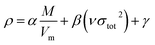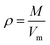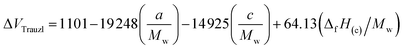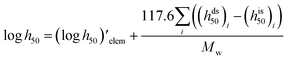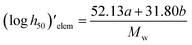DOI:
10.1039/D1RA05344B
(Paper)
RSC Adv., 2021,
11, 27420-27430
Design of functionalized bridged 1,2,4-triazole N-oxides as high energy density materials and their comprehensive correlations†
Received
12th July 2021
, Accepted 23rd July 2021
First published on 11th August 2021
Abstract
The demand for high energy density materials (HEDMs) remains a major challenge. Density functional theory (DFT) methods were employed to design a new family of bridged 1,2,4-triazole N-oxides by the manipulation of the linkage and oxygen-containing groups. The optimized geometry, electronic properties, energetic properties and sensitivities of new 40 molecules in this study were extensively evaluated. These designed compounds exhibit high densities (1.87–1.98 g cm−3), condensed-phase heat of formation values (457.31–986.40 kJ mol−1), impressive values for detonation velocity (9.28–9.49 km s−1) and detonation pressure (21.22–41.31 GPa). Their sensitivities (impact, electrostatic, and shock) were calculated and compared with 1,3,5-triamino-2,4,6-trinitrobenzene (TABT) and 4,6-dinitrobenzofuroxan (DNBF). Some new compounds 4,4′-trinitro-5,5′-bridged-bis-1,2,4-triazole-2,2′-diol (TN1–TN8) and 4,4′-dinitro-5,5′-ammonia-bis-1,2,4-triazole-2,2′-diol (DN3) were distinguished from this system, making them promising candidates for HEDMs. In addition, we found that the gas-relative parameters (detonation heat, oxygen balance, φ) were as important as the density, which were highly correlated to the detonation properties (P, D). Their comprehensive correlations should also be considered in the design of new energetic molecules.
1. Introduction
Researches concerning high energy density materials (HEDMs) have attracted tremendous attention in the past decades due to the demand for military purposes as well as civilian applications (mining, construction, demolition, and safety equipment).1,2 The main challenge is achieving an ideal combination of the large energy content and maximum possible chemical stability to ensure safe synthesis and handling.3 Traditional energetic materials are based on the oldest strategy in the presence of fuel (hydrocarbon component) and oxidizer (NO2, ONO2, etc.) on a molecular scaffold.4 Modern heterocyclic energetic compounds derive their energy not only from the oxidation of the carbon backbone, ring or cage strain but also additionally from the high nitrogen content and high heat of formation.5 In addition, the contrary nature of the desired parameters for HEDMs leads to the fact that the molecular design based on the computer-calculated properties has to be used to find a balance between performance and safety.6,7
Nitrogen-rich heterocycles, especially acknowledged azole-based compounds, have the advantages of high positive heat of formation and high densities, low sensitivities towards outer stimuli, and hence, become desired backbones for the construction of new HEDMs.8–11 Prominent families are triazole and tetrazole compounds that have been studied over the last couple of years with growing interest.12–16 Compared to the single heterocycle ring, bis-azoles with C–C connection show that promising properties arose from the higher heat of formation, which can be proved in good examples 5,5′-bistetrazoles17 and 5,5′-bistriazoles.18
A further way of developing energetic azoles is introducing N-oxides onto the ring to improve the oxygen balance without losing energy or stability.19 The oxidation of tetrazoles has been successfully accomplished, resulting in high performance explosives and low sensitivities.20,21 However, only a few examples of the oxidation of 1,2,4-triazoles to 1-hydroxy-1,2,4-triazoles are known in literature as a result of low yields and different isomers.22,23 Klapötke et al.24 reported the synthesis of dinitro-bis-1,2,4-triazole-1,1′-diol and derivatives. Their exceedingly powerful but safe characteristics demonstrated that the 1,2,4-triazole N-oxide would be an attractive building block in the search of the new generation of energetic materials with excellent comprehensive performance.
Motivated by this, we have initiated a computational program for the design of bridged 1,2,4-triazole N-oxides functionalized with linkage groups and oxygen-containing substituents. In this study, we designed 40 novel molecules, which consisted of abundant groups (–OH, –NHNO2, –NO2, –C(NO2)2, –C(NO2)3) to regulate the energy and sensitivity, and each of which corresponds to 8 types of bridged 1,2,4-triazole skeletons. The optimized structures and electronic characters have been calculated via density functional theory (DFT). Their physical–chemical and detonation properties, explosive power and sensitivities were evaluated based on the empirical equations. Furthermore, we also investigated the correlation coefficients between important parameters and detonation velocity (D) and detonation pressure (P).
2. Computational methods
2.1. Computational detail
The geometrical optimization and frequency analysis of the compounds were performed by Gaussian 09 set of programs25 using B3LYP function with 6-311G(d,p) as the basis set. All stationary points were confirmed as energy minimums on the potential surface. To ensure the reliability of the molecular structures, the initial configurations were established based on published crystallographic information files. We first set each bis-1,2,4-triazoles in conjugated configurations since they were found with lower molecular energies.
In this study, the predicted electronic and zero-point energies were obtained via density functional theory (DFT) based on the optimized structures mentioned above. The calculated energies were used for predicting crystal density and heat of formation (HOF). The electronic structures (electrostatic potentials and HOMO–LUMO gap) were calculated based on wave function output with the above optimization progresses.
2.2. Density and heats of formation
The crystal densities were calculated by the multifunctional wave-function analyzer,26 and predicted using eqn (1):| |
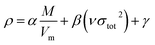 | (1) |
| |
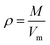 | (2) |
Eqn (2) was proposed by Bader et al.27 and this equation could describe the density but was proved with errors higher than 0.05 g cm−3. Politzer et al.28 introduced the electrostatic interaction correction to eqn (1), which represented intermolecular interactions within the crystal, and produced a marked improvement.28 In eqn (1), M is the molecular mass in g per molecule, Vm is the volume of the isolated gas phase molecule in cm3 per molecule, σtot2 is the total variance of the electrostatic potential in (kcal mol−1)2, ν is the degree of balance between the positive and the negative potentials on a molecular surface,28 and the values of α, β and γ are fitting parameters, which were 0.9183, 0.0028, and 0.0443, respectively.
The heat of formation (HOF) is an important factor in determining the chemical energy of detonation. In this study, we used the atomization energies method29 to covert quantum computational calculations to heat of formation in gas and condensed phases. The gas-phase heat of formation of the designed molecules was calculated by steps shown in eqn (3)–(5):
| | |
ΔfHm(298 K,M) = ΔfHm(0 K,M) + Hcorr(M) − ∑νiHcorr(Atom)
| (3) |
| | |
ΔfHm(0 K,M) = ∑νiΔfHm(0 K,Atom) − ΔrHm(0 K)
| (4) |
| | |
ΔrHm(0 K) = ∑νiE0(Atom) − E0(M)
| (5) |
where
E0 (kJ mol
−1) is the sum of electronic and zero-point energy,
Hcorr (kJ mol
−1) is the thermal correction to enthalpy from 0 K to 298 K, Δ
fHm,0 K (kJ mol
−1) of C, H, O, and N atoms are the experimental heat of formation values at 0 K, and were taken from the NIST webbook (https://webbook.nist.gov/chemistry/). The condense-phase heat of formation, Δ
fH(c) (kJ mol
−1) could be obtained using the Hess's law in
eqn (6):
| | |
ΔfH(c) = ΔfH(g) − ΔH(sublimation)
| (6) |
The equation of the predicted heat of sublimation was proposed by Rice et al. using ESP method30 which is shown in eqn (7):
| | |
ΔH(sublimation) = a(SA)2 + b(νσtot2)1/2 + c
| (7) |
where SA is the molecular surface area for this structure in Å
2.
a,
b, and
c are the empirical constants and were taken from Byrd and Rice,
30 in which
a = 0.000267,
b = 1.650087, and
c = 2.966078.
2.3. Energetic properties and sensitivities
Energetic properties indicate how powerful the designed molecules are and provide a feasible way to estimate whether a compound was a high energy density material (HEDM). The detonation velocity (D, km s−1) and pressure (P, GPa) were calculated using the Kamlet–Jacobs equations31 shown in eqn (8)–(10):| | |
D = 1.01φ0.5(1 + 1.30ρ)
| (8) |
where N is the mole of gaseous detonation products per gram of explosive in mol g−1, M is the average molecular weight of gaseous products in g mol−1, Q is the chemical energy of detonation in kcal g−1, ρ is the predicted crystal density in g cm−3, and φ is a parameter to evaluate the gaseous components.
The strength of energetic materials was calculated using the Trauzl block method,32 which is most widely used to determine the strength of high explosives. For 1,2,4-triazoles, which have unusual bonds (poly-nitrogen), we used a novel computer code developed by Keshavarz et al.32 as shown in eqn (11):
| |
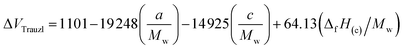 | (11) |
where
Mw is the molecular weight,
a and
c are the numbers of C and N, respectively. Δ
fH(c) is the condensed-phase heat of formation calculated in the above method in kJ mol
−1.
Impact, electrostatic, and shock sensitivities are three important parameters for the assessment of energetic materials.33 Impact sensitivities were calculated with a computer code proposed by Keshavarz et al., as eqn (12) and (13):
| |
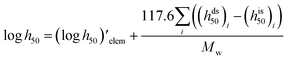 | (12) |
| |
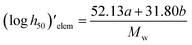 | (13) |
where
a and
b are numbers of C and H, respectively.
The prediction of electrostatic sensitivity is given as follows:
| | |
EES = 4.60 − 0.733a + 0.724d + 9.16rb/d − 5.14CR,OR
| (14) |
where
EES is the electric spark sensitivity in
J,
rb/d is the ratio of the number of H to O atoms,
CR,OR is the existence of alkyl (–R) or alkoxy groups (–OR), while in this study the values of
CR,OR were zero.
The equations of predicting shock sensitivities are given as eqn (15)–(19):
| | |
P90% TMD = 1679.0 + 226.3Λ − 631.4Eα-CH/NNO2 + 1771.9Γpure
| (15) |
| | |
P95% TMD = 2196.4 + 247.9Λ − 636.8Eα-CH/NNO2 + 3292.1Γpure
| (16) |
| | |
P98% TMD = 2544.9 + 221.1Λ − 416.2Eα-CH/NNO2 + 4639.2Γpure
| (17) |
| | |
Γpure = 1.93nNH2 – nNO2
| (19) |
where
P90% TMD,
P95% TMD and
P98% TMD are the pressures in MPa required to initiate the material pressed to 90%, 95%, and 98% of theoretical maximum density (TMD), respectively.
Eα-CH/NNO2 is equal to 1.0 for nitroamines or α-CH linkage in nitroaromatic compounds.
33
3. Results and discussion
We have designed a series of nitrogen-rich molecules by introducing five oxygen containing groups, –OH (H), –NO2 (N), –NHNO2 (NA), –C(NO2)2 (DN), and –C(NO2)3 (TN), into the framework of bridged-1,2,4-triazole-N-oxides with different linkage groups (bis-1, diazene-2, ammonia-3, hydrazine-4, methane-5, tetrazine-6, furazan-7, and 1,2-diazine-8), resulting in 40 new molecules including hydroxyl derivatives (H1–H8), nitroamine derivatives (NA1–NA8), nitro derivatives (N1–N8), dinitro derivatives (DN1–DN8), and trinitro derivatives (TN1–TN8) (Scheme 1).
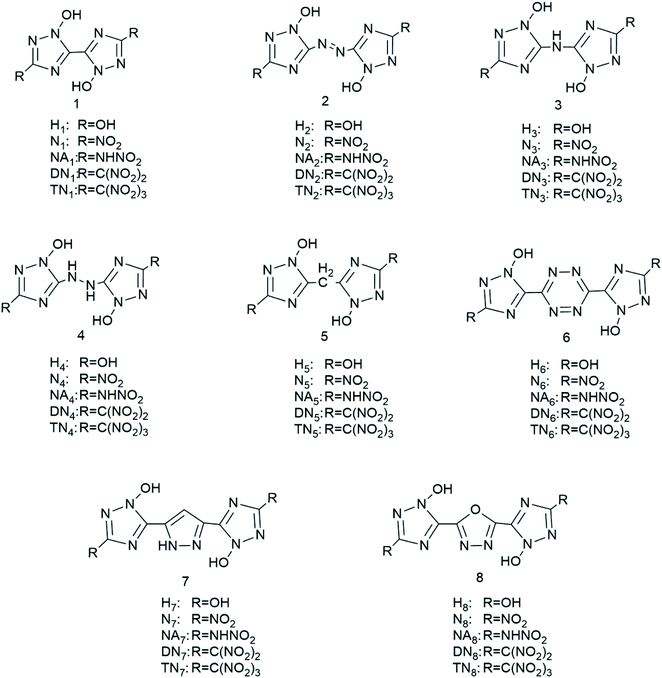 |
| | Scheme 1 Molecular frameworks of the 40 designed compounds. | |
3.1. Optimized structures
Compounds with linkage groups bis 1, diazene 2, tetrazine 6, furazan 7 and 1,2-diazine 8 remained conjugated rings after geometrical optimization. These compounds have their atoms on the ring skeleton in the same plane. The optimized structures of the TN series are given in Fig. 1. While compounds with linkage groups ammonia 3, hydrazine 4, methane 5 were not conjugated, and their ring skeletons fold at their bridge groups. However, there was a little correlation showing between the conjugation and detonation properties or sensitivities in this designed system. The optimized structures of the –C(NO2)3 (TN) series are shown in Fig. 1.
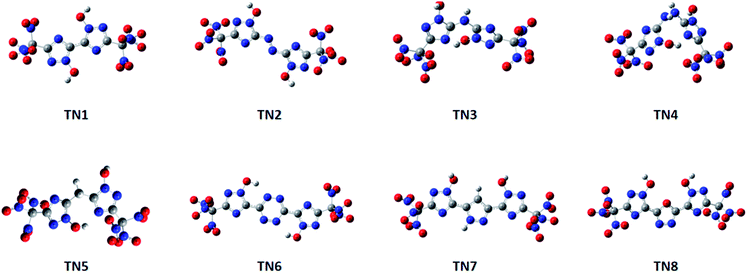 |
| | Fig. 1 Optimized structures of the –C(NO2)3 (TN) series. | |
3.2. Electronic structures
The electrostatic potential surface (ESP), highest occupied orbital (HOMO) and lowest unoccupied orbital (LUMO) of the TN series were calculated to analyze their electronic properties. The electrostatic potential values were mapped on the density isosurface defined by ρ = 0.001 e per Bohr3, output by VMD,34 and the –C(NO2)3 (TN) series is shown as a typical case in Fig. 2. Negative regions (blue part) were observed in case of the oxygenated substituted groups, as expected, indicating that this area tended to give out electrons. While the positive regions (red part) were observed in bridged-1,2,4-triazol rings, particularly the N-oxidized group, which was easier to obtain electrons compared to other regions. It could be expected that the oxygenated substituted groups were prone to nucleophilic reactions, and the N-oxidized groups preferred electrophilic reactions.
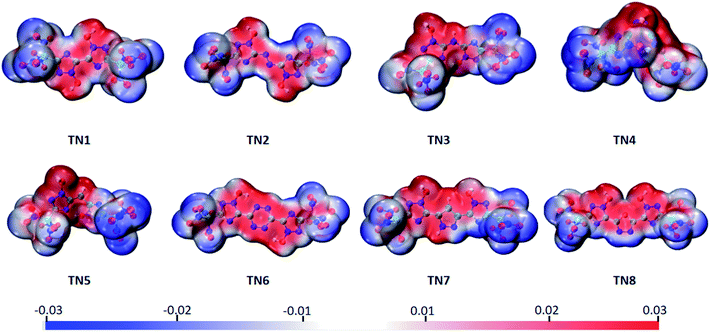 |
| | Fig. 2 Molecular electrostatic potential of the –C(NO2)3 (TN) series ranging from −0.03 a.u. (blue) to 0.03 a.u. (red), isosurface = 0.001. | |
The HOMO–LUMO orbitals of the –C(NO2)3(TN) series are shown as a typical case in Fig. 3. LUMO orbitals of TN3, TN4, TN5, and TN7 are contributed by one –C(NO2)3 group, and LUMO orbital of TN1 was contributed by both –C(NO2)3 groups. While LUMO orbital of TN2 occupied the 1,2,4-triazole rings and the bridged group, LUMO orbital of TN6 occupied only the bridged group, and LUMO orbital of TN8 occupied both bridged group and the –C(NO2)3 group. However, HOMO orbitals showed consistency in occupying 1,2,4-triazole rings, while the HOMO orbital of TN5 occupied only one 1,2,4-triazole and –C(NO2)3 group on the same side. The HOMO–LUMO gap ranged from 3.3 eV to 4.62 eV, which could be considered that these molecules are stable.
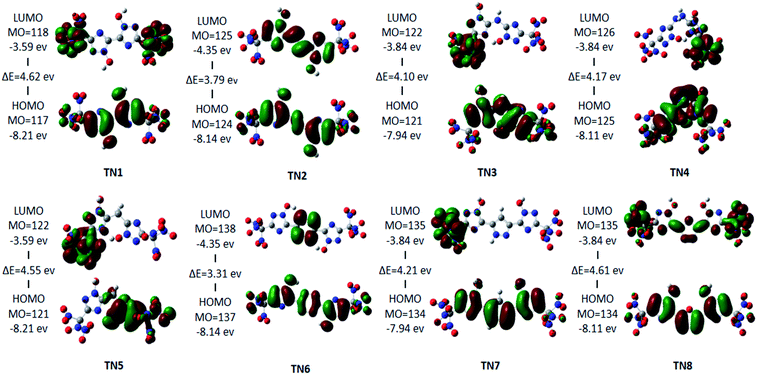 |
| | Fig. 3 HOMO–LUMO orbitals and HOMO–LUMO energy gap of the –C(NO2)3 (TN) series. | |
3.3. Heat of formation
The gas and condensed-phase heat of formation, as well as the relative parameters of all molecules are listed in Table S1.† The ΔfH(298 K,g) and ΔfH(298 K,c)of the molecules are shown in Fig. 4. All compounds were found to have positive heat of formation values in gas-phase range from 81.67 kJ mol−1 to 1444.98 kJ mol−1. Except for H1, H3, and H5, all compounds had positive HOFs in condensed-phase, ranging from 121.70 kJ mol−1 to 1229.32 kJ mol−1. Gas and solid-phase heat of formation showed similar trends in variations. Compounds with linkage group 6 (H6, N6, NA6, DN6, and TN6) had the highest heat of formation in each substituted group series. Compounds with linkage groups 2, 6, 7, and 8 showed higher values of HOF in each substituted series, and these compounds were all conjugated. While compounds with linkage groups 3, 4, and 5 showed lower HOF values and non-conjugated structures.
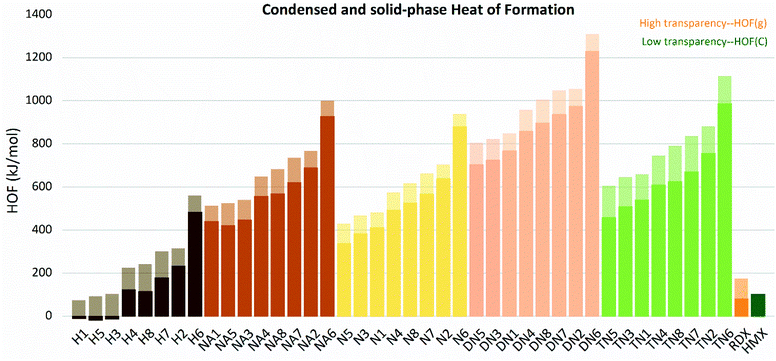 |
| | Fig. 4 Gas and condensed-phase heat of formation (HOF) of the molecules sorted by substituted groups –OH (H), –NO2 (N), –NHNO2 (NA), –C(NO2)2 (DN), –C(NO2)3 (TN). | |
3.4. Detonation properties
The values of crystal density, oxygen balance, detonation heat, detonation velocity, detonation pressure, and strength of compounds are listed in Table S2.† Among the designed molecules, the TN series showed the best detonation performances compared to other substituted groups (H, N, NA, and DN), as a result of polynitro groups in their molecules. Compounds DN3 and TN1–7 had higher detonation velocity and detonation pressure than HMX (9.1 km s−1, 39.3 GPa), as shown in Fig. 5, which were potential HEDMs. Besides, they also had a higher strength value than that of HMX, which indicates that these compounds tend to do more useful work during a detonation process.
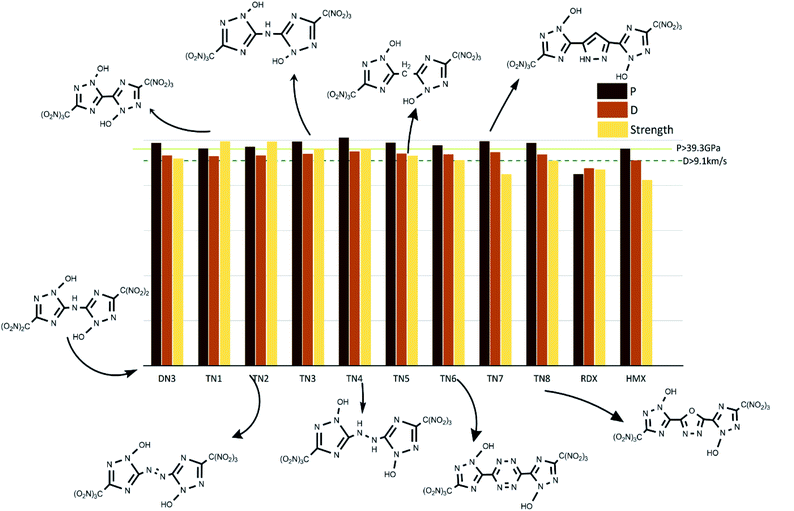 |
| | Fig. 5 Potential HEDMs which have higher strength, detonation velocity, and detonation pressure than HMX. | |
3.5. Influence factors
In order to find out which factors affect the detonation properties in this system, detonation parameters were simulated based on the Kamlet–Jacobs equation, in which detonation pressure (P) is proportional to the second power of density (ρ), and detonation velocity (D) is proportional to the density (ρ). Fig. 7–9 are detonation parameters of all the designed molecules (Table 1).
Table 1 The values of all 40 designed compounds of predicted crystal density (ρ) in g cm−3, oxygen balance (OB) in % (calculated based on CO2), heat of formation (HOF(c,298 K)) in kJ mol−1, detonation heat (Q) in cal g−1, detonation velocity (D) in km s−1, detonation pressure (P) in GPa, impact sensitivity (h50) in cm and electrostatic sensitivity (EES) in J
| No. |
ρ |
OB |
HOF(c,298 K) |
Q |
D |
P |
h50 |
EES |
| H1 |
1.76 |
−48.00 |
−10.85 |
1035.24 |
7.45 |
24.22 |
47.61 |
13.72 |
| H2 |
1.78 |
−42.11 |
231.81 |
1162.47 |
7.82 |
26.92 |
29.62 |
13.72 |
| H3 |
1.90 |
−48.37 |
−13.34 |
985.29 |
7.87 |
28.40 |
51.10 |
16.01 |
| H4 |
1.80 |
−48.70 |
121.70 |
1084.77 |
7.83 |
27.19 |
54.34 |
18.30 |
| H5 |
1.75 |
−67.29 |
−19.28 |
1008.43 |
7.23 |
22.78 |
128.30 |
17.57 |
| H6 |
1.82 |
−57.14 |
483.13 |
1161.11 |
7.67 |
26.23 |
37.19 |
12.26 |
| H7 |
1.86 |
−78.20 |
178.32 |
988.83 |
7.27 |
23.87 |
122.40 |
16.11 |
| H8 |
1.95 |
−53.73 |
114.59 |
1059.90 |
7.88 |
28.90 |
43.73 |
11.15 |
| N1 |
1.88 |
−18.60 |
411.08 |
1515.62 |
8.79 |
35.17 |
92.37 |
9.07 |
| N2 |
1.88 |
−16.78 |
637.67 |
1556.51 |
8.92 |
36.15 |
59.30 |
9.07 |
| N3 |
1.91 |
−20.51 |
382.73 |
1427.25 |
8.84 |
35.92 |
94.17 |
10.59 |
| N4 |
1.87 |
−22.21 |
491.82 |
1462.09 |
8.81 |
35.23 |
95.81 |
12.12 |
| N5 |
1.86 |
−35.28 |
337.71 |
1412.71 |
8.46 |
32.42 |
194.75 |
11.39 |
| N6 |
1.88 |
−33.12 |
879.05 |
1487.60 |
8.55 |
33.26 |
64.35 |
7.60 |
| N7 |
1.86 |
−49.36 |
566.41 |
1354.56 |
8.11 |
29.69 |
175.23 |
9.92 |
| N8 |
1.90 |
−29.44 |
524.52 |
1426.78 |
8.51 |
33.15 |
75.02 |
7.89 |
| NA1 |
1.81 |
−22.22 |
439.04 |
1418.83 |
8.54 |
32.37 |
95.81 |
12.12 |
| NA2 |
1.85 |
−20.25 |
687.56 |
1481.08 |
8.81 |
34.94 |
63.95 |
12.12 |
| NA3 |
1.85 |
−23.76 |
445.89 |
1371.76 |
8.67 |
33.90 |
97.31 |
13.65 |
| NA4 |
1.82 |
−25.16 |
556.03 |
1406.77 |
8.65 |
33.44 |
98.70 |
15.17 |
| NA5 |
1.81 |
−37.09 |
420.07 |
1373.71 |
8.35 |
30.97 |
187.26 |
14.44 |
| NA6 |
1.83 |
−34.78 |
927.41 |
1427.56 |
8.43 |
31.89 |
68.20 |
10.65 |
| NA7 |
1.86 |
−49.72 |
619.67 |
1306.68 |
8.18 |
30.25 |
170.98 |
12.97 |
| NA8 |
1.90 |
−31.46 |
568.33 |
1366.71 |
8.55 |
33.50 |
78.64 |
10.50 |
| DN1 |
1.89 |
−12.83 |
766.37 |
1775.90 |
9.17 |
38.45 |
43.11 |
9.27 |
| DN2 |
1.87 |
−11.94 |
973.13 |
1775.13 |
9.15 |
38.02 |
33.17 |
9.27 |
| DN3 |
1.95 |
−14.40 |
723.89 |
1695.17 |
9.32 |
40.36 |
45.01 |
10.19 |
| DN4 |
1.90 |
−15.84 |
858.16 |
1724.99 |
9.22 |
38.92 |
46.83 |
11.11 |
| DN5 |
1.89 |
−24.74 |
702.92 |
1700.50 |
8.97 |
36.69 |
74.77 |
10.37 |
| DN6 |
1.88 |
−24.67 |
1229.32 |
1706.68 |
8.90 |
36.08 |
37.68 |
7.81 |
| DN7 |
1.85 |
−36.36 |
935.98 |
1626.12 |
8.54 |
32.86 |
77.46 |
8.91 |
| DN8 |
1.88 |
−21.72 |
895.90 |
1679.12 |
8.84 |
35.56 |
41.58 |
8.37 |
| TN1 |
1.89 |
3.43 |
539.40 |
1611.63 |
9.28 |
39.35 |
20.51 |
11.65 |
| TN2 |
1.89 |
3.24 |
755.12 |
1624.65 |
9.32 |
39.66 |
17.28 |
11.65 |
| TN3 |
1.92 |
1.66 |
507.69 |
1605.69 |
9.39 |
40.60 |
21.73 |
12.30 |
| TN4 |
1.91 |
0.00 |
608.92 |
1664.17 |
9.49 |
41.31 |
22.95 |
12.96 |
| TN5 |
1.89 |
−6.67 |
457.31 |
1840.09 |
9.40 |
40.39 |
32.71 |
12.22 |
| TN6 |
1.88 |
−8.79 |
986.40 |
1915.67 |
9.37 |
39.92 |
20.44 |
10.18 |
| TN7 |
1.87 |
−18.05 |
670.35 |
2109.52 |
9.46 |
40.65 |
36.52 |
10.76 |
| TN8 |
1.92 |
−5.99 |
624.83 |
1796.89 |
9.36 |
40.34 |
21.88 |
10.82 |
As shown in these figures, both detonation pressure and detonation velocity showed a tendency in TN > DN > N ≈ NA > H, and a similar tendency in detonation heat is shown in Fig. 6. In this system, there was no obviously consistent trend between density and detonation properties. For example, in the hydroxyl (H) series, compounds have higher density than HMX; however, H3 and H8 showed a similar performance to H2 and H4.
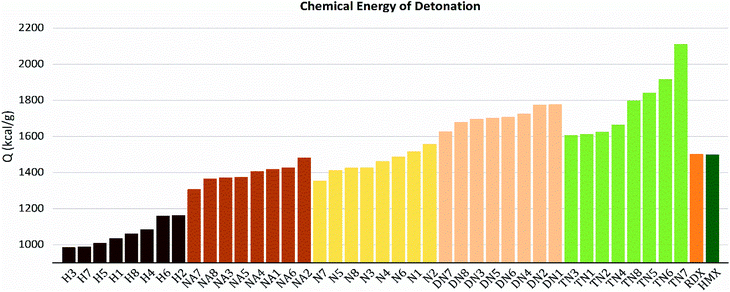 |
| | Fig. 6 Detonation heat (Q) sorted by substituted groups –OH (H), –NO2 (N), –NHNO2 (NA), –C(NO2)2 (DN), –C(NO2)3 (TN). | |
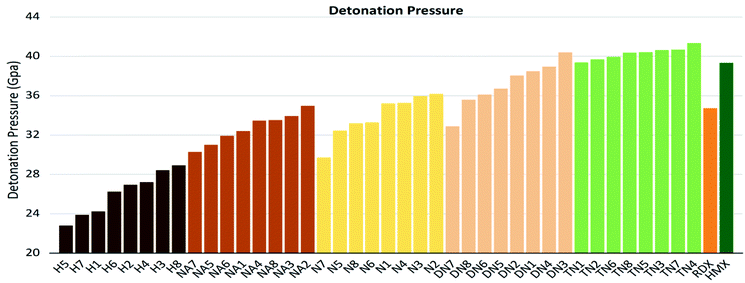 |
| | Fig. 7 Detonation pressure (P) sorted by substituted groups –OH (H), –NO2 (N), –NHNO2 (NA), –C(NO2)2 (DN), –C(NO2)3 (TN). | |
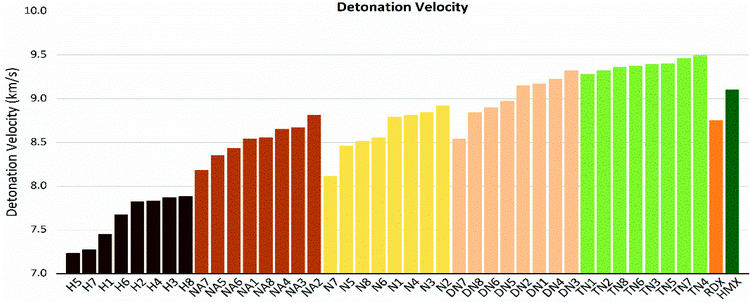 |
| | Fig. 8 Detonation velocity (D) sorted by substituted groups –OH (H), –NO2 (N), –NHNO2 (NA), –C(NO2)2 (DN), –C(NO2)3 (TN). | |
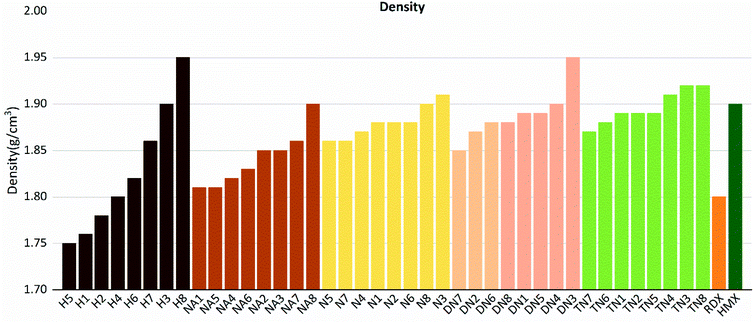 |
| | Fig. 9 Densities (ρ) sorted by substituted groups –OH (H), –NO2 (N), –NHNO2 (NA), –C(NO2)2 (DN), –C(NO2)3 (TN). | |
If we set skeleton 1 (no linkage group) of each series as the zero point of the reference frame, for H, NA, N, and DN series with nitrogen-rich linkage groups in 2, 3, and 4 had positive influence to detonation properties (D, P), while carbon-rich linkage groups in 5, 6, 7, and 8 tended to have a negative influence. Particularly, 7 has the highest C%; therefore, the lowest value in the detonation pressure and detonation velocity in the above series. The TN series are quite special since all 7 linkage groups tend to have positive influence compared to TN1, and we considered that the result of different linkage groups is negligible under the strong electron-withdrawing effect of the trinitromethyl group.
It is also interesting to notice that H7, NA7, N7, and DN7 have the lowest values in terms of detonation pressure and detonation velocity, while TN7 has the highest value compared to other molecules of this series; apart from its extremely unique high value of φ, TN7 has a special high value of detonation heat (Q), while the detonation heat values (Q) of H7, NA7, N7, DN7 are the lowest ones in each series.
Compounds with linkage group 8 tend to have the highest densities in each substituted group, and are proved with a smaller volume. TN8 and TN7 have nearly the same molecule weight and electrostatic correction, while their volumes shown evident difference. The difference might be from the angle of the 1,2,4-triazole and the linkage group due to the electron-negativity.
3.6. Correlation coefficient
Since detonation is a type of violent combustion, which accumulates a large amount of heat in a short period of time, causing the gas volume to expand rapidly, we think that there should be more attention focused on the gas-relative parameters. Fig. 10 and 11 show the correlation between detonation properties and gas-related parameters (detonation heat Q, oxygen balance OB, and φ), respectively. The correlation coefficients between oxygen balance, detonation heat, density, φ and detonation pressure were 0.8556, 0.8851, 0.4989, and 0.9322, respectively. The correlation coefficients between oxygen balance, detonation heat, density, φ and detonation velocity were 0.883, 0.9038, 0.4528, and 0.9594, respectively. This indicates oxygen balance, detonation heat and φ are highly related to detonation properties, which are results of the comprehensive influence.
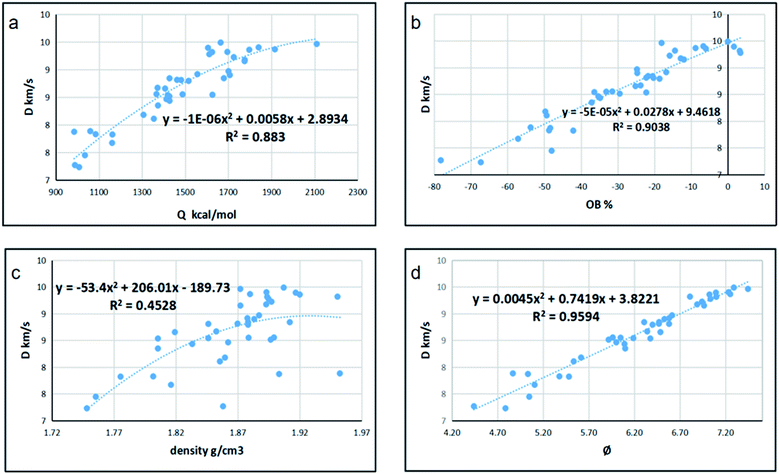 |
| | Fig. 10 Correlation coefficients and trend lines between (a) detonation heat (Q), (b) oxygen balance (OB), (c) density and (d) φ with detonation velocity (D). | |
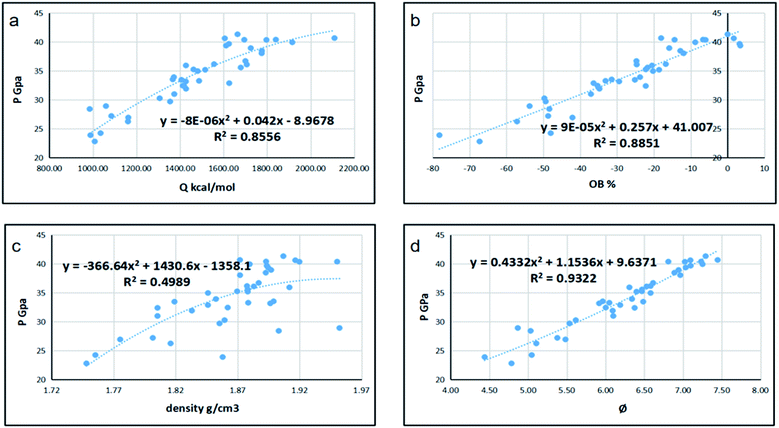 |
| | Fig. 11 Correlation coefficients and trend lines between (a) detonation heat (Q), (b) oxygen balance (OB), (c) density and (d) φ with detonation pressure (P). | |
3.7. Sensitivities
Table S3† lists the predicted values of impact (h50), electrostatic (EES), and shock (P90% TMD, P95% TMD, P98% TMD) sensitivities of all 40 compounds compared to TMBT and DNBF.
The values of impact sensitivity h50 and electrostatic sensitivity EES are sorted by substituted groups –OH (H), –NO2 (N), –NHNO2 (NA), –C(NO2)2 (DN), –C(NO2)3 (TN) in Fig. 12 and 13, respectively. Compounds with linkage groups 5 and 7 showed extremely high impact sensitivities in each substituted groups, and the NA series have the highest value towards impact sensitivity. The TN series had great detonation properties in 40 molecules designed in this work, and their electrostatic sensitivities were surprisingly higher than the N and DN series. Compounds with linkage groups 3, 4, 5, and 7, tend to have a higher stability to impact sensitivity and electrostatic sensitivity. It might be the result from the fact that HOMO–LUMO orbitals of the above compounds are contributed by one substituted group only, rather than distributing on the ring skeleton which may be sensitive to impact and electric.
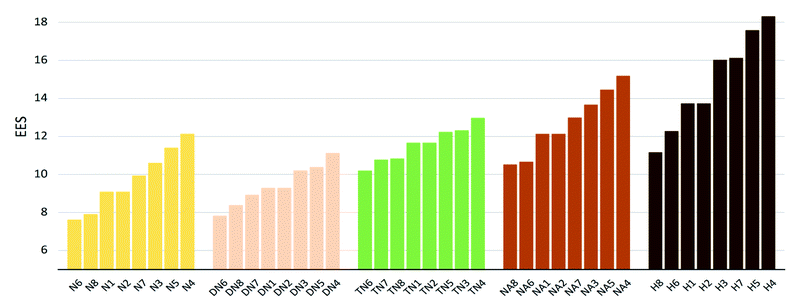 |
| | Fig. 12 Electronic sensitivities (EES) sorted by substituted groups –NO2 (N), –C(NO2)2 (DN), –C(NO2)3 (TN), –NHNO2 (NA), –OH (H). | |
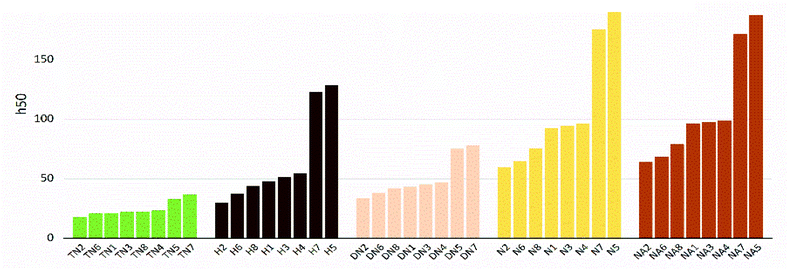 |
| | Fig. 13 Impact sensitivities (h50) sorted by substituted groups –C(NO2)3 (TN), –OH (H), –C(NO2)2 (DN), –NO2 (N),-NHNO2 (NA). | |
4. Conclusions
In this study, we designed a series of new 4,4′-substituted-bridged-1,2,4-triazole-2,2′-N-oxide compounds through regulating linkage groups and different types of oxygen-containing substituents. We also investigated the correlation between their detonation properties and chemical characters of energetic compounds. All trinitromethyl derivatives tend to have the most superior detonation property; the dinitromethyl derivatives are quite different from each other, among which DN3 was very alike to the TN series; the nitroamino group series and nitro group series are in moderate level but much better than the hydroxyl group series. Among them, DN3 and TN1–7 are considered as potential HEDMs since their detonation pressure and detonation velocity were higher than values of HMX. The most promising compound with stability and great energy performances was TN7. In addition, we found that the gas-relative parameters of detonation heat, oxygen balance and φ were highly correlated to the detonation properties (P, D), which should be considered in the design of new energetic molecules.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The support of the National Natural Science Foundation of China (22005345) and the Rapid Support Projects (61406190403) is gratefully acknowledged.
Notes and references
- H. Gao and J. M. Shreeve, Chem. Rev., 2011, 111, 7377–7436 CrossRef CAS PubMed.
- W. Huang, Y. Tang, G. H. Imler, D. A. Parrish and J. M. Shreeve, J. Am. Chem. Soc., 2020, 142, 3652–3657 CrossRef CAS PubMed.
- C. M. Sabate, T. M. Klapötke, In New Trends in Research of Energetic Materials, Proceedings of the 12th Seminar, University of Pardubice, Czech Republic, 2009 Search PubMed.
- T. M. Klapötke, Chemistry of High-Energy Materials, De Gruyter, 2015 Search PubMed.
- A. A. Dippold and T. M. Klapötke, J. Am. Chem. Soc., 2013, 135, 9931–9938 CrossRef CAS PubMed.
- J. Zhang, Q. Zhang, T. T. Vo, D. A. Parrish and J. M. Shreeve, J. Am. Chem. Soc., 2015, 137, 1697–1704 CrossRef CAS PubMed.
- M. Reichel, D. Dosch, T. Klapötke and K. Karaghiosoff, J. Am. Chem. Soc., 2019, 141, 19911–19916 CrossRef CAS PubMed.
- C. Jiang, L. Zhang, C. Sun, C. Zhang, C. Yang, J. Chen and B. Hu, Science, 2018, 359, 8953 CrossRef PubMed.
- Y. W. S. Li, C. Qi, X. Zhao, J. Zhang, S. Zhang and S. Pang, Angew. Chem., Int. Ed., 2014, 52, 13831–13851 Search PubMed.
- L. Hu, P. Yin, G. Zhao, C. He, G. H. Imler, D. A. Parrish, H. Gao and J. n. M. Shreeve, J. Am. Chem. Soc., 2018, 140, 15001–15007 CrossRef CAS PubMed.
- A. Miyoshi, K. Kato, T. Yokoi, J. J. Wiesfeld, K. Nakajima, A. Yamakara and K. Maeda, J. Mater. Chem. A, 2020, 8, 11996–12002 RSC.
- M. H. H. Wurzenberger, M. Lommel, M. S. Gruhne, N. Szimhardt and J. Stierstorfer, Angew. Chem., Int. Ed., 2020, 59, 12367–12370 CrossRef CAS PubMed.
- Y. Tang, W. Huang, G. H. Imler, D. A. Parrish and J. n. M. Shreeve, J. Am. Chem. Soc., 2020, 142, 7153–7160 CrossRef CAS PubMed.
- Y. Tang, Z. Yin, A. K. Chinnam, R. J. Staples and J. n. M. Shreeve, Inorg. Chem., 2020, 59, 17766–17774 CrossRef CAS PubMed.
- J. R. Yount, M. Zeller, E. F. C. Byrd and D. G. Piercey, J. Mater. Chem. A, 2020, 8, 19337–19347 RSC.
- S. E. Braley, D. C. Ashley, K. M. Kulesa, E. Jakubikova and J. M. Smith, Chem. Commun., 2021, 57, 4332 RSC.
- N. Fischer, D. Izsák, T. M. Klapötke and J. Stierstorfer, Chem.–Eur. J., 2013, 19, 8948–8957 CrossRef CAS PubMed.
- R. Wang, H. Xu, Y. Guo, R. Sa and J. N. M. Shreeve, J. Am. Chem. Soc., 2010, 132, 11904–11905 CrossRef CAS PubMed.
- P. He, J.-G. Zhang, X. Yin, J.-T. Wu, L. Wu, Z.-N. Zhou and T.-L. Zhang, Chem.–Eur. J., 2016, 22, 7670–7685 CrossRef CAS PubMed.
- N. Fischer, D. Fischer, T. M. Klapötke, D. G. Piercey and J. Stierstorfer, J. Mater. Chem., 2012, 22, 20418 RSC.
- M. Göbel, K. Karaghiosoff, T. M. Klapötke, D. G. Piercey and J. Stierstorfer, J. Am. Chem. Soc., 2010, 132, 17216–17226 CrossRef PubMed.
- J. Neubauer, U. Kardorff, J. Leyendecker, U. Baus, C. Kuenast, P. Hofmeister, W. Krieg, R. Kirstgen and W. Reuther, Substituted N-hydroxypyrazoles and N-hydroxytriazoles for controlling pests, European Patent, EP19900103758, 1991 Search PubMed.
- M. Begtrup and P. Vedsø, J. Chem. Soc., Perkin Trans. 1, 1995, 243–247, 10.1039/P19950000243.
- A. A. Dippold and T. M. Klapötke, J. Am. Chem. Soc., 2013, 135, 9931–9938 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- R. F. W. Bader, M. T. Carroll, J. R. Cheeseman and C. Chang, J. Am. Chem. Soc., 1987, 109, 7968–7979 CrossRef CAS.
- P. Politzer, J. Martinez, J. S. Murray, M. C. Concha and A. Toro-Labbé, Mol. Phys., 2009, 107, 2095–2101 CrossRef CAS.
- B. M. Rice, S. V. Pai and J. Hare, Combust. Flame, 1999, 118, 445–458 CrossRef CAS.
- E. F. C. Byrd and B. M. Rice, J. Phys. Chem. A, 2006, 110, 1005–1013 CrossRef CAS PubMed.
- M. J. Kamlet and S. J. Jacobs, J. Chem. Phys., 1968, 48, 23–35 CrossRef CAS.
- M. Kamalvand, M. H. Keshavarz and M. Jafari, Propellants, Explos., Pyrotech., 2015, 40, 551–557 CrossRef CAS.
- M. H. Keshavarz, H. Motamedoshariati, R. Moghayadnia, M. Ghanbarzadeh and J. Azarniamehraban, Propellants, Explos., Pyrotech., 2014, 39, 95–101 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra05344b |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Lishan Gonga,
Xiufang Moa and
Jianguo Zhang
*a,
Lishan Gonga,
Xiufang Moa and
Jianguo Zhang b
b