Open Access Article
Open Access ArticleQuantum mechanical modelling of phosphorus qubits in silicene under constrained magnetization
Anton A. Gnidenko *ab,
Andrey N. Chibisov
*ab,
Andrey N. Chibisov a,
Mary A. Chibisova
a,
Mary A. Chibisova c and
Anastasiia V. Prokhorenkoa
c and
Anastasiia V. Prokhorenkoa
aPacific National University, 136 Tihookeanskaya Street, Khabarovsk 680042, Russia. E-mail: agnidenko@mail.ru
bInstitute of Material Science of Khabarovsk Scientific Centre, Far Eastern Branch, Russian Academy of Sciences, 153 Tihookeanskaya Street, Khabarovsk 680042, Russia
cComputing Center, Far Eastern Branch, Russian Academy of Sciences, 65 Kim Yu Chen Street, Khabarovsk, 680000, Russia
First published on 18th October 2021
Abstract
A non-collinear density functional theory calculation of the electronic and magnetic structure of phosphorus-doped silicene was performed using atomic constrained magnetization. The antiferromagnetic state for the local magnetic moments of a pair of phosphorus atoms was found to be preferable both without and with constrained magnetization. A spatial change in the charge densities in the regions of substituting phosphorus atoms was shown. It was found that upon rotation from the |0〉 state to the |1〉 state, the charge density in the intermediate state changes asymmetrically relative to the bonds of the P atom with the neighbouring Si atoms.
Introduction
The creation of high-speed quantum computers requires studying the processes of electron and spin-exchange interactions between qubits. Understanding the features and mechanisms of these processes will allow the creation of adequate quantum information protocols for qubit logical gates.1 The development of quantum computers opens up broad potential for the design of new materials with specific properties, the production of new types of drugs, etc. A solid-state quantum system based on phosphorus atoms2–5 embedded in crystalline silicon is of particular interest to researchers. To produce quantum computers based on this approach, the current silicon semiconductor technology can be used with minor modifications to the manufacturing process. The resultant Si:P systems have exceptionally long coherence times and high fidelities.6,7 These materials can be manufactured by encapsulating phosphorous using solid source molecular beam epitaxy into the silicon surface.8 An analysis of electron transport through two weakly coupled precision-placed phosphorus donors in silicon was carried out;9 this study showed that the transfer process is regulated by the Pauli spin blockade. The electrical control of the exchange coupling between donor-bound electrons in silicon has been investigated with a detuning gate bias,10 the difference between asymmetric 2P–1P and symmetric 1P–1P qubits has been shown.Silicene, a 2D form of silicon, has a hexagonal structure with a low-buckled geometry, with a distance between two atomic sublattices of 0.44 Å. It is a metastable structure that can be synthesized on various substrates such as Ag(111)11 or ZrB2(0001)12 surfaces. In silicene, a spin–orbit interaction is observed, which opens the gap at the Dirac point of 1.55 meV.13 In contradistinction to graphene, in silicene, there is the ability to control the gap bandwidth14,15 by functionalization with hydrogen, fluorine, or CH3 groups, application of an external electric field, or mechanical stretching. It was shown by the quantum mechanical method that vacancies, depending on their concentration, significantly increase the gap bandwidth and can turn silicene into a ferromagnetic state.16 In bilayer silicene, a strong covalent interlayer bond destroys the original π-bond net of each layer, leaving unbound electrons unpaired. This leads to the formation of intrinsic magnetism and the appearance of a gap of 0.55 eV.17
In this study, we use quantum mechanical calculation methods based on the density functional theory, taking into account the non-collinear spin–orbit interaction, to investigate the spin dynamics of phosphorus atom nuclei to reveal the regularities of changes in the charge density and magnetization in the environment of quantum phosphorus qubits in the silicene structure. This information will help to improve predictions of processing and transmission of quantum information through qubits based on the Si:P system.
Methods and calculation details
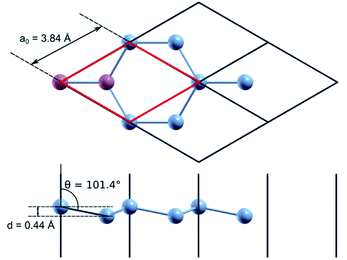
Quantum mechanical calculations based on the density functional theory (DFT)18,19 and the pseudopotential method were performed using the Quantum ESPRESSO (QE) software package.20 For exchange–correlation description, the generalized gradient approximation in the PBEsol form21 was used. All calculations were performed taking into account the spin–orbit non-collinear interaction.22,23 The corresponding full-relativistic ultrasoft pseudopotential values for silicon and phosphorus were taken from the QE library24 and tested for a correct description of the atomic and electronic structure of both crystalline silicon and silicon doped with phosphorus. The cutoff energy of the plane wave basis in all calculations was 476 eV. Integration over the Brillouin zone was performed using a uniform k-point grid, generated according to the Monkhorst–Pack25 scheme, which was varied in accordance with the size of the calculated supercell.For test calculation using a primitive silicene cell, a 36 × 36 × 1 k-points grid was used. In the direction perpendicular to the silicene plane, the supercell size was chosen as 15.88 Å; this distance is sufficient to exclude interaction with silicene layers in neighbouring periodic images. We obtained the following optimized parameters for a primitive diatomic unit cell (Fig. 1): the lattice parameter, a0, equals 3.84 Å, the Si–Si interatomic bond length is 2.26 Å, the buckling height, d, is 0.44 Å, and the angle between the normal to the silicene plane and the Si–Si bond is 101.4°. The calculated structural parameters of silicene are in good agreement with similar calculations from previous studies.26 The cohesion energy of nanostructured silicon materials tends to decrease with a decrease in the linear dimensions of the nanostructure (nanowires, films, nanoparticles). The calculated cohesion energy for silicene is −4.30 eV, this value fits into the range of values obtained by other authors.27,28 It is lower than the cohesion energy of bulk silicon, which is equal to −4.96 eV according to our calculations.
To simulate phosphorus-doped silicene, a supercell with dimensions of 4 × 4 × 1 was built, and one of the 32 silicon atoms was substituted by phosphorus. The k-point grid in this case was reduced to 9 × 9 × 1 in proportion to the increase in the supercell size. In addition, a further model was used in the study, with one side doubled, comprising 64 atoms and containing 2 phosphorus atoms; this model was used in order to change the local moments of phosphorus atoms independently of each other. In this case, the k-point grid was 4 × 9 × 1 in size.
Results and discussion
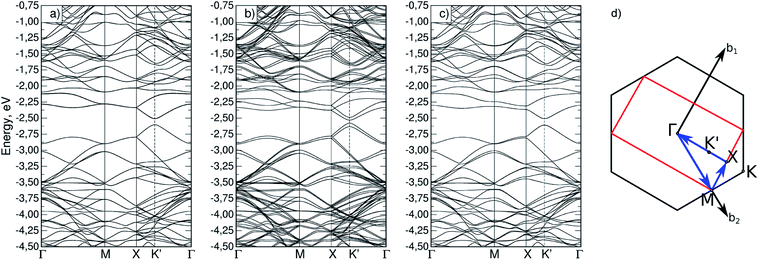
Firstly, the appearance of magnetization in silicene upon phosphorus substitution was considered. To do so, band structures were calculated for both a defect-free cell (Si32) and a cell with a phosphorus atom (Si31P). In the latter case, the calculation was performed with and without initial magnetization on the phosphorus atom; it was found that a non-collinear calculation with an initial magnetization gives a total energy value 31.7 meV lower than in the non-magnetic case. The obtained band structures are shown in Fig. 2a–c; the path in the reciprocal space, Γ–M–K–Γ, is typical for a two-dimensional hexagonal crystal lattice (Fig. 2d). A bandgap at point K of 1.5 meV was obtained for the Si32 cell, which is in agreement with similar previously calculated data.14,29 It is seen that the magnetization in Si31P leads to splitting of the degenerate energy levels (Fig. 2c). The dashed lines show the highest occupied (HOMO) and the lowest unoccupied (LUMO) molecular orbital bands; in the case of Si31P without magnetization, they coincide; for magnetization, the bandgap at point K is 27.2 meV.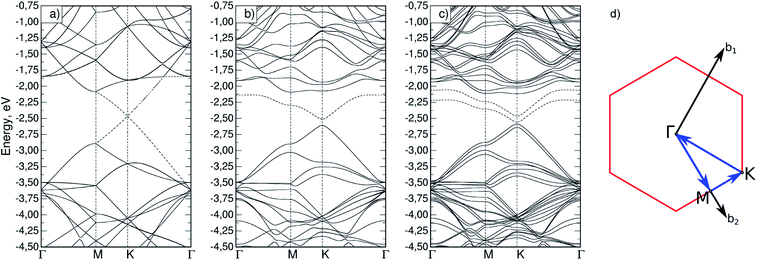 | ||
| Fig. 2 Band structure for (a) Si32 cell; (b) Si31P cell without magnetization; (c) Si31P cell with starting magnetization; (d) path in reciprocal space for hexagonal cell. | ||
If a silicon atom in Si crystal lattice is substituted by phosphorus, the magnetization of the Si:P system is determined by the presence of one unpaired electron and equals 1 μB per cell. Despite the partial violation of the sp3 hybridization and the redistribution of the electron density in silicene compared to a silicon lattice, the total magnetization upon substitution of phosphorus for a silicon atom is also equal to 1 μB per cell. Local magnetic moments are distributed as follows: 0.058 μB per cell on a phosphorus atom, 0.032 μB per cell on the three nearest silicon atoms, and 0.024 μB per cell on neighbouring silicon atoms of the next order. Local magnetic moments of the indicated group of atoms are codirectional and make up a total of 71% of all local magnetization. For comparison, the local moment of a phosphorus atom upon substitution in a silicon crystal lattice (supercell of 64 atoms) is 0.019 μB per cell, and 0.010 μB per cell on the nearest neighbouring silicon atoms.
In our calculations, we relate the local magnetic moment to the total atomic spin. Performing a non-collinear quantum mechanical calculation allows us to set up the direction and value of the initial magnetization of the atom, and introduce constraints for magnetization. The rotation of the local moment of the phosphorus atom leads to a reorientation of the local moments of its surrounding atoms to the same direction. Considering the direction of the total phosphorus atomic spin, the energy of the system remains isotropic to a total energy calculating accuracy value of ∼1 × 10−5 eV.
The next step was the study of an enlarged cell containing two phosphorus atoms (Si62P2). The distance between phosphorus atoms within one cell and neighbouring periodic images was 15.38 Å. According to our calculations, in this configuration, the contributions of the excess electrons of two phosphorus atoms compensate each other, and, as a result, the total magnetization is either absent or close to zero. To assess the effects of the magnetization presence, we used the atomic-type magnetization constraint implemented in Quantum Espresso. Two configurations were considered: (0,0), where local atomic moments on phosphorus atoms are codirectional and are perpendicular to the silicene plane, and (−90,90), where local moments of phosphorus atoms inside the Si62P2 cell are in opposite directions and lie within the silicene plane. In the first case, the angle between the local moments of phosphorus atoms is 0°, and in the second is 180°. Table 1 shows the results for the case without and for three cases with constrained (increasing) magnetization; for each case, the absolute magnitude of the local moment of phosphorus atoms (|MP|), the total magnetization value (MTOT), and the difference in total energies (ΔE) for (0,0) and (−90,90) configurations are presented.
| Configuration | |MP|, μB per cell | MTOT, μB per cell | ΔE, meV | |
|---|---|---|---|---|
| No constrained magnetization | (0,0) | 0.0022 | 0.06 | |
| (−90,90) | 0.0113 | 0.00 | + 0.17 | |
| Constrained magnetization (increasing) | (0,0) | 0.0395 | 0.28 | |
| (−90,90) | 0.0507 | 0.00 | −0.13 | |
| (0,0) | 0.0746 | 0.39 | ||
| (−90,90) | 0.0870 | 0.00 | −0.38 | |
| (0,0) | 0.1494 | 0.83 | ||
| (−90,90) | 0.1555 | 0.00 | −4.78 |
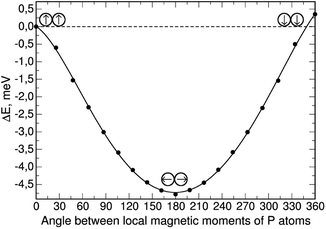
As shown, without constrained magnetization, the configuration (0,0) has a very small gain in total energy, but as the magnetization constraint increases, the (−90,90) configuration becomes preferable. For the case with the highest constrained magnetization, we calculated the dependence of the total energy on the angle between the local magnetic moments of phosphorus atoms; the local moments were rotated symmetrically about the axis perpendicular to the silicene plane with a step of 20° from an initial (0,0) configuration where the local moments of phosphorus are“up” (|0〉 state), to (−180,180) where the local moments are “down” (|1〉 state); the resulting dependence is shown in Fig. 3.
The total energy of the (0,0) configuration was taken as the zero level. Symmetric rotation of the local magnetic moment of phosphorus atoms from the initial position leads to a decrease in the total energy, as well as the total magnetization in the system, down to a value of zero. Further rotation of the phosphorus local moments leads to an almost symmetrical increase in the total energy. In this case, the “down” configuration has an energy value 0.35 meV higher than the “up” configuration. This suggests that in the presence of uniformly distributed phosphorus atoms in the two-dimensional silicene matrix, the antiferromagnetic orientation of their local moments will be preferable, leading to the removal of the total magnetization in the system.
For the Si62P2 cell, a band structure was also calculated (Fig. 4a–c). Fig. 4d shows the Brillouin zone (red marked rectangle) for this cell and the path in reciprocal space. Points M coincide for Si31P and Si62P2 cells, and the X–Γ line contains a point marked as K′, which is equivalent to point K. The band structures also indicate the absence of total magnetization in the configuration without constraint and the removal of the total magnetization in the (−90,90) configuration with constrained atomic magnetization, as indicated by the degeneracy of bands (Fig. 4c).
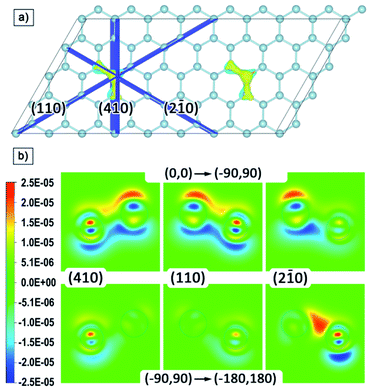
For a qualitative analysis of the electron density redistribution upon rotation of the local moments of phosphorus atoms from the (0,0) configuration to the (−90,90) configuration, and then to the (−180,180) configuration, the density difference of these configurations was found. Spatial changes occur in the regions of interatomic bonds of phosphorus and three neighbouring silicon atoms, therefore, for visualization, we built cross-sections in planes perpendicular to the silicene plane and passing through these three bonds; these planes and their indices are shown in Fig. 5a.
The cross-sections of differences in electron density are shown in Fig. 5b. The transition from cold to warm tones corresponds to the charge transfer upon rotation of the local moment of phosphorus atoms. The redistribution of electron density occurs in the same way on both phosphorus atoms, so we limited ourselves to cross-sections for only one of the atoms. It is possible to distinguish the plane (2–10) and the corresponding direction [210], for which the changes occur asymmetrically relative to the other two. At the (0,0) to (−90,90) transition, the charge from the regions under the phosphorus and two neighbouring silicon atoms transfers upward, and further rotation from (−90,90) to (−180,180) leads to upward charge transfer from the third neighbouring silicon atom. Thus, in general, the rotation of local moments from the |0〉 to |1〉 state leads to a close to symmetric upward transfer of charge density relative to the silicene plane. However, if we consider this process in stages, we can distinguish the formation of an intermediate redistribution of the electron density with a preferred direction [210], in which changes involve one of the neighbouring silicon atoms to a much lesser extent.
Conclusions
A series of quantum mechanical calculations shows that a phosphorus atom doped into silicene has higher local magnetization compared to a phosphorus atom in crystalline silicon. However, phosphorus atoms uniformly distributed in the silicene matrix remove the total magnetization by compensating for the local magnetic moments of each other. By constraining (i.e. enhancing) the magnetization on the phosphorus atom, we obtained the dependence of total energy on the angle between the local moments of a pair of phosphorus atoms. It was shown that, with an increase in magnetization, an antiferromagnetic state also stays more favourable for phosphorus atoms; the band structure showed a corresponding degeneracy of energy levels.The rotation of the local moments of phosphorus atoms from the |0〉 state to state |1〉 leads to charge transport in the opposite direction. In the intermediate state, in the (−90,90) configuration, the redistribution of the charge occurs asymmetrically relative to the 3 bonds of the phosphorus atom with its neighbouring silicon atoms. In the [210] direction, charge from the nearby Si atom from the P–Si bond starts to transfer with the rotation from the (−90,90) configuration to the (−180,180) configuration. In summary, our study shows the dependent behaviour of a pair of phosphorus atoms substituting silicon in the structure of silicene under constrained magnetization. Our results may have important implications for the design of qubits based on phosphorus atoms embedded in silicon structures.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The part of this work devoted to calculations of the atomic and electronic structure was supported in accordance with the State assignment for research work implementation from the Ministry of Science and Higher Education of the Russian Federation (project no. 0818-2020-0005). Computations were performed using methods and techniques developed under the State assignment for research work implementation from the Computing Centre Far Eastern Branch of the Russian Academy of Sciences (KhFRC FEB RAS). The studies were carried out using the resources of the Center for Shared Use of Scientific Equipment and the Center for Processing and Storage of Scientific Data of the Far Eastern Branch of the Russian Academy of Sciences, funded by the Russian Federation represented by the Ministry of Science and Higher Education of the Russian Federation under project No. 075-15-2021-663.References
- K. Nowack, M. Shafiei, M. Laforest, G. Prawiroatmodjo, L. Schreiber, C. Reichl, W. Wegscheider and L. Vandersypen, Science, 2011, 333, 1269–1272 CrossRef CAS PubMed
.
- B. Kane, Nature, 1998, 393, 133–137 CrossRef CAS
.
- L. Oberbeck, T. Hallam, N. Curson, M. Simmons and R. Clark, Appl. Surf. Sci., 2003, 212–213, 319–324 CrossRef CAS
.
- M. Fuechsle, J. Miwa, S. Mahapatra, H. Ryu, S. Lee, O. Warschkow, L. Hollenberg, G. Klimeck and M. Simmons, Nat. Nanotechnol., 2012, 7, 242–246 CrossRef CAS PubMed
.
- M. Broome, S. Gorman, M. House, S. Hile, J. Keizer, D. Keith, C. Hill, T. Watson, W. Baker, L. Hollenberg and M. Simmons, Nat. Commun., 2018, 9, 980 CrossRef CAS PubMed
.
- Y. He, S. Gorman, D. Keith, L. Kranz, J. Keizer and M. Simmons, Nature, 2019, 571, 371–375 CrossRef CAS PubMed
.
- D. Keith, M. House, M. Donnelly, T. Watson, B. Weber and M. Simmons, Phys. Rev. X, 2019, 9, 041003 CAS
.
- M. House, T. Kobayashi, B. Weber, S. Hile, T. Watson, J. van der Heijden, S. Rogge and M. Simmons, Nat. Commun., 2015, 6, 8848 CrossRef CAS PubMed
.
- S. Gorman, M. Broome, W. Baker and M. Simmons, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 125413 CrossRef
.
- Y. Wang, A. Tankasala, L. Hollenberg, G. Klimeck, M. Simmons and R. Rahman, npj quantum Inf., 2016, 2, 16008 CrossRef
.
- B. Lalmi, H. Oughaddou, H. Enriquez, A. Kara, S. Vizzini, B. Ealet and B. Aufray, Appl. Phys. Lett., 2010, 97, 223109 CrossRef
.
- A. Fleurence, R. Friedlein, T. Ozaki, H. Kawai, Y. Wang and Y. Yamada-Takamura, Phys. Rev. Lett., 2012, 108, 245501 CrossRef PubMed
.
- H. Kelardeh, V. Apalkov and M. Stockman, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045413 CrossRef
.
- J. Yan, M. Cruz, S. Barraza-Lopez and L. Yang, Appl. Phys. Lett., 2015, 106, 183107 CrossRef
.
- E. Zaminpayma and P. Nayebi, Phys. E, 2016, 84, 555–563 CrossRef CAS
.
- M. Ali, X. Pi, Y. Liu and D. Yang, AIP Adv., 2017, 7, 045308 CrossRef
.
- X. Wang and Z. Wu, Phys. Chem. Chem. Phys., 2017, 19, 2148–2152 RSC
.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef
.
- W. Kohn and L. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef
.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. Seitsonen, A. Smogunov, P. Umari and R. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed
.
- J. Perdew, A. Ruzsinszky, G. Csonka, O. Vydrov, G. Scuseria, L. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed
.
- T. Oda, A. Pasquarello and R. Car, Phys. Rev. Lett., 1998, 80, 3622–3625 CrossRef CAS
.
- R. Gebauer and S. Baroni, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, R6459–R6462 CrossRef CAS
.
- A. Dal Corso, Comput. Mater. Sci., 2014, 95, 337–350 CrossRef CAS
.
- H. Monkhorst and J. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef
.
- C. Liu, W. Feng and Y. Yao, Phys. Rev. Lett., 2011, 107, 076802 CrossRef PubMed
.
- S. Haldar, R. G. Amorim, B. Sanyal, R. H. Scheicher and A. R. Rocha, RSC Adv., 2016, 6, 6702 RSC
.
- N. D. Drummond, V. Zólyomi and V. I. Fal'ko, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 075423 CrossRef
.
- J. Sivek, H. Sahin, B. Partoens and F. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 085444 CrossRef
.
| This journal is © The Royal Society of Chemistry 2021 |