Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Controllable crystal form transformation and luminescence properties of up-conversion luminescent material K3Sc0.5Lu0.5F6: Er3+, Yb3+ with cryolite structure
Zhaoliang Yana,
Qingfeng Guo b,
Libing Liao
b,
Libing Liao *a,
Pengfei Shuaia,
Feifei Huanga and
Lefu Meia
*a,
Pengfei Shuaia,
Feifei Huanga and
Lefu Meia
aBeijing Key Laboratory of Materials Utilization of Nonmetallic Minerals and Solid Wastes, National Laboratory of Mineral Materials. School of Materials Sciences and Technology, China University of Geosciences, Beijing 100083, China. E-mail: clayl@cugb.edu.cn
bSchool of Gemology, China University of Geosciences, Jewelry and Mineral Materials Laboratory of Experimental Teaching Demonstration Center, Beijing 100083, China
First published on 8th September 2021
Abstract
In this paper, a novel cryolite-type up-conversion luminescent material K3Sc0.5Lu0.5F6: Er3+, Yb3+ with controllable crystal form was synthesized by a high temperature solid state method. K3Sc0.5Lu0.5F6: Er3+, Yb3+ can crystallize in monoclinic or cubic form at different temperatures. The composition, structure and up-conversion luminescence (UCL) properties of K3Sc0.5Lu0.5F6: Er3+, Yb3+ samples with different crystal form were investigated in detail. It is impressive that both monoclinic and cubic forms of K3Sc0.5Lu0.5F6: Er3+, Yb3+ show green emission (2H11/2/4S3/2→4I15/2). The luminescence intensity of cubic K3Sc0.5Lu0.5F6 is much higher than that of the monoclinic form, and the reasons are also discussed in detail. The results show that the luminescence intensity of up-conversion materials can be effectively tuned by controlling the crystal form. According to the power dependent UCL intensity, the UCL mechanism and electronic transition process were discussed. In addition, the fluorescence decay curves were characterized and the thermal coupling levels (TCLs) of Er3+ (2H11/2/4S3/2 → 4I15/2) in the range of 304–574 k were used to study the optical temperature sensing characteristics. All the results show that K3Sc0.5Lu0.5F6: Er3+, Yb3+ can be used in electronic components and have potential application value in temperature sensing fields.
1. Introduction
Lanthanides are usually used as the luminescence center of up-conversion luminescent materials due to their abundant energy levels, efficient energy conversion, and unique optical properties.1,2 Lanthanides can be excited by an external light source and the electrons of lanthanides can jump between different energy levels, showing the absorption of photons and up-conversion luminescence characteristics. Lanthanides have different electron configuration and energy level structure, therefore exhibit different up-conversion luminescence properties.3–8 Er3+/Yb3+ pairs are the most attractive lanthanide ions for up-conversion luminescence. Er3+ can absorb near-infrared photons around 980 nm and emit green and red light through the up-conversion process. Therefore, Er3+ is considered to be a superior up-conversion luminous center. However, Er3+ has weak absorption in the visible and near-infrared region, and it needs to be sensitized by other ions. Yb3+ is the most effective sensitizing ion because it has a large absorption cross-section and a wide absorption region and the energy level of Yb3+ and Er3+ matches well. Therefore, there is an effective energy transfer between Er3+ and Yb3+, and the up-conversion luminous efficiency of Er3+ is significantly improved.9–15The most common way to improve the efficiency of up-conversion is to use a host with low phonon energy.16 We hope to find materials with suitable crystal field environment and higher temperature sensitivity around Er3+, which can further improve the performance of optical temperature sensor. The fluoride host has significant physical and chemical properties and low phonon energy, which makes it suitable for non-contact optical temperature measurement. Many previous works have reported the application of fluoride in temperature sensing. Baziulyte-Paulaviciene successfully synthesized Er3+ doped hexagonal NaYbF4 particles, which can work in the temperature range of 175–475 K, and reach the maximum relative sensor sensitivity of 3.46% K−1 at 175 K.17 Qiang synthesized Mn2+ co-doped hexagonal NaGdF4: Yb3+, Ho3+ nano-phosphor, and proved that high-concentration Mn2+ doping can improve the sensing sensitivity of the sample.18 Kumar successfully doped GdF3: Ho3+, Yb3+ phosphors with Ag+ to achieve emission enhancement and real-time temperature sensing through magnetic field adjustment.19 Besides, Du synthesized SrF2: Yb3+, Ho3+ and realized wide-range temperature sensing.20
Cryolite is a promising host material in the field of luminescent materials due to its low phonon energy, good optical transparency, high mechanical and chemical stability.21,22 The general structural formula of cryolite is A3BF6 (A = Li+, Na+, K+, NH4+, etc. B = Al3+, Sc3+, Ga3+, In3+, etc.),23 and up-conversion luminescent ion pairs can occupy the B site easily, forming a coupled isomorphic replacement in the cryolite crystal lattice. In recent years, research on cryolite structure compound as a luminescent host material has been widely reported, such as K3ScF6: Tm3+, Yb3+,24 K3YF6: Er3+, Yb3+ 23, K3LuF6: Tb3+, Eu3+,25 K3GaF6: Mn4+,26 Na3GaF6: Eu3+,27 K3GdF6,28 K3AlF6: Mn4+.29 The luminescence characteristics of up-conversion depend on the complex interactions between different doping ions and the host lattice.30 Therefore, the luminescence of these particles can be adjusted by the crystal structure of the host lattice, the size of the particles and the ratio of different lanthanide dopants.
Polymorphism refers to the phenomenon that substances with the same chemical composition can crystallize into two or more crystals structures under different physical and chemical conditions. Rare-earth ions in different polymorphic structures will bring about particularly interesting luminescence phenomena. Therefore, the influence of the polymorphism transition on the luminescence properties of rare-earth ions has attracted attention from scholars, such as Gao changed the content ratio of ZnO/Na2O in the Tb3+–Yb3+ co-doped NaYF4 nanocrystal-containing zinc fluoride hydroxide glass ceramics to achieve the cubic to hexagonal form transition and the enhancement of up-conversion luminescence;31 Janjua prepared ultrafine pure hexagonal NaYF4 by the solvothermal method: the up-conversion luminescence intensity of hexagonal NaYF4: Er3+, Yb3+ is 10 times than cubic nanocrystals of the same size.32
For cryolite, the most common crystal structures are monoclinic and cubic, and in different crystal form, the up-conversion luminescence properties of cryolite materials maybe different. At present, many cryolite materials with different crystal forms were obtained by substitution of monovalent and trivalent cations, but the comparison of up-conversion luminescence properties of cryolite materials with polymorphism has not been reported. In this article, we synthesized cryolite material: K3Sc0.5Lu0.5F6: Er3+, Yb3+ (KSLF: Er3+, Yb3+). By changing the synthesis temperature, the monoclinic and cubic KSLF: Er3+, Yb3+ were obtained. We systematically compared the chemical composition, crystal structure, micromorphology, and up-conversion luminescence properties of KSLF: Er3+, Yb3+ with different crystal forms. In addition, we also discussed the possible luminescence mechanisms in the two crystal forms, the reasons for the difference in the electronic transition process and the up-conversion luminescence performance, and the application possibility of KSLF: Er3+, Yb3+ in temperature-sensitive areas.
2. Material synthesis and characterization
A series of Er3+ and Yb3+ co-doped KSLF powders were prepared by high-temperature solid-state method. Potassium carbonate (K2CO3, A.R.), scandium oxide (Sc2O3, 99.99), lutetium oxide (Lu2O3, 99.99), oxidizing bait (Er2O3, 99.99), ytterbium oxide (Yb2O3, 99.99), ammonium hydrogen fluoride (NH4HF2, A.R.) are the raw material, and the above materials are all purchased from Aladdin industrial corporation. Based on the stoichiometric ratio of the target compound, the raw materials are weighed and placed in a mortar and ground for 10 minutes until the mixture is uniformly mixed. Then, the well-mixed ingredients are placed into a crucible and transferred to the muffle furnace. The synthesis temperature of samples with different crystal structures were kept at 800 °C and 900 °C for 3 h and cooling in furnace to room temperature. The obtained samples were ground for subsequent characterization.X-ray diffraction (XRD) patterns of the synthesized samples were obtained by X-ray powder diffraction (D8 Advance, Bruker, Germany), with the Cu kα = 0.15406 nm, tube current = 40 mA, tube voltage = 40 kV, and the tested 2θ range from 10° to 70°, with 0.05° step scan mode. For XRD patterns analysis, the data from JCPDS (Joint Committee on Powder Diffraction Standards) were used as a reference. The size, morphology, energy dispersive X-ray spectroscopy (EDX) and element mapping of the samples were characterized by field emission scanning electron microscopy (SEM, JSM-6701F, Hitachi, Japan), operated at 10 kV. The X-ray photoelectron spectroscopy analyses (XPS, Thermo Escalab 250Xi, American) were performed for elements identification and valence state analysis. TEM images were obtained on a JEM2100F transmission electron microscope. The fluorescence emission spectra of samples were measured on Hitachi F4600 fluorescence spectrophotometer with 980 nm tunable infrared laser as excitation source.
3. Results and discussion
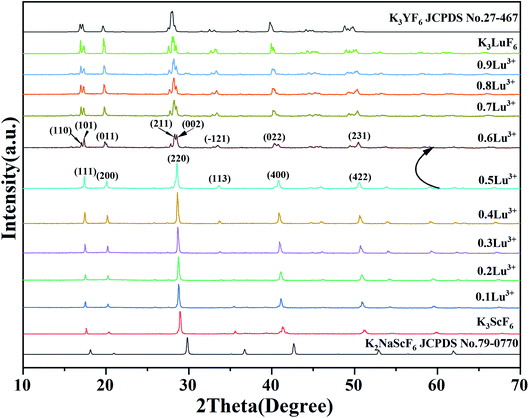
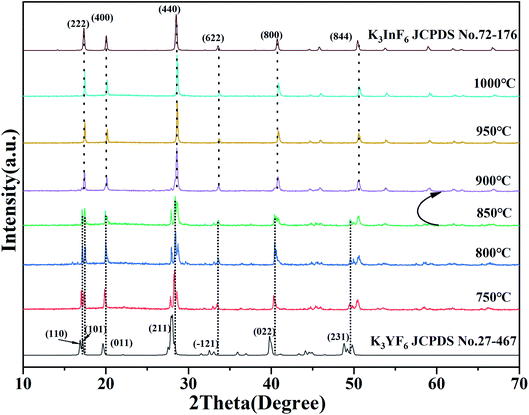
Fig. 1 show the XRD patterns of a series of K3Sc(1−x)LuxF6 samples synthesized by the high-temperature solid-phase method and the calculated standard profile of cubic K2NaScF6 (JCPDS no. 79-0770) and monoclinic K3YF6 (JCPDF no. 27-467) is shown as a reference. All diffraction peaks of the as-prepared samples are in consistent with the standard profile and no other diffraction peaks. When the doping concentration of Lu3+ is 50 mol%, the crystal structure of the sample changes from cubic to monoclinic in K3Sc(1−x)LuxF6. The result shows that replacing Sc3+ with Lu3+ can effectively affect the transformation of cubic form to monoclinic form.33,34 With the increase of Lu3+ doping concentration, the XRD diffraction peaks of the sample shift to lower diffraction angles. This can be explain that the Sc3+ in the lattice is replaced by a larger Lu3+, which leads to the expansion of the unit cell volume, the crystal interplanar spacing (d) becomes larger.35,36Fig. 2 shows the XRD patterns of K3Sc0.5Lu0.5F6 (KSLF) at different synthesis temperatures. The results showed when the temperature was below 850 °C, the main strong diffraction peaks of KSLF were consistent with the standard card of the monoclinic K3YF6 (JCPDF no. 27-467). Meanwhile, when the synthesis temperature was above 900 °C, the diffraction peaks of KSLF were consistent with the standard card of cubic K3InF6 (JCPDS no. 72-176). It shows that as the synthesis temperature increases, the crystal structure of the sample changes from monoclinic to cubic and all diffraction peaks become sharper which indicates that the crystallinity becomes better.34,37
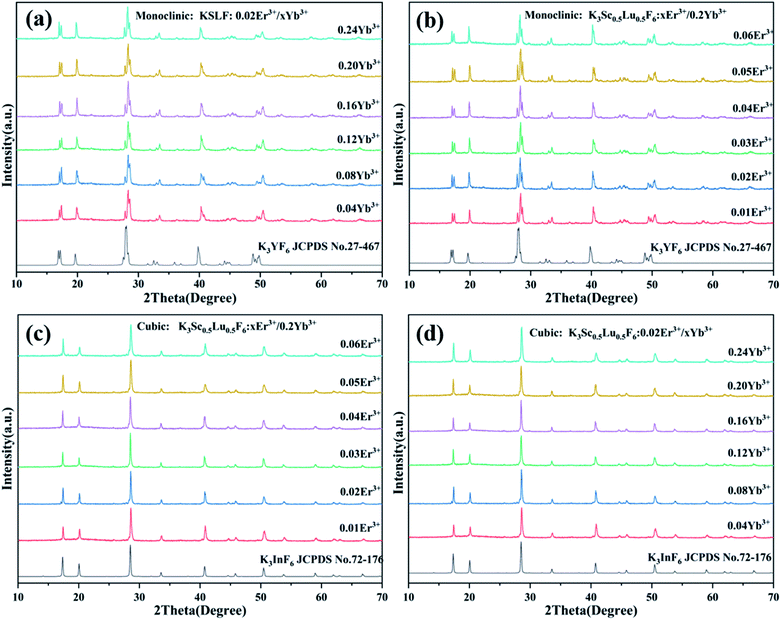
The luminous efficiency of up-conversion luminescent materials is not only related to the host structure, but also related to the phase purity of the prepared materials. Fig. 3(a and b) shows the XRD patterns of the monoclinic KSLF: 0.02Er3+, xYb3+ and KSLF: xEr3+, 0.2Yb3+, and the data of monoclinic K3YF6 (JCPDF no. 27-467) is shown as a reference. It is clear that the XRD diffraction peaks of KSLF: 0.02Er3+, xYb3+ (x = 0.04, 0.08, 0.12, 0.16, 0.20 and 0.24) and KSLF: xEr3+, 0.2Yb3+ (x = 0.01, 0.02, 0.03, 0.04, 0.05 and 0.06) match well with the standard card of K3YF6 (JCPDF no.27-467), indicating all the samples belong to the monoclinic form with a space group of P21/n. Fig. 3(c and d) shows the XRD patterns of the cubic KSLF: 0.02Er3+, xYb3+ and KSLF: xEr3+, 0.2Yb3+, and the with cubic K3InF6 (JCPDS no. 72-176) as a standard. According to the patterns, we can learned: XRD diffraction peaks of cubic KSLF: 0.02Er3+, xYb3+ (x = 0.04, 0.08, 0.12, 0.16, 0.20 and 0.24) and KSLF: xEr3+, 0.2Yb3+ (x = 0.01, 0.02, 0.03, 0.04, 0.05 and 0.06) match well with the standard card of K3YF6 (JCPDF no.27-467). It shows that the synthesized samples belong to the cubic system, with a space group of Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) .38–40 The samples for the two different crystal structures are all pure phases. The introduction of Er3+, Yb3+ did not have any significant influence on the crystal form of KSLF.29
.38–40 The samples for the two different crystal structures are all pure phases. The introduction of Er3+, Yb3+ did not have any significant influence on the crystal form of KSLF.29
The crystal structure of monoclinic and cubic KSLF: 0.04Er3+, 0.2Yb3+, and coordination environments of K, Sc, Lu, Er, Yb and F are presented. Fig. 4(a) is the crystal structure of monoclinic KSLF, the space group is P21/n, Sc, Lu, Er and Yb coordinate to six F to form [Sc, Lu, Er, YbF6] regular octahedra. There are two non-equivalent positions of K in the crystal structure of KSLF: 0.04Er3+, 0.2Yb3+, one with twelve-fold coordination and another with six-fold coordination.41 Fig. 4(b) is the crystal structure of cubic KSLF: 0.04Er3+, 0.2Yb3+, the space group is Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , K occupies four different crystallographic sites named K (1), K (2), K (3) and K (4), respectively. Sc1, Lu1, Er1 and Yb1 are situated in the center of the regular octahedron with 6-fold coordination by F−, Sc2, Lu2, Er2 and Yb2 are situated in the center of the deformed octahedron with 6-fold coordination by F−.42
, K occupies four different crystallographic sites named K (1), K (2), K (3) and K (4), respectively. Sc1, Lu1, Er1 and Yb1 are situated in the center of the regular octahedron with 6-fold coordination by F−, Sc2, Lu2, Er2 and Yb2 are situated in the center of the deformed octahedron with 6-fold coordination by F−.42
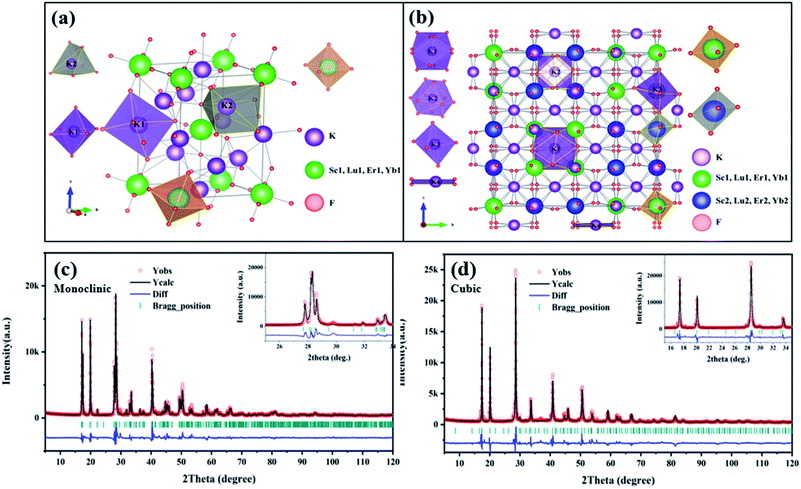 | ||
| Fig. 4 (a and b) The crystallographic structure of monoclinic and cubic KSLF: 0.04Er3+, 0.2Yb3+; (c and d) Rietveld refinement XRD patterns of monoclinic and cubic KSLF: 0.04Er3+, 0.2Yb3+. | ||
Fig. 4 shows the Rietveld refinement of monoclinic and cubic KSLF: 0.04 Er3+, 0.2Yb3+, where the red circles, black solid line, short green vertical and blue solid lines represent the observed pattern obtained from XRD measurements, the calculated pattern, the Bragg positions, and the difference between the observed and calculated patterns, respectively. In Fig. 4(c), all peaks were indexed by monoclinic crystal with parameters close to those of previously reported K3InF6 compound, and the structural parameters of K3InF6 were used as initial parameters in the Rietveld analysis. In Fig. 4(d), all peaks were indexed by cubic crystal with parameters close to those of previously reported K3YF6 compound, and the structural parameters of K3YF6 were used as initial parameters in the Rietveld analysis. Sites of Sc/Lu ions in monoclinic and cubic KSLF: 0.04 Er3+/0.2Yb3+ are occupied by Er, Yb ions. The final refinement is stable and convergent well with low residual factors Rp = 7.804%, χ2 = 3.032 and Rp = 9.331%, χ2 = 3.452, indicating no unidentified diffraction peaks from impurity. The final refined crystallographic data are listed in Table 1. The cell parameters of monoclinic KSLF: 0.04 Er3+, 0.2Yb3+ are determined to be a = 6.257 Å, b = 6.439 Å, c = 8.930 Å and V = 359.79 Å3, and the cell parameters of cubic KSLF: 0.04 Er3+, 0.2Yb3+ are determined to be a = 17.707 Å and V = 5551.4 Å3. The crystallographic site coordinates, occupancy factors, and equivalent isotropic displacement parameters of monoclinic and cubic KSLF: 0.04 Er3+, 0.2Yb3+ are summarized in Tables 2 and 3.43,44 Based on the site occupation fraction in Rietveld refinement, the Er3+ ions take up ∼5% Sc/Lu sites and Yb3+ ions take up ∼24.9% Sc/Lu sites in monoclinic KSLF. In cubic KSLF, the Er13+ ions take up ∼2.7% Sc1/Lu1 sites and Yb13+ ions take up ∼20.2% Sc1/Lu1 sites, the Er23+ ions take up ∼3.6% Sc2/Lu2 sites and Yb23+ ions take up ∼20.3% Sc2/Lu2 sites.45,46
| Compound | Monoclinic | Cubic |
|---|---|---|
| 2θ | 5–120 | 5–120 |
| Symmetry | Monoclinic | Cubic |
| Space group | P21/n | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
| a/Å | 6.257 (2) | 17.707 (1) |
| b/Å | 6.439 (1) | |
| c/Å | 8.930 (2) | |
| β (degree) | 90.304 (2) | |
| Volume/Å3 | 359.79 (3) | 5551.4 (1) |
| Z | 2 | 32 |
| Rp (%) | 7.804% | 9.331% |
| Rwp (%) | 11.194% | 12.670% |
| χ2 | 3.032 | 3.452 |
| Atom | Mult. | x | y | z | Occ. | Biso |
|---|---|---|---|---|---|---|
| Sc1 | 0 | 0 | 0 | 0 | 0.320(4) | 0.50(14) |
| Lu1 | 0 | 0 | 0 | 0 | 0.425(7) | 0.50(14) |
| Yb1 | 0 | 0 | 0 | 0 | 0.249(15) | 0.50(14) |
| Er1 | 0 | 0 | 0 | 0 | 0.05(2) | 0.50(14) |
| K1 | 0 | 0.5 | 0.5 | 0 | 1 | 1.00(28) |
| K2 | 0 | 0.0111(11) | 0.55233(60) | 0.74408(58) | 1 | 1.00(26) |
| F1 | 0 | 0.2163(18) | 0.3223(18) | 0.5250(16) | 1 | 1.00(44) |
| F2 | 0 | 0.3648(21) | 0.7871(19) | 0.5504(13) | 1 | 1.00(47) |
| F3 | 0 | 0.4273(17) | 0.5318(15) | 0.2775(13) | 1 | 0.60(40) |
| Atom | Mult. | x | y | z | Occ. | Biso |
|---|---|---|---|---|---|---|
| Sc1 | 16 | 0 | 0 | 0 | 0.326 | 0.17(46) |
| Sc2 | 16 | 0.5 | 0.5 | 0.5 | 0.231 | 0.10(43) |
| Lu1 | 16 | 0 | 0 | 0 | 0.445 | 0.17(46) |
| Lu2 | 16 | 0.5 | 0.5 | 0.5 | 0.5304 | 0.10(43) |
| Yb1 | 16 | 0 | 0 | 0 | 0.202(12) | 0.17(46) |
| Yb2 | 16 | 0.5 | 0.5 | 0.51 | 0.203(11) | 0.10(43) |
| Er1 | 16 | 0 | 0 | 0 | 0.027 | 0.17(46) |
| Er2 | 16 | 0.5 | 0.5 | 0.5 | 0.036 | 0.10(43) |
| K1 | 8 | 0.125 | 0.125 | 0.125 | 1 | 1.0(23) |
| K2 | 8 | 0.625 | 0.625 | 0.625 | 1 | 1.0(24) |
| K3 | 32 | 0.25 | 0.25 | 0.25 | 1 | 1.00(27) |
| K4 | 48 | 0.375 | 0.125 | 0.125 | 1 | 1.00(65) |
| F1 | 96 | 0.1112(14) | 0.0140(15) | 0.9626(10) | 1 | 1.00(64) |
| F2 | 96 | 0.6131(12) | 0.4981(13) | 0.5069(10) | 1 | 1.00(44) |
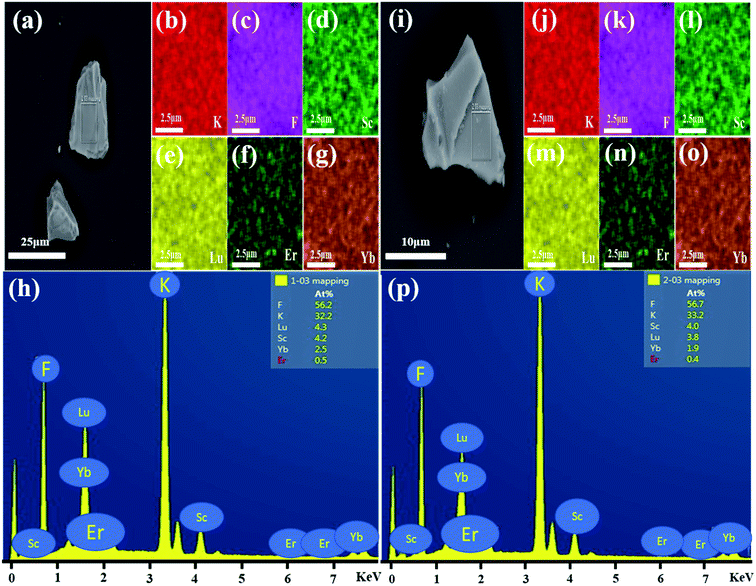
Fig. 5(a) shows the SEM image of monoclinic KSLF: 0.04Er3+, 0.2Yb3+, the prepared sample is irregularly granular, with a particle size of about tens of microns. In order to understand the distribution of all elements in the sample, a square is selected as the area for element mapping and EDS testing. Fig. 5(b–g) shows the element mapping images, it can be seen that K, Sc, Lu, F, Er can be observed in monoclinic KSLF: 0.04Er3+, 0.2Yb3+ and all the elements in the sample are homogenously distributed over the granules. Fig. 5(h) depicts the EDX spectrum and the atomic composition ratios of monoclinic KSLF: 0.04 Er3+, 0.2Yb3+ sample. Fig. 5(i) shows the SEM image of cubic KSLF: 0.04Er3+, 0.2Yb3+, choose a square as the area for element mapping and EDS testing. According to the mapping results of Fig. 5(j–o), all elements are evenly distributed, and the existence of Er illustrates that Er3+ ions were successfully doped into the crystal lattice. Fig. 5(p) shows the EDX spectrum and the atomic composition ratios of cubic KSLF: 0.04 Er3+, 0.2Yb3+ sample. For both monoclinic and cubic KSLF: 0.04Er3+, 0.2Yb3+, the molar ratio of Sc to Lu is close to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and the actual doping amount of Er and Yb is also close to the theoretical doping amount, which further shows that the measured atomic ratio of the corresponding element is close to the calculated value.
1, and the actual doping amount of Er and Yb is also close to the theoretical doping amount, which further shows that the measured atomic ratio of the corresponding element is close to the calculated value.
The microstructures of monoclinic and cubic KSLF: 0.04Er3+, 0.2Yb3+ were further characterized by TEM. In Fig. 6, the enlarged HRTEM image showed the characteristic lattice fringe of monoclinic and cubic KSLF: 0.04Er3+, 0.2Yb3+. The monoclinic KSLF: 0.04Er3+, 0.2Yb3+ has a lattice plane spacing of 0.318 nm, and the corresponding lattice plane index is (211). The cubic KSLF: 0.04Er3+, 0.2Yb3+ has a lattice plane spacing of 0.181 nm, and the corresponding lattice plane index is (844).
 | ||
| Fig. 6 (a and b) are TEM and HR-TEM images of monoclinic KSLF: 0.04Er3+, 0.2Yb3+; (c and d) are TEM and HR-TEM images of cubic KSLF: 0.04Er3+, 0.2Yb3+. | ||
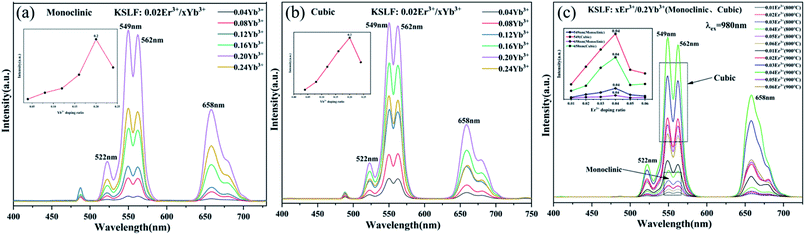
Fig. 7(a and b) shows the up-conversion emission spectra of monoclinic and cubic KSLF: 0.02Er3+, xYb3+(x = 0.04, 0.08, 0.12, 0.16, 0.20 and 0.24) for different Yb3+ doping ratio. As Yb3+ concentration changes from 0.04 to 0.24 mol, the emission intensity of the sample first increases and then decreases. When the doping ratio of Yb3+ is 0.20 mol, the emission intensity centered at 549 nm reaches the maximum. Fig. 7(c) shows the up-conversion luminescence performance of cubic and monoclinic KSLF: xEr3+, 0.2Yb3+ (x = 0.01, 0.02, 0.03, 0.04, 0.05 and 0.06) under 980 nm excitation. Er3+, Yb3+ co-doped KSLF showed bright green emission at 549 nm, and a weak red emission peak appeared at 657 nm. Keeping the doping ratio of Yb3+ at 0.2, it can be clearly seen that in monoclinic and cubic forms, as Er3+ increases from 0.01 to 0.06, the emitted up-conversion luminous intensity at 549 nm first increases and then shows a downward trend. When the Er3+ doping ratio is 0.04, the up-conversion luminescence intensity reaches the maximum value, and then the concentration quenching effect appears. This is because as Er3+ concentration increases, the central ion distance decreases to be less than the critical distance. In the process of energy transfer, the possibility of energy transfer in quenching center increases.47 The energy is released from the quenching center, resulting in the decrease of up-conversion luminescence intensity. This can be visually illustrated by the trend graph of the peak intensity at 549 nm and 658 nm with the concentration of Er3+ for monoclinic and cubic form. It can be observed that crystal form has no effect on the position of spectral peaks, but the luminescence intensity of cubic form is significantly higher than that of monoclinic form. This is because in monoclinic and cubic system, the crystal field environments are different, which affects the up-conversion energy transfer process, especially the non-radiation transition process of Er3+. The probability of the non-radiation transition of Er3+ in monoclinic crystal field environment is greater than that in cubic system, which leads to the stronger luminescent intensity of cubic form.
The photoluminescence decay curves of the prepared monoclinic and cubic KSLF: 0.04Er3+, 0.2Yb3+ are shown in Fig. 8. The attenuation curve is fitted with a double exponential eqn (1):
I(t) = I0 + A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ1) + A2 exp(−t/τ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ2) exp(−t/τ2)
| (1) |
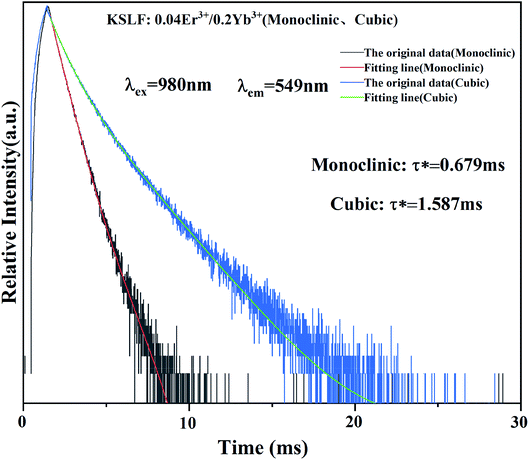 | ||
| Fig. 8 Fluorescence decay curve of monoclinic and cubic KSLF: 0.04Er3+, 0.2Yb3+ under the excitation of 980 nm. | ||
Among them, I(t) and I0 are the luminous intensity and background intensity at time t, respectively, A1 and A2 are the emission intensity factors, and τ1 and τ2 are the decay time of the exponential component, respectively.48 The average life span can be calculated as follows:
| τave = (A1τ12 + A2τ22)/(A1τ2 + A2τ1) | (2) |
Based on the equations, the calculated average lifetimes are about 0.679 ms and 1.587 ms for monoclinic and cubic KSLF: 0.04Er3+, 0.2Yb3+ phosphors. For samples with monoclinic form, the fluorescence lifetimes are comparatively shorter (0.679 ms), and the lifetimes for samples with the cubic form are notably longer (1.587 ms).
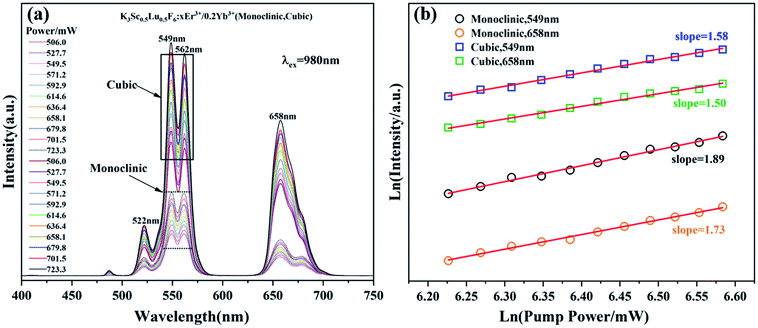
The up-conversion emission spectra of monoclinic and cubic KSLF: 0.04Er3+, 0.2Yb3+ samples under different pump powers are shown in Fig. 9. In the excitation power range is 506.0–723.3 mW, the influence of the pump power on the up-conversion emission intensity is studied. It can be seen from Fig. 9(a) that the Er3+ in the two samples with different crystal structures has obvious green and red emission at 549 nm and 658 nm, and the emission intensity shows an obvious linear upward trend. According to the relationship between the up-conversion luminous intensity (I) and the excitation power (P), I ∝ Pn, where n is the number of photons required from the ground state to the emission state during the up-conversion period.22 The integrated emission intensity of green and red light of KSLF: 0.04Er3+, 0.2Yb3+ at 549 nm and 658 nm is plotted with different pump powers in the form of Ln–Ln (pump power–emission intensity) curves. For monoclinic KSLF: 0.04Er3+, 0.2Yb3+, the slopes of green light and red light are 1.89 and 1.73 respectively, indicating that both green light (549 nm) and red light (658 nm) are two-photon processes produced. For cubic KSLF: 0.04Er3+, 0.2Yb3+, the slopes of green light and red light are 1.58 and 1.50, respectively, indicating that green light (549 nm) and red light (658 nm) are also two-photon processes produced.
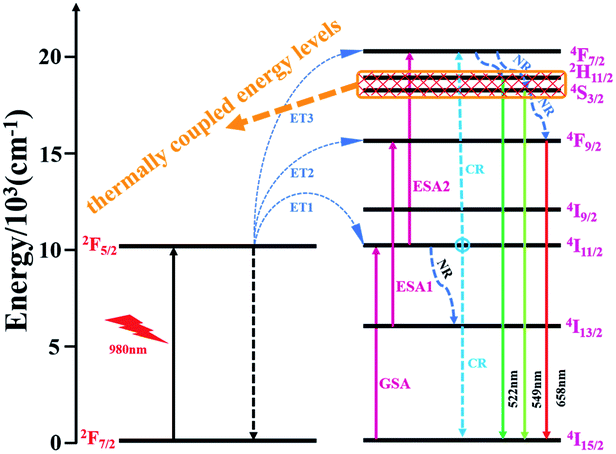
In order to illustrate the luminescence mechanism of KSLF: 0.04Er3+, 0.2Yb3+, the possible UC processes and energy levels diagram are described in detail in Fig. 10. The main UC processes include energy transfer (ET), ground state absorption (GSA), excited state absorption (ESA) and cross relaxation (CR). In the energy levels diagram, the energy gap of Er3+ (4I15/2 and 4I11/2) is match well with the energy gap of Yb3+ (2F7/2 and 2F5/2), so the ET from Yb3+ to Er3+ may occur: ET1: Er3+(4I15/2) + Yb3+(2F5/2) → Er3+(4I11/2) + Yb3+(2F7/2). For 522 nm, 549 nm and 562 nm emission peaked of the Er3+, 4F7/2 can populate the excited energy levels 2H11/2 and 4S3/2 by non-radiative (NR). And the 4F7/2 states could follow three processes: excitation states absorption (ESA2), ET3 and cross relaxation (CR). For red emitting centered at 658 nm from Er3+, the population of 4F9/2 level involves three processes: ESA1, ET2 and NR.
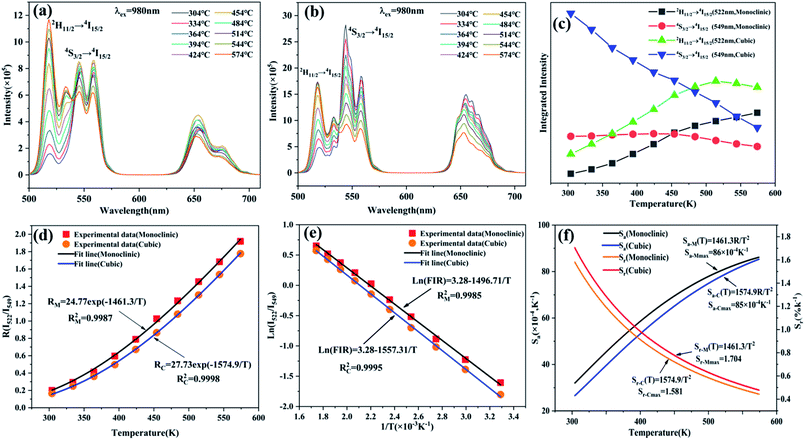
Depending on the excellent up-conversion luminescence performance of KSLF: Er3+, Yb3+, which can crystallize into two crystal forms, the temperature sensing performance has been investigated. Fig. 11(a) and (b) shows the green UC emission spectra of monoclinic KSLF: Er3+, Yb3+ and cubic KSLF: Er3+, Yb3+ under 980 nm excitation at 304–574 K. The spectra show systematic changes as the temperature increased from 304 to 574 K. With the increase of temperature, the intensity at 549 nm of the two crystal forms of KSLF: Er3+, Yb3+ decreased, while the intensity at 522 nm increased significantly (Fig. 11 c). Temperature sensing mainly uses two emission lines, and the energy gap between the two is small. As the temperature increases, the higher energy levels become denser due to the thermalization of the lower energy levels. Because the energy gap between 2H11/2 and 4S3/2 is small, the 2H11/2 state could be populated from 4S3/2 by thermal excitation, which leads to the variations of emission intensity of 2H11/2 and 4S3/2 transitions at elevated temperature.49 The relative population of the “thermally coupled” 2H11/2 and 4S3/2 levels is a quasithermal equilibrium obeying Boltzmann-type distribution, because the emission intensity varies as a function of temperature.50 Potential temperature measurement applications are related to fluorescence intensity ratio (FIR), which can be evaluated using the following formula:
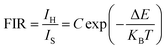 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1461.3/T), and the cubic form can be determined as RC = 27.73
exp(−1461.3/T), and the cubic form can be determined as RC = 27.73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1574.9/T). It can be clearly seen that FIR increases significantly with temperature.51 Here, the emission intensity at 522 nm and 549 nm is used to evaluate the 2H11/2 and 4S3/2 transitions for simplification. Eqn (4) can be derived from eqn (3) as follow:
exp(−1574.9/T). It can be clearly seen that FIR increases significantly with temperature.51 Here, the emission intensity at 522 nm and 549 nm is used to evaluate the 2H11/2 and 4S3/2 transitions for simplification. Eqn (4) can be derived from eqn (3) as follow:
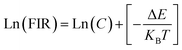 | (4) |
Fig. 11(e) shows the relationship between Ln(FIR) and 1/T of monoclinic and cubic KSLF: 0.04Er3+, 0.2Yb3+ sample in the temperature range of 304–574 K. The monoclinic data can be fitted as: Ln(FIR) = 3.28–1496.71/T, the slope −ΔE/k = −1123.6 and the intercept Ln(C) = 3.28, ΔE = 1040 cm−1. The cubic data can be well fitted as: Ln(FIR) = 3.28–1557.31/T, the slope −ΔE/k = −1557.31 and the intercept Ln(C) = 3.28, ΔE = 1082 cm−1. It is close to the actual energy gap between 4S3/2 and 2H11/2 levels in the current case. In order to evaluate the actual sensing ability of sensor materials, absolute sensitivity (Sa) and relative sensitivity (Sr) are usually used to study the sensitivity change with temperature, which is defined as follows:52
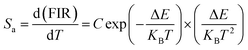 | (5) |
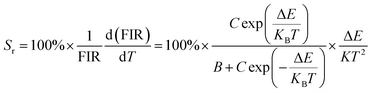 | (6) |
Fig. 11(f) is the calculated absolute temperature sensitivity and relative temperature sensitivity, and their fitting curves with temperature from 304 K to 574 K. With the increase of temperature from 304 K to 574 K, Sa displays a monotonous downward trend and Sr displays a monotonous upward trend for both monoclinic and cubic forms. For monoclinic form, the maximum value of Sa reaches 86 × 10−4 K−1, while the maximum relative sensitivity Sr is 1.704% K−1. For cubic form, the maximum value of Sa reaches 85 × 10−4 K−1, while the maximum relative sensitivity Sr is 1.581% K−1. The Sa in monoclinic and cubic forms is not much different, and the Sr in monoclinic form is greater than that in cubic form. Several classics optical thermometers are listed in Table 4. The results demonstrate that the monoclinic and cubic KSLF: Er3+, Yb3+ are promising in temperature sensing.
| RE doped samples | Maximum absolute sensitivity (×10−4 K−1) | Temperature range (K) | Ref. |
|---|---|---|---|
| CaMoO4: Er3+, Yb3+ | 72 | 300–760 | 53 |
| KSLF: Er3+, Yb3+ (monoclinic) | 86 | 304–574 | This work |
| KSLF: Er3+, Yb3+ (cubic) | 85 | 304–574 | This work |
| NaGdTiO4: Er3+, Yb3+ | 45 | 300–510 | 54 |
| Gd2MoO4: Er3+, Yb3+ | 53 | 303–703 | 14 |
| Na0.5Bi0.5TiO3: Er3+, Yb3+ | 35 | 173–553 | 55 |
| Y2O3: Er3+, Yb3+ | 97 | 314–573 | 1 |
| La2O2S: Er3+, Yb3+ | 80 | 290–573 | 56 |
| CaLa2ZnO5: Er3+, Yb3+ | 59 | 298–513 | 57 |
| LuVO4: Er3+, Yb3+ | 67 | 100–500 | 2 |
| Ba3Y4O9: Er3+, Yb3+ | 45.8 | 298–573 | 13 |
| NaY(WO4)2: Er3+, Yb3+ | 61 | 30–300 | 58 |
| Ba5Gd8Zn4O21: Er3+, Yb3+ | 24 | 298–573 | 59 |
| Na2Gd2Ti3O10: Er3+, Yb3+ | 58 | 290–490 | 60 |
| YVO4: Er3+, Yb3+ | 117 | 300–485 | 61 |
4. Conclusions
In summary, monoclinic and cubic KSLF: Er3+, Yb3+ were prepared by high temperature solid state method, a combination of XRD, SEM, TEM, XPS shows that KSLF: Er3+, Yb3+ with monoclinic (P21/n) and cubic (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) systems can be mutual transformed at different temperatures. Up-conversion fluorescence spectrum shows that the luminescence intensity of the cubic form is significantly higher than that of the monoclinic form, that may be because the probability of the non-radiation transition of Er3+ in the monoclinic crystal field environment is greater than that in the cubic system. The average lifetimes are about 0.679 ms and 1.587 ms for monoclinic and cubic KSLF: 0.04Er3+, 0.2Yb3+ phosphors. According to the fitting result of pump power dependence of up-conversion intensity, the green and red up-conversion emission of monoclinic and cubic KSLF: Er3+, Yb3+ all belong to the two-photon process. For the monoclinic and cubic forms, the maximum value of Sa reaches 86 × 10−4 K−1 and 85 × 10−4 K−1, indicating that the as-prepared KSLF: Er3+, Yb3+ phosphor is appropriate for practical application in optical temperature sensors.
) systems can be mutual transformed at different temperatures. Up-conversion fluorescence spectrum shows that the luminescence intensity of the cubic form is significantly higher than that of the monoclinic form, that may be because the probability of the non-radiation transition of Er3+ in the monoclinic crystal field environment is greater than that in the cubic system. The average lifetimes are about 0.679 ms and 1.587 ms for monoclinic and cubic KSLF: 0.04Er3+, 0.2Yb3+ phosphors. According to the fitting result of pump power dependence of up-conversion intensity, the green and red up-conversion emission of monoclinic and cubic KSLF: Er3+, Yb3+ all belong to the two-photon process. For the monoclinic and cubic forms, the maximum value of Sa reaches 86 × 10−4 K−1 and 85 × 10−4 K−1, indicating that the as-prepared KSLF: Er3+, Yb3+ phosphor is appropriate for practical application in optical temperature sensors.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The current work has been supported by the National Natural Science Foundation of China project (Grant No. 41672044).References
- X. X. Li, P. Gao, J. T. Li, L. Guan, X. L. Li, F. H. Wang, D. W. Wang, Z. Q. Li and X. Li, Enhancing upconversion emission and temperature sensing modulation of the La2(MoO4)3:Er3+, Yb3+ phosphor by adding alkali metal ions, Ceram. Int., 2020, 46(13), 20664–20671 CrossRef CAS.
- J. Wu, X. R. Cheng, F. C. Jiang, X. C. Feng, Q. Huang and Q. Y. Lin, Optical temperature sensing properties of Er3+/Yb3+ co-doped LuVO4 up-conversion phosphors, Physica B, 2019, 561, 97–102 CrossRef CAS.
- A. Mbarek and D. Zambon, New insight into polymorphism in LnP5O14 (Ln = Gd, Eu) ultraphosphates: Synthesis, crystal structure and site-selective spectroscopy of Eu3+-doped GdP5O14, Polyhedron, 2021, 196 DOI:10.1016/j.poly.2020.115012.
- C. N. Xie, S. K. Xie, R. X. Yi, R. P. Cao, H. L. Yuan and F. Xiao, Site-Selective Occupation for Broadband Upconversion Luminescence in Ca3Y(GaO)3(BO3)4:Yb3+,Mn2+ Phosphors, J. Phys. Chem. C, 2020, 124(12), 6845–6852 CrossRef CAS.
- T. H. Wang, Y. J. Li, T. Liu, Y. H. Peng, Z. Y. Yin, Z. W. Yang, J. B. Qiu and Z. G. Song, NIR-NIR upconverting optical temperature sensing based on the thermally coupled levels of Yb3+–Tm3+ codoped Bi7F11O5 nanosheets, J. Lumin., 2020, 221, 7 Search PubMed.
- Y. Lv, Y. H. Jin, Z. Z. Li, S. A. Zhang, H. Y. Wu, G. T. Xiong, G. F. Ju, L. Chen, Z. F. Hu and Y. H. Hu, Reversible photoluminescence switching in photochromic material Sr6Ca4(PO4)6F2:Eu2+ and the modified performance by trap engineering via Ln3+ (Ln = La, Y, Gd, Lu) co-doping for erasable optical data storage, J. Mater. Chem. C, 2020, 8(19), 6403–6412 RSC.
- J. Lee, H. Sa, H. Jo, D. Moon, K. M. Ok and T. S. You, Site-Selective n-Type “Heavy” Rare-Earth-Metal Doping in the Complex Zintl Phase Ca11−xRExSb10−y (RE = Tb, Dy, Ho, Er, Tm), Cryst. Growth Des., 2020, 20(7), 4503–4511 CrossRef CAS.
- G. C. Adhikari, P. A. Vargas, H. Y. Zhu, A. Grigoriev and P. F. Zhu, Tetradic phosphor white light with variable CCT and superlative CRI through organolead halide perovskite nanocrystals, Nanoscale Adv., 2019, 1(5), 1791–1798 RSC.
- Y. Tong, W. N. Zhang, R. F. Wei, L. P. Chen and H. Guo, Na2YMg2(VO4)3:Er3+,Yb3+ phosphors: up-conversion and optical thermometry, Ceram. Int., 2021, 47(2), 2600–2606 CrossRef CAS.
- X. Liu, J. W. Wang, R. S. Lei, S. L. Zhao, F. F. Huang, D. G. Deng and S. Q. Xu, Comparison study on the different strategies designed for ratiometric luminescence thermometry in Er3+/Yb3+: SrMoO4 phosphor, Sens. Actuators, A, 2020, 315, 7 Search PubMed.
- F. Shang, Y. Chen, J. W. Xu, T. Yang, Y. Yang and G. H. Chen, Up-conversion luminescence and highly sensing characteristics of Er3+/Yb3+ co-doped borophosphate glass-ceramics, Opt. Commun., 2019, 441, 38–44 CrossRef CAS.
- M. W. Pin, E. J. Park, S. Choi, Y. I. Kim, C. H. Jeon, T. H. Ha and Y. H. Kim, Atomistic evolution during the phase transition on a metastable single NaYF4:Yb, Er upconversion nanoparticle, Sci. Rep., 2018, 8, 10 CrossRef PubMed.
- S. F. Liu, H. Ming, J. Cui, S. B. Liu, W. X. You, X. Y. Ye, Y. M. Yang, H. P. Nie and R. X. Wang, Color-Tunable Upconversion Luminescence and Multiple Temperature Sensing and Optical Heating Properties of Ba3Y4O9:Er3+/Yb3+ Phosphors, J. Phys. Chem. C, 2018, 122(28), 16289–16303 CrossRef CAS.
- P. Du, X. Y. Huang and J. S. Yu, Yb3+-Concentration dependent upconversion luminescence and temperature sensing behavior in Yb3+/Er3+ codoped Gd2MoO6 nanocrystals prepared by a facile citric-assisted sol–gel method, Inorg. Chem. Front., 2017, 4(12), 1987–1995 RSC.
- G. C. Adhikari, S. Thapa, H. Y. Zhu and P. F. Zhu, Mg2+-Alloyed All-Inorganic Halide Perovskites for White Light-Emitting Diodes by 3D-Printing Method, Adv. Opt. Mater., 2019, 7(20), 9 CrossRef.
- G. C. Adhikari, P. A. Vargas, H. Y. Zhu and P. F. Zhu, Saponification Precipitation Method for CsPbBr3 Nanocrystals with Blue-Green Tunable Emission, J. Phys. Chem. C, 2019, 123(2), 1406–1412 CrossRef CAS.
- D. Baziulyte-Paulaviciene, N. Traskina, R. Vargalis, A. Katelnikovas and S. Sakirzanovas, Thermal decomposition synthesis of Er3+-activated NaYbF4 upconverting microparticles for optical temperature sensing, J. Lumin., 2019, 215, 8 CrossRef.
- Q. P. Qiang and Y. H. Wang, Enhanced optical temperature sensing and upconversion emissions based on the Mn2+ codoped NaGdF4: Yb3+, Ho3+ nanophosphor, New J. Chem., 2019, 43(13), 5011–5019 RSC.
- A. Kumar, S. P. Tiwari, K. Kumar and J. da Silva, Magnetic tuning in upconversion emission enhanced through Ag+ ions co-doped in GdF3: Ho3+/Yb3+ phosphor and a real-time temperature sensing demonstration, J. Alloys Compd., 2019, 776, 207–214 CrossRef CAS.
- S. S. Du and Y. H. Wang, A broad-range temperature sensor dependent on the magnetic and optical properties of SrF2:Yb3+, Ho3+, Crystengcomm, 2019, 21(9), 1452–1457 RSC.
- G. Tessitore, G. A. Mandl, M. G. Brik, W. Park and J. A. Capobianco, Recent insights into upconverting nanoparticles: spectroscopy, modeling, and routes to improved luminescence, Nanoscale, 2019, 11(25), 12015–12029 RSC.
- E. H. Song, J. Q. Wang, J. H. Shi, T. T. Deng, S. Ye, M. Y. Peng, J. Wang, L. Wondraczek and Q. Y. Zhang, Highly Efficient and Thermally Stable K3AIF6:Mn4+ as a Red Phosphor for Ultra-High-Performance Warm White Light-Emitting Diodes, ACS Appl. Mater. Interfaces, 2017, 9(10), 8805–8812 CrossRef CAS PubMed.
- P. F. Shuai, D. Yang, L. B. Liao, Q. F. Guo, L. F. Mei, Y. D. Zhang and H. K. Liu, Preparation, structure and up-conversion luminescence properties of novel cryolite K3YF6:Er3+, Yb3+, RSC Adv., 2020, 10(3), 1658–1665 RSC.
- D. Yang, L. B. Liao, Y. D. Zhang, Q. F. Guo, L. F. Mei and H. K. Liu, Synthesis and up-conversion luminescence properties of a novel K3ScF6: Yb3+, Tm3+ material with cryolite structure, J. Lumin., 2020, 224, 6 CrossRef.
- D. Yang, L. B. Liao, Q. F. Guo, L. F. Mei, H. K. Liu, T. S. Zhou and H. Ye, Luminescence properties and energy transfer of K3LuF6:Tb3+,Eu3+ multicolor phosphors with a cryolite structure, RSC Adv., 2019, 9(8), 4295–4302 RSC.
- T. T. Deng, E. H. Song, Y. Y. Zhou, L. Y. Wang, S. Ye and Q. Y. Zhang, Stable narrowband red phosphor K3GaF6: Mn4+ derived from hydrous K2GaF5(H2O) and K2MnF6, J. Mater. Chem. C, 2017, 5(37), 9588–9596 RSC.
- D. Yang, L. B. Liao, Q. F. Guo, L. J. Wang, L. F. Mei, H. K. Liu and T. S. Zhou, A novel phosphor of Eu3+-activated Na3GaF6: Synthesis, structure, and luminescence properties, J. Lumin., 2018, 203, 391–395 CrossRef CAS.
- M. A. Gusowski, G. Dominiak-Dzik, P. Solarz, R. Lisiecki and W. Ryba-Romanowski, Luminescence and energy transfer in K3GdF6:Pr3+, J. Alloys Compd., 2007, 438(1–2), 72–76 CrossRef CAS.
- Y. M. Liu, T. M. Wang, X. Z. Zhang, C. C. Cao, L. Yang, Y. H. Huang, S. Liao and H. X. Zhang, Synthesis, luminescence properties and nephelauxetic effect of nano stick phosphors K3AlF6:Mn4+ for warm white LED, J. Mater. Sci.: Mater. Electron., 2019, 30(2), 1870–1877 CrossRef CAS.
- Q. F. Guo, C. L. Zhao, Z. Q. Jiang, L. B. Liao, H. K. Liu, D. Yang and L. F. Mei, Novel emission-tunable oxyapatites-type phosphors: synthesis, luminescent properties and the applications in white light emitting diodes with higher color rendering, Dyes Pigm., 2017, 139, 361–371 CrossRef CAS.
- Y. Gao, Y. B. Hu, P. Ren, D. C. Zhou and J. B. Qiu, Phase transformation and enhancement of luminescence in the Tb3+–Yb3+ co-doped oxyfluoride glass ceramics containing NaYF4 nanocrystals, J. Eur. Ceram. Soc., 2016, 36(11), 2825–2830 CrossRef CAS.
- R. A. Janjua, C. Gao, R. C. Dai, Z. L. Sui, M. A. A. Raja, Z. P. Wang, X. X. Zhen and Z. M. Zhang, Na+-Driven Nucleation of NaYF4:Yb,Er Nanocrystals and Effect of Temperature on Their Structural Transformations and Luminescent Properties, J. Phys. Chem. C, 2018, 122(40), 23242–23250 CrossRef CAS.
- R. A. Janjua, C. Gao, R. Dai, Z. Sui, M. A. Ahmad Raja, Z. Wang, X. Zhen and Z. Zhang, Na+-Driven Nucleation of NaYF4:Yb,Er Nanocrystals and Effect of Temperature on Their Structural Transformations and Luminescent Properties, J. Phys. Chem. C, 2018, 122(40), 23242–23250 CrossRef CAS.
- S. Jiang, M. J. F. Digonnet, X. Xue, T. Cheng, W. Gao, T. Suzuki and Y. Ohishi, Luminescent properties and phase transition in Er3+–Yb3+-co-doped NaYF4/SiO2 core–shell nanoparticles, in Optical Components and Materials XIV, 2017 Search PubMed.
- D. Yang, L. Liao, Y. Zhang, Q. Guo, L. Mei and H. Liu, Synthesis and up-conversion luminescence properties of a novel K3ScF6: Yb3+, Tm3+ material with cryolite structure, J. Lumin., 2020, 224 DOI:10.1016/j.jlumin.2020.117285.
- Y. Wu, Y. Ji, J. Xu, J. Liu, Z. Lin, Y. Zhao, Y. Sun, L. Xu and K. Chen, Crystalline phase and morphology controlling to enhance the up-conversion emission from NaYF4:Yb,Er nanocrystals, Acta Mater., 2017, 131, 373–379 CrossRef CAS.
- J. Wang, H. Song, W. Xu, B. Dong, S. Xu, B. Chen, W. Yu and S. Zhang, Phase transition, size control and color tuning of NaREF4:Yb3+, Er3+ (RE = Y, Lu) nanocrystals, Nanoscale, 2013, 5(8), 3412–3420 RSC.
- D. Zhang, M. Cai, Y. Zhang, D. Zhang and L. Duan, Sterically shielded blue thermally activated delayed fluorescence emitters with improved efficiency and stability, Mater. Horiz., 2016, 3(2), 145–151 RSC.
- Y. Zhu, C. Li, D. Deng, B. Chen, H. Yu, H. Li, L. Wang, C. Shen, X. Jing and S. Xu, A high-sensitivity dual-mode optical thermometry based on one-step synthesis of Mn2+:BaAl12O19–Mn4+:SrAl12O19 solid solution phosphors, J. Alloys Compd., 2021, 853, 157262 CrossRef CAS.
- S. Cao, C. C. Dai, J. L. Zhao and B. S. Zou, Synthesis of dual-emission Ag- and Mn-codoped Zn–In–S nanocrystals and their optical radiometric temperature sensors, J. Nanopart. Res., 2019, 21(11), 8 CrossRef.
- P. Shuai, D. Yang, L. Liao, Q. Guo, L. Mei, Y. Zhang and H. Liu, Preparation, structure and up-conversion luminescence properties of novel cryolite K3YF6:Er3+, Yb3+, RSC Adv., 2020, 10(3), 1658–1665 RSC.
- D. Yang, Q. Guo, L. Liao, Y. Zhang, L. Mei and H. Liu, Crystal structure and up-conversion luminescence properties of K3ScF6:Er3+,Yb3+ cryolite, J. Alloys Compd., 2020, 848, 156336 CrossRef CAS.
- L. Chantelle, A. L. M. de Oliveira, B. J. Kennedy, J. Maul, M. R. S. da Silva, T. M. Duarte, A. R. Albuquerque, J. R. Sambrano, R. Landers, M. Siu-Li, E. Longo and I. M. G. dos Santos, Probing the Site-Selective Doping in SrSnO3:Eu Oxides and Its Impact on the Crystal and Electronic Structures Using Synchrotron Radiation and DFT Simulations, Inorg. Chem., 2020, 59(11), 7666–7680 CrossRef CAS PubMed.
- K. Ueda, S. Tanaka, T. Yoshino, Y. Shimizu and T. Honma, Site-Selective Doping and Site-Sensitive Photoluminescence of Eu3+ and Tb3+ in Perovskite-Type LaLuO3, Inorg. Chem., 2019, 58(16), 10890–10897 CrossRef CAS PubMed.
- X. X. Sheng, P. P. Dai, Z. Y. Sun and D. W. Wen, Site-selective occupation of Eu2+ activators toward full-visible-spectrum emission in well-designed borophosphate phosphors, Chem. Eng. J., 2020, 395, 10 CrossRef.
- H. Ming, S. F. Liu, L. L. Liu, J. Q. Peng, J. X. Fu, F. Du and X. Y. Ye, Highly Regular, Uniform K3ScF6:Mn4+ Phosphors: Facile Synthesis, Microstructures, Photoluminescence Properties, and Application in Light-Emitting Diode Devices, ACS Appl. Mater. Interfaces, 2018, 10(23), 19783–19795 CrossRef CAS PubMed.
- P. A. Loiko, N. M. Khaidukov, J. Mendez-Ramos, E. V. Vilejshikova, N. A. Skoptsov and K. V. Yumashev, Stokes and anti-Stokes luminescence from cubic elpasolite Cs2NaYF6 crystals doped with Er3+ and Yb3+ ions, J. Lumin., 2016, 175, 260–266 CrossRef CAS.
- Y. Chen, X. Y. Liu, J. W. Xu, T. Yang, Z. C. Li and G. H. Chen, Yb3+/Tb3+/Ho3+: phosphate nanophase embedded glass ceramics: enhanced upconversion emission and temperature sensing behavior, J. Mater. Sci.: Mater. Electron., 2019, 30(1), 778–785 CrossRef CAS.
- K. Li and R. Van Deun, Site-Bi3+ and Eu3+ dual emissions in color-tunable Ca2Y8(SiO4)6O2:Bi3+, Eu3+ phosphors prepared via sol–gel synthesis for potentially ratiometric temperature sensing, J. Alloys Compd., 2019, 787, 86–95 CrossRef CAS.
- Y. J. Wang, V. Tsiumra, Q. Peng, H. B. Liang, Y. Zhydachevskyy, M. Chaika, P. Dluzewski, H. Przybylinska and A. Suchocki, Hole Trapping Process and Highly Sensitive Ratiometric Thermometry over a Wide Temperature Range in Pr3+-Doped Na2La2Ti3O10 Layered Perovskite Microcrystals (vol. 123, pg 4021, 2019), J. Phys. Chem. A, 2019, 123(23), 5012 CrossRef CAS PubMed.
- M. Sekulic, Z. Ristic, B. Milicevic, Z. Antic, V. Dordevic and M. D. Dramicanin, Li1.8Na0.2TiO3:Mn4+: the highly sensitive probe for the low-temperature lifetime-based luminescence thermometry, Opt. Commun., 2019, 452, 342–346 CrossRef CAS.
- P. Du, L. H. Luo, H. K. Park and J. S. Yu, Citric-assisted sol–gel based Er3+/Yb3+-codoped Na0.5Gd0.5MoO4: a novel highly-efficient infrared-to-visible upconversion material for optical temperature sensors and optical heaters, Chem. Eng. J., 2016, 306, 840–848 CrossRef CAS.
- S. Sinha, M. K. Mahata, K. Kumar, S. P. Tiwari and V. K. Rai, Dualistic temperature sensing in Er3+/Yb3+ doped CaMoO4 upconversion phosphor, Spectrochim. Acta, Part A, 2017, 173, 369–375 CrossRef CAS PubMed.
- D. He, C. F. Guo, S. Jiang, N. M. Zhang, C. K. Duan, M. Yin and T. Li, Optical temperature sensing properties of Yb3+–Er3+ co-doped NaLnTiO4 (Ln = Gd, Y) up-conversion phosphors, RSC Adv., 2015, 5(2), 1385–1390 RSC.
- P. Du and J. S. Yu, Effect of molybdenum on upconversion emission and temperature sensing properties in Na0.5Bi0.5TiO3:Er/Yb ceramics, Ceram. Int., 2015, 41(5), 6710–6714 CrossRef CAS.
- Y. M. Yang, C. Mi, F. Yu, X. Y. Su, C. F. Guo, G. Li, J. Zhang, L. L. Liu, Y. Z. Liu and X. D. Li, Optical thermometry based on the upconversion fluorescence from Yb3+/Er3+ codoped La2O2S phosphor, Ceram. Int., 2014, 40(7), 9875–9880 CrossRef CAS.
- L. Li, C. Guo, S. Jiang, D. K. Agrawal and T. Li, Green up-conversion luminescence of Yb3+–Er3+ co-doped CaLa2ZnO5 for optically temperature sensing, RSC Adv., 2014, 4(13), 6391–6396 RSC.
- H. Y. Yao, H. L. Shen, Q. T. Tang, C. Feng and Y. F. Li, Effect of Li co-doping with Er on up-conversion luminescence property and its temperature dependence of NaY(WO4)2, J. Phys. Chem. Solids, 2019, 126, 189–195 CrossRef CAS.
- B. Tian, B. Chen, Y. Tian, X. Li, J. Zhang, J. Sun, S. Fu, H. Zhong, X. Zhang, H. Yu and R. Hua, Intense red upconversion emission and temperature sensing in Er3+/Yb3+ co-doped Ba5Gd8Zn4O21 phosphor, Mater. Express, 2013, 3(3), 241–246 CrossRef CAS.
- Z. Y. Zhang, C. F. Guo, H. Suo, X. Q. Zhao, N. M. Zhang and T. Li, Thermometry and up-conversion luminescence of Yb3+–Er3+ co-doped Na2Ln2Ti3O10 (Ln = Gd, La) phosphors, Phys. Chem. Chem. Phys., 2016, 18(28), 18828–18834 RSC.
- M. K. Mahata, K. Kumar and V. K. Rai, Er3+–Yb3+ doped vanadate nanocrystals: a highly sensitive thermographic phosphor and its optical nanoheater behavior, Sens. Actuators, B, 2015, 209, 775–780 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |