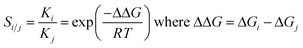Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
B12X11(H2)−: exploring the limits of isotopologue selectivity of hydrogen adsorption†
Toshiki Wulf *ab,
Jonas Warneke
*ab,
Jonas Warneke ac and
Thomas Heine
ac and
Thomas Heine *bd
*bd
aWilhelm Ostwald Institute of Physical and Theoretical Chemistry, Leipzig University, Linnéstr. 2, 04103 Leipzig, Germany. E-mail: toshiki.wulf@uni-leipzig.de
bInstitute of Resource Ecology, Research Site Leipzig, Helmholtz-Zentrum Dresden-Rossendorf, Permoserstr. 15, 04318 Leipzig, Germany. E-mail: thomas.heine@tu-dresden.de
cLeibniz Institute of Surface Engineering (IOM), Permoserstr. 15, 04318 Leipzig, Germany
dFaculty of Chemistry and Food Chemistry, School of Science, TU Dresden, 01062 Dresden, Germany
First published on 16th September 2021
Abstract
We study the isotopologue-selective binding of dihydrogen at the undercoordinated boron site of B12X11− (X = H, F, Cl, Br, I, CN) using ab initio quantum chemistry. With a Gibbs free energy of H2 attachment reaching up to 80 kJ mol−1 (ΔG at 300 K for X = CN), these sites are even more attractive than most undercoordinated metal centers studied so far. We thus believe that they can serve as an edge case close to the upper limit of isotopologue-selective H2 adsorption sites. Differences of the zero-point energy of attachment average 5.0 kJ mol−1 between D2 and H2 and 2.7 kJ mol−1 between HD and H2, resulting in hypothetical isotopologue selectivities as high as 2.0 and 1.5, respectively, even at 300 K. Interestingly, even though attachment energies vary substantially according to the chemical nature of X, isotopologue selectivities remain very similar. We find that the H–H activation is so strong that it likely results in the instantaneous heterolytic dissociation of H2 in all cases (except, possibly, for X = H), highlighting the extremely electrophilic nature of B12X11− despite its negative charge. Unfortunately, this high reactivity also makes B12X11− unsuitable for practical application in the field of dihydrogen isotopologue separation. Thus, this example stresses the two-edged nature of strong H2 affinity, yielding a higher isotopologue selectivity on the one hand but risking dissociation on the other, and helps define a window of adsorption energies into which a material for selective adsorption near room temperature should ideally fall.
Introduction
As the element with the lowest mass, hydrogen has the most pronounced isotope effect of all elements. This leads to numerous applications of heavy hydrogen isotopes, deuterium (2H = D) and tritium (3H = T): in spectroscopy; structural analysis and the elucidation of reaction mechanisms, especially in biochemistry and pharmaceutical research;1,2 and – more recently – even in pharmaceuticals,3,4 where an effort is ongoing to exploit the slower rate of reaction of deuterated compounds to delay or alter metabolic pathways in order to increase potency and/or reduce side effects.The continuous need for heavy hydrogen for energy production, science and medicine has motivated a revision of state-of-the-art separation processes5 by employing nanostructured materials. In a relatively recent approach, penetration and tunneling through two-dimensional materials such as graphene or hexagonal boron nitride are used to separate hydrogen isotopes.6,7 Other separation techniques involve kinetic sieving in the interstitial space of layered materials8 or in apertures in metal–organic frameworks (MOFs),9 or isotopologue-selective adsorption (chemical affinity quantum sieving, CAQS)10 at strong metal sites in MOFs11–13 and zeolites.14,15
CAQS relies on the different zero-point energies of the H2 isotopologues, which approximately correlate with the square root of the mass of the isotopologue. This leads to a stronger adsorption of the heavier isotopes and results in higher selectivities when the zero-point energy of adsorption is higher. The adsorption energy itself also positively correlates with the selectivity (albeit more loosely), because a higher adsorption energy leads to a steeper potential energy surface, which in turn increases the zero-point energy. (Although the stretching of the H–H bond decreases the frequency of the corresponding vibrational mode and thereby the zero-point energy, this effect is overcompensated by the contributions from other modes.16,17).
Recent progress has been made to enable CAQS significantly above the boiling temperature of liquid nitrogen. For example, Cu(I)-MFU-4l with an H2 adsorption enthalpy on the order of 30–35 kJ mol−1 and a zero-point energy difference of 2.5–3.0 kJ mol−1 between D2 and H2 reaches a D2/H2 selectivity of 10 at 100 K. However, since both selectivity and uptake decline with increasing temperature, operating temperatures must remain well below 200 K.12 Nevertheless, these experiments raised hopes that an appreciable selectivity at or near room temperature could be achieved if materials or adsorption sites with higher adsorption energies could be found. With this publication, we want to make a contribution towards the search of such materials.
B12X11− is a fascinating ion. Derived from the highly stable18–20 dianion B12X122− by abstraction of X−, its reactivity is driven by the strong preference for a double negative charge.21,22 Despite its negative charge, the monoanion is therefore highly electron-deficient. The partial positive charge at the undercoordinated boron atom would be expected to lead to strong H2 attraction in a way similar to undercoordinated metal cations.17 The significant interaction between the undercoordinated boron site and noble gas atoms reported by experiment and theory21–24 suggests that this system will also strongly bind dihydrogen, and that gas-phase experiments addressing this interaction should be feasible. A particularly attractive feature of these systems is the prospect of modifying the substituents X in order to form a cavity that sterically confines the bound dihydrogen to further increase isotopologue selectivity. For these reasons, we consider B12X11− a suitable model system to study the limits of isotopologue-selective H2 adsorption.
In this article, we computationally study H2 attachment at B12X11− (X = H, F, Cl, Br, I, CN). Using ab initio methods, we calculate thermodynamic parameters of the attachment reaction, analyze the influence of X on these parameters and of the different vibrational modes on the isotopologue selectivity. Furthermore, we investigate entropy effects, calculate isotopologue selectivities of the hypothetical adsorption of molecular H2 and examine potential dissociation pathways for H2 bound at B12X11−. Therefore, the present study highlights a wide range of aspects that are useful for the rational design of materials for dihydrogen isotopologue separation, including some rather surprising findings on the relation of attachment energy and selectivity, parameters that can be adjusted to enhance selectivity, and obstacles such as dihydrogen dissociation.
Methods
B12X11− (with X = H, F, Cl, Br, I and CN) and their H2 adducts have been optimized with hybrid density functional theory using the PBE0 (ref. 25) functional. Dispersion interactions have been accounted for with Grimme's D3 approach and Becke–Johnson damping, commonly referred to as D3(BJ).26 Equilibrium structures, their energies and Hirshfeld charges have been obtained using geometry optimization employing Ahlrich's def2-QZVP split-valence quadruple-zeta basis set.27 Potential energy surface scans have been performed using the smaller def2-TZVP basis set from the same series. For all DFT calculations we have made use of the resolution-of-identity and chain-of-spheres approximations, RIJCOSX,28 in conjunction with the def2/J29 auxiliary basis.Thermal and zero-point energy contributions to enthalpies and entropies have been calculated at the above-mentioned DFT level using numerical harmonic vibrational frequency analysis. Standard increments of 0.005 Bohr have been used except for B12H11(H2)− and B12F11(H2)− where this led to imaginary frequencies; 0.002 and 0.001 Bohr, respectively, have been used in those cases to ensure consistent treatment in thermodynamic calculations by ORCA. The Gibbs free energy has been calculated using the quasi-rigid-rotor-harmonic-oscillator (QRRHO) approximation30 as implemented in ORCA. This approximation treats the entropy (but not internal energy) contributions of low-frequency vibrational modes as free internal rotations by default. In line with such treatment, the zero-point and thermal vibrational contributions of the internal rotation to the internal energy have been subtracted from the value calculated by ORCA and ½RT has been added instead. Finally, entropy contributions have been corrected for an external symmetry number of 5 for B12X11− and an internal symmetry number for B12X11(H2)−: 10 for homoisotopic cases and 5 for heteroisotopic ones.31 For the B12X11(H2)− species, the Gibbs energies have been calculated for both symmetrical orientations of H2 with respect to B12X11− and the average has been used subsequently.
The hypothetical separation factors between two isotopologues of H2 (below referred to as i and j) have been calculated from the Gibbs energies of attachment of H2 (for the reaction leading to the local minima with undissociated H2) via the respective equilibrium constants:
Correlated single-point calculations have been performed using the DLPNO-CCSD(T)32,33 method as implemented in ORCA in conjunction with the def2-QZVPP and def2-QZVPP/C34 basis sets based on a Hartree–Fock calculation with VeryTightSCF settings. SCF convergence issues, which arose in some cases, have been cured using the SlowConv setting and employing the SOSCF algorithm late in the SCF procedure (SOSCFStart 0.0001). For X = H, NormalPNO and TightPNO35 settings have been compared and found to give almost identical results; NormalPNO has therefore been used throughout. Similarly, def2-TZVPP, def2-QZVPP, aug-cc-pVTZ and aug-cc-pVQZ basis sets have been found to yield very similar reaction energies for X = H, which has been taken as justification for using def2-QZVPP results without further refinement or correction for basis set effects.
Calculations employed ORCA36 version 4.2.1, except for energy decomposition analysis (EDA). The latter calculations have been performed with the Amsterdam Density Functional (ADF) program from the Amsterdam Modeling Suite (AMS), version 2019.104 (r76620),37,38 performing single-point calculations at the PBE0-D3(BJ) level in conjunction with scalar ZORA39 for relativistic effects and the TZ2P40 basis set with native Slater-type orbitals.
Results and discussion
Structure of B12X11− and B12X11(H2)−
The structure of B12X11− (X = F, Cl, Br, I, CN) with and without attached noble gas atoms has been computationally investigated several times21–23 and discussed in detail recently:24 Compared to B12X122−, the undercoordinated boron atom (B0) in B12X11− moves toward the center of the cluster. Meanwhile, the substituents X of the surrounding boron atoms slightly bend towards B0, thereby decreasing the angle α(X–Ctr–B0) between X, the center of the cluster (Ctr) and B0 from 63.4° to 60.5°. Upon binding of noble gas atoms, this angle remains practically unchanged.Given the similar size of He, Ne and H2, one might expect B12X11(H2)− to behave similarly to B12X11He− and B12X11Ne−. However, the latter two complexes show distinct differences in their B0–noble gas bond length. Moreover, H2 has a much higher HOMO, lower LUMO and is more polarizable. Therefore, it should bind much more strongly to B12X11−. This expectation is reflected in the B0–H2 distances, which are much shorter than those of B0–He despite similar sizes.
The structure of B12X11(H2)− is shown in Fig. 1. For all X investigated, the H–H bond is elongated by more than 9 pm, that is at least 3 pm more than for H2 coordinated at (C4H8O2)Cu+ (C4H8O2 = 1,4-dioxane; calculated value from ref. 17). A comparison of the geometric parameters, which are listed in Table 1, reveals that X = F is an outlier with a much longer H–H bond length and a shorter B0–H2 distance, which has consequences for the thermodynamic properties and isotopologue selectivity as discussed below.
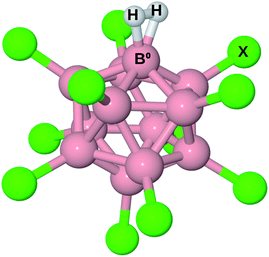 | ||
| Fig. 1 Illustration of B12X11− with H2 attached. B0 is the boron atom which is undercoordinated in B12X11− and to which H2 is bound in B12X11(H2)−. | ||
| X | r(H–H) | R(B0–H2) |
|---|---|---|
| (Free H2) | 74.4 | |
| H | 85.0 | 125.7 |
| F | 91.0 | 119.6 |
| Cl | 85.2 | 125.2 |
| Br | 84.5 | 126.4 |
| I | 84.1 | 127.6 |
| CN | 84.2 | 127.3 |
Analysis of the dihydrogen–B12X11− interaction
Attachment energies for H2 coordinating side-on at B12X11− are shown in Table 2 and have, with the exception of X = H, a magnitude of ≈100 kJ mol−1, which is much stronger than for most interactions of H2 with undercoordinated metal sites.11,12 As would be expected from the significantly elongated H–H bonds, the title compounds are predicted to strongly attract H2. However, the order CN ≈ F > Cl ≳ Br > I ≫ H from strongest to weakest interaction differs from what would be expected from the bond lengths (Table 1). This surprising lack of correlation, which is shown in Fig. 2a, is contrary to systems where undercoordinated metal sites serve as attractors and where bond length and binding energy are evidently correlated.| X = | ΔadU (H2) | ΔadU (D2) | ΔΔE0 | ΔadG (H2) | ΔadG (D2) | ΔΔG | S (D2/H2) |
|---|---|---|---|---|---|---|---|
| H | −36.6 | −41.5 | −4.9 | −9.1 | −10.8 | −1.72 | 1.99 |
| F | −110.0 | −114.6 | −4.6 | −81.3 | −82.6 | −1.31 | 1.69 |
| Cl | −101.4 | −106.6 | −5.2 | −72.5 | −74.3 | −1.81 | 2.06 |
| Br | −98.5 | −103.6 | −5.2 | −70.1 | −71.9 | −1.77 | 2.04 |
| I | −90.4 | −95.4 | −5.1 | −62.0 | −63.7 | −1.67 | 1.96 |
| CN | −108.5 | −113.9 | −5.3 | −80.0 | −81.8 | −1.87 | 2.12 |
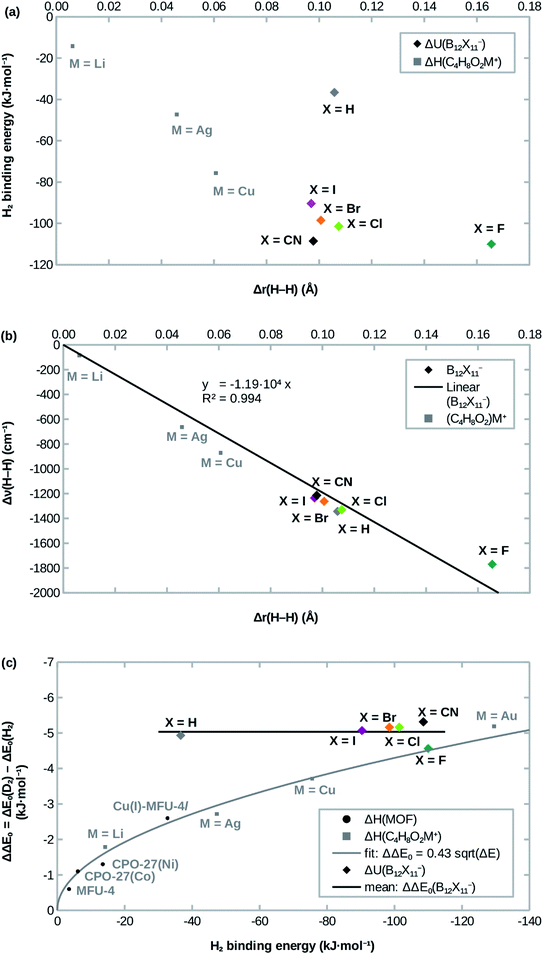 | ||
| Fig. 2 Correlation of (a) the H2 attachment energy and (b) the red-shift of H–H stretch frequency Δν(H–H) with the H–H bond length elongation Δr(H–H) w.r.t. free H2 in B12X11− and dioxane complexes. (c): Comparison of H2 attachment energies and differences of zero-point energies of attachment ΔΔE0 between D2 and H2. Experimental values for MOFs are from ref. 12,13,41, calculated values for dioxane complexes (C4H8O2M+) are from ref. 17. | ||
Interestingly, the H–H bond is much more elongated for X = F compared to other X, despite a binding energy which is only slightly higher. Conversely, X = H shows a substantially lower binding energy (36 kJ mol −1 vs. > 90 kJ mol −1) despite geometric parameters which are very similar to X = Cl. Furthermore, X = CN, which has the second-highest H2 binding energy after X = F, lies in between the least strongly binding halogens X = Br and X = I in terms of the H–H bond length. Only for X = Cl, Br, I does the binding energy follow the trend expected from the DFT-predicted bond lengths, that is: among the three, B12Cl11(H2)− has the highest binding energy, the shortest B0–H2 distance and the most elongated H–H bond, followed by B12Br11(H2)− with B12I11(H2)− being last.
If the interaction between H2 and all investigated B12X11− was mainly driven by σ bonding (from H2 to B0), one would expect a strong correlation between the charge at B0 and the H2 attachment energy. At least for Cl, Br and I, a reasonable correlation between attachment energy and Hirshfeld charge at B0 is found (see ESI; Fig. S1†). However, the correlation is poor for other X and different charge trends are obtained when using orbital-based charges such as NPA charges (Fig. S2†). Furthermore, this does not explain the significant elongation of the H–H bond for X = F.
Since these unintuitive findings warrant a deeper investigation of the underlying binding properties, we have performed energy decomposition analysis (EDA) of the Gibbs energy of the attachment reaction of H2 at B12X11−. Results are shown in Table 3: With one exception (ΔEdef of B12X11−, for discussion see below), the contributions of dispersion interaction and geometry deformation of the reactants as well as zero-point and thermal contributions are very similar.
| X = | ΔEPauli | ΔEelstat | ΔEoi | ΔEdisp | ΔEdef (B12X11−) | ΔEdef (H2) | ΔEel | ΔE0 | ΔEtherm | ΔG |
|---|---|---|---|---|---|---|---|---|---|---|
| CN | 400 | −166 | −402 | −10 | 13 | 19 | −146 | 22 | 29 | −95 |
| Cl | 435 | −185 | −405 | −10 | 16 | 16 | −134 | 22 | 29 | −84 |
| Br | 444 | −185 | −406 | −11 | 14 | 14 | −130 | 21 | 28 | −81 |
| I | 476 | −192 | −420 | −13 | 13 | 13 | −122 | 21 | 28 | −73 |
| H | 490 | −205 | −385 | −7 | 15 | 19 | −72 | 21 | 27 | −23 |
| F | 480 | −213 | −462 | −7 | 34 | 18 | −150 | 23 | 29 | −99 |
The greatest variability is afforded by the Pauli repulsion term, which results from the antisymmetry requirement of the wave function and closely matches the intuitive understanding of steric repulsion. For CN, Cl, Br and I, Pauli repulsion is the dominating contributor to the overall trend in the reaction Gibbs energies. It is partly compensated by the electrostatic interaction, which may sound surprising at first, but is justified given the well-known fact42 that molecules attract each other more strongly the more diffuse their charge clouds are.
EDA shows two main reasons for the B12X11−–H2 interaction being weakest for X = H. One is the weaker orbital interaction. The other is the stronger Pauli repulsion, which is caused by the larger electron density at B0 due to the less electron-withdrawing nature of X = H (see also ESI; Fig. S3†).
Finally, the case of X = F is characterized by a substantially stronger orbital interaction with H2. This is unlike what has been observed for the attraction of noble gas atoms, which is weakest for X = F. This striking difference is in line with results from a recent publication,43 which compared the binding of noble gases, N2 and CO at B12X11−. It was found that X = F shows the weakest binding of noble gas atoms but the strongest binding of N2 and CO due to π-like backbonding from B0 into the antibonding σ* orbitals of the attached molecule (something which is not possible for noble gases). This binding of N2 and CO for X = F is unlike the strong binding for X = CN, which is based almost solely on strong σ bonding, a binding mode which is much weaker for X = F. We expect similar behavior for the binding of H2, i.e. strong σ bonding and weak backbonding with modest H–H elongation for X = CN (and to a lesser degree Cl, Br, I) and weaker σ bonding but strong backbonding for X = F. The stronger backbonding would also explain the much greater elongation of the H–H bond for X = F.
Very similar zero-point energies of attachment
Previous studies of undercoordinated metal sites show a substantial (albeit sublinear) increase of the adsorption zero-point energy with the adsorption energy in paddlewheel MOFs16 and zeolites17 (see also Fig. 2c). By contrast, all B12X11− investigated here have very similar zero-point energies of attachment, which are almost independent of X (see Fig. 2c).In the case of X ≠ H, this could be interpreted as entering a region of saturation where an increase in the attachment energy yields smaller and smaller gains in the selectivity. However, this does not explain the case of X = H, where a lower zero-point energy of attachment would have been expected.
An explanation is given by the ZPE contributions of the different vibrational modes (see below for a detailed discussion). The greatest ZPE variability is afforded by the asymmetrical B0–H stretch mode, which works in favor of the overall selectivity. However, most of this contribution is compensated by the weakening of the H–H bond with an opposite contribution (see Fig. 3b).
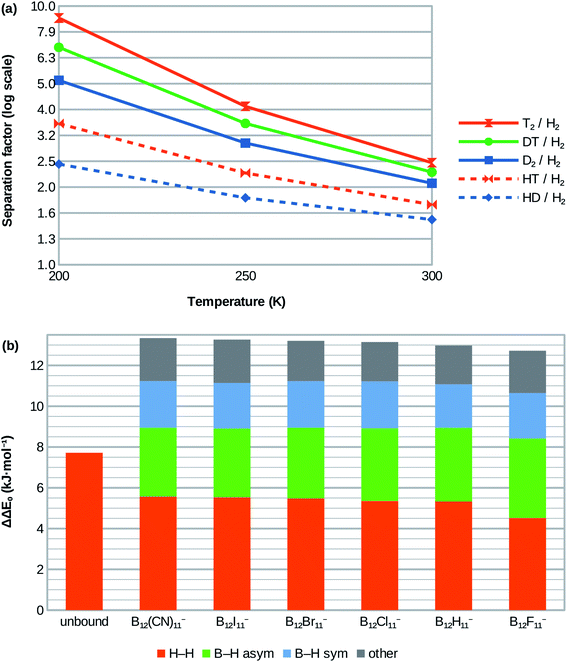 | ||
| Fig. 3 (a) Calculated isotopologue selectivities for the H2 attachment at B12X11− using X = Cl as example. Very similar selectivities are obtained for X = H, Br, I, CN and lower ones for X = F (see ESI; Table S1†). (b) Contribution of vibrational modes to zero-point energy difference between D2 and H2 isotopologues for free (unbound) dihydrogen in the gas phase (left bar) and when coordinated at the various B12X11−. | ||
Vibrational modes in detail
When discussing the vibrational modes of B12X11−, the internal rotation (φ in previous publications12,17) of H2 about the B0–H2 axis is of some interest. The combination of five-fold symmetry of B12X11− and two-fold symmetry of H2 results in a ten-fold internal rotational symmetry (36° period) about the B0–H2 axis31 for homoisotopic H2 (five-fold internal rotational symmetry for heteroisotopic H2). The high symmetry leads to an exceptionally flat potential energy surface for this mode, which is confirmed by a scan of the potential energy surface using DFT: the obtained differences between highest and lowest energy are below 0.02 kJ mol−1 in all cases, which is indistinguishable from numerical noise (see NEB paths for the internal rotation in the ESI†). A comparison of the vibrational behavior of B12X11(H2)− for φ = 0° and φ = 90° (equivalent to φ = 18°) shows almost identical results for the frequencies of the other modes (differences of less than 5 cm−1). These small differences suggest that the coupling between the quasi-free rotational mode along φ and the remaining vibrational modes is negligible. This allows for treatment of the other modes independent of φ and thereby greatly simplifies the calculation of the ZPE and of the thermal contributions to the Gibbs energies.H2 coordinated at B12X11− exhibits a vibrational behavior that qualitatively matches that observed in previous studies of highly attractive metal centers.12,16 The highest-frequency mode is the H–H stretch vibration (νHH along r), which is strongly red-shifted with respect to the free molecule. It is followed by the asymmetrical B0–H stretch vibration (νBH,asym, which in the case of weaker interaction would have been denoted as rotation of H2 in the B0–H2 plane along the angle ϑ) and the (symmetrical) stretch vibration of the B0–H2 bond (νBH,sym along R).
As shown in Fig. 2b, the frequency shift of the H–H stretch vibration correlates almost linearly with the H–H distance, not only for different B12X11−, but also when expanding the dataset using data from different (C4H8O2)M+ calculated in ref. 17. Near-linearity holds true even across different classes of compounds and breaks down only at extreme elongations (H2 at B12F11− and C4H8O2Au+; the latter is not shown in Fig. 2b because of the extreme values of Δr = 100 pm and Δν = 3722 cm−1). These cases, where the H–H stretch frequency approaches zero and the H–H distance goes to infinity, however, are still very well described by Badger's rule,44 which implies ν ∝ r−3/2 for H2.
Likewise, it could be expected that the frequencies of the B0–H stretching modes correlate with the B0–H2 distance. This is indeed the case for νBH,asym, but surprisingly not for νBH,sym.
The two remaining degrees of freedom, which can be interpreted as the hindered translations of H2 perpendicular to the B0–H2 axis, are expected to correlate more with the degree of steric hindrance than with the attractiveness of the undercoordinated site itself. Unfortunately, the substituents X are too far away from the H2 binding site to exert any significant influence leading to little variation in the frequencies of these modes.
Zero-point energies of attachment, entropies and high predicted D2/H2 selectivities
Although H2 attachment energies at B12X11− vary widely with X, the differences between the Gibbs energies of attachment of H2 and D2 for a given X and therefore the selectivities are in a very narrow range (with X = F being a slight outlier). This may be surprising at the face of it, but is in line with the very similar zero-point energies of attachment of all species.The entropy of H2 attachment is negative because the translational and rotational entropies of the free H2 are higher than the vibrational entropy of the bound H2, an effect which is more pronounced the higher the temperature. This fight against entropy is one of the key obstacles towards adsorptive H2 isotopologue sieving at high temperatures. Therefore, the high predicted D2/H2 selectivity – which is approximately 2.0 at 300 K for X = H, Cl, Br, I, CN – is truly remarkable. Selectivities of about 2.9 and 5.1 are predicted for 250 K and 200 K, respectively. Note, that the selectivities at 250 K and 200 K are much higher than would be expected based on the room temperature value if only the direct influence of temperature T on the separation factor via α = exp(-ΔΔG/RT) was considered. This is because most of the selectivity loss at higher temperatures is due to the above-mentioned entropy effects, which result in lower absolute values of ΔΔG as temperature increases and therefore lower selectivities.
HD/H2 selectivities are predicted to be about 1.4 at 300 K, 1.8 at 250 K and 2.4 at 200 K. Even at 200 K, T2/D2 and DT/D2 selectivities are much lower at around 1.7 and 1.3, respectively. More information is given in Fig. 3a and in the ESI (Table S1†).
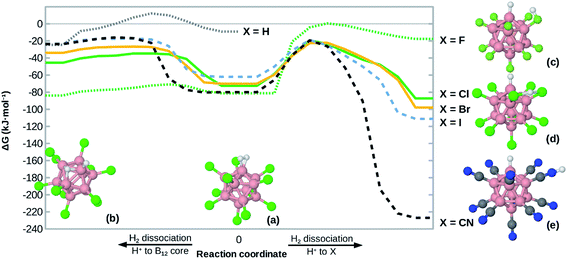
Heterolytic dissociation of H2 at B12X11(H2)−
Given the high H2 binding energies, one might expect that the title compounds show a substantial propensity towards dissociation of coordinated H2. Indeed, we found local minimum structures with a negatively polarized H− at B0 and a positively polarized H+. As shown in Fig. 4, that H+ can coordinate at one X (for X = F, CN), between two X (for X = Cl, Br, I) or directly at the boron core (preferred only for X = H, F), behavior which is in line with observations on B12X12H− (X = F, Cl, Br, I)45 and B12X11RH− (R = alkyl group).46The dissociation behavior of H2 at B12X11− is, however, unlike what has been observed in the case of undercoordinated metal sites. In a previous publication we have predicted particularly strong H2 interaction at zeolitic Au+ sites17 and observed strong elongation of the H–H bond to the point of dissociation using local coupled-cluster calculations. However, dissociation was homolytic in that case and attempts to create structures with H+/H− polarization failed (geometry optimization reverted to structures with equivalent H atoms). This shows the uniquely strong ability of B12X11− to polarize H2 and stabilize a H− ion at the B0 site.
For H2 bound at B12X11−, the activation energy for heterolytic dissociation is below (or only slightly above in the case of X = H) the H2 attachment energy, which means that an incoming H2 would have enough energy to overcome the barrier and dissociate. We therefore expect that B12X11(H2)− (X = F, Cl, Br, I, CN) will not be observed in experiment and a technological application requiring multiple adsorption cycles is not realistic. As indicated by its potential energy surface, B12H11(H2)− may be somewhat metastable against dissociation and it could therefore be interesting to study the dynamic behavior of this ion at low temperatures. Harmonic values of characteristic vibrational frequencies are given in the ESI (Table S2†).
Compared to other X, the potential energy surface for X = F is much flatter towards H2 dissociation and the formation of the structure shown in Fig. 4(b), which is in line with the much longer H–H bond length in this case.
It is interesting to note that the heterolytic dissociation of heteronuclear H2 isotopologues (i.e. HD, HT and DT) shows a preference for the heavier nucleus to occupy the position where the vibrational frequency of the corresponding stretch frequency is higher, thereby minimizing the overall zero-point energy. Especially for B12X11HD− with X = Cl, Br and I, this results in a pronounced preference for D to occupy the H− position (coordinated at B0 as D−) and for H to take the H+ position between two X as the latter is characterized by a very shallow potential energy surface. Equilibrium constants are given in Table S3.†
Related species
Preliminary calculations on related species (B12X112−, B12X102− and B12X10−) showed a similar propensity towards dissociative binding of H2, albeit with even lower dissociation barriers. Given the added computational expense of treating radical systems and/or multiple isomers, they have not been studied in detail.For the octahedral B6X5−, no local minimum structure with undissociated H2 has been found at all. Their smaller structures lead to smaller B–B–B angles, stronger pre-hybridization and therefore much stronger interaction.
Conclusion
We have investigated the interaction of B12X11− with H2 with a special focus on the different interaction strengths of H2 and D2. Internal energies of attachment are highest for X = CN and X = F (ΔU (1H2) = −110 kJ mol−1 at 0 K), decrease with increasing mass for the halogens (down to −90 kJ mol−1 for X = I) and are lowest for X = H (−36 kJ mol−1). Despite widely varying attachment energies, zero-point energy differences between D2 and H2 attachment are very similar at ≈5.0 kJ mol−1 (in contrast to results from other materials where a positive correlation between both parameters was typically found). Gibbs energies for different isotopologues are reported as well, corresponding to D2/H2 selectivities of ≈2.0 at 300 K.Unfortunately, the strong H2 activation leads to heterolytic dissociation with activation energies below the interaction energy; that is, H2 approaching the cluster has enough kinetic energy to overcome the activation barrier and form a compound with dissociated H2. This highlights the very high electrophilicity of B12X11− despite its negative charge, even exceeding that known from many strong H2-adsorbing metals like Au+ in zeolitic environments.
Although heterolytic dissociation likely precludes experimental investigation of B12X11(H2)− (with undissociated H2) and practical application for hydrogen isotopologue separation, the example is instructive as it shows the limits of increased adsorption energy with regards to enhancing isotopologue selectivity: not only do higher adsorption energies run the risk of leading to H2 dissociation, but there also seems to be a limit to the adsorption zero-point energy between H2 and D2 of around 5 kJ mol−1. However, already this 5 kJ mol−1 difference is very encouraging as it leads to predicted D2/H2 separation factors of 2.0 at 300 K and 3.0 at 250 K, figures that might be further enhanced by steric confinement and would even be high enough to enable HD/H2 separation if a suitable material could be found that does not lead to H2 dissociation.
Outlook
Since the smaller B6X5− show much stronger H2 affinity than B12X11−, we would expect higher closo-borates to bind H2 less strongly. Therefore, it could be interesting to investigate clusters like B16X15−, B32X31− and B42X41− (which derive from polyhedra dual to C28, C60 and C70, respectively).47,48 Unfortunately, the synthesis of higher closo-borates is faced with huge thermodynamic and kinetic obstacles.49 To the best of our knowledge, none of these compounds have been synthesized to date, leaving little prospect for eventual application.Nevertheless, we believe that the two known cases of Cu(I)-MFU-4l (adsorption enthalpy of ≈35 kJ mol−1 and appreciable selectivity around 200 K) and B12X11(H2)− (internal energy adsorption of ≈110 kJ mol−1 and appreciable selectivity at 300 K for X = CN, but dissociation and saturation of zero-point energy of adsorption) give us an estimate of the window of adsorption energies within which the search for materials enabling isotopologue-selective adsorption should be focused.
Author contributions
JW proposed to investigate the H2 affinity of B12(CN)11−. TW performed all calculations and prepared the first draft of the manuscript. The authors jointly discussed results and revised the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
TW thanks the European Social Fund for a PhD fellowship. JW is grateful to a Freigeist Fellowship of the Volkswagen foundation. We thank the Center for Information Services and High Performance Computing (ZIH) at TU Dresden for computational resources.References
- M. I. Blake, H. L. Crespi and J. J. Katz, Studies with deuterated drugs, J. Pharm. Sci., 1975, 64, 367–391 CrossRef CAS PubMed
.
- J. Atzrodt, V. Derdau, W. J. Kerr and M. Reid, Deuterium- and Tritium-Labelled Compounds: Applications in the Life Sciences, Angew. Chem., Int. Ed., 2018, 57, 1758–1784 CrossRef CAS PubMed
.
- T. Pirali, M. Serafini, S. Cargnin and A. A. Genazzani, Applications of Deuterium in Medicinal Chemistry, J. Med. Chem., 2019, 62, 5276–5297 CrossRef CAS PubMed
.
- J. F. Liu, S. L. Harbeson, C. L. Brummel, R. Tung, R. Silverman and D. Doller, in Platform Technologies in Drug Discovery and Validation, Elsevier, 2017, pp. 519–542 Search PubMed
.
- A. I. Miller, Heavy Water: A Manufacturers' Guide for the Hydrogen Century, Published in the Canadian Nuclear Society Bulletin, 2001, vol. 22 Search PubMed
.
- M. Lozada-Hidalgo, S. Hu, O. Marshall, A. Mishchenko, A. N. Grigorenko, R. A. W. Dryfe, B. Radha, I. V. Grigorieva and A. K. Geim, Sieving hydrogen isotopes through two-dimensional crystals, Science, 2016, 351, 68–70 CrossRef CAS PubMed
.
- Y. An, A. F. Oliveira, T. Brumme, A. Kuc and T. Heine, Stone-Wales Defects Cause High Proton Permeability and Isotope Selectivity of Single-Layer Graphene, Adv. Mater., 2020, 32, e2002442 CrossRef PubMed
.
- S. Hu, K. Gopinadhan, A. Rakowski, M. Neek-Amal, T. Heine, I. V. Grigorieva, S. J. Haigh, F. M. Peeters, A. K. Geim and M. Lozada-Hidalgo, Transport of hydrogen isotopes through interlayer spacing in van der Waals crystals, Nat. Nanotechnol., 2018, 13, 468–472 CrossRef CAS PubMed
.
- J. Teufel, H. Oh, M. Hirscher, M. Wahiduzzaman, L. Zhechkov, A. Kuc, T. Heine, D. Denysenko and D. Volkmer, MFU-4 – A Metal-Organic Framework for Highly Effective H2/D2 Separation, Adv. Mater., 2013, 25, 635–639 CrossRef CAS PubMed
.
- I. Savchenko, A. Mavrandonakis, T. Heine, H. Oh, J. Teufel and M. Hirscher, Hydrogen isotope separation in metal–organic frameworks: kinetic or chemical affinity quantum-sieving?, Microporous Mesoporous Mater., 2015, 216, 133–137 CrossRef CAS
.
- S. A. FitzGerald, C. J. Pierce, J. L. C. Rowsell, E. D. Bloch and J. A. Mason, Highly selective quantum sieving of D2 from H2 by a metal–organic framework as determined by gas manometry and infrared spectroscopy, J. Am. Chem. Soc., 2013, 135, 9458–9464 CrossRef CAS PubMed
.
- I. Weinrauch, I. Savchenko, D. Denysenko, S. M. Souliou, H.-H. Kim, M. Le Tacon, L. L. Daemen, Y. Cheng, A. Mavrandonakis, A. J. Ramirez-Cuesta, D. Volkmer, G. Schütz, M. Hirscher and T. Heine, Capture of heavy hydrogen isotopes in a metal–organic framework with active Cu(I) sites, Nat. Commun., 2017, 8, 14496 CrossRef CAS PubMed
.
- H. Oh, I. Savchenko, A. Mavrandonakis, T. Heine and M. Hirscher, Highly effective hydrogen isotope separation in nanoporous metal–organic frameworks with open metal sites: direct measurement and theoretical analysis, ACS Nano, 2014, 8, 761–770 CrossRef CAS PubMed
.
- R. Xiong, R. Balderas Xicohténcatl, L. Zhang, P. Li, Y. Yao, G. Sang, C. Chen, T. Tang, D. Luo and M. Hirscher, Thermodynamics, kinetics and selectivity of H2 and D2 on zeolite 5A below 77 K, Microporous Mesoporous Mater., 2018, 264, 22–27 CrossRef CAS
.
- R. Xiong, L. Zhang, P. Li, W. Luo, T. Tang, B. Ao, G. Sang, C. Chen, X. Yan, J. Chen and M. Hirscher, Highly effective hydrogen isotope separation through dihydrogen bond on Cu(I)-exchanged zeolites well above liquid nitrogen temperature, Chem. Eng. J., 2020, 391, 123485 CrossRef CAS
.
- T. Wulf and T. Heine, Toward separation of hydrogen isotopologues by exploiting zero-point energy difference at strongly attractive adsorption site models, Int. J. Quantum Chem., 2018, 118, e25545 CrossRef
.
- T. Wulf and T. Heine, Small Crown-Ether Complexes as Molecular Models for Dihydrogen Adsorption in Undercoordinated Extraframework Cations in Zeolites, J. Phys. Chem. C, 2020, 124, 9409–9415 CrossRef CAS
.
- J. Warneke, G.-L. Hou, E. Aprà, C. Jenne, Z. Yang, Z. Qin, K. Kowalski, X.-B. Wang and S. S. Xantheas, Electronic Structure and Stability of B12X122− (X = F-At): A Combined Photoelectron Spectroscopic and Theoretical Study, J. Am. Chem. Soc., 2017, 139, 14749–14756 CrossRef CAS PubMed
.
- E. Aprà, J. Warneke, S. S. Xantheas and X.-B. Wang, A benchmark photoelectron spectroscopic and theoretical study of the electronic stability of B12H122, J. Chem. Phys., 2019, 150, 164306 CrossRef PubMed
.
- V. Geis, K. Guttsche, C. Knapp, H. Scherer and R. Uzun, Synthesis and characterization of synthetically useful salts of the weakly-coordinating dianion B12Cl122−, Dalton Trans., 2009, 2687–2694 RSC
.
- M. Mayer, V. van Lessen, M. Rohdenburg, G.-L. Hou, Z. Yang, R. M. Exner, E. Aprà, V. A. Azov, S. Grabowsky, S. S. Xantheas, K. R. Asmis, X.-B. Wang, C. Jenne and J. Warneke, Rational design of an argon-binding superelectrophilic anion, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 8167–8172 CrossRef CAS PubMed
.
- M. Rohdenburg, M. Mayer, M. Grellmann, C. Jenne, T. Borrmann, F. Kleemiss, V. A. Azov, K. R. Asmis, S. Grabowsky and J. Warneke, Superelectrophilic Behavior of an Anion Demonstrated by the Spontaneous Binding of Noble Gases to B12Cl11, Angew. Chem., Int. Ed., 2017, 56, 7980–7985 CrossRef CAS PubMed
.
- M. Mayer, M. Rohdenburg, V. van Lessen, M. C. Nierstenhöfer, E. Aprà, S. Grabowsky, K. R. Asmis, C. Jenne and J. Warneke, First steps towards a stable neon compound: observation and bonding analysis of B12(CN)11Ne, Chem. Commun., 2020, 56, 4591–4594 RSC
.
- K. Wöhner, T. Wulf, N. Vankova and T. Heine, Strong Binding of Noble Gases to B12X11−: A Theoretical Study, J. Phys. Chem. A, 2021, 125, 4760–4765 CrossRef PubMed
.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS
.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange, Chem. Phys., 2009, 356, 98–109 CrossRef CAS
.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC
.
- S. Grimme, Supramolecular binding thermodynamics by dispersion-corrected density functional theory, Chemistry, 2012, 18, 9955–9964 CrossRef CAS PubMed
.
- M. K. Gilson and K. K. Irikura, Symmetry numbers for rigid, flexible, and fluxional molecules: theory and applications, J. Phys. Chem. B, 2010, 114, 16304–16317 CrossRef CAS PubMed
.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, Natural triple excitations in local coupled cluster calculations with pair natural orbitals, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed
.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, Communication: an improved linear scaling perturbative triples correction for the domain based local pair-natural orbital based singles and doubles coupled cluster method DLPNO-CCSD(T), J. Chem. Phys., 2018, 148, 11101 CrossRef
.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Optimized accurate auxiliary basis sets for RI-MP2 and RI-CC2 calculations for the atoms Rb to Rn, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed
.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. L. Martin and F. Neese, Exploring the Accuracy Limits of Local Pair Natural Orbital Coupled-Cluster Theory, J. Chem. Theory Comput., 2015, 11, 1525–1539 CrossRef CAS PubMed
.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2018, 8, 33 Search PubMed
.
- SCM, ADF 2019.103, Theoretical Chemistry, Vrije Universiteit, Amsterdam, Netherlands Search PubMed
.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS
.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic total energy using regular approximations, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS
.
- E. van Lenthe and E. J. Baerends, Optimized Slater-type basis sets for the elements 1-118, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed
.
- D. Denysenko, M. Grzywa, M. Tonigold, B. Streppel, I. Krkljus, M. Hirscher, E. Mugnaioli, U. Kolb, J. Hanss and D. Volkmer, Elucidating gating effects for hydrogen sorption in MFU-4-type triazolate-based metal-organic frameworks featuring different pore sizes, Chemistry, 2011, 17, 1837–1848 CrossRef CAS PubMed
.
- D. B. Boyd and K. B. Lipkowitz, Reviews in computational chemistry, Wiley-VCH, New York, 2000, vol. 15 Search PubMed
.
- M. Mayer, M. Rohdenburg, S. Kawa, F. Horn, H. Knorke, C. Jenne, R. Tonner, K. R. Asmis and J. Warneke, Relevance of π-Backbonding for the Reactivity of Electrophilic Anions B12 X11 - (X=F, Cl, Br, I, CN), Chem.–Eur. J., 2021, 27, 10274–10281 CrossRef CAS PubMed
.
- R. M. Badger, A Relation Between Internuclear Distances and Bond Force Constants, J. Chem. Phys., 1934, 2, 128–131 CrossRef CAS
.
- C. Jenne, M. Keßler and J. Warneke, Protic anions H(B12X12)- (X = F, Cl, Br, I) that act as Brønsted acids in the gas phase, Chemistry, 2015, 21, 5887–5891 CrossRef CAS PubMed
.
- J. Warneke, M. Mayer, M. Rohdenburg, X. Ma, J. K. Y. Liu, M. Grellmann, S. Debnath, V. A. Azov, E. Apra, R. P. Young, C. Jenne, G. E. Johnson, H. I. Kenttämaa, K. R. Asmis and J. Laskin, Direct functionalization of C-H bonds by electrophilic anions, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 23374–23379 CrossRef CAS PubMed
.
- W. N. Lipscomb and L. Massa, Examples of large closo boron hydride analogs of carbon fullerenes, Inorg. Chem., 1992, 31, 2297–2299 CrossRef CAS
.
- W. N. Lipscomb and L. Massa, Closo Boron Hydrides and Carbon Fullerenes, Phosphorus, Sulfur Silicon Relat. Elem., 1994, 87, 125–128 CrossRef CAS
.
- P. v. R. Schleyer, K. Najafian and A. M. Mebel, The Large closo-Borane Dianions, B(n)H(n)(2-) (n = 13-17) Are Aromatic, Why Are They Unknown?, Inorg. Chem., 1998, 37, 6765–6772 CrossRef CAS PubMed
.
- Jmol. An open-source Java viewer for chemical structures in 3D, http://www.jmol.org/ Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Additional tables and figures as quoted in the article (PDF); sample input files (TXT); atomic coordinates and NEB paths (XYZ); and vibration files (7-column XYZ, which can be read and visualized e.g. with Jmol50 using tools → vibrate). See DOI: 10.1039/d1ra06322g |
| This journal is © The Royal Society of Chemistry 2021 |