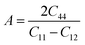Ultra-violet to visible band gap engineering of cubic halide KCaCl₃ perovskite under pressure for optoelectronic applications: insights from DFT

Abstract

Density functional theory is utilized to explore the effects of hydrostatic pressure on the structural, electrical, optical, and mechanical properties of cubic halide perovskite KCaCl₃ throughout this study. The interatomic distance is decreased due to the pressure effect, which dramatically lowers the lattice constant and unit cell volume of this perovskite. Under pressure, the electronic band gap shrinks from the ultra-violet to visible region, making it easier to move electrons from the valence band to the conduction band, which improves optoelectronic device efficiency. Furthermore, the band gap nature is switched from indirect to direct around 40 GPa pressure, which is more suitable for a material to be exploited in optoelectronic applications. The use of KCaCl₃ in microelectronics, integrated circuits, QLED, OLED, solar cells, waveguides, solar heat reduction materials, and surgical instruments has been suggested through deep optical analysis. The use of external hydrostatic pressure has a considerable impact on the mechanical properties of this material, making it more ductile and anisotropic.

---

1. Introduction

The physical properties of materials, such as structural, electronic, optical and mechanical are studied in depth to gain deep knowledge of their uses. The analysis of a material's physical properties can be done by both experimental^1–5 and theoretical investigations.^6–10 Theoretical studies aid experimental work in gaining a better understanding of physical properties.^1,6 The physical properties of materials are associated with crystal structure.^11–15 Perovskite compounds comprise conductors, insulators, semiconductors, and superconductors;^16–20 therefore, they are considered the most important materials among various types of crystal structures in terms of uses.^21–23 Because of their immense physical properties, such as photocatalytic, dielectric, ferroelectric, pyroelectric, piezoelectric, magnetic, superconductivity, and ionic conductivity,^24–31 perovskites are often referred to as “the department store of physical properties”.³² The simple cubic perovskite with space group Pm3̄m (#221) could be oxide based (general formula ABO₃)³³ or halide based (general formula ABX₃),³⁴ where A and B are cations, while X is a monovalent halogen anion.³⁵ The first-principle calculations were successfully implemented to cubic perovskite compounds to analyze different physical properties.^35–54 The substitution of element,^35,36 doping,^10,37,38 or applying hydrostatic pressure^39–53 can change the physical properties of cubic perovskites. Linh et al.³⁵ found that substituting of bigger ionic radius alkali metals (M = Li, Na, and K) to (Bi_0.5M_0.5)TiO₃ increased its direct band gap. The substitution of K to Cs site in MCaF₃ (M = K, Cs) improved the optical characteristics by altering the band gap from indirect to direct.³⁶ Gillani et al. also reported that the doping of alkaline earth metals (Mg, Ca, Ba) into SrZrO₃ shifted the band gap from indirect to direct.^37,38 Furthermore, using hydrostatic pressure to alter the band gap from indirect to direct proved beneficial, as seen in a number of cubic perovskites.^39–44 The band gap of halide cubic perovskites CsBX₃ (B = Sn, Ge; X= Cl, Br) was decreased to zero by applying external pressure, resulting in a semiconductor to metallic transition.^45–49 The first-principle investigations under hydrostatic pressure have also been done for Ca based cubic alkali halide perovskites KCaX₃ (X = F, Cl)^50,51 and ACaF₃ (A = Rb, Cs).^52,53 The band gap of KCaF₃ and RbCaF₃ were shifted from indirect to direct by applying hydrostatic pressure of 13.5 and ≥14 GPa, respectively.^51,53 Furthermore, ACaF₃ (A = K, Rb, Cs) exhibited improved mechanical properties under increased hydrostatic pressure.^51,53 The photoluminescence of another halide perovskite RbCaCl₃ phosphor activated with 3d elements Cu⁺ and Mn²⁺ was discussed in the reported literature.⁵⁴ The investigations of physical properties and structural stability have been done at ambient pressure^50,55,56 for experimentally synthesized Ca based alkali halide perovskite KCaCl₃,⁵⁷ but the attempt of applying pressure on this perovskite has yet to be done. As a result, the goal of this research is to use the first-principles calculations to examine the geometric structure, electronic, optical, and mechanical properties of non-toxic cubic halide perovskite KCaCl₃ under hydrostatic pressure and assess the results to explore the effects of pressure.

2. Computational method

The first-principle calculations are carried out with the Cambridge Serial Total Energy Package (CASTEP) code,⁵⁸ which is an implementation of the plane-wave pseudo-potential total energy approach based on density functional theory (DFT). The Vanderbilt-type ultrasoft-pseudopotential is used to model the interaction of valence electrons with ion cores.⁵⁹ The generalized gradient approximation (GGA) suggested by Perdew–Burke–Ernzerhof (PBE) is used to treat the exchange–correlation effect.⁶⁰ The plane-wave basis set cut-off is fixed to 900 eV to distinguish core states from valence ones. The Monkhorst–Pack method⁶¹ with 12 × 12 × 12 k-point mesh is used to integrate special points sampling over the Brillouin zone. In geometry optimization, the Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization technique⁶² is used, which allows quick search for the lowest energy structure. The convergence factors are set as the difference in total energy within 5 × 10⁻⁶ eV per atom, maximum ionic Hellmann–Feynman force within 0.01 eV Å⁻¹, maximum displacement within 5 × 10⁻⁴ Å, and maximum stress within 0.02 GPa. In this study, the hydrostatic pressure up to 120 GPa with an interval of 40 GPa is used. The optimized crystal structure is visualized by using VESTA software.⁶³ The two-dimensional (2D) and three-dimensional (3D) anisotropic contour plots of Young's modulus, shear modulus, and Poisson's ratio are constructed by using the ELATE program.⁶⁴

3. Result and discussion

3.1 Structural properties

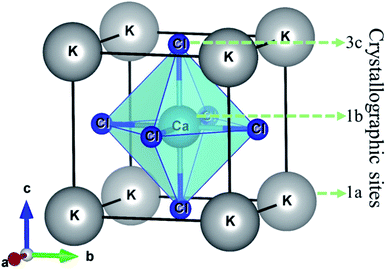
The halide perovskite compound KCaCl₃ is crystallized in cubic structure with the space group Pm3̄m (#221).^50,55 The optimized crystal structure of KCaCl₃ with crystallographic sites is represented in Fig. 1. The unit cell of KCaCl₃ is made up of five atoms, which has one formula unit. In the structure, K atom occupies the corner with 1a Wyckoff position (0, 0, 0), Ca atom locates at the body center with 1b Wyckoff position (0.5, 0.5, 0.5), and Cl atom holds the face center with 3c Wyckoff position (0, 0.5, 0.5).

Fig. 1 Crystal structure of cubic perovskite KCaCl₃ with crystallographic sites.

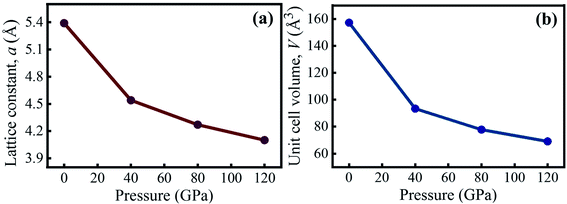
Table 1 summarizes the pressure-dependent simulated values of the lattice constant and unit cell volume of KCaCl₃ in comparison to experimental and theoretical data. The estimated data are clearly in agreement with the experimental⁵⁷ and available theoretical results.^50,55 The calculated lattice parameter is slightly larger than the experimental data due to the general tendency of GGA functional.⁴⁵ At 0 GPa, the computed lattice constant differs from the experimental value by only 0.60%, indicating that the present simulation is valid. Fig. 2(a) and (b) illustrates the effects of applied hydrostatic pressure (0–120 GPa) on the lattice constant and unit cell volume, respectively. As the pressure rises, both the lattice constant and unit cell volume are found to be reduced, indicating that the distance between atoms is getting decreased as represented in Table 2.

Table 1 The simulated and the available experimental with theoretical values of lattice constant, and unit cell volume of KCaCl₃ at different hydrostatic pressure

Pressure (GPa)	Lattice constant, a (Å)			Volume, V (Å^3)
	This work (GGA-PBE)	Theoretical study (GGA-PBE)	Experimental
00	5.397	5.410 (ref. 50) 5.407 (ref. 55)	5.365 (ref. 57)	157.20
40	4.537	—	—	93.39
80	4.269	—	—	77.78
120	4.101	—	—	69.00

---

Fig. 2 Variation of (a) lattice constant and (b) unit cell volume of KCaCl₃ with pressure.

Table 2 The calculated bond lengths in halide perovskite KCaCl₃ under different pressure

Bonds	Bond length (Å)
	0 GPa	40 GPa	80 GPa	120 GPa
K–Cl	3.81626	3.20811	3.01834	2.90029
Ca–Cl	2.69850	2.26848	2.13429	2.05082

---

3.2 Electronic properties

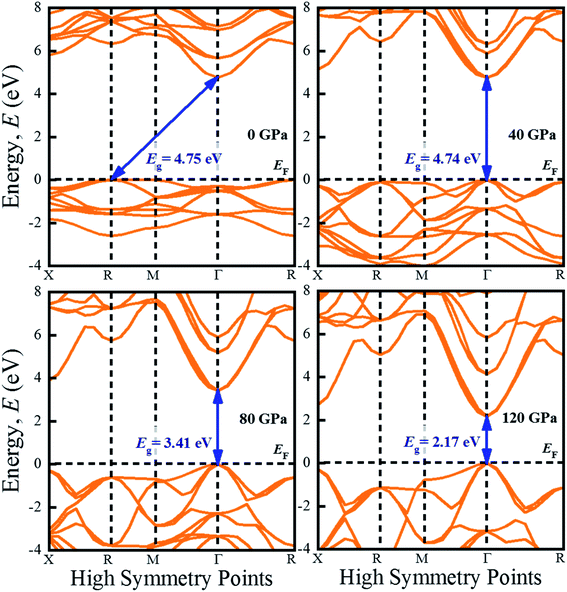
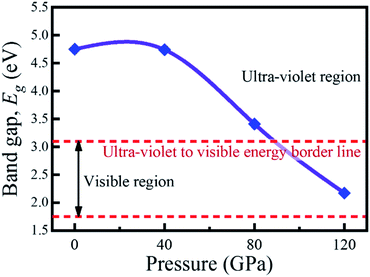
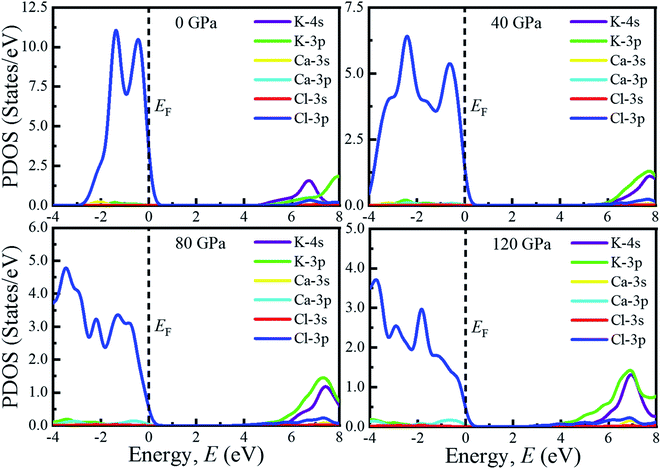
The investigation of electronic properties including band structure, density of states, and electronic density map is crucial to get a clear idea about the optical properties. The band structure variations of KCaCl₃ under various hydrostatic pressures calculated by GGA-PBE functional are displayed in Fig. 3. The band structure configuration ranging from −4 to +8 eV is displayed. The Fermi level (E_F) is displayed at zero photon energy indicating by horizontal dashed line. The band structure at 0 GPa pressure reveals the wide band gap (E_g) of KCaCl₃ with a value of 4.75 eV. Since, the valence band maximum (VBM) and conduction band minimum (CBM) are located at R and Γ point, respectively, indicating indirect band gap of KCaCl₃. The equivalent band gap of 4.76 eV⁵⁰ and 4.811 eV⁵⁴ was also found in the previous investigations using the same functional showing the authenticity of the present calculations. The applied pressure shows a major impact on the energy band gap and its nature. The value of E_g becomes significantly reduced from ultra-violet (4.75 eV) to visible (2.71 eV) region under pressure up to 120 GPa (Fig. 4), which allows electrons easily transport from valence band (VB) to conduction band (CB). Thus, the optical absorption and conductivity becomes higher, which is advantageous for optoelectronic applications. It is well-known that there exists an inverse relationship between the band gap and external applied pressure.⁶⁵ By applying the external pressure, the potential between the electron-ion is enhanced and hence the lattice parameters are reduced (Table 1). Due to this reduction in lattice parameters the band gap is reduced at the Brillouin zone symmetry points. Moreover, the nature of band gap is switched from indirect to direct after the application of 40 GPa pressure, as VBM is shifted from R to Γ point.

Fig. 3 Band structure of KCaCl₃ under various applied pressures.

Fig. 4 Variation of band gap of KCaCl₃ under various applied pressures.

The applied external pressure elongates the VB that shows a linear extension to higher energies at the Γ point. Such states shifting in energy induce specific rearrangement of states, resulting in an indirect to direct band gap transformation. The transition of band gap from indirect to direct under pressure was also observed for cubic halide perovskites ACaF₃ (A = K, Rb).^51,53 This transition reduces the energy required for electrons to move from the VB to the CB, which may improve device performance.^45,46 Since the VBM and CBM move forward to the E_F under pressure, the separation between certain VBs as well as certain CBs is increased. The prominent feature is observed at R and Γ points of the Brillouin zone.

For more clarification the partial density of states (PDOS) of KCaCl₃ at various applied pressures are plotted in Fig. 5. The vertical dashed line at 0 eV represents the Fermi level (E_F). The reducing tendency of E_g under pressure is also observed in the PDOS diagram, as the VBs and CBs move towards the E_F. By increasing external pressure the hybridization between K-3p and Cl-3p is enhanced, which lifts the CBs towards the E_F and hence the band gap is reduced. Moreover, the reduction in K–Cl bond length under pressure (Table 2) would enhance the hybridization between the K-3p and Cl-3p orbitals. The increased hybridization lifts up the VBM and down the CBM at Γ point of the Brillouin zone (Fig. 3), consequently reducing the band gap from 4.75 eV to 2.17 eV. This phenomenon is supported by the band diagrams. The VB of both non-pressurized and pressurized system is originated mostly from Cl-3p state with negligible share of K-3p and Ca-3p states. On the other hand, the CB is dominated by 4s, 3p orbitals of K atoms with small contribution of Cl-3p state.

Fig. 5 The partial density of states of cubic perovskite KCaCl₃ under pressure.

The charge density mapping is also studied in order to understand the behavior of chemical bonding. Fig. 6 shows the charge density distribution of KCaCl₃ at 0 and 120 GPa pressure along the crystallographic planes (100) and (200). The intensity of charge (electron) density is represented by the scale on the right side of the density map. At ambient pressure the electron charge distributions of K and Cl atoms are not overlapped along (100) plane, representing ionic bonding of K–Cl (Fig. 6(a)). In contrast, a slight overlapping of Ca and Cl atoms is observed along (200) plane (Fig. 6(b)), indicating covalent nature of Ca–Cl bonds. However, the spacing between K and Cl atoms reduces and begins to overlap along (100) plane (Fig. 6(c)) under pressure (120 GPa), converting the ionic character of K–Cl to covalent. Furthermore, the overlapping between Ca and Cl atoms increases along (200) plane (Fig. 6(d)) under hydrostatic pressure, intensifying the covalent nature of Ca–Cl bonds.

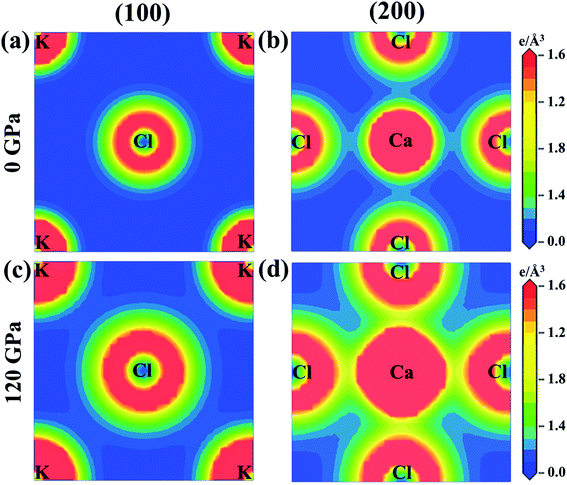Fig. 6 The electron density map of KCaCl₃ (a) and (b) at 0 GPa and (c) and (d) at 120 GPa along the crystallographic planes (100) and (200).

3.3 Optical properties

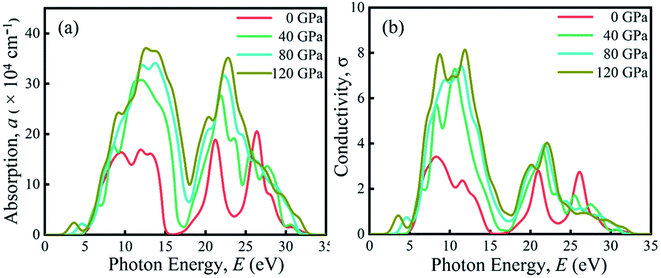
Due to the large band gap (4.75 eV) in the ultra-violet range, halide perovskite KCaCl₃ is not suited for optoelectronic applications. As a result, more advancement is required for improved performance in solar cell and other optoelectronic applications. The application of hydrostatic pressure might be a simple and effective approach to reduce the band gap for this purpose.^45–49 The exploration of optical profiles is a high-impact criterion for obtaining suitable concept about a material's compatibility in order to improve device efficiency. Therefore, the optical functions, namely absorption (α), conductivity (σ), reflectivity (R), refractive index (η), and dielectric function (ε) of KCaCl₃ are studied under induced pressure ranging from 0 to 120 GPa. The absorption coefficient (α) is a critical measure for determining a material's ability to absorb light energy and gives essential information on solar energy conversion efficiency.⁴⁸ Fig. 7(a) shows the variation of α of KCaCl₃ as a function of photon energy under pressure up to 120 GPa. It begins at band gap due to the absorption of ultra-violet radiation at 0 GPa, which causes transition of charges from VB to CB. Consequently, the optical conductivity also starts at band gap value because of the availability of charges in the CB. As the pressure increases the fundamental absorption shifts from ultra-violet to visible range of the electromagnetic spectrum. With the rise in pressure, the edge of α has clearly migrated to the low energy zone known as red shift^45–49 that is consistent to the pressure-dependent band gap variation. Moreover, the calculated α of KCaCl₃ shows linear increase due to the illustrated direct band gap after the increasing application of pressure that is better than that of indirect band gap nature at 0 GPa. The induced pressure dramatically boosts the absorption, implying that applying pressure significantly improve the potentiality of KCaCl₃ perovskite in solar cell or other optoelectronic devices. Furthermore, KCaCl₃ can be an efficient material for sterilizing the surgical instruments due to the wide absorption peak in the ultra-violet region. The optical conductivity or photoconductivity (σ) of KCaCl₃ under pressure is displayed in Fig. 7(b). The σ spectrum exhibits the similar pattern of α spectrum (Fig. 7(a) and (b)), as a material releases free carriers for conduction during photon absorption. However, both α and σ are not started at 0 eV for the system under pressure from 0–120 GPa, reconfirming the insulating/semiconducting nature of KCaCl₃. It can be seen from Fig. 7(b) that at zero pressure the σ starts from 4.75 eV and moves towards lower energies, as the pressure is increased. It is also observed that the σ shows maximum value when KCaCl₃ stabilizes direct band gap after the pressure being applied, which has a linear increasing tendency with increased pressure. Because of its improved conductivity under pressure, KCaCl₃ is expected to be an effective halide perovskite for improving optoelectronic device efficiency.

Fig. 7 The pressure-induced (a) absorption and (b) conductivity spectra of KCaCl₃.

The surface nature of the KCaCl₃ perovskite can be determined in relation to the reflected light energy from the surface.⁶⁶ The reflectivity (R) spectrum of KCaCl₃ as a function of photon energy under pressure is displayed in Fig. 8(a). The studied compound shows the best reflecting behavior in the energy range of 13–16 eV. It can be clearly seen from Fig. 7(a) and 8(a) that when the α edge is at 0 eV then at the same energy point the R has some value, which reveals the inverse relationship of absorption and reflectivity. Therefore, it is required to have high absorption and low reflectivity at low energy region for high performance photovoltaic devices. However, the R increases at low energy region with applied pressure, which may decrease the effectiveness of the photovoltaic efficiency. Therefore, further research should be done to reduce the R, which can increase absorption and photovoltaic performance. Importantly, as the R increases under pressure in the high energy zone, the titled material appears to be more promising for reducing solar heating. The refractive index (η) describes the speed with which light passes through a material⁶⁷ and also provides information about a material's suitability for device applications.⁶⁸ It is seen from Fig. 8(b) that at 0 eV, with the increase of pressure from 0.0–10 GPa, the η(0) increases from 1.55 to 2.15. The increased, η(0) under pressure can make KCaCl₃, more appropriate for application in QLED, OLED, solar cells, and waveguides.^69,70 The trend of η is similar to the real part of dielectric function ε₁ (Fig. (8b) and (c)). It starts with a static value of 1.55 at 0 GPa and reaches to a maximum of 2.15 at ∼7 eV energy, which increases with increase in pressure. However, the η decreases below unity in energy range 25–35 eV. In this region, the group velocity of incident radiations is greater than the velocity of light because the η is less than unity.^71,72 As a result, the group velocity transfers to the negative domain and the nature of medium changes from linear to nonlinear.

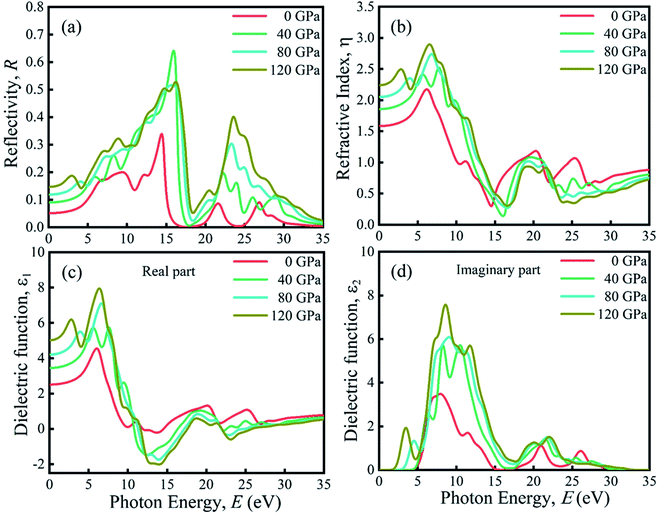Fig. 8 The pressure-induced (a) reflectivity, (b) refractive index, (c) real part of dielectric function, and (d) imaginary part of dielectric function of KCaCl₃.

The rate of charge-carrier recombination is governed by the dielectric function, which is a crucial optical parameter.^45–49,73 It provides a clear picture of optoelectronic device performance.⁷⁴ Solar cells with a higher static dielectric constant have lower recombination rates.⁷⁵ Fig. 8(c) and (d) show the real (ε₁) and imaginary (ε₂) part of dielectric constant of non-toxic KCaCl₃ under applied pressure, respectively. Pressure causes a higher static dielectric function, ε₁(0) of KCaCl₃ than that of non-pressurized system (Fig. 8(c)), which could improve device efficiency. It can be seen that the value of ε₁(0) increases with increasing pressure, viewing the band gap is inversely associated to ε₁(0); a smaller energy gap results in a higher ε₁(0) value. Moreover, the pressure-induced KCaCl₃ exhibits higher ε₁ in the visible region. The ε₂ is also linked to the optical absorption and the band gap of a material. Similar to the optical absorption, the applied pressure raises ε₂ in the visible region, and the peaks transfer to a low photon energy area, which concludes that KCaCl₃ is a good absorber of visible light under pressure. The ε₂ drops to zero as the photon energy increases because the absorption under all applied pressures is very low in the high photon energy region. Furthermore, the higher ε₁ and ε₂ at low photon energy as well as lower ε₁ and ε₂ at high energy region explicit the potential of KCaCl₃ in microelectronics and integrated circuits¹⁰

3.4 Mechanical properties

Elastic constants (C_ij) are a crucial element in calculating mechanical properties, such as brittleness, ductility, stiffness, and anisotropy.^45–49 C_ij can be used to identify mechanical stability and internal forces in solids.^45–49 The finite strain theory⁷⁶ is used to determine the mechanical properties in this study. Because the lattice parameters of KCaCl₃ decrease with induced pressure (Fig. 2), it is critical to understand how pressure affects the C_ij in order to gain better understanding of the mechanical properties. The three independent elastic constants of cubic KCaCl₃ perovskite are C₁₁, C₁₂, and C₄₄. The calculated C_ij at various applied pressure are listed in Table 3. The mechanical stability of cubic crystals is determined by the Born stability criterion⁷⁷ listed below.

C₁₁ > 0, C₄₄ > 0, (C₁₁ − C₁₂) > 0, (C₁₁ + 2C₁₂) > 0

Table 3 The calculated elastic constants (C_ij) and Cauchy pressure (C₁₂ − C₄₄) of KCaCl₃ at various applied pressures compared with previously reported data of halide perovskites CsXCl₃ (X = Sn,Ge,Ca)

Compound	Pressure (GPa)	C11	C12	C44	C12 − C44	Ref.
CsSnCl3	0	50.66	8.71	6.01	2.70	45
CsGeCl3	0	54.86	12.95	12.00	0.95	48
CsCaCl3	0	56.905	9.692	10.233	—	80
KCaCl3	0	54.06	9.26	7.80	1.46	This work
	40	356.87	67.29	8.17	59.12	This work
	80	606.10	120.29	7.40	112.89	This work
	120	818.07	170.96	6.82	164.14	This work

---

The calculated elastic constants meet the aforementioned criteria over the whole pressure range, confirming structural stability of KCaCl₃ at high pressure. Since, the reported elastic constants are not available; this study cannot compare the present results. However, the calculated elastic constants at 0 GPa are comparable with the halide perovskites CsXCl₃ (X = Sn, Ge, Ca).^45,48,80 The difference between C₁₂ and C₄₄ is known as Cauchy pressure and it can be used to determine whether a material is ductile (positive value) or brittle (negative value).^45–49 Under all applied pressures, the KCaCl₃ possesses positive Cauchy pressure, indicating its ductile character and the ductility becomes intensive with increased pressure (Table 3).

The elastic moduli, such as bulk modulus (B), shear modulus (G), Young's modulus (E) can be determined using Voight–Reuss–Hill approximation (VHR).⁷⁸ The fundamental mechanical properties, namely Pugh's ratio (B/G), Poisson's ratio (ν), and anisotropy factor (A) are calculated using the expressions in the previous literature.⁷⁹ The calculated B, G, E, B/G, ν, and A are listed in Table 4 having almost similar values with previously studied halide perovskites CsXCl₃ (X = Sn, Ge, Ca).^45,48,80 The value of B, G, and E increase as the applied pressure is increased, indicating that applying hydrostatic pressure incorporates the hardness, stiffness, and higher resistance to KCaCl₃ against tensile deformation under high pressure.^45,48 Unfortunately, there is no literature data of elastic moduli to compare with the pressure induced results. To the best of our knowledge, this is the first theoretical work on this compound under high pressure. Therefore, this study can serve as a prediction for future works. Pugh's ratio (B/G) and Poisson's ratio (ν) are crucial parameters to investigate the ductile/brittle character of a material.

Table 4 The calculated bulk modulus B (GPa), shear modulus G (GPa), Young's modulus E (GPa), Poisson's ratio (ν), Pugh's ratio (B/G), and elastic anisotropy (A) of KCaCl₃ at different applied pressures compared with previously reported data of halide perovskites CsXCl₃ (X = Sn, Ge, Ca)

Compound	Pressure (GPa)	B	G	E	B/G	ν	A	Ref.
CsSnCl3	0	22.70	10.20	26.61	2.22	0.300	—	45
CsGeCl3	0	26.92	15.03	38.01	1.79	0.265	—	48
CsCaCl3	0	25.430	14.406	36.353	1.765	0.363	0.433	80
KCaCl3	0	24.20	12.10	31.11	2.00	0.285	0.35	This work
	40	163.81	37.97	105.74	4.31	0.392	0.06	This work
	80	282.23	56.85	159.81	4.96	0.405	0.03	This work
	120	386.66	72.36	204.33	5.34	0.411	0.02	This work

---

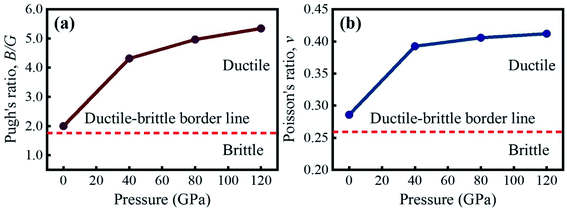
The critical value of B/G and ν to recognize the brittle/ductile nature of a material is 1.75 and 0.26, respectively.^45–49 A material is termed as ductile if the B/G and ν surpass the critical value, otherwise it is brittle. According to the computed B/G and ν, KCaCl₃ is a ductile material that becomes more ductile when the applied pressure is raised, as seen in Fig. 9(a) and (b), respectively. The increased ductility of KCaCl₃ under pressure makes it more suitable for use in optoelectronic devices.⁸¹ Moreover, the value of ν should be in the range of 0.25–0.50 to detect the presence of central force within a crystal.⁸² It is seen from Table 4 that the value of ν lies within 0.25–0.50 over the entire pressure range, confirming the presence of central force inside KCaCl₃.

Fig. 9 Variation of (a) Poisson's ratio and (b) Pugh's ratio of KCaCl₃ under pressure.

The Zener anisotropy index (A) indicates whether a substance is isotropic or anisotropic. It is calculated by using the following Zener equation^83,84 and listed in Table 4.

The compound is classified as isotropic when the value of A is unity; however, the deviation from unity reflects the degree of anisotropy.⁸³ The value of A manifests the anisotropic nature of KCaCl₃, which become more anisotropic under pressure.

In order to visually explore the anisotropic nature of KCaCl₃, the 2D and 3D anisotropic contour plots of Young's modulus (E), shear modulus (G), and Poisson's ratio (ν) at 0 and 120 GPa pressure are presented in Fig. 10(a) and (b), respectively. The 2D plots are constructed along the xy-, yz-, and xz-planes, but the projections are taken on the xy-plane. The isotropy of a material is represented by the circular 2D and spherical 3D plots, whereas the departure from those reveals anisotropy.^47,48 The 2D and 3D contour plots clearly show that the investigated KCaCl₃ has anisotropic character in all directions. However, the deviation of circular 2D and spherical 3D is more intensive in the case of 120 GPa than that of 0 GPa pressure, implying that pressure induces more anisotropy in KCaCl₃.

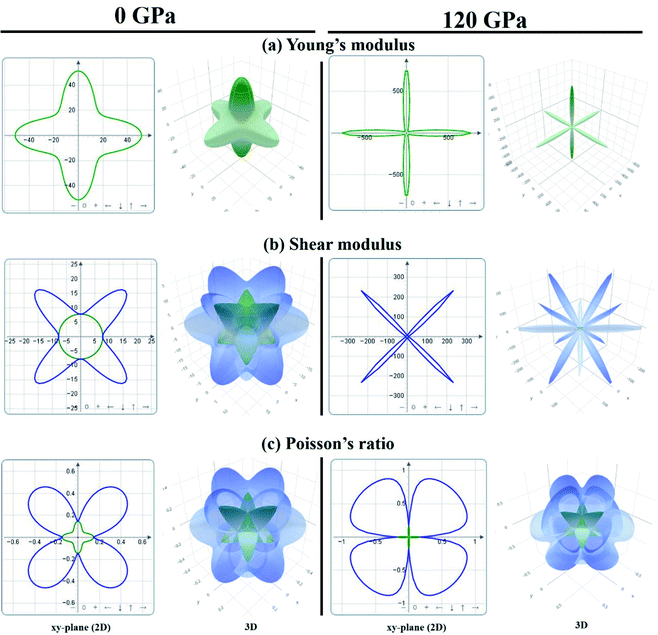Fig. 10 The anisotropic 2D and 3D representation of (a) Young's modulus, (b) shear modulus, and (c) Poisson's ratio of KCaCl₃ at 0 and 120 GPa pressure.

4. Conclusions

For the first time, a DFT-based simulation was used to examine the effect of pressure (up to 120 GPa) on the structural, electronic, optical, and mechanical properties of the cubic halide perovskite KCaCl₃. The optimized lattice parameters demonstrate good agreement with reported experimental and theoretical evidences, but being reduced under pressure. According to the examination of electronic behavior, the band gap of KCaCl₃ can be tuned by applying pressure. The band gap narrows dramatically from ultra-violet to visible light under pressure, which is advantageous for solar cell applications. The indirect band gap is also found to be converted into a direct band gap, which is helpful for optoelectronic applications. The pressure-induced optical functions are also studied, yielding some intriguing results as well as a variety of feasible applications. The estimated elastic constants maintain the Born stability criterion, ensuring the mechanical stability of KCaCl₃ over the whole pressure range. The application of pressure makes the compound more ductile and anisotropic.

Data availability

The datasets generated and/or analyzed in this study are available from the corresponding author upon reasonable request.

Author contributions

Muhtasim Ali Haq: investigation, methodology, data curation, writing original draft; Md Saiduzzaman: formal analysis, conceptualization, supervision, writing original draft, reviewing and editing; Tariqul Islam Asif & Ismile Khan Shuvo: formal analysis, investigation; Khandaker Monower Hossain: formal analysis, validation, supervision, writing the original draft, reviewing and editing.

Conflicts of interest

There is no conflict of interest to declare.

References

1. M. S. Ali, S. Das, Y. F. Abed and M. A. Basith, Lead-free CsSnCl₃ perovskite nanocrystals: rapid synthesis, experimental characterization and DFT simulations, Phys. Chem. Chem. Phys., 2021, 23, 22184–22198.
2. B. Yue, Q. Hu, L. Ji, Y. Wang and J. Liu, Facile synthesis of perovskite CeMnO₃ nanofibers as an anode material for high performance lithium-ion batteries, RSC Adv., 2019, 9, 38271–38279.
3. S. Thirumalairajan, K. Girija, N. Y. Hebalkar, D. Mangalaraj, C. Viswanathana and N. Ponpandian, Shape evolution of perovskite LaFeO₃ nanostructures: a systematic investigation of growth mechanism, properties and morphology dependent photocatalytic activities, RSC Adv., 2013, 3, 7549–7561.
4. X. Du, G. Wu, J. Cheng, H. Dang, K. Ma, Y. W. Zhang, P. F. Tan and S. Chen, High-quality CsPbBr₃ perovskite nanocrystals for quantum dot light-emitting diodes, RSC Adv., 2017, 7, 10391–10396.
5. Z. Wen, W. Zhai, C. Liu, J. Lin, C. Yu, Y. Huang, J. Zhang and C. Tang, Controllable synthesis of CsPbI₃ nanorods with tunable photoluminescence emission, RSC Adv., 2019, 9, 24928–24934.
6. T. G. Liashenko, E. D. Cherotchenko, A. P. Pushkarev, V. Pakštas, A. Naujokaitis, S. A. Khubezhov, R. G. Polozkov, K. B. Agapev, A. A. Zakhidov, I. A. Shelykhae and S. V. Makarov, Electronic structure of CsPbBr_3−xCl_x perovskites: synthesis, experimental characterization, and DFT simulations, Phys. Chem. Chem. Phys., 2019, 21, 18930–18938.
7. S. A. Khandy and D. C. Gupta, Analysing cation-modified magnetic perovskites A₂SnFeO₆ (A = Ca, Ba): a DFT study, RSC Adv., 2021, 11, 27499–27511.
8. M. I. Kholil, M. T. H. Bhuiyan, M. A. Rahman, M. S. Ali and M. Aftabuzzaman, Influence of molybdenum and technetium doping on visible light absorption, optical and electronic properties of lead-free perovskite CsSnBr₃ for optoelectronic applications, RSC Adv., 2021, 11, 2405–2414.
9. S. A. Khandy and D. C. Gupta, Structural, elastic and thermo-electronic properties of paramagnetic perovskite PbTaO₃, RSC Adv., 2016, 6, 48009–48015.
10. S. A. Khandy and D. C. Gupta, Investigation of the transport, structural and mechanical properties of half-metallic REMnO₃ (RE = Ce and Pr) ferromagnets, RSC Adv., 2016, 6, 97641–97649.
11. H. Pan, B. Gu and Z. Zhang, Phase-Dependent Photocatalytic Ability of TiO₂: A First-Principles Study, J. Chem. Theory Comput., 2009, 5, 3074–3078.
12. J. Yi, X. Zhu, M. Zhou, S. Zhang, L. Li, Y. Song, H. Chen, Z. Chen, H. Li and H. Xu, Crystal phase dependent solar driven hydrogen evolution catalysis over cobalt diselenide, Chem. Eng. J., 2020, 396, 125244.
13. Q. Zhang, K. Kusada, D. Wu, S. Kawaguchi, Y. Kubota and H. Kitagawa, Crystal Structure-dependent Thermal Stability and Catalytic Performance of AuRu₃ Solid-solution Alloy Nanoparticles, Chem. Lett., 2018, 47, 559–561.
14. C. Thelander, P. Caroff, S. Plissard, A. W. Dey and K. A. Dick, Effects of Crystal Phase Mixing on the Electrical Properties of InAs Nanowires, Nano Lett., 2011, 11, 2424–2429.
15. M. Mattila, T. Hakkarainen, M. Mulot and H. Lipsanen, Crystal-structure-dependent photoluminescence from InP nanowires, Nanotechnology, 2006, 17, 1580.
16. P. Goel, S. Sundriyal, V. Shrivastav, S. Mishra, D. P. Dubal, K. H. Kim and A. Deep, Perovskite materials as superior and powerful platforms for energy conversion and storage applications, Nano Energy, 2021, 80, 105552.
17. A. S. Bhalla, R. Guo and R. Roy, The perovskite structure-a review of its role in ceramic science and technology, Mater. Res. Innovations, 2000, 4, 3–26.
18. J. Sunarso, S. S. Hashim, N. Zhu and W. Zhou, Perovskite oxides applications in high temperature oxygen separation, solid oxide fuel cell and membrane reactor: a review, Prog. Energy Combust. Sci., 2017, 61, 57–77.
19. P. Kanhere and Z. Chen, A Review on Visible Light Active Perovskite-Based Photocatalysts, Molecules, 2014, 19, 19995–20022.
20. J. Tian, Q. Xue, Q. Yao, N. Li, C. J. Brabec and H. L. Yip, Inorganic Halide Perovskite Solar Cells: Progress and Challenges, Adv. Energy Mater., 2020, 10, 2000183.
21. Y. G. Shi, Y. F. Guo, S. Yu, M. Arai, A. A. Belik, A. Sato, K. Yamaura, E. Takayama-Muromachi, H. F. Tian, H. X. Yang, J. Q. Li, T. Varga, J. F. Mitchell and S. Okamoto, Continuous metal-insulator transition of the antiferromagnetic perovskite NaOsO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 161104.
22. C. C. Stoumpos, C. D. Malliakas, J. A. Peters, Z. Liu, M. Sebastian, J. Im, T. C. Chasapis, A. C. Wibowo, D. Y. Chung, A. J. Freeman, B. W. Wessels and M. G. Kanatzidis, Crystal Growth of the Perovskite Semiconductor CsPbBr₃: A New Material for High-Energy Radiation Detection, Cryst. Growth Des., 2013, 13, 2722–2727.
23. A. N. Baranov, D. C. Kim, J. S. Kim, H. R. Kang, Y. W. Park, J. S. Pshirkov and E. V. Antipov, Superconductivity in the Ba_1−xK_xBiO₃ system, Phys. C, 2001, 357–360, 414–417.
24. C. G. Solís, J. Oliva, L. A. D. Torres, J. B. Alvarado, V. R. Zamudio, A. Abidov and L. M. T. Martinez, Efficient photocatalytic activity of MSnO₃(M: Ca, Ba, Sr) stannates for photoreduction of 4-nitrophenol and hydrogen production under UV light irradiation, J. Photochem. Photobiol., A, 2019, 371, 365–373.
25. W. Dong, B. Li, Y. Li, X. Wang, L. An, C. Li, B. Chen, G. Wang and Z. Shi, General Approach to Well-Defined Perovskite MTiO₃ (M = Ba, Sr, Ca, and Mg) Nanostructures, J. Phys. Chem. C, 2011, 115, 3918–3925.
26. V. V. Lemanov, A. V. Sotnikov, E. P. Smirnova, M. Weihnacht and R. Kunze, Perovskite CaTiO₃ as an incipient ferroelectric, Solid State Commun., 1999, 110, 611–614.
27. J. Jia, S. Guo, S. Yan, F. Cao, C. Yao, X. Dong and G. Wang, Simultaneous large pyroelectric response and high depolarization temperature in sodium bismuth titanate-based perovskites, Appl. Phys. Lett., 2019, 114, 032902.
28. K. Wieczorek, A. Ziebiniska, Z. Ujma, K. Szot, M. Górny, I. Franke, J. Koperski, A. Soszyński and K. Roleder, Electrostrictive and Piezoelectric Effect in BaTiO₃ and PbZrO₃, Ferroelectrics, 2006, 336, 61–67.
29. R. M. Kusters, J. Singleton, D. A. Keen, R. McGreevy and W. Hayes, Magnetoresistance measurements on the magnetic semiconductor Nd_0.5Pb_0.5MnO₃, Phys. B, 1989, 155, 362–365.
30. H. Hayashi, H. Inaba, M. Matsuyama, N. G. Lan, M. Dokiya and H. Tagawa, Structural consideration on the ionic conductivity of perovskite-type oxides, Solid State Ionics, 1999, 122, 1–15.
31. L. M. Feng, L. Q. Jiang, M. Zhu, H. B. Liu, X. Zhou and C. H. Li, Formability of ABO₃ cubic perovskites, J. Phys. Chem. Solids, 2008, 69, 967–974.
32. M. Saiduzzaman, T. Takei and N. Kumada, Hydrothermal magic for the synthesis of new bismuth oxides, Inorg. Chem. Front., 2021, 8, 2918–2938.
33. X. G. Zhao, G. M. Dalpian, Z. Wang and A. Zunger, Polymorphous nature of cubic halide perovskites, Phys. Rev. B, 2020, 101, 155137.
34. A. Oleaga, A. Salazar and D. Skrzypek, Critical behaviour of magnetic transitions in KCoF₃ and KNiF₃ perovskites, J. Alloys Compd., 2015, 629, 178–183.
35. N. H. Linh, N. H. Tuan, D. D. Dung, P. Q. Bao, B. T. Cong and L. T. H. Thanh, Alkali metal-substituted bismuth-based perovskite compounds: a DFT study, J. Sci.: Adv. Mater. Devices, 2019, 4, 492–498.
36. G. Murtaza, I. Ahmad and A. Afaq, Shift of indirect to direct bandgap in going from K to Cs in MCaF₃ (M = K, Rb, Cs), Solid State Sci., 2013, 16, 152–157.
37. S. S. A. Gillani, R. Ahmad, M. Rizwan, M. Rafique, G. Ullah, C. B. Cao and H. B. Jin, Effect of magnesium doping on band gap and optical properties of SrZrO₃ perovskite: a first-principles study, Optik, 2019, 191, 132–138.
38. S. S. A. Gillani, R. Ahmad, I. Zeba, Islah-u-din, M. Rizwan, M. Rafique, M. Shakil, S. Jabbar and M. Siddique, Structural stability of SrZrO₃ perovskite and improvement in electronic and optical properties by Ca and Ba doping for optoelectronic applications: a DFT approach, Philos. Mag. Lett., 2019, 99, 3133–3145.
39. N. A. Noor, M. Rashid, S. M. A. Abbas, M. Raza, A. Mahmood, S. M. Ramay and G. Murtaza, Shift of indirect to direct bandgap and thermoelectric response of the cubic BiScO₃ via DFT-mBJ studies, Mater. Sci. Semicond. Process., 2016, 49, 40–47.
40. A. Batool, M. A. Faridi, Q. Mahmood, B. U. Haq, A. Laref and S. E. Awan, The pressure-induced indirect to direct bandgap transition and thermoelectric response in SrTiO₃: an ab initio study, J. Phys. Chem. Solids, 2018, 123, 70–75.
41. N. A. Noor, M. Rashid, G. M. Mustafa, M. I. Khan, A. Mahmood and S. M. Ramay, Study of pressure induced physical properties of ZnZrO₃ perovskite using density functional theory, Chem. Phys. Lett., 2020, 753, 137601.
42. M. Yaseen, M. K. Butt, A. Ashfaq, J. Iqbal, M. M. Almoneef, Misbah, M. Iqbal, A. Murtaza and A. Laref, Phase transition and thermoelectric properties of cubic KNbO₃ under pressure: DFT approach, J. Mater. Res. Technol., 2021, 11, 2106–2113.
43. M. Yaseen, H. Shafiq, J. Iqbal, Misbah, F. Batool, A. Murtaza, M. Iqbal, H. Althib, S. M. Ramay and A. Mahmood, Pressure induced electronic, optical and thermoelectric properties of cubic SrZrO₃: DFT investigation, Phys. Rev. B, 2021, 612, 412626.
44. N. A. Noor, Q. Mahmood, M. Rashid, B. U. Haq and A. Laref, The pressure-induced mechanical and optoelectronic behavior of cubic perovskite PbSnO₃ via ab initio investigations, Ceram. Int., 2018, 44, 13750–13756.
45. J. Islam and A. A. Hossain, Semiconducting to metallic transition with outstanding optoelectronic properties of CsSnCl₃ perovskite under pressure, Sci. Rep., 2020, 10, 14391.
46. M. Kholil and M. Bhuiyan, Effects of pressure on narrowing the band gap, visible light absorption, and semi-metallic transition of lead-free perovskite CsSnBr₃ for optoelectronic applications, J. Phys. Chem. Solids, 2021, 154, 110083.
47. M. A. Islam, M. Z. Rahaman and S. K. Sen, A comparative study of hydrostatic pressure treated environmentally friendly perovskites CsXBr₃ (X = Ge/Sn) for optoelectronic applications, AIP Adv., 2021, 11, 075109.
48. M. A. Islam, J. Islam, M. N. Islam, S. K. Sen and A. K. M. A. Hossain, Enhanced ductility and optoelectronic properties of environment-friendly CsGeCl₃ under pressure, AIP Adv., 2021, 1, 045014.
49. M. S. Hossain, M. M. H. Babu, T. Saha, M. S. Hossain, J. Podder, M. S. Rana, A. Barik and P. Rani, Pressure induced semiconductor to metal phase transition in cubic CsSnBr₃ perovskite, AIP Adv., 2021, 11, 055024.
50. A. A. Mousa, First-principles study of structural, electronic and optical properties of the KCaX₃ (X= F and Cl) compounds, Int. J. Mod. Phys. B, 2014, 28, 1450139.
51. S. Soleimanpour and F. Kanjouri, Elastic, electronic and optical properties of the cubic fluoro-perovskite KCaF₃ under pressure, Indian J. Phys., 2015, 89, 687–697.
52. L. Li, Y. J. Wang, D. X. Liu, C. G. Ma, M. G. Brik, A. Suchocki, M. Piasecki and A. H. Reshak, Comparative first-principles calculations of the electronic, optical, elastic and thermodynamic properties of XCaF₃ (X=K, Rb, Cs) cubic perovskites, Mater. Chem. Phys., 2017, 188, 39–48.
53. A. A. Mousa, J. M. Khalifeh, N. T. Mahmoud and H. K. Juwhari, First principles study of structural, electronic and optical properties of the fluoroperovskite RbCaF₃ crystal, Am. J. Condens. Matter Phys., 2013, 3, 151–162.
54. J. R. Raipurkar, R. G. Atram, P. L. Muthal, S. M. Dhopte and S. V. Moharil, Luminescence of some 3d activators in RbCaCl₃, J. Lumin., 2013, 136, 365–368.
55. A. H. Larbi, S. Hiadsi, M. Hadjab and M. A. Saeed, Optical study of cubic, and orthorhombic structures of XCaCl₃ (X=K, Rb) compounds: comparative ab initio calculations, Optik, 2018, 166, 169–176.
56. S. Grishina, P. Kodera, L. M. Uriarte, J. Dubessy, A. Oreshonkov, S. Goryainov, F. Simko, I. Yakovlev and E. M. Roginskii, Identification of anhydrous CaCl₂ and KCaCl₃ in natural inclusions by Raman spectroscopy, Chem. Geol., 2018, 493, 532–543.
57. H. Seifert, H. Fink, G. Thiel and J. Uebach, Thermodynamische und strukturelle Untersuchungen an den Verbindungen der Systeme KCl/MCl₂ (M=Ca, Cd, Co, Ni), Z. Anorg. Allg. Chem., 1985, 520, 151–159.
58. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, First-principles simulation: ideas, illustrations and the CASTEP code, J. Condens. Matter Phys., 2002, 14, 2717.
59. D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892.
60. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865.
61. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188.
62. T. H. Fischer and J. Almlof, General methods for geometry and wave function optimization, J. Phys. Chem., 1992, 96, 9768–9774.
63. K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276.
64. R. Gaillac, P. Pullumbi and F. X. Coudert, ELATE: an open-source online application for analysis and visualization of elastic tensors, J. Phys.: Condens. Matter, 2016, 28, 275201.
65. S. S. A. Gillani, R. Ahmad, I. Zeba, Islah-u-din, M. Shakil, M. Rizwan, M. Rafique, M. Sarfraz and S. S. Hassan, Effect of external pressure on the structural stability, electronic structure,band gap engineering and optical properties of LiNbO₃: an ab initio calculations, Mater. Today Commun., 2020, 23, 100919.
66. M. Roknuzzaman, K. K. Ostrikov, H. Wang, A. Du and T. Tesfamichael, Towards lead-free perovskite photovoltaics and optoelectronics by ab initio simulation, Sci. Rep., 2017, 7, 14025.
67. M. M. Rahaman, M. H. Rubel, M. A. Rashid, M. A. Alam, K. M. Hossain, M. I. Hossain, A. A. Khatun, M. M. Hossain, A. K. M. Islam, S. Kojima and N. Kumada, Mechanical, electronic, optical, and thermodynamic properties of orthorhonmbic LiCuBiO₄ crystal: a first–principles study, J. Mater. Res. Technol., 2019, 8, 3783–3794.
68. M. Roknuzzaman, K. K. Ostrikov, K. C. Wasalathilake, C. Yan, H. Wang and T. Tesfamichael, Insight into lead-free organic-inorganic hybrid perovskites for photovoltaics and optoelectronics: a first-principles study, Org. Electron., 2018, 59, 99–106.
69. M. I. Naher and S. H. Naqib, Structural, elastic, electronic, bonding, and optical properties of topological CaSn₃ semimetal, J. Alloys Compd., 2020, 829, 154509.
70. M. H. K. Rubel, K. M. Hossain, S. K. Mitro, M. M. Rahman, M. A. Hadi and A. A. Islam, Comprehensive first-principles calculations on physical properties of ScV₂Ga₄ and ZrV₂Ga₄ in comparison with superconducting HfV₂Ga₄, Mater. Today Commun., 2020, 24, 100935.
71. L. J Wang, A. Kuzmich and A. Dogariu, Gain-assisted superluminal light propagation, Nature, 2000, 406, 277–279.
72. D. Mugnai, A. Ranfagni and R. Ruggeri, Observation of superluminal behaviors in wave propagation, Phys. Rev. Lett., 2000, 84, 4830.
73. X. Liu, B. Xie, C. Duan, Z. Wang, B. Fan, K. Zhang, B. Lin, F. Colberts, W. Ma, R. A. J. Janssen, F. Huang and Y. Cao, A high dielectric constant non-fullerene acceptor for efficient bulk-heterojunction organic solar cells, J. Mater. Chem. A, 2018, 6, 395–403.
74. F. D. Murnaghan, Finite deformations of an elastic solid, Am. J. Math., 1937, 59, 235–260.
75. N. Pandech, K. Sarasamak and S. Limpijumnong, Elastic properties of perovskiteATiO₃ (A=Be, Mg, Ca, Sr, and Ba )and PbBO₃ (B =Ti, Zr, and Hf): first principles calculations, J. Appl. Phys., 2015, 117, 174108.
76. F. D. Murnaghan, Finite deformations of an elastic solid, Am. J. Math., 1937, 59, 235–260.
77. M. Born, On the stability of crystal lattices. I, Math. Proc. Cambridge Philos. Soc., 1940, 36, 160–172.
78. R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349.
79. M. Rasheduzzaman, K. M. Hossain, S. K. Mitro, M. A. Hadi, J. K. Modak and M. Z. Hasan, Structural, mechanical, thermal, and optical properties of inverse-Heusler alloys Cr₂CoZ (Z = Al, In): a first-principles investigation, Phys. Lett. A, 2021, 385, 126967.
80. K. E. Babu, N. Murali, K. V. Babu, P. T. Shibeshi and V. Veeraiah, Structural, elastic, electronic, and optical properties of cubic perovskite CsCaCl₃ compound: an ab initio study, Acta Phys. Pol., A, 2014, 125, 1179–1185.
81. M. N. Islam, M. A. Hadi and J. Podder, Influence of Ni doping in a lead-halide and a lead-free halide perovskites for optoelectronic applications, AIP Adv., 2019, 9, 125321.
82. H. Fu, D. Li, F. Peng, T. Gao and X. Cheng, Ab initio calculations of elastic constants and thermodynamic properties of NiAl under high pressures, Comput. Mater. Sci., 2008, 44, 774–778.
83. M. Zener and S. Siegel, Elasticity and anelasticity of metals, J. Phys. Colloid Chem., 1949, 53, 1468.
84. C. M. Kube, Elastic anisotropy of crystals, AIP Adv., 2016, 6, 095209.

---