Open Access Article
Open Access ArticleInsights into the thermal conductivity of MOF-5 from first principles†
Shenglong Zhang ab,
Jian Liu
ab,
Jian Liu *ab and
Linhua Liu
*ab and
Linhua Liu *ab
*ab
aSchool of Energy and Power Engineering, Shandong University, Jinan, Shandong 250061, China. E-mail: Jian.Y.Liu@sdu.edu.cn; liulinhua@sdu.edu.cn
bOptics and Thermal Radiation Research Center, Institute of Frontier and Interdisciplinary Science, Shandong University, Qingdao, Shandong 266237, China
First published on 17th November 2021
Abstract
Metal–organic frameworks (MOFs) have been extensively studied in many fields due to their abundant porous structures. The mechanism underlying the thermal conduction properties of MOFs, which plays an essential role in a wide variety of applications such as adsorbents and thermoelectric devices, remains elusive. It is also highly desirable to achieve the efficient modulation of thermal conductivity in MOFs via experimentally accessible methods such as metal substitution and strain engineering. In this work, we perform first-principles calculations to investigate the thermal transport properties of MOF-5, a representative prototype of MOFs. We find an ultralow thermal conductivity (κ) of 0.33 W m−1 K−1 at room temperature, in excellent agreement with the experimental measurement. Such ultralow κ is attributed to the strong phonon–phonon scattering that arises from the dense and intertwined low-frequency phonons. The phonon dispersion leads to unusual tuning strategies of κ, since conventional designing guidelines (e.g. substitution of heavier atoms or application of tensile strain is preferred in pursuit of lower thermal conductivity) are not fully obeyed in MOF-5. We find that isovalent substitutions of Zn atoms with (lighter) Mg and (heavier) Cd atoms both result in significant reduction of κ, due to the enhanced phonon scattering rates that are associated with the stronger bond strength and the larger atomic mass, respectively. We further demonstrate that the so-called “guitar string” vibrations are responsible for the anomalous non-monotonic variation of κ in MOF-5 under tensile strain. This work provides fundamental insights into the thermal transport mechanisms in MOF-5, which may have some important implications for the thermal management applications utilizing MOFs.
I. Introduction
Metal–organic frameworks (MOFs) constructed from metal nodes and organic ligands have recently attracted intensive interest,1 due to their high porosity and large surface areas that hold promising potentials in various applications such as catalysis,2,3 gas capture,4,5 water harvesting,6 and energy storage.7–9 The thermal transport property of MOFs is crucial for their performance in practical applications. For example, as an emerging class of porous adsorbents, MOFs with high κ may efficiently transfer the latent heat produced in the exothermic gas adsorption or the endothermic gas desorption (and thus maintain the isothermal conditions).10 On the other hand, as promising candidates for thermoelectric materials,8 MOFs with ultralow κ are highly desirable in order to achieve a high thermoelectric figure of merit.11Experimental measurements of κ in MOFs are challenging due to the difficulty in growing high-quality single crystals to large-enough size in millimeters.12 Existing measurements report κ of 0.32, 0.33, and 0.11 W m−1 K−1 for MOF-5,13 ZIF-8,14 and UiO-66,15 respectively. Such ultralow κ in MOFs, according to force-field-based molecular dynamics (MD) simulations, has been attributed to the short phonon mean free path,16 the mass mismatch between metal and oxygen atoms,17 and the interface thermal resistance between metal nodes and organic linkers.18 Only a limited number of parameter-free investigations exist, and hence first-principles calculations are welcome in order to provide insights into the underlying mechanism responsible for the ultralow κ in MOFs. Besides, κ in MOFs is intimately related to the structural (such as pore size19 and pore shape20) and chemical (such as the type of the functional group21) properties. It is hence highly desirable to investigate the tailoring strategies of κ in MOFs. Cation substitution22,23 and strain engineering24,25 have been demonstrated to be promising methods in tuning the thermal properties of semiconductors. According to the widely accepted guidelines,26 generally speaking, in pursuit of low κ, materials with large atomic mass or weak chemical bonding (giving rise to low phonon group velocity) and complex structure (giving rise to strong anharmonicity and hence phonon–phonon scattering) are desired. Another approach is via phonon engineering,27 e.g. via tailoring the phonon dispersion with small acoustic-optic frequency gap (a–o gap) and large width of the acoustic branches. The complex structures of MOFs render the controlled tuning of κ a challenging task, and hence unraveling the microscopic mechanism of thermal transport in MOFs would benefit the establishment of the structure–property relation.
In this study, using first-principles calculations, we investigate the thermal transport property of MOF-5 (representative of MOFs). The calculated lattice κ at room temperature is 0.33 W m−1 K−1, in line with the reported measurement. We find that κ in MOF-5 decreases with temperature (T), in contrast to previous classical MD results where κ exhibits barely no temperature dependence. The main contribution comes from acoustic phonons whose scattering rates increase with T. The ultralow κ in MOF-5 arises from the significant phonon–phonon scattering among the dense and intertwined low-lying phonons. Such complex phonon dispersion plays a vital role in the tailoring strategy of κ, giving rise to an unusual variation of κ with respect to metal substitution (κ reduces with heavier Cd or lighter Mg substitution) and strain engineering (κ non-monotonically decreases with volumetric tensile strain), in contrast to the conventional wisdom. Notably, the reduction of κ upon Mg substitution is due to the strong metal–oxygen chemical bonding that enlarges the width of acoustic branches and thus enhances the phonon–phonon scattering, while the so-called “guitar string” effect (phonon of transverse motion stiffens upon stretching) gives rise to the initial increase of κ under 4% strain. The unraveled mechanism underlying the thermal transport in MOF-5 may offer novel avenues for the thermal management applications utilizing MOFs.
II. Methods
Density-functional theory calculations are performed using the Quantum ESPRESSO package.28 The Perdew–Burke–Ernzerhof parametrization of the generalized gradient approximation29 is used to describe the exchange-correlation functional. The kinetic energy cut-off for the plane-wave expansion of the electronic wave functions is 120 Ry. The Γ point is used for Brillouin zone sampling. All structural parameters are relaxed until the energy difference is converged within 1 × 10−4 Ry, with a Hellman–Feynman force convergence threshold of 1 × 10−3 Ry Bohr−1. Then, the harmonic and anharmonic interatomic force constants (IFCs) are obtained from the 106-atom unit cell using Phonopy30 and Sheng BTE31 packages, respectively. For the harmonic IFCs, Born effective charges and dielectric tensor contributions to the dynamical matrix are considered. For the anharmonic IFCs, up to the third-nearest neighbors are taken into consideration. The lattice thermal conductivity is obtained by solving the linearized Boltzmann transport equation within the relaxation time approximation. All structures given in figures are produced using VESTA.32The lattice thermal conductivity κ reads
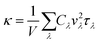 | (1) |
III. Results and discussion
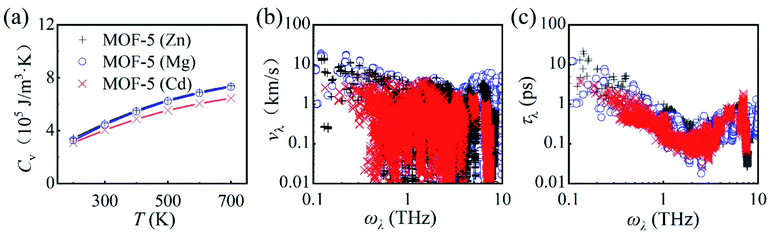
We start with the temperature dependence of κ in MOF-5. For MOF-5 with Zn metal nodes, the optimized lattice parameter is 26.08 Å (see Fig. S1† for the optimized structure), in good agreement with the experimental value of 25.91 Å. The calculated κ reads 0.33 W m−1 K−1 at room temperature, in excellent agreement with the experimental measurement13 of 0.32 W m−1 K−1 at 292 K, as shown in Fig. 1(a). A similar value of 0.31 W m−1 K−1 was reported using classical MD simulations, and the ultralow κ was attributed to the mass mismatch between the metal nodes and the organic linkers,17 in line with the expected trend (a large mass difference leads to a low value of κ).33,34 It was also found that κ slightly increases with T (a character often found in amorphous solids35) due to the suppressed acoustic contributions and the weak temperature-dependent optic contributions.17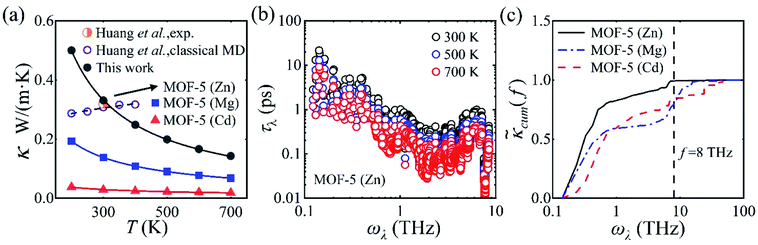 | ||
Fig. 1 (a) Calculated thermal conductivity κ for MOF-5 with different metal atoms (Zn, Mg, or Cd) as a function of temperature (represented by solid symbols), in comparison with experimental measurement13 and classical MD simulations.17 We note that κ obtained from this work, experiment, and classical MD simulation are almost identical (0.33, 0.32, and 0.31 W m−1 K−1, respectively). (b) Phonon transport lifetime τλ of MOF-5 (Zn) at 300, 500, and 700 K. (c) Normalized cumulative thermal conductivity 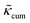 for MOF-5 with different metal atoms (Zn, Mg, or Cd) as a function of phonon frequency at room temperature. All the values are normalized by their lattice thermal conductivities. for MOF-5 with different metal atoms (Zn, Mg, or Cd) as a function of phonon frequency at room temperature. All the values are normalized by their lattice thermal conductivities. | ||
In strong contrast to classical MD simulations,17 we find that κ in MOF-5 decreases with T following the trend κ ∼ T−1. This is reasonable considering that more phonons are excited at elevated temperatures, which results in stronger phonon–phonon scattering rates as shown in Fig. 1(b). We find that κ in MOF-5 is dominated by phonons with vibrational frequency below 8.0 THz which contribute 99.2% of κ, as shown in Fig. 1(c). Phonon dispersion curves above 8.0 THz are rather flat, and hence contribute little to κ. Among these low-frequency phonons, the acoustic phonons contribute nearly 92% of κ, larger than that (62%) obtained with classical MD simulations.17 Thus, κ in MOF-5 exhibits the conventional temperature dependence, suggesting that the Umklapp phonon–phonon scattering dominants the thermal transport.36
It is of fundamental interest to understand the underlying mechanism responsible for the ultralow κ in MOF-5. We find that there exists a marginal overlap in the phonon partial density of states between Zn and O atoms [see Fig. S2(a)†]. Such mismatch between the metal nodes and the organic linkers gives rise to bottlenecks for thermal transport.37,38 Moreover, the specific heat capacity CV and the group velocity vλ are both small (comparable to that of SnSe, a well-known low-κ thermoelectric material in which κ is 0.70 W m−1 K−1, CV is 1.37 × 106 J m−3 K−1, and the highest vλ is 4.1 km s−1).39,40 Note also that, unlike many thermal conductors with high κ, the low-frequency phonon bands in MOF-5 are dense and intertwined as shown in Fig. S2† a characteristic feature that can be found in other MOFs such as MOF-74),41 enforcing the absence of the a–o gap. These low-frequency phonons constitute the major contribution, whereas the optic phonons provide important scattering pathways (in particular through the aao scattering), giving rise to strong phonon–phonon scattering. The overall effect is the ultralow κ in MOF-5.
It can be readily expected that MOFs may not follow the conventional guidelines of tuning κ due to the dense and intertwined phonon band structures. We first investigate the effect of metal substitution (a widely accepted method for structural modulation) on κ in MOF-5. Unexpectedly, a significant reduction of κ is found upon metal substitution, regardless of the mass of the isovalent substitute atom (lighter Mg or heavier Cd), as shown in Fig. 1(a). As low-frequency (below 8 THz) phonons constitute the major contribution to κ in MOF-5 (Zn), we can hence focus on the properties of phonons within this frequency range. Low-frequency (below 8 THz) phonons still constitute the major contribution of 80% and 83% for MOF-5 (Mg) and MOF-5 (Cd), respectively, as shown in Fig. 1(c). Upon metal substitution, the specific heat capacity CV exhibits barely no difference, while the group velocity vλ is in general inversely correlated with the mass of the metal atom, as shown in Fig. 2. The significant reduction of κ hence may only arise from the enhanced phonon–phonon scattering (as discussed below in detail).
We find that metal substitution alters significantly the phonon band structure of low-frequency phonons. In particular, upon Mg (Cd) substitution, the optic branches stiffen (soften) while the acoustic branches widen (narrow), as shown in Fig. S2.† This can be explained as follows. The optic and acoustic vibrations involve mainly motions of the light organic linkers and the heavy metal atoms, respectively. Hence, the width of the acoustic branch varies inversely with the mass of the metal substitute, while the frequency of the optic branch varies proportionally with the strength of the metal–oxygen bond (characterized by the bond dissociation energy,42 i.e. the energy penalty per bond of removing a metal atom from the binding site to vacuum), as shown in Table 1. The softening of the optic branches upon Cd substitution and the widening of the acoustic branches upon Mg substitution facilitates the aao and the aaa scattering processes, respectively. We note that due to the complex and intertwined phonon band structure in MOF-5, the identified mechanism being responsible for facilitating one scattering process may concurrently suppress the other, but the net effect is the overall reduction of phonon lifetime (upon metal substitution).
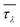 in the range below fo at room temperature. wa describes the width between the lowest and highest acoustic branches at X point in the Brillouin zone
in the range below fo at room temperature. wa describes the width between the lowest and highest acoustic branches at X point in the Brillouin zone
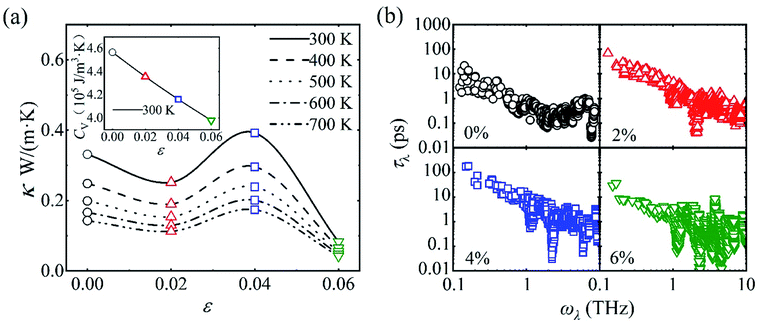
We then investigate the modulation of κ via applying volumetric tensile strains ε. Such response is generally monotonic in bulk materials such as silicon, diamond and zinc oxide.43,44 Interestingly, we obtain an unusual non-monotonic variation of κ with ε in MOF-5, as shown in Fig. 3(a). Notably, the temperature dependence of κ becomes increasingly weaker with the low-frequency optic phonons constituting increasingly more contribution to κ (i.e. κ decreases with T following the trend κ ∼ T−0.8 at ε = 0.06, since optic phonons contribute 29.4% of κ). This may partly explain the weak temperature dependence of MOF-5 found in the previous classical MD study (which is attributed to the relatively less contribution from acoustic phonons).17 Moreover, the anomalous response of κ with respect to ε can be attributed to the interplay between the monotonic decrease of CV and the non-monotonic variation of τλ, as shown in Fig. 3(b).
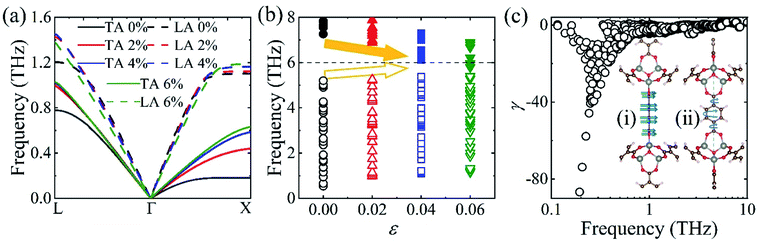
In particular, there exists an anomalous enhancement of κ at ε = 0.04 due to the weakened phonon–phonon scattering. This arises from the so-called “guitar string” effect, namely phonons of transverse motion stiffen upon longitudinal stretching, as shown in Fig. 4. Generally speaking, phonons soften upon volumetric stretching due to the weakened bonding. However, in framework materials, low-frequency transverse or twisting vibration of the organic linkers [see the inset in Fig. 4(c)] may stiffen due to the imposed restoring forces that restrict the motion of the organic linkers (like a stretched string). This is manifested as the negative Grüneisen parameter (γ, defined as −d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω/d ln
ω/d ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V, where ω is the frequency of a phonon mode), as shown in Fig. 4(c). We note here that the large (in magnitude) γ is indicative of strong anharmonicity (and hence low κ),45 and the negative γ is responsible for the negative thermal expansion in MOF-5.46 The stiffening (softening) of phonons below (above) 6 THz upon volumetric stretching is shown in Fig. 4(b). Notably, such “guitar string” effect becomes most pronounced at ε = 0.04 (and almost saturates after that). This narrows the width of the low-frequency phonons, effectively suppressing the phonon–phonon scattering and eventually resulting in the anomalous enhancement of κ.
V, where ω is the frequency of a phonon mode), as shown in Fig. 4(c). We note here that the large (in magnitude) γ is indicative of strong anharmonicity (and hence low κ),45 and the negative γ is responsible for the negative thermal expansion in MOF-5.46 The stiffening (softening) of phonons below (above) 6 THz upon volumetric stretching is shown in Fig. 4(b). Notably, such “guitar string” effect becomes most pronounced at ε = 0.04 (and almost saturates after that). This narrows the width of the low-frequency phonons, effectively suppressing the phonon–phonon scattering and eventually resulting in the anomalous enhancement of κ.
IV. Conclusions
In summary, via first-principles calculations, we have obtained the room-temperature thermal conductivity of 0.33 W m−1 K−1 for MOF-5, in agreement with the experimental measurement. We find that low-frequency phonons constitute the major contribution to κ, giving rise to enhanced scattering (and suppressed thermal conductivity) with increasing temperature. The ultralow κ is attributed to the strong phonon–phonon scattering that arises from the dense and intertwined phonon band structure at low frequencies with the absence of the a–o gap. As a result, the conventional design principles for thermal conductivity modulation are not fully followed. We find that substituting the metal Zn atoms with heavier Cd or lighter Mg atoms both results in a significant reduction of κ, due to the softening of the optic branches and the widening of the acoustic branches that facilitates the aao and the aaa scattering processes, respectively. We also demonstrate an anomalously non-monotonic response of κ with respect to volumetric tensile strains, namely there exists an unusual enhancement of κ under 4% strain that can be attributed to the so-called “guitar string” effect. This study sheds some new light on the mechanism of thermal transport in MOF-5, which may provide useful information for the thermal management utilizing MOFs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by the National Natural Science Foundation of China [Grant No. 52076123]. J. L. was supported by the Qilu Young Scholar Program of Shandong University.References
- T. Tian, Z. X. Zeng, D. Vulpe, M. E. Casco, G. Divitini, P. A. Midgley, J. Silvestre-Albero, J. C. Tan, P. Z. Moghadam and D. Fairen-Jimenez, Nat. Mater., 2018, 17, 174–179 CrossRef CAS PubMed.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- Y. Li, G. Hou, J. Yang, J. Xie, X. Yuan, H. Yang and M. Wang, RSC Adv., 2016, 6, 16395–16403 RSC.
- C. L. Hobday, C. H. Woodall, M. J. Lennox, M. Frost, K. Kamenev, T. Düren, C. A. Morrison and S. A. Moggach, Nat. Commun., 2018, 9, 1429 CrossRef PubMed.
- M. Du, L. Li, M. Li and R. Si, RSC Adv., 2016, 6, 62705–62716 RSC.
- H. Kim, S. Yang, S. R. Rao, S. Narayanan, E. A. Kapustin, H. Furukawa, A. S. Umans, O. M. Yaghi and E. N. Wang, Science, 2017, 356, 430–432 CrossRef CAS PubMed.
- L. F. Yang, S. H. Qian, X. B. Wang, X. L. Cui, B. L. Chen and H. B. Xing, Chem. Soc. Rev., 2020, 49, 5359–5406 RSC.
- A. A. Talin, A. Centrone, A. C. Ford, M. E. Foster, V. Stavila, P. Haney, R. A. Kinney, V. Szalai, F. El Gabaly, H. P. Yoon, F. Leonard and M. D. Allendorf, Science, 2014, 343, 66–69 CrossRef CAS PubMed.
- R. Mehek, N. Iqbal, T. Noor, M. Z. B. Amjad, G. Ali, K. Vignarooban and M. A. Khan, RSC Adv., 2021, 11, 29247–29266 RSC.
- J. Wieme, S. Vandenbrande, A. Lamaire, V. Kapil, L. Vanduyfhuys and V. Van Speybroeck, ACS Appl. Mater. Interfaces, 2019, 11, 38697–38707 CrossRef CAS PubMed.
- E. Redel and H. Baumgart, APL Mater., 2020, 8, 060902 CrossRef CAS.
- J. Huang, X. Xia, X. Hu, S. Li and K. Liu, Int. J. Heat Mass Transf., 2019, 138, 11–16 CrossRef CAS.
- B. L. Huang, Z. Ni, A. Millward, A. J. H. McGaughey, C. Uher, M. Kaviany and O. Yaghi, Int. J. Heat Mass Transf., 2007, 50, 405–411 CrossRef CAS.
- B. Y. Cui, C. O. Audu, Y. J. Liao, S. T. Nguyen, O. K. Farha, J. T. Hupp and M. Grayson, ACS Appl. Mater. Interfaces, 2017, 9, 28139–28143 CrossRef CAS PubMed.
- J. Huang, X. X. Xia, X. J. Hu, S. Li and K. Liu, Int. J. Heat Mass Transf., 2019, 138, 11–16 CrossRef CAS.
- X. Zhang and J. Jiang, J. Phys. Chem. C, 2013, 117, 18441–18447 CrossRef CAS.
- B. L. Huang, A. J. H. McGaughey and M. Kaviany, Int. J. Heat Mass Transf., 2007, 50, 393–404 CrossRef CAS.
- S. Wieser, T. Kamencek, J. P. Duerholt, R. Schmid, N. Bedoya-Martinez and E. Zojer, Adv. Theor. Simul., 2021, 4, 2000211 CrossRef CAS.
- K. B. Sezginel, S. Lee, H. Babaei and C. E. Wilmer, J. Phys. Chem. C, 2020, 124, 18604–18608 CrossRef CAS.
- H. Babaei, A. J. H. McGaughey and C. E. Wilmer, Chem. Sci., 2017, 8, 583–589 RSC.
- P. Ying, J. Zhang, X. Zhang and Z. Zhong, J. Phys. Chem. C, 2020, 124, 6274–6283 CrossRef CAS.
- B. Peng, H. Zhang, H. Shao, Y. Xu, X. Zhang and H. Zhu, RSC Adv., 2016, 6, 5767–5773 RSC.
- N. K. Ravichandran and D. Broido, Phys. Rev. X, 2020, 10, 021063 CAS.
- H. Xie, T. Ouyang, É. Germaneau, G. Qin, M. Hu and H. Bao, Phys. Rev. B, 2016, 93, 075404 CrossRef.
- Y. Han, J.-Y. Yang and M. Hu, Nanoscale, 2018, 10, 5229–5238 RSC.
- D. R. Clarke, Surf. Coat. Technol., 2003, 163–164, 67–74 CrossRef CAS.
- M. Nomura, J. Shiomi, T. Shiga and R. Anufriev, Jpn. J. Appl. Phys., 2018, 57, 080101 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Solid State, 2008, 78, 134106 CrossRef.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- K. Aryana, D. A. Stewart, J. T. Gaskins, J. Nag, J. C. Read, D. H. Olson, M. K. Grobis and P. E. Hopkins, Nat. Commun., 2021, 12, 2817 CrossRef CAS PubMed.
- Z. Tian, H. Hu and Y. Sun, Int. J. Heat Mass Transf., 2013, 61, 577–582 CrossRef CAS.
- J. J. Freeman and A. C. Anderson, Phys. Rev. B: Solid State, 1986, 34, 5684–5690 CrossRef CAS PubMed.
- T. M. Tritt, Theory, Properties, and Applications, 2004 Search PubMed.
- Y. Hong, J. Zhang and X. C. Zeng, Nanoscale, 2016, 8, 19211–19218 RSC.
- B. Li, J. Lan and L. Wang, Phys. Rev. Lett., 2005, 95, 104302 CrossRef PubMed.
- C. W. Li, J. Hong, A. F. May, D. Bansal, S. Chi, T. Hong, G. Ehlers and O. Delaire, Nat. Phys., 2015, 11, 1063–1069 Search PubMed.
- P.-C. Wei, S. Bhattacharya, J. He, S. Neeleshwar, R. Podila, Y. Y. Chen and A. M. Rao, Nature, 2016, 539, E1–E2 CrossRef CAS PubMed.
- X. Wang, R. Guo, D. Xu, J. Chung, M. Kaviany and B. Huang, J. Phys. Chem. C, 2015, 119, 26000–26008 CrossRef CAS.
- B. M. Rice, S. Sahu and F. J. Owens, J. Mol. Struct.: THEOCHEM, 2002, 583, 69–72 CrossRef CAS.
- X. Li, K. Maute, M. L. Dunn and R. Yang, Phys. Rev. B: Solid State, 2010, 81, 245318 CrossRef.
- J. A. Seijas-Bellido, R. Rurali, J. Íñiguez, L. Colombo and C. Melis, Phys. Rev. Mater., 2019, 3, 065401 CrossRef CAS.
- J. Callaway, Phys. Rev., 1959, 113, 1046–1051 CrossRef CAS.
- W. Zhou, H. Wu, T. Yildirim, J. R. Simpson and A. R. H. Walker, Phys. Rev. B: Solid State, 2008, 78, 054114 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra07022c |
| This journal is © The Royal Society of Chemistry 2021 |