Open Access Article
Open Access ArticleThe dolabellane diterpenes as potential inhibitors of the SARS-CoV-2 main protease: molecular insight of the inhibitory mechanism through computational studies†
Nanik Siti Aminah *ab,
Muhammad Ikhlas Abdjanac,
Andika Pramudya Wardanaac,
Alfinda Novi Kristantiab,
Imam Siswantoad,
Khusna Arif Rakhmane and
Yoshiaki Takayaf
*ab,
Muhammad Ikhlas Abdjanac,
Andika Pramudya Wardanaac,
Alfinda Novi Kristantiab,
Imam Siswantoad,
Khusna Arif Rakhmane and
Yoshiaki Takayaf
aDepartment of Chemistry, Faculty of Science and Technology, Universitas Airlangga, Surabaya 60115, Indonesia. E-mail: nanik-s-a@fst.unair.ac.id
bBiotechnology of Tropical Medicinal Plants Research Group, Universitas Airlangga, Indonesia
cPh.D. Student of Mathematics and Natural Sciences, Faculty of Science and Technology, Universitas Airlangga, Komplek Kampus C UNAIR, Jl. Mulyorejo, 60115, Surabaya, Indonesia
dBioinformatic Laboratory, UCoE Research Center for Bio-Molecule Engineering, Universitas Airlangga, Surabaya, Indonesia
eDepartment of Chemistry Education, Universitas Khairun, Ternate, Indonesia
fFaculty of Pharmacy, Meijo University, Nagoya, Japan
First published on 10th December 2021
Abstract
An investigation has been carried out on natural products from dolabellane derivatives to understand their potential in inhibiting the SARS-CoV-2 main protease (3CLpro) using an in silico approach. Inhibition of the 3CLpro enzyme is a promising target in stopping the replication of the SARS-CoV-2 virus through inhibition of the subsite binding pocket. The redocking process aims to determine the 3CLpro active sites. The redocking requirement showed a good pose with an RMSD value of 1.39 Å. The combination of molecular docking and MD simulation shows the results of DD13 as a candidate which had a good binding affinity (kcal mol−1) to inhibit the 3CLpro enzyme activity. Prediction of binding free energy (kcal mol−1) of DD13 using the Molecular Mechanics-Poisson Boltzmann/Generalized Born Surface Area (MM-PB/GBSA) approach shows the results ΔGbind(MM-GBSA): −52.33 ± 0.34 and ΔGbind(MM-PBSA): −43.52 ± 0.42. The key residues responsible for the inhibition mechanism are Hie41, Ser46, Met49, Asn142, Cys145, Hie163, Met165, and Gln189. Additionally, pharmacokinetic prediction recommended that DD13 had promising criteria as a drug candidate. The results demonstrated in this study provide theoretical information to obtain a potential inhibitor against the SARS-CoV-2 main protease.
Introduction
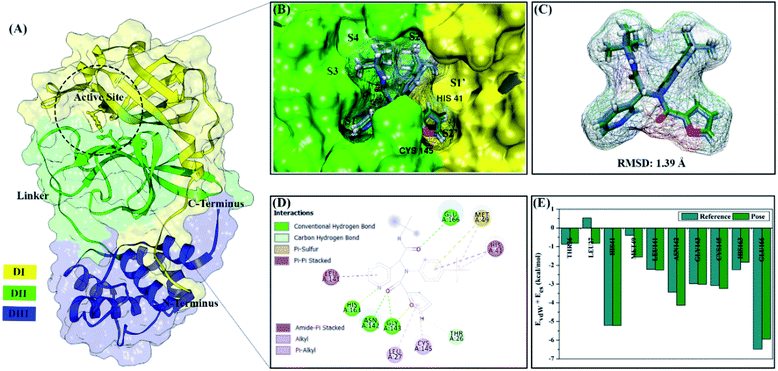
Coronavirus disease 2019 (COVID-19) is a pandemic that has been going on since 2019. The disease is caused by acute respiratory syndrome coronavirus 2 (SARS-CoV-2).1,2 In general, the coronaviruses are positive-sense single-stranded RNA viruses in the coronavirus genus.2,3 The coronavirus has multiple open reading frames (ORF), such as ORF1 and ORF2. These frames are responsible for producing the two polypeptides pp1a and pp1ab.4,5 Then, these polypeptides are processed by the main protease or 3C-like protease (MPro or 3CLPro), which is responsible for the coronavirus replication cycle.6,7 Therefore, the main protease SARS-CoV-2 becomes a promising target of COVID-19 disease drug development.7,8Structurally, the SARS-CoV-2 main protease has three domains, such as domain I (residues 10–99), domain II (residues 100–184), and domain III (residues 201–300) (Fig. 1A). Additionally, residue 185–200 is a long loop region that connects domain I and domain II.9 More specifically, the subsite binding pocket SARS-CoV-2 main protease contains His41 and Cys145 residues, which play a crucial role as catalysis centers.10 Mutations that occurred in amino acid residues for the main proteases of SARS-CoV-2 and SARS-CoV showed a similarity percentage of 83% with 12 amino acid residue mutations in each sequence (residue number: 35, 46, 65, 86, 88, 94, 134, 180, 202, 267, 285, and 286).11,12 It had been reported, the mutation of the Ser46 amino acid residue causes a conformational change in the subsite binding pocket of SARS-CoV-2 main protease.13 These changes can increase the surface area and volume in the subsite binding pocket of SARS-CoV-2 main protease. It is the main focus variable needed to understand because the subsite binding pocket plays a crucial role in the inhibitory mechanism of SARS-CoV-2 main protease.14 Studies on the interaction of inhibitors with amino acid residues in the subsite binding pocket are expected to be a solution to increase the development possibility of SARS-CoV-2 main protease inhibitors.
The development of SARS-CoV-2 main protease inhibitors was reported by several previous studies.15,16 One of them is the compound ML188, which has an inhibitory activity of the 3CLpro enzyme with an IC50 value of 2.5 μM.12 Besides, several reports state that natural product compounds have potential as SARS-CoV-2 main protease inhibitor.17–20 Some of them that have been reported are diterpene derivatives that have the inhibitor activity of SARS-CoV main protease.21 The report provides information that the diterpene derivative has the potential to inhibit the main protease of SARS-CoV-2. Several works of literature give similar recommendations about the potential of diterpenes as a promising SARS-CoV-2 main protease inhibitor.19,20 The selection of inhibitor candidates from natural products is starting with the consideration that compounds already have biological activity against some diseases or infections.22 The dolabellane (subclass diterpene) can be isolated from Caribbean Eunicea laciniata23 and Nigella damascena.24 These compounds are the main focus to investigate their potential as candidate inhibitors in this study. Some research reported dolabellane compounds had potential as antivirals.20,24,25 Hopefully, this research can provide information about the potential of dolabellane derivatives as inhibitors against the main protease SARS-CoV-2.
Theoretical studies using in silico approach provide another alternative in finding candidate compounds that have potential as main protease inhibitors of SARS-CoV-2.26–28 The combination of molecular docking and Molecular Dynamic (MD) simulation provides a comprehensive, structure-based approach in studying the interaction of inhibitors with the SARS-CoV-2 main protease at the molecular level.11,22 Several previous studies have offered an MD simulation approach for Mpro or 3CLpro enzymes to study their conformational dynamics.22,29–31 In particular, the interaction of the inhibitor with amino acid residues at the subsite binding pocket. Additionally, structure-based studies can provide a more detailed description of the inhibition mechanism through interactions with residues of the catalytic centre (His41 and Cys145), which regulate the replication of the COVID-19 virus.10,13 An important variable that is considered in this study is binding free energy (ΔGbind) to predict the inhibitor–receptor binding affinity. It is a crucial point to evaluate the criteria for a promising inhibitor of SARS-CoV-2 main protease. Besides, pharmacokinetic studies are expected to provide initial information of selected inhibitors as drug candidates that meet the criteria.
Methodology
Inhibitor and protein preparation
The selection of a target protein using co-crystal SARS-CoV-2 main protease (3CLpro) from the protein data bank (PDB ID: 7L0D). The complex crystal contains a native ligand (PDB ID: 0EN), namely N-[(1R)-2-(tert-butylamino)-2-oxo-1-(pyridine-3-yl)ethyl]-N-(4-tert-butylphenyl)furan-2-carboxamide or ML188 on the active site of the 3CLpro enzyme as a non-covalent inhibitor. The ML188 (0EN) ligand was a reference in this study because it has known as an inhibitor of the 3CLpro enzyme.12 ML188 inhibitor coordinates and amino acid residues (receptors) were extracted from the crystal structure 3CLpro using the Chimera version 1.13 package for docking and MD simulation purposes. Meanwhile, the candidate ligands used in this study were 14 diterpene derivatives (Fig. S1†) of the dolabellane type obtained from the literature review.20 Calculation of electrostatic potential (ESP) charges for candidate ligands uses the Semiempirical Quantum Parametric Method-3 (SQM-PM3) contained in the Gaussian 16 package.32 The AMBER FF14SB force field and Austin Model 1-bond charge correction are needed to calculate coordinate parameters of ligand and receptor.Molecular docking
The molecular docking study involves two stages: (i) the redocking process and (ii) docking candidate ligands through the DOCK6 package. The redocking process aims to determine the coordinates of the active site of the 3CLpro enzyme based on the selected sphere (a radius 10 Å from the 0EN coordinate). The scoring function based on the grid score function with the grid spacing used is 0.3 Å. The minimization process aims to minimize energy in each system. The redocking criteria evaluate through the best pose with RMSD criteria 2.0 Å.33,34 The footprint analysis was carried out to investigate the interaction between native ligands and amino acid residues on the active site. The redocking process that meets the criteria is used as the initial coordinate for the candidate docking process. The flexible conformational type is used in molecular docking to determine the interaction between the inhibitor and 3CLpro in the gas phase.Molecular dynamics simulation
Topology preparation (ligand, receptor, receptor-solvated, complex, and complex-solvated) on each system using tleap tools in the AMBER18 package. The application of the general AMBER force field (GAFF) to each ligand is used as the initial coordinates for the topology preparation of each system.35 These coordinates are the integration of the score function from the molecular docking results. Especially in receptor-solvated topology, it aims to see the dynamical conformation of the 3CLpro enzyme without the influence of inhibitors that bind to the active site. The solvent model used is TIP3P water solvent using a minimum distance of 12 Å. The ion neutralizing system used is the sodium ions (Na+) randomly added. The water molecules were minimized by 500 steps of steepest descent and 1500 steps of conjugated gradient, while the rest of the atoms were restrained. Then, the receptor and ligand were minimized by 500 steps of steepest descent and 1500 steps of the conjugated gradient with the restrained solvent. In the last step of minimization, the entire system was fully minimized by the same procedure.The simulation process is carried out through several stages, such as heating, equilibrium, and production. The heating stage of the system uses a gradual heating step from 10 K to 310 K (200 ps) with a harmonic restraint of 30 kcal mol−1 Å−2. The equilibrium stage (1300 ps) for each system was carried out periodically through four steps with harmonic restraint of 30, 20, 10, and 5 kcal mol−1 Å−2. Finally, the entire system is simulated under the NPT ensemble (310 K and 1 atm) until reaching 100 ns. The production stage (0–100 ns) aims to produce trajectories for further analysis and evaluation.36
Trajectories analysis
Trajectories analysis uses several tools available in the AMBER18 package for calculation purposes, such as processs mdout.perl and cpptraj tools. The overall analysis of trajectories (0–100 ns) aims to evaluate the stability of each system through several variables, such as total energy and root-meant-square displacement (RMSD). Meanwhile, the analysis of other variables, such as flexibility, compactness, solvent accessibility, binding free energy, energy decomposition, atom contacts, hydrogen bonding uses the last 20 ns (80–100 ns) trajectories. This consideration is taken based on the efficiency of calculation time.37 Besides, the trajectories used are trajectories that have achieved good stability. Its characterized by no significant fluctuations in the RMSD complex. To evaluate several variables such as percentage of atom contacts (PAC) and percentage of hydrogen bonding (PHB) can be calculated using eqn (1) and (2). The number of frames per H-bond or atom contact (Nfra) is divided by the total number of frames (Ntot) during the simulation time of 2000 frames.
 | (1) |
 | (2) |
Calculation of binding free energy (ΔGbind) and energy decomposition (ΔGresiduebind) using the MMPBSA.py tools available in the AMBER18 package.38 The binding free energy was calculated using the Molecular Mechanics-Poisson Boltzmann/Generalized Born Surface Area (MM-PB/GBSA) approach. Several key parameters were used for each approach: MM-GBSA (the generalized Born solvation model: 2, the concentration of mobile counterions in solution: 0.00 M, and nonpolar contribution of solvation free energy: 0.0072) and MM-PBSA (molecule dielectric constant: 1, solvent dielectric constant: 80.0, solvent probe radius: 1.4 Å, and nonpolar contribution of solvation free energy: 0.0072). Mathematically, binding free energy can be calculated using eqn (3). However, the entropy change (−TΔS) is ignored because of the high computational cost and low prediction accuracy.39 Specifically, the energy components that affect binding free energy are described in the gas phase (eqn (4)) and the solvation phase (eqn (5)). Energy components in the gas phase show energy components consisting of bonded energy (ΔEbonded), van der Waals energy (ΔEvdW), and electrostatic energy (ΔEele). In particular, bonded energy identifies bond, angle, and torsion energies, which are assumed to have conformational energy equal to zero. Meanwhile, the solvent phase is the total of Poisson Boltzmann/generalized Born models (ΔGelesol) and solvent-accessible surface area energy (ΔGnonpolarsol). The energy decomposition uses the MM-GBSA approach, which can be calculated completely using eqn (6).
| ΔGbind = ΔGgas + ΔGsolv − TΔS | (3) |
| ΔGgas = ΔEbonded + ΔEvdW + ΔEele | (4) |
| ΔGsol = ΔGelesol + ΔGnonpolarsol | (5) |
| ΔGresiduebind = ΔEvdW + ΔGnonpolarsol(GB) + ΔEele + ΔGelesol(GB) | (6) |
ADMET calculation
The study of absorption, distribution, metabolism, excretion and toxicity (ADMET) is also studied to see the ability of the candidate's biological activity as a drug in the body. Prediction of these pharmacokinetic properties using the pkCSM web service, which can describe in detail the ADMET properties.40Results and discussion
Molecular docking study
All steps of molecular docking are performed by the DOCK6 package. The active site determination using initial coordinates of the native ligand (0EN) extracted from the crystal structure is based on a cluster sphere selection. The redocking process provides convenience and accuracy in determining the active site of the receptor.33 Structurally, the active site of the 3CLpro enzyme has His41 and Cys145 residues as catalytic canters located on the subsite binding pocket.10 The redocking results showed that the native ligand was docked very well to the active site of the receptor (Fig. 1B). The data is supported by the redocking results of the native ligand showing a good pose with an RMSD value of 1.39 Å and a grid score: −72.58 kcal mol−1 using a flexible conformation (Fig. 1C). This value explains that the pose ligand coordinates have coordinates that are close to the crystal coordinates. It can describe more the accuracy of the interaction between the ligand and amino acid residues on the 3CLpro subsite binding pocket. In particular, the interaction of native ligands with amino acid residues on the subsite binding pocket, including S2′ (Thr25 and Leu27), S2 (His41 and Met49), S1 (Leu141, Asn142, Gly143, Cys145, His163), and S3 (Glu166). These amino acid residues are the main amino acid residue that responsible for the 0EN–3CLpro interaction. Besides, the amino acid residues on the S1′ and S4 binding subsites only show a van der Waals interaction. There are four residues, such as Asn142, Gly143, His163, and Glu166 responsible for hydrogen bonding interactions (Fig. 1D). Hydrogen bonding (H-bond) variables have a crucial role in explaining the inhibition mechanism of the 3CLpro enzyme.14,22 The footprint analysis was showed on ten amino acid residues on the 3CLpro active site. This variable was performed by comparing the van der Waals energy and electrostatic energy (EvdW + Ees) ligand reference and pose in the gas phase (Fig. 1E). Overall, the redocking process showed good criteria in determining the active site of the 3CLpro enzyme. However, these results need to be studied more comprehensively using molecular dynamic simulation (discussed in more detail below).The coordinates and parameters obtained from the redocking results are used as the main reference in the docking candidate process. The optimized candidates docked into the active site of the 3CLpro enzyme using a flexible conformation (Fig. 2A). The results show that two candidates have good interactions with 3CLpro, such as DD9: −72.66 kcal mol−1 and DD13: −74.53 kcal mol−1 (Fig. 2B). This consideration is taken based on the grid score pose < grid score candidate. The lower value of the grid score shows better interaction with the receptor.41 Overall, the energy contribution (higher negativity value) is shown by EvdW compared to Ees in the gas phase. The results of the candidate docking based on the grid score function are described in detail in Table S1.†
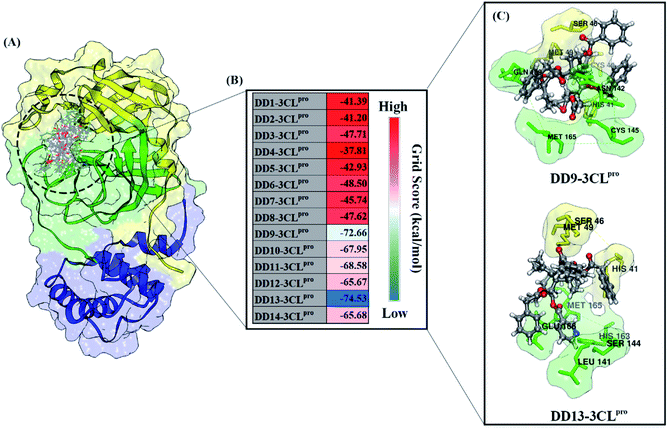 | ||
| Fig. 2 Molecular docking analysis: (A) candidates–3CLpro interaction in the active site, (B) heat map of grid score, and (C) selected candidates based on lowest grid score value. | ||
The inhibitory mechanism of candidate against the 3CLpro enzyme was studied through the interaction of amino acid residues on the subsite binding pocket.42 Each candidate shows that there are amino acid residues responsible for the inhibitor–receptor interaction: DD9–3CLpro (His41, Cys44, Ser46, Met49, Asn142, Cys145, Met165, and Gln189) and DD9–3CLpro (His41, Ser46, Met49, Leu141, Ser144, His163, Met165, and Glu166) (Fig. 2C). Specifically, there are residues responsible for H-bond interactions with each candidate ligand, including DD9–3CLpro (Ser46, Cys146, Asn142, and Gln189) and DD13–3CLpro (Ser46, His163, and Glu166) (Fig. S2†). These results provide a good initial image in understanding the interaction of keys residues at the molecular level. Molecular docking studies are effective in obtaining the initial coordinates through relatively fast calculations. It aims to facilitate the process of further analysis using MD simulation.
Conformational dynamic study: stability, compactness, and flexibility of each system
The quality of the conformational dynamics of each system is evaluated through several variables, such as stability,11,43 compactness,44 and flexibility.45,46 The calculation of the root-mean-square deviation (RMSD) aims to determine the stability of each system in the form of complex, backbone, and ligand RMSD (Fig. 3). Notably, the all atoms RMSD did not show any significant fluctuation in the last 20 ns of trajectories (80–100 ns). Additionally, each complex showed similar fluctuations with the apo protein (3CLpro enzyme). This data is reinforced by the average value of all atoms RMSD (nm), which is relatively the same for each system: 3CLpro: 0.25 ± 0.04, 0EN–3CLpro: 0.26 ± 0.04, DD9–3CLpro: 0.26 ± 0.04, and DD13–3CLpro: 0.27 ± 0.04. These results describe that the level of stability in each complex (inhibitor–3CLpro) showed good results. The presence of an inhibitor on the 3CLpro active site did not give a significant change in the 3CLpro structure. It becomes an important parameter in evaluating other variables. Good system stability will provide a clear image of the interaction between the inhibitor and the 3CLpro enzyme. The same fluctuation is also shown by the average value of the backbone and ligand RMSD (Table S2†). The total energy analysis was carried out to see the system stability from the thermodynamic aspect (Fig. S3†). The data shows that each system has converged and has not experienced excessive fluctuations (Table S2†). The stability achieved in each system, especially in the last 20 ns trajectories, was used for further analysis purposes.11,37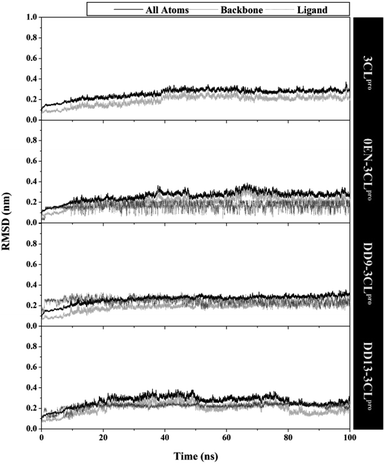 | ||
| Fig. 3 The root-mean-square displacement of all atoms, backbone (Cα, C, N, and O), and ligand for each system plotted along the 100 ns of MD simulation. | ||
The radius of gyration (RoG) analysis aims to obtain more information about equilibrium conformation and structure compactness during the last 20 ns of simulation.37 The results show that each system has a relatively compact structure with insignificant fluctuation (∼2.23 nm) (Fig. S4†). It is further strengthened by the average value of RoG on Apo protein (without inhibitor) and complex (with inhibitor) (Table S2†). Additionally, the results of the RoG analysis also show that each system has a stable folded structure.
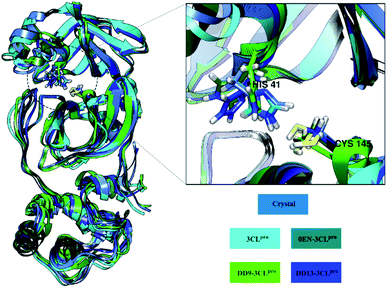
The root-mean-square fluctuation (RMSF) and B-factor calculation aim to see the flexibility of each system.46,47 The DD13–3CLpro complex showed significant RMSF and B-factor fluctuations compared to 3CLpro, 0EN–3CLpro, and DD9–3CLpro (Fig. S5†). In contrast, Apo protein (3CLpro) has a more rigid structure because it has lower fluctuations. Overall, the flexibility for each system is 3CLpro > 0EN–3CLpro, and DD9–3CLpro (Table S2†). Meanwhile, an explanation of the fluctuations that occur in each system is found in the DI loop region (47–53, 60–62, 92) and DIII (215–222 and 274–280). However, overall there was no significant conformational change during the simulation time for each structure (Fig. 4). Especially in the backbone (Cα, C, N, and O), fluctuations show that the average structure has coordinates that are similar to the crystal structure. It indicates that the conformational flexibility of the structure in each system is quite stable during the simulation time. This data is supported by the stability of the complex RMSD and backbone RMSD at the last 20 ns simulation (Fig. 4). It should be noted, the high structural flexibility leads to high conformational complexity. More specifically, flexibility at the enzyme active site may play a crucial role in the potential binding of the inhibitor.30 Therefore, it is necessary to carry out a more in-depth analysis of the key residues on the 3CLpro active site. It aims to see the flexibility of the key residues, especially residues His41 and Cys145. The RMSF residues of His41 and Cys145 on the active site were investigated to see the fluctuation of the two residues as a catalytic centre. The results showed that the RMSF (nm) of the two residues for each structure: 3CLpro (His41: ∼0.30, Cys145: ∼0.17), 0EN–3CLpro (His41: ∼0.48, Cys145: ∼0.30), DD9–3CLpro (His41: ∼0.39, Cys145: ∼0.28), and DD13–3CLpro (His41: ∼0.55, Cys145: ∼0.29). The comparison of coordinates (His41 and Cys145 residues) between each system with the initial coordinates of the crystal structure shows that there are differences in conformation. It is possible because along the last 20 ns simulation, there is an interaction with the inhibitor that affects the force field (steric) on the two residues. Additionally, it could be caused by the presence of a water molecule on the 3CLpro active site, which affects the dynamic conformation of each system.13,48 Hopefully, the study on the conformation dynamics of each system during the simulation can explain the interaction of inhibitor–3CLpro at the molecular level.
Solvent accessibility of inhibitor–3CLpro enzyme
The simulation process considers the solvent phase (water molecules) as a parameter that plays an important role in mediating the interaction of the inhibitor with the 3CLpro enzyme.48,49 Based on the previous section, the influence of water molecules plays an important role in influencing the interaction of inhibitors with amino acids residue on the active site. Solvent accessibility surface area (SASA) is one of the variables that can describe the water's ability to access all surface and active site surfaces during the simulation time (Fig. 5). Overall, the access capability on the entire surface shows that each system has a value of all surface > ∼140.00 nm2 (DD9–3CLpro > 3CLpro > DD13–3CLpro > 0EN–3CLpro) and active site > ∼9.00 nm2 (DD9–3CLpro > DD13–3CLpro > 3CLpro > 0EN–3CLpro). Especially the SASA of the active site (radius 5 Å) is the main focus. The candidate ligands are more accessible to water solvent than Apo protein and native ligands based on the average SASA value of each system (Table S2†).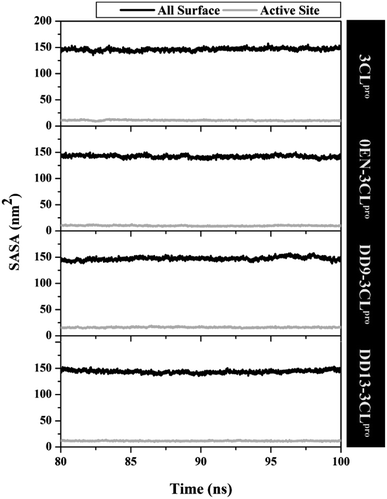 | ||
| Fig. 5 The solvent-accessible surface area using the last 20 ns trajectories. A radius of 5 Å was used to calculate the SASA in the active site of each system. | ||
The fluctuation of the key residues on the enzyme active site causes a water molecule traffic that is important for maintaining protein structure.30 Additionally, the effect of water molecules causes the stability of the protein structure to increase through the interaction of hydrogen bonds, salt bridges, and π–π stacking.31,50 It affects the conformation of the inhibitor at the active site of the 3CLpro enzyme. The presence of water molecules on the enzyme active site provides more opportunities to interact with the inhibitor interface. It is necessary to analyse the water molecules when approaching the inhibitor during the simulation.
The water molecules close to the inhibitor heteroatoms (O and N) in each complex are evaluated through the radial distribution function (RDF).11 The analysis of this variable was performance based on the assumption that the inhibitor present on the active site of the complex could interact directly with water molecules. To test the RDF value, it can show by the integration number on the first minimum value of heteroatoms in each inhibitor.51 The 0EN–3CLpro complex showed that the N2 atom in the first peak at a distance of ∼0.3 nm had relatively high access to water molecules. In contrast, the rest of the heteroatoms in the 0EN–3CLpro complex (N1, N3, O1, O2, and O3) suggest low water molecule access to these atoms (Fig. S6†). Meanwhile, the DD9–3CLpro complex showed atoms O15, O19, O26, O32, and O35 (the first peak was consistent at the distance: ∼0.27 nm) having relatively high access of water molecules on the active site compared to the rest of the atoms, such as O16, O18, O20, O21, and O30 (Fig. S7†). On the other hand, the DD13–3CLpro complex showed atoms O25, O27, and O54 O35 (the first peak was consistent at a distance: ∼0.27 nm) having relatively high access of water molecules on the active site compared to the rest of the atoms O15, O16, O18, O19, O20, O30, and N59 (Fig. S8†). Finally, we can assume that the inhibitor, which is relatively accessible to water molecules belongs to the complex DD9–3CLpro > DD13–3CLpro > 0EN–3CLpro based on the total integration number. This data is also supported by the average value of SASA on the active site, which shows the same conclusion (Table S2†). This consideration was taken on the assumption that the more water molecules contained in the active site of the complex (SASA-active site), the greater the chance of water molecules interacting with the inhibitor. Investigation of the presence of water molecules at the active site of the complex provides a more comprehensive image of the effect of water solvent on molecular level interactions.
The binding affinity of inhibitor against the 3CLpro enzyme
Determination of the binding affinity of each inhibitor to the 3CLpro enzyme was calculated based on 100 frames extracted from the last 20 ns trajectories. The binding affinity calculation process uses the MM-PB/GBSA approach in the gas and solvent phases.52 The calculation process is showed in detail by considering several energy components described in Table 1. The calculation process for each energy component is the main focus to describe binding free energy (ΔGbind). The energy component in the gas phase (ΔGgas) shows that a good energy contribution is found in the van der Waals energy (EvdW) compared to electrostatic energy (Eele). On the other hand, the energy contribution to the solvent phase (ΔGsol) shows a less favourable contribution to the polar energy for the Poisson Boltzmann/generalized Born model (Eelesol(PB) and Eelesol(GB)). Centrally, this has an unfavourable impact on the affinity binding of the inhibitor–3CLpro.| Energy component | 0EN–3CLpro | DD9–3CLpro | DD13–3CLpro |
|---|---|---|---|
| Gas phases | |||
| EvdW | −47.15 ± 0.22 | −43.40 ± 0.29 | −67.80 ± 0.31 |
| Eelec | −35.22 ± 0.41 | −8.34 ± 0.35 | −32.03 ± 0.39 |
| ΔGgas | −82.37 ± 0.42 | −51.75 ± 0.38 | −99.83 ± 0.50 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Solvation phases | |||
| Eelesol(GB) | 44.85 ± 0.22 | 27.56 ± 0.25 | 55.19 ± 0.31 |
| Enonpolarsol(GB) | −5.77 ± 0.02 | −5.40 ± 0.03 | −7.68 ± 0.02 |
| ΔGsol(GB) | 39.08 ± 0.22 | 22.16 ± 0.24 | 47.50 ± 0.30 |
| Eelesol(PB) | 48.19 ± 0.26 | 29.41 ± 0.37 | 64.63 ± 0.37 |
| Enonpolarsol(PB) | −6.53 ± 0.01 | −6.66 ± 0.03 | −8.32 ± 0.02 |
| ΔGsol(PB) | 41.66 ± 0.25 | 22.75 ± 0.36 | 56.31 ± 0.36 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Binding free energy | |||
| ΔGbind(GB) | −43.29 ± 0.29 | −29.59 ± 0.26 | −52.33 ± 0.34 |
| ΔGbind(PB) | −40.71 ± 0.33 | −28.99 ± 0.40 | −43.52 ± 0.42 |
The contribution of each energy component provides a clear picture of the binding free energy. The DD13–3CLpro complex showed promising ΔGbind using the MM-GBSA and MM-PBSA approaches. It is taken from the consideration that DD13–3CLpro ΔGbind is smaller than 0EN–3CLpro ΔGbind as a reference. Thus, the candidate DD13 inhibitor has a promising potential in inhibiting the 3CLpro enzyme. On the other hand, the DD9–3CLpro complex showed a less favourable ΔGbind because it had a higher ΔGbind value than the 0EN–3CLpro ΔGbind value. It is caused by the contribution of Eelec, which is less favourable than the contribution of DD13 Eelec. Thus, the candidate DD9 is not recommended as an effective inhibitor of the 3CLpro enzyme based on binding affinity calculation. Specifically, there are differences in the value of ΔGbind in each approach. The results show that the MM-GBSA approach has a more favourable ΔGbind value than the MM-PBSA approach. It is due to the unfavourable energy contribution of Eelesol (solvation terms) from the Poisson Boltzmann model. Additionally, a recent study reports that the standard MM-PBSA may not be very accurate in the charged systems and needs to be modified to improve its calculation accuracy.53,54 However, the overall strength order of ΔGbind using the MM-GBSA and MM-PBSA approaches showed the same trend towards each inhibitor, such as DD13–3CLpro > 0EN–3CLpro > DD9–3CLpro. The candidate with a good binding affinity (higher negativity value) can bind strongly to the 3CLpro enzyme subsite.55 The goal is to inactivate the regulation of the main protease SARS-CoV-2 in the form of replication by blocking the active site of the 3CLpro enzyme. More specifically, the process of inhibiting the main protease SARS-CoV-2 by inhibitors focuses on subsite binding pocket through interactions with amino acids.
Inhibitor–3CLpro interaction in the binding pocket
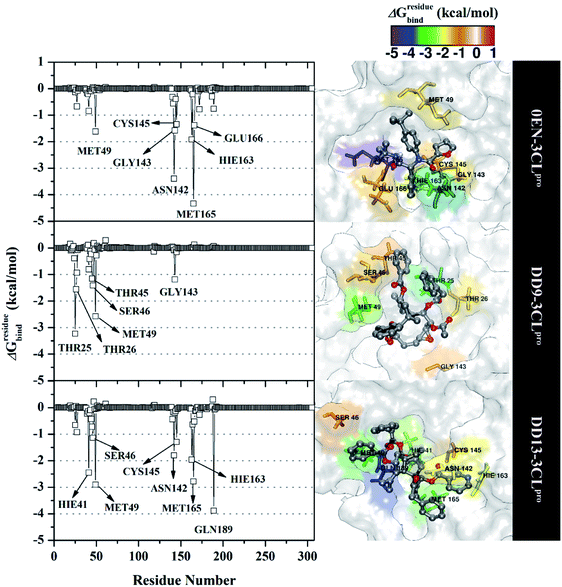
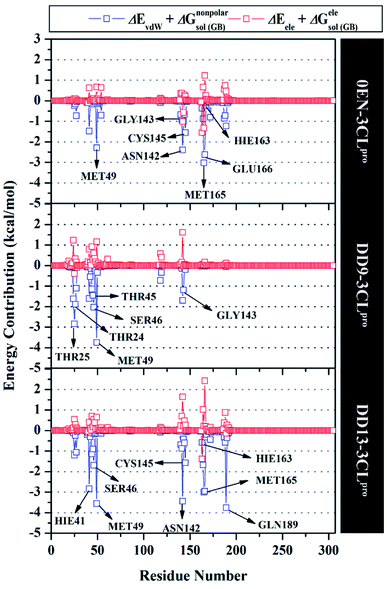
The inhibition mechanism of the 3CLpro enzyme was evaluated through the binding pattern of the inhibitor at the subsite binding pocket.56 Some of the variables analysed in this section are energy decomposition, atom contacts, and hydrogen bonding. Energy decomposition was analysed using the MM-GBSA approach through 100 frames extracted from the last 20 ns trajectories. In detail, a per-residue analysis of the subsite binding showed that the van der Waals contact contributed to the inhibitor–3CLpro interaction (Fig. S9†).The calculation of energy decomposition, which is responsible for inhibitor–3CLpro binding affinity shows that there are keys residues on the subsite that play a crucial role in the inhibition mechanism of the 3CLpro enzyme (Fig. 6). The evaluation process on amino acid residues that have a good binding affinity with criteria for the value of ΔGresiduebind ≤ 1.00 kcal mol−1.11 Each complex showed several keys residues (stronger binding affinity) found on the 3CLpro enzyme subsite, such as 0EN–3CLpro: seven key residues (S2: Met49, Met165, S1: Asn142, Gly143, Cys145, Hie163, and S3: Glu166), DD9–3CLpro: six key residues (S2′: Thr25, Thr26, S2: Thr45, Ser46, Met49, and S1: Gly163), and DD9–3CLpro: eight key residues (S2: Hie41, Ser46, Met49, Met165, S1: Asn142, Cys145, Hie163, and S4: Gln189). These data suggest that the contribution of keys residues in binding affinity inhibitor–3CLpro plays a crucial role in the binding free energy of each complex. In particular, the candidate ligands show that the DD13 candidate has a good energy decomposition compared to the DD9 candidate. It can show in the number of keys residues involved in direct interaction with candidate ligands. Especially, the DD13 inhibitor has more interaction with keys residues compared to the DD9 inhibitor. In particular, Gln189 has a value: −3.88 kcal mol−1 with a strong binding affinity category. Additionally, Hie41 and Cys145 residues as catalytic canters are included in the keys residues involved in the interaction with the DD13 inhibitor. Therefore, these data can explain why DD13 inhibitors have more promising free energy (ΔGbind) than DD9 inhibitors (Table 1). More specifically, energy decomposition key residues are described in detail in the form of energy contributions to each complex. The energy contribution is described through the energy contribution in the gas and solvent phases, such as ΔEvdW + ΔGnonpolarsol(GB) and ΔEele + ΔGelesol(GB) (Fig. 7).
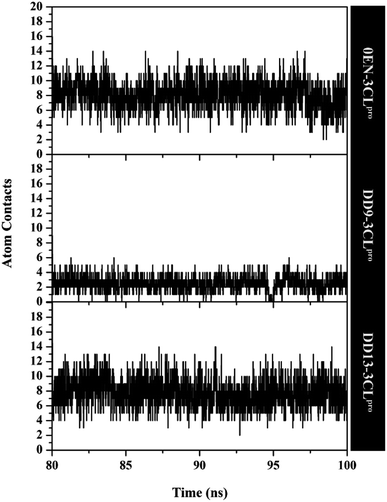
The atom contacts variable provides information to describe the inhibitor–3CLpro interaction stability at the atomistic level.57 The DD9 inhibitor had lower atom contacts with the amino acid residue on the active site of the 3CLpro enzyme compared to the 0EN and DD13 inhibitors during the last 20 ns of simulation time (Fig. 8). These data can be seen in the average value of the atom contacts in each complex described in Table S2.† In contrast, the DD13 shows more intensive atom contacts with some of the keys residues on the subsite binding pocket. Overall, the atom contacts of each inhibitor show 0EN–3CLpro: 16 contacts, DD9–3CLpro: 9 contacts, and DD13–3CLpro: 20 contacts (Table S3†). Atom contacts that have occupation ≥80% indicate a strong category. This further strengthens the assumption that DD13 candidate has a good interaction on the 3CLpro subsite binding with more atom contacts.
More specifically, hydrogen bonding (H-bond) was calculated using the last 20 ns trajectories for each complex (Fig. 9). Hydrogen bonding plays a crucial role in inhibitor–receptor interactions.11,37,57,58 The analysis of the occupation of the H-bond played a major role in the evaluation of the inhibitor–3CLpro interaction during the simulation time. The H-bond evaluation that has an occupancy value ≥80% indicates a strong category. In detail, the 0EN–3CLpro interaction involves five H-bond: (i) O2⋯H–N(Glu166) at 89.55%, 2.90 Å, 159.22°, (ii) O1⋯H–N(Gly143) at 86.15%, 3.04 Å, 156.91°, (iii) N3–HE2–NE2(Hie163) at 82.50%, 3.02 Å, 141.92°, (iv) O1⋯HD22–ND2(Asn142) at 50.50%, 2.96 Å, 154.99°, and (v) O3⋯H–N(Gly143) at 29.50%, 3.27 Å, 129.45°. The H-bond results from the simulated MD showed consistent results with molecular docking as the initial reference (Fig. 1D). Meanwhile, the analysis results for candidate inhibitors showed three H-bond interactions for the DD9–3CLpro complex: (i) O35⋯HD21–ND2(Asn142) at 5.20%, 3.01 Å, 149.09°, (ii) O32⋯HG–OG(Ser46) at 3.40%, 2.88 Å, 152.46°, and (iii) O35⋯HD22–ND2(Asn142) at 2.10%, 2.99 Å, 150.36°. Unfortunately, the three H-bonds show a weak category because they have a small H-bond occupancy (PHB < 10%). In contrast, the DD13–3CLpro complex only involved one H-bond: N59⋯HE2–NE2(Hie163) at 88.85%, 3.09 Å, 147.28°. However, the hydrogen bond shows a good H-bond occupation with a strong bond category. It is because, during the H-bond simulation, 1777 frames out of 2000 total frames were recorded. Thus, this further strengthens the DD13 candidate to have a more dominant interaction than the DD9 candidate as an inhibitor.
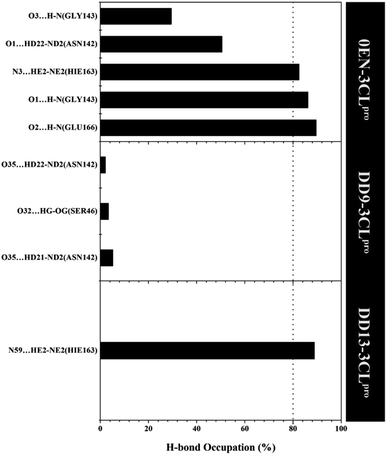 | ||
| Fig. 9 The percentage of hydrogen bond over the last 20 ns trajectories (cut-off value: distance < 3.5 Å and angle > 120°). | ||
Pharmacokinetic study of selected inhibitor
Based on several descriptions of molecular docking and MD simulation, the DD13 inhibitor is recommended as a selected candidate that has the potential to be an inhibitor of the SARS-CoV-2 main protease. The pharmacokinetic study aims to provide an initial prediction of the ADMET properties of the DD13 inhibitor (Table 2). One of them is the pkCSM server web service, which is widely applied to study the ADMET properties as a drug candidate.59–61| Parameters | DD13 |
|---|---|
a High-Caco-2 permeability: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Papp > 0.90 and poor-Caco-2 permeability: log Papp > 0.90 and poor-Caco-2 permeability: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Papp < 0.90. Intestinal absorption-human (+): HIA > 30% and intestinal absorption-human (−): HIA < 30%. BBB permeability (+): log Papp < 0.90. Intestinal absorption-human (+): HIA > 30% and intestinal absorption-human (−): HIA < 30%. BBB permeability (+): log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BB > 0.3 and BBB permeability (−): log BB > 0.3 and BBB permeability (−): log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BB < −1.0. BB < −1.0. |
|
| Absorption | |
Caco-2 permeability (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Papp in 10−6 cm s−1) Papp in 10−6 cm s−1) |
1.20 |
| Intestinal absorption-human (% absorbed) | 100 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Distribution | |
BBB permeability (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BB) BB) |
−1.46 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Metabolism | |
| CYP1A2 inhibitor | No |
| CYP2C19 inhibitor | No |
| CYP2C9 inhibitor | No |
| CYP2D6 inhibitor | No |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Excretion | |
| Total clearance (log mL min−1 kg−1) | −0.093 |
| Renal OCT2 substrate | No |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Toxicity | |
| AMES toxicity | No |
| Skin sensitisation | No |
Prediction results show that the candidate absorbed very well into the human small intestine (+HIA category). The predicted distribution of candidates does not cross the blood–brain barrier (−BBB). This indicates that the candidate does not interfere with the performance of the central nervous system.60 Additionally, a crucial parameter such as the effect of the candidate on the body's metabolic processes showed that the candidate did not inhibit the activity of cytochrome isoenzymes (CYP), such as the CYP1A2, CYP2C19, CYP2C9, and CYP2D6. Toxicity prediction shows that the candidate is not toxic because the prediction results show promising results with the criteria of non-AMES toxicity and non-skin sensation. This information is a promising advantage of candidate properties to treat COVID-19 patients. However, the prediction results need to be tested in clinical trials. Hopefully, the prediction data in the ADMET properties study can be used as an initial reference in understanding the candidate's ability as a drug candidate.
Conclusions
A combination of molecular docking and MD simulation is performed to study the interaction of dolabellane derivatives as the inhibitors of SARS-CoV-2 main protease. Determination of the active site using the selected sphere shows that the flexible conformation has good criteria with the RMSD pose of 1.39 Å. The molecular docking study showed that the DD9 and DD13 candidates showed a lower grid score than the native ligand. Meanwhile, the calculation of binding affinity using the MM-PB/GBSA approach showed that the DD13 candidate ΔGbind showed more promising inhibition criteria for the 3CLpro enzyme than the DD9 candidate. This result was strengthened by the interaction of the DD13 on the subsite binding pocket of the 3CLpro enzyme. Evaluation of energy decomposition showed that residue Hie41 and Cys145 had strong binding affinity interactions with the DD13 candidate. Besides, the H-bond analysis of the DD13 candidate with Hie163 residue showed a strong category with 88.85% occupation. Furthermore, the DD13 candidate showed promising ADMET properties criteria as a drug candidate with criteria +HIA, −BBB, non-inhibitor of cytochrome isoenzymes, and non-toxic.Conflicts of interest
The authors declare no conflict of interest.References
- G. Vargas, L. H. Medeiros Geraldo, N. Gedeão Salomão, M. Viana Paes, F. Regina Souza Lima and F. Carvalho Alcantara Gomes, Brain Behav. Immun. Health., 2020, 7, 100127 CrossRef.
- B. Hu, H. Guo, P. Zhou and Z. L. Shi, Nat. Rev. Microbiol., 2021, 19, 141–154 CrossRef CAS.
- Y. Chen, Q. Liu and D. Guo, J. Med. Virol., 2020, 92, 418–423 CrossRef CAS PubMed.
- R. Lu, X. Zhao, J. Li, P. Niu, B. Yang, H. Wu, W. Wang, H. Song, B. Huang, N. Zhu, Y. Bi, X. Ma, F. Zhan, L. Wang, T. Hu, H. Zhou, Z. Hu, W. Zhou, L. Zhao, J. Chen, Y. Meng, J. Wang, Y. Lin, J. Yuan, Z. Xie, J. Ma, W. J. Liu, D. Wang, W. Xu, E. C. Holmes, G. F. Gao, G. Wu, W. Chen, W. Shi and W. Tan, Lancet, 2020, 395, 565–574 CrossRef CAS.
- Y. Tan, S. G. Lim and W. Hong, Antiviral Res., 2005, 65, 69–78 CrossRef CAS PubMed.
- M. Miczi, M. Golda, B. Kunkli, T. Nagy, J. Tőzsér and J. A. Mótyán, Int. J. Mol. Sci., 2020, 21, 1–19 Search PubMed.
- W. Vuong, M. B. Khan, C. Fischer, E. Arutyunova, T. Lamer, J. Shields, H. A. Saffran, R. T. McKay, M. J. van Belkum, M. A. Joyce, H. S. Young, D. L. Tyrrell, J. C. Vederas and M. J. Lemieux, Nat. Commun., 2020, 11, 1–8 Search PubMed.
- V. Mody, J. Ho, S. Wills, A. Mawri, L. Lawson, M. C. C. J. C. Ebert, G. M. Fortin, S. Rayalam and S. Taval, Commun. Biol., 2021, 4, 1–10 CrossRef.
- Z. Jin, Y. Zhao, Y. Sun, B. Zhang, H. Wang, Y. Wu, Y. Zhu, C. Zhu, T. Hu, X. Du, Y. Duan, J. Yu, X. Yang, X. Yang, K. Yang, X. Liu, L. W. Guddat, G. Xiao, L. Zhang, H. Yang and Z. Rao, Nat. Struct. Mol. Biol., 2020, 27, 529–532 CrossRef CAS.
- J. C. Ferreira, S. Fadl, A. J. Villanueva and W. M. Rabeh, Front. Chem., 2021, 9, 1–11 Search PubMed.
- B. Nutho, P. Mahalapbutr, K. Hengphasatporn, N. C. Pattaranggoon, N. Simanon, Y. Shigeta, S. Hannongbua and T. Rungrotmongkol, Biochemistry, 2020, 59, 1769–1779 CrossRef CAS PubMed.
- G. J. Lockbaum, A. C. Reyes, J. M. Lee, R. Tilvawala, E. A. Nalivaika, A. Ali, N. K. Yilmaz, P. R. Thompson and C. A. Schiffer, Viruses, 2021, 13, 174 CrossRef CAS PubMed.
- A. Gahlawat, N. Kumar, R. Kumar, H. Sandhu, I. P. Singh, S. Singh, A. Sjöstedt and P. Garg, J. Chem. Inf. Model., 2020, 60, 5781–5793 CrossRef CAS.
- H. M. Mengist, T. Dilnessa and T. Jin, Front. Chem., 2021, 9, 1–19 Search PubMed.
- Purwati, A. Miatmoko, Nasronudin, E. Hendrianto, D. Karsari, A. Dinaryanti, N. Ertanti, I. S. Ihsan, D. S. Purnama, T. P. Asmarawati, E. Marfiani, Yulistiani, A. N. Rosyid, P. A. Wulaningrum, H. W. Setiawan, I. Siswanto and N. N. T. Puspaningsih, PLoS One, 2021, 16, 1–27 CrossRef.
- Z. Li, X. Li, Y. Y. Huang, Y. Wu, R. Liu, L. Zhou, Y. Lin, D. Wu, L. Zhang, H. Liu, X. Xu, K. Yu, Y. Zhang, J. Cui, C. G. Zhan, X. Wang and H. Bin Luo, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 27381–27387 CrossRef CAS PubMed.
- S. H. Ghoran, M. El-shazly, N. Sekeroglu and A. Kijjoa, Molecules, 2021, 26, 1754 CrossRef CAS.
- M. Omrani, M. Keshavarz, S. Nejad Ebrahimi, M. Mehrabi, L. J. McGaw, M. Ali Abdalla and P. Mehrbod, Front. Pharmacol., 2021, 11, 2115 Search PubMed.
- A. D. S. Antonio, L. S. M. Wiedemann and V. F. Veiga-Junior, RSC Adv., 2020, 10, 23379–23393 RSC.
- A. P. Wardana, N. S. Aminah, M. Rosyda, M. I. Abdjan, A. N. Kristanti, K. N. W. Tun, M. I. Choudhary and Y. Takaya, Heliyon, 2021, 7, 1–14 CrossRef.
- C. C. Wen, Y. H. Kuo, J. T. Jan, P. H. Liang, S. Y. Wang, H. G. Liu, C. K. Lee, S. T. Chang, C. J. Kuo, S. S. Lee, C. C. Hou, P. W. Hsiao, S. C. Chien, L. F. Shyur and N. S. Yang, J. Med. Chem., 2007, 50, 4087–4095 CrossRef CAS PubMed.
- M. A. A. Ibrahim, A. H. M. Abdelrahman, M. A. M. Atia, T. A. Mohamed, M. F. Moustafa, A. R. Hakami, S. A. M. Khalifa, F. A. Alhumaydhi, F. Alrumaihi, S. H. Abidi, K. S. Allemailem, T. Efferth, M. E. Soliman, P. W. Paré, H. R. El-Seedi and M. E. F. Hegazy, Mar. Drugs, 2021, 19, 391 CrossRef CAS.
- L. Santacruz, D. X. Hurtado, R. Doohan, O. P. Thomas, M. Puyana and E. Tello, Sci. Rep., 2020, 10, 1–11 CrossRef.
- K. Ogawa, S. Nakamura, K. Hosokawa, H. Ishimaru, N. Saito, K. Ryu, M. Fujimuro, S. Nakashima and H. Matsuda, J. Nat. Med., 2018, 72, 439–447 CrossRef CAS.
- A. Pardo-Vargas, F. A. Ramos, C. C. Cirne-Santos, P. R. Stephens, I. C. P. Paixão, V. L. Teixeira and L. Castellanos, Bioorg. Med. Chem. Lett., 2014, 24, 4381–4383 CrossRef CAS.
- N. Rahman, Z. Basharat, M. Yousuf, G. Castaldo, L. Rastrelli and H. Khan, Molecules, 2020, 2, 1–12 Search PubMed.
- T. L. Augustin, R. Hajbabaie, M. T. Harper and T. Rahman, Molecules, 2020, 25, 5501 CrossRef CAS PubMed.
- I. A. Guedes, L. S. C. Costa, K. B. dos Santos, A. L. M. Karl, G. K. Rocha, I. M. Teixeira, M. M. Galheigo, V. Medeiros, E. Krempser, F. L. Custódio, H. J. C. Barbosa, M. F. Nicolás and L. E. Dardenne, Sci. Rep., 2021, 11, 1–20 CrossRef PubMed.
- C. H. Zhang, E. A. Stone, M. Deshmukh, J. A. Ippolito, M. M. Ghahremanpour, J. Tirado-Rives, K. A. Spasov, S. Zhang, Y. Takeo, S. N. Kudalkar, Z. Liang, F. Isaacs, B. Lindenbach, S. J. Miller, K. S. Anderson and W. L. Jorgensen, ACS Cent. Sci., 2021, 7, 467–475 CrossRef CAS.
- D. El Ahdab, L. Lagardère, T. J. Inizan, F. Célerse, C. Liu, O. Adjoua, L. H. Jolly, N. Gresh, Z. Hobaika, P. Ren, R. G. Maroun and J. P. Piquemal, J. Phys. Chem. Lett., 2021, 12, 6218–6226 CrossRef CAS PubMed.
- T. Jaffrelot Inizan, F. Célerse, O. Adjoua, D. El Ahdab, L. H. Jolly, C. Liu, P. Ren, M. Montes, N. Lagarde, L. Lagardère, P. Monmarché and J. P. Piquemal, Chem. Sci., 2021, 12, 4889–4907 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- S. R. Brozell, S. Mukherjee, T. E. Balius, D. R. Roe, D. A. Case and R. C. Rizzo, J. Comput.-Aided Mol. Des., 2012, 26, 749–773 CrossRef CAS PubMed.
- K. Liu and H. Kokubo, J. Comput.-Aided Mol. Des., 2020, 34, 1195–1205 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS.
- D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS.
- D. Mishra, R. R. Maurya, K. Kumar, N. S. Munjal, V. Bahadur, S. Sharma, P. Singh and I. Bahadur, J. Mol. Liq., 2021, 335, 116185 CrossRef CAS PubMed.
- B. R. Miller, T. D. McGee, J. M. Swails, N. Homeyer, H. Gohlke and A. E. Roitberg, J. Chem. Theory Comput., 2012, 8, 3314–3321 CrossRef CAS PubMed.
- H. Luo, D. F. Liang, M. Y. Bao, R. Sun, Y. Y. Li, J. Z. Li, X. Wang, K. M. Lu and J. K. Bao, Int. J. Oral Sci., 2017, 9, 53–62 CrossRef CAS PubMed.
- D. E. V. Pires, T. L. Blundell and D. B. Ascher, J. Med. Chem., 2015, 58, 4066–4072 CrossRef CAS.
- W. J. Allen, T. E. Balius, S. Mukherjee, S. R. Brozell, D. T. Moustakas, P. T. Lang, D. A. Case, I. D. Kuntz and R. C. Rizzo, J. Comput. Chem., 2015, 36, 1132–1156 CrossRef CAS.
- J. He, L. Hu, X. Huang, C. Wang, Z. Zhang, Y. Wang, D. Zhang and W. Ye, Int. J. Antimicrob. Agents, 2020, 56, 106055 CrossRef CAS PubMed.
- Y. Kumar, H. Singh and C. N. Patel, J. Infect. Public Health, 2020, 13, 1210–1223 CrossRef PubMed.
- A. Kumari, V. S. Rajput, P. Nagpal, H. Kukrety, S. Grover and A. Grover, J. Biomol. Struct. Dyn., 2020, 1–13 Search PubMed.
- J. Tan, K. H. G. Verschueren, K. Anand, J. Shen, M. Yang, Y. Xu, Z. Rao, J. Bigalke, B. Heisen, J. R. Mesters, K. Chen, X. Shen, H. Jiang and R. Hilgenfeld, J. Mol. Biol., 2005, 354, 25–40 CrossRef CAS.
- M. E. Abouelela, H. K. Assaf, R. A. Abdelhamid, E. S. Elkhyat, A. M. Sayed, T. Oszako, L. Belbahri, A. E. El Zowalaty and M. S. A. Abdelkader, Molecules, 2021, 26, 1767 CrossRef CAS.
- A. Bornot, C. Etchebest and A. G. De Brevern, Proteins: Struct., Funct., Bioinf., 2011, 79, 839–852 CrossRef CAS.
- J. Lee, L. J. Worrall, M. Vuckovic, F. I. Rosell, F. Gentile, A. T. Ton, N. A. Caveney, F. Ban, A. Cherkasov, M. Paetzel and N. C. J. Strynadka, Nat. Commun., 2020, 11, 1–9 Search PubMed.
- D. Suárez and N. Díaz, J. Chem. Inf. Model., 2020, 60, 5815–5831 CrossRef.
- N. Ansari, V. Rizzi, P. Carloni and M. Parrinello, J. Am. Chem. Soc., 2021, 143, 12930–12934 CrossRef CAS.
- B. Nutho, S. Pengthaisong, A. Tankrathok, V. S. Lee, J. R. K. Cairns, T. Rungrotmongkol and S. Hannongbua, Biomolecules, 2020, 10, 1–19 CrossRef.
- C. Wang, D. Greene, L. Xiao, R. Qi and R. Luo, Front. Mol. Biosci., 2018, 4, 1–18 Search PubMed.
- H. M. Ding, Y. W. Yin, S. Di Ni, Y. J. Sheng and Y. Q. Ma, Chin. Phys. Lett., 2021, 38, 018701 CrossRef CAS.
- Y. J. Sheng, Y. W. Yin, Y. Q. Ma and H. M. Ding, J. Chem. Inf. Model., 2021, 61, 2454–2462 CrossRef CAS.
- M. I. Choudhary, M. Shaikh, A.-T. Wahab and A.-U. Rahman, PLoS One, 2020, 15, 1–15 CrossRef.
- Y. L. Weng, S. R. Naik, N. Dingelstad, M. R. Lugo, S. Kalyaanamoorthy and A. Ganesan, Sci. Rep., 2021, 11, 1–22 CrossRef.
- T. Somboon, P. Mahalapbutr, K. Sanachai, P. Maitarad, V. S. Lee and T. Rungrotmongkol, J. Mol. Liq., 2020, 322, 114999 CrossRef.
- S. Ahmad, Y. Waheed, S. Ismail, S. Bhatti, S. W. Abbasi and K. Muhammad, Molecules, 2021, 26, 1446 CrossRef CAS PubMed.
- M. A. Guimarães, R. N. De Oliveira, R. L. De Almeida, A. C. Mafud, A. L. V. Sarkis, R. Ganassin, M. P. Da Silva, D. B. Roquini, L. M. Veras, T. C. H. Sawada, C. D. Ropke, L. A. Muehlmann, G. A. Joanitti, S. A. S. Kuckelhaus, S. M. Allegretti, Y. P. Mascarenhas, J. de Moraes and J. R. S. A. Leite, PLoS One, 2018, 13, 1–19 Search PubMed.
- Y. Han, J. Zhang, C. Q. Hu, X. Zhang, B. Ma and P. Zhang, Front. Pharmacol., 2019, 10, 1–12 CrossRef.
- A. Mohammad, E. Alshawaf, S. K. Marafie, M. Abu-Farha, F. Al-Mulla and J. Abubaker, Biomolecules, 2021, 11, 573 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra07584e |
| This journal is © The Royal Society of Chemistry 2021 |