Open Access Article
Open Access ArticlePhase behavior and interfacial tension of ternary polymer mixtures with block copolymers†
Dongmei Liu a,
Ye Lina,
Kai Gonga,
Huifeng Bo*a,
Deyang Lia,
Zhanxin Zhanga and
Wenduo Chen*b
a,
Ye Lina,
Kai Gonga,
Huifeng Bo*a,
Deyang Lia,
Zhanxin Zhanga and
Wenduo Chen*b
aSchool of Science, North China University of Science and Technology, Tangshan 063210, P. R. China. E-mail: bohuifeng@ncst.edu.cn
bSchool of Materials, Sun Yat-sen University, Guangzhou 510275, P. R. China. E-mail: chenwd29@mail.sysu.edu.cn
First published on 29th November 2021
Abstract
The phase behavior and interfacial tension of ternary polymeric mixtures (polystyrene/polystyrene-b-poly(methyl methacrylate)/poly(methyl methacrylate), PS/PS-b-PMMA/PMMA) are investigated by dissipative particle dynamics (DPD) simulations. Our simulation results show that, as the PS-b-PMMA diblock copolymer concentration increases, the interfacial tension decreases due to the decayed correlations between homopolymers PS and PMMA. When the chain lengths of copolymers are fixed, with the increase of the chain lengths of PS and PMMA homopolymers the interfacial width becomes wider and the interfacial tension becomes smaller, due to the copolymers presenting more stretched and swollen structures in the mixtures with the short length of homopolymers. However, with simultaneously increasing chain lengths of both diblock copolymer and homopolymers with a fixed ratio, the interfacial tension increases because the copolymer chains with longer chain length penetrate more deeply into the homopolymer phase and the interactions between diblock copolymers become weaker. These results will provide a way to mix incompatible homopolymers to improve material performances.
1. Introduction
In recent years, polymeric mixtures composed of block copolymers and homopolymers have become one of the most popular research issues in the field of polymer science and engineering.1–4 It is known that chemically different polymers are usually immiscible,5 which inhibits the increase in mixing entropy6 and forms a thin interface with larger interfacial tension. The formation of thermodynamically stable polymeric mixtures is generally caused by the substantial decrease of the interfacial tension by the addition of copolymer compatibilizers between incompatible homopolymers, which results in the improved performance of the polymer composite materials.7 The copolymer compatibilizers at the interface could change the aggregation states of the immiscible homopolymers to minimize the interfacial energy. Thus, it is important to investigate the interfacial tension and structure of phase-separated polymeric mixtures at the molecular level.Experimental studies of the ternary homopolymer/block copolymer (homopolymer/block copolymer/homopolymer) mixtures have been extensively performed. By using neutron reflectivity and elastic recoil detection, Russell et al.8–12 investigated the density distribution of symmetric PS-b-PMMA chains, the width between the PS and PMMA homopolymers, and the interfacial tension. They found that the interfacial width between the PS and PMMA homopolymers broadens with the addition of the PS-b-PMMA chains, which increases from 50 Å at the absence of the PS-b-PMMA chains up to ∼85 Å at interfacial saturation. When the copolymer chains segregate to the interface, the interfacial tension decreases, which is consistent with the changing of interfacial tension in similar experimental works. Liu et al.13 investigated the dependence of phase behavior and dimensional scaling for PS/PS-b-PMMA/PMMA ternary mixtures on the χN (χ and N represent the Flory–Huggins interaction parameter and the degree of polymerization of PS-b-PMMA chain, respectively), the α (the ratio of the degree of polymerization of the PS and PMMA chains to that of the PS-b-PMMA chains), and the volume fraction of homopolymers in the mixtures. They found that the phase of the mixtures depends weakly on χN and α, but as the volume fraction of homopolymers increases, the phase transitions from lamellae to microemulsion and then to macrophase-separated domains. Morse et al.14 measured the interfacial tension between polystyrene and polybutadiene homopolymers in the presence of poly(styrene-b-butadiene) copolymer. The results showed that as the copolymer is premixed with PS, the interfacial tension presents a decrease with increasing concentration until an apparent CMC (critical micelles concentration) and then saturating at higher concentrations.
With the rapid development of computer hardware and software technology, molecular simulations have become a vital method for studying the phase morphology and mechanical properties of polymeric mixtures. Fischel et al.15 employed the self-consistent field method to investigate PS/PS-b-PMMA/PMMA mixtures. They found an excellent qualitative and quantitative agreement with the experimental data for the volume fraction profiles of both homopolymers and blocks of the copolymer at the interface. Balazs et al.16–20 reported a series of Monte Carlo simulations for the ternary block copolymer/homopolymer mixtures. Doi et al.21 derived the expression for the free energy of copolymer blends as a function of the density distribution of the monomer on each block. This expression can be used to calculate the micro- and macro-phase separation of any blends of homopolymers and block copolymers with arbitrary topological structures. Matsen et al.22,23 and Fredrickson et al.24–26 reported a series of field theoretic simulations to predict the equilibrium phase diagram of symmetric blends of AB diblock copolymer with A and B homopolymers. Their results are in qualitative agreement with the results of experiments in this system. Tanaka et al.27 investigated the local orientation of PS segments of the PS-b-PMMA chains at the interface by atomistic molecular dynamics simulation. It is found that the PS-b-PMMA chains which are located on the interfacial region, are in-plane oriented. In recent years, dissipative particle dynamics (DPD) simulations have been successfully used to study the interfacial and structural properties of immiscible mixtures.28–39 Specifically, Qian et al.28 calculated the interfacial tension of homopolymer/diblock copolymer/homopolymer mixtures via DPD simulation, and the results show that, as the number of the AB copolymer is fixed, the interfacial tension decreases with the increase of chain length of AB copolymer. Guo et al.29 systematically investigated the segregation of block copolymers in binary immiscible homopolymer blends through DPD simulations. They found that swollen block copolymers are more efficient in reducing the interfacial tension than nonswollen block copolymers. Pinto et al.30 investigated the effects of copolymer structure and concentration on the homopolymer/copolymer/homopolymer mixtures by DPD simulation. They proved that the microstructural properties of the copolymer exert a decisive impact on molecular interactions and the characteristics of the mesophases generated during the blending process. Goodson et al.31 performed a DPD simulation to study the effect of the interaction parameters of beads, chain length, and content of homopolymers on morphological stability and phase diagram of symmetric ternary mixtures PS/PS-b-PMMA/PMMA, which reproduce the key features of the experiment.
The above studies have increased our understanding of interfacial properties for homopolymer/block copolymer/homopolymer mixtures, whereas there are still many questions remaining unclear. In this research, we employ the DPD method to systematically explore the phase behavior and interfacial tension of the ternary polymeric mixtures PS/PS-b-PMMA/PMMA (Sn/SmMm/Mn). The methods are constructed based on Goodson's31 and our previous works.40–44 The dependence of the interfacial tension, the interfacial width, and the detailed chain conformations on the copolymer concentration, the chain lengths of homopolymers, and the simultaneous change of chain length of PS-b-PMMA, PS, and PMMA are systematically examined. The result elucidates that the more addition of the PS-b-PMMA copolymers, the shorter the PS-b-PMMA, PS, PMMA chain lengths, the lower the interfacial tension when the ternary mixtures occur macrophase segregation. Finally, the summary of our results and some concluding remarks are given in conclusions.
2. Model and simulation
2.1 Model
Dissipative particle dynamics is developed to study mesoscale problems in complex fluids and soft matter,45 which has the following two important features, compared with traditional all-atom molecular dynamics. First, a coarse-grained bead generally represents tens of monomer units in a DPD simulation system, which means that a larger time and a longer length scale can be achieved. Second, the beads in the system can overlap in a large amount, since the interactions between the paired beads occur through a soft potential.30DPD method can be used to study highly dispersed polymer mixtures without significant influence on mathematical formulas and calculation procedures, which is another special advantage. In a DPD simulation, all beads follow Newton's equations of motion,
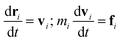 | (1) |
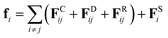 | (2) |
The conservative force FCij, represented by a soft potential, which is generally expressed as32
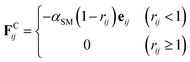 | (3) |
The dissipative force FDij depicts viscous drag and the random force FRij signifies the stochastic impulse, usually are given as follows:
| FDij = −γωD(rij)(vij·eij)eij | (4) |
| FRij = σωR(rij)ξijΔt−1/2eij | (5) |
| ωD(r) = [ωR(r)]2, σ2 = 2γkBT | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) is the Boltzmann constant and T is the thermodynamics temperature.
is the Boltzmann constant and T is the thermodynamics temperature.
The dimensionless weighting functions ωR(rij) and ωR(rij) can be simply taken from the research of Groot and Warren,32
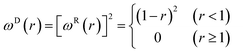 | (7) |
The harmonic spring force between the bonded beads enforces bead connectivity and is expressed as
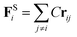 | (8) |
The repulsion interaction parameter αSM can be mapped to the Flory–Huggins parameter χSM via the following correlation32
| αSM ≈ αSS + 3.50χSM | (9) |
2.2 Simulation details
In this work, the DPD simulations are operated in a periodic cubic box with a side length L = 30 by Materials Studio (Accelrys Inc.) software. For simplicity, the radius of interaction is taken as rc = 1 and the temperature kBT = 1. The simulated bead density ρ = 3.28 The friction coefficient γ = 4.5. In this simulation, the program is first performed 2.0 × 105 steps to ensure that the system has reached equilibration with the time steps 0.05 (in reduced units). Then, the program is performed 5 × 104 steps as the production runs. We calculate the square of the radius of gyration of copolymers to show that the equilibration and production phase are sufficiently long (as illustrated in Fig. S1 in the ESI†), the evolution of the blend's morphology also show that the systems have reached equilibration [Fig. S2†]. To ensure the accuracy of the results, we ran 5 parallel simulations and averaged.In all cases, the Sn/SmMm/Mn mixtures contain equal amounts of PS, PMMA homopolymers, and the chain length of the homopolymers PS and PMMA are equal, the PS-b-PMMA diblock also consists of the same number of S and M beads.
To characterize the structure of PS/PS-b-PMMA/PMMA mixtures, we calculated the static structure factor, which obeys the following relationship,
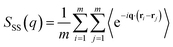 | (10) |
The interfacial tension is one of the most important parameters which can directly reflect the mechanical properties and stability of the interface in the phase-separated mixtures with a flat interface. Here, the interfacial tension was calculated by the following formula,46
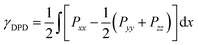 | (11) |
To characterize the detailed conformations of the PS-b-PMMA chain, the mean-square radii of gyration 〈Rg2〉, the mean-square end-to-end distance 〈Ree2〉, and the chain orientation parameter Θ were also calculated. The orientation parameter Θ of the PS-b-PMMA chain is calculated by the equation,28
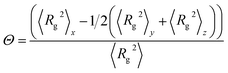 | (12) |
In addition, the interfacial width w between the PS and PMMA homopolymers was calculated by fitting the function tanh ((x + d)/w) to the profile (ρA(x) − ρB(x))/ρ(x) across the two interfaces, where d is the position of the interface center in x-directions.29
3. Results and discussion
3.1 Morphology and structures of Sn/SmMm/Mn ternary mixtures
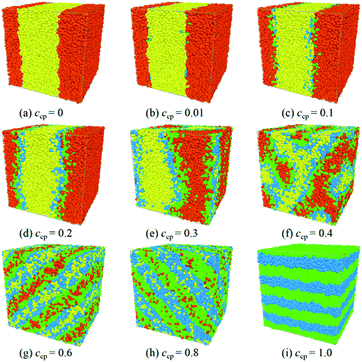
To investigate how the diblock copolymer concentration ccp (ccp is referred as the number density of the copolymer) influences the phase behavior and structural properties of the mixtures, we vary the PS-b-PMMA chains concentration from ccp = 0.0 to ccp = 1.0 for S2/S5M5/M2 mixtures. Fig. 1 and 2 show the representative morphology snapshots and structure-factor SSS(q) for S2/S5M5/M2 mixtures at different S5M5 copolymer concentrations ccp, respectively.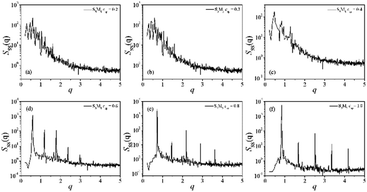 | ||
| Fig. 2 Structure-factor SSS(q) of the S beads in copolymer with S5M5 concentration of (a) ccp = 0.2 (b) ccp = 0.3 (c) ccp = 0.4 (d) ccp = 0.6 (e) ccp = 0.8 (f) ccp = 1.0. | ||
It is clear that the mixtures of homopolymers S2 and M2 show phase separation in the absence of S5M5 copolymers Fig. 1(a). When the content of the S5M5 chains increases from ccp = 0.01 to 0.2, two flat interfaces formed between the S2 and M2 homopolymers, which populated with the S5M5 copolymers. The S beads of the S5M5 copolymers penetrate into the S2 homopolymer phase, and the M beads penetrate into the M2 homopolymer phase Fig. 1(b)–(d). This phenomenon verifies the simulation results by Albert et al.31
As the S5M5 chains concentration increases from ccp = 0.2 to ccp = 0.3, the interfacial geometry starts to change and no longer remains a flat shape Fig. 1(e). However, as shown in Fig. 2, the structure factor SSS(q) in this concentration still displays its maximum at the smallest value of q, which indicates that the mixtures remain in a state of macrophase segregation.30,47
When the S5M5 diblock concentration is ccp = 0.4, several peaks appear in the structure factor SSS(q), indicating that the mixtures have formed a bicontinuous structure Fig. 1(f) and 2(c). When ccp ≥ 0.6, the mixtures form lamellar structures Fig. 1(g)–(i). The S2 homopolymers disperse in the S beads in S5M5 diblock copolymers. The scattering intensity displays five peaks Fig. 2(d), with the thickness of lamellae is 2π/q > 10.5. When ccp = 1.0, the thickness of lamellae decreases to around 7, which indicates that as the S5M5 diblock concentration increases, the width of the lamellar domains decreases.
We have verified that the S5M5 diblock copolymers are segregated at the interfaces between the S2 and M2 homopolymers phase when ccp ≤ 0.2. According to the experimental research of Russell et al.,8–12 when the SmMm chains aggregate at the interfaces, they can significantly change the density distribution of the Sn and Mn homopolymers and then affect the interfacial tension. Therefore, in the next part of the manuscript, we investigate the effect of increasing the S5M5 chains concentration ccp on the interfacial tension, etc., interfacial properties. We define the direction of perpendicular to the interfaces is x-direction in the lamellar structures.
3.2 Interfacial tension for Sn/SmMm/Mn mixtures
Fig. 3(a) and (b) show the density profiles (ρ) of beads S and M of S5M5 chains and S2, M2 homopolymers as a function of ccp. As the concentration of S5M5 chains increases from ccp = 0.01 to ccp = 0.2, the densities of the beads S and M of S5M5 chains at the interfaces exhibit significant increases Fig. 3(a), while the densities of the beads S and M of homopolymers S2 and M2 at the interface decreases Fig. 3(b). It can be understood that the accumulation of S5M5 diblock copolymers at the interface pushes the S2 and M2 homopolymers further away from the interfaces. This result also illustrates the decayed correlations between homopolymers S2 and M2 with increasing the S5M5 chain concentration ccp.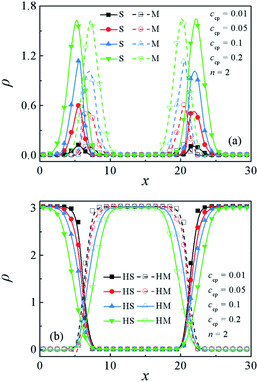 | ||
| Fig. 3 Density profiles of beads S and M of (a) S5M5 copolymers and (b) S2 and M2 homopolymers in the x-direction as a function of the concentration of the S5M5 chains. | ||
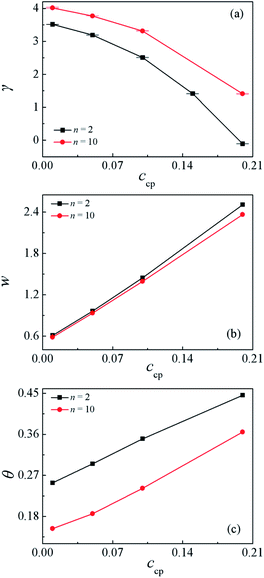
In order to quantify the effect of increasing the SmMm chains concentration ccp on the interfacial properties for the Sn/SmMm/Mn mixtures. The interfacial tension γ and interfacial width w at different S5M5 chains concentrations ccp with n = 2 and n = 10 are calculated, as shown in Fig. 4(a) and (b). Apparently, the interfacial tension γ decreases while the interfacial width w increases between the Sn and Mn homopolymers with increasing the S5M5 concentration ccp in the mixture systems. We infer that the decrease of the interfacial tension γ and the increase of the interfacial width w are related to the density distribution of the S5M5 copolymers and Sn, Mn homopolymers as illustrated in Fig. 3(a) and (b). That is, as the S5M5 diblock copolymer concentration ccp increases from 0.01 to 0.2, the densities of the S, M beads of S5M5 diblock at the interfaces exhibit a significant increase, while the densities of the homopolymers Sn, Mn near the center of the interfaces decrease, which results in the decayed correlations between Sn and Mn homopolymers. Hence, the interfacial tension γ decreases, the interfacial width w increases. We also find that the interfacial tension γ has a smaller value for shorter homopolymer chain length n = 2 at the fixed S5M5 diblock concentration, which implies that the S5M5 diblock shows better performance in lowering the interfacial tension γ for the mixtures with the shorter S2 and M2 homopolymer. These results for the interfaces are in good agreement with the previous studies.29
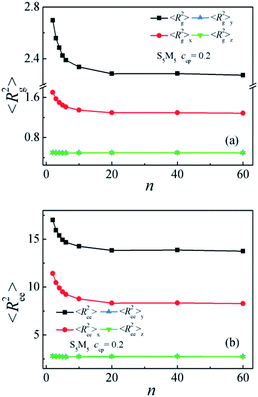
Moreover, to characterize the configurations of the S5M5 chains, we calculate the chain orientation parameter Θ, mean-square radii of gyration 〈Rg2〉 and its three components 〈Rg2〉x, 〈Rg2〉y, 〈Rg2〉z of the S5M5 diblock copolymer. Fig. 4(c) and 5 depict the dependence of the chain orientation parameter Θ and the dimension of the S5M5 diblock copolymers on the copolymer concentration ccp. We found that the S5M5 chain orientation parameter Θ is greater than 0, and increases with increasing ccp Fig. 4(c), which indicates that the S5M5 diblock copolymer with higher concentration is more stretched in the x-direction (perpendicular to the interface). Fig. 5 shows that the S5M5 copolymers exhibit almost the same sizes in y and z directions, which are parallel to the interfaces, and both y and z components are smaller than the perpendicular x component see Fig. 5(a) and (b). The 〈Rg2〉 and 〈Rg2〉x increase with increasing the S5M5 diblock copolymer concentration ccp as illustrated in Fig. 5(a) and (b). This result also indicates that increasing the S5M5 diblock copolymer concentration ccp causes the S5M5 diblock copolymer to extend along the x-direction.
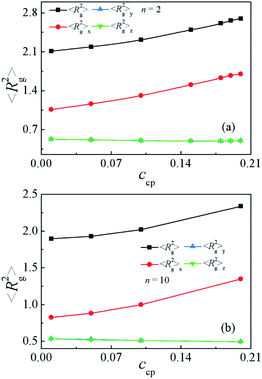 | ||
| Fig. 5 Mean-square radii of gyration 〈Rg2〉 and the three principal components 〈Rg2〉x, 〈Rg2〉y, 〈Rg2〉z as a function of the S5M5 chain concentration ccp with (a) n = 2 and (b) n = 10. | ||
As shown by Fig. 4 and 5, the chain length of PS and PMMA homopolymers exhibit a significant effect on the interfacial properties of the Sn/SmMm/Mn ternary mixtures. Therefore, in the following part of the manuscript, we explored the effects of increasing the homopolymer chain length n (the SmMm chain length is fixed as 10) and the simultaneous change of chain lengths of SmMm, Sn, Mn chain lengths (m = n) on the interfacial properties.
3.3 Effects of increasing the Sn and Mn homopolymers chain length n
In this section, the effect of increasing the Sn and Mn homopolymers chain length n on the interfacial properties of Sn/S5M5/Mn ternary mixtures is discussed. Here, we vary the chain length of PS and PMMA homopolymers from n = 2 to 60 with ccp = 0.2.Fig. 6 shows the density distribution of beads S + M of the S5M5 diblock copolymer with different chain lengths n. We found that the density of S + M beads of the S5M5 copolymer at the center of the interface increases with the Sn and Mn homopolymers chain length increases from n = 2 to n = 20. However, as the chain length of the PS and PMMA homopolymers n increases from 20 to 60, the density of S + M beads of the S5M5 chains at the center of the interfaces remains almost unchanged.
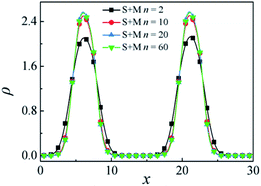 | ||
| Fig. 6 Density profiles of beads S + M in the x-direction as a function of the PS and PMMA chain length n in mixture systems of S5M5. | ||
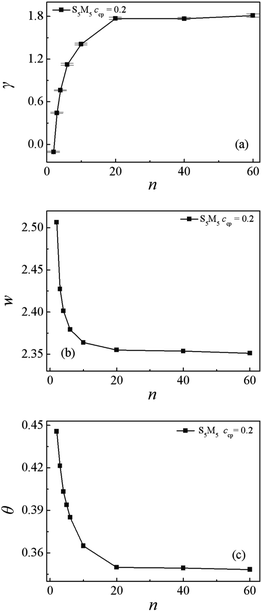
Fig. 7(a) and (b) show the γ and w for the mixtures as a function of n, respectively. The obtained γ rapidly increases and the w decreases with increasing the n = 2 to 20, whereas both the γ and w almost remain unchanged when n increases from 20 to 60. These results show that Sn/S5M5/Mn ternary mixtures composed of shorter Sn and Mn homopolymers exhibit lower interfacial tension γ. It is also revealed that the S5M5 diblock copolymers show better performance in lowering the γ for the mixtures with shorter Sn and Mn homopolymers. This is because that the shorter Sn and Mn homopolymers can cause a decayed correlation between the immiscible Sn and Mn homopolymers Fig. S3 in the ESI,† which results in a wider interfacial width w and a smaller interfacial tension γ.
Fig. 7(c) and 8 depict the dependence of the Θ and dimension of the S5M5 chains on the Sn and Mn homopolymer chain length n. It is found that the Θ, 〈Rg2〉, 〈Rg2〉x, 〈Ree2〉 and 〈Ree2〉x decrease significantly with the increase of the Sn and Mn chain length from n = 2 to 20, while as the Sn and Mn chain length n further increases from 20 to 60, the Θ, 〈Rg2〉, 〈Rg2〉x, 〈Ree2〉 and 〈Ree2〉x remain almost unchanged. Fig. 8(a) and (b) also show that as the n increases, the y and z components of the 〈Rg2〉 and the 〈Ree2〉 always remain almost unchanged. These results can be interpreted as follows: when the chain length of the Sn and Mn homopolymers is very short n = 2, the S5M5 diblock copolymer at the interface resembles a “wet brush” (the homopolymers can penetrate the copolymer blocks layer),48,49 and the S5M5 diblock copolymers are swollen by the short homopolymer chain length. Thus, the S5M5 diblock copolymers are more stretched, accompanied by the larger Θ, the broader density distribution of the diblock copolymer, the wider interfacial width, and the smaller interfacial tension γ. When the n ≥ 20, which are longer than the chain length of the S5M5 diblock copolymers 10, the homopolymers are expelled from the “dry brush”,48,49 i.e., the Sn and Mn can't penetrate the S5M5 copolymers layer, therefore the density distribution of the S5M5 copolymers, the interfacial tension, and the configuration of the S5M5 copolymers remain unchanged as n further increases from 20 to 60.
We find that the interfacial properties of the Sn/SmMm/Mn mixtures are strongly related to the Sn and Mn chain length n. And the study of Qian et al.28 indicates that the interfacial tension of the A/AB/B ternary mixtures increases with the increasing of AB diblock copolymer chain length. However, the influence of simultaneously increasing SmMm, Sn, Mn chain lengths on the interfacial properties remains unclear. Therefore, in the next part, we investigate the effects of simultaneously increasing the SmMm, Sn, Mn chain length on the interfacial properties with the chain length ratio of the SmMm and Sn, Mn fixed as m = n.
3.4 Effects of increasing the chain length of mixtures with m = n
The number of S and M beads for the copolymer and homopolymer used in this part are shown in Table 1.| System | m = n | |
|---|---|---|
| m | n | |
| 1 | 5 | 5 |
| 2 | 6 | 6 |
| 3 | 7 | 7 |
| 4 | 8 | 8 |
Fig. 9 depicts the density profiles of the SmMm copolymer with different chain lengths with m = n at a fixed SmMm chain concentration of ccp = 0.2, which illustrates that the density of beads S + M of the SmMm diblock copolymer at the interfaces decreases with increasing m = n. According to Fig. 6, the density of beads S + M of the SmMm at the interfaces increases with increasing the n. Hence, we inferred that the decrease of the density of beads S + M of the SmMm chain at the center of the interfaces is mainly related to the increase of the SmMm chain length.28
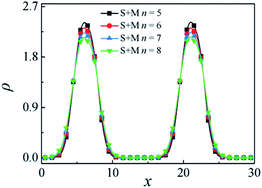 | ||
| Fig. 9 Density profiles of beads S + M of the diblock copolymers in the x-direction as a function of the n with m = n. | ||
Fig. 10(a) shows the dependence of the γ on the chain length m = n. Apparently, the obtained interfacial tension γ rapidly increases with the increase of m = n. This result is in agreement with the findings of increasing the chain length of diblock copolymers,28 which can be interpreted as follows: as the chain length m = n increases, the 〈Rg2〉x increases, as shown in Fig S4.† It means that the copolymer chains with longer chain length penetrate more deeply into the homopolymer phase. Thus the number of the copolymers at the center of the interfaces decreases, and the interfacial tension increases.28 Fig. 10(b) shows the relationship of the interfacial width w with the different chain lengths of m = n. We find that the interfacial width w increases with increasing the diblock copolymer and homopolymer chain length m = n. According to the result in the previous part, we know that as the chain length of the Sn and Mn homopolymers increase from 2 to 10 at a fixed chain length of diblock copolymers, the interfacial width w decreases. It means that the increase of the interfacial width w is also mainly related to the increase of the chain length of diblock copolymers. Fig. 10(c) shows the orientation parameter Θ of the diblock copolymers at the different chain lengths of m = n. We found that as m = n increases from 5 to 8, the orientation parameter Θ decreases, which is in contrast to the result of increasing diblock copolymer chain length with the homopolymer chain length n fixed.28 Therefore, we deduce that the decayed stretching of the diblock copolymer is mainly dependent on increasing the Sn and Mn homopolymer chain length n.
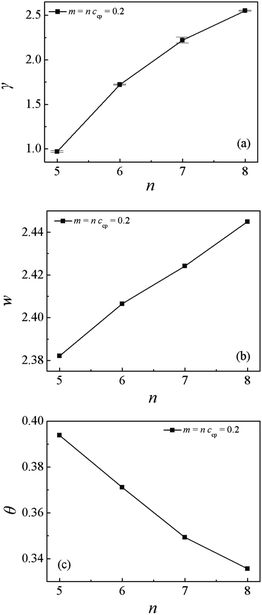 | ||
| Fig. 10 (a) Interfacial tension γ, (b) interfacial width w, and (c) orientation parameter of the SmMm chain as a function of m = n (m = n = 5, 6, 7, 8). | ||
4. Conclusions
In this paper, we conducted dissipative particle dynamics (DPD) simulations to study the three effects on the interfacial properties, including: the increase of the SmMm diblock copolymer concentration; the chain lengths of homopolymers Sn and Mn (the chain length of the SmMm copolymer is fixed as 10); and the simultaneous change of chain lengths of SmMm, Sn, and Mn with m = n.Our simulation results show that when the concentration of the SmMm diblock copolymers ccp ≤ 0.2, the SmMm diblock copolymers are segregated at the flat interfaces, and the S and M beads of the SmMm chains segregate into the homopolymers bulk Sn and Mn phases, respectively. As the SmMm diblock copolymer concentration ccp increases from 0.01 to 0.2, the density of S + M beads of the SmMm copolymer at the center of the interfaces increases, which results in the decayed correlations between Sn and Mn homopolymers, hence the interfacial tension decreases.
We then explore the interfacial properties of the Sn/SmMm/Mn mixtures with different chain lengths. (1) For the case of increasing the Sn and Mn homopolymers chain length n, when the n ≤ 10, the S5M5 diblock copolymers at the interface are swollen by the shorter homopolymers and resemble a “wet brush”. As the homopolymer chain length is shorter with n = 2, the S5M5 diblock copolymers are more stretched, accompanied by the larger Θ, the broader density distribution of the diblock copolymer, the wider interfacial width w, and the smaller interfacial tension γ. When n > 10, the homopolymers are expelled from the “dry brush”. Furthermore, as n further increases from 20 to 60, the density distribution of the S5M5 copolymers, the interfacial tension, and the configuration of the S5M5 copolymers remain unchanged. (2) For the case of simultaneously increasing chain lengths of SmMm, Sn, Mn with m = n, the deep of copolymer penetrate into the homopolymer phase increases with increasing m = n, which results in the weakened interactions between diblock copolymers and the increased interfacial tension, meanwhile, the orientation parameter Θ decreases, which is in contrast to the result of increasing diblock copolymer chain length with n fixed. It means that the decrease of the Θ is mainly related to the increase of the homopolymer chain length n.
Our simulation results indicate that the interfacial properties of Sn/SmMm/Mn mixtures are strongly correlated to the concentration of the SmMm chains and the chain lengths of SmMm, Sn, Mn, which raises important considerations concerning the use of the diblock copolymer as compatibilizers in the immiscible mixture systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is financially supported by the Basic Scientific Research Project of Hebei Provincial Department of Education (grant JQN2020021). We are grateful for the essential supports of Hebei Key Laboratory of Data Science and Application.References
- L. Sperling, in Recent Advances in Polymer Blocks, Grafts, and Blends, Plenum Press, 1974 Search PubMed.
- D. R. Paul and J. W. Barlow, J. Macromol. Sci., Polym. Rev., 1980, 18, 109 CrossRef.
- I. C. Sanchez, Annu. Rev. Mater. Res., 1983, 13, 387–412 CrossRef CAS.
- S. H. Wu, Polym. Eng. Sci., 1987, 27, 335–343 CrossRef CAS.
- K. Binder, M. Muller, F. Schmid and A. Werner, Phys. A, 1998, 249, 293–300 CrossRef CAS.
- N. Tan, S. K. Tai and R. M. Briber, Polymer, 1996, 37, 3509–3519 CrossRef CAS.
- H. Liang, B. D. Favis, Y. S. Yu and A. Eisenberg, Macromolecules, 1999, 32, 1637–1642 CrossRef CAS.
- T. P. Russell, A. Menelle, W. A. Hamilton and G. S. Smith, Macromolecules, 1991, 24, 5721–5726 CrossRef CAS.
- P. F. Green and T. P. Russell, Macromolecules, 1991, 24, 2931–2935 CrossRef CAS.
- T. P. Russell, S. H. Anastasiadis, A. Menelle, G. P. Felcher and S. K. Satija, Macromolecules, 1991, 24, 1575–1582 CrossRef CAS.
- S. H. Anastasiadis, T. P. Russell, S. K. Satija and C. F. Majkrzak, J. Chem. Phys., 1990, 92, 5677–5691 CrossRef CAS.
- S. H. Anastasiadis, T. P. Russell, S. K. Satija and C. F. Majkrzak, Phys. Rev. Lett., 1989, 62, 1852–1855 CrossRef CAS PubMed.
- G. L. Liu, M. P. Stoykovich, S. X. Ji, K. O. Stuen, G. S. W. Craig and P. F. Nealey, Macromolecules, 2009, 42, 3063–3072 CrossRef CAS.
- K. Chang, C. W. Macosko and D. C. Morse, Macromolecules, 2015, 48, 8154–8168 CrossRef CAS.
- L. B. Fischel and D. N. Theodorou, J. Chem. Soc., Faraday Trans., 1995, 91, 2381–2402 RSC.
- A. C. Balazs, C. P. Siemasko and C. W. Lantman, J. Chem. Phys., 1991, 94, 1653–1663 CrossRef CAS.
- Y. M. Wang, Y. Li and W. L. Mattice, J. Chem. Phys., 1993, 99, 4068–4075 CrossRef CAS.
- F. Schmid and M. Müller, Macromolecules, 1995, 28, 8639–8645 CrossRef CAS.
- M. Müller and M. Schick, J. Chem. Phys., 1996, 105, 8885–8901 CrossRef.
- A. Werner, F. Schmid, K. Binder and M. Müller, Macromolecules, 1996, 29, 8241–8248 CrossRef CAS.
- T. Uneyama and M. Doi, Macromolecules, 2005, 38, 196–205 CrossRef CAS.
- B. Vorselaars, R. K. W. Spencer and M. W. Matsen, Phys. Rev. Lett., 2020, 125, 117801 CrossRef CAS PubMed.
- R. K. W. Spencer and M. W. Matsen, J. Chem. Phys., 2018, 148, 204907 CrossRef PubMed.
- D. Duchs, V. Ganesan, G. H. Fredrickson and F. Schmind, Macromolecules, 2003, 36, 9237–9248 CrossRef.
- F. S. Bates, W. W. Maurer, P. M. Lipic, M. A. Hillmyer, T. P. Lodge, K. Almdal, K. Mortensen and G. H. Fredrickson, Phys. Rev. Lett., 1997, 79, 849–852 CrossRef CAS.
- D. Broseta and G. H. Fredrickson, J. Chem. Phys., 2018, 148, 204907 CrossRef PubMed.
- K. Uchida, K. Mita, S. Yamamoto and K. Tanaka, ACS Macro Lett., 2020, 9, 1576–1581 CrossRef CAS.
- H. J. Qian, Z. Y. Lu, L. J. Chen, Z. S. Li and C. C. Sun, J. Chem. Phys., 2005, 122, 187907 CrossRef PubMed.
- H. Guo and M. Cruz, J. Chem. Phys., 2005, 123, 753 Search PubMed.
- T. Lemos, C. Abreu and J. C. Pinto, Macromol. Theory Simul., 2020, 29, 1900042 CrossRef CAS.
- A. D. Goodson, G. Liu, M. S. Rick, A. W. Raymond, M. F. Uddin, H. S. Ashbaugh and J. Albert, J. Polym. Sci., Part B: Polym. Phys., 2019, 57, 794–803 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- X. H. Liu, Z. Q. Bai, K. D. Yang, J. Y. Su and H. X. Guo, Sci. China: Chem., 2013, 56, 1710–1721 CrossRef CAS.
- J. J. Wang, Z. Z. Li, X. P. Gu, L. F. Feng, C. L. Zhang and G. H. Hu, Polymer, 2012, 53, 4448–4454 CrossRef CAS.
- S. H. Anastasiadis, I. Gancarz and J. T. Koberstein, Macromolecules, 1988, 21, 2980–2987 CrossRef CAS.
- C. Zhou, S. K. Luo, Y. Sun, Y. Zhou and W. Qian, J. Appl. Polym. Sci., 2016, 133, 44098 Search PubMed.
- F. Paiva, A. Boromand, J. Maia, A. Secchi, V. Calado and S. Khani, J. Chem. Phys., 2019, 151, 114907 CrossRef CAS PubMed.
- Y. Zhou, X. P. Long and Q. X. Zeng, Polymer, 2011, 52, 6110–6116 CrossRef.
- Z. L. Luo and J. W. Jiang, Polymer, 2010, 51, 291–299 CrossRef CAS.
- D. M. Liu, X. Z. Duan, T. F. Shi, F. Jiang and H. Z. Zhang, Chem. J. Chin. Univ., 2015, 36, 2532–2539 CAS.
- D. M. Liu, L. J. Dai, X. Z. Duan, T. F. Shi and H. Z. Zhang, Chem. J. Chin. Univ., 2015, 36, 1752–1758 CAS.
- D. M. Liu, K. Gong, Y. Lin, T. Liu and X. Duan, Polymers, 2021, 13, 1516 CrossRef CAS PubMed.
- D. M. Liu, K. Gong, Y. Lin, H. F. Bo, T. Liu and X. Z. Duan, Polymers, 2021, 13, 2866 CrossRef CAS PubMed.
- D. M. Liu, M. Y. Yang, D. P. Wang, X. Y. Jing, Y. Lin, L. Feng and X. Z. Duan, Polymers, 2021, 13, 2333 CrossRef CAS PubMed.
- P. Espanol and P. B. Warren, J. Chem. Phys., 2017, 146, 150901 CrossRef PubMed.
- F. Goodarzi and S. Zendehboudi, Ind. Eng. Chem. Res., 2019, 58, 8817–8834 CrossRef CAS.
- A. G. Alexey, V. K. Yaroslav and V. C. Alexander, J. Chem. Phys., 2013, 139, 224901 CrossRef PubMed.
- P. K. Janert and M. Schick, Macromolecules, 1997, 30, 137–144 CrossRef CAS.
- I. Fortelny and J. Juza, Polymer, 2018, 150, 380–390 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra07671j |
| This journal is © The Royal Society of Chemistry 2021 |