Open Access Article
Open Access ArticleToward understanding the phase-selective growth mechanism of films and geometrically-shaped flakes of 2D MoTe2†
Tej B. Limbuab,
Bikram Adhikaria,
Seung Keun Songd,
Basant Chitaraa,
Yongan Tangc,
Gregory N. Parsonsd and
Fei Yan *a
*a
aDepartment of Chemistry and Biochemistry, North Carolina Central University, Durham, NC 27707, USA. E-mail: fyan@nccu.edu; tejblimbu@gmail.com
bDepartment of Physical and Applied Sciences, University of Houston-Clear Lake, Houston, TX 77058, USA
cDepartment of Mathematics and Physics, North Carolina Central University, Durham, NC 27707, USA
dDepartment of Chemical and Biomolecular Engineering, North Carolina State University, Raleigh, North Carolina 27695, USA
First published on 6th December 2021
Abstract
Two-dimensional (2D) molybdenum ditelluride (MoTe2) is an interesting material for fundamental study and applications, due to its ability to exist in different polymorphs of 2H, 1T, and 1T′, their phase change behavior, and unique electronic properties. Although much progress has been made in the growth of high-quality flakes and films of 2H and 1T′-MoTe2 phases, phase-selective growth of all three phases remains a huge challenge, due to the lack of enough information on their growth mechanism. Herein, we present a novel approach to growing films and geometrical-shaped few-layer flakes of 2D 2H-, 1T-, and 1T′-MoTe2 by atmospheric-pressure chemical vapor deposition (APCVD) and present a thorough understanding of the phase-selective growth mechanism by employing the concept of thermodynamics and chemical kinetics involved in the growth processes. Our approach involves optimization of growth parameters and understanding using thermodynamical software, HSC Chemistry. A lattice strain-mediated mechanism has been proposed to explain the phase selective growth of 2D MoTe2, and different chemical kinetics-guided strategies have been developed to grow MoTe2 flakes and films.
Introduction
Among various members of two-dimensional (2D) transition metal dichalcogenides (TMDs), molybdenum ditelluride (MoTe2) has sparked tremendous research interest in recent years, due to its structural variations and fascinating physical properties, such as existence of stable semiconducting 2H-phase to semi-metallic 1T and 1T′-phases,1,2 direct band gap similar to that of Si (∼1.1 eV) in single and bilayer semiconducting 2H-phases,3,4 high carrier mobility of 4000 cm2 V−1 s−1 and a giant magnetoresistance of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000% in a magnetic field of 14 T at 1.8 K,4 and room temperature phase change behavior from the 2H to 1T′-phase under applied strain5 and laser irradiation.6 Hence, 2D MoTe2 is a promising material for several frontier applications, including electronics,3,4 optoelectronics,7 spintronics,8 switching devices,9 and thermoelectric devices.10 2D MoTe2-based devices can be realized if a scalable method for the production of high quality flakes and large area films of the material is developed. Chemical vapor deposition (CVD) is a versatile and inexpensive method for the growth of flakes and large area films of 2D TMDs with high quality. However, the low chemical reactivity of transition metals with tellurium (Te) and the small electronegativity difference between them (for example, ≈0.3 eV between Mo and Te)1 imposes a challenge for a straightforward synthesis of highly crystalline transition metal ditellurides by the CVD process. Hence, an in-depth understanding of the CVD reaction is needed to overcome such a complex nature of chemical reaction between the transition metals and Te.
000% in a magnetic field of 14 T at 1.8 K,4 and room temperature phase change behavior from the 2H to 1T′-phase under applied strain5 and laser irradiation.6 Hence, 2D MoTe2 is a promising material for several frontier applications, including electronics,3,4 optoelectronics,7 spintronics,8 switching devices,9 and thermoelectric devices.10 2D MoTe2-based devices can be realized if a scalable method for the production of high quality flakes and large area films of the material is developed. Chemical vapor deposition (CVD) is a versatile and inexpensive method for the growth of flakes and large area films of 2D TMDs with high quality. However, the low chemical reactivity of transition metals with tellurium (Te) and the small electronegativity difference between them (for example, ≈0.3 eV between Mo and Te)1 imposes a challenge for a straightforward synthesis of highly crystalline transition metal ditellurides by the CVD process. Hence, an in-depth understanding of the CVD reaction is needed to overcome such a complex nature of chemical reaction between the transition metals and Te.
Researchers have developed different strategies for the phase-controlled CVD growth of 2D MoTe2. For example, Park et al.11 successfully synthesized centimeter-scale 2H- and 1T′-MoTe2 films by varying the Te partial pressure and quenching time, and Xu et al.12 reported the synthesis of the single crystals of 2H- and 1T′-MoTe2 in a two-step CVD process, where the 2D MoO2 single crystals were grown first and were tellurized at different temperatures for growing different phases. Large area 2H- and 1T′-MoTe2 films have also been controllably synthesized by adjusting the substrate location and the cooling rate after completion of the growth,13 and by tellurizing the Mo metal film and MoO3 films,14 respectively. There are a few more reports15–18 that also demonstrated the phase-controlled growth of large area 2H- and 1T′-MoTe2 films. Empante et al.2 has reported a successful synthesis of 2H-, 1T-, and 1T′- MoTe2 phases by varying the cooling rate after completion of the growth but has not demonstrated the controlled growth of films and flakes. 1T- phase of 2D MoTe2, which has been known to be less stable and can only be grown in the presence of an external agent, due to its low binding energy per unit cell (0.51 eV),2 has not been explored much. Although the previous works have demonstrated high-quality synthesis of various phases of 2D MoTe2, a thorough understanding on the phase-selective growth mechanism of 2H-, 1T-, and 1T′- 2D MoTe2 with controlled films and flakes formation has not been presented.
Herein, we report a detailed understanding on phase-selective growth of all three phases of 2D MoTe2, namely hexagonal structure 2H, trigonal 1T, and distorted trigonal 1T′ with controlled films and flakes formation for atmospheric-pressure CVD processes (APCVD). The growth processes have been explained by employing the knowledge of thermodynamics and kinetics. A thermodynamical software, HSC Chemistry has been employed to optimize and understand the necessary thermodynamic conditions and equilibria of the materials growth reactions. The associated homogeneous chemical reactions taking place in vapor-phase and heterogeneous reactions at the substrate surface, and the role of chemical kinetics have been discussed in detail. We have also optimized the growth routes of the 2D molybdenum dioxide (MoO2) and tellurene flakes that are always likely to form as byproduct materials during the growth effort of 2D MoTe2, and formation of the byproduct materials has been associated with our understanding of the phase-selective growth of 2D MoTe2. These findings have significant implications for predicting the phase-selective growth of films and geometrically-shaped flakes of other emerging 2D materials.
Experimental section
Phase- and morphology-controlled APCVD synthesis of 2H-, 1T-, and 1T′-MoTe2 was performed by using a tube furnace reactor (OTF-1200X, MTI corporation). For the synthesis of the flakes or rings of 2H-, 1T-, and 1T′-MoTe2, 1 mg of MoO3 powder (STREM chemicals Inc.) mixed with 5% NaCl was dispersed on a quartz boat (7 cm length, 1.5 cm height) with the help of a few drops of isopropanol. One piece of SiO2/Si substrate of dimension 0.8 cm × 1.5 cm was placed on the boat with SiO2 surface facing down. The quartz boat containing the Mo precursor and SiO2/Si substrates was placed at the center of the furnace consisting of a quartz tube (length 79 cm, internal diameter 3.2 cm, and external diameter 3.8 cm). Another quartz boat of the same size containing about 300 mg of Te powder (Fisher Scientific) was placed at about 10 cm upstream side from the edge of the furnace. For the synthesis of films, similar setup was used but with some changes. About 10 mg of a mixture of MoO3 + 5% NaCl was placed at the upstream edge of the quartz boat, and a SiO2/Si substrate was placed at 4 cm downstream with SiO2 surface facing up. The mount of Te in another boat was increased to about 1 g. For both cases, a carrier gas (a mixture of 10% H2 + 90% Ar) was flowed throughout the process at the rate of 40 sccm. 2H- and 1T′-MoTe2 were grown at the deposition temperatures of 650 and 730 °C, respectively for 15 minutes. The recorded temperatures of the region where Te powder was placed, were ∼420 °C and ∼450 °C for the set growth temperatures of 650 and 730 °C, respectively. The furnace was heated at the rate of 25 °C min−1 up to 400 °C and 10 °C min−1 up to 650 °C or 730 °C for 2H-MoTe2 and 1T′-MoTe2, respectively, and the cooling rate from the growth temperature to 300 °C was set at 15 °C min−1. After 300 °C, the furnace was opened to allow further cooling under ambient condition. A different strategy was used for the growth of 1T-MoTe2. The furnace was first ramped to 400 °C at the rate of 25 °C min−1 and then to 730 °C at 10 °C min−1. Then the furnace temperature was kept constant at 15 minutes and was suddenly cooled to 670 °C at the rate of 45 °C min−1, and the temperature was kept constant for next 15 minutes. The final cooling strategy was the same as in case of 2H and 1T′ phases.The deposition of 2D MoO2 was observed on the SiO2/Si placed on the quartz boat with SiO2 surface facing down. The deposition parameters were similar to those of 2H-MoTe2 flakes synthesis, except that the Te powder was placed upstream at a much lower temperature region and was not evaporated enough. The deposition of 2D tellurene nanobelts was observed on the SiO2/Si placed directly on the quartz tube around the furnace edge (about 20 cm from the center) with SiO2 surface facing up. Other deposition parameters were similar to those of 1T- and 1T′-MoTe2 films synthesis.
Gibbs free energy values and equilibrium amounts in reaction mixture were calculated using HSC Chemistry 7.1 software. For the equilibrium composition calculation, the initial concentrations of the reactants MoO3 and Te, NaCl, and gases H2 and Ar were 6.95 × 10−8, 7.83 × 10−8, 3.41 × 10−8, 2.68 × 10−6, and 2.14 × 10−5 kmol, respectively, for films growth. The corresponding initial concentrations for the flakes and rings growth were 6.95 × 10−9, 2.35 × 10−8, 3.41 × 10−8, 2.68 × 10−6, and 2.14 × 10−5 kmol, respectively. Amounts of the products have been plotted as a function of reaction temperature and have been labeled with different colors. Note that the software only shows thermodynamically favorable products (negative Gibbs free energy) and their amounts without kinetic consideration.
A combined RAMAN Microscope-Smart SPM atomic force microscope (LabRAm HR Evolution, Horiba Scientific) was used for the characterization of as-grown 2D MoTe2. The Raman measurements were carried out with a 532 nm excitation laser (0.27 mW laser power, and 20 s exposure time), using 1800 g mm−1 grating and 100× objective lens. The thickness of the MoTe2 films was measured using tapping mode AFM.
Elemental composition and chemical states of the elements were analyzed using X-ray photoelectron microscopy (XPS) (SPECS FlexMod XPS, Mg Ka excitation (1254 eV)) equipped with a hemispherical analyzer PHOIBIS 150. X-ray beam was generated at the accelerating potential of 10 kV and current of 30 mA. The base pressure and chamber pressure during analysis were ∼10−10 mbar and ∼10−9, respectively. The samples were sputtered with Ar+ ion for 1.5 minutes at a sputtering voltage of 5 kV and current of 4 μA before analysis.
Time-of-flight secondary ion mass spectrometry (ToF-SIMS) analyses of the samples were conducted using a TOF-SIMS instrument (ION TOF, Inc. Chestnut Ridge, NY) equipped with a bismuth analysis beam, Cs+ sputtering gun, and electron flood gun for charge compensation. Both the Bi and Cs ion columns are oriented at 45° with respect to the sample surface normal. The analysis chamber pressure is maintained below 5.0 × 10−9 mbar to avoid contamination of the surfaces to be analyzed. Current of Bi analysis beam was 14 nA over 500 μm × 500 μm of area. Ion flux was 1.2 ×1012 ions per cm2 for 100 μm × 100 μm sample and 6.0 × 1013 ions per cm2 for 100 μm × 100 μm sample. Ion flux for sputtering was 6.8 × 1015 ions per cm−2. For high lateral resolution mass spectral images acquired in this study, a Burst Alignment setting of 25 keV Bi3+ ion beam was used. The negative secondary ion mass spectra obtained were calibrated using C−, O−, OH−, Cn−. The positive secondary ion mass spectra were calibrated using C+, C2H3+, C3H5+, C4H7+.
Results and discussion
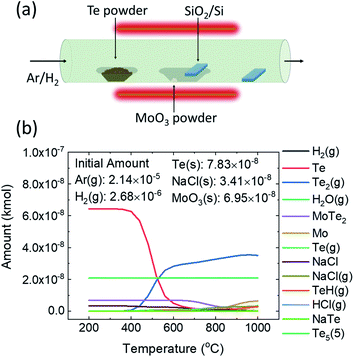
Fig. 1a shows a schematic of the CVD setup for the phase selective synthesis of 2D MoTe2 films with 2D tellurene obtained as a byproduct material. The schematic for the phase selective synthesis of 2D MoTe2 flakes or rings with 2D MoO2 as a byproduct material has been presented in Fig. 1Sa, ESI.† Although the details of the chemical reactions of this CVD process are not known yet, the following reaction steps are expected to occur:| MoO3(s) + NaCl(s) → xNaMoO3(s) + yMoOCl2(g) + zMoOCl4(g) + …. | (A.1) |
| MoOCl2(g) + MoOCl4(g) + 5Te(g) + 6H2(g) → 2MoTe2(s) + H2Te(g) + 6HCl(g) + 2H2O(g) | (A.2) |
| MoO3(g) + H2(g) + 3Te(g) → 0.5MoO2(g) + 0.5MoTe2(s) + TeO(g) + H2O(g) + 0.5Te2(g) | (B.1) |
| MoO2(g) + 2Te(g) + 2H2 → MoTe2(s) + 2H2O(g) | (B.2) |
The reactions (A.1) and (A.2) have been written based on the previously suggested reaction mechanism19 for MoTe2 synthesis, and the reactions (B.1) and (B.2) are the expected reactions written from our thermodynamic equilibrium product calculations. We suggest the additional reactions (B.1)–(B.2) for our CVD reactions based on the following reasoning: (1) HSC calculation shows that the Gibbs free energies are negative for these reactions, indicating that they are thermodynamically favorable, and (2) as predicted by the reaction (B.1), 2D MoO2 crystals were deposited under Te deficient reaction condition.
Fig. 1b shows a typical graph showing thermodynamic equilibrium product compositions calculated with HSC software for the reaction of 10 mg of MoO3 with 1 g of Te in the presence of promoter compound, NaCl, and gases H2 and Ar to form the films of MoTe2. The corresponding graph obtained with smaller amounts of MoO3 (1 mg) and Te (300 mg) for flakes or rings deposition has been presented in Fig. S1b, ESI.† From Fig. 1b, it is evident that the reaction leads to the formation of MoTe2 even at a low temperature, 200 °C, but due to slow reaction kinetics, a lower growth temperature is not suitable. The equilibrium concentration of the product, MoTe2 starts decreasing at 650 °C and almost vanishes at 900 °C. The effect of temperature on the reaction rate constant k is given by the Arrhenius equation, k = Ae−Ea/RT,20 where A is the pre-exponential factor, Ea is the activation energy, R is the molar gas constant, and T is the absolute temperature. Based on this equation, higher the temperature, faster is the reaction rate, which is generally intended for minimizing the total reaction time. However, the graph (Fig. 1b) shows that the formation of unintended byproducts, such as TeH(g), Te2(g), Mo(s), and NaCl(g) increase after the temperature of 730 °C. Based on this thermodynamic equilibrium calculation, we chose 650 to 730 °C as the maximum deposition temperature for the growth of 2D MoTe2.
Fig. 2a, c, and e show that flakes of the different phases of MoTe2 can exist in different geometrical structures, such as hexagonal for 2H-, hexagonal, triangular, and truncated-triangular (see Fig. S2, ESI†) for 1T-, and ring-like for 1T′-phases. The flakes were grown by controlling the amounts of the precursors to about 1 mg for MoO3 and 200 mg for Te powder, and the SiO2/Si substrates were placed upside down on the boat containing MoO3. For the film growth (see Fig. 2b, d, and f), the amounts of MoO3 and Te powders were increased to about 10 mg and 500 mg, respectively, and the SiO2/Si substrates were placed facing up on the boat. We note that despite a good controllability in film growth using the above-mentioned growth parameters and strategy, there remains a possibility of the formation of single crystals and/or streaks of the material in small areas, mostly near the edges of the substrates. However, films and flakes can be deposited with preference and with dominant morphology by following our growth parameters and strategies. Moreover, although it is known to be difficult to stabilize 1T-MoTe2,2 we successfully synthesized crystals and films of this phase. The detailed synthesis mechanism will be discussed later.
Raman spectroscopy is the necessary and sufficient characterization technique for the identification of 2D materials and their phases. Fig. 2g depicts the typical Raman spectra of 2H-, 1T-, and 1T′-2D MoTe2 phases for both flakes and films morphologies. We observed that Raman spectra of flakes and films for each phase are similar in terms of full width at half maximum (FWHM) of their corresponding vibrational bands, indicating similar qualities of both morphologies. FWHM of the Raman bands in the Raman spectra collected on different flakes and within a film of the same phase also vary slightly, and the Raman spectra are not significantly different, which could be due to local temperature variation on the substrates or unintended particles formation on the flakes and films. Hence, we presented typical Raman spectra for both flakes and films morphologies to represent only the phases. The samples grown at 630 °C show peaks at 171, 231, and 289 cm−1 corresponding to A1g, E12g, and B12g vibrational modes of 2H-MoTe2, consistent with previous reports.2,4–6 The samples grown at 750 °C are confirmed to be 1T′-MoTe2 as the Raman bands observed at 108, 125, and 160 cm−1 correspond to the Au, Ag, and Ag, respectively.2–6,19,21 The samples grown with the two-step growth strategy show a Raman spectrum with a sharp peak at 154 and a broad peak at 254 cm−1, which correspond to 1T-MoTe2 with an octahedral crystal structure.2 To our knowledge, this is the second report on the synthesis of 1T-MoTe2, and the previous work2 has shown a round structure for flakes, whereas our work shows perfect geometrically-shaped crystals, which suggests that the quality of 1T-MoTe2 grown by our method could be higher. With higher amounts of MoO3 and Te and SiO2/Si substrate facing up on the boat, continuous films were obtained for 2H, 1T, and 1T′ phases of 2D MoTe2 as shown in Fig. 2b, d, and f, respectively.
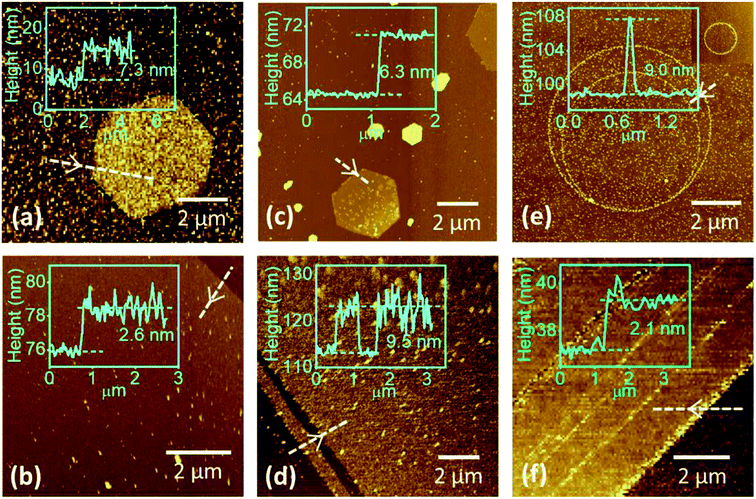
Fig. 3a–f show the tapping-mode AFM images and corresponding height profiles of the flakes and films of 2H-, 1T-, and 1T′-MoTe2. The images show that 2H-MoTe2 flakes are formed with hexagonal shape, and 1T-MoTe2 was formed with different geometrical shapes such as hexagon, triangle, and truncated triangle (see Fig. S2, ESI†). In contrast to 1T′-MoTe2 flakes formed in various shapes such as rectangular-,22 square-,12 star-like-,23 and irregular-shaped flakes1,19 reported previously, we obtained 1T′ phase with ring-like structures in our growth condition. The detailed growth mechanism of ring-shaped 1T′ phase of MoTe2 remains to be explored. We hypothesize that the loop formation could be the result of a spontaneous polarization process, which originates from the binding of the positively and negatively charged surfaces on the opposite sides of belt-like MoTe2 nanostructures. Fig. 3b shows the heights of the typical 2H-, 1T-, and 1T′-MoTe2 films are ∼2.6, ∼9.5, and ∼2.1 nm, which are equivalent to about 4, 15, and 3 layers, respectively. The measured root mean square (rms) roughness of the 2H-, 1T-, and 1T′-MoTe2 films are ∼0.8, ∼3.0, and ∼0.6 nm, respectively.
The bottom part of the Fig. 4a shows the Raman spectrum of the material grown at the downstream furnace edge obtained as a byproduct. The vibrational peaks appearing at 120 and 140 cm−1 resemble the longitudinal phonon mode (A1) and the high frequency vibrational mode (E2) of 2D tellurene.24
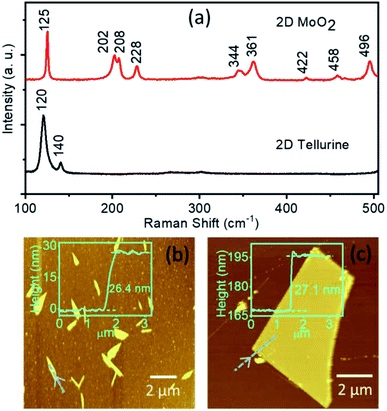 | ||
| Fig. 4 (a) Raman spectra of 2D tellurene and MoO2 showing characteristic vibrational bands. Tapping-mode AFM images and corresponding height profile of (b) tellurene nanobelts and (c) MoO2 flakes. | ||
The top part of the Fig. 4a shows the Raman spectrum of the byproduct obtained when Te was not well evaporated, i.e., with the minimal amount of Te supply. The peaks appearing at 125, 202, 208, 228, 344, 361, 422, 458, and 496 cm−1 are the characteristic vibrational bands of monoclinic structure of 2D MoO2.25 From our observation, it can be understood that the deposition of the quasi-2D crystals of MoO2 is due to the reduction of MoO3 by H2 gas, which is consistent with the previous reports.26,27 Fig. 4b and c show the AFM images of the 2D tellurene nanobelts and MoO2 flakes with a typical thickness of ∼26.4, and ∼27.1 nm, respectively.
XPS measurements were performed to analyze the elemental composition and chemical states of the synthesized samples, especially those that needed more characterization in addition to the Raman spectroscopy analysis and AFM measurements. We note that all the samples got oxidized to some extent when exposed to air for a few hours. During the course of various measurements, all samples were almost equally exposed to ambient, but 1T-MoTe2 was not found oxidized more heavily than other phases and 2D tellurene, indicating a good stability of this phase. We sputtered each sample with Ar+ ion before analyzing for XPS. Fig. 5a shows the XPS survey spectra of the Ar+ ion-sputtered 1T-MoTe2, 1T′-MoTe2, and tellurene films. The survey spectra show Mo and Te peaks at ∼232.8 eV and ∼573.8 eV, with 4.1 and 3.4 atomic%, respectively for 1T-MoTe2, and 3.3 and 2.9 atomic%, respectively, for 1T′-MoTe2 films. A slightly smaller value of the Te content with respect to Mo is due to Ar+ ion sputtering, which removes the top layer consisting of mostly oxidized Te and adventitious carbons. For this reason, no or negligibly small carbon peaks are observed in the spectra. For comparison purpose, we analyzed the 1T-MoTe2 film before Ar+ ion sputtering and observed Mo and Te atomic% as 1.9 and 4.1, respectively, with the Te to Mo atomic% ratio ∼2 as expected (see Fig. S3, ESI†). The survey spectrum of the tellurene film, on the other hand, does not show Mo content, confirming the nanobelts were purely of Te. Since we did not observe any tellurene nanobelts or crystals on the samples placed in the central region of the furnace or a higher temperature region, it is apparent that Te vapor crystalizes at a relatively lower temperature ∼500 °C and forms 2D tellurene nanostructures. Fig. 5b–d depict the high-resolution peaks of Te 3d region for 1T-MoTe2, 1T′-MoTe2, and tellurene films. The deconvolution of the Te peaks shows that a small amount of Te-O is still present in the samples even after the Ar ion sputtering.2,28 For 1T-MoTe2 film, the high-resolution XPS peaks (Fig. 5b) of Te are observed at 573.4 (3d5/2) and 583.7 (3d3/2) due to Te-Mo bonding, and we did not observe a significant shift of the Te peaks in 1T-MoTe2 with respect to 1T′-MoTe2. However, the Te peaks for tellurene nanobelts (Fig. 5d) appear at a slightly larger values of binding energy (B. E.), 574.1 (3d5/2) and 584.3 (3d3/2) compared to that of Te-Mo peak for 1T-MoTe2 or 1T′-MoTe2 phases, which agrees with the report.29
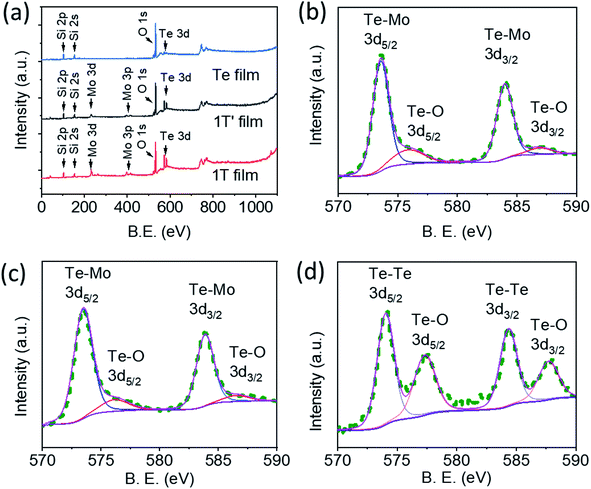 | ||
| Fig. 5 (a) XPS survey spectra of 1T, 1T′, and Te. High resolution peak of (b) Te 3d of 1T film, (c) Te 3d of 1T′ film, (d) Te 3d of tellurene film. | ||
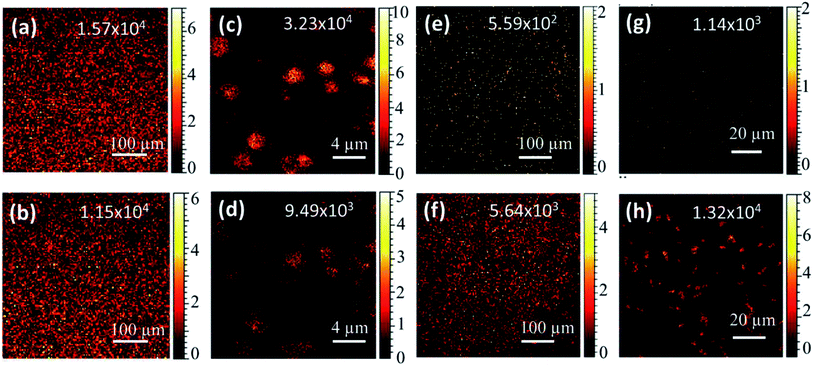
Elemental composition of the samples was further analyzed using ToF-SIMS. TOF-SIMS provides elemental, chemical state, and molecular information from surfaces of solid materials.30 Secondary ion ToF-SIMS maps of Mo and Te collected on 500 μm × 500 μm area of 1T-MoTe2 and tellurene films are presented in Fig. 6a, b, e and f, respectively, and the maps of 100 μm × 100 μm area of 1T-MoTe2 flakes and tellurene nanobelts are presented in Fig. 6c, d, g and h, respectively.
The values in the inset show the respective secondary ion (Mo+ and Te+) counts recorded, but the values do not correspond to the stoichiometry of the compound material, MoTe2. A much lower counts of Te+ may be ascribed to larger ionization energy (9.01 eV) of Te31 than that of Mo (7.09 eV)32 and the weak stability of Te+ ions, due to a low electron affinity (1.97 eV).33 For this reason, ToF-SIMS data alone are not ideal for determining stoichiometry of a compound. Hence, true amount of Te in the samples can be expected higher than what has been represented in Fig. 6b, d, f, and h. Secondary ion maps of Mo and Te for 1T-MoTe2 flakes shown in Fig. 6c and d support that the flakes are comprised of Mo and Te. A higher-resolution maps of Mo and Te for 1T-MoTe2 flakes deposited on SiO2/Si have been presented in Fig. S4a and b, ESI,† respectively. 2D tellurene growth on the substrates placed at the downstream furnace edge has also been confirmed by ToF-SIMS study. Secondary ion ToF-SIMS maps of Mo and Te in tellurene film deposited on SiO2/Si shown in Fig. 6e and f clearly indicate that the Mo+ ion counts is much smaller than that of Te+ ions. We note that the actual amount of Te in 2D tellurene film should be much larger than the one detected in our experiment for the aforementioned reason. Similar observation has been made for the Mo and Te secondary ion maps for 2D tellurene nanobelts deposited on SiO2/Si (Fig. 6g and h), confirming that the nanobelts are not a different polymorph of MoTe2. Secondary ion maps of Si and SiHO (Fig. S4c and d, ESI†) further show a clearer picture of small and belt-like structures of 2D tellurene nanobelts.
We observed that under ambient pressure conditions, different growth temperatures and a two-step growth strategy can lead to the phase-selective stabilization of 2D MoTe2. The phase selectivity may result from the lattice strain that influences the grown or growing crystals. Stress/strain-dependent phase transition rate in a material can be explained by the transition state theory (TST),34 according to which the phase transition rate is given by the relation, k(σ) ∝ e−Eσ/kBT, where σ is the stress acting on the growing material, Eσ is the barrier energy for phase transition, kB is the Boltzmann constant, and T is the absolute temperature. In the case of our CVD process, the growth temperature is a key parameter, which however, is proportional to the strain developed on the grown or growing material arising from the thermal expansivity mismatch between MoTe2 and the substrate SiO2/Si. Hence, at a different growth temperature condition, the grown or growing material experiences different stress/strain. According to TST, a larger stress/strain (or larger temperature) is expected to lower the phase transition barrier energy,34 facilitating the phase transition of the material. For example, a lower strain on the grown or growing material at a lower growth temperature of 650 °C is not strong enough to lower the phase transition barrier energy, which stabilizes the 2H phase. On the other hand, a higher stress/strain at a higher growth temperature of 750 °C would lower the phase transition barrier energy significantly, facilitating the phase transition and making 1T′-MoTe2 phase more thermodynamically favorable.4 This explanation is consistent with the observations made in previous reports,2,22 where 2H-MoTe2 and 1T′-MoTe2 were grown at lower and higher temperatures, respectively. Such a process of strain-mediated phase stabilization is also consistent with the report, where strain is found to have a strong influence on the phase change behavior of 2D MoTe2, i.e., 2H- to 1T′-MoTe2 phase change occurs under the application of strain and reverse phase transition occurs under removal of the strain.35 CVD growth of 1T-MoTe2 phase under a two-step growth strategy may be ascribed to the sudden strain relaxation and additional phase stabilization time provided during the second step of the growth process. When the temperature of the furnace is lowered to 670 °C, the strain on the grown or growing material is reduced facilitating the transition to 1T-MoTe2 phase, and the phase is stabilized when the furnace is maintained at 670 °C for 15 minutes. We performed several trials with a single step, i.e., at 730 °C or at 670 °C, but none of the trials led to the growth of 1T-MoTe2, which indicates that a two-step growth process was a key recipe to obtain this phase.
The controllable growth of flakes and films of 2H, 1T, and 1T′ phases of 2D MoTe2 may be understood considering the role of kinetic factors during the APCVD process. As mentioned above, it may be expected that the gaseous-phase reaction of MoO3 and Te in the presence of NaCl and H2 produces MoTe2 molecules as active species. The gaseous active species then diffuse through the boundary layer, which is a thin and active reaction zone in contact with the substrate of the growing material,36,37 due to the concentration gradient between its two opposite regions (above and below the boundary layer in our case). The active species are adsorbed onto the surface of the substrate and nucleate for crystal growth. The other incoming gaseous active species interact with the edges of the growing crystals and are incorporated. Inactive gaseous species are taken away by the carrier gas, however, they are sometimes incorporated into the crystal as impurities or form unintended crystals. In the process, only a part of the active species that cross the boundary layer is incorporated into the crystals, and the rest return to the bulk of the gases. A lower amount, 1 mg of MoO3 with 300 mg of Te supplies a much smaller concentration of the gaseous active species (Cg) than a larger amount, 10 mg of MoO3 with 500 mg of Te, provided the same ramping rate and furnace temperature. Hence, the concentration of the gaseous active species that crosses the boundary layer and interacts with the growing crystals at their edges (Cs) is proportional to the amounts of the precursors. For such a condition, Flux of the active species diffusing to the substrate surface through boundary layer (∅1) and flux of the unincorporated species returning from the substrate surface (∅1) are given by:38
| ∅1 = hg (Cg − Cs) | (1) |
| ∅2 = ksCs | (2) |
| Cs = hgCg/(ks + hg) | (3) |
Since we synthesized the flakes and films of each phase of 2D MoTe2 at the same temperature, the temperature dependent quantity, ks,20 can be treated constant for any amounts of precursors (e.g., 1 mg of MoO3 and 300 mg of Te or 10 mg of MoO3 and 1 g of Te). From eqn (3), it is apparent that the concentration of the gaseous active species that crosses the boundary layer and interacts with the growing crystals at their edges (Cs) is less for smaller amounts of the precursors. Furthermore, the mass transport coefficient is dependent upon the thickness of the boundary layer, δ, as hg = Dg/δ,39 where Dg is the gas diffusion coefficient. According to the Blasius model, the thickness of the laminar boundary layer (δ) is inversely proportional to the square root of the gas flow speed.40 Since the gas speed can be expected less below than above the SiO2/Si substrate placed with SiO2 surface facing down on the boat, hg is smaller for such a substrate orientation. Eqn (3) suggests that Cs is smaller as both factors Cg and hg are smaller, when a smaller amount of the precursors were used and the SiO2/Si substrate placed facing down on the ceramic boat. Hence, this growth strategy leads to a smaller nucleation density resulting in the growth of flakes or ring morphologies of the 2D MoTe2. On the other hand, when larger amounts of the precursors were used, and the materials were grown on the SiO2/Si substrate placed facing up on the boat, both the quantities Cg and hg are larger, making Cs much larger. As a result, this strategy leads to a much larger nucleation density, promoting the film growth of 2D MoTe2.
Conclusions
In summary, we demonstrated a facile approach for selective growth of few-layer flakes and films of 2H-, 1T-, and 1T′-MoTe2 by APCVD and presented a thorough understanding of the growth mechanism. A thermodynamical software, HSC Chemistry was used to optimize the growth parameters and understand the role of thermodynamics for materials growth. Lattice strain-mediated growth mechanism has been proposed to explain the phase selective growth of 2D MoTe2, and the strategies for selective growth for flakes or films have been developed based on the role of chemical kinetics. We also suggested the facile routes for the synthesis of 2D MoO2 and tellurene nanocrystals, based on the observation of these nanocrystals deposited as byproducts during our synthesis. Our investigation imparts knowledge on the growth strategies to overcome the complexity of the CVD reactions and will be useful for growing not only MoTe2 but also other layered 2D materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for the financial support of this project by the U.S. National Science Foundation (Awards #1831133 and #2122044). This work was performed in part at the Analytical Instrumentation Facilities (AIF) at NC State University, which is supported by the state of North Carolina and the National Science Foundation (Award ECCS-1542015). The authors would like to thank Dr Fred Stevie and Dr Chuanzhen Zhou for assisting with the XPS and ToF-SIMS measurements, respectively.References
- J. Zhou, F. Liu, J. Lin, X. Huang, J. Xia, B. Zhang, Q. Zeng, H. Wang, C. Zhu, L. Niu and X. Wang, Large area and high quality 2D transition metal telluride, Adv. Mater., 2017, 29, 1603471 CrossRef PubMed.
- T. A. Empante, Y. Zhou, V. Klee, A. E. Nguyen, I. H. Lu, M. D. Valentin, S. A. Naghibi Alvillar, E. Preciado, A. J. Berges, C. S. Merida and M. Gomez, Chemical vapor deposition growth of few-layer MoTe2 in the 2H, 1T′, and 1T phases: tunable properties of MoTe2 films, ACS Nano, 2017, 11, 900–905 CrossRef CAS PubMed.
- L. Zhou, A. Zubair, Z. Wang, X. Zhang, F. Ouyang, K. Xu, W. Fang, K. Ueno, J. Li, T. Palacios and J. Kong, Synthesis of high-quality large-area homogenous 1T′ MoTe2 from chemical vapor deposition, Adv. Mater., 2016, 28, 9526–9531 CrossRef CAS PubMed.
- D. H. Keum, S. Cho, J. H. Kim, D. H. Choe, H. J. Sung, M. Kan, H. Kang, J. Y. Hwang, S. W. Kim, H. Yang and K. J. Chang, Bandgap opening in few-layered monoclinic MoTe2, Nat. Phys., 2015, 11, 482–486 Search PubMed.
- S. Song, D. H. Keum, S. Cho, D. Perello, Y. Kim and Y. H. Lee, Room temperature semiconductor–metal transition of MoTe2 thin films engineered by strain, Nano Lett., 2016, 16, 188–193 CrossRef CAS PubMed.
- Y. Tan, F. Luo, M. Zhu, X. Xu, Y. Ye, B. Li, G. Wang, W. Luo, X. Zheng, N. Wu and Y. Yu, Controllable 2H-to-1T′ phase transition in few-layer MoTe2, Nanoscale, 2018, 10, 19964–19971 RSC.
- L. Yin, X. Zhan, K. Xu, F. Wang, Z. Wang, Y. Huang, Q. Wang, C. Jiang and J. He, Ultrahigh sensitive MoTe2 phototransistors driven by carrier tunneling, Appl. Phys. Lett., 2016, 108, 043503 CrossRef.
- D. MacNeill, G. M. Stiehl, M. H. D. Guimaraes, R. A. Buhrman, J. Park and D. C. Ralph, Control of spin–orbit torques through crystal symmetry in WTe2 ferromagnet bilayers, Nat. Phys., 2017, 13, 300–305 Search PubMed.
- X. Qian, J. Liu, L. Fu and J. Li, Quantum spin Hall effect in two-dimensional transition metal dichalcogenides, Science, 2014, 346, 1344–1347 CrossRef CAS PubMed.
- D. Shi, G. Wang, C. Li, X. Shen and Q. Nie, Preparation and thermoelectric properties of MoTe2 thin films by magnetron co-sputtering, Vacuum, 2017, 138, 101–104 CrossRef CAS.
- J. C. Park, S. J. Yun, H. Kim, J. H. Park, S. H. Chae, S. J. An, J. G. Kim, S. M. Kim, K. K. Kim and Y. H. Lee, Phase-engineered synthesis of centimeter-scale 1T′-and 2H-molybdenum ditelluride thin films, ACS Nano, 2015, 9, 6548–6554 CrossRef CAS PubMed.
- X. Xu, X. Li, K. Liu, J. Li, Q. Feng, L. Zhou, F. Cui, X. Liang, Z. Lei, Z. Liu and H. Xu, Thermodynamics and kinetics synergetic phase-engineering of chemical vapor deposition grown single crystal MoTe2 nanosheets, Cryst. Growth Des., 2018, 18, 2844–2850 CrossRef CAS.
- S. Cheng, L. Yang, J. Li, Z. Liu, W. Zhang and H. Chang, Large area phase-controlled growth of few-layer two-dimensional MoTe2 and lateral 1T′–2H heterostructures by chemical vapor deposition, CrystEngComm, 2017, 19, 1045–1051 RSC.
- J. P. Fraser, L. Masaityte, J. Zhang, S. Laing, J. C. Moreno-López, A. F. McKenzie, J. C. McGlynn, V. Panchal, D. Graham, O. Kazakova and T. Pichler, Selective phase growth and precise-layer control in MoTe2, Commun. Mater., 2020, 1, 1–9 CrossRef.
- L. Zhou, K. Xu, A. Zubair, A. D. Liao, W. Fang, F. Ouyang, Y. H. Lee, K. Ueno, R. Saito, T. Palacios and J. Kong, Large-area synthesis of high-quality uniform few-layer MoTe2, J. Am. Chem. Soc., 2015, 137, 11892–11895 CrossRef CAS PubMed.
- L. Yang, W. Zhang, J. Li, S. Cheng, Z. Xie and H. Chang, Tellurization velocity-dependent metallic–semiconducting–metallic phase evolution in chemical vapor deposition growth of large-area, few-layer MoTe2, ACS Nano, 2017, 11, 1964–1972 CrossRef CAS PubMed.
- T. Kim, H. Park, D. Joung, D. Kim, R. Lee, C. H. Shin, M. Diware, W. Chegal, S. H. Jeong, J. C. Shin and J. Park, Wafer-Scale Epitaxial 1T′, 1T′–2H Mixed, and 2H Phases MoTe2 Thin Films Grown by Metal–Organic Chemical Vapor Deposition, Adv. Mater. Interfaces, 2018, 5, 1800439 CrossRef.
- B. Adhikari, T. B. Limbu, K. Vinodgopal and F. Yan, Atmospheric-pressure CVD growth of two-dimensional 2H-and 1T′-MoTe2 films with high-performance SERS activity, Nanotechnology, 2021, 32, 335701 CrossRef CAS PubMed.
- K. Chen, Z. Chen, X. Wan, Z. Zheng, F. Xie, W. Chen, X. Gui, H. Chen, W. Xie and J. Xu, A Simple Method for Synthesis of High-Quality Millimeter-Scale 1T′ Transition-Metal Telluride and Near-Field Nano optical Properties, Adv. Mater., 2017, 29, 1700704 CrossRef PubMed.
- J. E. Crowell, Chemical methods of thin film deposition: Chemical vapor deposition, atomic layer deposition, and related technologies, J. Vac. Sci. Technol., A, 2003, 21, 88–95 CrossRef.
- L. Zhou, S. Huang, Y. Tatsumi, L. Wu, H. Guo, Y. Q. Bie, K. Ueno, T. Yang, Y. Zhu, J. Kong and R. Saito, Sensitive phonon-based probe for structure identification of 1T′ MoTe2, J. Am. Chem. Soc., 2017, 139, 8396–8399 CrossRef CAS PubMed.
- J. H. Sung, H. Heo, S. Si, Y. H. Kim, H. R. Noh, K. Song, J. Kim, C. S. Lee, S. Y. Seo, D. H. Kim and H. K. Kim, Coplanar semiconductor–metal circuitry defined on few-layer MoTe2 via polymorphic heteroepitaxy, Nat. Nanotechnol., 2017, 12, 1064–1070 CrossRef CAS PubMed.
- C. H. Naylor, W. M. Parkin, J. Ping, Z. Gao, Y. R. Zhou, Y. Kim, F. Streller, R. W. Carpick, A. M. Rappe, M. Drndic and J. M. Kikkawa, Monolayer single-crystal 1T′-MoTe2 grown by chemical vapor deposition exhibits weak antilocalization effect, Nano Lett., 2016, 16, 4297–4304 CrossRef CAS PubMed.
- H. Cui, K. Zheng, Z. Xie, J. Yu, X. Zhu, H. Ren, Z. Wang, F. Zhang, X. Li, L. Q. Tao and H. Zhang, Tellurene nanoflake-based NO2 sensors with superior sensitivity and a sub-parts-per-billion detection limit, ACS Appl. Mater. Interfaces, 2020, 12, 47704–47713 CrossRef CAS PubMed.
- Y. Zhu, X. Ji, S. Cheng, Z. Y. Chern, J. Jia, L. Yang, H. Luo, J. Yu, X. Peng, J. Wang and W. Zhou, Fast energy storage in two-dimensional MoO2 enabled by uniform oriented tunnels, ACS Nano, 2019, 13, 9091–9099 CrossRef CAS PubMed.
- N. S. Vorobeva, A. Lipatov, D. S. Muratov and A. Sinitskii, Chemical vapor deposition and characterization of two-dimensional molybdenum dioxide (MoO2) nanoplatelets, Nanotechnology, 2018, 29, 505707 CrossRef PubMed.
- J. Luo, H. Chen, J. Wang, F. Xia and X. Huang, Direct growth of 2D MoO2 single crystal on SiO2/Si substrate by atmospheric pressure chemical vapor deposition, Mater. Chem. Phys., 2020, 251, 123166 CrossRef CAS.
- S. Cho, S. Kim, J. H. Kim, J. Zhao, J. Seok, D. H. Keum, J. Baik, D. H. Choe, K. J. Chang, K. Suenaga and S. W. Kim, Phase patterning for ohmic homojunction contact in MoTe2, Science, 2015, 349, 625–628 CrossRef CAS PubMed.
- L. Yang, H. Wu, W. Zhang, Z. Chen, J. Li, X. Lou, Z. Xie, R. Zhu and H. Chang, Anomalous oxidation and its effect on electrical transport originating from surface chemical instability in large-area, few-layer 1T′-MoTe2 films, Nanoscale, 2018, 10, 19906–19915 RSC.
- C. Zhou, F. Stevie and R. Garcia, Analysis of permethrin treated fabric using ToF-SIMS, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2020, 38, 034006 CAS.
- T. Kieck, Y. Liu, D. W. Stracener, R. Li, J. Lassen and K. D. A. Wendt, Resonance laser ionization spectroscopy of tellurium, Spectrochim. Acta, Part B, 2019, 159, 105645 CrossRef CAS.
- D. M. Rayner, S. A. Mitchell, O. L. Bourne and P. A. Hackett, First-ionization potential of niobium and molybdenum by double-resonance, field-ionization spectroscopy, J. Opt. Soc. Am. B, 1987, 4, 900–905 CrossRef CAS.
- G. Haeffler, A. E. Klinkmüller, J. Rangell, U. Berzinsh and D. Hanstorp, The electron affinity of tellurium, Z. Phys. D: At., Mol. Clusters, 1996, 38, 211–214 CrossRef CAS.
- A. Ghasemi and W. Gao, Atomistic mechanism of stress modulated phase transition in monolayer MoTe2, Extreme Mechanics Letters, 2020, 40, 100946 CrossRef.
- S. Song, D. H. Keum, S. Cho, D. Perello, Y. Kim and Y. H. Lee, Room temperature semiconductor–metal transition of MoTe2 thin films engineered by strain, Nano Lett., 2016, 16, 188–193 CrossRef CAS PubMed.
- S. Kasap, H. Khaksaran, S. Çelik, H. Özkaya, C. Yanık and I. I. Kaya, Controlled growth of large area multilayer graphene on copper by chemical vapor deposition, Phys. Chem. Chem. Phys., 2015, 17, 23081–23087 RSC.
- T. B. Limbu, J. C. Hernández, F. Mendoza, R. K. Katiyar, J. J. Razink, V. I. Makarov, B. R. Weiner and G. Morell, A novel approach to the layer-number-controlled and grain-size-controlled growth of high-quality graphene for nanoelectronics, ACS Appl. Nano Mater., 2018, 1, 1502–1512 CrossRef CAS.
- S. Bhaviripudi, X. Jia, M. S. Dresselhaus and J. Kong, Role of kinetic factors in chemical vapor deposition synthesis of uniform large area graphene using copper catalyst, Nano Lett., 2010, 10, 4128–4133 CrossRef CAS PubMed.
- C. C. Chen, C. J. Kuo, C. D. Liao, C. F. Chang, C. A. Tseng, C. R. Liu and Y. T. Chen, Growth of large-area graphene single crystals in confined reaction space with diffusion-driven chemical vapor deposition, Chem. Mater., 2015, 27, 6249–6258 CrossRef CAS.
- R. K. Bansal, A Text-Book of Fluid Mechanics and Hydraulic Machines, Laxmi Publications Limited, New Delhi, India, 2005, pp. 607−632 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra07787b |
| This journal is © The Royal Society of Chemistry 2021 |