Open Access Article
Open Access ArticlePrediction of superconductivity in bilayer borophenes
Luo Yan abc,
Ruiqi Kud,
Jing Zoub,
Liujiang Zhou
abc,
Ruiqi Kud,
Jing Zoub,
Liujiang Zhou b,
Jijun Zhaoe,
Xue Jiang
b,
Jijun Zhaoe,
Xue Jiang *e and
Bao-Tian Wang
*e and
Bao-Tian Wang *acf
*acf
aInstitute of High Energy Physics, Chinese Academy of Science (CAS), Beijing 10049, China. E-mail: wangbt@ihep.ac.cn
bYangtze Delta Region Institute (Huzhou), University of Electronic Science and Technology of China, Huzhou 313001, China
cSpallation Neutron Source Science Center, Dongguan 523803, China
dSchool of Physics, Harbin Institute of Technology, Harbin 150001, China
eKey Laboratory of Material Modification by Laser, Ion and Electron Beams, Dalian University of Technology, Ministry of Education, Dalian 116024, China. E-mail: Jiangx@dlut.edu.cn
fCollaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan, Shanxi 030006, China
First published on 17th December 2021
Abstract
Borophenes and related two-dimensional materials have exhibited many exotic properties, especially for superconductivity, although the superconductivity of single-layer borophene is suppressed by the strains or doping from its substrates. Intriguingly, bilayer (BL) borophenes can be stabilized by appropriate pillar density and hexagonal holes density, rather than being supported by Ag(111) or Cu(111) substrates. Thus, we studied the two most stable structures, namely BL-B8 and BL-B30, stabilized by the above-mentioned two methods. Within density functional theory and Bardeen–Cooper–Schrieffer theory framework, their stability, electron structures, and phonon properties, as well as possible superconductivity are systematically scrutinized. The metallic BL-B8 and BL-B30 exhibit intrinsic superconducting features with superconductivity transition temperatures (Tc) of 11.9 and 4.9 K, respectively. The low frequency (below 400 cm−1) consisting of out-of-plane vibrations of boron atoms plays crucial rule in their superconductivity. In particular, a Kohn anomaly appears at the Γ point in BL-B8, leading to substantial electron–phonon coupling. Here, our findings will provide instructive clues for experimentally determining the superconductivity of borophene and will broaden the two-dimensional superconductor family.
1 Introduction
Inspired by the fascinating properties of graphene,1 explorations of related two-dimensional (2D) materials have sprung up in recent years.2–5 Boron, as a neighbor of carbon, also possesses a short covalent radius with sp2 hybridization, leading to the flexibility to form planar boron clusters,6,7 cage-like boron fullerene,8,9 and nanotubes.10 Moreover, similar to graphene, boron atoms can also exist in a 2D graphene-like monolayer, namely borophene. However, different to graphene, the one electron-deficient property of boron atoms results in the biggest challenge to synthesizing borophene. To balance the electrons, hexagonal hole incorporation is an effective method, in which the hexagonal holes can obtain extra electrons from the filled hexagons. In this way, 2D boron sheets (α-, β-,11,12 g-boron sheet13,14) have been predicted to be stable. Moreover, borophene deposited on metal substrates is an alternative method to balance the surplus electron of boron. Following the clues given by first-principle calculation,15 the single-layer (SL) borophene is stabilized by metal passivation of Cu(111),16 Ag(111),17,18 Ir(111),19 Al(111)20 and Au(111) surfaces.21 In addition, bilayer (BL) borophenes, whose stability is related to hexagonal holes and interlayer pillars, have been systematically investigated, greatly enlarging the family of 2D boron sheets (here, a pillar means a direct chemical bond, which connects the upper and lower boron atoms layers).22 Moreover, BL borophene has been successfully synthesized on atomically flat single-crystal Ag(111).23 More recently, single-crystalline bilayer borophene with large-size on the Cu(111) surface has been obtained by molecular beam epitaxy.24 However, their stable phases are supported by substrates, which provide additional electrons for the bonding of additional boron atoms.As discussed above, both SL and BL borophenes can exhibit various structural polymorphs depending on their supporting substrates, leading to intriguing physical and chemical properties,25 such as ideal strength, negative Poisson’s ratio26 and high thermal conductivity.27 Therefore, borophenes have been explored for desirable applications in many fields, such as as electrode materials,28–32 sensors,33–35 and in energy storage,36,37 flexible devices,38 etc. Furthermore, superconductivity, as one of the famous macroscopic quantum phenomena, has also been predicted to exist among the family of borophenes, due to its light atomic weight as well as the large density of states (DOS) near the Fermi level. SL β12 and χ3 borophenes with vacancy fractions of 1/6 and 1/5 are predicted to be phonon-mediated superconductors with superconducting transition temperatures Tc of 10–20 K.39,40 The Tc of SL borophenes as a function of the hexagon hole density shows a V-shape.41 A honeycomb borophene (h-B2) is also predicted to be a 30 K superconductor without considering the imaginary phonon modes.41 Besides, super-borophene has a critical temperature Tc of 25.3 K at ambient conditions.42 Moreover, some boron-based 2D superconductors are also predicted, such as Mo2B2,43 W2B2,44 AlB2,45 Li2B2,46 Li2B7,47 B2C,48 XB6 (X = Al, Ga, In),49,50 B2O,51 TiB4,52 TiB7,53 MnB3,54 etc., further indicating the rich superconductivity in boron families.
However, although the SL h-B2, α-, β12 and χ3 borophenes have been synthesized in experiments and predicted to be intrinsic superconductors with high Tc by many theoretical works, their superconductivity has not yet been unambiguously observed in experiments.55 The undetected superconductivity of SL borophene could be attributed to the interference from the substrates, which can introduce strains and/or dopings.41,45,56 Thus, more effective synthesis methods without the supportive substrates for SL borophenes are urgently required, but current structures of borophenes can only exist on a special substrate. In particular, BL borophene, synthesized by layer-by-layer techniques, could serve as a candidate to experimentally explore the superconductivity of borophene. Besides, some unique properties appear in few-layer borophenes. For example, the in-plane negative Poisson’s ratios in the monolayer become positive in the layered borophene, while out-of-plane negative Poisson’s ratios are preserved;57 the electronic and magnetic properties of BL borophene can be modulated by transition metal atoms intercalation;58 P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) -boron possesses a topologically nontrivial Dirac nodal line, which is protected by the mirror reflection symmetry.59 BL-α borophene has been synthesized recently and it has a higher crystallinity and local work function, but it can’t maintain a free-standing structure without the supportive substrate.23 Therefore, further studying the BL borophene will significantly expand the phase space for boron-based nanomaterials.
-boron possesses a topologically nontrivial Dirac nodal line, which is protected by the mirror reflection symmetry.59 BL-α borophene has been synthesized recently and it has a higher crystallinity and local work function, but it can’t maintain a free-standing structure without the supportive substrate.23 Therefore, further studying the BL borophene will significantly expand the phase space for boron-based nanomaterials.
In the present work, the most stable BL borophenes BL-B8 and BL-30, stabilized by appropriate pillar density and hexagonal holes, respectively, are theoretically dissected via first-principles calculations. Their bonding nature, stability, electronic, phonon vibrational properties and electron–phonon coupling (EPC) are systematically studied. Results indicate that they are not only 2D metals with high stability, but also are 2D intrinsic superconductors with Tc of 11.9 and 4.9 K, respectively. Their superconductivity originates from the coupling between electrons of B-p orbitals and soft or flat phonon modes in the low-frequency region occupied by out-of-plane vibrations. In particular, a Kohn anomaly appears at the Γ point in BL-B8 and provides substantial EPC, leading to a higher Tc than the SL borophenes.
2 Computational methods
The cell optimizations and electronic structure calculations were carried out using the ab initio plane-wave pseudopotential method as implemented in the Vienna ab initio simulation package (VASP).60,61 The plane-wave energy cutoff of 500 eV and generalized gradient approximation (GGA)62,63 formulated by Perdew–Burke–Ernzerhof (PBE)64 were used for the exchange correlations. A vacuum space of 15 Å along the z direction was adopted to avoid the unphysical interactions within the periodic images. For Brillouin zone (BZ) samplings, the Γ-centered 18 × 16 × 1 and 13 × 13 × 1 k-point meshes were used for rectangular and hexagonal primitive cells, respectively. The ab initio molecular dynamics (AIMD) simulations, with constant number, volume, temperature (NVT) ensemble, were carried out to assess the thermal stabilities, lasting for 5 ps with a time step of 1 fs. Some data post processing steps in the VASP calculations were dealt with using the VASPKIT code.65 The convergence criteria were set for an energy of 10−5 eV and force of 0.01 eV Å−1.Within density functional perturbation theory (DFPT)66 and the Bardeen–Cooper–Schrieffer (BCS) theory,67 the superconductivity was studied using the open source QUANTUM ESPRESSO (QE) package.68,69 Here, the phonon spectra were calculated by using the finite displacements method within its primitive cell. The norm-conserving PBE pseudopotentials were chosen to describe the electron–ion interactions. The plane-wave kinetic energy cutoff and the charge–density cutoff were tested to be 70 and 280 Ry, respectively. The self-consistent electron densities for rectangular and hexagonal cells were calculated on 36 × 32 × 1 and 24 × 24 × 1 k-meshes, respectively. Moreover, 9 × 8 × 1 and 6 × 6 × 1 q-meshes were selected for them to calculate the dynamical matrices and the EPC matrix elements.
3 Results and discussion
3.1 Atomic structures
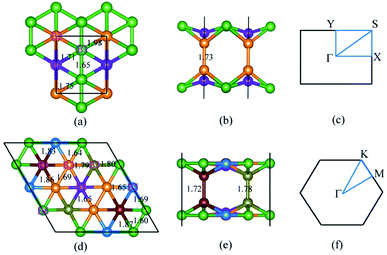
As reported by previous work,22 the BL borophene sheets can be obtained by optimal proportions of pillars and hexagonal holes to balance the surplus electrons. Therefore, we focus our study on the most stable crystals, obtained by the above two methods. As shown in Fig. 1(a and b), this BL is constructed with pillar density of 1/4, where pillar density is calculated by (number of atoms forming pillars)/(number of atoms in the unit cell).22 Based on the number of atoms within its primitive cell, we label it as BL-B8. Compared with other BL sheets, it is the most stable structure with the lowest energy stabilized by pillars.22 BL-B8 crystallizes in an orthorhombic space group, Pmmm (no. 47), and exhibits three types of B–B bonds with bond lengths of 1.65–1.98 Å, which are comparable to those of the SL borophene (1.62–1.88 Å)28,32 and bulk borophene (1.73 Å).70 The seven-coordinated boron atoms, marked as orange atoms in Fig. 1(a and b), serve as pillars to stabilize the top and bottom planes, which balance the surplus electrons and maintain the stability. The high-symmetry paths in its 2D BZ for BL-B8 are shown in Fig. 1(c).Another structure of BL borophene, also from ref. 22 and as shown in Fig. 1(d and e), is stabilized by isolated hexagonal holes separated by boron sheets, and has low formation energy among bilayer structures with different hexagonal holes density. For simplicity, we name it as BL-B30. The entitled BL-B30 optimizes in a hexagonal lattice and its high-symmetry paths are along Γ–M–K–Γ as presented in Fig. 1(f). As clearly distinguished in Fig. 1(d and e), there are seven different surroundings of boron atoms and the B–B bonds are in range of 1.65–1.87 Å. Different from BL-B8, here, the pillars are formed by two different B–B bonds: one is 1.72 Å and another 1.78 Å. Moreover, we compare atomic energy of per boron in BL-B8 and BL-B30 with typical SL borophenes (δ6, β12 and χ3). Their corresponding lattice constants and energies are listed in Table 1. Obviously, both our investigated BL borophenes are more stable than the SL borophenes, especially BL-B30. Besides, BL-B30 has more reliable stability when compared with BL-B8, which is in accordance with their bonds’ distributions. Thus, the combination of pillars and hexagonal holes with suitable ratios is beneficial for the stability of BL borophenes.11,22
| Configuration | Lattice constant (Å) | Energy (eV per atom) |
|---|---|---|
| δ6 | a = 2.97; b = 1.62 | −6.21 |
| β12 | a = b = 4.45 | −6.26 |
| χ3 | a = 2.93; b = 5.00 | −6.27 |
| BL-B8 | a = 2.85; b = 3.23 | −6.37 |
| BL-B30 | a = b = 6.56 | −7.12 |
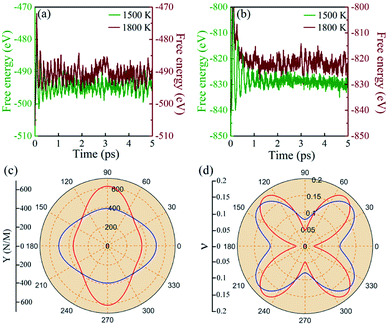
3.2 Thermal and mechanical properties
The stabilities of 2D materials are very important. Materials with good stability may be synthesized by experiments. AIMD simulations controlled by the Nosé-Hoover thermostat71 are adopted to study the thermal properties of BL-B8 and BL-B30. To take periodic boundary conditions into consideration, 3 × 3 × 1 supercells are built. As shown in Fig. 2(a and b), the free energies of BL-B8 and BL-B30 maintain nearly constant fluctuations during the 5 ps simulation period at about 1500 K. At about 1800 K, there may exist structural disruptions with collapsed fluctuations, indicating their theoretical melting temperatures at around 1500–1800 K.Moreover, the mechanical properties of BL-B8 and BL-B30 are explored within their rectangle unit cells. Then, the elastic constants Cij are obtained by
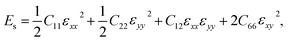 | (1) |
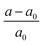 , (a and a0 are the lattice constants of the strained and non-strained crystals, respectively.) and εxx (εyy) is the uniaxial strain along the x(y) direction, and εxy is the shear strain. Then, the independent elastic constants (C11, C12, C22 and C66) within the rectangle cell can be calculated from the function of strain energy vs. applied strains.72 The corresponding elastic constants for BL-B8 and BL-B30, compared with SL borophenes, are listed in Table 2. Clearly, the C11, C22 and C66 of BL-B8 and BL-B30 are much larger than those of β12 and χ3.73 Additionally, both BL-B8 and BL-B30 satisfy the Born criteria,74 C11 > 0, C66 > 0 and C11C22 − C122 > 0,74,75 indicating they are mechanically stable.
, (a and a0 are the lattice constants of the strained and non-strained crystals, respectively.) and εxx (εyy) is the uniaxial strain along the x(y) direction, and εxy is the shear strain. Then, the independent elastic constants (C11, C12, C22 and C66) within the rectangle cell can be calculated from the function of strain energy vs. applied strains.72 The corresponding elastic constants for BL-B8 and BL-B30, compared with SL borophenes, are listed in Table 2. Clearly, the C11, C22 and C66 of BL-B8 and BL-B30 are much larger than those of β12 and χ3.73 Additionally, both BL-B8 and BL-B30 satisfy the Born criteria,74 C11 > 0, C66 > 0 and C11C22 − C122 > 0,74,75 indicating they are mechanically stable.
| Compounds | C11 | C12 | C22 | C66 | Yx | Yy | νx | νy |
|---|---|---|---|---|---|---|---|---|
| β12 | 188 | 36 | 214 | 64 | 182 | 241 | 0.17 | 0.18 |
| χ3 | 195 | 36 | 188 | 71 | 188 | 181 | 0.19 | 0.18 |
| BL-B8 | 356 | 17 | 618 | 161 | 355 | 618 | 0.03 | 0.05 |
| BL-B30 | 509 | 40 | 390 | 146 | 505 | 387 | 0.1 | 0.08 |
In addition, BL-B8 and BL-B30 belong to the orthogonal 2D system, their orientation-dependent Young’s moduli (Y) and Poisson’s ratios (ν) can be defined as51,72,76
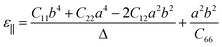 | (2) |
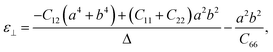 | (3) |
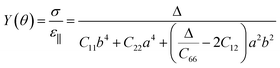 | (4) |
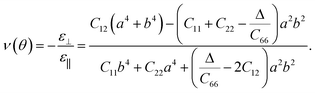 | (5) |
As shown in Fig. 2(c), the variations of Y for BL-B8 and BL-B30 are spindle-like shapes, which are similar to that of the B2O monolayer.51 However, the distributions of the orientation-dependent Y are opposite. For BL-B8, the in-plane minimal value of Y along the x direction is 355 N m−1, and the maximal value of 618 N m−1 is along y direction. Contrary to BL-B8, for BL-B30 the maximal value of 505 N m−1 and the minimal value of 387 N m−1 are along the x and y directions, respectively. Moreover, their orientation-dependent ν variations show butterfly-like shapes, as shown in Fig. 2(d), further indicating their fully anisotropic traits.
3.3 Electron structures
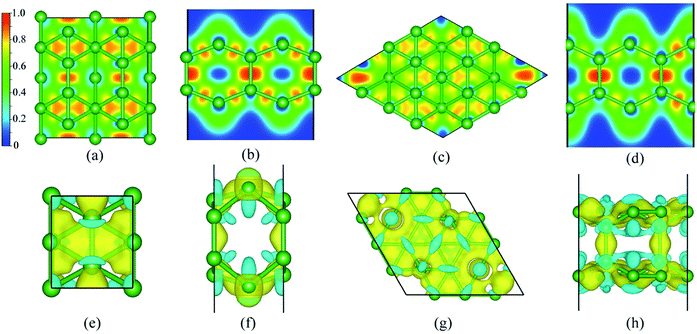
Based on the electron localization function (ELF),77 plotted in Fig. 3(a–d), the bonding natures in BL-B8 and BL-B30 are studied. In general, a region with ELF = 1 means strong localization of covalent bonding electrons, ELF values close to 0 are a low electron density, and regions with ELF = 0.5 indicates a homogeneous electron gas. Obviously, both in BL-B8 and BL-B30, all the ELF values for B–B bonds are close to 0.8, showing their covalent bonding nature. In particular, large ELF values around 1 are found along the pillars, meaning stronger covalent bonding than the B–B bonds within the planes. Such results indicate again that the pillars in BL-B8 and BL-B30 are important for their stability.22 Furthermore, the difference charge plots for BL-B8 and BL-B30 are exhibited in Fig. 3(e–h). Evidently, boron atoms in different locations show different electron transfer capabilities, but electron transfer occurs within layers, balancing the surplus electrons and enhancing stability for BL-B8 and BL-B30. Furthermore, the formations of pillars in BL-B8 and BL-B30 are beneficial to the electrons’ transfer and compensation for unsaturated valence electrons in sp2 hybridization.22 According to the Bader charges analysis,78 the net charge transfer between B–B covalent bonds in BL-B8 is 0.86|e|, much smaller than that of BL-B30 (2.4|e|). Interestingly, relatively large amounts of electron transfer happen in BL-B8 and BL-B30, hinting at their performances in superconductivity.The orbital-projected band structures and the electronic density of states (DOS) are exhibited in Fig. 4. The same as SL borophenes, BL-B8 and BL-B30 show intrinsic metallic features with large amounts of electron states concentrating near the Fermi level. Clearly, their metallic nature mainly originates from the B-p orbitals with small amounts of s orbitals [Fig. 4(b and f)]. Moreover, the in-plane B-p (B-pσ) and out-of-plane B-p (B-pπ) orbitals have almost equal proportion in the projected DOS of BL-B8 [Fig. 4(c)]. However, as for BL-B30, its metallicity mostly stems from B-pπ orbitals partially hybridized with few B-pσ orbitals [Fig. 4(g)]. Furthermore, the Rashba effect79,80 is explored, and the band structures calculated with spin–orbit coupling (SOC) interactions are presented in Fig. 4(d and h). Clearly, both in BL-B8 and BL-B30, extremely weak SOC effects happen and no bands split in proximity to the Fermi level. Thus, the Rashba effect will not be considered for the studied systems.
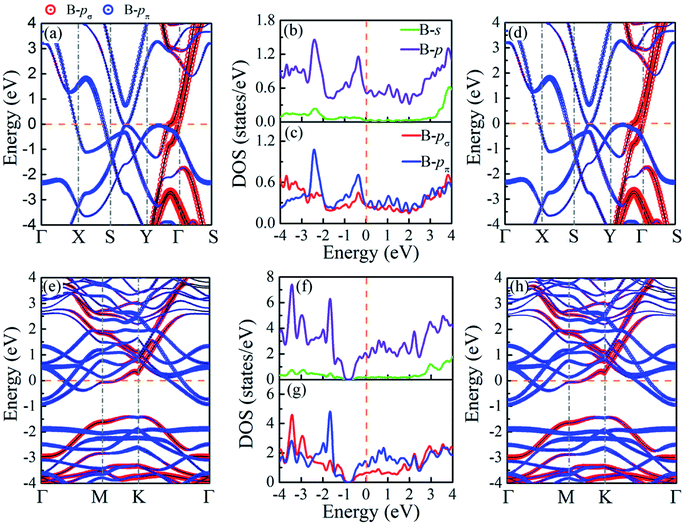 | ||
| Fig. 4 Orbital projected band structures without SOC (left panel), with SOC (right panel), as well as projected DOS without SOC (middle panel) of (a–d) BL-B8 and (e–h) BL-B30. | ||
3.4 Phonon properties and EPC
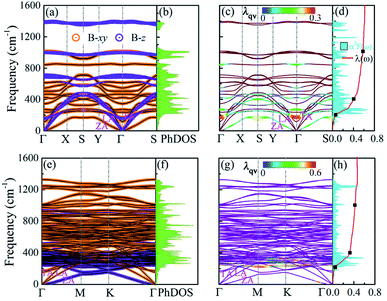
The phonon properties and possible superconductivity of the metallic BL-B8 and BL-B30 are further investigated. In terms of the displacement directions of B atoms,81,82 their resolved phonon spectra are given in Fig. 5(a and e). Here, the phonon kp theorem is adopted to sort the phonon branches based on their eigenvectors83–85
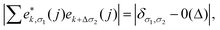 | (6) |
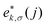 and Δ are the displacement of the atom j in the eigenvector of (k, σ) vibration modes and a small wave vector, respectively. Clearly, all the phonon modes in BL-B8 and BL-B30 are positive, further suggesting their stability without any dynamical instability. The three acoustic branches are formed by the out-of-plane (ZA), in-plane transverse (TA), and in-plane longitudinal (LA) modes. As shown in Fig. 5(a), in BL-B8, the low-frequency region (below 300 cm−1) is mostly dominated by the in-plane modes of B atoms (B-xy), whilst the LA and the first three optical branches are mainly occupied by the out-of-plane B modes (B-z). In the middle-frequency region (300–1000 cm−1), phonon vibrations also mainly originate from the B-xy. In the high-frequency region (larger than 1000 cm−1), contributions are mostly from B-z modes. As for BL-B30 (Fig. 5(e)), the low-frequency region below 400 cm−1 is related mainly to the B-z modes, along with some B-xy modes in TA, ZA and the first two optical branches. However, phonon frequencies higher than 400 cm−1 mainly consist of the in-plane vibrations of B atoms. The phonon density of states (PhDOS) distributions are in line with above analysis of the vibration modes [Fig. 5(b and f)]. Moreover, the highest vibration frequency in BL-B8 and BL-B30 with light weight reaches to ∼1400 cm−1, comparable to those of δ6 (∼1200 cm−1), β12 (∼1290 cm−1) and χ3 (∼1411 cm−1) borophenes, according well with their strong covalent bond features.49,51
and Δ are the displacement of the atom j in the eigenvector of (k, σ) vibration modes and a small wave vector, respectively. Clearly, all the phonon modes in BL-B8 and BL-B30 are positive, further suggesting their stability without any dynamical instability. The three acoustic branches are formed by the out-of-plane (ZA), in-plane transverse (TA), and in-plane longitudinal (LA) modes. As shown in Fig. 5(a), in BL-B8, the low-frequency region (below 300 cm−1) is mostly dominated by the in-plane modes of B atoms (B-xy), whilst the LA and the first three optical branches are mainly occupied by the out-of-plane B modes (B-z). In the middle-frequency region (300–1000 cm−1), phonon vibrations also mainly originate from the B-xy. In the high-frequency region (larger than 1000 cm−1), contributions are mostly from B-z modes. As for BL-B30 (Fig. 5(e)), the low-frequency region below 400 cm−1 is related mainly to the B-z modes, along with some B-xy modes in TA, ZA and the first two optical branches. However, phonon frequencies higher than 400 cm−1 mainly consist of the in-plane vibrations of B atoms. The phonon density of states (PhDOS) distributions are in line with above analysis of the vibration modes [Fig. 5(b and f)]. Moreover, the highest vibration frequency in BL-B8 and BL-B30 with light weight reaches to ∼1400 cm−1, comparable to those of δ6 (∼1200 cm−1), β12 (∼1290 cm−1) and χ3 (∼1411 cm−1) borophenes, according well with their strong covalent bond features.49,51
We now turn to their potential superconductivity, according to the magnitude of the electron–phonon coupling (EPC) λqν within the whole frequency region, the calculated Eliashberg spectral function α2F(ω) and the cumulative EPC strength λ(ω). Based on the Migdal–Eliashberg theory,86,87 the λqν can be calculated by
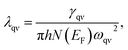 | (7) |
| Compounds | N(EF) | ωlog | λ | Tc |
|---|---|---|---|---|
| χ3 | 6.68 | 417.57 | 0.64 | 11.5 |
| δ6 | 2.61 | 409.29 | 0.82 | 20.1 |
| β12 | 7.51 | 371.71 | 0.71 | 13.7 |
| BL-B8 | 7.98 | 495.51 | 0.61 | 11.9 |
| BL-B30 | 27.01 | 541.05 | 0.47 | 4.9 |
In terms of α2F(ω), the EPC strength λ(ω) can be obtained by
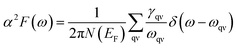 | (8) |
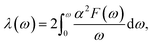 | (9) |
Then, the logarithmic average frequency ωlog is derived by
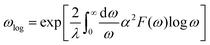 | (10) |
Four clearly distinguished regions in α2F(ω) are indicated by black dots [Fig. 5(d and h)]. Here, region I (below 200 cm−1) and II (200–400 cm−1) are both in the low-frequency region. Tthe intermediate region is from 400 to 1000 cm−1 (region III) and a high-frequency region is above 1000 cm−1 (region IV). Although the total EPC are attributed to all the phonon modes over the entire frequency range, the relative contributions of each region are considerably different.88 For BL-B8, region I is mainly dominated by the ZA modes and accounts for only about 10% of the total EPC constant (λ = 0.61), and region II with a Kohn anomaly at the Γ point leads to substantial EPC, and provides a contribution of 57% to the total λ. Thus, the low-frequency phonons make the main contribution to the total EPC, approximately 67%. At the same time, region III in the middle-frequency region also has a non-negligible contribution of 27.9% to the total EPC. However, region IV provides a negligible contribution, only about 5%. As mentioned above, the Kohn anomaly in region II dominated by the out-of-plane of boron atoms vibrations is the crucial factor for producing a high value of Tc for BL-B8. Therefore, based upon the above results, the Tc can be calculated by the McMillian–Allen–Dynes formula:89
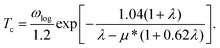 | (11) |
4 Conclusions
In summary, we have performed a systematic theoretical study on BL-B8 and BL-B30, including stability, electron, phonon properties and even EPC. They are both intrinsic 2D metals with good stability. Within the BSC microscopic theory, they are further determined to be 2D supercondutors with Tc of 11.9 K and 4.9 K. The EPC in low-frequency occupied by out-of-plane boron vibrations (below 400 cm−1) is crucial for their superconductivity. Here, a Kohn anomaly appears at a Γ point in BL-B8 which provides substantial EPC, while flat optical branches in BL-B30 contribute a little to the EPC with a great quantity of electrons near the Fermi level. In addition, their superconductivity can be tuned by strain and doping engineering with further efforts. Our work would fill in the blanks of superconductivity in BL borophenes, and provide clues for experimental explorations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. Z. acknowledges the financial support from the University of Electronic Science and Technology of China. B.-T.W. acknowledges financial support from the Natural Science Foundation of China (Grants No. 12074381).Notes and references
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D.-e. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- K. S. Novoselov, D. Jiang, F. Schedin, T. Booth, V. Khotkevich, S. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453 CrossRef CAS PubMed.
- J. N. Coleman, M. Lotya, A. O’Neill, S. D. Bergin, P. J. King, U. Khan, K. Young, A. Gaucher, S. De and R. J. Smith, et al., Science, 2011, 331, 568–571 CrossRef CAS PubMed.
- J. Zhao, H. Liu, Z. Yu, R. Quhe, S. Zhou, Y. Wang, C. C. Liu, H. Zhong, N. Han and J. Lu, et al., Prog. Mater. Sci., 2016, 83, 24–151 CrossRef CAS.
- Y. Huang, Y.-H. Pan, R. Yang, L.-H. Bao, L. Meng, H.-L. Luo, Y.-Q. Cai, G.-D. Liu, W.-J. Zhao and Z. Zhou, et al., Nat. Commun., 2020, 11, 1–9 Search PubMed.
- Z. A. Piazza, H.-S. Hu, W.-L. Li, Y.-F. Zhao, J. Li and L.-S. Wang, Nat. Commun., 2014, 5, 1–6 Search PubMed.
- H.-J. Zhai, B. Kiran, J. Li and L.-S. Wang, Nat. Mater., 2003, 2, 827–833 CrossRef CAS PubMed.
- N. G. Szwacki, A. Sadrzadeh and B. I. Yakobson, Phys. Rev. Lett., 2007, 98, 166804 CrossRef PubMed.
- H.-J. Zhai, Y.-F. Zhao, W.-L. Li, Q. Chen, H. Bai, H.-S. Hu, Z. A. Piazza, W.-J. Tian, H.-G. Lu and Y.-B. Wu, et al., Nat. Chem., 2014, 6, 727–731 CrossRef CAS PubMed.
- F. Liu, C. Shen, Z. Su, X. Ding, S. Deng, J. Chen, N. Xu and H. Gao, J. Mater. Chem., 2010, 20, 2197–2205 RSC.
- H. Tang and S. Ismail-Beigi, Phys. Rev. Lett., 2007, 99, 115501 CrossRef PubMed.
- X. Wu, J. Dai, Y. Zhao, Z. Zhuo, J. Yang and X. C. Zeng, ACS Nano, 2012, 6, 7443–7453 CrossRef CAS PubMed.
- E. S. Penev, S. Bhowmick, A. Sadrzadeh and B. I. Yakobson, Nano Lett., 2012, 12, 2441–2445 CrossRef CAS PubMed.
- X. Yu, L. Li, X.-W. Xu and C.-C. Tang, J. Phys. Chem. C, 2012, 116, 20075–20079 CrossRef CAS.
- Y. Liu, E. S. Penev and B. I. Yakobson, Angew. Chem., Int. Ed., 2013, 52, 3156–3159 CrossRef CAS PubMed.
- H. Liu, J. Gao and J. Zhao, Sci. Rep., 2013, 3, 1–9 Search PubMed.
- A. J. Mannix, X.-F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago and J. R. Guest, et al., Science, 2015, 350, 1513–1516 CrossRef CAS PubMed.
- B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Nat. Chem., 2016, 8, 563–568 CrossRef CAS PubMed.
- N. A. Vinogradov, A. Lyalin, T. Taketsugu, A. S. Vinogradov and A. Preobrajenski, ACS Nano, 2019, 13, 14511–14518 CrossRef CAS PubMed.
- W. Li, L. Kong, C. Chen, J. Gou, S. Sheng, W. Zhang, H. Li, L. Chen, P. Cheng and K. Wu, Sci. Bull., 2018, 63, 282–286 CrossRef CAS.
- B. Kiraly, X. Liu, L. Wang, Z. Zhang, A. J. Mannix, B. L. Fisher, B. I. Yakobson, M. C. Hersam and N. P. Guisinger, ACS Nano, 2019, 13, 3816–3822 CrossRef CAS PubMed.
- N. Gao, X. Wu, X. Jiang, Y. Bai and J. Zhao, FlatChem, 2018, 7, 48–54 CrossRef CAS.
- X. Liu, Q. Li, Q. Ruan, M. S. Rahn, B. I. Yakobson and M. C. Hersam, Nat. Mater., 2021 DOI:10.1038/s41563-021-01084-2.
- C. Chen, H. Lv, P. Zhang, Z. Zhuo, Y. Wang, C. Ma, W. Li, X. Wang, B. Feng, P. Cheng, X. Wu, K. Wu and L. Chen, Nat. Chem., 2021, 1–7, DOI:10.1038/s41557-021-00813-z.
- D. Li, J. Gao, P. Cheng, J. He, Y. Yin, Y. Hu, L. Chen, Y. Cheng and J. Zhao, Adv. Funct. Mater., 2020, 30, 1904349 CrossRef CAS.
- H. Wang, Q. Li, Y. Gao, F. Miao, X.-F. Zhou and X. Wan, New J. Phys., 2016, 18, 073016 CrossRef.
- H. Zhou, Y. Cai, G. Zhang and Y.-W. Zhang, npj 2D Mater. Appl., 2017, 1, 1–7 CrossRef.
- H. Jiang, W. Shyy, M. Liu, Y. Ren and T. Zhao, J. Mater. Chem. A, 2018, 6, 2107–2114 RSC.
- Y. Zhang, Z.-F. Wu, P.-F. Gao, S.-L. Zhang and Y.-H. Wen, ACS Appl. Mater. Interfaces, 2016, 8, 22175–22181 CrossRef CAS PubMed.
- H. Chen, W. Zhang, X.-Q. Tang, Y.-H. Ding, J.-R. Yin, Y. Jiang, P. Zhang and H. Jin, Appl. Surf. Sci., 2018, 427, 198–205 CrossRef CAS.
- B. Mortazavi, A. Dianat, O. Rahaman, G. Cuniberti and T. Rabczuk, J. Power Sources, 2016, 329, 456–461 CrossRef CAS.
- H. Jiang, Z. Lu, M. Wu, F. Ciucci and T. Zhao, Nano Energy, 2016, 23, 97–104 CrossRef CAS.
- H. Xiao, W. Cao, T. Ouyang, S. Guo, C. He and J. Zhong, Sci. Rep., 2017, 7, 45–986 CrossRef PubMed.
- V. Shukla, J. Warna, N. K. Jena, A. Grigoriev and R. Ahuja, J. Phys. Chem. C, 2017, 121, 26869–26876 CrossRef CAS.
- P. Ranjan, T. K. Sahu, R. Bhushan, S. S. Yamijala, D. J. Late, P. Kumar and A. Vinu, Adv. Mater., 2019, 31, 1900353 CrossRef PubMed.
- X. Chen, L. Wang, W. Zhang, J. Zhang and Y. Yuan, Int. J. Hydrogen Energy, 2017, 42, 20036–20045 CrossRef CAS.
- X. Sun, X. Liu, J. Yin, J. Yu, Y. Li, Y. Hang, X. Zhou, M. Yu, J. Li and G. Tai, et al., Adv. Funct. Mater., 2017, 27, 1603300 CrossRef.
- Z. Zhang, Y. Yang, E. S. Penev and B. I. Yakobson, Adv. Funct. Mater., 2017, 27, 1605059 CrossRef.
- M. Gao, Q.-Z. Li, X.-W. Yan and J. Wang, Phys. Rev. B, 2017, 95, 024505 CrossRef.
- E. S. Penev, A. Kutana and B. I. Yakobson, Nano Lett., 2016, 16, 2522–2526 CrossRef CAS PubMed.
- Y. Zhao, S. Zeng and J. Ni, Appl. Phys. Lett., 2016, 108, 242601 CrossRef.
- Z. Gao, M. Li and J.-S. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 47279–47288 CrossRef CAS PubMed.
- L. Yan, T. Bo, P.-F. Liu, B.-T. Wang, Y.-G. Xiao and M.-H. Tang, J. Mater. Chem. C, 2019, 7, 2589–2595 RSC.
- L. Yan, T. Bo, W.-X. Zhang, P.-F. Liu, Z.-S. Lu, Y.-G. Xiao, M.-H. Tang and B.-T. Wang, Phys. Chem. Chem. Phys., 2019, 21, 15327–15338 RSC.
- M. Gao, X.-W. Yan, J. Wang, Z.-Y. Lu and T. Xiang, Phys. Rev. B, 2019, 100, 024503 CrossRef CAS.
- W. Chen, L. Yan, Y. Li, J. Liu, D. Wu, W. Chen, G. Yu, L. Zhou and Z. Li, J. Phys. Chem. C, 2020, 124, 5870–5879 CrossRef CAS.
- C. Wu, H. Wang, J. Zhang, G. Gou, B. Pan and J. Li, ACS Appl. Mater. Interfaces, 2016, 8, 2526–2532 CrossRef CAS PubMed.
- J. Dai, Z. Li, J. Yang and J. Hou, Nanoscale, 2012, 4, 3032–3035 RSC.
- B. Song, Y. Zhou, H.-M. Yang, J.-H. Liao, L.-M. Yang, X.-B. Yang and E. Ganz, J. Am. Chem. Soc., 2019, 141, 3630–3640 CrossRef CAS PubMed.
- L. Yan, T. Bo, P.-F. Liu, L. Zhou, J. Zhang, M. Tang, Y. Xiao and B. Wang, J. Mater. Chem. C, 2020, 8, 1704–1714 RSC.
- L. Yan, P.-F. Liu, H. Li, Y. Tang, J. He, X. Huang, B.-T. Wang and L. Zhou, npj Comput. Mater., 2020, 6, 94 CrossRef CAS.
- L. Wang, M. Liu, J. Li, R. Li, H. Ma and X.-Q. Chen, Phys. Rev. B, 2021, 104, 195123 CrossRef CAS.
- J.-S. Yu, J.-H. Liao, Y.-J. Zhao, Y.-C. Zhao and X.-B. Yang, Phys. Chem. Chem. Phys., 2020, 22, 16236–16243 RSC.
- Z. Qu, F. Han, T. Yu, M. Xu, Y. Li and G. Yang, Phys. Rev. B, 2020, 102, 075431 CrossRef CAS.
- T. Chen, Q. Gu, Q. Chen, X. Wang, C. J. Pickard, R. J. Needs, D. Xing and J. Sun, Phys. Rev. B, 2020, 101, 054518 CrossRef CAS.
- C. Cheng, J.-T. Sun, H. Liu, H.-X. Fu, J. Zhang, X.-R. Chen and S. Meng, 2D Mater., 2017, 4, 025032 CrossRef.
- H. Zhong, K. Huang, G. Yu and S. Yuan, Phys. Rev. B, 2018, 98, 054104 CrossRef CAS.
- X. Zhang, Y. Sun, L. Ma, X. Zhao and X. Yao, Nanotechnology, 2018, 29, 305706 CrossRef PubMed.
- S.-G. Xu, B. Zheng, H. Xu and X.-B. Yang, J. Phys. Chem. C, 2019, 123, 4977–4983 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS.
- S. Baroni, S. de Gironcoli, A. D. Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- J. Bardeen, L. N. Cooper and J. R. Schrieffer, Phys. Rev., 1957, 108, 1175 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, et al., J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- L. Cui, T. Song, J. Cai, X. Cui, Z. Liu and J. Zhao, Phys. Rev. B, 2020, 102, 155133 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- V. Wang and W. Geng, J. Phys. Chem. C, 2017, 121, 10224–10232 CrossRef CAS.
- B. Peng, H. Zhang, H. Shao, Z. Ning, Y. Xu, G. Ni, H. Lu, D. W. Zhang and H. Zhu, Mater. Res. Lett., 2017, 5, 399–407 CrossRef CAS.
- M. Born and K. Huang, Dynamical theory of crystal lattices, Clarendon press, 1954 Search PubMed.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- L. Wang, A. Kutana, X. Zou and B. I. Yakobson, Nanoscale, 2015, 7, 9746–9751 RSC.
- A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832 CrossRef CAS.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084–204 Search PubMed.
- Y. A. Bychkov, JETP Lett., 1984, 39, 78–81 Search PubMed.
- P. Modak, A. K. Verma and A. K. Mishra, Phys. Rev. B, 2021, 104, 054504 CrossRef CAS.
- L. Feng Huang and Z. Zeng, J. Appl. Phys., 2013, 113, 083524 CrossRef.
- L. F. Huang, P. L. Gong and Z. Zeng, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 045409 CrossRef CAS.
- P.-F. Liu, T. Bo, Z. Liu, O. Eriksson, F. Wang, J. Zhao and B.-T. Wang, J. Mater. Chem. C, 2018, 6, 12689–12697 RSC.
- L. F. Huang, P. L. Gong and Z. Zeng, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 045409 CrossRef CAS.
- L. F. Huang and Z. Zeng, J. Appl. Phys., 2013, 113, 083524 CrossRef.
- F. Giustino, Rev. Mod. Phys., 2017, 89, 015003 CrossRef.
- G. Grimvall, The electron-phonon interaction in metals, North-Holland Amsterdam, 1981, vol. 8 Search PubMed.
- P.-F. Liu, J. Li, X.-H. Tu, H. Yin, B. Sa, J. Zhang, D. J. Singh and B.-T. Wang, Phys. Rev. B, 2020, 102, 155406 CrossRef CAS.
- P. B. Allen and R. Dynes, Phys. Rev. B: Condens. Matter Mater. Phys., 1975, 12, 905 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |