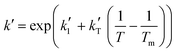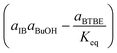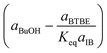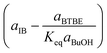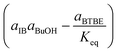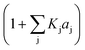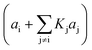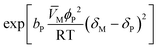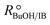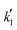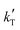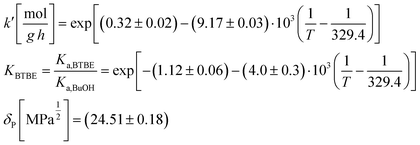Liquid-phase synthesis of butyl tert-butyl ether catalysed by ion-exchange resins: kinetic modelling through in-depth model discrimination†
Jordi Hug
Badia
 ,
Carles
Fité
,
Carles
Fité
 *,
Roger
Bringué
*,
Roger
Bringué
 ,
Eliana
Ramírez
,
Eliana
Ramírez
 and
Montserrat
Iborra
and
Montserrat
Iborra
Chemical Engineering and Analytical Chemistry Department, Faculty of Chemistry, University of Barcelona, Martí i Franquès 1 11, 08028 Barcelona, Spain. E-mail: fite@ub.edu
First published on 2nd November 2020
Abstract
The kinetics of the butyl tert-butyl ether (BTBE) synthesis reaction over Amberlyst™ 35 as the catalyst has been studied at 303–356 K in the liquid phase in two different reactor systems: batch and fixed-bed. Internal mass transfer effects were detected at temperatures above 333 K for catalyst particles larger than 0.25 mm. Particles smaller than 0.08 mm did not show mass transfer limitations under the whole assayed temperature range. The best kinetic model has been searched among a large number of kinetic equations resulting from the systematic combination of all possible elementary reactions, adsorbed species, and rate-determining step based, according to the Langmuir–Hinshelwood–Hougen–Watson and the Eley–Rideal formalisms. The significance of the temperature effect on the kinetic parameters and of the effect of the interaction between the catalyst and the reaction medium on the reaction rate has been checked. All proposed kinetic equations have been fitted to experimental rate data free from mass transfer limitations. The model discrimination procedure has been based on mathematical and physicochemical criteria. The resulting kinetic model is consistent with an Eley–Rideal type mechanism where one 1-butanol molecule adsorbs on one active site of the catalyst, it reacts with one isobutene molecule from the liquid phase to give one adsorbed BTBE molecule, which finally desorbs. The rate-determining step is the surface reaction. The catalyst activity is affected by the resin-medium interaction. 1-Butanol adsorption on the catalyst is more exothermic than BTBE adsorption, and isobutene adsorption is negligible.
Introduction
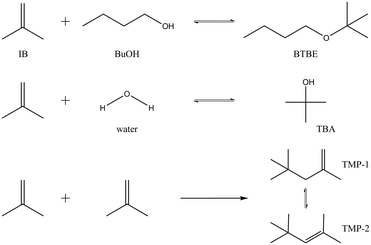
Reaction between isobutene (IB) and 1-butanol (BuOH) produces butyl tert-butyl ether (BTBE) and can be catalysed by acidic ion-exchange resins. BTBE is an interesting alternative to methyl and ethyl tert-butyl ethers (MTBE and ETBE, respectively) to be used as oxygenated high-octane component in current gasoline formulations. Since 1-butanol can be obtained through fermentation of non-edible biomass,1,2 it would allow a reduction of the fossil fuel use and dependence in gasoline production. BTBE can be produced at industrial scale in the same reaction units than MTBE or ETBE, in contrast to the next generation biofuels (stemmed from lignocellulose, non-food materials, algal biomass, and energy crops grown on marginal lands) that these days are receiving more attention, but still being under development.3,4 Thus, BTBE is a feasible option to find cleaner alternatives to traditional automotive fuels in the short- and midterm.In the course of the addition of IB to BuOH to form BTBE, two side reactions can take place simultaneously depending on the operating conditions (Fig. 1): isobutene hydration to form tert-butyl alcohol (TBA), and isobutene dimerisation to form 2,4,4-trimethyl-1-pentene (TMP1) and 2,4,4-trimethyl-2-pentene (TMP2). Few literature references focused on BTBE synthesis can be found. The most significant works are devoted to the reaction thermodynamics and to the reactivity of primary alcohols with isobutene.5–9 No data have been found concerning the BTBE etherification kinetics, which is crucial for the potential production of BTBE in industrial units. Due to the reaction similarities, BTBE synthesis is expected to proceed through a mechanism similar to that of MTBE or ETBE and, therefore, reaction rates could be explained by means of an analogous kinetic model.
MTBE and ETBE etherifications have been studied extensively throughout the years.10–16 More recently, the production of propyl tert-butyl ether (PTBE), the next ether in the analogous series, obtained by addition of 1-propanol to isobutene, has also been investigated.17 According to the literature, all these etherification reactions are reversible and exothermic, and the olefin–alcohol–ether mixtures behave strongly non-ideally. The reported reaction rate expressions are basically derived from Langmuir–Hinshelwood–Hougen–Watson (LHHW) or Eley–Rideal (ER) formalisms. It is expected that these reactions proceed through a similar mechanism. However, there are some discrepancies among the published works concerning mainly the number of active sites involved in the rate-determining step and the compounds that actually adsorb significantly on the resin. Possible reasons of such discrepancies are to have tested a limited number of candidate models, to have chosen a model among others with a similar goodness of fit, to have included non significant effects in the kinetic equation, or to have excluded significant effects. The present in-depth kinetic model discrimination study is motivated to assure that all plausible models are considered in the discrimination procedure, and that all parameters included in the proposed kinetic equation are significant.
Building the kinetic models
The candidate models of the BTBE synthesis have been developed from the LHHW and ER formalisms, because it is a heterogeneously catalysed system. The form of a given kinetic equation is characterised by a set of compounds that adsorb on the catalyst, a set of elementary reactions, and the reaction step being the rate-determining step. Following the approach of our previous works,17,18 the search of the best kinetic model starts with the proposal of all kinetic equations to be tested. They have been obtained from the systematic combination of all possible rate-determining steps, adsorbed and non-adsorbed species on the catalyst, and significant or non-significant temperature dependence of every parameter, as well as the possible inclusion of a term accounting for the effect on rates of the interaction between the resin and the liquid mixture. The aim of this procedure is to avoid dismissing the true model (i.e., the one that most accurately describes the physicochemical reality of the etherification reaction) from the set of candidate models. The BTBE reacting mixture is assumed to be highly non-ideal, similarly to the analogous etherification systems. Therefore, activities were used instead of concentrations and estimated by means of the UNIFAC-Dortmund method, which is an enhancement of the widely known UNIFAC method.19All proposed equations match the same general expression (eqn (1)). Models differ in the developed form of each term in the kinetic equation (Table 1).
 | (1) |
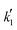 and
and 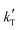 are the parameters to be fitted. The mean experimental temperature, Tm, is included to reduce the correlation between both parameters.
are the parameters to be fitted. The mean experimental temperature, Tm, is included to reduce the correlation between both parameters.
Regarding the driving force term, four different alternatives have been considered, given the considered rate-determining step for the global reaction process, i.e., surface reaction (eqn (3)), 1-butanol adsorption (eqn (4)), isobutene adsorption (eqn (5)), and BTBE desorption (eqn (6)). The parameter Keq in eqn (3) to (6) stands for the chemical equilibrium constant for the synthesis of BTBE, whose value had been determined experimentally in a previous work:7
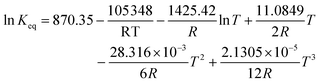 | (10) |
| No. | Adsorption term | No. | Adsorption term |
|---|---|---|---|
| 1 | 1 | 8 | 1 + KBuOHaBuOH |
| 2 | a BuOH | 9 | 1 + KBTBEaBTBE |
| 3 | a IB | 10 | 1 + KIBaIB |
| 4 | a BuOH + KBTBEaBTBE | 11 | 1 + KBuOHaBuOH + KBTBEaBTBE |
| 5 | a BuOH + KIBaIB | 12 | 1 + KBuOHaBuOH + KIBaIB |
| 6 | a BTBE + KIBaIB | 13 | 1 + KBTBEaBTBE + KIBaIB |
| 7 | a BuOH + KBTBEaBTBE + KIBaIB | 14 | 1 + KBuOHaBuOH + KBTBEaBTBE + KIBaIB |
Since Kj parameters are adsorption equilibrium constants or a quotient thereof, their temperature dependence has been expressed according to the van't Hoff equation, as follows:
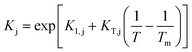 | (11) |
The exponent n in the adsorption term is related to the number of active sites, or clusters of active sites, involved in the reaction mechanism. Values of n of 1, 2, and 3 are the most likely, according to previous kinetic studies on similar reaction systems.11–13,18,20–22
The resin–medium interaction term (eqn (9)) accounts for the effect of the reaction medium on the catalyst activity promoted by the difference between the solubility parameters of the reaction medium, δM, and the catalyst, δP, as observed in analogous reaction systems where the Hildebrand solubility parameter was used.15,23 The binary parameter bP is equal to 0 if the effect of the interaction between the reaction medium and the catalyst is not significant, or equal to 1 if the interaction effect is significant; then, δP could be constant (kTP = 0) or linearly temperature dependent (kTP ≠ 0):15,23
| δP = kP1 + kPT(T − Tm) | (12) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) M, estimated from the species concentration and the temperature,24–26 the catalyst porosity in the swollen-state ϕP, the Hildebrand solubility parameter of the liquid mixture δM, estimated as described in the literature,26 and the gas constant R.
M, estimated from the species concentration and the temperature,24–26 the catalyst porosity in the swollen-state ϕP, the Hildebrand solubility parameter of the liquid mixture δM, estimated as described in the literature,26 and the gas constant R.
As a result of all possible combinations of the proposed forms of the general kinetic expression terms, a total of 1404 different kinetic equations are obtained, to be fitted individually to the experimental data with the aim of obtaining the best kinetic model.
Experimental section
Materials
Apparatus, procedure, and analysis
Experimental runs were carried out in two different reactor setups. Most of the experiments were run in a batch stirred tank reactor, the rest in a continuously operated fixed-bed catalytic reactor. The purpose of the experiments in the fixed-bed reactor was to validate the results in the batch reactor. The initial reaction mixture in batch experiments and the reactor feed in continuous experiments did not contain BTBE. The batch reactor experiments were carried out at 2.0 MPa and at constant temperature, in the range of 318 to 356 K. Initial alcohol to isobutene molar ratio,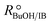 , varied between 1.0 and 2.0, and pure isobutene was used as reactant. The catalytic fixed-bed reactor experiments were carried out at 1.5 MPa and at constant temperature, between 303 and 333 K. The isobutene source was either pure isobutene or the synthetic C4 mixture, with an equimolar alcohol–isobutene mixture at the reactor inlet (
, varied between 1.0 and 2.0, and pure isobutene was used as reactant. The catalytic fixed-bed reactor experiments were carried out at 1.5 MPa and at constant temperature, between 303 and 333 K. The isobutene source was either pure isobutene or the synthetic C4 mixture, with an equimolar alcohol–isobutene mixture at the reactor inlet (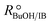 = 1.0).
= 1.0).
GC analyses of samples of the reaction medium in both setups allowed quantifying the reactants and products concentrations. Each GC was equipped with a capillary column (HP-PONA 19091S-001, J&W Scientific, Santa Clara, US; 100% dimethylpolysiloxane, 50 m × 0.20 mm × 0.50 μm), helium was used as the carrier gas, and the oven temperature was set at 333 K.
A detailed description of the experimental setup and procedure can be found elsewhere.17 Further details on the calculation of experimental reaction rates are shown in section A of the ESI,† and a list of all experimental conditions and calculated reaction rates in section B.
Results and discussion
Experimental results
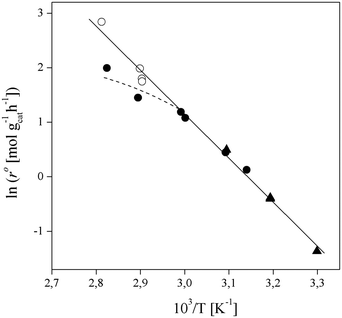
In order to focus the present study on the BTBE synthesis kinetics, the experimental conditions were chosen to minimize the side reactions extension, based on previous works on similar systems.27,28 Since the amount of byproducts at the end of the experiments was always below 5% wt, they have been further dismissed from the kinetic analysis. Other side reactions, such as 1-butanol dehydration or further isobutene oligomerisation, were not detected. Obtaining a kinetic model from experimental data requires that the calculated reaction rates are intrinsic kinetics, that is, free from mass and heat transfer effects. The consequence of such effects is to increase the resistance of the global reaction process, so the measured reaction rate would be lower than the reaction rate in the absence of transfer effects. In heterogeneous catalysis, external transfer effects can take place between the fluid bulk phase and the catalyst surface, so they can be avoided by sufficiently reducing the thickness of the film surrounding the catalyst: by increasing the stirring speed in a batch reactor, or by increasing the fluid flow rate in a fixed-bed reactor. In the present reaction system, external mass transfer effects are avoided with stirring speeds of 750 rpm in the batch reactor, and flow rates of 0.031 g s−1 in the fixed-bed setup, as determined in previous works.21,29,30Internal mass transfer effects occur inside the catalyst. They become more noticeable at larger catalyst bead size and at higher reaction temperature. Assuming that there are not external transfer effects, internal mass transfer effects can be easily checked by plotting the logarithm of measured reaction rates obtained at the same composition vs. the temperature inverse (Fig. 2). If a straight line is obtained, internal mass transfer effects are negligible. For this purpose, a set of experiments was carried out at different temperatures in both reactor systems, i.e., batch and fixed-bed, with the same reactants composition (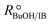 = 1.0) in the absence of product, and with 0.25–0.40 mm catalyst bead size (solid symbols in Fig. 2). Experimental points deviate at temperature higher than 333 K (1/T < 3.0 × 10−3 K−1 in Fig. 2), what indicates a significant effect of mass transfer resistances above 333 K. Additional experiments at the same composition and at about 343 K and 353 K were carried out using smaller catalyst particles (<0.08 mm, open symbols in Fig. 2), which resulted well aligned with those obtained at lower temperatures, thus free of mass transfer resistance. In the further kinetic analysis, reaction rates affected by transfer effects were dismissed. From the slope of the solid straight line in Fig. 2, the apparent activation energy, Eap, for the BTBE formation reaction has been estimated as (67 ± 2) kJ mol−1. This value is in the same range of those quoted in the literature for similar reaction systems using A35.14,17,18,22,31,32
= 1.0) in the absence of product, and with 0.25–0.40 mm catalyst bead size (solid symbols in Fig. 2). Experimental points deviate at temperature higher than 333 K (1/T < 3.0 × 10−3 K−1 in Fig. 2), what indicates a significant effect of mass transfer resistances above 333 K. Additional experiments at the same composition and at about 343 K and 353 K were carried out using smaller catalyst particles (<0.08 mm, open symbols in Fig. 2), which resulted well aligned with those obtained at lower temperatures, thus free of mass transfer resistance. In the further kinetic analysis, reaction rates affected by transfer effects were dismissed. From the slope of the solid straight line in Fig. 2, the apparent activation energy, Eap, for the BTBE formation reaction has been estimated as (67 ± 2) kJ mol−1. This value is in the same range of those quoted in the literature for similar reaction systems using A35.14,17,18,22,31,32
Fitting kinetic models to experimental rate data
The first step in the search of the kinetic model was to fit each of the 1404 built equations to all experimental reaction rates free from mass transfer limitations at once by optimisation of the parameter values. The Levenberg–Marquardt algorithm was used to minimize the residual sum of squares (RSS), defined as: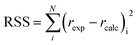 | (13) |
The discrimination of kinetic models has been carried out by applying the following mathematical and physicochemical criteria to conservatively discard inadequate models:
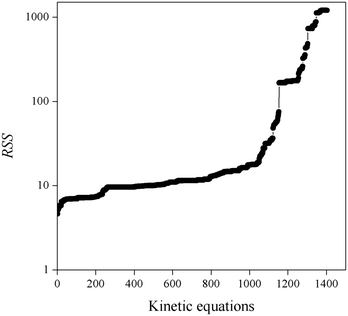
1. Fitted kinetic equations presenting large RSS values do not provide a satisfactory description of all experimental kinetic data. Fig. 3 shows the obtained RSS, where kinetic equations are ordered from lowest to highest RSS values. Consequently, equations presenting RSS values larger than 100 have been rejected.
2. In a suitable kinetic expression, all fitted parameter values should be statistically significant. Their standard error can be estimated from the covariance matrix of the parameters at the optimum. In this regard, models with at least one parameter with an associated standard uncertainty as large as the fitted value have been discarded.
3. Only kinetic equations producing positive values for the apparent activation energy, Eap, can be accepted, because of the experimental evidence that the reaction rate increases with temperature (Fig. 2), so models with positive fitted values for 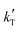 (eqn (2)) are directly discarded. In addition, positive Eap values clearly inconsistent with previously reported Eap for similar reaction systems (in the range of 69.3 to 84 kJ mol−1 for MTBE, ETBE, PTBE, and TAEE syntheses over A35)14,17,18,22,31,32 can also be rejected. In particular, Eap values well above 100 kJ mol−1 (i.e.,
(eqn (2)) are directly discarded. In addition, positive Eap values clearly inconsistent with previously reported Eap for similar reaction systems (in the range of 69.3 to 84 kJ mol−1 for MTBE, ETBE, PTBE, and TAEE syntheses over A35)14,17,18,22,31,32 can also be rejected. In particular, Eap values well above 100 kJ mol−1 (i.e., 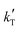 < −13
< −13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K−1) or below 45 kJ mol−1 (i.e.,
000 K−1) or below 45 kJ mol−1 (i.e., 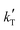 > −5000 K−1) have been rejected.
> −5000 K−1) have been rejected.
4. The adsorption process of a given compound on the resin is an exothermic process (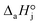 < 0). For models with a significant number of unoccupied active sites (eqn (7)), Kj is the adsorption equilibrium constant of compound j, and KT,j (eqn (11)) corresponds to
< 0). For models with a significant number of unoccupied active sites (eqn (7)), Kj is the adsorption equilibrium constant of compound j, and KT,j (eqn (11)) corresponds to 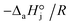 , thus it should be positive. Models whose range of any KT,j and its uncertainty clearly falls in negative values have been discarded. Models where all active sites are considered as occupied (eqn (8)) are not affected by this condition, because Kj is defined as a ratio of adsorption equilibrium constants and, therefore, KT,j = −(
, thus it should be positive. Models whose range of any KT,j and its uncertainty clearly falls in negative values have been discarded. Models where all active sites are considered as occupied (eqn (8)) are not affected by this condition, because Kj is defined as a ratio of adsorption equilibrium constants and, therefore, KT,j = −(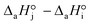 )/R, so it can be either positive or negative.
)/R, so it can be either positive or negative.
5. From its definition, the resin solubility parameter δP must be positive. In models where δP is temperature dependent, and it is expected to decrease with temperature,23 so the range of kPT and its uncertainty cannot fall completely in positive values. Models that do not meet these conditions have been discarded.
6. The Akaike information criterion (AIC), i.e., the relative likelihood of every model, can be used to rank a number of S kinetic equations from more to less plausible upon the basis of robust multimodel inferences.33,34 The following expressions apply in the Akaike procedure:
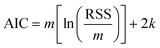 | (14) |
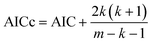 | (15) |
| Δi = AICci − AICcmin | (16) |
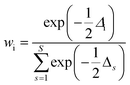 | (17) |
The consideration of the mathematical and physicochemical criteria applied in a conservative way allowed to reduce the number of candidate equations from 1404 to only a few. The best ranked models, their optimal parameter values and ranking criteria (RSS, Δi, and wi) are listed in Table 3, sorted from best to worst.
| Model no. | k′ (mol g−1 h−1) | {Driving force}a | {Adsorption term} | n | δ P (MPa1/2) | RSS | Δ i | w i | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1st adsb | K 1,BuOH | K T,BuOH | K 1,IB | K T,IB | K 1,BTBE | K T,BTBE | k P1 | k PT | ||||||||
| a Form of the driving force: (a) surface reaction (eqn (3)) and (c) isobutene adsorption (eqn (5)). b First summand of the adsorption term. | ||||||||||||||||
| 49 | 0.320 | −9171 | (a) | a BuOH | — | — | — | — | −1.119 | −4039 | 1 | 24.51 | — | 6.497 | 0 | 0.937 |
| 48 | 0.395 | −9031 | (a) | a BuOH | — | — | — | — | −0.540 | — | 1 | 24.18 | — | 6.981 | 8 | 0.021 |
| 290 | 1.917 | −8986 | (a) | 1 | −0.334 | — | — | — | −0.810 | — | 3 | 24.61 | — | 6.948 | 9 | 0.010 |
| 173 | 2.072 | −8994 | (a) | 1 | 0.332 | — | — | — | −0.144 | — | 2 | 24.53 | — | 6.954 | 9 | 0.009 |
| 56 | 3.408 | −9019 | (a) | 1 | 2.951 | — | — | — | 2.491 | — | 1 | 24.32 | — | 6.977 | 10 | 0.007 |
| 174 | 2.230 | −8498 | (a) | 1 | 0.495 | 530 | — | — | −0.096 | — | 2 | 24.50 | — | 6.920 | 11 | 0.004 |
| 978 | 0.412 | −9033 | (c) | 1 | — | — | — | — | −1.178 | — | 3 | 24.06 | — | 7.155 | 11 | 0.004 |
| 291 | 1.975 | −8707 | (a) | 1 | −0.272 | 308 | — | — | −0.804 | — | 3 | 24.60 | — | 6.933 | 11 | 0.004 |
| 861 | 0.428 | −9042 | (c) | 1 | — | — | — | — | −0.761 | — | 2 | 23.94 | — | 7.185 | 11 | 0.003 |
| 166 | 0.088 | −9318 | (a) | a BuOH | — | — | — | — | −1.655 | −3039 | 2 | 22.56 | — | 7.327 | 16 | <0.001 |
| 751 | 0.121 | −9346 | (c) | a BuOH | — | — | — | — | −0.981 | −3650 | 1 | 22.24 | — | 7.429 | 18 | <0.001 |
| 165 | 0.144 | −9196 | (a) | a BuOH | — | — | — | — | −1.207 | — | 2 | 22.26 | — | 7.749 | 22 | <0.001 |
| 750 | 0.182 | −9218 | (c) | a BuOH | — | — | — | — | −0.451 | — | 1 | 21.89 | — | 7.888 | 24 | <0.001 |
| 2 | 1.170 | −9770 | (a) | 1 | — | — | — | — | — | — | 1 | 20.06 | — | 9.566 | 48 | <10−10 |
A model is considered as substantially supported by empirical evidence when its Δi value is lower than 3.33,34 The first ranked model (Model 49) stands out as the most plausible one, because of its high probability (wModel49 = 93.7%) and ΔModel49 = 0 value, far from the second ranked model (wModel48 = 2.1%, ΔModel48 = 8). In addition, some common features are observed among the first ranked models that support the choice of Model 49: i) none of the equations includes the isobutene contribution in the adsorption term (Σwi = 0), whereas the 1-butanol and BTBE effect appears in the adsorption term for most of the candidate equations (Σwi = 0.993 and Σwi ≈ 1, respectively); ii) there is a high probability that the first summand in the adsorption term is aBuOH (Σwi = 0.959) in front of being 1 (Σwi = 0.041); iii) the exponent in the adsorption term is likely to be n = 1 (Σwi = 0.966); iv) the resin–medium interaction term is suitable (Σwi ≈ 1); and v) the most likely rate-determining step is the surface reaction (Σwi = 0.993; driving force type (a) in Table 3).
Fig. 4 shows the adequacy of the prediction of experimental reaction rates by Model 49, the low sensitivity of the model output due to the uncertainty of the fitted parameters and the randomly distributed residuals for each experimental point. Model 49 predicts simultaneously well the experimental data obtained in both batch and fixed-bed reactor systems.
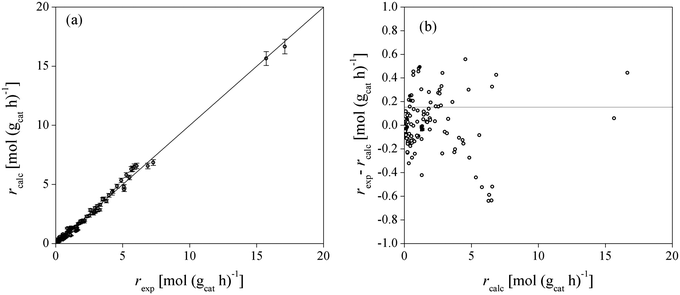 | ||
| Fig. 4 Comparison between experimental and calculated BTBE reaction rates for Model 49 (a), and residuals distribution (b). Symbols: experimental rates obtained in the batch reactor (○), in the fixed-bed reactor using the C4 as isobutene source (●), and in the fixed-bed reactor using pure isobutene (■). Error bars in (a) correspond to the sensitivity (standard deviation) of the model output due to the parameters uncertainty (see section C in ESI†). | ||
Selected kinetic model
The proposed kinetic equation Model 49, its parameter estimates, and their standard error are: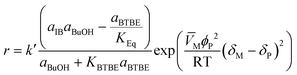 | (18) |
This expression derives from an ER reaction mechanism consisting of the following steps: i) one molecule of 1-butanol adsorbs on a resin active site (or cluster of active sites); ii) it reacts with one isobutene molecule from solution to give one molecule of adsorbed BTBE; and iii) the BTBE molecule desorbs. The surface reaction step is the rate-limiting step of the overall reaction process. This mechanism is in agreement with previous works on analogous reaction systems, e.g., syntheses of MTBE,14 ETBE,15 or PTBE.17
Since the exponent of the adsorption term n is 1, the apparent kinetic coefficient k′ is equal to the intrinsic kinetic constant k, as follows:
k′ = k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K1−na,BuOH = k K1−na,BuOH = k | (19) |
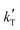 = −(9.17 ± 0.03) × 103 K, then Ea = (76.3 ± 0.3) kJ mol−1.
= −(9.17 ± 0.03) × 103 K, then Ea = (76.3 ± 0.3) kJ mol−1.
The parameter KBTBE in the adsorption term of eqn (18) corresponds to the ratio between the adsorption equilibrium constants of BTBE and 1-butanol, i.e., Ka,BTBE/Ka,BuOH. It is related to adsorption thermodynamic properties as follows:
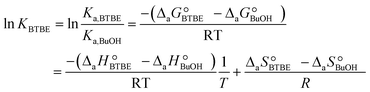 | (20) |
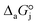 ,
, 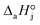 and
and 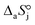 are the adsorption Gibbs free energy, enthalpy and entropy changes of compound j, respectively. The adsorption enthalpy and entropy changes of individual compounds cannot be obtained from the parameter estimates of the kinetic model. Instead, parameters provide differences between BTBE and 1-butanol adsorption enthalpy and entropy changes:
are the adsorption Gibbs free energy, enthalpy and entropy changes of compound j, respectively. The adsorption enthalpy and entropy changes of individual compounds cannot be obtained from the parameter estimates of the kinetic model. Instead, parameters provide differences between BTBE and 1-butanol adsorption enthalpy and entropy changes: 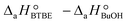 = (34 ± 2) kJ mol−1 and
= (34 ± 2) kJ mol−1 and 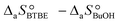 = (93 ± 7) J mol−1 K−1. Consequently, 1-butanol adsorption on the resin is more exothermic than BTBE adsorption, and the entropic loss due to adsorption for 1-butanol is larger than for BTBE. A positive difference between the adsorption enthalpies is consistent with values reported in a previous work on adsorption equilibrium of BTBE and 1-butanol on A35, but in the gas phase:
= (93 ± 7) J mol−1 K−1. Consequently, 1-butanol adsorption on the resin is more exothermic than BTBE adsorption, and the entropic loss due to adsorption for 1-butanol is larger than for BTBE. A positive difference between the adsorption enthalpies is consistent with values reported in a previous work on adsorption equilibrium of BTBE and 1-butanol on A35, but in the gas phase: 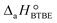 = −21.8 kJ mol−1 and
= −21.8 kJ mol−1 and 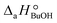 = −41.8 kJ mol−1.35
= −41.8 kJ mol−1.35
The estimate of the Hildebrand solubility parameter of A35, δP (eqn (12)), can be considered as constant in the assayed temperature range and equal to (24.51 ± 0.18) MPa1/2. This value is slightly larger than the published δP values for this catalyst in similar reaction systems, also being constant: (20.5 ± 0.3) MPa1/2 in the PTBE synthesis,17 (20.9 ± 2.0) MPa1/2 in the ETBE synthesis,31 and (21.16 ± 0.12) MPa1/2 in the simultaneous synthesis of ETBE and TAEE.18 However, it fully agrees with the Hildebrand solubility parameter estimated by means of the Hoftyzer and van Krevelen group contribution method,36 resulting in δP = 25.45 MPa1/2 at 298 K. The Hansen solubility parameter, which is considered as a refinement of the Hildebrand parameter, has also been estimated from group contribution,36 resulting in δP = 25.54 MPa1/2 at 298 K. With the aim of checking whether the choice of the selected model, and thus the reaction mechanism, would be affected in case that δP were roughly estimated, all kinetic equations have been fitted again to experimental rate data, but taking δP as a fixed value equal to 20.85 MPa1/2 (the average of the estimated values quoted in literature)17,18,29 if appearing in the model. The best ranked models obtained with this constraint are listed in Table S2 (section D in ESI†). Globally, the residual sum of squares (RSS) is now slightly higher due to the reduction of the degrees of freedom of the fit, but the group of best ranked models is coincident with the non-restricted case, and Model 49 is again the most plausible one (wModel49 = 44.7%, followed by wModel166 = 8.9%). This result reinforces the choice of the selected kinetic equation Model 49 as the best one.
Conclusions
The kinetics of the liquid-phase etherification reaction of isobutene with 1-butanol to produce butyl tert-butyl ether using Amberlyst™ 35 as the catalyst has been studied at 303–356 K in the liquid phase. Significant internal mass transfer limitations have been detected at temperatures above 333 K using 0.25–0.40 mm catalyst bead size, but this effect was not noticeable for bead size smaller than 0.08 mm. Reaction rates free from mass transfer effects obtained in two reaction setups (a batch reactor and a differential tubular reactor) have been used to fit a large number of candidate kinetic equations, each derived from a different mechanism and rate-determining step, based on the Langmuir–Hinshelwood–Hougen–Watson and Eley–Rideal formalisms. The possible effects of the reaction medium on the catalyst activity, and of the temperature on the parameters of the kinetic equations have also been considered. Discrimination of models has been accomplished by applying mathematical and physicochemical criteria in a conservative manner. The Akaike information criterion has been used to rank the reliability of the kinetic models. The best model is derived from an Eley–Rideal type mechanism, where one molecule of 1-butanol adsorbed on one active site reacts with one isobutene molecule from the liquid phase to form one BTBE molecule that, finally, desorbs. The rate-determining step is the surface reaction. The adsorption of 1-butanol on the resin is more exothermic than BTBE adsorption. The interaction between the reaction medium and the resin has a significant effect on the catalytic activity.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank The Dow Chemical Company, now DuPont, for providing the ion exchange resin used as the catalyst in this work.Notes and references
- J. Zheng, Y. Tashiro, Q. Wang and K. Sonomoto, J. Biosci. Bioeng., 2015, 119, 1 CrossRef CAS.
- B. Ndaba, I. Chiyanzu and S. Marx, Biotechnol. Rep., 2015, 8, 1 CrossRef CAS.
- A. Démolis, M. Eternot, N. Essayem and F. Rataboul, New J. Chem., 2016, 40, 3747 RSC.
- G. W. Huber, S. Iborra and A. Corma, Chem. Rev., 2006, 106, 4044 CrossRef CAS.
- K. G. Sharonov, Y. B. Mishentseva, A. M. Rozhnov, E. A. Miroshnichenko and L. I. Korchatova, J. Chem. Thermodyn., 1991, 23, 141 CrossRef CAS.
- K. G. Sharonov, Y. B. Mishentseva, A. M. Rozhnov, E. A. Miroshnichenko and L. I. Korchatova, J. Chem. Thermodyn., 1991, 23, 636 CrossRef.
- J. H. Badia, C. Fité, R. Bringué, E. Ramírez and F. Cunill, J. Chem. Eng. Data, 2016, 61, 1054 CrossRef CAS.
- F. Ancillotti, M. Massi Mauri and E. Pescarollo, J. Catal., 1977, 46, 49 CrossRef CAS.
- F. Ancillotti, M. Massi Mauri, E. Pescarollo and L. Romagnoni, J. Mol. Catal., 1978, 4, 37–48 CrossRef CAS.
- A. Gicquel and B. Torck, J. Catal., 1983, 83, 9 CrossRef CAS.
- O. Françoisse and F. C. Thyrion, Chem. Eng. Process., 1991, 30, 141 CrossRef.
- A. Rehfinger and U. Hoffmann, Chem. Eng. Sci., 1990, 45, 1605 CrossRef CAS.
- C. Fité, M. Iborra, J. Tejero, J. F. Izquierdo and F. Cunill, Ind. Eng. Chem. Res., 1994, 33, 581 CrossRef.
- D. Parra, J. Tejero, F. Cunill, M. Iborra and J. F. Izquierdo, Chem. Eng. Sci., 1994, 49, 4563 CrossRef CAS.
- C. Fité, J. Tejero, M. Iborra, F. Cunill and J. F. Izquierdo, AIChE J., 1998, 44, 2273 CrossRef.
- K. Sundmacher, R. S. Zhang and U. Hoffmann, Chem. Eng. Technol., 1995, 18, 269 CrossRef CAS.
- J. H. Badia, C. Fité, R. Bringué, M. Iborra and F. Cunill, Chem. Eng. J., 2019, 356, 219 CrossRef CAS.
- R. Soto, C. Fité, E. Ramírez, R. Bringué and F. Cunill, Chem. Eng. J., 2017, 307, 122 CrossRef CAS.
- D. Constantinescu and J. Gmehling, J. Chem. Eng. Data, 2016, 61, 2738 CrossRef CAS.
- A. M. Al-Jarallah, M. A. B. Siddiqui and A. K. K. Lee, Can. J. Chem. Eng., 1988, 66, 802 CrossRef CAS.
- J. A. Linnekoski, A. O. Krause and L. K. Rihko, Ind. Eng. Chem. Res., 1997, 36, 310 CrossRef CAS.
- G. Bozga, A. Motelica, R. Dima, V. Plesu, A. Toma and C. Simion, Chem. Eng. Process., 2008, 47, 2247 CrossRef CAS.
- C. Fité, J. Tejero, M. Iborra, F. Cunill, J. F. Izquierdo and D. Parra, Appl. Catal., A, 1998, 169, 165 CrossRef.
- R. C. Reid, J. M. Prausnitz and B. E. Poling, The Properties of Gases and Liquids, McGraw-Hill, New York, 4th edn, 1987 Search PubMed.
- B. E. Poling, J. M. Prausnitz, J. P. O'Connell and R. C. Reid, The Properties of Gases and Liquids, McGraw-Hill, New York, 5th edn, 2001 Search PubMed.
- C. L. Yaws, Thermophysical Properties of Chemicals and Hydrocarbons, William Andrew Inc., Norwich, NY, 2008 Search PubMed.
- M. Vila, F. Cunill, J.-F. Izquierdo, J. González and A. Hernández, Appl. Catal., A, 1994, 117, L99 CrossRef CAS.
- J. H. Badia, C. Fité, R. Bringué, E. Ramírez and F. Cunill, Appl. Catal., A, 2013, 468, 384 CrossRef CAS.
- J. H. Badia, C. Fité, R. Bringué, E. Ramírez and M. Iborra, J. Ind. Eng. Chem., 2016, 42, 36 CrossRef CAS.
- M. Umar, A. R. Saleemi and S. Qaiser, Catal. Commun., 2008, 9, 721 CrossRef CAS.
- R. González, Performance of Amberlyst™ 35 in the Synthesis of ETBE from Ethanol and C4 Cuts (Ph.D. Thesis), University of Barcelona, 2011 Search PubMed.
- Ó. Santín, Estudio del control de las etapas físicas en las síntesis de MTBE y ETBE (M.Sc. Thesis), University of Barcelona, 2005 Search PubMed.
- M. R. E. Symonds and A. Moussalli, Behav. Ecol. Sociobiol., 2011, 65, 13 CrossRef.
- K. P. Burnham and D. R. Anderson, Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, Springer-Verlag, New York, 2nd edn, 2002 Search PubMed.
- R. Soto, N. Oktar, C. Fité, E. Ramírez, R. Bringué and J. Tejero, Chem. Eng. Technol., 2017, 40, 889 CrossRef CAS.
- D. W. van Krevelen and K. te Nijenhuis, Properties of Polymers: Their Correlation with Chemical Structure; their Numerical Estimation and Prediction from Additive Group Contributions, Elsevier Science, Amsterdam, The Netherlands, 4th edn, 2009 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0re00318b |
| This journal is © The Royal Society of Chemistry 2021 |