Open Access Article
Open Access ArticleRapid chiral analysis based on liquid-phase cyclic chemiluminescence†
Runkun
Zhang
,
Yanhui
Zhong
,
Zhenyu
Lu
,
Yanlong
Chen
and
Gongke
Li
 *
*
School of Chemistry, Sun Yat-sen University, Guangzhou 510275, People's Republic of China. E-mail: cesgkl@mail.sysu.edu.cn
First published on 22nd October 2020
Abstract
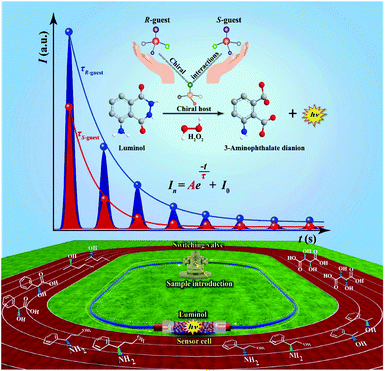
Rapid chiral analysis has become one of the important aspects of academic and industrial research. Here we describe a new strategy based on liquid-phase cyclic chemiluminescence (CCL) for rapid resolution of enantiomers and determination of enantiomeric excess (ee). A single CCL measurement can acquire multistage signals that provide a unique way to examine the intermolecular interactions between chiral hosts and chiral guests, because the lifetime (τ) of the multistage signals is a concentration-independent and distinguishable constant for a given chiral host–guest system. According to the τ values, CCL allows discrimination between a wide range of enantiomeric pairs including chiral alcohols, amines and acids by using only one chiral host. Even the chiral systems hardly distinguished by nuclear magnetic resonance and fluorescence methods can be distinguished easily by CCL. Additionally, the τ value of a mixture of two enantiomers is equal to the weighted average of each enantiomer, which can be used for the direct determination of ee without the need to separate the chiral mixture and create calibration curves. This is extremely crucial for the cases without readily available enantiomerically pure samples. This strategy was successfully applied to monitoring of the Walden inversion reaction and analysis of chiral drugs. The results were in good agreement with those obtained by high-performance liquid chromatography, indicating the utility of CCL for routine quick ee analysis. Mechanism study revealed that the τ value is possibly related to the activity of the chiral substance to catalyze a luminol–H2O2 reaction. Our research provides an unprecedented and general protocol for chirality differentiation and ee determination, which is anticipated to be a useful technology that will find wide application in chirality-related fields, particularly in asymmetric synthesis and the pharmaceutical industry.
Introduction
Chirality is a universal phenomenon in nature, and most biological species, such as amino acids, nucleic acids, proteins, and drugs, are chiral and intermolecular chiral–chiral interactions occur ubiquitously among biological processes.1–3 The simultaneous determination of the absolute configuration and enantiopurity of chiral substrates is highly significant in the fields of synthetic, biological and pharmaceutical chemistry.4–6 However, chiral analysis remains a great challenge because enantiomers have nearly identical physical properties.7In the past several decades, many effective methods have been developed for chiral analysis, such as gas chromatography,8,9 high-performance liquid chromatography (HPLC),10,11 capillary electrophoresis,12–14 nuclear magnetic resonance (NMR) spectroscopy7,15–17 and mass spectrometry.18,19 However, these methods are time-consuming and technically complex, and the instrumentation required is expensive and bulky and requires well-trained operators.20,21 Optical sensing methodologies, such as circular dichroism,22–24 fluorescence25,26 and colorimetry,27 have attracted considerable research interest as a result of their advantages of rapidity, simplicity, and low cost. In such a strategy, molecules or materials containing the chiral unit are used as chemosensory hosts that can interact with the chiral targets and then induce distinguishable optical signals.21 Although great efforts and achievements that have been made in this field, some problems still remain to be solved. For instance, most methods suffer from narrow substrate scope and limitedly differentiable enantiomers.28 In addition, the output signal for chiral discrimination is strongly influenced by the analyte concentration, and this would normally need two independent methods to simultaneously determine both enantiomeric configuration and enantiopurity.28,29 Especially, these assays usually require highly pure samples to construct calibration curves for enantiomeric excess (ee) determination.4,30,31 It would be particularly significant to acquire a concentration-independent parameter for chiral discrimination and enantiopurity determination, because such a technique can simplify and speed up the measurement and thereby find wide application in rapid screening of ee for asymmetric synthesis, the pharmaceutical industry etc. In this paper, we report an unprecedented strategy of liquid-phase cyclic chemiluminescence (CCL) that does not suffer from the above limitations in chiral analysis. To the best of our knowledge, this paper is the first to report a chemiluminescence-based sensing methodology that provides a concentration-independent constant for the simultaneous determination of the enantiomeric configuration and ee value.
As an important optical analytical technology, chemiluminescence (CL) have been widely used for pharmaceutical analysis,32 clinical analysis33–35 and biological analysis.36,37 However, typical CL kinetic curves lack the characteristic features of the analytes. To overcome this drawback, our group proposed a new concept of cyclic chemiluminescence (CCL) for rapid discrimination of structurally similar compounds.38 In contrast to conventional flow CL systems, the direction of the carrier in the CCL system is in a state of periodical change, which triggers a succession of CL reactions in a single sample introduction to produce multistage signals. We found that the multistage signals on the CCL kinetic curve satisfy the first-order exponential decay law:
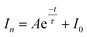 | (1) |
Experimental section
The fabrication of the liquid-phase CCL system can be seen in the ESI.† In the present work, immobilized luminol (5-amino-2,3-dihydro-1,4-phthalazinedione; immobilization method is detailed in the ESI†) was packed into a homemade flow-through reactor to fabricate a sensor cell. H2O2 was used as a carrier and oxidant, and it was catalyzed by a sample containing a metal–organic complex to produce reactive oxygen species. Subsequently, immobilized luminol in a sensor cell was oxidized by reactive oxygen species to form a 3-aminophthalate dianion in an excited state, which emitted light when returning to the ground state.40 Specifically, a circular pipeline was designed for the CCL system, and the direction of the carrier in the CCL system can be changed automatically at the indicated cycle period. Through automatically changing the carrier direction at the indicated period, the chemical species at different stages flowed through the sensor cell repeatedly to induce the CL reactions in succession. Multistage signals that satisfy the exponential decay law were measured over time. The design of the CCL system extends the observable time, and therefore the distinctions between different luminous reactions that are usually not easy to observe by conventional CL-based detection can be observed by CCL detection. The flow paths of liquid-phase CCL detection at different stages are shown in the ESI (Fig. S1).†For chiral analysis, chiral metal–organic complexes that are able to enhance the luminescence intensity of luminol–H2O2 reactions were used as hosts, and new complexes were formed via chiral–chiral interactions between the chiral host and chiral guest, when chiral guests were mixed with chiral hosts. The τ values of the CCL kinetic curves of luminol–H2O2 reactions catalyzed by the new complexes were used for chiral analysis. The schematic representation of liquid-phase CCL for chiral analysis is shown in Fig. 1.
Results and discussion
Resolution of enantiomers
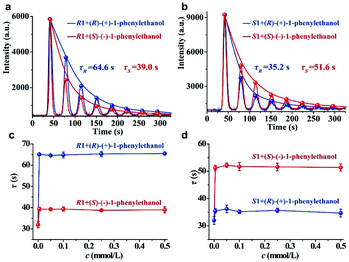
To examine the feasibility of our strategy for chiral analysis, three pairs of commercially available chiral metal–organic complexes (R1 and S1, R2 and S2, and R3 and S3; the detailed information of these chiral complexes can be seen in Table S1 of the ESI†) were used as hosts. The original CCL kinetic curves of the luminol–H2O2 system catalyzed by these chiral metal–organic complexes are shown in the ESI (Fig. S2).† It shows that the two enantiomers of one chiral substrate of metal–organic complexes have the same τ value without adding chiral guests. This because the differences between enantiomers are difficult to observe under normal circumstance, but these differences become much more marked in a chiral environment. Thus, chiral guests were added into the solutions of chiral hosts. We found that additions of (R)-(+)-1-phenylethanol and (S)-(−)-1-phenylethanol into R1 outputting τ values of 64.6 and 39.0 s (Fig. 2a), respectively. τ values of 35.2 and 51.6 s were observed when (R)-(+)-1-phenylethanol and (S)-(−)-1-phenylethanol were added into S1 (Fig. 2b).We further investigated the effects of the concentration of the guest on the response behaviors of the hosts in a much broader concentration range. We have plotted the τ values of R1 and S1 versus the increasing concentrations of (R)-(+)-1-phenylethanol and (S)-(−)-1-phenylethanol in Fig. 2c and d, respectively. We found that the τ value is independent of the concentration of the chiral guest in the range of 0.005 to 0.5 mmol L−1 but is only dependent on the chiral configuration. In addition, the τ value is also independent of the H2O2 concentration within a certain range (Fig. S3, detailed discussion can be seen in the ESI†). These results demonstrate that each chiral system has a unique and constant τ value, and the distinction in the τ value confirms the chiral discrimination. Quite different from other sensing methodologies based on intensity quenching/enhancement or spectral changes, the parameter (τ value) of CCL for chiral analysis is a concentration-independent constant characteristic of a given chiral system, which functions as characteristic labelling for directly determining the identity of enantiomers.
The reproducibility of the immobilized luminol was investigated by the measurement of (R)-(+)-1-phenylethanol using S1. We found that the background noise increases and luminescence intensity (A) decreases gradually with increasing testing number (ESI, Fig. S4†), but τ could remain stable within 25 replicates with an RSD of 3.7% (ESI, Fig. S5a†). It means that τ has good stability, possibly because τ depends on the rate of luminescence depletion related to the characteristics of the reaction, but not the apparent intensity. The τ values measured from 5 different batches of immobilized luminol was 4.2% (ESI, Fig. S5b†). The sufficient stability of τ within the same batch and between different batches of immobilized luminol make CCL qualified for chiral differentiation. It is worth noting that the A value is easily fluctuant and the τ value depends on the decay rate of the multistage signal, and therefore the multistage signal can be normalized for nonlinear curve fitting to obtain the τ value.
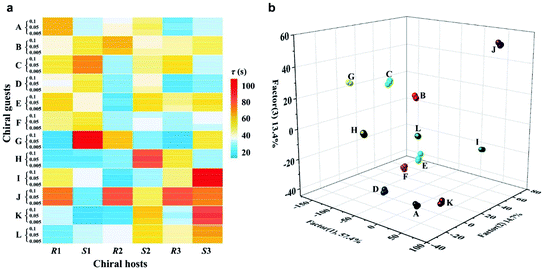
An ideal method for chiral sensing should be capable of discrimination of different kinds of chiral molecules accompanied by the resolution of the two enantiomers of one chiral substrate.21 However, current methods usually suffer from narrow substrate scope and limitedly differentiable enantiomers.15 We next turned attention to demonstrate the ability of CCL to discriminate a wide range of enantiomers with broad substrate applicability. The chiral metal–organic complexes shown in the ESI (Table S1)† were used as hosts for sensing two pairs of chiral alcohols, chiral amines and chiral acids, respectively. As expected, each enantiomer can be correlated with a distinct τ value when it is mixed with a given chiral host (Fig. 3), enabling easy discrimination of chiral compounds. For example, when the chiral complex R1 was used as a chiral host, τ values of 64.6 and 39.0 s were observed for (R)-(+)-1-phenylethanol and (S)-(−)-1-phenylethanol; 52.7 and 38.2 s for (R)-(−)-2-pentanol and (S)-(+)-2-pentanol; 58.3 and 46.5 s for (R)-(−)-2-phenylglycinol and (S)-(+)-2-phenylglycinol; 12.1 and 21.4 s for (R)-3-amino-3-phenylpropan-1-ol and (S)-3-amino-3-phenylpropan-1-ol; 49.6 and 73.9 s for D-(−)-tartaric acid and L-(+)-tartaric acid; 31.6 and 23.7 s for D-(−)-mandelic acid and L-(+)-mandelic acid, respectively. Satisfactory resolution of the two enantiomers of one chiral substrate is easily achieved by simply comparing the τ values.
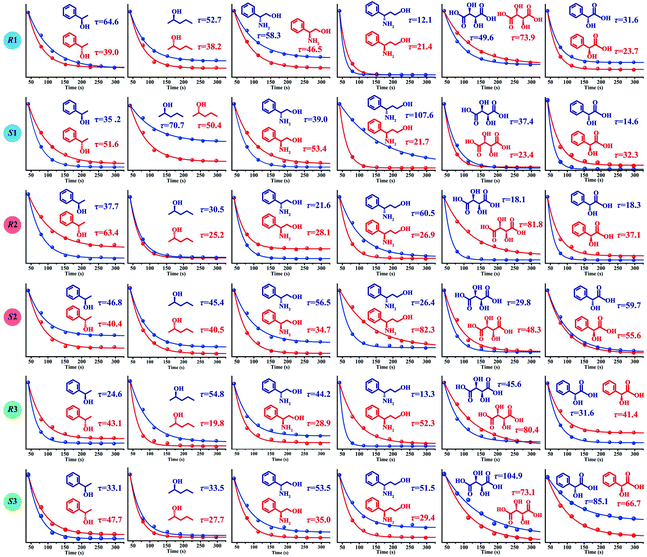 | ||
| Fig. 3 The τ values of different chiral host–guest systems. The concentration of all hosts and guests is 0.1 mmol L−1, and the concentration of H2O2 is 0.05 mmol L−1. The unit of τ is seconds. | ||
Noteworthily, each chiral host–guest system has a corresponding τ value, that is different hosts show different values of τ to a given guest, and the same host exhibits different values of τ to different guests. The above results demonstrate that each chiral host–guest system has a corresponding exponential decay equation with a unique τ value. Thus, we can establish a database of τ values of various chiral host–guest systems in future, which provides facilitation for quick recognition of unknown chiral compounds. For example, if the τ values of an analyte were measured to be 64.6 and 35.2 s when using R1 and S1 as hosts, respectively, the identity of the analyte could be confirmed to be (R)-(+)-1-phenylethanol by searching the database.
Fig. 3 illustrates the broad substrate applicability and the satisfactory enantio-differentiating ability of our strategy. Usually, we can discriminate most enantiomeric pairs by only using one chiral host. However, the τ values of some chiral compounds on a certain host are close. For example, although the host S2 allows discrimination between enantiomers of 1-phenylethanol or 2-pentanol, it is unable to resolve (S)-(−)-1-phenylethanol (τ = 40.4 s) and (S)-(+)-2-pentanol (τ = 40.5 s). Our aim is to realize unambiguous discrimination among a large variety of chiral compounds, not just limited to the two enantiomers of one chiral substrate. In consideration of the cross-reactivity of the hosts, we combined all the hosts (R1, S1, R2, S2, R3 and S3) to construct a sensor array, expecting to unambiguously discriminate between various chiral compounds. Three concentrations (low: 0.005 mmol L−1, medium: 0.05 mmol L−1 and high: 0.1 mmol L−1) of 12 chiral compounds were tested by using the sensor array, and the resulting τ values are summarized in the ESI (Table S2).† For easier visualization, the τ value of each response is depicted in the form of a heat map according to the scale bar on the right. As shown in Fig. 4a, each of the chiral guests creates a unique multidimensional response pattern, and different concentrations of the same chiral guest induce similar response patterns. Linear discriminant analysis (LDA) was then used to further digitize and visualize the response patterns (6 host units × 12 chiral guests × 3 concentrations). Fig. 4b shows the 3-D discrimination plot constructed from the first three factors. The first three factors account for 85.5% of the total variance.
The same colored symbol within the LDA graphical output is assigned to specific chiral guests. These chiral guests are classified into 12 groups with 100% accuracy, and small spatial distances are observed within the same group. This demonstrates the satisfactory discrimination capacity of the sensor array based on the CCL strategy.
NMR spectroscopy and fluorescence spectroscopy are common techniques used for chiral discrimination. However, we found that the 1H NMR spectroscopy cannot effectively resolve the chiral systems of R1 (and S1) with 1-phenylethanol enantiomers (ESI, Fig. S6†). The same chiral systems also cannot be resolved by the fluorescence method, because R1, S1 and 1-phenylethanol are non-fluorescent substances. These results demonstrate that CCL can distinguish some chiral host–guest systems, which would be difficult for NMR and fluorescence spectroscopy. Compared with the method for chiral discrimination using a QD enhanced-CL system,41 the commercial chiral metal–organic complexes used in the present work are easily available. In addition, they allow facile discrimination between a wide range of enantiomeric pairs. It is well known that static injection CL can provide a full intensity kinetic curve. However, we found that the CL kinetic curves obtained by static injection lack enough discriminability to differentiate chiral compounds, mainly due to the short lifetime of the CL kinetic curve. The τ values of different kinetic curves obtained by static injection are in the range from 1.0 to 3.6 s (ESI, Fig. S7†), and the narrow τ-range means low resolution. The detailed discussion can also be seen in the ESI.† Thus, CCL will be a powerfully complementary technology for chiral discrimination.
Determination of ee
The determination of ee is performed routinely in many scientific fields, especially in asymmetric synthesis and the pharmaceutical industry.42–45 Chiral separation is the most common method for ee determination. However, chiral separation is a cost-intensive and time-consuming process due to the long analysis time and the use of expensive chiral columns.21,46 Simple and inexpensive techniques for rapid determination of ee are attractive for their potential applications in academic and industrial fields. In order to probe the application value of our strategy in rapid determination of ee, R1 and S2 were used to measure a series of mixtures consisting of different percentages of 1-phenylethanol enantiomers, and the trends of the τ value of the mixture (τm) versus the percentages of (R)-(+)-1-phenylethanol and (S)-(−)-1-phenylethanol are plotted in Fig. 5, respectively. Linear-regression analysis shows that τm is linearly related to the percentages of the enantiomers in the mixture. Further study found that the slope of the linear regression equation is equal to the difference between the τ values of the two enantiomers, and the intercept equals the τ value of one of the enantiomers. The τm of the mixture composed of arbitrary proportions of enantiomers can be expressed as:| τm = ω(R)(τ(R) − τ(S)) + τ(S) = ω(R)τ(R) + (1 − ω(R))τ(S) | (2) |
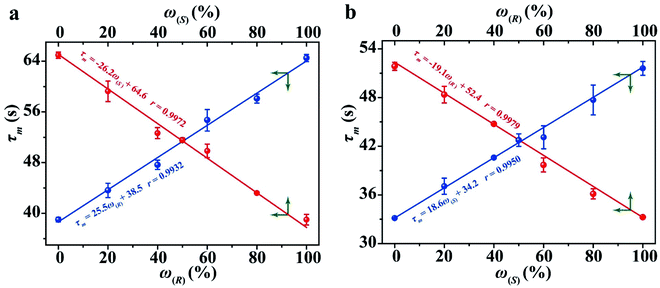 | ||
| Fig. 5 The relationship between the τ value and the percentages of 1-phenylethanol enantiomers using R1 (a) and S1 (b) as hosts. | ||
Or can be presented in the following form:
| τm = ω(S)(τ(S) − τ(R)) + τ(R) = (1 − ω(S))τ(R) + ω(S)τ(S) | (3) |
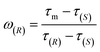 | (4) |
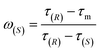 | (5) |
The ee (%) is defined as:47
| ee = ω(R) − ω(S) | (6) |
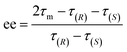 | (7) |
Applications
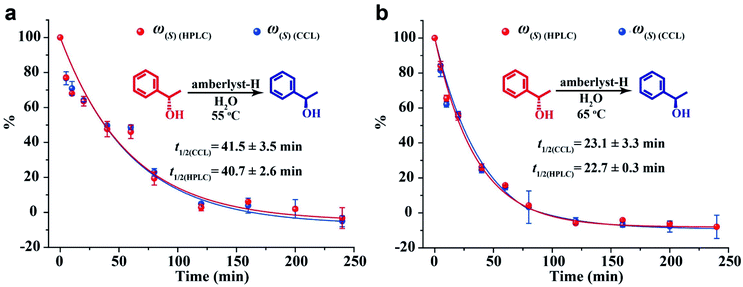
To validate the utility of CCL in enantiopurity determination, an amberlyst-catalyzed Walden inversion was selected as a prototype reaction because of its industrial application in the production of pharmaceutical and agrochemical building blocks.48 1.0 g of amberlyst-H was added to 100 mL solution of (S)-(−)-1-phenylethanol at 0.2 mmol L−1, the above solutions were prepared in duplicate and were heated to 55 °C and 65 °C under stirring condition, respectively. At various times, 2 mL of the reaction mixture aliquots were withdrawn and added to cuvettes containing 2 mL of deionized water or a chiral host (S1 at 0.2 mmol L−1). A specific chiral separation column was used for HPLC measurement, and the enantiopurities were calculated according to the calibration curves constructed in advance (the details can be seen in the ESI, Table S4, Fig. S9 and S10†). For CCL measurement, the percentages and the ee values of the 1-phenylethanol enantiomers were directly calculated by using eqn (4), (5) and (7) according to the τ values of the aliquots. Three replicates of the above assay were performed. The reaction curves obtained by the two methods are shown in Fig. 6. The general shape of the curves obtained by the two methods is surprisingly similar, showing that the conversion of (S)-(−)-1-phenylethanol follows first order reaction kinetics. The relative content of (S)-(−)-1-phenylethanol steadily decreases, meaning that the yield of (R)-(+)-1-phenylethanol steadily increases with the conversion of (S)-(−)-1-phenylethanol. Complete substrate conversion within 240 min was observed. The half-lives calculated by CCL (t1/2(CCL)) and HPLC (t1/2(HPLC)) are in good agreement. The ee values at different reaction times measured by the two methods are listed in the ESI (Table S5).† The CCL determined ee values correlated well with chiral HPLC results with absolute errors ranging from −7.1% to 7.0%.It is worth noting that during the processes of the above assays, the analytical time of each HPLC measurement was 13 min (ESI, Fig. S9†), and the total time spent on every HPLC assay was about 377 min (13 min of each detection × 7 standard solutions + 13 min of each detection × 22 samples). The time taken for a single CCL measurement was about 5 min, moreover, chiral separation and calibration curve are not necessary for CCL measurement, the total analytical time of every CCL assay was 110 min (5 min of each detection × 22 samples). The above results demonstrate that CCL represents a fast and reliable tool that can reduce the cost and time of chiral analysis.
The analysis of ee of chiral drugs plays an important role in the pharmaceutical industry and clinical pharmacy, because only one of the two enantiomers is the pharmaceutically active ingredient in many cases.49 Ibuprofen is one of the most potent anti-inflammatory drugs used for the treatment of acute and chronic pain, fever and inflammatory diseases. It has been proved that (S)-(+)-ibuprofen is almost entirely responsible for the anti-inflammatory activity.50 In order to further explore the utility of our strategy in enantiopurity determination, we used S1 as the host to analyze ibuprofen samples. First, the standard samples of (R)-(−)-ibuprofen and (S)-(+)-ibuprofen were measured by CCL, and their τ values are found to be 44.6 and 26.1 s, respectively (ESI, Fig. S11†). Next, samples containing ibuprofen were dissolved in ethanol, and then diluted with deionized water. Finally, the prepared solutions were simultaneously analyzed by CCL and HPLC. Similarly, a specific chiral column was used and calibration curves were constructed in advance for HPLC determination (the details can be seen in the ESI, Table S6, Fig. S12 and S13†). For CCL measurement, the ee values were directly calculated by using eqn (7) according to the τ values of samples. The results obtained by the two methods are in good agreement with absolute errors ranging from −4.2% to 4.0% (Table 1). This example illustrates the promising application of our strategy in the analysis of chiral drugs.
| Samples | ee (%) measured by CCL | ee (%) measured by HPLC | Absolute error (%) |
|---|---|---|---|
| a Samples 1 and 2 are two commercially available ibuprofen tablets; samples 3 and 4 are two commercially available ibuprofen capsules; sample 5 was prepared by mixing analytical grade (R)-(−)-ibuprofen with (S)-(+)-ibuprofen at random. | |||
| 1 | −4.5 ± 2.7 | 4.2 ± 1.9 | −0.3 |
| 2 | 5.6 ± 3.8 | 1.6 ± 5 | 4.0 |
| 3 | −1.6 ± 6.0 | −1.7 ± 8.2 | 0.1 |
| 4 | −5.6 ± 2.7 | −1.4 ± 0.32 | −4.2 |
| 5 | −42.1 ± 3.5 | −45.6 ± 2.3 | 3.5 |
Mechanism study
One of the major approaches to chirality sensing is based on the formation of diastereomeric complexes generated by intermolecular chiral–chiral interactions between a chiral host and chiral guest.5,21,51,52 In order to explore the working mechanism of CCL for chiral discrimination, density functional theory and the B3LYP method in the Gaussian 09 program were employed to gain insight into the possible modes of interactions between R1 (or S1) and 1-phenylethanol enantiomers. Geometry optimization was performed using the basis set of LANL2DZ for cobalt atoms and 6-31G for other atoms. Further frequency analysis was done to insure optimized structures have only real frequencies. The optimized geometries for the new complexes are presented in Fig. 7, which points out that 1-phenylethanol enantiomers can be linked to chiral cobalt complexes (R1 and S1) via hydrogen bonds to form adducts. The binding geometries in the formative adducts are different, and their binding energies are higher than −4 kcal mol−1, indicating that stable complexes with different spatial structures were formed.53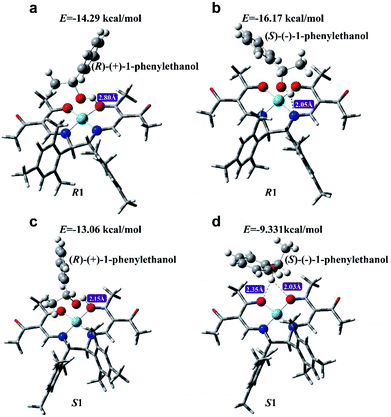 | ||
| Fig. 7 The optimized structures of R1 with (R)-(+)-1-phenylethanol (a), R1 with (S)-(−)-1-phenylethanol (b), S1 with (R)-(+)-1-phenylethanol (c) and S1 with (S)-(−)-1-phenylethanol (d). | ||
In order to further explore the interaction between R1 (or S1) and 1-phenylethanol enantiomers, the mixtures of R1 and (R)-(+)-1-phenylethanol (R1+R), R1 and (S)-(−)-1-phenylethanol (R1+S), S1 and (R)-(+)-1-phenylethanol (S1+R), and S1 and (S)-(−)-1-phenylethanol (S1+S), were measured by surface-enhanced Raman spectroscopy (SERS), and density functional theory at the B3LYP/6-31++G(d,p) level was employed to calculate the Raman bands of the new adducts. As Fig. S14 in the ESI† shows, the Raman spectra of R1+R and R1+S exhibit features at 1296 and 1278 cm−1, respectively. Similarly, characteristic bands at 1281.1 and 1296.7 are observed for S1+R and S1+S, respectively. This further demonstrates the formation of different adducts. Molecular modeling revealed that the stretching vibration of C–O in 1-phenylethanol enantiomers brings the hydroxyl radical close to the nitrogen atom in the hosts, forming hydrogen bonds with different spatial structures, and therefore the new adducts exhibit differential Raman bands (Video S1†).
It is well known that different complexes show different activities to catalyze luminol–H2O2 reactions, and we speculate that the difference in τ values among different chiral systems may be related to their catalytic activities. Thus, the reaction kinetics of luminol–H2O2 reactions catalyzed by different chiral systems were investigated by using HPLC to monitor the consumption rate of luminol, and the results are shown in the ESI (Fig. S15).† In order to facilitate the comparison, the reaction rate was expressed as lifetime using the τ value. The results showed that luminol–H2O2 reactions catalyzed by R1 (τ = 14.7 min) and S1 (τ = 15.2 min) have almost similar τ values. The τ values of luminol–H2O2 reactions catalyzed by R1 with (R)-(+)-1-phenylethanol, R1 with (S)-(−)-1-phenylethanol, S1 with (R)-(+)-1-phenylethanol, and S1 with (S)-(−)-1-phenylethanol are 28.9, 19.2, 17.8 and 22.4 min. A high level of consistency exists between the τ value of reaction kinetics monitored by HPLC and the τ value of the CCL kinetic curve, which confirms our hypothesis. According to the above results, we conclude that new adducts with different spatial structures can be formed via intermolecular chiral–chiral interaction between the chiral hosts and chiral guests. These new adducts show different catalytic activities for luminol–H2O2 reactions, and the distinction in the catalytic activities can be reflected by the decay speeds of the multistage signals measured by CCL, expressing as distinguishable τ values.
Compared with static injection CL, it seems that CCL detection makes the whole reaction proceed through a staged process, which expands the differences related to reaction kinetics after the multistage reaction. In addition, additional features, such as diffusion, convection and interaction between the sample and resin, can probably occur in the CCL system. The difference in these features may also affect the observed analytical signal. Therefore, extensive work is still needed to further explore the mechanism.
Conclusion
In conclusion, we have described a brand-new optical strategy of liquid-phase CCL for chiral analysis. This strategy provides a concentration-independent parameter (τ value) to discriminate a large variety of chiral substrates. Importantly, our strategy allows rapid determination of the ee value without the need for chiral separation and calibration curves, thereby paving the way for rapid ee analysis. Further development can focus on establishing a standard database of τ values to quickly and accurately recognize unknown chiral compounds. Mechanism study revealed that new adducts with different spatial structures can be formed via intermolecular chiral–chiral interactions between the chiral hosts and chiral guests. The new adducts exhibit different catalytic activity for luminol–H2O2 reactions, resulting in distinguishable τ values of the multistage signals measured by CCL. Since CCL allows examine the intermolecular interactions between host and guest through outputting distinguishable τ values. We are currently exploring this strategy to discriminate chiral biological substrates, expecting to find applications in the study of protein structures, molecular dynamics, drug design etc. based on host–guest interactions. Further studies in this direction are currently underway in our laboratory and will be reported in due course. We believe that the combination of our strategy and diversified chiral hosts will offer a powerful platform to address some challenges of chirality analysis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 21605163, 21675178 and 21976213), the Research and Development Plan for Key Areas of Food Safety in Guangdong Province of China (No. 2019B020211001), and the National Key Research and Development Program of China (No. 2019YFC1606101), respectively.Notes and references
- J. L. Stymiest, V. Bagutski, R. M. French and V. K. Aggarwal, Nature, 2008, 456, 778–783 CrossRef CAS.
- J. Q. Dong, C. X. Tan, K. Zhang, Y. Liu, P. J. Low, J. W. Jiang and Y. Cui, J. Am. Chem. Soc., 2017, 139, 1554–1564 CrossRef CAS.
- M. Planchestainer, E. Hegarty, C. M. Heckmann, L. J. Gourlay and F. Paradisi, Chem. Sci., 2019, 10, 5952–5958 RSC.
- L. You, J. S. Berman, A. Lucksanawichien and E. V. Anslyn, J. Am. Chem. Soc., 2012, 134, 7126–7134 CrossRef CAS.
- J. Y. C. Lim, I. Marques, V. Félix and P. D. Beer, Angew. Chem., Int. Ed., 2018, 130, 593–597 CrossRef.
- Z. Liu, J. Ai, P. Kumar, E. You, X. Zhou, X. Liu, Z. Tian, P. Bouř, Y. Duan and S. Ding, Angew. Chem., Int. Ed., 2020, 132, 15338–15343 CrossRef.
- Y. C. Zhao and T. M. Swager, J. Am. Chem. Soc., 2015, 137, 3221–3224 CrossRef CAS.
- H. L. Qian, C. X. Yang and X. P. Yan, Nat. Commun., 2016, 7, 12104–12110 CrossRef CAS.
- J. H. Zhang, S. M. Xie, L. Chen, B. J. Wang, P. G. He and L. M. Yuan, Anal. Chem., 2015, 87, 7817–7824 CrossRef CAS.
- L. Capriotti, C. M. Montone, M. Antonelli, C. Cavaliere, F. Gasparrini, G. L. Barbera, S. Piovesana and A. Laganà, Anal. Chem., 2018, 90, 8326–8330 CrossRef.
- X. Han, J. J. Huang, C. Yuan, Y. Liu and Y. Cui, J. Am. Chem. Soc., 2018, 140, 892–985 CrossRef CAS.
- R. B. Yu and J. P. Quirino, Trends Anal. Chem., 2019, 118, 779–792 CrossRef CAS.
- S. J. Xu, Y. Y. Wang, W. Li and Y. B. Ji, J. Chromatogr. A, 2019, 1602, 481–488 CrossRef CAS.
- C. Sonnendecker, S. Thürmann, C. Przybylski, F. D. Zitzmann, N. Heinke, Y. Krauke, K. Monks, A. A. Robitzki, D. Belder and W. Zimmermann, Angew. Chem., Int. Ed., 2019, 131, 6477–6480 CrossRef.
- J. Axthelm, H. Görls, U. S. Schubert and A. Schiller, J. Am. Chem. Soc., 2015, 137, 15402–15405 CrossRef CAS.
- G. L. Bian, S. W. Yang, H. Y. Huang, H. Zong, L. Song, H. J. Fan and X. Q. Sun, Chem. Sci., 2016, 7, 932–938 RSC.
- M. S. Seo and H. Kim, J. Am. Chem. Soc., 2015, 137, 14190–14915 CrossRef CAS.
- C. Ebner, C. A. Müller, C. Markert and A. Pfaltz, J. Am. Chem. Soc., 2011, 133, 4710–4713 CrossRef CAS.
- S. T. Phillips, J. N. Dodds, B. M. Ellis, J. C. May and J. A. McLean, Chem. Commun., 2018, 54, 9398–9401 RSC.
- I. Boussouar, Q. J. Chen, X. Chen, Y. L. Zhang, F. Zhang, D. M. Tian, H. S. White and H. B. Li, Anal. Chem., 2017, 89, 1110–1116 CrossRef CAS.
- X. Zhang, J. Yin and J. Yoon, Chem. Rev., 2014, 114, 4918–4959 CrossRef CAS.
- H. T. Z. Zhu, Q. Li, Z. C. Gao, H. L. Wang, B. B. Shi, Y. T. Wu, L. Q. Shangguan, X. Hong, F. Wang and F. H. Huang, Angew. Chem., Int. Ed., 2020, 59, 10868–10872 CrossRef CAS.
- T. R. Schulte, J. J. Holstein and G. H. Clever, Angew. Chem., Int. Ed., 2019, 58, 5562–5566 CrossRef CAS.
- F. Y. Thanzeel, A. Sripada and C. Wolf, J. Am. Chem. Soc., 2019, 141, 16382–16387 CrossRef CAS.
- Y. Sasaki, S. Kojima, V. Hamedpour, R. Kubota, S. Takizawa, I. Yoshikawa, H. Houjou, Y. Kubo and T. Minami, Chem. Sci., 2020, 11, 3790–3796 RSC.
- A. Akdeniz, T. Minami, S. Watanabe, M. Yokoyama, T. Ema and P. Anzenbacher Jr, Chem. Sci., 2016, 7, 2016–2022 RSC.
- F. F. Xie, Q. Bai, X. M. Jiang, X. S. Yu, Z. N. Xia and W. L. Wei, ACS Appl. Mater. Interfaces, 2018, 10, 11872–11879 CrossRef CAS.
- S. S. Yu, W. Plunkett, M. Kim and L. Pu, J. Am. Chem. Soc., 2012, 134, 20282–20285 CrossRef CAS.
- K. L. Wen, S. S. Yu, Z. Huang, L. M. Chen, M. Xiao, X. Q. Yu and L. Pu, J. Am. Chem. Soc., 2015, 137, 4517–4524 CrossRef CAS.
- P. Zardi, K. Wurst, G. Licini and C. Zonta, J. Am. Chem. Soc., 2017, 139, 15616–15619 CrossRef CAS.
- Z. A. De Los Santos, C. C. Lynch and C. Wolf, Angew. Chem., Int. Ed., 2019, 58, 1198–1202 CrossRef CAS.
- E. Al-Hetlani, M. O. Amin and M. Madkour, Nanophotonics, 2018, 7, 683–692 CAS.
- F. M. Chen, S. F. Mao, H. L. Zeng, S. H. Xue, J. M. Yang, H. Nakajima, J. M. Lin and K. Uchiyama, Anal. Chem., 2013, 85, 7413–7418 CrossRef CAS.
- R. Yang, F. Li, W. C. Zhang, W. Shen, D. Yang, Z. P. Bian and H. Cui, Anal. Chem., 2019, 91, 13006–13013 CrossRef CAS.
- Y. Y. Su, D. Y. Deng, L. C. Zhang, H. J. Song and Y. Lv, Trends Anal. Chem., 2016, 82, 394–411 CrossRef CAS.
- J. Y. Sun, Z. A. Hu, S. C. Zhang and X. R. Zhang, ACS Sens., 2019, 4, 87–92 CrossRef CAS.
- W. J. Zhou, Y. Q. Cao, D. D. Sui and C. Lu, Angew. Chem., Int. Ed., 2016, 55, 4236–4241 CrossRef CAS.
- R. K. Zhang, Y. F. Hu and G. K. Li, Anal. Chem., 2014, 86, 6080–6087 CrossRef CAS.
- Y. H. Zhong, Y. F. Hu, G. K. Li and R. K. Zhang, Anal. Chem., 2019, 91, 12063–12069 CrossRef CAS.
- L. Rose and T. D. Waite, Anal. Chem., 2001, 73, 5909–5920 CrossRef.
- M. Shahrajabian, F. Ghasemi and M. R. Hormozi-Nezhad, Sci. Rep., 2018, 8, 14011–14019 CrossRef.
- B. T. Herrera, S. R. Moor, M. McVeigh, E. K. Roesner, F. Marini and E. V. Anslyn, J. Am. Chem. Soc., 2019, 141, 11151–11160 CrossRef CAS.
- N. Eccles, L. F. A. B. Bailly, D. F. Sala, J. I. Vitórica-Yrezábal, J. Clayden and J. S. Webb, Chem. Commun., 2019, 55, 9331–9334 RSC.
- P. M. Mower and D. G. Blackmond, ACS Catal., 2018, 8, 5977–5982 CrossRef.
- A. Akdeniz, T. Minami, S. Watanabe, M. Yokoyama, T. Ema and P. Anzenbacher, Chem. Sci., 2016, 7, 2016–2022 RSC.
- Z. A. De Los Santos, S. MacAvaney, K. Russell and C. Wolf, Angew. Chem., Int. Ed., 2020, 59, 2440–2448 CrossRef CAS.
- A. Comby, E. Bloch, C. M. M. Bond, D. Descamps, J. Miles, S. Petit, S. Rozen, J. B. Greenwood, V. Blanchet and Y. Mairesse, Nat. Commun., 2018, 9, 5212–5225 CrossRef CAS.
- F. Biedermann and W. M. Nau, Angew. Chem., Int. Ed., 2014, 53, 5694–5699 CrossRef CAS.
- M. Hu, Y. X. Yuan, W. Z. Wang, D. M. Li, H. C. Zhang, B. X. Wu, M. H. Liu and Y. S. Zheng, Nat. Commun., 2020, 11, 161–170 CrossRef CAS.
- J. M. Padró, J. Osorio-Grisales, J. A. Arancibia, A. C. Olivieri and C. B. Castells, J. Chromatogr. A, 2016, 1467, 255–260 CrossRef.
- J. M. Wollschlãger, K. Simon, M. Gaedke and C. A. Schalley, Chem. Commun., 2018, 54, 4967–4970 RSC.
- Z. Chen, Q. Wang, X. Wu, Z. Li and Y. B. Jiang, Chem. Soc. Rev., 2015, 44, 4249–4263 RSC.
- Y. L. Li, J. P. Wu, D. L. Cao and J. L. Wang, J. Phys. Chem. A, 2016, 120, 8444–8449 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Fabrication and working principle of the liquid-phase CCL system; method for the immobilization of luminol; Fig. S1–S10 and Tables S1–S5. See DOI: 10.1039/d0sc03496g |
| This journal is © The Royal Society of Chemistry 2021 |