Molecular and supported Ti(III)-alkyls: efficient ethylene polymerization driven by the π-character of metal–carbon bonds and back donation from a singly occupied molecular orbital

Abstract

While Ti(III) alkyl species are the proposed active sites in Ziegler–Natta ethylene polymerization catalysts, the corresponding well-defined homogeneous catalysts are not known. We report that well-defined neutral β-diiminato Ti(III) alkyl species, namely [Ti(nacnac)(CH₂^tBu)₂] and its alumina-grafted derivative [(Al_sO)Ti(nacnac)(CH₂^tBu)], are active towards ethylene polymerization at moderate pressures and temperatures and possess an electron configuration well-adapted to insertion of ethylene. Advanced EPR spectroscopy showed that ethylene insertion into a Ti(III)–C bond takes place during polymerization from Ti(nacnac)(CH₂^tBu)₂. A combination of pulsed EPR spectroscopy and DFT calculations, based on a crystal structure of [Ti(nacnac)(CH₂^tBu)₂], enabled us to reveal details about the structure and electronic configurations of both molecular and surface-grafted species. For both compounds, the α-agostic C–H interaction, which involves the singly occupied molecular orbital, indicates a π character of the metal–carbon bond; this π character is enhanced upon ethylene coordination, leading to a nearly barrier-less C₂H₄ insertion into Ti(III)–C bonds after this first step. During coordination, back donation from the SOMO to the π*(C₂H₄) occurs, leading to stabilization of π-ethylene complexes and to a significant lowering of the overall energy of the C₂H₄ insertion transition state. In d¹ alkyl complexes, ethylene insertion follows an original “augmented” Cossee–Arlman mechanism that involves the delocalization of unpaired electrons between the SOMO, π*(C₂H₄) and σ*(Ti–C) in the transition state, which further favors ethylene insertion. All these factors facilitate ethylene polymerization on Ti(III) neutral alkyl species and make d¹ alkyl complexes potentially more effective polymerization catalysts than their d⁰ analogues.

---

Introduction

Since the discovery of Ziegler–Natta ethylene polymerization catalysts in the early 1950s,^1,2 the nature of the active site(s) has been a matter of debate. Later, group IV transition-metal metallocenes were developed as efficient homogeneous,^3–7 as well as supported,^8,9 olefin polymerization catalysts for which cationic M(IV) alkyl species have been proposed as the active sites.¹⁰ Such species have been isolated in the form of Lewis base adducts and have been shown to be competent in olefin polymerization; one noteworthy example is Ti(IV) amidinate species [(Cp*)Ti{NC(Ph)NⁱPr₂}(OPPh₃)Me][BArF₄] (Scheme 1a).¹¹ Taking into account the strong ionic character of MgCl₂, the key support of Ziegler–Natta catalysts, surface Ti(IV) cationic alkyl species are sometimes proposed as the active sites in these systems in analogy to their metallocene equivalents.¹²

Scheme 1 Known Ti(IV) (a) and Ti(III) (b) alkyl species, competent in olefin polymerization, together with synthesis of well-defined neutral supported Ti(III) alkyl species 1@Al₂O_3-700 (c) from molecular complex 1via surface organometallic chemistry.

However, the evidence for Ti(IV) cationic species in Ziegler–Natta heterogeneous catalysts has remained elusive. In fact, the reaction with triethyl aluminum, a common cocatalyst used in the Ziegler–Natta process, undoubtedly leads to reduction and/or alkylation of certain sites, and Ti(III) centers have previously been observed by XPS and EPR.^13–18 Since their role as active sites in the polymerization of ethylene has not been evidenced so far, it remains unclear whether or not titanium d¹ complexes can be efficient in ethylene polymerization.^19,20 In parallel, cationic monocyclopentadienyl Ti(III) compounds show high activities towards styrene polymerization and are catalytically comparable to or better than the corresponding Ti(IV) derivatives (Scheme 1b).²¹ Furthermore, it has been recently shown by pulsed EPR spectroscopy, combined with DFT calculations, that Ti(III)-alkyl surface species are formed when silica-supported titanium(III) hydride comes into contact with ethylene.²² This finding is consistent with previous calculations that show Ti(III) hydrides as competent for initiating ethylene polymerization;²³ it further implies that Ti(III) d¹ alkyl complexes could polymerize olefins such as ethylene.

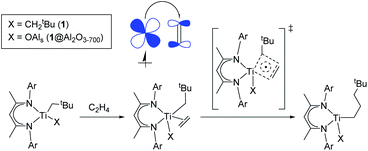
Among well-defined Ti(III) alkyl species, the neutral β-diiminato Ti(III) dialkyl species (Scheme 1c, 1) are noteworthy for their stability.^24,25 While reported to be unreactive towards ethylene polymerization without a cocatalyst at room temperature under 6 bar of ethylene,²⁴ the presence of two alkyl ligands in this compound makes it particularly attractive to generate a supported Ti(III) alkyl catalyst through surface organometallic chemistry (SOMC)²⁶ and to evaluate its polymerization activity. Indeed, SOMC has been shown to provide access to many active and stable catalysts through isolation of metal sites at the surface of oxide supports.^26–29 In addition, the presence of strong Lewis acid surface sites, such as in alumina, can also help promote the formation of more active species.^30–32 Alternatively, cationic surface sites can be stabilized using sulfated metal oxides as a support.^32–34

Herein, we show that the molecular β-diiminato Ti(III) alkyl complex (Scheme 1c, 1) efficiently promotes ethylene polymerization without the need for co-catalysts at 80 °C and pressures higher than 4 bar and that its alumina-supported analogue, prepared via the SOMC²⁶ approach (Scheme 1c, 1@Al₂O_3-700), shows significantly improved productivity. Using pulsed EPR spectroscopy, combined with DFT calculations and polymerization tests, we demonstrate that neutral Ti(III) alkyl species are indeed able to initiate ethylene polymerization to produce ultra-high molecular weight polyethylene via ethylene insertion into a Ti(III)–C bond. Detailed DFT calculations show that ethylene insertion into the Ti(III)–C bond, a key step of ethylene polymerization, is favored by a partial alkylidenic character of the metal–carbon bond, as in its d⁰ analogues,^35,36 and the added possibility of a partial electron transfer to the coordinated olefin in Ti(III) compounds, which can be viewed as the π-back donation from the SOMO into the coordinated ethylene. This “augmented” Cossee–Arlman mechanism of olefin polymerization, possible for d¹ metal-alkyl complexes, involves the delocalization of unpaired electrons in the transition state of olefin insertion into the metal–carbon bond with a strong alkylidenic character.

Results and discussion

Synthesis and characterization of neutral Ti(III) species and examination of their polymerization activity

Synthesis and characterization. The molecular complex [Ti(nacnac)(CH₂^tBu)₂] (nacnac = [Ar]NC(Me)CHC(Me)N[Ar], Ar = 2,6-(CHMe₂)₂C₆H₃), 1 (see Scheme 1c), and its ¹³C-labelled analogue [Ti(nacnac)(¹³CH₂^tBu)₂], 1*, were prepared from [Ti(nacnac)Cl₂] and LiCH₂^tBu or its ¹³C-labeled analogue, Li¹³CH₂^tBu, respectively, according to literature procedures.²⁵ Complex 1 was characterized by NMR (see Fig. S1‡) and room-temperature CW EPR (see Fig. S2‡), consistent with its previous characterization.²⁵ Complex 1 was further grafted onto alumina, partially dehydroxylated at 700 °C (Al₂O_3-700), resulting in material 1@Al₂O_3-700 (Scheme 1c). During grafting, the emerald green solution of 1 becomes colorless, while the alumina support turns grey. This reaction is accompanied by the release of 0.54 equivalents of ^tBuCH₃ per initial surface OH group (for further experimental details see ESI Part 2.1‡).

Elemental analysis of 1@Al₂O_3-700 gives 0.24 wt% Ti, 2.06 wt% C, 0.20 wt% N and 0.24 wt% H, corresponding to 41.0 ± 1 C/Ti (34 expected), 3.4 ± 1 N/Ti (2 expected) and 57.0 H/Ti (52 expected). The grafting of 0.54 Ti per surface OH group is thus consistent with the formation of a monografted species, [(Al_sO)Ti(nacnac)(CH₂^tBu)] (Al_s = surface aluminium). Further characterization of 1@Al₂O_3-700 by Fourier transform infrared spectroscopy (FTIR) shows the disappearance of the initial isolated hydroxyl groups and the appearance of a broad band from 3420 to 3760 cm⁻¹, associated with hydroxyl groups interacting with the ligands of the grafted Ti centres (e.g. nacnac ligand).³⁷ These fragments are also revealed via ν(C–H) vibrations at 3081–2874 cm⁻¹ (Fig. S3‡).

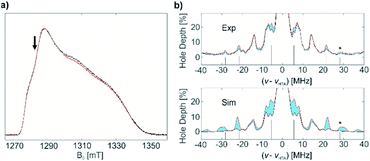
Both materials 1 and 1@Al₂O_3-700 were then characterized with CW EPR spectroscopy. The X-band CW EPR spectrum of complex 1 recorded at 10 K (Fig. 1a, blue) originates from an S = 1/2 electron spin system with a nearly axial g tensor, having its principal values g_x = 1.898 ± 0.023, g_y = 1.981 ± 0.016, and g_z = 1.996 ± 0.012 (the given intervals indicate Gaussian distributions of g principal values; the simulation of the EPR spectrum is shown in Fig. 1a, red).

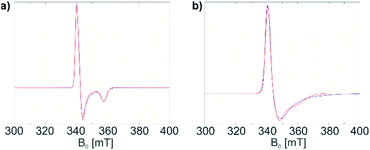Fig. 1 (a) CW EPR spectrum of 1 in a frozen toluene solution (blue) and simulation (red); (b) CW EPR spectrum of 1@Al₂O_3-700 (blue) and simulation (red). See text for simulation parameters.

For the surface-grafted material 1@Al₂O_3-700, the X-band CW EPR spectrum (Fig. 1b blue) was measured at 10 K; the spectrum is consistent with the presence of an S = 1/2 system, with g_x = 1.880 ± 0.087, g_y = 1.970 ± 0.049 and g_z = 1.984 ± 0.016 (the simulation is shown in Fig. 1b, red) associated with a paramagnetic Ti(III) surface species. Significant line broadening is observed in the grafted material 1@Al₂O_3-700 compared to molecular complex 1 which may result from the presence of different Ti³⁺ surface species, possibly due to small differences in local surface environments and thereby coordination geometry. In spite of replacing one Ti-coordinated carbon atom by a more electronegative oxygen atom, the g principal values for both 1 and 1@Al₂O_3-700 agree with each other within the given line widths, thus indicating a similar electronic structure and symmetry of molecular complex 1 and alumina-supported species 1@Al₂O_3-700.

Polymerization activity. We further examined the polymerization activity of 1 and its supported analogues. Molecular complex 1 was found to be active in ethylene polymerization in the temperature range 80–100 °C and at ethylene pressures higher than 4 bar (Fig. 2a). The reaction was carried out in either benzene or toluene solutions. The formation of white films of polyethylene (PE) was observed after 2 hours. Within the range tested, a maximal calculated productivity of 11 kg_PE (mol_Ti h)⁻¹ was achieved at 80 °C under 7 bars of ethylene in toluene solution (Fig. 2a, green). Note that heating a toluene solution of 1 under the same conditions (80 °C), but in the absence of ethylene, showed neither a white film nor the formation of any new species visible by EPR or NMR spectroscopies (Fig. S4‡). We can therefore propose that 1 is a direct precursor of the active species that are formed under ethylene pressure.

Fig. 2 (a) Ethylene consumption of a toluene solution of 1 with time under different pressure and temperature conditions. (b) Molecular weight distribution of polyethylene produced by 1 under 7 bar of ethylene pressure and at 100 °C (blue), together with molecular weight distribution of polyethylene produced by 1@Al₂O_3-700 under 6 bar of ethylene pressure and at 50 °C (red). (c) SEM image of the 1@Al₂O_3-700 material before polymerization. (d) SEM image of the 1@Al₂O_3-700 material after polymerization under 1 bar of ethylene pressure and at room temperature. The changes in ethylene consumption curves up to minute 12 in (a) are due to the pressure changes in the system while reaching the reaction temperature.

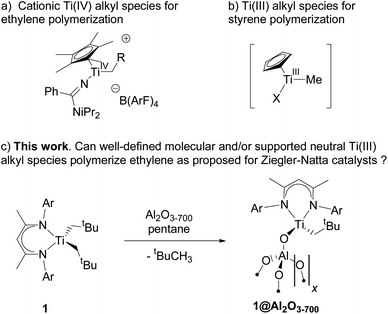
The material 1@Al₂O_3-700 is significantly more active towards ethylene polymerization than its molecular analogue 1, and the polymerization stops within minutes due to the formation of a dense PE layer that can be directly observed with scanning electron microscopy (SEM) (Fig. 2c and d). Overall, this material displays a productivity of ca. 36 kg_PE (mol_Ti h)⁻¹ under 6 bar of ethylene at 50 °C. Note that, in contrast to 1, 1@Al₂O_3-700 initiates ethylene polymerization even under very mild conditions, i.e. room temperature, 80 mbar of ethylene.

The molecular weight distribution for PE, produced by 1 and 1@Al₂O_3-700, is obtained with size-exclusion chromatography (SEC, Fig. 2b). For both catalysts, the distribution is asymmetric with a main heavy fraction and a broad distribution of molecular weights of lighter PE fractions, possibly being the products of chain termination reactions. The main fraction of PE has a molecular weight of ca. 1130 kg mol⁻¹ for 1 and ca. 5660 kg mol⁻¹ for 1@Al₂O_3-700, which is typical for ultra-high molecular weight polyethylene (UHMWPE).³⁸ As the PE molecular weight distribution has similar character for both 1 and 1@Al₂O_3-700, and as UHMWPE is produced in both cases, we propose that the polymerization on both catalysts takes place via a similar mechanism. The higher molecular weight of the main fraction of PE, produced with 1@Al₂O_3-700, can be explained by the absence and/or the slower rate of possible chain termination reactions, one example being the α-H abstraction reaction.

Detailed EPR characterization and evaluation of the structures of 1 and 1@Al₂O_3-700. We further characterize complex 1 and the associated surface species in 1@Al₂O_3-700 by pulse EPR spectroscopy, namely by HYSCORE (Hyperfine Sublevel Correlation Spectroscopy).³⁹ This method was selected for its ability to observe weak hyperfine couplings (e.g. weakly coupled ¹⁴N and ¹H) that are usually not resolved in the CW EPR spectra. The X-band HYSCORE spectra of 1 and 1@Al₂O_3-700, shown in Fig. 3b and d, respectively, were measured at 10 K at the field positions corresponding to the maxima of the echo-detected EPR spectra (Fig. 3a and c; the field positions are marked with arrows). Both spectra shown in Fig. 3b and d were measured with an interpulse delay of τ = 128 ns. The X-band HYSCORE spectra were also measured with three τ values τ = 128 ns, 160 ns and 224 ns to avoid loss of spectral information due to blind spots (see Fig. S5‡ for the τ-summation spectra); however, it appeared that the spectra with τ = 128 ns contained all peak patterns present in the τ-summation spectra except for the ¹H matrix peak, whose suppression is favorable.

Fig. 3 (a) Echo-detected EPR spectrum of a frozen toluene solution of 1; (b) HYSCORE spectrum of 1, τ = 128 ns; (c) echo-detected EPR spectrum of 1@Al₂O_3-700; (d) HYSCORE spectrum of solid 1@Al₂O_3-700, τ = 128 ns. Arrows on the echo-detected EPR spectra (a and c) indicate the magnetic field positions for HYSCORE measurements. Antidiagonal lines on the HYSCORE spectra (b and d) correspond to nuclear frequencies indicated on the spectra (black arrows).

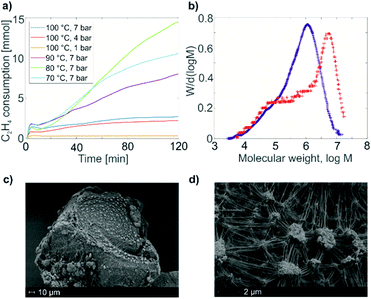
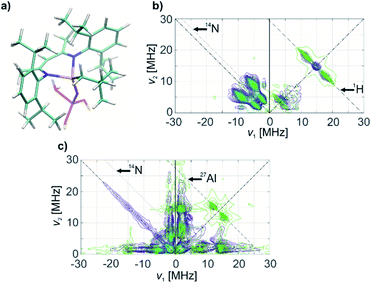
The HYSCORE spectrum of complex 1 (Fig. 3b) shows the presence of ¹H and ¹⁴N nuclei in the Ti(III) coordination sphere, revealed by cross peaks along the ¹H antidiagonal in the weak coupling (+, +) quadrant, corresponding to ¹H hyperfine couplings, and by peaks in the low-frequency region both in the weak coupling (+, +) and strong coupling (−, +) quadrants, corresponding to ¹⁴N hyperfine and quadrupole couplings. For the material 1@Al₂O_3-700, the HYSCORE spectrum (Fig. 3d) reveals the presence of ¹⁴N hyperfine and quadrupole couplings as well, which are close to the ones observed for molecular complex 1 before grafting. This indicates that the (nacnac) ligand remains coordinated to the Ti(III) center after grafting onto the Al₂O_3-700 surface. For 1@Al₂O_3-700, a different set of ¹H hyperfine couplings is observed, with a loss of strongly coupled ¹H being the most prominent change after grafting. Most probably, this is due to the loss of one of the CH₂^tBu ligands upon grafting, as shown in Scheme 1. Furthermore, ²⁷Al couplings are observed for 1@Al₂O_3-700 as a matrix peak on the ²⁷Al antidiagonal line (Fig. 3d) and are well-resolved in Q-band HYSCORE spectra (Fig. 5c). This is consistent with the presence of nearby surface Al atoms in the surroundings of Ti(III), as expected for a grafted species.

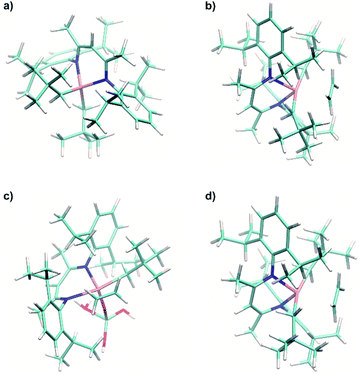
Using the experimental HYSCORE spectra, we could further estimate the conformation of molecular complex 1 in toluene solution and provide detailed structural information regarding the surface species in 1@Al₂O_3-700 by comparing experimental and calculated hyperfine and quadrupole tensors. In order to find the explicit structure of complexes 1 and 1@Al₂O_3-700, the X-ray crystal structures of 1 (ref. 25) (see Fig. S6‡) and the derived model for the species in 1@Al₂O_3-700 were optimized with unrestricted Kohn–Sham density functional theory (DFT), using the functional PBE0 (ref. 40) in ORCA 3.^41,42 For these geometry optimizations, a polarized triple-ζ def2-TZVPP basis set⁴³ was used for all atoms, together with Becke's three-center dispersion correction.⁴⁴ The COSMO continuum solvation model⁴⁵ was applied for complex 1. Furthermore, the hyperfine and quadrupole tensor parameters were calculated with the def2-TZVPP basis set for Ti and Al atoms and the EPR-II basis set⁴⁶ for all other atoms. Based on the calculated parameters, the simulations of HYSCORE spectra were carried out in EasySpin.⁴⁷ Hyperfine and nuclear quadrupole couplings were previously found to be highly sensitive to small structural changes.²² Here we find that rotation of one of the CH₂^tBu ligands of 1 has a tremendous effect on the calculated isotropic part of the ¹H hyperfine tensors of α-H atoms of the CH₂^tBu ligands (see Fig. S7‡). Together with their dipolar part, which is sensitive to the Ti–H distances, the calculated hyperfine tensors act as fingerprints of α-H positions in the calculated structures of 1 and 1@Al₂O_3-700. The calculated multiple-quantum (e.g. double-quantum) ¹⁴N transitions are affected by such a rotation as well (see Fig. S7‡), and hence are an effective probe for the molecular structure and conformation through both hyperfine and quadrupole tensors. This allows us to use DFT-based simulations of the experimental HYSCORE spectra as a tool for evaluation of the molecular structures of 1 and 1@Al₂O_3-700. After such an evaluation, the explicit structures and the Kohn–Sham molecular orbital sets for 1 and 1@Al₂O_3-700 were obtained simultaneously, both verified by a comparison of the experimental and simulated HYSCORE spectra.

The crystal structure of 1, however, does not yield the correct set of ¹H hyperfine coupling parameters, since it fails to fully predict the experimental HYSCORE spectrum (Fig. S6‡). This indicates that complex 1 possesses a different conformation in frozen toluene solution than in the solid state. However, after the geometry optimization using the parameters indicated above, the obtained conformation (Fig. 4a) generates hyperfine and quadrupole tensors for ¹⁴N and ¹H nuclei (Table 1), which simulate the entire X-band HYSCORE spectrum rather nicely (Fig. 4b). Both the isotropic and dipolar parts of ¹H hyperfine tensors fit well to the experimental spectrum in Fig. 4b, thus indicating the correct positions of the α-H atoms of CH₂^tBu ligands in the optimized structure (Fig. 4a). Furthermore, the calculated ¹⁴N hyperfine and quadrupole tensor parameters are found to simulate both the X-band (Fig. 4b) and Q-band (see Fig. S8‡) HYSCORE spectra. We therefore propose that in a frozen toluene solution, molecular compound 1 is present in the form of the conformer shown in Fig. 4a, which differs from the solid-state structure by a slight rotation of the CH₂^tBu ligands around the Ti–C axis (see ESI Part 2.3‡).

Fig. 4 (a) Molecular structure of 1, based on DFT optimizations and on the agreement with HYSCORE spectra. (b) X band HYSCORE spectrum of 1 (blue) and simulation (green), based on DFT calculations on the structure in (a).

Table 1 Calculated hyperfine and quadrupole couplings for EPR active nuclei (in MHz) for the structures of 1 and 1@Al₂O_3-700, together with ²⁷Al hyperfine couplings for 1@Al₂O_3-700, based on least squares fitting of the experimental Q-band HYSCORE spectrum

	1	1@Al2O3-700
^1H	a iso = 7.77	a iso = 5.80
	a dip = [−4.94; −3.08; 8.02]	a dip = [−3.87; −2.57; 6.44]
^1H	a iso = 13.37	a iso = −3.34
	a dip = [−3.85; −2.57; 6.42]	a dip = [7.65; −3.34; −4.30]
^1H	a iso = 18.76	—
	a dip = [−3.93; −2.82; 6.76]
^1H	a iso = 1.27	—
	a dip = [−3.40; −5.71; 9.11]
^14N	a iso = −7.98	a iso = −6.37
	a dip = [2.05; 1.74; −3.79]	a dip = [0.61; −0.17; −0.43]
	P = 2.72 (η = 0.316)	P = 2.50 (η = 0.470)
^14N	a iso = −7.07	a iso = −7.03
	a dip = [1.08; 0.74; −1.82]	a dip = [0.80; 0.50; −1.30]
	P = 2.69 (η = 0.276)	P = 2.60 (η = 0.354)
^27Al (least squares fit)	—	a iso = 2.68
		a dip = [−2.23; 3.56; −1.34]
		P = 7.66 (η = 0.01)

---

A similar approach of evaluating the molecular structure was used for the grafted species 1@Al₂O_3-700. We considered two possible types of 1@Al₂O_3-700 species, either neutral [(Al_sO)Ti(nacnac)(CH₂^tBu)] surface Ti complexes obtained via grafting of 1 through surface OH groups (Scheme 1c) or cationic [Ti(nacnac)(OAl_s)]⁺⋯[(CH₂^tBu)Al_s]⁻ where the alkyl group is transferred onto alumina (see Fig. S9‡) as previously observed for other complexes.^31,48,49 Geometry optimizations with subsequent calculations of EPR parameters were performed for both cationic and neutral models. It appeared that the cationic model, however, does not result in ¹H hyperfine couplings that are strong enough to simulate the elongated experimental HYSCORE ridges (see Fig. S9‡). The α-H atoms of the CH₂^tBu fragment in this model are far from the Ti center such that both dipolar and isotropic parts of the ¹H hyperfine tensors appear too small (see ESI Part 2.3‡). Only the neutral models exhibit ¹H hyperfine couplings that are strong enough to simulate the experimental HYSCORE spectrum.

The geometry optimization of the neutral [(Al_sO)Ti(nacnac)(CH₂^tBu)] model was performed as described above for complex 1, followed by a DFT-based calculation of EPR parameters. The complex nature of the Al₂O₃ surface results in a number of different types of OH groups that can participate in grafting.³¹ Here, we represent the (OH)Al_s surface atom by the simplest possible tetracoordinated neutral Al model, namely (HO)Al_s = (HO)Al(OH)₂(H₂O). Within this approximation, the symmetry of the {AlO₄} cluster may be decreased compared to the structure of an alumina surface center due to different Al–OH₂ and Al–OH bond lengths; this may result in overestimation of quadrupole coupling for the ²⁷Al nucleus. Furthermore, it is worth noting that the spin density on Al nuclei tends to be underestimated even with basis sets that contain diffuse functions, which are expected to better describe spin density near the nucleus.⁵⁰ Taking this into account, it appeared to be better to rely on experimentally determined ²⁷Al hyperfine and quadrupole couplings rather than to evaluate these from DFT calculations.

The ¹H and ¹⁴N couplings (Table 1) computed for the thus-obtained model (Fig. 5a) simulate the experimental X-band HYSCORE spectrum quite well (Fig. 5b). Similar to molecular complex 1, this indicates the correct positions of α-H atoms of a CH₂^tBu ligand in the optimized structure. Although ²⁷Al couplings are not detected in the X-band HYSCORE spectrum, Q-band HYSCORE (Fig. 5c) provides the necessary information to determine the ²⁷Al hyperfine couplings by least squares fitting (Fig. S10‡). Together with the calculated ¹⁴N hyperfine couplings, they fit reasonably to the Q-band HYSCORE spectrum (Fig. 5c, green). This allows us to consider the obtained model (Fig. 5a) as an explicit structure of Ti(III) surface species observed in our EPR studies. Therefore, we confirm that grafting of 1 onto the Al₂O_3-700 surface yields a neutral Ti(III) alkyl species, namely [(Al_sO)Ti(nacnac)(CH₂^tBu)], with the structure shown in Fig. 5a. The production of UHMWPE by 1@Al₂O_3-700 as well as by 1, together with a high polymerization activity of 1@Al₂O_3-700, is consistent with a predominant presence of Ti(III) neutral alkyl species on the Al₂O_3-700 surface after grafting.

Fig. 5 (a) Model for 1@Al₂O_3-700 species representing a neutral [(Al_sO)Ti(nacnac)(CH₂^tBu)] complex based on agreement with HYSCORE spectra. (b) X-band HYSCORE spectrum of 1@Al₂O_3-700 (blue) and simulation (green), based on DFT calculations on the obtained model. (c) Q-band HYSCORE spectrum of 1@Al₂O_3-700 (blue) and simulation (green), based on DFT computed EPR parameters from the obtained model (a) for ¹⁴N, combined with EPR parameters for ²⁷Al, obtained from a least squares fit of the experimental spectrum. The ridge on the anti-diagonal in the left quadrant is due to an echo crossing that was not fully suppressed by phase cycling.

¹³C labelling as a tool to probe Ti-alkyl chains and the polymerization mechanism. In order to gain further insight into the polymerization mechanism and the active state of the catalyst, we performed EPR studies on the molecular complex [Ti(nacnac)(CH₂^tBu)₂] after reaction with C₂H₄, in combination with ¹³C isotope labelling. Among two possible labelling schemes (Scheme S1‡), we decided to use the one that involves the reaction of non-labelled ethylene with selectively ¹³C-labelled complex [Ti(nacnac)(¹³CH₂^tBu)₂] (1*) and that should yield (Ti^III–(CH₂CH₂)_n−1(¹³CH₂^tBu)) with a labelled ¹³CH₂^tBu terminating group. This reaction should lead to reduction of the initial ¹³C signal intensity in the EPR spectra of 1*, which may be observed with pulse hyperfine EPR methods and interpreted by comparison of the spectra before and after the reaction. Using the alternative labelling scheme, which involves the reaction of ¹³C labelled ethylene with the unlabelled complex [Ti(nacnac)(CH₂^tBu)₂] (1), proved to be difficult and did not allow the detection of ¹³C hyperfine couplings (see the ESI‡ for details), possibly due to a broad distribution of conformations associated with the flexibility of PE ligands ((¹³CH₂)_n(CH₂^tBu)). Such distribution would result in a broad set of ¹³C hyperfine couplings and thereby broad spectral lines unobservable in our hyperfine EPR experiments.

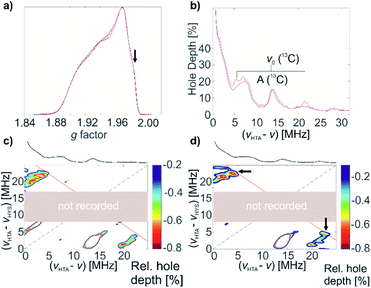
¹³C-labeled complex 1* was characterized by pulse EPR spectroscopy. It exhibits the same echo-detected EPR spectrum and, consequently, the same g tensor parameters as non-labelled complex 1 (Fig. 6a). Detection of the ¹³C couplings of the coordinating (¹³CH₂^tBu) ligands proved difficult. According to DFT calculations for the optimized structure of 1 (Fig. 4a), the ¹³C hyperfine tensors for both α-C atoms of (¹³CH₂^tBu) ligands of complex 1* show large couplings that are mostly isotropic (a_iso = −20.51 MHz, a_dip = [1.26 0.54 –1.80] MHz and a_iso = −21.69 MHz, a_dip = [1.52 0.50 –2.01] MHz for the two ¹³C nuclei). This leads to a low probability of the forbidden electron-¹³C-nuclear spin transitions, making direct observation of the ¹³C signals with ESEEM-based techniques (e.g. HYSCORE) difficult (in the Q band) or impossible (in the X band). Furthermore, strong ¹⁴N ESEEM modulations in both the X- and Q-band may suppress the ¹³C modulations due to a cross-suppression effect.⁵¹ For this reason, we used an alternative EPR methodology based on the recently developed hyperfine technique CHEESY-detected NMR (CHEESY = chirp echo EPR spectroscopy).⁵² This method is based on long selective hole burning pulses that drive forbidden transitions, similar to ELDOR-detected NMR, but the detection is based on broadband chirp echoes and subsequent Fourier transform. This leads to a multiplex advantage and, consequently, to higher sensitivity (see ESI Part 2.4‡ for more details). Indeed, the ¹³C signals were observed already in the 1D CHEESY-detected NMR spectrum of 1*, revealed in comparison with the same spectrum of non-labelled complex 1 where the ¹³C signals were not observed (Fig. 6b).

Fig. 6 (a) Q-band echo-detected EPR spectra of 1 (blue) and 1* (red), intensities normalized; the position of further measurements is indicated with an arrow. (b) 1D CHEESY-detected NMR spectra of 1 (blue) and 1* (red); the ¹³C signals are marked on the spectrum. (c) Q-band 2D CHEESY-detected NMR spectrum of 1; the ¹³C nuclear Zeeman frequency is shown by a red antidiagonal line. (d) Q-band 2D CHEESY-detected NMR spectrum of 1*; the ¹³C nuclear Zeeman frequency is shown by a red antidiagonal line along which cross peaks due to ¹³C hyperfine coupling are observed (marked with arrows). The gray area has not been recorded during the experiment in order to optimize sensitivity and the spectra were recorded at slightly different fields and frequencies.

These ¹³C signals, observed at the orientation corresponding to g = 1.983 (Fig. 6a, marked with an arrow), are better resolved in two-dimensional HYSCORE-type CHEESY-detected NMR spectra (Fig. 6c and d), which are obtained by applying a selective π pulse with variable frequency before the HTA pulse (see ESI Part 2.4‡ for the details of CHEESY-detected NMR experiments). The comparison of the spectra for 1 (Fig. 6c) and 1* (Fig. 6d) reveals the peaks at (21, 5) MHz, corresponding to the signals of ¹³C in [Ti(nacnac)(¹³CH₂^tBu)₂]. Based on the obtained spectra (Fig. 6b–d), the ¹³C hyperfine coupling was estimated to be a_iso(¹³C) = 16 MHz. This allowed us to confirm the assignment by Q-band HYSCORE and Q-band Davies ENDOR⁵³ (see Fig. S11‡), where the weak spectral signals corresponding to ¹³C hyperfine couplings were identified by comparison to the 1D- and 2D-CHEESY detected NMR spectra.

Next, a benzene solution of 1* was brought into contact with C₂H₄ (1000 equivalents) at 80 °C for 2 hours. After the reaction, the excess C₂H₄ was removed and EPR measurements of (1* + C₂H₄) were performed. The similarities in the echo-detected Q-band EPR spectra (Fig. 7a) of complex 1* before and after polymerization indicate similar g tensor parameters consistent with conservation of the symmetry of Ti(III). Using the same methodology as before, 1D CHEESY-detected NMR spectra before and after the polymerization were measured (Fig. 7b) at the same frequency and field positions, with an identical microwave resonator profile (Fig. S12‡). Although the absolute echo intensities for both samples may still be slightly different, the CHEESY-detected NMR signals, being essentially the ratio of the spectra with and without a high turning-angle pulse, can be considered a quantitative tool to probe the amount of EPR active nuclei in the Ti(III) coordination sphere before and after the reaction with C₂H₄.

Fig. 7 (a) Q-band echo-detected EPR spectra of 1* (red) and 1* + C₂H₄ (black), intensities normalized; the position of further measurements is indicated by an arrow. (b) Top: experimental 1D CHEESY-detected NMR spectra of 1* (red) and 1* + C₂H₄ (black); no normalization was applied. Bottom: simulated 1D CHEESY-detected NMR spectra of 1* (red) and 1 (black). ¹³C signals, corresponding to A(¹³C) = 16 MHz are marked with lines under the spectra; the combination signal of (¹³C + ¹⁴N) is marked with an asterisk. The difference between the spectra due to difference in ¹³C signal intensities is colored in blue.

An obvious decrease of the ¹³C signal intensity is observed after polymerization (Fig. 7b, top) for all previously observed ¹³C lines of 1*, corresponding to a_iso(¹³C) = 16 MHz, as well as for the combination signal of (¹³C + ¹⁴N). At the same time, the spectral lines, determined by ¹⁴N hyperfine and quadrupole couplings (e.g. double-quantum ¹⁴N signals around 14 MHz), are the same before and after polymerization both regarding their frequencies and intensities. Since the frequencies of these ¹⁴N signals are sensitive even to small changes in the structure and conformation of 1* (see Fig. S7‡) we can conclude that the structure of the Ti(III) coordination sphere experiences minimal change upon polymerization. These ¹⁴N signals were reasonably simulated with the calculated values for the previously estimated conformation of 1 (Fig. 4a) in the spectra both before and after polymerization of ethylene (Fig. 7b, bottom). Together with the observed decrease of the ¹³C signal intensity, this indicates that ligand exchange of ¹³CH₂^tBu to (CH₂CH₂)_n−1(¹³CH₂^tBu) occurs with preservation of the initial structure and conformation of 1*. Indeed, the experimentally observed decrease of ¹³C signals is simulated well as a difference between 1D CHEESY-detected NMR simulations for labelled complex 1* and non-labelled complex 1 (Fig. 7b, bottom). To that end, the experimental a_iso(¹³C) = −16 MHz, together with DFT computed a_dip(¹³C) parameters, was used for the simulation of the spectrum of 1* (see ESI Part 2.4‡ for the details of the simulation). The comparison of the simulated and experimentally observed decrease of the ¹³C signal intensity implies that probably not all the complex 1* present is affected by the ligand exchange, but only a part of it. This indicates that only a part of molecules of 1* acts as active centres of ethylene polymerization under the aforementioned reaction conditions. This is consistent with the presence of an induction period at the beginning of polymerization, revealed by changes in ethylene consumption (Fig. 2a). It is also consistent with the calculated energy barrier for the first olefin insertion (vide infra). An exact quantification is difficult without precise knowledge of the full ¹³C hyperfine tensor, which also affects line intensities.

Based on the discussed experimental results, we propose that olefin polymerization takes place via C₂H₄ insertion into the Ti(III)–C bond in the molecular system Ti(nacnac)(CH₂R)₂–1. Unfortunately, we were not able to study ethylene polymerization with 1@Al₂O_3-700 due to T₂ electron spin relaxation times, which are ca. 6 times shorter for 1@Al₂O_3-700 than for 1. This limits the observation window length and, consequently, the resolution of CHEESY-detected NMR²⁶ such that the separation of ¹³C, ¹⁴N and ²⁷Al signals becomes rather uncertain. However, the molecular weight distributions of produced PE are quite close for both 1 and 1@Al₂O_3-700, with UHMWPE being produced in both cases. This indicates a similar type of active center and polymerization mechanism for both catalysts. As we determined a neutral [(Al_sO)Ti(nacnac)(CH₂^tBu)] species to be present in 1@Al₂O_3-700, which is similar in terms of structure and electronic properties to molecular complex 1, we propose that ethylene polymerization on 1@Al₂O_3-700 proceeds via the same mechanism as for 1, i.e. through C₂H₄ insertion into the Ti(III)–C bond in [(Al_sO)Ti(nacnac)(CH₂^tBu)].

Electronic structures and the polymerization mechanism for 1 and 1@Al₂O_3-700

α-Agostic C–H interaction and π character of Ti–C bonds of 1 and 1@Al₂O_3-700. The estimated structure of molecular complex 1 (Fig. 4a) is notable because of the presence of unusually small Ti–C–H angles in both Ti alkyls. These angles of 95.56° and 96.95° are associated with relatively short Ti⋯H distances (2.500 Å and 2.503 Å, respectively) as well as with elongated C_α–H distances (up to 1.104 Å and 1.107 Å, respectively), in comparison with typical distances of 1.091–1.103 Å for all the other aliphatic C–H distances in 1. Such observations are consistent with the presence of so-called α-agostic C–H bonds in this Ti(III) compound. A similar, but weaker, α-H agostic Ti⋯H interaction is found for the refined structure of alumina-grafted neutral species [(Al_sO)Ti(nacnac)(CH₂^tBu)] of 1@Al₂O_3-700 (further named 1@Al₂O_3-700), with one of the α-H atoms of the CH₂^tBu ligand having a Ti–C–H angle of 101.80° and a Ti–H distance of 2.603 Å.

Essentially, α-agostic C–H bonds are described^35,54 as the donation of electrons from the filled molecular orbital corresponding to the C–H bond to a metal d-orbital of appropriate symmetry that is empty for d⁰ metals. This agostic interaction has been recently related to a metal–carbon bond acquiring a π (or alkylidene) character,^35,55 which favors the olefin insertion process. The degree of this π character could be indirectly estimated from the deviation of the Ti–C–H angle from 109° towards ca. 90°. In order to estimate directly the π character of Ti(III)–C bonds of 1 and 1@Al₂O_3-700, a Natural Bond Orbital (NBO) analysis⁵⁶ was performed, using the program NBO 7.0.⁵⁷ The molecular orbital sets for NBO analyses were generated using ORCA 4 (ref. 42) with the same parameters for the DFT calculations as the ones used for the simulations of the HYSCORE spectra (PBE0 functional together with the def2-TZVPP basis set for Ti and Al atoms and EPR-II basis set for all other atoms). Given the good agreement between the measured and calculated HYSCORE spectra, this computational method describes the electronic structures of 1 and 1@Al₂O_3-700 with sufficient accuracy.

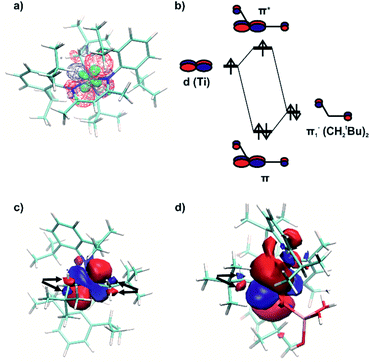
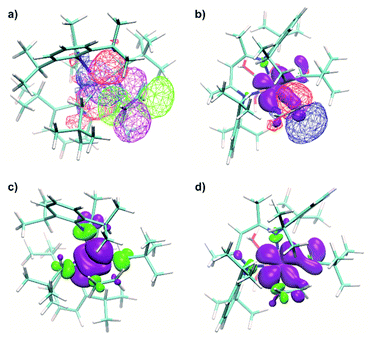
The NBO analysis revealed a natural orbital, related to a singly occupied molecular orbital (SOMO) of paramagnetic complex 1 (Fig. 8a, red and blue). Its shape correlates well with the calculated distribution of spin density in space (Fig. 8a, green), thus confirming the close relation of this natural orbital to the SOMO. This orbital is nearly axially symmetric, which is consistent with the experimentally observed axial symmetry of the g tensor.

Fig. 8 (a) A natural spin-α orbital, related to the SOMO of 1 (red for positive and blue for negative signs of the wavefunction, the same in all the panels), together with the spin density distribution (green). (b) Qualitative molecular orbital diagram, illustrating the formation of the π*(Ti–(CH₂^tBu)₂) orbital being the SOMO component of 1. (c) Natural SOMO of 1 as visible from the (CH₂^tBu)₂ side, showing a central d-type part and two carbon p-type parts (marked with arrows). (d) Natural SOMO of 1@Al₂O_3-700, showing a carbon p-type part (marked with arrows).

The spatial distribution of the SOMO-related natural orbital of 1 includes four lobes of the p-type on two nitrogen atoms and two carbon atoms of CH₂^tBu ligands, all being in antiphase with the central d-type lobes (Fig. 8a and c). The part of this orbital, which includes the central d-type part and the two carbon p-type parts (Fig. 8c), can be understood as a product of interaction of the half-filled d_xy-type Ti orbital and one of two degenerate filled π⁻ orbitals of the (CH₂^tBu)₂ fragment (Fig. 8b). This orbital features π* symmetry with respect to the Ti–C bond.

Therefore, the presence of the π* orbital, as part of the SOMO and delocalized between two CH₂^tBu ligands, reveals the existence of π bonding in Ti–(CH₂^tBu)₂. This π interaction, although being weakened by the unpaired electron in the antibonding π* orbital (Fig. 8b), stabilizes the structure with the α-agostic C–H bonds for 1. Compared to metal d⁰ complexes³⁵ this α-H agostic interaction involves a half-filled metal d orbital instead of an empty one, as revealed by the NBO analysis for the refined structure of 1. Such an interaction brings a π character into both Ti–C bonds of 1. This π character is also evidenced by the deviation of the natural hybrid orbital (NHO) on carbon from the Ti–C axis (θ_NHO–C–Ti = 15.0° and 14.4° for the two Ti–C bonds of 1) – for a pure σ-bond no deviation would be expected (0.0°).³⁵

A natural orbital of similar type, including a p-type lobe on the carbon atom of the single CH₂^tBu ligand, is also found for 1@Al₂O_3-700 (Fig. 8d). This indicates the presence of a π* orbital and, consequently, a π interaction in the [Ti–(CH₂^tBu)] system. However, the π character acquired by the Ti–C bond of 1@Al₂O_3-700 is less pronounced compared to that of complex 1 (θ_NHO–C–Ti = 9.2° for 1@Al₂O_3-700). The described π interaction, which involves half-filled metal d orbitals, might be present for all paramagnetic transition metal alkyl complexes, provided that the corresponding half-filled d orbitals have appropriate symmetry.

Olefin polymerization pathways of 1 and 1@Al₂O_3-700. The presence of π character in the metal–carbon bonds has been found to play a crucial role in the reactivity of d⁰ compounds, making them reactive towards olefin insertion.³⁵ It was also used as an explanation for C–H activation pathways, including α-H abstraction in dialkyl compounds, that have been shown to be isolobal reactions.⁵⁸ Indeed, the α-H abstraction is a known synthetic pathway of Ti(IV) d⁰ alkylidenes, prepared via oxidation of 1 by AgOTf.²⁵ However, the transition state (TS) energy for the α-H abstraction process for d¹ complex 1, calculated in ORCA 3 (ref. 41) with the same DFT parameters as the ones used for ground state optimizations, was found to be relatively high (ΔH^‡₂₉₈ = 31.5 kcal mol⁻¹; ΔG^‡₂₉₈ = 31.5 kcal mol⁻¹, Fig. S13‡). This should make the process slow and indicate the relative stability of 1 even under the elevated temperatures used in ethylene polymerization. In contrast, the transition state for C₂H₄ insertion into the Ti(III)–C bond of 1 (Fig. S13‡) appeared to have an overall energy barrier with respect to the initial reagents (1 + C₂H₄) of ΔH^‡₂₉₈ = 22.5 kcal mol⁻¹ and ΔG^‡₂₉₈ = 33.7 kcal mol⁻¹. The large difference of 9.0 kcal mol⁻¹ in the TS enthalpies (ΔH^‡₂₉₈) suggests that the reaction of C₂H₄ insertion into the Ti(III)–C bond is more facile than α-H abstraction. Looking at the free energy, where entropy factors in solution are typically overestimated,⁵⁹ one would expect that both processes can be competitive. Overall, the calculated ΔH^‡₂₉₈ and ΔG^‡₂₉₈ values of the ethylene insertion for complex 1 are consistent with a slow polymerization reaction at 80 °C as well as the need to use high pressure to conduct the reaction. In fact, similar calculated energetics are reported for the Ti(IV) homogeneous catalysts of ethylene polymerization (e.g. ΔH^‡₂₉₈ and ΔG^‡₂₉₈ = 16 and 28 kcal mol⁻¹, respectively, for the [H₂Si(C₅H₄)(^tBuN)]TiCH₃⁺⋯H₃CB(C₆F₅)₃⁻ ion pair⁶⁰). This supports our experimental evidence of ethylene insertion into the Ti(III)–C bond as the mechanism of ethylene polymerization of molecular catalyst 1.

It is noteworthy that for the model Ti(IV) cationic analogue of complex 1, namely [Ti(nacnac)(CH₂^tBu)₂]⁺ (1⁺), the ethylene insertion reaction is predicted to be less favorable compared to the α-H abstraction process, as revealed by calculations on the optimized structure (Fig. 9a). The calculated energy barrier for the α-H abstraction in d⁰ complex 1⁺ is ΔH^‡₂₉₈ = 29.7 kcal mol⁻¹ and ΔG^‡₂₉₈ = 30.3 kcal mol⁻¹, being slightly less than the one calculated for d¹ complex 1. This is consistent with a stronger degree of π character in the Ti–C bonds (θ_NHO–C–Ti = 23.5° and 17.5° for the two Ti–C bonds) of 1⁺. For ethylene insertion involving 1⁺, the TS barrier is ΔH^‡₂₉₈ = 28.3 kcal mol⁻¹ and ΔG^‡₂₉₈ = 41.7 kcal mol⁻¹ with respect to the initial reagents. Despite having a stronger degree of π character of the Ti–C bonds, the TS energy of ethylene insertion is strongly increased by ΔG = + 8.0 kcal mol⁻¹ for the d⁰ complex compared to the analogous d¹ complex. This indicates that the unpaired electron in a singly occupied molecular orbital of complex 1 plays an important role in its reactivity towards ethylene insertion, significantly lowering the TS energy for d¹ active species compared to similar d⁰ species.

Fig. 9 (a) Calculated structure of the model Ti(IV) complex [Ti(nacnac)(CH₂^tBu)₂]⁺ (1⁺). (b) Calculated structure of π-ethylene complex 1⋯C₂H₄. (c) Calculated structure of π-ethylene complex 1@Al₂O_3-700⋯C₂H₄. (d) Calculated structure of model Ti(IV) π-ethylene complex 1⁺⋯C₂H₄.

For the neutral supported alkyl species in 1@Al₂O_3-700, the overall energy barriers for C₂H₄ insertion into the Ti–C bond are ΔH^‡₂₉₈ = 16.7 kcal mol⁻¹ and ΔG^‡₂₉₈ = 29.7 kcal mol⁻¹ and thus both are lower than those found for molecular complex 1. This is consistent with the high polymerization activity of 1@Al₂O_3-700.

Ethylene insertion into the Ti–C bonds for both 1 and 1@Al₂O_3-700 follows the formation of π-ethylene complexes. The structures of the complexes 1⋯C₂H₄ (Fig. 9b) and [(Al_sO)Ti(nacnac)(CH₂^tBu)(C₂H₄)] (1@Al₂O_3-700⋯C₂H₄, Fig. 9c) were obtained through DFT geometry optimizations along the TS imaginary modes (see ESI Part 2.6‡ for details of the optimization). These structures are close to those of the transition states for C₂H₄ insertion (see Fig. S13‡) with two CH₂^tBu ligands being trans to each other for complex 1⋯C₂H₄ and with the CH₂^tBu ligand being trans to the Ti–N bond of the nacnac ligand for complex 1@Al₂O_3-700⋯C₂H₄. In fact, for complex 1⋯C₂H₄, the calculated enthalpy and Gibbs free energy of formation with respect to the initial reagents (1 + C₂H₄) are ΔH⁰₂₉₈ = 21.4 kcal mol⁻¹ and ΔG⁰₂₉₈ = 34.0 kcal mol⁻¹ and very close to those of the TS (the corresponding TS energies are ΔH^‡₂₉₈ = 1.1 kcal mol⁻¹ and ΔG^‡₂₉₈ = −0.3 kcal mol⁻¹ with respect to the 1⋯C₂H₄ complex). The same is found for the 1@Al₂O_3-700⋯C₂H₄ π complex, with its CH₂^tBu ligand being trans to the Ti–N bond of the nacnac ligand. With ΔH⁰₂₉₈ = 16.4 kcal mol⁻¹ and ΔG⁰₂₉₈ = 28.2 kcal mol⁻¹ the energy barriers remaining to reach the TS are almost zero and calculated to be ΔH^‡₂₉₈ = 0.3 kcal mol⁻¹ and ΔG^‡₂₉₈ = 1.5 kcal mol⁻¹. Therefore, the energy cost for ethylene polymerization is mostly due to the initial formation of the π complexes followed by an almost barrier-less insertion, which is again in agreement with the observed induction period. The relatively high barrier of formation of the π-ethylene complex 1⋯C₂H₄ could be overcome by elevated ethylene pressure and increased temperature; this is consistent with the high temperatures and pressures (e.g. 80 °C, 7 bar) required for efficient polymerization on 1 (see Fig. 2a).

For the calculated Ti(IV) model cationic complex [Ti(nacnac)(C₂H₄)(CH₂^tBu)₂]⁺ (1⁺⋯C₂H₄, Fig. 9d), the TS energy of ethylene insertion with respect to this complex is close to that of its d¹ analogue 1⋯C₂H₄ (ΔH^‡₂₉₈ = 0.9 kcal mol⁻¹ and ΔG^‡₂₉₈ = 2.4 kcal mol⁻¹). Again, as soon as a π-ethylene complex is formed, the ethylene insertion into the Ti–C bond is nearly barrier-less; this behavior occurs in both d¹ and d⁰ complexes. At the same time, while the structure is similar to that of the 1⋯C₂H₄ complex, the formation energy of 1⁺⋯C₂H₄ is much higher than that for 1⋯C₂H₄ (ΔH⁰₂₉₈ = 27.4 kcal mol⁻¹, ΔG⁰₂₉₈ = 39.3 kcal mol⁻¹). We thus further examine the π-ethylene complexes 1⋯C₂H₄, 1⁺⋯C₂H₄ and 1@Al₂O_3-700⋯C₂H₄via NBO analyses.

Back donation from the unpaired electron orbital and the enhanced π character in Ti–C bonds of the π-ethylene complexes support the “augmented” Cossee–Arlman polymerization mechanism. For both 1⋯C₂H₄ and 1@Al₂O_3-700⋯C₂H₄, the degree of the π character of the Ti–C bonds may be indirectly estimated through the corresponding Ti–C–H angles in the calculated structures of the complexes, which acts as a marker of the α-agostic C–H interaction. For the complex 1⋯C₂H₄, the corresponding acute angles are 85.73° for the shortened (2.188 Å) Ti–C bond and 82.04° for the elongated (2.239 Å) Ti–C bond. For 1@Al₂O_3-700⋯C₂H₄, the Ti–C–H angle is 90.30°. This points towards an increase of the π character in the metal–carbon bonds in the 1⋯C₂H₄ and 1@Al₂O_3-700⋯C₂H₄ complexes compared to the initial 1 and 1@Al₂O_3-700.

The degree of π character in Ti–C bonds of both the π complexes is further shown via the deviation of the corresponding NHO on C from the Ti–C axis, being θ_NHO–C–Ti = 31.3° for the shortened and 38.5° for the elongated Ti–C bonds of 1⋯C₂H₄, and θ_NHO–C–Ti = 26.1° for the Ti–C bond of 1@Al₂O_3-700⋯C₂H₄. For the Ti(IV) 1⁺⋯C₂H₄ complex, these values are θ_NHO–C–Ti = 25.6° and 39.7° for the two Ti–C bonds, being close to the ones for 1⋯C₂H₄. Therefore, a significant increase of the π character is observed for both d¹ and model d⁰ π-ethylene complexes. These values are close to the ones previously found for the cationic Zr(IV) and Ti(IV) d⁰ complexes [Cp₂MEt(C₂H₄)]⁺, with θ_NHO–C–Ti = 40.9° for M = Ti and θ_NHO–C–Ti = 40.4° for M = Zr.³⁵ Note that all mentioned π-ethylene complexes, while having an enhanced degree of the π character in their Ti–C bonds, provide nearly barrier-less ethylene insertion with rather low calculated or reported³⁵ TS energies. This indicates that ethylene insertion in neutral Ti(III) alkyl species or cationic Ti(IV) and Zr(IV) alkyls depends on the extent of the π character in Ti–C bonds. Therefore, a strong π character is a general reason for the facile ethylene insertion in d¹ and d⁰ metal alkyl complexes after the coordination of C₂H₄.

It is noteworthy that for Ti(III) d¹ complexes 1 and 1@Al₂O_3-700 “back donation” of the unpaired electron from a SOMO to the π* orbital of coordinated C₂H₄ is also involved in the insertion process. These two orbitals have a constructive overlap, as revealed by the NBO analysis for complex 1⋯C₂H₄via the overlap of negative parts of the corresponding natural orbitals (Fig. 10a). This results in some weakening of the C=C double bond of the C₂H₄ ligand (C–C distance is 1.344 Å compared to the calculated value of 1.333 Å for free ethylene), together with a population of the π*(C₂H₄) orbital (see ESI Part 2.7‡). The NBO energetic analysis reveals the stabilization effect, caused by the presence of a π*(C₂H₄) orbital in 1⋯C₂H₄, of 30.0 kcal mol⁻¹. At the same time, the stabilization effect, caused by the presence of the π*(C₂H₄) orbital in the d⁰1⁺⋯C₂H₄ complex, is 23.1 kcal mol⁻¹. Therefore, the energy of the back donation of unpaired electron density in 1⋯C₂H₄ could be estimated through the difference of these two as a stabilization by 6.9 kcal mol⁻¹, consistent with the difference of formation enthalpies ΔH⁰₂₉₈ of 1⋯C₂H₄ and 1⁺⋯C₂H₄ of 6.0 kcal mol⁻¹. This indicates that the back donation of the unpaired electron from the SOMO to the π* orbital of C₂H₄ is the main reason for relative stabilization of the π-ethylene complex 1⋯C₂H₄ compared to its d⁰ analogue 1⁺⋯C₂H₄. As the TS energies of ethylene insertion after the formation of π-ethylene complexes 1⋯C₂H₄ and 1⁺⋯C₂H₄ differ only by 2.7 kcal mol⁻¹ (ΔG^‡₂₉₈ = −0.3 kcal mol⁻¹ for 1⋯C₂H₄, compared to ΔG^‡₂₉₈ = 2.4 kcal mol⁻¹ for 1⁺⋯C₂H₄), the principal reason for the lowering of the overall TS energy for d¹ catalyst 1 by ΔG = 8.0 kcal mol⁻¹ is the back donation of the unpaired electron to the π* orbital of C₂H₄.

Fig. 10 (a) Natural orbital, related to a SOMO (red for positive and blue for negative signs of the wavefunction), together with a natural orbital, related to π*(C₂H₄) (purple for positive and green for negative signs of the wavefunction) of 1⋯C₂H₄. (b) Calculated spin density distribution (purple for positive and green for negative, contour levels 0.2%), together with the natural orbital, related to π*(C₂H₄) (red for positive and blue for negative signs of the wavefunction), of the 1@Al₂O_3-700⋯C₂H₄ complex. (c) Calculated spin density distribution (purple for positive and green for negative signs, contour levels 0.1%) for the TS of ethylene insertion for 1. (d) Calculated spin density distribution (purple for positive and green for negative signs, contour levels 0.1%) for the TS of ethylene insertion for 1@Al₂O_3-700. The degree of delocalization of the unpaired electron could be estimated from the spin density distribution in the first coordination sphere of Ti, including ethylene.

An even higher degree of back donation to π*(C₂H₄) is observed for the 1@Al₂O_3-700⋯C₂H₄ complex, since a strong spin density transfer from the initial SOMO to π*(C₂H₄) is revealed by the calculated spin density distribution (Fig. 10b). Similar to the molecular 1⋯C₂H₄ complex, this leads to a weakening of the C=C double bond of the C₂H₄ molecule (C–C distance is 1.364 Å) and to the appearance of a bonding interaction between Ti in 1@Al₂O_3-700 and C₂H₄. In fact, NBO analysis, being one of the possible ways of representation of the electronic structure of 1@Al₂O_3-700⋯C₂H₄, shows a breaking of the π system of ethylene, followed by formation of a bonding set of natural orbitals, corresponding to a Ti–C(C₂H₄) bond (Fig. S14 and Table S2‡), and a partially occupied natural lone pair on the other carbon atom of C₂H₄, derived from π*(C₂H₄) (Fig. 10b). This indicates more favorable coordination of C₂H₄ to 1@Al₂O_3-700 where the stronger back donation in 1@Al₂O_3-700⋯C₂H₄ is caused by better orbital overlap between the initial SOMO and π*(C₂H₄). The better overlap between the SOMO and π*(C₂H₄) in the supported catalyst is mostly caused by the difference in geometry of the π-ethylene complexes induced by replacing one of the strong σ-donor alkyl ligands (CH₂^tBu) by a weaker O anionic surface ligand OAl_s. This is consistent with the lower formation energy of 1@Al₂O_3-700⋯C₂H₄ of ΔH⁰₂₉₈ = 16.4 kcal mol⁻¹ compared to ΔH⁰₂₉₈ = 21.4 kcal mol⁻¹ for complex 1 and with the ability of 1@Al₂O_3-700 to catalyze ethylene polymerization under milder conditions.

In fact, the unpaired electron in the 1@Al₂O_3-700⋯C₂H₄ complex appears to be strongly delocalized between the Ti d orbital, π*(C₂H₄) and σ*(Ti–C_CH2^tBu), as revealed by the spin density distribution (Fig. 10b) and the occupancies of the related natural orbitals (see Table S2‡). The same delocalization is also found in the structure of the TS of ethylene insertion for both 1 and 1@Al₂O_3-700, as revealed by the calculated spin density distributions (Fig. 10c and d). This delocalization appears to be stronger for the TS for 1@Al₂O_3-700 (Fig. 10d), while being weaker for the TS for 1 (Fig. 10c). It appears that the unpaired electron, while weakening the C=C double bond of C₂H₄ and facilitating the formation of a Ti–C(C₂H₄) bond due to its presence at π*(C₂H₄), also favors the cleavage of the Ti–C bond of the CH₂^tBu ligand by occupation of the σ*(Ti–C) orbital before ethylene insertion. These factors together facilitate the C₂H₄ insertion into the Ti–C bond, in addition to the previously mentioned factor of its π character, which is consistent with a lowered energy of the TS of ethylene insertion in 1⋯C₂H₄, compared to 1⁺⋯C₂H₄, by ΔG = 2.7 kcal mol⁻¹. We, therefore, propose that the mechanism of ethylene polymerization for 1 and 1@Al₂O_3-700 catalysts involves the delocalization of the unpaired electron in the TS (Scheme 2).

Scheme 2 “Augmented” Cossee–Arlman mechanism of ethylene polymerization for 1 and 1@Al₂O_3-700. A partial electron transfer process from the SOMO to π*(C₂H₄) (“back donation”) is shown in the molecular orbital picture.

In general, the mechanism of ethylene insertion in d¹ Ti(III) alkyl complexes 1 and 1@Al₂O_3-700 is determined by two key factors: the π character in Ti–C bonds of (CH₂^tBu) ligands and the back donation of the unpaired electron. While the presence of the π character facilitates the insertion of ethylene into Ti–C bonds after its coordination, making the insertion in π-ethylene complexes nearly barrier-less at the TS, the back donation significantly lowers the formation energies of the π-ethylene complexes, which facilitates the overall reaction of C₂H₄ insertion. The delocalization of the unpaired electron in the TS structure, being noticeable for the systems with a high degree of back donation (i.e.1@Al₂O_3-700⋯C₂H₄), also has an effect on this reaction, favoring the cleavage of Ti–C and C=C bonds and slightly lowering the TS barrier. We denote this process (Scheme 2) as an “augmented” Cossee–Arlman mechanism, being essentially a [2σ + 2π + d¹] cycloaddition involving a partially alkylidenic σ(Ti–C) bond and a π(C₂H₄) bond together with a delocalized d¹ electron.

The described delocalization of the unpaired electron is likely an important feature in d¹ systems able to polymerize olefins, with a degree of the back donation (electron density transfer) that depends on the overlap of the SOMO and π*(C₂H₄), which in turn depends on the geometry of the system. For instance, a higher polymerization activity towards styrene polymerization was observed experimentally for Cp*Ti(OCH₃)₂/MAO and Cp₂TiCl/MAO catalytic systems compared to Cp*Ti(OCH₃)₃/MAO and Cp₂TiCl₂/MAO, respectively.²¹ It is likely that the Ti(III) species, active towards styrene polymerization, show better performance compared to similar Ti(IV) systems due to a strong back donation (electron transfer), favored by the aromatic system of styrene. Therefore, under the same polymerization conditions, a d¹ catalyst may be more active than a d⁰ catalyst of a similar structure. This finding also further suggests that Ti(III) alkyl species have competent electronic structures to act as efficient polymerization catalysts and may indeed be active species in the classical Ziegler–Natta heterogeneous catalysts.

Conclusions

In this work, we report the polymerization activity of molecular and the corresponding alumina-supported well-defined Ti(III) neutral alkyl species prepared via surface organometallic chemistry. Both of them were characterized and studied in detail by pulse EPR spectroscopy, combined with DFT calculations. This approach enabled us to identify the prevalent conformation of the molecular complex [Ti(nacnac)(CH₂^tBu)₂] in a frozen toluene solution and to reveal the structure of the alumina-supported species that correspond predominantly to a neutral Ti(III) alkyl compound, i.e. [(Al_sO)Ti(nacnac)(CH₂^tBu)]. To the best of our knowledge, these are the first examples of well-defined Ti(III) alkyl species able to efficiently polymerize ethylene, producing ultra-high molecular weight polyethylene. The ethylene insertion into the Ti(III)–C bond of [Ti(nacnac)(CH₂^tBu)₂] was further evidenced by EPR hyperfine spectroscopy (CHEESY-detected NMR), using isotope-labeled Ti(nacnac)(¹³CH₂^tBu)₂ in contact with C₂H₄.

These Ti(III)-based polymerization pre-catalysts display α-agostic C–H bonds in their (CH₂^tBu) ligands, supporting the presence of π character in the corresponding metal–carbon bonds.³⁵ Such a π character was further supported by DFT calculations via NBO analysis. It is noteworthy that the presence of the half-filled d¹ Ti orbital does not prevent α-agostic C–H bonding. After coordination of C₂H₄, the degree of π character in the Ti–C bonds of (CH₂^tBu) ligands is significantly increased, which allows a nearly barrier-less insertion of C₂H₄ into the Ti–C bonds. Hence, the slow step is olefin coordination, consistent with the need for high pressure to carry out this reaction and with the observation of an induction period. The back donating interaction (electron transfer) between the SOMO and the π* orbital of C₂H₄ results in a significant lowering of the formation energies of π-ethylene complexes, which facilitates an overall reaction of ethylene insertion in these Ti(III) systems. Due to the back donation, the unpaired electron could be delocalized between the Ti d orbital and π*(C₂H₄) and σ*(Ti–C) orbitals in both π-ethylene complexes and transition states, which also lowers the energy barriers for ethylene insertion. All these factors, which combine to give an “augmented” Cossee–Arlman mechanism, facilitate the overall reaction of C₂H₄ insertion into the Ti–C bond, making the ethylene polymerization in d¹ metal complexes potentially more efficient than that in d⁰ complexes of a similar structure under the same conditions.

This study shows that neutral d¹ Ti alkyl complexes are competent in ethylene polymerization, being favored by a combination of the π character in the Ti–C bonds and the back donation of the unpaired electron. These findings lend further support to the notion that d¹ Ti-alkyls are possible active sites in the heterogeneous Ziegler–Natta polymerization catalysts.

Author contributions

A. A. and F. A. contributed equally. A. A. carried out CW EPR and polymerization tests for 1, HYSCORE measurements, DFT computations, NBO analysis and wrote the manuscript. F. A. performed synthesis and characterization of 1, 1* and 1@Al₂O_3-700 and polymerization tests for 1@Al₂O_3-700. N. W. conducted CHEESY-detected NMR measurements. D. K. supervised the project. S. K. proposed the Ti(nacnac)(CH₂^tBu)₂ complex as a stable Ti(III) alkyl compound to be tested for ethylene polymerization activity. G. J. and C. C. coordinated the project and provided guidance. All the authors revised the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. A. was supported by a SNF—ANR grant (Mr CAT 2-77275-15). We acknowledge David Trummer (ETHZ) and Gina Noh (ETHZ) for their assistance with the ethylene polymerization experiments; John Severn and Tigran Margossian (DSM) for SEC of the produced PE; Frank Krumeich (ETHZ) for SEM of 1@Al₂O_3-700; Christopher P. Gordon (ETHZ) and Erwin Lam (ETHZ) for discussions.

Notes and references

1. K. Ziegler, Bel. Pat., 533 362, 1953; K. Ziegler, E. Holzkamp, H. Breil and H. Martin, Angew. Chem., 1955, 67, 541–547.
2. G. Natta, P. Pino and G. Mazzanti, Ita. Pat., 537 425, 1954; G. Natta and F. Danusso, Stereoregular Polymers and Stereospecific Polymerizations, Pergamon Press, Oxford, 1967.
3. H. Sinn, W. Kaminsky, H.-J. Vollmer and R. Woldt, Angew. Chem., 1980, 92, 396–402.
4. R. F. Jordan, W. E. Dasher and S. F. Echols, J. Am. Chem. Soc., 1986, 108, 1718–1719.
5. W. Kaminsky, J. Chem. Soc., 1998, 9, 1413–1418.
6. S. Mecking, Macromol. Rapid Commun., 1999, 20, 139–143.
7. J. Klosin, P. P. Fontaine and R. Figueroa, Acc. Chem. Res., 2015, 48, 2004–2016.
8. T. J. Marks, Acc. Chem. Res., 1992, 25, 57–65.
9. O. Olabisi, M. Atiqullah and W. Kaminsky, J. Macromol. Sci., Polym. Rev., 1997, 37, 519–554.
10. R. F. Jordan, J. Chem. Educ., 1988, 65, 285–289.
11. R. A. Collins, A. F. Russell, R. T. W. Scott, R. Bernardo, G. H. J. van Doremaele, A. Berthoud and P. Mountford, Organometallics, 2017, 36, 2167–2181.
12. Yu. V. Kissin, J. Catal., 2012, 292, 188–200.
13. E. Magni and G. Somorjai, Appl. Surf. Sci., 1995, 89, 187–195.
14. E. Magni and G. Somorjai, Catal. Lett., 1995, 35, 205–214.
15. T. I. Korányi, E. Magni and G. A. Somorjai, Top. Catal., 1999, 7, 179–185.
16. T. Risse, J. Schmidt, H. Hamann and H.-J. Freund, Angew. Chem., Int. Ed., 2002, 41, 1517–1520.
17. S. Maurelli, E. Morra, S. Van Doorslaer, V. Busico and M. Chiesa, Phys. Chem. Chem. Phys., 2014, 16, 19625–19633.
18. E. Morra, E. Giamello, S. Van Doorslaer, G. Antinucci, M. D'Amore, V. Busico and M. Chiesa, Angew. Chem., Int. Ed., 2015, 54, 4857–4860.
19. E. P. Moore, in Polypropylene handbook: polymerization, characterization, properties, processing, applications, Hanser-Gardner, Cincinnati, 1996, ch. 2, pp. 61–73.
20. G. Cecchin, G. Morini and F. Piemontesi, in Kirk-Othmer Encyclopedia of Chemical Technology, John Wiley & Sons, Hoboken, 2000, vol. 26, pp. 502–554.
21. J. Schellenberg and N. Tomotsu, Prog. Polym. Sci., 2002, 27, 1925–1982.
22. F. Allouche, D. Klose, C. P. Gordon, A. Ashuiev, M. Wörle, V. Kalendra, V. Mougel, C. Copéret and G. Jeschke, Angew. Chem., Int. Ed., 2018, 57, 14533–14537.
23. N. Bahri-Laleh, M. Nekoomanesh-Haghighi and S. A. Mirmohammadi, J. Organomet. Chem., 2012, 719, 74–79.
24. P. H. M. Budzelaar, A. B. van Oort and A. G. Orpen, Eur. J. Inorg. Chem., 1998, 1998, 1485–1494.
25. F. Basuli, B. C. Bailey, J. Tomaszewski, J. C. Huffman and D. J. Mindiola, J. Am. Chem. Soc., 2003, 125, 6052–6053.
26. C. Copéret, A. Comas-Vives, M. P. Conley, D. P. Estes, A. Fedorov, V. Mougel, H. Nagae, F. Núñez-Zarur and P. A. Zhizhko, Chem. Rev., 2016, 116, 323–421.
27. D. G. H. Ballard, J. Polym. Sci., 1975, 13, 2191–2212.
28. J. D. A. Pelletier and J.-M. Basset, Acc. Chem. Res., 2016, 49, 664–677.
29. F. Allouche, K. W. Chan, A. Fedorov, R. A. Andersen and C. Copéret, Angew. Chem., Int. Ed., 2018, 57, 3431–3434.
30. M. Jezequel, V. Dufaud, M. J. Ruiz-Garcia, F. Carrillo-Hermosilla, U. Neugebauer, G. P. Niccolai, F. Lefebvre, F. Bayard, J. Corker, S. Fiddy, J. Evans, J.-P. Broyer, J. Malinge and J.-M. Basset, J. Am. Chem. Soc., 2001, 123, 3520–3540.
31. J. Joubert, F. Delbecq, P. Sautet, E. Le Roux, M. Taoufik, C. Thieuleux, F. Blanc, C. Coperet, J. Thivolle-Cazat and J.-M. Basset, J. Am. Chem. Soc., 2006, 128, 9157–9169.
32. M. M. Stalzer, M. Delferro and T. J. Marks, Catal. Lett., 2015, 145, 3–14.
33. B. D. Culver, H. Tafazolian and M. P. Conley, Organometallics, 2018, 37, 1001–1006.
34. C. P. Nicholas, H. Ahn and T. J. Marks, J. Am. Chem. Soc., 2003, 125, 4325–4331.
35. C. P. Gordon, S. Shirase, K. Yamamoto, R. A. Andersen, O. Eisenstein and C. Copéret, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5867–5876.
36. C. P. Gordon, C. Raynaud, R. A. Andersen, C. Copéret and O. Eisenstein, Acc. Chem. Res., 2019, 52, 2278–2289.
37. B. Rhers, A. Salameh, A. Baudouin, E. A. Quadrelli, M. Taoufik, C. Copéret, F. Lefebvre, J.-M. Basset, X. Solans-Monfort, O. Eisenstein, W. W. Lukens, L. P. H. Lopez, A. Sinha and R. R. Schrock, Organometallics, 2006, 25, 3554–3557.
38. S. M. Kurtz, in The UHMWPE handbook: ultra-high molecular weight polyethylene in total joint replacement, Academic Press, Cambridge, 2004, ch. 1, pp. 1–12.
39. P. Höfer, A. Grupp, H. Nebenführ and M. Mehring, Chem. Phys. Lett., 1986, 132, 279–282.
40. J. P. Perdew and M. Ernzerhof, J. Chem. Phys., 1996, 105(22), 9982–9985; C. Adamo and V. Barone, J. Chem. Phys., 1991, 110, 6158–6170.
41. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
42. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327.
43. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
44. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 105104; S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
45. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
46. N. Rega, M. Cossi and V. Barone, J. Chem. Phys., 1996, 105, 11060–11067.
47. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.
48. K. H. Dahmen, D. Hedden, R. L. Burwell Jr and T. J. Marks, Langmuir, 1988, 4, 1212–1214.
49. G. Tosin, M. Delgado, A. Baudouin, C. Catherine, C. C. Santini, F. Bayard and J.-M. Basset, Organometallics, 2010, 29, 1312–1322.
50. G. Rao, A. B. Altman, A. C. Brown, L. Tao, T. A. Stich, J. Arnold and R. D. Britt, Inorg. Chem., 2019, 58, 7978–7988.
51. S. Stoll, C. Calle, G. Mitrikas and A. Schweiger, J. Magn. Reson., 2005, 177, 93–101.
52. N. Wili and G. Jeschke, J. Magn. Reson., 2018, 289, 26–34.
53. G. Feher, Phys. Rev., 1956, 103, 834.
54. M. Brookhart and M. L. H. Green, J. Organomet. Chem., 1983, 250, 395–408.
55. W. W. Lukens Jr, M. R. Smith III and R. A. Andersen, J. Am. Chem. Soc., 1996, 118, 1719–1728.
56. F. Weinhold, C. R. Landis and E. D. Glendening, Int. Rev. Phys. Chem., 2016, 35, 399–440.
57. E. D. Glendening, F. Weinhold and C. R. Landis, J. Comput. Chem., 2019, 40, 2234–2241.
58. C. P. Gordon, K. Yamamoto, K. Searles, S. Shirase, R. A. Andersen, O. Eisenstein and C. Copéret, Chem. Sci., 2018, 9, 1912–1918.
59. M. Besora, P. Vidossich, A. Lledós, G. Ujaque and F. Maseras, J. Phys. Chem. A, 2018, 122, 1392–1399; L. Falivene, V. Barone and G. Talarico, Mol. Catal., 2018, 452, 138–144.
60. G. Lanza, I. L. Fragalà and T. J. Marks, Organometallics, 2002, 21, 5594–5612.

---

Footnotes

† We dedicate this work to the memory of Prof. Richard A. Andersen.

‡ Electronic supplementary information (ESI) available: Details of experimental procedures and additional experimental data. See DOI: 10.1039/d0sc04436a

§ These authors contributed equally to this work.

---