Open Access Article
Open Access ArticleBinding site exchange kinetics revealed through efficient spin–spin dephasing of hyperpolarized 129Xe†
Martin
Kunth
 and
Leif
Schröder
and
Leif
Schröder
 *
*
Leibniz-Forschungsinstitut für Molekulare Pharmakologie im Forschungsverbund Berlin e.V. (FMP), Campus Berlin-Buch, Robert-Roessle-Str. 10, 13125 Berlin, Germany. E-mail: kunth@fmp-berlin.de; lschroeder@fmp-berlin.de; Tel: +49 30 94793 121
First published on 19th October 2020
Abstract
Spin exchange between different chemical environments is an important observable for characterizing chemical exchange kinetics in various contexts, including protein folding, chelation chemistry, and host–guest interactions. Such spins experience effective spin–spin relaxation rate, R2,eff, that typically shows a dispersive behavior which requires detailed analysis. Here, we describe a class of highly simplified R2,eff behavior by relying on hyperpolarized 129Xe as a freely exchanging ligand reporter. It provides large chemical shift separations that yield reduced expressions of both the Swift–Connick and the Carver–Richards treatment of exchange-induced relaxation. Despite observing a diamagnetic system, R2,eff is dominated by large Larmor frequency jumps and thus allows detection of otherwise inaccessible analyte concentrations with a single spin echo train (only 0.01% of the overall hyperpolarized spins need to be transiently bound to the molecule). The two Xe hosts cryptophane-A monoacid (CrA-ma) and cucurbit[6]uril (CB6) represent two exemplary families of container molecules (the latter one also serving as drug delivery vehicles) that act as highly efficient phase shifters for which we observed unprecedented exchange-induced relaxivity r2 (up to 866 s−1 mM−1). By including methods of spatial encoding, multiple data points can be collected simultaneously to isolate the exchange contribution and determine the effective exchange rate in partially occupied binding sites with a single delivery of hyperpolarized nuclei. The relaxivity is directly related to the guest turnover in these systems and temperature-dependent measurements yield an activation energy of EA = 41 kJ mol−1 for Xe@CrA-ma from simple relaxometry analysis. The concept is transferable to many applications where Xe is known to exhibit large chemical shifts.
1 Introduction
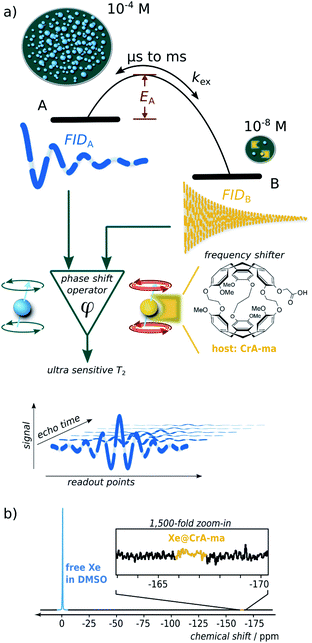
Nuclear magnetic resonance (NMR) is one of the most versatile and powerful analytical techniques with applications in chemistry, materials sciences, life sciences, and medical diagnostics. The ability of many nuclei to report exchange-induced fluctuations in the local magnetic field via spin dephasing is of particular interest for characterizing dynamic processes such as conformational changes in enzymes during catalysis1 or low-populated (“hidden”) intermediate states of protein folding.2 Reversible binding in coordination chemistry or in host guest complexes are further examples where exchanging NMR-active nuclei experience enhanced spin relaxation at a paramagnetic center3 and/or transient changes in their Larmor frequency.4 Both effects cause signal loss summarized in the spin–spin relaxation rate, R2. Altogether, these dynamics are essential for the functions of biochemical macromolecules or for drug carriers with regard to ligand complexation and release. Studying relaxation under different RF pulse perturbations of the system provides insights into the kinetics (exchange rate), thermodynamics (population of the involved pools), and structure (change in Larmor frequency). The total exchange rate of a two-site exchange system, kex = kon + koff (with on- and off-rates, respectively), is characteristic for the system and is linked to the activation energy (see Fig. 1a) as well as to the accessibility at the binding site5 that can be impaired by competing binding partners, the solvent, or conformational changes.Overall, the effective spin–spin dephasing or transverse relaxation rate, R2,eff, of the detected transverse magnetization in a dominant pool A depends on the lifetime, τex (which equals 1/kex), of transiently formed states/complexes (the dilute pool B) and on the magnetic interaction strengths therein. R2,eff can be quantified through the decay of spin echoes with the Carr–Purcell (–Meiboom–Gill) (CP(MG)) method. The effect is modulated by the Carr–Purcell frequency of the magnetization refocusing RF pulses, νCP, and the transition from infrequent pulsing (low νCP; maximum observed R2,eff) to frequent pulsing (high νCP; minimum R2,eff) is called relaxation dispersion (RD).6,7 Two-site exchange is described in a general form by the Carver–Richards equation that usually requires careful sampling of the RD curve to extrapolate the upper and lower relaxation rate limits.
However, in the limits of either fast (Δω ≪ kex; with Δω denoting the relative chemical shift difference between the Larmor frequencies in both pools) or slow exchange (Δω ≫ kex), simplifications apply to isolate the exchange contribution and to obtain kex.8 Whereas the latter case is mathematically convenient because R2,ex = [B]/([A] + [B]) × kex (with [j] denoting the concentration of j and j ∈ A or B) becomes independent of the (not necessarily known) change in Δω, it is challenging to find a suitable spin label with such conditions at room temperature. However the measurable effect practically vanishes for [B] ≪ [A] and direct line broadening for the A pool is also insignificant in such cases where the analyte is only available in highly dilute solutions (see ESI, Fig. S1†).
We here introduce a new powerful approach that relies on noble gas spins (in our case 129Xe) and provides important insights for highly dilute states even for biochemically relevant exchange kinetics. It provides multiple critical improvements over other RD approaches for analyzing hydrophobic binding sites: (1) a large chemical shift range redefines even sub-ms dynamics as “slow”; (2) minimal starting relaxation rates due to inefficient spin interactions are promptly dominated by the desired R2,ex contribution; (3) the ability to include spin hyperpolarization (HP) for significant sensitivity enhancement, including easy re-delivery for time-resolved studies; (4) the combination with spatial encoding enables the option to study multiple conditions with one delivery of HP nuclei; (5) the bare isotope itself (26% natural abundance) represents the reporter for ligand-based relaxometry and the molecule of interest can remain at even lower concentrations than the dissolved gas; (6) a highly simplified mathematical description yields a dispersion-free behavior over wide ranges of νCP.
Key feature of this system is the large Δω that dominates all other critical rates and becomes particularly convenient for [A] ≫ [B]. Whereas slow exchange has been described with an equation by Tollinger et al.,9 such previous work did not apply to highly dilute pools. The conditions studied here apply to many systems with limited water solubility that is problematic for concentrations typically required for NMR. In cases where the population of B represents the occupancy of a hydrophobic binding site, Xe can be used as a neutral surrogate to report on the net turnover of a small guest entering and leaving such a site. The noble gas with its usually weak spin–spin interactions is ideally suited to detect exchange-induced spin–spin dephasing even if these are minor changes (<10−1 s in T2,eff) at low concentrations and thus require a low spin–spin relaxation rate in the absence of any exchanging site, R2,0 to start with for accumulating a sufficient signal difference.
Hyperpolarized Xe can be detected in single-shot experiments at μM concentrations and thus allows to combine the HP sensitivity enhancement with the advantages of ligand-based relaxometry which is the favorable way to introduce a spin label into the molecular system.10,11 Importantly, this system can be called exchange-dominated because R2,eff is easily dominated by large fluctuations in the Larmor frequency induced by Δω, even at sub-μM concentrations of the B pool. This allows easy characterization of the apparent exchange rate constant, kex (similar to the gas turnover rate, β × kBA, with host occupancy, β; see below), of Xe interacting with dilute binding sites at conditions that would otherwise be inaccessible. A careful combination with spatially encoded NMR further broadens the application range: it solves the limitation of one-time useable HP magnetization and allows the side-by-side quantification of exchange conditions for variable concentrations with a single HP Xe delivery. This replaces elaborate sampling of the RD curve because the Xe system exhibits a non-dispersive relaxation behavior over wide ranges of experimental conditions. Hence, isolation of the R2,ex contribution for obtaining kex only requires a small set of concentrations (minimum: 2) to subtract the exchange-free relaxation. Moreover, because of the simple linear relationship between the exchange-induced relaxivity, r2 (the slope of R2,eff along the concentration series) as the observable and the system parameter kex, further thermodynamic insights such as the activation energy, EA, can be readily derived from an Arrhenius plot.
Whereas R2,eff relaxation of transiently bound 129Xe has been reported in previous work,12 the relaxivity r2 itself has to the best of our knowledge never been examined in the context of a detailed analysis of chemical exchange with a related theoretical description. We have chosen two commonly known Xe hosts (cryptophane-A monoacid, CrA-ma, and cucurbit[6]uril, CB6) to demonstrate our generalizable findings such as for the exemplary cases in the seminal relaxation analysis papers from 1962 (Swift–Connick)3 and 1972 (Carver–Richards).13
One of the systems studied herein even serves as efficient MRI contrast agent that actually surpasses the most efficiently known paramagnetic T2,ex agents such as EuDOTA chelates14 and natural D-glucose15 by 2–3 orders of magnitude. Moreover, the accelerated spatial encoding techniques developed herein are also beneficial for other hyperpolarized agents generated via dynamic nuclear polarization (DNP) or parahydrogen induced polarization (PHIP) that could complement the minimalistic RD analysis with hp nuclei by Liu et al.16 by replacing multiple RF channels with multiple samples. It also paves the way for ultra-sensitive MRI with such tracers from various HP techniques. We further demonstrate the advantages of HP Xe as an easy deliverable spin reporter to perform time-resolved R2,eff relaxometry on a sample with a self-reducing accessible host concentration. This yields a gas turnover-rate from variable relaxivities from only one sample.
2 Theory
2.1 Simplification of the Swift–Connick equation and of relaxation dispersion in the “diamagnetic extreme limit”
To fully appreciate the extend of the simplifications for the R2,eff exchange effects in 129Xe NMR, it is worthwhile to briefly consider important previous work on spin echo train relaxation measurements. In essence, the systems described herein behaves similar to one of the four limiting cases already discussed with the introduction of the Swift–Connick equation:3 two of them (either dominant Δω due to large paramagnetic shifts or dominant spin–spin relaxation rate in spin pool B, R2,B, at a metal center) can be treated as practically complete loss of phase coherence for bound spins when they exchange back into the detected bulk pool. In Swift's and Connick's description, R2,eff is derived from the exchange broadening of the bulk pool line width and then directly given by the rate of chemical exchange. The dominant Δω encountered in our work will eventually yield an analogue result for R2,eff being proportional to kex, but for a diamagnetic system.Moreover, we can neglect dispersion effects due to the rather convenient conditions provided by the Xe chemical shift range and exchange kinetics. For this non-dispersive exception (as demonstrated by simulations in the ESI S1†), the key aspect is that the Carver–Richards equation contains a cosh−1 term (using a notation such as that by Millet et al. in ref. 8) for the relaxation dispersion that is scaled with 1/τCP. We will use herein that this cosh−1 term simplifies significantly over a wide range of pulsing frequencies. Moreover, recently introduced correction terms by Baldwin17 can also be neglected in a diamagnetic system with broadly dominant Δω such as 129Xe as well as correction terms in a generalized approach for N-site chemical exchange by Koss et al.18
Critically, Xe serves as a reporter that is not covalently bound to the analyte (as in isotopically labeled ligands detection) and is thus an ideal surrogate for other less sensitive NMR-active guests to explore access to binding sites (even if a direct signal of bound Xe is undetectable; see ESI S1†). An accurate determination of kex is the key element to characterize the kinetics and derive the activation energy. When characterizing the exchange kinetics, the exact value of Δω is of minor importance for us but it is convenient that it is often the dominant frequency in Xe systems. Other RD data is usually in the intermediate to fast exchange regime for 1H, 13C, 15N detection.2 Such dispersion curves lack a clearly defined plateau for slow pulsing (<102 Hz) and require an entire curve fit to isolate kex with limited accuracy. For “slow exchange”, kex < Δω, this simplifies significantly because evaluating the plateau value versus a single measurement without exchange directly yields the exchange contribution R2,ex = fB × kex,8,19 with fB denoting the factional size of pool B. In fact, exchange rates can still occur faster than the ms time regime for Xe and still be “slow” because of the large chemical shift difference Δω.
The slow pulsing regime has been the focus of a gradually refined theoretical description to match the experimentally observed relaxation dispersion under various conditions.20–22 A widely used solution allowing different intrinsic relaxation in both pools has been introduced by Carver and Richards.13 Their description agrees for slow CPMG pulse repetition with the Swift–Connick result for R2,eff. Whereas the limit of slow pulsing comes with the maximum possible R2,ex contribution, this adds up to the intrinsic spin–spin relaxation rate in pool A, R2,0, and thus determines an inherent maximum time window for sampling the spin echo decay with sufficient accuracy. To some extent, fast(er) pulsing is desirable for high relaxation, but too fast pulsing can unfortunately lead to underestimation of the exchange effects. It is therefore highly beneficial to detect nuclei such as 129Xe that exhibit slow relaxation in the absence of exchange. Thus, even significant R2,ex contributions do not require prohibitive short spin echo times that would be in conflict with any hardware limitations. At the same time, the large Δω > 10 kHz stretches the dispersion plateau far towards the fast pulsing regime (see ESI S1†). This allows moderate fast pulsing for the acquisition of extended spin echo trains, providing high accuracy for decay analysis and high data density to include spatial encoding options.
Millet et al. in ref. 8 use a modified notation of the Carver–Richards equation that eventually yields R2,ex = fB × kex for dominant Δω. They also emphasize that R2,ex “is not overly sensitive” to the intrinsic R2,0 in both separate pools as long as |R2,0 − R2,B| ≪ Δω(fA − fB). Here, our system benefits again from Δω > 104 Hz. We only have to ensure that Δω dominates R2,B, a condition that is likely but also easy to verify in chemical exchange saturation transfer (CEST) experiments (see ESI S1†).
We thus use R2,eff = R2,0 + fB × kex (where in the extreme limit of no host concentration, i.e., [host] → 0, the following relaxation rates are equal: R2,A = R2,0) in the limit of large Δω. This is identical to the Swift–Connick equation for a dominant chemical shift term:
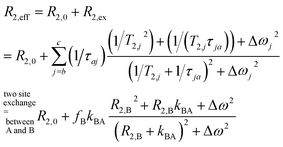 | (1) |
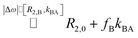 | (2) |
We demonstrate in the ESI S1† that the pulsing frequency νCP can be neglected for a wide range and thus we work with a practically non-dispersive behavior. Experimentally, we will show that the relaxation follows a linear dependence on the host concentration:
| R2,eff = R2,0 + R2,ex = R2,0 + fB × kBA = R2,0 + [host] × r2 | (3) |
Moreover, we do not need to know the exact R2 in the B pool, R2,B, because the large Δω acts similar to a “crusher”, quickly dephasing the magnetization and releasing it with a significant loss of phase coherence relative to the bulk pool. This is convenient because the systems studied here are exemplary for conditions where the dilute state cannot be studied in the absence of exchange.
2.2 Adaptation for exchange sites with variable “loading”
It should be mentioned that there is a certain analogy to diagnostic applications of strong R2,ex effects that have been implemented with paramagnetic chelates that coordinate water molecules for fast relaxation of protons.23 In such systems, the Swift–Connick equation is also used to describe the exchange contribution24 but does not simplify as in our case of the diamagnetic extreme limit with “slow” exchange.Regarding R2,ex = fB × kBA for paramagnetic R2,ex agents, fB is proportionally given by the agent concentration because each chelate has a fixed hydration number (typically q = 1). For host–guest systems (and others relying on chemical affinity than on bonding through electrons), however, fB = β × ([host]/[Xe])25 depends on the host (or site) occupancy β (in %) and we obtain
| β × kBA = [Xe] × r2 | (4) |
It should be mentioned that although we work with a strongly simplified version of eqn (1), the corresponding Swift–Connick plot is still useful for illustrating into which regime a certain molecular system falls. This plot will be used in the discussion to compare the systems.
3 Experimental section
3.1 Xenon hyperpolarization and gas delivery
A Xe gas mix of {2, 10, 88}-vol.% of {Xe, N2, He} (with 26.4% of 129Xe at natural abundance) was hyperpolarized (HP) by spin-exchange optical pumping using a custom-designed continuous-flow polarizer.27,28 A 150 W Laser (QPC Lasers, 795 nm; emission bandwidth ∼ 0.5 nm) was used to obtain a Xe polarization degree of ∼20%, which corresponds to ≈104-fold 129Xe-NMR signal enhancement. HP Xe gas was continuously guided through 1/4 inch PFA tubing and dispersed into the sample via fused silica glass capillaries (inner/outer diameter of 250/350 μm, respectively; Polymicro Technologies/Molex; Part#: 1068150030) at a flow rate of 100 mL min−1 for a bubbling time of 10 s, followed by a waiting time of 1 s to allow remaining bubbles to collapse.27 With a xenon Ostwald solubility coefficient in dimethyl sulfoxide (DMSO) of 0.66 L per atm at room temperature,29,30 and a total pressure of the Xe gas mix of 4.5 bar, the Xe concentration in DMSO solution was ca. 2.3 mM.25,313.2 Sample preparations
Experiments for demonstrating the simplified relaxation behavior in the diamagnetic extreme limit were done with cryptophane-A monoacid (CrA-ma) in DMSO at various concentrations and at various temperatures (291–310 K). CrA-ma (molecular weight of 939 g M−1; provided by Kang Zhao, Tianjin University, China) was prepared as a stock solution of 150 μM (i.e., 2 mg of CrA-ma were dissolved in 14.2 mL DMSO and sonicated for >30 minutes). This stock solution was used to obtain a concentration series with 2, 4, 8, 16-fold dilution for determining the spin–spin relaxivity, r2, for [CrA-ma] = {75, 37.5, 18.75, 9.375} μM. For this series, measurements were performed at temperatures of T = {295, 303, 310} K (using the spectrometer's variable temperature unit (VTU) with a minimum waiting time of 20 min in between changing temperatures to allow for thermal equilibrium). An experiment to demonstrate a relaxometry map including the host free reference sample was performed with 50 μM CrA-ma at r.t. of 291 K.DMSO was chosen as the solvent predominantly for two reasons: (1) it demonstrates the method for a system with a rather weak binding constant (previously published as 38 M−1 (ref. 26)) where only ≈10% of the binding sites are actually occupied and still yield a measurable relaxation effect. (2) This solvent provides experimental conditions for higher accuracy as the relaxivity can be determined from a wider range of concentrations without facing precipitation issues that otherwise occur for various Xe hosts when they have not been fitted with any solubilizing units. However, we expect the method to also provide important insights for comparative studies in aqueous conditions. Regarding the freezing point of DMSO, it should be mentioned that the elevated pressure in the sample (4.5 bar abs) as well as the repeated gas delivery prevented the solution from freezing at 291 K.
The re-evaluated time-resolved observation of a host–guest system with increasing guest competition was originally performed with a solution containing 16 μM cucurbit[6]uril (CB6) and 6 mM lysine (Lys) dissolved in a buffer of 10 mM ammonium acetate in H2O at pH = 6.0. Lys serves as substrate reservoir for lysine decarboxylase (LDC, from Bacillus cadaveris, 1.6 U mg−1; Lys and LDC were obtained from Sigma-Aldrich, Steinheim, Germany). This sample was kept at 298 K inside the magnet to follow the conversion of Lys into cadaverine (Cad) which gradually blocks the CB6 cavity for Xe.
3.3 Spatial encoding for relaxometry mapping
The basic concept of R2,eff mapping is to acquire a series of MRI scans with increasing effective spin echo time (TE). This enables collection of data from different samples that have all been simultaneously supplied with HP nuclei. Multiple data points for relaxometry can then be collected to characterize the exchange contribution without facing the limitations of non-self-renewing magnetization. Each pixel in this type of quantitative MRI data then exhibits an exponential signal decay S(x, y, TE) = S0(x, y) × exp{−TE × R2,eff(x, y)}. The spatial encoding has advantages even for uniform samples: it provides decay curves for each pixel and is thus also beneficial due to the improved statistics of many individual R2,eff decays S(x, y, TE). Whereas the spin echo decay is the desired effect to measure R2,eff(x, y) for various concentrations [host](x, y), a continuous decrease in the spin echo intensity comes with challenges for image encoding when relying on the sensitivity advantages of hyperpolarized nuclei. For self-renewing magnetization (longitudinal relaxation time T1 recovery after each excitation), Cartesian sampling of the image raw data (k-space) with CPMG sequences is the gold-standard for R2,eff mapping. One runs multiple experiments, each with a certain spin echo train length and, depending on how fast the signal decays in each spin echo train, a certain degree of k-space segmentation is applied. For HP Xe, however, this type of data recording requires multiple HP Xe deliveries. This is problematic because two critical consequences arise: (1) the hyperpolarization level (i.e., detectable magnetization) can vary from one measurement to the other making reliable T2,eff estimation challenging, and (2) the method becomes time consuming. For this reason, we aim for a single-shot method that does full T2,eff mapping after a single HP Xe delivery.However, in single shot Cartesian turbo-spin echo encoding significant signal decay during the acquisition of different sections of k-space causes signal blurring in the reconstructed MR image as a well-known artefact.32 It also seriously increases the spin echo spacing between individual images and would allow only coarse temporal sampling of S(x, y, TE) for each pixel. We thus employ an approach including undersampling and k-space data sharing.
The low frequency components of Fourier space (i.e., in the center of k-space) contain the main contrast intensity in image space; the high frequency components of Fourier space contribute in image space to resolution and sharp edges. Hence, R2,eff mapping is mainly interested to update frequent changes of the k-space center signal intensity between adjacent images S(x, y, n × TE) and S(x, y, (n + 1) × TE). This makes radial (non-Cartesian) sampling the method of choice. In this scheme, every single readout, be it the first or the last acquired “projection”, traverses the center of k-space, which updates the low frequency components. The reconstruction of radial k-space data is also suitable for undersampling techniques for fast dynamic studies.
For pushing the time-resolution limits, we took advantage of the Golden-Angle (GA) based sampling in conjunction with non-conventional MR image reconstruction including a k-space weighted image contrast (KWIC) filter.33–35 Details are given in the ESI S2.1.† In brief, this encoding scheme avoids acquisition of any redundant k-space information and enables a “sliding” reconstruction window to obtain images for any desired TE by combining data from different readouts with different emphasis of either the center or the periphery of k-space. S(x, y, TE) can be obtained for small increments along the time dimension for accurate evaluation of R2,eff and the derived gas turnover rate.
The filter is necessary to avoid artefacts linked to the Nyquist–Shannon sampling theorem which requires a minimum number p of projections to be acquired from radial k-space data (p = matrix size × π/2). It enables dense sampling of the signal decay based on artifact-free MR image reconstruction of highly undersampled radial k-space data. To further improve the quality of R2,eff mapping (enabling higher resolution down to 150 μm (i.e., with up to 1282 matrix size; see ESI Fig. S12†) for identifying regional differences in chemical exchange), we introduce a modified version of the KWIC filter that we call smoothed KWIC (sKWIC)-filter. To our knowledge, a sKWIC-filter has not been reported yet. The full description of the sKWIC filter is given in ESI S2.2.† It allows significant undersampling (factor 25) with only 8 projections including the center of k-space for accurate R2,eff mapping with both high spatial resolution and dense spin echo spacing to extract maximum information regarding the exchange-related effects. The MR image reconstruction was done using Fessler's and Sutton's nonuniform fast Fourier transform toolbox.36
Data were post-processed on a GNU/Linux (Debian 8.3.0-6) workstation using custom-designed scripts in C++ (version 8.3.0), gnuplot (version 5.2 patchlevel 6), and Matlab (R2012a). A pixel-wise analysis of the generated image series was done with a decay with the following equation
| S(x, y, TE) = M0(x, y)exp{−TE × R2,eff(x, y)} + offset(x, y) | (5) |
When focusing on the use of Xe hosts as T2,eff contrast agents, there is a spin echo time with maximum image contrast. Following the quantitative R2,eff analysis, it can be used together with the sliding reconstruction window as described in the ESI S2† to generate the image with maximum contrast.
3.4 NMR acquisition parameters
All studies were done on a B0 = 9.4 T wide bore NMR spectrometer (Bruker Biospin, Ettlingen, Germany; software: ParaVision 5) equipped with a gradient setup for spatial encoding. For detection, we used a 10 mm double-resonant 129Xe/1H transmit/receive probe head. Prior to detection, each sample was shimmed and a flip angle calibration was performed. The 129Xe-MR images were acquired from free Xe in solution serving as the bulk pool (referenced to 0 ppm) that experiences exchange-enhanced relaxation in the presence of the host molecule.The experiments for T2,eff mapping investigating exchange with CrA-ma (see Fig. 2) used a rapid acquisition with relaxation enhancement (RARE) pulse sequence that was modified for golden-angle based radial k-space sampling. The sequence parameters were: 90° RF Gaussian excitation pulse (length: 1 ms; bandwidth: 2740 Hz); 180° RF Gaussian refocussing pulse (length: 1 ms; bandwidth: 1610 Hz); effective spectral bandwidth: 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 161 Hz; field-of-view: 20 × 20 mm2; slice thickness: 20 mm; (minimum) spin echo time (TE): 9 ms.
161 Hz; field-of-view: 20 × 20 mm2; slice thickness: 20 mm; (minimum) spin echo time (TE): 9 ms.
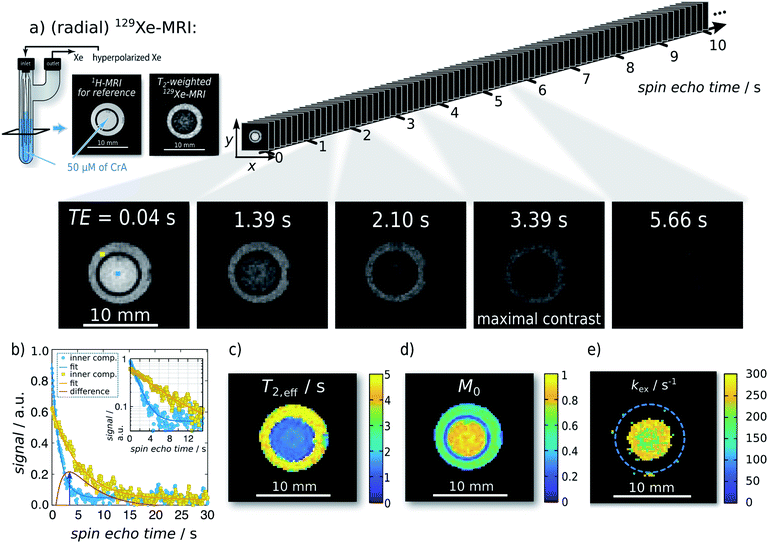 | ||
| Fig. 2 Single-shot Xe T2,eff quantification and mapping at 291 K. Representative radial sKWIC filter reconstructed 129Xe MR images for different spin echo times TE are shown in (a); signal intensities were normalized to that of the first spin echo time TE = 0.04 s. The image of maximal contrast between the inner and the outer compartment is shown at TE = 3.39 s. (b) Signal intensity of two individual pixels (marked by blue and yellow squares in first Xe MR image in (a)) with respect to the echo time. T2,eff analysis yielded a T2,eff of (5.95 ± 0.10) s without CrA-ma in the outer compartment, and of (1.85 ± 0.02) s in the presence of 50 μM of CrA-ma in the inner compartment (initial magnetization: M0,IC = 0.80 ± 0.01; M0,OC = 0.609 ± 0.007). Pixelwise T2,eff analysis yielded the T2,eff and M0 maps in (c) and (d), respectively. Since the total field-of-view was 20 mm2 (here, a zoom in is shown), a matrix size of 962 yields a spatial resolution of 208 μm2. (e) kex-map (derived with factional size of pool B, fB = 2.1 × 10−3, which was obtained with qHyper-CEST; see ESI S4†). | ||
The matrix size ranged from 322 (TEmin: 9 ms; spatial resolution: 625 μm2; number of projections: 2230; total acq. time: ∼20 s), 642 (TEmin: 9 ms; spatial resolution: 312 μm2; number of projections: 2230; total acq. time: ∼20 s), 962 (TEmin: 10.2 ms; spatial resolution: 208 μm2; number of projections: 1970; total acq. time: ∼20 s) to 1282 (TEmin: 20.0 ms; spatial resolution: 156 μm2; number of projections: 1004; total acq. time: ∼20 s). At spatial resolutions starting with 210 μm2 (i.e., in our setup at matrix sizes 962 and 1282), the resolution is sufficient to even begin to resolve the silica glass capillaries (see Fig. 2 and similarly in Fig. S12†).
Once the 90° RF pulse has been applied, the pulse sequence continuously records data (up to ∼103 of projections) over several seconds for an arbitrary time period (depending on how fast the recorded signal decays). Each single-shot GA-based radial encoding for T2,eff mapping acquires data that is matrix size-independent. The whole measurement lasts less than 20 s and requires only a single HP Xe delivery. This is a significant acceleration (e.g., when the matrix size of Cartesian k-space sampling was 32 × 32, then the acceleration with our method is 32-fold; when the matrix size was 64 × 64, then our method is 64-fold faster, etc.) of the data acquisition time required for quantification.
3.5 Determination of the activation energy
In exchange processes, the activation energy EA for the transition between pools A and B can be determined with an Arrhenius plot of ln(kex) versus inverse temperature, 1/T. The slope m of this plot is linked to EAvia m = EA/R with R being the ideal gas constant.In our case, kex is dominated by kBA (because kex = kAB + kBA = fB × kBA + kBA = kBA × (fB + 1) ∼ kBA, due to the dominant A pool). The exchange contribution in the relaxivity measurement now allows to isolate kex to a good approximation. From eqn (3) we know fB × kBA = [host] × r2 ≈ fB × kex. Thus, we can write the sum of several parameters as a function of the variable (1/T) in Arrhenius's equation ln(kex)(1/T) ≈ ln(r2)(1/T) + ln([host]) − ln(fB). The term ln([host]) just causes an offset in the Arrhenius plot and ln(fB) is expected to vary very little with (1/T). If the latter is confirmed experimentally, the activation energy can be directly calculated from the slope 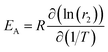 .
.
4 Results and discussion
4.1 Reliability of relaxometry mapping
For achieving accurate relaxometry, the signal decay with increasing spin echo number should be detected with minimum artefacts and a sufficiently dense sampling along the time domain. Given we are in the slow exchange regime and ΔR2,eff([host]) is small compared to Δω to warrant the assumption R2,A = R2,B, the exchange contribution increases linearly with fB, i.e., the host concentration. It should thus be possible to extract β × kBA from the difference in R2,eff for two different host concentrations with a single delivery of HP nuclei. To this end, we implemented spatial encoding for relaxometry mapping with highly undersampled data from a two-compartment sample setup. We first tested the reliability of the spatial encoding that we also used afterwards for reasons of comparability to quantify relaxation in uniform samples at different temperatures. An attempt to reconstruct images for quantifying the early onset of signal decay with using only eight spin echoes without any filter showed serious artefacts even for coarse spatial resolution (image matrix size of 322, see ESI Fig. S9†). These problems aggravate for larger matrix sizes and prevent accurate quantification of R2,eff. Full sampling according to the Nyquist theorem was done by combining more spin echoes from the same data set. However, this increases the minimum spin echo time seriously and yields an averaged signal intensity over a longer evolution time that does not accurately represent any more the true signal evolution in both samples. Using a filter is thus unavoidable and we compared two implementations: 129Xe MR images that were reconstructed from the very same spin echo train with either the KWIC filter or the proposed smoothed KWIC (sKWIC) filter (see ESI S2.1/S2.2†) were inspected for residual artefacts that would hamper R2,eff quantification. Subtraction of two MR images (signal intensities normalized two their maximum signal) of the very same TE revealed reduction of noise of over 20% of the sKWIC over the KWIC filter (see ESI Fig. S11;† the standard error for the fitting results was also reduced, see ESI Fig. S13†). We therefore exclusively used the sKWIC filter for the reconstruction of 129Xe MR images from here on.We also performed one experiment where the 2-compartment phantom was filled with two identical solutions to verify that the applied method would yield the same T2,eff throughout the sample. Region-of-interest (ROI)-evaluated data demonstrated that systematic errors due to temperature differences or wall interactions could be excluded in the setup (see ESI S3 and Fig. S14†). Moreover, neither the matrix size of the recorded R2,eff mapping nor the choice of the selective excitation and refocussing pulses had an impact on the quantitative results (Table S1†).
4.2 Transverse relaxation enhancement of reversibly bound Xe
For the first analytical experiment, the method was applied to a two-compartment phantom with the inner compartment containing 50 μM of CrA-ma and the outer one serving as host-free reference for determination of R2,0 (see Fig. 2a). Even-though this host concentration does not yield any detectable bound Xe in direct 129Xe-NMR (Fig. 1b; 16 averages; signal expected at ca. −166 ppm (ref. 25)), there was a significant loss of signal in T2-weighted 129Xe MR scans at areas where CrA-ma was present. This clearly demonstrates the advantages of using this type of hp spin reporters and its combination with imaging where multiple conditions can be analyzed simultaneously. Hyperpolarization (via DNP) has been implemented for RD measurements in a previous study.16 However, it mentioned the challenges of such single shot techniques: the non-self-renewing magnetization has to be used with care when multiple data points are required to isolate R2,ex. Whereas a significant sensitivity enhancement could be achieved, the system was still in fast exchange and showed only moderate amplitudes of R2,ex.The spin echo time series of sKWIC filter-reconstructed 129Xe MR images with two compartments (Fig. 2a) was evaluated for the signal evolution. Two exemplary selected pixels (blue: inner compartment; yellow: outer compartment) including corresponding fitting curves according to eqn (5) are plotted in Fig. 2b. The red curve additionally shows the difference signal with a maximum contrast between both pixels at TE = 3.39 s (4th Xe MR image in a). Pixelwise fitting yields the T2,eff and M0 maps shown in Fig. 2c and d, respectively. We reproducibly saw that the initial magnetization was higher in the inner compartment which we attributed to a difference in the HP Xe delivery. Overall, the maps show two areas of clearly distinct, homogeneous T2,eff distributions that allow further exchange quantification. It should be noticed that the long acquisition window for following the slow decay causes a large fraction of noise in the fast decaying signal. Moreover, pixel-wise evaluation shows a relative high noise level (compared to the ROI-based evaluation in the ESI S3†) and the dynamic range is relative small. The positive noise level causes a systematic error in the time constant when the starting amplitude is not orders of magnitude larger than the noise offset. We thus applied a careful analysis prior to fitting the data as explained in the ESI Fig. S15.†
Investigation of the slow and fast decaying spin echo trains yield T2,eff,S (6.18 s), T2,eff,F (1.80 s), M0,S, and M0,F for the inner and the outer compartment, respectively. With 1/T2,eff,S serving as the internal reference, 1/T2,eff,F − 1/T2,eff,S = 0.394 s−1 yields the relaxation enhancement for 50 μM CrA-ma and thus a relaxivity of r2 = 7.9 (s mM)−1 at 291 K. Solving the partial derivative of the difference of these two decays for ∂ΔS/∂TE = 0 yields TE = 3.3879 s for maximum signal contrast between both solutions, which shows excellent agreement between two individually picked pixels and the ensemble average throughout the compartments.
4.3 Relaxivity-derived Xe exchange rates
For a more detailed analysis of the effective R2,eff relaxation under different exchange conditions, we recorded T2,eff maps for different concentration of CrA-ma and at different temperatures controlled by the VTU. Data given in the ESI Fig. S1† illustrates that even for [CrA-ma] = 100 μM, no significant change in the line width of free Xe could be observed and that the signal of bound Xe was still too noisy under these conditions to directly quantify the exchange. Quantitative results for CrA-ma in DMSO are shown in Fig. 3a including relaxivities r2 obtained by linear fitting the data to eqn (3) (results also listed in Table 1). As expected, the exchange-induced relaxation increases with increasing temperature. Even at 10 μM host concentration, the relaxation rate is already more than doubled compared to the exchange-free conditions. At the same time, most observed values are still within a range R2,eff ≤ 1 s−1. This illustrates the high sensitivity that Xe provides for relaxometry measurements. The relaxivities for Xe with CrA-ma in DMSO ranged from 10.9 s−1 mM−1 at 295 K to 23.2 s−1 mM−1 at 310 K. The value for 295 K using the VTU is consistent with the 2-point determination from the relaxivity map in Fig. 2c including the host-free reference standard at room temperature (291 K). In comparison to 1H-MRI EuDOTA-agents (reported relaxivities range from 0.064 s−1 mM−1 to 0.167 s−1 mM−1 for comparable temperature range14), Xe's relaxivities are at least 2 orders of magnitude higher.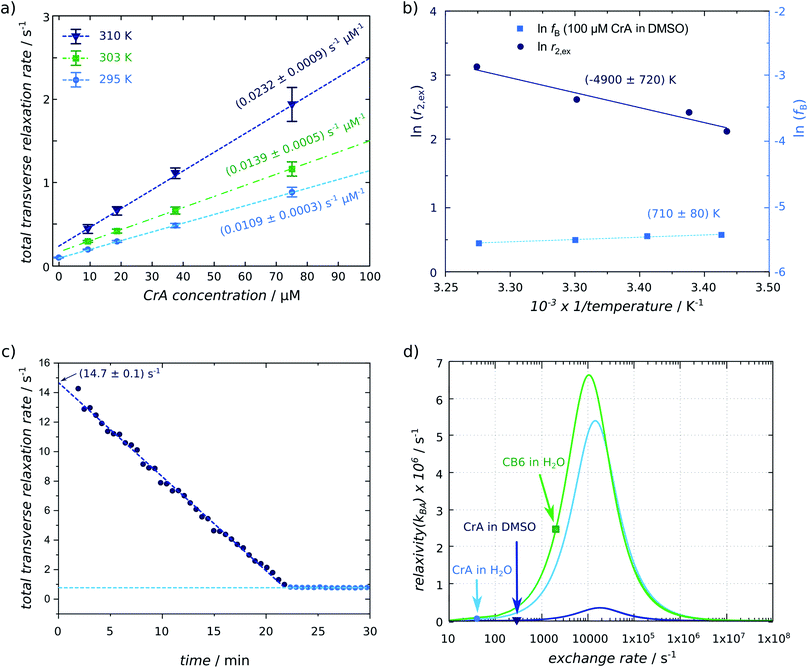 | ||
Fig. 3 (a) Xe relaxivity r2 (listed in Table 1) determined by a linear fit to eqn (3) for different concentrations of CrA-ma at three different temperatures (T = 295 K (light-blue circles), 303 K (green squares), 310 K (blue triangles)) (derived from 322 matrix size data sets). The error bars were derived from the standard deviation of the T2,eff fit for individual pixels. (b) Arrhenius plot for determining the activation energy from relaxivities obtained in (a) and from the relaxivity determined from data in Fig. 2; the additional term ln(fB) does not show a strong dependence on 1/T. (c) Linearly decaying relaxation rate of Xe for 16 μM CB6 in the presence of Lys being converted to Cad by LDC. The extrapolated starting relaxivity is 14.7 s−1. (d) Numerical simulation of the Swift–Connick relationship (using eqn (1) and substituting fB with β × ([host]/[Xe])25 and separating [host]) using the following parameters: CrA-ma in DMSO: Δω = −166 ppm = −18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 Hz, β = 9%, [Xe] = 2340 μM; CrA-ma in H2O: Δω = −132 ppm = −14 260 Hz, β = 9%, [Xe] = 2340 μM; CrA-ma in H2O: Δω = −132 ppm = −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520 Hz, β = 29%, [Xe] = 309 μM; CB6 in H2O: Δω = −96 ppm = −10 520 Hz, β = 29%, [Xe] = 309 μM; CB6 in H2O: Δω = −96 ppm = −10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 560 Hz, β = 49%, [Xe] = 309 μM; all systems at the same ambient temperature of 295 K exhibit very different exchange rates that are indicated by each marker (R2,B was small compared to kBA and Δω and, therefore, neglected). 560 Hz, β = 49%, [Xe] = 309 μM; all systems at the same ambient temperature of 295 K exhibit very different exchange rates that are indicated by each marker (R2,B was small compared to kBA and Δω and, therefore, neglected). | ||
The measured relaxation rate may include some small spin-diffusion (SD) contribution such as R2,eff,1 = R2,eff,1 + RSD. However, since we consider only the slope, this is irrelevant in the concentration series and thus the spin-diffusion contributions cancel each other out.
The relaxivities readily yield the gas turnover rate β × kBAviaeqn (4) because the Xe concentration in the sample is directly given through the applied pressure and Ostwald coefficient ([Xe] = 2.34 mM in our case). The experiment at 295 K yields β × kBA = 25.52 (% s−1) (units according to previous introduction of the gas turnover rate26,37). This is in excellent agreement with the value of 23 (% s−1) from a previous quantitative CEST with hyperpolarized Xe (qHyper-CEST) analysis.26 Notably, the slope in the relaxivity experiment can be determined with higher accuracy (0.8% standard deviation for the room temperature measurement) than β × kBA from qHyper-CEST.
The relationship fB × kBA = [host] × r2 from eqn (3) together with eqn (4) allows to derive fB × kBA for three different temperatures studied here. Further isolation of kBA is possible once fB is known (Fig. 2e). The latter can be achieved through a qHyper-CEST analysis. The results for both the pure Hyper-CEST and the combined Hyper-CEST/relaxivity determinations of kBA(T) are given in Table 1 and in the ESI S4.† They yield values that reflect the consistency of both approaches.
This technique has a potential for many applications since Xe is often used as a surrogate for O2 to study gas binding proteins.38,39 Significant chemical shifts have been observed in such proteins40–42 (with 60–80 ppm downfield shift) or macrocyclic hosts in ternary systems that are of pharmacological interest43,44 (ca. 100 ppm upfield shift). In these examples, protein/chemical engineering demonstrated efficient tuning of the exchange conditions that could be studied with this method.
4.4 Activation energy from Arrhenius plot
The set of T-dependent relaxivities in Fig. 3a was used to quantify the activation energy EA for the exchange of Xe with CrA-ma as outlined in the methods section. Fig. 3b shows a plot of ln(r2) versus 1/T with a slope m that yields EA = m × R = (41 ± 10) kJ mol−1. Critically, the values for fB determined from qHyper-CEST analysis at variable temperature T for 100 μM CrA-ma in DMSO do not show a great variance when plotting ln(fB) as a function of (1/T). In fact, its slope vanishes within the error of m and thus the Arrhenius plot of ln(r2) yields EA to a good approximation. The obtained value is comparable to that observed for a system with similar host–guest inclusion size, i.e. CH2Cl2 binding to cryptophane-C in 1,1,2,2-tetrachloroethane-d2 with 46–60 kJ mol−1.45,46The ability to determine EA from simple T2 relaxation measurements is particularly appealing for comparative studies between samples with different solvent conditions. Water can mediate host and guest solvation while other solvents presumably neither indirectly impact the exchange kinetics nor have a chance to enter the binding site themselves. Whereas this will be an important for many host–guest systems, we consider it beyond the scope of this proof-of-principle study to include a wider range of solvent conditions but encourage future studies to apply this technique for understanding the role of water in kinetic features.
4.5 Exchange kinetics with competitive binding
To further demonstrate the consistency between relaxometry and previous Hyper-CEST-based quantification of exchange dynamics, we also applied the R2,eff analysis to another host system for Xe, i.e., CB6. The CB[n]s are a family of macrocyclic hosts with reversible binding capabilities that are also considered for drug delivery. This host can also bind lysine (Lys) weakly but cadaverine (Cad) is a strong competitor that displaces Xe from the cavity. In a previous study, we had also monitored the changes in transverse 129Xe relaxation during the enzymatic conversion of Lys into Cad in the presence of lysine decarboxylase (LDC). However, the T2,eff values were not further analyzed to quantify the gas turnover. We have now re-evaluated this data and plotted R2,eff(t) for the reaction using 10 μg mL−1 of LDC (see Fig. 3c). This data set is also an impressive example how Xe provides useful conditions for easy and reliable re-delivery of HP magnetization to perform time-resolved studies despite the unavoidable one-time use of the specially prepared spin system. Knowing the starting condition [CB6] = 16 μM of Xe-accessible host and the end condition of totally Cad-occupied CB6, the difference R2,eff(t = 0) − R2,eff (t > 23 min) yields the relaxivity r2 for CB6. A highly linear behavior can be seen for this time curve until it reaches a stable plateau. A piece-wise fit yields R2,eff(t = 0) = 14.65 s−1 from the y-intercept and a plateau value R2,eff = 0.79 s−1. Thus, this host has a very high relaxivity of r2 = 13.86/16 (s mM)−1 = 866 (s mM)−1 under these buffer conditions.We see that whereas CrA-ma in DMSO showed already significantly higher relaxivity compared to reported 1H agents, CB6 in H2O was even 20-times higher than CrA-ma in DMSO. The magnitude of the different exchange contributions to r2 relaxivity can be compared in a Swift–Connick plot. Fig. 3d gives the plot of eqn (1) from the Swift–Connick equation for the three systems (CrA-ma in DMSO; CrA-ma in H2O; CB6 in H2O) studied so far in more detail. They all have their maximum when kex matches Δω. The three highlighted conditions represent the observed exchange rates. Both CrA-ma and CB6 can reach much larger values in water than CrA-ma in DMSO. This is because the occupancy of CrA-ma in DMSO is low while the solubility of Xe in this solvent is high. Pool B is thus inefficient to impact relaxation in pool A. We notice that the experimental conditions for CB6 in water are close to the maximum in this curve. It should thus be verified if the Swift–Connick equation still simplifies to fB × kBA for the exchange contribution. Δω is still the dominant term and R2,B can be neglected for noble gases that do not reside in immediate vicinity of a paramagnetic relaxation center. In the extreme case Δω = kex, the fraction in eqn (1) approaches the factor 1/2. For the general case of kex = Δω/x (x as a scaling factor), the fraction simplifies to (1 + 1/x2)−1. For CB6 in water, we have x ≈ 5 and thus the fraction is 25/26, i.e. a ca. 4% deviation from the approximation for slow exchange.
We thus assume that we can still evaluate the gas turnover to a good approximation even for this “faster” exchange condition. The amount of dissolved Xe was ca. 975 μM (from 5% Xe dissolved at 4.5 bar in water). This yields β × kBA = [Xe] × r2 = 840.15 (% s−1). This value is lower than β × kBA = 1029 (% s−1) from a previous qHyper-CEST analysis. However, the latter study was performed on a sample without ions or Lys that partially limits the Xe exchange efficiency.43 We thus indeed expect a reduced gas turnover rate from this present analysis. Again, the simple relaxometry study yields straightforward quantification of the gas exchange.
4.6 Advantages for detecting dilute populations
The high sensitivity of Xe relaxometry does not only come from hyperpolarization. We see that for detecting “hidden states”, it approaches the sensitivity of CEST experiments but does not require a saturation RF field to actively drive a magnetization decay. It is noteworthy that the Δω ∼ 10 kHz means that the transiently bound spins are set into anti-phase after only 50 μs and any exchange on the ms time scale causes rather efficient spin dephasing in the bulk pool while still fulfilling slow exchange conditions. Usually, slow exchange (Δω ≪ kex) implies that kex is limited. This has at least three undesirable consequences, particularly for dilute pools [B] that are limited due to solubility or availability of sample material: (1) only exchange dynamics outside the most common biochemically relevant regime fall into this category; (2) [B] ≪ [A] causes a practically undetectable exchange-induced spin–spin relaxation rate according to R2,ex = [B]/([A] + [B]) × kex that hardly differs from the exchange-free R2; (3) direct detection that could become feasible in slow exchange due to well defined separate Larmor frequencies is also impossible due the small peak of B that experiences prohibitive line broadening due to a small host occupancy (ca. < 10%; see ESI Fig. S1†). Regarding the additional sensitivity enhancements provided by hyperpolarization, our work benefits even more from such a HP ligand than the previous HP 19F approach by Liu et al.16 when taking the overall conditions into account. We demonstrate in the ESI S1† that with the accuracy of the linear fits in Fig. 3a, the detection limit for CrA-ma is ca. 2 μM around r.t. This is already quite impressive for a single shot NMR technique with spatial encoding. However, it is noteworthy that the use of Xe leaves room for significant improvements. First, one has to consider that the occupancy of this host in these solvent conditions is only β ≈ 9% (ref. 26) and thus only ca. 0.2 μM of CrA-ma are actively dephasing the unbound Xe spins that were present at comparatively high concentrations. This low efficiency is also illustrated by the comparative plots in Fig. 3d. A reduction of the bulk Xe concentration – while still maintaining a reasonable signal intensity – would allow to decrease the host concentration and still observe enhanced relaxation. Here, it pays off that Xe can be easily introduced into solvent samples in the high μM to low mM range by simple dispersion and the concentration can be regulated by the gas pressure. The fB values give some orientation what sensitivity might be achievable: Hyper-CEST analysis (ESI S4†) quantified a bound fraction of fB = 4 × 10−3 for 100 μM CrA-ma in DMSO. Hence, ≈2 μM correspond to fB = 8 × 10−5 as the detection limit from data in Fig. 3a. A conservative extrapolation of what sensitivity might be reachable is the following: unlocalized NMR requires less dissolved Xe and should presumably work with at least 100-fold reduced concentrations of what was used in this study (this is also supported by recent reports of optimized polarizers that easily achieve 3-fold higher polarization than the setup used here).47 The bulk pool could thus be reduced to 20 μM of dissolved Xe (which is comparable to the HP ligand concentration in the 19F DNP study). The same fB of 8 × 10−5 would then correspond to 1.6 nM for the analyte that induces the exchange relaxation (in a single-shot spin echo train acquisition).Such sensitivity is hardly achievable with other nuclei in relaxometry. The limited chemical shift range of typically detected nuclei (13C, 15N) in combination with typically occurring fluctuations (μs to ms timescale) implies fast exchange conditions. The dispersion curve is then gradual, follows a complex function, and the exchange-compensated relaxation rates for high νCP are already comparable or larger than the additional, exchange-induced spin–spin relaxation rate, R2,ex, contributions. This yields lower detection limits of 0.5% for the dilute pool when investigating sparsely populated states.18
To put the diamagnetic Xe systems into a perspective of T2,eff exchange agents, L-glutamine and glutamate have been investigated in a recent study and their T2,eff relaxivity caused by the exchange has been reported at 310 K to not exceed 0.102 s−1 mM−1 at pH = 7.2, respectively.48 This illustrates how potent these Xe hosts are as MRI contrast agents. However, it should be mentioned that in vivo conditions already start with much accelerated T2,eff relaxation compared to the reference sample in this study. It is thus also necessary to work with potent agents such that the change in the effective rate R2,eff is significant from the reference condition. The result could be like superparamagnetic iron oxide particles that cause signal cancellation in MRI scans for nearby water molecules.
5 Conclusions
A method has been proposed that quantifies relaxation of hyperpolarized Xe in a “single-shot” in a few seconds after a single supply of HP Xe. We could obtain very accurate relaxivity values for gas-binding hosts due to the exchange-dominated spin dephasing where the intrinsic, exchange-free relaxation readily becomes dominated by the terms of the highly simplified Carver–Richards equation. This allows determination of the gas turnover rate and can also be expanded to obtain activation energies from Arrhenius plots of the temperature-dependent change in this turnover. The golden angle-based radial k-space sampling single-shot quantification mapping immensely speeds up the acquisition time for quantitative data, being at least 32-fold faster than Cartesian k-space sampling as gold standard method. More importantly, it solves T2,eff quantification problems with “single use” magnetization that does not self-renew, and thus make optimum use of the enhanced magnetization. The single-shot encoding makes this type of T2,eff quantification also very suitable for other HP NMR protocols that rely on either DNP or PHIP as HP technique where a re-delivery is challenging or impossible – a very important capability for biochemical or in vivo applications. NMR of dissolved Xe does, nonetheless, comprise the option of easy re-delivery and allowed time-resolved relaxometry studies to follow an enzymatic reaction through relaxometry. Applications will have great impact to quantify suitable host–guest exchange rates and single-shot mapping of their binding activation energy. We envision this method with broad range of possible applications and becoming useful for various other systems in which Xe has already been used to explore hydrophobic binding sites.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Jörg Döpfert and Christopher Witte for discussions regarding implementation and evaluation of the spatial encoding. The Deutsche Forschungsgemeinschaft is acknowledged for support of this work through the Koselleck Program under grant no. SCHR 995/5-1. Part of this work was also supported by the Human Frontiers Science Program through program grant no. RGP0050/2016.Notes and references
- E. Z. Eisenmesser, D. A. Bosco, M. Akke and D. Kern, Science, 2002, 295, 1520–1523 CrossRef CAS.
- D. M. Korzhnev, X. Salvatella, M. Vendruscolo, A. A. Di Nardo, A. R. Davidson, C. M. Dobson and L. E. Kay, Nature, 2004, 430, 586–590 CrossRef CAS.
- T. J. Swift and R. E. Connick, J. Chem. Phys., 1962, 37, 307–320 CrossRef CAS.
- J. Döpfert, M. Schnurr, M. Kunth, H. M. Rose, A. Hennig and L. Schröder, Magn. Reson. Chem., 2018, 56, 679–688 CrossRef.
- Z. Lin, M. L. Shelby, D. Hayes, K. A. Fransted, L. X. Chen and M. J. Allen, Dalton Trans., 2014, 43, 16156–16159 RSC.
- K. Henzler-Wildman and D. Kern, Nature, 2007, 450, 964–972 CrossRef CAS.
- A. J. Baldwin, Nat. Chem. Biol., 2009, 5, 808–814 CrossRef CAS.
- O. Millet, J. P. Loria, C. D. Kroenke, M. Pons and A. G. Palmer, J. Am. Chem. Soc., 2000, 122, 2867–2877 CrossRef CAS.
- M. Tollinger, N. R. Skrynnikov, F. A. A. Mulder, J. D. Forman-Kay and L. E. Kay, J. Am. Chem. Soc., 2001, 123, 11341–11352 CrossRef CAS.
- J. S. Zintsmaster, B. D. Wilson and J. W. Peng, J. Am. Chem. Soc., 2008, 130, 14060–14061 CrossRef CAS.
- T. Moschen, C. H. Wunderlich, R. Spitzer, J. Levic, R. Micura, M. Tollinger and C. Kreutz, Angew. Chem., Int. Ed., 2015, 54, 560–563 CAS.
- M. D. Gomes, P. Dao, K. Jeong, C. C. Slack, C. C. Vassiliou, J. A. Finbloom, M. B. Francis, D. E. Wemmer and A. Pines, J. Am. Chem. Soc., 2016, 138, 9747–9750 CrossRef CAS.
- J. Carver and R. Richards, J. Magn. Reson., 1972, 6, 89–105 CAS.
- T. C. Soesbe, M. E. Merritt, K. N. Green, F. A. Rojas-Quijano and A. D. Sherry, Magn. Reson. Med., 2011, 66, 1697–1703 CrossRef CAS.
- N. N. Yadav, J. Xu, A. Bar-Shir, Q. Qin, K. W. Chan, K. Grgac, W. Li, M. T. McMahon and P. C. van Zijl, Magn. Reson. Med., 2014, 72, 823–828 CrossRef CAS.
- M. Liu, Y. Kim and C. Hilty, Anal. Chem., 2017, 89, 9154–9158 CrossRef CAS.
- A. J. Baldwin, J. Magn. Reson., 2014, 244, 114–124 CrossRef CAS.
- H. Koss, M. Rance and A. G. Palmer, Biochemistry, 2018, 57, 4753–4763 CrossRef CAS.
- D. Davis, M. Perlman and R. London, J. Magn. Reson., Ser. B, 1994, 104, 266–275 CrossRef CAS.
- Z. Luz and S. Meiboom, J. Chem. Phys., 1963, 39, 366–370 CrossRef CAS.
- A. Allerhand and H. S. Gutowsky, J. Chem. Phys., 1964, 41, 2115–2126 CrossRef CAS.
- A. Allerhand and H. S. Gutowsky, J. Chem. Phys., 1965, 42, 1587–1599 CrossRef CAS.
- T. C. Soesbe, S. J. Ratnakar, M. Milne, S. Zhang, Q. N. Do, Z. Kovacs and A. D. Sherry, Magn. Reson. Med., 2014, 71, 1179–1185 CrossRef CAS.
- I. Daryaei and M. Pagel, Res. Rep. Nucl. Med., 2015, 5, 19–32 Search PubMed.
- M. Kunth, C. Witte and L. Schröder, J. Chem. Phys., 2014, 141, 194202 CrossRef CAS.
- M. Kunth, C. Witte, A. Hennig and L. Schröder, Chem. Sci., 2015, 6, 6069–6075 RSC.
- C. Witte, M. Kunth, J. Döpfert, F. Rossella and L. Schröder, J. Visualized Exp., 2012, 67, e4268 Search PubMed.
- C. Witte, M. Kunth, F. Rossella and L. Schröder, J. Chem. Phys., 2014, 140, 084203 CrossRef CAS.
- H. L. Clever, Krypton, Xenon and Radon – Gas Solubilities, Pergamon, Oxford, Chemistry Department, Emory University, Atlanta, GA, USA, 2nd edn, 1979 Search PubMed.
- B. M. Goodson, J. Magn. Reson., 2002, 155, 157–216 CrossRef CAS.
- M. Kunth, C. Witte and L. Schröder, NMR Biomed., 2015, 28, 601–606 CrossRef CAS.
- A. Farhadi, G. Ho, M. Kunth, B. Ling, A. Lakshmanan, G. J. Lu, R. W. Bourdeau, L. Schröder and M. G. Shapiro, AIChE J., 2018, 64, 2927–2933 CrossRef CAS.
- S. Winkelmann, T. Schaeffter, T. Koehler, H. Eggers and O. Doessel, IEEE Trans. Med. Imag., 2007, 26, 68–76 Search PubMed.
- M. Kunth, N. Seiberlich, P. Ehses, V. Gulani and M. Griswold, ISMRM - Stockholm, 2010, p. 2895 Search PubMed.
- P. Ehses, N. Seiberlich, D. Ma, F. A. Breuer, P. M. Jakob, M. A. Griswold and V. Gulani, Magn. Reson. Med., 2013, 69, 71–81 CrossRef.
- J. A. Fessler and B. P. Sutton, IEEE Trans. Signal Process., 2003, 51, 560–574 CrossRef.
- M. Kunth, G. J. Lu, C. Witte, M. G. Shapiro and L. Schröder, ACS Nano, 2018, 12, 10939–10948 CrossRef CAS.
- J. Cohen, A. Arkhipov, R. Braun and K. Schulten, Biophys. J., 2006, 91, 1844–1857 CrossRef CAS.
- B. W. Roose, S. D. Zemerov and I. J. Dmochowski, Methods Enzymol., 2018, 602, 249–272 CAS.
- Y. Wang, B. W. Roose, E. J. Palovcak, V. Carnevale and I. J. Dmochowski, Angew. Chem., 2016, 55, 8984–8987 CrossRef CAS.
- B. W. Roose, S. D. Zemerov, Y. Wang, M. A. Kasimova, V. Carnevale and I. J. Dmochowski, ChemPhysChem, 2019, 20, 260–267 CrossRef CAS.
- B. W. Roose, S. D. Zemerov and I. J. Dmochowski, Chem. Sci., 2017, 8, 7631–7636 RSC.
- M. Schnurr, J. Sloniec-Myszk, J. Döpfert, L. Schröder and A. Hennig, Angew. Chem., 2015, 54, 13444–13447 CrossRef CAS.
- K. Kim, N. Selvapalam, Y. H. Ko, K. M. Park, D. Kim and J. Kim, Chem. Soc. Rev., 2007, 36, 267–279 RSC.
- Z. Takacs, M. Soltesova, J. Kowalewski, J. Lang, T. Brotin and J.-P. Dutasta, Magn. Reson. Chem., 2013, 51, 19–31 CrossRef CAS.
- J. Canceill, L. Lacombe and A. Collet, J. Am. Chem. Soc., 1985, 107, 6993–6996 CrossRef CAS.
- J. R. Birchall, R. K. Irwin, P. Nikolaou, E. V. Pokochueva, K. V. Kovtunov, I. V. Koptyug, M. J. Barlow, B. M. Goodson and E. Y. Chekmenev, J. Magn. Reson., 2020, 316, 106755 CrossRef CAS.
- C. G. Joo, S.-H. Yang, Y. Choi, H.-Y. Son, D.-H. Kim and Y.-M. Huh, Magn. Reson. Med., 2020, 84, 2055–2062 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc04835f |
| This journal is © The Royal Society of Chemistry 2021 |