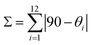Open Access Article
Open Access ArticleInterplay between spin crossover and proton migration along short strong hydrogen bonds†
Verónica
Jornet-Mollá
 a,
Carlos
Giménez-Saiz
a,
Carlos
Giménez-Saiz
 a,
Laura
Cañadillas-Delgado
a,
Laura
Cañadillas-Delgado
 b,
Dmitry S.
Yufit
b,
Dmitry S.
Yufit
 c,
Judith A. K.
Howard
c,
Judith A. K.
Howard
 *c and
Francisco M.
Romero
*c and
Francisco M.
Romero
 *a
*a
aInstituto de Ciencia Molecular, Universitat de València, P. O. Box 22085, 46071 València, Spain. E-mail: fmrm@uv.es
bInstitut Laue-Langevin, 6 Rue Jules Horowitz, BP 156, 38042 Grenoble Cedex 9, France
cDepartment of Chemistry, Durham University, Durham DH1 3LE, UK
First published on 16th November 2020
Abstract
The iron(II) salt [Fe(bpp)2](isonicNO)2·HisonicNO·5H2O (1) (bpp = 2,6-bis(pyrazol-3-yl)pyridine; isonicNO = isonicotinate N-oxide anion) undergoes a partial spin crossover (SCO) with symmetry breaking at T1 = 167 K to a mixed-spin phase (50% high-spin (HS), 50% low-spin (LS)) that is metastable below T2 = 116 K. Annealing the compound at lower temperatures results in a 100% LS phase that differs from the initial HS phase in the formation of a hydrogen bond (HB) between two water molecules (O4W and O5W) of crystallisation. Neutron crystallography experiments have also evidenced a proton displacement inside a short strong hydrogen bond (SSHB) between two isonicNO anions. Both phenomena can also be detected in the mixed-spin phase. 1 undergoes a light-induced excited-state spin trapping (LIESST) of the 100% HS phase, with breaking of the O4W⋯O5W HB and the onset of proton static disorder in the SSHB, indicating the presence of a light-induced activation energy barrier for proton motion. This excited state shows a stepped relaxation at T1(LIESST) = 68 K and T2(LIESST) = 76 K. Photocrystallography measurements after the first relaxation step reveal a single Fe site with an intermediate geometry, resulting from the random distribution of the HS and LS sites throughout the lattice.
Introduction
Interest in switchable molecular materials is being fuelled by the potential applications of these compounds as smart sensors and in high-density information storage devices.1 One of the most important advantages of molecule-based switchable solids is the modular approach to their synthesis. This makes it possible to introduce multiple functions in the same material.2 Attention is being drawn to the simultaneous observation of switchable dielectric and magnetic transformations in molecular materials.3 In particular, to the subject of magneto(di)electric coupling, a phenomenon that can help to reduce the energy needed for the electronic readout of information.4Spin crossover (SCO) metal complexes are suitable candidates for these synergic effects. These well-known bistable materials are able to interconvert between different spin states under an external perturbation, such as light irradiation, temperature change or application of pressure.5 Further, SCO is always accompanied by strong distortions of the metal coordination sphere that can lead to changes in the local electric dipoles. In many cases, SCO is associated with structural phase transitions that involve a breaking of symmetry and/or a concerted displacive motion of the molecules.6–8 This may result in enhanced dielectric responses.
Among the different compounds exhibiting SCO behaviour, we turned our attention to [Fe(bpp)2]2+ complexes (bpp = 2,6-bis(pyrazol-3-yl)pyridine, Chart 1).9,10 The reasons for that are manifold: first, these iron(II) complexes show light-induced excited-state spin trapping (LIESST) effects with relatively high relaxation temperatures;11 secondly, they have four pyrazolyl N–H moieties that can act as hydrogen-bond donors towards polytopic anionic hydrogen-bond acceptors.12 The high directionality and strength of hydrogen bonds allow for designing SCO salts with non-centrosymmetric structures.13 Further, the adventitious presence of solvent molecules acting as H-bond acceptors is responsible for the marked dependence of the magnetic properties of these materials on the extent of solvation.14,15 Following these design principles, we have recently obtained acentric packings based on low-spin [Fe(bpp)2]2+ isonicotinate salts. Reversible removal of solvent molecules yields a polar structure where half of the Fe2+ cations undergo crossover to the high-spin state. This allows for switching the electric polarisation and the magnetic moment of the material in the same temperature range.13
One of the main drawbacks of our approach is the high stabilisation of the polar phase, in such a way that the ferroelectric phase transition could not be detected even at high temperatures (T = 493 K). The high strength of hydrogen bonding hinders the relative displacement of positive and negative charges needed for reversal of electric polarisation.
In order to circumvent these problems, we focus now our interest in the dynamic processes at the basis of ferroelectric phase transitions. One of these processes is proton displacement between ditopic hydrogen-bond acceptors. Indeed, Rochelle salt and KH2PO4, the first ferroelectrics to be discovered, rely on hydrogen bonding.16 One of the first examples of a single-component organic ferroelectric crystal was dabcoHClO4 (dabco = 1,4-diazabicyclo[2.2.2]octane), in which the polarisation of the material depends on proton displacement along hydrogen-bonded chains.17 Also, ferroelectric cocrystals, with two or more components, that undergo a change of polarisation when protons shuttle between an acid and a base are being investigated.18 In these systems, it is important to match the pKa of the hydrogen bond acceptor and donor. Thus, binary systems composed of anilic acids and several hydrogen-bond acceptors like phenazine,19 5,5′-dimethyl-2,2′-bipyridine20 or the ‘proton sponge’ 2,3,5,6-tetra(2-pyridinyl)pyrazine21 show ferroelectric behaviour based on proton dynamics. Proton displacement usually takes place along short strong hydrogen bonds (SSHBs), in which the proton is trapped between the HB donor and the HB acceptor in a single or a low-barrier double potential well.22 As in the case of SCO, this effect can also be responsive to an external perturbation, including the application of an electric field or changes in temperature and pressure.23,24 Further, many enzymatic reactions involve proton transfer in SSHBs.25 The study of systems combining SCO and proton transfer can thus provide interesting synergies in terms of physical properties and also models of enzymatic action (considering SCO as mimicking the allosteric changes that activate the enzyme towards proton transfer). With these ideas in mind, we undertake now the study of a cocrystal comprising a [Fe(bpp)2]2+ SCO typical cation and a carboxyl(ate)-based SSHB. Herein, we describe the structural and (photo)magnetic properties of [Fe(bpp)2](isonicNO)2·HisonicNO·5H2O (1), a SCO salt containing isonicotinic acid N-oxide (Chart 1) both in its free and deprotonated form. We will show that spin crossover in 1 is accompanied by proton migration and hydrogen bond formation in two steps, with breaking of symmetry and formation of a metastable high-spin/low-spin (HS/LS) pair. Details of the synthesis and characterisation of 1 are provided in the ESI.†
Results and discussion
X-ray crystal structure at 240 K and 210 K
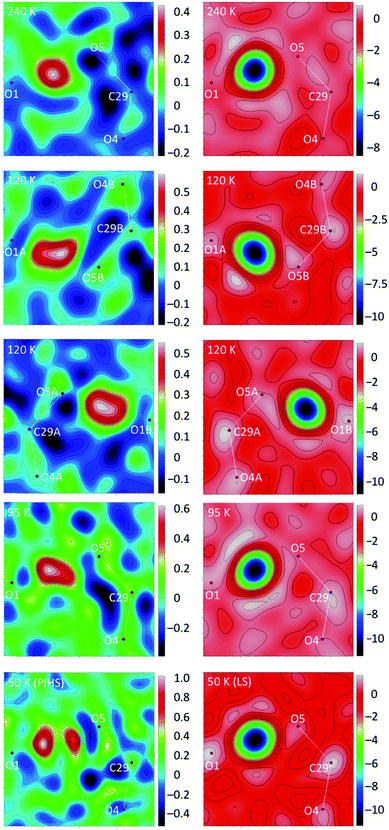
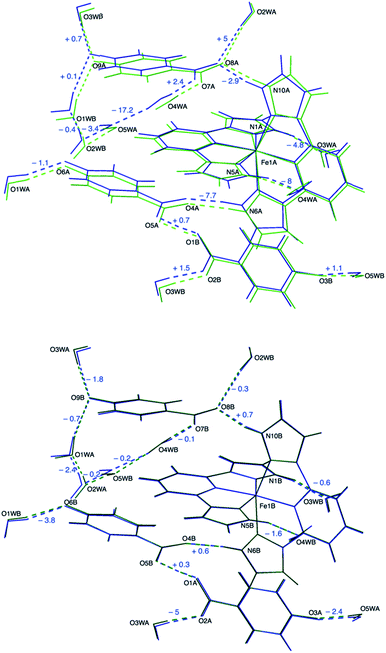
The crystal structure of 1 at 240 K (triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , Table S1†) contains a single [Fe(bpp)2]2+ cation (Fig. 1) lying in a general position, five water molecules and three inequivalent isonicotinate N-oxide anions denoted (3), (6) and (9) after the numbering of the oxygen atoms of the corresponding N-oxide groups. In isonicNO(3), the N-oxide function acts as a monotopic H-bond acceptor towards a water molecule (O5W), while the carboxylate unit establishes two hydrogen bonds in a syn, syn bridging mode: one with a H2O molecule (O3W) and a very strong one with isonicNO(6). The strength of this H-bond and its marked covalent character are confirmed by the very short distance between the two heteroatoms (O1⋯O5: 2.4247(17) Å), well below the threshold proposed for temperature-dependent proton migration along O–H⋯O SSHBs.23 It is known that the X-ray refined positions of this type of H atom are unable to model the normally anisotropic shape of the bonding electron density, giving atomic coordinates that are unpredictably shifted from their real values.26 This translates into very high atomic displacement parameters in comparison to other H atoms present in the structure, as it is indeed our case (Table S2†). A proper description of this interaction relies then on the study of Fourier differential density maps and their comparison to neutron data. Fig. 2 shows an image of the electron density across the O1⋯O5 bond obtained by a Fourier differential analysis. It shows a spherical shape, corresponding to a H atom (H1O) located in an almost linear arrangement and approximately halfway between the two carboxylate anions, with O–H distances that are similar (distances to the maximum density peak are listed in Table S3†). This is consistent with very strong three-center four-electron σ-bonding (Speakman–Hadzi bond).27 In agreement with this picture, the two C–O bond distances of the carboxylate anions involved in this hydrogen bond interaction (C23–O1: 1.281(2) Å; C29–O5: 1.279(2) Å) are similar and much longer than those observed for the corresponding C
, Table S1†) contains a single [Fe(bpp)2]2+ cation (Fig. 1) lying in a general position, five water molecules and three inequivalent isonicotinate N-oxide anions denoted (3), (6) and (9) after the numbering of the oxygen atoms of the corresponding N-oxide groups. In isonicNO(3), the N-oxide function acts as a monotopic H-bond acceptor towards a water molecule (O5W), while the carboxylate unit establishes two hydrogen bonds in a syn, syn bridging mode: one with a H2O molecule (O3W) and a very strong one with isonicNO(6). The strength of this H-bond and its marked covalent character are confirmed by the very short distance between the two heteroatoms (O1⋯O5: 2.4247(17) Å), well below the threshold proposed for temperature-dependent proton migration along O–H⋯O SSHBs.23 It is known that the X-ray refined positions of this type of H atom are unable to model the normally anisotropic shape of the bonding electron density, giving atomic coordinates that are unpredictably shifted from their real values.26 This translates into very high atomic displacement parameters in comparison to other H atoms present in the structure, as it is indeed our case (Table S2†). A proper description of this interaction relies then on the study of Fourier differential density maps and their comparison to neutron data. Fig. 2 shows an image of the electron density across the O1⋯O5 bond obtained by a Fourier differential analysis. It shows a spherical shape, corresponding to a H atom (H1O) located in an almost linear arrangement and approximately halfway between the two carboxylate anions, with O–H distances that are similar (distances to the maximum density peak are listed in Table S3†). This is consistent with very strong three-center four-electron σ-bonding (Speakman–Hadzi bond).27 In agreement with this picture, the two C–O bond distances of the carboxylate anions involved in this hydrogen bond interaction (C23–O1: 1.281(2) Å; C29–O5: 1.279(2) Å) are similar and much longer than those observed for the corresponding C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups (C23–O2: 1.233(2) Å; C29–O4: 1.235(2) Å). One carbonyl group is hydrogen-bonded to a pyrazol NH fragment of a bpp ligand with a relatively high distance (N6⋯O4: 2.8357(18) Å), in agreement with its poor electron donating character. Finally, O(6), the N-oxide oxygen atom, establishes only one hydrogen-bond with another H2O molecule (O1W). The third anion, isonicNO(9), is the only one where the N-oxide moiety acts as a ditopic H-bond acceptor towards two H2O molecules (O1W and O3W). In general, N-oxides are poor electron donors and this is translated here in long H-bond distances, higher than 2.8 Å. The carboxylate fragment O7–C35–O8 of isonicNO(9) binds to three H-bond donors. Both carboxylate oxygen atoms O7 and O8 are connected to water molecules (O4W and O2W, respectively) but the latter is also bound in a bifurcated manner to the second pyrazol NH fragment of the same bpp ligand (N10⋯O8: 2.7179(18) Å). Thus, one of the bpp ligands is hydrogen-bonded through its pyrazol NH groups to two different isonicNO molecules, whereas the second bpp ligand is connected via hydrogen bonding to two distinct water molecules (N5⋯O4W: 2.832(2) Å and N1⋯O3W: 2.7031(19) Å).
O groups (C23–O2: 1.233(2) Å; C29–O4: 1.235(2) Å). One carbonyl group is hydrogen-bonded to a pyrazol NH fragment of a bpp ligand with a relatively high distance (N6⋯O4: 2.8357(18) Å), in agreement with its poor electron donating character. Finally, O(6), the N-oxide oxygen atom, establishes only one hydrogen-bond with another H2O molecule (O1W). The third anion, isonicNO(9), is the only one where the N-oxide moiety acts as a ditopic H-bond acceptor towards two H2O molecules (O1W and O3W). In general, N-oxides are poor electron donors and this is translated here in long H-bond distances, higher than 2.8 Å. The carboxylate fragment O7–C35–O8 of isonicNO(9) binds to three H-bond donors. Both carboxylate oxygen atoms O7 and O8 are connected to water molecules (O4W and O2W, respectively) but the latter is also bound in a bifurcated manner to the second pyrazol NH fragment of the same bpp ligand (N10⋯O8: 2.7179(18) Å). Thus, one of the bpp ligands is hydrogen-bonded through its pyrazol NH groups to two different isonicNO molecules, whereas the second bpp ligand is connected via hydrogen bonding to two distinct water molecules (N5⋯O4W: 2.832(2) Å and N1⋯O3W: 2.7031(19) Å).
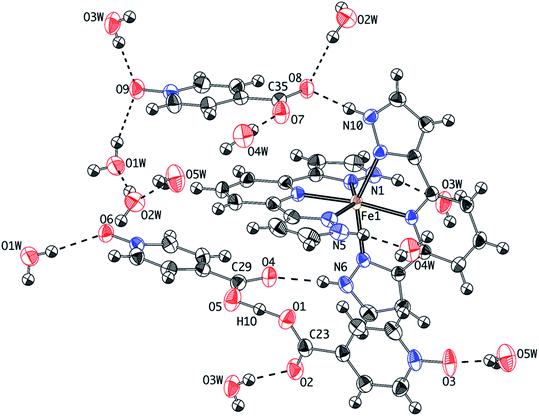 | ||
| Fig. 1 Thermal ellipsoid plot of the crystal structure of 1 at 240 K showing the hydrogen-bonding connectivity. | ||
As expected, the two terdentate bpp ligands bind in meridional positions of the iron(II) coordination sphere and are arranged in almost perpendicular planes, with Fe–N bond lengths ranging from 2.115 Å to 2.190 Å (Table S4†). This is in agreement with 100% of the Fe2+ cations in the HS state being determined from magnetic measurements. A HS phase stable at 240 K is unusual for [Fe(bpp)2]2+ salts of simple anions in their hydrated forms.14,28 For comparison, the isonicotinate salt [Fe(bpp)2](isonic)2·2H2O exists only in the LS state even at temperatures much higher than room temperature.13 Noteworthy is the fact that the N-oxide moiety is not involved in hydrogen bonds with the [Fe(bpp)2]2+ cation, probably due to the weaker H-bond accepting character of pyridine N-oxides with respect to pyridines. This decreases the electron density of the non-coordinating nitrogen atoms and leads to weaker N–Fe donor-metal σ-interactions, destabilising the LS state.29
Another aspect of the crystal packing of [Fe(bpp)2]2+ salts with an impact on the SCO abruptness and hysteretic behaviour is the presence of π–π stacking interactions between adjacent bpp ligands. In 1, these contacts organise alternating chains of [Fe(bpp)2]2+ complexes along the c axis (Fig. S1a†). Isonicotinate N-oxide anions are located in the interchain space, preventing the formation of the terpyridine embrace motif commonly found in these salts. A description of these intermolecular contacts and their variation with temperature is given in Fig. S1.†
At 210 K, the crystal structure of 1 is essentially the same. The Fe–N lengths are slightly shorter, ranging from 2.106 Å to 2.182 Å, but still pointing to a HS state for this cation (Table S4†). All H-bond distances (Table 1), including those involving only isonicNO anions and/or H2O molecules, show a small decrease with respect to the values observed at 240 K. This is expected as a consequence of thermal contraction.
| H-bond | 240 K (HS) | 210 K (HS) | 120 K (HS/LS)a | 120 K (HS/LS)b | 95 K (LS) | 50 K (PIHS)c | 50 K (PIHSrel)d | 95 K (LS)e |
|---|---|---|---|---|---|---|---|---|
| a Contacts within the A sublattice, except for O1WA⋯O9B, O3WA⋯O9B and O5WA⋯O2WB. b Contacts within the B sublattice, except for O1WB⋯O9A, O3WB⋯O9A and O5WB⋯O2WA. c Photoinduced high-spin phase. d Structure obtained from partial relaxation of the PIHS phase. e Structure obtained after full relaxation of the PIHS phase. | ||||||||
| N1⋯O3W | 2.7031(19) | 2.6982(18) | 2.6845(19) | 2.6427(19) | 2.638(3) | 2.6880(18) | 2.662(2) | 2.645(3) |
| N5⋯O4W | 2.832(2) | 2.825(2) | 2.808(2) | 2.7442(19) | 2.727(3) | 2.8188(18) | 2.777(2) | 2.741(3) |
| N6⋯O4 | 2.8357(18) | 2.8320(16) | 2.8335(18) | 2.7507(18) | 2.758(3) | 2.8324(17) | 2.8017(19) | 2.757(3) |
| N10⋯O8 | 2.7179(18) | 2.7155(16) | 2.7235(18) | 2.6883(17) | 2.697(3) | 2.7091(17) | 2.711(2) | 2.714(3) |
| O1W⋯O6 | 2.8488(18) | 2.8402(16) | 2.7889(17) | 2.8158(17) | 2.778(2) | 2.8272(16) | 2.8037(17) | 2.780(3) |
| O1W⋯O9 | 2.838(2) | 2.8311(17) | 2.8231(17) | 2.8153(17) | 2.816(3) | 2.8055(17) | 2.8054(18) | 2.823(3) |
| O2W⋯O1W | 2.814(2) | 2.8030(18) | 2.7890(18) | 2.7694(18) | 2.765(3) | 2.7955(17) | 2.7780(18) | 2.771(3) |
| O2W⋯O8 | 2.892(2) | 2.8883(17) | 2.8786(17) | 2.9321(18) | 2.928(3) | 2.8616(17) | 2.8857(18) | 2.938(3) |
| O3W⋯O9 | 2.892(2) | 2.8832(18) | 2.8696(18) | 2.8453(17) | 2.853(3) | 2.8579(17) | 2.8503(19) | 2.857(3) |
| O3W⋯O2 | 2.7630(18) | 2.7563(16) | 2.7603(17) | 2.6946(17) | 2.710(3) | 2.7511(17) | 2.7313(18) | 2.713(3) |
| O4W⋯O7 | 2.723(2) | 2.7181(17) | 2.7135(18) | 2.7384(17) | 2.737(3) | 2.7136(17) | 2.7222(18) | 2.736(3) |
| O4W⋯O5W | 3.062(2) | 3.044(2) | 3.0256(19) | 2.8562(19) | 2.858(3) | 3.0070(18) | 2.934(2) | 2.853(3) |
| O5W⋯O3 | 2.743(2) | 2.7372(18) | 2.7437(18) | 2.7091(18) | 2.722(3) | 2.7397(17) | 2.7313(17) | 2.709(3) |
| O5W⋯O2W | 2.854(2) | 2.8455(19) | 2.8387(19) | 2.8072(18) | 2.803(3) | 2.8410(18) | 2.8204(19) | 2.802(3) |
X-ray crystal structure at 120 K
Upon cooling to 120 K, 1 undergoes a crystallographic phase transition. The space group (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) remains the same but the unit cell volume is almost doubled with respect to 240 K (Table S1†). There are now two crystallographically independent [Fe(bpp)2]2+ cations, ten water molecules and six inequivalent isonicotinate N-oxide anions (with two protons) but the changes in the crystal packing are minor. However, the coordination spheres of the two independent Fe2+ cations, Fe1A and Fe1B, are very different (Fig. 3). Whereas the Fe1A–N bond distance range (2.116 Å to 2.188 Å) is very similar to that observed at 240 K (Table S4†), Fe1B–N bond distances (between 1.934 Å and 2.001 Å) are considerably shorter and typical of Fe(II) LS centers. As expected for a 1A1g electronic ground state resulting from the d6 electron configuration, the LS site Fe1B shows a less distorted octahedral coordination sphere. It has been shown that the ground spin state of [Fe(bpp)2]2+ SCO complexes can be correlated to two independent parameters: (i) the trans N–Fe–N angle φ, given by the coordination of the pyridine fragments; (ii) the octahedral distortion parameter Σ, defined by the sum of deviations from 90° of the 12 cis angles of the coordination sphere.30
) remains the same but the unit cell volume is almost doubled with respect to 240 K (Table S1†). There are now two crystallographically independent [Fe(bpp)2]2+ cations, ten water molecules and six inequivalent isonicotinate N-oxide anions (with two protons) but the changes in the crystal packing are minor. However, the coordination spheres of the two independent Fe2+ cations, Fe1A and Fe1B, are very different (Fig. 3). Whereas the Fe1A–N bond distance range (2.116 Å to 2.188 Å) is very similar to that observed at 240 K (Table S4†), Fe1B–N bond distances (between 1.934 Å and 2.001 Å) are considerably shorter and typical of Fe(II) LS centers. As expected for a 1A1g electronic ground state resulting from the d6 electron configuration, the LS site Fe1B shows a less distorted octahedral coordination sphere. It has been shown that the ground spin state of [Fe(bpp)2]2+ SCO complexes can be correlated to two independent parameters: (i) the trans N–Fe–N angle φ, given by the coordination of the pyridine fragments; (ii) the octahedral distortion parameter Σ, defined by the sum of deviations from 90° of the 12 cis angles of the coordination sphere.30For Fe1B the φ angle increases (approaching to 180°) in comparison with Fe1A and the HS site at 240 K (Table S5†). The parameter Σ equals 100.54°, a value characteristic of a LS configuration and much lower than those observed for HS centers.9
A very interesting point arises after examining the second coordination sphere, defined by the hydrogen bonds between the four NH pyrazole functions and the four H-bond acceptors (two water molecules and two isonicotinate N-oxide anions). It is found (Table 1) that hydrogen bonds are stronger for the Fe1B site (mean distance N⋯O: 2.706 Å) as compared to the Fe1A site (mean distance N⋯O: 2.762 Å), the latter being similar to the H-bond distances observed at 240 K (mean value N⋯O: 2.772 Å). The increase in H-bond strength as the Fe(II) complex undergoes SCO to the LS state can be explained in terms of an electrostatic model: the LS state has a lower volume and, therefore, a higher charge density. This reinforces electrostatic attraction to the negative charges of the anions (and water dipoles), thus leading to shorter H-bond distances.
There are only a couple of examples in the literature reporting HS and LS phases of the same hydrogen-bonded [Fe(bpp)2]2+ complex in the same environment. For instance, the structure of [Fe(bpp)2](ClO4)2·1.75CH3COCH3·1.5Et2O displays a gradual and incomplete spin transition near 205 K.31 The HS and LS phases are isostructural and both contain two inequivalent Fe2+ cations in the asymmetric unit. Hydrogen bonds (mean distance N⋯O: 2.834 Å) are stronger for the LS phase as compared to the HS phase (mean distance N⋯O: 2.871 Å). Another example is the anhydrous isonicotinate salt [Fe(bpp)2](isonic)2, that presents a partial spin crossover centered at 324 K. In this case, the HS and LS phases are isostructural and possess only one independent Fe center at both temperatures. Here again, an increase in H-bond strength (mean distance N⋯acceptor: 2.669 Å) is observed in the LS phase in comparison with the HS phase (mean distance N⋯acceptor: 2.708 Å).13
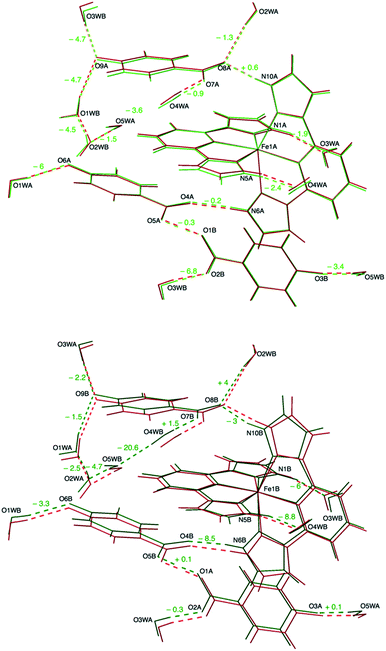
In our case, the main consequence of the increase of the hydrogen bond strength in the second coordination sphere of the LS Fe1B center is a shortening of most other hydrogen bonds with respect to the values obtained for equivalent positions near the HS Fe1A cation, the latter being closer to those measured at 240 K (Table 1). An elongation of the hydrogen bond distance is only observed in two cases. For instance, in the bifurcated H bond mentioned above, as the distance between the carboxylate anion and the LS Fe1B complex becomes shorter (N10B⋯O8B: 2.6883(17) Å versus N10A⋯O8A: 2.7235(18) Å), the distance with respect to the water molecule increases (O2WB⋯O8B: 2.9321(18) Å versus O2WA⋯O8A: 2.8786(17) Å). Besides this, the most significant difference between A and B sublattices is the formation of a hydrogen bond between O4WB and O5WB (O4WB⋯O5WB: 2.8562(19) Å) that it is not present between their A counterparts (O4WA⋯O5WA: 3.0256(19) Å). This in turn causes a slight elongation of a second hydrogen bond (O4WB⋯O7B: 2.7384(17) Å versus O4WA⋯O7A: 2.7135(18) Å).
The short strong H-bond involving the two carboxylates is now split in two different interactions with similar strengths (O1A⋯O5B: 2.4257(16) Å; O1B⋯O5A: 2.4216(16) Å). Their geometrical parameters after structure refinement are very similar to those observed at 240 K but now the electron density distributions around H1OA and H1OB obtained by differential Fourier analysis are elongated along the bonds (indicating their bonding character) and less symmetric (Fig. 2). Indeed, the positions of the electron density maxima shift from O1A and O1B to, respectively, O5B and O5A (Table S3†). Smearing out of the electron density upon cooling is very rare. Often the opposite behavior is detected due to decreased thermal motion.32 This may be an indication of dynamic disorder (if a double well potential appears below the phase transition) and/or a shift of the potential energy minimum towards one of the carboxylate anions as a consequence of the spin crossover. In any case, this shift takes place without breaking the centrosymmetric character of the crystal structure.
X-ray crystal structure at 95 K
Magnetic susceptibility measurements (vide infra) have shown that the mixed HS/LS phase measured at 120 K is metastable at lower temperatures. In fact, when the temperature of a single crystal of 1 is kept at 95 K during 4 h, a new triclinic phase of this compound is obtained. The crystal structure of 1 at 95 K belongs to the centrosymmetric P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group. Now the unit cell is halved with respect to that observed at 120 K (Table S1†). The crystal packing is very similar to the 240 K structure but the cell volume has decreased by a factor of 2.6%. A study of the temperature dependence of the crystal cell parameters (vide infra) shows that the relative decrease of volume is higher than that expected for thermal contraction and agrees with a complete SCO process. Indeed, the Fe–N bond distances (Table S4†) in the Fe2+ coordination sphere lie in the expected range (1.940 Å to 2.006 Å) for a LS configuration. The value of the Σ parameter (103°) and the trans N–Fe–N angle φ (172.62°) are also in agreement with a LS ground state, but deviate further, in comparison to the LS site present at 120 K (Table S5†), from the ideal octahedral geometry, approaching the limiting values.9 This can be attributed to a small fraction of HS molecules present in the crystal, that translates also into an increase of esd values for distances and angles.
space group. Now the unit cell is halved with respect to that observed at 120 K (Table S1†). The crystal packing is very similar to the 240 K structure but the cell volume has decreased by a factor of 2.6%. A study of the temperature dependence of the crystal cell parameters (vide infra) shows that the relative decrease of volume is higher than that expected for thermal contraction and agrees with a complete SCO process. Indeed, the Fe–N bond distances (Table S4†) in the Fe2+ coordination sphere lie in the expected range (1.940 Å to 2.006 Å) for a LS configuration. The value of the Σ parameter (103°) and the trans N–Fe–N angle φ (172.62°) are also in agreement with a LS ground state, but deviate further, in comparison to the LS site present at 120 K (Table S5†), from the ideal octahedral geometry, approaching the limiting values.9 This can be attributed to a small fraction of HS molecules present in the crystal, that translates also into an increase of esd values for distances and angles.
The hydrogen-bonding distances are very similar to those observed for the B sublattice at 120 K (Fig. 4). The mean distance between the pyrazole NH units and the H-bond acceptors in the second coordination sphere of the [Fe(bpp)2]2+ cation has almost the same value (2.705 Å). The remaining H-bonding distances are very similar to those observed in the crystal structure at 120 K between equivalent positions near the LS Fe1B center. This means a shrinkage of these contacts with respect to high temperature, except for the few cases already mentioned. Now, 100% of O4W molecules are bonded to O5W with a distance of 2.858(3) Å.
The strong 3c–4e− H-bond interaction is maintained (O1⋯O5: 2.429(2) Å). The shape of the electron density changes with respect to 120 K and is more similar to the 240 K data, becoming more spherical but slightly unsymmetric (Fig. 2). Also, the position of the maximum density (Table S3†) is shifted back towards O1, as expected for a reentrant phase transition.
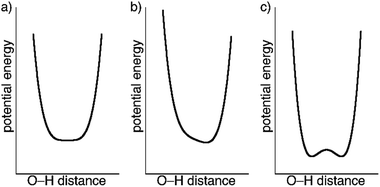
The crystal structures of 1 determined by X-ray diffraction have clearly shown the presence of a strong H-bond interaction of quasi covalent nature with a proton being trapped between the two isonicotinate anions isonicNO(3) and isonicNO(6). Although this hydrogen atom H1O was found in Fourier differential density maps, its position could not be determined precisely. Further, the value of the atomic displacement parameter for H1O for the different temperatures (Table S2†) is much larger than those observed for the other refined H atoms (those of water molecules). These facts point to the presence of H1O in a single potential energy well with an energy minimum located approximately halfway between the H-bond acceptors (Fig. 5a). This is an interesting situation as any subtle variation in the crystal structure (such as spin crossover) can lead to proton displacement (Fig. 5b) and/or the appearance of static disorder due to the change of the potential energy curve or to the difficulty to overcome the activation energy barrier (Fig. 5c) at low temperatures. Since these phenomena are at the basis of H-bonded ferroelectrics,18–21 a neutron crystallography study is justified.
Neutron crystallography
Single-crystal neutron diffraction experiments of 1 were undertaken at T = 240, 120 and 95 K (the latter after thermal relaxation for 4 h). Similar cell parameters (Table S6†) to those obtained from the X-ray study were observed, confirming the presence of the HS, mixed-spin and LS phases at the three working temperatures, respectively. The coordinates of the non-hydrogen atoms are thus virtually the same (within the experimental error) in all cases but the positions of the H atoms differ significantly. A comparative (neutron vs. X-ray) analysis (Fig. S2 and S3†) of the hydrogen-bonding parameters involving bpp ligands (D: distance between non-hydrogen atoms; dN–H and dH⋯O) reveals that N–H distances obtained from X-ray data refinement are underestimated by 0.1–0.2 Å with respect to values determined by neutron diffraction. In turn, H⋯O distances are overestimated by the same amount. There is a rough negative correlation between these shifts and the strength of hydrogen bonding: as the distance between the heteroatoms increases, so does increase the divergence between XRD and neutron diffraction values. It is well-known that XRD determines the electron density distribution whereas neutron diffraction locates the position of nuclei.33 These may differ largely for hydrogen atoms bonded to electronegative elements. In any case, neutron diffraction data clearly confirm that hydrogen bonds involving the second coordination sphere of [Fe(bpp)2]2+ cations are shorter for the LS species. Thus, the mean NH⋯O distance decreases from 1.744 Å at 240 K to 1.694 Å at 95 K, whereas in the mixed-spin phase the mean NH⋯O distances are 1.737 Å and 1.693 Å for the HS and LS centers, respectively (Table S7†). The formation of the hydrogen bond between O4W and O5W in the LS phase is also observed: the (O4W)H⋯O5W distance decreases from 2.122(11) Å at 240 K to 1.898(8) Å at 95 K. The remaining (OH⋯O) hydrogen bond distances involving water molecules parallel the results obtained by XRD: distances are shorter for the LS phase with the few exceptions already mentioned. These changes are also detected in the B sublattice of the mixed-spin phase at 120 K.Other important hydrogen-bonding parameters to discuss are the N–H⋯O and O–H⋯O bond angles (θ), which can be accurately determined from neutron diffraction and can differ randomly from the estimated XRD values by as much as 6°. It was found that the N–H⋯O bond angles in the second coordination sphere are lower for the LS species (Table S8†). They decrease from an average value of 170° at 240 K to a value of 164° at 95 K. This is striking, as in most cases shorter H bonds tend to be more linear. The depart from linearity on going from the HS to the LS state can be ascribed to the change of the bpp bite angle below the phase transition. Concerning the O–H⋯O angles, their variation does not seem to correlate with the change in H bond distances. The formation of the H bond between O4W and O5W in the LS structure entails an increase of the O4W–H⋯O5W θ angle (172.4(6)°) with respect to the value at 240 K (167.7(7)°), in this case approaching linearity.
The most remarkable observation concerns the SSHB interaction O1⋯O5. In the HS phase at 240 K, the H1O proton is located halfway between the two oxygen atoms (Table 2), in qualitative agreement with the XRD study. For this very strong H bond, with the H atom lying in an almost symmetric environment, the position of the nucleus and the center of the electron density distribution are almost coincident. In the mixed-spin phase at 120 K, this contact is split into two. While the O1A⋯H1OB⋯O5B interaction keeps the proton practically in the middle of the H bond, in the O1B⋯H1OA⋯O5A interaction the proton separates slightly from O1B. In the reentrant LS phase at 95 K, the symmetry is restored but the H1O proton still deviates from the center of the H bond. SSHBs with O⋯O distances smaller than 2.45 Å are expected to show broad single-well potentials suitable for proton migration. Normally, the proton is located halfway between the heteroatoms at high temperature and becomes off-centered as temperature decreases.32,34 Additional neutron diffraction data of 1 were thus collected at 50 K for both the mixed-spin and LS phases (the latter being obtained after thermal relaxation at 95 K for 4 h). For the mixed-spin phase, the geometries of the SSHBs are similar to those described at 120 K, with a clearly symmetric O1A⋯H1OB⋯O5B interaction (Table 2) and a slightly more asymmetric O1B⋯H1OA⋯O5A interaction. For the LS phase, the asymmetry of the SSHB increases and is larger than that observed at 95 K.
| T (K) | d(O1⋯H1O) (Å) | d(H1O⋯O5) (Å) | D(O1⋯O5) (Å) |
|---|---|---|---|
| a The O1⋯H1O⋯O5 interaction is split into two: O1A⋯H1OB⋯O5B (top line) and O1B⋯H1OA⋯O5A (bottom line) due to symmetry breaking. b Temperature was held at 95 K for 4 h prior to data collection. | |||
| 240 | 1.203(7) | 1.206(7) | 2.407(4) |
| 120a | 1.216(7) | 1.213(7) | 2.427(4) |
| 1.221(7) | 1.198(7) | 2.416(4) | |
| 95b | 1.222(6) | 1.200(6) | 2.420(4) |
| 50a | 1.213(8) | 1.209(8) | 2.420(5) |
| 1.227(8) | 1.191(8) | 2.414(5) | |
| 50b | 1.237(7) | 1.184(7) | 2.419(4) |
At all working temperatures (Fig. 2), the nuclear density of the H atom is well localized, with thermal parameters that are similar to those corresponding to other protons present in the structure (Table S9†). This clearly discards a temperature-dependent proton disorder resulting from the presence of a low-activation energy barrier and confirms a genuine proton migration. This can be due either to an asymmetric potential energy well; or to a change of the potential energy surface with temperature.32 The latter seems to apply in our case, given the rather symmetric environment of the H atom. The similar behaviour of the LS phase and the LS sublattice of the mixed-spin phase confirms that the modulation of the potential energy surface and the subsequent proton migration is a consequence of the SCO process. The shift in the proton position is small (Table 2) but significant (8 times the experimental error) and compares well with similar shifts observed in H-bonded ferroelectrics.18–21
Variable temperature neutron diffraction data down to 10 K were also collected using the single-crystal Laue technique. No further transformations were observed upon cooling down to 10 K (ESI†).
Interplay between SCO and H-bond cooperativity
The correlation observed between the SCO phenomenon and proton displacement in 1 suggests that it could be possible to trace the interaction path between the iron(II) cations by looking at the H-bond cooperativity.33 For instance, as one of the Fe2+ cations undergoes crossover to the LS site Fe1B, the H-bond distance N10B⋯O8B becomes shorter (Table 1, row 4) due to the increasing charge density. This in turn pushes the electron density of the O7B–C35B–O8B carboxylate anion towards O8B, thus decreasing the H-bond acceptor character of O7B. Consequently, the distance O4WB⋯O7B increases (row 11) and O4WB moves towards N5B (row 2), stabilising the LS state of an adjacent Fe2+ cation (Fig. S4a†). This is the shortest H-bond pathway between neighbouring Fe complexes and builts centrosymmetric π-stacked dimeric BB units. Interestingly, there is no such a short H-bond pathway between Fe1A and Fe1B sites, the shortest one involving three water molecules and one carboxylate ligand. In this case, the presence of the LS Fe1B site increases the strength of the N5B⋯O4WB H-bond and this induces by σ-bond cooperativity the formation of the new H-bond between O4WB and O5WB (Fig. S4b†), releasing the chemical pressure of the system and hindering the propagation of H-bond cooperativity to the A sublattice.Temperature dependence of unit cell parameters
The thermal variation of the crystal cell parameters was measured by single-crystal X-ray diffraction in the 240–120 K range (Fig. S5†). A clear discontinuity is observed for all the parameters between 160 K and 170 K, indicating a crystallographic phase transition in this temperature range. Below 160 K, the temperature dependence of the unit cell volume can be fitted to the linear expression V (Å3) = 4171.6 + 0.53T. This yields a volumetric thermal expansion coefficient for the mixed HS/LS phase αHS/LS = 125 × 10−6 K−1. Since in the 120–160 K temperature range (vide infra) the magnetic moment of the sample is constant, this value of αHS/LS can be considered as an intrinsic coefficient associated solely to thermal expansion. Instead, above 170 K, the thermal variation of the unit cell volume can be fitted to the expression V (Å3) = 2086.4 + 0.29881T, yielding a coefficient for the high-spin phase αHS = 139 × 10−6 K−1. This higher value indicates that, in the 170–240 K range, there is also a partial depopulation of the HS state. This is in agreement with the magnetic behaviour, as shown below.Differential scanning calorimetry (DSC) measurements
DSC measurements were performed in the 120–300 K temperature range in order to determine precisely the temperature of the crystallographic phase transition. Upon cooling the sample from 240 K to 180 K, a very broad feature is observed, corresponding probably to the partial depopulation of the HS state mentioned in the last paragraph. A further decrease of the temperature yields a sharp exothermic peak centered at T↓ = 162 K (Fig. 6). The value of the enthalpy change associated to this transformation is ΔH = 1.75 KJ mol−1, a relatively small value in comparison to other SCO systems, even for a partial crossover.35 The variation of entropy (ΔS = 10.8 J K−1 mol−1) is also low but still higher than the value expected for the electronic contribution (ΔS = 1/2R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5). In the heating curve, a similar sharp endothermic peak is observed around T↑ = 167 K, with values of the thermodynamic functions ΔH = 2.13 KJ mol−1 and ΔS = 12.7 J K−1 mol−1. Thus, both sharp features correspond to the crystallographic phase transition from the HS phase to the mixed HS/LS phase. A second temperature cycle (not shown) indicates that this is a reversible process.
5). In the heating curve, a similar sharp endothermic peak is observed around T↑ = 167 K, with values of the thermodynamic functions ΔH = 2.13 KJ mol−1 and ΔS = 12.7 J K−1 mol−1. Thus, both sharp features correspond to the crystallographic phase transition from the HS phase to the mixed HS/LS phase. A second temperature cycle (not shown) indicates that this is a reversible process.
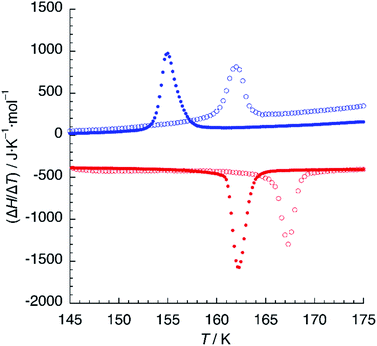 | ||
| Fig. 6 DSC plot of 1 (empty circles) and 1d (solid circles). Blue and red colours refer to cooling and heating modes, respectively. Scan rate: 10 K min−1. | ||
When hydrogen bonding influences spin crossover, thermodynamic properties can be very sensitive to isotopic composition.36 We thus undertook DSC measurements on samples crystallised from deuterated solvents (1d). A similar calorimetric plot was obtained with T↓ = 155 K and T↑ = 162 K (Fig. 6), with similar values of ΔH = 2.24 KJ mol−1 and ΔS = 13.8 J K−1 mol−1. The thermal hysteresis (ΔT = 7 K) is higher than that observed for 1 but the most striking result is the 6 K decrease of the critical temperature of the phase transition for 1d, indicating a destabilisation of the mixed HS/LS phase.
Since the FeN6 environment in the iron(II) coordination sphere should be the same, this destabilisation has to be ascribed to the free energy gain associated to the reorganisation of hydrogen bonds, particularly to the formation of the H-bond between O4WB and O5WB. As a result of the lower zero-point vibrational energy of O–D bonds relative to O–H bonds,33 it is known that hydrogen bond lengths increase upon deuteration (Ubbelohde effect). Hence, H-bond enthalpies should decrease and this could be the reason for the destabilisation effect observed in the thermal properties. However, the enthalpy variation ΔH is very similar or even higher for 1d. It seems then that the shift in T1/2 is due to differences in vibrational entropy (note that ΔS increases in our case for 1d). This is in contrast with the seminal report on the isotope effects of the tris(picolylamine)iron(II) complex, in which the SCO shifts to higher temperatures upon deuteration.37 In this and other cases,38 the isotope effect has been ascribed to differences between the zero-point vibrational levels of the HS and LS sites in their deuterated and non-deuterated forms, while here we are focusing on the intermolecular hydrogen-bond interactions. In any case, the existence of isotope effects demonstrates the crucial role of hydrogen bonding in defining the magnetic behaviour of the salts.
Magnetic properties
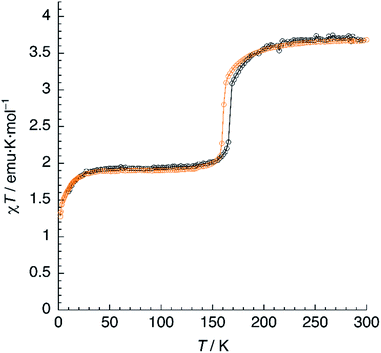
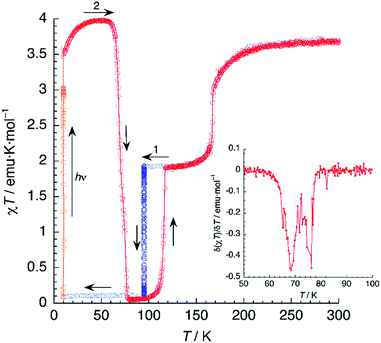
Magnetic susceptibility measurements of 1 (Fig. 7) were performed in the 2–300 K range under an applied field of 1000 Oe. At 300 K, the product of molar magnetic susceptibility and temperature (χT) approaches a constant value of 3.67 emu K mol−1, far above the expected value for a ‘spin-only’ Fe2+ cation (χT = 3.0 emu K mol−1). Upon cooling, χT decreases very steeply near an inflection point located at T1 = 167 K, then it reaches a plateau for a χT value of 1.95 emu K mol−1, corresponding to the one expected for the mixed HS/LS state characterised by X-ray diffraction at 120 K.Below 25 K, the magnetic moment of the sample decreases fast and this is a signature of the zero-field splitting (ZFS) expected for the HS fraction present in the material. An essentially identical curve is obtained after heating the sample from 2 K to 300 K and even after subsequent temperature cycles (not depicted), showing the reversibility of the process. The lack of hysteresis contrasts with the small value (ΔT = 5 K) observed in the DSC measurements, the latter being performed at a much higher sweeping rate (10 K min−1).
The magnetic properties of 1d were studied exactly in the same conditions and a very similar plot was obtained (Fig. 7). The limiting value of χT at 300 K equals 3.68 emu K mol−1, matching that observed for 1. On lowering the temperature, χT decreases and reaches an inflection point at T1 = 161 K. Note the 6 K decrease in the SCO temperature, in perfect agreement with the DSC measurements. Further cooling yields a constant value of χT = 1.90 emu K mol−1, corresponding to a HS fraction γHS ≈ 0.5. Finally, at very low temperatures, an additional decrease due to ZFS is observed. Again, the full process is reversible as confirmed by the equivalent heating and cooling curves (not shown). Clearly, magnetic properties show the higher stability of the HS phase for the deuterated material, thus confirming the crucial role of hydrogen-bonding in the SCO process.
Photomagnetism
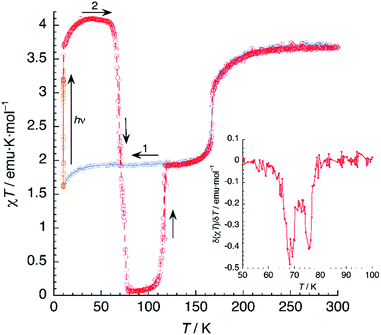
A sample of 1 was prepared for photomagnetic experiments in a SQUID magnetometer. At first, the magnetic susceptibility of the compound was measured without irradiation between 300 K and 2 K (in the cooling and heating modes, not depicted) in order to check the integrity of the material. Then, the sample was cooled down to 10 K (Fig. 8, in blue) and irradiated at this temperature with a red laser source (λ = 630 nm). This resulted in an increase of χT from an initial value of 1.61 emu K mol−1 to 3.56 emu K mol−1 after 10 min irradiation (in orange), where saturation of the signal is observed, indicating a fast excitation to the HS state. Then, light was switched off and the thermal variation of the susceptibility of 1 was measured by heating in the dark at 0.3 K min−1, following the standard T(LIESST) procedure.39 After an initial increase, ascribed to ZFS of the quintet ground state, χT reaches a value of 4.10 emu K mol−1 at 40 K, corresponding to the one expected for γHS ≈ 1. Between 40 and 55 K, χT remains constant, indicating an efficient trapping of the photoexcited 100% HS state. Above 60 K, χT decreases very abruptly and vanishes completely at 80 K, indicating a fast relaxation to the 100% LS state. Note that relaxation goes beyond the initial mixed HS/LS phase present before irradiation. The compound becomes diamagnetic until 105 K, where a sudden increase of χT to reach a value of 1.93 emu K mol−1 at 118 K is observed. Above this temperature, the thermal variation of χT matches perfectly that recorded for the non-irradiated material, being constant in the 120–160 K range (where γHS ≈ 0.5) and increasing sharply at T1 = 167 K to a limiting value of 3.67 emu K mol−1 at room temperature.The photomagnetic experiments clearly suggest three intervals of stability: (i) at T > 167 K, the HS phase is the stable one; (ii) 116 K < T < 167 K, where the stable phase has a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 HS
50 HS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LS distribution of the Fe2+ sites; (iii) at T < 116 K, where this mixed spin phase becomes metastable and the most stable phase is LS. This behavior is very similar to that previously observed for an iron(II) bischelated complex of 2,6-bis(3-methylpyrazol-1-yl)pyridine.40 Of interest for our discussion is the fact that the magnetic properties of this compound were strongly dependent of the presence of H2O molecules in the crystal. However, in that case, the crucial role of hydrogen bonding could not be studied due to crystallographic disorder.
LS distribution of the Fe2+ sites; (iii) at T < 116 K, where this mixed spin phase becomes metastable and the most stable phase is LS. This behavior is very similar to that previously observed for an iron(II) bischelated complex of 2,6-bis(3-methylpyrazol-1-yl)pyridine.40 Of interest for our discussion is the fact that the magnetic properties of this compound were strongly dependent of the presence of H2O molecules in the crystal. However, in that case, the crucial role of hydrogen bonding could not be studied due to crystallographic disorder.
It is known that, for these bischelated iron(II) complexes, T(LIESST) can be correlated to the SCO temperature T1/2 by the expression T(LIESST) = T0 − 0.3T1/2, where T0 = 150 K. For T1/2 = T2 = 116 K, a value of T(LIESST) = 115 K should be expected. It has been pointed out that when the expected T(LIESST) and T1/2 are similar, the thermal SCO depends strongly on kinetic factors and this often results in partial spin conversion,41 as observed in the present case, and reduction of the T(LIESST) parameter with respect to the expected values. Alternatively, an increase of T(LIESST) resulting from reorientation of solvent molecules during the HS to LS relaxation has been recently observed in [FeL2][BF4]2·CH3CN (L = 4-{isopropylsulfanyl}-2,6-di{pyrazol-1-yl}-pyridine).42 Interestingly, in our case, the determination of T(LIESST) from the first derivative plot (Fig. 8, inset) shows clearly a relaxation in two steps: a first process with T1(LIESST) = 68 K, in which the photoexcited HS phase relaxes to a mixed HS/LS material; and a second process with T2(LIESST) = 76 K, where the remaining HS Fe2+ cations relax to their LS states. Clearly stepped LIESST plots, generally ascribed to the successive relaxation of inequivalent Fe2+ ions, are not very common.43 An example showing two clearly separated relaxation events differing in more than 40 K has been reported in iron(II) complexes derived from dipyrazolylpyrazine.44 Most often, however, the LIESST curve exhibits an inflexion point indicating the presence of two relaxation processes.45 Normally, the presence of this characteristic point in the LIESST plot reflects the stepped character of the thermal SCO. The parameters defining the thermal SCO (T1/2 and cooperativity) are generally mirrored in the LIESST properties.46 We can thus ascribe the first relaxation process at T1(LIESST) = 68 K to the partial SCO observed at T1 = 167 K. Here also, the data fall outside the T(LIESST) vs. T line, as expected for kinetically trapped spin states.
In another experiment, compound 1 was cooled down to 95 K and kept at this temperature for 4.5 h (Fig. 9). In these conditions, 1 relaxes completely to the LS phase. Then, the compound was cooled further to 10 K and irradiated with red laser light (λ = 630 nm). A 30-fold increase of the magnetic susceptibility was observed after 10–15 min, as fast as that measured by irradiating the HS/LS phase. Further, there was no evidence of a plateau that would indicate a two-step process. It seems then that the photoswitching process proceeds directly from the LS to the PIHS phase.
Then, the T(LIESST) curve was recorded in the dark. After an initial increase owing to ZFS effects, χT reached a plateau in the 40–55 K region, with a value of 3.97 emu K mol−1, corresponding to 100% population of the HS state. Heating further yields a drastic decrease of the magnetic signal, vanishing again at 80 K. The values of T(LIESST) obtained from the first derivative plot (T1(LIESST) = 68 K, T2(LIESST) = 76 K) are the same, irrespective of the initial phase present before irradiation. This is not always the case: in a similar compound showing also two-step relaxation, the sample can undergo photoexcitation from the low-spin phase or from a metastable mixed-spin phase with different results (the latter being more effective).47 Thus, the fact that T(LIESST) curves of 1 obtained from photoexcitation of, respectively, the LS phase and the mixed HS/LS phase are identical in the whole temperature range, strongly suggests that the photoexcited HS phase is the same in both cases.
Relaxation kinetics of the photoinduced HS phase
Assuming a common photoexcited HS phase, we studied the relaxation kinetics of the compound obtained after light irradiation of the metastable mixed HS/LS material. Relaxation measurements were performed at different temperatures between 60 K and 72 K. At the selected temperature, light was switched off and the time dependence of γHS was recorded (Fig. 10). Based on the LIESST plot, the relaxation curves were fitted using a sum of two exponential terms, with temperature-dependent rate constants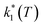 and
and 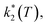 corresponding to the faster and slower process, respectively.
corresponding to the faster and slower process, respectively.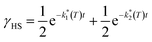 | (1) |
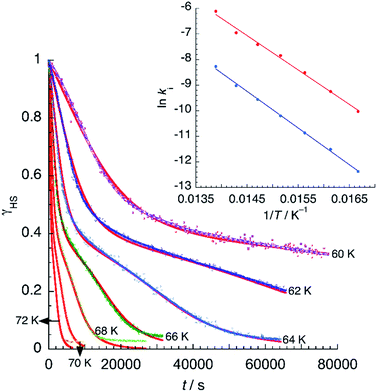 | ||
| Fig. 10 Time dependence of the high-spin fraction of Fe2+ cations at different temperatures. Red lines correspond to the best-fit data according to eqn (1). The inset shows Arrhenius plots corresponding to the fast (red) and slow (blue) processes, together with the best-fit to Arrhenius equation. | ||
However, due to cooperative effects, both rate constants depend also on the remaining fraction of HS centers (γHS) in such a way that the two exponential curves become sigmoidal and dependent on a self-acceleration factor, 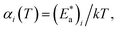 that is also a function of temperature:48
that is also a function of temperature:48
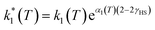 | (2) |
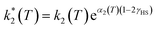 | (3) |
The observed behaviour is very similar to that reported for [Fe(bppI)2](BF4)2, a complex showing two T(LIESST) values of 65 and 75 K. In that example, simulation of the relaxation curves was accomplished with a model consisting in the sum of a fast exponential decay and a slow self-accelerated process.49
From the best-fit data shown in Fig. 10, values of ki and αi can be extracted at different temperatures below Ti(LIESST). Results are gathered in Table S10.† Note that the two rate constants k1 and k2 differ in one order of magnitude. This justifies the fit to a double exponential law. The calculated values of the rate constants follow an Arrhenius law (inset Fig. 10) indicating a thermally activated process with apparent activation energies, Ea1 = 935.7 cm−1 and Ea2 = 997.9 cm−1, that compare well with values reported for similar systems.49,50 The apparent preexponential factors k1(∞) and k2(∞) are 2.563 × 105 s−1 and 1.059 × 105 s−1, respectively. The ratio k1(∞)/k2(∞) is close to 2, the expected statistical value for these similar processes. The energy associated to cooperativity, 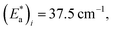 lies in the expected range observed for these complexes. Instead, the α2 parameter does not follow a simple thermal variation.
lies in the expected range observed for these complexes. Instead, the α2 parameter does not follow a simple thermal variation.
Photocrystallography studies
The crystal structure of 1 in the photoinduced high-spin state (PIHS) was investigated in the dark at 50 K by single-crystal X-ray diffraction after light irradiation with a laser source (λ = 630 nm) for 90 min. The photoinduced crystal phase is isostructural to the HS phase solved at 240 K (Fig. S6 and Table S1†). The 2.7% cell volume difference between the two structures (V = 2153.0 Å3 at 240 K; V = 2095.3 Å3 at 50 K) agrees well with the thermal expansion coefficient discussed previously. There is a single independent Fe(II) complex, occupying an octahedral site with Fe–N bond distances ranging between 2.114 and 2.195 Å (Table S4†), as expected for a HS state. The values of the parameter φ and Σ match those calculated for the HS phase at 240 K (Table S5†). The H-bond distances in the second coordination sphere of the iron complex are also very similar. The mean N⋯O value (2.762 Å) is exactly the same than that corresponding to the HS Fe1A site present at 120 K (Table 1). This again proves the correlation between the strength of the H-bonding interactions and the spin state. All other H-bonds have also similar distances to those observed at 240 K and 120 K (for the A sublattice). It is worth noting that the H-bond between O4W and O5W present in the LS phase is cleaved (H-bond distance: 3.0070(18) Å) under light irradiation. Concerning the short strong hydrogen bond, Fourier maps (Fig. 2) show clearly the presence of two distinct maxima of electron density. A disorder model including two, partially occupied, hydrogen atoms was introduced and the quality of structure refinement improved slightly. This is an evidence of static disorder present at 50 K and confirms the presence of a low-value energy barrier for proton migration between the two carboxylates. Since, at the same temperature, neutron diffraction data give a single location for the proton, the energy barrier is not intrinsic and appears as a result of the photoinduced excitation, meaning that the LIESST effect modifies the potential energy curve of the SSHB.As seen previously, the photomagnetic studies reveal a two-step relaxation process with T1(LIESST) = 68 K and T2(LIESST) = 76 K. After the first step, the value of γHS = 0.5 suggests the presence of a mixed 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 HS/LS material similar to the metastable phase measured at 120 K. In order to characterise this mixed-spin phase by photocrystallography, a single crystal of 1 mounted on a X-ray diffractometer was irradiated (λ = 630 nm) at 50 K for 1 h. Then, it was heated to 69 K (scan rate of 0.3 K min−1), allowing for partial relaxation. Then, the crystal was quenched rapidly to 50 K and measured. The structure is still centrosymmetric (P
1 HS/LS material similar to the metastable phase measured at 120 K. In order to characterise this mixed-spin phase by photocrystallography, a single crystal of 1 mounted on a X-ray diffractometer was irradiated (λ = 630 nm) at 50 K for 1 h. Then, it was heated to 69 K (scan rate of 0.3 K min−1), allowing for partial relaxation. Then, the crystal was quenched rapidly to 50 K and measured. The structure is still centrosymmetric (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) but the unit cell volume (V = 2090.17 Å3) decreases with respect to the value of the PIHS phase. There is a single independent Fe(II) center, exhibiting Fe–N bond lengths in the 2.034–2.106 Å range (Table S4†). The mean length dFe–N = 2.075 Å and the octahedral distortion parameters are intermediate between those corresponding to the HS and LS structures (Table S5†), confirming the efficient trapping of a mixed-spin phase with 50% of the iron sites in each spin state. Similar considerations apply to the second sphere H-bonding N⋯O distances, with a mean value (2.738 Å) that lies exactly between those observed for the HS and LS phases (Table 1). An intermediate distance between O4W and O5W water molecules (2.934(2) Å) is also observed. Isotropic displacement parameters are much higher than those measured for the other structures (Table S2†). This translates into larger ellipsoids (Fig. S7†), specially for those pyrazolyl C and N atoms that undergo a higher displacement with the change of the bpp bite angle, and for water molecules (O3W and O4W) located in the second coordination sphere of the complex.
) but the unit cell volume (V = 2090.17 Å3) decreases with respect to the value of the PIHS phase. There is a single independent Fe(II) center, exhibiting Fe–N bond lengths in the 2.034–2.106 Å range (Table S4†). The mean length dFe–N = 2.075 Å and the octahedral distortion parameters are intermediate between those corresponding to the HS and LS structures (Table S5†), confirming the efficient trapping of a mixed-spin phase with 50% of the iron sites in each spin state. Similar considerations apply to the second sphere H-bonding N⋯O distances, with a mean value (2.738 Å) that lies exactly between those observed for the HS and LS phases (Table 1). An intermediate distance between O4W and O5W water molecules (2.934(2) Å) is also observed. Isotropic displacement parameters are much higher than those measured for the other structures (Table S2†). This translates into larger ellipsoids (Fig. S7†), specially for those pyrazolyl C and N atoms that undergo a higher displacement with the change of the bpp bite angle, and for water molecules (O3W and O4W) located in the second coordination sphere of the complex.
These results point to a random distribution of HS and LS Fe(II) complexes in the crystal lattice. We did not found any evidence of superstructure reflections that might indicate an ordering of the two spin species in the crystal, even in a modulated manner. A possible explanation for the two-step relaxation in the magnetic properties and the lack of a symmetry breaking event in the structural analysis can be the existence of a short-range interaction defining LS dimers that distributes randomly throughout the lattice. This explanation is consequent with the cooperativity of H-bonds. Indeed, the analysis of thermal parameters for the different isonicNO anions shows higher values for atoms (O7 and O8) involved in the H-bonding cooperative pathway described above. This illustrates how the analysis of a metastable structure obtained after partial relaxation can be useful in the definition of the cooperative interactions present in the solid.
Finally, the crystal structure of 1 was measured after full relaxation at 95 K. As expected, an isostructural phase to that measured at the same temperature without irradiation was observed (Fig. S8 and Table S1†).
Relaxation kinetics of the metastable mixed-spin phase
In contrast to previous examples,51 the 100% HS phase could not be obtained by fast cooling of 1 (thermally induced excited spin-state trapping, TIESST). Instead, quenching the sample to 10 K in a few seconds afforded a γHS fraction close to 0.5, indicating the presence of a metastable HS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LS mixed-spin phase. Heating now the material (Fig. 11) under the same conditions used in the LIESST experiment, yielded T(TIESST) = 96 K. The same TIESST experiment was performed after cooling the sample at a standard rate (2 K min−1) instead of quenching it. Curiously, a similar TIESST plot was observed, but now T(TIESST) = 100 K, indicating a faster relaxation for the first experiment, probably due to the mechanical stress induced by fast cooling. In any case, these values are considerably higher than T2(LIESST), confirming that the metastable material obtained by thermal trapping is different from the metastable phase induced by irradiation, then partial relaxation. At 100–104 K, the T(TIESST) plots exhibit a minimum, dependent on the cooling procedure, and at 114–116 K, both merge with the T(LIESST) curve, showing that the stable phases (LS, stable at T < 114–116 K, and HS
LS mixed-spin phase. Heating now the material (Fig. 11) under the same conditions used in the LIESST experiment, yielded T(TIESST) = 96 K. The same TIESST experiment was performed after cooling the sample at a standard rate (2 K min−1) instead of quenching it. Curiously, a similar TIESST plot was observed, but now T(TIESST) = 100 K, indicating a faster relaxation for the first experiment, probably due to the mechanical stress induced by fast cooling. In any case, these values are considerably higher than T2(LIESST), confirming that the metastable material obtained by thermal trapping is different from the metastable phase induced by irradiation, then partial relaxation. At 100–104 K, the T(TIESST) plots exhibit a minimum, dependent on the cooling procedure, and at 114–116 K, both merge with the T(LIESST) curve, showing that the stable phases (LS, stable at T < 114–116 K, and HS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LS, stable between 114–116 K and 167 K) are the same regardless of the initial conditions (thermal- vs. light-induced spin trapping).
LS, stable between 114–116 K and 167 K) are the same regardless of the initial conditions (thermal- vs. light-induced spin trapping).
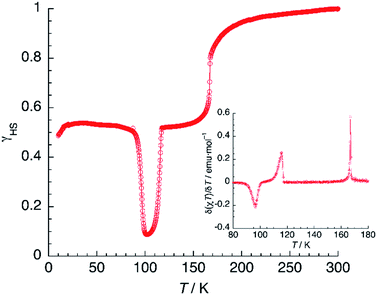 | ||
| Fig. 11 TIESST experiment: thermal variation of χT after quenching a sample of 1 at 10 K, then heating it at 0.3 K min−1. The inset shows the first derivative of the TIESST plot. | ||
Marked differences between the relaxation kinetics of the metastable HS phases obtained by photoinduced (LIESST) or thermal (TIESST) trapping have been reported.52 The HS Fe2+ sites obtained by irradiation of the LS material at low temperatures have a less distorted octahedral environment in comparison to the Fe2+ sites obtained by supercooling, the latter being frozen in a coordination environment similar to that observed in the HS phase stable at high temperature. These subtle differences in the coordination spheres propagate throughout the lattice, making the whole structure of the photoinduced HS phase more similar to that of the LS phase, thus decreasing the apparent activation energy of the SCO process.
The divergence between T(TIESST) and T(LIESST) is indicative of different relaxation mechanisms for the metastable phases obtained by thermal quenching and light irradiation. This can be confirmed by measuring the relaxation of a precooled sample at different temperatures within the metastability region (T < 114 K). For instance, the relaxation curve γHS = f(t) at 72 K of the photoinduced material decays completely after 72 min, whereas that corresponding to the thermally quenched sample at 75 K contains less than 10% LS centers even after 10.5 h (Fig. S9†). At higher temperatures, 85 K and 95 K, complete decay is reached in 8 h and 4 h, respectively. Instead, at 102.5 K, 20% of Fe2+ cations still remain in the HS state after 12 h, whereas a change of only 1% in the magnetic signal is observed at 105 K after 3.2 h. For the last two points, relaxation rates decrease when the temperature is increased, indicating that the compound enters into the thermal range corresponding to thermodynamic equilibrium, its behaviour being governed by the master equation.53
At T < 114 K, the shape of the χT = f(T) plot strongly depends on the cooling procedure and, at a sufficiently low cooling rate, thermal hysteresis should be measured. Fig. 12 shows the thermal variation of χT of 1 at a low cooling rate. First, the material was cooled down to 105 K at 3 K min−1. Then, the rate was changed to 0.04 K min−1 and the sample cooled further to 85 K. Below 101 K, χT decreases steadily, reaches an inflection point at T↓ = 97 K, and diminishes further to reach a constant value of 0.17 emu K mol−1 at 85 K. Heating now the sample results in a fast increase of the magnetic signal around T↑ = 111 K to yield an apparent thermal hysteresis ΔT = 14 K. The observation of a low-temperature HS residue indicates that kinetic effects are noticeable even in such a slow cooling conditions. This can be best appreciated by the superimposition of isothermal relaxation experiments, starting from the mixed-spin phase, in the same plot. It is possible to notice that, at 85 and 95 K, relaxation proceeds to values below those observed in the hysteresis plot. At 97.5 K, the quasistatic χT value matches the heating branch of the loop, indicating that the hysteresis has a purely kinetic origin at this temperature. At 102.5 K, complete relaxation is not observed even after 12 h, confirming that the quasistatic hysteresis loop is much thinner than the apparent one. Above 114 K, the χT plot merges with the one obtained at higher sweeping rates, suggesting that, at least in the range 105 K < T < 114 K, true bistability is observed.
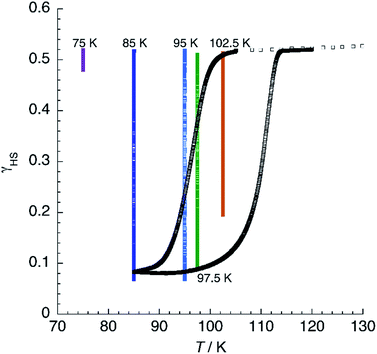 | ||
| Fig. 12 Thermal variation of χT for 1 at a slow scan rate (0.04 K min−1) showing the thermal hysteresis. Superimposed are isothermal relaxation experiments at the given temperatures. | ||
General discussion
There is an increasing number of reports concerning multistep transitions.43 Usually, they result from crystallographically independent Fe2+ cations showing distinct coordination environments, thus leading to different T1/2 values that define a plateau in the χT vs. T curve. Our system belongs to another category, in which the presence of competing elastic interactions stabilises a mixed-spin phase that arises from a structural symmetry breaking transition. In these cases, the coordination environments of the FeII sites are very similar, but HS and LS states coexist in the crystal lattice in an ordered pattern. The presence of clearly distinct two sublattices in the mixed-spin phase has been very helpful in establishing correlations between SCO and structural properties, not only in terms of Fe–N distances but also with respect to H-bond interactions, including the evidence for proton migration in a SSHB.A clear correlation between intermolecular interactions, particularly hydrogen bonding, and the presence of multistep SCO is present in several studies concerning Hofmann-type frameworks based on triazole ligands. In these systems, the reversible exchange of guest species allows for tuning the competing ferro- and antiferroelastic interactions in such a way that elastic frustration can be reversibly switched.54 It seems clear that hydrogen bonding is playing a crucial role also in our case.
A strong dependence of the SCO properties on the temperature scan rate is usually associated to large structural differences between the HS and LS phases. Of course, this dissimilarity has its origin in specific intermolecular interactions with a strong impact on the respective crystal packings.55 The wide temperature range of metastability of our mixed-spin phase is thus probably correlated to the formation of the hydrogen bond between O4W and O5W. Indeed, it has been shown that changes in the location of solvent molecules and/or anions can lead to very impressive thermomagnetic properties such as wide hysteresis loops or even double spin transitions.56
The possibility of populating different metastable states depending on the external perturbation (multimetastability) has been verified in some SCO Fe2+ complexes.52,57 In the present case, due to the high difference in T(LIESST) and T(TIESST) values, it seems clear that the mixed-spin metastable phases obtained by, respectively, light irradiation and thermal trapping are markedly different. This has been confirmed by photocrystallography measurements.
An important outcome of our work is the impact of SCO on proton migration along a SSHB. Although neutron diffraction is the method of choice for the study of these processes, a temperature-dependent X-ray diffraction analysis gives some complementary information. Electronic and nuclear densities do not necessarily follow the same pattern.32 While neutron diffraction reflects only vibrational (thermal) effects, X-ray yields information on electron sharing. For compound 1, SCO induces a small displacement of the proton position but has a strong impact on the electron density being more delocalised and shifted towards O5A and O5B in the mixed-spin phase. The advantage of neutron diffraction is that it can discard the presence of disorder of the H atoms over two positions in a double-well potential, a situation that is not commonly observed in SSHB but seems to appear here as a consequence of the lattice expansion induced by irradiation.
Very recently, Sato and coworkers have described the first examples of coupling between proton transfer and spin crossover.58 They have shown that the change in the spin state of an Fe(II) bischelated complex triggers an intramolecular proton transfer from a coordinated hydrazone unit to an appended pyridine moiety. The disymmetric character of this H-bond enables an unambiguous assignment of proton location, without the need of neutron crystallography experiments. While in this study the driving force for proton transfer is the change of the bite angle of the chelating ligand, in our case the effect seems to be purely electrostatic. An advantage of our intermolecular approach is that the proton can be located in a strictly symmetric environment, occupying a special position that becomes general after the SCO process, lowering the symmetry of the system, a situation that is needed in the design of ferroelectrics.
Conclusions
A new SCO compound based on the [Fe(bpp)2]2+ cation has been synthesised and its structural and magnetic properties have been studied. This compound deserves special attention for several reasons: (i) it undergoes a crystallographic phase transition at T1 = 167 K with symmetry breaking and formation of a HS-LS phase; (ii) this mixed-spin phase is stable in a limited thermal range and becomes metastable at temperatures below T2 = 116 K, where it transforms to a LS phase restoring the initial symmetry; (iii) important structural rearrangements accompany the phase transformations, with formation of a hydrogen bond between two water molecules that can be reversed on heating or irradiating the sample; (iv) an interplay between spin crossover and proton displacement across a short strong H-bond is demonstrated, including the formation of a photoinduced activation energy barrier for proton motion; (v) hydrogen-bond cooperativity seems to play a major role in the transmission of elastic interactions, as evidenced by the X-ray structural analysis at different temperatures, neutron crystallography and measurements on deuterated samples.Further, the present work establishes that SCO can have an impact on proton displacement even on remote positions, mimicking the allosteric changes that activate enzymes towards proton transfer, and opening the way to the design of SCO systems exhibiting proton conductivity and/or H-bonded ferroelectricity.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank José M. Martínez-Agudo and Gloria Agustí for the magnetic measurements. We acknowledge financial support from the Spanish Ministerio de Ciencia, Innovación y Universidades (MICINN project CTQ2017-87201-P) and Generalitat Valenciana (Prometeo/2019/076 project). V. J.-M. thanks also the MICINN for a FPU fellowship (FPU15/02804).Notes and references
- J.-F. Létard, P. Guionneau and L. Goux-Capes, Top. Curr. Chem., 2004, 235, 221 CrossRef CAS; K. Szacilowski, Chem. Rev., 2008, 108, 3481 CrossRef; M. S. Alam, M. Stocker, K. Gieb, P. Müller, M. Haryono, K. Student and A. Grohmann, Angew. Chem., Int. Ed., 2010, 49, 1159 CrossRef; T. Miyamachi, M. Gruber, V. Davesne, M. Bowen, S. Boukari, L. Joly, F. Scheurer, G. Rogez, T. K. Yamada, P. Ohresser, E. Beaurepaire and W. Wulfhekel, Nat. Commun., 2012, 3, 938 CrossRef; A. Rotaru, J. Dugay, R. P. Tan, I. A. Gural'skiy, L. Salmon, P. Demont, J. Carrey, G. Molnár, M. Respaud and A. Bousseksou, Adv. Mater., 2013, 25, 1745 CrossRef; J. Dugay, M. Giménez-Marqués, T. Kozlova, H. W. Zandbergen, E. Coronado and H. S. J. van der Zant, Adv. Mater., 2015, 27, 1288 CrossRef; M. M. Khusniyarov, Chem.–Eur. J., 2016, 22, 15178 CrossRef; M. D. Manrique-Juárez, S. Rat, L. Salmon, G. Molnár, C. M. Quintero, L. Nicu, H. J. Shepherd and A. Bousseksou, Coord. Chem. Rev., 2016, 308, 395 CrossRef.
- S. Hayami, K. Danjobara, K. Inoue, Y. Ogawa, N. Matsumoto and Y. Maeda, Adv. Mater., 2004, 16, 869 CrossRef CAS; S. Dorbes, L. Valade, J. A. Real and C. Faulmann, Chem. Commun., 2005, 69 10.1039/b412182a; J. A. Rodríguez-Velamazán, O. Fabelo, C. M. Beavers, E. Natividad, M. Evangelisti and O. Roubeau, Chem.–Eur. J., 2014, 20, 7956 CrossRef; H. Phan, S. M. Benjamin, E. Steven, J. S. Brooks and M. Shatruk, Angew. Chem., Int. Ed., 2015, 54, 823 CrossRef; J.-L. Wang, Q. Liu, X.-J. Lv, R.-L. Wang, C.-Y. Duan and T. Liu, Dalton Trans., 2016, 45, 18552 RSC; M. Estrader, J. Salinas Uber, L. A. Barrios, J. Garcia, P. Lloyd-Williams, O. Roubeau, S. J. Teat and G. Aromí, Angew. Chem., Int. Ed., 2017, 56, 15622 CrossRef; Y.-S. Meng and T. Liu, Acc. Chem. Res., 2019, 52, 1369 Search PubMed.
- X. Zhang, T. Palamarciuc, J.-F. Létard, P. Rosa, E. Vega Lozada, F. Torres, L. G. Rosa, B. Doudin and P. A. Dowben, Chem. Commun., 2014, 50, 2255 RSC; H. Zheng, Y.-S. Meng, G.-L. Zhou, C.-Y. Duan, O. Sato, S. Hayami, Y. Luo and T. Liu, Angew. Chem., Int. Ed., 2018, 57, 8468 CrossRef CAS.
- D.-W. Fu, W. Zhang, H.-L. Cai, Y. Zhang, J.-Z. Ge, R.-G. Xiong, S. D. Huang and T. Nakamura, Angew. Chem., Int. Ed., 2011, 50, 11947 CrossRef CAS; G.-C. Xu, W. Zhang, X.-M. Ma, Y.-H. Chen, L. Zhang, H.-L. Cai, Z.-M. Wang, R.-G. Xiong and S. Gao, J. Am. Chem. Soc., 2011, 133, 14948 CrossRef; H.-L. Cai, Y. Zhang, D.-W. Fu, W. Zhang, T. Liu, H. Yoshikawa, K. Awaga and R.-G. Xiong, J. Am. Chem. Soc., 2012, 134, 18487 CrossRef; R. Shang, S. Chen, Z.-M. Wang and S. Gao, Chem.–Eur. J., 2014, 20, 15872 CrossRef; J. A. Rodríguez-Velamazán, O. Fabelo, A. Millán, J. Campo, R. D. Johnson and L. Chapon, Sci. Rep., 2015, 5, 14475 CrossRef; Y.-X. Wang, Y. Ma, Y. Chai, W. Shi, Y. Sun and P. Cheng, J. Am. Chem. Soc., 2018, 140, 7795 CrossRef.
- P. Gütlich and H. A. Goodwin, Spin Crossover in Transition Metal Compounds, Topics in Current Chemistry, Springer, Berlin, 2004, pp. 233–235 Search PubMed.
- D. Chernyshov, M. Hostettler, K. W. Törnroos and H.-B. Bürgi, Angew. Chem., Int. Ed., 2003, 42, 3825 CrossRef CAS; K. W. Törnroos, M. Hostettler, D. Chernyshov, B. Vangdal and H.-B. Bürgi, Chem.–Eur. J., 2006, 12, 6207 CrossRef.
- M. Shatruk, H. Phan, B. A. Chrisostomo and A. Suleimenova, Coord. Chem. Rev., 2015, 289, 62 CrossRef; N. Ortega-Villar, M. C. Muñoz and J. A. Real, Magnetochemistry, 2016, 2, 16 CrossRef.
- R. Pritchard, C. A. Kilner and M. A. Halcrow, Chem. Commun., 2007, 577 RSC; S. Bonnet, M. A. Siegler, J. Sánchez Costa, G. Molnár, A. Bousseksou, A. L. Spek, P. Gamez and J. Reedijk, Chem. Commun., 2008, 5619 RSC; N. Bréfuel, H. Watanabe, L. Toupet, J. Come, N. Matsumoto, E. Collet, K. Tanaka and J.-P. Tuchagues, Chem.–Eur. J., 2009, 48, 9304 Search PubMed; N. Bréfuel, E. Collet, H. Watanabe, M. Kojima, N. Matsumoto, L. Toupet, K. Tanaka and J.-P. Tuchagues, Chem.–Eur. J., 2010, 16, 14060 CrossRef CAS; M. Griffin, S. Shakespeare, H. J. Shepherd, C. J. Harding, J.-F. Létard, C. Desplanches, A. E. Goeta, J. A. K. Howard, A. K. Powell, V. Mereacre, Y. Garcia, A. D. Naik, H. Müller-Bunz and G. G. Morgan, Angew. Chem., Int. Ed., 2011, 50, 896 CrossRef; K. Bhar, S. Khan, J. Sánchez Costa, J. Ribas, O. Roubeau, P. Mitra and B. K. Ghosh, Angew. Chem., Int. Ed., 2012, 51, 2142 CrossRef; N. F. Sciortino, K. R. Scherl-Gruenwald, G. Chastanet, G. J. Halder, K. W. Chapman, J.-F. Létard and C. J. Kepert, Angew. Chem., Int. Ed., 2012, 51, 10154 CrossRef; A. Lennartson, A. D. Bond, S. Piligkos and C. J. McKenzie, Angew. Chem., Int. Ed., 2012, 51, 11049 CrossRef; Z.-Y. Li, J.-W. Dai, Y. Shiota, K. Yoshizawa, S. Kanegawa and O. Sato, Chem.–Eur. J., 2013, 19, 12948 CrossRef; Y. M. Klein, N. F. Sciortino, F. Ragon, C. E. Housecroft, C. J. Kepert and S. M. Neville, Chem. Commun., 2014, 50, 3838 RSC; T. Romero-Morcillo, F. J. Valverde-Muñoz, M. C. Muñoz, J. M. Herrera, E. Colacio and J. A. Real, RSC Adv., 2015, 5, 69782 RSC; Z.-Y. Li, H. Ohtsu, T. Kojima, J.-W. Dai, T. Yoshida, B. K. Breedlove, W.-X. Zhang, H. Iguchi, O. Sato, M. Kawano and M. Yamashita, Angew. Chem., Int. Ed., 2016, 55, 5184 CrossRef; E. Trzop, D. Zhang, L. Piñeiro-Lopez, F. J. Valverde-Muñoz, M. C. Muñoz, L. Palatinus, L. Guerin, H. Cailleau, J. A. Real and E. Collet, Angew. Chem., Int. Ed., 2016, 55, 8675 CrossRef; J. E. Clements, J. R. Price, S. M. Neville and C. J. Kepert, Angew. Chem., Int. Ed., 2016, 55, 15105 CrossRef; F.-L. Liu and J. Tao, Chem.–Eur. J., 2017, 23, 18252 CrossRef; W. Phonsri, C. G. Davies, G. N. L. Jameson, B. Moubaraki, J. S. Ward, P. E. Kruger, G. Chastanet and K. S. Murray, Chem. Commun., 2017, 53, 1374 RSC.
- M. A. Halcrow, Coord. Chem. Rev., 2009, 253, 2493 CrossRef CAS; G. A. Craig, O. Roubeau and G. Aromí, Coord. Chem. Rev., 2014, 269, 13 CrossRef.
- K. H. Sugiyarto, W.-A. McHale, D. C. Craig, D. Rae, M. L. Scudder and H. A. Goodwin, Dalton Trans., 2003, 2443 RSC; A. Bhattacharjee, V. Ksenofontov, K. H. Sugiyarto, H. A. Goodwin and P. Gütlich, Adv. Funct. Mater., 2003, 13, 877 CrossRef CAS; A. Kaiba, H. J. Shepherd, D. Fedaoui, P. Rosa, A. E. Goeta, N. Rebbani, J.-F. Létard and P. Guionneau, Dalton Trans., 2010, 39, 2910 RSC.
- C. Carbonera, J. Sánchez Costa, V. A. Money, J. Elhaïk, J. A. K. Howard, M. A. Halcrow and J.-F. Létard, Dalton Trans., 2006, 3058 RSC; D. Fedaoui, Y. Bouhadja, A. Kaiba, P. Guionneau, J.-F. Létard and P. Rosa, Eur. J. Inorg. Chem., 2008, 1022 CrossRef CAS.
- E. Coronado, M. C. Giménez-López, C. Giménez-Saiz and F. M. Romero, CrystEngComm, 2009, 11, 2198 RSC; V. Jornet-Mollá, Y. Duan, C. Giménez-Saiz, J. C. Waerenborgh and F. M. Romero, Dalton Trans., 2016, 45, 17918 RSC.
- V. Jornet-Mollá, Y. Duan, C. Giménez-Saiz, Y.-Y. Tang, P.-F. Li, F. M. Romero and R.-G. Xiong, Angew. Chem., Int. Ed., 2017, 56, 14052 CrossRef.
- M. L. Scudder, D. C. Craig and H. A. Goodwin, CrystEngComm, 2005, 7, 642 RSC.
- S. A. Barrett, C. A. Kilner and M. A. Halcrow, Dalton Trans., 2011, 40, 12021 RSC; T. D. Roberts, F. Tuna, T. L. Malkin, C. A. Kilner and M. A. Halcrow, Chem. Sci., 2012, 3, 349 RSC; C. Bartual-Murgui, C. Codina, O. Roubeau and G. Aromí, Chem.–Eur. J., 2016, 22, 12767 CrossRef CAS.
- J. Valasek, Phys. Rev., 1921, 17, 475 CrossRef CAS; M. E. Lines and A. M. Glass, Principles and Applications of Ferroelectric and Related Materials, Oxford University Press, New York, 1977 Search PubMed.
- A. Katrusiak and M. Szafranski, Phys. Rev. Lett., 2002, 89, 215507 CrossRef.
- S. Horiuchi, R. Kumai and Y. Tokura, Chem. Commun., 2007, 2321 RSC; A. S. Tayi, A. Kaeser, M. Matsumoto, T. Aida and S. I. Stupp, Nat. Chem., 2015, 7, 281 CrossRef CAS.
- R. Kumai, S. Horiuchi, H. Sagayama, T. Arima, M. Watanabe, Y. Noda and Y. Tokura, J. Am. Chem. Soc., 2007, 129, 12920 CrossRef CAS; S. Horiuchi, R. Kumai and Y. Tokura, J. Mater. Chem., 2009, 19, 4421 RSC.
- S. Horiuchi, R. Kumai and Y. Tokura, Angew. Chem., Int. Ed., 2007, 46, 3497 CrossRef CAS.
- S. Horiuchi, R. Kumai, Y. Tokunaga and Y. Tokura, J. Am. Chem. Soc., 2008, 130, 13382 CrossRef CAS.
- M. Schmidtmann, D. S. Middlemiss and C. C. Wilson, CrystEngComm, 2015, 17, 5273 RSC.
- L. K. Saunders, H. Nowell, L. E. Hatcher, H. J. Shepherd, S. J. Teat, D. R. Allan, P. R. Raithby and C. C. Wilson, CrystEngComm, 2019, 21, 5249 RSC.
- D. M. S. Martins, D. S. Middlemiss, C. R. Pulham, C. C. Wilson, M. T. Weller, P. F. Henry, N. Shankland, K. Shankland, W. G. Marshall, R. M. Ibberson, K. Knight, S. Moggach, M. Brunelli and C. A. Morrison, J. Am. Chem. Soc., 2009, 131, 3884 CrossRef CAS; Z.-S. Yao, K. Yamamoto, H.-L. Cai, K. Takahashi and O. Sato, J. Am. Chem. Soc., 2016, 138, 12005 CrossRef.
- G. Zundel, Adv. Chem. Phys., 2000, 111, 1 CAS.
- A. Parkin, S. M. Harte, A. E. Goeta and C. C. Wilson, New J. Chem., 2004, 28, 718 RSC.
- J. C. Speakman, J. Chem. Soc., 1949, 3357 RSC; D. Hadzi, Pure Appl. Chem., 1965, 11, 435 Search PubMed; F. J. Savage, R. H. Blessing and H. Wunderlich, Trans. Am. Crystallogr. Assoc., 1987, 23, 97 Search PubMed.
- K. H. Sugiyarto, D. C. Craig, A. D. Rae and H. A. Goodwin, Aust. J. Chem., 1994, 47, 869 CrossRef CAS; K. H. Sugiyarto, K. Weitzner, D. C. Craig and H. A. Goodwin, Aust. J. Chem., 1997, 50, 869 CrossRef; P. King, J. J. Henkelis, C. A. Kilner and M. A. Halcrow, Polyhedron, 2013, 52, 1449 CrossRef.
- M. Clemente-León, E. Coronado, M. C. Giménez-López and F. M. Romero, Inorg. Chem., 2007, 46, 11266 CrossRef.
- P. Guionneau, M. Marchivie, G. Bravic, J.-F. Létard and D. Chasseau, Top. Curr. Chem., 2004, 234, 97 CrossRef CAS.
- G. A. Craig, J. Sánchez Costa, O. Roubeau, S. J. Teat and G. Aromí, Chem.–Eur. J., 2012, 18, 11703 CrossRef CAS.
- A. O. F. Jones, M.-H. Lemée-Cailleau, D. M. S. Martins, G. J. McIntyre, I. D. H. Oswald, C. R. Pulham, C. K. Spanswick, L. H. Thomas and C. C. Wilson, Phys. Chem. Chem. Phys., 2012, 14, 13273 RSC.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48 CrossRef CAS.
- A. O. F. Jones, N. Blagden, G. J. McIntyre, A. Parkin, C. C. Seaton, L. H. Thomas and C. C. Wilson, Cryst. Growth Des., 2013, 13, 497 CrossRef CAS.
- E. König, Struct. Bonding, 1991, 76, 51 CrossRef.
- P. Gütlich, H. Köppen and H. G. Steinhäuser, Chem. Phys. Lett., 1980, 74, 475 CrossRef CAS; B. Weber, W. Bauer, T. Pfaffeneder, M. M. Dîrtu, A. D. Naik, A. Rotaru and Y. Garcia, Eur. J. Inorg. Chem., 2011, 3193 CrossRef.
- C. P. Köhler, R. Jakobi, E. Meissner, L. Wiehl, H. Spiering and P. Gütlich, J. Phys. Chem. Solids, 1990, 51, 239 CrossRef.
- A. Bousseksou, L. Tommasi, G. Lemercier, F. Varret and J.-P. Tuchagues, Chem. Phys. Lett., 1995, 243, 493 CrossRef CAS.
- J.-F. Létard, P. Guionneau, O. Nguyen, J. S. Costa, S. Marcén, G. Chastanet, M. Marchivie and L. Goux-Capes, Chem.–Eur. J., 2005, 11, 4582 CrossRef.
- V. A. Money, C. Carbonera, J. Elhaïk, M. A. Halcrow, J. A. K. Howard and J.-F. Létard, Chem.–Eur. J., 2007, 13, 5503 CrossRef CAS.
- N. Paradis, G. Chastanet and J.-F. Létard, Eur. J. Inorg. Chem., 2012, 3618 CrossRef CAS; N. Paradis, G. Chastanet, F. Varret and J.-F. Létard, Eur. J. Inorg. Chem., 2013, 968 CrossRef; N. F. Sciortino, S. M. Neville, C. Desplanches, J.-F. Létard, V. Martínez, J. A. Real, B. Moubaraki, K. S. Murray and C. J. Kepert, Chem.–Eur. J., 2014, 20, 7448 CrossRef.
- R. Kulmaczewski, E. Trzop, E. Collet, S. Vela and M. A. Halcrow, J. Mater. Chem. C, 2020, 8, 8420 RSC.
- S. Pillet, E.-E. Bendeif, S. Bonnet, H. J. Shepherd and P. Guionneau, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 064106 CrossRef.
- R. Mohammed, G. Chastanet, F. Tuna, T. L. Malkin, S. A. Barrett, C. A. Kilner, J.-F. Létard and M. A. Halcrow, Eur. J. Inorg. Chem., 2013, 819 CrossRef CAS.
- J. Klingele, D. Kaase, M. Schmucker, Y. Lan, G. Chastanet and J.-F. Létard, Inorg. Chem., 2013, 52, 6000 CrossRef CAS; D. Zhang, E. Trzop, F. J. Valverde-Muñoz, L. Piñeiro-López, M. C. Muñoz, E. Collet and J. A. Real, Cryst. Growth Des., 2017, 17, 2736 CrossRef.
- B. A. Leita, S. M. Neville, G. J. Halder, B. Moubaraki, C. J. Kepert, J.-F. Létard and K. S. Murray, Inorg. Chem., 2007, 46, 8784 CrossRef CAS; K. D. Murnaghan, C. Carbonera, L. Toupet, M. Griffi, M. M. Dîrtu, C. Desplanches, Y. Garcia, E. Collet, J.-F. Létard and G. G. Morgan, Chem.–Eur. J., 2014, 20, 5613 CrossRef.
- M. Nihei, H. Tahira, N. Takahashi, Y. Otake, Y. Yamamura, K. Saito and H. Oshio, J. Am. Chem. Soc., 2010, 132, 3553 CrossRef CAS.
- A. Hauser, J. Jeftic, H. Romstedt, R. Hinek and H. Spiering, Coord. Chem. Rev., 1999, 190–192, 471 CrossRef CAS.
- L. J. Kershaw Cook, H. J. Shepherd, T. P. Comyn, C. Baldé, O. Cespedes, G. Chastanet and M. A. Halcrow, Chem.–Eur. J., 2015, 21, 4805 CrossRef CAS.
- L. J. Kershaw Cook, F. L. Thorp-Greenwood, T. P. Comyn, O. Cespedes, G. Chastanet and M. A. Halcrow, Inorg. Chem., 2015, 54, 6319 CrossRef CAS.
- J.-F. Létard, S. Asthana, H. J. Shepherd, P. Guionneau, A. E. Goeta, N. Suemura, R. Ishikawa and S. Kaizaki, Chem.–Eur. J., 2012, 18, 5924 CrossRef.
- G. A. Craig, J. Sánchez Costa, O. Roubeau, S. J. Teat and G. Aromí, Chem.–Eur. J., 2011, 17, 3120 CrossRef CAS; G. A. Craig, J. Sánchez Costa, S. J. Teat, O. Roubeau, D. S. Yufit, J. A. K. Howard and G. Aromí, Inorg. Chem., 2013, 52, 7203 CrossRef.
- C. Enachescu, F. Varret, E. Codjovi, J. Linarès, S. Floquet, P. Manikandan and P. T. Manoharan, J. Phys. Chem. B, 2006, 110, 5883 CrossRef CAS.
- N. F. Sciortino, F. Ragon, Y. M. Klein, C. E. Housecroft, C. G. Davies, G. N. L. Jameson, G. Chastanet and S. M. Neville, Inorg. Chem., 2018, 57, 11068 CrossRef CAS.
- M. Seredyuk, M. C. Muñoz, M. Castro, T. Romero-Morcillo, A. B. Gaspar and J. A. Real, Chem.–Eur. J., 2013, 19, 6591 CrossRef CAS.
- A. Bialonska and R. Bronisz, Inorg. Chem., 2012, 51, 12630 CrossRef CAS; M. Weselski, M. Ksiazek, D. Rokosz, A. Dreczko, J. Kusz and R. Bronisz, Chem. Commun., 2018, 54, 3895 RSC.
- E. Milin, V. Patinec, S. Triki, E.-E. Bendeif, S. Pillet, M. Marchivie, G. Chastanet and K. Boukheddaden, Inorg. Chem., 2016, 55, 11652 CrossRef CAS.
- T. Nakanishi, Y. Hori, H. Sato, S.-Q. Wu, A. Okazawa, N. Kojima, T. Yamamoto, Y. Einaga, S. Hayami, Y. Horie, H. Okajima, A. Sakamoto, Y. Shiota, K. Yoshizawa and O. Sato, J. Am. Chem. Soc., 2019, 141, 14384 CrossRef CAS; T. Nakanishi, Y. Hori, S. Wu, H. Sato, A. Okazawa, N. Kojima, Y. Horie, H. Okajima, A. Sakamoto, Y. Shiota, K. Yoshizawa and O. Sato, Angew. Chem., Int. Ed., 2020, 59, 14781 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental section; Tables S1–S9: crystallographic data; Table S10: kinetic parameters derived from relaxation after LIESST; Fig. S1 and S4: details of crystal packing and H-bond cooperativity; Fig. S2 and S3: comparative plot of H-bonding parameters obtained from neutron and X-ray data; Fig. S5: thermal variation of crystal cell parameters; Fig. S6–S8: crystal structures under different conditions; Fig. S9: thermal relaxation experiments at different temperatures. CCDC 1873604, 1832988, 1873602 and 1832962 contain X-ray crystal data for 1 at 95, 120, 210 and 240 K, respectively. CCDC 1984961, 1984960 and 1984957 contain the neutron crystal data for 1 at 240 K, 120 K and 50 K, respectively. CCDC 1984959 and 1984958 contain the neutron crystal data for 1 at 95 K and 50 K after full relaxation to the LS state, respectively. CCDC 1984962, 1984963 and 1984964 contain the X-ray data for PIHS 1 at 50 K, 1 at 50 K after partial relaxation and at 95 K upon full relaxation to the LS state, respectively. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc04918b |
| This journal is © The Royal Society of Chemistry 2021 |