The atomic-level structure of bandgap engineered double perovskite alloys Cs₂AgIn_1−xFe_xCl₆

Abstract

Although lead-free halide double perovskites are considered as promising alternatives to lead halide perovskites for optoelectronic applications, state-of-the-art double perovskites are limited by their large bandgap. The doping/alloying strategy, key to bandgap engineering in traditional semiconductors, has also been employed to tune the bandgap of halide double perovskites. However, this strategy has yet to generate new double perovskites with suitable bandgaps for practical applications, partially due to the lack of fundamental understanding of how the doping/alloying affects the atomic-level structure. Here, we take the benchmark double perovskite Cs₂AgInCl₆ as an example to reveal the atomic-level structure of double perovskite alloys (DPAs) Cs₂AgIn_1−xFe_xCl₆ (x = 0–1) by employing solid-state nuclear magnetic resonance (ssNMR). The presence of paramagnetic alloying ions (e.g. Fe³⁺ in this case) in double perovskites makes it possible to investigate the nuclear relaxation times, providing a straightforward approach to understand the distribution of paramagnetic alloying ions. Our results indicate that paramagnetic Fe³⁺ replaces diamagnetic In³⁺ in the Cs₂AgInCl₆ lattice with the formation of [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains, which show different sizes and distribution modes in different alloying ratios. This work provides new insights into the atomic-level structure of bandgap engineered DPAs, which is of critical significance in developing efficient optoelectronic/spintronic devices.

---

Introduction

Lead (Pb) halide perovskites have received considerable attention for photovoltaics field.^1–3 However, the presence of toxic Pb and intrinsic poor stability are the main bottlenecks for their further application.⁴ A promising approach to solve these issues is to replace divalent Pb²⁺ with monovalent B⁺ and trivalent B³⁺ metal ions, forming a double perovskite with the formula of A₂B⁺B³⁺X₆ (A = Cs⁺, CH₃NH₃⁺; B = metal ions; X = Cl⁻, Br⁻, I⁻).^5–7 Unfortunately, the large bandgaps of the current double perovskites limit their practical applications.

Alloying/doping is a simple yet efficient method to tune the bandgaps of a wide range of materials, including traditional inorganic semiconductors,^8,9 oxide-based perovskites,¹⁰ Pb-based perovskites,¹¹ as well as lead-free halide double perovskites.^12–15 For example, trivalent Sb³⁺-alloying has been employed to decrease the bandgap of Cs₂AgBiBr₆ and Cs₂AgInCl₆. However, the bandgaps of the alloys in both cases are still large for photovoltaic applications.^12,13 In addition, multivalent Tl (Tl⁺/Tl³⁺) has also been introduced to decrease the bandgap of Cs₂AgBiBr₆ from 2.0 eV to 1.40 eV by Karunadasa and coworkers.¹⁴ Considering the high toxicity of Tl, they further doped less toxic Sn²⁺ into Cs₂AgBiBr₆ crystals, reaching a promising bandgap of 1.48 eV.¹⁵ However, the oxidatively unstable Sn²⁺ makes the doped perovskites highly sensitive to the ambient atmosphere. Therefore, finding rational alloying ions to tune the bandgaps of benchmark double perovskites remains challenging. During the preparation of this manuscript, Fe³⁺-alloying strategy was reported to reduce the bandgap of double perovskite Cs₂AgInCl₆.²¹

In parallel with the material development using the alloying strategy, fundamental understanding of these double perovskite alloys is also of critical importance. However, the atomic-level understanding of various dopants/alloys in halide DPAs is at a very early stage; recently, Michaelis and coworkers provided the first report for the long- to short-range structural elucidation of white-light-emitting DPAs.¹⁶ In this aspect, solid-state NMR (ssNMR), where very small chemical shifts within a given nucleus type record precisely the local chemical environment of its chemically inequivalent sites,^17–20 provide a unique and powerful approach to understand the local atomic-level structures of double perovskite alloys.

Herein, we alloy magnetic ions (Fe³⁺-alloying) into the benchmark Cs₂AgInCl₆,²¹ and tune the bandgap of Cs₂AgIn_1−xFe_xCl₆ over a range from 2.8 eV to 1.6 eV. We investigate the atomic-level structure of these double perovskite alloys using ¹³³Cs and ¹¹⁵In ssNMR spectroscopy, where the paramagnetic Fe³⁺ provides rich information on nuclear relaxation times. We find that Fe³⁺ replaces In³⁺ in the Cs₂AgIn_1−xFe_xCl₆ matrix, easily forming [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains. We also reveal that the sizes and distribution modes of [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains are different in different amounts of Fe³⁺ alloying. Our findings provide fundamental understanding of the atomic-level structure in double perovskite alloys, and are important for rational development of novel alloying elements for optoelectronic applications.

Results and discussion

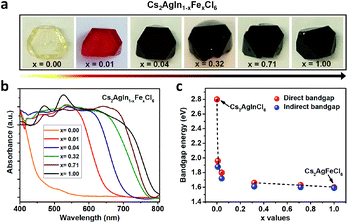
Double perovskite alloys (DPAs) Cs₂AgIn_1−xFe_xCl₆ (x = 0–1) single crystals were synthesized by the hydrothermal method from CsCl, AgCl, InCl₃, FeCl₃ and HCl precursor solutions (more details in ESI†). As shown in Fig. 1a, all the resulting crystals exhibit similar truncated octahedral morphology, and the crystal color changes from transparent to black with increasing Fe³⁺ concentration. It is worth noting that the Fe³⁺ can completely substitute In³⁺ in Cs₂AgInCl₆ with the formation of Cs₂AgFeCl₆, probably due to comparable ion radii between In³⁺ and Fe³⁺.²² The accurate concentrations (x values) of Fe³⁺ in different crystals are obtained from inductively coupled plasma optical emission spectrometer (ICP-OES) (Table S1†).

Fig. 1 Photographs (a) and normalized UV-Vis absorption spectra (b) of Cs₂AgIn_1−xFe_xCl₆ (x = 0.00, 0.01, 0.04, 0.32, 0.71 and 1.00) crystals. (c) Bandgaps of DPAs Cs₂AgIn_1−xFe_xCl₆ (x = 0.00, 0.01, 0.04, 0.32, 0.71 and 1.00) extracted by linear fits to both direct bandgap and indirect bandgap Tauc plots.

In order to understand different crystal colors between DPAs Cs₂AgIn_1−xFe_xCl₆, we investigate their optical absorption properties through UV-Visible (UV-Vis) reflectance spectra (Fig. S1†), which are further transformed to pseudo-absorption values by the Kubelka–Munk theorem.²³ As shown in Fig. 1b, there is a nonlinear change in the absorption for these alloys with increasing Fe³⁺ concentration. Specifically, the absorption edges broaden rapidly (from original ∼460 nm to ∼700 nm) with low Fe³⁺-concentrations (x ≤ 0.04) (Fig. 1b and S2†), consistent with the observed color changes in Fig. 1a. With increasing Fe³⁺ concentration, the absorption edges of Cs₂AgIn_1−xFe_xCl₆ slowly broaden. We further determine the optical bandgaps of DPAs Cs₂AgIn_1−xFe_xCl₆ (x = 0.00, 0.01, 0.04, 0.32, 0.71 and 1.00) by plotting α^r as the function of photon energy (hν), where α is the pseudo-absorption coefficient, the values for r are 2 and 1/2 for a direct and indirect bandgap, respectively. Considering the uncertainty of the direct or indirect property of DPAs Cs₂AgIn_1−xFe_xCl₆ (x > 0), we fit the absorption results by both functions (Fig. S3 and S4†). Both analyses indicate that the bandgap decreases quickly at low Fe³⁺-concentrations (x ≤ 0.04), followed by a slow decrease at high Fe-concentrations (x ≥ 0.32), reaching the smallest bandgap of ∼1.6 eV (Fig. 1c).

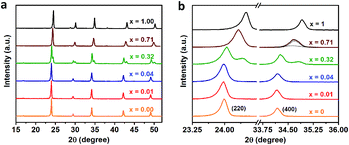
We further perform the powder X-ray diffraction (PXRD) measurements to investigate how Fe³⁺-alloying affects the crystal structures of DPAs Cs₂AgIn_1−xFe_xCl₆. As shown in Fig. 2a, all patterns show a similar diffraction behavior for the entire 2θ range, indicating that all DPAs retain the original cubic structure of Cs₂AgInCl₆. Interestingly, the change of lattice parameters with increasing concentrations of Fe-alloying can be regarded as two stages (Fig. S5†), in accordance with the absorption results. For low Fe³⁺-concentrations (x ≤ 0.04), all the diffraction peaks are almost the same, with no obvious peak shifts (Fig. 2b). Further increasing the Fe³⁺-concentration (x ≥ 0.32), the diffraction peaks shift to the high-angle side gradually, which can be understood by the smaller ionic radius of Fe³⁺ (0.65 Å) compared with In³⁺ (0.80 Å). Particularly, both (220) and (400) diffraction peaks split into two peaks for 32% Fe³⁺-alloyed Cs₂AgInCl₆, suggesting the segregation of In³⁺-rich and Fe³⁺-rich phases. According to the Scherrer equation, we can estimate the average domain size of In³⁺-rich and Fe³⁺-rich phases are about 37 nm and 24 nm, respectively. These split diffraction peaks tend to merge into a single peak again with further increasing the Fe³⁺ concentration to 71% (Fig. 2b and S6†). In other words, the diffraction peaks split when the Fe³⁺ concentration is comparable with the In³⁺ concentration, implying possible formation of In³⁺-rich and Fe³⁺-rich phases, as confirmed by the following ssNMR measurements.

Fig. 2 (a) XRD patterns of Cs₂AgIn_1−xFe_xCl₆ (x = 0.00, 0.01, 0.04, 0.32, 0.71 and 1.00) powders with different Fe³⁺-concentrations. (b) The enlarged view of the (220) and (400) diffraction peaks in the PXRD patterns.

To investigate the distribution of different phases and atomic-level structures, we perform ¹³³Cs, ¹¹⁵In solid-state NMR (ssNMR) experiments.¹⁶ As shown in Fig. 3, a relatively narrow, symmetric signal at ca. δ_iso = 41.6 ppm appears in pristine Cs₂AgInCl₆ in ¹¹⁵In ssNMR spectra which shifts slightly to lower frequencies with increasing concentrations of Fe. While these signals seem very similar, they contain useful structural information. We observe not only slight changes in the chemical shifts of the detected signal, but also signal broadening, suggesting increasing presence of dopant species (diamagnetic Fe²⁺/paramagnetic Fe³⁺) incorporated in the matrix. The increasing broadening of ¹¹⁵In signals with growing amount of Fe dopant species is induced by changes in static chemical disorder (distribution of local environments) as well as second order quadrupolar broadening of the central transition.¹⁶ In the case of 4% Fe-alloyed perovskite, the resulting ¹¹⁵In ssNMR spectrum shows broadened and less resolved spectral line (Fig. 3c and S7†). The increase of alloyed Fe concentration (32% and 71%) highlights this effect as recorded spectra become increasingly broad. This is further documented by increasing signal half-width in ¹¹⁵In ssNMR spectra (Fig. 3d and e), induced by the presence of Fe ions in the matrix.

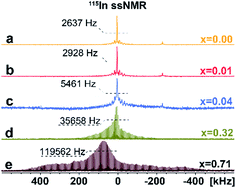Fig. 3 Experimental ¹¹⁵In ssNMR spin-echo (a–c) and WURST-QCPMG (d and e) spectra of Cs₂AgIn_1−xFe_xCl₆ (x = 0.00, 0.01, 0.04, 0.32, 0.71), conducted at static conditions. The ¹¹⁵In WURST-QCPMG NMR spectra are shown for better clarity. The magnification of ¹¹⁵In ssNMR spin-echo spectra (a–c) and comparison of ¹¹⁵In ssNMR spectra (spin-echo vs. WURST-QCPMG) for (d and e) are listed in ESI, see Fig. S7 and S8,† respectively.

Additional structural information is provided from ¹³³Cs NMR spectra. As shown in Fig. 4a–f, the symmetric peak at δ_iso = 120.2 ± 0.5 ppm for pristine Cs₂AgInCl₆ splits, broadens and finally disappears with increasing concentration of Fe ions while at high concentrations a new peak at δ_iso = 2973 ± 1.0 ppm (Fig. 4d–f) grows. Single, narrow signals for the pristine Cs₂AgInCl₆ (Fig. 4a) and the completely substituted Cs₂AgFeCl₆ (Fig. 4f) confirm the existence of one crystallographic position of the Cs⁺ ions in both structures. The significant shift of peak from δ_iso = 120.2 ± 0.5 ppm (Cs₂AgInCl₆) to δ_iso = 2973 ± 1.0 ppm (Cs₂AgFeCl₆) in ¹³³Cs MAS NMR spectra suggests presence of paramagnetic Fe³⁺ in perovskite matrix. Moreover, with increasing concentration of Fe ions alloyed into Cs₂AgInCl₆ lattice, the chemical environment of Cs⁺ becomes more complex as seen by additional signals appearing in the range of 100–120 ppm (Fig. S9†). Specifically, at low Fe concentration (x = 0.01), two signals are observed in the ¹³³Cs MAS NMR spectra, first remaining at δ_iso = 120.2 ± 0.5 ppm and a new, less intensive peak appearing at δ_iso = 117.74 ± 0.5 ppm (Fig. 4b). As the Fe ion concentration increases (x ≥ 0.04), the latter signal becomes more significant. For 4% and 32% Fe alloyed systems, a third signal is resolved (Fig. 4c and d), at 111.0 ± 2.0 ppm. The second and third signal (δ_iso = 117.74 ± 0.5 ppm and 111.0 ± 2.0 ppm) suggest the presence of Fe ions located close to Cs ions. Furthermore, in cases of 32% and 71% Fe alloyed systems, the above mentioned new shifted signal(s) appear at low-frequency position of ca. 2950 ± 50 ppm (Fig. 4d and e). These new shifted signal(s) (δ_iso = 2950 ± 50, 2973 ± 1 and 3002 ± 1 ppm) seem to correspond to the splitting of peaks in the PXRD patterns (Fig. 2b and S6†). In addition, the small changes of ¹³³Cs chemical shift in the diamagnetic region (ranging from 200 to (−100) ppm) can be explained by two ways: (i) through-space (pseudo-contact) interactions with paramagnetic Fe³⁺.^24–26 and/or (ii) the diamagnetic effect of substitution and lattice contraction.¹⁶ The signals in the diamagnetic region as well as in paramagnetic spectral range around 2950 ppm, indicate multi-component nature of the DPAs, agreeing well with the PXRD results. Based on ¹¹⁵In and ¹³³Cs ssNMR results, we conclude that the Fe³⁺ ions are incorporated into the matrix replacing In³⁺ ions.

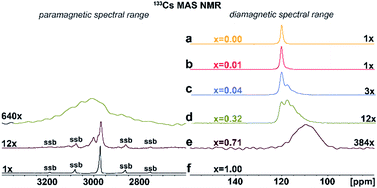Fig. 4 (a)–(f) Experimental ¹³³Cs MAS NMR spectra of Cs₂AgIn_1−xFe_xCl₆ (x = 0.00, 0.01, 0.04, 0.32, 0.71 and 1.00). The major detected ¹³³Cs NMR signals were confirmed using ¹³³Cs–¹³³Cs SD/MAS NMR experiments (The ¹³³Cs–¹³³Cs SD/MAS NMR spectra are listed in ESI, Fig. S9†).

To confirm the presence of paramagnetic Fe³⁺ ions and provide further information on their distribution in DPAs matrix, we perform ¹³³Cs NMR T₁-relaxation measurements.^27,28 These are based on the fact that the presence of paramagnetic metal centers (e.g. Fe³⁺) usually causes extremely rapid longitudinal and transverse relaxation of the nearby nuclei due to electron-spin couplings. This approach was developed by Emsley and co-workers and it is based on the reduction of ¹H and ¹³³Cs NMR T₁-relaxation times to detect paramagnetic dopants in lead halide perovskites.^27,28 The saturation-recovery build–up curves of the detected ¹³³Cs NMR signal(s) are analyzed by single and/or multi-exponential functions and values of T₁ (¹³³Cs) relaxation times as well as the corresponding fractions of individual components are obtained, see Table 1. Corresponding well with the symmetric single peaks of the Cs₂AgInCl₆ and Cs₂AgFeCl₆ systems in ¹³³Cs MAS NMR spectra, the relaxation decays were fitted by a single exponential function. However, both systems provide significantly different relaxation times with a long T₁ (¹³³Cs) relaxation time of 100 s for Cs₂AgInCl₆ and a very short T₁ (¹³³Cs) relaxation time of 11 ms for Cs₂AgFeCl₆. These results further confirm one crystallographic position of the Cs⁺ ions in both systems in an altered unit cell.

Table 1 ¹³³Cs T₁ relaxation times of Cs₂AgIn_1−xFe_xCl₆ (x = 0.00, 0.01, 0.04, 0.32, 0.71 and 1.00)

Materials	^133Cs δiso (ppm)	^133Cs T1^a (s ms^−1)	Rel. amount (%)
a The plots of the ^133Cs T1 relaxation datasets with the fitted curves are depicted in ESI, see Fig. S10. b The ^133Cs T1 relaxation time cannot be determined due to low concentration and poor resolution of 1D ^133Cs MAS NMR spectrum (see Fig. 4d).
Cs2AgInCl6	120.2 ± 0.5	101 s	100
Cs2AgIn0.99Fe0.01Cl6	120.2 ± 0.5	7.7 s	60 ± 10
	117.7 ± 0.5	1.4 s	40 ± 10
Cs2AgIn0.96Fe0.04Cl6	120.2 ± 0.5	420 ms	50 ± 10
	117.7 ± 0.5	63 ms	25 ± 10
	111.0 ± 2.0	58 ms	25 ± 10
Cs2AgIn0.68Fe0.32Cl6	120.2 ± 0.5	119 ms	30 ± 10
	117.7 ± 0.5	56 ms	40 ± 10
	111.0 ± 2.0	34 ms	30 ± 10
	2950 ± 50^b	—	<5 ± 10
Cs2AgIn0.29Fe0.71Cl6	111.0 ± 2.0	1.2 s	10 ± 10
	2973 ± 1.0	8.4 ms	60 ± 10
	3002 ± 1.0	7.2 ms	30 ± 10
Cs2AgFeCl6	2973 ± 1.0	11 ms	100

---

Contrary to the pristine materials, alloyed Cs₂AgIn_1−xFe_xCl₆ systems exhibit multi-exponential behavior reflected by a dispersion of observed T₁ (¹³³Cs) relaxation times corresponding to distinct distributions of paramagnetic species in the matrix. The 1% Fe³⁺-alloyed Cs₂AgInCl₆ system is characterized by a double exponential decay with T₁ (¹³³Cs) relaxation times of 7.7 s (60%) and 1.4 s (40%), confirming a two-component character of the matrix. The rapid-relaxation (1.4 s) and the slow-relaxation phases (7.7 s) correspond to a phase extensively occupied by well-dispersed Fe³⁺ ions and the presence of Cs⁺ ions more distant from Fe³⁺ species, respectively. It is noted that the observed significant shortening of both T₁ (¹³³Cs) spin-lattice relaxation times as compared to the Cs₂AgInCl₆ parent system (100 s) indicates almost homogeneous distribution of Fe³⁺ ions (isolated [FeCl₆]³⁻ octahedrons and/or small [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains in size up to two unit cells) in the perovskite matrix. With increasing amount of alloyed Fe³⁺ ions (4% and 32%) in the matrix, the multi-component relaxation is further accelerated. The relaxation process is in range of tens and/or hundreds of milliseconds, representing ¹³³Cs species in strong interaction with the dispersed Fe³⁺ ions. The significant shortening of relaxation times indicates presence of larger [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains, which mean that the [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains grow larger as the Fe³⁺-concentration increases.

Moreover, for the 4% Fe³⁺ alloyed perovskite, no signal at position 2950 ± 50 ppm was detected and a relatively long T₁ relaxation time (420 ms) for signal at 120.2 ± 0.5 ppm was observed, which suggests the existence of large, homogeneously distributed [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains in Cs₂AgInCl₆ parent matrix. In contrast, a new and broad signal at 2950 ± 50 ppm observed for 32% Fe³⁺ alloyed perovskite system, points to formation of a secondary Fe³⁺-rich phase, also confirmed by observed very short relaxation times (120–30 ms). Besides, the visible broadening of the signal at 2950 ± 50 ppm indicates the presence of static disorder which implies random distribution of these [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains in the matrix. Combining the short relaxation times and additional peaks in ¹³³Cs MAS NMR spectra (Table 1 and Fig. 4d), we can conclude that for 32% Fe³⁺ alloyed perovskite system the [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains have grown to form a second, interconnected microscopic phase (Fe³⁺-rich phase). These results correspond well with the feature in PXRD data, caused mainly by interconnection between these larger [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains.

In case of 71% Fe³⁺ alloyed system, we also conclude a two-component system based on ¹³³Cs MAS NMR spectra (Fig. 4e) and T₁ (¹³³Cs) spin-lattice relaxation times. In ¹³³Cs MAS NMR spectra, two relatively well-ordered phases of Cs₂AgFeCl₆ are confirmed by two sharp signals at 2973 and 3002 ppm while the [InCl₆]³⁻·[AgCl₆]⁵⁻ domains are represented by the signal at 111.0 ± 2.0 ppm. The matrix can be defined as an inverted-phase system as compared to the above-mentioned systems. The distribution of [InCl₆]³⁻·[AgCl₆]⁵⁻ domains can also be derived from the unexpectedly relatively long ¹³³Cs T₁ relaxation time (1.2 s, see Table 1.) of the corresponding signal. Considering that similarly long relaxation time was detected for the second phase of the 1% Fe alloyed Cs₂AgInCl₆, we conclude that the formation of relatively large [InCl₆]³⁻·[AgCl₆]⁵⁻ domains surrounded by [FeCl₆]³⁻ matrix. Within these domains some substitution by Fe³⁺ ions can be presumed based on the value of the corresponding relaxation time. On the other hand, the very short relaxation times for the peaks at 2973 ± 1.0 and 3002 ± 1.0 ppm confirm formation of large [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains with slightly different local environments.

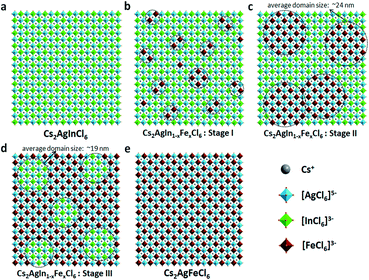
In short, based on the above observations, both pure Cs₂AgInCl₆ and Cs₂AgFeCl₆ are homogeneous systems (Fig. 5a and e). Meanwhile, the Fe-alloying process in DPAs Cs₂AgIn_1−xFe_xCl₆ can be divided into the following three stages with different Fe³⁺ concentrations:

Fig. 5 (a)–(e) Schematic presentations of possible scenarios for Fe³⁺ distribution inside the DPAs Cs₂AgIn_1−xFe_xCl₆ (x = 0–1) matrix. The [FeCl₆]³⁻·[AgCl₆]⁵⁻ or [InCl₆]³⁻·[AgCl₆]⁵⁻ domains are highlighted in balck circles.

(i) For low Fe³⁺ concentration DPAs (x ≤ 0.04), Fe³⁺ ions exist in the form of isolated [FeCl₆]³⁻ octahedrons and/or small [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains, which are almost homogeneously distributed in the perovskite matrix (Fig. 5b, stage I).

(ii) For medium Fe³⁺ concentration DPAs, the isolated [FeCl₆]³⁻ octahedrons or small [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains grow into larger [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains. The growth of these domains forms microscopically segregated phases with different sizes, leading to nonhomogeneous distribution in the matrix (Fig. 5c, stage II). A typical example is DPAs Cs₂AgIn_1−xFe_xCl₆ with 32% Fe³⁺ concentration. The average domain size of [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains in the 32% Fe³⁺ alloyed sample is about 24 nm.

(iii) For high Fe³⁺ concentration DPAs (x ≥ 0.71), the structure can be viewed as low concentration In³⁺-alloyed Cs₂AgFeCl₆. In this case, DPAs become a relatively uniform phase with almost homogeneous distribution of small and/or relatively large [InCl₆]³⁻·[AgCl₆]⁵⁻ domains in the Cs₂AgFeCl₆ matrix (Fig. 5d, stage III).

Conclusions

In conclusion, we successfully tune the bandgap of Cs₂AgInCl₆ from 2.8 eV to 1.6 eV through Fe³⁺-alloying, which is attractive for optoelectronic device applications. Moreover, we provide fundamental understanding of the atomic-level structure of DPAs with paramagnetic alloying ions (Cs₂AgIn_1−xFe_xCl₆), as revealed by the ¹³³Cs/¹¹⁵In ssNMR spectroscopy. Our results indicate that paramagnetic Fe³⁺ replaces diamagnetic In³⁺ in Cs₂AgIn_1−xFe_xCl₆ matrix and forms [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains, which grow larger as the Fe³⁺ concentration increases. Meanwhile, the connection of these larger [FeCl₆]³⁻·[AgCl₆]⁵⁻ domains leads to the formation of microscopically segregated Fe³⁺-rich phases in DPAs. We believe that ssNMR is also widely suitable for atomic-level structure study in traditional magnetic semiconductors (e.g. GaAs : Mn), molecular magnets, etc.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by Knut and Alice Wallenberg Foundation, the Swedish Energy Agency (2018-004357), VR Starting Grant (2019–05279), Carl Tryggers Stiftelse, Olle Engkvist Byggmästare Stiftelse, the STINT grant (CH2018-7655), the National Natural Science Foundation of China (61704078), the Grant Agency of the Czech Republic (Grant GA19-05259S), and the Swedish Government Strategic Research Area in Materials Science on Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU No. 2009-00971). F. G. is a Wallenberg Academy Fellow. F. J. was supported by the China Scholarship Council (CSC).

Notes and references

1. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051.
2. N. J. Jeon, J. H. Noh, W. S. Yang, Y. C. Kim, S. Ryu, J. Seo and S. I. Seok, Nature, 2015, 517, 476–480.
3. S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Science, 2013, 342, 341–344.
4. A. H. Slavney, R. W. Smaha, I. C. Smith, A. Jaffe, D. Umeyama and H. I. Karunadasa, Inorg. Chem., 2017, 56, 46–55.
5. A. H. Slavney, T. Hu, A. M. Lindenberg and H. I. Karunadasa, J. Am. Chem. Soc., 2016, 138, 2138–2141.
6. F. Ji, J. Klarbring, F. Wang, W. Ning, L. Wang, C. Yin, J. S. M. Figueroa, C. K. Christensen, M. Etter, T. Ederth, L. Sun, S. I. Simak, I. A. Abrikosov and F. Gao, Angew. Chem., 2020, 132, 15303–15306.
7. J. Luo, X. Wang, S. Li, J. Liu, Y. Guo, G. Niu, L. Yao, Y. Fu, L. Gao, Q. Dong, C. Zhao, M. Leng, F. Ma, W. Liang, L. Wang, S. Jin, J. Han, L. Zhang, J. Etheridge, J. Wang, Y. Yan, E. H. Sargent and J. Tang, Nature, 2018, 563, 541–545.
8. K.-F. Berggren and B. E. Sernelius, Phys. Rev. B, 1981, 24, 1971–1986.
9. V. Palankovski, G. Kaiblinger-Grujin and S. Selberherr, Mater. Sci. Eng., B, 1999, 66, 46–49.
10. R. Guo, R. Tian, D. Shi, H. Li and H. Liu, ACS Appl. Nano Mater., 2019, 2, 7755–7765.
11. F. Ji, L. Wang, S. Pang, P. Gao, H. Xu, G. Xie, J. Zhang and G. Cui, J. Mater. Chem. A, 2016, 4, 14437–14443.
12. K. Du, W. Meng, X. Wang, Y. Yan and D. B. Mitzi, Angew. Chem., Int. Ed., 2017, 56, 8158–8162.
13. T. T. Tran, J. R. Panella, J. R. Chamorro, J. R. Morey and T. M. McQueen, Mater. Horiz., 2017, 4, 688–693.
14. A. H. Slavney, L. Leppert, D. Bartesaghi, A. Gold-Parker, M. F. Toney, T. J. Savenije, J. B. Neaton and H. I. Karunadasa, J. Am. Chem. Soc., 2017, 139, 5015–5018.
15. K. P. Lindquist, S. A. Mack, A. H. Slavney, L. Leppert, A. Gold-Parker, J. F. Stebbins, A. Salleo, M. F. Toney, J. B. Neaton and H. I. Karunadasa, Chem. Sci., 2019, 10, 10620–10628.
16. A. Karmakar, G. M. Bernard, A. Meldrum, A. O. Oliynyk and V. K. Michaelis, J. Am. Chem. Soc., 2020, 142, 10780–10793.
17. D. J. Kubicki, D. Prochowicz, E. Salager, A. Rakhmatullin, C. P. Grey, L. Emsley and S. D. Stranks, J. Am. Chem. Soc., 2020, 142, 7813–7826.
18. A. Q. Alanazi, D. J. Kubicki, D. Prochowicz, E. A. Alharbi, M. E. F. Bouduban, F. Jahanbakhshi, M. Mladenović, J. V. Milić, F. Giordano, D. Ren, A. Y. Alyamani, H. Albrithen, A. Albadri, M. H. Alotaibi, J.-E. Moser, S. M. Zakeeruddin, U. Rothlisberger, L. Emsley and M. Grätzel, J. Am. Chem. Soc., 2019, 141, 17659–17669.
19. D. J. Kubicki, D. Prochowicz, A. Hofstetter, P. Péchy, S. M. Zakeeruddin, M. Grätzel and L. Emsley, J. Am. Chem. Soc., 2017, 139, 10055–10061.
20. D. J. Kubicki, D. Prochowicz, A. Hofstetter, S. M. Zakeeruddin, M. Grätzel and L. Emsley, J. Am. Chem. Soc., 2017, 139, 14173–14180.
21. H. Yin, Y. Xian, Y. Zhang, W. Chen, X. Wen, N. U. Rahman, Y. Long, B. Jia, J. Fan and W. Li, Adv. Funct. Mater., 2020, 11.
22. W. Ning and F. Gao, Adv. Mater., 2019, 31, 1900326.
23. P. Kubelka and F. Munk, Z. Tech. Phys., 1931, 12, 16.
24. Y. Ishii, N. P. Wickramasinghe and S. Chimon, J. Am. Chem. Soc., 2003, 125, 3438–3439.
25. R. J. Holmberg, T. Burns, S. M. Greer, L. Kobera, S. A. Stoian, I. Korobkov, S. Hill, D. L. Bryce, T. K. Woo and M. Murugesu, Chem.–Eur. J., 2016, 22, 7711–7715.
26. L. Kobera, S. Abbrent, L. Holcova, M. Urbanova, D. Kolousek, B. Dousova and J. Brus, Microporous Mesoporous Mater., 2017, 241, 115–122.
27. D. J. Kubicki, D. Prochowicz, A. Pinon, G. Stevanato, A. Hofstetter, S. M. Zakeeruddin, M. Grätzel and L. Emsley, J. Mater. Chem. A, 2019, 7, 2326–2333.
28. W. Xiang, Z. Wang, D. J. Kubicki, W. Tress, J. Luo, D. Prochowicz, S. Akin, L. Emsley, J. Zhou, G. Dietler, M. Grätzel and A. Hagfeldt, Joule, 2019, 3, 205–214.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc05264g

---