Open Access Article
Open Access ArticleStatistical analysis of C–H activation by oxo complexes supports diverse thermodynamic control over reactivity†
Joseph E.
Schneider
,
McKenna K.
Goetz
and
John S.
Anderson
 *
*
Department of Chemistry, University of Chicago, Chicago, IL 60637, USA. E-mail: jsanderson@uchicago.edu
First published on 29th January 2021
Abstract
Transition metal oxo species are key intermediates for the activation of strong C–H bonds. As such, there has been interest in understanding which structural or electronic parameters of metal oxo complexes determine their reactivity. Factors such as ground state thermodynamics, spin state, steric environment, oxygen radical character, and asynchronicity have all been cited as key contributors, yet there is no consensus on when each of these parameters is significant or the relative magnitude of their effects. Herein, we present a thorough statistical analysis of parameters that have been proposed to influence transition metal oxo mediated C–H activation. We used density functional theory (DFT) to compute parameters for transition metal oxo complexes and analyzed their ability to explain and predict an extensive data set of experimentally determined reaction barriers. We found that, in general, only thermodynamic parameters play a statistically significant role. Notably, however, there are independent and significant contributions from the oxidation potential and basicity of the oxo complexes which suggest a more complicated thermodynamic picture than what has been shown previously.
Introduction
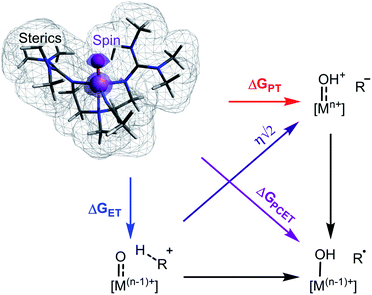
The activation of C–H bonds through proton-coupled electron transfer (PCET) underpins a wide range of biological and synthetic processes. The applications of this reaction include drug metabolism by cytochrome P450 enzymes as well as synthetic methods for the preparation of fine chemicals.1–3 In many cases PCET reactions are mediated by transition metal oxo intermediates generated within either protein-based or synthetic ligand scaffolds. In these reactions, both a proton and an electron are transferred to an oxo complex resulting in the net removal of a hydrogen atom from the organic substrate. The generality of this reaction combined with the ubiquity of C–H bonds in synthesis has led to considerable interest in determining what properties govern the PCET reactivity of transition metal oxo species.A large body of work supports that the free energy of reaction (ΔGPCET) is central to transition metal oxo mediated C–H activation and also offers a great deal of explanatory and predictive power.4–7 Recently however, additional properties have been cited as important although it is not clear if any have a widespread effect on reactivity. Individual cases support the influence of O-centered spin density,8 spin state,9–11 steric environment,12–14 the free energies of proton and electron transfer (ΔGPT and ΔGET),15–20 or the asynchronicity (η) of the reaction,21–24 but there is a lack of consensus regarding their generality and relative importance (Scheme 1).8,25–27 Very few studies have explored these parameters outside of a narrow range of complexes,4,6,10,20,21,28 and none have statistically examined the significance of parameters other than ΔGPCET on the reactivity of a broad set of metal oxo complexes.
We previously found an atypical dependence on ΔGPT in the concerted C–H activation reactivity of a terminal CoIII oxo complex which contrasts with the expected rate dependence on ΔGPCET.15 Given the disparity of this result with the literature, we sought to understand the interplay of characteristics affecting a broad range of transition metal oxo mediated PCET reactions using multivariable linear free energy relationships (LFERs). These models can be used to relate experimentally determined data, such as reaction rates, to multiple predictor variables simultaneously. LFER models have recently been used as versatile tools to optimize organic methodology, predict reaction barrier heights, and investigate underlying mechanisms.29–33,116,117
We have applied this analysis to examine trends in rates of PCET mediated C–H activation for a broad dataset of previously reported metal oxo complexes. This analysis enables a statistical examination of several hypotheses regarding what parameters of metal oxo species determine their PCET reactivity. Unsurprisingly, we observe that ΔGPCET is the most important factor. However, we also observe a significant role for ΔGPT and ΔGET beyond and independent of their contribution to ΔGPCET. Furthermore, the other parameters investigated do not have broad significance. These results suggest that thermodynamic factors are generally the dominant contributors to transition metal oxo C–H activation reactivity, but also demonstrate that thermodynamic parameters beyond the commonly invoked ΔGPCET are influential.
Results and discussion
We began our analysis by compiling an extensive data set of second order rate constants (k2) for the oxidation of 9,10-dihydroanthracene (DHA) by thirty well-characterized metal oxo complexes.12,13,15,17,34–51 This diverse data set comprises complexes of five different transition metals, tetragonal and trigonal geometries, spin multiplicities from 1 to 5, charges from −1 to +3, and d-electron counts from 0 to 6. We manually divided the data set into a training set of seventeen metal oxo complexes and a test set of thirteen metal oxo complexes such that each set had a diverse mix of species. For our analysis, we calculated the values of parameters that have been hypothesized as important to metal oxo mediated PCET reactivity for each metal oxo complex. The investigated parameters include the steric environment (quantified by percent buried volume, %BV),52 the spin density on the oxygen atom (via intrinsic bond order (IBO) analysis),53,54 the energetic cost of accessing a higher spin state if one lies closer to the product spin multiplicity than the reactant ground spin state (spin excitation), the thermodynamic free energies ΔGPCET, ΔGPT, and ΔGET, and the magnitude of the asynchronicity parameter (|η|).21 The detailed approaches used to determine the values for these parameters are provided in the methods section. Importantly, none of these parameters require transition state optimizations which are relatively difficult and less reliable than ground state calculations.55,56 While this precludes a direct estimation of transition state effects, we expect to indirectly capture some of them. For instance, parameters such as ΔGPCET and |η| have been shown to correlate with tunneling.23,57We examined the effect of each of these parameters on experimental reaction barriers by building multivariable free energy models via ordinary least squares regression of the barrier heights against the parameters. Each model consists of a set of coefficients (with variable units such that the product with the respective parameter gives units of kcal mol−1) and an intercept (with units kcal mol−1). These models were used to generate predicted reaction barriers for each data point, which could be compared with experimental reaction barriers to assess the utility of the model. Because ΔGPCET has strong theoretical and experimental support for affecting reaction barrier heights,4–6 we analyzed each parameter in combination with ΔGPCET and compared the resulting model to regression against ΔGPCET alone.
We evaluated each regression based on R2, leave-one-out (LOO) R2 (sometimes referred to as Q2), and a statistical F-test.58–61R2 is a goodness of fit measure which quantifies the amount of variation explained by a model. The predictive ability of a model is gauged with LOO R2, in which each data point is left out and predicted by the remaining data points and the goodness of fit is then reevaluated. Critically, unlike regular R2 this metric does not necessarily improve with an increase in parameters; overfitted models with too many parameters perform poorly with LOO R2. For each R2, a value close to 1 indicates a good fit. Finally, we report the p-value from an F-test on each model, which shows the probability the observed correlation arises from statistical noise. The lower this p-value is, the more significant a given parameter. Additionally, the calculation of p-values considers the number of parameters added to a model, so, as with LOO R2, an F-test is not biased in favor of adding more parameters.
A summary of our findings is presented in Table 1. In line with previous reports, we find a strong correlation between the experimental reaction barriers and ΔGPCET. This parameter alone explains 70% of the variation in reaction barriers within the training set (R2 = 0.70) and has high predictive ability (LOO R2 = 0.60). Interestingly, most other parameters do not significantly improve the model. While we do observe a small correlation with %BV steric metrics, the magnitude of the effect is too small to be statistically significant. Compared to the ΔGPCET only model, spin-based parameters and |η| barely improve R2 and perform similarly or worse in LOO cross-validation. While it is difficult to rule out the importance of these parameters in individual cases, an F-test indicates they do not have a statistically significant effect across our entire data set.
| Parameter(s) Regressed with ΔGPCET | Training set on DHAa | All data for multiple substratesb | |||
|---|---|---|---|---|---|
| R 2 | LOOcR2 | p-valued | R 2 | LOOeR2 | |
| a A subset of the reactions of 17 metal oxo complexes with DHA. b Excluding outlier metal oxo complexes (Ru oxos and oxo complexes of 13-TMC); substrates are DHA, 1,4-cyclohexadiene, xanthene, and fluorene. c Leave-one-out. d From an F-test where the null hypothesis is that only ΔGPCET has an effect. e Leave-one-out, slightly modified such that all reactions for a given metal oxo are left out together. f From an F-test where the null hypothesis is that ΔGPCET has no effect. g From an F-test where the null hypothesis is that ΔGPT has no effect. h From an F-test where the null hypothesis is that ΔGET has no effect. | |||||
| ΔGPCET only | 0.70 | 0.60 | <0.001f | 0.45 | 0.36 |
| %BV steric metrics | 0.77 | 0.64 | 0.15 | 0.48 | 0.28 |
| Oxo spin density | 0.70 | 0.55 | 0.78 | 0.53 | 0.37 |
| Spin excitation | 0.71 | 0.50 | 0.49 | 0.50 | 0.39 |
| |η| | 0.73 | 0.53 | 0.22 | 0.50 | 0.30 |
| ΔGPT, ΔGET | 0.86 | 0.71 | 0.0082 | 0.64 | 0.50 |
| 0.023g | |||||
| 0.0038h | |||||
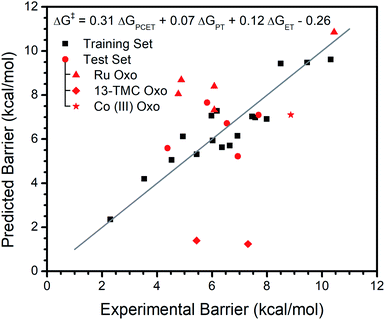
In contrast, addition of ΔGPT and ΔGET does significantly improve the fit. For this {ΔGPCET, ΔGPT, ΔGET} model, R2 increases from 0.70 to 0.86 and LOO R2 increases from 0.60 to 0.71, indicating both better explanation of the available data and better predictive ability. An F-test gives p < 0.01 which suggests the observed effect is statistically significant. The equation from this fit is ΔG‡ = 0.31ΔGPCET + 0.07ΔGPT + 0.12ΔGET − 0.26 (all coefficients unitless; free energies and intercept in kcal mol−1). Typically, ΔGPCET is a negative value while ΔGPT and ΔGET are positive values. Thus, the coefficients' positive signs mean a more exergonic reaction will have a lower barrier while increases in ΔGPT and ΔGET will raise the barrier. The larger coefficient of ΔGPCET indicates the reaction barrier is most sensitive to this free energy. Satisfyingly, the ΔGPCET coefficient agrees with experimental data: for metal oxo complexes that have a demonstrated trend of log(kobs) vs. substrate bond dissociation free energy (BDFE), the average slope of ΔG‡vs. substrate BDFE is ∼0.3 (see Table S1†), very similar to the 0.30 observed in our analysis. The intercept of −0.26 contains contributions to the average error not accounted for by the three free energies.
The significance of ΔGPT and ΔGET is intriguing because the literature discussion of these values has often been framed in terms of how they contribute to ΔGPCET rather than in terms of their intrinsic contribution to reaction barrier heights.16–19,27 However, ΔGPT and ΔGET as defined here are the energies to form the intermediates involved in stepwise reactivity – the protonated metal oxo with the deprotonated substrate, or the reduced metal oxo with the oxidized substrate (Scheme 1). Critically, ΔGPT and ΔGET do not form a full thermodynamic cycle with ΔGPCET and thus are fundamentally distinct. This fact is statistically supported by poor correlations between ΔGPCET and ΔGPT and between ΔGPCET and ΔGET (−0.12 and 0.31, respectively, see Regression S6†). Finally, we find that ΔGPT and ΔGET have importance independent of a contribution to ΔGPCET as clearly demonstrated by the LOO R2s and F-tests. All of our analyses therefore suggest that the combination of ΔGPT and ΔGET is an independent and significant contributor to C–H activation barrier heights.
While the observation of a dependence on ΔGPT and ΔGET that arises from our linear regressions is principally empirical, it is consistent with prior theoretical models in the literature. The physical underpinning of this dependency on ΔGPT and ΔGET is likely due to mixing of proton transfer and electron transfer intermediates into the concerted transition state despite these intermediates never being fully realized.62–64 Within transition state theory, this can be envisioned by a More-O’Ferrall–Jencks plot in which the transition state lies not on a one-dimensional line connecting reactant and product but on a two-dimensional plane containing reactant, product, and intermediates.65,66 In this case, the intermediates arise from proton transfer and electron transfer, and when either ΔGPT or ΔGET lowers in energy the transition state can adopt structural and electronic components of these intermediates resulting in a lower barrier height. While the use of these classical structure–energy relationships to analyse PCET reactions has been questioned recently,26,27 proton transfer and electron transfer states and their energies also have roles in nonadiabatic rate theories of PCET which treat proton transfer in a quantum mechanical fashion.67,68 Therefore, the use of ΔGPT and ΔGET to predict barrier heights of PCET is consistent with prior theoretical foundations.
Assigning a direct role for ΔGPT and ΔGET is in line with recent computational studies of PCET transition states which invoke off-ΔGPCET diagonal thermodynamic terms from Scheme 1, such as asynchronicity (η), as key contributors to DFT derived reaction barriers.21–24 Asynchronicity is derived not from the sum of ΔGPT and ΔGET, but rather their difference. Conversely, we instead find that the sum of ΔGPT and ΔGET have a more significant effect than |η|. The reason for this discrepancy is unclear, but a possible explanation is that experimental noise prevents us from observing a comparatively more subtle trend between |η| and the experimental reaction barrier heights. Furthermore, the well-controlled nature of the series of complexes previously investigated for asynchronicity may have too little variation in (ΔGPT + ΔGET) to manifest similarly to the effects we observe here.
Another way in which our data may not be amenable to investigating the effect of |η| is the variable reorganization energy of the metal oxo complexes examined here. |η| is specifically framed as an adjustment to the Marcus reorganization energy;21 therefore |η|'s effect may only be clear when reorganization is properly accounted for. While it is clear that the reorganization energy is important to PCET reactivity, there is no established way to compute it without computationally expensive transition state geometries.11,67–69 We have made multiple attempts to derive reorganization or deformation parameters using the optimized metal oxo and metal hydroxide geometries and frequencies, but none of these parameters have statistically significant contributions to predicted reaction barriers with or without |η| (see ESI†). Therefore, a combination of noise in the experimental data and our inability to compute a reliable reorganization parameter could preclude us from observing an effect of |η| on the barrier heights. Nonetheless, previous studies as well as this current work offer increasing support that off-ΔGPCET diagonal thermodynamic terms such as ΔGPT and ΔGET have important effects on reactivity independent of ΔGPCET.
The all-thermodynamic model we find here provides insights and possible alternative explanations for previously reported trends in PCET reactivity. In one study,12 steric and spin state effects were invoked to explain the comparatively high reactivity of the S = 2 complex [FeIV(O)(TMG2dien)(CH3CN)]2+. A higher rate of C–H activation as compared to S = 2 [FeIV(O)(TMG3tren)]2+ was ascribed to reduced steric hinderance in the TMG2dien complex,13 and the higher rate of C–H activation as compared to the S = 1 complexes [FeIV(O)(N4Py)]2+ and [FeIV(O)(TMC)(CH3CN)]2+ was ascribed to the S = 2 spin state in the TMG2dien complex.36,44 However, it was noted that the even faster reactivity of [FeIV(O)(Me3NTB,CH3CN)]2+, which is S = 1 and has a similar %BV profile to [FeIV(O)(TMG2dien)(CH3CN)]2+,34 is not easily explained by either hypothesis. Our analysis suggests that the thermodynamic properties of these complexes may provide an alternative explanation in these comparisons (see Table S9†). The Me3NTB complex has by far the most exergonic reaction with DHA (ΔGPCET = −16 kcal mol−1), followed by the TMG2dien complex (ΔGPCET = −9 kcal mol−1), followed by the complexes of TMG3tren, TMC, and N4Py (ΔGPCET = −7, −6, and −6 kcal mol−1, respectively). Thus, thermodynamic parameters would predict the Me3NTB complex to have the lowest reaction barrier and fastest rate of reaction, with the TMG2dien complex being the next most reactive, and the remaining complexes the least reactive as is observed experimentally.
In another study, it was observed that the rates of PCET reactions performed by [FeIV(O)(TMC)(X)]n+ decrease with more strongly donating axial ligands X.36 Variation in ΔGPCET was ruled out as a cause of this trend, as it was calculated to be similar for all complexes investigated. It was suggested that the accessibility of a high-spin state may explain this variation in the rates, as the energy of the quintet excited state decreased with stronger X ligands. However, our calculations indicate that while stronger axial donors increase ΔGET, ΔGPT decreases more substantially (see Table S9†). In our model, these changes result in a net decrease in the reaction barrier, suggesting that despite a similar ΔGPCET, the reactivity trend could be explained by thermodynamic effects. These analyses do not rule out that spin state or steric effects may be important in the previous studies, but suggest that thermodynamics may also play an important role.
The fit of the training data to {ΔGPCET, ΔGPT, ΔGET} and this model's performance on the test set is depicted graphically in Fig. 1. It is clear that the reaction barriers for most metal oxo complexes in the test set are well predicted. Nonetheless, several metal oxo complexes (given unique symbols in Fig. 1) deserve further discussion.
The {ΔGPCET, ΔGPT, ΔGET} model behaves the poorest in predicting reaction barriers for the FeIV oxo and CoIV oxo complexes of the ligand 13-TMC.49,70 Essentially no barrier is predicted for these reactions which is not observed experimentally. This is due to a large negative calculated ΔGPCET in both cases; in fact, these complexes are outliers even in the ΔGPCET only fit (see Regression S1†). The cause of this discrepancy is not entirely clear. However, it appears to be systemic to the particular ligand scaffold rather than the identity of the metal center, which suggests this discrepancy could arise from ambiguity in the primary coordination sphere of these complexes. No structural characterization is reported for the FeIV complex, and while a short Co–O bond is identified by EXAFS for the CoIV complex, it is difficult to conclusively determine the primary coordination sphere. Any discrepancy in coordination sphere would render our calculated parameters incorrect, potentially explaining their inability to predict the experimental reaction barriers.
The reaction barrier is overestimated for all Ru oxo complexes, and for three of them by more than two kcal mol−1. As Ru is the only second row transition metal in our data set, we suspect this overestimation is due to a consistent difference between first and second row transition metals rather than Ru examples not following the same trends. For instance, it is possible that the Ru oxo complexes have relatively low structural reorganization energy or that relativistic effects influence the coefficients. It may also simply be a change in the systemic DFT error upon going to the second row. Regardless, regression of barriers from the kinetics of an individual Ru oxo complex reacting with several different substrates reveals there is a trend with ΔGPCET, ΔGPT, and ΔGET with similar coefficients to those obtained from the more general model with multiple different oxo complexes (see ESI†). This supports that the same trends in free energies are at play in the Ru oxo complexes.
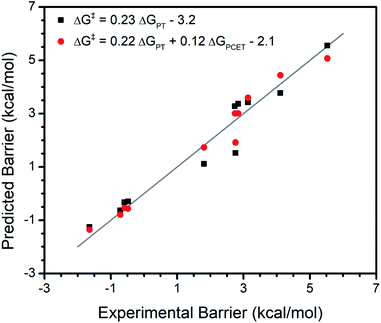
Interestingly, the {ΔGPCET, ΔGPT, ΔGET} model only moderately underestimates the reaction barrier (by ∼2 kcal mol−1) for a terminal CoIII oxo complex which has unusual trends in its reactivity with various substrates.15 Unlike most metal oxo complexes, the reactivity of this complex does not have a clear trend with ΔGPCET; its kinetics are instead dominated by ΔGPT. Therefore, its adherence to trends in {ΔGPCET, ΔGPT, ΔGET} as seen for the broad set of metal oxo complexes deserves further investigation. We regressed the experimental reaction barriers for the reactivity of this complex with several substrates against only ΔGPT as well as against {ΔGPT, ΔGPCET} (Fig. 2). We find that the inclusion of ΔGPCET significantly improves the model, increasing R2 from 0.94 to 0.97 and LOO R2 from 0.93 to 0.95 and having an F-test p-value of 0.02 (see ESI†). However, the relative weighting of the contribution from ΔGPCET is quite different than for the broader set of complexes.
In the broader set we observe that ΔGPCET has a larger effect on the reaction barriers than either ΔGPT or ΔGET, which is reflected in the larger coefficient for the ΔGPCET term than for the ΔGPT and ΔGET terms in the fit equation (Fig. 1). In contrast, ΔGPT has a greater effect than ΔGPCET on the reaction barriers for the CoIII oxo complex, again reflected in the magnitude of their coefficients (Fig. 2). Furthermore, the addition of ΔGET significantly improves the model for the broader set of metal oxo complexes (Table 1) but is insignificant for the series of substrates reacting with the CoIII oxo complex (p-value > 0.05, see Regressions S42 and S43†). Overall, this CoIII oxo complex is not so dissimilar from the broader set of metal oxo complexes in that the same thermodynamic free energies explain the reactivity of both. However, this individual case demonstrates a different weighting of parameters than those observed in the broad set.
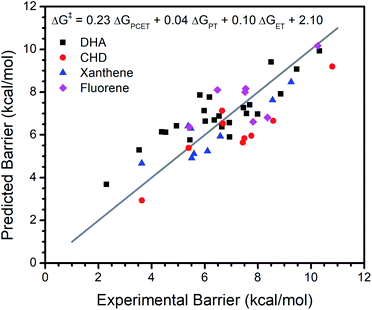
Our analysis of the CoIII reactivity rests on the assumption that the coefficients of the model do not change appreciably from substrate to substrate. To test this assumption, we extended our analysis of the larger set of metal oxo complexes to include reactivity with 1,4-cyclohexadiene (CHD), fluorene, and xanthene in addition to DHA. We refit the model with reported data for the reactions between each substrate and all metal oxo complexes (excluding the previously discussed Ru and 13-TMC oxo complexes). As with our regressions for DHA alone, the inclusion of ΔGPT and ΔGET notably improves the fit (Table 1, Fig. 3). Other parameters offer comparably little improvement to the fit and do not perform well by LOO cross validation. The equation for this model is ΔG‡ = 0.23ΔGPCET + 0.04ΔGPT + 0.10ΔGET + 2.10, which is satisfyingly similar to the equation of the fit to DHA data alone, supporting the assumption that the coefficients of the model are not appreciably affected by the identity of the substrate.
Conclusions
Overall, this thorough analysis of the reported C–H activation reactivity of transition metal oxo complexes demonstrates that ΔGPCET, ΔGPT, and ΔGET have a statistically significant correlation with the reaction barrier. Interestingly, no other parameters examined here, including steric environment and spin-based parameters, provide a significant improvement to a ΔGPCET only model. This is in contrast to previous literature reports which implicate such factors in explaining metal oxo mediated PCET. The {ΔGPCET, ΔGPT, ΔGET} model predicts all but five of the reaction barrier heights for reactivity with DHA within 2 kcal mol−1, and predicts most of these barrier heights within 1 kcal mol−1. We find that the asynchronous reactivity of a CoIII oxo complex is also well-predicted, although a fit to just this complex alone reveals changes in the relative importance of ΔGPCET, ΔGPT, and ΔGET. The structural and electronic bases for such variation, and whether concomitant changes in selectivity can be leveraged, are exciting avenues for future research.While the relative importance of these thermodynamic parameters can vary between specific cases, this study on a broad set of metal oxo complexes suggests that thermodynamic parameters provide the most general contribution to reaction barriers. Furthermore, while a strong dependence on ΔGPCET is observed, as is expected based on literature precedent, significant and independent contributions from ΔGPT and ΔGET are observed. This conclusion adds to the growing body of literature supporting the importance of thermodynamic parameters beyond ΔGPCET.
Methods
Tabulation of experimental kinetics
In this study we used thirty reported k2 values of metal oxo species reacting with DHA.12,13,15,17,34–51 For each of these oxo complexes, we tabulated various descriptors (metal, valency, d-count, coordination number, etc.), experimental parameters (M–O bond length and vibrational frequency, BDFE, pKa, etc.), and the reported kinetics for reactions with various substrates (k2, and, if reported, the statistical correction to this k2, experimental ΔH‡ and ΔS‡, and the KIE) along with the conditions these data were reported in (temperature and solvent). A full tabulation is found in the ESI.† We excluded a few metal oxo species from our analysis despite having reported kinetic data for reactivity with DHA. The reasons for these exclusions were varied: several did not have a well-defined primary coordination sphere,71–74 we were unable to calculate the reduced form of MnIII oxo complexes without deprotonation of the hydrogen-bonding ligands,17,20 one VV oxo has too much experimental uncertainty in its k2 value,75 corrolazine complexes were too large to calculate their vibrational frequencies using our methods,16,76 vibrational frequencies did not converge for the reduced form of two RuVI dioxo complexes,50 we did not include third row complexes or complexes with ligand radicals,37,77–79 and in one case saturation was reported at higher concentrations of DHA.80 We also found several reports of metal oxo mediated C–H activation of substrates besides DHA14,39,70,81–94 and useful reviews.95,96All rate constants utilized here were reported as k2 values with the exception of several rate constants used in the CoIII oxo reactivity analysis.15 In this case, for substrates which did not have a reported k2, the pseudo-first order rate constant kobs at 0.0125 M of substrate was divided by 0.0125 M to obtain an approximate k2. We used all substrates with reported kinetic data in this analysis except for 1,1,3,3-tetraphenylpropene. This substrate reacts unusually slowly, which we believe to be due to large steric hindrance of the reacting C–H bond. The remaining substrates were sterically similar enough that there is no steric effect on their kinetics (see Regression S41†).
Determination of experimental barrier heights
Before determining barrier heights from experimental k2 values, we first multiplied each k2 by any reported stoichiometric and statistical adjustments so as to start from consistently unadjusted k2 rate constants (experimental k2 rate constants are often reported with statistical corrections to facilitate comparisons between substrates, either for the stoichiometry of the substrate's reactivity or for the number of benzylic C–H bonds). We assume that where no adjustment is noted in a paper, none has been made. The barriers of PCET reactivity were then determined from the unadjusted experimental k2 values by solving the Eyring equation97 and subtracting approximate expressions for the free energy of metal oxo-substrate association: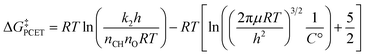 | (1) |
The second term in eqn (1) is an approximation for the free energy of association of the metal oxo and the substrate.97 This adjustment allows us to compare kinetic data collected at different temperatures. As C–H bonds are poor hydrogen bond donors, we assume that the cost of association is purely entropic (or at least that enthalpic components vary minimally between different metal oxo complexes and substrates) and further assume this entropy cost is solely the loss of translational entropy. This neglects the loss of rotational entropy and the gain of low frequency metal oxo-substrate vibrational modes, but these effects will partially cancel. Regression with ΔGPCET and RT does not fit DHA reaction barrier heights significantly better than a fit to ΔGPCET alone (see Regression S10†), indicating that this adjustment satisfactorily accounts for the temperature dependence of the reaction barrier.
We do not take into account hydrogen bonding between the metal oxo complexes and protic solvents as we were unable to derive a suitably accurate correction. However, in the ESI† we demonstrate that our best attempt to do so does not change the main conclusions herein (see Table S11†).28,98–100
Calculation of parameters
For each of these oxo complexes we calculated the values of parameters that have been proposed to influence metal oxo mediated PCET reactivity. Specifically, the parameters investigated were %BV steric metrics, spin density on the oxygen atom, available spin states, thermodynamic free energies ΔGPCET, ΔGPT, and ΔGET, and the magnitude of the asynchronicity parameter (|η|). Geometry optimization and frequency calculations were performed in ORCA using the def2 basis sets of Weigend and Ahlrichs and the O3LYP functional.101–106 For the wider set of metal oxo complexes, all transition metals were given the def2-TZVPP basis set, all metal-bonded atoms and the transferring hydrogen atom the def2-TZVP basis set, and the remaining atoms the def2-SV(P) basis set. Substrates were calculated entirely with the def2-TZVP basis set. For calculations regarding the CoIII oxo and various substrates, Co, N, O, the carbene carbons of the ligand, and the carbon undergoing C–H activation was given def2-TZVPP; all other atoms were given def2-SVP. For both sets of calculations solvent effects were included as a polarizable continuum (CPCM with the dielectric constant of acetonitrile for the broader set of metal oxo complexes; COSMO with the dielectric constant of THF for the CoIII oxo with substrates). This is primarily to mitigate the effect of self-interaction error;107 we assume that the solvent dielectric has little effect on the rate of PCET, as reported solvent effects on similar reactions are typically limited to hydrogen bonding.28,100,108 The def2 ECP was used for ruthenium.109 The resolution of identity approximation was used for coulomb integrals and the chain of spheres approximation for exchange integrals (with def2/J as the auxiliary basis). No change was made to ORCA's default grid settings. Free energies were derived from the electronic energies and vibrational calculations using the quasi-harmonic oscillator formulation of Grimme and coworkers.110Unfortunately, several of our optimized structures have small imaginary frequencies (see ESI†), which we believe is due to numerical noise of CPCM solvation. Occasionally these frequencies lie below −100 cm−1 but in each of these cases the mode is isolated to a soft dihedral motion, e.g. methyl rotation on an acetonitrile ligand. We used the absolute value of these frequencies when calculating the thermodynamic enthalpy and entropy values, believing that to be a better approximation for these modes than either nonexistence or a frequency of 0 cm−1. We were unable to reoptimize these structures to remove the imaginary frequencies.
In many cases, the correct ground state multiplicity of a species was not immediately clear. In such cases we confirmed our initial assignment by running ten geometry optimization cycles on alternate spin states and confirming these alternate assignments were several kcal mol−1 uphill of the assigned spin state. In a few cases were the energy was within 5 kcal mol−1 and the optimization was not close to convergence, we fully optimized the alternate spin state. Whenever two spin states had nearly the same energy, we chose the higher spin state as the ground state due to the typically higher entropy of high spin states.
To quantify the steric environment around each metal oxo center or substrate reactive C–H bond, we calculated percent buried volume (%BV) steric metrics using the online SambVCA web application.52 We centered the calculation on the oxygen atom (for oxos) or the transferring hydrogen (for substrates), defined the negative z-axis as going through the metal center (for oxos) or the reacting carbon center (for substrates), and defined the xz plane as containing another atom bonded to the metal or carbon (the first such atom in the .xyz file). We had the center oxygen or hydrogen atom deleted from the calculation, included hydrogen atoms in the calculation, and left all other settings to their default value (using Bondi radii scaled by 1.17, a sphere radius of 3.5 angstroms, and a mesh setting of 0.10 angstroms). The application returns a total percent buried volume, as well as that for individual quadrants of the sphere. For metal oxo complexes, we used the total percent buried volume (%BV Tot) and the standard deviation of these four quadrants (%BV Dev) in our regressions in order to capture both overall steric bulk and how evenly distributed this bulk is around the metal oxo moiety. For substrates, we solely used %BV Tot. See the ESI† for a further discussion of steric parameters and their effect on reaction barrier heights.
To evaluate the effect of spin and spin state on reactivity, we used two parameters that have been discussed in the literature: spin density on the oxo ligand and the energy to excite to a higher spin state.8,10 Atomic spin populations were determined via IBO analysis using the freely available IBO Viewer software.53,54 We recorded the spin density on the metal and on oxygen for each metal oxo complex as well as how much spin both atoms gain upon PCET reduction; we also tabulated similar values for the IBO charges. In the regression analysis we solely used the spin density on the oxo ligand. The “Spin Excitation Energy” is the vertical energy from the ground spin state of the initial oxo complex to the lowest lying excited spin state that is within one spin multiplicity of the resulting metal hydroxide ground spin state. If the ground spin state is already one spin multiplicity greater or lower than the product hydroxide spin state, then the spin excitation energy is taken to be zero. For instance, in the case of a triplet FeIV oxo reacting to give a sextet FeIII hydroxide the spin excitation energy is the energy of the quintet FeIV oxo relative to the triplet FeIV oxo at the ground state optimized geometry. This is the scenario for most FeIV oxos in the data set. But in the case of the two non-heme FeIV quintet oxos,12,13 the spin excitation energy is zero because the ground spin state is already within one spin multiplicity of the sextet hydroxide product. Essentially, the spin excitation energy is the energy needed to reach a spin surface on which reduction to the metal hydroxide's ground spin state is spin allowed. While this simple metric ignores the nuances of two state reactivity theory (such as the spin inversion probability) it is relatively simple to compute and has precedent as a quantitative measure of PCET reactivity.10,36
For each metal oxo-substrate combination assessed here, we tabulated the free energies of proton coupled electron transfer (ΔGPCET, eqn (2)), proton transfer (ΔGPT, eqn (3)), electron transfer (ΔGET, eqn (4)), and the asynchronicity as defined by Srnec and coworkers (η, eqn (5)):21
ΔGPCET = GM–OH + GC· − GM![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O − GC–H O − GC–H | (2) |
ΔGPT = GM–OH+ + GC:− − GM![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O − GC–H O − GC–H | (3) |
ΔGET = GM–O− + GC–H+ − GM![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O − GC–H O − GC–H | (4) |
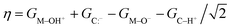 | (5) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O is the calculated free energy of the oxo species, GC–H is the calculated free energy of the substrate, and all other free energies are defined analogously. We also tabulated the absolute value of the asynchronicity (|η|), the average of ΔGPT and ΔGET (ΔGCT Average), and the analogous electronic energies (same notation, with G replaced with E).
O is the calculated free energy of the oxo species, GC–H is the calculated free energy of the substrate, and all other free energies are defined analogously. We also tabulated the absolute value of the asynchronicity (|η|), the average of ΔGPT and ΔGET (ΔGCT Average), and the analogous electronic energies (same notation, with G replaced with E).
Statistical analysis
All statistical analysis was performed in Python using the Numpy, Scipy, Pandas, Sklearn, and Matplotlib packages.111–115 A script ran a prescribed set of regression models and reported statistics on each model. All regressions were performed with ordinary least squares. Prior to fitting any regression, we separated the data into a test set and a training set of metal oxo species. While we show both test and training sets for each regression in the ESI,† we initially did not plot the test set or calculate statistics with it. We solely used the training set in the earlier stages of our analysis, where we determined which parameters improved a fit to ΔGPCET only and which did not. We then examined if the good fits to the training set extrapolated well to the test set. We had to make a few changes to the initial division of the training and test sets, however. Initially, the CoIV oxo was included in the training set,49 but that was interfering with the fit to ΔGPCET. We moved it to the test set, and to provide insight into this poor fit we calculated the FeIV oxo complex of 13-TMC and added it to the test set.70 We also saw, visually, that the inclusion of a RuIV oxo in the training set was interfering with the addition of other parameters and moved all Ru oxo complexes to the test set.38,43,45,50,51The simplest metrics reported from these models are the mean square error (MSE) and the goodness of fit R2.58–61 These both give an indication of how well a model fits the available data but are prone to overfitting; more complicated models can only improve these metrics, regardless of whether or not the model is actually better.
We also evaluated each model with cross validation (CV) metrics, which can become worse upon overfitting. In K-fold cross validation, the training data is further subdivided into K subsets, and each subset is predicted by the K − 1 remaining subsets.59,61 When K is the number of data points, i.e. each data point being predicted by the rest of the data points, this is known as leave-one-out (LOO) cross validation. These predicted data points can be used to calculate the MSE and R2 as above. The MSE from LOO cross validation is an approximately unbiased estimate of the expected error of a test set; however, it has high variability from training set to training set because each prediction uses nearly every point in a given training set. By repeatedly subdividing into larger groups and averaging the resultant K-fold MSEs, one obtains a pessimistic but less variable estimate of the expected test error. As we see similar trends for both LOO and 5-fold CV, we only report LOO R2 in the main text but show all metrics in the ESI.†
Another way to determine the significance of the model is to use a statistical F-test.58,60 This allows one to compare an unrestricted model with a more restricted one (fewer parameters used as regressors, or no parameters regressed, or restrictions placed on the relationship between coefficients, etc.). In the language of hypothesis testing, the null hypothesis is that the unrestricted model offers no improvement on the restricted model and the alternate hypothesis is that there is an improvement. When both models are fit to the data, the unrestricted model will have less total squared error than the restricted model. Assuming said error of each data point is normally distributed (or that there is enough data such that the error is approximately normally distributed), that the average error is zero, and that the model is properly formulated, it is possible to determine the probability that this reduction in total squared error is spurious. This probability is known as the p-value. The test relies on a well-defined number of degrees of freedom in both the restricted and unrestricted model to draw out what the statistical distribution of total squared error ought to be.
For regressions on multiple substrates at once, the unequal weighting of different metal oxo complexes (depending on how many substrates are reported for them) renders these statistical metrics unreliable.61 We ameliorate this issue for LOO cross validation by leaving out all reaction barriers for a given metal oxo complex together rather than one at a time. That is, we leave one metal oxo complex out and predict its reaction barrier heights based on all other metal oxos' reaction barrier heights rather than leave one reaction barrier height out and predict this barrier based off all other barriers. We accordingly only report LOO CV metrics for this set of regressions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the National Institutes of Health (R35 GM133470), the National Science Foundation (1654144), and the University of Chicago. J. E. S. thanks the Department of Defense for a National Defense Science and Engineering Graduate Fellowship (00003765) and J. S. A. thanks the Sloan Foundation for a Research Fellowship (FG-2019-11497). Computations were generously supported by the UChicago Research Computing Center. We also acknowledge useful discussions with Dr Daniel Bím.Notes and references
- M. Milan, M. Salamone, M. Costas and M. Bietti, Acc. Chem. Res., 2018, 51, 1984–1995 CrossRef CAS.
- H. B. Gray and J. R. Winkler, Acc. Chem. Res., 2018, 51, 1850–1857 CrossRef CAS.
- G. Yin, Coord. Chem. Rev., 2010, 254, 1826–1842 CrossRef CAS.
- W. Lai, C. Li, H. Chen and S. Shaik, Angew. Chem., Int. Ed., 2012, 51, 5556–5578 CrossRef CAS.
- J. M. Mayer, J. Phys. Chem. Lett., 2011, 2, 1481–1489 CrossRef CAS.
- J. M. Mayer, Acc. Chem. Res., 2011, 44, 36–46 CrossRef CAS.
- D. Dhar, G. M. Yee, A. D. Spaeth, D. W. Boyce, H. Zhang, B. Dereli, C. J. Cramer and W. B. Tolman, J. Am. Chem. Soc., 2016, 138, 356–368 CrossRef CAS.
- N. Dietl, M. Schlangen and H. Schwarz, Angew. Chem., Int. Ed., 2012, 51, 5544–5555 CrossRef CAS.
- S. N. Dhuri, M. S. Seo, Y.-M. Lee, H. Hirao, Y. Wang, W. Nam and S. Shaik, Angew. Chem., Int. Ed., 2008, 47, 3356–3359 CrossRef CAS.
- K.-B. Cho, E. J. Kim, M. S. Seo, S. Shaik and W. Nam, Chem.–Eur. J., 2012, 18, 10444–10453 CrossRef CAS.
- D. Usharani, D. Janardanan, C. Li and S. Shaik, Acc. Chem. Res., 2013, 46, 471–482 CrossRef CAS.
- J. England, Y. Guo, K. M. Van Heuvelen, M. A. Cranswick, G. T. Rohde, E. L. Bominaar, E. Münck and L. Que, J. Am. Chem. Soc., 2011, 133, 11880–11883 CrossRef CAS.
- J. England, M. Martinho, E. R. Farquhar, J. R. Frisch, E. L. Bominaar, E. Münck and L. Que, Angew. Chem., Int. Ed., 2009, 48, 3622–3626 CrossRef CAS.
- J. P. Bigi, W. H. Harman, B. Lassalle-Kaiser, D. M. Robles, T. A. Stich, J. Yano, R. D. Britt and C. J. Chang, J. Am. Chem. Soc., 2012, 134, 1536–1542 CrossRef CAS.
- M. K. Goetz and J. S. Anderson, J. Am. Chem. Soc., 2019, 141, 4051–4062 CrossRef CAS.
- D. E. Lansky and D. P. Goldberg, Inorg. Chem., 2006, 45, 5119–5125 CrossRef CAS.
- T. H. Parsell, M.-Y. Yang and A. S. Borovik, J. Am. Chem. Soc., 2009, 131, 2762–2763 CrossRef CAS.
- T. H. Yosca, J. Rittle, C. M. Krest, E. L. Onderko, A. Silakov, J. C. Calixto, R. K. Behan and M. T. Green, Science, 2013, 342, 825–829 CrossRef CAS.
- R. A. Baglia, C. M. Krest, T. Yang, P. Leeladee and D. P. Goldberg, Inorg. Chem., 2016, 55, 10800–10809 CrossRef CAS.
- S. K. Barman, J. R. Jones, C. Sun, E. A. Hill, J. W. Ziller and A. S. Borovik, J. Am. Chem. Soc., 2019, 141, 11142–11150 CrossRef CAS.
- D. Bím, M. Maldonado-Domínguez, L. Rulíšek and M. Srnec, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E10287–E10294 CrossRef.
- D. Bím, M. Maldonado-Domínguez, R. Fučík and M. Srnec, J. Phys. Chem. C, 2019, 123, 21422–21428 CrossRef.
- M. Maldonado-Domínguez, D. Bím, R. Fučík, R. Čurík and M. Srnec, Phys. Chem. Chem. Phys., 2019, 21, 24912–24918 RSC.
- M. Maldonado-Domínguez and M. Srnec, J. Am. Chem. Soc., 2020, 142, 3947–3958 CrossRef.
- C. T. Saouma and J. M. Mayer, Chem. Sci., 2013, 5, 21–31 RSC.
- C. Costentin and J.-M. Savéant, Chem. Sci., 2020, 11, 1006–1010 RSC.
- R. Tyburski, T. Liu, S. D. Glover and L. Hammarström, J. Am. Chem. Soc., 2021, 143(2), 560–576 CrossRef CAS.
- J. J. Warren and J. M. Mayer, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 5282–5287 CrossRef CAS.
- J. P. Reid and M. S. Sigman, Nature, 2019, 571, 343–348 CrossRef CAS.
- A. G. Maldonado and G. Rothenberg, Chem. Soc. Rev., 2010, 39, 1891–1902 RSC.
- K. Jorner, T. Brinck, P.-O. Norrby and D. Buttar, Chem. Sci., 2021, 12, 1163–1175 RSC.
- C. B. Santiago, J.-Y. Guo and M. S. Sigman, Chem. Sci., 2018, 9, 2398–2412 RSC.
- B. P. Roberts and A. J. Steel, J. Chem. Soc., Perkin Trans. 2, 1994, 2155–2162 RSC.
- M. Sook Seo, N. Hee Kim, K.-B. Cho, J. Eun So, S. Kyung Park, M. Clémancey, R. Garcia-Serres, J.-M. Latour, S. Shaik and W. Nam, Chem. Sci., 2011, 2, 1039–1045 RSC.
- S. Kundu, J. V. K. Thompson, L. Q. Shen, M. R. Mills, E. L. Bominaar, A. D. Ryabov and T. J. Collins, Chem.–Eur. J., 2015, 21, 1803–1810 CrossRef CAS.
- C. V. Sastri, J. Lee, K. Oh, Y. J. Lee, J. Lee, T. A. Jackson, K. Ray, H. Hirao, W. Shin, J. A. Halfen, J. Kim, L. Que, S. Shaik and W. Nam, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 19181–19186 CrossRef CAS.
- C. Fertinger, N. Hessenauer-Ilicheva, A. Franke and R. van Eldik, Chem.–Eur. J., 2009, 15, 13435–13440 CrossRef CAS.
- T. Kojima, K. Nakayama, K. Ikemura, T. Ogura and S. Fukuzumi, J. Am. Chem. Soc., 2011, 133, 11692–11700 CrossRef CAS.
- Y. J. Jeong, Y. Kang, A.-R. Han, Y.-M. Lee, H. Kotani, S. Fukuzumi and W. Nam, Angew. Chem., Int. Ed., 2008, 47, 7321–7324 CrossRef CAS.
- K. A. Gardner, L. L. Kuehnert and J. M. Mayer, Inorg. Chem., 1997, 36, 2069–2078 CrossRef CAS.
- C. Arunkumar, Y.-M. Lee, J. Y. Lee, S. Fukuzumi and W. Nam, Chem.–Eur. J., 2009, 15, 11482–11489 CrossRef CAS.
- K.-B. Cho, H. Kang, J. Woo, Y. J. Park, M. S. Seo, J. Cho and W. Nam, Inorg. Chem., 2014, 53, 645–652 CrossRef CAS.
- S. N. Dhuri, Y.-M. Lee, M. S. Seo, J. Cho, D. D. Narulkar, S. Fukuzumi and W. Nam, Dalton Trans., 2015, 44, 7634–7642 RSC.
- D. Wang, K. Ray, M. J. Collins, E. R. Farquhar, J. R. Frisch, L. Gómez, T. A. Jackson, M. Kerscher, A. Waleska, P. Comba, M. Costas and L. Que, Chem. Sci., 2013, 4, 282–291 RSC.
- J. R. Bryant and J. M. Mayer, J. Am. Chem. Soc., 2003, 125, 10351–10361 CrossRef CAS.
- G. Yin, A. M. Danby, D. Kitko, J. D. Carter, W. M. Scheper and D. H. Busch, J. Am. Chem. Soc., 2008, 130, 16245–16253 CrossRef CAS.
- S. Hong, H. So, H. Yoon, K.-B. Cho, Y.-M. Lee, S. Fukuzumi and W. Nam, Dalton Trans., 2013, 42, 7842–7845 RSC.
- D. F. Leto, R. Ingram, V. W. Day and T. A. Jackson, Chem. Commun., 2013, 49, 5378–5380 RSC.
- B. Wang, Y.-M. Lee, W.-Y. Tcho, S. Tussupbayev, S.-T. Kim, Y. Kim, M. S. Seo, K.-B. Cho, Y. Dede, B. C. Keegan, T. Ogura, S. H. Kim, T. Ohta, M.-H. Baik, K. Ray, J. Shearer and W. Nam, Nat. Commun., 2017, 8, 14839 CrossRef CAS.
- C.-M. Che, J.-L. Zhang, R. Zhang, J.-S. Huang, T.-S. Lai, W.-M. Tsui, X.-G. Zhou, Z.-Y. Zhou, N. Zhu and C. K. Chang, Chem.–Eur. J., 2005, 11, 7040–7053 CrossRef CAS.
- W. W. Y. Lam, S.-M. Yiu, D. T. Y. Yiu, T.-C. Lau, W.-P. Yip and C.-M. Che, Inorg. Chem., 2003, 42, 8011–8018 CrossRef CAS.
- L. Falivene, Z. Cao, A. Petta, L. Serra, A. Poater, R. Oliva, V. Scarano and L. Cavallo, Nat. Chem., 2019, 11, 872–879 CrossRef CAS.
- G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843 CrossRef CAS.
- G. Knizia and J. E. M. N. Klein, Angew. Chem., Int. Ed., 2015, 54, 5518–5522 CrossRef CAS.
- F. Jensen, Introduction to computational chemistry, John Wiley & Sons, Chichester, 2007 Search PubMed.
- J. N. Harvey, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2006, 102, 203–226 RSC.
- R. P. Bell, The tunnel effect in chemistry, Chapman and Hall, London, New York, 1980 Search PubMed.
- D. Freedman, Statistical models: theory and practice, Cambridge University Press, Cambridge, 2005 Search PubMed.
- T. Hastie, J. Friedman and R. Tisbshirani, The elements of statistical learning: data mining, inference, and prediction, Springer, New York, 2018 Search PubMed.
- R. Carter Hill, W. E. Griffiths and G. C. Lim, Principles of econometrics, Wiley, Hoboken, NJ, 4th edn, 2011 Search PubMed.
- L. Buitinck, G. Louppe, M. Blondel, F. Pedregosa, A. Mueller, O. Grisel, V. Niculae, P. Prettenhofer, A. Gramfort, J. Grobler, R. Layton, J. Vanderplas, A. Joly, B. Holt and G. Varoquaux, 2013, arXiv:1309.0238 [cs].
- D. Usharani, D. C. Lacy, A. S. Borovik and S. Shaik, J. Am. Chem. Soc., 2013, 135, 17090–17104 CrossRef CAS.
- J. W. Darcy, S. S. Kolmar and J. M. Mayer, J. Am. Chem. Soc., 2019, 141, 10777–10787 CrossRef CAS.
- A. Cembran, M. R. Provorse, C. Wang, W. Wu and J. Gao, J. Chem. Theory Comput., 2012, 8, 4347–4358 CrossRef CAS.
- E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, Mill Valley, California, 2006 Search PubMed.
- W. P. Jencks, Chem. Rev., 1985, 85, 511–527 CrossRef CAS.
- S. Hammes-Schiffer and A. A. Stuchebrukhov, Chem. Rev., 2010, 110, 6939–6960 CrossRef CAS.
- S. Hammes-Schiffer, Acc. Chem. Res., 2001, 34, 273–281 CrossRef CAS.
- C. R. Waidmann, X. Zhou, E. A. Tsai, W. Kaminsky, D. A. Hrovat, W. T. Borden and J. M. Mayer, J. Am. Chem. Soc., 2009, 131, 4729–4743 CrossRef CAS.
- S. Hong, Y.-M. Lee, K.-B. Cho, K. Sundaravel, J. Cho, M. J. Kim, W. Shin and W. Nam, J. Am. Chem. Soc., 2011, 133, 11876–11879 CrossRef CAS.
- A. Company, I. Prat, J. R. Frisch, D. R. Mas-Ballesté, M. Güell, G. Juhász, X. Ribas, D. E. Münck, J. M. Luis, L. Que and M. Costas, Chem.–Eur. J., 2011, 17, 1622–1634 CrossRef CAS.
- A. T. Fiedler and L. Que, Inorg. Chem., 2009, 48, 11038–11047 CrossRef CAS.
- O. Planas, M. Clémancey, J.-M. Latour, A. Company and M. Costas, Chem. Commun., 2014, 50, 10887–10890 RSC.
- S. C. Sawant, X. Wu, J. Cho, K.-B. Cho, S. H. Kim, M. S. Seo, Y.-M. Lee, M. Kubo, T. Ogura, S. Shaik and W. Nam, Angew. Chem., Int. Ed., 2010, 49, 8190–8194 CrossRef CAS.
- C. R. Waidmann, X. Zhou, E. A. Tsai, W. Kaminsky, D. A. Hrovat, W. T. Borden and J. M. Mayer, J. Am. Chem. Soc., 2009, 131, 4729–4743 CrossRef CAS.
- K. A. Prokop, S. P. de Visser and D. P. Goldberg, Angew. Chem., Int. Ed., 2010, 49, 5091–5095 CrossRef CAS.
- Y. Liu, S.-M. Ng, W. W. Y. Lam, S.-M. Yiu and T.-C. Lau, Angew. Chem., 2016, 128, 296–299 CrossRef.
- K. Cho, P. Leeladee, A. J. McGown, S. DeBeer and D. P. Goldberg, J. Am. Chem. Soc., 2012, 134, 7392–7399 CrossRef CAS.
- J. P. T. Zaragoza, M. A. Siegler and D. P. Goldberg, Chem. Commun., 2016, 52, 167–170 RSC.
- I. Garcia-Bosch, A. Company, C. W. Cady, S. Styring, W. R. Browne, X. Ribas and M. Costas, Angew. Chem., Int. Ed., 2011, 50, 5648–5653 CrossRef CAS.
- X. Wu, M. S. Seo, K. M. Davis, Y.-M. Lee, J. Chen, K.-B. Cho, Y. N. Pushkar and W. Nam, J. Am. Chem. Soc., 2011, 133, 20088–20091 CrossRef CAS.
- J. Chen, Y.-M. Lee, K. M. Davis, X. Wu, M. S. Seo, K.-B. Cho, H. Yoon, Y. J. Park, S. Fukuzumi, Y. N. Pushkar and W. Nam, J. Am. Chem. Soc., 2013, 135, 6388–6391 CrossRef CAS.
- J. England, J. O. Bigelow, K. M. V. Heuvelen, E. R. Farquhar, M. Martinho, K. K. Meier, J. R. Frisch, E. Münck and L. Que, Chem. Sci., 2014, 5, 1204–1215 RSC.
- G. K. Cook and J. M. Mayer, J. Am. Chem. Soc., 1995, 117, 7139–7156 CrossRef CAS.
- S. N. Dhuri, M. S. Seo, Y.-M. Lee, H. Hirao, Y. Wang, W. Nam and S. Shaik, Angew. Chem., Int. Ed., 2008, 47, 3356–3359 CrossRef CAS.
- S. A. Wilson, J. Chen, S. Hong, Y.-M. Lee, M. Clémancey, R. Garcia-Serres, T. Nomura, T. Ogura, J.-M. Latour, B. Hedman, K. O. Hodgson, W. Nam and E. I. Solomon, J. Am. Chem. Soc., 2012, 134, 11791–11806 CrossRef CAS.
- W. Nam, S.-E. Park, I. K. Lim, M. H. Lim, J. Hong and J. Kim, J. Am. Chem. Soc., 2003, 125, 14674–14675 CrossRef CAS.
- M. Ghosh, K. K. Singh, C. Panda, A. Weitz, M. P. Hendrich, T. J. Collins, B. B. Dhar and S. Sen Gupta, J. Am. Chem. Soc., 2014, 136, 9524–9527 CrossRef CAS.
- A. N. Biswas, M. Puri, K. K. Meier, W. N. Oloo, G. T. Rohde, E. L. Bominaar, E. Münck and L. Que, J. Am. Chem. Soc., 2015, 137, 2428–2431 CrossRef CAS.
- M. Mitra, H. Nimir, S. Demeshko, S. S. Bhat, S. O. Malinkin, M. Haukka, J. Lloret-Fillol, G. C. Lisensky, F. Meyer, A. A. Shteinman, W. R. Browne, D. A. Hrovat, M. G. Richmond, M. Costas and E. Nordlander, Inorg. Chem., 2015, 54, 7152–7164 CrossRef CAS.
- J. Kaizer, E. J. Klinker, N. Y. Oh, J.-U. Rohde, W. J. Song, A. Stubna, J. Kim, E. Münck, W. Nam and L. Que, J. Am. Chem. Soc., 2004, 126, 472–473 CrossRef CAS.
- K. Nehru, M. S. Seo, J. Kim and W. Nam, Inorg. Chem., 2007, 46, 293–298 CrossRef CAS.
- J. Serrano-Plana, W. N. Oloo, L. Acosta-Rueda, K. K. Meier, B. Verdejo, E. García-España, M. G. Basallote, E. Münck, L. Que, A. Company and M. Costas, J. Am. Chem. Soc., 2015, 137, 15833–15842 CrossRef CAS.
- T. Kurahashi, A. Kikuchi, Y. Shiro, M. Hada and H. Fujii, Inorg. Chem., 2010, 49, 6664–6672 CrossRef CAS.
- A. Gunay and K. H. Theopold, Chem. Rev., 2010, 110, 1060–1081 CrossRef CAS.
- X.-S. Xue, P. Ji, B. Zhou and J.-P. Cheng, Chem. Rev., 2017, 117, 8622–8648 CrossRef CAS.
- T. L. Hill, An Introduction to Statistical Thermodynamics, Dover Publications, Newburyport, 2012 Search PubMed.
- M. H. Abraham, P. L. Grellier, D. V. Prior, P. P. Duce, J. J. Morris and P. J. Taylor, J. Chem. Soc., Perkin Trans. 2, 1989, 699–711 RSC.
- M. H. Abraham, P. L. Grellier, D. V. Prior, J. J. Morris and P. J. Taylor, J. Chem. Soc., Perkin Trans. 2, 1990, 521–529 RSC.
- D. W. Snelgrove, J. Lusztyk, J. T. Banks, P. Mulder and K. U. Ingold, J. Am. Chem. Soc., 2001, 123, 469–477 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- N. C. Handy and A. J. Cohen, Mol. Phys., 2001, 99, 403–412 CrossRef CAS.
- A. J. Cohen and N. C. Handy, Mol. Phys., 2001, 99, 607–615 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- A. J. Johansson, M. R. A. Blomberg and P. E. M. Siegbahn, J. Chem. Phys., 2008, 129, 154301 CrossRef.
- D. V. Avila, C. E. Brown, K. U. Ingold and J. Lusztyk, J. Am. Chem. Soc., 1993, 115, 466–470 CrossRef CAS.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- S. van der Walt, S. C. Colbert and G. Varoquaux, Comput. Sci. Eng., 2011, 13, 22–30 Search PubMed.
- W. McKinney, Proc. Python Sci. Conf., 2010, pp. 56–61 Search PubMed.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, Nat. Methods, 2020, 17, 261–272 CrossRef CAS.
- T. Z. H. Gani and H. J. Kulik, ACS Catal., 2018, 8(2), 975–986 CrossRef CAS.
- A. Nandy and H. J. Kulik, ACS Catal., 2020, 10(24), 15033–15047 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed summary of LFER models; additional methodological details; further analysis of hydrogen bonding, steric effects, and reorganization effects; spreadsheets containing experimental and computational data; optimized geometries and the output of frequency calculations; and python scripts used to perform the regression. See DOI: 10.1039/d0sc06058e |
| This journal is © The Royal Society of Chemistry 2021 |