Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A redox-active ionic liquid manifesting charge-transfer interaction between a viologen and carbazole and its effect on the viscosity, ionic conductivity, and redox process of the viologen†
Hironobu
Tahara
 *a,
Yudai
Tanaka
a,
Shoko
Yamamoto
a,
Shigeki
Yonemori
b,
Bun
Chan
*a,
Yudai
Tanaka
a,
Shoko
Yamamoto
a,
Shigeki
Yonemori
b,
Bun
Chan
 a,
Hiroto
Murakami
a,
Hiroto
Murakami
 a and
Takamasa
Sagara
a and
Takamasa
Sagara
 *a
*a
aGraduate School of Engineering, Nagasaki University, 1-14 Bunkyo, Nagasaki, 852-8521, Japan. E-mail: h-tahara@nagasaki-u.ac.jp; sagara@nagasaki-u.ac.jp
bSchool of Engineering, Nagasaki University, 1-14 Bunkyo, Nagasaki, 852-8521, Japan
First published on 18th February 2021
Abstract
Redox-active ionic liquids (RAILs) are gaining attention as a material that can create a wide range of functions. We herein propose a charge-transfer (CT) RAIL by mixing two RAILs, specifically a carbazole-based ionic liquid ([CzC4ImC1][TFSI]) as a donor and a viologen-based ionic liquid ([C4VC7][TFSI]2) as an acceptor. We investigated the effect of CT interaction on the physicochemical properties of the CT ionic liquid (CT-IL) using the results of temperature-dependent measurements of UV-vis absorption, viscosity, and ionic conductivity as well as cyclic voltammograms. We employed the Walden analysis and the Grunberg–Nissan model to elucidate the effect of the CT interaction on the viscosity and ionic conductivity. The CT interaction reduces the viscosity by reducing the electrostatic attraction between the dicationic viologen and TFSI anion. It also reduces the ionic conductivity by the CT association of the dicationic viologen and carbazole. The electrochemically reversible responses of the viologens in [C4VC7][TFSI]2 and CT-IL are consistent with the Nernstian and the interacting two-redox site models. Notably, the transport and electrochemical properties are modulated by CT interaction, leading to unique features that are not present in individual component ILs. The inclusion of CT interaction in RAILs thus provides a powerful means to expand the scope of functionalized ionic liquids.
1. Introduction
Charge transfer (CT) interaction between a donor and acceptor has been of great interest because it can determine the material structures, electric conduction, and photoconduction in solid state.1 In addition, it can give rise to unique dynamical physicochemical properties of Stoddart's supramolecules,2,3 intermediate complex of chemical reaction,4 and photochemically active species5–8 in solution phase. CT interaction never emerges in its individual component species but appears as a synergetic effect. The CT interaction depends on the combination of a donor and acceptor, and one can exploit such combinations in ionic liquids to produce new photoactivity and to modulate their physicochemical properties.A myriad of ionic liquids (ILs) with various physicochemical properties have been synthesized. Because ILs are designer solvents9 that can be readily created by combining organic cations and anions, one can straightforwardly tune their viscosity, ionic conductivity, and melting point, as well as the solubility of substrate molecules. This leads to some notable advantages over typical organic solvents. For example, ILs are often preferred due to the higher solubility of solutes such as cellulose10 and CO2.11,12 Therefore, they are frequently applied to extraction and separation chemistry.13 ILs also provide interesting functionalities rarely found in organic molecular solvents,14 leading to unique IL-based liquid materials. In addition, organic cations can be modified to further transform ILs into functionalized ionic liquids (FILs) or task-specific ionic liquids.15
Extensive developments of FILs have led to functional liquid materials that are not merely a solvent or medium. The high concentrations in FILs (around 1–2 M) lead to strong interactions between functional groups and ions; these interactions can play dominant roles in new IL-based functional materials. For example, magnetic ILs consisting of metal complexes have been reported.16–18 Hisamitsu et al. reported photo-functionalized ionic liquids with photon-up-conversion characteristics,19,20 with concentrated chromophores being a critical design in their FILs. Murray et al. reported conductive redox-active ILs (RAILs) that comprise metal complexes and viologens.21–23 In addition, Saielli et al. reported the thermal properties of various viologen-based ILs and ionic liquid crystals, which are correlated with their structure.24–26 These findings demonstrate the potential of viologens to be a potent basic component for developing and creating FILs.
Several applications of RAILs in electrochemical reactions and devices have also been reported; they are used as components in supercapacitors,27,28 redox flow batteries,29 and electrochromic devices,30–32 and as electron mediators for photochemical catalysts.33 Additional examples have been given in recent reviews.34,35 They highlight the extended utility of RAILs as a class of FILs. We note that, in most of the cases, functionalities of FILs originate from individual functional groups and ions.
Let us now consider the use of CT interaction in ILs to create a new class of FILs. Kato et al. first reported an ion pair formation between an imidazolium and iodide in a neat imidazolium-based IL ([BMIM][I]), resulting from CT interaction between them.36 They indicate that the Madelung potential of [BMIM][I] determines the stabilization of the CT complex. Ogura et al. reported CT interaction between pyridinium as an acceptor and iodide as a donor in neat pyridinium-based IL ([Epy][I]) at 100 °C.37 They found that the CT complex in the neat [Epy][I] shows a different photo-absorption band from the diluted solution in dichloromethane, and they pointed out the importance of CT interaction between cation and anion in the neat [Epy][I]. Aster and Vauthey studied the CT interaction between anions of ILs and electron accepting additives in a photo-induced electron transfer reaction between the species.38 They concluded that the ILs play an active role in such photochemical systems rather than being an inert medium. With the incorporation of CT interactions into ILs, we may create a new functionality that is not possessed by individual donors and acceptors, and thereby modulate the physicochemical properties of the materials. In this study, we aim to exploit the functionality of viologens to design FILs based on CT interaction. In this regard, CT interactions between donors and viologens have been applied for assembling molecules,2,39 photo-induced electron transfer reactions,5–8,40,41 alkali metal sensing,42 and thermochromism.43 These studies demonstrated the potential of incorporating CT interactions into viologen-based ILs to pave a new path in IL research. To the best of our knowledge, research into RAILs with externally introduced CT interaction has not been attempted.
Intermolecular and interionic interactions in ILs have been investigated to understand the relationship between the structures and dynamic transport properties such as viscosity and ionic conductivity. In these species, electrostatic, van der Waals, hydrogen bonding, dipole–dipole, and π–π interactions all play important roles in the formation of microstructures, leading to unanticipated transport features and functionalities.44,45 Understanding these strong and weak interactions will provide new insights into the transport properties and functionalities in ILs. In this regard, it is noteworthy that the effect of CT interaction in ILs on the physicochemical and electrochemical properties is presently unclear.
In this study, we present a “RAIL with CT interaction” (CT-IL) originating from two redox centers, a carbazole and viologen; it is based on an equimolar mixture of a viologen-based IL and a carbazole-based IL. As we shall see, in the CT-IL, the CT interaction between the carbazole and viologen modulates the physicochemical properties such as viscosity and ionic conductivity, as well as redox properties including redox reversibility of viologens. Our approach provides a convenient means for creating and tuning of CT-IL, with properties that are distinct from those of the components.
2. Experimental
Chemical structures of the carbazole-based RAIL ([CzC4ImC1][TFSI]) and the viologen-based RAIL ([C4VC7][TFSI]2) in this study are shown in Scheme 1, with a photo of the combined CT-IL straightforwardly prepared from an equimolar mixture between them. Synthetic procedures of the RAILs, water content in the RAILs, and experimental setups are described in the ESI.† All measurements in this study were conducted in neat RAILs, namely without any solvent, unless otherwise mentioned. [C4VC7][TFSI]2 remains in a supercooled liquid state for a few hours at room temperature after it was heated above the melting point (52 °C).46 Although the melting points of [CzC4ImC1][TFSI] and CT-IL could not be determined by differential scanning calorimetry (DSC) because of the absence of any peak assignable to the melting point, their solidification was not observed at room temperature (see the DSC thermograms in Fig. S1†). Therefore, [C4VC7][TFSI]2, [CzC4ImC1][TFSI], and CT-IL can be handled as room temperature ILs.32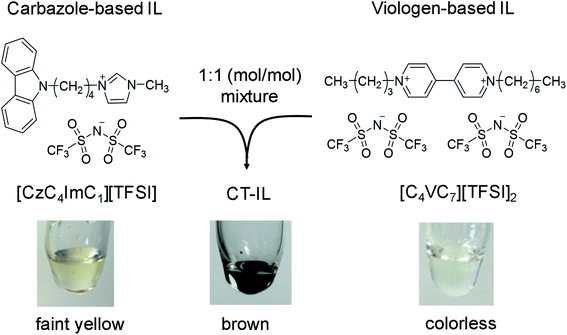 | ||
| Scheme 1 Preparation of a redox-active ionic liquid (RAIL) with charge transfer (CT) interaction from carbazole-based and viologen-based RAILs. | ||
3. Results and discussion
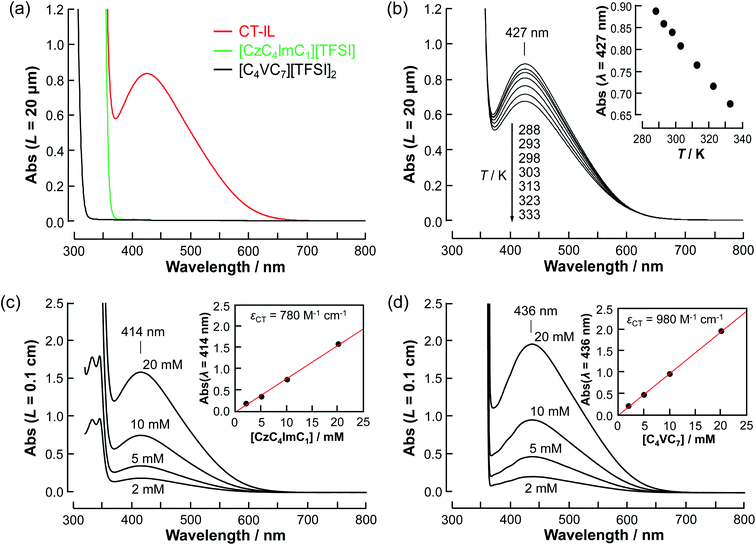
3.1 Optical properties
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex of carbazole and viologen, the same as in the diluted system. Taking these considerations into account, the temperature dependence can be explained by the association/dissociation equilibrium of the carbazole and viologen (Cz + V++ ⇌ CzV++).
1 complex of carbazole and viologen, the same as in the diluted system. Taking these considerations into account, the temperature dependence can be explained by the association/dissociation equilibrium of the carbazole and viologen (Cz + V++ ⇌ CzV++).
As a first approximation, we do not consider carbazole–carbazole interaction and viologen–viologen interaction. The total concentration (c0) of the carbazoles and viologens of CT-IL here was 0.92 M in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (molar ratio) mixture (c0 = [Cz]0 = [V++]0) (see the ESI†). The concentration of the CT complex (cCT) can be described by the thermodynamic equilibrium constant.
1 (molar ratio) mixture (c0 = [Cz]0 = [V++]0) (see the ESI†). The concentration of the CT complex (cCT) can be described by the thermodynamic equilibrium constant.
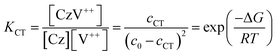 | (1) |
The molar absorption coefficient (εCT) of the CT complex between carbazoles and viologens was reported to be around 400 ± 70 M−1 cm−1 at 420 nm.7 However, the absorption coefficient is invalid in our CT-IL because if we use it as an approximated value, the concentration of the CT complex is estimated to be over 1.0 M at 298 K with the Lambert–Beer relation (AbsCT = εCTLcCT) despite c0 = 0.92 M. Usually, those parameters can be determined from the concentration dependence of the donor and acceptor in the same solvent. However, CT-IL here consists of only the donor ([CzC4ImC1][TFSI]) and acceptor ([C4VC7][TFSI]2) without solvent. That is, the donor and the acceptor themselves play the role of a medium as well. Thus, the concentration and the fraction changes give rise to the polarity changes of the solvent (medium). To approximate εCT and KCT of the CT-IL, we prepared two sets of diluted solutions, (1) x mM [CzC4ImC1][TFSI] diluted by [C4VC7][TFSI]2 (x = 2, 5, 10, 20) and (2) y mM [C4VC7][TFSI]2 diluted by [CzC4ImC1][TFSI] (y = 2, 5, 10, 20), and measured the absorption spectra. Note that two sets of solutions satisfy the following concentration relationship: [CzC4ImC1] (x mM, solute) ≪ [C4VC7] (1.8 M, solvent) in system (1) and [C4VC7] (y mM, solute) ≪ [CzC4ImC1] (2.7 M, solvent) in system (2). Besides, the polarity of [C4VC7][TFSI]2 and [CzC4ImC1][TFSI] could be close to that for the CT-IL. Fig. 1(c) and (d) show absorption spectra of the CT complex in systems (1) and (2). The absorbances were proportional to the concentration of the diluted species. In these cases, i.e. with a large excess of C4VC7 or CzC4ImC1, the absorbance of the CT complex can be described as follows.
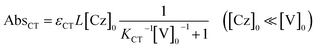 | (2) |
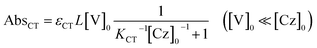 | (3) |
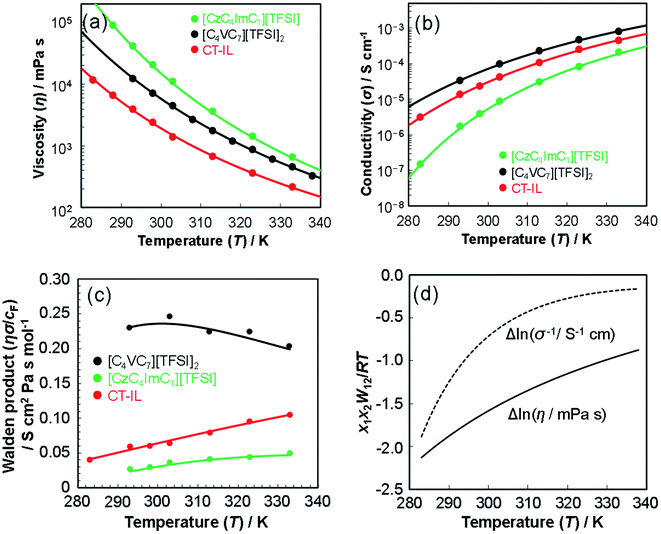
3.2 Viscosity and ionic conductivity
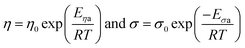 | (4) |
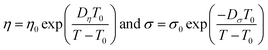 | (5) |
The best fit parameter-sets are listed in Table 1. The Arrhenius plot of the viscosities and ionic conductivities (Fig. S6†) shows a little deviation from straight lines. The coefficient of determination (R2) for the viscosity of CT-IL is 0.9914, and that for the ionic conductivity of [CzC4ImC1][TFSI] is 0.9761 on the basis of the Arrhenius equation. Taking these into consideration, we can see that these RAILs obey VFT formalism resulting in better R2 values over 0.999.
| RAILs | Arrhenius parameter set | Vogel–Fulcher–Tammann parameter set | |||||
|---|---|---|---|---|---|---|---|
η = η0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Eηa/RT) exp(Eηa/RT) |
η = η0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(DηT0/(T − T0)) exp(DηT0/(T − T0)) |
||||||
σ = σ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Eσa/RT) exp(−Eσa/RT) |
σ = σ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−DσT0/(T − T0)) exp(−DσT0/(T − T0)) |
||||||
| E ηa/kJ mol−1 | ln(η0/Pa s) | R 2 | D η T 0/K | T 0/K | ln(η0/Pa s) | R 2 | |
| E σa/kJ mol−1 | ln(σ0/S cm−1) | D σ T 0/K | ln(σ0/S cm−1) | ||||
| a Viscosity data and the VTF parameters were taken from ref. 46. | |||||||
| [C4VC7][TFSI]2a | 63.1 | −23.58 | 0.9941 | 1147 | 193.9 | −9.053 | 0.9997 |
| 64.2 | 16.21 | 0.9917 | 659.0 | 219.8 | −1.303 | 0.9999 | |
| [CzC4ImC1][TFSI] | 87.0 | −32.03 | 0.9952 | 1413 | 194.7 | −10.66 | 0.9999 |
| 109 | 31.42 | 0.9761 | 774.5 | 230.3 | −1.005 | 0.9996 | |
| CT-IL | 62.8 | −24.44 | 0.9914 | 880.8 | 200.6 | −8.217 | 0.9995 |
| 77.0 | 20.36 | 0.9896 | 1019 | 203.8 | 0.1992 | 0.9997 | |
The activation energy (Eηa) for the viscosity follows the order CT-IL ≈ [C4VC7][TFSI]2 < [CzC4ImC1][TFSI]. In comparison, activation energy (Eσa) for the conductivity shows a different order [C4VC7][TFSI]2 < CT-IL < [CzC4ImC1][TFSI]. This suggests that the activation processes of viscosity and conductivity are different. This tentative conclusion is also supported by the difference in the trends for DηT0 and DσT0 in VTF formalism, as interpreted from the activation energy, i.e., CT-IL < [C4VC7][TFSI]2 < [CzC4ImC1][TFSI] for the viscosity and [C4VC7][TFSI]2 < [CzC4ImC1][TFSI] < CT-IL for the conductivity. The activation energy (Eηa) of the viscosity of CT-IL is reduced by mixing the two RAILs. To examine the characteristics of the ionic transportation, we use the Walden analysis and the Grunberg–Nissan48–51 analysis below.
In comparison, the Walden product of CT-IL increased with increasing temperature, while that of [CzC4ImC1][TFSI] remains nearly constant with a slight increase, and that of [C4VC7][TFSI]2 slightly decreases. To put these results into perspective, the Walden product of a conventional IL [BMIM][BF4] remains almost constant.52 In CT-IL, the ionic association and the CT complex formation can be deeply involved in the transport properties. Therefore, the temperature dependent Walden product of CT-IL is attributable to both equilibria: association and dissociation of (1) ionic components (between the viologen, imidazolium, and TFSI), and (2) CT complex (between the carbazole and viologen).
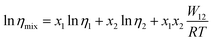 | (6) |
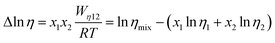 | (7) |
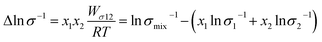 | (8) |
Fig. 2(d) shows the temperature dependence of Δln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η and Δln
η and Δln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ−1 for CT-IL, obtained using the continuous data interpolated with the VTF formula of the viscosity and conductivity as well as the fitted parameters in Table 1. The interaction parameters were negative, and the magnitudes of both viscosity and conductivity decreased monotonically with increasing the temperature. The curvatures of Δln
σ−1 for CT-IL, obtained using the continuous data interpolated with the VTF formula of the viscosity and conductivity as well as the fitted parameters in Table 1. The interaction parameters were negative, and the magnitudes of both viscosity and conductivity decreased monotonically with increasing the temperature. The curvatures of Δln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η and Δln
η and Δln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ−1 are different, where Δln
σ−1 are different, where Δln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ−1 shows more convex behavior.
σ−1 shows more convex behavior.
In the CT-IL system, two kinds of equilibria should be considered: (1) electrostatic cation–anion pair association and dissociation and (2) formation of the CT complex. In ionic liquids, electrostatic attraction between anions and cations dominates the attractive interaction that leads to the association of cations and anions (Fig. 3(a) and (b)). The associations can be examined in terms of ionicity by the impedance technique and nuclear magnetic resonance.53 The decreased viscosity in CT-IL upon mixing [CzC4ImC1][TFSI] and [C4VC7][TFSI]2 can be attributed to decreasing electrostatic attraction because of the formation of the CT complex between the carbazole and the viologen (Fig. 3(c)). Our DFT calculation supports the decrease of the interionic attraction. We employed a fragment molecular orbital (FMO) calculation to evaluate the CT interaction which contributes to the charge donation from the carbazole to the viologen. We found that the carbazole donates 0.163 electrons to the viologen resulting in decreasing its cationic charge, i.e. the formal charge can be depicted as Cz+0.163V+1.837. Besides, the attraction enthalpy difference between the viologen and TFSI is 63.4 kJ mol−1 with carbazole and 65.9 kJ mol−1 without carbazole (geometries of the contact ionic pairs are shown in Fig. S17†). Thus, the CT attraction can weaken the electrostatic attraction between the viologen and TFSI. Therefore, we may expect that decreased viscosity would lead to increasing ionic conductivity. However, the ionic conductivity of CT-IL was in fact smaller than that of [C4VC7][TFSI]2.
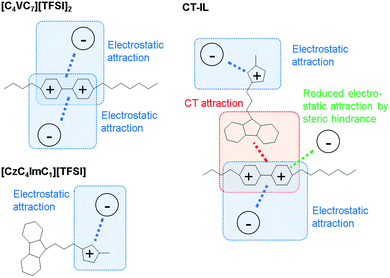 | ||
| Fig. 3 Illustration of attractions between the cations (imidazolium and viologen) and the anion (TFSI). | ||
To explain the smaller ionic conductivity of CT-IL than [C4VC7][TFSI]2, we note that the actual concentration of free ionic species is important for ionic conductivity. Formation of the CT complex would lead to decreasing concentration of the free dicationic viologens and suppressing the movement and migration of the viologens and imidazoliums linked with carbazole. Because increasing temperature leads to dissociation of both the ions and the CT complex, this results in a steeper temperature dependence on Δln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ−1 than on Δln
σ−1 than on Δln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η.
η.
The viscosity and ionic conductivity of those RAILs can be affected by the temperature-dependent microstructural and dynamic heterogeneities of the ILs.44,45 For our [CzC4ImC1][TFSI] and [C4VC7][TFSI]2 systems, however, no data suggest the presence of the such phase-separated structures in these RAILs.
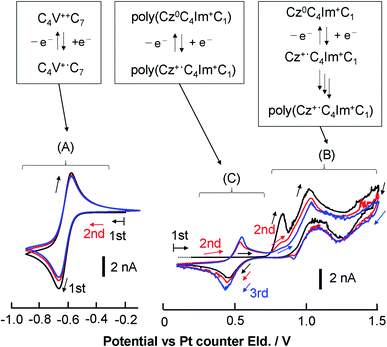
3.3 Redox properties
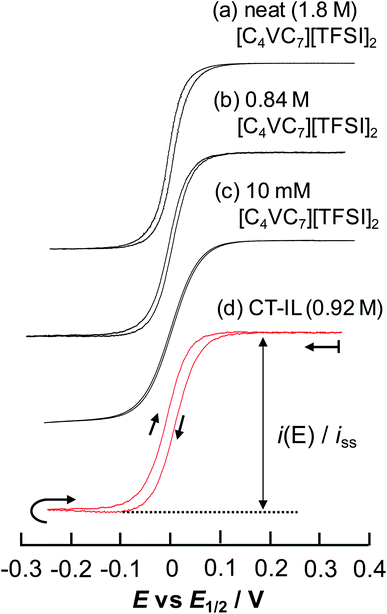 | ||
Fig. 5 Steady-state CVs of [C4VC7][TFSI]2 at various concentrations at 333 K with a Au-UME using a slow scan rate within the reduction region of viologens. (a) Neat [C4VC7][TFSI]2 at 0.1 mV s−1, (b) 0.84 M [C4VC7][TFSI]2 in [BMIM][TFSI] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio mixture of [C4VC7][TFSI]2 and [BMIM][TFSI]) at 0.5 mV s−1, (c) 10 mM [C4VC7][TFSI]2 in [BMIM][TFSI] at 1 mV s−1, and (d) CT-IL at 0.5 mV s−1. The currents were normalized by the steady-state limiting current. Nernstian parameters related to the CVs are listed in Table 2. 2 molar ratio mixture of [C4VC7][TFSI]2 and [BMIM][TFSI]) at 0.5 mV s−1, (c) 10 mM [C4VC7][TFSI]2 in [BMIM][TFSI] at 1 mV s−1, and (d) CT-IL at 0.5 mV s−1. The currents were normalized by the steady-state limiting current. Nernstian parameters related to the CVs are listed in Table 2. | ||
In principle, when the electrochemical reaction is described by a simple electrochemical equilibrium (Ox + e− ⇄ Red) of a redox couple and the redox species are not interacting with each other, the Nernst equation is established and can provide the concentration ratio of the redox species on the electrode surface [Ox]surf/[Red]surf. In that situation, a steady-state voltammogram can be described by the ideal Nernst response eqn (9) under the assumption of equal diffusion coefficients DOx = DRed with napp = 1.
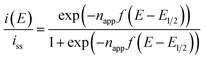 | (9) |
| V2+ + e−(eld) ⇄ V+˙ (step 1) |
| V+˙ + V2+(neighbor) ⇄ V+˙⋯V2+ (step 2) |
| V+˙⋯V2+ + e−(eld) ⇄ V+˙⋯V+˙ (step 3) |
| RAILs | Concentration of C4VC7/M | i ss/nA | D app/cm2 s−1 | n app | ΔE = E1 − E2/mV | Viscosity (η)/mPa s | Conductivity (σ)/S cm−1 |
|---|---|---|---|---|---|---|---|
| a Forward scan. b Reverse scan. c Pure [BMIM][TFSI] from ref. 58 using the VFT equation. d Pure [BMIM][TFSI] from ref. 59 using the VFT equation. | |||||||
| (a) Neat [C4VC7][TFSI]2 | 1.8 | −8.38 | 2.4 × 10−8 | 1.60a | −55.6a | 456 | 8.0 × 10−4 |
| 1.66b | −64.6b | ||||||
(b) Mixture of [C4VC7][TFSI]2 and [BMIM][TFSI] (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio) 2 molar ratio) |
0.84 | −13.0 | 8.0 × 10−8 | 1.43a | −20.0a | N/A | N/A |
| 1.39b | −15.6b | ||||||
| (c) Diluted [C4VC7][TFSI]2 in [BMIM][TFSI] | 0.010 | −0.466 | 2.4 × 10−7 | 1.00 | +39.9 | 15.4c | 1.1 × 10−2d |
| (d) CT-IL | 0.92 | −1.85 | 1.0 × 10−8 | 1.22a | +13.2a | 214 | 4.5 × 10−4 |
| 1.23b | +7.6b | ||||||
Step 3 is the dimerization reaction of the reduced viologen as discussed below. If ΔG in step 3 is negatively large and the reactions from step 1 to step 3 are regarded as a sequential redox process with two redox sites, we can approximately describe the reaction as a two-consecutive one-electron transfer process. In that case, the reduction potential difference ΔE = E1 − E2, the first and second reduction potentials E1 and E2, can negatively increase with increasing the attractive interaction which means the system prefers the dimerized viologens (V+˙⋯V+˙). The two steps of the reduction reaction eventually cannot be distinguished from each other but seen to be coalescent apparently resulting in an indistinguishable two-electron reduction reaction. Under the assumption that diffusion coefficients of all species involved in the reaction are the same, the steady-state voltammogram can be described as follows.56,57
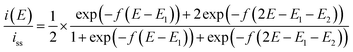 | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2)RT/F = +39.8 mV at 333 K and napp becomes unity. If the inter-site interaction is repulsive/attractive, i.e. one reduced site discourages/encourages the reduction reaction on another site, then ΔE > +39.8 mV for repulsive and ΔE < +39.8 mV for attractive interaction.
2)RT/F = +39.8 mV at 333 K and napp becomes unity. If the inter-site interaction is repulsive/attractive, i.e. one reduced site discourages/encourages the reduction reaction on another site, then ΔE > +39.8 mV for repulsive and ΔE < +39.8 mV for attractive interaction.
The results from analyzing the CVs in Fig. 5 are listed in Table 2. The diluted solution of 10 mM [C4VC7][TFSI]2 exhibited a typical Nernstian CV with napp = 1 and ΔE = +39.8 mV, which indicates the absence of interaction between viologens. Other viologen systems exhibit ΔE < +39.8 mV and napp > 1, which suggest attractive interaction between viologens. A possible attraction of viologens was the dimerization between reduced species (V+˙ + V+˙ ⇌ V+˙⋯V+˙). In relation to such dimerization, the dimerization constants of viologens (KD = [V+˙⋯V+˙]/[V+˙]2) in water and organic solvent systems are typically 103 to 105 M−1 (ref. 60–62) with the corresponding Gibbs energy changes being −18.8 to −29.1 kJ mol−1.61 In our previous electroreflectance spectroscopy experiments, we have also observed, in the steady-state CV, intramolecular dimerization of a diluted bis-viologen in water as a result of attractive interaction.57 In addition, we have also reported electrochromic devices based on viologen-based RAILs, with dimerizations being observed as a result of highly concentrated viologens.31,33
The concentrated viologens in this study reached around 1–2 M, and we therefore deem dimerization as induced by reduction possible. The order of −ΔE and napp values is (c) 10 mM [C4VC7][TFSI]2 (no attraction) < (d) CT-IL < (b) 0.84 M [C4VC7][TFSI]2 < (a) neat [C4VC7][TFSI]2. Neat [C4VC7][TFSI]2 (a) exhibited the greatest napp and smallest ΔE because of its highest viologen concentration. Interestingly, the concentration of C4VC7 in (d) CT-IL (0.92 M) is similar to that for (b) 0.84 M [C4VC7][TFSI]2, while the napp and ΔE values were quite different. This can be explained by the CT complexation between the viologen and carbazole, which weakened the inter-viologen dimerization. Three such mechanisms were plausible. One mechanism is that CT complexation weakens the attraction of free V++ species to V+˙; the other mechanism is that the reduction potential of the CT complex (CzV++) might be more negative than that for free V++, which then results in the increase of ΔE greater than the value in 0.84 M [C4VC7][TFSI]2.
The diffusion coefficients can be evaluated by the steady state limiting current (iss) with the Saito equation (iss = 4nFrcD) for microelectrodes.63 The migration effect in the absence of the supporting electrolyte system should not be ignored but the contribution to the limiting current in our system could be small.64 Therefore, we directly used the observed limiting current to evaluate the diffusion coefficient without any migration correction. The diffusion coefficients of the viologen (DV) in [C4VC7][TFSI]2 and CT-IL at 60 °C are, respectively, 2.4 × 10−8 and 1.0 × 10−8 cm2 s−1 in the CVs of Fig. 5. The diffusion coefficients of the concentrated system can be explained by the Dahms–Ruff model (DV = Dphys + Dex)65,66 as the sum of physical diffusion and electron hopping processes. Although we cannot clarify the details of the process in the redox reaction at this stage, we need to mention the relation between the diffusion coefficient in the CVs and the transport properties such as viscosity and ionic conductivity. Interpretation of these diffusion coefficients should be presently made for two limiting cases.
In the case of Dphys ≫ Dex. The above-mentioned magnitude relation, DV([C4VC7][TFSI]2) > DV(CT-IL), cannot be simply explained by the magnitude relation of the viscosities (456 and 214 mPa s) with the Stokes–Einstein equation (Dphys = kBT/6πaη, a is the molecular radius) for the physical diffusion process. To explain the diffusion coefficients within the Stokes–Einstein framework, we can write the following relation aV,CT-IL/aV,C4VC7 = DV,CT-ILηCT-IL/DV,C4VC7ηC4VC7 and we obtained aV,CT-IL/aV,C4VC7 = 5.1. This can be translated by association of C4VC7 with not only CzC4ImC1 but also TFSI anions in the CT-IL.
In the case of Dex ≫ Dphys. The diffusion coefficient electron hopping can be described by the Ruff equation (Dex = δ2kexc/6).66,67 Center-to-center distances between viologens in [C4VC7][TFSI]2 and CT-IL were estimated using the equation δ = (NAc)−1/3 (where NA is the Avogadro constant and c is the molar concentration), respectively, to be 0.97 and 1.2 nm. Thus, the electron hopping rate constants kB were, respectively, 8.5 and 4.6 ×106 M−1 s−1. The electron hopping rate constant kex in viscous solution can be described by an atmosphere relaxation model68,69 which is an ion-pairing process to hold the electroneutrality in the electron hopping process. The magnitude relation of the diffusion coefficients agrees with that of ionic conductivities not that of the viscosities.
The details of the relationship among the transportation properties require further experiments such as diffusion ordered spectroscopy (DOSY)-NMR. We will perform and report it elsewhere in the future. Although the detailed mechanism of the redox process is at present not clear, what is clear is that CT interaction can notably modulate the physicochemical properties of ILs.
4. Conclusions
We demonstrated CT interactions in an IL produced by equimolar mixing of a carbazole-based ([CzC4ImC1][TFSI]) and a viologen-based ([C4VC7][TFSI]2) RAIL. The existence of a CT complex between the carbazole and viologen was confirmed by UV-vis absorption spectra, which neither [CzC4ImC1][TFSI] nor [C4VC7][TFSI]2 exhibited. The decrease of absorption with increasing temperature suggested the CT complex dissociation with increasing temperature. Transport properties are modulated by the new interaction; we found the viscosity and ionic conductivity of CT-IL to be different from those of the individual RAILs. The viscosity of CT-IL was smaller than those of [CzC4ImC1][TFSI] and [C4VC7][TFSI]2. Likewise, the ionic conductivity of CT-IL was also smaller than those of [CzC4ImC1][TFSI] and [C4VC7][TFSI]2. CV with a microelectrode showed that the redox response of the viologen was also modulated by CT interaction with the carbazoles. The apparent number of electrons involved in the redox reaction was larger than unity in concentrated solutions of [C4VC7][TFSI]2, indicating an attractive interaction between the redox species in accordance with a two-site redox model. In turn, this implies that dimerization of reduced viologens occurred much faster than the CV timescale. In comparison, CT-IL showed less attractive behavior than neat [C4VC7][TFSI]2, because CT complexation between the viologens and carbazoles suppresses viologen dimerization. Overall, the introduction of CT interaction into RAILs changes a wide range of chemical and physical properties. Thus, it represents a useful design tool for expanding the scope of FILs; a deep understanding of the relationship between the structures and the functions would be beneficial in advancing such systems.Author contributions
H. Tahara conceived and designed this study. S. Yonemori and S. Yamamoto synthesized the compounds. H. Tahara performed viscosity and spectroscopic measurements. H. Tahara, Y. Tanaka, and S. Yamamoto performed electrochemical measurements. H. Tahara and C. Bun performed the quantum chemical calculations. H. Tahara and T. Sagara analyzed the data. H. Tahara produced the manuscript. H. Murakami, C. Bun and T. Sagara checked and modified the manuscript.Funding sources
This work was supported by a Japan Society for the Promotion of Science (JSPS) Grant-in-Aid for Young Scientists (B) no. 26810052 (H. T.), Grant-in-Aid for Scientific Research (C) no. 20K05649 (H. T.), and the Hattori Hokokai Foundation (H. T.).Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was the result of using research equipment (1H NMR, elemental analysis, mass spectroscopy) shared in the MEXT Project for promoting public utilization of advanced research infrastructure (Program for supporting introduction of the new sharing system) Grant Number JPMXS0422500320.References
- K. P. Goetz, D. Vermeulen, M. E. Payne, C. Kloc, L. E. McNeil and O. D. Jurchescu, J. Mater. Chem. C, 2014, 2, 3065–3076 RSC.
- M. M. Cetin, Y. Beldjoudi, I. Roy, O. Anamimoghadam, Y. J. Bae, R. M. Young, M. D. Krzyaniak, C. L. Stern, D. Philp, F. M. Alsubaie, M. R. Wasielewski and J. F. Stoddart, J. Am. Chem. Soc., 2019, 141, 18727–18739 CrossRef CAS.
- C. P. Collier, G. Mattersteig, E. W. Wong, Y. Luo, K. Beberly, J. Sampaio, F. M. Raymo, J. F. Stoddart and J. R. Heath, Science, 2000, 289, 1172–1175 CrossRef CAS.
- U. M. Rabie, J. Mol. Struct., 2013, 1034, 393–403 CrossRef CAS.
- H. Yonemura, M. Kasahara, H. Saito, H. Nakamura and T. Matsuo, J. Phys. Chem., 1992, 96, 5765–5770 CrossRef CAS.
- F. Ito and T. Nagamura, J. Photochem. Photobiol., C, 2007, 8, 174–190 CrossRef CAS.
- J. W. Park, H. J. Song, Y. J. Cho and K. K. Park, J. Phys. Chem. C, 2007, 111, 18605–18614 CrossRef CAS.
- H. Yonemura and M. D. E. Forbes, Photochem. Photobiol., 2015, 91, 672–677 CrossRef CAS.
- M. Freemantle, Chem. Eng. News, 1998, 76, 32–37 CrossRef.
- J. Zhang, J. Wu, J. Yu, X. Zhang, J. He and J. Zhang, Mater. Chem. Front., 2017, 1, 1273–1290 RSC.
- E. D. Bates, R. D. Mayton, I. Ntai and J. H. Davis, Jr, J. Am. Chem. Soc., 2002, 124, 926–927 CrossRef CAS.
- Q. R. Sheridan, W. F. Schneider and E. J. Maginn, Chem. Rev., 2018, 118, 5242–5260 CrossRef CAS.
- S. Ventura, F. A. e. Silva, M. V. Quental, D. Mondal, M. G. Freire and J. A. P. Coutinho, Chem. Rev., 2017, 117, 6984–7052 CrossRef CAS.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629 CrossRef CAS.
- A. E. Visser, R. P. Swatlowski, W. M. Reichert, R. Mayton, S. Sheff, A. Wierzbicki, J. H. Davis, Jr and R. D. Rogers, Chem. Commun., 2001, 135–136 RSC.
- S. Hayashi and H. Hamaguchi, Chem. Lett., 2004, 33, 1590–1591 CrossRef CAS.
- E. Santos, J. Albo and A. Irabien, RSC Adv., 2014, 4, 40008–40018 RSC.
- K. D. Clark, O. Nacham, J. A. Purslow, S. A. Pierson and J. L. Anderson, Anal. Chim. Acta, 2016, 934, 9–21 CrossRef CAS.
- S. Hisamitsu, N. Yanai and N. Kimizuka, Angew. Chem., Int. Ed., 2015, 54, 11550–11554 CrossRef CAS.
- S. Hisamitsu, J. Miyano, K. Okumura, J. K.-H. Hui, N. Yanai and N. Kimizuka, ChemistryOpen, 2020, 9, 14–17 CrossRef CAS.
- T. Hatazawa, R. H. Terrill and R. W. Murray, Anal. Chem., 1996, 68, 597–603 CrossRef CAS.
- A. M. Leone, S. C. Weatherly, M. E. Williams, H. H. Thorp and R. W. Murray, J. Am. Chem. Soc., 2001, 123, 218–222 CrossRef CAS.
- R. Balasubramanian, W. Wang and R. W. Murray, J. Am. Chem. Soc., 2006, 128, 9994–9995 CrossRef CAS.
- V. Causin and G. Saielli, J. Mater. Chem., 2009, 19, 9153–9162 RSC.
- I. Pibiri, A. Beneduci, M. Carraro, V. Causin, G. Casella, G. A. Corrente, G. Chidichimo, A. Pace, A. Riccobono and G. Saielli, J. Mater. Chem. C, 2019, 7, 7974–7983 RSC.
- G. Saielli, Adv. Theory Simul., 2018, 1, 1800081 Search PubMed.
- H. J. Xie, B. Gélinas and D. Rochefort, Electrochem. Commun., 2016, 66, 42–45 CrossRef CAS.
- E. Mourad, L. Coustan, P. Lannelongue, D. Zigah, A. Mehdi, A. Vioux, S. A. Freunberger, F. Favier and O. Fontaine, Nat. Mater., 2017, 16, 446–453 CrossRef CAS.
- K. Takechi, Y. Kato and Y. Hase, Adv. Mater., 2015, 27, 2501–2506 CrossRef CAS.
- B. Gélinas, D. Das and D. Rochefort, ACS Appl. Mater. Interfaces, 2017, 9, 28726–28736 CrossRef.
- H. Tahara, R. Baba, K. Iwanaga, T. Sagara and H. Murakami, Chem. Commun., 2017, 53, 2455–2458 RSC.
- H. Tahara, K. Uranaka, M. Hirano, T. Ikeda, T. Sagara and H. Murakami, ACS Appl. Mater. Interfaces, 2019, 11, 1–6 CrossRef CAS.
- H. Shimakoshi, N. Houfuku, L. Chen and Y. Hisaeda, Green Energy & Environment, 2019, 4, 116–120 Search PubMed.
- D. Rochefort, Curr. Opin. Electrochem., 2019, 15, 125–132 CrossRef CAS.
- A. P. Doherty, Curr. Opin. Electrochem., 2018, 7, 61–65 CrossRef CAS.
- R. Kato, M. Hara and S. Tsuzuki, J. Phys. Chem. B, 2008, 112, 15426–15430 CrossRef.
- T. Ogura, N. Akira, K. Shibuya and A. Kawai, J. Phys. Chem. B, 2013, 117, 8547–8554 CrossRef CAS.
- A. Aster and E. Vauthey, J. Phys. Chem. B, 2018, 122, 2646–2654 CrossRef CAS.
- H. R. Wessels, C. Slebodnick and H. W. Gibson, J. Am. Chem. Soc., 2018, 140, 7358–7370 CrossRef CAS.
- W. G. Santos, D. S. Budkina, V. M. Deflon, A. N. Tarnovsky, D. R. Cardoso and D. E. Forbes, J. Am. Chem. Soc., 2017, 139, 7681–7684 CrossRef CAS.
- H. Yao and T. Enseki, Langmuir, 2017, 33, 219–227 CrossRef CAS.
- Y. S. Park, S. Y. Um and K. B. Yoon, J. Am. Chem. Soc., 1999, 121, 3193–3200 CrossRef CAS.
- T. Kinuta, T. Sato, N. Tajima, R. Kuroda, Y. Matsubara and Y. Imai, J. Mol. Struct., 2010, 982, 45–49 CrossRef CAS.
- R. Clark, M. A. Nawawi, A. Dobre, D. Pugh, Q. Liu, A. P. Ivanov, A. J. P. White, J. B. Edel, M. K. Kuimova, A. J. S. McIntosh and T. Welton, Chem. Sci., 2020, 11, 6121–6133 RSC.
- Y.-L. Wang, B. Li, S. Sarman, F. Mocci, Z.-Y. Lu, J. Yuan, A. Laaksonen and M. D. Fayer, Chem. Rev., 2020, 120, 5798–5877 CrossRef CAS.
- N. Bodappa, P. Broekmann, Y. Fu, J. Furrer, Y. Furue, T. Sagara, H. Siegenthaler, H. Tahara, S. Vesztergom, K. Zick and T. Wandlowski, J. Phys. Chem. C, 2015, 119, 1067–1077 CrossRef CAS.
- T. Miyashita, T. Yatsue and M. Matsuda, J. Phys. Chem., 1991, 95, 2448–2451 CrossRef CAS.
- L. Grunberg and A. H. Nissan, Nature, 1949, 164, 799–800 CrossRef CAS.
- R. J. Fort and W. R. Moore, Trans. Faraday Soc., 1966, 62, 1112–1119 RSC.
- H. Niedermeyer, J. P. Hallett, I. J. Villar-Garcia, P. A. Hunt and T. Welton, Chem. Soc. Rev., 2012, 41, 7780–7802 RSC.
- M. T. Clough, C. R. Crick, J. Gräsvik, P. A. Hunt, H. Nie-dermeyer, T. Welton and O. P. Whitaker, Chem. Sci., 2015, 6, 1101–1114 RSC.
- Y. O. Andriyko, W. Reishl and G. E. Nauer, J. Chem. Eng. Data, 2009, 54, 855–860 CrossRef CAS.
- K. Ueno, H. Tokuda and M. Watanabe, Phys. Chem. Chem. Phys., 2010, 12, 1649–1658 RSC.
- R. Kirankumar, T. Tsuda, C.-Y. Chen, C.-Y. Lu, S. Kuwabata and P.-Y. Chen, RSC Adv., 2016, 6, 15735–15744 RSC.
- R. Kirankumar, W.-C. Huang, H.-F. Chen and P.-Y. Chen, J. Electroanal. Chem., 2018, 826, 198–206 CrossRef CAS.
- T. Sagara and H. Eguchi, Electrochim. Acta, 2019, 295, 215–223 CrossRef CAS.
- D. E. Richardson and H. Taube, Inorg. Chem., 1981, 20, 1278–1285 CrossRef CAS.
- G. Yu, D. Zhao, L. Wen, S. Yang and X. Chen, AIChE J., 2012, 58, 2885–2899 CrossRef CAS.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2005, 109, 6103–6110 CrossRef CAS.
- P. M. S. Monk, N. M. Hodgkinson and S. A. Ramzan, Dyes Pigm., 1999, 43, 207–217 CrossRef CAS.
- K. Nchimi-Nono, P. Dalvand, K. Wadhwa, S. Nuryyeva, S. Alneyadi, T. Prakasam, A. C. Fahrenbach, J.-C. Olsen, Z. Asfari, C. Platas-Iglesias, M. Elhabiri and A. Trabolsi, Chem.–Eur. J., 2014, 20, 7334–7344 CrossRef CAS.
- M. Geraskina, A. S. Dutton, M. J. Juetten, S. A. Wood and A. H. Winter, Angew. Chem., Int. Ed., 2017, 56, 9435–9439 CrossRef CAS.
- Y. Saito, Rev. Polarogr., 1968, 15, 177–187 CrossRef CAS.
- N. Bodappa, Y.-C. Fu, P. Broekmann, J. Furrer, K. Zick, S. Vesztergom, H. Tahara and T. Sagara, Electrochim. Acta, 2019, 320, 134559 CrossRef CAS.
- H. Dahms, J. Phys. Chem., 1968, 72, 362–364 CrossRef CAS.
- I. Ruff and V. J. Friedrich, J. Phys. Chem., 1971, 75, 3297–3302 CrossRef CAS.
- I. Ruff, V. J. Friedrich, K. Demeter and K. Csillag, J. Phys. Chem., 1971, 75, 3303–3309 CrossRef CAS.
- J. E. F. Weaver, D. Breadner, F. Deng, B. Ramjee, P. J. Ragogna and R. W. Murray, J. Phys. Chem. C, 2011, 115, 19379–19385 CrossRef CAS.
- R. A. Marcus, J. Phys. Chem. B, 1998, 102, 10071–10077 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental method; DSC thermograms of [C4VC7][TFSI]2, [CzC4ImC1][TFSI], and CT-IL; absorption spectra of a diluted solution of the RAILs; equilibrium constant of CT complex formation in CT-IL; fluorescence spectra of [CzC4ImC1][TFSI] in neat and diluted solutions; water content and IR spectra of RAILs; Arrhenius plots of the viscosities and ionic conductivities; Walden plots of the RAILs; multiple CV cycles of neat [CzC4ImC1][TFSI] in potential region B; ionic conductivity apparatus; two-electrode cell for electrochemical measurements; fitting diagrams of experimental CVs by the simple Nernst model; fitting diagrams of experimental CVs by the two redox-site model; uncompensated resistance effects of CVs by DigiElch; uncompensated resistance effects of Nernst analysis by DigiElch; scan rate dependence of CVs in neat [C4VC7][TFSI]2 and CT-IL by DigiElch; DFT models of the viologen and carbazole for evaluating the Gibbs energy of the CT complex formation. See DOI: 10.1039/d0sc06244h |
| This journal is © The Royal Society of Chemistry 2021 |