Open Access Article
Open Access ArticleUsing internal electrostatic fields to manipulate the valence manifolds of copper complexes†
Alexander B.
Weberg
,
Samuel P.
McCollom
,
Laura M.
Thierer
,
Michael R.
Gau
,
Patrick J.
Carroll
and
Neil C.
Tomson
 *
*
Roy and Diana Vagelos Laboratories, Department of Chemistry, University of Pennsylvania, 231 South 34th Street, Philadelphia, Pennsylvania 19104, USA. E-mail: tomson@upenn.edu
First published on 26th January 2021
Abstract
A series of tetradentate tris(phosphinimine) ligands (R3P3tren) was developed and bound to CuI to form the trigonal pyramidal, C3v-symmetric cuprous complexes [R3P3tren-Cu][BArF4] (1PR3) (PR3 = PMe3, PMe2Ph, PMePh2, PPh3, PMe2(NEt2), BArF4 = B(C6F5)4). Electrochemical studies on the CuI complexes were undertaken, and the permethylated analog, 1PMe3, was found to display an unprecedentedly cathodic CuI/CuII redox potential (−780 mV vs. Fc/Fc+ in isobutyronitrile). Elucidation of the electronic structures of 1PR3via density functional theory (DFT) studies revealed atypical valence manifold configurations, resulting from strongly σ-donating phosphinimine moieties in the xy-plane that destabilize 2e (dxy/dx2−y2) orbital sets and uniquely stabilized a1 (dz2) orbitals. Support is provided that the a1 stabilizations result from intramolecular electrostatic fields (ESFs) generated from cationic character on the phosphinimine moieties in R3P3tren. This view is corroborated via 1-dimensional electrostatic potential maps along the z-axes of 1PR3 and their isostructural analogues. Experimental validation of this computational model is provided upon oxidation of 1PMe3 to the cupric complex [Me3P3tren-Cu][OTf]2 (2PMe3), which displays a characteristic Jahn–Teller distortion in the form of a see-saw, pseudo-Cs-symmetric geometry. A systematic anodic shift in the potential of the CuI/CuII redox couple as the steric bulk in the secondary coordination sphere increases is explained through the complexes' diminishing ability to access the ideal Cs-symmetric geometry upon oxidation. The observations and calculations discussed in this work support the presence of internal electrostatic fields within the copper complexes, which subsequently influence the complexes' properties via a method orthogonal to classic ligand field tuning.
Introduction
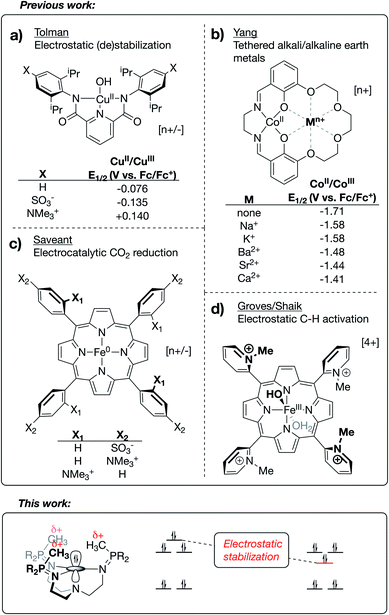
Frontier orbitals are at the heart of chemical reactivity. Many reactions can be simplified to an interaction between the highest occupied molecular orbital (HOMO) of one species and the lowest unoccupied molecular orbital (LUMO) of another. Deliberate control of the frontier orbital energies is therefore crucial to facilitating desirable chemistry and preventing side reactions. The development of new tools for manipulating valence manifolds may be envisioned to support the creation of unique catalysts, photochemical reagents, and separations technologies.The active site architectures of metalloenzymes have historically provided much inspiration to this task. Current design principles such as metal choice, active-site geometries, use of pH-responsive ligands, incorporation of hydrogen-bonding moieties into secondary coordination spheres, and the use of multinuclear clusters have all received inspiration or analogy in bioinorganic chemistry. An underexplored concept from enzymology is the use of properly aligned electric fields for reaction site engineering. As described in detail below, the application of this burgeoning method to transition metal chemistry provides a promising new avenue for exerting precise control over the electronic structures and reactivity profiles of homogeneous systems. Inasmuch as orbital energies reflect the energy of a single electron experiencing the waveform and potential energy environment of the orbital, the structure of the valence manifold should be susceptible to the application of a properly aligned electrostatic field. The general importance of local electrostatic fields to enzymatic function was originally proposed by Warshel1 and has since been studied in detail by Boxer.2–4 Accumulated work in this area has even been used in support of the argument that electrostatic effects may be general to enzyme catalysis.3–5
Research outside of the biochemical field has investigated the effects of electrostatic fields on the electronic structure and reactivity of various materials. This work has included (i) the use of bulk, homogeneous electric fields,6–8 (ii) the study of anion effects on reaction selectivity,9 (iii) the study of electrostatic stabilization of in situ-generated radical species,10–14 and (iv) in-depth computational studies on reaction barrier (de)stabilization of organic molecules bearing charged functional groups.15–20 Limited examples are known of transition metal complexes that use oriented internal electrostatic fields to tune the properties of the system. The Tolman group reported cupric hydroxide compounds bound by NNN pincer-type bis(carboxamide)pyridine ligands, wherein charged residues were incorporated at the para positions of the carboxamide aryl rings.21 A shift of ∼0.3 V in the CuII/CuIII redox couple was observed upon switching between substitution of a cationic group (–NMe3+) with an anionic group (–SO3−), implicating a through-space electrostatic effect on the potential of this redox couple (Fig. 1a). Similarly, using a salen-based ligand containing a crown-ether moiety, Yang and coworkers showed a systematic anodic shift in the CoII/CoIII redox couples across a series of CoII complexes as alkali and alkaline earth metals were tethered in the secondary coordination sphere (Fig. 1b).22 These anodic shifts correlated with the strength of electrostatic fields emanating from the redox-innocent metal, as opposed the Lewis acidity of these metals. Impressively, securing redox-innocent metals in the crown-ether pocket of this ligand was also shown to improve aerobic oxidation catalysis with FeIII complexes23 and promote stability across a series of MnV-nitride complexes.24
Success in this field has also been realized through incorporation of charges into the secondary coordination spheres of heme-based complexes. Savéant published an elegantly designed series of iron/porphyrin-based CO2 electro-reduction catalysts, wherein charged functional groups were placed at different distances from the catalyst active site.25 In this case, a dramatic decrease in overpotential was observed when the cationic charges were placed in closest proximity to the CO2 binding site (Fig. 1c). Mayer reported this same complex to be a fast and efficient catalyst for the oxygen reduction reaction (ORR).26 The Shaik group recently published a computational study27 characterizing two Fe/porphyrin complexes that contain cationic pyridinium residues in the secondary coordination sphere. Groves, in his original report on these complexes, showed that they undergo unprecedentedly fast C–H activation kinetics (Fig. 1d for the FeIII–OH complex).28,29 Shaik's study was able to reproduce activation energies from the experimental data through replacement of the charged functional groups with external oriented electrostatic fields, thereby implicating the catalytic effect as being almost purely electrostatic in origin.27
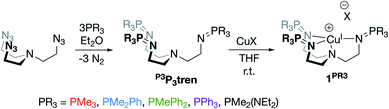
Beyond the electrostatic effects proposed by Tolman, Yang Savéant, and Groves/Shaik, little is known about the origin, magnitude, and impact of internal electrostatic fields on transition metal centers. Herein, we report a series of CuI complexes bound by novel tetradentate, tren-based tris(phosphinimine) ligands that exhibit a dramatic effect on the CuI/CuII redox potential. The major resonance contributors of the phosphinimine moieties of the ligands are the charge-separated, zwitterionic forms, in which a substantial amount of cationic charge on phosphorous results in the development of a cationic electrostatic field near an open coordination site at the metal center. The use of classical coordination chemistry, electrochemistry, and a textbook Jahn–Teller distortion allowed for an in-depth view into the effects brought by the development of strong, local electrostatic fields within this series of molecules.
Results and discussion
Ligand design and syntheses
Phosphinimines are often employed as strong, neutral, organic bases. Some are commercially available, and their pKa values can range from 26 to 50, allowing for a multitude of applications.30,31 These high basicities are on par with, or stronger than, the neutral bases 1,8-diazabicyclo(5.4.0)undec-7-ene (DBU), 1,1,3,3-tetramethylguanidine (TMG), and triazabicyclodecene (TBD),32 and can be attributed to significant anionic character at the nitrogen atoms. Dyson and coworkers used DFT calculations to support the presence of significant ylidic character at the N–P bond of HN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PH3 (δN = −1.28; δP = +1.14).33 We calculated similar charge distributions for a series of P-substituted N-methyl phosphinimines, with the most notable change from the parent phosphinimine being an increase in the partial positive charge on phosphorus (δP) as alkyl/aryl/amido groups are introduced on phosphorus (Fig. 2).
PH3 (δN = −1.28; δP = +1.14).33 We calculated similar charge distributions for a series of P-substituted N-methyl phosphinimines, with the most notable change from the parent phosphinimine being an increase in the partial positive charge on phosphorus (δP) as alkyl/aryl/amido groups are introduced on phosphorus (Fig. 2).
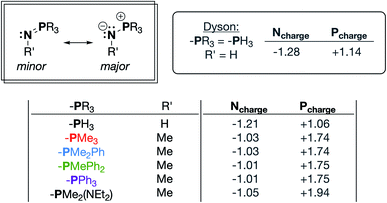 | ||
| Fig. 2 Important resonance structures and select partial charges of truncated phosphinimine ligands as determined by natural population analyses (NPA). These charges are consistent with those calculated by Dyson and coworkers.33 | ||
We next sought to incorporate phosphinimine moieties into a multidentate ligand scaffold34–41 with the intention of positioning multiple cationic phosphonium residues about a single open coordination site at a metal center. Ideally, the ligand would simultaneously take advantage of the strong σ-donation offered by the Lewis basic phosphinimine nitrogens.42–47 A tris(2-aminoethyl)amine (tren) ligand backbone was selected due to the multitude of complexes bound by related ligands that have been described in the literature. The novel series of tren-based tris(phosphinimine)ligands (R3P3tren) were synthesized via the Staudinger reaction (Scheme 1), wherein the ratio of aryl:alkyl substituents bound to the phosphorous atoms in the secondary coordination sphere was systematically modulated (PR3 = PMe3, PMe2Ph, PMePh2, PPh3). Additionally, in order to probe the impact of incorporating a strong electron-donating group bound to phosphorous, a PR3 = PMe2(NEt2) substituted ligand was synthesized following the same reaction scheme. These ligands were characterized using standard analytical techniques (see ESI†). The 31P{1H} NMR spectral resonances were identified at ca. 3 ppm, with a modest upfield shift as the number of aryl groups bound to phosphorous was increased. Notably, the 31P{1H} NMR spectral resonance for the PR3 = PMe2(NEt2) derivative was observed significantly downfield of the rest (20.79 ppm), indicative of a more electron-deficient phosphorous atom. This is consistent with the calculated δP values, which showed a marked increase for the PMe2(NEt2)-substituted phosphinimine compared to the all-alkyl/aryl-substituted analogs.
Synthesis of [R3P3tren-Cu]+ complexes (1PR3) and electrochemical studies
Treatment of R3P3tren with 1 equiv. of CuBArF4·4MeCN (BArF4 = B(C6F5)4−) in tetrahydrofuran (THF) afforded the cuprous complexes 1PR3 as white (1PMe3) or yellow (1PMe2Ph, 1PMePh2, 1PPh3, 1PMe2(NEt2)) solids (Scheme 1). Crystallographic analyses of 1PMe3, 1PMe2Ph, and 1PPh3 revealed trigonal pyramidal complexes (Fig. 3). The Cu–Nax distances range from 2.175–2.236 Å (1PMe2Ph < 1PMe3 < 1PPh3), and the Cu–Neq distances range from 2.017–2.081 Å (1PMe3 < 1PPh3 < 1PMe2Ph). Neither trend was found to correlate with the steric bulk of the phosphorus substituents. Notably, the vacant axial coordination site of 1PMe3 is retained in the solid state, irrespective of the identity of the anion or the presence of Lewis basic solvents (see ESI†). NMR spectra of 1PR3 were obtained in CD3CN and found to display C3v symmetry on the NMR timescale; single 31P{1H} resonances were located downfield (between 20 and 25 ppm) of those for the free ligands (R3P3tren). For 1PMe2(NEt2), the single spectral resonance corresponding to the phosphorous environment is observed further downfield at 38.11 ppm.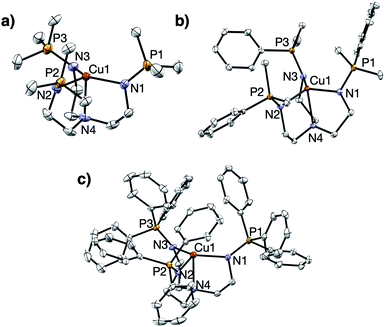 | ||
| Fig. 3 Solid state structures of (a) 1PMe3, (b) 1PMe2Ph, and (c) 1PPh3. Ellipsoids shown at 50% probability; hydrogen atoms and anions omitted for clarity. | ||
Electrochemical studies of 1PR3 were undertaken in isobutyronitrile (IBN) and are reported relative to Fc/Fc+. As shown in Fig. 4, 1PR3 displayed quasi-reversible E1/2 features that we assign as the CuI/CuII redox couples. The most anodic feature was observed for 1PPh3 at −415 mV. As the ratio of alkyl:aryl substituents bound to phosphorous increased, a cathodic shift in the CuI/CuII redox potential was observed, culminating with 1PMe3 at −780 mV. This E1/2 value is remarkably reducing, and to the best of our knowledge represents the most cathodic CuI/CuII redox couple for this geometry reported to date. The trend in redox potentials suggested that an increase in the number of alkyl groups on phosphorus caused an increase in the σ-donation of the phosphinimine nitrogen to Cu, thereby creating increasingly electron-rich metal centers across the series. However, 1PMe2(NEt2), which would be expected to have the strongest σ-donation due to the increased anionic character on the nitrogen donor atom, was found to have a CuI/CuII couple of −740 mV, a value that is 40 mV more anodic than the CuI/CuII redox couple of 1PMe3 and similar to the redox couple observed for 1PMe2Ph. Combined with the structural data, these results indicate that the secondary coordination sphere plays a role in the electronic structures of the metal centers across this series. We thus turned to density functional theory (DFT) to generate an impression of the valence manifold that could be carried into further experimental studies with this system.
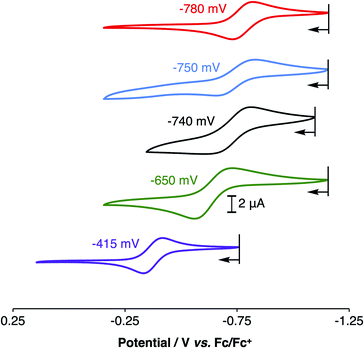 | ||
| Fig. 4 Cyclic voltammograms of 1PMe3 (red), 1PMe2Ph (blue), 1PMe2(NEt2) (black), 1PMePh2 (green), and 1PPh3 (purple), showing their CuI/CuII redox couples in isobutyronitrile (IBN). | ||
DFT calculations on 1PR3 and comparison to literature analogs
DFT calculations on 1PR3 were compared to a series of literature examples selected for the similarities they offer in terms of structure and donor type (Fig. 5a). The most facile point of comparison is tren-CuI, which shares the architecture and N4 donor set of P3tren. We have similarly included the TMG3tren-CuI complex due to parallels between the basic guanidyl groups of this ligand and the phosphinimine groups on 1PR3. Other recent ligand design efforts have generated CuI centers in similar geometries but with widely varying redox potentials. Karlin and coworkers reported a series of XTMPA-CuI complexes (TMPA = tris(2-pyridylmethyl)amine) wherein a systematic change in the CuI/CuII redox couple was attained through substitution at the para-positions of the TMPA pyridyl rings.48 Introducing electron-donating groups at these positions resulted in a shift of the CuI/CuII couple to more negative potentials, ultimately attaining a potential of −0.70 V (vs. Fc/Fc+) for the dimethylamino-substituted XTMPA derivative (NMe2TMPA). This value was ∼0.3 V more cathodic than the CuI complex bound by the parent ligand (HTMPA).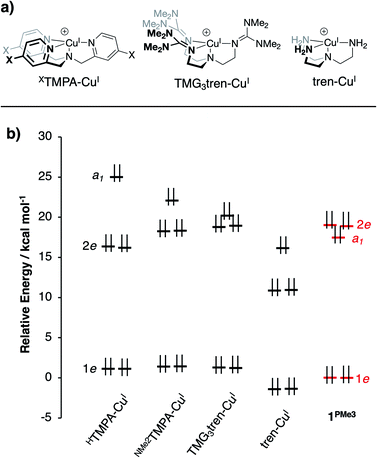 | ||
| Fig. 5 (a) CuI complexes from the literature for computational comparison to 1PR3, and (b) DFT-calculated MO diagram for CuI complexes (energies referenced arbitrarily to 1e of 1PMe3). | ||
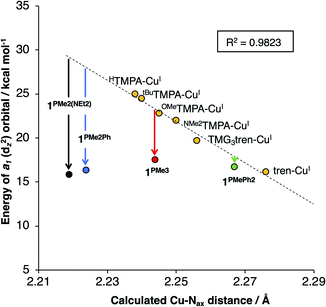
DFT geometry optimizations were performed on the cations of 1PR3, tren-CuI, TMG3tren-CuI, HTMPA-CuI, tBuTMPA-CuI, OMeTMPA-CuI, and NMe2TMPA-CuI. In accord with available experimental data, it was found that MeCN coordination to HTMPA-CuI was energetically favorable, forming a 20 e− complex. The other CuI complexes preferentially retained an open coordination site trans to the tertiary nitrogen. The geometries for all four-coordinate complexes were best described as trigonal pyramidal, and the five-coordinate MeCN adduct of HTMPA-CuI adopted a C3v geometry that is best described as trigonal bipyramidal. In all cases, the calculated bond distances about copper provided excellent agreement with experimental data (see ESI†). One observation that will be important to the ensuing discussion is that the trend in Cu–Nax distances observed experimentally (1PMe2Ph < 1PMe3 < 1PPh3) was reproduced using these computational methods.
The calculations revealed an interesting trend in the ligand field splitting pattern. The pseudo-C3v-symmetric geometries allow for valence manifolds containing nearly degenerate e-sets of dxz/dyz character (1e) and dx2−y2/dxy character (2e), along with an a1-symmetric dz2 orbital. For HTMPA-CuI-MeCN, tBuTMPA-CuI, OMeTMPA-CuI, NMe2TMPA-CuI, TMG3tren-CuI, and tren-CuI, 1e is lowest in energy, followed by 2e, and then a1 as the HOMO, creating 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 d-manifold splitting pattern. As expected, HTMPA-CuI–MeCN exhibits the highest energy a1 due to the ligand field effect of the additional axial donor. Removal of MeCN leads to the trigonal pyramidal HTMPA-CuI model compound suitable for comparison to the other four-coordinate complexes in this series (Fig. 5b); this four-coordinate species retains the 2
1 d-manifold splitting pattern. As expected, HTMPA-CuI–MeCN exhibits the highest energy a1 due to the ligand field effect of the additional axial donor. Removal of MeCN leads to the trigonal pyramidal HTMPA-CuI model compound suitable for comparison to the other four-coordinate complexes in this series (Fig. 5b); this four-coordinate species retains the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 splitting pattern of the other XTMPA congeners.
1 splitting pattern of the other XTMPA congeners.
For 1PR3, the d-manifolds switch to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 configurations, with the 2e set containing the HOMO and HOMO−1 (Fig. 5b for 1PMe3). This inversion in the valence manifold splitting pattern may be thought to result from two primary contributors. First, the stronger ligand field strength of the partially anionic phosphinimine nitrogen σ-donors creates a larger split between 1e and 2e, effectively raising the energy of 2e in 1PR3 relative to 2e in the reference compounds. Second, a significant variation in the relative energy of a1 (dz2) was observed. The energy of a1 decreases from TMPA-CuI to tBuTMPA-CuI, OMeTMPA-CuI, NMe2TMPA-CuI, TMG3tren-CuI, and tren-CuI. As expected, this trend was found to correlate closely with the Cu–Nax bond distance, as the ligand field strength in the axial direction will exert the most influence on the destabilization of dz2 (R2 = 0.98; Fig. 6, yellow); i.e. the longer the Cu–Nax distance, the lower the a1 energy. The 1PR3 complexes, however, provide notable deviations from this trend. Using 1PMe3 as an example, the predicted Cu–Nax distance of 2.244 Å would be expected to result in an a1 energy of ca. 23.3 kcal mol−1, but the energy of a1 is instead calculated to lie nearly 6 kcal mol−1 lower in energy (17.5 kcal mol−1, Fig. 6, red). This unexpected and significant decrease in the energy of a1 appears to work in concert with the aforementioned destabilization of 2e to create the 2
2 configurations, with the 2e set containing the HOMO and HOMO−1 (Fig. 5b for 1PMe3). This inversion in the valence manifold splitting pattern may be thought to result from two primary contributors. First, the stronger ligand field strength of the partially anionic phosphinimine nitrogen σ-donors creates a larger split between 1e and 2e, effectively raising the energy of 2e in 1PR3 relative to 2e in the reference compounds. Second, a significant variation in the relative energy of a1 (dz2) was observed. The energy of a1 decreases from TMPA-CuI to tBuTMPA-CuI, OMeTMPA-CuI, NMe2TMPA-CuI, TMG3tren-CuI, and tren-CuI. As expected, this trend was found to correlate closely with the Cu–Nax bond distance, as the ligand field strength in the axial direction will exert the most influence on the destabilization of dz2 (R2 = 0.98; Fig. 6, yellow); i.e. the longer the Cu–Nax distance, the lower the a1 energy. The 1PR3 complexes, however, provide notable deviations from this trend. Using 1PMe3 as an example, the predicted Cu–Nax distance of 2.244 Å would be expected to result in an a1 energy of ca. 23.3 kcal mol−1, but the energy of a1 is instead calculated to lie nearly 6 kcal mol−1 lower in energy (17.5 kcal mol−1, Fig. 6, red). This unexpected and significant decrease in the energy of a1 appears to work in concert with the aforementioned destabilization of 2e to create the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ligand field splitting pattern. Similar effects for 1PMe2Ph, 1PMe2(NEt2), and 1PMe2Ph are observed, to varying degrees (Fig. 6, blue, black, and green).
2 ligand field splitting pattern. Similar effects for 1PMe2Ph, 1PMe2(NEt2), and 1PMe2Ph are observed, to varying degrees (Fig. 6, blue, black, and green).
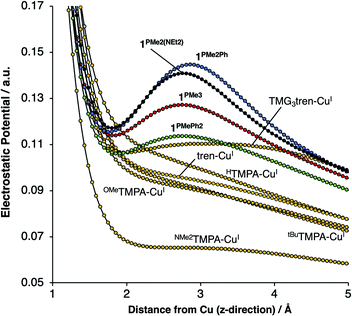
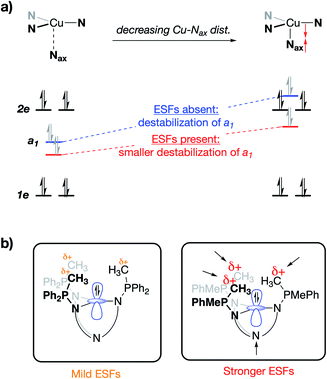
On considering the ylidic character of the phosphinimines and the geometric constraints imposed by the tren backbone of the R3P3tren ligands, the possibility arose that the deviations in the energy of a1 may reflect stabilization from cationic electrostatic fields emanating from the phosphonium residues. This view is supported by evaluation of the electrostatic potential along the canonical z-axis radiating away from the copper centers in the complexes evaluated above. In the absence of electrostatic fields in the secondary coordination sphere, one would expect the potential experienced by a test charge placed along this vector to diminish with a ca. 1/r dependence, according to the coulombic interaction of that test charge with the Cu ion. Indeed, this behavior is observed for HTMPA-CuI, tBuTMPA-CuI, OMeTMPA-CuI, NMe2TMPA-CuI, and tren-CuI (Fig. 7). However, deviations from 1/r behavior of the electrostatic potential are apparent in the cases of 1PR3 (Fig. 7). In these cases, clear maxima along the z-axis are observed at ca. 2.75 Å, a position that lies in-plane with the three nearest phosphonium carbon atoms, which are ca. 2.5 Å from the z-axes. Evaluation of the electrostatic potential gradients along the z-axes for 1PR3 predicts the presence of local electrostatic fields, located at ca. 2.2 Å from the copper centers, ranging in magnitude from 3–12 V nm−1 (Fig. S1–S3†). These field strengths are on par with what has been measured both in enzymes using vibrational Stark spectroscopy2–4 and in organized matter via neutron and synchrotron/X-ray diffraction studies,5 and it would therefore be large enough in magnitude to interact with the electron pair in a1. The TMG3tren-CuI complex also shows a modest deviation from the expected 1/r dependence in electrostatic potential, rising at ca. 2 Å to a plateau in electrostatic potential that persists to ca. 4 Å from the copper center (Fig. 7). This may be thought to result from the contribution of ionic resonance pictures available to the guanidinyl units in which a cationic charge is located on one of the amino nitrogen atoms. The modest deviation in electrostatic potential in this case is consistent with the crystallographic data, which indicate that the TMG groups show minor contributions from these ionic resonance structures.
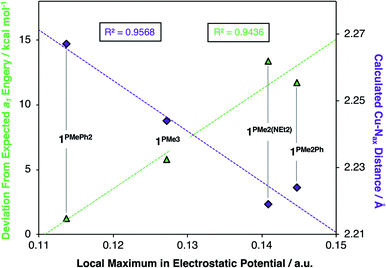
Deviations in the a1 orbital energies (Fig. 6) increase in order from 1PMePh2 < 1PMe3 < 1PMe2Ph ≈ 1PMe2(NEt2). This ordering was found to directly correlate with the calculated strength of the electrostatic field present along the canonical z-axes of the molecules (Fig. 8, green triangles), thereby implicating the cationic phosphonium residues as having a through-space electrostatic stabilizing effect on a1 (Fig. 9a). The strengths of the electrostatic fields in 1PR3 were also found to inversely correlate with the calculated Cu–Nax distances (Fig. 8, purple diamonds). This observation suggests that electrostatic attractions between the occupied a1 orbitals and the phosphonium residues work in concert with the rigidity of the ligand backbones to pull the Nax atoms closer to the copper centers (Fig. 9b). This stereoelectronic effect is significant in that it represents a physical consequence of electrostatic stabilization of a1. Together, the observations discussed within this section support a direct relationship between the physical properties observed in this system and the magnitude of the electrostatic fields emanating from the cationic phosphonium residues in the secondary coordination spheres in 1PR3.
Chemical oxidation of 1PMe3 and DFT analysis of the CuII products
To validate the computationally predicted valence manifolds for 1PR3, we performed chemical oxidations of one of the P3tren-CuI complexes. The 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 d-orbital splitting patterns calculated for 1PR3 suggest that 1 e− oxidations would generate holes with significant 2e character. The resulting CuII complexes would contain doubly degenerate electronic ground states, which would then be susceptible to primary Jahn–Teller distortions. By contrast, the 2
2 d-orbital splitting patterns calculated for 1PR3 suggest that 1 e− oxidations would generate holes with significant 2e character. The resulting CuII complexes would contain doubly degenerate electronic ground states, which would then be susceptible to primary Jahn–Teller distortions. By contrast, the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 d-orbital splitting pattern predicted for the other compounds in this class would yield singly degenerate S = 1/2 states upon oxidation, precluding Jahn–Teller distortions from occurring. Thus, the presence or absence of a Jahn–Teller distortion in the CuII analog of 1PMe3 may be used to resolve the structure of the CuI valence manifold.
1 d-orbital splitting pattern predicted for the other compounds in this class would yield singly degenerate S = 1/2 states upon oxidation, precluding Jahn–Teller distortions from occurring. Thus, the presence or absence of a Jahn–Teller distortion in the CuII analog of 1PMe3 may be used to resolve the structure of the CuI valence manifold.
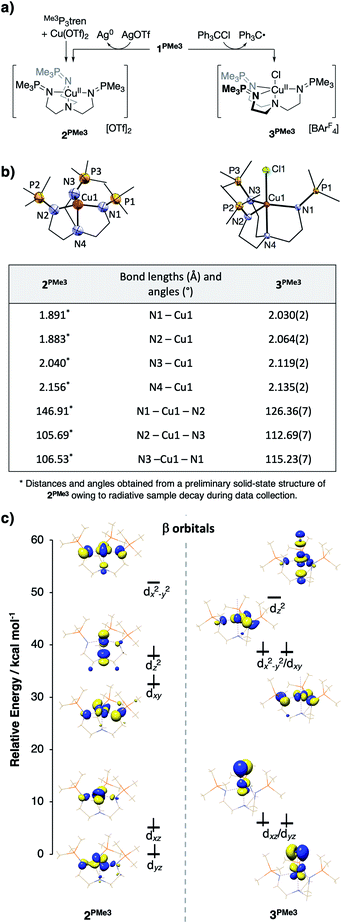
Upon treatment of 1PMe3 with AgBArF4·4MeCN in THF, the colorless solution immediately turned red, concomitant with precipitation of a dark solid (Ag0). The CuII product proved resistant to crystallization, but independent synthesis of the dication through ligation of cupric triflate with Me3P3tren in MeCN afforded [(Me3P3tren)Cu][OTf]2 (2PMe3, Fig. 10a). This red material shows the same UV-vis spectral features as the oxidation product described above and the same cyclic voltammetry trace as 1PMe3 (Fig. S15†). Single crystals of 2PMe3 were grown by diffusion of pentane into a 1,2-difluorobenzene (DFB) solution of the complex; however, radiative decay of the crystalline sample during X-ray diffraction experiments (Cu-Kα radiation source, λ = 1.5406 Å) resulted in incomplete data set collection and subsequently poor X-ray model refinement (R = 27%). Although the exact bond lengths and angles derived from the preliminary solid-state structure of 2PMe3 are not statistically reliable, the data were adequate to reveal a four-coordinate CuII complex clearly distorted to a pseudo-Cs symmetry via a Jahn–Teller distortion (Fig. 10b).
This result may be contrasted with the 1-electron oxidation of 1PMe3 using triphenylmethyl chloride, which resulted in the formation of the yellow/green five-coordinate complex [(Me3P3tren)CuCl][OTf] (3PMe3, Fig. 10a), which exists in the solid-state as a pseudo-C3v-symmetric complex with an axial chloride ligand. Significant differences in the solid-state geometries between 2PMe3 and 3PMe3 are highlighted in the selected bond distances and angles shown in Fig. 10b. Complex 2PMe3 exhibits shorter Cu–Neq distances, a longer Cu–Nax distance, and a marked distortion of the equatorial donors from a nearly trigonal geometry in 3PMe3 (<Neq–Cu–Neq = 113°–126°) to a T-shaped geometry in 2PMe3 (<Neq–Cu–Neq = 106°–147°).
DFT geometry optimization calculations on the cationic portion of 2PMe3 replicated the Jahn–Teller distortion observed experimentally, regardless of the starting geometry (Fig. 10c, left, β (spin down) orbitals). As expected, the distortion lifted the degeneracy of 2e, increasing the energy of the singly occupied dx2−y2 and decreasing the energy of dxy. In an effort to examine the uniqueness of the Jahn–Teller distortion observed in 2PMe3, the analogous, four-coordinate CuII complexes bound by HTMPA, tBuTMPA-CuI, OMeTMPA-CuI, NMe2TMPA, TMG3tren, and tren were evaluated by the same methods as those used for 2PMe3. The calculated CuII ions were found to exhibit C3v symmetry, closely matching the experimental geometries, and consistent with the presence of an a1-symmetric vacancy. Comparable DFT analysis of the five-coordinate complex 3PMe3 supports the conclusion that its 3-fold symmetry results from Cl− destabilization of dz2, thereby reverting the ligand field splitting to a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 : 1 pattern (Fig. 10c, right, β orbitals) that is inactive toward a Jahn–Teller distortion for a d9 metal ion.
2 : 1 pattern (Fig. 10c, right, β orbitals) that is inactive toward a Jahn–Teller distortion for a d9 metal ion.
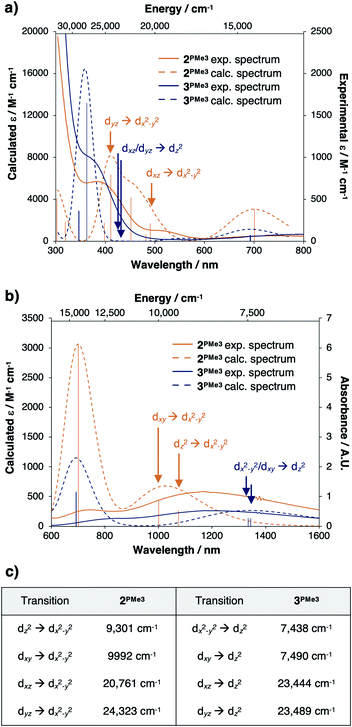
Time-dependent density functional theory (TD-DFT) predictions added support that the valence manifold structures of the red CuII species 2PMe3 and the green CuII species 3PMe3 both persist in the solution phase. The experimentally measured UV-vis spectrum of 2PMe3 (Fig. 11a and b, solid orange trace) contains three prominent features at ca. 400 nm (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1), 526 nm (19
000 cm−1), 526 nm (19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1), and 700 nm (14
000 cm−1), and 700 nm (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1) that were reproduced computationally (Fig. 11a and b, dashed orange trace). The feature at 400 nm is assigned as the dyz → dx2−y2 transition, and the feature at 526 nm is assigned as the dxz → dx2−y2 transition. The feature calculated at 700 nm is best described as a ligand to metal charge transfer (LMCT) from the phosphinimine moieties to the empty dx2−y2 β orbital, though the experimental and calculated intensities are both predicted to be low. A single broad feature is observed in the near infrared spectrum (NIR) (Fig. 11b, solid orange trace) at ca. 1190 nm (8403 cm−1) that was reproduced computationally (Fig. 11b, dashed orange trace) as a combination of the dxy → dx2−y2 and dz2 → dx2−y2 transitions.
200 cm−1) that were reproduced computationally (Fig. 11a and b, dashed orange trace). The feature at 400 nm is assigned as the dyz → dx2−y2 transition, and the feature at 526 nm is assigned as the dxz → dx2−y2 transition. The feature calculated at 700 nm is best described as a ligand to metal charge transfer (LMCT) from the phosphinimine moieties to the empty dx2−y2 β orbital, though the experimental and calculated intensities are both predicted to be low. A single broad feature is observed in the near infrared spectrum (NIR) (Fig. 11b, solid orange trace) at ca. 1190 nm (8403 cm−1) that was reproduced computationally (Fig. 11b, dashed orange trace) as a combination of the dxy → dx2−y2 and dz2 → dx2−y2 transitions.
The experimental UV-vis spectrum of 3PMe3 (Fig. 11a, solid blue trace) contains prominent features at ca. 360 nm (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1) and 750 nm (13
800 cm−1) and 750 nm (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1), which were also reproduced computationally (27
300 cm−1), which were also reproduced computationally (27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1 and 14
800 cm−1 and 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 388 cm−1) (Fig. 11a, dashed blue trace). Although the dxz/dyz → dz2 transitions are predicted to be within this energy range (23
388 cm−1) (Fig. 11a, dashed blue trace). Although the dxz/dyz → dz2 transitions are predicted to be within this energy range (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 444, 23
444, 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 489 cm−1), they are likely not observed due to low intensities (εcalc = 13–14 M−1 cm−1). A single broad feature is observed in the NIR spectrum of 3PMe3 (Fig. 11b, solid blue trace) that was reproduced computationally (Fig. 11b, dashed blue trace) as the dxy/dx2−y2 → dz2 transitions. The calculated energies of the various d–d transitions for 2PMe3 and 3PMe3 are tabulated in Fig. 11c and are marked on the spectra in Fig. 11a and b with arrows (orange for 2PMe3, blue for 3PMe3).
489 cm−1), they are likely not observed due to low intensities (εcalc = 13–14 M−1 cm−1). A single broad feature is observed in the NIR spectrum of 3PMe3 (Fig. 11b, solid blue trace) that was reproduced computationally (Fig. 11b, dashed blue trace) as the dxy/dx2−y2 → dz2 transitions. The calculated energies of the various d–d transitions for 2PMe3 and 3PMe3 are tabulated in Fig. 11c and are marked on the spectra in Fig. 11a and b with arrows (orange for 2PMe3, blue for 3PMe3).
DFT evaluation of the CuI/CuII redox potentials
The calculated redox potentials for this series of complexes were evaluated as a way to gauge the extent to which the Jahn–Teller distortions, the phosphinimine donor strengths, and the through space electrostatic effects individually contribute to the highly cathodic CuI/CuII couples. As mentioned above, Karlin and co-workers have shown that variations in the donor strength of TMPA-based ligands significantly impacts CuI/CuII redox potentials, and the Tolman group has used distal charged residues to influence CuII/CuIII redox potentials as a function of the sign of the charged group. Jahn–Teller effects have also been shown to impact the thermodynamics of electron transfer. For example, a ∼0.6 V shift in redox potentials for a series of CuI bis(1,10-phenanthroline) complexes has been ascribed to the varying extent of Jahn–Teller distortion available to the complexes as a function of the steric bulk in their secondary coordination spheres.49–51In the present case, the trends in the experimental redox potentials were reproduced computationally for 1PMe3 and the XTMPA-CuI complexes48 discussed above (Table 1). The mean unsigned error of 120 mV is on par with the current state-of-the-art.52 In order to evaluate the impact of the Jahn–Teller distortion in 2PMe3 on the CuI/CuII redox potential, a C3v-symmetric analog of 2PMe3 was evaluated by constraining the Neq–Cu–Neq angles to 120°. The structure optimized with this constraint was then used to calculate a hypothetical CuI/CuII redox potential in which the CuI symmetry is maintained upon oxidation of 1PMe3 (denoted as C3v-CuI/C3v-CuII). This redox couple (−630 mV) is on par with the calculated redox potential for NMe2TMPA-CuI (−617 mV), indicating that the phosphinimine donors act as strong σ-donors to create electron-rich CuI centers. Importantly, however, the C3v-CuI/C3v-CuII potential is calculated to be substantially more anodic than the CuI/CuII redox potential that takes into account the Jahn–Teller distortion on oxidation (C3v-CuI/Cs-CuII, −890 mV; Table 1). This 260 mV shift in potential indicates that the geometric change accompanying oxidation provides a substantial driving force (ca. 6 kcal mol−1) for electron transfer from 1PMe3.
| Complex | Calc. pot. (mV) | Exp. pot. (mV) | Error (mV) |
|---|---|---|---|
| 1PMe3 (C3v-CuI/Cs-CuII) | −890 | −780 | −110 |
| 1PMe3 (C3v-CuI/C3v-CuII) | −630 | +150 | |
| 1PMe2Ph | −579 | −750 | +171 |
| 1PMe2(NEt2) | −822 | −740 | −82 |
| 1PMePh2 | −640 | −650 | +10 |
| HTMPA-CuI | −232 | −400 | +168 |
| tBuTMPA-CuI | −303 | −460 | +157 |
| OMeTMPA-CuI | −311 | −490 | +179 |
| NMe2TMPA-CuI | −617 | −700 | +83 |
It remained to consider the origin of the >350 mV range in redox potentials for 1PR3. The potentials do not clearly track with the donor strengths of the phosphinimines, and the characterization of the oxidation as being 2e (dx2−y2/dxy)-based suggests that the extent of electrostatic stabilization of a1 is not responsible. This is supported by the observation that the magnitude of the electrostatic potential along the canonical z-axis does not scale with the CuI/CuII redox couple. We thus hypothesized that the steric bulk of the phosphinimine substitutions was responsible for modulating the extent to which the Jahn–Teller distortion stabilized the oxidized CuII ions.
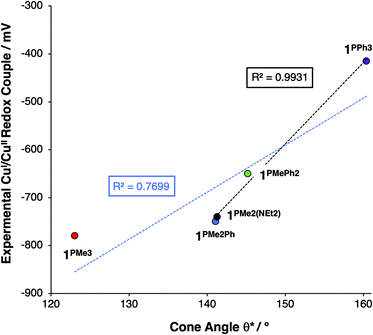
This steric effect was evaluated through calculation of a modified Tolman cone angle (θ*) for the phosphinimine substituents in the R3P3tren ligands (see ESI† for details on the calculation of θ*). Upon plotting the experimental CuI/CuII redox potentials versus θ*, a direct relationship between steric bulk in the secondary coordination sphere and the CuI/CuII redox potential is realized (Fig. 12). Indeed, for cone angles >140°, a linear relationship (R2 = 0.99) is observed. This observation can be explained by considering that the maximum amount of stabilization of the CuII species (and thus the most cathodic CuI/CuII redox potential) will occur for ligands with small values of θ*, for which the limited steric profile of the ligand allows for the most distortion by the tethered arms of the ligand backbone. As the steric profile of the ligand increases, the CuII species become increasingly prohibited from accessing Jahn–Teller-distorted geometries (Fig. 13), resulting in a systematic anodic shift in the CuI/CuII redox potentials. The non-linearity of the data shown in Fig. 12 on inclusion of 1PMe3 suggests that a lower bound for the cone angle at which the Jahn–Teller distortion is inhibited lies between 123° and 141°. Overall, these data indicate that while electrostatic effects appear to be critical for engendering a Jahn–Teller distortion in 2PR3, the steric profile of the secondary coordination sphere is responsible for fine-tuning the CuI/CuII redox potentials.
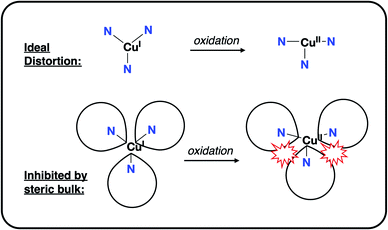 | ||
| Fig. 13 Depiction of the inhibition of an “ideal” Jahn–Teller distortion with increased steric bulk in the secondary coordination sphere. | ||
Conclusions
This study demonstrates the ability of strategically-placed charged residues to directly impact the valence manifolds of homogeneous inorganic complexes. This technique is independent of the specific donor bound to the metal center, allowing for orthogonal control of valence orbital energies by way of through-bond and through-space effects. In the present example, electrostatic fields (ESFs) emanating from cationic phosphonium residues in the secondary coordination spheres of 1PR3 stabilize the valence MO a1 (dz2) orbitals. This stabilization would typically result in an anodic shift in redox potential, but the strong σ-donation from the phosphinimine donors provides an orthogonal destabilization of the CuI 2e set, producing counter-intuitive shifts in CuI/CuII redox potentials. The resulting inversion of the valence manifold brought by these complementary effects generates a system capable of undergoing a Jahn–Teller distortion upon oxidation, providing an additional thermodynamic driving force for electron transfer. Studies to assess the impact of ESFs on small molecule binding and reactivity are underway.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was financially supported by the National Institute of General Medical Sciences of the National Institutes of Health (award number R35GM128794), the Charles E. Kaufman Foundation of the Pittsburgh Foundation (award number KA2016-85227), and the University of Pennsylvania. We also thank the Vagelos Institute for Energy Science and Technology (VIEST) for a Graduate Research Fellowship, awarded to ABW.References
- A. Warshel, P. K. Sharma, M. Kato, Y. Xiang, H. Liu and M. H. M. Olsson, Chem. Rev., 2006, 106, 3210–3235 CrossRef CAS.
- S. D. Fried, S. Bagchi and S. G. Boxer, Science, 2014, 346, 1510–1514 CrossRef CAS.
- M. G. Romei, C.-Y. Lin, I. I. Mathews and S. G. Boxer, Science, 2020, 367, 76–79 CrossRef CAS.
- S. D. Fried and S. G. Boxer, Annu. Rev. Biochem., 2017, 86, 387–415 CrossRef CAS.
- M. W. Shi, S. P. Thomas, V. R. Hathwar, A. J. Edwards, R. O. Piltz, D. Jayatilaka, G. A. Koutsantonis, J. Overgaard, E. Nishibori, B. B. Iversen and M. A. Spackman, J. Am. Chem. Soc., 2019, 141, 3965–3976 CrossRef CAS.
- C. F. Gorin, E. S. Beh, Q. M. Bui, G. R. Dick and M. W. Kanan, J. Am. Chem. Soc., 2013, 135, 11257–11265 CrossRef CAS.
- C. F. Gorin, E. S. Beh and M. W. Kanan, J. Am. Chem. Soc., 2012, 134, 186–189 CrossRef CAS.
- A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Nature, 2016, 531, 88–91 CrossRef.
- V. M. Lau, W. C. Pfalzgraff, T. E. Markland and M. W. Kanan, J. Am. Chem. Soc., 2017, 139, 4035–4041 CrossRef CAS.
- M. Klinska, L. M. Smith, G. Gryn’ova, M. G. Banwell and M. L. Coote, Chem. Sci., 2015, 6, 5623–5627 RSC.
- G. Gryn’ova and M. L. Coote, Aust. J. Chem., 2017, 70, 367–372 CrossRef.
- K. Zhang, B. B. Noble, A. C. Mater, M. J. Monteiro, M. L. Coote and Z. Jia, Phys. Chem. Chem. Phys., 2018, 20, 2606–2614 RSC.
- L. Zhang, E. Laborda, N. Darwish, B. B. Noble, J. H. Tyrell, S. Pluczyk, A. P. Le Brun, G. G. Wallace, J. Gonzalez, M. L. Coote and S. Ciampi, J. Am. Chem. Soc., 2018, 140, 766–774 CrossRef CAS.
- L. Zhang, Y. B. Vogel, B. B. Noble, V. R. Gonçales, N. Darwish, A. Le Brun, J. J. Gooding, G. G. Wallace, M. L. Coote and S. Ciampi, J. Am. Chem. Soc., 2016, 138, 9611–9619 CrossRef CAS.
- M. T. Blyth, B. B. Noble, I. C. Russell and M. L. Coote, J. Am. Chem. Soc., 2020, 142, 606–613 CrossRef CAS.
- N. S. Hill and M. L. Coote, Aust. J. Chem., 2019, 72, 627–632 CrossRef CAS.
- M. T. Blyth and M. L. Coote, J. Org. Chem., 2019, 84, 1517–1522 CrossRef.
- L.-J. Yu and M. L. Coote, J. Phys. Chem. A, 2019, 123, 582–589 CrossRef CAS.
- N. S. Hill and M. L. Coote, J. Am. Chem. Soc., 2018, 140, 17800–17804 CrossRef CAS.
- H. M. Aitken and M. L. Coote, Phys. Chem. Chem. Phys., 2018, 20, 10671–10676 RSC.
- D. Dhar, G. M. Yee and W. B. Tolman, Inorg. Chem., 2018, 57, 9794–9806 CrossRef CAS.
- A. H. Reath, J. W. Ziller, C. Tsay, A. J. Ryan and J. Y. Yang, Inorg. Chem., 2017, 56, 3713–3718 CrossRef CAS.
- T. Chantarojsiri, J. W. Ziller and J. Y. Yang, Chem. Sci., 2018, 9, 2567–2574 RSC.
- T. Chantarojsiri, A. H. Reath and J. Y. Yang, Angew. Chem., Int. Ed., 2018, 57, 14037–14042 CrossRef CAS.
- I. Azcarate, C. Costentin, M. Robert and J.-M. Savéant, J. Am. Chem. Soc., 2016, 138, 16639–16644 CrossRef CAS.
- D. J. Martin, B. Q. Mercado and J. M. Mayer, Sci. Adv., 2020, 6, eaaz3318 CrossRef CAS.
- T. Stuyver, R. Ramanan, D. Mallick and S. Shaik, Angew. Chem., Int. Ed., 2020, 59, 7915–7920 CrossRef CAS.
- H. Gao and J. T. Groves, J. Am. Chem. Soc., 2017, 139, 3938–3941 CrossRef CAS.
- S. R. Bell and J. T. Groves, J. Am. Chem. Soc., 2009, 131, 9640–9641 CrossRef CAS.
- J. Verkade, Angew. Chem., Int. Ed., 2009, 48, 9221 CrossRef CAS.
- I. Kaljurand, J. Saame, T. Rodima, I. Koppel, I. A. Koppel, J. F. Kögel, J. Sundermeyer, U. Köhn, M. P. Coles and I. Leito, J. Phys. Chem. A, 2016, 120, 2591–2604 CrossRef CAS.
- H. Wittmann, V. Raab, A. Schorm, J. Plackmeyer and J. Sundermeyer, Eur. J. Inorg. Chem., 2001, 1937–1948 CrossRef CAS.
- A. B. Chaplin, J. A. Harrison and P. J. Dyson, Inorg. Chem., 2005, 44, 8407–8417 CrossRef CAS.
- M. Sauthier, F. Leca, R. Fernando de Souza, K. Bernardo-Gusmão, L. F. Trevisan Queiroz, L. Toupet and R. Réau, New J. Chem., 2002, 26, 630–635 RSC.
- M. T. Reetz and E. Bohres, Chem. Commun., 1998, 935–936 RSC.
- M. J. Sgro and D. W. Stephan, Dalton Trans., 2011, 40, 2419–2421 RSC.
- R. Cariou, F. Dahcheh, T. W. Graham and D. W. Stephan, Dalton Trans., 2011, 40, 4918–4925 RSC.
- R. Cariou, T. W. Graham and D. W. Stephan, Dalton Trans., 2013, 42, 4237–4239 RSC.
- R. Cariou, T. W. Graham, F. Dahcheh and D. W. Stephan, Dalton Trans., 2011, 40, 5419–5422 RSC.
- T. Cheisson and A. Auffrant, Dalton Trans., 2014, 43, 13399–13409 RSC.
- T. Cheisson, L. Mazaud and A. Auffrant, Dalton Trans., 2018, 47, 14521–14530 RSC.
- M. J. Aroney, I. E. Buys, M. S. Davies and T. W. Hambley, J. Chem. Soc., Dalton Trans., 1994, 2827–2834 RSC.
- B. A. Arndtsen, H. F. Sleiman, L. McElwee-White and A. L. Rheingold, Organometallics, 1993, 12, 2440–2444 CrossRef CAS.
- R. Tonner and G. Frenking, Organometallics, 2009, 28, 3901–3905 CrossRef CAS.
- H. V. Huynh, Chem. Rev., 2018, 118, 9457–9492 CrossRef CAS.
- P. Imhoff, C. J. Elsevier and C. H. Stam, Inorg. Chim. Acta, 1990, 175, 209–216 CrossRef CAS.
- M. J. Aroney, M. S. Davies, T. W. Hambley and R. K. Pierens, J. Chem. Soc., Dalton Trans., 1994, 91–96 RSC.
- C. X. Zhang, S. Kaderli, M. Costas, E. Kim, Y.-M. Neuhold, K. D. Karlin and A. D. Zuberbühler, Inorg. Chem., 2003, 42, 1807–1824 CrossRef CAS.
- B. R. James and R. J. P. Williams, J. Chem. Soc., 1961, 2007–2019 RSC.
- D. V Scaltrito, D. W. Thompson, J. A. O'Callaghan and G. J. Meyer, Coord. Chem. Rev., 2000, 208, 243–266 CrossRef.
- G. D. Stroscio, R. D. Ribson and R. G. Hadt, Inorg. Chem., 2019, 58, 16800–16817 CrossRef CAS.
- L. Yan, Y. Lu and X. Li, Phys. Chem. Chem. Phys., 2016, 18, 5529–5536 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2045438–2045442. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc06364a |
| This journal is © The Royal Society of Chemistry 2021 |