Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Single-molecule junctions of multinuclear organometallic wires: long-range carrier transport brought about by metal–metal interaction†‡
Yuya
Tanaka
 *ab,
Yuya
Kato
ab,
Kaho
Sugimoto
ab,
Reo
Kawano
ab,
Tomofumi
Tada
c,
Shintaro
Fujii
*ab,
Yuya
Kato
ab,
Kaho
Sugimoto
ab,
Reo
Kawano
ab,
Tomofumi
Tada
c,
Shintaro
Fujii
 d,
Manabu
Kiguchi
d,
Manabu
Kiguchi
 d and
Munetaka
Akita
d and
Munetaka
Akita
 *ab
*ab
aLaboratory for Chemistry and Life Science, Institute of Innovative Research, Tokyo Institute of Technology, 4259 Nagatsuta, Midori-ku, Yokohama 226-8503, Japan. E-mail: ytanaka@res.titech.ac.jp; akitatit@icloud.com
bDepartment of Chemical Science and Engineering, School of Materials and Chemical Technology, Tokyo Institute of Technology, 4259 Nagatsuta, Midori-ku, Yokohama 226-8503, Japan
cKyushu University Platform of Inter/Transdisciplinary Energy Research, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka 819-0395, Japan
dDepartment of Chemistry, School of Science, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo 152-8551, Japan
First published on 8th February 2021
Abstract
Here, we report multinuclear organometallic molecular wires having (2,5-diethynylthiophene)diyl-Ru(dppe)2 repeating units. Despite the molecular dimensions of 2–4 nm the multinuclear wires show high conductance (up to 10−2 to 10−3G0) at the single-molecule level with small attenuation factors (β) as revealed by STM-break junction measurements. The high performance can be attributed to the efficient energy alignment between the Fermi level of the metal electrodes and the HOMO levels of the multinuclear molecular wires as revealed by DFT–NEGF calculations. Electrochemical and DFT studies reveal that the strong Ru–Ru interaction through the bridging ligands raises the HOMO levels to access the Fermi level, leading to high conductance and small β values.
Introduction
One of the goals of molecular devices is to control carrier transport through molecular junctions.1–4 Molecular conductance, however, strongly depends on the dimensions of the molecules according to the following equation: G = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βL), where G, A, β, and L refer to conductance, contact resistance, attenuation factor, and molecular length, respectively. To realize molecular wires with efficient long-range electron-transport performance, it is essential to minimize the β factor as much as possible. The coherent tunneling process dominates for molecules with small dimensions, while the incoherent hopping process additionally contributes to the conductance of molecules with dimensions greater than ∼3 nm.5–7 The former process often causes a large β factor mainly due to the energy mismatch between the molecules and electrodes.
exp(−βL), where G, A, β, and L refer to conductance, contact resistance, attenuation factor, and molecular length, respectively. To realize molecular wires with efficient long-range electron-transport performance, it is essential to minimize the β factor as much as possible. The coherent tunneling process dominates for molecules with small dimensions, while the incoherent hopping process additionally contributes to the conductance of molecules with dimensions greater than ∼3 nm.5–7 The former process often causes a large β factor mainly due to the energy mismatch between the molecules and electrodes.
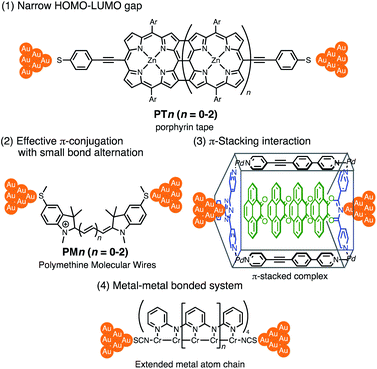
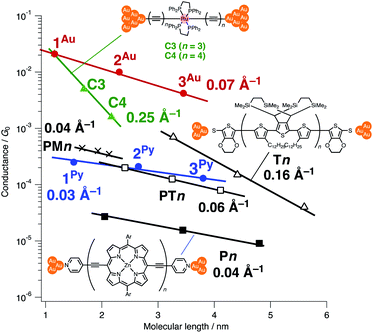
Thus far, extensive single-molecule conductance studies have unveiled general strategies for organic and inorganic molecular wires with small β values such as (1) narrowing the HOMO–LUMO gap,8–10 (2) extending π-conjugated systems (e.g. less bond alternation),11,12 and making use of (3) π-stacking interactions13–15 and (4) metal–metal bonded systems (Fig. 1).16,17 These strategies have led to the successful development of efficient but relatively short molecular wires (<2 nm). On the other hand, those longer than 2 nm remain to be developed due to the instability of longer derivatives and synthetic difficulty.
Insertion of metal fragments into organic molecular wires is an effective way to make the β factor smaller while increasing the molecular dimensions.18,19 Single-molecule conductance studies of multimetallic complexes containing metal fragments as repeating units are scarce20 in contrast to those of self-assembled monolayer systems.21–26 Berke, Stadler, Lörtscher et al. reported the single-molecule conductance of multinuclear molecular wires of a diiron complex (Fe2), which dimerized to form a tetrairon complex (Fe4) during break-junction (BJ) measurements using a scanning tunneling microscope (STM) (Fig. 2 top).27 In this case, however, the poor characterization of the in situ formed dimer Fe4 prevented the detailed study of a series of multinuclear molecular wires.28
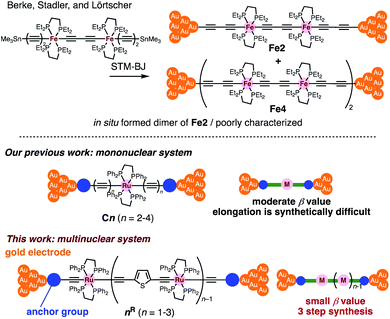 | ||
| Fig. 2 (Top) Examples of multimetallic molecular wires. (Bottom) Concept of our previous and present studies. | ||
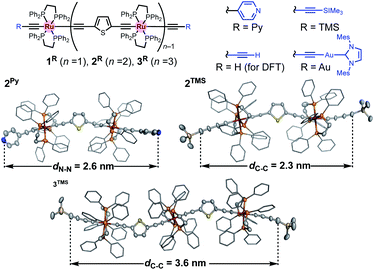
Recently, we reported metallapolyyne wires Cn with electron-rich Ru(dppe)2 fragments (dppe: 1,2-bis(diphenylphosphino)ethane) end-capped with gold groups, which facilitated covalent linkage with gold electrodes. The molecular wires shorter than 2 nm turned out to be highly conductive (10−2 to 10−3G0, 1 G0 = 77.5 μS).29,30 The synthetic difficulty, however, hampered the elongation of the system and the β value was moderate (0.25 Å−1). To address these issues, we designed a series of mono-, di- and tri-nuclear molecular wires nR (n = 1–3) consisting of (2,5-diethynylthiophene)diyl-Ru(dppe)2 repeating units (Fig. 2 bottom and 3). To examine the effect of the terminal anchor groups, pyridine- (nPy) and gold-terminated complexes (nAu) were prepared. Notably, these molecular wires were accessible within three steps from their known precursors and showed significantly small β values as a result of metal–metal interaction as will be discussed later.
Results and discussion
Synthesis and characterization
We prepared multinuclear molecular wires 2Py and 3Py in two steps from the known vinylidene complex [trans-ClRu(dppe)2(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2)][PF6].31–34 Treatment of the vinylidene complex with H–C
CH2)][PF6].31–34 Treatment of the vinylidene complex with H–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Th–C
C–Th–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–H 4 (for 2Py; Th: 2,5-thiophenediyl) and trans-(H–C
C–H 4 (for 2Py; Th: 2,5-thiophenediyl) and trans-(H–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Th–C
C–Th–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)2Ru(dppe)25 (for 3Py) followed by Sonogashira coupling reaction with 4-bromopyridine afforded 2Py and 3Py, respectively. On the other hand, gold-terminated complexes 2Au and 3Au with N-heterocyclic carbene auxiliaries were prepared via sequential desilylation and auration of the TMS-protected precursors 2TMS and 3TMS, respectively, which were obtained from trans-ClRu(dppe)2(C
C)2Ru(dppe)25 (for 3Py) followed by Sonogashira coupling reaction with 4-bromopyridine afforded 2Py and 3Py, respectively. On the other hand, gold-terminated complexes 2Au and 3Au with N-heterocyclic carbene auxiliaries were prepared via sequential desilylation and auration of the TMS-protected precursors 2TMS and 3TMS, respectively, which were obtained from trans-ClRu(dppe)2(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CC
CC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CTMS) and 4/5.35 We characterized these complexes by conventional spectroscopic methods. Notably, the complexes prepared here were stable under ambient conditions in both solution and solid state. Molecular structures of 2Py, 2TMS, and 3TMS determined by X-ray crystallography are shown in Fig. 3. The distances between the atoms to be connected to the gold electrodes during the subsequent STM-BJ measurements are 2.6 (2Py; N⋯N), 2.3 (2TMS; C⋯C), and 3.6 nm (3TMS; C⋯C), and separations of the Ru atoms are around 1.2 nm. While the thiophene parts may come into contact with gold electrodes,36 they are sufficiently protected by the bulky dppe ligands.
CTMS) and 4/5.35 We characterized these complexes by conventional spectroscopic methods. Notably, the complexes prepared here were stable under ambient conditions in both solution and solid state. Molecular structures of 2Py, 2TMS, and 3TMS determined by X-ray crystallography are shown in Fig. 3. The distances between the atoms to be connected to the gold electrodes during the subsequent STM-BJ measurements are 2.6 (2Py; N⋯N), 2.3 (2TMS; C⋯C), and 3.6 nm (3TMS; C⋯C), and separations of the Ru atoms are around 1.2 nm. While the thiophene parts may come into contact with gold electrodes,36 they are sufficiently protected by the bulky dppe ligands.
STM-break junction study
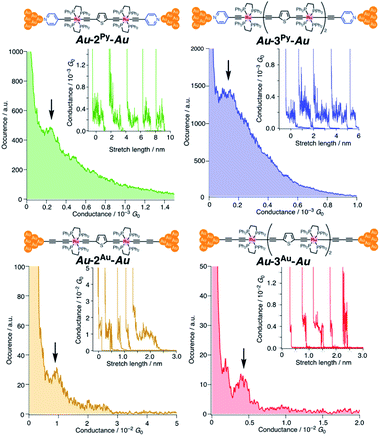
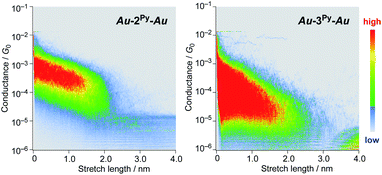
We performed single-molecule conductance measurements of the obtained wires nR using the STM break-junction method (bias voltage: 100 mV).37 Individual traces for 0.25 M tetraglyme solutions of the pyridine-terminated complexes 2Py and 3Py (Fig. 4 and S11‡) showed steps with high probabilities for the formation of molecular junctions (>90%). Both of the linear and log histograms showed peaks in the 10−4G0 region. The 2D histograms for 2Py and 3Py revealed that the molecular junction formation was extended over the 2 nm region (Fig. 5), indicating junction formation at the terminal pyridine anchors rather than at the thiophene linker parts (dN–S ∼1.3 nm). Single-molecule conductance of 2Py and 3Py was 2.1 (±0.6) and 1.3 (±0.6) × 10−4G0, respectively, as determined by statistical analysis of the linear-scale histograms.Next, molecular wires 2Au and 3Au were subjected to an STM-break junction study (1.0 mM in tetraglyme, Fig. 4 and S12‡). The lack of coordinating anchor groups, like those in the pyridine-anchor in 2Py and 3Py, lowered the formation probability of the molecular junctions Au–2Au–Au and Au–3Au–Au through the C(acetylide)–Au(electrode) covalent bonds to 5–10% (via e.g. transmetalation and fusion).35 Nevertheless, in the individual traces, the steps were observed in the 10−2 to 10−3G0 region, and single-molecule conductance of 2Au and 3Au was determined to be 1.0 (±0.3) × 10−2 and 4.2 (±1.2) × 10−3G0, respectively, from the statistical analysis of the linear-scale histograms. The virtually linear relationship between the conductance in the logarithmic scale and the junctions' dimensions suggests the occurrence of the tunneling process for molecular junctions of 1R–3R (R = Py, Au).38,39 Thus, the β values for 1Py–3Py and 1Au–3Au are determined to be 0.03 and 0.07 Å−1, respectively.
When compared with the representative molecular wires with low β values obtained with low bias voltage (<200 mV) (Fig. 6),40 the obtained β value turns out to be significantly smaller than that for the mononuclear polyyne wires Cn (0.25 Å−1) and comparable to or even smaller than those for porphyrin wires Pn (0.04 Å−1)8 and porphyrin tapes PTn (0.06 Å−1).9 Furthermore, the β value for 1R–3R is smaller than those of the related 1,4-diethynylbenzene-bridged wire with Ru(dppe)2 fragments PhRn (0.09–0.16 Å−1, Fig. 7) estimated by conductive probe AFM measurements of the self-assembled monolayer.22,23 Two factors are considered for the smaller β factor for 1R–3R. One is that thienylene linkers were reported to support metal–metal interactions compared to phenylene linkers.41 The other is the terminal anchor groups: PhRn bear electronically weakly coupling thioacetate ester and cyanide groups. Details are still unclear, and the terminal anchor groups were also reported to affect the β values.42
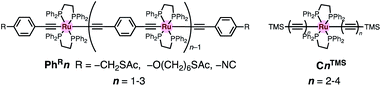 | ||
| Fig. 7 Molecular structures of the related 1,4-diethynylbenzene-bridged wire with the Ru(dppe)2 fragments PhRn and metallapolyynes with trimethylsilyl end groups CnTMS. | ||
The excellent performance of nAu can be ascribed to the two following factors: (1) the small contact resistance of the covalent C(acetylide)–Au electrode bonds and (2) the performance of the bridging linkers. For the former factor, the absolute conductance of the organometallic wires 1Au–3Au is significantly larger than that for the molecules compared herein due to the small contact resistance brought about by the strong coupling between the acetylide anchors and the gold electrodes as discussed previously by Lörtscher, Venkatesan, Berke, et al.43 For the bridging linkers, when compared with the porphyrin wires Pn with the same pyridine anchor groups,8 the conductance of 1Py–3Py is larger by one order of magnitude. Furthermore, the conductance of 1Py–3Py is comparable to that of the wires with the less resistive thiolate and thioether anchor groups44 such as the porphyrin tapes PTn, polymethine wires PMn,11 and oligo(thiophene) wires Tn.6,45 Thus, wires nAu are superior to the related wires in these two aspects.
DFT–NEGF study
According to the approximated Landauer–Büttiker formula, zero bias conductance (G) can be expressed by eqn (1),46,47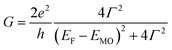 | (1) |
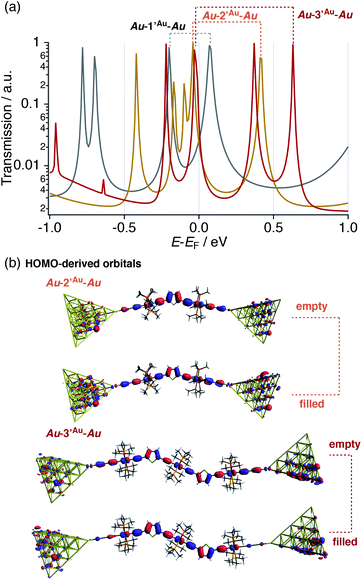
In this respect, DFT–NEGF calculations were carried out in order to gain insights into the highly conductive nature and small β value of the multinuclear molecular junctions Au–nAu–Au.49 The truncated model complexes, where the Ph groups of the dppe ligands were replaced with Me groups for the sake of calculation cost, were used as molecular junction models (denoted as 1′Au–3′Au). Because acetylide anchor groups form stable σ bonds with Au electrodes,50 the on-top σ-attachment to Au35 pyramidal clusters has been adopted as the molecular junction models. Transmission spectra are shown in Fig. 8a. As we reported previously,29 the metallapolyyne junction Au–1Au–Au shows a unique transmission spectrum with the two peaks closely located above and below the Fermi level (EF) of the electrodes (highlighted with the dashed line). This phenomenon is due to the splitting of the HOMO of the 1Au caused upon molecular junction formation as a result of charge transfer interaction between the Ru center and the electrodes through the acetylide anchor groups.51 In a manner similar to the dppe junction Au–1Au–Au, the truncated dmpe analogues Au–n′Au–Au (n = 1–3) also undergo orbital splitting (Fig. 8a) to generate the filled and empty conduction peaks located within 0.5 eV from EF, and these conduction peaks originate from the HOMO and HOMO−1 orbitals of the corresponding molecules n′H (n = 1–3, Fig. 8b).52 The orbital characteristics for the HOMO of n′H and the conduction orbitals of Au–n′Au–Au are almost the same (Fig. S19‡). The empty conduction orbitals are pushed up and away from EF as the number (n) of repeating units increases (Au–n′Au–Au; 0.07 (n = 1) → 0.41 (n = 2) → 0.63 eV (n = 3)), while the filled conduction orbitals get closer to EF (−0.20 → −0.05 → −0.03 eV) (Fig. 8a). In particular, the latter factor predominantly contributes to the large transmission factors of Au–n′Au–Au at EF and, as a result, the theoretically estimated β value becomes small (0.02 Å−1 for 1′Au–3′Au). The pyridine derivatives show similar features (β = 0.01 Å−1 for 1′Py–3′Py, Fig. S23‡).53 These features are in stark contrast to those of the mononuclear series (C2 (= 1Au), C3 and C4).29 In this case, the energies of the transmission peaks (Efilled, Table 1) are rather insensitive to the dimensions of the acetylene linkers, leading to the moderate theoretically estimated β value (0.14 Å−1).
| Complex | In (mV) | K C1 | K C2 | In (eV) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E onset | E 1/2 1 | E 1/2 2 | E 1/2 3 | ΔE1a | ΔE2a | HOMOCVc | HOMODFTd (for terminal H analogues) | E filled | E empty | |||
| a ΔEn = E1/2n+1 − E1/2n. b K Cn = exp(ΔEn(V)·F/RT). c HOMOCV = –(Eonset/V + 5.1) eV. d DFT calculations performed for the terminal H analogues at the B3LYP/LanL2DZ, 6-31G(d) levels of theory. e Conduction orbital energies estimated using the DFT–NEGF method. f Ref. 25. g Calculations were performed for the truncated dmpe models. h Calculations were performed for the dppe models. | ||||||||||||
| 1TMS/C2TMSf | 80 | 150 | −5.18 | −4.49 | −0.20g/−0.23h | 0.07g/0.09 h | ||||||
| 2TMS | −430 | −360 | 10 | 370 | 1.8 × 106 | −4.67 | −3.96 | −0.05g | 0.41g | |||
| 3TMS | −510 | −440 | −200 | 100 | 240 | 300 | 1.2 × 104 | 1.2 × 105 | −4.59 | −3.75 | −0.03g | 0.63g |
| C3TMS | 195 | 270 | −5.30 | −4.59 | −0.22h | 0.09h | ||||||
| C4TMS | 253 | 325 | −5.35 | −4.70 | −0.10h | 0.15h | ||||||
Metal–metal interaction
To gain further insight into the energy shift of the conduction orbitals of the multinuclear systems (nAu, n = 1–3), we carried out electrochemical and DFT studies for the TMS (nTMS) and H analogues (nH), respectively (Fig. 9 and Table 1). While the mononuclear complex 1TMS shows a single redox wave, the di- (2TMS) and tri-nuclear complexes (3TMS), respectively, show successive two and three reversible oxidation waves.54 The large separations (ΔEn = E1/2n − E1/2n−1; 370 mV for the dinuclear complex 2TMS; 240 (ΔE1) and 300 mV (ΔE2) for the trinuclear complex 3TMS) reveal significant Ru–Ru interaction with large comproportionation constants (KC > 104).32,55 This metal–metal interaction makes the HOMO energies higher than that of the mononuclear wire 1TMS (−5.18 eV) by 0.49 eV (2TMS) and 0.61 eV (3TMS). In contrast, the HOMO energy level of the mononuclear system is slightly lowered, as the acetylene linkers are elongated from C2TMS to C3TMS and C4TMS (Fig. 7) by 0.12 and 0.18 eV, respectively.29 Thus, the significant higher-energy shifts of the HOMO level are the key for the energy level alignment of the molecular junction.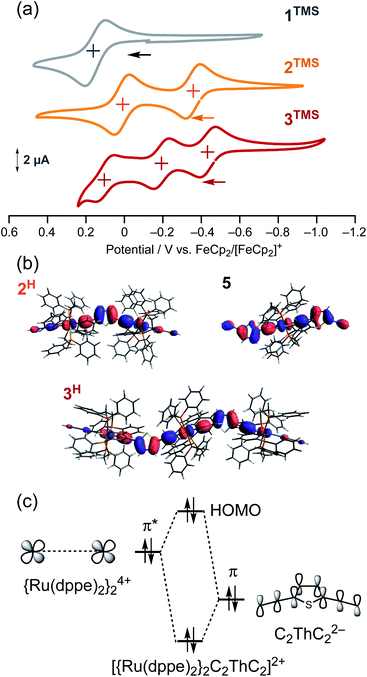 | ||
| Fig. 9 (a) Cyclic voltammograms of 1TMS–3TMS. (b) HOMO orbitals of 2H, 3H and 5. (c) Qualitative orbital interaction diagram of {Ru(dppe)2}24+ and C2ThC22−. | ||
To gain insight into the high-lying HOMO energies for the multinuclear wires, we carried out a DFT study.56 Two factors can be considered for this observation: extension of the π-conjugated systems and/or metal–metal interactions. For the multinuclear complexes 2H and 3H, the HOMOs are delocalized over the conjugated systems (Fig. 9b), leading to higher HOMO energy levels compared to that of 1H (−4.49 eV; ΔE(HOMODFT) = 0.53 eV for 2H and 0.74 eV for 3H) (Table 1). Furthermore, the E(HOMO)DFT level for trans-(H–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Th–C
C–Th–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)2Ru(dppe)25 (−4.39 eV) is comparable to that of 1H and much lower than that of 3H (−3.75 eV). Because the HOMO of 5, a substructure of 3H, is highly delocalized over the (C
C)2Ru(dppe)25 (−4.39 eV) is comparable to that of 1H and much lower than that of 3H (−3.75 eV). Because the HOMO of 5, a substructure of 3H, is highly delocalized over the (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Th–C
C–Th–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)2Ru moiety as also observed for 3H (Fig. 9b), the extension of the π-system and substituent effects on the E(HOMODFT) level for 3H are negligible. The HOMOs of 2H and 3H are composed of the π*-orbitals of the ruthenium fragments and the π-orbitals of the diethynylthienylene bridging linkers, and the anti-bonding orbital interaction between them raises the HOMO energy levels (Fig. 9c).41 Thus, the high-lying HOMOs for 2H and 3H, which are caused by the metal–metal interactions through the diethynylthiophene-diyl linkers push up both of the filled and empty conduction orbitals' energies for the molecular junction, leading to effective energy alignment between the filled conduction orbitals and the Fermi energy.
C)2Ru moiety as also observed for 3H (Fig. 9b), the extension of the π-system and substituent effects on the E(HOMODFT) level for 3H are negligible. The HOMOs of 2H and 3H are composed of the π*-orbitals of the ruthenium fragments and the π-orbitals of the diethynylthienylene bridging linkers, and the anti-bonding orbital interaction between them raises the HOMO energy levels (Fig. 9c).41 Thus, the high-lying HOMOs for 2H and 3H, which are caused by the metal–metal interactions through the diethynylthiophene-diyl linkers push up both of the filled and empty conduction orbitals' energies for the molecular junction, leading to effective energy alignment between the filled conduction orbitals and the Fermi energy.
Conclusions
In summary, we have described the synthesis, and the results of single-molecule conductance measurements, and electrochemical and theoretical study of multinuclear molecular wires and junctions with the (2,5-diethynylthiophene)diyl-Ru(dppe)2 repeating units, Au–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C
C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Ru(dppe)2–{C
C–Ru(dppe)2–{C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Th–C
C–Th–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Ru(dppe)2}n−1–C
C–Ru(dppe)2}n−1–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C
C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Au (n = 1–3). Their high single-molecule conductance with small β factors is shown. The DFT–NEGF study reveals that elongation by insertion of the organometallic repeating units causes a shift of the HOMO conduction peaks towards the electrode's Fermi level. The high HOMO energy levels of the multinuclear systems were ascribed to the Ru–Ru interaction as revealed by the CV and DFT study. Further study to unveil the relationship between the metal–metal interaction and single-molecule conductance is ongoing in our laboratory.
C–Au (n = 1–3). Their high single-molecule conductance with small β factors is shown. The DFT–NEGF study reveals that elongation by insertion of the organometallic repeating units causes a shift of the HOMO conduction peaks towards the electrode's Fermi level. The high HOMO energy levels of the multinuclear systems were ascribed to the Ru–Ru interaction as revealed by the CV and DFT study. Further study to unveil the relationship between the metal–metal interaction and single-molecule conductance is ongoing in our laboratory.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Hiroyasu Sato (Rigaku Corp.) for the help in solving the X-ray crystal structure. This work was supported by JSPS KAKENHI (grant number 18K05139) and a research grant from the JGC-S Scholarship Foundation and Kato Foundation for Promotion of Science. YT acknowledges financial support from a Tokyo Tech Research Award. This work was performed under the Cooperative Research Program of “Network Joint Research Center for Materials and Devices”. The computations were performed using the computer at the Research Center for Computational Science, Okazaki, Japan.References
- C. Joachim, J. K. Gimzewski and A. Aviram, Nature, 2000, 408, 541–548 CrossRef CAS.
- M. S. Hybertsen and L. Venkataraman, Acc. Chem. Res., 2016, 49, 452–460 CrossRef CAS.
- R. Frisenda, D. Stefani and H. S. J. van der Zant, Acc. Chem. Res., 2018, 51, 1359–1367 CrossRef CAS.
- S. Marqués-González and P. J. Low, Aust. J. Chem., 2016, 69, 244–253 CrossRef.
- X. Zhao, C. Huang, M. Gulcur, A. S. Batsanov, M. Baghernejad, W. Hong, M. R. Bryce and T. Wandlowski, Chem. Mater., 2013, 25, 4340–4347 CrossRef CAS.
- S. K. Lee, R. Yamada, S. Tanaka, G. S. Chang, Y. Asai and H. Tada, ACS Nano, 2012, 6, 5078–5082 CrossRef CAS.
- Y. Ie, Y. Okamoto, T. Inoue, S. Tone, T. Seo, Y. Honda, S. Tanaka, S. K. Lee, T. Ohto, R. Yamada, H. Tada and Y. Aso, J. Phys. Chem. Lett., 2019, 10, 3197–3204 CrossRef CAS.
- G. Sedghi, V. M. García-Suárez, L. J. Esdaile, H. L. Anderson, C. J. Lambert, S. Martín, D. Bethell, S. J. Higgins, M. Elliott, N. Bennett, J. E. Macdonald and R. J. Nichols, Nat. Nanotechnol., 2011, 6, 517–523 CrossRef CAS.
- E. Leary, B. Limburg, A. Alanazy, S. Sangtarash, I. Grace, K. Swada, L. J. Esdaile, M. Noori, M. T. González, G. Rubio-Bollinger, H. Sadeghi, A. Hodgson, N. Agraït, S. J. Higgins, C. J. Lambert, H. L. Anderson and R. J. Nichols, J. Am. Chem. Soc., 2018, 140, 12877–12883 CrossRef CAS.
- S. Fujii, S. Marqués-González, J.-Y. Shin, H. Shinokubo, T. Masuda, T. Nishino, N. P. Arasu, H. Vázquez and M. Kiguchi, Nat. Commun., 2017, 8, 15984 CrossRef CAS.
- S. Gunasekaran, D. Hernangomez-Peíez, I. Davydenko, S. Marder, F. Evers and L. Venkataraman, Nano Lett., 2018, 18, 6387–6391 CrossRef CAS.
- W. Xu, E. Leary, S. Hou, S. Sangtarash, M. T. González, G. Rubio-Bollinger, Q. Wu, H. Sadeghi, L. Tejerina, K. E. Christensen, N. Agraït, S. J. Higgins, C. J. Lambert, R. J. Nichols and H. L. Anderson, Angew. Chem., Int. Ed., 2019, 58, 8378–8382 CrossRef CAS.
- M. Kiguchi, T. Takahashi, Y. Takahashi, Y. Yamauchi, T. Murase, M. Fujita, T. Tada and S. Watanabe, Angew. Chem., Int. Ed., 2011, 50, 5708–5711 CrossRef CAS.
- S. T. Schneebeli, M. Kamenetska, Z. Cheng, R. Skouta, R. A. Friesner, L. Venkataraman and R. Breslow, J. Am. Chem. Soc., 2011, 133, 2136–2139 CrossRef CAS.
- M. Carini, M. P. Ruiz, I. Usabiaga, J. A. Fernández, E. J. Cocinero, M. Melle-Franco, I. Diez-Perez and A. Mateo-Alonso, Nat. Commun., 2017, 8, 15195 CrossRef CAS.
- I.-W. P. Chen, M.-D. Fu, W.-H. Tseng, J.-Y. Yu, S.-H. Wu, C.-J. Ku, C.-H. Chen and S.-M. Peng, Angew. Chem., Int. Ed., 2006, 45, 5814–5818 CrossRef CAS.
- M. Kiguchi, J. Inatomi, Y. Takahashi, R. Tanaka, T. Osuga, T. Murase, M. Fujita, T. Tada and S. Watanabe, Angew. Chem., Int. Ed., 2013, 52, 6202–6205 CrossRef CAS.
- Y. Tanaka, M. Kiguchi and M. Akita, Chem.–Eur. J., 2017, 23, 4741–4749 CrossRef CAS.
- D. C. Milan, A. Vezzoli, I. J. Planje and P. J. Low, Dalton Trans., 2018, 47, 14125–14138 RSC.
- X. Yao, X. Sun, F. Lafolet and J.-C. Lacroix, Nano Lett., 2020, 20, 6899–6907 CrossRef CAS.
- N. Tuccitto, V. Ferri, M. Cavazzini, S. Quici, G. Zhavnerko, A. Licciardello and M. A. Rampi, Nature Mat., 2009, 8, 41–46 CrossRef CAS.
- L. Luo, A. Benameur, P. Brignou, S. H. Choi, S. Rigaut and C. D. Frisbie, J. Phys. Chem. C, 2011, 115, 19955–19961 CrossRef CAS.
- B. S. Kim, J. M. Beebe, C. Olivier, S. Rigaut, D. Touchard, J. G. Kushmerick, X.-Y. Zhu and C. D. Frisbie, J. Phys. Chem. C, 2007, 111, 7521–7526 CrossRef CAS.
- K. Terada, H. Nakamura, K. Kanaizuka, M. Haga, Y. Asai and T. Ishida, ACS Nano, 2012, 6, 1988–1999 CrossRef CAS.
- H. Nakamura, T. Ohto, T. Ishida and Y. Asai, J. Am. Chem. Soc., 2013, 135, 16545–16552 CrossRef CAS.
- R. Sakamoto, K.-H. Kuo-Hui, R. Matsuoka, H. Maeda and H. Nishihara, Chem. Soc. Rev., 2015, 44, 7698–7714 RSC.
- F. Schwarz, G. Kastlunger, F. Lissel, H. Riel, K. Venkatesan, H. Berke, R. Stadler and E. Lörtscher, Nano Lett., 2014, 14, 5932–5940 CrossRef CAS.
- The β value was reported to be 0.44 Å−1.
- Y. Tanaka, Y. Kato, T. Tada, S. Fujii, M. Kiguchi and M. Akita, J. Am. Chem. Soc., 2018, 140, 10080–10084 CrossRef CAS.
- Y. Tanaka, K. Ohmura, T. Tada, S. Fujii, M. Kiguchi and M. Akita, Inorg. Chem., 2020, 59, 13254–13261 CrossRef CAS.
- K. Sugimoto, H. Idei, Y. Tanaka and M. Akita, J. Organomet. Chem., 2017, 847, 121–131 CrossRef CAS.
- See the ESI‡ for details.
- D. Touchard, P. Haquette, S. Guesmi, L. Le Pichon, A. Daridor, L. Toupet and P. H. Dixneuf, Organometallics, 1997, 16, 3640–3648 CrossRef CAS.
- Synthesis of 1Py was previously reported. K. Sugimoto, Y. Tanaka, S. Fujii, T. Tada, M. Kiguchi and M. Akita, Chem. Commun., 2016, 52, 5796–5799 RSC.
- D. Millar, L. Venkataraman and L. H. Doerrer, J. Phys. Chem. C, 2007, 111, 17635–17639 CrossRef CAS.
- S. Bock, O. A. Al-Owaedi, S. G. Eaves, D. C. Milan, M. Lemmer, B. W. Skelton, H. M. Osorio, R. J. Nichols, S. J. Higgins, P. Cea, N. J. Long, T. Albrecht, S. Martin, C. J. Lambert and P. J. Low, Chem.–Eur. J., 2017, 23, 2133–2143 CrossRef CAS.
- B. Xu and N. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS.
- T. Hines, I. Diez-Perez, J. Hihath, H. Liu, Z.-S. Wang, J. Zhao, G. Zhou, K. Müllen and N. Tao, J. Am. Chem. Soc., 2010, 132, 11658–11664 CrossRef CAS.
- The single-molecule conductance data for 1Py34 and 1Au29 are taken from the literature. The conditions for the STM-break junction measurements are the same as in this study.
- Depending on the bias voltages and solvents, negative β values were reported. See ref. 9 and 11.
- J.-F. Halet and C. Lapinte, Coord. Chem. Rev., 2013, 257, 1584–1613 CrossRef CAS.
- P. Moreno-García, M. Gulcur, D. Z. Manrique, T. Pope, W. Hong, V. Kaliginedi, C. Huang, A. S. Batsanov, M. R. Bryce, C. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2013, 135, 12228–12240 CrossRef.
- F. Lissel, F. Schwarz, O. Blacque, H. Riel, E. Lortscher, K. Venkatesan and H. Berke, J. Am. Chem. Soc., 2014, 136, 14560–14569 CrossRef CAS.
- W. Hong, D. Z. Manrique, P. Moreno-García, M. Gulcur, A. Mishchenko, C. J. Lambert, M. R. Bryce and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 2292–2304 CrossRef CAS.
- R. Yamada, H. Kumazawa, S. Tanaka and H. Tada, Appl. Phys. Express, 2009, 2, 025002 CrossRef.
- R. Landauer, IBM J. Res. Dev., 1957, 1, 223–231 Search PubMed.
- M. Kiguchi and S. Kaneko, Phys. Chem. Chem. Phys., 2013, 15, 2253–2267 RSC.
- T. Tada and K. Yoshizawa, Phys. Chem. Chem. Phys., 2015, 17, 32099–32110 RSC.
- T. Tada, M. Kondo and K. Yoshizawa, J. Chem. Phys., 2004, 121, 8050 CrossRef CAS.
- W. Hong, H. Li, S.-X. Liu, Y. Fu, J. Li, V. Kaliginedi, S. Decurtins and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 19425–19431 CrossRef CAS.
- The high HOMO energy levels of the organometallic molecular wires are one of the reasons for the orbital splitting behavior. See ref. 30.
- For Au–3′Au–Au, HOMO−1 also undergoes orbital splitting and the filled and empty conduction peaks are located at –0.22 and 0.37 eV, respectively.
- The HOMO conduction peaks shift as follows: –0.72 (Au–1′Py–Au) → –0.48 (Au–2′Py–Au) → –0.42 eV (Au–3′Py–Au) (Fig. S23‡).
- The electrochemical study of pyridine derivatives 2Py and 3Py showed virtually the same ΔE and KC values as those obtained for 2TMS and 3TMS. See the ESI‡ for details.
- Spectroelectrochemical studies revealed the appearance of intense NIR bands upon electrochemical 1e-oxidation of neutral species 2R and 3R (R = Py, TMS), suggestive of strong electronic interaction between the metal centers (Fig. S14–17‡).32 DFT and TD-DFT analyses revealed electronic interaction between the adjacent metal fragments, while those between the terminal metal centers in 3Py and 3TMS turned out to be small (Fig. S18–22‡).
- DFT calculations were performed for 1H–3H at the B3LYP/LanL2DZ (Ru), 6-31G(d) (others) levels of theory.
Footnotes |
| † This article is dedicated to Professor Pierre H. Dixneuf on the occasion of his 80th birthday for his invaluable contribution to the development of organometallic chemistry. |
| ‡ Electronic supplementary information (ESI) available. CCDC 2039830–2039832. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc06613c |
| This journal is © The Royal Society of Chemistry 2021 |