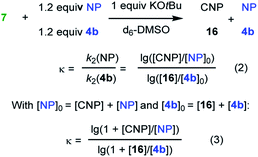Open Access Article
Open Access ArticleElectrophilic reactivities of cyclic enones and α,β-unsaturated lactones†
Robert J.
Mayer
 a,
Patrick W. A.
Allihn
a,
Patrick W. A.
Allihn
 b,
Nathalie
Hampel
a,
Peter
Mayer
a,
Stephan A.
Sieber
b,
Nathalie
Hampel
a,
Peter
Mayer
a,
Stephan A.
Sieber
 b and
Armin R.
Ofial
b and
Armin R.
Ofial
 *a
*a
aDepartment Chemie, Ludwig-Maximilians-Universität München, Butenandtstr. 5-13, 81377 München, Germany. E-mail: ofial@lmu.de
bDepartment Chemie, Technische Universität München, Lichtenbergstraße 4, 85748 Garching, Germany
First published on 9th February 2021
Abstract
The reactivities of cyclic enones and α,β-unsaturated lactones were characterized by following the kinetics of their reactions with colored carbon-centered reference nucleophiles in DMSO at 20 °C. The experimentally determined second-order rate constants k2 were analyzed with the Mayr–Patz equation, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = sN(N + E), to furnish the electrophilicity descriptors E for the Michael acceptors. Cyclic enones and lactones show different reactivity trends than their acyclic analogs. While cyclization reduces the reactivity of enones slightly, α,β-unsaturated lactones are significantly more reactive Michael acceptors than analogously substituted open-chain esters. The observed reactivity trends were rationalized through quantum-chemically calculated Gibbs energy profiles (at the SMD(DMSO)/M06-2X/6-31+G(d,p) level of theory) and distortion interaction analysis for the reactions of the cyclic Michael acceptors with a sulfonium ylide. The electrophilicities of simplified electrophilic fragments reflect the general reactivity pattern of structurally more complex terpene-derived cyclic enones and sesquiterpene lactones, such as parthenolide.
k = sN(N + E), to furnish the electrophilicity descriptors E for the Michael acceptors. Cyclic enones and lactones show different reactivity trends than their acyclic analogs. While cyclization reduces the reactivity of enones slightly, α,β-unsaturated lactones are significantly more reactive Michael acceptors than analogously substituted open-chain esters. The observed reactivity trends were rationalized through quantum-chemically calculated Gibbs energy profiles (at the SMD(DMSO)/M06-2X/6-31+G(d,p) level of theory) and distortion interaction analysis for the reactions of the cyclic Michael acceptors with a sulfonium ylide. The electrophilicities of simplified electrophilic fragments reflect the general reactivity pattern of structurally more complex terpene-derived cyclic enones and sesquiterpene lactones, such as parthenolide.
Introduction
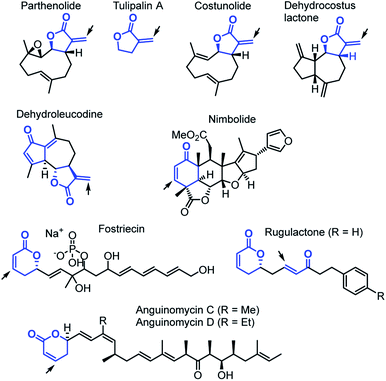
Cyclic carbonyl compounds with α,β-unsaturated positions are important motifs within many natural products (Chart 1).1–3 Previous studies of their cellular reactivities with endogenous proteins revealed intriguing insights into their target profiles.4,5 The ability of these biomolecules to react as electrophiles with nucleophilic sites furnishes them with a multitude of biological functions,6,7e.g. the recently reported inhibition of focal adhesion kinase 1 by parthenolide,5a,b the cytotoxic activity of dehydroleucodine against human leukemia cells,8 or the ability of nimbolide to inhibit metastasis.5c Nature has structurally tailored the reactivity of α,β-unsaturated cyclic carbonyl compounds in different variants. In particular, α-methylene-γ-butyrolactones exhibit superior cellular protein binding compared to lactones with endocyclic π-system, likely associated with an elevated reactivity.4a,9 For the sesquiterpene lactones costunolide and dehydrocostus lactone,10 α,β-unsaturated δ-lactones such as leptomycin, fostriecin or the anguinomycins,11–15 as well as for simple fragments, such as tulipalin A,16 it has been analyzed that their biological activities mainly depend on the ability to alkylate biomacromolecules through Michael additions. Sometimes these Michael additions are coupled with subsequent steps to achieve irreversible covalent enzyme inhibition.15 On the other hand, in modified rugulactones the α,β-unsaturated δ-lactone unit does not contribute to the antibacterial effects and bioactivities of rugulactone were instead assigned to the reactivity of the α,β-unsaturated ketone unit.17Despite these insights into proteome reactivity, a systematic analysis of the individual electrophilicity of the Michael acceptor moieties in different natural products or their truncated analogs is lacking. Knowledge of the reactivity of such biologically occurring electrophilic fragments would facilitate the identification of pharmacophores and is, therefore, of fundamental interest in biochemistry, toxicology, medicinal chemistry, and drug discovery.9,18 Moreover, Michael acceptors with endo- and exocyclic unsaturation are also a structural motif of significant importance for synthetic chemists.3
In life-sciences, rate constants for the reactions of electrophiles with glutathione (GSH) are frequently used for estimating the reactivity and potential toxicity of various electrophilic compounds.19–23 However, the most comprehensive overview of polar organic reactivity is currently given by Mayr and co-workers who used eqn (1) to characterize the reactivities of more than 1200 nucleophiles and over 300 electrophiles in solution phase.24
lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2(20 °C) = sN(N + E) k2(20 °C) = sN(N + E) | (1) |
Eqn (1) is a linear free energy relationship that allows for the semi-quantitative prediction of second-order rate constants k2 for the reactions of electrophiles with nucleophiles from three parameters: the electrophilicity parameter E and the solvent-dependent nucleophilicity parameters N and sN (susceptibility).
Recently, we determined the nucleophilic reactivity parameters N and sN of GSH in aqueous solution, which facilitates to interconnect both approaches. Bioassay-derived GSH kinetics can now be used to roughly estimate Mayr electrophilicity parameters E, and vice versa. In this way, Mayr electrophilicities E for more than 70 acyclic Michael acceptors were estimated based on their previously determined kinetics toward GSH.25 More precise electrophilicities E for a series of structurally simple acyclic Michael acceptors were determined from the kinetics of their reactions with carbon-centered one-bond nucleophiles (reference nucleophiles), that is, mainly with pyridinium and sulfonium ylides.26,27
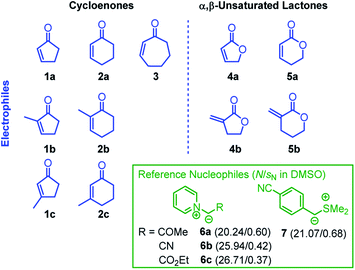
We now set out to determine the Mayr electrophilicity parameters E of cyclic enones 1–3 and α,β-unsaturated lactones 4–5 by studying the kinetics of their reactions with the reference nucleophiles 6–7 (Chart 2). We then tested whether the Mayr E parameters obtained for the electrophilic core structures 1–5 are also representative of the reactivity profile of structurally more complex natural products that bear these fragments in their molecular scaffold. Quantum-chemical calculations were used to rationalize the observed reactivity trends which significantly differ from those for analogous acyclic (open chain) ketones and esters.
Results and discussion
Product studies
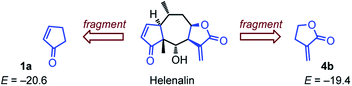
The formal 1,3-dipolar cycloadditions (Huisgen reactions) of simple electron-deficient alkenes with pyridinium ylides, generated from N-alkylated pyridinium salts under basic conditions, are well-known to yield tetrahydroindolizines. Subsequent oxidation (e.g. with air or chloranil) efficiently aromatizes the newly formed heterocycles to afford diversely substituted indolizines.27–31 In contrast, formation of the analogous tricyclic cyclopenta-, cyclohexa-, or cyclohepta-indolizines has rarely been studied. Only Tamura reported the formation of cyclohexaindolizines in low yield (10%) in a vinylic substitution reaction that used the pyridinium ylide 6c (R = CO2Et) and 3-chlorocyclohexanone as educts.32 Direct 1,3-dipolar cycloaddition reactions of pyridinium ylides with cyclic enones or α,β-unsaturated lactones have not been reported to the best of our knowledge.We planned to use the pyridinium ylides 6 as colored reference nucleophiles to follow the kinetics of their reactions with cyclic Michael acceptors by photometric methods. Given the lack of knowledge about the outcome of these reactions, we decided to characterize the products of a subset of the electrophile/nucleophile combinations under the conditions of the kinetic experiments, that is, in DMSO at 20 °C (Scheme 1).
 | ||
| Scheme 1 Products for the reactions of the pyridinium ylides 6 (generated by deprotonation of 6·HY) with cyclic Michael acceptors (yields of isolated products after chromatography, see ESI† for details). Insert: Single-crystal X-ray structure of 8. Thermal ellipsoids drawn at a 50% probability level. | ||
Treatment of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-mixture of the pyridinium salt 6b·HY (HY = HCl, HBr) and sodium carbonate with a DMSO solution of cyclopentenone (1a, 2 equiv.) resulted in a (3+2)-cycloaddition to give a mixture of diastereomeric tetrahydroindolizines. Due to their high sensitivity toward oxidation33 and to facilitate the product purification, we oxidized these initial adducts to the aromatic indolizine 8, which was isolated in 18% yield and characterized by single-crystal X-ray diffraction. We were delighted to find that analogous reactions of 6b with cyclohexenone (2a), cycloheptenone (3) as well as with the lactone 5a gave the corresponding indolizines 9b, 10, and 11, respectively, in significantly higher yields (72–86% of isolated products). Furthermore, cyclohexaindolizines 9a and 9c were isolated in high yields from the reactions of the ester- and keto-stabilized pyridinium ylides 6a and 6c with cyclohexenone (2a).
1-mixture of the pyridinium salt 6b·HY (HY = HCl, HBr) and sodium carbonate with a DMSO solution of cyclopentenone (1a, 2 equiv.) resulted in a (3+2)-cycloaddition to give a mixture of diastereomeric tetrahydroindolizines. Due to their high sensitivity toward oxidation33 and to facilitate the product purification, we oxidized these initial adducts to the aromatic indolizine 8, which was isolated in 18% yield and characterized by single-crystal X-ray diffraction. We were delighted to find that analogous reactions of 6b with cyclohexenone (2a), cycloheptenone (3) as well as with the lactone 5a gave the corresponding indolizines 9b, 10, and 11, respectively, in significantly higher yields (72–86% of isolated products). Furthermore, cyclohexaindolizines 9a and 9c were isolated in high yields from the reactions of the ester- and keto-stabilized pyridinium ylides 6a and 6c with cyclohexenone (2a).
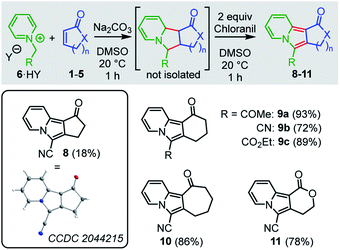
To diversify the types of reference nucleophiles in our kinetic studies, we also investigated the reactions of the cyclic electrophiles with the sulfonium ylide 7. Treatment of a solution of the sulfonium tetrafluoroborate 7·HBF4 and a cyclic Michael acceptor in DMSO with potassium tert-butoxide generated the sulfonium ylide 7 which then underwent cyclopropanation reactions with the electrophiles 1a, 2a, 4a, and 5a (Scheme 2). The cyclopropanes 12–15 were obtained as mixtures of diastereomers. Separation of the diastereomers by column chromatography was not always possible. However, purified diastereomers of 12 and 15 could be crystallized and characterized by single-crystal X-ray crystallography, providing unequivocal evidence for the cyclopropanation reaction.
 | ||
| Scheme 2 Products for the reactions of the sulfonium ylide 7 with the electrophiles 1–5 (yields of isolated products after column chromatography, thermal ellipsoids drawn at 50% probability level, see ESI† for details). [a] 5 equiv., [b] 10 equiv., [c] d.r. determined after extraction, [d] d.r. determined after column chromatography. | ||
The lactones 4b and 5b reacted with the sulfonium ylide 7 at their exo-methylene groups to give diastereomeric mixtures of 16 (46%) and 17 (69%), respectively. Owing to their sufficiently different polarity these diastereomeric mixtures were separable by column chromatography. One diastereomer of 16 and one of 17 were crystallized and analyzed by single-crystal X-ray diffraction (Scheme 2).
As a general trend, the yields of the cyclopropanes 12–17 depended on two factors: (a) the excess and (b) the absolute concentration of the electrophiles. A survey of the reaction conditions showed that highest yields were obtained when the cyclic Michael acceptor was present in excess (up to 10 equiv.) over the pronucleophile 7 and/or at low concentrations (<0.01 M). Experimental protocols with higher concentrations of the Michael acceptors or reduced excess (1.5 equiv.) resulted in complete consumption of the colored ylide 7, too, but the cyclopropanes were only formed as minor products under these conditions. Instead, 7 isomerized in a background reaction to furnish the sulfide 18,34,35 presumably through a Sommelet–Hauser type of rearrangement (Scheme 3).36
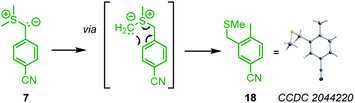 | ||
| Scheme 3 Isomerization of the sulfonium ylide 7 to the benzyl methyl sulfide 18 (thermal ellipsoids drawn at 50% probability level). | ||
The sulfide 18 is the starting material for BAY 85-8501, a candidate for the treatment of inflammatory diseases such as acute lung injury.35 We characterized 18 by single-crystal X-ray diffraction. Solutions with low concentrations of 7 in DMSO isomerized slower (t1/2 = 30 min at [7]0 = 1 × 10−4 M) than solutions with higher concentrations of 7 (t1/2 = 4 min at [7]0 = 0.057 M, monitored by time-resolved 1H NMR spectroscopy). Thus, the isomerization of 7 into 18 partially consumed the nucleophile when 7 was combined with weakly or only moderately reactive electrophiles, whose cyclopropanations proceeded at comparable time scale as the Sommelet–Hauser rearrangement of 7.
Kinetics
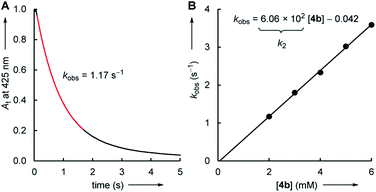
The kinetics of the reactions of the colorless electrophiles 1–5 with the pyridinium (6) and sulfonium (7) ylides were determined by following the decay of the UV-vis absorbance of the colored nucleophiles. Reactions at the seconds to minutes timescale were followed by conventional photometry. Stopped-flow photometric methods were employed for faster reactions in the millisecond regime. DMSO was used as the solvent for all electrophile–nucleophile combinations, which were uniformly studied at 20 °C.Solutions of the ylides 6 and 7 in DMSO were generated by adding stoichiometric amounts of potassium tert-butoxide to the corresponding pyridinium or sulfonium salts. In the next step, these DMSO solutions were mixed with an excess (>10 equiv.) of the electrophiles 1–5. With this ratio of reactants, the concentration of the excess compound can be assumed to remain practically constant during the kinetic measurements, which simplifies the kinetics and makes it possible to determine rate constants kobs under pseudo-first order conditions. In general, the time-dependent change of the nucleophile's absorbance followed a mono-exponential decay. The first-order rate constants kobs were then determined by a least-squares fitting of the mono-exponential decay function At = A0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kobs × t) + C to the experimental absorbances At (Fig. 1A).
exp(−kobs × t) + C to the experimental absorbances At (Fig. 1A).
The correlation of kobs with the concentration of the electrophiles 1–5 revealed a linear relationship, the slope of which corresponds to the second-order rate constant kexp2 (Fig. 1B, Table 1). Isomerization (of 7) and/or decomposition of the colored reference nucleophiles proceed concurrently and impede the kinetic study of slower reactions. Therefore, only the highly reactive nucleophile 6c was available to study the rather unreactive 2- and 3-methylated cyclic enones 1c, 2b, and 2c.
| Electrophiles | Nucleophiles | k exp2 (M−1 s−1) | k eqn (1)2 (M−1 s−1) | k exp2/keqn (1)2 |
|---|---|---|---|---|
| a This work. b Electrophilicity E estimated on the basis of only one rate constant kexp2. | ||||
| 1a, E = −20.6a | 6a | 1.51 ± 0.05 | 6.1 × 10−1 | 2.5 |
| 7 | 1.06 ± 0.05 | 2.1 | 0.51 | |
| 6c | (1.62 ± 0.01) × 102 | 1.8 × 102 | 0.89 | |
| 1b, E = −22.1a | 6a | (3.69 ± 0.19) × 10−2 | 7.7 × 10−2 | 0.48 |
| 7 | 1.05 ± 0.02 | 2.0 × 10−1 | 5.3 | |
| 6c | 7.83 ± 0.85 | 5.1 × 101 | 0.15 | |
| 1c (E = −28.9)a,b | 6c | (1.55 ± 0.18) × 10−1 | — | — |
| 2a, E = −22.1a | 6a | (7.60 ± 0.36) × 10−2 | 7.7 × 10−2 | 0.99 |
| 7 | (5.16 ± 0.12) × 10−1 | 2.0 × 10−1 | 2.6 | |
| 6c | (1.07 ± 0.01) × 101 | 5.1 × 101 | 0.21 | |
| 2b (E = −27.5)a,b | 6c | (5.00 ± 0.49) × 10−1 | — | — |
| 2c (E = −29.6)a,b | 6c | (8.70 ± 1.31) × 10−2 | — | — |
| 3, E = −22.0a | 6a | (8.13 ± 0.49) × 10−2 | 8.8 × 10−2 | 0.92 |
| 7 | (5.31 ± 0.17) × 10−1 | 2.3 × 10−1 | 2.3 | |
| 6c | (1.19 ± 0.05) × 101 | 5.5 × 101 | 0.22 | |
| 4a, E = −20.7a | 6a | (4.14 ± 0.10) × 10−1 | 5.3 × 10−1 | 0.78 |
| 7 | 2.89 ± 0.16 | 1.8 | 1.6 | |
| 6c | (8.09 ± 0.02) × 101 | 1.7 × 102 | 0.48 | |
| 4b, E = −19.4a | 6a | 5.47 ± 0.27 | 3.2 | 1.7 |
| 7 | 8.39 ± 0.38 | 1.4 × 101 | 0.61 | |
| 6c | (6.06 ± 0.12) × 102 | 5.1 × 102 | 1.2 | |
| 5a, E = −21.8a | 6a | (9.68 ± 0.27) × 10−2 | 1.2 × 10−1 | 0.84 |
| 7 | (4.12 ± 0.08) × 10−1 | 3.2 × 10−1 | 1.3 | |
| 5b, E = −19.5a | 6a | 6.62 ± 0.23 | 2.8 | 2.4 |
| 7 | 5.10 ± 0.04 | 1.2 × 101 | 0.44 | |
| 6c | (6.01 ± 0.14) × 102 | 4.7 × 102 | 1.3 | |
Based on the set of experimental second-order rate constants kexp2, we calculated the electrophilicity parameters E for compounds 1–5 by applying eqn (1) and the reported Mayr nucleophilicity parameters N and sN of the reference nucleophiles.24d,30,37
Electrophilicity of natural products
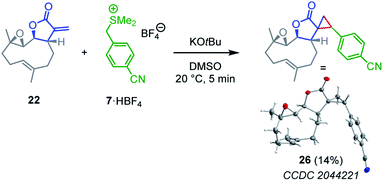 | ||
| Scheme 4 Cyclopropanation of parthenolide (22) by the sulfonium ylide 7 (yield of isolated product after chromatographic workup, thermal ellipsoids drawn at 50% probability level, see ESI† for details). | ||
| Electrophile (NP) | Nucleophile | k exp2 , (M−1 s−1) | κ | Mayr E |
|---|---|---|---|---|
a Kinetics were determined photometrically by following the decay of the absorbance of the nucleophile 6c.
b Determined by competition experiments with 4b as competition partner.
c
E = E(4b) + (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κ)/sN(7). κ)/sN(7).
|
||||
| 19 | 6c | (5.5 ± 0.1) × 10−1 | −27.4 | |
| 20 | 6c | (8.3 ± 1.2) × 10−2 | −29.6 | |
| 21 | 6c | (2.8 ± 0.1) × 10−2 | −30.9 | |
| 22 | 6c | (7.3 ± 0.3) × 102 | −19.0 | |
| 7 | 4.4 | (−18.5)c, av −18.8 | ||
| 23 | 7 | 1.3 | (−19.2)c | |
| 24 | 7 | 4.6 | (−18.4)c | |
| 25 | 7 | 1.9 | (−19.0)c | |
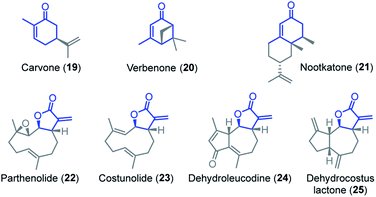
Competition experiments were performed to estimate the Mayr electrophilicities E of the exo-methylene lactones 22–25 (= natural products, NP). The lactone 4b (E = −19.4) was chosen as the competition partner because it contains the entire core structure of the electrophilic moiety in the natural products. As outlined in Scheme 5,38 the experiments were performed such that the reference nucleophile 7 (generated in solution from 7·HBF4 with KOtBu) was completely consumed in reactions with an excess of the two competing electrophiles NP and 4b. Consequently, the product mixture contained the remaining electrophiles NP and 4b as well as both products, the respective cyclopropanated natural product CNP (from NP + 7) and 16 (from 4b + 7). The reaction mixture was analyzed by 1H NMR spectroscopy to determine the competition constant κ according to eqn (3). The competition constants κ were then used to estimate the E parameters for the electrophilic NPs 22–25 (Table 2).
The reactivity of parthenolide (22) was characterized by both approaches. An electrophilicity E = −19.0 was determined from the direct kinetic measurements with 6c and E = −18.5 resulted from the competition experiment (vs.4b) with the nucleophile 7. Thus, the E values determined by the two different experimental methods agreed within one order of magnitude, and an averaged E = −18.8 is a realistic semiquantitative estimate for the electrophilicity of parthenolide (22).
Substituents remote from the electrophilic π-system have only a minor impact on the observed reactivity. Carvone (19) is almost as reactive as 2-methylcyclohexenone (2b) and verbenone (20) has a similar reactivity as 3-methylcyclohexenone (2c). Only a significant increase of the steric hindrance in the vicinity to the reaction center, for example in nootkatone (21), causes another slight decrease in electrophilicity in comparison with the model fragment 2c.
Application of electrophilicity parameters in synthesis
The levels of electrophilicity derived from the ranking of 1–5 in the Mayr electrophilicity scale (Fig. 2) facilitate assessing the reaction times and experimental conditions required for successful reactions with C-nucleophiles (see comment box in Fig. 2).24d Usually, reactions with predicted second-order rate constants of k2 < 10−5 M−1 s−1 (at 20 °C) will need catalytic activation, heating or significantly extended reaction times to furnish products. In the subsequent summary, the reaction conditions of reported procedures are compared with predictions based on the Mayr–Patz eqn (1).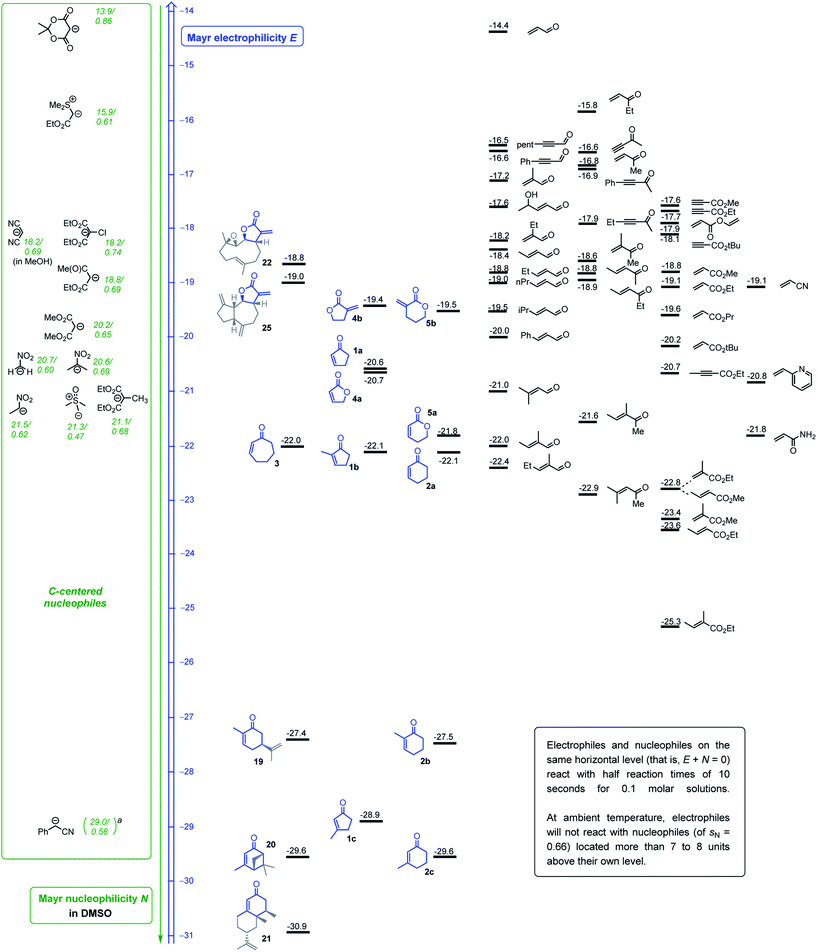 | ||
| Fig. 2 Michael acceptors studied in this work (blue) or previously (ref. 25 and 27), ranked according to their electrophilicity parameters E and combined with a reactivity scale for C-centered nucleophiles (ordered by their N parameters, reactivity given as N/sN). aEstimated N/sN based on reactivity data for the carbanion derived from 2-phenylpropionitrile (ref. 24d). | ||
In accord with the determined electrophilicity, tulipalin A (4b, α-methylene-γ-butyrolactone, E = −19.4) was reported to undergo high yielding DBU-catalyzed Michael reactions with the nitromethane- (N/sN = 20.7/0.60 in DMSO) (−25 to 20 °C, 16 h)39 and 2-nitropropane-derived carbanions (N/sN = 20.6/0.69 in DMSO) (20 °C, 48 h).40 The Michael adduct from the reaction of 4b with the deprotonated diethyl 2-chloromalonate (N/sN = 18.2/0.74 in DMSO) (in THF, r.t., 6 h, 85% yield) was accompanied by traces of the corresponding 4-oxo-5-oxaspiro[2,4]heptane, generated via a cyclopropanation reaction. This sequence of nucleophilic attack at 4b with subsequent ring closure was exclusively observed when diethyl 2-bromomalonate was used as the pronucleophile in the analogous reaction with 4b (in THF, r.t., 10 h, 75% yield).41 Furthermore, the piperidine-catalyzed Michael addition of malononitrile (N/sN = 18.2/0.69 in MeOH) at 4b was reported to be facile at ambient temperature in ethanol. The reaction did not stop at the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stage and furnished the two-fold alkylated malononitrile (piperidine cat, EtOH, 2–3 min, product precipitates, 75% yield).42 The carbon–carbon bond-formation between 4b and the weakly nucleophilic Meldrum's acid-derived enolate ion (N/sN = 13.9/0.86 in DMSO) is predicted by eqn (1) to be very slow at 20 °C (keqn (1)2 = 4 × 10−7 M−1 s−1), and effective product formation required phase transfer catalysis and elevated reaction temperatures (TEBA–Cl in MeCN, 50 °C, 10 h, 64% yield).43 Reactions of dehydrocostus lactone (25, E = −19.0) with the anion of nitromethane (N/sN = 20.7/0.60 in DMSO, 90% yield) were carried out under the same experimental conditions as applied for 4b, the core electrophilic fragment of 25.39
1 stage and furnished the two-fold alkylated malononitrile (piperidine cat, EtOH, 2–3 min, product precipitates, 75% yield).42 The carbon–carbon bond-formation between 4b and the weakly nucleophilic Meldrum's acid-derived enolate ion (N/sN = 13.9/0.86 in DMSO) is predicted by eqn (1) to be very slow at 20 °C (keqn (1)2 = 4 × 10−7 M−1 s−1), and effective product formation required phase transfer catalysis and elevated reaction temperatures (TEBA–Cl in MeCN, 50 °C, 10 h, 64% yield).43 Reactions of dehydrocostus lactone (25, E = −19.0) with the anion of nitromethane (N/sN = 20.7/0.60 in DMSO, 90% yield) were carried out under the same experimental conditions as applied for 4b, the core electrophilic fragment of 25.39
Given the almost identical electrophilic reactivities, it is unsurprising that reported Michael additions or cyclopropanation reactions of α-methylene-pyranone (5b, E = −19.5) cover the same spectrum of carbon-nucleophiles as for 4b. Carbanions generated by deprotonation of diethyl 2-chloro- and 2-bromomalonate (for 2-Br-malonate: in THF, r.t., 10 h, 85% yield)41 and 2-nitropropane (DBU-catalyzed in MeCN, r.t., 4.5 h, 81% yield)44 were successfully used to functionalize 5b.
Michael additions of nitroethane to cyclopentenone (1a, E = −20.6) and cyclohexenone (2a, E = −22.1) under basic conditions were reported.45 Enantioselective additions of the anion generated by deprotonation of dimethyl malonate (N/sN = 20.2/0.65 in DMSO) to 1a were carried out in the presence of a bifunctional amine-thiourea catalysts (toluene, 50 °C, 20 h, 84% yield).46 Alkylations of the cyclic enones 1a, 2a, and 3 (E = −22.0) at their β-positions were also reported when dimethyl malonate was deprotonated by potassium tert-butoxide (in THF, r.t., 92–95% yield)47a or when 3 reacted with the slightly less reactive ethyl acetoacetate-derived carbanion (in ethanol, 25 °C, 21 h, 52% yield).47b Furthermore, the cyclic enones 1a and 2a were used as substrates for cyclopropanation reactions with the sulfonium ylide generated from trimethylsulfoxonium iodide (N/sN = 21.3/0.47 in DMSO).48 Elongated reaction times were needed (DBU, CHCl3, r.t., overnight, 82% yield), however, when a bicyclic framework was constructed from cyclopentenone 1a with the less nucleophilic sulfonium ylide derived from ethyl (dimethylsulfonium)acetate bromide (N/sN = 15.9/0.61 in DMSO).49
With the same sulfonium ylide as the nucleophile, the butenolide 4a (E = −20.7) was reported to produce only a poor yield (22%) of the attempted cyclopropanation product (Cs2CO3, DMF, r.t., reaction time not given).50 Conjugate additions of silyl ketene acetals (N/sN = 9.0/0.98 in CH2Cl2 for Me2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(OMe)OSiMe3) to 4a and 5,6-dihydro-2H-pyran-2-one 5a (E = −21.8) required activation e.g. by Lewis acid catalysts to be productive.51
C(OMe)OSiMe3) to 4a and 5,6-dihydro-2H-pyran-2-one 5a (E = −21.8) required activation e.g. by Lewis acid catalysts to be productive.51
The highly reactive phenyl lithium reacted with 2-methyl cyclohexenone (2b) through 1,2-addition at the carbon atom of the carbonyl group.52 The electron-poor olefin 2b (E = −27.5) underwent conjugate additions, however, with the anion of dimethyl malonate (N/sN = 18.2/0.64 in MeOH) in methanol or ethanol after initial heating and long overall reaction times (MeOH, 16 h (ref. 53) and EtOH, 60 °C for 5 h + 20 °C, 12 h).54 The Michael addition of nitroethane (N/sN = 21.5/0.62 in DMSO) to 2b was accomplished by deprotonation of the pronucleophile with N,N,N′,N′-tetramethylguanidine and stirring the acetonitrile solution for 3 days at ambient temperature (62% yield).45 Analogous reactions of deprotonated nitroethane with the even less electrophilic 3-methylcycloalkenones 1c (E = −28.9) and 2c (E = −29.6) were carried out under phase transfer catalysis to avoid too long reaction times (K2CO3/TEBA–Cl in benzene, r.t. for 4 days, 51% yield from 1c).45
Accordingly, 2c (E = −29.6) requires a reaction time of 9 days for the Michael addition of the diethyl malonate-derived anion (N/sN = 18.2/0.64 in MeOH) in ethanol at ambient temperature (74–76% yield).55a In an alternative procedure, the diethyl 2-methylmalonate-derived carbanion (N/sN = 21.1/0.68 in DMSO) added to 2c under 15 kbar pressure (DBN, MeCN, 45 °C, 36 h) in a yield of 50%.55b
The reaction of 2c with the highly nucleophilic lithiated phenylacetonitrile (N/sN = 29.0/0.58 in DMSO, estimated based on data for 2-phenylpropionitrile)24d delivers within a few minutes the allyl alcohols via kinetically controlled 1,2-addition (−90 °C in THF). The 1,2-addition is reversible, however, and extended reaction times or slightly higher temperatures furnish the corresponding ketone via the thermodynamically favored 1,4-attack (THF, −60 °C, 120 min, 95%).56
This survey of reported reactions of C-nucleophiles with the cyclic Michael acceptors characterized in this work shows, that the determined Mayr electrophilicities E for the electrophiles 1–5 and the dehydrocostus lactone (25) are well in accord with practical experience in organic synthesis.
Quantum chemical calculations
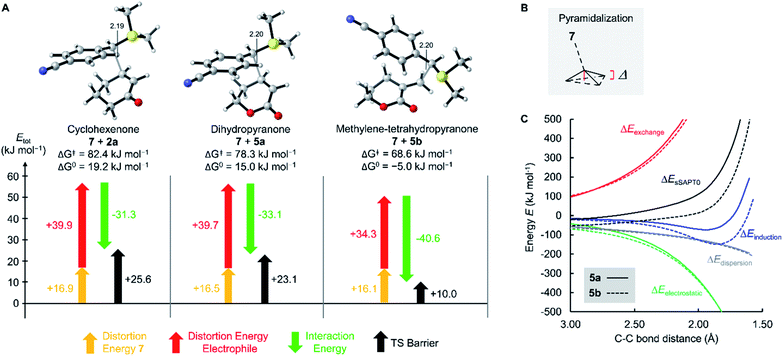
As depicted in Fig. 4 for the reaction of 7 with cyclopentenone 1a, zwitterionic intermediates IM are generated in the first step of the reaction mechanism (viaTS1). The newly formed C–C bond connects two stereocenters, and the reaction can proceed through a cis- and a trans-attack. As displayed in Table 3, the computational results indicate that the trans-attack is slightly favored over the cis-attack for the cyclic Michael acceptors, except for the 2- and 3-methyl substituted electrophiles 1b, 2b and 2c. In general, however, the computed differences between the cis- and the trans-pathways are small, in accord with the experimental observation that mixtures of diastereomeric products were isolated in moderate yields (Scheme 2). Hence, we refrained from interpreting the stereoselectivity of the cyclopropanation reactions and used the most favorable pathway for our subsequent analyses (if not stated otherwise).
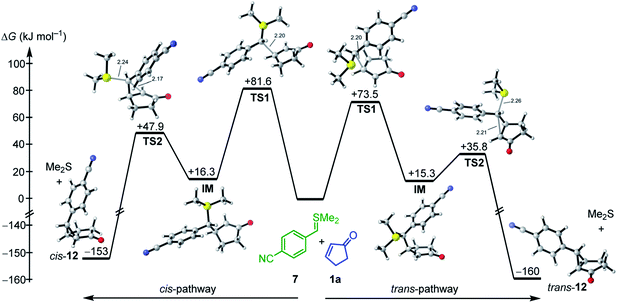 | ||
| Fig. 4 Gibbs energy profile for the reaction of 7 with cyclopentenone (1a) at the SMD(DMSO)/M06-2X/6-31+G(d,p) level of theory (see ESI, Fig. S1,† for a distortion/interaction analysis). | ||
| Electrophiles | Mayr E | k 2 (M−1 s−1) | ΔG‡expb | Trans-pathway | Cis-pathway | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔG‡(TS1)c | ΔG°(IM) | ΔG‡(TS2) | ΔG° | ΔG‡(TS1)c | ΔG°(IM) | ΔG‡(TS2) | ΔG° | ||||
| a k 2 calculated by using eqn (1), the nucleophilicity parameters N and sN of 7 and the electrophilicity parameters E from Table 1. b Calculated by applying k2 in the Eyring equation. c Entries for ΔG‡(TS1) printed in bold indicate the favored transition state (trans vs. cis) used for the correlations in Fig. 5. | |||||||||||
| 1a | −20.6 | 1.1 | 71.5 | 73.5 | 15.3 | 35.8 | −160.0 | 81.6 | 16.3 | 47.9 | −152.7 |
| 1b | −22.1 | 1.1 | 71.6 | 83.7 | 28.8 | 51.1 | −150.9 | 82.1 | 34.9 | 61.2 | −144.3 |
| 1c | (−28.9) | 4.7 × 10−6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
101.7 | 101.1 | 46.7 | 66.8 | −140.5 | 101.5 | 41.9 | 70.7 | −137.7 |
| 2a | −22.1 | 0.52 | 73.4 | 82.4 | 19.2 | 42.9 | −161.4 | 82.9 | 18.8 | 62.2 | −145.0 |
| 2b | (−27.5) | 4.1 × 10−5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
96.4 | 92.4 | 42.9 | 54.8 | −151.3 | 88.5 | 39.4 | 74.6 | −139.7 |
| 2c | (−29.6) | 1.6 × 10−6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
104.3 | 103.4 | 46.3 | 70.0 | −143.9 | 102.1 | 48.7 | 83.1 | −133.1 |
| 3 | −22.0 | 0.53 | 73.3 | 80.7 | 19.0 | 45.5 | −172.8 | 85.8 | 12.4 | 56.7 | −151.7 |
| 4a | −20.7 | 2.9 | 69.2 | 72.8 | 20.3 | 40.1 | −159.5 | 79.9 | 17.7 | 56.8 | −156.9 |
| 4b | −19.4 | 8.4 | 66.6 | 73.8 | −1.0 | 24.8 | −179.7 | Ident. | Ident. | 25.8 | −179.3 |
| 5a | −21.8 | 0.41 | 73.9 | 78.3 | 15.0 | 44.3 | −165.6 | 79.5 | 17.6 | 57.2 | −153.3 |
| 5b | −19.5 | 5.1 | 67.8 | 68.6 | −5.0 | 15.4 | −176.0 | Ident. | Ident. | 24.0 | −181.9 |
In the final step, an intramolecular SN2 reaction eliminates dimethyl sulfide from IMviaTS2 to yield the highly exergonic products, namely, dimethyl sulfide and cyclopropanes with cis- or trans-configuration. For all entries in Table 3, the relative Gibbs activation energies for TS1 and TS2 indicate that the addition (viaTS1) is the rate-determining step in the reactions of 7 with 1a.
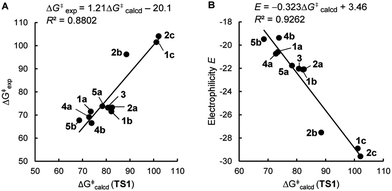
As shown in Table 3 and graphically in Fig. 5A, the quantum-chemically calculated activation barriers ΔG‡(TS1) agree reasonably well (±11 kJ mol−1; mean deviation: ±3.3 kJ mol−1) with the experimental ΔG‡ determined either by experiment (kexp2) or by utilizing eqn (1) (keqn (1)2). Accordingly, there is also a reasonable correlation of ΔG‡(TS1) with the electrophilicity parameters E from Table 1 (Fig. 5B).
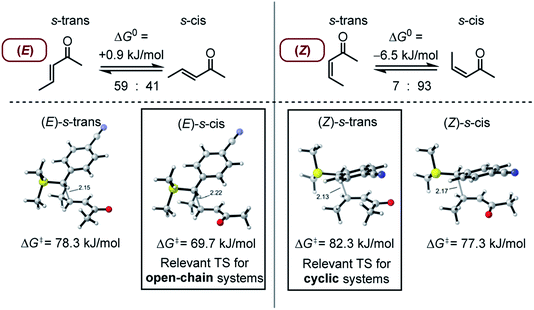
As discussed by Bienvenüe on the basis of UV and IR spectroscopic data, (E)- and (Z)-enones exist in both the s-trans and s-cis form owing to the hindered rotation around the central carbon–carbon σ-bond (Fig. 6, top).58 Experimental data58 as well as computations (this work) agree that for (E)-pentenone both s-cis and s-trans conformers are of comparable energy. For (Z)-pentenone, however, the calculations indicate a significant preference for the s-cis form (cis/trans = 93![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7). We then computed Gibbs energies for the transition states of the addition of 7 at both (E)- and (Z)-pentenone. We found that the s-cis conformers of (E)- and (Z)-pentenone both react with 7via lower energy barriers than the respective s-trans conformers. As shown in Fig. 6 (bottom, left), the transition state energy for the s-cis-(E)-pentenone is 8.6 kJ mol−1 lower than that for the s-trans-(E)-conformer. The difference between the transition states for s-trans-(Z)- and s-cis-(Z)-pentenone amounts to 5.0 kJ mol−1 (Fig. 6, bottom, right). When the most favored transition states for (E)- and (Z)-pentenone are compared, the (E)-isomer of pentenone can be expected to be by approximately one order of magnitude more reactive than the (Z)-configured isomer (ΔΔG‡ = 7.6 kJ mol−1).
7). We then computed Gibbs energies for the transition states of the addition of 7 at both (E)- and (Z)-pentenone. We found that the s-cis conformers of (E)- and (Z)-pentenone both react with 7via lower energy barriers than the respective s-trans conformers. As shown in Fig. 6 (bottom, left), the transition state energy for the s-cis-(E)-pentenone is 8.6 kJ mol−1 lower than that for the s-trans-(E)-conformer. The difference between the transition states for s-trans-(Z)- and s-cis-(Z)-pentenone amounts to 5.0 kJ mol−1 (Fig. 6, bottom, right). When the most favored transition states for (E)- and (Z)-pentenone are compared, the (E)-isomer of pentenone can be expected to be by approximately one order of magnitude more reactive than the (Z)-configured isomer (ΔΔG‡ = 7.6 kJ mol−1).
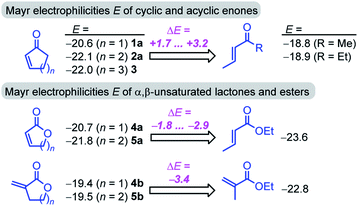
Furthermore, the calculations suggest that the experimentally characterized (E)-pentenone reacts via the s-cis transition state (ΔG‡ = 69.7 kJ mol−1) with nucleophiles (such as 7). Conformationally locked cyclic species, such as 1a or 2a, adopt transition states similar to the unfavorable s-trans pathway for (Z)-pentenone (ΔG‡ = 82.3 kJ mol−1). Thus, we can roughly estimate that cyclic enones are at minimum by two orders of magnitude less reactive than analogously substituted α,β-unsaturated open-chain ketones. The Mayr E values for (E)-pentenone (E = −18.8), cyclopentenone (1a, E = −20.6), cyclohexenone (2a, E = −22.1), and cycloheptenone (3, E = −22.0) are in acceptable accord with this naïve analysis.
In line with the relative reactivity ranking in our work, lactones are well-known to undergo significantly faster alkaline hydrolysis than acyclic esters. This finding was explained by unfavorable orbital interactions in the transition state59 or through differences in the dipole moments leading to ground state destabilization of (Z)-configured ester units.60 More recently, stereoelectronic effects were suggested to explain the higher reactivity of unsaturated lactones.61
For acyclic esters, the s-(Z) conformation is generally preferred, in which the n → σ* interaction donates electron density from the oxygen lone pair into the antiperiplanar antibonding 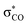 orbital (Fig. 7). This negative hyperconjugation reduces the electron-deficiency of the π-system and, in consequence, electrophilicity. In contrast, the locked s-(E) conformation in lactones impedes such a transfer of electron density and gives rise to an unattenuated electrophilic reactivity of the conjugated π-system (Fig. 7).61
orbital (Fig. 7). This negative hyperconjugation reduces the electron-deficiency of the π-system and, in consequence, electrophilicity. In contrast, the locked s-(E) conformation in lactones impedes such a transfer of electron density and gives rise to an unattenuated electrophilic reactivity of the conjugated π-system (Fig. 7).61
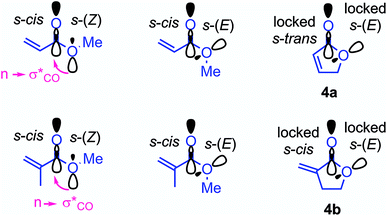 | ||
| Fig. 7 Conformational dependency of the negative hyperconjugation in methyl (meth)acrylates and γ-butyrolactones. | ||
The oxygen atom of the alkoxy group can affect the reactivity of the π-system only through a minor inductive effect. In line with this interpretation, the quantum-chemically calculated transition state structures for the addition of 7 at the ketone 2a and the lactone 5a are highly similar in geometry and energetics (Table 3, Fig. 8) in agreement with the almost identical experimentally determined second-order rate constants kexp2 for both reactions (Table 1).
The unsaturated lactones 4b and 5b bearing an exo-methylene group are more electrophilic than the lactones 4a and 5a with endocyclic unsaturation. The higher reactivity can be attributed to the favorable interplay of two effects. First, the s-trans geometry is locked in lactones 4b and 5b in both the reactants and the transition states. Additionally, we assumed that the absence of substituents at the site of nucleophilic attack introduces less steric constraints in 4b/5b than in 4a/5a.
To assess this hypothesis, a distortion interaction analysis (DIA)62 was performed, which compared the transition states of the first step in the reactions of the S-ylide 7 with 2a, 5a, and 5b, respectively (Fig. 8A). While the distortion energy of ylide 7 is identical in the reactions with 2a, 5a and 5b, the distortion energy of the electrophile is significantly lower for 5b than for 2a or 5a. It can be expected, that variable demand for geometrical changes at the electrophiles' reactive carbon atom upon C–C bond formation is key for the observed distortion energy difference in the comparison of 5bvs.5a. We used the distance of the attacked C-atom of the electrophile from the plane defined by the three surrounding atoms in the transition state, as depicted in Fig. 8B, to describe the degree of pyramidalization Δ in the transition state. In line with Hine's principle of least nuclear motion (PLNM), which predicts ‘that those elementary reactions will be favored that involve the least change in atomic position’,63 we observed a higher requirement for pyramidalization in the transition state of the reaction of 7 with 5a (Δ = 0.227 Å, distortion energy: +39.7 kJ mol−1) than in the analogous transition state for the faster reaction of 7 with 5b (Δ = 0.174 Å, distortion energy: +34.3 kJ mol−1).
Let's now analyze the higher interaction energy in the reaction of 7 with 5b (−40.6 kJ mol−1) than in the reaction of 7 with 5a (−33.1 kJ mol−1). It has previously been shown, that interaction energies can be further decomposed by energy decomposition analysis (EDA).64 In this work, we applied symmetry-adapted perturbation theory (SAPT) at the sSAPT0/jun-cc-pVDZ level of theory, which decomposes an interaction into its electrostatic, exchange, induction, and dispersion components.64 The SAPT analysis was performed in gas-phase with an entirely different theoretical method and, therefore, absolute numbers of the interaction energies differ from the results of our DFT method. Nevertheless, we expected the relative trends to hold. As shown in Fig. 8C, the interaction energy (ΔEsSAPT0) for 5b is generally more negative than for 5a. Depending on the extent of bond formation, this is due to different origins. (1) During the approach to the transition state (located at 2.20 Å), it is the stronger electrostatic interaction that favors 5b over 5a. (2) At the transition state and in the further course of the reaction, however, the induction component becomes the decisive factor. In the transition state, the LUMO energy of the distorted 5b is lower (εLUMO = −0.03527 Hartree) than that of the distorted 5a (εLUMO = −0.03309 Hartree) while the HOMO energies of 7 are essentially identical (with 5b: εHOMO = −0.21875 Hartree; with 5a: εHOMO = −0.21867 Hartree). The smaller energetic gap for 7 + 5b (4.99 eV) indicates a more favorable HOMO–LUMO interaction for the couple 7 + 5b than for the combination 7 + 5a (5.05 eV), in accord with the relative ΔEinduction for 5b and 5a in the SAPT analysis.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond drastically lowers electrophilicity of cyclic enones. A methyl group in the α-position reduces the electrophilicity E of cycloenones by 2 to 6 units (cf.Fig. 2). For substituents placed in the β-position this effect is even more pronounced: the reactivity of β-methyl cycloenones 1c and 2c is reduced by approximately 8 units on the Mayr E scale if compared to the unsubstituted analogs 1a and 2a, respectively. The retarding effect of α- and β-alkyl substituents at the cyclic enones may be caused by steric constraints and/or the electron donating ability of the alkyl group.
C double bond drastically lowers electrophilicity of cyclic enones. A methyl group in the α-position reduces the electrophilicity E of cycloenones by 2 to 6 units (cf.Fig. 2). For substituents placed in the β-position this effect is even more pronounced: the reactivity of β-methyl cycloenones 1c and 2c is reduced by approximately 8 units on the Mayr E scale if compared to the unsubstituted analogs 1a and 2a, respectively. The retarding effect of α- and β-alkyl substituents at the cyclic enones may be caused by steric constraints and/or the electron donating ability of the alkyl group.
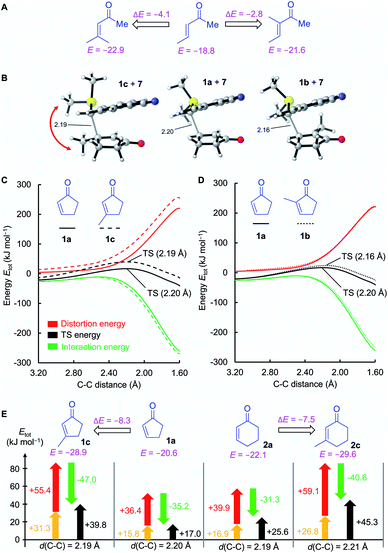 | ||
| Fig. 9 (A) Reactivity trends for open-chain enones. (B) Structures of the trans-transition states for the reaction of 7 with the cyclopentenones 1a, 1b, and 1c (the shown trans-TS for 1b is by 1.6 kJ mol−1 higher in energy than the preferred cis-TS). (C) Distortion interaction analysis (SMD(DMSO)/M06-2X/6-31+G(d,p)) on the pathways of the reactions of 7 with 1a and 1c. (D) Distortion interaction analysis (SMD(DMSO)/M06-2X/6-31+G(d,p)) on the pathways of the reactions of 7 with 1a and 1b. (E) DIA of the transition states of the reaction of 7 with 1c, 1a, 2a and 2c. For the color legend of the DIA, see Fig. 8 (purple: Mayr electrophilicity descriptors E, black: electronic energies Etot). | ||
Again, DIA was used to quantify the effects. To keep the transition-state conformations comparable (Fig. 9B), the trans-TS for the reaction 1b + 7 was evaluated in the DIA instead of the (by 1.6 kJ mol−1) preferred cis-TS. As the C–C bond length in the transition state of the reaction 1a + 7 differs from that of the reaction 1b + 7, the entire pathways of the reactions of 7 with 1a, 1b, and 1c, respectively, were analyzed. The positions of the distortion and interaction energy curves of 1c (Fig. 9C) and 1b (Fig. 9D) relative to those of 1a reveal the reasons responsible for the reduced reactivity in both cases. Let us first discuss the effect of 3-substitution (Fig. 9C): the distortion energy for 1c is significantly more positive than that for 1a while the interaction energy is slightly more negative for 1c than for 1a.
As the C–C bond lengths in the transition states are similar for the reactions of 7 with the 3-substituted cycloenones and their unsubstituted analogs, these observations can also be assessed in a DIA of the respective transition state geometries of 1a and 1c (and analogously for 2a and 2c). As shown in Fig. 9E, the significant decrease of reactivity of β-substituted enones is mostly due to an increase of the distortion energy in both the enone fragments and the ylide 7. As previously discussed for 5a and 5b, pyramidalization Δ and Hine's PLNM can be utilized to rationalize the higher distortion energies of the 3-methyl substituted cycloenones. The reaction of 1a with 7 requires a minor extent of pyramidalization (Δ = 0.222 Å) than for the much less electrophilic 1c (Δ = 0.303 Å).65 Moreover, the higher distortion energy of 7 in the reaction with 1c than in that with 1a can be rationalized by comparing the structures of the transition states (Fig. 9B). Different from the transition states for the reactions of 7 with 1a or 1b, the SMe2 group of 7 is rotated in the transition state of the reaction with 1c to avoid a clash with the methyl group of the electrophile.
Also 2-substituted cyclic enones were found to be weaker electrophiles than the unsubstituted analogs, though, for a different reason. The distortion energy curves for 1a/1b (Fig. 9D) are highly similar or, for 2a/2b (not depicted) even indicate a lower distortion component for 2b. Hence, the nucleophilic β-attack is not sterically hindered by the presence of an α-methyl group. However, the reaction path for 1b suffers from a slightly less negative interaction energy than for the analogous reactions of 7 with 1a.66 Analysis of the involved HOMO/LUMO interactions of the fragments in the transition state resulted in a slightly stronger orbital interaction in the reaction of 7 with 1a (5.14 eV) than in the reaction of 7 with 1b (5.19 eV). Moreover, Hirshfeld atomic charge analysis of the fragments showed that in the transition state the reactive center of 1b (+0.0391) is less positively charged than that of 1a (+0.0472), presumably due to the electron-donating effect of the methyl group in 1b (ESI, Fig. S3†).
Rate constants toward glutathione (GSH)
Helenalin is a sesquiterpene lactone isolated, e.g., from Arnica montana, which embodies two different electrophilic units.67 GSH was reported to attack faster, yet reversible,67–69 at the cyclopentenone moiety of helenalin than at the α-methylene butyrolactone part.68 This kinetic preference differs from the ordering of electrophilicities derived from our measurements, which predict higher reactivity for the unsaturated lactone from E = −19.4 for 4b and E = −20.6 for 1a (Fig. 10).We, therefore, set out to evaluate whether the electrophilicity parameters E for the cyclic Michael acceptors, which we determined from their reactions with carbon-centered nucleophiles in DMSO solution, would enable us to also predict their reactivity toward glutathione (GSH) in aqueous solution. The rate constants for the reaction of GSH with the selected electrophiles were measured in aqueous, buffered solution at pH 7.4 by utilizing a modified bioassay.19c,21b An excess of the electrophile was added to an aqueous buffered (pH 7.4) solution of GSH. After certain time intervals, 5,5′-dithio-bis-(2-nitrobenzoic acid) (DTNB, Ellman's reagent) was added to allow for photometric quantification of unreacted GSH. The time dependent decay of the GSH concentration at 15–20 points was then evaluated by fitting a mono-exponential decay function, which furnished the first-order rate constants kobs (s−1). The kinetic procedure was repeated to collect kobs at four different concentrations for each electrophile. The slope of the linear correlations of kobs with the electrophile concentrations furnished the second-order rate constants kGSH for the reactions of GSH with the cyclic Michael acceptors. Considering the small fraction of reactive thiolate GSH(NH3+/S−) at pH 7.4 (kexp2 = kGSH/F, with F = 0.028 at pH 7.4)25 finally converts kGSH to kexp2.
The reactivity of glutathione GSH(NH3+/S−) in aqueous solution has recently been rated with N = 20.97 (sN = 0.56) on the Mayr nucleophilicity scale.25 Thus eqn (1) was used to calculate keqn (1)2 for the Michael addition of GSH(NH3+/S−) with a set of cyclic unsaturated carbonyl compounds.
Typically, eqn (1) allows one to calculate second-order rate constants within a precision of factor <100 for reactions in which one new σ-bond is formed. Table 4 shows that eqn (1) estimated the second-order rate constants for the additions of GSH at cyclopentenone (1a), cyclohexenone (2a), the dihydropyranone 5a and the α-methylene-pyranone 5b within a factor of 20. For 2-methyl-cyclopentenone (1b) and the exo- and endocyclic lactones 4a and 4bkexp2 and the calculated keqn (1)2 agreed within a factor of 2. It can, thus, be concluded that the general reactivity pattern of cyclic electrophiles toward GSH is represented by their E parameters.
| Enone | Electrophilicity E | k GSH (M−1 s−1) | k exp2 (M−1 s−1) | k exp2/keqn (1)2 |
|---|---|---|---|---|
| a Calculated from kinetic data reported in ref. 19d. b Calculated from kinetic data in ref. 21b. | ||||
| 1a | −20.6 | (9.34 ± 0.66) × 10−1, (4.3 × 10−1)a | 33 (15)a | 21 (9.3)a |
| 1b | −22.1 | 3.33 × 10−3a | 0.12a | 1/1.9a |
| 2a | −22.1 | (1.18 ± 0.07) × 10−1, (3.4 × 10−1)b | 4.2 (12)b | 18 (52)b |
| 4a | −20.7 | (1.93 ± 0.09) × 10−2 | 0.69 | 1/2.0 |
| 4b | −19.4 | (5.75 ± 0.40) × 10−1 | 21 | 2.8 |
| 5a | −21.8 | (1.77 ± 0.17) × 10−1 | 6.3 | 18 |
| 5b | −19.5 | 1.43 ± 0.11 | 51 | 7.7 |
In agreement with previous studies by Schmidt on the dual electrophilicity of helenalin toward GSH,67,68 we determined kGSH (1a) > kGSH (4b). Hence, we have to note that small reactivity differences within one or two orders of magnitude are not unequivocally resolved by the simple three-parameter eqn (1). Changing the experimental method for determining the kinetics, swapping from a C- to an S-centered reference nucleophile as well as the neglect of constraint conformational space in natural products by the fragment approach may twist the relative reactivity order of similarly reactive Michael acceptors. Also the influence of solvents on the reactivity of carbonyl compounds needs further investigation.
The relative position of the lactone 5a (E = −21.8) and (E)-pent-3-en-2-one (E = −18.8) or (E)-hex-4-en-3-one (E = −18.9) in the electrophilicity scale (Fig. 2) is in accord with the preferential binding of the ketone unit of rugulactone by nucleophilic sites in the course of covalent enzyme inhibition.17 This illustrates that ΔE > 2.5 enables a safe prognosis of the reactive site in a natural product with dual electrophilicity.
Conclusions
In summary, sulfonium and pyridinium ylides were utilized as one-bond reference nucleophiles in kinetic experiments to characterize the Mayr electrophilicity parameters E for various cyclic enones and α,β-unsaturated lactones in DMSO at 20 °C. By combining the electrophilicity parameters E with tabulated nucleophilicity descriptors N (and sN) eqn (1) can be used to predict the rate constants for the reactions of 1–5 with various C-nucleophiles, as demonstrated by comparison with reported synthetic protocols.Most valuable, the reactivities of cyclic core fragments of the Michael acceptors 1–5 agree with the observed electrophilicities of natural products (terpenes) of more complex structure and considerably higher molecular weight that contain the same reactive moiety. The distinct different reactivity of cyclic enones and unsaturated lactones compared to their acyclic analogs was analyzed by quantum-chemical calculations, distortion interaction analysis, and by considering stereoelectronic effects.
The most important structural effects on the reactivity of α,β-unsaturated carbonyl compounds are summarized in Fig. 11. The locked conformations of cyclic Michael acceptors have a significant impact on their electrophilic reactivities. If compared to analogous open-chain enones, the electrophilicity of cyclic enones is significantly reduced by the fixed (Z)-geometry of the s-trans configured π-system. Alkyl groups in either α- or β-position of the cyclic enones further attenuate the electrophilicity of cyclic enones by positive inductive effects and steric bulk in vicinity or directly at the electrophilic reaction center. Thus, β-alkylated cyclohexenones are among the least electrophilic species characterized so far in Mayr's reactivity scales.24
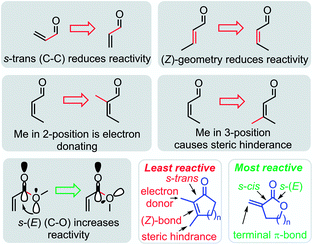 | ||
| Fig. 11 Summary of stereoelectronic and steric effects on the electrophilic reactivity of cyclic enones and α,β-unsaturated lactones. | ||
In contrast, the rigid cyclic structures of α-methylene-γ-butyrolactones facilitate synergistic stereoelectronic effects which favorably combine with a lack of steric hindrance at the reactive site to furnish a privileged class of highly potent electrophiles. In contrast to simple alkyl acrylates of comparable electrophilic reactivity, the cyclic scaffold of sesquiterpene lactones can be loaded with stereochemical information needed for recognition processes and selective reactions in living organisms. It is, therefore, not surprising that plants have chosen α-methylene-γ-butyrolactones as most abundant electrophilic fragment in biologically active sesquiterpene lactones.
The reactivity parameters determined in this work, together with those of previously characterized acyclic Michael acceptors, now provide an extensive basis for the systematic development of reactions with various classes of nucleophiles. Derivatization of natural products with the studied electron-deficient cyclic core fragments can in future be exploited in a more straightforward manner, thus saving limited natural resources, energy, and human effort. Knowledge of the electrophilic potential of these cyclic Michael acceptors to undergo reactions with nucleophiles in combination with considering the thermodynamics of the intended reactions thus facilitates the rational design of synthesis with difficult to access and costly natural products and, in this way, fosters the development in discovery medicinal and pharmaceutical chemistry.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Prof. Herbert Mayr (LMU München) and Prof. Claude Y. Legault (Université de Sherbrooke) for helpful discussions. Financial support by the Deutsche Forschungsgemeinschaft (SFB 749, projects A3 and B1; OF 120/1-1, project number 410831260), the Fonds der Chemischen Industrie (Kekulé fellowship to RJM), the Department Chemie (LMU München), and the Department Chemie (TU München) is gratefully acknowledged.Notes and references
- Sesquiterpene Lactones, ed. V. P. Sülsen and V. S. Martino, Springer, Cham (CH), 2018 Search PubMed.
- J. A. Marco and M. Carda, in Natural Lactones and Lactams: Synthesis, Occurrence and Biological Activity, ed. T. Janecki, Wiley-VCH, Weinheim, 1st edn, 2014, ch. 2, pp. 51–100 Search PubMed.
- Ł. Albrecht, A. Albrecht and T. Janecki, in Natural Lactones and Lactams: Synthesis, Occurrence and Biological Activity, ed. T. Janecki, Wiley-VCH, Weinheim, 1st edn, 2014, ch. 4, pp. 147–192 Search PubMed.
- (a) M. H. Kunzmann, I. Staub, T. Böttcher and S. A. Sieber, Biochemistry, 2011, 50, 910–916 CrossRef CAS; (b) A. Janecka, A. Wyrebska, K. Gach, J. Fichna and T. Janecki, Drug Discovery Today, 2012, 17, 561–572 CrossRef CAS; (c) M. H. Kunzmann, N. C. Bach, B. Bauer and S. A. Sieber, Chem. Sci., 2014, 5, 1158–1167 RSC; (d) A. Coricello, J. D. Adams, E. J. Lien, C. Nguyen, F. Perri, T. J. Williams and F. Aiello, Curr. Med. Chem., 2020, 27, 1501–1514 CrossRef CAS; (e) R. R. A. Freund, P. Gobrecht, D. Fischer and H.-D. Arndt, Nat. Prod. Rep., 2020, 37, 541–565 RSC.
- (a) A. Ghantous, A. Sinjab, Z. Herceg and N. Darwiche, Drug Discovery Today, 2013, 18, 894–905 CrossRef CAS; (b) C. A. Berdan, R. Ho, H. S. Lehtola, M. To, X. Hu, T. R. Huffman, Y. Petri, C. R. Altobelli, S. G. Demeulenaere, J. A. Olzmann, T. J. Maimone and D. K. Nomura, Cell Chem. Biol., 2019, 26, 1027–1035 CrossRef CAS; (c) J. N. Spradlin, X. Hu, C. C. Ward, S. M. Brittain, M. D. Jones, L. Ou, M. To, A. Proudfoot, E. Ornelas, M. Woldegiorgis, J. A. Olzmann, D. E. Bussiere, J. R. Thomas, J. A. Tallarico, J. M. McKenna, M. Schirle, T. J. Maimone and D. K. Nomura, Nat. Chem. Biol., 2019, 15, 747–755 CrossRef CAS.
- P. A. Jackson, J. C. Widen, D. A. Harki and K. M. Brummond, J. Med. Chem., 2017, 60, 839–885 CrossRef CAS.
- (a) J. Krysiak and R. Breinbauer, Top. Curr. Chem., 2012, 324, 43–84 CrossRef CAS; (b) R. Lagoutte and N. Winssinger, Chimia, 2017, 71, 703–711 CrossRef CAS; (c) D. K. Nomura and T. J. Maimone, in Activity-Based Protein Profiling (Curr. Top. Microbiol. Immun., vol. 420), ed. B. F. Cravatt, K.-L. Hsu and E. Weerapana, Springer, Cham (CH), 2018; pp. 351–374, DOI:10.1007/82_2018_121.
- P. E. Ordóñez, K. K. Sharma, L. M. Bystrom, M. A. Alas, R. G. Enriquez, O. Malagón, D. E. Jones, M. L. Guzman and C. M. Compadre, J. Nat. Prod., 2016, 79, 691–696 CrossRef.
- (a) S. M. Kupchan, D. C. Fessler, M. A. Eakin and T. J. Giacobbe, Science, 1970, 168, 376–377 CrossRef CAS; (b) R. R. A. Kitson, A. Millemaggi and R. J. K. Taylor, Angew. Chem., Int. Ed., 2009, 48, 9426–9451 CrossRef CAS.
- Q. Li, Z. Wang, Y. Xie and H. Hu, Biomed. Pharmacother., 2020, 125, 109955 CrossRef CAS.
- (a) N. Kudo, N. Matsumori, H. Taoka, D. Fujiwara, E. P. Schreiner, B. Wolff, M. Yoshida and S. Horinouchi, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 9112–9117 CrossRef CAS; (b) Q. Sun, Y. P. Carrasco, Y. Hu, X. Guo, H. Mirzaei, J. MacMillan and Y. M. Chook, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1303–1308 CrossRef CAS.
- S. B. Buck, C. Hardouin, S. Ichikawa, D. R. Soenen, C.-M. Gauss, I. Hwang, M. R. Swingle, K. M. Bonness, R. E. Honkanen and D. L. Boger, J. Am. Chem. Soc., 2003, 125, 15694–15695 CrossRef CAS.
- T. J. Schmidt, in Studies in Natural Products Chemistry, ed. Atta-ur-Rahman, Elsevier, Amsterdam, 2006, vol. 33, pp. 309–392 Search PubMed.
- T. J. Schmidt, in Sesquiterpene Lactones, ed. V. P. Sülsen, V. S. Martino, Springer, Cham (CH), 2018, ch. 15, pp. 349–371 Search PubMed.
- E. A. Crane and K. Gademann, Angew. Chem., Int. Ed., 2016, 55, 3882–3902 CrossRef CAS.
- J.-T. Feng, D.-L. Wang, Y.-L. Wu, Y. He and Z. Xing, Bioorg. Med. Chem. Lett., 2013, 23, 4393–4397 CrossRef CAS.
- M. B. Nodwell, H. Menz, S. F. Kirsch and S. A. Sieber, ChemBioChem, 2012, 13, 1439–1446 CrossRef CAS.
- (a) X. Li, D. T. Payne, B. Ampolu, N. Bland, J. T. Brown, M. J. Dutton, C. A. Fitton, A. Gulliver, L. Hale, D. Hamza, G. Jones, R. Lane, A. G. Leach, L. Male, E. G. Merisor, M. J. Morton, A. S. Quy, R. Roberts, R. Scarll, T. Schulz-Utermoehl, T. Stankovic, B. Stevenson, J. S. Fossey and A. Agathanggelou, MedChemComm, 2019, 10, 1379–1390 RSC; (b) C. Tian, R. Sun, K. Liu, L. Fu, X. Liu, W. Zhou, Y. Yang and J. Yang, Cell Chem. Biol., 2017, 24, 1416–1427 CrossRef CAS.
- (a) T. W. Schultz, J. W. Yarbrough and E. L. Johnson, SAR QSAR Environ. Res., 2005, 16, 313–322 CrossRef CAS; (b) J. W. Yarbrough and T. W. Schultz, Chem. Res. Toxicol., 2007, 20, 558–562 Search PubMed; (c) A. Böhme, D. Thaens, A. Paschke and G. Schüürmann, Chem. Res. Toxicol., 2009, 22, 742–750 Search PubMed; (d) A. Böhme, A. Laqua and G. Schüürmann, Chem. Res. Toxicol., 2016, 29, 952–962 Search PubMed.
- V. J. Cee, L. P. Volak, Y. Chen, M. D. Bartberger, C. Tegley, T. Arvedson, J. McCarter, A. S. Tasker and C. Fotsch, J. Med. Chem., 2015, 58, 9171–9178 CrossRef CAS.
- (a) M. Friedman, J. F. Cavins and J. S. Wall, J. Am. Chem. Soc., 1965, 87, 3672–3682 CrossRef CAS; (b) H. Esterbauer, H. Zollner and N. Scholz, Z. Naturforsch., C: J. Biosci., 1975, 30, 466–473 CAS.
- (a) G. Eisenbrand, J. Schuhmacher and P. Gölzer, Chem. Res. Toxicol., 1995, 8, 40–46 Search PubMed; (b) K. Chan, R. Poon and P. J. O'Brien, J. Appl. Toxicol., 2008, 28, 1027–1039 CAS.
- J. A. H. Schwöbel, D. Wondrousch, Y. K. Koleva, J. C. Madden, M. T. D. Cronin and G. Schüürmann, Chem. Res. Toxicol., 2010, 23, 1576–1585 Search PubMed.
- (a) H. Mayr and M. Patz, Angew. Chem., Int. Ed. Engl., 1994, 33, 938–957 CrossRef; (b) H. Mayr, T. Bug, M. F. Gotta, N. Hering, B. Irrgang, B. Janker, B. Kempf, R. Loos, A. R. Ofial, G. Remennikov and H. Schimmel, J. Am. Chem. Soc., 2001, 123, 9500–9512 CrossRef CAS; (c) H. Mayr and A. R. Ofial, SAR QSAR Environ. Res., 2015, 26, 619–646 CrossRef CAS; (d) The database of reactivity parameters (E, N, and sN) is freely accessible under, www.cup.lmu.de/oc/mayr/reaktionsdatenbank2/, accessed Jan., 2021.
- R. J. Mayer and A. R. Ofial, Angew. Chem., Int. Ed., 2019, 58, 17704–17708 CrossRef CAS.
- Q. Chen, P. Mayer and H. Mayr, Angew. Chem., Int. Ed., 2016, 55, 12664–12667 CrossRef CAS.
- D. S. Allgäuer, H. Jangra, H. Asahara, Z. Li, Q. Chen, H. Zipse, A. R. Ofial and H. Mayr, J. Am. Chem. Soc., 2017, 139, 13318–13329 CrossRef.
- A. Kakehi, Heterocycles, 2012, 85, 1529–1577 CrossRef CAS.
- D. S. Allgäuer and H. Mayr, Eur. J. Org. Chem., 2013, 6379–6388 CrossRef and ref. cited therein.
- D. S. Allgäuer and H. Mayr, J. Am. Chem. Soc., 2013, 135, 15216–15224 CrossRef.
- D. S. Allgäuer and H. Mayr, Eur. J. Org. Chem., 2014, 2956–2963 CrossRef.
- Y. Tamura, Y. Sumida, S.-I. Haruki and M. Ikeda, J. Chem. Soc., Perkin Trans. 1, 1975, 575–579 RSC.
- R.-B. Hu, S. Sun and Y. Su, Angew. Chem., Int. Ed., 2017, 56, 10877–10880 CrossRef CAS.
- T. Zincke and H. Rollhäuser, Chem. Ber., 1912, 45, 1495–1511 CrossRef CAS.
- F. von Nussbaum, V. M.-J. Li, S. Allerheiligen, S. Anlauf, L. Bärfacker, M. Bechem, M. Delbeck, M. F. Fitzgerald, M. Gerisch, H. Gielen-Haertwig, H. Haning, D. Karthaus, D. Lang, K. Lustig, D. Meibom, J. Mittendorf, U. Rosentreter, M. Schäfer, S. Schäfer, J. Schamberger, L. A. Telan and A. Tersteegen, ChemMedChem, 2015, 10, 1163–1173 CrossRef CAS.
- (a) V. K. Aggarwal, H. W. Smith, G. Hynd, R. V. H. Jones, R. Fieldhouse and S. E. Spey, J. Chem. Soc., Perkin Trans. 1, 2000, 3267–3276 RSC; (b) M. Liao, L. Peng and J. Wang, Org. Lett., 2008, 10, 693–696 CrossRef CAS.
- R. Appel, N. Hartmann and H. Mayr, J. Am. Chem. Soc., 2010, 132, 17894–17900 CrossRef CAS.
- R. Huisgen, Angew. Chem., Int. Ed., 1970, 9, 751–762 CrossRef CAS.
- A. Otto, B. Abegaz, B. Ziemer and J. Liebscher, Tetrahedron: Asymmetry, 1999, 10, 3381–3389 CrossRef CAS.
- E. S. Beh, L. Tong and R. G. Gordon, Organometallics, 2017, 36, 1453–1456 CrossRef CAS.
- J.-C. Le Menn, A. Tallec and J. Sarrazin, Can. J. Chem., 1991, 69, 761–767 CrossRef CAS.
- N. Martin-Leon, M. Quinteiro, C. Seoane and J. L. Soto, Liebigs Ann. Chem., 1990, 101–104 CrossRef CAS.
- C. Bigogno, B. Danieli, G. Lesma and D. Passarella, Heterocycles, 1995, 41, 973–982 CrossRef CAS.
- D. M. Altshuler, C. D. Anderson, W. G. Chen, J. J. Clemens, T. Cleveland, T. R. Coon, B. Frieman, P. Grootenhuis, S. S. Hadida Ruah, B. J. Hare, R. Kewalramani, J. Mccartney, M. T. Miller, P. Paraselli, F. Pierre, S. M. Robertson, P. R. Sosnay, S. E. Swift and J. Zhou, WO 2020/102346A1, Vertex Pharmaceutical Inc., 2020, p. 46.
- K. E. Bailey and B. R. Davis, Aust. J. Chem., 1995, 48, 1827–1834 CrossRef CAS.
- K. Dudzinski, A. M. Pakulska and P. Kwiatkowski, Org. Lett., 2012, 14, 4222–4225 CrossRef CAS.
- (a) M. Puppala, A. Murali and S. Baskaran, Chem. Commun., 2012, 48, 5778–5780 RSC; (b) H. O. House, W. A. Kleschick and E. J. Zaiko, J. Org. Chem., 1978, 43, 3653–3661 CrossRef CAS.
- (a) J. Cossy, N. Furet and S. BouzBouz, Tetrahedron, 1995, 51, 11751–11764 CrossRef CAS; (b) P. J. Crowley, I. H. Aspinall, K. Gillen, C. R. A. Godfrey, I. M. Devillers, G. R. Munns, O.-A. Sageot, J. Swanborough, P. A. Worthington and J. Williams, Chimia, 2003, 57, 685–691 CrossRef CAS.
- R. González, I. Collado, B. López de Uralde, A. Marcos, L. M. Martín-Cabrejas, C. Pedregal, J. Blanco-Urgoiti, J. Pérez-Castells, M. A. Fernández, S. L. Andis, B. G. Johnson, R. A. Wright, D. D. Schoepp and J. A. Monn, Bioorg. Med. Chem., 2005, 13, 6556–6570 CrossRef.
- I. Collado, C. Pedregal, A. B. Bueno, A. Marcos, R. González, J. Blanco-Urgoiti, J. Pérez-Castells, D. D. Schoepp, R. A. Wright, B. G. Johnson, A. E. Kingston, E. D. Moher, D. W. Hoard, K. I. Griffey and J. P. Tizzano, J. Med. Chem., 2004, 47, 456–466 CrossRef CAS.
- R. Gnaneshwar and S. Sivaram, Synth. Commun., 2006, 36, 885–890 CrossRef CAS.
- S. Kawanishi, K. Sugiyama, Y. Oki, T. Ikawa and S. Akai, Green Chem., 2017, 19, 411–417 RSC.
- S. J. Robbins and D. M. S. Wheeler, Synth. Commun., 1989, 19, 769–775 CrossRef CAS.
- B. R. Davis, S. R. Gupta and T. G. Halsall, J. Chem. Soc., 1961, 4211–4214 RSC.
- (a) M.-A. Poupart, G. Lassalle and L. A. Paquette, Org. Synth., 1990, 69, 173 CrossRef CAS; (b) W. G. Dauben and J. M. Gerdes, Tetrahedron Lett., 1983, 24, 3841–3844 CrossRef CAS.
- (a) R. Sauvetre, M.-C. Roux-Schmitt and J. Seyden-Penne, Tetrahedron, 1978, 34, 2135–2140 CrossRef CAS; (b) M.-C. Roux-Schmitt, L. Wartski and J. Seyden-Penne, Synth. Commun., 1981, 11, 85–94 CrossRef CAS.
- (a) A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS; (b) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed; (c) M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed; (d) C. Y. Legault, CYLview 1.0b, Université de Sherbrooke, 2009, http://www.cylview.org Search PubMed.
- A. Bienvenüe, J. Am. Chem. Soc., 1973, 95, 7345–7353 CrossRef.
- H. K. Hall Jr, M. K. Brandt and R. M. Mason, J. Am. Chem. Soc., 1958, 80, 6420–6427 CrossRef.
- (a) R. Huisgen, Angew. Chem., 1957, 69, 341–359 CrossRef CAS; (b) R. Huisgen and H. Ott, Tetrahedron, 1959, 6, 253–267 CrossRef CAS.
- I. Alabugin, Stereoelectronic Effects: A Bridge Between Structure and Reactivity, Wiley, Chichester (UK), 2016, ch. 6, pp. 149–150 Search PubMed.
- (a) D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646–10647 CrossRef CAS; (b) D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187–10198 CrossRef CAS; (c) Y. Lan, L. Zou, Y. Cao and K. N. Houk, J. Phys. Chem. A, 2011, 115, 13906–13920 CrossRef CAS; (d) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS; (e) P. Vermeeren, S. C. C. van der Lubbe, C. F. Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649–667 CrossRef CAS.
- J. Hine, Adv. Phys. Org. Chem., 1977, 15, 1–61 CrossRef CAS.
- (a) B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS; (b) T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 094106 CrossRef; (c) R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince III, E. G. Hohenstein, U. Bozkaya, A. Yu. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer III, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS.
- Pyramidalization Δ in the transition states of the reactions of 7 with the cyclohexenones 2a, 2b, and 2c follows an analogous pattern as discussed for the cyclopentenones, that is, decreasing electrophilic reactivity is correlated with increasing pyramidalization Δ (see ESI, Table S1†).
- Presumably due to the very small differences in the interaction energies, SAPT analysis of the reaction pathways of the reactions of 7 with 1a and 1b did not provide sufficient insight to reveal the underlying reasons for the difference in interaction energies (see ESI, Fig. S2†).
- G. Lyss, T. J. Schmidt, I. Merfort and H. L. Pahl, Biol. Chem., 1997, 378, 951–961 CAS.
- (a) T. J. Schmidt, Bioorg. Med. Chem., 1997, 5, 645–653 CrossRef CAS; (b) T. J. Schmidt, G. Lyß, H. L. Pahl and I. Merfort, Bioorg. Med. Chem., 1999, 7, 2849–2855 CrossRef CAS.
- (a) J. C. Widen, A. M. Kempema, J. W. Baur, H. M. Skopec, J. T. Edwards, T. J. Brown, D. A. Brown, F. A. Meece and D. A. Harki, ChemMedChem, 2018, 13, 303–311 CrossRef CAS; (b) In this work, we observed a half-life time of the 1a-GSH adduct of t1/2 = 40 min (under the conditions of the kinetic GSH chemoassay).
Footnote |
| † Electronic supplementary information (ESI) available: Details of synthetic procedures and product characterization, kinetic measurements, quantum-chemical calculations, geometries of all optimized structures and X-ray crystallographic data. CCDC 2044215–2044221. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc06628a |
| This journal is © The Royal Society of Chemistry 2021 |