Open Access Article
Open Access ArticleRevealing the role of excited state proton transfer (ESPT) in excited state hydrogen transfer (ESHT): systematic study in phenol–(NH3)n clusters
Christophe
Jouvet
 *ab,
Mitsuhiko
Miyazaki
*ab,
Mitsuhiko
Miyazaki
 cd and
Masaaki
Fujii
cd and
Masaaki
Fujii
 *bd
*bd
aCNRS, Aix Marseille Université, Physique des Interactions Ioniques et Moleculaires (PIIM), UMR 7345, 13397 Marseille Cedex, France. E-mail: christophe.jouvet@univ-amu.fr
bWorld Research Hub Initiatives, Institute of Innovative Research, Tokyo Institute of Technology, 4259-R1-15, Nagatsuta-cho, Midori-ku, Yokohama 226-8503, Japan
cNatural Science Division, Faculty of Core Research, Ochanomizu University, 2-1-1 Ohtsuka, Bunkyo-ku, Tokyo 112-8610, Japan
dLaboratory for Chemistry and Life Science, Institute of Innovative Research, Tokyo Institute of Technology, 4259-R1-15, Nagatsuta-cho, Midori-ku, Yokohama 226-8503, Japan. E-mail: mfujii@res.titech.ac.jp
First published on 10th February 2021
Abstract
Excited State Hydrogen Transfer (ESHT), proposed at the end of the 20th century by the corresponding authors, has been observed in many neutral or protonated molecules and become a new paradigm to understand excited state dynamics/photochemistry of aromatic molecules. For example, a significant number of photoinduced proton-transfer reactions from X–H bonds have been re-defined as ESHT, including those of phenol, indole, tryptophan, aromatic amino acid cations and so on. Photo-protection mechanisms of biomolecules, such as isolated nucleic acids of DNA, are also discussed in terms of ESHT. Therefore, a systematic and up-to-date description of ESHT mechanism is important for researchers in chemistry, biology and related fields. In this review, we will present a general model of ESHT which unifies the excited state proton transfer (ESPT) and the ESHT mechanisms and reveals the hidden role of ESPT in controlling the reaction rate of ESHT. For this purpose, we give an overview of experimental and theoretical work on the excited state dynamics of phenol–(NH3)n clusters and related molecular systems. The dynamics has a significant dependence on the number of solvent molecules in the molecular cluster. Three-color picosecond time-resolved IR/near IR spectroscopy has revealed that ESHT becomes an electron transfer followed by a proton transfer in highly solvated clusters. The systematic change from ESHT to decoupled electron/proton transfer according to the number of solvent molecules is rationalized by a general model of ESHT including the role of ESPT.
1. Introduction
Excited state proton transfer (ESPT) and excited state hydrogen transfer (ESHT) play important roles in photochemistry and biology. These photochemical reactions have been explored for 30 years via the spectroscopy of molecular clusters. The initial idea was that aromatic alcohols are more acidic in the excited state than in the ground state and therefore, in a molecular cluster, it should be possible to induce a proton transfer reaction by optical excitation, i.e. ESPT. However, following developments in experimental techniques and progress in computational chemistry, controversial results were reported, particularly in phenol (PhOH) hydrogen-bonded (H-bonded) clusters, and finally ESHT took over ESPT in the description of many photochemical processes. This research topic – started in around 1985 – has since provided many surprises, with the results having had a significant impact on our understanding of the photochemistry and photophysics of substituted aromatic molecules, including biomolecules.Due to the importance of this topic, as will be shown below, a substantial number of papers on ESHT and ESPT have been published. Despite all that has been published on this subject over a period of around forty years, it seems that only the most recent studies have given rise to an accurate understanding of ESHT. It should also be noted that the understanding of the experimental results is now facilitated by ab initio calculations of excited states, a technique that has made considerable progress in recent years. Theoretical calculations well reproduce not only the energy of the electronic transitions but also the intensities of the active vibrational modes in spectroscopy. From the theoretical calculations and advanced experimental results, we can understand the relation between ESHT and ESPT, which has not been previously discussed in a systematic manner. In this review, the role of the ESPT underlying the ESHT process will be discussed using the benchmark molecular system PhOH–(NH3)n (n = 1–5). The review will begin by giving an overview of progress in this research field from the initial idea of ESPT to the establishment of ESHT.
2. Research history from ESPT to ESHT
2.1 Proton transfer in the condensed phase
Since the pioneering work of Förster,1 the protolytic processes (displacement of the acid–base equilibrium or proton transfer in hydrogen-bonded complexes) induced by optical electronic excitation have been studied in the condensed phase.2 Emission from neutral photoexcited 1-naphthol (1-NpOH*) is shifted from its gas phase value at 350 nm in the near ultraviolet (UV) to the visible (blue) in an aqueous solution. The blue emission after UV excitation was initially interpreted as the formation of the naphtholate anion3 and accompanying proton release from the excited state, i.e. ESPT. This implies a dramatic decrease in pKa (9.1 (S0) to 0.5 (S1)) upon photoexcitation to the first excited state of 1-NpOH. The decrease of pKa was also found in aromatic hydroxy, amino, and carboxy derivatives, and thus ESPT was established in the condensed phase.2.2 Gas phase PT
Since the 1980s, molecular beam laser spectroscopy has been applied to aromatic molecular clusters and ESPT has been studied in both the frequency and time domains. A combination of several factors explains the success of this technique. Collisional relaxation can be neglected in a molecular beam. The number of molecules in the cluster is clearly specified when coupling with mass-selected multiphoton ionization detection. The relative orientations and geometries of molecules in the cluster are well defined because of the low temperature. Furthermore, an excited state reaction implies that the optical excitation is triggering the reaction, thus the reaction dynamics can be followed in real time, from a well-defined t = 0 of the reaction. Due to these advantages, the ESPT mechanism can be revealed at the molecular level by using molecular beam laser spectroscopy.2.3 ESPT in naphthol/phenol–ammonia clusters and the contradictions
Leutwyler and coworker4 provided the first example of ESPT in the gas phase by the study of the fluorescence spectra of AH–B clusters (AH = 1-NpOH, B = (NH3)n, (piperidine)n). A red-shifted emission assigned to the proton-transfer process AH*–B → A−*–(HB)+ was observed only from the excited state of sufficiently large clusters (n ≥ 4 or 2 for ammonia or piperidine, respectively). The observation of a threshold number of solvent molecules for an intracluster ESPT attracted the research groups specializing in time-resolved spectroscopy combined with the mass-selected multiphoton ionization technique. The dynamics in S1 were measured by picosecond (ps) pump–probe spectroscopy of NpOH–(NH3)n. However, not only n = 4 but also n = 3 were reported to be the threshold size of ESPT in NpOH–(NH3)n.4–7 High-resolution time-of-flight mass spectroscopy revealed the influence of NH3 evaporation after ionization in these experiments, and eventually it was concluded that the threshold size was n = 5.8 This threshold size was also supported by recent theoretical calculations.9It was expected that solvated clusters of PhOH and NpOH show similar behavior as far as ESPT is concerned. For PhOH solvated clusters, ESPT was postulated from the lowering of the ionization potential which was measured by the two-color resonance-enhanced multiphoton ionization (REMPI) technique.10,11 Since a strong H-bond lowers the ionization potential of the proton donor (acid), one can expect a large shift of the ionization thresholds when the ion pair is formed in the clusters. As expected, a strong lowering of the IP was found in PhOH–(NH3)n at n = 4 and was interpreted as the ionization from the proton-transferred structure (PT structure).
There was, however, a notable difference between PhOH–(NH3)n and NpOH–(NH3)n clusters: free NH4+(NH3)n−1 clusters formed after photoexcitation were detected only for PhOH–(NH3)n clusters and not for NpOH–(NH3)n clusters.12 Moreover, a ps rise time of the NH4+(NH3)n−1 signal was similar to the decay signal of the parent PhOH–(NH3)n. The formation of NH4+(NH3)n−1 clusters after the ionization of the PhOH–(NH3)n cluster was observed, and the energy dependence of the ps dynamics was probed. The observation of NH4+(NH3)n−1 implies the presence of a high barrier in the ionic state at a size where the barrier is very small in the excited state. However, it is well established that the acidity of ionic species is larger than that of neutrals13 thus the barrier should be lower than that in S1. In addition, Schmitt14et al. found that the action spectra of PhOH–(NH3)n clusters obtained by monitoring NH4+(NH3)n−1 show well-resolved vibronic structures in S1. This posed a problem, as no ESPT is expected for small cluster sizes (n ≤ 3), whereas the appearance of protonated fragments was supposed to be a signature of the proton transfer mechanism either in the excited or in the ionic state. These contradictions suggest the presence of dynamics other than ESPT. A full discussion of these contradictions can be found in two reviews.12,15
2.4 Discovery of ESHT
These contradictions were resolved upon the discovery of ESHT at the end of the 20th century. The first key experiment was the observation of the ˙NH4(NH3)n hypervalent cluster produced by excitation of the S1 state of PhOH–(NH3)n.16,17 In 1999, Pino et al. observed the formation of a long-lived species from the S1 excited state by a delayed ionization of PhOH–(NH3)n clusters.16 Serendipitously, they measured the pump–probe photoionization mass spectra not only at a short delay (Δt = 0) but also at very long delay (200 nanosecond (ns)), which is obviously longer than the lifetime of the parent cluster in S1 (see Fig. 1). When they measured the mass spectra without delay Δt = 0, both parent ions PhOH–(NH3)n and fragment ions NH4+(NH3)n−1 were detected (see Fig. 1). The typical lifetime of hydrogen-bonded PhOH clusters is ∼10 ns therefore all the signals should be very weak with a delay of 200 ns. Indeed, the mass peaks of parent ions PhOH+–(NH3)n become significantly weaker. However, even with such a long delay, the mass peaks of the fragment ions remain. This indicates that long-lived neutral species are generated from the photoexcited PhOH–(NH3)n, and photoionization of these species produces NH4+(NH3)n−1. From the various possibilities of long-lived species (including a triplet state of the clusters), they concluded that these neutral species are hydrogenated ammonia clusters generated by neutral cleaving of the OH bond, followed by a successive H atom transfer to the NH3 moiety: PhOH–(NH3)n → PhO˙ + ˙NH4(NH3)n−1. This result was soon confirmed18 by studying the electronic spectra of the reaction products using UV-near infrared (NIR)/IR-UV′ three-color ion dip spectroscopy. The NIR transition is the signature of a surplus electron in ˙NH4(NH3)n−1, which occupies the 3s orbital and gives rise to Rydberg transitions, such as 3p–3s in the NIR region. Fig. 2 displays the NIR spectra obtained by UV-NIR-UV ion dip spectroscopy of PhOH–(NH3)n (n = 2–5). Regardless of the number of ammonia molecules in the cluster, broad NIR transitions are observed. The spectra are very similar to the NIR spectra of ˙NH4(NH3)n−1 generated by photodissociation of pure NH3 clusters,19,20 which are traced in the same figure in dotted lines. This strongly supports the formation of ˙NH4(NH3)n−1 and neutral cleaving of the OH bond after photodissociation, i.e. ESHT. The infrared (IR) spectra measured by UV-IR-UV spectroscopy also confirmed the formation of ˙NH4(NH3)n−1.21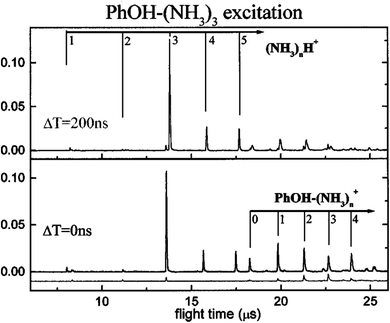 | ||
| Fig. 1 Demonstration of the formation of ˙NH4(NH3)n−1 clusters from a two color ionization of PhOH–(NH3)nvia S1.16,17 – The lower trace: a second ns laser at 355 nm, with no delay, ionizes the PhOH*–(NH3)n excited by the first laser (281.75 nm) within the S1 lifetime. Simultaneously, NH4+(NH3)n cluster ions are observed. – Upper trace: The second (ionization) laser is delayed by 200 ns from the first laser. It cannot excite the PhOH*–(NH3)n, of which the lifetime is a ns, thus PhOH+–(NH3)nmostly disappears. In contrast, NH4+(NH3)n ions remain at almost the same intensity. This suggests the production of long-lived species, i.e. ˙NH4(NH3)n−1. Reproduced from ref. 17 with permission from the PCCP owner Societies, copyright 2000. | ||
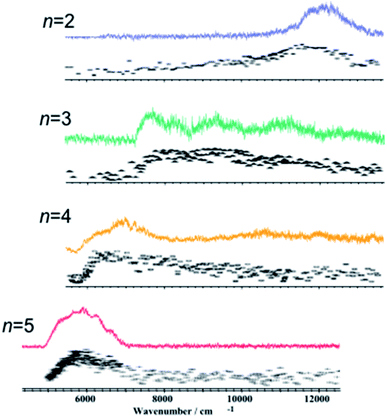 | ||
| Fig. 2 Electronic spectra of the reaction products from photo-excited PhOH–(NH3)n are shown in color.18 Electronic spectra of the reaction products from photo-excited pure (NH3)n clusters assigned to the excitation of the ˙NH4(NH3)n radical cluster are shown in black.19,20 Reproduced from ref. 18 with the permission of AIP Publishing, copyright 2002 and from ref. 20 with permission of Springer Nature, copyright 1999. | ||
2.5 The S.D.D.J. model
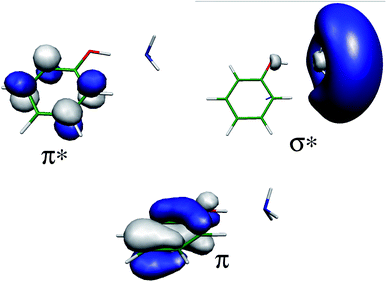
Theoretical approaches also support the existence of ESHT. Ab initio calculations were performed on PhOH–(H2O),22,23 with a diffuse function on the H atom in order to properly describe the Rydberg character of the 1πσ* state (see Fig. 3 for the orbital shapes). The calculations revealed a new predissociation pathway from the S1 (ππ*) state to a low-lying 1πσ* state through a conical intersection, which leads to a concerted electron- and proton-transfer reaction from the chromophore to the solvent. Theoretical calculations also show that the excited-state reaction is endothermic in PhOH–(H2O) complex but exothermic in the PhOH–NH3 complex. Thus, ESHT in PhOH–(NH3)n clusters is also validated by the theoretical results. Combining experimental and theoretical results, a general model – the SDDJ model23 – was proposed in 2002. In this model, a key role is played by excited singlet states of πσ* character, which have repulsive potential-energy functions with respect to the stretching of OH or NH bonds (see Fig. 4). The 1πσ* potential-energy functions intersect not only the bound potential-energy functions of the 1ππ* excited states, but also that of the electronic ground state. The S1 surface typically exhibits a local minimum of 1ππ* character in the vicinity of the equilibrium geometry of the ground state. The second excited state is a dissociative 1πσ* which induces a barrier on the S1 surface by its conical intersection with the 1ππ* potential surface. The excited state lifetime is governed by the rate of tunneling through the barrier from the ππ* to the πσ*.23–25 The barrier is also responsible for pronounced isotope effects on the fluorescence lifetime and quantum yield.26 The πσ* state crosses the ground state at a greater distance, leading to the second conical intersection. Classically, at this point, the H atom can pursue the πσ* potential curve and will retain quite a high kinetic energy or be trapped on the ground state surface leading to a hot molecule which undergoes statistical evaporation of the H atom. From the theoretical point of view, the potential energy surfaces calculated by different methods are quite similar and vary only in details.27–31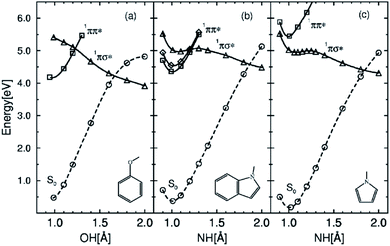 | ||
| Fig. 4 Potential energy profiles of the lowest 1ππ* states (squares), the lowest 1πσ* state (triangles) and the electronic ground state (circles) as a function of the OH stretch (PhOH) or NH stretch (indole, pyrrole) reaction coordinate. Geometries have been optimized in the excited electronic states at the CASSCF level; the PE profiles have been obtained with the CASPT2 method. Reproduced from ref. 23 with permission from the PCCP owner Societies, copyright 2002. | ||
2.6 H-loss in the free PhOH molecule and its relation to ESHT
ESHT was established through the experimental and theoretical studies performed on solvated clusters. In monomers, the ESHT of clusters turns into an H loss channel from the excited state. H atom dissociation in photoexcited PhOH has been well characterized by the measurement of the kinetic energy of the H atom. A bimodal distribution is observed. For the first component, the fast H atoms, the kinetic energy reflects the vibrational progression in the remaining PhO˙ along the out of plane vibration. Here, out of plane vibrations are necessary in order to couple the ππ* and the πσ* states because of the difference in Cs symmetry.29,32–34 Such a well-defined and structured kinetic energy distribution is characteristic of bond rupture on a dissociative potential. The H-loss channel is also evidenced by the formation of the PhO˙ radical, as detected by VUV photoionization.35,36 The second component of the distribution, the slow H atoms, is assigned to a statistical fragmentation which occurs after internal conversion following the crossing of the πσ* and the ground state. By measuring both the ps transients of parent and fragment and the total translational energy distribution of products as a function of the reaction time, it was evidenced that both the slow and fast components of the H fragment have the same tunneling origin and that the ground state is populated at the second πσ*–S0 crossing and not through a direct ππ*–S0 internal conversion process.24,37The H-loss dynamics have also been studied in the time domain. The ps time-evolution of the S1 excited state of PhOH shows that the lifetime decreases from 2 ns at the band origin 000 down to 600 ps at the band located 3500 cm−1 above the origin.38 These surveys show that the excitation of vibrational levels of A′′ symmetry shortens the lifetime, mainly through S1–S2 (πσ*) vibronic coupling. At high energy, the direct excitation of the πσ* leads to very fast dynamics of about 150 fs at 207 nm (excess energy of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1).39,40 The dynamics of the PhOH monomer has become a good example to test different theoretical methods for excited state dynamics, such as the quantum wave packet propagation method41 or the multistate semiclassical trajectory method. Xu31et al. clearly confirm that hydrogen tunneling from the ππ* to the πσ* potential surface is the main reaction mechanism in the PhOH H-loss photodissociation at the 000 band origin, and agree with experiments on the bimodal nature of the kinetic energy spectral distribution. They also show that the low kinetic energy release is due to both statistical dissociations to the ground state and direct dissociation to the first excited state of the phenoxyl radical. This interpretation is consistent with the translational energy distributions and branching ratios of the phenoxyl radicals produced in the different electronic states.38
000 cm−1).39,40 The dynamics of the PhOH monomer has become a good example to test different theoretical methods for excited state dynamics, such as the quantum wave packet propagation method41 or the multistate semiclassical trajectory method. Xu31et al. clearly confirm that hydrogen tunneling from the ππ* to the πσ* potential surface is the main reaction mechanism in the PhOH H-loss photodissociation at the 000 band origin, and agree with experiments on the bimodal nature of the kinetic energy spectral distribution. They also show that the low kinetic energy release is due to both statistical dissociations to the ground state and direct dissociation to the first excited state of the phenoxyl radical. This interpretation is consistent with the translational energy distributions and branching ratios of the phenoxyl radicals produced in the different electronic states.38
Besides ππ* to πσ* internal conversion, another mechanism to explain H loss was proposed for the PhOH monomer.33 In this model, the first step was S1–S0 internal conversion and the H loss was assumed to take place on the ground state surface. This model could not account for experimental observations such as the reaction in the ammonia cluster or the decrease of the reaction time upon the intermolecular OH⋯N vibration excitation and increase upon deuteration.15 This model was ultimately dismissed following the demonstration of the correlation of the excited state lifetime of PhOH and its derivatives with the ππ*/πσ* gap.24,34,37 It should be stressed that the ˙NH4(NH3)n clusters can be seen as a very good messenger for characterizing the H loss on a πσ* potential. Indeed, the H transfer requires a fairly direct process (the dynamics occur on a repulsive surface) since a process going through hot ground state molecules (H loss mediated by internal conversion to the ground state33) would lead to a statistical process (Intramolecular Vibrational Redistribution: IVR) and the immediate evaporation of the whole cluster or some of the NH3 molecules. A strong driving force is imperative in order to attach the H atom and repel the ˙NH4(NH3)n cluster from the chromophore, and this cannot be achieved in a statistical process. One can also suppose that the kinetic energy of the ˙NH4(NH3)n clusters follows an impulsive type distribution, but the confirmatory experiment has yet to be performed. As we will show below, the variation of the dynamics with cluster size can be very well understand within this ππ*/πσ* internal conversion framework.
2.7 Forgotten ESPT behind ESHT
Through extensive experimental and theoretical research, ESHT (or H loss in a monomer) has been characterized in terms of tunneling or internal conversion from the optically bright S1 ππ* state to the dissociative πσ* potential surface. In solvated clusters, the dissociative πσ* potential will bring the H atom to the solvent moiety, the process terminating in H atom transfer. For monomers, the πσ* state crosses the ground state potential surface, and internal conversion to the ground state is induced. This is the quenching process of photoexcited aromatic molecules, and is discussed as the built-in mechanism of aromatic biomolecules which have to remain photostable upon UV excitation. The first publications concerning ESHT described this reaction as the “Forgotten channel”16,17 but now it is a popularly invoked photochemical process, particularly in gas phase studies. On the other hand, ESPT has become a somewhat “forgotten” process now, and the relation between ESPT and ESHT has yet not been discussed, although both processes should be considered in the description of aromatic molecular systems. We should discuss their relations in aromatic molecular systems: which of ESHT or ESPT occurs, why so, where is the key on the potential surface, and how do ESHT and ESPT influence each other. PhOH–(NH3)n clusters, at the origin of the ESHT issue, are one of the best systems with which to unravel these aspects, because the ππ* and πσ* states are systematically controlled by the number of NH3 molecules in the cluster, and the reaction products ˙NH4(NH3)n−1 are well characterized by both experimental spectroscopy and theory. In particular, their low ionization potentials42 and characteristic near infrared electronic absorption20 are important for experiments. Here, we will present the photodynamics for individual clusters of increasing size and discuss pertinent aspects of the ESHT/ESPT issue accordingly.3. Methods
3.1 Experimental
Although the experimental setups used to study PhOH–(NH3)n clusters have been slightly different depending upon the experimental groups, the typical conditions are always the same. Clusters are produced by expansion of a gas mixture of NH3-seeded He/Ne which has been flowed over a room temperature reservoir containing PhOH. The backing pressure is typically 2 bars and the nozzle diameter is around 500 μm. The cluster size is varied by changing the backing pressure and the partial pressure of NH3 in the mixture, with the highest pressures giving rise to the largest clusters. The clusters are then laser excited and ionized in a second chamber, between the extraction plates of a TOF mass spectrometer.Picosecond time-resolved IR/NIR (ps-TRIR or ps TRNIR) spectroscopy of PhOH–(NH3)n was performed by utilizing time-resolved ultraviolet (UV)-IR/NIR-UV′ ion dip spectroscopy. The principle of the spectroscopy and details of the spectrometer are described elsewhere.43 The clusters obtained in the supersonic expansion have been studied by different excitation schemes which are illustrated in Fig. 5. Briefly, PhOH–(NH3)n was excited to the ππ* state by a ps UV pulse, νexc, and the ESHT reaction was triggered. The reaction product, ˙NH4(NH3)n−1, was ionized by a ns UV laser pulse, νion, which was fired at (typically) 30 ns after νexc. The population of the reaction product was monitored at masses of NH4+(NH3)n−1 using a time-of-flight mass spectrometer. A ps tunable NIR laser, νNIR, whose frequency was fixed to that of the 3p–3s Rydberg transition of ˙NH4(NH3)n−1 in the NIR region, was fired for Δt ps after νexc. The population of ˙NH4(NH3)n−1 was depleted by excitation to the 3p Rydberg state. If νNIR is sufficiently strong, population of ˙NH4(NH3)n−1 is generated until the νNIR irradiation (at Δt) is completely depleted. Then, the ion signal of NH4+(NH3)n−1 corresponds to the amount of ˙NH4(NH3)n−1 produced after Δt ps until 30 ns after from the νexc irradiation. Therefore, the ESHT dynamics can be monitored by measuring the intensity of ˙NH4+(NH3)n−1 as a function of Δt.
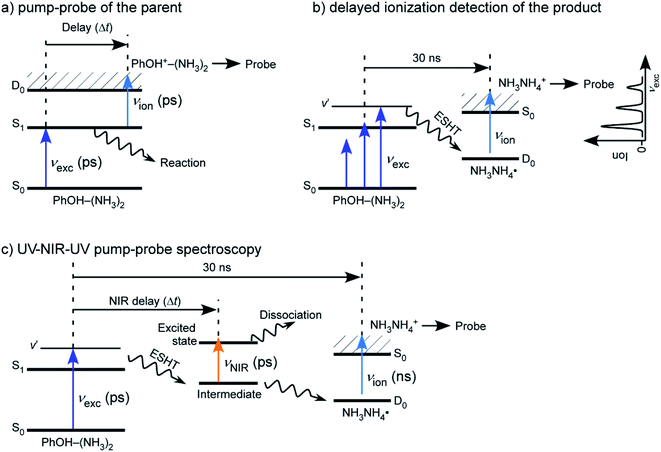 | ||
| Fig. 5 Different experimental schemes for studying the reaction dynamics in PhOH–(NH3)n clusters: (a) simple pump–probe experiment: this allows the study of the decay of the parent ion, (b) ionization after a long delay between the pump and the probe. The excited state parent ions have decayed and only the reaction product can be ionized, (c) three color experiment. A NIR laser between the first and second UV lasers excites the ˙NH4(NH3)n−1 product immediately after the H transfer and leads to the depopulation of the reaction product. Reproduced from ref. 54 with permission from the PCCP Owner Societies, copyright 2020. | ||
This spectroscopy has several variations. If νNIR is changed to a pulse from a tunable ps IR laser, νIR, the time-resolved vibrational (IR) spectra can be measured. In the time-domain, we can measure the femtosecond dynamics by replacing νexc and νNIR by femtosecond UV and NIR laser pulses. The static IR and NIR spectra can be measured by using ns tunable lasers for all three laser pulses. It should be noted that the femtosecond UV/NIR lasers do not have high enough energy resolution to distinguish individual vibrational transitions. Thus, femtosecond spectroscopy is used only in the measurement of time-resolved electronic spectra in the NIR region.
3.2 Theoretical
The first calculations on the PhOH–NH3 system showing evidence of the role of the πσ* and of the H transfer process were performed by Sobolewski et al.44 but these phenomena were inferred long ago by Evleth and collaborators on the basis of semi empirical molecular-orbital calculations.45 Using multi configuration methods (CASSCF/CASPT2) the calculations performed on PhOH–solvent, where solvent is NH3 or H2O, showed that the reaction of excited PhOH-solvent was exothermic for NH3 clusters and endothermic for H2O clusters. The role of the πσ* state could only be evidenced by the addition of diffuse functions in the basis set, necessary to fully describe the Rydberg character of this state. It was also shown that there is no barrier to the proton transfer in the ionic state (PhOH+–NH3), adding one more piece of information dismissing the ESPT mechanism discussed in an earlier paper.13 It should be noted that earlier calculations were focused on the ESPT process and did not mention the πσ* state.46,47 For clusters, the ground state geometries and the ground state vibrations have been mostly calculated at the MP2 level, and these calculations were used to assign the vibrational bands in the IR hole burning experiments and determine the cluster structure.21,43 For the excited state, two main methods were used: either (CASSCF/CASPT2) or Coupled Cluster (CC2). Both methods give good agreement with experiments. With CC2, the absorption of the excited state can be calculated and the nature of the excited state (ππ* or πσ*) compared with the experimental results.24 For large clusters, DFT/M06-2X/cc-pVTZ has also been used, with these calculations predicting a stable ground state proton transfer structure (zwitterionic structure) for PhOH–(NH3)n where n > 8.48It is interesting to note that most of the theoretical work is published alongside experiments. The experimental and theoretical work has made progress together, nicely illustrating the interest of studying clusters, for which both approaches are directly comparable.
4. Experimental findings
The ESHT mechanism has been observed to vary as a function of cluster size. As we will describe below, the study of each cluster size of PhOH–(NH3)n reveals some new information on the reaction dynamics, from the n = 1 complex in which the role of the intermolecular vibration is evidenced, to the n = 5 cluster in which the role of the proton transfer state in the ESHT is demonstrated.4.1 PhOH–(NH3)1: lifetime variation with intermolecular vibration
For the PhOH–(NH3)1 complex (hereafter “the n = 1 complex”), the time-evolution of the H transfer reaction can only be measured with the pump–probe scheme monitoring the decay of the parent ion. Indeed, since the lifetime of the ˙NH4 product is very short (13 ps), i.e. a lot shorter than the tunneling time from the ππ* to the πσ* potential surface, the concentration of the product is negligible. One should mention that this method (Fig. 5a) measures the lifetime of the parent ion after the initial excitation pulse, which corresponds to the time for the tunneling, and subsequent dissociation, to occur. The latter (dissociation) corresponds to the time necessary for the ˙NH4 moiety to be far enough from the PhO˙. Examples of such an effect are demonstrated in the case of the NaI49 diatomic molecule or in NaI–(NH3)n clusters.50The excited state lifetime of the n = 1 complex has been measured to be 1.2 ns (ref. 51) which is shorter than the lifetime of the free PhOH molecule (2 ns (ref. 52) or 2.2 ns (ref. 24)). The excitation of the intermolecular vibration at +182 cm−1 above the origin leads to a shortening of the lifetime down to 391 ± 100 ps. This vibration is the intermolecular OH⋯N stretching mode which is directly connected to the reaction path. Indeed, one can expect that when the OH⋯N distance decreases, the tunneling barrier decreases, as observed. This observation is very convincing evidence that the reaction proceeds via a tunneling mechanism. A similar observation was also made for the PhOH–(NH3)2 complex.51
Another strong argument for a tunneling process in the reaction was the observation of the change in the reaction speed upon deuteration. For the n = 1 deuterated complex, the lifetime is 7 ns (compared to 1.2 ns for the hydrogenated species), and for the n = 2 cluster, it is 7 ns instead of 400 ps.15 Thus, the simplest explanation for this observation is the presence of a tunneling barrier.
4.2 PhOH–(NH3)2: biexponential lifetime and the role of the triplet state
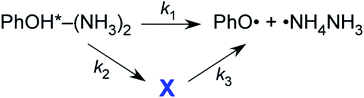
The S1 lifetime of PhOH–(NH3)2 was measured by two groups using a pump–probe ionization method.51,53 Both groups monitored the parent ion, PhOH+–(NH3)2, and measured the decay of S1 by the loss of the parent ion (pump–probe method, see Fig. 5a). The reported lifetimes are significantly different: 80 ps (ref. 53) and 400 ps.51 The main reason for the difference is the simultaneous excitation of larger clusters. Even after careful preparation of the experimental conditions, it is very difficult to avoid the coexistence of clusters of various sizes. The transitions of the PhOH–(NH3)n (n = 2–5) clusters appear in almost the same frequency range, thus, multiple species are invariably excited at the same time. Furthermore, larger clusters (n > 2) easily dissociate after ionization, and contaminate the PhOH+–(NH3)2 mass channel. The latter group51 subtracted the contributions from the larger clusters by measuring the time-evolution of the background signal, and obtained the longer lifetime. This lifetime is the convolution of the tunneling and the dissociation times. The pure H transfer lifetime (i.e. tunneling in this case) was measured by time-resolved UV-NIR-UV ion dip spectroscopy (Fig. 5c) which indicates the H transfer directly by NIR absorption. This method is insensitive to interference from larger clusters, thus the difference in the lifetimes corresponds to the dissociation lifetime.All the time-evolutions of ˙NH4NH3 formation detected by NIR absorption are biexponential.54 Here, the biexponential time evolution from the S1 origin means that an electronic relaxation would be feasible to explain this behavior, while IVR makes no contribution (Fig. 6a). The single exponential fit to the early part of the time-evolution from the S1 origin gives a lifetime of ∼270 ps, thus the 130 ps difference from the lifetime measured by the conventional method51 is the contribution of ˙NH4NH3 dissociation.
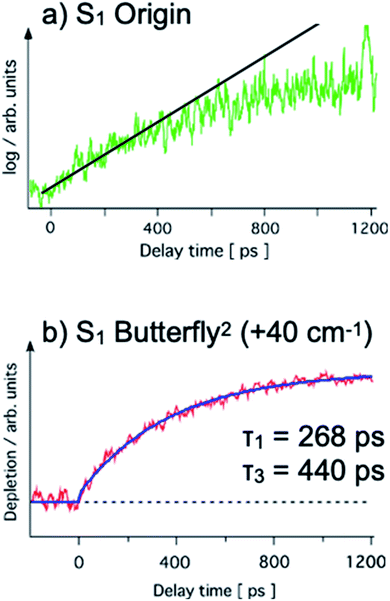 | ||
| Fig. 6 Biexponential appearance of the ˙NH4NH3 product on the pps time scale from the (a) S1 origin (log scale on vertical axis) and (b) S1 overtone of the butterfly vibration (40 cm−1 excess vibrational energy, linear scale on vertical axis) taken from ref. 54. A single exponential (267 ps) and biexponential fit (τ1 = 268 ps, τ2 = 440 ps) are shown by the solid straight line (a) and curve (b), respectively. Reproduced from ref. 54 with permission from the PCCP Owner Societies, copyright 2020. | ||
Two reaction paths and a contribution from the unknown state X in one of the paths are assumed to explain the biexponential time-evolution (see below).
The first reaction path with reaction rate k1 is the simple ESHT reaction via the conical intersection from S1 ππ* to πσ*. The second path including the state X also has an ESHT reaction for the decay of state X, but the formation of state X occurs via electronic relaxation. By solving the rate equations54 and fitting with a biexponential growth, the observed time-evolutions are fitted for the time-evolutions from several vibronic levels. Here, we assumed that k2 is common for the dynamics from all vibronic levels, and applied a global fit.54 The example of the fitted results for the time-evolution from the overtone of the butterfly vibration in S1 is shown in Fig. 6b along with the observed time-evolution on a linear vertical scale. The fitted values are τ1 = 1/k1 = 268 ps and τ3 = 1/k3 = 440 ps, and the common parameter of τ2 = 1/k2 converges at 125 ps. τ1 and τ3 vary according to the vibronic levels, but all of them are on the order of hundreds of ps.
What is state X? As mentioned above, IVR is not responsible for the biexponential behavior, thus a vibrational bath mode is not responsible. The high energy vibrational states of S0 are also not a suitable candidate for X, because such states relax quickly by the fast IVR process, thus it is not possible to access the πσ* state which promotes the ESHT reaction. A triplet state (3ππ*) of the PhOH–(NH3)2 cluster is also not reasonable, because k2 must be the rate of the intersystem crossing, which would be much slower than ps.
The last candidate is a triplet πσ* state (3πσ*). The σ* orbital is diffuse and located far away from the cluster (see Fig. 3). Thus, the 3πσ* is expected to be energetically degenerate with the 1πσ*. As a consequence, there is almost no energy gap in the intersystem crossing and thus the relaxation can be accelerated to the sub-ns order.55 The potential surface of 3πσ* crosses that of 3ππ* at a longer OH distance, and a bound state can be produced because of the avoided crossing. Then, those molecules converted to 3πσ* can be trapped in this bound state before dissociating to PhO˙ + ˙NH4NH3 along the repulsive 3πσ* potential surface (see Fig. 7).
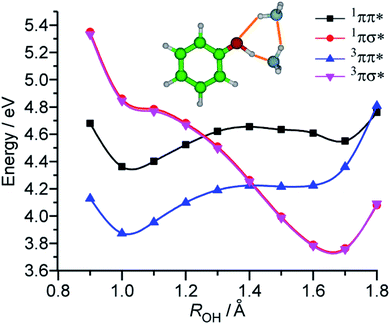 | ||
| Fig. 7 Potential curves of the PhOH–(NH3)2 cluster along the OH bond length ROH in different electronic states and spin multiplicities obtained at the RI-CC2/aug-cc-pVDZ level. Cs symmetry has been imposed for the calculations, thus avoided crossing should be considered between 1,3ππ* and 1,3πσ* states. Reproduced from ref. 54 with permission from the PCCP Owner Societies, copyright 2020. | ||
This model was confirmed by the theoretical calculations of the potential curves of 1,3ππ* and 1,3πσ* along the OH distance shown in Fig. 7. The potential curves were obtained by stretching the OH distance around the excited state equilibrium distance. The black curve represents the 1ππ* state and a local minimum at ROH = 1.7 Å corresponds to the proton transfer state. This PT state is not energetically accessible from the ππ* obtained by ground state excitation. The blue curve shows a triplet 3ππ* state that does not exhibit a local PT state minimum. The red and pink curves correspond to the singlet and triplet 1,3πσ* states, respectively. The potential curves of the singlet and triplet πσ* states are almost degenerate in energy. The dissociative potential curves of 1,3πσ* cross those of both 1ππ* and 3ππ*, thus confirming the mechanism detailed above: the biexponential time-evolutions are due to the triplet πσ* formation and successive trapping in the triplet manifold.
4.3 PhOH–(NH3)3: isomerization within the reaction products
The PhOH–(NH3)2 cluster discussed above has no isomers, and the reaction product of ESHT is a single species, ˙NH4(NH3), rendering the study of this species relatively simple. For clusters containing more than two ammonia molecules, the ESHT reaction becomes complicated in two ways. The first is the coexistence of several conformers of PhOH–(NH3)n. Excitation of different conformers leads to a difference in the initial geometry of the cluster undergoing the ESHT reaction. This complication can be minimized if the electronic transition of each conformer is well separated in energy and can be selectively excited. The second point is the conformational variety of the reaction product ˙NH4(NH3)n−1 (n ≥ 3). Isomerization between these conformers is also possible, according to the excess energy available after ESHT. This second point is essential and cannot be avoided experimentally.For PhOH–(NH3)3, hole burning spectroscopy indicates that this cluster exists in only a single geometry in the ground state.56 Its cyclic hydrogen-bonded structure, shown in the lower left of Fig. 8, was determined by interpretation of the IR spectrum with the help of theoretical calculations.21
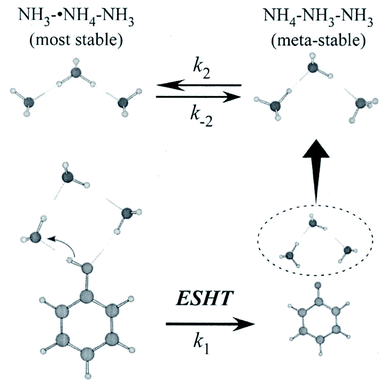 | ||
| Fig. 8 ESHT reaction scheme for the PhOH–(NH3)3 cluster. The initial cluster (lower left) reacts at a rate k1 to give the PhO˙⋯˙NH4(NH3)2 product (lower right). The ˙NH4(NH3)2 dissociates from PhO˙ (upper right) and then isomerizes to NH3˙NH4NH3, the most stable isomer (upper left) at a rate k2. Reproduced from ref. 43 with the permission of AIP Publishing, copyright 2007. | ||
Fig. 9a shows the NIR transition probing the electronic structure obtained by scanning the νNIR frequency in the UV-IR-UV pump–probe spectroscopy of PhOH–(NH3)3. The NIR absorptions at 7800 cm−1 and 9000 cm−1 are assigned to 3p–3s transitions of NH3–˙NH4–NH3 while those at 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and 12
000 cm−1 and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 originate from that of ˙NH4–NH3–NH3. The NIR absorption of ˙NH4–NH3–NH3 (Fig. 9c) rises faster than that of NH3–˙NH4–NH3 (Fig. 9b). Thus, the time-evolution shows the fast generation of ˙NH4–NH3–NH3 rather than of NH3–˙NH4–NH3. Another important point is that both species exist even after a long delay time. This suggests an equilibrium between the two species.
000 cm−1 originate from that of ˙NH4–NH3–NH3. The NIR absorption of ˙NH4–NH3–NH3 (Fig. 9c) rises faster than that of NH3–˙NH4–NH3 (Fig. 9b). Thus, the time-evolution shows the fast generation of ˙NH4–NH3–NH3 rather than of NH3–˙NH4–NH3. Another important point is that both species exist even after a long delay time. This suggests an equilibrium between the two species.
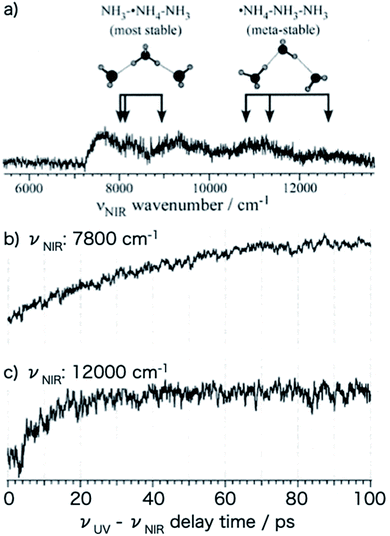 | ||
| Fig. 9 Time-evolution of the reactive products of photoexcited PhOH–(NH3)3. (a) Electronic spectrum of the ˙NH4(NH3)2 cluster. The structure at 12000 cm−1 is ˙NH4–NH3–NH3 while that at lower energy is NH3–˙NH4–NH3. The time-evolution curves (b and c) show that ˙NH4–NH3–NH3 is obtained before the generation of NH3–˙NH4–NH3. Reproduced from ref. 43 with the permission of AIP Publishing, copyright 2007. | ||
The fast formation of ˙NH4–NH3–NH3 demonstrates the memory effect of the initial geometry in the parent PhOH–(NH3)3 cluster (see Fig. 8). After photoexcitation to S1, O–H bond radical dissociation in the cyclic PhOH–(NH3)3 induces H atom transfer to the terminal NH3. This reaction generates the initial product ˙NH4–NH3–NH3 exclusively. The ˙NH4–NH3–NH3 species is less stable and thus isomerizes to the more stable NH3–˙NH4–NH3 (the barrier height is 3.1 kcal mol−1 (ref. 43 and 63)). The back reaction to the initial product under an isolated condition, leads to an equilibrium between the two species at long delay times.
The three-state model is confirmed by the application of rate equations,43 using the rate constants k1 (ESHT), k2 (isomerization), and k−2 (back-reaction) shown in Fig. 8. The details of the analysis and fitting procedures are reported in the reference, thus we will show only the fitted results here. Fig. 10 shows the time-evolution of (a) the meta-stable product ˙NH4–NH3–NH3 and (b) the final product NH3–˙NH4–NH3. The experimental time evolutions were obtained by the averaging of the time evolutions of both the NIR and IR spectra. The fitted curves obtained by the global fit of the rate equation analysis are shown by solid curves as well as the residual errors between the observations and the fit functions. The fits reasonably reproduce the time-evolution of the meta-stable and the final products with 24 ps, 6 ps, and 9 ps for the inverse of rate constants 1/k1, 1/k2 and 1/k−2, respectively. Thus, we conclude that the initial formation of the metastable product is due to the memory effect, followed by isomerization to the most stable species, and final equilibrium is attained by the back reaction.
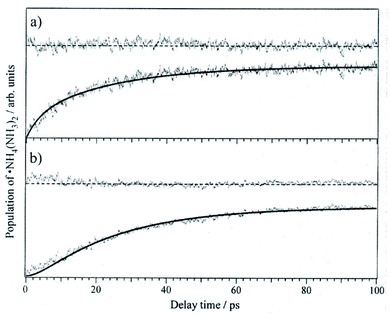 | ||
Fig. 10 The time evolutions of the products (a) ˙NH4–NH3–NH3 monitored at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, (b) the final product NH3–˙NH4–NH3 monitored at 6000 cm−1, for ESHT in the PhOH–(NH3)3 cluster. The fitted results are shown as solid curves along with the residual. Reproduced from ref. 43 with permission of AIP Publishing, copyright 2007. 000 cm−1, (b) the final product NH3–˙NH4–NH3 monitored at 6000 cm−1, for ESHT in the PhOH–(NH3)3 cluster. The fitted results are shown as solid curves along with the residual. Reproduced from ref. 43 with permission of AIP Publishing, copyright 2007. | ||
4.4 PhOH–(NH3)4: an even more complex system
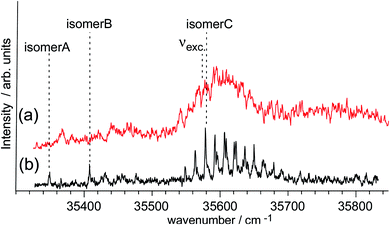
While time-resolved spectroscopy has been applied to ESHT reactions in PhOH–(NH3)2,3,5 clusters, no time-resolved spectroscopy has yet been reported for the PhOH–(NH3)4 system. To complete the systematic study of PhOH–(NH3)n, the ps TRIR and TRNIR spectroscopy of PhOH–(NH3)4 has been performed for this review. Before presenting the time resolved data, we would like to summarize the previous nanosecond spectroscopy of PhOH–(NH3)4 associated with theoretical calculations.21,56The UV action spectra of PhOH–(NH3)4 obtained by the monitoring by delayed ionization detection of the product with (a) ps and (b) ns lasers are shown in Fig. 11 (see Fig. 5b for the spectroscopic method). Four color hole burning spectroscopy shows that PhOH–(NH3)4 has three isomers, whose bands are indicated in the figure.56 Due to the lower spectral resolution of the ps laser (15 cm−1), a low frequency progression of isomer C cannot be resolved in Fig. 11a. Also, sharp and weak bands of isomers A and B cannot be seen in Fig. 11a. As a result, the ESHT time-evolution can be measured only for isomer C.
Theoretical calculations at the MP2/6-31++G(d,p) level show that a cyclic hydrogen bonded structure is the most stable for this cluster. In the early stages of the ESHT studies in PhOH–(NH3)n, the coexistence of isomers was not known. For this reason, the IR spectrum obtained by labeling the band at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 348 cm−1 (isomer A) was assigned to the cyclic hydrogen-bonded structure. However, this assignment should be re-considered because the most stable species should appear more strongly than other isomers. In this case, isomer A is significantly weaker than isomer C. Also, no IR spectra of isomers B and C have been measured. Thus, we proceed in the analysis with a tentative assignment of the isomer C as the cyclic hydrogen-bonded structure.
348 cm−1 (isomer A) was assigned to the cyclic hydrogen-bonded structure. However, this assignment should be re-considered because the most stable species should appear more strongly than other isomers. In this case, isomer A is significantly weaker than isomer C. Also, no IR spectra of isomers B and C have been measured. Thus, we proceed in the analysis with a tentative assignment of the isomer C as the cyclic hydrogen-bonded structure.
The cyclic hydrogen-bonded structure shown in Fig. 12 is similar to that of PhOH–(NH3)3. Fig. 12 also shows possible conformations of the reaction products ˙NH4(NH3)3 with their relative energies. If ESHT takes place in the parent cluster of the cyclic structure, the H atom will transfer to the terminal NH3 in the ammonia moiety. In this case, only the meta-stable product ˙NH4–NH3–NH3–NH3 (4c in Fig. 12) is produced. The NIR spectrum of reaction products from PhOH–(NH3)4 measured by ns laser systems is also shown in the figure. Theoretically predicted 3p–3s Rydberg transitions for the products 4a to 4d are also indicated in the spectrum. The spectrum clearly shows the co-existence of all four reaction products 4a to 4d. Therefore, it is reasonable to consider the isomerization of the meta-stable product 4c to the other products. However, it is too complicated to trace all the possible isomerization paths and equilibria after ESHT because of the multiple isomers of ˙NH4(NH3)3. Thus, we neglected the contributions of species 4b and 4c, and applied the three-state model to the photoexcited PhOH–(NH3)4, the meta-stable product 4c and the most stable product for this cluster, 4d.
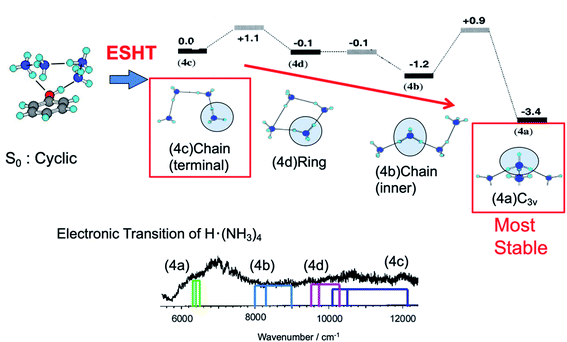 | ||
| Fig. 12 Reaction scheme for the PhOH–(NH3)4 cluster. – The initial cluster (upper left) reacts at the rate k1 to give the PhO˙–˙NH4(NH3)3 species. The initial ESHT product starting from ˙NH4(NH3)3 (4c) evolves to structures 4d and 4b and then isomerizes to the most stable C3v isomer 4a (upper right). – Lower trace: electronic spectrum of the ˙NH4(NH3)3 species, which includes the contributions of the four isomers. The colored sticks are the calculated excited states of the different isomers. Reproduced from ref. 18 and 63 with the permission of AIP Publishing, copyright 2002 and 2003, respectively. | ||
Time-evolutions of the meta-stable product 4c and the most stable product 4d were monitored by following the NIR absorption at 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and 7000 cm−1, respectively. The observed time-evolutions and the best fit of the three-state model are shown in Fig. 13. The absorption of the meta-stable product 4c rises quickly after the photoexcitation to S1 and decays gradually after 30 ps. On the other hand, the absorption of the most stable product 4d increases slowly. This is essentially the same mechanism as that observed in PhOH–(NH3)3: selective generation of the metastable 4c product due to the memory effect, and successive isomerization towards the most stable product, 4d. Good reproduction of the observed time-evolutions by the rate equations confirms the equivalent ESHT mechanism to PhOH–(NH3)3. The inverse of the rate constants 1/k1, 1/k2 and 1/k−2 are determined to be 15 ps, 25 ps and 38 ps, respectively.
000 cm−1 and 7000 cm−1, respectively. The observed time-evolutions and the best fit of the three-state model are shown in Fig. 13. The absorption of the meta-stable product 4c rises quickly after the photoexcitation to S1 and decays gradually after 30 ps. On the other hand, the absorption of the most stable product 4d increases slowly. This is essentially the same mechanism as that observed in PhOH–(NH3)3: selective generation of the metastable 4c product due to the memory effect, and successive isomerization towards the most stable product, 4d. Good reproduction of the observed time-evolutions by the rate equations confirms the equivalent ESHT mechanism to PhOH–(NH3)3. The inverse of the rate constants 1/k1, 1/k2 and 1/k−2 are determined to be 15 ps, 25 ps and 38 ps, respectively.
As compared to PhOH–(NH3)3, 1/k1, the time constant for the tunneling is two times faster (15 ps instead of 30 ps) whereas the isomerization constants (1/k2 and 1/k−2) are longer (25/38 ps instead of 6/9 ps for PhOH–(NH3)3). The shorter tunneling time implies that the tunneling barrier for PhOH–(NH3)4 is smaller than that in PhOH–(NH3)3, in agreement with the interpretation given in Section 4.7 “General model for ESHT and ESPT”. Concerning the isomerization, the barriers are nearly the same for ˙NH4(NH3)2 and ˙NH4(NH3)3 so the slower reaction rate can be accounted for by the higher density of states in ˙NH4(NH3)3 compared to NH4(NH3)2.
4.5 PhOH–(NH3)5: the return of proton transfer
S1–S0 electronic spectra of PhOH–(NH3)n (n ≤ 4) exhibit well-resolved structures. This is consistent with the picosecond order of the ESHT reaction rate. In contrast, PhOH–(NH3)5 gives rise to a broad absorption, which indicates a significant change of the reaction mechanism for this cluster. Here, we would like to summarize the structural information obtained from nanosecond “static” spectroscopy. The structure of the PhOH–(NH3)5 cluster in S0 has been assigned to a bicyclic hydrogen-bonded structure (see Fig. 14).21 Photoexcitation of the cluster triggers O–H cleaving by ESHT, with the H atom transferred to the nearest ammonia in the ammonia moiety. From this geometry, the expected nascent product is the structure where the fifth ammonia molecule is hydrogen bonded to one of the NH3 in ˙NH4(NH3)3 in C3v symmetry, which is shown in Fig. 14 as C3v+1. However, the NIR spectrum obtained by ns UV-NIR-UV pump–probe spectroscopy (Fig. 2 and lower right panel in Fig. 14) shows a strong and broad band at ∼6000 cm−1 which is assigned to ˙NH4(NH3)3 in the most stable tetrahedral structure Td, not C3v+1. Therefore, several intermediate species are expected to play a role in the ESHT reaction of PhOH–(NH3)5.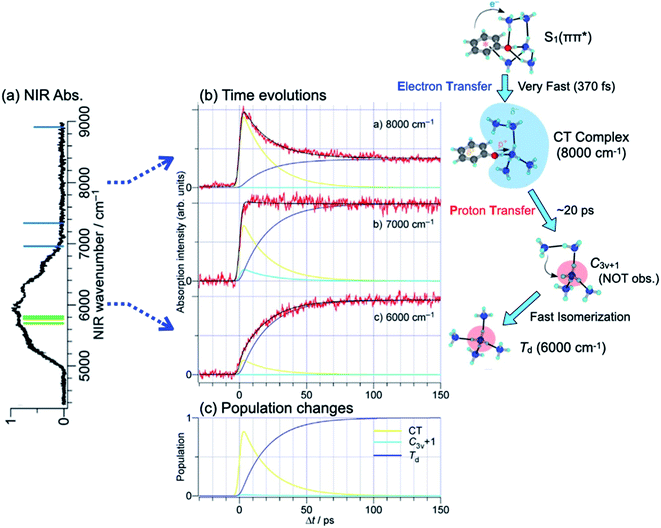 | ||
| Fig. 14 H transfer dynamics of PhOH–(NH3)5: (a) absorption spectrum of the Td ˙NH4(NH3)4 species, the most stable structure, (b) time evolutions of the electronic structures: at 8000 cm−1 excitation of the charge transfer state within PhOH–(NH3)5, at 6000 cm−1 the final Td structure, and at 7000 cm−1 the overlap of both contributions. The right panel shows a scheme of the reaction events and time evolution of the electronic structures. (c) shows the population evolution deduced from the fit. The C3v+1 structure is barely populated. Reproduced from ref. 58 with the permission of Wiley-VCH Verlag GmbH & Co, copyright 2018. | ||
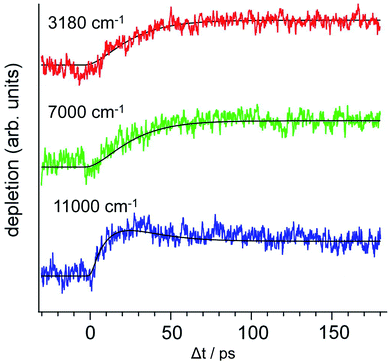
The time-evolutions of the NIR signals at 6000 cm−1, 7000 cm−1 and 8000 cm−1 are shown in Fig. 14.57,58 The signal at 6000 cm−1, which corresponds to the most stable Td product, grows gradually and becomes constant at around 100 ps. The signal at 8000 cm−1 rises rapidly and decays slowly. The ultrafast rise of the signal is consistent with the broad spectral feature of the UV absorption transition of PhOH–(NH3)5. The time-evolution at 7000 cm−1 shows a sharp rise and the signal is constant after the rise. This is explained by an overlapping of the decreasing signal at 8000 cm−1 and the increasing signal of the Td species at 6000 cm−1. Quantum chemical calculations suggest two possible transient species in this region. One is the nascent ESHT product of C3v+1 symmetry, of which the 3px,y,z–3s transitions are shown by blue bars in Fig. 14a. Another is the 4p Rydberg–σ* transition of the CT complex originating from the occupation of an electron in the πσ* orbital, of which the transition energy is 0.85 eV (6900 cm−1). These two species are considered potential candidates for the 8000 cm−1 absorption. In both cases, this signal is a signature of electron transfer from the aromatic π* to the σ* orbitals.
The NIR transitions are a good indicator of electron transfer. On the other hand, the real N–H bond formation dynamics can be observed independently by IR spectroscopy in the 3 μm region. Fig. 15 shows the ps-TRIR spectra of PhOH–(NH3)5. The theoretical IR spectra of both the C3v+1 and Td products are also shown in Fig. 15b. Here, the Td product will exhibit intense vibrational transitions at 2965 cm−1 (H-bonded NH stretching of ˙NH4) and 3260 cm−1 (free NH stretching of NH3), while the C3v+1 species is calculated to give rise to IR absorption at 3217 cm−1 (free NH stretching of NH3). The ps-TRIR spectra show a strong transition at ∼3200 cm−1 and a broad absorption at ∼3000 cm−1. Time-evolutions at 2983 cm−1 (A in Fig. 15a), 3165 cm−1 (B) and 3248 cm−1 (C) are shown in Fig. 15c. Both signals at A and C gradually grow in intensity with increasing delay time, and no sharp rise was found. The signal at B should be sensitive to the presence of the nascent C3v+1 product. However, the time-evolution does not show an ultrafast rise, and can be fitted by single exponential functions with lifetimes of ∼20 ps. This suggests that the ps-TRIR spectra reflect mainly the vibrational transitions of the Td product.
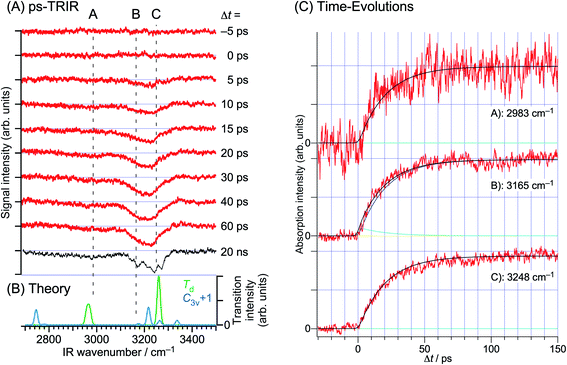 | ||
| Fig. 15 H transfer dynamics of PhOH–(NH3)5 monitored through the free NH vibrations. Left: (a) experimentally-derived time-evolution of the IR spectrum as a function of the delay between the pump and the probe, and (b) the calculated transitions for the two postulated geometries. Right: time-evolution of the vibrational absorption at different wavelengths shown in the left-hand spectra. In contrast to the electronic absorption, there are no very short dynamics. Reproduced from ref. 58 with the permission of Wiley-VCH Verlag GmbH & Co, copyright 2018. | ||
The right panel in Fig. 14 summarizes the ESHT reaction mechanism and spectroscopic signatures for the possible species involved. The time-evolutions are analyzed by rate equations with the rate constants kS1–CT, kCT–C3v+1, and kisomerization. The global fit reproduced the observed time-evolutions, as shown by black solid curves in Fig. 14 and 15, with 1/kS1–CT ≪ 3 ps, 1/kCT−C3v+1 = 20.2 ps, and 1/kisomerization (=1/kC3v+1–Td) = 0.4 ps. The population changes of CT, C3v+1 and Td species extracted from the fit are also illustrated in Fig. 14c. The fit shows that the electron transfer from PhOH to the ammonia moiety is very fast (≪3 ps). However, the proton transfer is slower (20 ps) and is decoupled from the electron transfer. It is clearly a different mechanism compared to that observed in the smaller clusters (n ≤ 4). It should be noted that the time resolved experiment in the femtosecond regime later determined the time constant of the initial electron transfer as 370 fs.59
The electron-proton decoupling for n = 5 is rationalized by the strong distortion of the potential surfaces of the S1 and S2 states. Fig. 16 shows the calculated potential energy curves obtained by stretching the OH distance, ROH.58 The other coordinates are fixed at the geometry in S0, of which the symmetry is C1. Due to the C1 symmetry, π/σ symmetry does not exist, but we distinguish the major character of the excited states from the shape of their orbitals. If the orbital is mainly localized on the aromatic ring, like the valence orbital, we call it π or π* and it is denoted by blue squares. In the case where the orbital is diffuse like the Rydberg orbital, it is denoted as σ* and is indicated by red circles. Where ROH is smaller than 1.2 Å, S1 and S2 have ππ* and πσ* characters, respectively. This character is reversed beyond the conical intersection (CI) at ∼1.2 Å and the S1 becomes πσ* in character. From the Franck–Condon (FC) position (∼1.0 Å), the reaction takes place without any barrier in S1. This means that the proton moves fast along the reaction coordinate. When the proton crosses over the CI, the character of S1 changes to πσ*. This means that the π* electron is transferred to the Rydberg-like σ* orbital, and the CT complex is generated. The CT complex gives rise to the NIR transitions at ∼8000 cm−1 which corresponds to the fast rise of 370 fs.59 At that time, the proton – which goes over the CI with significant speed – proceeds into the S2 state rather than following the S1 potential curve. Here, S2 has ππ* character beyond the CI, thus this corresponds to the classical ESPT reaction. The proton can be trapped in S2 for a while, and due to the Coulomb attraction this cluster cannot dissociate. The S2 state relaxes by internal conversion to S1 (of πσ* character), which immediately causes dissociation and the successive formation of the final Td product. In this scenario, the observed ∼20 ps lifetime for the formation of the Td product corresponds to the rate of the IC, i.e. the lifetime of S2. Further detailed discussion allowing a systematic understanding of the ESHT mechanism will be given in the next section.
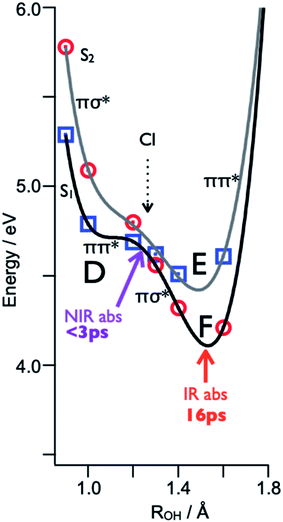 | ||
| Fig. 16 Excited state potential curve for the PhOH–(NH3)5 cluster along the OH coordinate. The cluster is excited in the Franck–Condon (FC) region (D) on the ππ* surface (black curve). It evolves within 3 ps toward the Conical Intersection (CI). Then, diabatically, it can continue to the ππ* proton transfer state (E) or stay on the adiabatic surface and relax to the bottom of the πσ* state (F). The tunneling barrier present for the smaller cluster sizes has disappeared, since the ππ* proton transfer energy (E) is lower in energy than the ππ* in the FC region (D). Reproduced from ref. 58 with the permission of Wiley-VCH Verlag GmbH & Co, copyright 2018. | ||
4.6 Larger clusters: proton transfer in the ground state
ESHT has not been detected in PhOH–(NH3)n when n = 6 or larger, because NH4+(NH3)n−1 (n ≥ 6) are not observed in the mass-spectrum after two-photon ionization of PhOH–(NH3)nvia the S1 state (see Fig. 1, for n = 6, 7, …). The absence of NH4+(NH3)n−1 suggests two possibilities: ESPT or proton transfer in the neutral ground state (GSPT). However, theoretical calculations show that ππ* states which promote ESPT are higher in energy than the πσ* state for clusters of n ≥ 6, as shown in Fig. 17. Thus, ESPT cannot be responsible for the absence of the reaction products NH4+(NH3)n−1.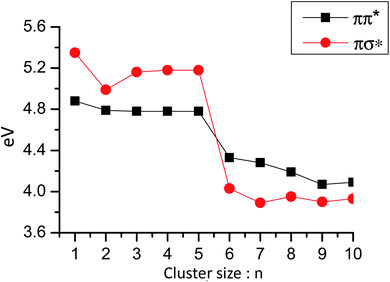 | ||
| Fig. 17 Vertical excitation energies of ππ* and πσ* states in PhOH–(NH3)n clusters as a function of the number of ammonia molecules. For n ≤ 5 the calculated ground state structure is PhOH–(NH3)n and for n > 5 the zwitterionic PhO−–(NH4+)(NH3)n−1 structure. For these structures the lowest energy excited state is the πσ* state, which has a Rydberg character, a very small oscillator strength and a very long lifetime (around 50 ns).60 Reproduced from ref. 60 with permission from the PCCP Owner Societies, copyright 2009. | ||
GSPT is reasonable to explain the observed results. At a certain size, the proton affinity of the ammonia moiety in the cluster will be large enough to induce proton transfer from PhOH in the ground state, leading to the formation of a zwitterion. When the zwitterionic cluster PhO−–NH4+(NH3)n−1 is excited, there is no driving force to dissociate the cluster, since the most stable NH4+ structure is already formed and this system relaxes in the excited state by evaporation of NH3 fragments.12,15 This is consistent with the absence of the fragments NH4+(NH3)n−1.
The obvious question, just like in the case of ESPT, is: what is the threshold size for GSPT? The results of the mass-spectra naturally suggest the threshold size n = 6. This is supported by the measurement of the ionization potential (IP) of PhOH–(NH3)n (ref. 61) through a one photon experiment using synchrotron light to avoid the excited state reaction in a two photon process through S1. The measured IP drops for n = 6 and larger clusters. This can be explained by the formation of the PT structure in the ground state. It is clear from calculations13,44,60 and experiments that the most stable form in the ionic state is the PT structure (PhO–NH4+) by around 0.8 eV compared to the PhOH+–NH3 form. Thus, a PT structure in S0 has a good FC factor to access the adiabatic ionic minimum (i.e. the PT structure), whereas the non-PT structure of ground state PhOH–NH3 cannot access the adiabatic IP (PT structure) in the ion and this leads to a higher IP.
However, the size-selected IR spectra of PhOH–(NH3)n (n = 0–11) measured by IR-UV dip spectroscopy raised a doubt about the threshold size of n = 6.62 The IR spectra showed the signature of PhOH vibrations (such as C–O stretching) even for clusters of n = 6 and the expected marker band (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching) of PhO− was not found. The disappearance of the C–O stretching band was not clear, even in larger sized clusters, whereas the C–O–H bending vibration, another vibrational signature of PhOH, disappeared at n ≥ 9. From these results, it was suggested that n = 6 may be the beginning of GSPT, but that both PT and non-PT structures co-exist for n = 6–8, and all the co-existing species become PT structures at n = 9.
O stretching) of PhO− was not found. The disappearance of the C–O stretching band was not clear, even in larger sized clusters, whereas the C–O–H bending vibration, another vibrational signature of PhOH, disappeared at n ≥ 9. From these results, it was suggested that n = 6 may be the beginning of GSPT, but that both PT and non-PT structures co-exist for n = 6–8, and all the co-existing species become PT structures at n = 9.
A recent theoretical paper,48 at the M06-2X/cc-pVTZ level of theory, has revealed that clusters of n ≥ 9 exhibit zwitterionic structures. In this paper, a rather impressive number of cluster structures were investigated and the energy of zwitterionic structures becomes comparable to the non-PT structures only for clusters of n ≥ 9. There is obviously a discrepancy compared to previous studies and a few possibilities could be responsible for this. One is that the evaporation processes following either ionization or excited state reaction are very important and have been overly neglected in the experimental interpretations. In this hypothesis, the ions observed at n = 6 come from larger ones: this may be tested experimentally but has not been done yet. Another possibility might be that the DFT method is not appropriate for describing such a system and the energy of some structures can be tested with other methods (MP2, CCSD(T), …), although this requires huge computational power at the present time. These possibilities have not been investigated, leaving work to be done by the next generation.
4.7 General model for ESHT and ESPT
We have determined the following three points on the ESHT process mainly from experiments: (1) the reaction speed increases as the cluster size increases, (2) the reaction mechanism changes at n = 5 and (3) the H transfer proceeds through a tunneling mechanism for small clusters (n < 5).Let us discuss the cluster size dependence of the ESHT lifetime, which is summarized in Table 1. The ESHT lifetimes for n = 2, 3, 4, and 5 (electron transfer ET and proton transfer PT) are measured by the rise of the reaction products ˙NH4(NH3)n−1, while that of n = 1 is extracted from the pump–probe experiment in which the size selection of the cluster is not perfect because of the evaporation of NH3 after ionization. Thus, the lifetime of n = 1 may not be “clean” in comparison to other values, however, the order of the lifetime can be trusted. Thus, the ESHT lifetime exhibits a tendency to drop significantly upon increasing the number of solvent molecules in the cluster: nanosecond at n = 1, sub-nanosecond at n = 2, tens of ps at n = 3 and 4, and finally femtosecond for n = 5.
At first, this change was attributed to the efficient stabilization of πσ* by the higher solvation. It sounds reasonable because the diffuse σ* electron can easily be stabilized by solvents. Nevertheless, such a sharp stabilization was not found in the theoretical calculations;60,63 the absolute energy is lowered by the solvation but the energy gaps between ππ* and πσ* are not changed much at the vertical excitation.
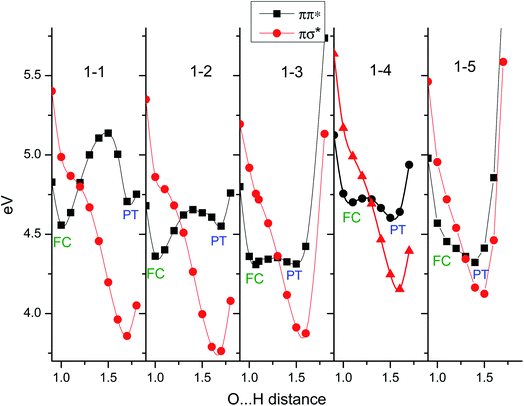
This is shown in Fig. 18. Here, the clusters are maintained in Cs symmetry and the initial structures are optimized in the ground state.60 The clusters are then optimized in the ππ*(A′) state and the potentials are obtained by stretching the OH distance. For the PhOH–(NH3)5, there is no barrier, so that the FC ππ* region optimization requires the constraint of the OH distance at 1 Å. It should be noted that the potential curves for n = 5 (1–5 in the figure) are essentially the same as those in Fig. 16 but are calculated with simpler assumptions, such as Cs symmetry. As one can see, the πσ* potential curves at long O–H distances have a minimum which corresponds to the attachment of the H to N (i.e. formation of ˙NH4) but along the O–N coordinate, this πσ* state is dissociative and this is responsible for the separation of the ˙NH4(NH3)n−1 cluster away from PhO˙; the one dimension calculations does not take into account this dissociation of ˙NH4(NH3)n−1 from the clusters. Although these curves cannot be compared directly with the experiments, an essential picture emerges from these calculations:
(a) At the equilibrium of the ππ* geometry (around the FC region), the ππ*/πσ* gap does not change as the cluster size increases, being 0.5 eV for the free molecule, 0.4 for n = 2, 3, 4 and rising back to 0.5 eV for n = 5.
(b) The PT structures (ππ* at long OH distance) gradually decrease in energy, being of comparable energy to the ππ* state for n = 3 and being lower in energy for n ≥ 4.
(c) The minimum of the PT structure (ππ*) is obtained at 1.75 A for n = 1 (1–1 in Fig. 18) and is shifted to 1.5 Å for n = 5, indicating a shrinking of the O–N distance as the cluster size increases in the PT structure.
(d) Since the reaction is controlled by tunneling,21 both (b) and (c) favor a lowering of the barrier and thus the HT reaction becomes faster.
In Fig. 18, it can be seen that the shape of the πσ* remains approximately the same as the cluster size changes, although the energies are shifted by the cluster size. This is opposite to the pattern observed for the ππ* state. The ππ* potential curves each have two minima, except for n = 5: one at around the FC region and another for the PT (PhO−–NH+4(NH3)n−1) structures at greater OH distance. In contrast to the πσ* case, along the O–N coordinate this is a bound state because ionic character prevents fragmentation. For n = 1–3, the minima in the FC region are the global minima but the relative energies of the PT minima gradually decrease and become comparable at n = 3. The PT minimum becomes the global minimum at n = 4 and further stabilization of the PT structure makes the ππ* potential barrier-less at n = 5.
The H transfer tunneling barrier along the OH coordinate is generated by the potential crossing (conical intersection) between the ππ* and the πσ* potential curves. Therefore, the height of the barrier strongly depends on the steepness of the ππ* state as the OH is stretched. Another barrier in this system is that to the PT structure in the ππ* potential curves. For small sizes (n = 1), the PT structure is higher in energy than the FC region and the barrier to the PT structure on the ππ* is also quite high. Thus, the PT reaction cannot take place after optical excitation to S1. The HT reaction is possible but the barrier is quite high because of the steep ππ* potential. This is a reasonable explanation for the slowest HT reaction in the series. As the cluster size increases, the PT structure and the barrier on the ππ* potential decrease, which also suppresses the barrier height of the H transfer. This tendency terminates in the absence of any barrier for n ≥ 5. Gradual suppression of the barrier can be used to rationalize the size dependence of the ESHT rate as shown in Table 1. This means that the ESHT dynamics vary according to the ππ* potential curve, which in turn is controlled by the stability of the PT structure.
This systematic understanding of the ESHT reaction rate provides a comprehensive understanding of the relation between ESHT and ESPT. It is interesting to note that the initial idea of ESPT which started this research in the 1980s was dismissed at the beginning of the 21st century. However, this review has revealed “The return of ESPT” in a quite different form as being a key mechanism in ESHT.
4.8 Other examples
The lifetime of the first excited state in the 3-methylindole–NH3 complex is strongly dependent on the intermolecular vibrations. As experimentally observed,73 the excitation of the NH⋯N stretching coordinate is expected to favor the H transfer reaction. High-level ab initio optimization of the equilibrium geometry in the S1 state and calculated vibrational frequencies compared with the experimental observations seem to indicate that the in-plane bending vibration also favors the H transfer from the aromatic chromophore (3-methylindole) to the solvent (ammonia), the reaction being 530 ps on the 0–0, 145 ps for 1 quantum in the N–H⋯NH3 stretch and 205 ps for 1 quantum in the N–H⋯NH3 bend.
5. Concluding remarks
PhOH–(NH3)n is a very rich system in which many subtleties of the reaction dynamics of the hydrogen mediated reaction exist. The excited state dynamics is systematically changed by the size of the ammonia moiety, of which the basicity increases with the number of molecules. Although this idea, initiated in Leutwyler's group4,79 was used for the study of ESPT in clusters, it also explains systematic variation in the ESHT mechanism. This is because the change in the basicity distorts the potential surface of the optically active ππ* state due to stabilization of the PT local minimum. The potential distortion gives rise to a significant change in the tunneling barrier to H atom release, which is produced by the crossing to the πσ* potential surface.The lowering in energy of the PT structure is strongly size dependent. For n = 1, the PT structure at O–H = 1.8 Å is higher in energy by 0.15 eV than the FC structure (PhOH*–(NH3)n), and its energy decreases as the cluster size increases. At n = 4, this structure seems to be more stable than that of the FC, although a barrier to PT transfer still exists, and at n = 5 the energy of the PT structure is so low (−0.22 eV) that the PT reaction becomes barrierless. In contrast to the ππ* state, the πσ* state is relatively insensitive to the cluster size, primarily because the potential shape of this repulsive state is essentially independent of the molecular system. This insensitive character is given by the energy of its asymptote at long distance. It corresponds to the bond dissociation energy of the OH (NH) which is more or less the same for many molecules (OH bond energy 4.8 eV, or 3.2 for NH). Thus, the systematic change of the ππ* potential surface directly gives the clear size dependence of the ESHT mechanism, as well as the ESPT (rather than ESHT) reaction in naphthol.
Quite unexpectedly, the role of the hypervalent dissociative Rydberg state – evidenced experimentally and theoretically for the PhOH–(NH3)n system – has been found to be key to processes in the excited states of many protonated ions such as the aromatic amino acids. In these cases, the excess proton on the amino group (NH3+) can easily accept an electron after optical excitation to a hypervalent dissociative state which leads to H loss or H transfer depending on the nearby atom. This first step controls both the ensuing long term dynamics, and the selectivity of the fragmentation processes.78 This work is a benchmark, demonstrating the role of the excited state reaction in leading to the formation of radical pairs through the H loss, which was too often neglected before. The H loss from aromatic molecule is now quite a standard paradigm. Extension of the ESHT reaction to describe other processes is now occurring, notably in the description of excited state H abstraction by aromatic molecules, which is the reverse process of ESHT and is demonstrated in photoexcited pyridine–H2O system.80–83 These reverse process studies are still in their infancy but might grow rapidly to resolve the world energy crisis. We hope that the up-to-date mechanism of the ESHT reaction and re-definition of the role of ESPT will thus provide a firm base for the understanding and design of this new direction of excited state dynamics.
Author contributions
C. J., M. M. and M. F. conceived and designed the project. M. M. measured and analysed the spectra. C. J. performed and analysed the quantum chemical calculations. C. J. and M. F. co-wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are deeply indebted to their collaborators who were the work force of all these studies. This group is an international team which includes Dr C. Dedonder (U. Aix-Marseille), Dr G. Gregoire (U. Paris-Saclay), Dr S. Martrenchard (U. Paris-Sud), and Dr D. Solgadi (U. Paris-Sud) from France, Prof. G. A. Pino (Cordova U.) from Argentina, Prof. Dr A. L. Sobolewski (Inst. Physics Polish Acad. Sci.) from Poland, Prof. Dr W. Domcke (T. U. München) from Germany, and Prof. Shun-ichi Ishiuchi (Tokyo Tech.), Prof. Makoto Sakai (Okayama Sci. U), Prof. Kenro Hashimoto (Open U. Japan), and Mr Ryuhei Ohara (Tokyo Tech.) from Japan, as well as their graduate students. The authors would like to thank Dr Jennifer Noble (U. Aix-Marseille) for careful reading of the manuscript and her useful comments. This work was supported in part by KAKENHI (JP205104008) on innovative area (2503), KAKENHI (JP19H05527, JP18H01938, JP19K23624) of the JSPS, World Research Hub Initiatives at Tokyo Institute of Technology, the Cooperative Research Program of the “Network Joint Research Center for Materials and Devices” from the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan, and the RIKEN Pioneering Project, “Fundamental Principles Underlying the Hierarchy of Matter: A Comprehensive Experimental Study”. We also acknowledge the use of the computing facility cluster Meso-LUM of the LUMAT federation (LUMAT FR 2764).References
- T. Förster, Die pH-Abhängigkeit der Fluoreszenz von Naphthalinderivaten, Z. Elektrochem. Angew. Phys. Chem., 1950, 54, 531–535 Search PubMed.
- H. Beens, K. H. Grellmann, M. Gurr and A. H. D. Weller, Effect of solvent and temperature on proton transfer reactions of excited molecules, Discuss. Faraday Soc., 1965, 39, 183–193 RSC.
- N. Mataga, Y. Kawasaki and Y. Torihashi, On the mechanism of proton transfer reactions in the excited hydrogen bonded complexes, Theor. Chim. Acta, 1964, 2, 168–176 CrossRef CAS.
- O. Cheshnovsky and S. Leutwyler, Transfer in neutral microsolvent clusters, Chem. Phys. Lett., 1985, 121, 1–8 CrossRef CAS.
- S. K. Kim, J. J. Breen, D. M. Willberg, L. W. Peng, A. Heikal, J. A. Syage and A. H. Zewail, Solvation Ultrafast Dynamics Reactions. 8. Acid-Base Reactions in Finite-Sized Clusters Naphthol in Ammonia, Water, and Piperidine, J. Phys. Chem., 1995, 99, 7421–7435 CrossRef CAS.
- J. A. Syage, Ultrafast Measurements of Chemistry in Clusters: Excited-State Proton Transfer, J. Phys. Chem., 1995, 99, 5772–5786 CrossRef CAS.
- D. C. Lührs, R. Knochenmuss and I. Fischer, Excited-state proton transfer in 1-naphthol(NH3)n clusters: Wavelength-dependence of the picosecond pump–probe spectra, Phys. Chem. Chem. Phys., 2000, 2, 4335–4340 RSC.
- C. Dedonder-Lardeux, D. Grosswasser, C. Jouvet, S. Martrenchard and A. Teahu, Evaporation after ionization in molecular clusters: application to 1-naphthol–(NH3)n, Phys. Chem. Chem. Phys., 2001, 3, 4316–4324 RSC.
- T. Shimizu, M. Miyazaki and M. Fujii, Theoretical Study on the Size Dependence of Excited State Proton Transfer in 1-Naphthol-Ammonia Clusters, J. Phys. Chem. B, 2015, 119, 2415–2424 CrossRef CAS.
- C. Jouvet, C. Lardeux-Dedonder, M. Richard-Viard, D. Solgadi and A. Tramer, Reactivity of molecular clusters in the gas phase: proton-transfer reaction in neutral phenol-(ammonia)n and phenol-(ethylamine)n, J. Phys. Chem., 1990, 94, 5041–5048 CrossRef CAS.
- D. Solgadi, C. Jouvet and A. Tramer, Resonance-Enhanced Multiphoton Ionization Spectra and Ionization Thresholds of Phenol–(NH3)n Clusters, J. Phys. Chem., 1988, 92, 3313–3315 CrossRef CAS.
- O. David, C. Dedonder-Lardeux and C. Jouvet, Is there an Excited State Proton Transfer in phenol clusters? Hydrogen Detachment and Transfer to Solvent: A key for non-radiative processes in clusters, Int. Rev. Phys. Chem., 2002, 21, 499–523 Search PubMed.
- J. Steadman and J. A. Syage, Picosecond Studies of Proton Transfer in Clusters. 2. Dynamics and Energetics of Solvated Phenol Cation, J. Am. Chem. Soc., 1991, 113, 6786–6795 CrossRef CAS.
- M. Schmitt, C. Jacoby, M. Gerhards, C. Unterberg, W. Roth and K. Kleinermanns, Structures and vibrations of phenol(NH3)2–4 clusters, J. Chem. Phys., 2000, 113, 2995–3001 CrossRef CAS.
- G. Grégoire, C. Dedonder-Lardeux, C. Jouvet, S. Martrenchard and D. Solgadi, Has the Excited State Proton Transfer Ever Been Observed in Phenol−(NH3)n Molecular Clusters?, J. Phys. Chem. A, 2001, 105, 5971–5976 CrossRef.
- G. A. Pino, C. Dedonder-Lardeux, G. Grégoire, C. Jouvet, S. Martrenchard and D. Solgadi, Intracluster hydrogen transfer followed by dissociation in the Phenol–(NH3)3 Excited State PhOH(S1)–(NH3)3→PhO˙+(NH4)(NH3)2, J. Chem. Phys., 1999, 111, 10747–10749 CrossRef CAS.
- G. Pino, G. Grégoire, C. Dedonder-Lardeux, C. Jouvet, S. Martrenchard and D. Solgadi, A forgotten channel in the excited state dynamics of phenol–(ammonia)n clusters: Hydrogen transfer, Phys. Chem. Chem. Phys., 2000, 2, 893–900 RSC.
- S. Ishiuchi, K. Daigoku, M. Saeki, M. Sakai, K. Hashimoto and M. Fujii, Hydrogen transfer in photoexcited phenol/ammonia clusters by UV–IR–UV ion dip spectroscopy and ab initio molecular orbital calculations. I. Electronic transitions, J. Chem. Phys., 2002, 117, 7077–7082 CrossRef CAS.
- S. Nonose, T. Taguchi, F. Chen, S. Iwata and K. Fuke, Electronic Spectra and Structures of Solvated NH4 Radicals, NH4(NH3)n (n = 1–8), J. Phys. Chem., 2002, 106, 5242–5248 CrossRef CAS.
- S. Nonose, T. Taguchi, K. Mizuma and K. Fuke, Electronic spectra of solvated NH4 radicals NH4(NH3)n for n = 1–6, Eur. Phys. J. D, 1999, 9, 309–311 CrossRef CAS.
- S. Ishiuchi, K. Daigoku, M. Saeki, M. Sakai, K. Hashimoto and M. Fujii, Hydrogen transfer in photo-excited phenol/ammonia clusters by UV–IR–UV ion dip spectroscopy and ab initio molecular orbital calculations. II. Vibrational transitions, J. Chem. Phys., 2002, 117, 7083–7093 CrossRef CAS.
- W. Domcke and A. L. Sobolewski, Unraveling the molecular mechanisms of photoacidity, Science, 2003, 302, 1693–1694 CrossRef CAS.
- A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Excited-state hydrogen detachment and hydrogen transfer driven by repulsive 1πσ* states: A new paradigm for nonradiative decay in aromatic biomolecules, Phys. Chem. Chem. Phys., 2002, 4, 1093–1100 RSC.
- G. A. Pino, A. N. Oldani, E. Marceca, M. Fujii, S. Ishiuchi, M. Miyazaki, M. Broquier, C. Dedonder and C. Jouvet, Excited state hydrogen transfer dynamics in substituted phenols and their complexes with ammonia: ππ*–πσ* energy gap propensity and ortho-substitution effect, J. Chem. Phys., 2010, 133, 124313 CrossRef CAS.
- G. M. Roberts, A. S. Chatterley, J. D. Young and V. G. Stavros, Direct Observation of Hydrogen Tunneling Dynamics in Photoexcited Phenol, J. Phys. Chem. Lett., 2012, 3, 348–352 CrossRef CAS.
- R. J. Lipert and S. D. Colson, Deuterium isotop effects on S1 radiationless decay in phenol and on intermolecular vibrations in the phenol–water complex, J. Phys. Chem., 1989, 93, 135–139 CrossRef CAS.
- Z. Lan, W. Domcke, V. Vallet, A. L. Sobolewski and S. Mahapatra, Time-dependent quantum wave-packet description of the 1πσ* photochemistry of phenol, J. Chem. Phys., 2005, 122, 224315 CrossRef.
- O. P. J. Vieuxmaire, Z. Lan, A. L. Sobolewski and W. Domcke, Ab initio characterization of the conical intersections involved in the photochemistry of phenol, J. Chem. Phys., 2008, 129, 224307 CrossRef.
- G. A. King, T. A. A. Oliver, M. G. D. Nix and M. N. R. Ashfold, High Resolution Photofragment Translational Spectroscopy Studies of the Ultraviolet Photolysis of Phenol-d5, J. Phys. Chem., 2009, 113, 7984–7993 CrossRef CAS.
- K. R. Yang, X. Xu, J. Zheng and D. G. Truhlar, Full-dimensional potentials and state couplings and multidimensional tunneling calculations for the photodissociation of phenol, Chem. Sci., 2014, 5, 4661–4680 RSC.
- X. Xu, J. Zheng, K. R. Yang and D. G. Truhlar, Photodissociation Dynamics of Phenol: Multistate Trajectory Simulations including Tunneling, J. Am. Chem. Soc., 2014, 136, 16378–16386 CrossRef CAS.
- M. N. R. Ashfold, G. A. King, D. Murdock, M. G. D. Nix, T. A. A. Oliver and A. G. Sage, πσ* excited states in molecular photochemistry, Phys. Chem. Chem. Phys., 2010, 12, 1218–1238 RSC.
- M. N. R. Ashfold, B. Cronin, A. L. Devine, R. N. Dixon and M. G. D. Nix, The role of πσ* excited states in the photodissociation of heteroaromatic molecules, Science, 2006, 312, 1637–1640 CrossRef CAS.
- R. N. Dixon, T. A. A. Oliver and M. N. R. Ashfold, Tunnelling under a conical intersection: Application to the product vibrational state distributions in the UV photodissociation of phenols, J. Chem. Phys., 2011, 134, 194303 CrossRef.
- C.-M. Tseng, Y. T. Lee, C.-K. Ni and J.-L. Chang, Photodissociation dynamics of the chromophores of the amino acid tyrosine: p-methylphenol, p-ethylphenol, and p-(2-aminoethyl)phenol, J. Phys. Chem. A, 2007, 111, 6674–6678 CrossRef CAS.
- C. M. Tseng, Y. T. Lee and C. K. Ni, H atom elimination from the πσ* state in the photodissociation of phenol, J. Chem. Phys., 2004, 121, 2459–2461 CrossRef CAS.
- K. C. Woo and S. K. Kim, Multidimensional H Atom Tunneling Dynamics of Phenol: Interplay between Vibrations and Tunneling, J. Phys. Chem. A, 2019, 123, 1529–1537 CrossRef CAS.
- Y.-C. Lin, C. Lee, S.-H. Lee, Y.-Y. Lee, Y. T. Lee, C. M. Tseng and C. K. Ni, Excited-state dissociation dynamics of phenol studied by a new time-resolved technique, J. Chem. Phys., 2018, 148, 074306 CrossRef.
- C. P. Schick, S. D. Carpenter and P. M. Weber, Femtosecond multiphoton ionization photoelectron spectroscopy S2 state phenol, J. Phys. Chem., 1999, 103, 10470–10476 CrossRef CAS.
- R. A. Livingstone, J. O. F. Thompson, M. Iljina, R. J. Donaldson, B. J. Sussman, M. J. Paterson and D. Townsend, Time-resolved photoelectron imaging of excited state relaxation dynamics in phenol, catechol, resorcinol, and hydroquinone, J. Chem. Phys., 2012, 137, 184304 CrossRef.
- H. An and K. K. Baeck, Quantum Wave Packet Propagation Study of the Photochemistry of Phenol: Isotope Effects (Ph-OD) and the Direct Excitation to the 1 πσ* State, J. Phys. Chem. A, 2011, 115, 13309–13315 CrossRef CAS.
- K. Fuke, R. Takasu and F. Misaizu, Photoionization of hypervalent molecular clusters: electronic structure and stability of NH4(NH3)n, Chem. Phys. Lett., 1994, 229, 597–603 CrossRef CAS.
- S. Ishiuchi, M. Sakai, K. Daigoku, K. Hashimoto and M. Fujii, Hydrogen transfer dynamics in a photoexcited phenol/ammonia (1:3) cluster studied by picosecond time-resolved UV-IR-UV ion dip spectroscopy, J. Chem. Phys., 2007, 127, 234304 CrossRef.
- A. L. Sobolewski and W. Domcke, Photoinduced Electron and Proton Transfer in Phenol and Its Clusters with Water and Ammonia, J. Phys. Chem. A, 2001, 105, 9275–9283 CrossRef CAS.
- E. Kassab and E. M. Evleth, Theoretical Study of the Ammoniated NH4 Radical and Related Structures, J. Am. Chem. Soc., 1987, 109, 1653–1661 CrossRef CAS.
- W. Siebrand, M. Z. Zgierski, Z. K. Smedarchina, M. Vener and J. Kaneti, The structure phenol ammonia clusters before and after proton transfer. A theoretical investigation, Chem. Phys. Lett., 1997, 266, 47–52 CrossRef CAS.
- W. Siebrand and M. Z. Zgierski, Theoretical study structure phenol-ammonia complexes subject to proton transfer, Chem. Phys. Lett., 2001, 334, 127–135 CrossRef CAS.
- T. Shimizu, K. Hashimoto, M. Hada, M. Miyazaki and M. Fujii, A theoretical study on the size-dependence of ground-state proton transfer in phenol-ammonia clusters, Phys. Chem. Chem. Phys., 2018, 20, 3265–3276 RSC.
- C. Jouvet, S. Martrenchard, D. Solgadi, C. Dedonder-Lardeux, M. Mons, G. Grégoire, I. Dimicoli, F. Piuzzi, J. P. Visticot, J.-M. M. Mestdagh, P. D'Oliveira, P. Meynadier and M. Perdrix, Experimental Femtosecond Photoionization of NaI, J. Phys. Chem. A, 1997, 101, 2555–2560 CrossRef CAS.
- G. Grégoire, M. Mons and I. Dimicoli, Real time monitoring of the evaporative cooling: Application to the dynamics of NaI–(NH3)n clusters, J. Chem. Phys., 1999, 110, 1521–1525 CrossRef.
- G. Grégoire, C. Dedonder-Lardeux, C. Jouvet, S. Martrenchard, A. Peremans and D. Solgadi, Picosecond hydrogen transfer in the phenol–(NH3)n (n = 1–3) excited state, J. Phys. Chem. A, 2000, 104, 9087–9090 CrossRef.
- H. Y. Lai, W. R. Jhang and C. M. Tseng, Communication: Mode-dependent excited-state lifetime of phenol under the S1/S2 conical intersection, J. Chem. Phys., 2018, 149, 031104 CrossRef.
- M. F. Hineman, D. F. Kelley and E. R. Bernstein, Proton transfer dynamics and cluster ion fragmentation in phenol/ammonia clusters, J. Chem. Phys., 1993, 99, 4533–4538 CrossRef CAS.
- S. Ishiuchi, J. Kamizori, N. Tsuji, M. Sakai, M. Miyazaki, C. Dedonder, C. Jouvet and M. Fujii, Excited state hydrogen transfer dynamics in phenol–(NH3)2 studied by picosecond UV-near IR-UV time-resolved spectroscopy, Phys. Chem. Chem. Phys., 2020, 22, 5740–5748 RSC.
- R. Englman and J. Jortner, The energy gap law for radiationless transitions in large molecules, Mol. Phys., 1970, 18, 285–287 CrossRef.
- S. Ishiuchi, K. Daigoku, K. Hashimoto and M. Fujii, Four-color hole burning spectra of phenol/ammonia 1:3 and 1:4 clusters, J. Chem. Phys., 2004, 120, 3215–3220 CrossRef CAS.
- M. Miyazaki, R. Ohara, K. Daigoku, K. Hashimoto, J. R. Woodward, C. Dedonder, C. Jouvet and M. Fujii, Electron-Proton Decoupling in Excited-State Hydrogen Atom Transfer in the Gas Phase, Angew. Chem., Int. Ed., 2015, 54, 15089–15093 CrossRef CAS.
- M. Miyazaki, R. Ohara, C. Dedonder, C. Jouvet and M. Fujii, Electron-Proton Transfer Mechanism of Excited-State Hydrogen Transfer in Phenol–(NH3)n (n = 3 and 5), Chem.–Eur. J., 2018, 24, 881–890 CrossRef CAS.
- M. Miyazaki, N. Washio and M. Fujii, Electron-proton transfer mechanism of excited-state hydrogen transfer in Phenol–(NH3)n (n = 3 and 5), studied by delayed ionization detected femtosecond time-resolved NIR spectroscopy, Chem. Phys., 2018, 515, 580–585 CrossRef CAS.
- A. Carrera, I. B. Nielsen, P. Carcabal, C. Dedonder, M. Broquier, C. Jouvet, W. Domcke and A. L. Sobolewski, Biradicalic excited states of zwitterionic phenol-ammonia clusters, J. Chem. Phys., 2009, 130, 024302 CrossRef CAS.
- S. Martrenchard-Barra, C. Dedonder-Lardeux, C. Jouvet, D. Solgadi, M. Vervloet, G. Grégoire and I. Dimicoli, Proton-transfer reaction in the ground state of phenol-ammonia clusters: an experimental study, Chem. Phys. Lett., 1999, 310, 173–179 CrossRef CAS.
- M. Miyazaki, A. Kawanishi, I. Nielsen, I. Alata, S. Ishiuchi, C. Dedonder, C. Jouvet and M. Fujii, Ground state proton transfer in phenol–(NH3)n (n ≤ 11) clusters studied by mid-IR spectroscopy in 3–10 μm range, J. Phys. Chem. A, 2013, 117, 1522–1530 CrossRef CAS.
- K. Daigoku, S. Ishiuchi, M. Sakai, M. Fujii and K. Hashimoto, Photochemistry of phenol–(NH3)n clusters: Solvent effect on a radical cleavage of an OH bond in an electronically excited state and intracluster reactions in the product NH4(NH3)n−1 (n ≤ 5), J. Chem. Phys., 2003, 119, 5149–5158 CrossRef CAS.
- H. Kang, C. Jouvet, C. Dedonder-Lardeux, S. Martrenchard, G. Grégoire, C. Desfrançois, J. P. Schermann, M. Barat and J. A. Fayeton, Ultrafast deactivation mechanisms of protonated aromatic amino acids following UV excitation, Phys. Chem. Chem. Phys., 2005, 7, 394–398 RSC.
- N. Tsuji, S. Ishiuchi, C. Jouvet, C. Dedonder-Lardeux, M. Miyazaki, M. Sakai and M. Fujii, Hole-Burning Spectra of m-Fluorophenol/Ammonia (1:3) Clusters and Their Excited State Hydrogen Transfer Dynamics., ChemPhysChem, 2011, 12, 1928–1934 CrossRef CAS.
- N. Tsuji, S. Ishiuchi, M. Sakai, M. Fujii, T. Ebata, C. Jouvet and C. Dedonder-Lardeux, Excited state hydrogen transfer in fluorophenol-ammonia clusters studied by two-color REMPI spectroscopy, Phys. Chem. Chem. Phys., 2006, 8, 114–121 RSC.
- D. A. Blank, S. W. North and Y. T. Lee, The Ultraviolet Photodissociation Dynamics Pyrrole, Chem. Phys., 1994, 187, 35–47 CrossRef CAS.
- H. Lippert, H. H. Ritze, I. V. Hertel and W. Radloff, Femtosecond time-resolved hydrogen-atom elimination from photoexcited pyrrole molecules, ChemPhysChem, 2004, 5, 1423–1427 CrossRef CAS.
- I. Lamas, A. Longarte, A. Peralta Conde, G. Muga, D. Townsend and R. Montero, Dynamics of Pyrroles Excited to the 3s/πσ* State, J. Phys. Chem. A, 2019, 123, 8982–8993 CrossRef CAS.
- O. David, C. Dedonder-Lardeux, C. Jouvet, H. Kang, S. Martrenchard, T. Ebata and A. L. Sobolewski, Hydrogen transfer in excited pyrrole-ammonia clusters, J. Chem. Phys., 2004, 120, 10101–10110 CrossRef CAS.
- M. G. D. Nix, A. L. Devine, B. Cronin and M. N. R. R. Ashfold, High resolution photofragment translational spectroscopy of the near UV photolysis of indole: dissociation via the 1πσ* state, Phys. Chem. Chem. Phys., 2006, 8, 2610–2618 RSC.
- C. Dedonder-Lardeux, D. Grosswasser, C. Jouvet and S. Martrenchard, Dissociative hydrogen transfer in indole–(NH3)n clusters, PhysChemComm, 2001, 4, 1–3 RSC.
- O. David, C. Dedonder-Lardeux, C. Jouvet and A. L. Sobolewski, Role of the intermolecular vibrations in the hydrogen transfer rate: the 3-methylindole–NH3 complex, J. Phys. Chem. A, 2006, 110, 9383–9387 CrossRef CAS.
- H. Lippert, V. Stert, L. Hesse, C. P. Schulz, W. Radloff and I. V. Hertel, Hydrogen atom transfer in indole clusters: formation dynamics of (NH3)n−1NH4, n = 1–6, fragments, Eur. Phys. J. D, 2002, 20, 445–448 CrossRef CAS.
- V. Stert, L. Hesse, H. Lippert, C. P. Schulz and W. Radloff, Dynamics of Hydrogen Atom Transfer in indole–(NH3)n Clusters, J. Phys. Chem. A, 2002, 106, 5051–5053 CrossRef CAS.
- H. Lippert, V. Stert, L. Hesse, C. P. Schulz, I. V. Hertel and W. Radloff, Isotope effect of the photoinduced H(D)-transfer reaction in indole–ammonia clusters, Chem. Phys. Lett., 2003, 371, 208–216 CrossRef CAS.
- H.-H. Ritze, H. Lippert, V. Stert, W. Radloff and I. V. Hertel, Theoretical study of the hydrogen atom transfer in the heterodimer indole–ammonia and comparison with experimental results, J. Chem. Phys., 2004, 120, 3619–3629 CrossRef CAS.
- S. Soorkia, C. Jouvet and G. Grégoire, UV Photoinduced Dynamics of Conformer-Resolved Aromatic Peptides, Chem. Rev., 2020, 120, 3296–3327 CrossRef CAS.
- T. Droz, R. Knochenmuss and S. Leutwyler, Excited state proton transfer in gas phase clusters 2-Naphthol–(NH3)n, J. Chem. Phys., 1990, 93, 4520–4532 CrossRef CAS.
- X. Liu, T. N. V. Karsili, A. L. Sobolewski and W. Domcke, Photocatalytic Water Splitting with the Acridine Chromophore: A Computational Study, J. Phys. Chem. B, 2015, 119, 10664–10672 CrossRef CAS.
- X. Liu, A. L. Sobolewski, R. Borrelli and W. Domcke, Computational investigation of the photoinduced homolytic dissociation of water in the pyridine–water complex, Phys. Chem. Chem. Phys., 2013, 15, 5957–5966 RSC.
- N. Esteves-lópez, S. Coussan, C. Dedonder-lardeux and C. Jouvet, Photoinduced water splitting in pyridine water clusters, Phys. Chem. Chem. Phys., 2016, 18, 25637–25644 RSC.
- X. Huang, A. Juan-Pablo, J. Ehrmaier, J. A. Noble, W. Xie, A. L. L. Sobolewski, C. Dedonder-Lardeux, C. Jouvet and W. Domcke, Photoinduced water oxidation in pyrimidine–water clusters: a combined experimental and theoretical study, Phys. Chem. Chem. Phys., 2020, 22, 12502–12514 RSC.
| This journal is © The Royal Society of Chemistry 2021 |