Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Metallofullerene photoswitches driven by photoinduced fullerene-to-metal electron transfer†
Michal
Zalibera
 *ab,
Frank
Ziegs
c,
Sandra
Schiemenz
c,
Vasilii
Dubrovin
*ab,
Frank
Ziegs
c,
Sandra
Schiemenz
c,
Vasilii
Dubrovin
 c,
Wolfgang
Lubitz
c,
Wolfgang
Lubitz
 b,
Anton
Savitsky
bd,
Shihu H. M.
Deng
e,
Xue-Bin
Wang
b,
Anton
Savitsky
bd,
Shihu H. M.
Deng
e,
Xue-Bin
Wang
 e,
Stanislav M.
Avdoshenko
e,
Stanislav M.
Avdoshenko
 c and
Alexey A.
Popov
c and
Alexey A.
Popov
 *c
*c
aInstitute of Physical Chemistry and Chemical Physics, Slovak University of Technology in Bratislava, Radlinského 9, 81237 Bratislava, Slovakia. E-mail: michal.zalibera@stuba.sk
bMax Planck Institute for Chemical Energy Conversion, Mülheim (Ruhr), Germany
cLeibniz Institute for Solid State and Materials Research, Helmholtzstraße 20, 01069 Dresden, Germany. E-mail: a.popov@ifw-dresden.de
dFaculty of Physics, Technical University Dortmund, Otto-Hahn-Str. 4a, 44227 Dortmund, Germany
ePhysical Sciences Division, Pacific Northwest National Laboratory, Richland, Washington 99352, USA
First published on 30th April 2021
Abstract
We report on the discovery and detailed exploration of the unconventional photo-switching mechanism in metallofullerenes, in which the energy of the photon absorbed by the carbon cage π-system is transformed to mechanical motion of the endohedral cluster accompanied by accumulation of spin density on the metal atoms. Comprehensive photophysical and electron paramagnetic resonance (EPR) studies augmented by theoretical modelling are performed to address the phenomenon of the light-induced photo-switching and triplet state spin dynamics in a series of YxSc3−xN@C80 (x = 0–3) nitride clusterfullerenes. Variable temperature and time-resolved photoluminescence studies revealed a strong dependence of their photophysical properties on the number of Sc atoms in the cluster. All molecules in the series exhibit temperature-dependent luminescence assigned to the near-infrared thermally-activated delayed fluorescence (TADF) and phosphorescence. The emission wavelengths and Stokes shift increase systematically with the number of Sc atoms in the endohedral cluster, whereas the triplet state lifetime and S1–T1 gap decrease in this row. For Sc3N@C80, we also applied photoelectron spectroscopy to obtain the triplet state energy as well as the electron affinity. Spin distribution and dynamics in the triplet states are then studied by light-induced pulsed EPR and ENDOR spectroscopies. The spin–lattice relaxation times and triplet state lifetimes are determined from the temporal evolution of the electron spin echo after the laser pulse. Well resolved ENDOR spectra of triplets with a rich structure caused by the hyperfine and quadrupolar interactions with 14N, 45Sc, and 89Y nuclear spins are obtained. The systematic increase of the metal contribution to the triplet spin density from Y3N to Sc3N found in the ENDOR study points to a substantial fullerene-to-metal charge transfer in the excited state. These experimental results are rationalized with the help of ground-state and time-dependent DFT calculations, which revealed a substantial variation of the endohedral cluster position in the photoexcited states driven by the predisposition of Sc atoms to maximize their spin population.
Introduction
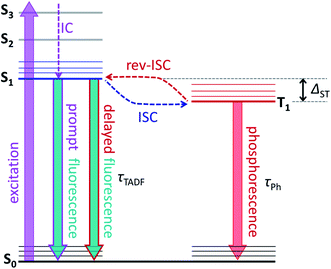
The molecular structure of endohedral metallofullerenes (EMFs) is built from two components, the carbon cage and the endohedral cluster.1–7 EMF molecules often have certain structural flexibility associated with the motion of the endohedral species, whose dynamics is apparently decoupled from that of the fullerene cage. For instance, nitride clusterfullerenes M3N@C80 (M = Sc, Y, lanthanides) exhibit a quasi-free rotation of the M3N cluster inside the fullerene near room temperature as evidenced experimentally by NMR spectroscopy8,9 and variable-temperature single-crystal X-ray diffraction studies,10,11 or computationally by molecular dynamics simulations.12–15 But such a dynamic situation does not mean that there is no interaction between the fullerene host and its guest. Endohedral metal atoms transfer their valence electrons to the carbon cage and exhibit substantial d–π orbital overlap and bonding interaction with the fullerene π-system. If the fullerene cage is rather uniform – as is the case for the icosahedral C80(Ih) – it has many equivalent or almost equivalent binding sites, and the quasi-free rotation of the cluster means that metal atoms can move easily between these sites. Depending on the temperature and the depths of the energy minima, metal dynamics in EMFs can show different regimes. For M3N@C80, experimental and computational estimations give the barrier to the cluster rotation on the order of 10 kJ mol−1 or less,9,16,17 which can be easily reached by the thermal energy in a broad temperature range leading to spontaneous motion of the endohedral clusters down 30–50 K.18,19 But the switching of the M3N cluster position inside the fullerene can be also induced by more specific external stimuli, which however require experiments to be performed at low temperature to disentangle their effect from thermal motion. Petek et al. demonstrated switching of the Sc3N cluster positions under the influence of the tunnelling current in the STM study of Sc3N@C80.17,20 Greber et al. showed that a magnetic field can affect the orientation of endohedral clusters in HoLu2N@C80 and TbSc2N@C80.18 Morton et al. found that laser irradiation of ErSc2N@C80 at 5 K changes the ratio of two kinds of EMF species with different EPR spectra.19A possibility to switch the position of endohedral units in EMFs with light is very attractive and can potentially lead to control over molecular structure and properties at the level realized in well-established photoswitching materials and molecular machines.21–26 But currently, surprisingly little is known about the photophysics of EMFs. Their role as electron donors or acceptors in molecular dyads undergoing photoinduced charge transfer had been studied comprehensively,27–38 but the properties of pristine EMFs, including those of iconic Sc3N@C80, are not well known.35,37,39–41 For empty fullerenes, very efficient S1 → T1 intersystem crossing leads to almost 100% yield of a triplet state after photoexcitation.42 The heavy-metal effect in metallofullerenes is expected to further enhance the triplet state formation and facilitate the non-radiative decay. Thus, it is hard to expect that EMFs can show appreciable photoluminescence. The situation can be changed if endohedral metal atoms have low-energy emitting states, and near-infrared lanthanide-based luminescence had been observed in Er- and Tm-based EMFs.19,43–48 Surprisingly, Y3N@C80 was found to show unusually strong luminescence and long fluorescence lifetimes, but the reasons for this unexpected behaviour first remained unclear.49,50 Recently we found that the strong photoemission of Y3N@C80 is caused by the small singlet-triplet S1–T1 gap of less than 0.1 eV, which enables thermally activated delayed fluorescence (TADF) via thermal population of the emitting S1 state from the T1 “reservoir”.51 As the triplet state plays a crucial role in the process, in the same work we also characterized its dynamics and spin distribution by light-induced EPR and ENDOR spectroscopy and found that yttrium atoms have negligible spin populations. TADF is a crucial phenomenon for this work, and Fig. 1 illustrates key processes involved in delayed fluorescence. Note that TADF is a rather common mechanism in many compounds with small S1–T1 energy difference, including empty fullerenes,52–56 and is actively pursued as the way to increase the efficiency of exciton harvesting in OLEDs.57–59
In this work, we report on the photophysical and light-induced EPR studies of a series of YxSc3−xN@C80 (x = 0–3) nitride clusterfullerenes.60,61 Unexpectedly, we found that when Sc atoms are present in the endohedral cluster, the EMF molecules undergo photoswitching. In the photoexcited state, the endohedral cluster acquires a position which ensures the maximal degree of spin density localization on the Sc atoms, and this position is different from the cluster position in the ground-state. We first describe variable-temperatures steady-state and time-resolved photophysical studies, revealing that TADF is a universal scenario for all M3N@C80 molecules. Then, computations of molecular and electronic structures of EMFs molecules in the ground and excited state are presented, revealing conformer switching and spin density accumulation on the Sc atoms in the excited state. The triplet state energy and close correspondence to the triplet excited state to the Sc3N@C80− anion are established by photoelectron spectroscopy. Finally, a light-induced time-resolved EPR study addressing dynamics of the photoexcited triplet state is described, concluded by the analysis of the spin distribution in the triplet states using light-induced ENDOR spectroscopy.
Results and discussion
Room temperature spectroscopic properties
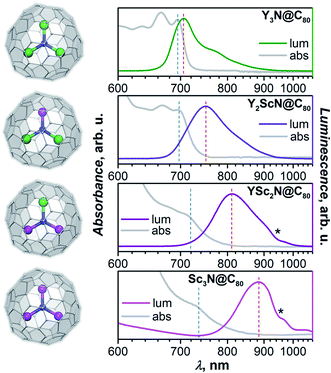
Absorption and photoluminescence (PL) emission spectra of the whole YxSc3−xN@C80 series (x = 0–3) are shown in Fig. 2. Despite the same formal charge state of metal and fullerene cage, considerable variations of the spectroscopic properties are observed with the increase of the Sc content in the endohedral nitride cluster as summarized in Table 1 and Fig. 2.| Y3N@C80 | Y2ScN@C80 | YSc2N@C80 | Sc3N@C80 | |
|---|---|---|---|---|
| a λ abs and λlum denote maxima positions of the absorption and luminescence peaks, ΔStokes is the Stokes shift determined from λabs and λlum, Tmax is the temperature, at which luminescence has the maximum intensity and is equal to 120 K for Y3N@C80, Y2ScN@C80, YSc2N@C80, and 60 K for Sc3N@C80; ΔST is the S1–T1 energy difference determined either form the fluorescence and phosphorescence peak positions in the spectra (“optical”) or by fitting the temperature dependence of luminescence lifetimes with eqn (1) (“τ-fit”); τTADF is the fluorescence lifetime at RT; τPh is the phosphorescence lifetime; Tthr is the temperature, at which luminescence lifetime reaches a plateau and TADF is quenched; τ1 is the spin–lattice relaxation time of the triplet state at 20 K in d8-toluene and τT1 is the triplet state lifetime from the time-resolved light-induced W-band EPR study. b Precision of the peak positions is ≈±1 nm for absorption in the whole range, ±2 nm for emission at λ < 800 nm, ±5 nm for emission at 800 nm < λ < 900 nm, and ±10 nm for emission at λ > 900 nm; PL lifetime uncertainty is ≈2–3% for single-exponential decays; temperature uncertainty in PL measurements is near 1 K above 100 K, but the measured values can be underestimated by up to 5–8 K close to liquid helium temperature. c For Sc3N@C80, the TADF is most probably not completely quenched even at the lowest accessible temperature of 4 K, so the lifetimes may not be the intrinsic τPh. d Measurement in h8-toluene gave a τT1 lifetime of 180 ± 7 ms. | ||||
| h 8 -Toluene, RT | ||||
| λ abs, nm (eV) | 695 (1.784) | 696 (1.782) | 713 (1.739) | 730 (1.699) |
| λ lum, nm (eV) | 704 (1.761) | 750 (1.653) | 810 (1.531) | 910 (1.394) |
| Δ Stokes, nm (eV) | 9 (0.023) | 54 (0.128) | 97 (0.208) | 180 (0.306) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Polystyrene, VT | ||||
| λ lum, RT; nm (eV) | 705 (1.759) | 748 (1.658) | 799 (1.552) | 869 (1.427) |
| λ lum, Tmax; nm (eV) | 701 (1.769) | 752 (1.649) | 804 (1.542) | 904 (1.372) |
| λ lum, 4 K; nm (eV) | 739 (1.678) | 775 (1.600) | 821 (1.510) | 915 (1.355) |
| Δ ST, optical; eV | 0.091 ± 0.006 | 0.049 ± 0.006 | 0.032 ± 0.006 | n/a |
| Δ ST, τ-fit; eV | 0.098 ± 0.003 | 0.054 ± 0.002 | 0.028 ± 0.002 | n/a |
| τ TADF, RT; μs | 1.1 | 10.5 | 1.2 | 0.3 |
| τ Ph, 4 K; ms | 192 | 78 | 26 | 0.4/1.8c |
| T thr, K | 60 | 40 | 30 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| d 8 -Toluene, 20 K (W-EPR) | ||||
| τ T1 ≈ τPh, ms | 240 ± 3 (h8: 180 ± 7)d | 120 ± 6 | 38 ± 6 | 10 ± 6 |
| τ 1, μs | 97 ± 1 | 556 ± 72 | 1200 ± 140 | 78 ± 4 |
Y3N@C80 shows a well-structured group of absorption features at 600–700 nm with the lowest energy one at 695 nm. The emission spectrum is also relatively narrow with the lowest energy maximum at 704 nm, very close to the absorption maximum. The absorption spectrum of Y2ScN@C80 is very similar to that of Y3N@C80 with marginal shifts and somewhat redistributed linewidth. The lowest-energy absorption feature is found at 696 nm. The PL spectrum of Y2ScN@C80 shows more pronounced differences from that of Y3N@C80, the peak at 750 nm and a shoulder at 718 nm are considerably broader and shifted to longer wavelengths. Further replacement of Y by Sc results in stronger changes in the absorption spectrum of YSc2N@C80. The low-energy bands become broader and hence almost smeared. The lowest energy feature can be distinguished at 713 nm. The emission spectrum of YSc2N@C80 has one broad peak with a maximum at 810 nm. Thus, there is a further red shift of the bands and further broadening. The absorption spectrum of Sc3N@C80 resembles that of YSc2N@C80 but is shifted to lower energy, with the single resolved feature at 730 nm. The PL spectrum is further broadened and red-shifted, the maximum is detected near 890 nm (note that due to the strong decrease of the detector sensitivity beyond 800 nm, the position of the maximum for Sc3N@C80 is less accurate than for other compounds).
A similar variation of absorption spectra with broadening and a red shift was already observed before in the MxSc3−xN@C80 series (M = Y, Gd, Dy, Ho, Er, Lu; x = 0–3),60,62–64 but emission spectra of mixed-metal nitride clusterfullerenes have not been studied yet and reveal a surprisingly strong dependence on the Sc content in the nitride cluster. There is an overall tendency of the red shift for both absorption and emission bands, but the effect for the PL is much stronger (Table 1). As a result, the Stokes shift is also increasing dramatically from 0.02 eV in Y3N@C80 through 0.13 eV in Y2ScN@C80 and 0.21 eV in YSc2N@C80 to ≈0.31 eV in Sc3N@C80. The reasons for these changes will be analysed and explained below.
Luminescence lifetimes measurements were performed in degassed polystyrene films prepared by mixing fullerene and polymer solutions in CS2 and evaporating the solvent under vacuum. For Y3N@C80, we also performed PL lifetime measurements in degassed toluene solution and obtained the lifetimes similar to those measured in the polymer film (Table S1†). At room temperature, PL lifetimes span the range from 0.3 μs in Sc3N@C80 to 10.5 μs in Y2ScN@C80. These values are orders of magnitude longer than normally observed for prompt fluorescence and indicate that the triplet states are likely to be involved in the emission. Thermally-activated delayed fluorescence (TADF) described for Y3N@C80 (ref. 51) and empty fullerenes56 probably take place in all YxSc3−xN@C80 compounds. This hypothesis is further corroborated via temperature-dependent PL study.
Variable temperature photoluminescence (VT-PL)
A small energy difference between T1 and S1 states enables thermally-activated reversible intersystem crossing from T1 to S1 with subsequent delayed fluorescence known as TADF (Fig. 1). Unlike the short prompt fluorescence, TADF is characterized by a strongly increased lifetime, which essentially reflects the lifetime of the T1 state. In the presence of TADF and the absence of prompt fluorescence, three distinct PL regimes can be expected at different temperatures:(i) While the temperature is high enough to allow fast thermally-activated rev-ISC from the T1 to the S1 state, TADF dominates in the PL spectrum. The measured fluorescence lifetime (τTADF) in this regime grows with cooling following the increase of the triplet state lifetime at lower temperatures. With the growth of the T1 lifetime, the probability that T1 decays via TADF increases, which leads to the increase of the TADF quantum yield and growth of the PL intensity.
(ii) Once the temperature decreases below a certain limit, the efficiency of the T1 → S1 rev-ISC starts to decrease fast, and the TADF intensity goes down. At the same time, phosphorescence can appear as a visible contribution to the PL competing with TADF. The PL lifetime in this regime still increases upon cooling.
(iii) At the threshold temperature Tthr, rev-ISC and TADF are quenched completely, and below this temperature the phosphorescence remains the only radiative decay mechanism. At Tthr, the luminescence lifetime becomes equal to the intrinsic phosphorescence lifetime τPh and is not changing with further cooling.
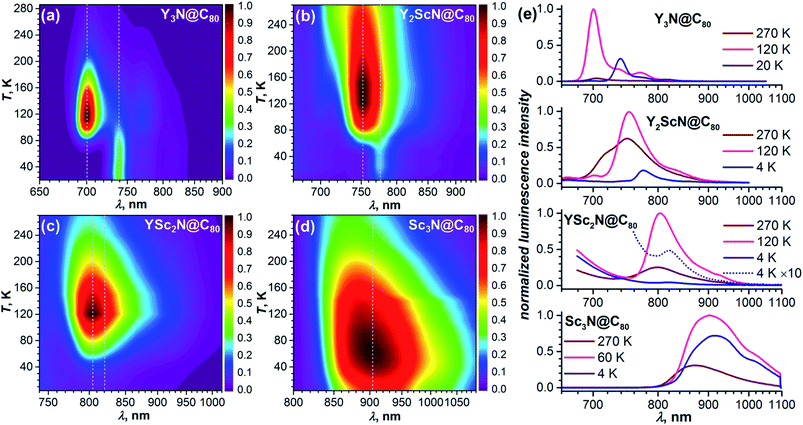
As TADF is characterized by strong changes of emission intensity and PL lifetime with temperature, we performed variable-temperature (VT) PL studies of YxSc3−xN@C80 compounds. The VT-PL spectra measured during the heating of the samples from helium to room temperatures are presented in Fig. 3a–d in the form of 2D contour plots with colour-coded normalized intensity. Spectra at three selected temperatures (270 K, the temperature of the highest luminescence intensity, and the lowest-temperature used in the studies) are plotted in Fig. 3e. Luminescence lifetimes measured at different temperatures are listed in Tables S1–S4† and plotted in Fig. 4.
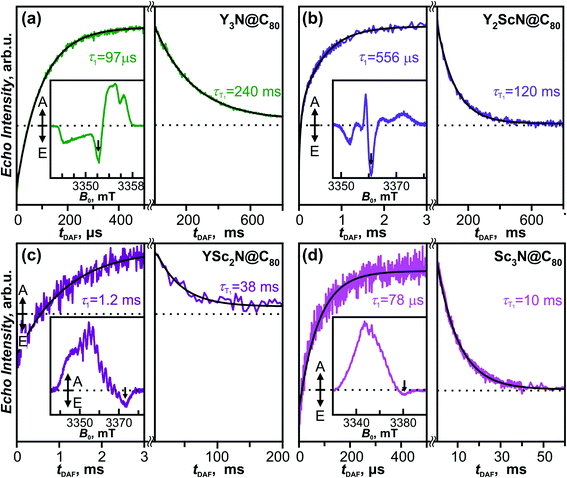
 | ||
| Fig. 4 Luminescence lifetimes of YxSc3−xN@C80 compounds measured in polystyrene film at different temperatures. For Sc3N@C80, two sets of lifetimes are determined below 60 K. Thin dashed lines are shown to guide the eye, thick solid lines are fits of the low-temperature part based on eqn (1). | ||
The VT-PL studies of Y3N@C80 reported by us earlier revealed three regimes outlined above.51 When cooling from room temperature down to 120 K, the PL peak of Y3N@C80 at 705 nm enhances its intensity approximately 20-fold, which is accompanied by a gradual shift to 701 nm and narrowing of the emission peaks. In this temperature range, TADF is the only emissive pathway. As temperature decreases below 120 K, the intensity of the PL peak at 701 nm starts to decrease. At the same time, a new feature appears at 739 nm. This behaviour is caused by a decrease of the rev-ISC efficiency, leading to a decrease of the delayed fluorescence yield and appearance of the phosphorescence (the new peak at 739 nm). At 60 K, the peak at 701 nm disappears completely, whereas the peak at 739 nm is not changing with further cooling. Note that the prompt fluorescence usually does not show a strong temperature dependence, and the complete disappearance of the Y3N@C80 fluorescence below 60 K indicates that the compound does not show prompt fluorescence.
The VT-PL evolution for Y2ScN@C80 and YSc2N@C80 is qualitatively similar to that of Y3N@C80. The shoulder at 716 nm in the PL spectrum of Y2ScN@C80 decreases with cooling and essentially disappears by 120 K, whereas the intensity of the peak at 750 nm increases and reaches the maximum at 120–150 K. The increase of the luminescence intensity from RT to 120 K of ca. 80% is not as dramatic as for Y3N@C80. At further cooling, the peak at 750 nm decreases and disappears completely at 50 K, whereas a new feature at 775 nm becomes visible at 78 K first as a shoulder, and then as the only remaining PL peak below 50 K. The intensity of this peak remains almost constant between 50 and 4 K. In analogy to Y3N@C80 and based on the PL lifetimes (see below), we assign the peak at 775 nm to the phosphorescence and the peak at 750 nm to the delayed fluorescence of Y2ScN@C80. PL intensity of YSc2N@C80 near 800 nm also increases with cooling and reaches the maximum around 120 K, when its intensity becomes about 4 times higher than at room temperature. The band position is shifting gradually from 799 nm at RT to 804 nm at 120 K. Below 120 K, the PL intensity decreases, but the peak at 804 nm remains detectable down to 30–20 K. Only at the lowest temperatures, a new weak emission feature at 821 nm assigned to the phosphorescence of YSc2N@C80 can be distinguished. Its intensity is ≈100 times lower than that of the 804 nm peak at 120 K.
Sc3N@C80 shows a different thermal evolution of the PL spectra. Upon cooling, we observed an increase in the intensity and gradual shift of the peak position from 869 nm at RT to 904 nm at 60 K. The peak has an asymmetrical shape indicating either a complicated vibronic structure or coexistence of several emitting states with similar energy. The PL intensity increases threefold from RT to 60 K and then decreases to lower temperatures. Below 60 K, the broad PL peak changes its shape with the low-energy shoulder at 915 nm gaining in intensity, but the spectrum remains broad and unresolved even at the lowest temperature.
Luminescence lifetimes and S1–T1 gap
The temperature dependence of luminescence lifetimes shown in Fig. 4 has a similar pattern for three YxSc3−xN@C80 molecules (x = 1–3) and confirms the TADF mechanism. The lifetime increases from 1–10 μs at RT to tens of ms below 100 K (Fig. S1 and Tables S1–S4†). At the threshold temperature Tthr, the lifetime is levelled off and no further changes were observed at lower temperatures. The threshold temperature decreases with the increase of the Sc content in the endohedral cluster from 60 K for Y3N@C80, to 40 K for Y2ScN@C80, and 30 K for YSc2N@C80. Likewise, the luminescence lifetime at the plateau also decreases from 192 ms in Y3N@C80, 78 ms in Y2ScN@C80, to 26 ms in YSc2N@C80. These lifetimes can be interpreted as intrinsic phosphorescence lifetimes, τPh.The key TADF parameter, the S1–T1 energy gap (ΔST), can be determined as the energy difference of the fluorescence and phosphoresce peak maxima (marked with white dashed lines in Fig. 3a–c), giving 0.09 eV for Y3N@C80, 0.05 eV for Y2ScN@C80, and 0.03 eV for YSc2N@C80. Independent estimation of ΔST is possible from the temperature dependence of luminescence lifetimes using eqn (1):65
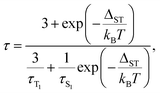 | (1) |
The temperature dependence of the Sc3N@C80 luminescence lifetimes is more complex. Upon cooling from room temperature, the lifetime first decreases from 0.3 μs at 296 K to 0.13 μs at 225 K, but then shows a gradual increase to 13 μs at 65 K. Below this temperature, the decay of the PL intensity after the laser pulse has a double-exponential shape giving two sets of lifetimes (Fig. 4). In both sets the values continue to increase at cooling, giving lifetimes of 0.4 and 1.8 ms near 4 K. Levelling off at the plateau similar to other YxSc3−xN@C80 molecules is not observed. Considering that the lifetimes, ΔST gaps, and the threshold temperature Tthr decrease systematically with the increasing number of Sc atoms in the cluster, we suggest that the ΔST gap in Sc3N@C80 is very small, and TADF remains efficient even at 4 K. Decrease of the PL intensity below 60 K indicates that the efficiency of the T1 → S1 rev-ISC decreases here as well, but cooling below the lowest temperature accessible with our setup would be needed to freeze this process completely. In the absence of a clear transition between TADF and phosphorescence in the available temperature range, the ΔST gap of Sc3N@C80 cannot be determined experimentally. However, we can speculate that it is smaller than 0.03 eV obtained for YSc2N@C80.
Another feature of Sc3N@C80 not found in other YxSc3−xN@C80 molecules is the appearance of the fast radiative decay channel below 200 K with the lifetime of 8.8 ns, which decreases to 1.4 ns at 4 K. The assignment of this low-yield process remains open. A nanosecond timescale is typical for a prompt fluorescence. However, a transient absorption study of Sc3N@C80 showed that the S1 → T1 intersystem crossing is very fast and occurs within only 48 ps,34,37 which leaves no possibility for a nanosecond-long prompt fluorescence.
Computational studies
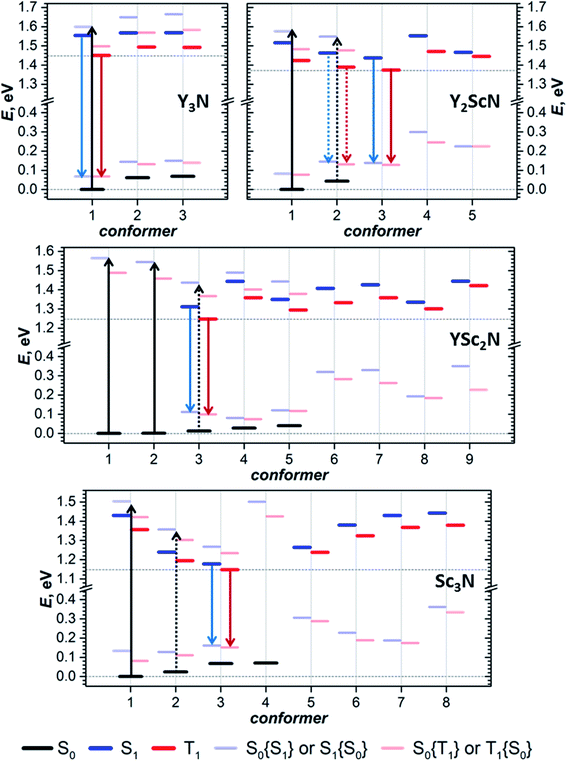
The photophysical study of YxSc3−xN@C80 molecules revealed several systematic trends in the optical properties associated with the cluster composition. An increase of the number of Sc atoms leads to a modest red shift of the absorption and a much more pronounced red shift of the luminescence, a strong increase of the Stokes shift, a decrease of the S1–T1 gap, and a systematic decrease of luminescence lifetimes. To find the connection between these phenomena and the molecular and electronic structure of the metallofullerenes, detailed DFT modelling was performed.Preferable orientations of the M3N cluster inside the fullerene cage, which we will refer to as conformers, can vary substantially with the electronic state of the molecule. For instance, the lowest energy conformer of the Sc3N@C80 anion is different from that of the neutral molecule.16,66 To find the most preferable conformers, we used Fibonacci sampling67 to generate a set of 120 starting geometries with different cluster orientations for each YxSc3−xN@C80 molecule. All these structures were then optimized in the S0 and T1 electronic states at the PBE level using the Priroda code.68,69 Unique T1 conformers were then re-optimized in the S1 state using the time-dependent (TD)-DFT approach. In the course of TD-DFT optimization, the structures of S1 conformers remained very similar to corresponding T1 structures, and we will not distinguish them in the following discussion. Single point energy calculations at the PBE/def2-TZVPP level with ZORA scalar-relativistic corrections were then performed for all unique conformers in S0, S1, and T1 states using the ORCA suite.70–76 To treat S1 and T1 states at the same theoretical level, their energies were computed with TD-DFT. For estimation of vertical transition energies, the energies of S1 and T1 states in S0 geometry and the energy of the S0 state in S1 and T1 geometries were also calculated. Computed energies are summarized in Fig. 5 and listed in Table S5.† The conformers are numbered first in ascending order according to their relative energies in the S0 state and are labelled in the further discussion as conf N. In particular, conf 1 is always the lowest energy conformer for the ground electronic state. If the vibrational structure of the electronic transition is not resolved, the point of the highest intensity in the broad band corresponds to the vertical transition. For absorption, it will be denoted as S0 → S1{S0}, which means that the S0 and S1 energies are computed in the optimized geometry of the S0 state. Likewise, vertical transitions corresponding to fluorescence are denoted as S1 → S0{S1}, which means that the energies of S1 and S0 states are computed in the optimized S1 geometry. In the following discussion, the theoretical Stokes shift, ΔStokes, is calculated as E(S0 → S1{S0}) − E(S1 → S0{S1}) for the lowest energy S0 and S1 conformers, whereas the adiabatic S1–T1 energy gap, ΔST, is the energy difference of S1 and T1 states in their optimized geometries.
For Y3N@C80, computations revealed three conformers for the ground state and analogous conformers for excited states. Conf 1 with C3 symmetry (Fig. 2) has the lowest energy in both S0 and S1/T1 states, which means that Y3N@C80 retains its structure upon photoexcitation. Relative energies of conf 2 and conf 3 in the ground state are 0.062 and 0.069 eV, and these conformers may also contribute to the absorption spectra at room temperature. Adiabatic S1 ↔ S0 excitation is predicted at 1.554 eV, whereas vertical transitions S0 → S1{S0} and S1 → S0{S1} are predicted at 1.599 and 1.487 eV, respectively, giving ΔStokes of 0.112 eV. The computed ΔST gap is 0.104 eV, very close to the experimental estimation near 0.09–0.10 eV (Table 1).
For Y2ScN@C80, we found two S0 conformers with the energy difference of 0.044 eV and their counterparts for S1/T1 states, but also three other S1/T1 conformers without analogous structures in the ground state. Conf 1 resembles the C3-symmetric structure of Y3N@C80 with one Y replaced by Sc. Adiabatic and vertical S0 → S1 excitations for conf 1 at 1.516 and 1.576 eV, respectively, are very close to the Y3N@C80 values in line with the similarity of the absorption spectra (Fig. 2). Conf 3 has the lowest energy in the S1/T1 excited states (1.438 eV for S1), and its vertical S1 → S0{S1} transition has an energy of 1.300 eV. Thus, computed ΔStokes is 0.276 eV, and its considerable increase in comparison to Y3N@C80 is caused by switching from conf 1 in the ground state to conf 3 in the excited state. The ΔST gap in conf 3 is 0.063 eV, again in good agreement with the experimental value of ≈0.05 eV. Note that conf 2 of Y2ScN@C80 is only slightly higher in energy than conf 3 in the excited state and hence may also contribute to the luminescence. But its transition energy and ΔST gap are very similar to the values of conf 3.
YSc2N@C80 has the most diverse manifold of conformers in the whole YxSc3−xN@C80 series. We found 5 ground state conformers and 7 excited state conformers, of which only 3 have corresponding S0 structures. Conf 1 and conf 2 are equally stable and have similar S0 → S1{S0} energies of 1.564 and 1.544 eV, respectively. At the same time, three other S0 conformers also have close relative energies within 0.041 eV, but smaller excitation energies (down to 1.402 eV for conf 5). All five S0 conformers may contribute to the absorption spectrum at room temperature, causing broadening and red shift when compared to the spectra of Y3N@C80 and Y2ScN@C80. The lowest energy S1/T1 conformer of YSc2N@C80 is conf 3 with an S1 → S0{S1} transition at 1.201 eV and ΔST gap of 0.062 eV. Rearrangement from conf 1 in S0 into conf 3 in the S1 state leads to a rather large value of the computed ΔStokes, 0.363 eV.
Sc3N@C80 also shows a rich structural variability with 4 S0 and 7 S1/T1 conformers. S0 conformers coincide with those found in our earlier computational study,16 which used a less extended set of starting configurations. Conf 1 and conf 2 have close relative energies in the ground state, but considerably different energies of S0 → S1{S0} transitions at 1.503 and 1.333 eV, respectively. Thus, calculations predict a further red shift of absorptions in comparison to other YxSc3−xN@C80 molecules and broadening of the spectral profile, in good agreement with experimental observations. Conf 3 is the lowest energy conformer in the S1 excited states, followed by conf 2 at 0.025 eV higher. The S1 → S0{S1} transitions of conf 3 and conf 2 occur at 1.017 and 1.123 eV, respectively, giving further red shift of the emission and the ΔStokes value of 0.486 eV. The calculated ΔST gap in conf 3 is only 0.030 eV.
The structural flexibility of M3N@C80 molecules associated with the motion of the endohedral cluster16,66 leads to a possibility of switching between conformers when the thermal motion of the cluster is frozen at low temperatures.17–20 Our work proves that this conformational flexibility indeed appears in the excited states. Each of the YxSc3−xN@C80 molecules we studied has several conformers with close energies in both S0 and T1/S1 states. Since conformers have significantly different spectroscopic properties, as can be concluded from the different S0 ↔ S1 transition energies discussed above, this conformational variability should have a profound influence on the optical spectra. The changes in the spectral shape and shift of the peak positions at lower temperatures can be rooted in the changes in the conformer composition. For example, the shoulder at higher energy in the emission spectrum of Y2ScN@C80 and its disappearance at a lower temperature may be caused by a higher-energy conformer, whose thermal population decreases during cooling. The gradual shift of the Sc3N@C80 emission to longer wavelengths upon cooling may be also rooted in a similar variation of conformational composition. A more definitive answer is hardly possible at this moment because the spectra have unresolved vibronic structure, which can also change with temperature (for instance, by freezing out hot transitions).
Switching between conformers driven by their thermodynamic stability requires equilibration of the system. Since emission takes place on a relatively long timescale of μs and ms, and since barriers for reorganization between conformers are expected to be rather low,9,16,17 we believe that thermal equilibrium between conformers in the T1 state is established between excitation and emission and that the emission proceeds with the lowest energy conformers of the triplet state. Excess energy which may be needed to overcome the barriers between conformers is granted by the internal conversion, which follows after the molecule is excited by a photon to some higher energy electronic state (Fig. 1). Equilibration in the ground state is more questionable, and the system can stay in the non-equilibrium conformer distribution after emission. Morton et al. reported that ErSc2N@C80 changes conformer composition when irradiated by a 532 nm laser at 5 K, and that annealing at 30 K in the dark restores the original composition.19 Magnetic studies of HoLu2N@C80 and TbSc2N@C80 also showed that rotation of the endohedral cluster is frozen near 50 K.18 Thus, likely, the conformer distribution of YxSc3−xN@C80 molecules in the ground electronic state is also not completely restored in our experiments below 30 K. For instance, the population of conf 3 can be enhanced in the S0 state of YSc2N@C80 and Sc3N@C80 after continuous irradiation. But our photoluminescence studies cannot follow the ground state conformer composition, whereas results for the excited states will not be affected by this effect.
To summarize, our computations show that only in Y3N@C80 the molecular structure is not changing in the excited state. The lowest energy conformers of Y2ScN@C80, YSc2N@C80, and Sc3N@C80 molecules are different in the ground (S0) and excited (S1/T1) electronic states, which results in the photoswitching. The metal cluster in these molecules rotates upon photoexcitation to adopt a lower energy configuration (Fig. 6). The S0 → S1{S0} excitation energy of the most stable ground state conformer (conf 1) is weakly affected by the cluster composition in the whole YxSc3−xN@C80 series, decreasing by 0.098 eV from Y3N@C80 to Sc3N@C80. On the other hand, the S1 → S0{S1} transition energy for the most stable exited-state conformer decreases in the same row by as much as 0.470 eV. Altogether, this results in a considerable increase in the difference between absorption and emission energies for YxSc3−xN@C80 molecules with the decrease of x. These computational findings are in perfect agreement with the spectroscopic observations (Fig. 2 and 3) and confirm the switching of the endohedral cluster position in the excited state.
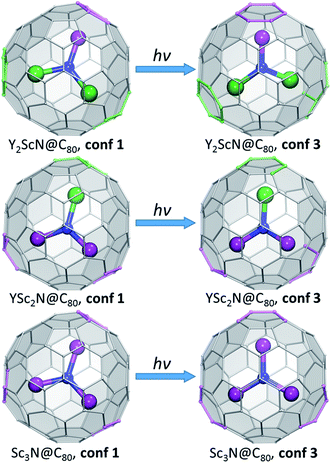 | ||
| Fig. 6 Switching between the lowest-energy conformers of S0 (conf 1) and S1/T1 (conf 3) electronic states in Y2ScN@C80, YSc2N@C80, and Sc3N@C80. Carbon atoms with Y–C distance less than 2.6 Å and Sc–C distance less than 2.5 Å are highlighted in green and magenta, respectively. The fullerene cage is shown in the same orientation in all figures. Conf 1 has C3 symmetry in Sc3N@C80 and Y3N@C80 (not shown here, see Fig. 2), and a similar cluster orientation is also realized in YSc2N@C80 and Y2ScN@C80. In conf 3 of Sc3N@C80, the cluster is rotated around the C3-axis to adopt C3v symmetry. For YSc2N and Y2ScN, the analogous cluster position inside the cage is not stable because of the larger cluster size. | ||
To understand what may be the reason behind the change of the endohedral cluster position in the excited state, we analyzed frontier molecular orbitals, spin densities in the triplet state (ρspin(T1)), and the difference electron charge density (ρel) for the S0 → S1 excitation (Δρel(S0 → S1) = ρel(S1) − ρel(S0)). The difference density gives the most informative description of the changes in the electronic structure upon excitation, and Δρel(S0 → S1) isosurfaces for the key conformers of YxSc3−xN@C80 molecules are plotted in Fig. 7, whereas frontier MOs and spin densities are shown in ESI (Fig. S2 and S3).† In Δρel(S0 → S1) plots, blue lobes denote areas where the electron charge density is accumulated in the excited state, whereas dark orange lobes mark areas where the electron charge density is depleted. Since S0 → S1 excitations in the studied molecules have mainly HOMO → LUMO character, Δρel(S0 → S1) is approximately equal to the difference of the orbital densities of the LUMO and HOMO, and hence the blue and orange lobes in Fig. 7 reflect the spatial localization of the LUMO and HOMO, respectively. On the other hand, ρspin(T1) has a similar shape to Δρel(S0 → S1), but has the same sign almost everywhere and therefore is less informative. In the discussion below, we will refer to the belt connecting metal-coordinated fragments of the fullerene cage as the equator, whereas the parts of the fullerene above and below the plane of the M3N cluster as poles.
 | ||
| Fig. 7 Difference electron charge density Δρel(S0 → S1) = ρel(S1) − ρel(S0) computed with TD-DFT for the lowest-energy S0 and S1/T1 conformers of YxSc3−xN@C80. Blue lobes denote areas where the electron density is accumulated in the excited state, dark orange lobes mark areas where the electron density is depleted upon excitation. If the excited state is described as a formation of the electron–hole pair (exciton), blue lobes in Δρel(S0 → S1) isosurfaces illustrate the spatial localization of the electron, and orange lobes describe (de)localization of the hole. The isosurfaces are visualized with VMD.77 | ||
In the M3N@C80 molecules with M = Y and other heavy metals (but not Sc), the HOMO and LUMO are localized on the poles and equator, respectively. Therefore, photoexcitation results in the electron transfer from the poles to the equator, as can be well seen in the Δρel(S0 → S1) isosurface plot for Y3N@C80, conf 1 (Fig. 7). Metal contributions to the difference density are very small and hardly seen. The situation changes when a Sc atom replaces Y. The HOMO of Y2ScN@C80 (conf 1) is still localized on the poles and the LUMO on the equator, but the latter also has a noticeable Sc contribution, which results in a partial localization of Δρel(S0 → S1) on Sc. The same pattern is observed in Δρel(S0 → S1) isosurfaces of YSc2N@C80 and Sc3N@C80, which show that each Sc atom has a contribution in the LUMO (hence blue lobes on Sc atoms in Fig. 7), but has a little effect on the HOMO. Another immediate conclusion from the analysis of Δρel(S0 → S1) isosurfaces in Fig. 7 is that in all YxSc3−xN@C80 molecules (x = 0–2), localization of the excess charge density on Sc atoms in the lowest-energy T1 conformer (conf 3) is substantially larger than in the ground state conformers (conf 1).
Thus, Δρel(S0 → S1) isosurfaces show that in Sc-containing M3N@C80 molecules the first excitation has a considerable charge-transfer character. In analogy to ligand-to-metal charge transfer (LMCT) in the photophysics of coordination compounds, this kind of excitation can be called “fullerene-to-metal charge transfer” (FMCT). The FMCT character of the photoexcitation increases incrementally with the number of Sc atoms in YxSc3−xN@C80 molecules and is further enhanced in those conformers of YxSc3−xN@C80, which are stabilized in the excited state. The maximization of the excess charge density on Sc atoms appears to be a driving force for the cluster rearrangement in the excited state.
The spatial separation of the HOMO and LUMO over the fullerene cage leads to the relatively small ΔST gap in Y3N@C80 and enables efficient TADF.51 Enhancement of the spatial separation of the frontier orbitals due to the adherence of the LUMO to Sc atoms and the increase of the FMCT character of the first excitation across the YxSc3−xN@C80 series is the reason for an even further decrease of the ΔST gap in the YxSc3−xN@C80 molecules as x decreases from 3 to 0. And since the FMCT character is enhanced in excited-state conformers such as conf 3 (Fig. 7), these conformers also feature the smallest ΔST gaps (Fig. S4†). To summarize, preferential localization of the excess electron charge and spin density in the excited state on Sc atoms and further enhancement of this effect in the conformers stabilized in the excited states leads to a decrease of the ΔST gaps for these structures, which agrees perfectly with our spectroscopic results (Table 1). In Sc3N@C80 this effect is so strong that the ΔST gap is below the limit which can be determined in our experiments.
Photoelectron spectroscopy (PES) of the Sc3N@C80− anion
The lowest-energy T1-conformer of Sc3N@C80 from this work, conf 3, has the same C3v-symmetric arrangement of the Sc3N cluster inside fullerene as was earlier found in the lowest energy conformer of the Sc3N@C80− anion.16,66 Further comparison shows that there is indeed a close parallelism between optimal conformers for the neutral fullerene in the T1 excited state and the monoanion (see Table S6† for comparison of conformer energies). Similar to the triplet state of Sc3N@C80, the Sc3N@C80− monoanion also has a much higher spin density on the cluster in conf 3 (C3v conformer) than in conf 1 (C3 configuration). Thus, the structure with the largest spin population on the endohedral cluster has the lowest energy both in the anionic state and the triplet excited state, which leads to a similar structural rearrangement upon negative charging or photoexcitation of a Sc3N@C80 molecule.We can establish a further connection between anion and triplet state geometries of Sc3N@C80 by a low-temperature photoelectron spectroscopic (PES) study78 of the Sc3N@C80− anion. In the PES experiment, laser photoionization of the anion M− cooled to helium temperature results in the ejection of an electron with a certain binding energy. Fig. 8a summarizes the photoelectron ejection mechanisms possible in the low energy range. Electron ejection from the SOMO of the anion leaves the molecule M in the ground electronic state, and the binding energy for this process is equal to the electron affinity (EA) of the molecule. However, an electron can be also ejected from the low-lying two-fold occupied orbital, which will give either the triplet or the singlet excited state of the neutral molecule, M*. The binding energy, in this case, corresponds to the sum of EA and electronic excitation energy Eex of the neutral molecule.
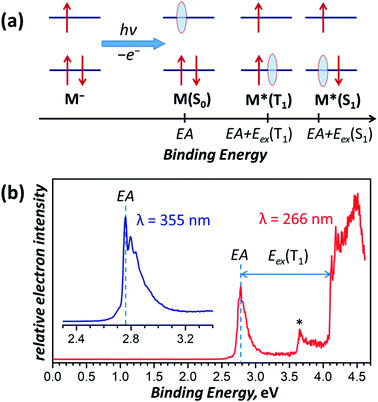 | ||
| Fig. 8 (a) Schematic description of the electron photoemission process with an anion M− resulting in a neutral molecule M in different electronic states (S0, T1, S1, etc.) and correspondence of the binding energies with the molecular electronic properties, such as the electron affinity (EA) and excitation energies S0 → T1 and S0 → S1 denoted as Eex(T1) and Eex(S1), respectively; red arrows denote electrons, whereas light blue ovals show “holes” left behind the photo-emitted electrons. (b) Photoelectron spectrum of Sc3N@C80− measured at 12 K with laser excitations at 355 nm (3.49 eV, inset) and 266 nm (4.66 eV). The asterisk denotes an auto-detachment peak similar to that observed in PES spectra of C60−.88,89 | ||
The photoelectron spectrum of Sc3N@C80− in Fig. 8b gives the EA of 2.76 ± 0.01 eV, which agrees well with an earlier estimation of EA = 2.81 ± 0.05 eV from the high-temperature ion-molecular equilibrium analyzed by Knudsen-cell mass spectrometry.79 To our knowledge, this is the first determination of the EMF electron affinity by high-resolution PES, although the method had been widely used for EA measurements of empty fullerenes and their derivatives.80–86 For comparison, the most accurate EA of C60 determined by a similar technique is 2.684 ± 0.001 eV.87 Since Sc3N@C80− is cooled down to 12 K and equilibrated before the photoionization, it is reasonable to assume that the most intense feature in the PES spectrum corresponds to the Sc3N@C80− → Sc3N@C80 process of the C3v conformer (conf 3) in both anion and neutral states. Photoionization yielding lower-energy conformers of the neutral Sc3N@C80 should give somewhat smaller EA but is expected to have much lower intensity by the Franck–Condon principle and may be responsible for the tail of the main peak at 2.60–2.75 eV.
The PES peak at binding energy above 4 eV corresponds to the T1 excited state of Sc3N@C80. The large width and complex structure of the peak are likely to be caused by the distribution of conformers, vibronic transitions, and overlap with the S1 state, which should appear at essentially the same energies because of the small ΔST gap. The lowest energy peak likely to correspond to the conf 3 in the T1 state, which yields 1.35 eV as the Eex(S0 → T1) transition energy of the conf 3. This value is very close to the emission energy of Sc3N@C80 determined in low-temperature PL studies (Table 1).
Light-induced EPR spectroscopy
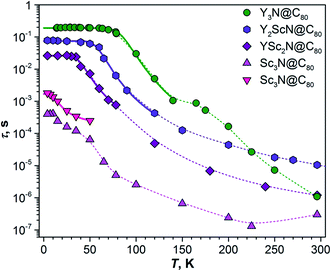
The fullerene-to-metal charge transfer in the S1/T1 excited states of YxSc3−xN@C80 molecules implies that the spin density in the T1 states has large Sc contribution, which should lead to strong hyperfine interactions. Spin density in the Sc3N@C80− anion is mainly localized on the endohedral cluster resulting in a large 45Sc hyperfine coupling constant of 5.3–5.6 mT (≈150 MHz).90–93 If the analogy between triplet state and anion holds, enhanced hyperfine constants for Sc atoms are expected in the T1 state of YxSc3−xN@C80. To study the electronic structure and the dynamics of the triplet states we have employed light-induced pulsed W-band EPR spectroscopy (94 GHz/3.4 T). Experiments were performed in toluene-d8 solutions frozen at 20 K to ensure sufficiently long T1 lifetimes.The field-swept Electron Spin Echo (ESE) detected W-band EPR spectra of the YxSc3−xN@C80 series, recorded upon laser excitation in frozen toluene-d8 at 20 K, are shown in Fig. 9 (insets) and Fig. S5.† Reference spectra measured in the dark showed no EPR signal, and the spectra recorded upon irradiation are therefore assigned to the corresponding excited triplet states. Directly after the laser flash (delay after flash time, tDAF, of 500 ns), the EPR spectra show spin-polarized character, featuring both absorption (A) and emission (E) lines (Fig. 9 insets). The polarization pattern stems from the non-equilibrium population of the triplet energy levels built during the intersystem crossing from the excited singlet state. A detailed analysis of the polarized EPR patterns is non-trivial due to the complex cluster conformational dynamics discussed above and is thus out of the scope of this work. The ESE signals evolve through two distinct time regimes as illustrated for the emissive line intensities in Fig. 9. During the first few hundreds of μs (or in the low ms range) after the laser flash, the polarized pattern diminishes due to the spin–lattice relaxation characterized by the τ1 time. The purely absorptive EPR signal formed after this first period (Fig. S5†) then corresponds to the Boltzmann population of the triplet energy levels. Its exponential decay during the next tens to hundreds of ms corresponds to the relaxation of the T1 to the S0 ground state and is characterized by the triplet lifetime τT1.
The τ1 times obtained for the YxSc3−xN@C80 series span over an order of magnitude from 78 μs for the Sc3N@C80 to 1.2 ms for YSc2N@C80. The trend shows no apparent correlation with the cluster composition and the difference between the shortest and the longest τ1 is rather surprising. The position of the emission feature within the polarized spectra varies considerably among the fullerene series, being close to the center for Y3N@C80 and Y2ScN@C80 and near the high-field edge for YSc2N@C80 and Sc3N@C80 excited triplets. Given the powder-like character of the EPR spectra, generally, the microwave pulse excitation closer to the center covers more molecular orientations than at the edge, where single crystal-like orientation-selected data can be achieved. If a significant spin–lattice relaxation anisotropy occurs and depends on the molecular orientations, the different positions within the spectrum may result in incompatible data. Thus, a more detailed study with different field positions is needed to yield insight into the relationship between the cluster composition and/or motion and relaxation dynamics, which is beyond the scope of this work.
The trend of the triplet lifetimes τT1 is more straightforward. At 20 K, τT1 decreases with the increasing number of Sc atoms in the cluster from 240 ms for Y3N@C80 to 10 ms for Sc3N@C80. This trend agrees with the results from the phosphorescence measurements, and the τT1 and τPh values show a reasonable quantitative match (Table 1), if we keep the different experimental conditions in mind, particularly the different solvent matrix (frozen toluene-d8 in EPR vs. polystyrene in luminescence experiments).
The long lifetimes of the YxSc3−xN@C80 triplets at 20 K provide an additional advantage for the light-induced EPR experiments. The spectra obtained under continuous irradiation (Fig. 10, compare with Fig. S5†) correspond to the equilibrium population of the triplet energy levels and are easier to analyze due to the absence of polarization effects. Besides, EPR signal acquisition is no longer limited by the laser pulse repetition rate, giving improved signal-to-noise ratio under continuous illumination. Already a brief inspection of the EPR spectra in Fig. 10 reveals several interesting trends. The increasing number of Sc atoms in the cluster leads to the broadening of the EPR spectra. Their central position moves towards lower g values and a regular signal splittings appear for YSc2N@C80 and Sc3N@C80. The splittings were already apparent in the polarized EPR spectra in Fig. 9 and S5.† They become best resolved when we process the absorption data from Fig. 10a using a pseudo-modulation procedure to resemble cw-like EPR spectra (Fig. 10b). The splittings indicate a significant hyperfine interaction between the triplet exciton (two unpaired electrons) and the 45Sc nuclear spin(s) (I = 7/2, natural abundance 100%). The broadening and the rather isotropic character of YSc2N@C80 and Sc3N@C80 EPR spectra most likely stems from a combined effect of the 45Sc hyperfine splitting and a larger zero-field splitting. Together with the shifts of the spectrum towards the g < 2 region these observations suggest a larger metal contribution to the spin-bearing orbitals as the cluster composition changes from Y3N to Sc3N.
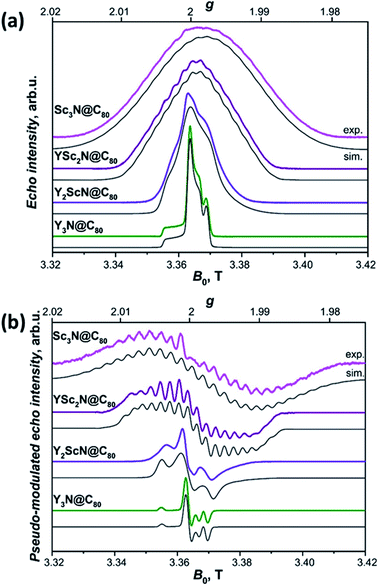 | ||
| Fig. 10 (a) W-band ESE-detected EPR spectra of the Y3N@C80 (green line), Y2ScN@C80 (violet line), YSc2N@C80 (purple line) and Sc3N@C80 (magenta line) excited triplet states recorded in frozen toluene-d8 solution at 20 K under continuous 510 nm laser illumination. Grey lines represent EPR spectra calculated using the spin Hamiltonian in eqn (2) and the magnetic parameters summarized in Table 2. (b) The same ESE EPR spectra processed by a field pseudo-modulation procedure (modulation amplitude of 1.5 mT) to resemble continuous-wave (CW) EPR spectra. The 45Sc hyperfine multiplets are clearly resolved in the YSc2N@C80 and Sc3N@C80 traces. Reduced spin density on Y atoms together with smaller nuclear g-factor (gn = −0.27 for 89Y versus gn = 1.36 for 45Sc) lead to much smaller 89Y hyperfine couplings, which cannot be resolved in the EPR spectra. | ||
Interpretation of the EPR spectra of triplets with strong hyperfine interactions and nuclear spin I > 1/2 requires a spin Hamiltonian (Ĥspin), which includes electron Zeeman (ĤEZ), zero-field splitting (ĤZFS), hyperfine (ĤHFI), nuclear Zeeman (ĤNZI), and nuclear quadrupole (ĤNQI) terms:
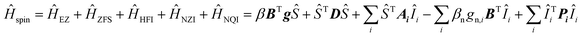 | (2) |
| ĤZFS = ŜTDŜ = D[Ŝz2 − S(S + 1)/3] + E(Ŝx2 − Ŝy2) | (3) |
| ĤNQI = ÎTPÎ = K[3Îz2 − I(I + 1) + η(Îx2 − Îy2)] | (4) |
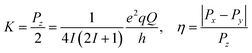 | (5) |
| g | ZFS parametersb, MHz | Hyperfine coupling, MHz | Nuclear quadrupole coupling, MHz | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 89Yc | 45Scd | 14Nc | 45Sce | 14Nf | |||||||
| a The estimated error ±0.0002. b The estimated error ±10 MHz for Sc-containing molecules because of Sc hyperfine broadening. c The estimated error ±0.1 MHz. d The estimated error ±3 MHz. e The estimated error ±3 MHz. f The estimated error ±0.05 MHz. | |||||||||||
| Y3N@C80 | g x | 2.0004 | D | +128 | A ⊥ | +1.02 | — | +0.15 | |e2Qq/h| | — | 1.46 |
| g y | 2.0008 | E | 0 | A ∥ | +1.02 | — | +0.62 | η | — | 0 | |
| g z | 2.0030 | ||||||||||
| Y2ScN@C80 | g x | 1.9964 | D | +131 | A ⊥ | −0.75 | +35 | +0.10 | |e2Qq/h| | 75 | 1.30 |
| g y | 1.9984 | E | 0 | A ∥ | −0.75 | +49 | −0.54 | η | 0 | 0 | |
| g z | 2.0025 | ||||||||||
| YSc2N@C80 | g x | 1.9986 | D | +133 | A ⊥ | — | +58 | −0.64 | |e2Qq/h| | 75 | 1.21 |
| g y | 1.9986 | E | 0 | A ∥ | — | +58 | −0.83 | η | 0 | 0 | |
| g z | 2.0003 | ||||||||||
| Sc3N@C80 | g x | 1.9969 | D | +291 | A ⊥ | — | +71 | — | |e2Qq/h| | 72 | — |
| g y | 1.9969 | E | 0 | A ∥ | — | +71 | — | η | 0 | — | |
| g z | 2.0002 | ||||||||||
Light-induced ENDOR
A quantitative description of the spin density distribution within the M3N clusters requires determination of hyperfine and quadrupolar couplings in eqn (2). As the EPR spectra do not provide sufficient resolution, the problem was addressed with Electron Nuclear Double Resonance spectroscopy (ENDOR). In pulsed ENDOR, the microwave electron-spin excitation pulse is followed by irradiation of the sample with a radiofrequency pulse, which changes the populations of nuclear spin levels and reduces the ESE intensity at the frequencies corresponding to the nuclear spin transitions. The frequencies of the ENDOR nuclear transitions, calculated to the first order of perturbation theory, are given by eqn (6):97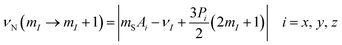 | (6) |
Mims ENDOR
Mims-type pulse W-band ENDOR data of the YxSc3−xN@C80 (x = 1–3) excited triplets are shown in Fig. 11. The spectra obtained with Y3N@C80 were already analyzed in our previous work51 and are reproduced here for completeness. The EPR spectrum of Y3N@C80 shows a well resolved ZFS fine structure and the ENDOR spectra were recorded at field positions corresponding to the turning points of the ZFS pattern, providing a sufficient orientation selection. Signals found at frequencies below 13.0 MHz reflect the hyperfine and quadrupole couplings of the cluster nuclei, 89Y and 14N. | ||
| Fig. 11 Mims-type (b) 89Y and (c) 14N ENDOR spectra of the Y3N@C80 (green lines), Y2ScN@C80 (violet lines) and YSc2N@C80 (purple lines) light-excited triplets recorded at magnetic field positions indicated by the arrows in panel (a) displaying the EPR spectra. The arrow colour tone matches with the corresponding experimental ENDOR trace. All spectra were obtained under continuous 510 nm irradiation at 20 K in frozen toluene-d8. Grey lines show the ENDOR spectra calculated using the spin Hamiltonian parameters summarized in Table 2. The splitting due to the corresponding hyperfine (A) and quadrupolar (P) interactions are illustratively indicated for Y3N@C80 in (c). The dashed lines indicate the Larmor frequencies of the corresponding nuclei. | ||
Following eqn (6) for the S = 1 triplet state with I = 1/2 nuclei, the sharp line at 7 MHz (Fig. 11b, green) corresponds to the Larmor frequency of 89Y (I = 1/2, 100% natural abundance) and originates from the degenerate NMR transitions within the electron spin manifold mS = 0. The two broader lines, spaced by A(89Y) from the mS = 0 line, result from the 89Y hyperfine interaction at mS = ±1. The invariant frequency position of these lines throughout the field-swept ENDOR series suggests the predominantly isotropic character of the 89Y hyperfine interaction, A⊥ ≈ A∥ ≈ Aiso. Simulations of the spectra reveal a small positive isotropic hyperfine coupling (hfc) constant of Aiso(89Y) = +1.02 MHz, with the three Y nuclei in the cluster being magnetically equivalent. In theory, the isotropic hyperfine coupling for the nucleus X is defined by the generalized Fermi contact term Aiso(X) ∼ S−1gn(X)ρspin(X),98,99 where S is the electron spin, gn(X) is the nuclear g-factor, and ρspin(X) is the spin density at nucleus X. The factor gn(89Y) is negative, and the positive sign of the Aiso(89Y) suggests that the electron spin density ρspin(Y) at the Yttrium of the endohedral cluster is negative. This is in line with the results of our DFT calculations, which predict the positive sign for Aiso(89Y) and thus a negative ρspin(Y) generated by the spin polarization of 89Y s-orbitals (Table S7, ESI†).
The orientation selection obtained in the Mims ENDOR spectra of Y3N@C80 triplet also allows for a detailed analysis of the hyperfine and quadrupole tensor of the central cluster nitrogen (14N, I = 1, natural abundance 99.63%, Larmor frequency around 10.4 MHz, Fig. 11c, green lines). The simulation of experimental ENDOR recordings (Fig. 11c grey lines) reveals a rather small positive axial hfc with A∥(14N) = +0.62 MHz, A⊥(14N) = +0.15 MHz (Aiso(14N) = +0.31 MHz), and a somewhat larger nuclear quadrupole of |e2Qq/h| = 1.46 MHz (asymmetry η = 0). The small positive Aiso(14N) and the magnitude of the quadrupole coupling are also well predicted by DFT as detailed in Table S7.†
When compared to the Y3N@C80 data, the Mims ENDOR spectra of Y2ScN@C80 triplet (Fig. 11b) are of poorer quality. This is due to the shorter triplet lifetime, lower triplet quantum yield and a broader EPR spectrum resulting in a lower EPR intensity at the selected magnetic field position. Despite the lower signal-to-noise ratio, one can identify two 89Y hfc lines positioned closer to the central mS = 0 line (Fig. 11b) suggesting a smaller Aiso(89Y) of −0.75 MHz. While the claim on the isotropic character of the tensor and the equivalence of the two Y in the cluster is less justified, given the fewer field positions explored, we believe they hold. In this case, the negative sign of the Aiso(89Y) is compatible with a small positive electron spin density ρspin(Y) at Yttrium atoms. The negative sign of Aiso(89Y) is also predicted by DFT (Table S7†), although the hfc values are overestimated by the calculation, and the two nuclei are predicted to be magnetically inequivalent. In contrast to Y3N@C80, the 14N ENDOR data (Fig. 11b) of Y2ScN@C80 show a stronger powder character. This is in line with the appearance of the EPR spectrum where the ZFS pattern, and thus the accessible orientation selection, smear out due to the hyperfine splitting from 45Sc. Simulations of the ENDOR data reveal an axial hyperfine tensor with A∥(14N) = −0.54 MHz, A⊥(14N) = +0.10 MHz (Aiso(14N) = −0.11 MHz), and the nuclear quadrupole coupling of |e2Qq/h| = 1.30 MHz (asymmetry parameter η = 0) for the central nitrogen.
The experimental difficulties in obtaining high-quality ENDOR data are even more pronounced for YSc2N@C80, due to the physical limits given by the photophysical properties of its T1 state. We could not detect the mS = ±1 89Y hfc lines, even though the central mS = 0 line is observable (Fig. 11b, purple). The 14N ENDOR data (Fig. 11b) show powder Pake patterns compatible with A∥(14N) = −0.83 MHz, A⊥(14N) = −0.64 MHz (Aiso(14N) = −0.70 MHz), and the quadrupole coupling of |e2Qq/h| = 1.21 (asymmetry η = 0). The trend in the 89Y hyperfine couplings (Table 2), observed in the YxSc3−xN@C80 (x = 1–3) series, and particularly the switch of the sign of Aiso(89Y) suggests an increase of the spin density on Y with increasing content of Sc in the cluster, supporting the idea of spin density transfer from the fullerene cage to the cluster. The interpretation of the differences in 14N couplings is less straightforward, but the DFT predicted small negative spin density ρspin(N) at the nitrogen in Sc-containing molecules (negative Aiso(14N), Table S7†) is reflected in the experimental data. In general, both 89Y and 14N hfc's are rather small. Therefore, we conclude that these are certainly not the spin-bearing nuclei in the T1 states of YxSc3−xN@C80 (x = 1–3).
Davies ENDOR
The key data to evaluate the hypothesis on the spin density transfer from cage to the Sc-containing cluster come from 45Sc ENDOR spectroscopy. The splittings in the EPR spectra of YSc2N@C80 and Sc3N@C80 triplets show that 45Sc hyperfine couplings are about 50 MHz. The ENDOR data for the YxSc3−xN@C80 (x = 0–2) triplets recorded at different magnetic field positions within the EPR spectra are shown in Fig. 12. To the best of our knowledge, these are the first ENDOR data reported for the 45Sc nucleus. In general, the spectra show well-resolved patterns at around 35 MHz and broad lines with linewidths exceeding 15 MHz above 60 MHz. With the 45Sc Larmor frequency around 34.8 MHz, the obtained data correspond to ENDOR spectroscopy in the high coupling regime with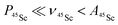 . In this regime, according to eqn (6), the spectrum of the S = 1 triplet is expected to feature a doublet signal centered at the frequency of the hyperfine coupling and split by double the Larmor frequency, as indicated in Fig. 12f (magenta, bottom panel). Additionally, the nuclear transitions within the mS = 0 manifold generate a signal at the 45Sc nuclear Larmor frequency, that is influenced by nuclear quadrupole coupling and higher-order hyperfine shifts.
. In this regime, according to eqn (6), the spectrum of the S = 1 triplet is expected to feature a doublet signal centered at the frequency of the hyperfine coupling and split by double the Larmor frequency, as indicated in Fig. 12f (magenta, bottom panel). Additionally, the nuclear transitions within the mS = 0 manifold generate a signal at the 45Sc nuclear Larmor frequency, that is influenced by nuclear quadrupole coupling and higher-order hyperfine shifts.
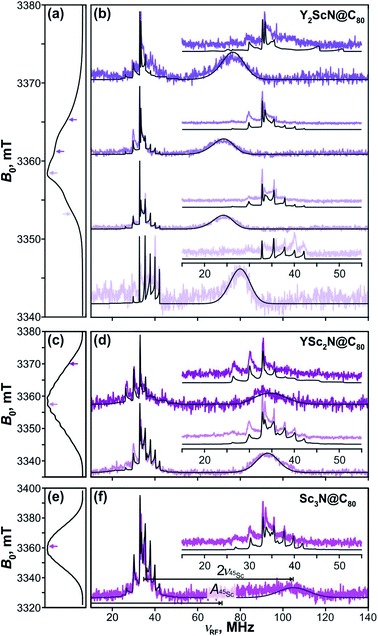 | ||
Fig. 12 Davies-type 45Sc-ENDOR spectra (b) of Y2ScN@C80 (violet lines), (d) YSc2N@C80 (purple lines) and (f) Sc3N@C80 (magenta lines) excited triplet states detected at the arrow-marked magnetic field positions in W-band ESE EPR spectra in panels (a), (c), and (e), respectively. All spectra were obtained in frozen toluene-d8 at 20 K under continuous 510 nm laser irradiation. Insets in panels (b), (d), (f) show expansions of the signals around the 45Sc Larmor frequency, corresponding to the transitions within the mS = 0 manifold. The well-resolved splitting patterns originate from the quadrupolar interaction. Grey lines show spectra calculated using the spin Hamiltonian parameters summarized in Table 2. The evaluation of the 45Sc hyperfine coupling 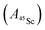 is illustratively indicated for Sc3N@C80. is illustratively indicated for Sc3N@C80. | ||
The 45Sc ENDOR spectra of Y2ScN@C80 (Fig. 12b, violet lines) reveal a shift of the position of the high-frequency line (mS = −1) from 65 to 80 MHz, depending on the field position within the EPR spectrum, indicating a minor anisotropy of the 45Sc hyperfine coupling. The line broadening is likely the consequence of a complex quadrupolar splitting combined with a hyperfine strain. The signal is readily detectable, despite the broadening, due to the hyperfine-enhancement effect100,101 producing larger ENDOR intensity for the high-frequency component of the hyperfine doublet. The low-frequency counterpart (mS = +1) essentially vanishes in the noise at the low-frequency end of the ENDOR spectrum and partially overlaps with the well-resolved mS = 0 feature at the Larmor frequency. The spectral simulations revealed that an axial hyperfine tensor with A∥(45Sc) = 49 MHz and A⊥(45Sc) = 35 MHz is compatible with the field-dependent shifts of the high-frequency line. The well resolved Pake patterns at the 45Sc Larmor frequency reflect an axial quadrupolar coupling tensor of the high-spin I = 7/2 45Sc nucleus defined by |e2Qq/h| = 75 MHz and asymmetry η = 0 (Fig. 12b, violet lines).
The 45Sc ENDOR spectra of YSc2N@C80 show less pronounced variations of the position of the high-frequency line and the spectra calculated with isotropic hyperfine tensors for both Sc atoms, Aiso(45Sc) = A∥(45Sc) = A⊥(45Sc) = 58 MHz, match reasonably well with the experimental traces (Fig. 12d, purple lines). The isotropic character of the coupling is also in line with the well-resolved and regular splitting observed in the corresponding EPR spectrum (Fig. 10). The quadrupolar coupling extracted from the sharp peaks around the Larmor frequency is essentially identical with the Y2ScN cluster |e2Qq/h| = 75 MHz (η = 0).
The ENDOR spectrum of Sc3N@C80 triplet (Fig. 12f, magenta line) recorded at the field position of the maximum EPR signal shows the high-frequency line at 104 MHz and suggest a hyperfine tensor with Aiso(45Sc) = A∥(45Sc) = A⊥(45Sc) = 71 MHz. Since here we have the data only from a single magnetic field position, the isotropic character of the tensor is an estimate based on the well-resolved hyperfine pattern observed in the EPR (Fig. 10). The low-frequency hyperfine ENDOR line (mS = +1) is in this case completely covered by the mS = 0 multiplet, which can be reproduced in the calculated spectrum with the quadrupolar coupling of |e2Qq/h| = 72 MHz (η = 0). Note that the Aiso(45Sc) in the triplet state is about twice smaller than in the Sc3N@C80− anion with Aiso(45Sc) ≈ 150 MHz.90–93 The DFT-predicted spin density and spin population at Sc in both species are almost identical, but the S−1 scaling of the hfc constant leads to a two-fold decrease of the Aiso(45Sc) value for the triplet (S = 1) in comparison to the anion radical (S = 1/2). Alternatively, it can be recalled that the hfc constant in the triplet state is expected to be close to an average of the hfc constants of the anion and cation radicals (see ref. 102 for an example). As the HOMO in Sc3N@C80 is localized on the fullerene cage, the 45Sc hfc constant of the cation should be very small (experimental value is not known yet), which gives Aiso(45Sc, T1) ≈ 0.5Aiso(45Sc, anion).
Summarizing, the 45Sc ENDOR of the YxSc3−xN@C80 (x = 0–2) reveals an increase in the magnitude of the 45Sc hyperfine coupling with the increasing number of Sc atoms in the cluster, in line with the predicted fullerene-to-metal spin density transfer in the photoexcited triplets. The ENDOR spectroscopy of triplet S = 1 states additionally provides a unique method to obtain detailed information about the nuclear quadrupolar interaction, since the corresponding splittings are well resolved with the mS = 0 multiplet. The 45Sc quadrupolar coupling in YxSc3−xN@C80 (x = 0–2) excited triplet series is essentially identical and is very close to the value for the parent ground state of Sc3N@C80 revealed by solid state-NMR (|e2Qq/h| = 67.9 MHz, η = 0).103 This similarity suggests that the electric field gradients around the Sc nuclei are of similar magnitude and are not dramatically influenced by the electron and spin density redistribution in the S0 → T1 excitation.
Utilizing the detailed data on the hyperfine and quadrupolar tensors (Table 2) obtained from the ENDOR investigation we were able to calculate the EPR spectra of all the YxSc3−xN@C80 (x = 0–3) triplets shown in Fig. 10 (grey lines). The calculated EPR spectra match well with the experimental recordings, when we assume that the Sc atoms in the YSc2N and Sc3N clusters are magnetically equivalent. The zero-field splitting tensors were considered axially symmetric and the D values grow from +128 MHz in Y3N@C80 to +291 MHz in Sc3N@C80. The D value appears similar for Y3N@C80, YSc2N@C80, and Y2Sc@NC80, but precise details cannot be discussed because of the uncertainty in the value introduced by the broadening of the spectra by Sc-hyperfine interaction. Additionally, a decrease in all principal values of the g-tensor is observed with increasing content of Sc in the cluster. Together with the increase of the 45Sc hyperfine coupling throughout the series, these data confirm the progressive shift of the spin density from the fullerene cage to the Sc-containing cluster and are fully consistent with the conclusions from the photochemical investigations and the DFT-modelling. Hyperfine and quadrupolar parameters and g-tensors of the lowest-energy triplet conformers were also computed with DFT and listed in Table S7.† The computations qualitatively reproduce the experimental trends, including a decrease of the g-factor from Y3N@C80 to Y2ScN@C80 to YSc2N@C80 as well as the increase of the A(45Sc) hyperfine constants. DFT calculations also point out that the A(45Sc)-tensors do not show a large anisotropy, thus justifying an isotropic approximation employed in simulations of the experimental EPR and ENDOR spectra. Finally, the DFT calculated quadrupolar parameters are also in close agreement with the experimental values. The predicted asymmetry parameter η is close to 0 in all studied structures for both 14N and 45Sc, which agrees with experimental observations.
Conclusions
A systematic study of the photophysical properties of metallofullerenes YxSc3−xN@C80 (x = 0–3) showed that the cluster composition has a very strong influence on the emission properties of these, seemingly similar nitride clusterfullerene. Utilizing variable-temperature steady-state and time-resolved measurements we proved that luminescence from all four compounds follows the thermally-activated delayed fluorescence mechanism, replaced by phosphorescence only at very low temperature. All YxSc3−xN@C80 molecules feature a very small S1–T1 gap of less than 0.1 eV, which indicates that TADF may be a universal phenomenon in metallofullerenes. Emission studies also revealed a strong increase of the luminescence wavelength with the increase of the number of Sc atoms in the endohedral cluster, which is not reflected in the absorption spectra. Such changes point to a potential structural reorganization upon excitation, and this hypothesis was thoroughly analyzed by theoretical modelling of the ground and excited states. Indeed, we found that for all M3N clusters with Sc atoms, the M3N cluster has different preferential positions inside the fullerene cage in the S0 and S1/T1 states. Furthermore, computations revealed that the conformers with lower energy in the excited state tend to increase the localization of the excess electron charge and spin density on Sc atoms compared to the conformers preferred in the ground state. Light-induced pulsed W-band EPR spectroscopy was applied to further corroborate the properties of the triplet states. The triplet lifetimes found by electron spin echo detected EPR are in good agreement with optical measurements, thus confirming the correct assignment of the emitting states. Mims and Davies-type 14N, 45Sc, and 89Y ENDOR measurements provided a detailed characterization of the spin distribution in the triplet states and showed a systematic increase of the spin density localization on Sc atoms when going from Y2ScN@C80 to Sc3N@C80, in perfect agreement with computational results. Altogether, our study demonstrates that the position of the endohedral cluster in metallofullerenes can be controlled by light excitation, and that the driving force for the photoswitching is the fullerene-to-cluster charge transfer and localization of the electron charge and spin density on the metal atoms.The flexibility of the metal cluster in EMFs often results in disorder of the metal positions, which substantially affects the studies of their molecular structure and physical properties, such as electron transport or magnetism. Whereas conventional cooling of metallofullerene assemblies usually results in disordered cluster positions, light-induced switching can be used for better control of such assemblies. For instance, light-assisted annealing can be developed to selectively increase the population of particular cluster orientations, whereas a combination of this effect with lanthanide-based magnetism in metallofullerenes104,105 opens a way to magnetooptical switching on a nanoscale.
Author contributions
F. Z. and S. S. performed luminescence studies; V. D., S. M. A. and A. A. P. performed DFT calculations; S. H. D. and X. B. W. performed the PES study; M. Z., A. S. and W. L. performed EPR study; M. Z. and A. A. P. conceived the study and written the manuscript with contributions from all coauthors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding from the Deutsche Forschungsgemeinschaft (grants PO 1602/5-1 and PO 1602/6-1 to A. A. P.), the Slovak Research and Development Agency (grants APVV-17-0513, APVV-19-0024 to M. Z.), the Slovak Scientific Grant Agency VEGA (grant 1/0466/18 to M. Z.) and the Max Planck Society. Computational facilities were partially provided by the Center for High Performance Computing at the TU Dresden. We appreciate the technical support with local computational resources in IFW Dresden by Ulrike Nitzsche. The PES work was supported by U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, and performed using EMSL, a national scientific user facility sponsored by DOE's Office of Biological and Environmental Research and located at Pacific Northwest National Laboratory, which is operated by Battelle Memorial Institute for the DOE.References
- A. A. Popov, S. Yang and L. Dunsch, Endohedral Fullerenes, Chem. Rev., 2013, 113(8), 5989–6113 CrossRef CAS PubMed.
- S. Yang, T. Wei and F. Jin, When metal clusters meet carbon cages: endohedral clusterfullerenes, Chem. Soc. Rev., 2017, 46(16), 5005–5058 RSC.
- X. Lu, W. Shen and S. Hu, Endohedral Metallofullerenes: New Structures and Unseen Phenomena, Chem.–Eur. J., 2020, 26(26), 5748–5757 CrossRef PubMed.
- M. R. Cerón, F.-F. Li and L. A. Echegoyen, Endohedral fullerenes: the importance of electronic, size and shape complementarity between the carbon cages and the corresponding encapsulated clusters, J. Phys. Org. Chem., 2014, 27, 258–264 CrossRef.
- J. Zhang, S. Stevenson and H. C. Dorn, Trimetallic Nitride Template Endohedral Metallofullerenes: Discovery, Structural Characterization, Reactivity, and Applications, Acc. Chem. Res., 2013, 46(7), 1548–1557 CrossRef CAS PubMed.
- X. Lu, L. Feng, T. Akasaka and S. Nagase, Current status and future developments of endohedral metallofullerenes, Chem. Soc. Rev., 2012, 41(23), 7723–7760 RSC.
- A. Rodriguez-Fortea, A. L. Balch and J. M. Poblet, Endohedral metallofullerenes: a unique host-guest association, Chem. Soc. Rev., 2011, 40, 3551–3563 RSC.
- J. Zhang and H. C. Dorn, NMR Studies of the Dynamic Motion of Encapsulated Ions and Clusters in Fullerene Cages: A Wheel Within a Wheel, Fullerenes, Nanotubes, Carbon Nanostruct., 2014, 22(1–3), 35–46 CrossRef CAS.
- W. Fu, X. Wang, H. Azuremendi, J. Zhang and H. C. Dorn, 14N and 45Sc NMR study of trimetallic nitride cluster (M3N)6+ dynamics inside a icosahedral C80 cage, Chem. Commun., 2011, 47(13), 3858–3860 RSC.
- F. Liu and L. Spree, Molecular spinning top: visualizing the dynamics of M3N@C80 with variable temperature single crystal X-ray diffraction, Chem. Commun., 2019, 55(86), 13000–13003 RSC.
- Y. Hao, Y. Wang, L. Spree and F. Liu, Rotation of fullerene molecules in the crystal lattice of fullerene/porphyrin: C60 and Sc3N@C80, Inorg. Chem. Front., 2021, 8, 122–126 RSC.
- K. Vietze and G. Seifert, Fluxional behaviour of Sc3N in endohedral Sc3N@C80, AIP Conf. Proc., 2002, 633(1), 39–42 CrossRef CAS.
- T. Heine, K. Vietze and G. Seifert, 13C NMR fingerprint characterizes long time-scale structure of Sc3N@C80 endohedral fullerene, Magn. Reson. Chem., 2004, 42, S199–S201 CrossRef CAS PubMed.
- Y. Zhang, D. Krylov, S. Schiemenz, M. Rosenkranz, R. Westerstrom, J. Dreiser, T. Greber, B. Buchner and A. A. Popov, Cluster-size dependent internal dynamics and magnetic anisotropy of Ho ions in HoM2N@C80 and Ho2MN@C80 families (M = Sc, Lu, Y), Nanoscale, 2014, 6, 11431–11438 RSC.
- A. D. Pykhova, O. O. Semivrazhskaya, N. A. Samoylova, A. V. Rybalchenko, M. Rosenkranz, I. N. Ioffe, A. A. Popov and A. A. Goryunkov, Addition of CF2 group to endohedral fullerene Sc3N@Ih-C80, Dalton Trans., 2020, 49, 9137–9147 RSC.
- A. A. Popov and L. Dunsch, Hindered Cluster Rotation and 45Sc Hyperfine Splitting Constant in Distonoid Anion Radical Sc3N@C80, and Spatial Spin Charge Separation as a General Principle for Anions of Endohedral Fullerenes with Metal-Localized Lowest Unoccupied Molecular Orbitals, J. Am. Chem. Soc., 2008, 130(52), 17726–17742 CrossRef CAS PubMed.
- T. Huang, J. Zhao, M. Feng, A. A. Popov, S. Yang, L. Dunsch and H. Petek, A Molecular Switch Based on Current-Driven Rotation of an Encapsulated Cluster within a Fullerene Cage, Nano Lett., 2011, 11, 5327–5332 CrossRef CAS PubMed.
- A. Kostanyan, R. Westerström, Y. Zhang, D. Kunhardt, R. Stania, B. Büchner, A. A. Popov and T. Greber, Switching Molecular Conformation with the Torque on a Single Magnetic Moment, Phys. Rev. Lett., 2017, 119(23), 237202 CrossRef PubMed.
- J. G. M. Morton, A. Tiwari, G. Dantelle, K. Porfyrakis, A. Ardavan and G. A. D. Briggs, Switchable ErSc2N Rotor within a C80 Fullerene Cage: An Electron Paramagnetic Resonance and Photoluminescence Excitation Study, Phys. Rev. Lett., 2008, 101, 013002 CrossRef PubMed.
- T. Huang, J. Zhao, M. Feng, A. A. Popov, S. Yang, L. Dunsch and H. Petek, A multi-state single-molecule switch actuated by rotation of an encapsulated cluster within a fullerene cage, Chem. Phys. Lett., 2012, 552, 1–12 CrossRef CAS.
- A. Goulet-Hanssens, F. Eisenreich and S. Hecht, Enlightening Materials with Photoswitches, Adv. Mater., 2020, 32(20), 1905966 CrossRef CAS PubMed.
- Z. L. Pianowski, Recent Implementations of Molecular Photoswitches into Smart Materials and Biological Systems, Chem.–Eur. J., 2019, 25(20), 5128–5144 CrossRef CAS PubMed.
- A. Gonzalez, E. S. Kengmana, M. V. Fonseca and G. G. D. Han, Solid-state photoswitching molecules: structural design for isomerization in condensed phase, Mater. Today Adv., 2020, 6, 100058 CrossRef.
- S. Erbas-Cakmak, D. A. Leigh, C. T. McTernan and A. L. Nussbaumer, Artificial Molecular Machines, Chem. Rev., 2015, 115(18), 10081–10206 CrossRef CAS PubMed.
- S. Castellanos, F. Kapteijn and J. Gascon, Photoswitchable metal organic frameworks: turn on the lights and close the windows, CrystEngComm, 2016, 18(22), 4006–4012 RSC.
- A. M. Rice, C. R. Martin, V. A. Galitskiy, A. A. Berseneva, G. A. Leith and N. B. Shustova, Photophysics Modulation in Photoswitchable Metal–Organic Frameworks, Chem. Rev., 2020, 120(16), 8790–8813 CrossRef CAS PubMed.
- M. Rudolf, S. V. Kirner and D. M. Guldi, A multicomponent molecular approach to artificial photosynthesis - the role of fullerenes and endohedral metallofullerenes, Chem. Soc. Rev., 2016, 45(3), 612–630 RSC.
- O. Trukhina, M. Rudolf, G. Bottari, T. Akasaka, L. Echegoyen, T. Torres and D. M. Guldi, Bidirectional Electron Transfer Capability in Phthalocyanine–Sc3N@Ih–C80 Complexes, J. Am. Chem. Soc., 2015, 137(40), 12914–12922 CrossRef CAS PubMed.
- B. Liu, H. Fang, X. Li, W. Cai, L. Bao, M. Rudolf, F. Plass, L. Fan, X. Lu and D. M. Guldi, Synthesis and Photophysical Properties of a Sc3N@C80-Corrole Electron Donor–Acceptor Conjugate, Chem.–Eur. J., 2014, 21(2), 746–752 CrossRef PubMed.
- S. Kirner, M. Sekita and D. M. Guldi, 25th Anniversary Article: 25 Years of Fullerene Research in Electron Transfer Chemistry, Adv. Mater., 2014, 26(10), 1482–1493 CrossRef CAS PubMed.
- C. Schubert, M. Rudolf, D. M. Guldi, Y. Takano, N. Mizorogi, M. Á. Herranz, N. Martín, S. Nagase and T. Akasaka, Rates and energetics of intramolecular electron transfer processes in conjugated metallofullerenes, Philos. Trans. R. Soc., A, 2013, 371(2038), 20120490 CrossRef PubMed.
- M. Rudolf, S. Wolfrum, D. M. Guldi, L. Feng, T. Tsuchiya, T. Akasaka and L. Echegoyen, Endohedral Metallofullerenes—Filled Fullerene Derivatives towards Multifunctional Reaction Center Mimics, Chem.–Eur. J., 2012, 18(17), 5136–5148 CrossRef CAS PubMed.
- S. Wolfrum, J. R. Pinzon, A. Molina-Ontoria, A. Gouloumis, N. Martin, L. Echegoyen and D. M. Guldi, Utilization of Sc3N@C80 in long-range charge transfer reactions, Chem. Commun., 2011, 47(8), 2270–2272 RSC.
- J. R. Pinzón, C. M. Cardona, M. A. Herranz, M. E. Plonska-Brzezinska, A. Palkar, A. J. Athans, N. Martin, A. Rodriguez-Fortea, J. M. Poblet, G. Bottari, T. Torres, S. Shankara Gayathri, D. M. Guldi and L. Echegoyen, Metal Nitride Cluster Fullerene M3N@C80 (M = Y, Sc) Based Dyads: Synthesis, and Electrochemical, Theoretical and Photophysical Studies, Chem.–Eur. J., 2009, 15(4), 864–877 CrossRef PubMed.
- J. R. Pinzon, D. C. Gasca, S. G. Sankaranarayanan, G. Bottari, T. Torres, D. M. Guldi and L. Echegoyen, Photoinduced Charge Transfer and Electrochemical Properties of Triphenylamine Ih-Sc3N@C80 Donor-Acceptor Conjugates, J. Am. Chem. Soc., 2009, 131(22), 7727–7734 CrossRef CAS PubMed.
- R. B. Ross, C. M. Cardona, D. M. Guldi, S. G. Sankaranarayanan, M. O. Reese, N. Kopidakis, J. Peet, B. Walker, G. C. Bazan, E. Van Keuren, B. C. Holloway and M. Drees, Endohedral fullerenes for organic photovoltaic devices, Nat. Mater., 2009, 8(3), 208–212 CrossRef CAS PubMed.
- J. R. Pinzon, M. E. Plonska-Brzezinska, C. M. Cardona, A. J. Athans, S. S. Gayathri, D. M. Guldi, M. A. Herranz, N. Martin, T. Torres and L. Echegoyen, Sc3N@C80-Ferrocene Electron-Donor/Acceptor Conjugates as Promising Materials for Photovoltaic Applications, Angew. Chem., Int. Ed., 2008, 47(22), 4173–4176 CrossRef CAS PubMed.
- Y. Chai, X. Liu, B. Wu, L. Liu, Z. Wang, Y. Weng and C. Wang, In situ switching of photoinduced electron transfer direction by regulating redox state in fullerene-based dyads, J. Am. Chem. Soc., 2020, 142(9), 4411–4418 CrossRef CAS PubMed.
- M. Rudolf, L. Feng, Z. Slanina, T. Akasaka, S. Nagase and D. M. Guldi, A Metallofullerene Electron Donor that Powers an Efficient Spin Flip in a Linear Electron Donor–Acceptor Conjugate, J. Am. Chem. Soc., 2013, 135(30), 11165–11174 CrossRef CAS PubMed.
- B. Wu, J. Hu, P. Cui, L. Jiang, Z. Chen, Q. Zhang, C. Wang and Y. Luo, Visible-Light Photoexcited Electron Dynamics of Scandium Endohedral Metallofullerenes: The Cage Symmetry and Substituent Effects, J. Am. Chem. Soc., 2015, 137(27), 8769–8774 CrossRef CAS PubMed.
- Y. Takano, M. A. Herranz, N. Martin, S. G. Radhakrishnan, D. M. Guldi, T. Tsuchiya, S. Nagase and T. Akasaka, Donor-Acceptor Conjugates of Lanthanum Endohedral Metallofullerene and pi-Extended Tetrathiafulvalene, J. Am. Chem. Soc., 2010, 132(23), 8048–8055 CrossRef CAS.
- C. S. Foote, Photophysical and Photochemical Properties of Fullerenes, in Electron Transfer I, Springer-Verlag Berlin, Berlin, 1994, vol. 169, pp. 347–363 Search PubMed.
- Z. Wang, N. Izumi, Y. Nakanishi, T. Koyama, T. Sugai, M. Tange, T. Okazaki and H. Shinohara, Near-Infrared Photoluminescence Properties of Endohedral Mono- and Dithulium Metallofullerenes, ACS Nano, 2016, 10(4), 4282–4287 CrossRef CAS PubMed.
- A. Tiwari, G. Dantelle, K. Porfyrakis, A. Ardavan and G. A. D. Briggs, Temperature-dependent photoluminescence study of ErSc2N@C80 and Er2ScN@C80 fullerenes, Phys. Status Solidi B, 2008, 245(10), 1998–2001 CrossRef CAS.
- A. Tiwari, G. Dantelle, K. Porfyrakis, R. A. Taylor, A. A. R. Watt, A. Ardavan and G. A. D. Briggs, Configuration-selective spectroscopic studies of Er3+ centers in ErSc2N@C80 and Er2ScN@C80 fullerenes, J. Chem. Phys., 2007, 127(19), 194504 CrossRef PubMed.
- M. Nie, J. Xiong, C. Zhao, H. Meng, K. Zhang, Y. Han, J. Li, B. Wang, L. Feng, C. Wang and T. Wang, Luminescent single-molecule magnet of metallofullerene DyErScN@Ih-C80, Nano Res., 2019, 12(7), 1727–1731 CrossRef CAS.
- R. M. Macfarlane, D. S. Bethune, S. Stevenson and H. C. Dorn, Fluorescence spectroscopy and emission lifetimes of Er3+ in ErxSc3-xN@C80 (x = 1-3), Chem. Phys. Lett., 2001, 343(3–4), 229–234 CrossRef CAS.
- D. Xu, Y. Jiang, Y. Wang, T. Zhou, Z. Shi, H. Omachi, H. Shinohara, B. Sun and Z. Wang, Turning on the Near-Infrared Photoluminescence of Erbium Metallofullerenes by Covalent Modification, Inorg. Chem., 2019, 58(21), 14325–14330 CrossRef CAS PubMed.
- K. Toth, J. K. Molloy, M. Matta, B. Heinrich, D. Guillon, G. Bergamini, F. Zerbetto, B. Donnio, P. Ceroni and D. Felder-Flesch, A Strongly Emitting Liquid-Crystalline Derivative of Y3N@C80: Bright and Long-Lived Near-IR Luminescence from a Charge Transfer State, Angew. Chem., Int. Ed., 2013, 52(47), 12303–12307 CrossRef CAS.
- L. Bharadwaj and L. Novotny, Plasmon-Enhanced Photoemission from a Single Y3N@C80 Fullerene, J. Phys. Chem. C, 2010, 114(16), 7444–7447 CrossRef.
- M. Zalibera, D. S. Krylov, D. Karagiannis, P.-A. Will, F. Ziegs, S. Schiemenz, W. Lubitz, S. Reineke, A. Savitsky and A. A. Popov, Thermally Activated Delayed Fluorescence in a Y3N@C80 Endohedral Fullerene: Time-Resolved Luminescence and EPR Studies, Angew. Chem., Int. Ed., 2018, 57(1), 277–281 CrossRef CAS.
- C. Baleizao and M. N. Berberan-Santos, Thermally activated delayed fluorescence as a cycling process between excited singlet and triplet states: application to the fullerenes, J. Chem. Phys., 2007, 126(20), 8 CrossRef PubMed.
- F. A. Salazar, A. Fedorov and M. N. Berberan-Santos, A study of thermally activated delayed fluorescence in C60, Chem. Phys. Lett., 1997, 271(4–6), 361–366 CrossRef CAS.
- M. N. Berberan-Santos and J. M. M. Garcia, Unusually Strong Delayed Fluorescence of C70, J. Am. Chem. Soc., 1996, 118(39), 9391–9394 CrossRef CAS.
- S. M. Bachilo, A. F. Benedetto, R. B. Weisman, J. R. Nossal and W. E. Billups, Time-resolved thermally activated delayed fluorescence in C70 and 1,2-C70H2, J. Phys. Chem. A, 2000, 104(48), 11265–11269 CrossRef CAS.
- C. Baleizão and M. N. Berberan-Santos, Thermally Activated Delayed Fluorescence in Fullerenes, Ann. N. Y. Acad. Sci., 2008, 1130(1), 224–234 CrossRef PubMed.
- Z. Yang, Z. Mao, Z. Xie, Y. Zhang, S. Liu, J. Zhao, J. Xu, Z. Chi and M. P. Aldred, Recent advances in organic thermally activated delayed fluorescence materials, Chem. Soc. Rev., 2017, 46(3), 915–1016 RSC.
- Y. Tao, K. Yuan, T. Chen, P. Xu, H. Li, R. Chen, C. Zheng, L. Zhang and W. Huang, Thermally Activated Delayed Fluorescence Materials Towards the Breakthrough of Organoelectronics, Adv. Mater., 2014, 26(47), 7931–7958 CrossRef CAS PubMed.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Highly efficient organic light-emitting diodes from delayed fluorescence, Nature, 2012, 492(7428), 234–238 CrossRef CAS PubMed.
- N. Chen, L. Z. Fan, K. Tan, Y. Q. Wu, C. Y. Shu, X. Lu and C. R. Wang, Comparative Spectroscopic and Reactivity Studies of Sc3-xYxN@C80 (x = 0-3), J. Phys. Chem. C, 2007, 111(32), 11823–11828 CrossRef CAS.
- Y. Zhang, D. Krylov, M. Rosenkranz, S. Schiemenz and A. A. Popov, Magnetic Anisotropy of Endohedral Lanthanide Ions: Paramagnetic NMR Study of MSc2N@C80-Ih with M Running Through the Whole 4f Row, Chem. Sci., 2015, 6, 2328–2341 RSC.
- S. F. Yang, M. Kalbac, A. Popov and L. Dunsch, Gadolinium-based mixed metal nitride clusterfullerenes GdxSc3-xN@C80 (x = 1, 2), ChemPhysChem, 2006, 7(9), 1990–1995 CrossRef CAS PubMed.
- S. Yang, A. A. Popov, C. Chen and L. Dunsch, Mixed Metal Nitride Clusterfullerenes in Cage Isomers: LuxSc3-xN@C80 (x = 1, 2) As Compared with MxSc3-xN@C80 (M = Er, Dy, Gd, Nd), J. Phys. Chem. C, 2009, 113(18), 7616–7623 CrossRef CAS.
- Y. Zhang, A. A. Popov, S. Schiemenz and L. Dunsch, Synthesis, Isolation and Spectroscopic Characterization of Holmium-Based Mixed-Metal Nitride Clusterfullerenes: HoxSc3−xN@C80 (x = 1, 2), Chem.–Eur. J., 2012, 18(31), 9691–9698 CrossRef CAS PubMed.
- M. J. Leitl, F.-R. Küchle, H. A. Mayer, L. Wesemann and H. Yersin, Brightly Blue and Green Emitting Cu(I) Dimers for Singlet Harvesting in OLEDs, J. Phys. Chem. A, 2013, 117(46), 11823–11836 CrossRef CAS PubMed.
- R. Valencia, A. Rodriguez-Fortea, A. Clotet, C. de Graaf, M. N. Chaur, L. Echegoyen and J. M. Poblet, Electronic Structure and Redox Properties of Metal Nitride Endohedral Fullerenes M3N@C2n (M = Sc, Y, La, and Gd; 2n = 80, 84, 88, 92, 96), Chem.–Eur. J., 2009, 15(41), 10997–11009 CrossRef CAS PubMed.
- V. Dubrovin, L.-H. Gan, B. Büchner, A. A. Popov and S. M. Avdoshenko, Endohedral metal-nitride cluster ordering in metallofullerene–NiII(OEP) complexes and crystals: a theoretical study, Phys. Chem. Chem. Phys., 2019, 21, 8197–8200 RSC.
- D. N. Laikov and Y. A. Ustynuk, PRIRODA-04: a quantum-chemical program suite. New possibilities in the study of molecular systems with the application of parallel computing, Russ. Chem. Bull., 2005, 54(3), 820–826 CrossRef CAS.
- D. N. Laikov, Fast evaluation of density functional exchange-correlation terms using the expansion of the electron density in auxiliary basis sets, Chem. Phys. Lett., 1997, 281, 151–156 CrossRef CAS.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1327 Search PubMed.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(1), 73–78 CAS.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms, J. Chem. Theory Comput., 2008, 4(6), 908–919 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, Efficient and Accurate Approximations to the Molecular Spin-Orbit Coupling Operator and their use in Molecular g-Tensor Calculations, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- F. Neese, Prediction of Electron Paramagnetic Resonance g-values by Coupled Perturbed Hartree-Fock and Kohn-Sham Theory, J. Chem. Phys., 2001, 115, 11080–11096 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152(22), 224108 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD - Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- X.-B. Wang and L.-S. Wang, Development of a low-temperature photoelectron spectroscopy instrument using an electrospray ion source and a cryogenically controlled ion trap, Rev. Sci. Instrum., 2008, 79(7), 073108 CrossRef PubMed.
- I. N. Ioffe, A. S. Ievlev, O. V. Boltalina, L. N. Sidorov, H. C. Dorn, S. Stevenson and G. Rice, Electron affinity of some trimetallic nitride and conventional metallofullerenes, Int. J. Mass Spectrom., 2002, 213(2–3), 183–189 CrossRef CAS.
- X. B. Wang, H. K. Woo, J. Yang, M. M. Kappes and L. S. Wang, Photoelectron spectroscopy of singly and doubly charged higher fullerenes at low temperatures: C76−, C78−, C84− and C762−, C782−, C842−, J. Phys. Chem. C, 2007, 111(48), 17684–17689 CrossRef CAS.
- X.-B. Wang, C. Chi, M. Zhou, I. V. Kuvychko, K. Seppelt, A. A. Popov, S. H. Strauss, O. V. Boltalina and L.-S. Wang, Photoelectron Spectroscopy of C60Fn− and C60Fm2− (n = 17, 33, 35, 43, 45, 47; m = 34, 46) in the Gas Phase and the Generation and Characterization of C1-C60F47− and D2-C60F44 in Solution, J. Phys. Chem. A, 2010, 114(4), 1756–1765 CrossRef CAS PubMed.
- I. V. Kuvychko, J. B. Whitaker, B. W. Larson, T. C. Folsom, N. B. Shustova, S. M. Avdoshenko, Y.-S. Chen, H. Wen, X. Wang, L. Dunsch, A. A. Popov, O. V. Boltalina and S. H. Strauss, Substituent effects in a series of 1,7-C60(RF)2 compounds (RF = CF3, C2F5, n-C3F7, i-C3F7, n-C4F9, s-C4F9, n-C8F17): electron affinities, reduction potentials, and E(LUMO) values are not always correlated, Chem. Sci., 2012, 3(5), 1399–1407 RSC.
- T. T. Clikeman, S. H. M. Deng, A. A. Popov, X.-B. Wang, S. H. Strauss and O. V. Boltalina, Fullerene cyanation does not always increase electron affinity: an experimental and theoretical study, Phys. Chem. Chem. Phys., 2015, 17(1), 551–556 RSC.
- B. W. Larson, J. B. Whitaker, X.-B. Wang, A. A. Popov, G. Rumbles, N. Kopidakis, S. H. Strauss and O. V. Boltalina, Electron Affinity of Phenyl–C61–Butyric Acid Methyl Ester (PCBM), J. Phys. Chem. C, 2013, 117(29), 14958–14964 CrossRef CAS.
- T. T. Clikeman, S. H. M. Deng, S. Avdoshenko, X.-B. Wang, A. A. Popov, S. H. Strauss and O. V. Boltalina, Fullerene “Superhalogen” Radicals: The Substituent Effect on Electronic Properties of 1,7,11,24,27-C60X5, Chem.–Eur. J., 2013, 19(45), 15404–15409 CrossRef CAS PubMed.
- G.-L. Hou, L.-J. Li, S.-H. Li, Z.-M. Sun, X. Gao and X.-B. Wang, Regioisomer-specific electron affinities and electronic structures of C70 para-adducts at polar and equatorial positions with (bromo)benzyl radicals: photoelectron spectroscopy and theoretical study, Phys. Chem. Chem. Phys., 2016, 18(28), 18683–18686 RSC.
- D.-L. Huang, P. D. Dau, H.-T. Liu and L.-S. Wang, High-resolution photoelectron imaging of cold C60− anions and accurate determination of the electron affinity of C60, J. Chem. Phys., 2014, 140(22), 224315 CrossRef PubMed.
- X. B. Wang, C. F. Ding and L. S. Wang, High resolution photoelectron spectroscopy of C60−, J. Chem. Phys., 1999, 110(17), 8217–8220 CrossRef CAS.
- X. B. Wang, H. K. Woo and L. S. Wang, Vibrational cooling in a cold ion trap: vibrationally resolved photoelectron spectroscopy of cold C60− anions, J. Chem. Phys., 2005, 123(5), 4 Search PubMed.
- P. Jakes and K. P. Dinse, Chemically induced spin transfer to an encased molecular cluster: an EPR study of Sc3N@C80 radical anions, J. Am. Chem. Soc., 2001, 123(36), 8854–8855 CrossRef CAS PubMed.
- B. Elliott, L. Yu and L. Echegoyen, A Simple Isomeric Separation of D5h and Ih Sc3N@C80 by Selective Chemical Oxidation, J. Am. Chem. Soc., 2005, 127(31), 10885–10888 CrossRef CAS PubMed.
- A. A. Popov, N. B. Shustova, A. L. Svitova, M. A. Mackey, C. E. Coumbe, J. P. Phillips, S. Stevenson, S. H. Strauss, O. V. Boltalina and L. Dunsch, Redox-Tuning Endohedral Fullerene Spin States: From the Dication to the Trianion Radical of Sc3N@C80(CF3)2 in Five Reversible Single-Electron Steps, Chem.–Eur. J., 2010, 16(16), 4721–4724 CrossRef CAS PubMed.
- D. V. Konarev, A. A. Popov, L. V. Zorina, S. S. Khasanov and R. N. Lyubovskaya, Molecular Structure and Magnetic and Optical Properties of Endometallonitridofullerene Sc3N@Ih-C80 in Neutral, Radical Anion, and Dimeric Anionic Forms, Chem.–Eur. J., 2019, 25(65), 14858–14869 CrossRef CAS PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Claredon Press, Oxford, 1970 Search PubMed.
- S. Stoll and D. Goldfarb, EPR Interactions – Nuclear Quadrupole Couplings, eMagRes, 2017, vol. 6, iss. 4, pp. 495–510 Search PubMed.
- S. Stoll and A. Schweiger, EasySpin, a comprehensive software package for spectral simulation and analysis in EPR, J. Magn. Reson., 2006, 178(1), 42–55 CrossRef CAS PubMed.
- A. Schweiger and G. Jeschke, Principles of Pulse Electron Paramagnetic Resonance, Oxford University Press, Oxford, UK, 2001 Search PubMed.
- M. Bennati, EPR Interactions – Hyperfine Couplings, in eMagRes, 2017, vol. 6, pp. 271–282 Search PubMed.
- F. Neese, Quantum Chemistry and EPR Parameters, in eMagRes, ed. R. K. Harris and R. L. Wasylishen, 2017, vol. 6, pp. 1–22 Search PubMed.
- J. Harmer, G. Mitrikas and A. Schweiger, Advanced Pulse EPR Methods for the Characterization of Metalloproteins, in High Resolution EPR: Applications to Metalloenzymes and Metals in Medicine, ed. L. Berliner and G. Hanson, Springer New York, New York, NY, 2009, pp. 13–61, DOI:10.1007/978-0-387-84856-3_2.
- J. R. Harmer, Hyperfine Spectroscopy – ENDOR, eMagRes, 2016, 5(4), 1493–1514 Search PubMed.
- F. Lendzian, R. Bittl, A. Telfer and W. Lubitz, Hyperfine structure of the photoexcited triplet state 3P680 in plant PS II reaction centres as determined by pulse ENDOR spectroscopy, Biochim. Biophys. Acta, Bioenerg., 2003, 1605(1), 35–46 CrossRef CAS.
- K. R. Gorny, C. H. Pennington, J. A. Martindale, J. P. Phillips, S. Stevenson, I. Heinmaa and R. Stern, Molecular orientational dynamics of the endohedral fullerene Sc3N@C80 as probed by 13C and 45Sc NMR, 2006, arXiv:cond-mat/0604365v1.
- L. Spree and A. A. Popov, Recent advances in single molecule magnetism of dysprosium-metallofullerenes, Dalton Trans., 2019, 48(9), 2861–2871 RSC.
- F. Liu, L. Spree, D. S. Krylov, G. Velkos, S. M. Avdoshenko and A. A. Popov, Single-Electron Lanthanide-Lanthanide Bonds Inside Fullerenes toward Robust Redox-Active Molecular Magnets, Acc. Chem. Res., 2019, 52(10), 2981–2993 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc07045a |
| This journal is © The Royal Society of Chemistry 2021 |