Open Access Article
Open Access ArticleModulating the radical reactivity of phenyl radicals with the help of distonic charges: it is all about electrostatic catalysis†
Totan
Mondal
 a,
Sason
Shaik
a,
Sason
Shaik
 *a,
Hilkka
Kenttämaa
*a,
Hilkka
Kenttämaa
 b and
Thijs
Stuyver
b and
Thijs
Stuyver
 *a
*a
aInstitute of Chemistry, The Hebrew University, Jerusalem 91904, Israel. E-mail: sason.shaik@gmail.com; thijs.stuyver@mail.huji.ac.il
bDepartment of Chemistry, Purdue University, West Lafayette, Indiana 47907-1393, USA
First published on 23rd February 2021
Abstract
This manuscript reports the modulation of H-abstraction reactivity of phenyl radicals by (positive and negative) distonic ions. Specifically, we focus on the origins of this modulating effect: can the charged functional groups truly be described as “extreme forms of electron-withdrawing/donating substituents” – implying a through-bond mechanism – as argued in the literature, or is the modulation mainly caused by through-space effects? Our analysis indicates that the effect of the remote charges can be mimicked almost perfectly with the help of a purely electrostatic treatment, i.e. replacing the charged functional groups by a simple uniform electric field is sufficient to recover the quantitative reactivity trends. Hence, through-space effects dominate, whereas through-bond effects play a minor role at best. We elucidate our results through a careful Valence Bond (VB) analysis and demonstrate that such a qualitative analysis not only reveals through-space dominance, but also demonstrates a remarkable reversal in the reactivity trends of a given polarity upon a rational modification of the reaction partner. As such, our findings demonstrate that VB theory can lead to productive predictions about the behaviour of distonic radical ions.
1 Introduction
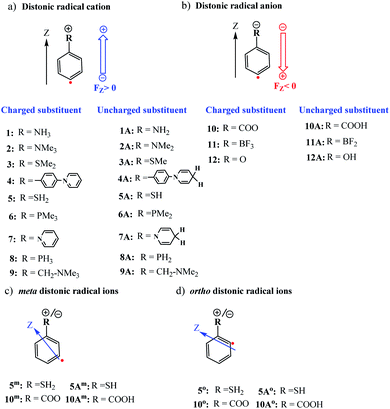
Distonic radical ions are a peculiar class of radical ions in which the charge and radical site are formally separated.1–3 First postulated in the early 1970s as likely intermediates in mass spectrometry experiments,4,5 it took almost an entire decade before conclusive experimental evidence of their existence was provided by Radom and co-workers.6 Since then, the interest in these exotic compounds – and the remarkable reactivity patterns they exhibit – has grown significantly.7 In recent years in particular, the research field has experienced a jolt of activity due to the potential offered by pH-controllable remote charges to modulate the stability of radicals.8,9One of the topics in distonic radical ion chemistry that sparked great interest from the onset was the interplay between the charge and radical site. Initial studies focused on unravelling the influence of the charge on the radical reactivity modes in so-called α-distonic radical ions,10i.e., radical ions in which the charge and radical site are adjacent, and subsequently in aliphatic distonic ions,11i.e., radical ions in which more than one atom separates these two sites. However, due to their close proximity in the former system, and the flexibility of the aliphatic chain in the latter, the charge and radical site were often found to interact simultaneously with (neutral) reaction partners.7 As such, neither of these two types of model systems proved suitable testbeds for probing the reaction modes associated with the radical site in an independent manner.
Consequently, more recent studies have generally focused on the reactivity of rigid aromatic carbon-centred σ-type radicals with a spatially separated (and chemically inert) charge site.7 Throughout the 1990s and early 2000s, Kenttämaa and co-workers performed a series of studies on charged phenyl radical compounds with the help of Fourier-transform ion cyclotron resonance mass spectrometry.12–15 Based on the emerging data from these experiments, it was concluded that charged phenyl radicals generally exhibit similar reaction modes as neutral phenyl radicals, but that the remote charged substituent is able to significantly enhance or temper the reaction rates, depending on the nature of the functional group, its distance from the radical site and the polarity of the transition state. These findings were rationalized with the help of valence bond-like state crossing diagrams.16–19 In short, the charge site was posited to either stabilize or destabilize the main charge-transfer (CT) state mixing into the wavefunction along the reaction coordinate. The lower the energy of these respective charge-transfer states, the more stabilized the transition state would become relative to the reactant complex, which translates into a lower activation energy for the considered reaction.
Importantly, what remained unaddressed in this elegant explanation of the observed reactivity trends is the detailed mechanism through which these charge-transfer states become stabilized. In their pioneering studies, Kenttämaa and co-workers generally interpreted the charged substituents on the phenyl radicals as “extreme forms of electron-withdrawing/donating substituents”,15 enhancing the electrophilicity/nucleophilicity at the radical site. This characterization implicitly appears to suggest an underlying through-bond (inductive/resonance-like) mechanism. Through-space, i.e., pure long-range electrostatic, effects emanating from the charged substituent, were not considered explicitly.
In recent years however, it has become increasingly clear that such through-space electrostatic interactions play a much bigger role in organic chemistry than previously thought, and even outrightly dominate in many phenomena which were previously ascribed almost exclusively to through-bond effects. For example, Wheeler and Houk demonstrated convincingly in 2008 that substituent effects in benzene dimer formation do not involve the π-system of the substituted benzene, but are instead caused by direct, i.e., through-space, interactions between the substituent itself and the unsubstituted ring.20–22 In other words, contrary to the common viewpoint, substituent-induced modulation of the electron density associated with the π-cloud in a substituted benzene ring, i.e., electron withdrawal/donation, plays no significant role in π-stacking; dimer formation is driven almost exclusively by electrostatics. In another series of papers, Schwarz et al. showed that the catalysis provided by metal oxides and carbides in C–H bond activation is essentially electrostatic in nature.23–25 Very recently, Stuyver and co-workers demonstrated that the local electric fields emanating from charged substituents present on the macrocyclic ligands in a couple of metalloenzyme analogues synthesized by Groves et al.26,27 could account fully for their remarkably enhanced reactivity, i.e., through-bond (inductive) effects were not needed to describe the enhanced rates of H-abstraction by these complexes.28 Around the same time, Cockroft and co-workers performed a set of elegant experiments to probe the relative significance of through-bond and through-space substituent effects in molecular interactions and reaction kinetics.29 The resulting data clearly revealed dominant through-space interactions for the considered systems; in fact, it turned out that, depending on the precise spatial orientation of specific substituents, their classically assigned electron-donating/electron-withdrawing character could be turned off – or even reversed altogether.
In the present computational study, we take a closer look at the radical reactivity exhibited by a set of charged phenyl radicals. More specifically, we will consider the impact of a variety of charged substituents on the H-abstraction reaction from a model reaction partner (CH4) and we will probe whether the observed modulation of the reactivity is governed by a through-space or through-bond mechanism. As will be demonstrated below, we find no compelling arguments for significant through-bond radical reactivity modulation; consideration of through-space electrostatics generally suffices to describe the impact of the charged substituents. Furthermore, we find that modelling the effect of the remote charge as an oriented external-electric field (OEEF) leads to quantitative correspondence in the calculated activation energies for most of our systems. Our results constitute yet another illustration of the pervasive role played by long-range electrostatic interactions in chemical structure and reactivity, and the insights gained could contribute to the design of new electric-field mediated catalysts.30–34
2 Computational methods
All calculations in this study were performed with the Gaussian 16 quantum chemical software package.35 The ωB97X-D functional36 in conjunction with Ahlrichs' formulated polarization-corrected triple-ζ basis set (def2-TZVP),37 was used to optimize the geometries of the stationary points associated with the H-abstraction reaction from CH4 by the considered distonic radical ions (1–12) and their corresponding uncharged radical analogues (1A–12A), cf.Fig. 1. A vibrational frequency analysis was performed at the same level-of-theory to verify the nature of the stationary points on the potential energy surface as real minima (Nimg = 0) or first-order saddle points (Nimg = 1).To confirm the robustness, i.e., functional independence, of our findings, a full comparison between the ωB97X-D results and the corresponding results obtained with the popular B3LYP-D3 functional38–40 has been included in the ESI (cf. Tables S1 and S2).† A correlation between the two sets of barrier heights is presented in Fig. S1.† Our analysis demonstrates that both functionals not only recover the exact same reactivity trends, but that the agreement is quantitative (R2 = 0.98, ΔEB3LYP-D3–ωB97X-D < 1.0 kcal mol−1). Additionally, we have also recalculated the barrier heights for two model systems with other popular functionals, i.e., PBE0-D3 (ref. 41 and 42) and M06-2X.43 These functionals give a similar energy and reproduce the same trend as well (Table S3†).
Since reactions involving distonic radical ions are known to occur under a wide variety of thermodynamic conditions (e.g., these compounds have been posited to be involved both in interstellar reactivity as well as in combustion processes),44 we refrained from adding thermodynamic corrections to the presented energy values and instead report all values simply as electronic energies + zero-point corrections.
Nevertheless, we included a comparison between the ΔE and corresponding ΔH and ΔG values, evaluated under standard conditions, cf. Table S4 in the ESI.† From this table, one can conclude that our results are insensitive – within reasonable bounds – to the specific thermodynamic conditions at which the reaction occurs.
One point of interest with regard to the thermodynamic corrections though is that at room temperature and atmospheric pressure, entropic factors render most of the reaction complexes (RC) unstable with respect of the isolated reactants (note that such RC instabilities were previously reported by Radom and co-workers45 as well). To verify whether this finding could affect our results, we compared the reactant complexes with the isolated reactants as references for the reaction barrier quantification (cf. Table S4†). Our analysis indicates that both potential reference points lead to the exact same conclusions. Finally, we also confirmed that inclusion of solvent environments does not affect the observed trends (Section S2†).
As such, one can conclude that, overall, our results are remarkably robust: the reactivity trends are retained irrespective of whether one uses isolated reactants or complexes as a reference, whether one focuses on electronic energy, enthalpy or Gibbs energy to quantify barrier heights and irrespective of the used functional.
The in-house developed TITAN code46 was utilized to quantify the net electric field at the reactive radical site, emanating from the remote charged substituents in the distonic radical ions as follows.
First, the optimized distonic radical cation geometries (1–9,Fig. 1) were neutralized by removing –H or –Me substituents from the charged substituents on the phenyl ring respectively. For the resulting uncharged molecules (1A–9A, Fig. 1), single-point calculations were performed. A similar approach was also taken for the negatively charged species. In this case, adding either H+ substituents (10A and 12A) or removing F− substituents (11A), from the charged substituents, to obtain the uncharged analogues of the original distonic radical (an)ions.
Subsequently, the natural (NBO)47 charges were calculated for both the charged and uncharged molecules. The two corresponding NBO charge distributions were then subtracted from one another. This way, a differential charge distribution associated with the charged substituent was obtained. The field strength exerted by the substituent part of the differential charge distribution was then quantified at the reactive radical site according to Coulomb's law for the respective distonic radical ions considered.
To examine whether the through-space electrostatics govern the reactivity modifications in the distonic radical ions compared to their uncharged analogues, single-point calculations were performed on the uncharged versions (i.e., 1A–12A) of the optimized charged molecules (i.e., 1–12), with inclusion of an oriented-external electric field (OEEF) mimicking the net field exerted by the charged substituents. In these single-point calculations, the mimicking OEEFs were included using the “Field” keyword available in Gaussian 16. Throughout this study, we adopt the Gaussian software convention for the field direction, i.e., the vector for electric fields (FZ) is defined to be directed from a negative charge to a positive one.31
Molecular electrostatic potentials (ESP) were also generated at UωB97X-D/def2-TZVP level-of-theory. The calculated ESPs were graphically mapped onto a molecular surface corresponding to an isodensity contour of 0.001 e per a.u.3 with the help of the GaussView software.48 Two different scales were used to visualize the ESPs: for the distonic radical cations, the red region was set to 0.10 a.u., the blue region was set to 0.25 a.u.; for the distonic radical anions, the red region was set to −0.20 a.u. and the blue region to 0.10 a.u.
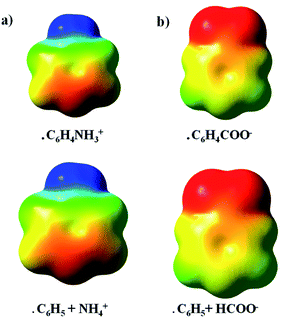
An additive ESP model was employed to scrutinize further the occurrence of π-resonance and inductive effects (vide infra). For example, in the case of distonic radical cation 1, this was done as follows. First, the ESPs for isolated C6H5, and NH4+ were evaluated on a rectangular grid, after which the fragments were positioned in a relative orientation corresponding to the geometry of the full C6H4NH3+ system. Subsequently, the individual ESPs were added, and the resulting map was compared to the ESP for the full C6H4NH3+ molecule.21,22
3 Results and discussion
3.1 The impact of generic OEEFs on the H-abstraction reaction profile
Let us start by considering the general mechanism through which through-space electrostatics can be expected to impact the activation energies of radical reactions. To facilitate our discussions, we focus first on so-called (uniform) oriented external electric fields (OEEF), i.e., idealized electric fields oriented in a specific direction and retaining a constant field strength at every point in (the considered) space. OEEFs impact the stability of molecular systems through interaction with their dipole moment,31,33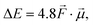 | (1) |
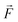 to the electric field (in V Å−1) and
to the electric field (in V Å−1) and 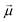 to the dipole moment (in D).
to the dipole moment (in D).
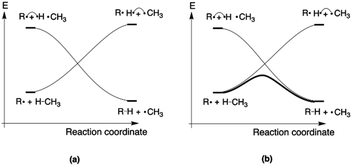
Since the activation energy generally corresponds to the energy difference between the reactant complex (RC) and the transition state (TS), one can identify three distinct scenarios for electrostatic reaction barrier modification, depending on the relative magnitudes of the dipole moments of the RC and TS species and their alignment with the electric field. In Fig. 2, these individual scenarios are depicted with respect to a common z-axis.
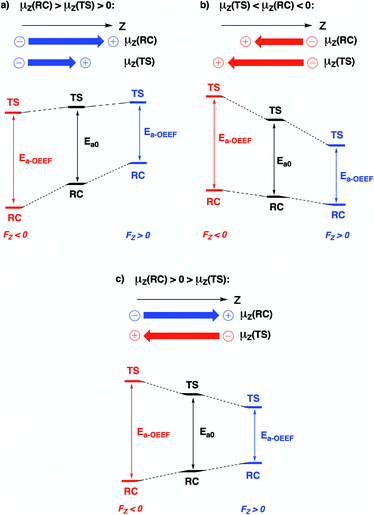 | ||
| Fig. 2 Schematic representation of the different distinct scenarios for electrostatic reaction barrier modification, depending on the relative magnitudes of the RC/TS dipole moments and the alignment with the electric field (cf. the electric field convention in Fig. 1). A common z-axis was set for clarity; note that rotating this axis by 180° would flip the signs of the individual (dipole moment/electric field) vectors but does not change the physical picture. For each of the panels, a positive electric field induces a decrease in the reaction barrier height (right-hand side), a negative field induces a barrier increase (left-hand side). | ||
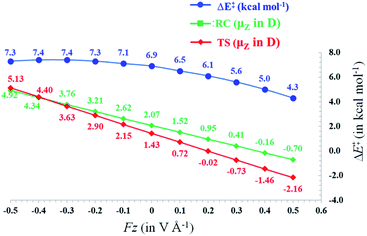
Thus, as long as the dipole moment associated with a chemical system, undergoing a reaction, changes upon proceeding from the RC to the TS, one can expect that applying an oriented electric field will alter the associated activation energy. In Table 1, the permanent dipole moments, i.e., the dipole moment in the absence of an electric field, are displayed for the neutral analogues of the distonic radical ions depicted in Fig. 1 (1A–12A). It should be clear that for each system, these values are indeed distinct for RC and TS, both in their total magnitude and in their magnitude along the axis connecting the substituent site and the radical site (i.e., the z-direction, cf.Fig. 1).
| Systems | RC | TS | ||
|---|---|---|---|---|
| |μ| (D) | μ z (D) | |μ| (D) | μ z (D) | |
| 1A | 2.30 | 2.07 | 1.74 | 1.43 |
| 2A | 2.72 | 2.70 | 2.08 | 2.06 |
| 3A | 1.55 | 0.74 | 1.32 | −0.05 |
| 4A | 0.70 | 0.70 | 0.19 | −0.19 |
| 5A | 0.77 | 0.01 | 1.14 | −0.81 |
| 6A | 1.27 | 0.32 | 1.30 | −0.54 |
| 7A | 0.39 | 0.39 | 0.40 | −0.40 |
| 8A | 0.78 | −0.30 | 1.36 | −1.17 |
| 9A | 0.45 | 0.39 | 0.45 | −0.40 |
| 10A | 1.52 | −0.56 | 2.05 | −1.46 |
| 11A | 1.52 | −1.52 | 2.43 | −2.43 |
| 12A | 1.53 | 0.84 | 1.32 | 0.13 |
Based on the dipole moments tabulated in Table 1, one can straightforwardly map the individual systems to the different scenarios outlined in Fig. 2: 1A, 2A and 12A correspond to scenario (a) in which μz(RC) > μz(TS) > 0, 8A, 10A and 11A correspond to scenario (b) in which μz(TS) < μz(RC) < 0, and 3A–7A and 9A correspond to scenario (c) wherein μz(RC) > 0 > μz(TS). Thus, for each of the neutral molecules, applying an electric field in the positive direction can be expected to lead to barrier reduction in first order. Flipping the field direction would then lead to an increase in the barrier height.
In Fig. 3, the evolution of the barrier height as a function of the magnitude of a generic uniform FZ (increments of 0.1 V Å−1) is plotted for uncharged molecule 1A. As expected from our analysis above, one can indeed observe that an increasingly positive field strength leads to a proportional lowering of the activation energy, whereas an increasingly negative field strength leads to an increase of the activation energy. Note that on the left-hand side of this plot, the activation energy does not continue to increase indefinitely; at a critical negative field strength, a maximum barrier height is reached. This behaviour can be attributed to higher-order effects: since the polarizability of the TS is higher than that of the RC, the magnitudes of the overall dipole moment crosses over at some point, so that the relative stabilization of one species over the other becomes reversed.
3.2 The role of the LEF emanating from the charged substituents in distonic radical ions
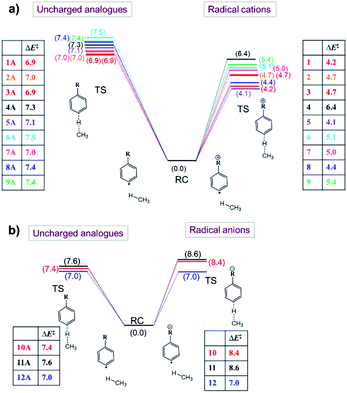
Now that we have constructed a rudimentary model for the impact of OEEFs on the activation energy for radical reactions, let us consider specifically the effect of the charged functional groups in selected para distonic radical ions (Fig. 1a and b). In Fig. 4, the barrier heights for the H-abstraction reaction from methane (CH4) by systems 1–12 are shown together with the corresponding barrier for their neutral analogues (1A–12A). The full reaction profiles are provided in Table S1 in the ESI.†From Fig. 4, one can conclude that for the cations (panel (a)), the barrier height is consistently reduced, whereas for the anions (panel (b)), the barrier heights are generally increased (for the 12/12A pair, the barrier stays roughly the same). Overall, the change in the reaction barrier upon inclusion of a charged substituent appears to follow (at least qualitatively) the paradigm outlined for the OEEFs in the previous subsection: a positively charged R substituent corresponds to a positive field applied along the z-direction, whereas a negatively charged R substituent corresponds to a negative field (cf.Fig. 1a).
From a more detailed consideration of the barrier height changes in Fig. 4, one can infer also that the magnitude of the barrier modification caused by the charged substituents is at least somewhat distance-dependent: whereas the distonic radical cations for which the (localized) charged substituents are attached directly to the phenyl ring (1–3, 5–8) consistently exhibit a reduction in barrier by 2–3 kcal mol−1 compared to their neutral analogues, the effect of the charged substituent in compound 4, in which an additional phenyl ring is inserted in between the radical site and the charge site (a pyridinium ring), the effect is reduced by 0.9 kcal mol−1. Similarly, in compound 9, in which the charged trimethylammonium group and the phenyl moiety are formally separated by a methylene unit, the activation barrier for H abstraction is 0.7 kcal mol−1 higher than in 2 (Fig. 1 and 4; Table S6 in the ESI†). In conclusion therefore, these computational results are perfectly in line with the experimental results previously reported by Kenttämaa13 and others,49,50 thus demonstrating the adequacy of our methodology (cf. Section S4 in the ESI†).
3.3 Is the effect of the charged functional groups mostly electrostatic in nature?
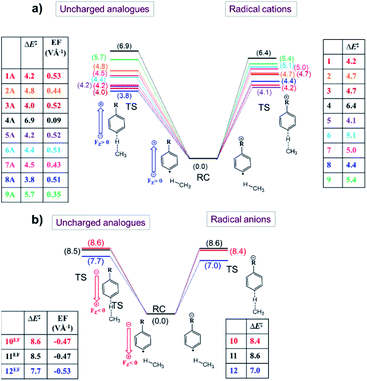
From the analysis in the previous subsections, one can clearly conclude that the effect of the charged functional groups in the considered distonic radical ions on the activation energy for the H-abstraction process qualitatively agrees with what one would expect from a simple OEEF model. Here, we will consider whether this correspondence is only qualitative, or whether there is also a quantitative agreement, i.e., can an OEEF mimic the effect of the charged substituent on the radical reactivity quantitatively? Put differently: are the through-space electrostatics sufficient to explain the impact of the charged substituent on the radical reactivity, or are the often-invoked through-bond (inductive) contributions essential to this end as well?To assess this point, we started by quantifying the net local electric fields (LEFs) exerted by the charged substituents at the reactive radical sites of the distonic radical ions (1–12) compared to their neutral analogues using the in-house developed TITAN code.46
First, we neutralized the respective distonic radical ions in their optimized RC geometry. For the cations, this was achieved by removing a hydrogen/methyl unit from the respective substituents, for the anions, this was achieved by adding an H+ or removing an F− substituent respectively. Subsequently, a so-called differential charge distribution was constructed (see the Computational methods section for the methodology used). For each of the distonic radical ions considered, we found that most of the charge remained on the charged substituent; the extent of charge transfer to or from the phenyl ring remained below 0.30 e in most cases. Furthermore, the fraction of the charge that effectively got transferred to the phenyl unit ended up being distributed fairly evenly over the different sites of the ring, so that each carbon atom carried a negligible net charge, usually significantly below 0.1 e (Table S7†). It should be noted that there is one compound couple, 12/12A, for which the net charge transfer is slightly more pronounced. However, even in this extreme case, the charge transferred to the radical site amounts to only a moderate 0.14 e.
Subsequently, the point-charges from this differential charge distribution belonging to the remote substituent domain were used to quantify the net oriented electric field experienced by the respective species along the z-axis shown in Fig. 1a at the radical site according to Coulomb's law.
Once the net electric fields were obtained for every species, single-point calculations were performed on neutralized versions of the respective RCs and TSs, with the calculated net electric field taken into account through mimicking OEEFs of the corresponding field strength.
The results from these calculations are summarized in Fig. 5. Note that the barrier heights calculated for the uncharged analogues + OEEF agree within a few tenths of a kcal mol−1 with those obtained for the original radical ion. This observation convincingly demonstrates that through-space electrostatics drive the reactivity modification in distonic radical ions.
3.4 What about the through-bond interactions?
The results presented so far indicate that through-space electrostatics are sufficient to explain the radical reactivity modulating effect of the remote charges in distonic radical ions. But what about the often invoked through-bond (e.g., resonance and inductive) effects then? Are they completely irrelevant in these systems, or do they somehow play a subtle (minor) contributing role as well?As already remarked, the TITAN-calculated differential charge distributions reveal only limited charge transfer from the charged substituent to the phenyl unit and an almost uniform distribution of this charge across the ring for every radical ion considered. This on its own already suggests that the impact of the charged substituent on the electronic structure of the phenyl unit in the distonic radical ion is rather limited. The ESP maps presented in Fig. 6 underscore this point. In this figure, the ESPs of benzene and isolated versions of respectively the charged substituents HCOO− and NH4+ are overlaid and compared with the ESPs for the corresponding full distonic radical ions 1 and 10 (cf. Computational methods section for more information). The striking agreement between the respective plots demonstrates unequivocally that the ESPs are merely a sum of their constituting parts; the substituents do not deform the π-clouds of the phenyl units in a discernible way, they only impact the ESP through-space (cf. the previous work by Wheeler and co-workers21,22).
A final indicator for the negligible impact of through-bond interaction is obtained from analysis of the spin densities ρ at the radical sites. As established in a recent contribution from this group, the spin density on a radical site acts as a probe of the “resonance penalty” to be paid throughout a reaction taking place at this location.51 A low spin-density indicates that a lot of resonance stabilization needs to be shed throughout the reaction, which translates into a (relatively) high reaction barrier. A high spin-density on the other hand indicates that the electronic wavefunction requires only limited modification in preparation of a reaction at this radical site, leading to a (relatively) low reaction barrier. For example, the resonance penalty associated with the delocalization of the radical electron in allyl˙ (ρterminal-C = 0.66 e) translates into an increase in the barrier height for H-abstraction from methane of almost 10 kcal mol−1 compared to its fully localized analogue H3C˙ (ρC = 1.08 e).
The distonic radical ions in the present study also exhibit some variation in the spin density residing on their radical sites, but the magnitude of these charge-induced shifts is extremely small compared to the reference values mentioned for the allyl˙/H3C˙ pair: the difference between the lowest and highest value for the spin density calculated for the considered set of distonic ions does not even exceed 0.05 e! Even for the 12/12A couple, exhibiting the highest extent of charge transfer to the phenyl ring (vide supra), one observes only a negligible change in spin density (<0.02 e). As such, this variation cannot account for the significant shifts in the barrier heights observed. Nevertheless, there is a correlation between the barriers and the spin density values, but as discussed in Section S6 of the ESI,† this correlation has to be non-causal.
3.5 Ortho- and meta-substituted distonic radical ions
Up to this point, we have limited our analysis to para-substituted distonic radical ions. Let us now turn our attention for a moment to distonic radical ions in which the charged substituent is placed in ortho- and meta-position and consider whether our previous conclusions hold in these cases as well.We selected two of the previously considered charged systems, 5 and 10, and considered the reaction barriers for the different isomeric forms (ortho, meta, para), cf.Table 2.
| x (5/10) | ΔE‡ (in kcal mol−1) | |||
|---|---|---|---|---|
| Isomer | Charged radical (x) | Uncharged radical (xA) | Uncharged radical (xA) + OEEF | |
| 5 | Para (5) | 4.1 | 7.1 | 4.2 |
| Meta (5m) | 3.5 | 7.4 | 4.3 | |
| Ortho (5o) | 3.3 | 6.7 | 3.7 | |
| 10 | Para (10) | 8.4 | 7.4 | 8.6 |
| Meta (10m) | 9.1 | 7.3 | 8.6 | |
| Ortho (10o) | 8.9 | 7.7 | 8.9 | |
From this table, it should be clear that the qualitative correspondence between the effect of the remote charged functional group and the OEEF model holds for each of the isomers considered. The maximal deviation between the reaction barrier obtained for the charged species and for the uncharged species with OEEF amounts to 0.8 kcal mol−1. It should be noted that the small discrepancies observed are not caused by the sudden emergence of through-bond effects, but can be attributed to the distinct through-space electrostatic patterns induced by the different positioning of the charged functional groups in the ortho- and meta-isomers compared to the para-isomer (see Section S7 of the ESI†).
3.6 Qualitative valence bond models reveal the distinctive impact of through-space and through-bond contributions on the potential energy surface
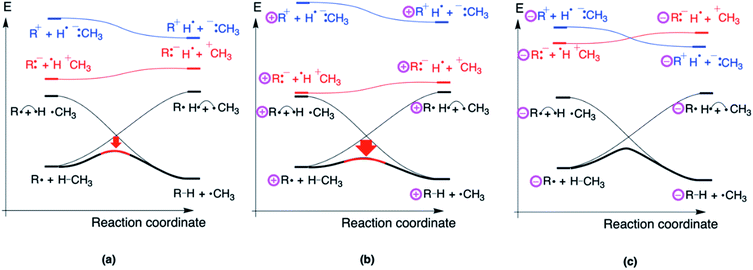
It is instructive to conclude this study by constructing a qualitative valence bond reactivity diagram (VBSCD) depicting a generic H-abstraction reaction involving a distonic radical ion. Recall from the Introduction that Kenttämaa and co-workers already used some elements of such a VB analysis to rationalize their experimental observations.14,15 In this final subsection, we will demonstrate that a refined VBSCD treatment17–19 of the H-abstraction reaction from CH4 by a generic distonic radical ion not only enables productive predictions to be made about the reactivity trends, but also elucidates straightforwardly the distinctive mechanisms through which through-bond and through-space interactions shape the potential energy surface and leads to the correct identification of the main driver of the reactivity modulation in an organic way.For regular H-abstraction reactions, e.g., R˙ + H–CH3 → R–H + ˙CH3, VBSCDs can be constructed by focusing on the evolution of only two diabatic energy curves along the reaction coordinate: one for the reactant and one for product. These reactant and product diabatic curves cross at the midpoint of the energy versus reaction coordinate plot: the reactant curve depicts the electronic configuration of the reactant and is by definition most stable in the optimal reactant geometry and correlates to the high-lying “promoted” product state in the optimal product geometry; the product curve on the other hand is most stable in the product geometry and correlates to the high-lying “promoted” reactant state in the optimal reactant geometry (cf.Fig. 7a). The two crossing diabatic curves interact and mix along the reaction coordinate; this mixing gives rise to the so-called adiabatic curve which corresponds to the ground-state potential energy surface (Fig. 7b). Note that in the reactant/product geometry, the adiabatic curve coincides with the reactant/product diabatic states respectively, but as one proceeds away from these extremes, the extent of mixing increases gradually.
It should be noted here that, even though the reactant and product curve are represented in Fig. 7 by the main covalent, i.e., uncharged, structure contributing to the respective electronic configurations associated with them, there are in fact a number of ionic structures which mix into these configurations. It is the contribution of these secondary structures which induces a permanent dipole moment in the considered species, cf.Table 1 for the dipole moments associated with the reactant complexes considered in this study.
In order to explain the reactivity trends for distonic radicals, another set of diabatic states needs to be considered explicitly: a pair of so-called charge transfer (CT) state, i.e., R:−H˙ +CH3 and R+H˙−:CH3. The CT classification of these states stems from their characterization in the reactant and product geometry; they involve an electron transfer from one isolated reactant/product to the other. In the reactant and product geometries, i.e., the limiting situation in which the reactants/products are infinitely separated, the mixing of these (high lying) states into the ground-state wave function is essentially zero, but in the intermediate region, i.e., in the region around the TS, these states can mix in significantly. The extent to which this mixing happens depends on the relative stability of these CT states compared to the states of the reactant and product, i.e., the energetic spacing between these states and the main diabatic curves.
Considering the H-abstraction from methane by a phenyl radical, R:−H˙ +CH3 is more stable than R+H˙−:CH3 due to the higher electron affinity of R = Ph˙ compared to H3C˙. As such, the former structure will push the energy hill in the VBSCD down the most (cf.Fig. 8a).
It is at this point that the effect of the charges in distonic radical ions on the reaction barrier height can be straightforwardly understood: placing a remote positive charge on R will stabilize this preferential CT state (Fig. 8b), whereas a remote negative charge will destabilize this state (Fig. 8c). As can be seen from this figure, the modulation of the height of the CT state will directly affect the extent of mixing of this state in the TS geometry and thus the energy spacing between the reactants and the TS.
Note that since we did not take all the secondary ionic structures into account, our VBSCD only reveals the relative movement of the TS compared to the RC-reference; considering the full electronic structure, one recovers the absolute dipole-moment induced stabilization/destabilization of the individual species we focused on in the beginning of this study.
From the VBSCDs drawn in Fig. 8, one can conclude that it is the preferential status of the CT state, R:−H˙+CH3, which results in barrier reduction in the case of a positive remote charge and in a barrier increase in the case of a negative charge. Logically, one can now expect that flipping the polarity of the reaction partners, i.e., considering a system in which Ra+H˙−:Rb is the preferential CT state, should lead to reversed trends. Indeed, that is exactly what we retrieve computationally: when we consider an H-abstraction reaction from nitrobenzene by a prototypical distonic radical cation (1/1A), the reaction barrier increases all of a sudden; for a prototypical anion (10/10A), the reaction barrier decreases (see Section S8 in the ESI† for more details). Additionally, experimental support for such a trend reversal can be found in the work of Petzold and co-workers.15 As such, this finding underscores unequivocally that our detailed VB analysis enables productive predictions to be made about distonic radical ions.
Now that full VBSCDs have been constructed and interpreted, we can consider the dichotomous PES-shaping effect of through-bond and through-space interactions.
As mentioned throughout this contribution, any resonance/inductive effect induced by substituents has to be inherently reflected in the electronic structure of the reactants (and/or the products). Hence, through-bond interactions by definition manifest themselves in the curvature of the reactant and product diabatic curve, since these curves respectively describe the evolution of the reactant and product electronic configuration. Thus, it is the resonance penalty43 induced modification of the shape of the reactant and product diabatic curves that causes the reaction barrier to H-abstraction for allyl˙ to be significantly higher than the corresponding barrier for H3C˙.
The main CT states on the other hand, which are the root cause of the reactivity modifications in distonic radical ions, do not mix into the adiabatic curve in the reactant and product geometry, which implies that they do not contribute to the ground-state wave function in these geometries. Consequently, their relative location is completely disjoint from any resonance/inductive through-bond effect reflected in the electronic structures of the reactants (or products); these states only start to manifest themselves when the optimal reactant/product geometry is abandoned, and one moves towards the TS in the diagram. The location of the CT states is thus governed exclusively by what we generally call through-space effects. By definition, these effects remain “hidden” in the reactant electronic structure: it is the long-range electric field emanating from the remote charge state which facilitates the dipole modulation induced exclusively by these CT diabatic states in the TS geometry.20,21,29
Thus, our in-depth VB analysis clearly demonstrates that identifying the CT states as responsible for the observed reactivity trends automatically implies that long-rang electrostatics drive the reactivity and that electron-donation/withdrawal is at best a minor contributor of limited significance.
4 Conclusions
Throughout this manuscript, we set out to answer the following question: can the charged functional groups in distonic radical ions be characterized as “extreme forms of electron-withdrawing/donating substituents” (implying dominant through-bond effects, cf. the description by Kenttämaa and co-workers), or is the radical reactivity modulation they induce mainly caused by through-space effects?A detailed analysis demonstrated that uniform oriented external electric fields can mimic the remote charges almost perfectly, indicating an electrostatic origin of the radical reactivity modulation. At the same time, the charge-induced modification of the electronic structure of the phenyl radical unit was shown to be far too small to cause the observed variability in charge-induced barrier heights. Hence, we are able to conclude unequivocally that through-space effects dominate over through-bond effects in distonic radical ions. This finding fits into a growing body of evidence, emerging from the recent literature, that through-space interactions are much more important and pervasive in chemistry than previously thought.
Finally, we constructed a lucid Valence Bond (VB) model and demonstrated that such a qualitative analysis not only reveals the dominance of through space effects in an organic manner, but also points to a remarkable reversal in the reactivity trends upon a rational modification of the reaction partner. As such, we were able to show that VB theory enables profound insights into the behaviour of distonic radical ions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. S. is supported by the Israel Science Foundation (ISF 520/18). T. M. thanks the Israeli PBC for a postdoctoral research fellowship. T. S. acknowledges the Research Foundation-Flanders (FWO) for a position as postdoctoral research fellow (1203419N). The authors thank Prof. Peter Chen for useful discussions.Notes and references
- K. M. Stirk, L. K. M. Kiminkinen and H. I. Kenttämaa, Chem. Rev., 1992, 92, 1649–1665 CrossRef CAS.
- B. F. Yates, W. J. Bouma and L. Radom, J. Am. Chem. Soc., 1984, 106, 5805–5808 CrossRef CAS.
- B. F. Yates, W. J. Bouma and L. Radom, Tetrahedron, 1986, 42, 6225–6234 CrossRef CAS.
- M. L. Gross, J. Am. Chem. Soc., 1972, 94, 3744–3748 CrossRef CAS.
- M. L. Gross and F. W. Mclafferty, J. Am. Chem. Soc., 1971, 93, 1267–1268 CrossRef.
- W. J. Bouma, J. K. MacLeod and L. Radom, J. Chem. Soc., Chem. Commun., 1978, 724–725 RSC.
- P. E. Williams, B. J. Jankiewicz, L. Yang and H. I. Kenttämaa, Chem. Rev., 2013, 113, 6949–6985 CrossRef CAS.
- G. Gryn'ova, D. L. Marshall, S. J. Blanksby and M. L. Coote, Nat. Chem., 2013, 5, 474–481 CrossRef.
- G. Gryn'ova and M. L. Coote, J. Am. Chem. Soc., 2013, 135, 15392–15403 CrossRef.
- D. M. Tomazela, A. A. Sabino, R. Sparrapan, F. C. Gozzo and M. N. Eberlin, J. Am. Soc. Mass Spectrom., 2006, 17, 1014–1022 CrossRef CAS.
- H. I. Kenttämaa, Org. Mass Spectrom., 1994, 29, 1–10 CrossRef.
- R. L. Smith and H. I. Kenttämaa, J. Am. Chem. Soc., 1995, 117, 1393–1396 CrossRef CAS.
- K. K. Thoen, R. L. Smith, J. J. Nousiainen, E. D. Nelson and H. I. Kenttämaa, J. Am. Chem. Soc., 1996, 118, 8669–8676 CrossRef.
- J. M. Price, K. E. Nizzi, J. L. Campbell, H. I. Kenttämaa, M. Seierstad and C. J. Cramer, J. Am. Chem. Soc., 2003, 125, 131–140 CrossRef CAS.
- C. J. Petzold, E. D. Nelson, H. A. Lardin and H. I. Kenttämaa, J. Phys. Chem. A, 2002, 106, 9767–9775 CrossRef CAS.
- N. M. Donahue, J. S. Clarke and J. G. Anderson, J. Phys. Chem. A, 1998, 102, 3923–3933 CrossRef CAS.
- S. Shaik and P. C. Hiberty, A Chemist's Guide to Valence Bond Theory, 2007 Search PubMed.
- S. S. Shaik, J. Am. Chem. Soc., 1981, 103, 3692–3701 CrossRef CAS.
- S. Shaik and A. Shurki, Angew. Chem., Int. Ed., 1999, 38, 586–625 CrossRef.
- S. E. Wheeler and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10854–10855 CrossRef CAS.
- S. E. Wheeler and K. N. Houk, J. Chem. Theory Comput., 2009, 5, 2301–2312 CrossRef CAS.
- S. E. Wheeler, Acc. Chem. Res., 2013, 46, 1029–1038 CrossRef CAS.
- J. Li, S. Zhou, J. Zhang, M. Schlangen, T. Weiske, D. Usharani, S. Shaik and H. Schwarz, J. Am. Chem. Soc., 2016, 138, 7973–7981 CrossRef CAS.
- H. Schwarz, S. Shaik and J. Li, J. Am. Chem. Soc., 2017, 139, 17201–17212 CrossRef CAS.
- C. Geng, J. Li, T. Weiske, M. Schlangen, S. Shaik and H. Schwarz, J. Am. Chem. Soc., 2017, 139, 1684–1689 CrossRef CAS.
- H. Gao and J. T. Groves, J. Am. Chem. Soc., 2017, 139, 3938–3941 CrossRef CAS.
- S. R. Bell and J. T. Groves, J. Am. Chem. Soc., 2009, 131, 9640–9641 CrossRef CAS.
- T. Stuyver, R. Ramanan, D. Mallick and S. Shaik, Angew. Chem., Int. Ed., 2020, 59, 7915–7920 CrossRef CAS.
- R. J. Burns, I. K. Mati, K. B. Muchowska, C. Adam and S. L. Cockroft, Angew. Chem., Int. Ed., 2020, 59, 16717–16724 CrossRef CAS.
- S. Shaik, D. Mandal and R. Ramanan, Nat. Chem., 2016, 8, 1091–1098 CrossRef CAS.
- S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Chem. Soc. Rev., 2018, 47, 5125–5145 RSC.
- T. Stuyver, D. Danovich, J. Joy and S. Shaik, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, 1–22 Search PubMed.
- S. Shaik, D. Danovich, J. Joy, Z. Wang and T. Stuyver, J. Am. Chem. Soc., 2020, 142, 12551–12562 CrossRef CAS.
- S. Ciampi, N. Darwish, H. M. Aitken, I. Díez-Perez and M. L. Coote, Chem. Soc. Rev., 2018, 47, 5146–5164 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Rev. B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- J. Da Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- P. E. Williams, B. J. Jankiewicz, L. Yang and H. I. Kenttämaa, Chem. Rev., 2013, 113, 6949–6985 CrossRef CAS.
- B. Chan, R. J. O'Reilly, C. J. Easton and L. Radom, J. Org. Chem., 2012, 77, 9807–9812 CrossRef CAS.
- T. Stuyver, J. Huang, D. Mallick, D. Danovich and S. Shaik, J. Comput. Chem., 2020, 41, 74–82 CrossRef CAS.
- E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1, Gaussian Inc., Pittsburgh, 2003 Search PubMed.
- R. Dennington, T. Keith and J. Millam, GaussView, Version 6.1, Semichem Inc., Shawnee. Mission, KS, 2016 Search PubMed.
- A. T. Maccarone, B. B. Kirk, C. S. Hansen, T. M. Griffiths, S. Olsen, A. J. Trevitt and S. J. Blanksby, J. Am. Chem. Soc., 2013, 135, 9010–9014 CrossRef CAS.
- P. E. Williams, D. L. Marshall, B. L. J. Poad, V. R. Narreddula, B. B. Kirk, A. J. Trevitt and S. J. Blanksby, J. Am. Soc. Mass Spectrom., 2018, 29, 1848–1860 CrossRef CAS.
- T. Stuyver, F. De Proft, P. Geerlings and S. Shaik, J. Am. Chem. Soc., 2020, 142, 10102–10113 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc07111k |
| This journal is © The Royal Society of Chemistry 2021 |