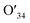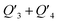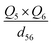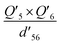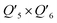Open Access Article
Open Access ArticleCoupling molecular rigidity and flexibility on fused backbones for NIR-II photothermal conversion†
Yonglin
He‡
 a,
Hailiang
Liao‡
b,
Shanzhi
Lyu
a,
Xiao-Qi
Xu
a,
Zhengke
Li
b,
Iain
McCulloch
c,
Wan
Yue
a,
Hailiang
Liao‡
b,
Shanzhi
Lyu
a,
Xiao-Qi
Xu
a,
Zhengke
Li
b,
Iain
McCulloch
c,
Wan
Yue
 *b and
Yapei
Wang
*b and
Yapei
Wang
 *a
*a
aDepartment of Chemistry, Renmin University of China, Beijing 100872, China. E-mail: yapeiwang@ruc.edu.cn
bState Key Laboratory of Optoelectronic Materials and Technologies, Key Laboratory for Polymeric Composite and Functional Materials of Ministry of Education, Guangzhou Key Laboratory of Flexible Electronic Materials and Wearable Devices, School of Materials Science and Engineering, Sun Yat-Sen University, Guangzhou 510275, China. E-mail: yuew5@mail.sysu.edu.cn
cDepartment of Chemistry, University of Oxford, 12 Mansfield Road, Oxford OX1 3TA, UK
First published on 17th February 2021
Abstract
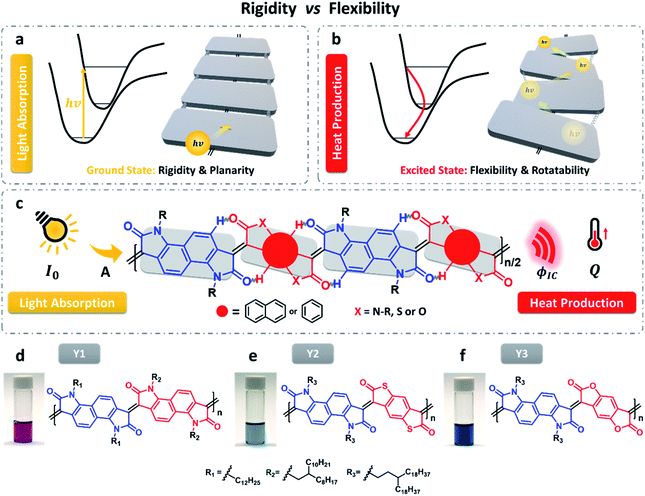
Great attention is being increasingly paid to photothermal conversion in the near-infrared (NIR)-II window (1000–1350 nm), where deeper tissue penetration is favored. To date, only a limited number of organic photothermal polymers and relevant theory have been exploited to direct the molecular design of polymers with highly efficient photothermal conversion, specifically in the NIR-II window. This work proposes a fused backbone structure locked via an intramolecular hydrogen bonding interaction and double bond, which favors molecular planarity and rigidity in the ground state and molecular flexibility in the excited state. Following this proposal, a particular class of NIR-II photothermal polymers are prepared. Their remarkable photothermal conversion efficiency is in good agreement with our strategy of coupling polymeric rigidity and flexibility, which accounts for the improved light absorption on going from the ground state to the excited state and nonradiative emission on going from the excited state to the ground state. It is envisioned that such a concept of coupling polymeric rigidity and flexibility will offer great inspiration for developing NIR-II photothermal polymers with the use of other chromophores.
Introduction
In terms of its low absorption by hemoglobin and water in tissue environments, near-infrared light (NIR) between 1000 and 1350 nm, or NIR-II for short, is generally regarded as a more biological transparent window than other wavelengths.1 Besides this, human tissues also exhibit a higher tolerance to NIR-II light in contrast to light with a shorter wavelength. These attractive advantages essentially satisfy the need for optically non-invasive diagnosis and treatment in deep tissues.2–7 The past few years have witnessed an explosive development in photothermal conversion, which is considered to be an innovative way to use NIR-II light with high quantum efficiency.4,8,9 Referring to the principles of photothermal conversion, photothermal materials with the ability to convert light energy to thermal energy are critically important. Benefiting from their easy modification, good biocompatibility, and potential biodegradability, organic photothermal materials are attracting great interest in addition to the investigation of inorganic nanoparticles.10–16 However, only a limited number of organic NIR-II photothermal materials have been exploited so far. The successful examples have mostly been formulated using conjugated polymers, which possess a low bandgap to meet the light absorption in the NIR window. Rarely has attention been paid to theoretical ideas for directing the molecular design of polymers that prefer to absorb NIR-II light, and also exhibit highly efficient photothermal conversion.2,17–19In principle, the photothermal conversion process of NIR-II molecules can be described using eqn (1),
| Q = I0 × (1 − 10A) × ϕIC | (1) |
Following the strategy of coupling rigidity and flexibility, we successfully developed a type of polymers that have low energy gaps and high photothermal conversion efficiency (Fig. 1c). As illustrated in Fig. 1d–f, the three polymers are all composed of a fused backbone structure in which the free rotation of molecular fragments is extremely restricted by the interconnected double bonds and intramolecular hydrogen bonding interaction, ensuring higher molecular planarity and electron delocalization along the polymer chain. However, the hydrogen bonding cannot fully lock the molecular skeleton and the length of the double bond becomes longer, with a certain degree of molecular torsion occurring in the excited state. This unique characteristic is beneficial for internal conversion by means of vibration relaxation.
Results and discussion
Polymer synthesis
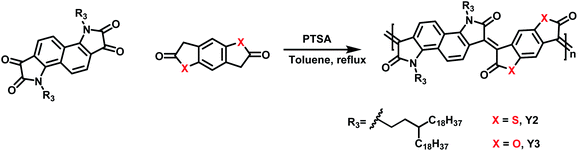
Three polymers with different heteroatoms were synthesized via an acid-catalyzed aldol polymerization from different precursor monomers (Schemes 1, S1–S3 and Fig. S1–S5†), including naphthalene bis-isatin,25,26 benzenedifurandione,27 and benzodithiophene-dione.28 As measured by high-temperature gel permeation chromatography (GPC), the molecular weights (Mn) of Y1, Y2, and Y3 are 67.3, 25.2, and 21.1 kDa, respectively. These polymers are all soluble in halogenated solvents, for example, chloroform, chlorobenzene (CB), and o-dichlorobenzene (DCB). The decomposition temperatures with a 5.0% weight loss are 377 °C for Y1, 345 °C for Y2, and 376 °C for Y3, according to the thermogravimetric analysis (TGA) (see Fig. S6–S8†). The lower decomposition temperature of Y2 might be attributed to the low stability of the thioester groups in the structure of 3,7-bis((E)-2-oxoindolin-3-ylidene)-3,7-dihydrobenzo[1,2-b:4,5-b′]dithiophene-2,6-dione (IBDT).28,29 In practice, these decomposition temperatures are high enough to ensure desirable thermal stability in the particular cases of biologically photothermal applications.Light absorption and electron excitation
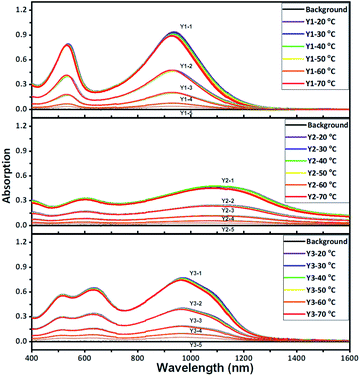
The light absorption properties of the three polymers were evaluated within a range from 400 to 1600 nm (Fig. S9 and S10†). As shown in Fig. 2 and S9,† the vis-NIR absorption spectra of Y1, Y2, and Y3 dissolved in chlorobenzene were investigated upon changing the polymer concentration as well as the temperature. The three polymers all exhibit remarkable absorption in the NIR-II window. As theoretically predicted in Fig. S11–S13,† the experimental spectra closely overlap with the calculated spectra of the dimers and trimers, suggesting that the effective conjugation lengths of these polymers are likely to fall between two and three repeating units. The ion potentials (IPs) of Y1, Y2, and Y3, as measured by X-ray photoelectron spectroscopy (XPS) in air, are 5.20, 5.36, and 5.71 eV, which are basically consistent with the estimation of the highest occupied molecular orbital (HOMO) (Fig. S14†). Referring to the theoretical light absorption spectra of the trimers (Fig. S15†), the three polymers are more likely to accept aromatic configuration rather than quinoid configuration.30 It is worth noting that the temperature has little influence on the absorption spectra of the three polymers at the given polymer concentrations. There is no blue shift when the temperature is increased, suggesting that the light absorption in the NIR-II window is not a result of J-aggregation.31,32 The linear correlation of the absorbance with the polymer concentration, which is entirely consistent with the Lambert–Beer law (Fig. S16†), also supports the assumption of negligible molecular aggregation in chlorobenzene.The maximum absorption peaks (λP) of Y1, Y2, and Y3 are 937, 1107, and 970 nm, respectively, obeying an order of λP-Y2 > λP-Y3 > λP-Y1. Whereas, the order of the molar extinction coefficient (εm) is the reverse, εm-Y1 > εm-Y3 > εm-Y2. Both the maximum absorption order and molar extinction order are also supported by theoretical calculations (Fig. S12 and S13†). In principle, λP and εm rely on the molecular rigidity and coplanar properties. In general, better coplanar property leads to greater delocalization of the electrons, thereby enabling intense light absorption at a longer wavelength.33,34 To decide if the order of λP and εm are influenced by the coplanar properties, the trimers of the three polymers were optimized in terms of their configurations via density functional theory (DFT) calculations (Fig. S21†). These trimers possess pronounced coplanarity, except for the dione groups, where small torsion is observed, which probably accounts for the indistinct molecular aggregation. The dihedral angle of the three polymers is in the order of θS0-Y3 < θS0-Y1 < θS0-Y2, unlike the orders of λP or εm. In this regard, the molecular coplanarity alone could not be used to explain the absorption difference of the three polymers directly.
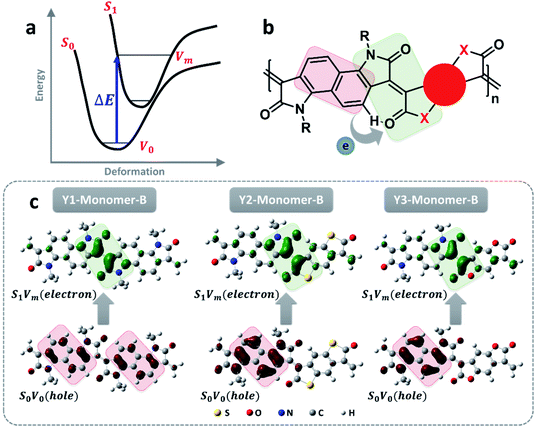
In principle, the distinct light absorption is relevant to electron transition from the ground state to the excited state under light irradiation. So, understanding the process of electron transition is favorable for explaining the order of the absorption wavelength as well as the molar extinction coefficient. As illustrated in Fig. 3a, the electron excitation generally follows the rule of Franck–Condon transitions from S0V0 to S1Vm, in which the energy gap corresponds to the absorption wavelength (λP). Because an excitation of electron transition mostly involves a number of molecular orbitals, the total electron cloud either in the ground state or the excited state is calculated by integrating all the molecular orbitals involved in the transition process based on hole–electron analysis.35 As summarized in Fig. 3c, the electron cloud in the ground state is originally distributed on the bonding region within the benzene ring, and then moves to individual atoms in the excited state. Similar electron cloud changes were also observed for polymers with different effective conjugation lengths (Fig. 3c and S17–S20†). This electron transition can be classified as a π–π* transition. Besides this, a distinct donor–acceptor electron transfer process from the donor segment, naphthalene, to the electron-deficient dione groups was also observed (Fig. 3b). This D–A electron transfer process reduces the energy gap, leading to a significant redshift in the absorption wavelength.36 The larger conjugation length is another factor that accounts for the absorption at a longer wavelength (Fig. S11–S13†).
Regardless of the influence of the dihedral angles within a conjugated repeating unit, the main structural difference among the three polymers lies in the heteroatoms near to the carbonyl group, referring to N, S, and O for Y1, Y2, and Y3, respectively. These three atoms all offer a positive conjugated effect and act as electron donors in the conjugated system. Concretely, the atomic radius of N is closer to C than O, and the π bonds between C and N, O are composed of their 2p orbitals. S possesses a larger radius than C, and its 3p orbitals take part in the formation of π bonds. The contribution of three atoms to the conjugation effect follows the order of N > O > S. As for the molecular structures in this work, the less conjugated the heteroatom is, the more electron deficient the dione group, corresponding to a lower lowest unoccupied molecular orbital (LUMO) energy level, namely LUMOY1 < LUMOY3 < LUMOY2 (Fig. S14†). In terms of the close HOMOs due to similar donor segments, a lower LUMO energy level corresponds to a narrower energy bandgap, which thus explains the order of λP-Y2 >λP-Y3 > λP-Y1.
The different extinction coefficients of the three polymers are also related to the factors of the donor–acceptor (D–A) structure and conjugation effect. Theoretically, the extinction coefficient (ε) is proportional to the overlap integral of the electron wave functions of the ground state φS0 and the excited state φS1, which can be expressed using eqn (2),
| ε ∝ 〈φS0|μ|φS1〉2 | (2) |
Photothermal conversion and vibrational relaxation
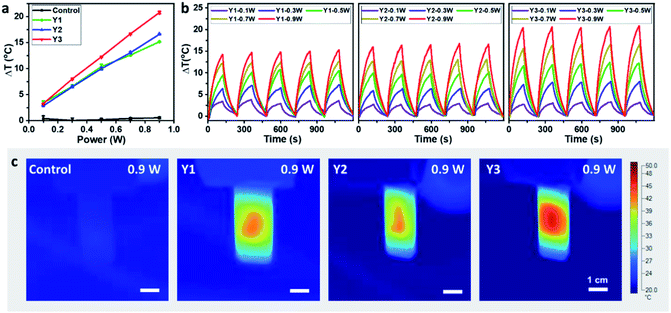
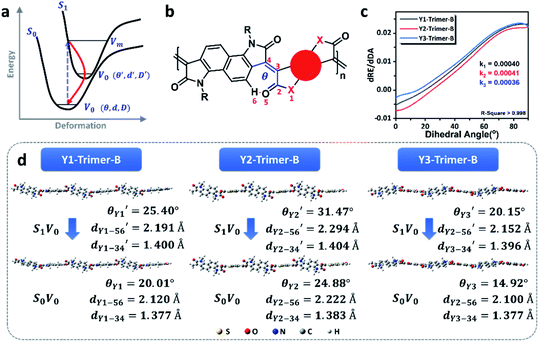
The photothermal conversion properties of these three polymers were investigated after the experimental and theoretical evaluation of their light absorption properties. As shown in Fig. 4, the three polymers dissolved in chlorobenzene with the same absorbance via adjusting polymer concentrations were compared and subjected to NIR-II light irradiation under different power densities. As recorded using an infrared (IR) camera, the temperature of each polymer solution rapidly rises under NIR light irradiation. The temperature difference compared to room temperature is positively related to the light power (Fig. S22†). For example, at a light power of 0.9 W, the temperature increases by 20.8 °C relative to room temperature for the Y3 solution, and 15.1 and 16.6 °C for the Y1 and Y2 solutions, respectively. Notably, the control group consisting of only chlorobenzene exhibits a negligible response to NIR light irradiation, as its temperature only increases by 0.5 °C, confirming that it is the polymers rather than chlorobenzene that are responsible for the photothermal effect. Reversible cycles of on–off NIR light irradiation under different light powers reveal that the three polymers possess excellent photostability (Fig. 4b). The completely reproducible temperature changes suggest that the photothermal effect results from a photophysical process rather than chemical reactions. The photothermal energy can be specified by summing the increased heat in polymer solution and thermal dissipation, as shown in eqn (3):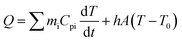 | (3) |
The photothermal effect is a result of relaxation from the excited to ground state. The pathways of intersystem crossing and fluorescent emission were ruled out in terms of the absence of singlet oxygen (Fig. S23†) and the unobserved fluorescence signal within the range of 1100–1800 nm under the excitation of a 1064 nm laser (Fig. S24†). So, the internal conversion is proposed to account for the electron relaxation along with non-irradiative emission in the form of thermal heat. As illustrated in Fig. 5a, the internal conversion process generally involves two steps, from the high vibrational energy level S1Vm to the lowest vibrational energy level S1V0 of the excited state, and then from S1V0 to the ground state S0V0. The internal conversion rate generally depends on the second step as the first step is much faster.14 The transformation of the molecular conformation between the ground and excited states is crucial to the internal conversion because it is closely related to the molecular vibrational energy level. As labeled in Fig. 5b, a dihedral angle, denoted as θ, is a representative parameter used to illustrate the primary conformation change between the ground and excited states. This assumption was confirmed using DFT calculations, as shown in Fig. 5d. The dihedral angles of the trimers of the three polymers decrease to a similar extent when they evolve from S1V0 to S0V0, in the order of Y2 > Y1 > Y3. In principle, the dihedral angle is a balanced result of two factors; one is the spatial repulsion of the molecular segments as bridged by the double bond, and the other is the hydrogen bond of the carbonyl group with the hydrogen atom on the neighboring benzene.
To further understand the photothermal process, the Laplacian bond orders (O) of the double bonds,37 the bond length (d), and atomic partial charges (Q) derived using the restrained electrostatic potential (RESP) approach in S1V0 (with a prime symbol) and S0V0 (without a prime symbol) were calculated (Fig. 5, Tables 1 and S1†). As shown in Fig. 5d, the length of the double bonds is longer than that of ethylene (1.339 Å) but indeed shorter than the carbon–carbon single bond of ethane (1.535 Å). This order is also applicable to the Laplacian bond orders of double bonds (Table 1). The weaker double bonds allow a certain degree of molecular distortion and are beneficial to the vibrational relaxation. It should be noted that these double bonds become even weaker in the excited states, which may be caused by the increase in the electron cloud on the two carbon atoms. Besides this, the hydrogen bonds in these polymers are assigned as being moderate in strength according to their length,38 of which the interaction is generally electrostatic and their strength should be proportional to the electrostatic potential energy, namely 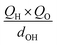 . According to Table 1, the bond strengths in the excited states are weaker than those in the ground states, while the QH × QO values are correspondingly larger. This trend indicates that the hydrogen bond changes can be mainly attributed to the difference in the oxygen–hydrogen distances. However, since the oxygen–hydrogen distances are dependent variables, the weakening of the hydrogen bonds are actually due to the molecular conformation changes resulting from the weaker double bonds. Once the molecular conformation changes, the polarized charges on the hydrogen and oxygen atoms will be increased to counter the change.
. According to Table 1, the bond strengths in the excited states are weaker than those in the ground states, while the QH × QO values are correspondingly larger. This trend indicates that the hydrogen bond changes can be mainly attributed to the difference in the oxygen–hydrogen distances. However, since the oxygen–hydrogen distances are dependent variables, the weakening of the hydrogen bonds are actually due to the molecular conformation changes resulting from the weaker double bonds. Once the molecular conformation changes, the polarized charges on the hydrogen and oxygen atoms will be increased to counter the change.
The analysis stated above provides more detailed information about the charge and conformation changes between the excited and ground states. In principle, the difference in these polymers in terms of their photothermal efficiency is a result of the total energy change. So, we further analyzed the relative energies of the molecules with different dihedral conformations. As shown in Fig. S26,† the dihedral angles corresponding to the points with zero relative energy follow the order of Y3 < Y1 < Y2, which is consistent with the previous calculation of S0V0. Increasing or decreasing the dihedral angle leads to a gradual increase in free energy, which indicates that the molecular distortion is restricted. However, since the hydrogen bond is a relatively weak bond and the double bond is weaker than that of ethylene, the rotation is not completely forbidden. There are more than 20 degrees below the gray dashed-dots for all of the polymers (Fig. S26†), indicating that the rotation is allowed within a certain range at room temperature. The high photothermal efficiencies of these polymers can be mainly attributed to the flexible hydrogen bonding, which allows the excited molecules back to the ground state through the pathway of vibrational relaxation. Furthermore, the curves in Fig. S26† are differentiated by the dihedral angle. The slopes of the linear regions that cover θ and θ′ in Fig. 5c represent the rate of relative energy change from S1V0 to S0V0, which can be used to evaluate the degree of difficulty of the molecular rotation. The slopes of Y1, Y2, and Y3 are 0.00040, 0.00041, and 0.00036, respectively. The smaller slope of Y3 represents easier molecular rotation along the 3–4 double bond at the same angle. In this regard, both the hydrogen and double bonds possess a certain flexibility in the excited state, which also provides preconditions and possibilities for the efficient photothermal conversion.
Conclusions
In conclusion, we have provided insights into three low bandgap polymers to understand the influence that intramolecular hydrogen bonding has on the light absorption and photothermal conversion properties. Following the rule of coupling molecular rigidity and flexibility, the three polymers all have remarkable absorption in the NIR-II window, and meanwhile possess excellent photothermal conversion capability. However, in view of the lack of theoretical research on the molecular design of NIR-II photothermal polymers and the scarcity of related studies on the structure–activity relationship, this work combines experiments with theoretical calculations to provide insights into the structure–property relationship and theoretical analysis of NIR-II photothermal molecular design, which is hoped to reinforce the photothermal knowledge relevant to conjugated polymers. Molecular structures in the ground and excited states were thoroughly analysed, and some new understanding in regard to the molecular structure has also been provided. Furthermore, the differences in the energy gap and dihedral angle are explained by the atomic conjugation effect and induction effect, which we believe will enlighten the design of functional photothermal polymers that exhibit higher light absorption and photothermal efficiency.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (22005336, 21875291, 21702240, and 21825503). Resources supporting this work were provided by the High-performance Computing Platform of Renmin University of China. The authors would like to thank Dr Ze-Fan Yao and Zhen Wang for their helpful discussion.Notes and references
- Y. Yang, P. He, Y. Wang, H. Bai, S. Wang, J.-F. Xu and X. Zhang, Angew. Chem., Int. Ed., 2017, 56, 16239–16242 CrossRef CAS PubMed.
- Y. He, Y. Cao and Y. Wang, Asian J. Org. Chem., 2018, 7, 2201–2212 CrossRef CAS.
- A. M. Smith, M. C. Mancini and S. Nie, Nat. Nanotechnol., 2009, 4, 710–711 CrossRef CAS PubMed.
- Y. Jiang, J. Li, X. Zhen, C. Xie and K. Pu, Adv. Mater., 2018, 30, 1705980 CrossRef PubMed.
- B. Li, L. Lu, M. Zhao, Z. Lei and F. Zhang, Angew. Chem., Int. Ed., 2018, 57, 7483–7487 CrossRef CAS PubMed.
- G. Wen, X. Li, Y. Zhang, X. Han, X. Xu, C. Liu, K. W. Y. Chan, C.-S. Lee, C. Yin, L. Bian and L. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 33492–33499 CrossRef CAS PubMed.
- C. Yin, X. Li, G. Wen, B. Yang, Y. Zhang, X. Chen, P. Zhao, S. Li, R. Li, L. Wang, C.-S. Lee and L. Bian, Biomaterials, 2020, 232, 119684 CrossRef CAS PubMed.
- Y. He and Y. Wang, Acta Polym. Sin., 2019, 50, 102–108 CAS.
- Z. Cao, L. Feng, G. Zhang, J. Wang, S. Shen, D. Li and X. Yang, Biomaterials, 2018, 155, 103–111 CrossRef CAS PubMed.
- T. Sun, J.-H. Dou, S. Liu, X. Wang, X. Zheng, Y. Wang, J. Pei and Z. Xie, ACS Appl. Mater. Interfaces, 2018, 10, 7919–7926 CrossRef CAS PubMed.
- B. Guo, Z. Sheng, Kenry, D. Hu, X. Lin, S. Xu, C. Liu, H. Zheng and B. Liu, Mater. Horiz., 2017, 4, 1151–1156 RSC.
- J. Wu, L. You, L. Lan, H. J. Lee, S. T. Chaudhry, R. Li, J.-X. Cheng and J. Mei, Adv. Mater., 2017, 29, 1703403 CrossRef PubMed.
- H. Zhu, P. Cheng, P. Chen and K. Pu, Biomater. Sci., 2018, 6, 746–765 RSC.
- Y. Cao, J.-H. Dou, N.-j. Zhao, S. Zhang, Y.-Q. Zheng, J.-P. Zhang, J.-Y. Wang, J. Pei and Y. Wang, Chem. Mater., 2017, 29, 718–725 CrossRef CAS.
- Y. Kai, X. Huan, C. Liang, S. Chunyang, W. Jun and L. Zhuang, Adv. Mater., 2012, 24, 5586–5592 CrossRef PubMed.
- L. Li, Y. Liu, P. Hao, Z. Wang, L. Fu, Z. Ma and J. Zhou, Biomaterials, 2015, 41, 132–140 CrossRef CAS PubMed.
- J. Li, J. Rao and K. Pu, Biomaterials, 2018, 155, 217–235 CrossRef CAS PubMed.
- Y. Wang, W. Zhu, W. Du, X. Liu, X. Zhang, H. Dong and W. Hu, Angew. Chem., Int. Ed., 2018, 57, 3963–3967 CrossRef CAS PubMed.
- G. Qian and Z. Y. Wang, Chem.–Asian J., 2010, 41, 1006–1029 CrossRef PubMed.
- Y. Cai, L. Huo, X. Sun, D. Wei, M. Tang and Y. Sun, Adv. Energy Mater., 2015, 5, 1500032 CrossRef.
- Y. Lin and X. Zhan, Adv. Energy Mater., 2015, 5, 1501063 CrossRef.
- L. Zhan, S. Li, H. Zhang, F. Gao, T.-K. Lau, X. Lu, D. Sun, P. Wang, M. Shi, C.-Z. Li and H. Chen, Adv. Sci., 2018, 5, 1800755 CrossRef PubMed.
- Z. Yao, X. Liao, K. Gao, F. Lin, X. Xu, X. Shi, L. Zuo, F. Liu, Y. Chen and A. K. Y. Jen, J. Am. Chem. Soc., 2018, 140, 2054–2057 CrossRef CAS PubMed.
- X. Li, F. Fang, B. Sun, C. Yin, J. Tan, Y. Wan, J. Zhang, P. Sun, Q. Fan, P. Wang, S. Li and C.-S. Lee, Nanoscale Horiz., 2021, 6, 177–185 RSC.
- A. Onwubiko, W. Yue, C. Jellett, M. Xiao, H.-Y. Chen, M. K. Ravva, D. A. Hanifi, A.-C. Knall, B. Purushothaman, M. Nikolka, J.-C. Flores, A. Salleo, J.-L. Bredas, H. Sirringhaus, P. Hayoz and I. McCulloch, Nat. Commun., 2018, 9, 416 CrossRef PubMed.
- N. M. Randell, P. C. Boutin and T. L. Kelly, J. Mater. Chem. A, 2016, 4, 6940–6945 RSC.
- T. Lei, J.-H. Dou, X.-Y. Cao, J.-Y. Wang and J. Pei, J. Am. Chem. Soc., 2013, 135, 12168–12171 CrossRef CAS PubMed.
- Y. He, J. Quinn, Y. Deng and Y. Li, Org. Electron., 2016, 35, 41–46 CrossRef CAS.
- E. A. Castro, Chem. Rev., 1999, 99, 3505–3524 CrossRef CAS PubMed.
- E. Wang, W. Mammo and M. R. Andersson, Adv. Mater., 2014, 26, 1801–1826 CrossRef CAS PubMed.
- M. Kasha, Radiat. Res., 1963, 20, 55–70 CrossRef CAS PubMed.
- K. Cai, J. Xie, D. Zhang, W. Shi, Q. Yan and D. Zhao, J. Am. Chem. Soc., 2018, 140, 5764–5773 CrossRef CAS PubMed.
- N. J. Turro, V. Ramamurthy and J. C. Scaiano, Modern Molecular Photochemistry of Organic Molecules, University Science Books, Mill Valley, California, 2009 Search PubMed.
- Y. Lu, Z. D. Yu, R. Z. Zhang, Z. F. Yao, H. Y. You, L. Jiang, H. I. Un, B. W. Dong, M. Xiong, J. Y. Wang and J. Pei, Angew. Chem., Int. Ed., 2019, 58, 11390–11394 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS.
- P. M. Beaujuge, C. M. Amb and J. R. Reynolds, Acc. Chem. Res., 2010, 43, 1396–1407 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Phys. Chem. A, 2013, 117, 3100–3108 CrossRef CAS PubMed.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc00060h |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |