Open Access Article
Open Access ArticleFacilitated inversion complicates the stereodynamics of an SN2 reaction at nitrogen center†
Dóra
Papp
 * and
Gábor
Czakó
* and
Gábor
Czakó
 *
*
MTA-SZTE Lendület Computational Reaction Dynamics Research Group, Interdisciplinary Excellence Centre and Department of Physical Chemistry and Materials Science, Institute of Chemistry, University of Szeged, Rerrich Béla tér 1, Szeged H-6720, Hungary. E-mail: dorapapp@chem.u-szeged.hu; gczako@chem.u-szeged.hu
First published on 24th March 2021
Abstract
Bimolecular nucleophilic substitution (SN2) reactions at carbon center are well known to proceed with the stereospecific Walden-inversion mechanism. Reaction dynamics simulations on a newly developed high-level ab initio analytical potential energy surface for the F− + NH2Cl nitrogen-centered SN2 and proton-transfer reactions reveal a hydrogen-bond-formation-induced multiple-inversion mechanism undermining the stereospecificity of the N-centered SN2 channel. Unlike the analogous F− + CH3Cl SN2 reaction, F− + NH2Cl → Cl− + NH2F is indirect, producing a significant amount of NH2F with retention, as well as inverted NH2Cl during the timescale within the unperturbed NH2Cl molecule gets inverted with only low probability, showing the important role of facilitated inversions via an FH…NHCl−-like transition state. Proton transfer leading to HF + NHCl− is more direct and becomes the dominant product channel at higher collision energies.
1. Introduction
The bimolecular nucleophilic substitution (SN2) reaction is one of the most important reaction types in organic and biological chemistry. The traditional stereo-selective back-side-attack Walden inversion mechanism of SN2 reactions at carbon center has been known for more than a hundred years,1 however, it took half a century to understand its atomic-level details: the process goes through a transition state with a nucleophile-central atom-leaving group geometry and results stereospecifically in the inversion of configuration around the central C atom.2 Although with a very low probability, the retention of the initial configuration around a C atom in a SN2 reaction is also possible: through the front-side-attack mechanism, known also for decades,2–4 or following the recently revealed double-inversion reaction path,5–7 where Walden-inversion is preceded by a proton-abstraction-induced first inversion. Double inversion, which is shown to be a non-IRC reaction route,8 is especially important in the case of a strong nucleophile, such as F−, when it becomes the lower-energy, and thus the primary retention pathway.6 Note that numerous reaction mechanisms resulting in inversion of configuration were also reported for SN2@C, such as roundabout,9 H-bonded complex formation,10 direct rebound11 and stripping11 pathways;12 as well as an interesting leaving-group effect13 and front-side complex formation14 have also been revealed. However, even with strong nucleophiles, in SN2@C reactions the system usually has to overcome a substantial energy barrier to follow a retention pathway, while Walden inversion is often a barrierless (energies of all involved stationary points are below the reactant asymptote) route, supported by deep pre- and post-reaction ion-dipole, or H-bonded minima.7,12 Thus, inversion is unequivocally the dominant outcome of a C-centered SN2 reaction ensuring almost exclusive stereospecificity. Replacing the central carbon atom with nitrogen, having at most three ligands and the capability of their self-inversion through a rather low-energy barrier,15 as well as different electronic structure and symmetry properties than carbon, is expected to make both the energetics and the stereodynamics of an SN2 reaction considerably distinct from those of SN2@C.SN2 reactions at N center were found to play an important role in carcinogenesis16–18 in the early 1990s arousing interest in these types of reactions. Double labeling experiments then suggested the presence of a classic transition state for an SN2 reaction at N center19 and later a twice larger reactivity was observed for the F− + NH2Cl reaction when compared to F− + CH3Cl in gas-phase selected ion flow tube experiments.20 Theoretical investigations of the SN2 reactions at N center began with the characterization of the potential energy surfaces (PESs) of X− + NH2Y and N(CH3)2Y [X, Y = F, Cl, Br, I] using lower-level ab initio21–24 and density functional theory (DFT) methods.25–27 Later, Bickelhaupt and co-workers studied the impact of replacing the central carbon atom in SN2 reactions with several other atoms by performing an activation strain analysis.28,29 In 2018 one of the present authors reported benchmark classical and adiabatic CCSD(T)-F12b/complete-basis-set-quality stationary-point energies and geometries taking also into account the correlation of core electrons both for identity and non-identity X− + NH2Y [X, Y = F, Cl, Br, I] reactions.30 The energetics of the OH− + NH2Cl31 and the F− + NH2Cl32 reactions was investigated in water as well by Wang and co-workers using a QM/MM approach. Not only the PESs, but the dynamics of SN2@N reactions were also studied in the framework of direct dynamics simulations, which compute the gradients of the PES “on-the fly” and therefore allow using only low-level ab initio or DFT methods, and running a few hundred/thousand of quasi-classical trajectories. First, the OH− + NH2Y [Y = F, Cl]33 and the F− + NH2F34 reactions were subjects of such calculations using the MP2 method with small basis sets, followed by the direct dynamics investigation of the F− + NH2Cl reaction in 2017 by Liu et al.35 at the B3LYP/aug-cc-pVDZ level of theory. They proposed indirect dynamics for the SN2 reaction and suggested minor competiveness of the proton-transfer channel even at the higher of the two collision energies considered. They also observed various SN2 mechanisms, such as direct rebound, direct stripping and indirect hydrogen-bonding. Li and Wang later proposed a proton-abstraction roundabout mechanism followed by Walden-inversion for the F− + NH2Cl → Cl− + NH2F reaction based on M06-2X/aug-cc-pVDZ-level direct dynamics simulations, along with identifying a double-inversion transition state and the corresponding reaction path.36
Taking a significant step forward from the previous direct dynamics investigations, here we report the first full-dimensional global analytical PES for the F− + NH2Cl reaction fitted on high-quality CCSD(T)-F12b/aug-cc-pVTZ energy points, which allows for a detailed and statistically reliable quasi-classical dynamics study based on more than half a million trajectories covering a wide range of collision energies. Moreover, our analysis makes it possible to track the change of the initial configuration, and therefore is capable of providing new insights into the so far unstudied stereodynamics of this prototypic SN2@N reaction.
2. Methods
As a starting point for the potential energy surface development we randomly displace the Cartesian coordinates of the CCSD(T)-F12b/aug-cc-pVTZ optimized geometries of the stationary points of the F− + NH2Cl reaction taken from ref. 30 in the 0.0–0.4 Å interval, and in the case of the reactants and products we also scatter the two fragments in random orientation around each other in the 2.5–15.0 Å distance range. The random geometries generated this way are then subjected to MP2/aug-cc-pVDZ37,38 single-point computations, and the obtained dataset is cut at a 100 kcal mol−1 energy threshold above the global minimum of the set. The energies of the remaining 5775 geometries are recalculated at the CCSD(T)-F12b/aug-cc-pVTZ38,39 level of theory, and then serve as the starting dataset for the automated PES development carried out with the ROBOSURFER program package,40 using also the same level of theory. For all quantum chemical computations the MOLPRO program package41 is used. The permutationally invariant polynomial method42,43 is applied for fitting the PES ensuring that it is invariant under the permutation of like atoms. For this, the potential energy points are fitted using a full-dimensional analytical function which is an expansion of the polynomials of the yij = exp(−rij/a) Morse-like variables with rij being the atom–atom distances and the a parameter, which defines the asymptotic behavior of the functions, is 3.0 bohr. The highest polynomial order used for this PES is 6, and the fit requires 4285 coefficients. A weighted least-squares fit is carried out, where a given energy E relative to the global minimum has a weight of (E0/(E0 + E)) × (E1/(E1 + E)) with E0 = 0.1 hartree and E1 = 0.5 hartree. In the ROBOSURFER program a hard upper limit of 100 kcal mol−1 is set relative to the energy of the reactants. During development a target accuracy of 0.5 kcal mol−1 is demanded up to 50 kcal mol−1 relative to the reactants. New geometries, carefully selected and added to improve the PES, are generated in quasi-classical trajectory (QCT) simulations and by the Holebuster subprogram.40 ROBOSURFER iterations are performed at the following collision energies (kcal mol−1) used in the dynamics computations with the maximal values of the b impact parameter (the distance between the velocity vectors of the reactants in bohr) in parentheses: 64, 27, 13, 11, 13, 27, 17, 62, 36, and 18 iterations with 1.0(20.0), 5.0(15.0), 10.0(10.0), 20(10.0), 30(10.0), 40(10.0), 50(10.0), 80(10.0), 100(10.0) and 50(10.0), in the last bunch of iterations executing the Holebuster subprogram too. The final PES is built of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 geometries and the corresponding CCSD(T)-F12b/aug-cc-pVTZ energies, and features 0.56(0.93) kcal mol−1 root mean square deviations in the 0–63(63–126) kcal mol−1 interval with respect to the global minimum of the final dataset.
780 geometries and the corresponding CCSD(T)-F12b/aug-cc-pVTZ energies, and features 0.56(0.93) kcal mol−1 root mean square deviations in the 0–63(63–126) kcal mol−1 interval with respect to the global minimum of the final dataset.
Quasi-classical trajectory simulations are performed at seven collision energies: 0.9, 6.9, 10.0, 20.0, 30.0, 40.0, and 46.1 kcal mol−1 to investigate the dynamics of the F− + NH2Cl reaction. The spatial orientation of the reactants is randomly sampled, and the initial distance between the F− ion and the center of mass of the NH2Cl molecule is set to 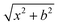 bohr, where x = 30.0 bohr and the b impact parameter is varied between 0 and bmax, the distance where the reaction probability becomes zero, with a step size of 1.0 bohr. 5000 trajectories are run at each b value; thus the total number of trajectories is more than half a million. At the beginning of the trajectories the zero-point energy (ZPE) of the NH2Cl molecule is set by using standard normal mode sampling.44 Each trajectory is propagated with a 0.0726 fs time step until the largest interatomic distance becomes larger than the largest initial one by 1 bohr. 2000 trajectories with zero collision energy are run until a 500
bohr, where x = 30.0 bohr and the b impact parameter is varied between 0 and bmax, the distance where the reaction probability becomes zero, with a step size of 1.0 bohr. 5000 trajectories are run at each b value; thus the total number of trajectories is more than half a million. At the beginning of the trajectories the zero-point energy (ZPE) of the NH2Cl molecule is set by using standard normal mode sampling.44 Each trajectory is propagated with a 0.0726 fs time step until the largest interatomic distance becomes larger than the largest initial one by 1 bohr. 2000 trajectories with zero collision energy are run until a 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time-step limit to monitor the configuration change of the unperturbed NH2Cl reactant in its ground vibrational state while the F− ion is placed 50 bohr far from NH2Cl. Integral cross-sections (ICSs) of the two reaction channels are calculated by a b-weighted numerical integration of the P(b) opacity functions at each collision energy. For the proton-transfer channel, three different ZPE-constraints are set for the reaction probabilities and ICSs: (1) soft: the sum of the classical vibrational energy of the NHCl− product and the internal energy of the HF product must be larger than the sum of the ZPE of NHCl− and the ZPE corresponding to the actual rotational state of HF, (2) hard: the above restrictions are set separately for each product, and (3) NHCl− ZPE: the restriction is set only for NHCl−. The variationally determined rovibrational energy levels of the HF molecule are taken from ref. 45. The scattering angle distributions of the products are obtained by binning the cosine of the angle (θ) of the relative velocity vectors of the products and the reactants into 10 equidistant bins from −1 to 1. Cos(θ) = −1 (θ = 180°) corresponds to backward scattering. The rotational quantum number of the HF product is determined as detailed in ref. 46. The configuration of the NH2Cl reactant (and the ‘product’ in non-reactive trajectories) and the NH2F product is identified as retained (retention) if the sign of the scalar product of the normal vector of the HNH plane and the NX (X = Cl, F) vector was the same as in the initial reactant configuration, otherwise it is identified as inverted (inversion).47
000 time-step limit to monitor the configuration change of the unperturbed NH2Cl reactant in its ground vibrational state while the F− ion is placed 50 bohr far from NH2Cl. Integral cross-sections (ICSs) of the two reaction channels are calculated by a b-weighted numerical integration of the P(b) opacity functions at each collision energy. For the proton-transfer channel, three different ZPE-constraints are set for the reaction probabilities and ICSs: (1) soft: the sum of the classical vibrational energy of the NHCl− product and the internal energy of the HF product must be larger than the sum of the ZPE of NHCl− and the ZPE corresponding to the actual rotational state of HF, (2) hard: the above restrictions are set separately for each product, and (3) NHCl− ZPE: the restriction is set only for NHCl−. The variationally determined rovibrational energy levels of the HF molecule are taken from ref. 45. The scattering angle distributions of the products are obtained by binning the cosine of the angle (θ) of the relative velocity vectors of the products and the reactants into 10 equidistant bins from −1 to 1. Cos(θ) = −1 (θ = 180°) corresponds to backward scattering. The rotational quantum number of the HF product is determined as detailed in ref. 46. The configuration of the NH2Cl reactant (and the ‘product’ in non-reactive trajectories) and the NH2F product is identified as retained (retention) if the sign of the scalar product of the normal vector of the HNH plane and the NX (X = Cl, F) vector was the same as in the initial reactant configuration, otherwise it is identified as inverted (inversion).47
3. Results and discussion
Compared to the analogous SN2 reaction at carbon center, F− + CH3Cl → Cl− + CH3F, the energy landscape of the F− + NH2Cl → Cl− + NH2F reaction, shown in Fig. 1, is markedly different. The F− + NH2Cl reaction also follows the two typical pathways of an ion–molecule reaction: SN2 and proton transfer (PT). The SN2 path features a −13.6 kcal mol−1 exothermicity, which is significantly less than the −31.9 kcal mol−1 value for the C-centered reaction, while the PT channel has only a 4.0 kcal mol−1 adiabatic endothermicity, opening at a much lower energy than in the case of carbon center.5 The F− + NH2Cl → HF + NHCl− reaction has a submerged barrier, −9.7 kcal mol−1, considerably deeper than for F− + CH3Cl → HF + CH2Cl− (12.6 kcal mol−5), and both lack a kinetic barrier. Based on the above, the proton-transfer channel promises to be much more competitive with the SN2 path at N-center. As also seen in Fig. 1, the adiabatic barrier height for the inversion of the reactant NH2Cl molecule is only 7.9 kcal mol−1, which makes self-inversion possible to occur even at low energies, turning the stereodynamics of the SN2 pathway more complex and thus more difficult to predict, in sharp contrast to the SN2 reaction at C-center, where there is no possibility for the reactant to be self-inverted. The barrier of the usual back-side-attack Walden-inversion mechanism of the N-centered SN2 reaction is also negative (−11.9 kcal mol−1) and is of similar relative energy to that of the C-centered one, however, the former reaction is missing the typical pre-reaction arrangement, a prior minimum structure with high symmetry,7,12,48 to reach the Walden transition state (W TS), where a nucleophile-central atom bond is being formed. In the case of the F− + NH2Cl reaction only a H-bonded minimum (H premin) is found in the entrance channel (−30.2 kcal mol−1),30 twice as deep as for the F− + CH3Cl reaction, relative to which the proton-transfer transition state (PT TS) lies only slightly higher than the Walden-TS, in contrast to the C-centered case, where the PT TS lies 12.6 kcal mol−1 above the reactant asymptote.5 In addition, the configurational space covered near the H premin is more favorable for proton transfer, which makes it more likely to occur while preventing the system from passing through the Walden-TS easily. Accordingly, it is not surprising that the visual analysis of the dynamics simulations shows that the system spends most of the ‘pre-reaction time’ near the H premin. On the other hand, from the H premin arrangement, the most favorable transformation is not proton-transfer, but an inversion through a H-bonded, FH…NHCl−-like transition state, called traditionally as the double-inversion TS (DI TS),5 also observed in the direct dynamics computations of Wang and co-workers.36 In contrast to the case of carbon center, where it has a 16.4 kcal mol−1 relative energy,5,6 the DI TS lies here quite deep, −23.8 kcal mol−1 below the reactants. As seen in Fig. 1, the H-bond forming between the reactants reduces the adiabatic inversion barrier of NH2Cl from 7.9 kcal mol−1 to 5.1 kcal mol−1 (owing probably to the weakened N–H bond), and thus due both to the configurational and energetic preferences (about one quarter of the barrier height) from the H premin to the pre-DI TS with respect to the Walden-TS, several induced inversion events through the pre-DI TS are expected to occur before finding a favorable arrangement for the substitution to take place. In the exit channel a similarly deep H-bonded post-reaction minimum (H postmin) can be found, however, with a considerably higher-lying post-DI TS, energetically close to the product asymptote. This is another major difference compared to the analogous F− + CH3Cl → Cl− + CH3F reaction, where the post-DI TS lies 66.1 kcal mol−1 higher than the reactants6 and 98.0 kcal mol−1 higher than the products,6,48 and thus inversion through this TS is almost negligible, while the product asymptote is only 9.7 kcal mol−1 above the H postmin complex, driving the system to form the products rather directly. In the F− + NH2Cl case a front-side pre-reaction complex (FS premin) featuring a halogen–halogen bond, known to have an important role in SN2 dynamics for C center,13,14 can also be identified submerged below the reactants (−12.1 kcal mol−1), significantly deeper than the −2.7 kcal mol−1 value observed for F− + CH3Cl.14 Such a deep minimum with a non-reactive orientation is expected to have a significant prohibiting effect on the reaction dynamics as it was shown for the F− + CH3I → I− + CH3F reaction.14 The front-side-attack transition state (FS TS) for the F− + NH2Cl → Cl− + NH2F reaction lies relatively high above the reactants (almost at the same height as for F− + CH3Cl5), thus if the NH2F product is found with retained configuration at low collision energies, the system is sure to have followed a double or more likely a multiple-inversion mechanism through the DI TSs. Taken together, owing to the deep non-reactively oriented and H-bonded minima, the H-bond-lowered barrier height of inversion at the pre-DI TS, the lack of the traditional N–F-bonded pre- and post-reaction minima, the relatively high Walden-TS from the H premin and the strongly competitive proton-transfer channel, we can expect much more indirect dynamics for the SN2 reaction at N-center than at C-center. Furthermore, the indirect reaction proceeding through a mechanism that is very likely to involve multiple configuration inversions also raises several questions regarding stereospecificity in SN2@N.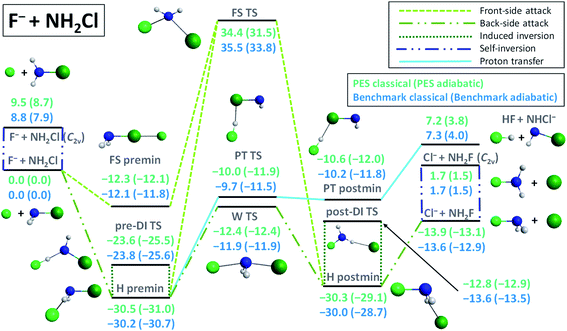 | ||
| Fig. 1 Schematic representation of the energetics and possible reaction paths of the F− + NH2Cl reaction showing classical and adiabatic relative energies of the minima and transition states comparing benchmark values30 with those obtained on the newly developed PES. For details about the stationary points see the ESI.† | ||
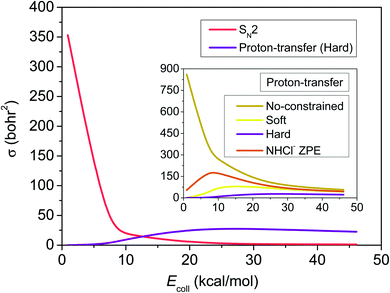
To test the hypotheses made based purely on the energy landscape characterized above, we investigate the dynamics of the F− + NH2Cl reaction in detail. For this we first develop a high-quality full-dimensional ab initio analytical PES using a permutationally invariant fitting of the gold-standard CCSD(T)-F12b/aug-cc-pVTZ energy points, on which we run quasi-classical trajectories at seven collision energies, 0.9, 6.9, 10.0, 20.0, 30.0, 40.0 and 46.1 kcal mol−1, covering the chemically interesting energy range of the reaction. Looking at Fig. 2 we can see that the excitation function, i.e. the integral cross-sections (ICSs) as a function of collision energy, of the SN2 channel decreases sharply, as it is expected in the case of a barrierless highly exothermic reaction. For the proton-transfer ICSs we applied different ZPE-constraints (see the Methods section), among which the hard-restricted ICSs, where each product must have higher vibrational energy then its own ZPE, are the most realistic. ZPE-constraints seem to have a significant effect on the reactivity, changing the fast decaying shape of the unrestricted excitation function to a much flatter one with a maximum and in the soft- and hard-constrained cases also with a threshold. After the proton-transfer channel becomes thermodynamically available at around 4 kcal mol−1 collision energy, it features a commeasurable reactivity with SN2, and slightly above 10 kcal mol−1 it turns to be the dominant reaction path, in contrast to the findings of the statistically considerably less reliable direct dynamics computations of Liu et al.35
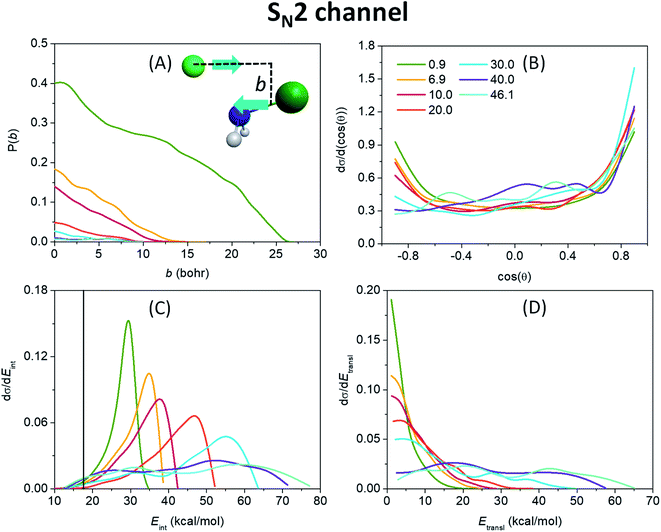
Fig. 3(A) shows that the probability for the SN2 reaction to occur is the highest at the lowest collision energy, reaching even 40% at zero impact parameter, and decreases rapidly with increasing collision energy. This demonstrates that translational energy basically inhibits a barrierless exothermic reaction by reducing the time available for finding a favorable condition (orientation or vibrational phase) for reaction. The maximum value of the impact parameter, where the reactivity vanishes, is the largest (26 bohr) at 0.9 kcal mol−1 collision energy, and decreases fast as translational energy increases, underlining the promoting effect of reaction time by allowing the ion–dipole interaction between the reactants to guide the substitution reaction. The monotonically decaying shape of the opacity functions, i.e. the reaction probability as a function of the impact parameter, of Fig. 3(A) along with the scattering angle distributions (Fig. 3(B)), which show an increasing preference for forward over backward scattering with increasing collision energy, give rise to a direct rebound mechanism at lower translational energies, occurring mostly at small impact parameters and a more and more dominative direct stripping mechanism at higher energies. The latter takes place at large impact parameters, where the approaching F− ion strips away the NH2 fragment of the reactant molecule while retaining its initial direction. However, the primarily isotropic scattering angles indicate a rather indirect reaction. This is in contrast to the C-centered analogous reaction,48 where forward scattering and the corresponding stripping mechanism are mostly observed at low collision energies, and the overall dynamics is essentially direct. The internal energy distribution of the NH2F product, seen in Fig. 3(C), peaks near the maximum accessible internal energies (the sum of the ZPE of the reactant, the collision energy and the absolute value of the classical reaction energy) at lower collision energies, which indicates a highly indirect reaction where almost all the available energy, which is considerable due to the high exothermicity, is trapped in the internal degrees of freedom while the system is stuck in the pre- and post-reaction H-bonded minima and/or DI TSs inducing repetitive inversions. The elongated N–F bond in the W TS structure with respect to that in NH2F30 is also expected to lead to vibrationally highly excited products.49 The translational energy distribution of the SN2 products, shown in Fig. 3(D), peaking near zero (except the two highest energies), also underlies the indirect mechanism, implying that the products can only separate with minimal translational energy at the rare occasions when enough of the excess internal energy flows into the translational degree of freedom. As collision energy increases, the maxima gradually shift toward higher energies and the internal energy distributions adopt a more Gaussian-like shape as a sign of an increasingly direct reaction, in consistence with the broadening relative translational energy distributions. As seen from the internal energy distributions, the number of ZPE violating trajectories is practically negligible.
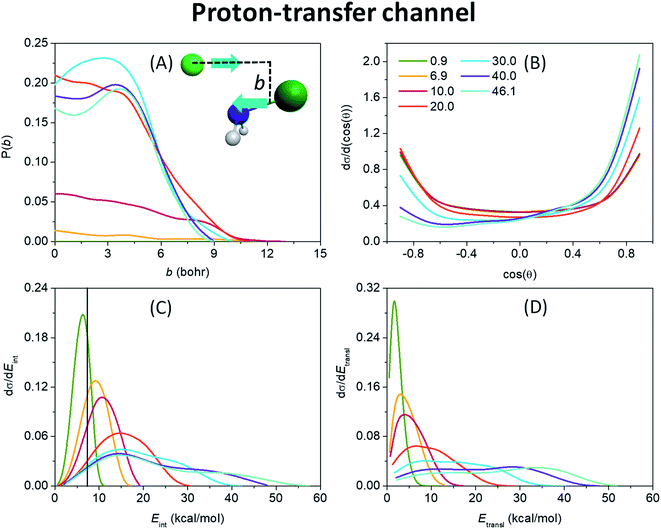
After the opening of the proton-transfer channel the hard ZPE-constrained opacity functions of Fig. 4(A) show enhancing reaction probability as collision energy increases. Note that at 0.9 kcal mol−1 the hard-restricted reaction probability is zero, in accord with the 3.8 kcal mol−1 adiabatic endothermicity and the experiments of ref. 20. We have seen in Fig. 1 that PT is also a barrierless reaction, however, the system is much less likely to stick in the deep H-bonded pre-reaction minimum, from which the PT TS is almost as far as the W TS, but the configuration of the H premin favors proton transfer. This and a shallower exit-channel well give rise to a more direct mechanism, that is why the increase of the initial translational energy promotes the reaction noticeably. At high collision energies the stripping mechanism becomes dominant as seen from the substantial reaction probabilities at relatively large impact parameters of 3–6 bohr and from the forward-scattering preference of the scattering angle distributions of the products (Fig. 4(B)) in these cases. The bmax values are much smaller for the PT reaction than for SN2, the largest is 13 bohr at 10 kcal mol−1 energy, as another sign of direct reaction dynamics. From the internal energy distributions of the NHCl− product, shown in Fig. 4(C), it is also clear that a large number of the low-energy trajectories is ZPE-violating, making it necessary to apply the above-described ZPE-constraints. Fig. 4(C) and (D) also suggest a more direct reaction than it is observed in the case of the SN2 channel with colder and broader Gaussian-like internal energy distributions along with hotter and broader relative translational energy distributions of the products both with blue-shifting maxima as collision energy increases.
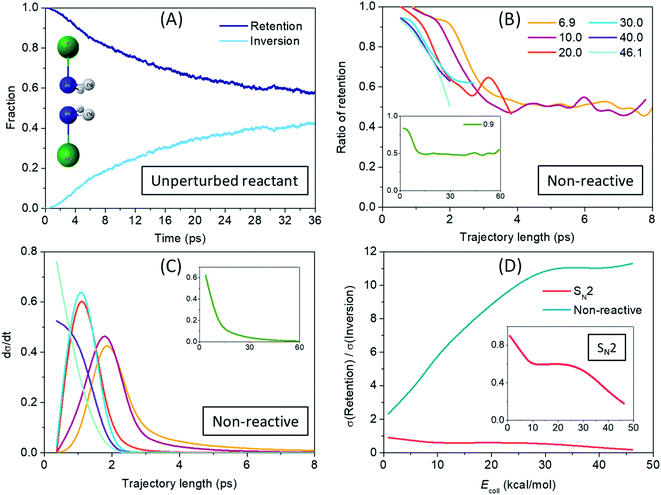
After revealing a considerably more indirect SN2 reaction dynamics, caused mainly by the deep H-bonded minima and low-lying submerged TSs for nitrogen center compared to C center, we arrive at the most interesting question: how much stereospecificity is affected by the central atom? The low-barrier umbrella motion of the ligands around the N atom has two consequences that could play an important role in the stereodynamics: (1) on one hand, unlike the case of carbon center, at nitrogen center self-inversion is a feasible internal motion of the NH2Cl reactant and of the NH2F product (with only 7.9 kcal mol−1 and 14.4 kcal mol−1 adiabatic barrier heights, respectively, the latter being higher due maybe to the stronger N–F bond relative to N–Cl); (2) on the other hand, the H-bond formed with the F− ion further lowers this barrier height for the reactant (to 5.1 kcal mol−1), while the somewhat weaker H-bond with Cl− does not really affect the inversion barrier of the product (15.2 kcal mol−1), but still leaves the door open for the inversion to take place in the exit channel as well. To investigate the time-scale and impact of (1), we analyzed the motion of the NH2Cl molecule in an unperturbed state, with zero collision energy and allowing only zero-point vibration. The fraction of retention and inversion of NH2Cl as the trajectories are propagated in time is shown in Fig. 5(A). It can be seen that the initial configuration starts to invert after 1 ps without any external action and the average retention–inversion ratio gradually converges to the racemic limit, however, at quite a low pace: it is still 58–42% after 36 ps. To study the effect of the inversion motion induced by the H-bond formed with F− we also analyze the non-reactive trajectories (with NH2Cl as ‘product’) run at different collision energies, and show the ratio of those that result in the retention of configuration in Fig. 5(B). Taking a look at the long trajectories of the low collision energies (the time distribution of the non-reactive trajectories is plotted in Fig. 5(C)) one can observe that above a certain trajectory length NH2Cl comes with roughly 50% probability in inverted or in retained configuration, which means that stereospecificity basically vanishes in these cases. With increasing collision energy, the length of the trajectories decreases, however, due to faster collisions, inversion may take place over a shorter period of time, which is indicated in Fig. 5(B) by a faster ‘convergence’ to the racemic limit with increasing trajectory length. By comparing Fig. 5(A) and (B) it is clear that induced inversion plays a significant role in the dynamics, since non-reactive trajectories reach a near racemic average outcome usually in 2–4 ps, while only 10% of the NH2Cl molecules are inverted after 4 ps in an unaffected zero-point vibrational state. It is also true for the lowest 0.9 kcal mol−1 collision energy (see insets of Fig. 5(B) and (C)), where the 50–50% probability is reached at about 12 ps trajectory length, and kept smoothly for longer trajectories as well, whereas the unperturbed reactant is found inverted only in 20% at 12 ps. The above observations suggest that a pre-reaction inversion can readily occur and it is most likely to happen through the pre-DI TS. As seen from Fig. 3(C), NH2F is produced with considerable internal energy owing to the high exothermicity, and, due to its formation via inversion at Walden-TS a significant part of the excess energy may be responsible to excite the umbrella motion of the ligands. Thus, inversion of the product, despite its higher barrier than that of the reactant, can also take place easily both through the post-DI TS or on its own. Moreover, not only one, but multiple inversions can and do occur both in the entrance and exit channels, since longer trajectories eventually reach a racemic outcome of the SN2 reaction, as shown in Fig. 5(B). These findings are also strengthened by the visual analysis of SN2 trajectories showing that the system frequently alters the configuration around the N atom through the pre-DI TS. Visual inspection also underlies the post-reaction inversion mechanisms, however, while the attacking F− ion recurrently abstracts one of the protons from N, the product Cl− ion seems very unlikely to be capable of that. We also observe a roaming/roundabout mechanism50 in the entrance channel: after proton-abstraction the HF molecule does not have enough energy to drift from the NHCl− fragment, and thus it begins to stroll around the rotating NHCl− until finally putting the proton back. This process can then be followed by actual proton-transfer, but can precede an SN2 reaction as well, in consistence with the observations of Li and Wang.36 Such an indirect pathway makes the reaction dynamics even more complex. Selected snapshots from QCT simulations of the above mechanisms are presented in Fig. S1 in the ESI.† As shown in Fig. 5(D) the impact of the multiple-inversion mechanism is also reflected in the ICS values of the SN2 channel: at the lowest collision energy the retention/inversion ICS ratio is almost 1 and it slowly decays to 0.2 as trajectories are getting shorter with increasing collision energy. This finding is in sharp contrast to what is observed for the analogous C-centered reaction, where the ICS fraction of retention is smaller than 2%,5 showing the clear stereospecificity of the Walden-inversion mechanism for SN2@C. The H-bond-induced inversion in the case of non-reactive trajectories is also substantial: the retention/inversion ratio at the lowest collision energy is only 2.3, indicating that if enough time is available, induced inversion is very likely to occur. With higher energies the trajectory length is dropping rapidly which prevents effectively the inversion of configuration. The energetics of the F− + NH2Cl → Cl− + NH2F reaction explored in water by Wang and co-workers32 suggests that although the barrier heights of both the pre-DI TS and the W TS become positive, the former is much less increased, and thus the difference between the two increases by about 50%, this way promoting the pre-reaction inversional motion in aqueous solution. Taken together, replacing the central carbon atom with nitrogen in an SN2 reaction inherently questions its stereospecificity, so far taken for granted regarding this family of chemical reactions, and although it raises new complexities, it might open new doors as well.
4. Conclusions
In the present study we have developed a full-dimensional global analytical potential energy surface fitted on CCSD(T)-F12b/aug-cc-pVTZ energy points for the F− + NH2Cl reaction, which allows for performing accurate dynamics simulations based on more than half a million quasi-classical trajectories covering a wide range of collision energies. The F− + NH2Cl → Cl− + NH2F reaction serves as a prototypic SN2@N reaction, for which we report the first detailed dynamical investigations. Furthermore, our newly developed PES and the size of the system open the route for studying the dynamics of the F− + NH2Cl reaction by quantum methods in the near future, even in full dimensions. Such simulations will be able to complement the present QCT results by capturing tunneling effects which can be important during inversion or when proton transfer takes place.It is clear from the internal, translational and scattering angle distributions of the products that, in contrast to its C-centered analogue, the N-centered SN2 reaction exhibits essentially indirect characteristics, originating from deep pre- and post-reaction H-bonded minima, low lying H-bonded inversion transition states, the lack of traditional ion–dipole minima, and a strongly competitive proton-transfer reaction. Increasing initial translational energy is found to counteract the exothermic barrierless SN2 reaction, allowing less time for finding a favorable condition for reaction; whereas it enhances the reactivity of the endothermic (but also barrierless) proton-transfer pathway, which becomes dominant above 10 kcal mol−1 collision energy. The latter turns out to feature more direct dynamics, being less likely to get stuck in deep minima.
Our simulations, capable of tracking the configurational changes around the central N atom, feasible even at room temperature and further facilitated by the H-bond formed with the attacking F− ion, also give new insights into the so far unstudied stereodynamics of this prototypical SN2@N reaction. Compared to SN2@C, where stereospecificity via Walden inversion is the conventional route, our simulations clearly demonstrate the important role of the H-bond-induced multiple-inversion mechanisms at N center, accelerating the inversion of NH2Cl compared to the unperturbed reactant and producing a significant fraction of the NH2F products with retention of the initial configuration. While double inversion is a minor pathway for SN2@C, its multiple-inversion analogue can be the key mechanism for N-centered SN2 reactions.
Author contributions
G. C. designed research, D. P. performed research and analyzed data, G. C. and D. P. discussed the results and D. P. wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the National Research, Development and Innovation Office−NKFIH, K-125317; the Ministry of Human Capacities, Hungary Grant 20391-3/2018/FEKUSTRAT; and the Momentum (Lendület) Program of the Hungarian Academy of Sciences for financial support.References
- P. Walden, Ber. Dtsch. Chem. Ges., 1896, 29, 133 CrossRef.
- C. K. Ingold, Structure and Mechanisms in Organic Chemistry, Cornell Univ. Press, Ithaca, NY, 1953 Search PubMed.
- M. N. Glukhovtsev, A. Pross, H. B. Schlegel, R. D. Bach and L. Radom, J. Am. Chem. Soc., 1996, 118, 11258 CrossRef CAS.
- A. P. Bento and F. M. Bickelhaupt, J. Org. Chem., 2008, 73, 7290 CrossRef CAS PubMed.
- I. Szabó and G. Czakó, Nat. Commun., 2015, 6, 5972 CrossRef PubMed.
- I. Szabó and G. Czakó, J. Phys. Chem. A, 2015, 119, 3134 CrossRef PubMed.
- I. Szabó and G. Czakó, J. Phys. Chem. A, 2017, 121, 9005 CrossRef PubMed.
- Y.-T. Ma, X. Ma, A. Li, H. Guo, L. Yang, J. Zhang and W. L. Hase, Phys. Chem. Chem. Phys., 2017, 19, 20127 RSC.
- J. Mikosch, S. Trippel, C. Eichhorn, R. Otto, U. Louderaj, J.-X. Zhang, W. L. Hase, M. Weidemüller and R. Wester, Science, 2008, 319, 183 CrossRef CAS PubMed.
- J. Zhang, J. Mikosch, S. Trippel, R. Otto, M. Weidemüller, R. Wester and W. L. Hase, J. Phys. Chem. Lett., 2010, 1, 2747 CrossRef CAS.
- J. Mikosch, J. Zhang, S. Trippel, C. Eichhorn, R. Otto, R. Sun, W. A. de Jong, M. Weidemüller, W. L. Hase and R. Wester, J. Am. Chem. Soc., 2013, 135, 4250 CrossRef CAS PubMed.
- J. Xie and W. L. Hase, Science, 2016, 352, 32 CrossRef CAS PubMed.
- M. Stei, E. Carrascosa, M. A. Kainz, A. H. Kelkar, J. Meyer, I. Szabó, G. Czakó and R. Wester, Nat. Chem., 2016, 8, 151 CrossRef CAS PubMed.
- I. Szabó, B. Olasz and G. Czakó, J. Phys. Chem. Lett., 2017, 8, 2917 CrossRef PubMed.
- S. A. Jarrett-Sprague and I. H. Hillier, J. Chem. Soc., Faraday Trans., 1990, 86, 3991 RSC.
- M. Novak, K. A. Martin and J. L. Heinrich, J. Org. Chem., 1989, 54, 5430 CrossRef CAS.
- J. S. Helmick, K. A. Martin, J. L. Heinrich and M. Novak, J. Am. Chem. Soc., 1991, 113, 3459 CrossRef CAS.
- R. Ulbrich, M. Famulok, F. Bosold and G. Boche, Tetrahedron Lett., 1990, 31, 1689 CrossRef CAS.
- P. Beak and J. Li, J. Am. Chem. Soc., 1991, 113, 2796 CrossRef CAS.
- R. Gareyev, S. Kato and V. M. Bierbaum, J. Am. Soc. Mass Spectrom., 2001, 12, 139 CrossRef CAS PubMed.
- M. Bühl and H. F. Schaefer III, J. Am. Chem. Soc., 1993, 115, 9143 CrossRef.
- M. Bühl and H. F. Schaefer III, J. Am. Chem. Soc., 1993, 115, 364 CrossRef.
- M. N. Glukhovtsev, A. Pross and L. Radom, J. Am. Chem. Soc., 1995, 117, 9012 CrossRef CAS.
- Y. Ren and H. Zhu, J. Am. Soc. Mass Spectrom., 2004, 15, 673 CrossRef CAS PubMed.
- J. Yang, Y. Ren, H. Zhu and S.-Y. Chu, Int. J. Mass Spectrom., 2003, 229, 199 CrossRef CAS.
- Y.-M. Xing, X.-F. Xu, Z.-S. Cai and X.-Z. Zhao, J. Mol. Struct.: THEOCHEM, 2004, 671, 27 CrossRef CAS.
- X. Liu, J. Zhang, L. Yang and R. Sun, J. Phys. Chem. A, 2016, 120, 3740 CrossRef CAS PubMed.
- J. Kubelka and F. M. Bickelhaupt, J. Phys. Chem. A, 2017, 121, 885 CrossRef CAS PubMed.
- T. A. Hamlin, M. Swart and F. M. Bickelhaupt, ChemPhysChem, 2018, 19, 1315 CrossRef CAS PubMed.
- B. Hajdu and G. Czakó, J. Phys. Chem. A, 2018, 122, 1886 CrossRef CAS PubMed.
- J. Lv, J. Zhang and D. Wang, Phys. Chem. Chem. Phys., 2016, 18, 6146 RSC.
- X. Niu, P. Liu and D. Wang, J. Phys. Chem. A, 2020, 124, 141 CrossRef CAS PubMed.
- F. Yu, L. Song and X. Zhou, Comput. Theor. Chem., 2011, 977, 86 CrossRef CAS.
- F. Yu, J. Comput. Chem., 2012, 33, 401 CrossRef CAS PubMed.
- X. Liu, C. Zhao, L. Yang, J. Zhang and R. Sun, Phys. Chem. Chem. Phys., 2017, 19, 22691 RSC.
- Y. Li and D. Wang, Phys. Chem. Chem. Phys., 2018, 20, 12106 RSC.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007 CrossRef.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- T. Győri and G. Czakó, J. Chem. Theory Comput., 2020, 16, 51 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schützet al., Molpro, version 2015.1, a package of ab initio programs, see http://www.molpro.net Search PubMed.
- B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577 Search PubMed.
- J. M. Bowman, G. Czakó and B. Fu, Phys. Chem. Chem. Phys., 2011, 13, 8094 RSC.
- W. L. Hase, Encyclopedia of Computational Chemistry, Wiley, New York, 1998, pp. 399−407 Search PubMed.
- G. Czakó, B. C. Shepler, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2009, 130, 084301 CrossRef PubMed.
- D. Papp, V. Tajti, T. Győri and G. Czakó, J. Phys. Chem. Lett., 2020, 11, 4762 CrossRef CAS PubMed.
- P. Papp, V. Tajti and G. Czakó, Chem. Phys. Lett., 2020, 755, 137780 CrossRef CAS.
- I. Szabó, A. G. Császár and G. Czakó, Chem. Sci., 2013, 4, 4362 RSC.
- J. C. Polanyi, Science, 1987, 236, 680 CrossRef CAS PubMed.
- D. Townsend, S. A. Lahankar, S. K. Lee, S. D. Chambreau, A. G. Suits, X. Zhang, J. Rheinecker, L. B. Harding and J. M. Bowman, Science, 2004, 306, 1158 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Structures, energies, harmonic frequencies and T1 diagnostics of the stationary points of the F− + NH2Cl reaction, entrance channel 1D scan of the PES and snapshots from a quasi-classical trajectory. See DOI: 10.1039/d1sc00490e |
| This journal is © The Royal Society of Chemistry 2021 |