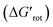Open Access Article
Open Access ArticleThe ortho effect in directed C–H activation†
Balázs L.
Tóth
 *a,
Anna
Monory
a,
Orsolya
Egyed
b,
Attila
Domján
*a,
Anna
Monory
a,
Orsolya
Egyed
b,
Attila
Domján
 b,
Attila
Bényei
b,
Attila
Bényei
 c,
Bálint
Szathury
d,
Zoltán
Novák
c,
Bálint
Szathury
d,
Zoltán
Novák
 *a and
András
Stirling
*a and
András
Stirling
 *be
*be
aELTE “Lendület” Catalysis and Organic Synthesis Research Group, Faculty of Science, Institute of Chemistry, Eötvös Loránd University, Pázmány Péter Sétány. 1/A, H-1117 Budapest, Hungary. E-mail: tothb@zng.elte.hu; novakz@elte.hu
bResearch Centre for Natural Sciences, Eötvös Loránd Research Network, Magyar Tudósok Körútja 2, H-1117 Budapest, Hungary. E-mail: stirling.andras@ttk.hu
cDepartment of Physical Chemistry, University of Debrecen, Egyetem Tér 1, H-4032 Debrecen, Hungary
dDepartment of Chemistry, University of Cambridge, Lensfield Rd, Cambridge CB2 1EW, UK
eDepartment of Chemistry, Eszterházy Károly University, Leányka u. 6, H-3300 Eger, Hungary
First published on 2nd March 2021
Abstract
The success of transition metal-catalysed ortho-directed C–H activation is often plagued by the effects of undesirable interactions between the directing group (DG) and other groups introduced into the aromatic core of the substrate. In particular, when these groups are in neighbouring positions, their interactions can affect profoundly the efficacy of the C–H activation by transition metals. In this work we introduce a simple substrate-only-based model to interpret the influence of steric hindrance of a group in ortho position to the DG in directed ortho-C–H bond activation reactions, and coined the term Ortho Effect (OE) for such situations. We consider simple descriptors such as torsion angle and torsional energy to predict and explain the reactivity of a given substrate in directed C–H activation reactions. More than 250 examples have been invoked for the model, and the nature of the ortho effect was demonstrated on a wide variety of structures. In order to guide organic chemists, we set structural and energetic criteria to evaluate a priori the efficiency of the metalation step which is usually the rate-determining event in C–H activations, i.e. we provide a simple and general protocol to estimate the reactivity of a potential substrate in C–H activation. For borderline cases these criteria help set the minimum reaction temperature to obtain reasonable reaction rates. As an example for the practical applicability of the model, we performed synthetic validations via palladium-catalysed 2,2,2-trifluoroethylation reactions in our lab. Furthermore, we give predictions for the necessary reaction conditions for several selected DGs.
Introduction
C–H activation reactions became one of the most important transformations in modern synthetic organic chemistry, which enable the cleavage of the inert aromatic C–H bond and its direct substitution with different carbon-containing functional groups such as the alkynyl, aryl, alkenyl, alkyl or acyl group with the aid of catalytic amounts of transition metals such as Pd, Rh, Ru, Co, Ir, Ni, Mn, and Cu.1 In aromatic compounds, there are many hydrogen atoms in similar chemical environments, which can raise problems of regioselectivity. However, the presence of a directing group (DG) in the aromatic core allows selective metalation in the ortho, meta or even in para positions.2–4 The efficacy of these processes critically depends on the C–H bond breaking and the formation of the metalated complex containing a carbon–metal bond, which is in many cases the rate limiting step of the catalytic cycle. This step could take place through various mechanistic scenarios such as electrophilic palladation, oxidative addition or CMD/AMLA mode,5 resulting in cyclometalated complexes. The electronic and steric properties of the substrates have a strong influence on the C–H activation step, on the stability of the metallacycle intermediates and on the synthetic outcome of the overall transformation. The beneficial electronic and steric properties could result in efficient functionalisations under mild reaction conditions, but often structural variations can prevent the C–H activation even under more forced reaction conditions. As an electrophilic metalation mechanism, the electronic effects on C–H activation reactions are well-understood.6 However, the more complex and less foreseeable effects of steric conflicts have remained often elusive without a general, thorough explanation. There is a very frequent situation in ortho C–H activation, when the substituent is located in the aromatic core at one of the ortho positions compared to the DG. For this particular situation we coin the term Ortho Effect (OE) referring to the steric influence of this group in ortho position to the DG on the metalation of C–H bond in the other ortho position of the aromatic substrate (Fig. 1A). As an example, the significant difference between the reactivity of acetanilide and 2-methyl-N-methylacetanilide provides a clear example for OE. While acetanilide can be functionalized in the ortho positions in various C–H activation reactions even under mild conditions, the functionalisation of 2-methyl-N-methylacetanilide remained unprecedented (Fig. 1B), which can be attributed to steric effects (additional examples representing situations between the two extremes are presented in the ESI†).7–17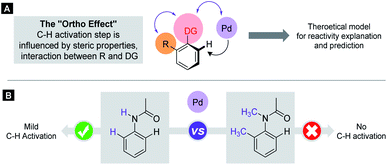 | ||
| Fig. 1 The substrate-dependent OE in Pd catalysed C–H activation. (A) General representation of OE. (B) Demonstration of OE with anilides. | ||
Generally, the steric interactions can be very complex. Small variations in their pattern can often lead to considerable changes in reactivities, hence their effects are difficult to predict.18 OE is easy to understand intuitively, but to the best of our knowledge, so far, no attempt has been made to identify, define and quantify its extent. On the other hand, a large body of empirical experience is available in a number of publications where the role of OE can be presumed.7–17 In view of this we raise the following questions:
Can a suitable, qualitative model of OE be devised by exploiting the available experimental data to establish correlation between reactivity and the relevant properties of the substrates?
Can simple descriptors be identified to predict the OE based on the properties of the substrates and the experimental results?
Characterizing the reactivity requires mechanistic insight transferable within a wide range of analogous reactions. In ortho-directed C–H activations the C–H bond breaking and the formation of the carbon–metal bond is a necessary and sufficient prerequisite of the successful ortho-metalation. Often this step is the kinetic bottleneck in these reactions.1i Hence, we focus on this step determining the rate and selectivity of the whole reaction to grasp the efficiency of the C–H activations. It is important to note that the isolation of metallic species as intermediates in the C–H activation step is a frequently used experimental strategy to obtain more detailed mechanistic insight into the catalytic transformations.
Assessing the reactivity requires large number of comparable and reliable data for both extremes (high and low) of reactivities. Although numerous examples have been disclosed for diverse substrate functionalisation using transition metal catalysed C–H bond activation under various reaction conditions,1 the compilation of the data is far from straightforward. The effects of the limiting structural molecular motifs are typically not scrutinized and the unsuccessful experiments are seldom reported. In the absence of details, the failed reaction setups are hidden to the public which hampers mechanistic interpretations.
Correlating selected descriptors with desired chemical properties has been a successful design strategy in various fields of chemistry, and especially in catalysis.19 In the present context we seek simple structural or energetic parameters of the substrate which correlate with the reactivities of the substrate in the carbon–metal bond formation step. For quantifying reactivities we need to select parameters representing the applied conditions of the reaction leading to the metallacycle formation (such as temperature or reaction time) and values representing the efficiency of the reactions (conversions or yields). This approach warrants some additional thoughts: we envision in principle two viable directions to follow:
(I) a reaction-based approach where we compute reaction routes for selected metals and ligands and make predictions on the basis of the results;
(II) a substrate-only-based approach where suitably selected properties of the substrate are used to predict reactivities.
The former approach has the advantage of being accurate whereas it has the disadvantage that the more specific (regarding ligand and metal selection) and accurate the strategy, necessarily the less general its scope is and the less general is the model it offers. In contrast, the substrate-only-based model is less accurate but it can be far wider in scope. We think that a substrate-only based model can address reactivity issues in typical synthetic problems more efficiently than a costly approach and the practice appreciates it more favourably.
In this study therefore we aimed to develop a theoretical substrate-only-based model to investigate the OE in Pd catalysed ortho C–H activation reaction with the analysis of a large number of available substrates. DFT calculations provided simple descriptors (torsional angles and torsional energies) which are shown here to perform surprisingly well to capture the experimentally observed reactivities for a large set (>250) of substrates. Our goal was to show how to assess the reactivity of a potential substrate using these descriptors and how to obtain a preliminary estimation of the reaction temperature in advance. In particular, we wish to demonstrate here that with this simple model:
(I) one can decide in a binary yes/no fashion whether a reaction is expected;
(II) in borderline cases the model helps to set the reaction temperature for a likely successful reaction;
(III) one can assess the regioselectivity when competing sites are available;
(IV) one can predict the outcome for single vs. double ortho-functionalisation reactions.
Results and discussion
Computational details
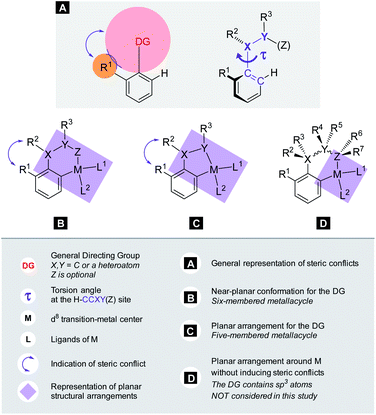
The calculations for constructing the model require optimizations of substrate conformers. The calculations have been performed using the Gaussian 09 software package.20 The ωB97XD functional21 with the 6-311++G** basis set has been employed for the geometry optimizations. Full optimizations have been done for all substrates and then a restricted optimization was performed where the chelating chain was forced to be in the plane of the ring by constraining the dihedral angle (τ) to be zero (Scheme 1) without any metal catalyst (M). Solvent effects were not included in the calculations. We assume that the solvents, employed in the experiments where yields were taken, are properly selected (during the optimization studies) for the ideal reactivity of the substrates and the solvents have similar effects on the equilibrium and planar conformers of a given substrate. In this study we will approximate the rotational Gibbs free energy (ΔGrot) by the computed Kohn–Sham energy difference of the equilibrium and constrained geometries, where the conformational angle (τ) is set to 0° (Scheme 1) and neglect the entropy, vibrational and zero-point energy differences between the equilibrium and constrained structures. We note that when formation of a six-membered metallacycle is expected all the three atoms of DG are forced to be in-plane with the aromatic ring requiring two dihedral angles to be 0°. In the following we will use either the equilibrium dihedral angle τ, or the term ΔGrot when discussing the effect of steric hindrance between DG and ortho groups. In addition, we also express ΔGrot in RT units (standardized ΔGrot;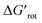 = ΔGrot/RT), i.e. we can compare torsional energies at different temperatures.
= ΔGrot/RT), i.e. we can compare torsional energies at different temperatures.
Theory for C–H activation with d8 metals
Our objective is to find suitable descriptors for the steric conflicts between DG and the ortho-substituents of the aromatic substrate. In principle, a number of structural parameters could be used to quantify the steric bulks of the ligands in question such as distances between selected atoms, specifically defined volumes or dimensional parameters.18a Still, simplicity and chemical intuition suggest that the equilibrium value of τ or the corresponding torsional energy ΔGrot can be suitable simple quantities to predict the effectiveness of ortho-functionalisation. In the following we verify this hypothesis, define its limitations and show examples how this concept can be efficiently exploited.Previous calculations and measurements have shown that after the coordination of the DG's heteroatom to M, the intermediates feature a planar ligand arrangement around M which is coplanar with the aryl group.15 Such a situation can arise for d8 metal centres (Scheme 1). This planarity represents an important constraint for chelate formation: the bond between M and DG must be coplanar with the aryl ring. However, this often comes at the prize of steric conflicts between groups that are not participating in the formation of the metallacycle as shown in Scheme 1. This is a crucial issue when the formation of the metallacycle is the rate-determining step because in such cases the efficiency of the whole functionalisation reaction is strongly dependent on the extent of the steric repulsion induced by the formation of the metallacycle in the C–H activation stage as explained in Fig. 2. In this spirit, the activation barrier can be hypothetically divided into two components: an energy term for the necessary conformational change of DG for chelation (ΔGrot) and the energy investment for the rest of the chemical changes (ΔG#chem) as pictorially shown in Fig. 2. Clearly, the smaller the energy for the conformational change (ΔGrot) is for a given ΔG#chem, the faster the reaction is as the total activation barrier (ΔG#) is smaller.
We note that similar theoretical decompositions have been proposed earlier and have been employed with great success.22 In these methods the activation energy is expressed in terms of distortion strains of the reactants (bond elongations, bond angle and torsional angle variations) and the interaction energy between the strained reactants. The main difference in our approach is that we seek parameters that are characteristic of the original substrate alone without invoking any metal catalyst, i.e. we focus on the equilibrium properties of the substrates only.
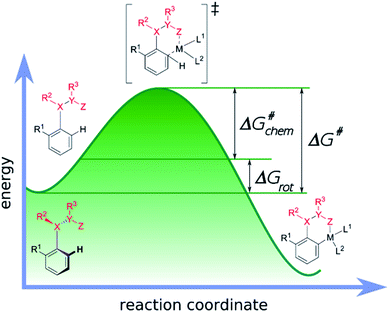 | ||
| Fig. 2 Energy profile of a typical transition-metal catalysed aryl C–H activation and its decomposition into two terms: the rotation (ΔGrot) and the chemical terms (ΔG#chem). | ||
This is why the activation barrier is dissected to an energy term representative of the initial reactant (ΔGrot) whereas the rest of the contributions to the barrier (e.g. additional strain and interaction energy components) are included in the term ΔG#chem. It is also important to note that this division implies the planarity of the TS-s. However, this assumption is only approximately valid, because the TS is not necessarily fully planar, hence a small portion of energy necessary to reach full planarity might be covered by the reaction heat liberated after the TS. On the other hand ΔGrot is a well-defined quantity for the substrates alone which is an advantageous factor for standardization of the model.
This decomposition can establish a conceptual model where a simple structural or energetic property of the substrate can predict the reaction performance in ortho-functionalisation. The goal is therefore to assess the extent to which τ or ΔGrot alone can be used to make prediction for the ortho-functionalisation without additional computations (e.g. transition state [TS] calculations).
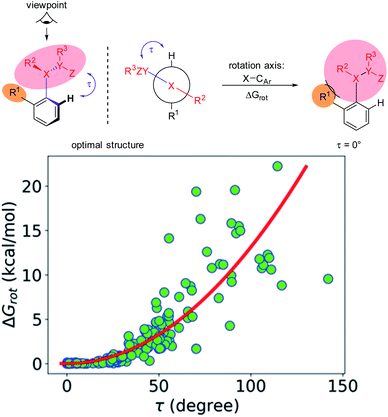
The first step along this line is to verify that the energy to constrain the DG into the necessary planar conformation for chelate formation (ΔGrot) indeed depends on the dihedral angle τ in a systematic fashion. For this we have considered the whole set of substrates curated for this study featuring an aromatic core suitable for the ortho-substitution. For many of these molecules experimental data are available but we have also included those which have not yet been employed in ortho-functionalisations. The full database is presented as part of the ESI† (Full Interactive Database). Fig. 3 displays the variation of ΔGrot as a function of τ calculated for each substrate.
It is seen that there is an apparent correlation between τ and the torsional energy (i.e. ΔGrot and τ are not independent parameters). At large angles however we can see larger scattering. In particular, there are cases where the distortion requires less energy than expected from the average tendency. This indicates that the deformation potential can be quite flat occasionally. Still, it is clear that approaching the coplanar equilibrium orientation, the torsional energy diminishes.
The partitioning of the energy barrier of the metallacycle formation into torsional (ΔGrot) and chemical (ΔG#chem) terms (Fig. 2) affords translation of the effect of the possible steric repulsions to a factorized reaction rate expression using the transition state theory (TST).23
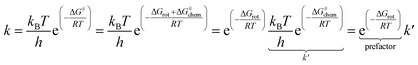 | (1) |
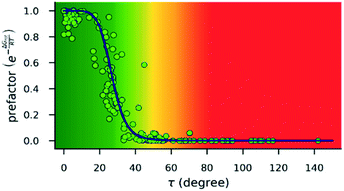 | ||
| Fig. 4 Dependence of the exponential prefactor exp(−ΔGrot/RT) of eqn (1) on the torsional angle (τ) calculated for 25 °C. Note that this plot is a nonlinear transformation of the plot in Fig. 3. The blue line is only a guide. The background color gradient is an indication of the effect of torsion on the kinetics, i.e. it is a qualitative measure of the magnitude of the prefactor: green range: small effect is expected; red range: reaction is expected to be inhibited; yellow range: transient region. | ||
Assessing the model
The next step in developing our reactivity model is to see whether there is correlation between the available experimental reaction performances and the calculated quantities (τ and ΔGrot) of the substrates. The reactivity or reaction performance can be defined in a number of ways (rate, turnover frequency, yield, etc.), however there are two important issues to consider:(I) Accurate kinetic measurements are seldom performed therefore experimental rates are not available; the only available information for deducing the reaction performance is the isolated yield. Consequently, our strategy is to employ the published yields as a measure of reactivity.24 We note that using the experimental yields instead of accurate kinetic data limits the predictive power of our model because yields only qualitatively represent the reactivity. However, in default of kinetic data the yields are used with their limitations in mind.
(II) In order to cover the full range of reaction efficiencies we need both high and low reactivity cases. Still, the vast majority of the published reactions report good to excellent yields for well-known reasons, and low yields are rarely published, therefore data for low reactivities are taken mostly from our laboratory.
The energy necessary to reach the planar conformations (ΔGrot) is meaningful if we know the reaction temperature. Indeed, the barrier of a given ΔGrot is easier to overcome at higher temperature resulting in higher yield in a given reaction time. In order to take into account this effect, we have to express ΔGrot in RT units (standardized ΔGrot, 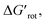 a dimensionless quantity).
a dimensionless quantity). 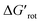 indicates how much larger ΔGrot is than the available thermal energy (RT), so it allows a meaningful comparison of the torsional hindrances for different temperatures. For example, if ΔGrot = 5 kcal mol−1, the standardized
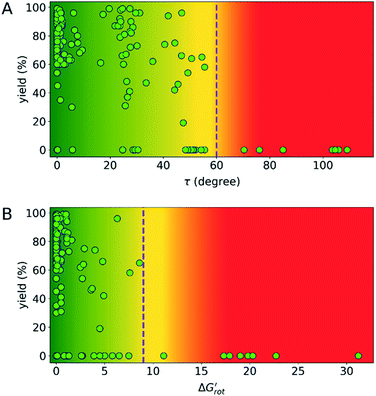
indicates how much larger ΔGrot is than the available thermal energy (RT), so it allows a meaningful comparison of the torsional hindrances for different temperatures. For example, if ΔGrot = 5 kcal mol−1, the standardized 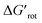 -s are 8.4 and 6.4 at 25 °C and 100 °C, respectively.25 These values indicate that at higher temperatures the same calculated barrier represents a smaller hindrance. Fig. 5A and B show the yields as a function of torsional angles and
-s are 8.4 and 6.4 at 25 °C and 100 °C, respectively.25 These values indicate that at higher temperatures the same calculated barrier represents a smaller hindrance. Fig. 5A and B show the yields as a function of torsional angles and 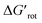 -s, respectively. Note that for these figures only those substrates were considered where experimental yields are available and the actual experimental temperatures were applied. Our first observation is that no clear correlation between the experimental yields and either the torsional angle τ or the standardized torsional energy can be detected in Fig. 5A and B. Still, a qualitative assessment can identify torsional angle or energy regions where we expect the reactions to occur (green and yellow regions) and the domain with larger torsional angle and energy values where reaction does not take place (indicated by the red background colour). To understand the origin of the peculiar scattering of the data points in Fig. 5A and B we recall that the outcome of a reaction is the function of both
-s, respectively. Note that for these figures only those substrates were considered where experimental yields are available and the actual experimental temperatures were applied. Our first observation is that no clear correlation between the experimental yields and either the torsional angle τ or the standardized torsional energy can be detected in Fig. 5A and B. Still, a qualitative assessment can identify torsional angle or energy regions where we expect the reactions to occur (green and yellow regions) and the domain with larger torsional angle and energy values where reaction does not take place (indicated by the red background colour). To understand the origin of the peculiar scattering of the data points in Fig. 5A and B we recall that the outcome of a reaction is the function of both 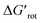 and ΔG#chem. Indeed, for a very favorable
and ΔG#chem. Indeed, for a very favorable 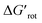 other factors (large ΔG#chem) can prevent a fast reaction and for a larger
other factors (large ΔG#chem) can prevent a fast reaction and for a larger 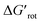 a reaction may be successful if the rest of the activation requires sufficiently small energy (small ΔG#chem).
a reaction may be successful if the rest of the activation requires sufficiently small energy (small ΔG#chem).
This implies that scattering of the points is inevitable and it is more instructive to compare reactions where the term ΔG#chem is expected to be very similar, i.e. for a given ortho-DG under similar conditions (see related calculations in the ESI,† where the contribution of the torsional energy ΔGrot to the barrier is studied). However, data for successful and unsuccessful synthesis of palladacycles are limited, and consequently the number of data-points for a given DG is seldom sufficient to demonstrate the effect. These individual distributions are given in the ESI† displaying the variations of the yields as a function of τ and 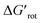 for the different classes of DGs.
for the different classes of DGs.
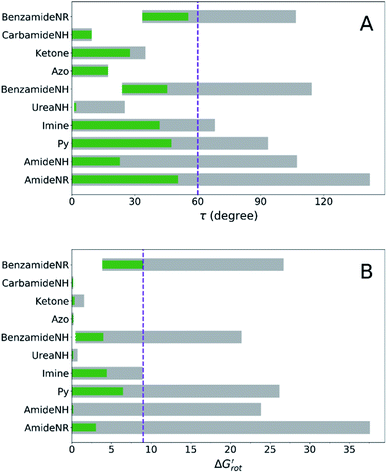
At this point our goal is to obtain an overall insight. To this end, we turn to a more qualitative assessment of the available experimental and computational data. We define a substrate active if it can form an isolable palladacycle intermediate with a non-zero experimental yield. Fig. 6 shows the range of dihedral angle τ and computed 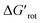 for selected classes of ortho-DGs. These plots show all the available computational data for each class by means of the grey bars. Within a class, the ranges where non-zero experimental yields are available (active substrates) are indicated by green bars. Both figures show that depending on the nature of the DGs the range covered by computations can be quite wide. However, it is clearly seen that experimentally only those substrates are active and form palladacycle intermediates, whose dihedral angle τ and
for selected classes of ortho-DGs. These plots show all the available computational data for each class by means of the grey bars. Within a class, the ranges where non-zero experimental yields are available (active substrates) are indicated by green bars. Both figures show that depending on the nature of the DGs the range covered by computations can be quite wide. However, it is clearly seen that experimentally only those substrates are active and form palladacycle intermediates, whose dihedral angle τ and 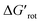 do not exceed specific thresholds (τ ≈ 60° and
do not exceed specific thresholds (τ ≈ 60° and 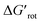 ≈ 9) as also indicated by Fig. 5A and B respectively. Although the thresholds can be refined by adding additional future examples, the current overall picture also reveals finer details: for some DGs the ranges cover a wide possible torsional interval starting from fully planar equilibrium conformations, whereas for other DGs a non-negligible equilibrium torsion is always present implying considerable OE. However, not all reactive substrates form isolable palladacycles due to various reasons, hence it cannot be excluded that substrates outside the green regions might be reactive, although as we move upward to the larger values in a given class its probability diminishes sharply (cf. with Fig. 4).
≈ 9) as also indicated by Fig. 5A and B respectively. Although the thresholds can be refined by adding additional future examples, the current overall picture also reveals finer details: for some DGs the ranges cover a wide possible torsional interval starting from fully planar equilibrium conformations, whereas for other DGs a non-negligible equilibrium torsion is always present implying considerable OE. However, not all reactive substrates form isolable palladacycles due to various reasons, hence it cannot be excluded that substrates outside the green regions might be reactive, although as we move upward to the larger values in a given class its probability diminishes sharply (cf. with Fig. 4).
Validation
Our theoretical model is designed to help synthetic chemists to design reactions and explain reactivities taking into account simple parameters such as τ,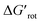 in such a way that the outcome of a C–H activation step can be explained on the basis of the actual values of these descriptors. Thus, the formation and stability of the corresponding palladacycle,26 moreover the functionalizability of the substrate subjected to the Pd catalysed transformation can also be predicted (Fig. 7). Following this flowchart, we aimed to assess the validity of our model with the design of two sets of experiments.
in such a way that the outcome of a C–H activation step can be explained on the basis of the actual values of these descriptors. Thus, the formation and stability of the corresponding palladacycle,26 moreover the functionalizability of the substrate subjected to the Pd catalysed transformation can also be predicted (Fig. 7). Following this flowchart, we aimed to assess the validity of our model with the design of two sets of experiments.
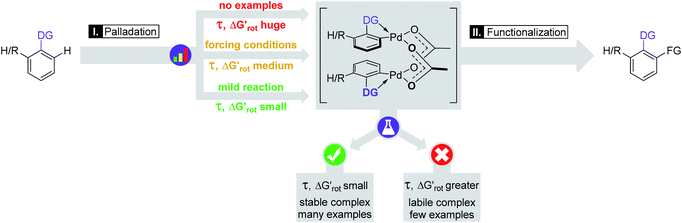
In the first series of experiments, we selected substrates with similar anilide DG with a wide-range of the OE due to the varying extent of steric conflicts between the DG and the substituents next to the anilide chains. First we applied Pd(OAc)2 catalyst in stoichiometric quantity and tested the reactivities of the substrates in forming palladacycles (Scheme 2). Note that the isolation of Pd complex intermediates is typical in mechanistic studies of C–H activation.
 | ||
| Scheme 2 The developing steric hindrance and ortho effect in aromatic amides.29 | ||
We found that 2-methylacetanilide (1), N-acetylindoline (2) and N-phenylpyrrolidin-2-one (3) underwent the palladation reaction and yielded the corresponding dimeric Pd complexes as yellow solids in 93%, 77% and 84% yields.15 These results are in line with the calculated small torsional angles (0°, 2°, 24°) and small torsional energies ( < 1) indicating a negligible OE. In the case of N-acetyl tetrahydroquinoline (4) the equilibrium torsional angle is 44° (
< 1) indicating a negligible OE. In the case of N-acetyl tetrahydroquinoline (4) the equilibrium torsional angle is 44° ( = 2.9) and the corresponding Pd complex could be isolated in 75% yield. For substrates with larger torsional angles and torsional barriers (N-methylacetanilide (5), N-(2-tolyl)pyrrolydin-2-one (6)27 and N-methyl-N-(2-tolyl)acetamide 7) isolation of the corresponding palladacycles failed even at 75 °C. Clearly, the efficiency of the complex formation follows the trend predicted by the torsional angles and torsional barriers of the substrates. An important observation is that the OE is a joint action of both ligands interacting with each other. Indeed, taking substrates 1, 6 and 7 as examples we can see that the methyl group in the ortho position does not necessarily signify OE (1), only if steric conflicts with the DG occur as in the case of substrates 6 and 7.
= 2.9) and the corresponding Pd complex could be isolated in 75% yield. For substrates with larger torsional angles and torsional barriers (N-methylacetanilide (5), N-(2-tolyl)pyrrolydin-2-one (6)27 and N-methyl-N-(2-tolyl)acetamide 7) isolation of the corresponding palladacycles failed even at 75 °C. Clearly, the efficiency of the complex formation follows the trend predicted by the torsional angles and torsional barriers of the substrates. An important observation is that the OE is a joint action of both ligands interacting with each other. Indeed, taking substrates 1, 6 and 7 as examples we can see that the methyl group in the ortho position does not necessarily signify OE (1), only if steric conflicts with the DG occur as in the case of substrates 6 and 7.
We then performed Pd-catalysed trifluoroethylation reactions on the selected substrates as a straightforward and efficient C–H activation reaction, to show the correlation between the key physical parameters obtained from the model and the reaction efficiency (Scheme 2).16 Performing a trifluoroethylation reaction on sterically less hindered substrates (1, 2, 3) with mesityl(trifluoroethyl)iodonium salt resulted in full conversion at 25 °C. However, the electrophilic trifluoroethylation of 4 provided 72% conversion under the same reaction conditions (25 °C, 24 h), which indicates a decreased reactivity shown by the somewhat larger τ and  values (44°, 2.9). Curiously, although Pd complexes could not be obtained from substrates 5 and 6, poor functionalisation could be achieved as shown by the yields (23% and 3%). This points to a reduced stability for the intermediate Pd complexes due to the non-planarity of the substrates which prevents their isolation. Finally, the highly distorted substrate 7 could not be functionalized, in agreement with the prediction of the model (very large τ torsional angle and ΔG# barrier height).
values (44°, 2.9). Curiously, although Pd complexes could not be obtained from substrates 5 and 6, poor functionalisation could be achieved as shown by the yields (23% and 3%). This points to a reduced stability for the intermediate Pd complexes due to the non-planarity of the substrates which prevents their isolation. Finally, the highly distorted substrate 7 could not be functionalized, in agreement with the prediction of the model (very large τ torsional angle and ΔG# barrier height).
In the second set of experiments, we selected a site-selective DG on substrates with two linked aromatic rings, where competition between the anilide-like (A) and benzamide-like (B) sites is expected (Scheme 3),28 and the outcome could be predicted on the basis of our model. Systematic variation of the OE could be achieved with strategical variation of the presence of a methyl group in ortho position to the amide-linker in both aryl-rings and on the amide-N. Again, we first applied Pd(OAc)2 in stoichiometric amount to form palladacycles and subsequently we explored the reactivity of the substrates in the trifluoroethylation reaction and correlated the site-selectivities with the OE operating in the anilide and benzamide moieties.
The benzamide moiety forms a five-membered palladacycle, whereas the anilide unit results in a six-membered palladacycle. The model could successfully predict the regioselective outcome for both the Pd complexes and for the functionalisation experiments. We found that palladation of the core-scaffold N-phenylbenzamide (8) without any additional group on the phenyl rings occurred at the A-side, the corresponding Pd complex was isolated in 84% yield, and B remained unsubstituted. The trifluoroethylation of the same substrate resulted in full conversion and provided the monosubstituted product in 87% yield. This is in agreement with the smaller OE on the A-side as shown by the calculated torsional angles and barriers. A methyl group in the ortho position of anilide (9), benzamide (10) or both in A and B parts (11) did not modify either the regioselectivity or the reactivity, in accordance with the preserved smaller OE on A. The expected anilide-Pd complexes could be isolated in 67%, 85%, and 63% yields, respectively. In parallel, the mono-trifluoroethylation of these substrates provided good and excellent yields (71%, 84%, 88%). By introducing a methyl group onto the linker amide-N (N-methyl-N-phenylbenzamide, 12) we have found that both the N-methyl benzamide (B) and N-methyl anilide (A) moieties feature a considerable OE albeit of different extent. While the Pd complex could not be isolated, mono-trifluoroethylation of the substrate at room temperature took place on either A or B and both AB rings in an approximately 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio (unseparable mixture) reflecting the more enhanced OE in the benzamide-moiety seen also in the theoretical descriptors. Further variation of the OE could be achieved by introducing additional methyl groups into the frame of compound 12.
2 ratio (unseparable mixture) reflecting the more enhanced OE in the benzamide-moiety seen also in the theoretical descriptors. Further variation of the OE could be achieved by introducing additional methyl groups into the frame of compound 12.
In this way, we studied the reactivity of all possible substrates (13, 14, 15). Similar to 12, none of these compounds afforded the isolation of Pd complexes (presumably due to the considerable OE present in each side). Remarkably, the site-selectivity could be swapped in the case of 13 where a methyl group is introduced into ring A, leading to the ortho-trifluoroethylation of the benzamide side (B) and the corresponding product was isolated in 46% yield. This is again in very nice agreement with the prediction of our model, which indicated a prohibitively large OE on the A-side but forecasted moderate reactivity for the ring B.
The methyl group installed on ring B further increased the OE at this side as shown by the large torsional angles and barrier and this resulted in the ortho-trifluoroethylation of the anilide side A with a yield of 34%. Installation of a methyl group in ring A increased the OE at this side as well and substrate 15 is thus inactive in the Pd-catalysed functionalisation, in agreement with the predictions of our model, i.e. both descriptors indicate inactivity for both aromatic rings.
In substrates 8, 10 and 14 two equivalent sites are available in the active ring A for ortho-functionalisation. Hence, we also tested if double equivalents of the trifluoroethyl reagent can afford the installation of two trifluoroethyl groups into the two ortho positions. We obtained bis-trifluoroethyl anilide 8b in 81% yield and 10b in 71% yield indicating only a moderate OE in mono-trifluoroethyl anilides 8m and 10m. In contrast, the bis-trifluoroethyl anilide 14b could not be obtained which points to an amplified OE in 14m.
In general, the steric hindrance and the OE of a functionalized arene can vary on a broad scale depending on the steric demands of the interacting groups.
General applicability and prediction
Beyond our designed experimental results in Scheme 4 we have collected a larger set of substrates along with the descriptors to quantify the extent of their OE to provide a more general picture of the applicability of the model. Herein we predict the possibility of successful functionalizations and the expected reaction temperatures in a pictorial way on the basis of the descriptors (for custom predictions use the attached Full Interactive Database equipped with Temperature Control Panel). We also indicate if literature precedents are available for such C–H functionalisation regardless of the incoming substituent.30–46 In fact literature examples have not been found any of the substrates predicted to be unreactive. We have also considered bis-functionalisations when equivalent ortho-positions and sites are available. Similar to the aromatic NH amides, methyl phenylcarbamate (16), tert-butyl phenylcarbamate (17) and N,N-dimethyl-N′H-N′-phenylurea (18) feature coplanar structures and zero torsional energy which suggest mild reaction conditions and a possible twofold C–H activation, which are supported by experimental results.30–32 However, the presence of an N-methyl group in N,N-dimethyl-N′-methyl-N′-phenylurea (19)33 induces structural distortion and a larger implying a slower reaction. Hence, we propose an elevated reaction temperature. For substrates 16–18 bis-functionalisation is possible. However, its success is strongly dependent on the steric demand of the first substituent. Comparison of cyclic aromatic imide (20)34 and its methylated variant 21 indicates a significant difference in the extent of the OE operating in the two substrates and 21 is predicted unreactive. There are known C–H activation reactions for azo and keto DGs such as 22 (ref. 35) and 23 (ref. 36) and the descriptors showing their planarity and also supporting their reactivity.
implying a slower reaction. Hence, we propose an elevated reaction temperature. For substrates 16–18 bis-functionalisation is possible. However, its success is strongly dependent on the steric demand of the first substituent. Comparison of cyclic aromatic imide (20)34 and its methylated variant 21 indicates a significant difference in the extent of the OE operating in the two substrates and 21 is predicted unreactive. There are known C–H activation reactions for azo and keto DGs such as 22 (ref. 35) and 23 (ref. 36) and the descriptors showing their planarity and also supporting their reactivity.
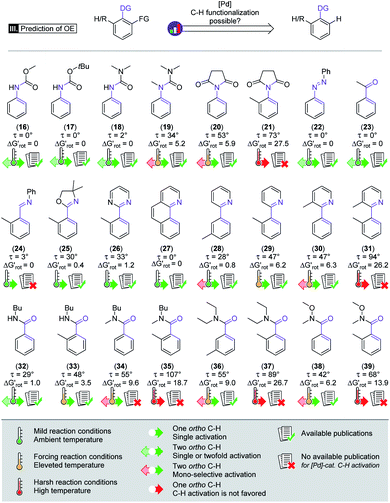 | ||
Scheme 4 Augmented demonstration and prediction of the steric repulsion and ortho effect. Values of  are calculated at 25 °C.30–46 are calculated at 25 °C.30–46 | ||
Similarly, only limited OE is predicted by the model for the nitrogen donor imines 24 and 25,37 for aromatic pyrimidine (26)38 and for benzo[h]quinoline (27).39
These predictions are aided by the experimental examples from the literature. The development of the steric hindrance and how it tunes the OE is quite spectacular in the case of phenyl pyridines: (28)40 has a slightly twisted geometry typical of linked aryl rings and the CH3 in the meta position is far from the DG. Hence the ortho-functionalisation is predicted to be feasible.
In addition, the success of a possible double functionalisation is again strongly dependent on the steric demand of the first installed substituent. The presence of ortho-methyl on either the aryl or pyridyl core (29 and 30)41,42 typically makes the C–H activation difficult, as also indicated by the descriptors. To overcome this barrier, elevated temperature is proposed. For 30 a second ortho-substitution is also a possibility if the overall OE allows it. If both rings of the phenylpyridine frame have o-CH3 (31) the torsional energy rises dramatically which might be compensated with harsh reaction conditions, although no literature precedent was found for the functionalisation of this substrate. Benzamides also feature an important DG in C–H activation reactions, although there are considerably less publications regarding their ortho-metalation reactions. The unsubstituted N-butyl benzamide (32)43 has a slightly nonplanar geometry implying small OE and a feasible mono- and bis-functionalisation. Introducing a CH3 group (33)44 induces a larger OE and suggests a somewhat higher reaction temperature. Substrate pairs 34–35, 36–37 and 38–3945,46 are good examples of how we can modify the OE by changing the interacting groups. For each pair we can see that the OE arising from the interaction of the alkyl groups on the amide-N moiety with the ortho-H atoms is considerable (34, 36, 38) but still within the productive range albeit indicating a reduced reactivity. Introduction of a larger group (35, 37, 39) however increases the OE, and further functionalisation in the ortho position is not feasible.
We note that increasing steric hindrance along the C–N axis can lead to restricted rotation and thus to the appearance of axial chirality.47 Therefore, the substrates which will be functionalized with a larger group in the ortho position can be considered as axial prochiral substances and this structural property can be exploited in diverse synthetic approaches too.48
Conclusions
In this work we have introduced the concept of Ortho Effect (OE) in C–H activation. We can define it as the interaction between the directing group (DG) and an atom or a larger group installed in the ortho position relative to the DG, if this interaction influences the outcome of the directed C–H activation in the aromatic core in question. The present work has considered various ortho-DGs, where the effect is readily discernible and likely the most frequent as compared to meta and para DGs. Development of the model focused on the metallacycle formation step because usually it is rate-determining in C–H functionalisations under kinetic control. We sought descriptors representing the substrates alone which can predict their reactivities. The rotational angle of the DG and the corresponding rotational barrier were found to be such descriptors. An evident correlation between them has been found for a set of more than 250 substrates. Employing the transition state theory, we have shown how the rotational barrier can be translated to an overall rate decrease. In addition, we introduced a dimensionless quantity, the standardized rotational barrier which takes into account the experimental reaction temperature. To characterize the reactivities of the substrates we used the experimental yields. While it is true that using the experimental yields propagates their shortcomings to our reactivity model preventing a fully quantitative analysis, reactivity domains could be identified successfully with this approach. On this basis, useful thresholds for the practice could be set for the torsional angles and torsional barriers which can predict likely successful C–H activations, and in borderline cases allows estimation of a necessary reaction temperature. Indeed, with a torsional barrier ΔGrot in hand one can estimate a minimal reaction temperature for a likely successful reaction from the fact that the threshold is for = ΔGrot/RT ≲ 9. Rearranging this relationship yields T ≳ ΔGrot/9R setting a lower bound for the reaction temperature.
= ΔGrot/RT ≲ 9. Rearranging this relationship yields T ≳ ΔGrot/9R setting a lower bound for the reaction temperature.
The model presented in this study provides a straightforward picture behind the OE. In a nutshell, if there is a coplanar or near coplanar arrangement formed by the aromatic ring and the sp2 hybridized DG of substrates then the C–H activation can easily occur; highly twisted arrangement prevents a successful metallacycle formation.
In summary, the crucial elements of our model are depicted pictorially in Fig. 8. These elements are the torsion angle, conformational energy, size of DG and ortho substituent, stability of palladacycles, reaction temperature and number of literature precedents. The study also verified our hypothesis that the outcome of a C–H activation reaction can be assessed from the properties of the substrate alone. This analysis can be done with simple geometry optimizations and energy calculations of the substrate molecules without extensive quantum chemical calculations of the free energy profile of whole reaction mechanisms including the metal catalysts. We note that with properly tuned force fields one could calculate equilibrium torsional angles with the extremely fast and cheap molecular mechanics engines built in chemical drawing programs.
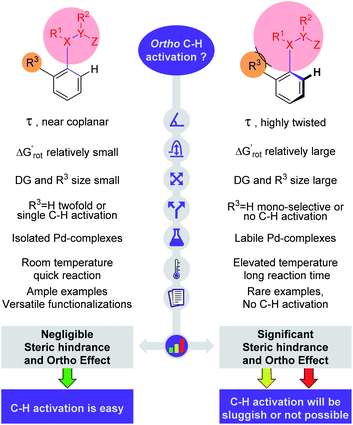 | ||
| Fig. 8 Crucial parameters for the description of steric hindrance and OE in directing group (DG, shown by a red circle) supported C–H activation. | ||
As a proof of concept, we have performed Pd-catalysed C–H functionalisations where the synthetic targets were strategically selected to verify the model. For a set of anilide compounds where differences between the electronic effects were minimized the correlations between the descriptors and reaction efficiencies were demonstrated. We have also shown how to apply the model to predict site-selectivity in functionalisations or how to tune mono vs. bis functionalisations. For a set of molecules, we have given a preliminary assessment of reactivity and selectivity in the functionalisations as well as reaction conditions on the basis of the model. We believe that our model can serve as a simple and useful tool for bench chemists and non-experts for a fast reactivity assessment in the field of ortho-directed C–H functionalisation.
Finally, we note that our database could be extended with further substrates and with the corresponding experimental and additional computed quantities. Including substrates showing moderate or no reactivities reported seldom in the literature would be highly useful and this provides additional argument favouring the publication of the so-called negative reactions. The value of such a database is that far better reactivity patterns could be obtained with more effective descriptors accounting for both reactive and unreactive situations. Certainly, modern machine learning tools could also be applied to such a sufficiently large database to obtain further suitable descriptors.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the National Research, Development and Innovation Office (K116034 and K125120); this work was completed in the ELTE Thematic Excellence Programme 2020 supported by the National Research, Development and Innovation Office – TKP2020-IKA-05, and Cooperation Excellence Program with Research Centre for Natural Sciences, Eötvös Loránd Research Network. The research was supported by the EU and co-financed by the European Regional Development Fund under the project GINOP-2.3.2-15-2016-00008. The authors thank Ágnes Gömöry for the analytical measurements, and Dr P. P. Fehér at the Research Centre for Natural Sciences, Eötvös Loránd Research Network for fruitful discussions.Notes and references
- (a) Q. Zheng, C.-F. Liu, J. Chen and G.-W. Rao, Adv. Synth. Catal., 2020, 362, 1406 CrossRef CAS; (b) P. Gandeepan, T. Müller, D. Zell, G. Cera, S. Warratz and L. Ackermann, Chem. Rev., 2018, 119, 2192 CrossRef; (c) C. Sambiagio, D. Schönbauer, R. Blieck, T. Dao-Huy, G. Pototschnig, P. Schaaf, T. Wiesinger, M. F. Zia, J. Wencel-Delord, T. Besset, B. U. W. Maes and M. Schnürch, Chem. Soc. Rev., 2018, 47, 6603 RSC; (d) Z. Dong, Z. Ren, S. J. Thompson, Y. Xu and G. Dong, Chem. Rev., 2017, 117, 9333 CrossRef CAS; (e) L. Ping, D. S. Chung, J. Bouffard and S.-G. Lee, Chem. Soc. Rev., 2017, 46, 4299 RSC; (f) F. Roudesly, J. Oble and G. Poli, J. Mol. Catal. A: Chem., 2017, 426, 275 CrossRef CAS; (g) B. Song and B. Xu, Chem. Soc. Rev., 2017, 46, 1103 RSC; (h) Y. Yang, J. Lan and J. You, J. Chem. Rev., 2017, 117, 8787–8863 CrossRef CAS; (i) T. Gensch, M. N. Hopkinson, F. Glorius and J. Wencel-Delord, Chem. Soc. Rev., 2016, 45, 2900 RSC; (j) J. R. Hummel, J. A. Boerth and J. A. Ellman, Chem. Rev., 2016, 117, 9163 CrossRef; (k) C. Liu, J. Yuan, M. Gao, S. Tang, W. Li, R. Shi and A. Lei, Chem. Rev., 2015, 115, 12138 CrossRef CAS; (l) S. H. Cho, J.-Y. Kim, J. Kwak and S. Chang, Chem. Soc. Rev., 2011, 40, 5068 RSC; (m) C. Liu, H. Zhang, W. Shi and A. Lei, Chem. Rev., 2011, 111, 1780 CrossRef CAS; (n) J. Wencel-Delord, T. Dröge, F. Liu and F. Glorius, Chem. Soc. Rev., 2011, 40, 4740 RSC; (o) T. W. Lyons and M. S. Sanford, Chem. Rev., 2010, 110, 1147 CrossRef CAS.
- (a) Z. Chen, B. Wang, J. Zhang, W. Yu, Z. Liu and Y. Zhang, Org. Chem. Front., 2015, 2, 1107 RSC; (b) W. Ma, P. Gandeepan, J. Li and L. Ackermann, Org. Chem. Front., 2017, 4, 1435 RSC.
- (a) G. Meng, N. Y. S. Lam, E. L. Lucas, T. G. Saint-Denis, P. Verma, N. Chekshin and J.-Q. Yu, J. Am. Chem. Soc., 2020, 142, 10571 CrossRef CAS; (b) A. Gholap, S. Bag, S. Pradhan, A. R. Kapdi and D. Maiti, ACS Catal., 2020, 10, 5347 CrossRef CAS; (c) L. Y. Liu, J. X. Qiao, K. S. Yeung, W. R. Ewing and J.-Q. Yu, Angew. Chem., Int. Ed., 2020, 59, 13831 CrossRef CAS; (d) K. Korvorapun, M. Moselage, J. Struwe, T. Rogge, A. Messinis and L. Ackermann, Angew. Chem., Int. Ed., 2020, 59, 18795 CrossRef CAS; (e) V. K. Tiwari and M. Kapur, Org. Biomol. Chem., 2019, 17, 1007 RSC; (f) A. Dey, S. Agasti and D. Maiti, Org. Biomol. Chem., 2016, 14, 5440 RSC; (g) C. J. Teskey, A. Y. W. Lui and M. F. Greaney, Angew. Chem., Int. Ed., 2015, 54, 11677 CrossRef CAS; (h) Z. Dong, J. Wang and G. Dong, J. Am. Chem. Soc., 2015, 137, 5887 CrossRef CAS; (i) J. Yang, Org. Biomol. Chem., 2015, 13, 1930 RSC; (j) Y.-J. Liu, H. Xu, W. J. Kong, M. Shang, H. X. Dai and J.-Q. Yu, Nature, 2014, 515, 389 CrossRef CAS; (k) J. Luo, S. Preciado and I. Larrosa, J. Am. Chem. Soc., 2014, 136, 4109 CrossRef CAS; (l) R. J. Phipps and M. J. Gaunt, Science, 2009, 323, 1593 CrossRef CAS; (m) A. Dey, S. K. Sinha, T. K. Achar and D. Maiti, Angew. Chem., Int. Ed., 2019, 58, 10820 CrossRef CAS; (n) S. Porey, X. Zhang, S. Bhowmick, V. K. Singh, S. Guin, R. S. Paton and D. Maiti, J. Am. Chem. Soc., 2020, 142, 3762 CrossRef CAS.
- (a) U. Dutta, S. Porey, S. Pimparkar, A. Mandal, J. Grover, A. Koodan and D. Maiti, Angew. Chem., Int. Ed., 2020, 59, 20831 CrossRef CAS; (b) M. T. Mihai, B. D. Williams and R. J. Phipps, J. Am. Chem. Soc., 2019, 141, 15477 CrossRef CAS; (c) U. Dutta, S. Maiti, S. Pimparkar, S. Maiti, L. R. Gahan, E. H. Krenske, D. W. Lupton and D. Maiti, Chem. Sci., 2019, 10, 7426 RSC; (d) K. Naksomboon, J. Poater, F. M. Bickelhaupt and M. Á. Fernández-Ibáñez, J. Am. Chem. Soc., 2019, 141, 6719 CrossRef CAS; (e) T. Patra, S. Bag, R. Kancherla, A. Mondal, A. Dey, S. Pimparkar, S. Agasti, A. Modak and D. Maiti, Angew. Chem., Int. Ed., 2016, 55, 7751 CrossRef CAS; (f) G. Tu, C. Yuan, Y. Li, J. Zhang and Y. Zhao, Angew. Chem., Int. Ed., 2018, 57, 15597 CrossRef CAS; (g) C. Yuan, L. Zhu, C. Chen, X. Chen, Y. Yang, Y. Lan and Y. Zhao, Nat. Commun., 2018, 9, 1189 CrossRef; (h) S. Bag, T. Patra, A. Modak, A. Deb, S. Maity, U. Dutta, A. Dey, R. Kancherla, A. Maji, A. Hazra, M. Bera and D. Maiti, J. Am. Chem. Soc., 2015, 137, 11888 CrossRef CAS.
- (a) D. Lapointe and K. Fagnou, Chem. Lett., 2010, 39, 1118 CrossRef; (b) Y. Boutadla, D. L. Davies, S. A. Macgregor and A. I. Poblador-Bahamonde, Dalton Trans., 2009, 30, 5820 RSC; (c) D. Stuart and K. Fagnou, Science, 2007, 316, 1172 CrossRef CAS; (d) D. L. Davies, S. M. A. Donald and S. A. Macgregor, J. Am. Chem. Soc., 2005, 127, 13754 CrossRef CAS; (e) S. A. Kurzeev, G. M. Kazankov and A. D. Ryabov, Inorg. Chim. Acta, 2002, 340, 192 CrossRef CAS; (f) A. D. Ryabov, Chem. Rev., 1990, 90, 403–424 CrossRef CAS.
- (a) D. García-Cuadrado, P. de Mendoza, P. A. A. C. Braga, F. Maseras and A. M. Echavarren, J. Am. Chem. Soc., 2007, 129, 6880 CrossRef; (b) J.-R. Wang, C.-T. Yang, L. Liu and Q.-X. Guo, Tetrahedron Lett., 2007, 48, 5449 CrossRef CAS; (c) L.-C. Campeau, M. Parisien, M. Leblanc and K. Fagnou, J. Am. Chem. Soc., 2004, 126, 9186 CrossRef CAS; (d) J. J. González, N. García, B. Gómez-Lor and A. M. Echavarren, J. Org. Chem., 1997, 62, 1286 CrossRef.
- H. Horino and N. Inoue, J. Org. Chem., 1981, 46, 4416 CrossRef CAS.
- W. Mossi, A. J. Klaus and P. Rys, Helv. Chim. Acta, 1992, 75, 2531 CrossRef CAS.
- F. Yang, F. Song, W. Li, J. Lan and J. You, RSC Adv., 2013, 3, 9649 RSC.
- S. J. Tremont and H. U. Rahman, J. Am. Chem. Soc., 1984, 106, 5759 CrossRef CAS.
- M. D. K. Boele, G. P. F. van Strijdonck, A. H. M. de Vries, P. C. J. Kamer, J. G. de Vries and P. W. N. M. van Leeuwen, J. Am. Chem. Soc., 2002, 124, 1586 CrossRef CAS.
- V. G. Zaitsev and O. Daugulis, J. Am. Chem. Soc., 2005, 127, 4156 CrossRef CAS.
- B. S. Kim, C. Jang, D. J. Lee and S. W. Youn, Chem.–Asian J., 2010, 5, 2336 CrossRef CAS.
- M. Tobisu, Y. Ano and N. Chatani, Org. Lett., 2009, 11, 3250 CrossRef CAS.
- C. S. Yeung, X. Zhao, N. Borduas and V. M. Dong, Chem. Sci., 2010, 1, 331 RSC.
- B. L. Tóth, S. Kovács, G. Sályi and Z. Novák, Angew. Chem., Int. Ed., 2016, 55, 1988 CrossRef.
- B. P. Mathew, H. J. Yang, J. Kim, J. B. Lee, Y.-T. Kim, S. Lee, C. Y. Lee, W. Choe, K. Myung, J.-U. Park and S. Y. Hong, Angew. Chem., Int. Ed., 2017, 56, 5007 CrossRef CAS.
- (a) A. V. Brethomé, S. P. Fletcher and R. S. Paton, ACS Catal., 2019, 9, 2313 CrossRef; (b) J. P. Reid and M. S. Sigman, Nature, 2019, 571, 343 CrossRef CAS.
- (a) D. J. Durand and N. Fey, Chem. Rev., 2019, 119, 6561 CrossRef CAS; (b) M. Foscato and V. R. Jensen, ACS Catal., 2020, 10, 2354 CrossRef CAS.
- M. J. Frisch et al. Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- (a) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070 CrossRef CAS; (b) D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187 CrossRef CAS; (c) F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114 CrossRef CAS.
- E. Pollak and P. Talkner, Chaos, 2005, 15, 26116 CrossRef.
- Discussion of a possible standardization of the published yields is given in the ESI.†.
- Note that the Gibbs free energy is a temperature dependent quantity but we neglect this dependence in this study..
- B. E. Haines, J. F. Berry, J.-Q. Yu and D. G. Musaev, ACS Catal., 2016, 6, 829 CrossRef CAS.
- D. G. Billing, J. C. A. Boeyens, L. Denner, K. E. D. Plooy, G. C. Long and J. P. Michael, Acta Crystallogr., 1991, 47, 284 Search PubMed.
- (a) Q. Lin, Z. Lin, M. Pan, Q. Zheng, H. Li, X. Chen, C. Darcel, P. H. Dixneuf and B. Li, Org. Chem. Front., 2021, 8, 514–521 RSC; (b) K. Sahoo, P. Pradhan and N. Panda, Org. Biomol. Chem., 2020, 18, 1820 RSC; (c) R. Gramage-Doria, Chem.–Eur. J., 2020, 26, 9688 CrossRef CAS; (d) A. Tomberg, M. É. Muratore, M. J. Johansson, I. Terstiege, C. Sköld and P.-O. Norrby, iScience, 2019, 20, 373 CrossRef CAS; (e) Y.-H. Sun, T.-Y. Sun, Y.-D. Wu, X. Zhang and Y. Rao, Chem. Sci., 2016, 7, 2229 RSC.
- C. Y. Legault, The optimized structures were visualized with CYLview, 1.0b, Université de Sherbrooke, 2009, http://www.cylview.org Search PubMed.
- (a) Q.-L. Li, Z.-Y. Li and G.-W. Wang, ACS Omega, 2018, 3, 4187 CrossRef CAS; (b) A. Polley, K. Varalaxmi and R. Jana, ACS Omega, 2018, 3, 14503 CrossRef CAS; (c) N. Uhlig and C.-J. Li, Chem.–Eur. J., 2014, 20, 12066 CrossRef CAS.
- E. Dubost, V. Babin, F. Benoist, A. Hebert, P. Barbey, C. Chollet, J.-P. Bouillon, A. Manrique, G. Pieters, F. Fabis and T. Cailly, Org. Lett., 2018, 20, 6302 CrossRef CAS.
- (a) S. Kovács, B. L. Tóth, G. Borsik, T. Bihari, N. V. May, A. Stirling and Z. Novák, Adv. Synth. Catal., 2017, 359, 527 CrossRef; (b) T. Nishikata, A. R. Abela, S. Huang and B. H. Lipshutz, Beilstein J. Org. Chem., 2016, 12, 1040 CrossRef CAS; (c) C. E. Houlden, M. Hutchby, C. D. Bailey, J. G. Ford, S. N. G. Tyler, M. R. Gagne, G. C. Lloyd-Jones and K. I. Booker-Milburn, Angew. Chem., Int. Ed., 2009, 48, 1830 CrossRef CAS.
- Z. Jiang, L. Zhang, C. Dong, X. Su, H. Li, W. Tang, L. Xu and Q. Fan, RSC Adv., 2013, 3, 1025 RSC.
- C. Zhang, Y. Song, Z. Sang, L. Zhan and Y. Rao, J. Org. Chem., 2018, 83, 2582 CrossRef CAS.
- (a) G. Hong, D. Mao, S. Wu and L. Wang, J. Org. Chem., 2014, 79, 10629 CrossRef CAS; (b) X.-T. Ma and S.-K. Tian, Adv. Synth. Catal., 2013, 355, 337 CAS; (c) H. Li, P. Li, H. Tan and L. Wang, Chem.–Eur. J., 2013, 19, 14432 CrossRef CAS.
- G. Shan, X. Yang, L. Ma and Y. Rao, Angew. Chem., Int. Ed., 2012, 51, 13070 CrossRef CAS.
- D. A. Gutierrez, W.-C. C. Lee, Y. Shen and J. J. Li, Tetrahedron Lett., 2016, 57, 5372 CrossRef CAS.
- (a) X. Wang, L. Truesdale and J.-Q. Yu, J. Am. Chem. Soc., 2010, 132, 3648 CrossRef CAS; (b) Q.-L. Yang, C.-Z. Li, L.-W. Zhang, Y.-Y. Li, X. Tong, X.-Y. Wu and T.-S. Mei, Organometallics, 2019, 38, 1208 CrossRef CAS.
- (a) D. C. Powers and T. Ritter, Nat. Chem., 2009, 1, 302 CrossRef CAS; (b) Q.-Y. Han, X. Hu, X.-S. Xue, C.-L. Zhao and C.-P. Zhang, Asian J. Org. Chem., 2019, 8, 665 CrossRef CAS.
- (a) X. Wang, X. Ji, C. Shao, Y. Zhang and Y. Zhang, Org. Biomol. Chem., 2017, 15, 5616 RSC; (b) A. Hossian, M. K. Manna, K. Manna and R. Jana, Org. Biomol. Chem., 2017, 15, 6592 RSC; (c) D. Kalyani and M. S. Sanford, Org. Lett., 2005, 7, 4149 CrossRef CAS.
- (a) S. R. Neufeldt, C. K. Seigerman and M. S. Sanford, Org. Lett., 2013, 15, 2302 CrossRef CAS; (b) X. Wang, X. Ji, C. Shao, Y. Zhang and Y. Zhang, Org. Biomol. Chem., 2017, 15, 5616 RSC.
- (a) D. Kalyani, N. R. Deprez, L. V. Desai and M. S. Sanford, J. Am. Chem. Soc., 2005, 127, 7330 CrossRef CAS; (b) X. Chen, C. E. Goodhue and J.-Q. Yu, J. Am. Chem. Soc., 2006, 128, 12634 CrossRef CAS; (c) C. K. Seigerman, T. M. Micyus, S. R. Neufeldt and M. S. Sanford, Tetrahedron, 2013, 69, 5580 CrossRef CAS.
- M. Maraswami, S. Pankajakshan, G. Chen and T.-P. Loh, Org. Lett., 2017, 19, 4223 CrossRef CAS.
- C. Luis and N. C. Misal Castro, Chem.–Eur. J., 2014, 20, 4548 CrossRef.
- (a) K. Jing, J.-P. Yao, Z.-Y. Li, Q.-L. Li, H.-S. Lin and G.-W. Wang, J. Org. Chem., 2017, 82, 12715 CrossRef CAS; (b) F.-C. Qiu, W.-C. Yang, Y.-Z. Chang and B.-T. Guan, Asian J. Org. Chem., 2017, 6, 1361 CrossRef CAS.
- (a) R. Das and M. Kapur, J. Org. Chem., 2017, 82, 1114 CrossRef CAS; (b) Y. Wang, K. Zhou, Q. Lan and X.-S. Wang, Org. Biomol. Chem., 2015, 13, 353 RSC.
- (a) J. E. Díaz, A. Mazzanti, L. R. Orelli and M. Mancinelli, ACS Omega, 2019, 4, 4712 CrossRef; (b) A. Iida, M. Matsuoka, H. Hasegawa, N. Vanthuyne, D. Farran, C. Roussel and O. Kitagawa, J. Org. Chem., 2019, 84, 3169 CrossRef CAS; (c) E. Bisz, A. Piontek, B. Dziuk, R. Szostak and M. Szostak, J. Org. Chem., 2018, 83, 3159 CrossRef CAS; (d) K. T. Barrett, A. J Metrano, P. R. Rablen and S. J. Miller, Nature, 2014, 509, 71 CrossRef CAS; (e) S. R. LaPlante, P. J. Edwards, L. D. Fader, A. Jakalian and O. Hucke, ChemMedChem, 2011, 6, 505 CrossRef CAS; (f) J. Clayden, Chem. Commun., 2004, 2, 127 RSC; (g) A. Ahmed, R. A. Bragg, J. Clayden, L. W. Lai, C. McCarthy, J. H. Pink, N. Westlund and S. A. Yasin, Tetrahedron, 1998, 54, 13277 CrossRef CAS.
- (a) M. I. Lapuh, S. Mazeh and T. Besset, ACS Catal., 2020, 10, 12898 CrossRef CAS; (b) R. Costil, A. J. Sterling, F. Duarte and J. Clayden, Angew. Chem., Int. Ed., 2020, 59, 18670 CrossRef CAS; (c) Q.-J. Yao, P.-P. Xie, Y.-J. Wu, Y.-L. Feng, M.-Y. Teng, X. Hong and B.-F. Shi, J. Am. Chem. Soc., 2020, 142, 18266 CrossRef CAS; (d) H. Li, X. Yan, J. Zhang, W. Guo, J. Jiang and J. Wang, Angew. Chem., Int. Ed., 2019, 58, 6732 CrossRef CAS; (e) Q. Dherbassy, J.-P. Djukic, J. Wencel-Delord and F. Colobert, Angew. Chem., Int. Ed., 2018, 57, 4668 CrossRef CAS; (f) Q.-Y. Sun, W.-Y. Ma, K.-F. Yang, J. Cao, Z.-J. Zheng, Z. Xu, Y.-M. Cui and L.-W. Xu, Chem. Commun., 2018, 54, 10706 RSC; (g) S.-X. Li, Y.-N. Ma and S.-D. Yang, Org. Lett., 2017, 19, 1842–1845 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: General reaction conditions, characterization and NMR spectra, full interactive database as a supplementary XLSX (MS Excel) file, zip compressed XYZ files containing atomic coordinates of substrates and CIF files for XRD coordinates. CCDC deposition numbers are 2044698–2044703 for 4-Pd, 8-Pd, 9-Pd, 11-Pd, 44, and 45, respectively. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc00642h |
| This journal is © The Royal Society of Chemistry 2021 |