Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A dynamic picture of the halolactonization reaction through a combination of ab initio metadynamics and experimental investigations†
Ruben
Van Lommel
 ab,
Jonathan
Bock
c,
Constantin G.
Daniliuc
d,
Ulrich
Hennecke
ab,
Jonathan
Bock
c,
Constantin G.
Daniliuc
d,
Ulrich
Hennecke
 *c and
Frank
De Proft
*c and
Frank
De Proft
 *a
*a
aEenheid Algemene Chemie (ALGC), Department of Chemistry, Vrije Universiteit Brussel (VUB), Pleinlaan 2, 1050 Brussels, Belgium. E-mail: fdeprof@vub.be
bMolecular Design and Synthesis, Department of Chemistry, KU Leuven, Celestijnenlaan 200F Leuven Chem&Tech, box 2404, 3001 Leuven, Belgium
cOrganic Chemistry Research Group (ORGC), Department of Chemistry, Department of Bioengineering Sciences, Vrije Universiteit Brussel (VUB), Pleinlaan 2, 1050 Brussels, Belgium. E-mail: Ulrich.Hennecke@vub.be
dInstitute for Organic Chemistry, University of Muenster, Corrensstr. 40, 48149 Münster, Germany
First published on 26th April 2021
Abstract
The halolactonization reaction is one of the most common electrophilic addition reactions to alkenes. The mechanism is generally viewed as a two-step pathway, which involves the formation of an ionic intermediate, in most cases a haliranium ion. Recently, an alternative concerted mechanism was proposed, in which the nucleophile of the reaction played a key role in the rate determining step by forming a pre-polarized complex with the alkene. This pathway was coined the nucleophile-assisted alkene activation (NAAA) mechanism. Metadynamics simulations on a series of model halolactonization reactions were used to obtain the full dynamic trajectory from reactant to product and investigate the explicit role of the halogen source and solvent molecules in the mechanism. The results in this work ratify the occasional preference of a concerted mechanism over the classic two-step transformation under specific reaction conditions. Nevertheless, as the stability of both the generated substrate cation and counter-anion increase, a transition towards the classic two-step mechanism was observed. NCI analyses on the transition states revealed that the activating role of the nucleophile is independent of the formation and stability of the intermediate. Additionally, the dynamic insights obtained from the metadynamics simulations and NCI analyses employed in this work, unveiled the presence of syn-directing noncovalent interactions, such as hydrogen bonding, between the alkenoic acid and the halogen source, which rationalized the experimentally observed diastereoselectivities. Explicit noncovalent interactions between the reactants and a protic solvent or basic additive are able to disrupt these syn-directing noncovalent interactions, affecting the diastereoselective outcome of the reaction.
Introduction
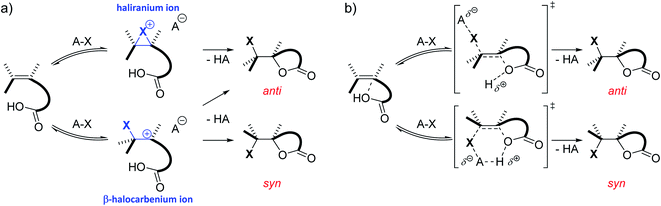
Besides substitution and elimination reactions, the addition of functional groups to unsaturated C–C bonds is one of the key chemical transformations.1,2 A well-known example of such a transformation is the electrophilic halogenation of alkenes. Classically, the mechanism of this reaction is supposed to proceed in two steps. In the first and rate determining step, a cationic intermediate is formed as the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond captures the electrophilic halogen atom. In the second step, a nucleophile attacks this positively charged intermediate, completing the addition reaction.3,4 This nucleophile can stem from either the halogen source, the solvent, an additive or the substrate itself. Depending on the type of substrate and reaction conditions, the cationic intermediate can be classified as the quintessential bridged haliranium or a β-halocarbenium ion. On the other hand, solvation determines whether these ions can be considered as tight ion pairs or solvent-separated ion pairs.5 Both the constitutional preference of the ion as well as its solvation determines the facial approach of the nucleophile with respect to the halogen, i.e. syn-versus anti-addition, and therefore the associated diastereomer of the product (Scheme 1a). If the alkene is prochiral and the halogen electrophile and nucleophilic species that add onto the double bond differ from one another, a total of up to eight isomeric products could be formed. Although the electrophilic halogen addition to alkenes has been studied for over 80 years, its regio- and stereochemical complexity and the control thereof make the transformation a challenging subject for synthetic chemists to this day.6–11
C double bond captures the electrophilic halogen atom. In the second step, a nucleophile attacks this positively charged intermediate, completing the addition reaction.3,4 This nucleophile can stem from either the halogen source, the solvent, an additive or the substrate itself. Depending on the type of substrate and reaction conditions, the cationic intermediate can be classified as the quintessential bridged haliranium or a β-halocarbenium ion. On the other hand, solvation determines whether these ions can be considered as tight ion pairs or solvent-separated ion pairs.5 Both the constitutional preference of the ion as well as its solvation determines the facial approach of the nucleophile with respect to the halogen, i.e. syn-versus anti-addition, and therefore the associated diastereomer of the product (Scheme 1a). If the alkene is prochiral and the halogen electrophile and nucleophilic species that add onto the double bond differ from one another, a total of up to eight isomeric products could be formed. Although the electrophilic halogen addition to alkenes has been studied for over 80 years, its regio- and stereochemical complexity and the control thereof make the transformation a challenging subject for synthetic chemists to this day.6–11
The halolactonization reaction is a class of electrophilic halogen additions which has attracted significant interest over the years.12–16 Herein, a carboxylic acid moiety of an alkenoic acid substrate acts as the nucleophile, resulting in an intramolecular cyclization forming a lactone. Recent research on the halolactonization reaction is particularly focussed on gaining stereoselective control by exploiting asymmetric catalysts.14,17–24 This field flourished greatly in the last decade with several types of highly selective chiral catalysts being developed by different research groups.25–34 Following these reports, enantioselective bromolactonization reactions of alkynes were developed by some of the authors of this work.35,36
Although numerous chiral catalysts have been developed for the enantioselective halolactonization reaction, their mode of action often remains elusive. Only very recently, the mechanistic aspects of the (DHQD)2PHAL catalysed asymmetric chlorolactonization reaction were unveiled by a joint effort by Jackson and Borhan.37 Kinetic studies were performed to establish that the reaction shows a first order dependence on both the catalyst and the halogen source. Furthermore, ROESY NMR spectroscopy and static DFT calculations provided a resting state complex and plausible transition states for the catalytic cycle. The foundation of this research is formed by other reports from both groups, investigating the reaction pathways of the non-catalysed halolactonization as well as other halocyclization reactions by means of a combination of experiments and static DFT calculations.38 In 2016, they proposed a concerted nucleophile-assisted alkene activation (NAAA) mechanism for a non-catalysed halolactonization reaction, supported by kinetic isotope effects and the nucleophile proximity observed during NMR experiments and static DFT calculations (Scheme 1b).39 Already more than 50 years ago, Shilov, among others, observed that the nucleophile could influence the rate and regioselectivity of electrophilic halogen additions, suggesting the classic mechanism was oversimplified in some cases.40–42 With the NAAA mechanism, a plausible alternative is introduced which can explain these early observations. Compared to the classic mechanism, the NAAA mechanism occurs concerted and no ionic intermediate is formed. Additionally, the nucleophile plays a vital role in the rate determining step of the reaction as it counter-intuitively forms a pre-polarized complex with the electron rich unsaturated bond. This complexation presumably activates the double bond by raising its HOMO energy level, enabling the electrophilic attack.
The elucidation of a reaction mechanism does not only improve the fundamental understanding of chemical transformations, it also aids in future catalyst design.43,44 State-of-the-art research, often uses an integrated computational and experimental approach to gain such knowledge, as exemplified by the collaborative works of Jackson and Borhan.37–39 On the computational side, static DFT calculations are routinely used, due to the availability of several user friendly software, limited hardware requirements and the extensive development of this approach.45–47 Most static DFT calculations simplify solvation effects by implicit solvation models, negating the possibility of observing explicit interactions between the solvent and reactants. In the past decade, researchers are paying more attention to previously overlooked solvent effects, by including explicit microsolvated clusters and developing new methods that maintain computational tractability at the DFT level of theory when adding explicit solvation molecules to the computed system.48–50 Notwithstanding that static DFT calculations provide valuable information concerning chemical reactions, they only provide knowledge limited to the stationary points of the potential energy surface. In this regard, ab initio molecular dynamics simulations has proven to be a valuable tool to study the full dynamical aspects of a chemical reaction, explicitly including all molecular entities that are present during the transformation.51–54 Recently, we have shown the usefulness of first-principles metadynamics (MtD) simulations to study the mechanisms of the electrophilic aromatic sulfonation and chlorination, with a focus on the formation of ionic intermediates during the reaction.55,56 In this work, a similar approach will be used to revisit the mechanism of the non-catalysed halolactonization. Emphasis will be put on the formation of a possible ionic intermediate, which differentiates the NAAA mechanism from the classic two-step mechanism. Furthermore, bond length and noncovalent interaction (NCI) analyses will reveal the specific role of the nucleophile and possible noncovalent interactions that might affect the diastereoselectivity of the reaction. Finally, the influence of the type of halogen source (chlorolactonization and bromolactonization), basic additives and the solvent will be investigated. The results of the MtD simulations will be compared to experimental observations made on the halolactonization reactions of the model substrates. In essence, we aim for this study to provide a better dynamic understanding of the prominent halolactonization reaction.
Results and discussion
Experimental results
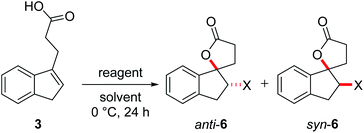
One parameter in halolactonization reactions that should be significantly influenced by the mechanism is the diastereoselectivity of the addition. On the one hand, if a haliranium ion is formed, its opening by backside attack leads to exclusive formation of the anti-diastereomer. Formation of the syn-product, on the other hand, can be explained either by reaction via an open-chain β-halocarbenium ion or, according to the results of Jackson and Borhan, by a concerted reaction pathway involving NAAA. Therefore, we have chosen to investigate the diastereoselective outcome of the reaction, by carrying out an extensive set of selected halolactonization reactions (detailed results of the full experimental analysis can be found in the ESI†). The substrates of choice are derived from aryl-substituted pent-4-enoic acid, which undergo clean 5-exo cyclization (Scheme 2). 4-Phenyl-pent-4-enoic acid 1a is a common substrate used in mechanistic studies and novel asymmetric halolactonization methods. To observe the diastereoselectivity of the reaction, a methyl group was introduced in the 5-position. This 4-phenyl-hex-4-enoic acid 1b can be synthesized with exclusive (E)-geometry of the alkene following a novel, high yielding synthetic route (Scheme 1). Furthermore, cyclic alkenoic acids 2 and 3 were chosen as previous investigations have shown that these substrates provide unusually high amounts of syn-products in electrophilic halogenation reactions.9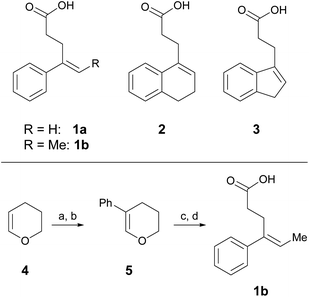 | ||
| Scheme 2 Alkenoic acids used as model starting materials. Synthesis of 1b: (a) Br2, pyridine, 45%; (b) Pd2dba3, SPhos, PhB(OH)2, K2CO3, 70%; (c) NiCl2, IPr·HCl, MeMgBr, 86%; (d) TEMPO, PIDA, 60%. | ||
Initial investigations quickly revealed that diastereoselectivity in the halolactonization of 1b, 2 and 3 was indeed sensitive to reaction conditions and the halolactonization of 3 showed in general the highest amount of syn-products. Therefore, 3 was chosen as the initial model substrate.
The halolactonization of 3 was studied at 0 °C in CH2Cl2 using different, electrophilic halogenating agents. 1,3-Dichloro-5,5-dimethylhydantoin (DCDMH) induced efficient 5-exo cyclization to provide chlorolactones anti-6a and syn-6a in good yield (69%) and with low diastereoselectivity (d.r. 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40; Table 1, entry 2). The identity of the diastereomers was confirmed by X-ray structure analysis of the isolated products (Fig. 1).† Subsequent experiments showed that the diastereoselectivity was strongly dependent on the electrophilic halogenating agent and the halogen used. N-Bromosuccinimide (NBS) led to the bromolactones anti-6b and syn-6b in moderate yield and a slightly higher diastereoselectivity (71
40; Table 1, entry 2). The identity of the diastereomers was confirmed by X-ray structure analysis of the isolated products (Fig. 1).† Subsequent experiments showed that the diastereoselectivity was strongly dependent on the electrophilic halogenating agent and the halogen used. N-Bromosuccinimide (NBS) led to the bromolactones anti-6b and syn-6b in moderate yield and a slightly higher diastereoselectivity (71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 d.r.; entry 3). Changing the relative amount of NBS with respect to the substrate 3 had a slight effect on the diastereoselectivity, with an increased formation of anti-6b when the relative amount of NBS increases (Table 1, entry 4 and 5). The more reactive 1,3-dibromo-5,5-dimethylhydantoin (DBDMH) provided a higher yield, but basically the same diastereoselectivity (d.r. 69
29 d.r.; entry 3). Changing the relative amount of NBS with respect to the substrate 3 had a slight effect on the diastereoselectivity, with an increased formation of anti-6b when the relative amount of NBS increases (Table 1, entry 4 and 5). The more reactive 1,3-dibromo-5,5-dimethylhydantoin (DBDMH) provided a higher yield, but basically the same diastereoselectivity (d.r. 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31, entry 6). A significant change in selectivity was observed when a reagent not based on a N-haloamide core was used. 2,4,4,6-Tetrabromo-2,5-cyclohexadienone (TBCO) induced bromolactonization in excellent yield (98%) and with very high diastereoselectivity (d.r. 97
31, entry 6). A significant change in selectivity was observed when a reagent not based on a N-haloamide core was used. 2,4,4,6-Tetrabromo-2,5-cyclohexadienone (TBCO) induced bromolactonization in excellent yield (98%) and with very high diastereoselectivity (d.r. 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, entry 7). A very high diastereoselectivity was also observed when an electrophilic iodinating agent such as N-iodosuccinimide (NIS) was used, leading to the formation of almost pure anti-6c (95%, d.r. 97
3, entry 7). A very high diastereoselectivity was also observed when an electrophilic iodinating agent such as N-iodosuccinimide (NIS) was used, leading to the formation of almost pure anti-6c (95%, d.r. 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, entry 8). For comparison, also an electrophilic fluorinating agent, N-fluorobenzenesulfonimide (NFSI) was used. Fluorine cannot form fluoriranium ions, excluding a reaction path involving such an ion.57–60 NFSI proved to be much less reactive and the reaction could only be observed at RT in MeCN.61,62 Nevertheless, fluorolactonization proceed under these conditions in acceptable yield (62%) and with decent diastereoselectivity (d.r. 79
3, entry 8). For comparison, also an electrophilic fluorinating agent, N-fluorobenzenesulfonimide (NFSI) was used. Fluorine cannot form fluoriranium ions, excluding a reaction path involving such an ion.57–60 NFSI proved to be much less reactive and the reaction could only be observed at RT in MeCN.61,62 Nevertheless, fluorolactonization proceed under these conditions in acceptable yield (62%) and with decent diastereoselectivity (d.r. 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21, entry 1).
21, entry 1).
| Entry | Halogen source | Solvent | d.r.b (anti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) syn) syn) |
Yieldc (%) |
|---|---|---|---|---|
| a Reaction conditions: 3 (1.0 equiv.), halogen source (1.2 equiv.), in CH2Cl2 at 0 °C for 24 h. b Determined by 1H-NMR of the crude reaction mixture. c Determined by 1H-NMR of the crude reaction mixture using mesitylene as internal standard. d Reaction at RT. e Reaction with 1.0 equiv. quinuclidine added. | ||||
| 1 | NFSI | MeCN | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 21 |
62 |
| 2 | DCDMH | CH2Cl2 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
6a, 69 |
| 3 | NBS | CH2Cl2 | 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 29 |
6b, 49 |
| 4 | NBS (0.5) | CH2Cl2 | 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 34 |
6b, 40 |
| 5 | NBS (2.0) | CH2Cl2 | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 25 |
6b, 75 |
| 6 | DBDMH | CH2Cl2 | 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31 31 |
6b, 99 |
| 7 | TBCO | CH2Cl2 | 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
6b, 98 |
| 8 | NIS | CH2Cl2 | 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
6c, 96 |
| 9 | NBS | MeOH | 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
6b, 99 |
| 10 | DCDMH | MeOH | 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
6a, 99 |
| 11 | NBS | CH2Cl2 | 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
6b, 99 |
| 12 | DCDMH | CH2Cl2 | 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
6a, 99 |
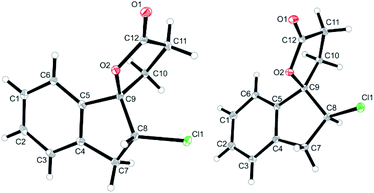 | ||
| Fig. 1 Solid state structures of anti-6a (left) and syn-6a (right) as obtained from X-ray crystallography (see ESI† for details, thermal ellipsoids are shown with 30% probability). | ||
While halolactonization of 3 using electrophilic chlorinating as well as brominating agents in CH2Cl2 provided mixtures of product diastereomers only slightly favouring the anti-addition products, a remarkably different behaviour was observed in MeOH. For DCDMH as well as NBS, almost fully selective formation of the anti-addition products anti-6a or anti-6b in excellent yields was observed (entries 9 and 10). The syn-addition products were only formed in traces. A similar switch of selectivity could also be induced in CH2Cl2, if one equivalent of quinuclidine was added to the reaction (it is used as a model for cinchona alkaloid catalysts in asymmetric halolactonizations). This sped up the reactions and led to the almost exclusive formation of anti-addition products when using DCDMH or NBS as reagent, respectively.
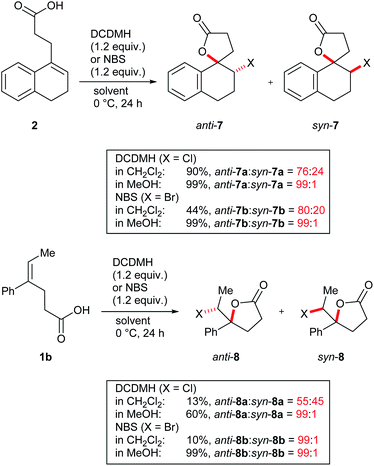
While the switch from a moderately diastereoselective halolactonization in CH2Cl2 to a fully selective reaction in MeOH was most pronounced for 3, similar observations were also made for model compounds 1b and 2 (Scheme 3 and ESI†). Cyclic alkenoic acid 2 underwent chlorolactonization using DCDMH in CH2Cl2 in good yield and with moderate diastereoselectivity (d.r. 76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24), while the reaction in MeOH was again highly selective towards anti-addition (d.r. 99
24), while the reaction in MeOH was again highly selective towards anti-addition (d.r. 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Compared to the cyclic alkenes 2 and 3, open-chain alkenoic acid 1b was less reactive and chlorolactonization using DCDMH in CH2Cl2 was slow and not diastereoselective (d.r. 55
1). Compared to the cyclic alkenes 2 and 3, open-chain alkenoic acid 1b was less reactive and chlorolactonization using DCDMH in CH2Cl2 was slow and not diastereoselective (d.r. 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45). In MeOH reactivity was much higher and the product anti-8a was obtained in 60% yield and excellent diastereoselectivity.
45). In MeOH reactivity was much higher and the product anti-8a was obtained in 60% yield and excellent diastereoselectivity.
Overall, two clear trends could be observed: while reactions in CH2Cl2 showed only low to moderate diastereoselectivities, reactions in MeOH were in all cases highly selective for the anti-addition. A similar effect was observed when quinuclidine was added as a base to the reaction. Furthermore, diastereoselectivities increased when going from smaller chlorine to the larger iodine electrophiles in line with the observation that longer C–X bonds lead to more stable cyclic (“bridging”) haliranium ions.63–65
Computational results: the halogen source matters
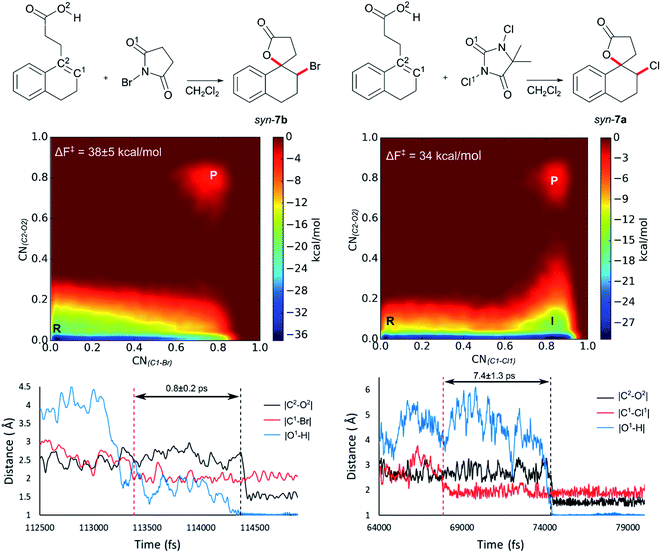
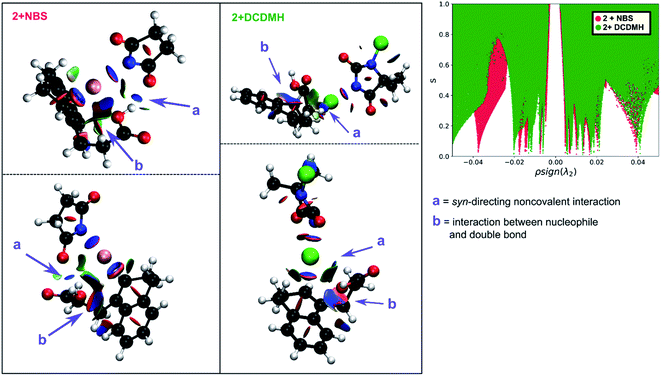
Initially 2 was chosen as a model substrate for the calculations as the experimental results indicated an intermediate behaviour with respect to the diastereoselectivity. To obtain a plausible mechanistic pathway for this reaction, ab initio metadynamics simulations were performed with a simulation box including 2, a halogenating agent, either NBS or DCDMH, and a number of CH2Cl2 molecules to match the experimental conditions and account for explicit solvation. The reaction coordinate was described by collective variables expressed as coordination numbers through which the reaction was driven. A more in-depth explanation of these collective variables can be found in the computational methods section. All simulations in this study were performed at the DFT level using the BLYP-D3 functional and the DZVP-MOLOPT-GTH plane wave basis set with the grid level cut-off set at 320 Ry (for detailed settings of the MtD simulations see ESI†).66,67 Surprisingly, the MtD simulations of 2 in CH2Cl2 with NBS as brominating source, always resulted in the formation of syn-7b, independent of the starting topology of the simulation. The full trajectory of the reaction shows that the syn-mechanism has an asynchronous concerted character (MV_S1). Before reaction takes place, an intermolecular hydrogen bond is present between the carboxylic acid moiety of 2 and an amide carbonyl group of NBS, which directs the syn-addition. Following this pre-reactive complexation, the electrophilic bromine is captured by the double bond. This event is rapidly followed by the simultaneous deprotonation of the carboxylic acid and intramolecular lactone formation. From the free energy surface (FES), only the reactant and product phase are observable minima, suggesting no intermediate is formed during the reaction (Fig. 2). Furthermore, through bond length analyses it is possible to determine the time between the initial electrophilic addition and nucleophilic ring closure, essentially quantifying the lifetime of the ionic intermediate phase. For the syn-selective reaction of 2 with NBS in CH2Cl2, a relative short average lifetime of 0.8 ± 0.2 ps is observed. Both the FES and bond length analyses indicate the concerted asynchronous character of the mechanism. Moreover, prior to bromine addition, the nucleophile (O2) and the double bond (C2–C1) are in proximity to each other as a distance of approximately 2.5 Å between them is observed. The latter could be interpreted as the nucleophile activating the double bond by forming a pre-polarized complex. Both the concerted asynchronous character of the reaction and the proximity of the nucleophile to the double bond, point towards the NAAA mechanism.By investigating the corresponding DCDMH chlorolactonization of 2 in CH2Cl2, we aimed to elucidate the effect of the halogenating source on the reaction mechanism. Our experimental results indicated that the preference towards the anti-product increases together with the size of the halogen for the halolactonization reaction of 3, following the trend Cl+ (DCDMH) < Br+ (NBS) < I+ (NIS) (Table 1). Notable, a similar trend was previously observed by Jackson and Borhan for the halolactonization of 1a.39 Their initial reasoning for this trend, was that for larger halogen atoms, the mechanism giving rise to the syn-product would be characterized by an increased steric repulsion, favouring the anti-product. To investigate whether the enhanced preference for the anti-product could be attributed to the size of the halogen atom, noncovalent interaction (NCI) analyses on the transition states for the syn-halolactonization reaction of 2 with NBS and DCDMH were performed. Latter technique allows to identify the noncovalent interactions in a molecular system by means of the relationship between the reduced density gradient (s) and the product of the electron density (ρ) and the sign of the second eigenvalue of the electron density Hessian matrix (sign![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ2).68 Peaks appearing in the corresponding 2D-plot at low absolute values of ρsign(λ2) are caused by noncovalent interactions. If the peak occurs at positive values of ρsign(λ2), the interaction is repulsive. If the peak occurs at negative values the interaction is attractive. Additionally, the interactions can be visualized by plotting an isosurface of s, with an RGB colour scale indicating if the interaction is repulsive (red), weakly attractive (green) or strongly attractive (blue).
λ2).68 Peaks appearing in the corresponding 2D-plot at low absolute values of ρsign(λ2) are caused by noncovalent interactions. If the peak occurs at positive values of ρsign(λ2), the interaction is repulsive. If the peak occurs at negative values the interaction is attractive. Additionally, the interactions can be visualized by plotting an isosurface of s, with an RGB colour scale indicating if the interaction is repulsive (red), weakly attractive (green) or strongly attractive (blue).
The analysis reveals that both transition states are characterized by similar repulsive interactions as peaks in the positive region of the 2D-plot of s against ρsign(λ2) overlap entirely (Fig. 3). This excludes steric repulsion induced by a larger halogen atom to be the reason behind the change in diastereoselectivity. However, when looking at the negative region of the 2D-plot, i.e. attractive interactions, significant differences are observable. Indeed, upon closer inspection of the 3D-NCI isosurfaces, it is clear that for the NBS syn-bromolactonization of 2, a syn-directing hydrogen bond between both reactants is present (highlighted in Fig. 3 by the purple arrow “a”). In contrast, a similar hydrogen bond is absent for the DCDMH syn-chlorolactonization of 2. In the latter case, however, an attractive noncovalent interaction between the α-hydrogen of the carboxylic acid and the incoming halogen is present, which is able to fulfil a similar role as the hydrogen bond in steering the syn-addition of the nucleophile (again this interaction is highlighted in Fig. 3 by the purple arrow “a”). These findings are a first indication that a fundamental change in the reaction mechanism occurs when altering the halogen source from NBS to DCDMH. Also, when comparing the free energy surfaces and bond length analyses of the above-mentioned reactions, clear differences are observable (Fig. 2). For the DCDMH chlorolactonization of 2, the presence of an intermediate phase (I) characterized by a high value of CN(C1–Cl1) and a low value of CN(C2–O2) is observable. From these values it is discerned that this structure corresponds to a classic ionic intermediate. Indeed, also from bond length analyses one can imply the existence of a more stable intermediate, as the lifetime of this phase (7.4 ± 1.3 ps) has increased considerably with respect to the NBS syn-bromolactonization of 2 (0.8 ± 0.2 ps).‡ We suspect this trend to be explained by the larger inherent stability of the dechlorinated counter-anion of DCDMH (MCDMH−) compared to the corresponding debrominated succinimide anion of NBS (succ−) (this statement is supported by static heterolytic BDE calculations, see ESI†). Due to the clear formation of an ionic intermediate during the reaction, it is concluded that the DCDMH syn-chlorolactonization of 2 follows a two-step reaction pathway. It must be mentioned, however, that bond length analyses indicated the nucleophile (O2) to be in proximity (∼3.0 Å) of the double bond before the halogen addition occurs. Also, from the 3D-NCI isosurface, a noncovalent attractive interacting area can be detected between the nucleophile (O2) and the double bond in the transition state (this interaction is highlighted in Fig. 3 by the purple arrow “b”). As such, the concerted nature of the NAAA reaction mechanism is not a prerequisite for the pre-activation of the double bond by the nucleophilic species.
The mechanistic disparities between the NBS and DCDMH syn-halolactonization of 2 showcase that the type of halogen source affects the mode of action. To determine whether the reaction pathway occurs through a two-step mechanism or the concerted NAAA mechanism, the stability of all ionic species that are generated during the course of the reaction need to be considered. This includes the cationic β-halocarbenium ion and the corresponding counter-anion generated from the halogen source. When the stability of both ionic species increases, a transition from the concerted NAAA mechanism towards a two-step mechanism occurs. On the other hand, syn-directing noncovalent interactions between the alkenoic acid and the halogen source rationalize the substantial formation of syn-product for the bromo- and chlorolactonization of 2. In the former case, a syn-directing hydrogen bond is present between the carboxylic acid and amide group of NBS. One can deduct that if a halogenating source were to be used where such interaction would be missing, an increased diastereoselectivity towards the anti-product could be observed. And indeed, when TBCO (a brominating agent which has no ortho carbonyl group to facilitate hydrogen bond formation) was used during the halolactonization of 3 (Table 1, entry 7), the amount of anti-diastereomer that is formed increases significantly compared to other brominating sources with an ortho-oriented carbonyl group (NBS, DBDMH).
In addition to 2, the bromo- and chlorolactonization reaction of 1a was explored by MtD simulations in order to study possible effects of the substrate on the mechanism. Again, for the NBS bromolactonization, the syn-mechanism was readily observed, guided by an intermolecular hydrogen bond between NBS and the substrate. Further analysis of the trajectory, bond lengths and free energy surface reveals other similar characteristics compared to the NBS syn-bromolactonization reaction of 2 (see ESI†). Indeed, no distinct intermediate phase is observed from the free energy surface and the corresponding average lifetime thereof is relatively small, being 0.9 ± 0.3 ps. Moreover, the carboxylic acid oxygen (O2), which acts as the nucleophile in the reaction, is near the alkene (∼3.0 Å) before electrophilic addition of the halogen to the double bond takes place. This indicates the activation of the double bond through complexation. With these features in mind, the concerted NAAA mechanism is suggested as the reaction pathway for the NBS syn-bromolactonization reaction of 1a in CH2Cl2. When the corresponding DCDMH chlorolactonization of 1a is studied, a similar pathway is obtained (see ESI†). An inter-molecular hydrogen bond between the halogen source and the substrate directs the syn-addition, the nucleophile is in proximity of the double bond and thus is able to activate the unsaturated bond by forming a pre-polarized complex. And finally, no distinct ionic intermediates are observed in the free energy surface and its limited lifetime (1.0 ± 0.5 ps). These observations indicate the DCDMH syn-chlorolactonization of 1a to follow the concerted NAAA mechanism. Notably, the same reaction with 2 occurs through a two-step mechanism. This highlights that both the stability of the cation generated from the substrate and the counter-anion from the halogen source need to be considered when investigating the mechanism of the halolactonization reaction.
Basic additives enable full anti-diastereoselectivity
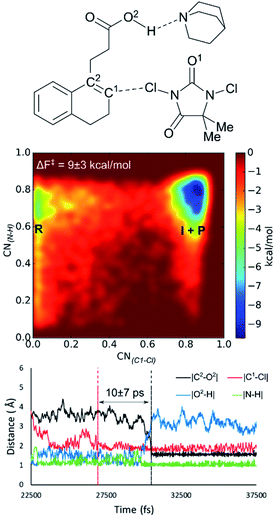
In previous sections only the syn-halolactonization mechanism was discussed as the anti-mechanism could not be retrieved from the MtD simulations. Not even by setting various geometrical constraints on the reactive system during the MtD simulation. Nevertheless, the experimental results showed a clear preference towards formation of the anti-diastereoisomer for all reactions, independent of the halogen source and substrate. Moreover, this effect is increased when quinuclidine is added to the reaction mixture as a base. Besides the diastereoselectivity towards the anti-product, the halolactonization shows a significant increase in yield when quinuclidine is added (Table 1, entry 12).When including a quinuclidine molecule in the system for the DCDMH halolactonization of 2 in CH2Cl2, the anti-mechanism was exclusively observed from the MtD simulations, coinciding with the experimental observed increased anti-diastereoselectivity (Fig. 4). Furthermore, the activation barrier is reduced significantly when quinuclidine is included in the simulation box (ΔF‡ = 9 kcal mol−1). The latter is consistent with the experimentally observed increased yield. Before the reaction takes place, deprotonation of the carboxylic acid by the quinuclidine base occurs. The resulting protonated quinuclidine remains connected to the carboxylate by means of hydrogen bonding in a pre-reactive complex, preventing the formation of any syn-directing interaction with the halogen source. This explains the diastereoselectivity of the reaction towards the anti-product. In the next step, halogen addition occurs without pre-polarization of the double bond by the nucleophile as the distance between the nucleophile and the double bond prior to halogen addition is relatively large (∼4 Å). Furthermore, a long-lived intermediate phase is formed (10 ± 7 ps), likely due to the inherent stability of MCDMH− and the cationic substrate-quinuclidine complex. In the final step, lactonization occurs which is accompanied by the simultaneous breaking of the substrate-quinuclidine hydrogen bond. These results suggest that when quinuclidine is added as a base to the DCDMH halolactonization reaction of 2, a two-step mechanism is followed, which results exclusively in the anti-product. The experimentally observed diastereoselectivity is explained by the absence of a syn-directing noncovalent interaction between the nucleophile and the halogen source. Summarized, molecules which are able to interact with the carboxylic acid group of the alkenoic acid through hydrogen bonding, facilitate formation of the anti-product by competing with syn-directing noncovalent interactions.
With these new insights, we again set out to retrieve a plausible mechanism for the non-catalysed anti-halolactonization. Inspired by Jackson and Borhan, who could only localize such a transition state by explicitly adding a second halogen source molecule to their static calculations, we were also able to suggest a plausible transition state for the anti-halolactonization of 2 with NBS and DCDMH using static DFT calculations (see ESI†). As such we thought it might be necessary to include two pairs of reactants in the simulation box to observe the dynamics of the anti-mechanism. Unfortunately, this approach did not yield the anti-addition, not when a second halogen source molecule was added to the system nor a second substrate molecule. Notably, in the latter case dimerization of the two substrate molecules occurred instantaneous through hydrogen bonding of their carboxylic acid groups. When a succinimide anion was included in the simulation as a base for the NBS bromolactonization of 2, a mechanism resulting in the anti-product was observable, where the succinimide base fulfils a similar role as the quinuclidine in the anti-halolactonization mechanism described above (see ESI†). Seemingly basic molecules that can disrupt the syn-directing interactions and deprotonate the substrate are necessary to retrieve the anti-addition from the MtD simulations. However, it remains ambiguous to us which molecule fulfils this role in the non-catalysed anti-halolactonization. It might be possible that there are molecules missing from the system which are crucial for the anti-mechanism and thus prevent us from observing it.
Protic solvation effects
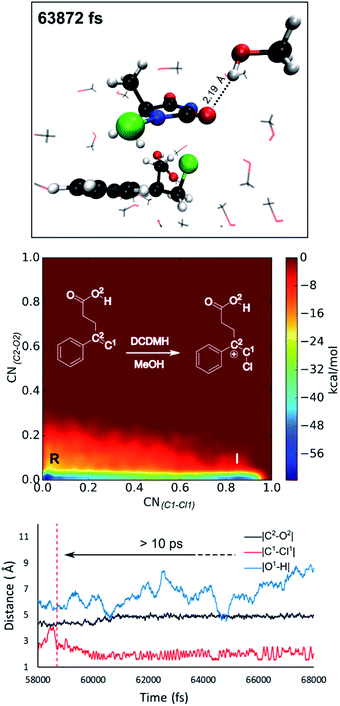
Reflecting on the afore mentioned findings, we conclude that noncovalent interactions between the reactants play an important role during the halolactonization reaction. For example, hydrogen bonding between the nucleophile and the halogen source directs the syn-addition. If the reaction is performed in an aprotic medium such as CH2Cl2, the solvent will most likely not significantly influence these noncovalent interactions. Indeed, in all MtD simulations where CH2Cl2 was included as a solvent, no explicit interactions between the solvent and reactants were observed. Results also indicate that the diastereoselectivity towards the anti-product increases when these syn-directing noncovalent interactions are disrupted. Naturally, the question arises whether a solvent can be used to accomplish this. As the experimental diastereoselectivities of the model reactions in MeOH all showed almost exclusive anti-product formation as well as an increase in yield compared to when the reaction is performed in CH2Cl2, one would assume that this were to be the case. Therefore, in this paragraph, MtD simulations will be used to investigate how a protic solvent (MeOH) affects the diastereoselective outcome and mode of action of the halolactonization reaction.From an MtD simulation of the DCDMH chlorolactonization of 1a in MeOH, the clear formation of a halonium intermediate is observed. This conclusion is based on the free energy surface as well as the extended lifetime of the intermediate phase that can be determined from bond length analyses (>10 ps) (Fig. 5). Notably, the nucleophile is not in proximity of the double bond before halogen addition takes place (∼4.5 Å) and no syn-directing intermolecular interactions between the nucleophile and halogen source are observed during the transition towards the halonium intermediate. Therefore, it is concluded that the DCDMH chlorolactonization of 1a in MeOH follows the classic mechanism without pre-activation of the double bond by the nucleophile or any syn-directing interactions. Note that when the simulations were carried out in CH2Cl2, the concerted NAAA mechanism was favoured. When scrutinizing the explicit role of the protic solvent on the reaction mechanism, hydrogen bonds between MeOH and the acid functionality of the substrate are observable. Seemingly the solvent competes with and disrupts any syn-directing interactions such as hydrogen bonding between the substrate and the halogen source. Similar to when the reaction is performed in presence of a quinuclidine base, the absence of syn-directing interactions can rationalize the experimental diastereoselectivity towards the anti-product. Moreover, after halogen addition has taken place, a stable hydrogen bond is observed between a MeOH molecule and the dechlorinated MCDMH− molecule, which sustains the anionic species (Fig. 5). This stabilizing effect explains the considerable lifetime of the ionic intermediate phase and the preference towards the two-step mechanism.
Conclusion
In this work, an elaborate experimental and computational investigation was performed on the halolactonization of alkenoic acids. By carrying out a set of halolactonization reactions and performing the corresponding ab initio metadynamics simulations, we aimed to elucidate the diastereoselectivity and mechanistic aspects of this chemical transformation. Focus was put on two viable reaction pathways, being the textbook two-step mechanism and a recently proposed concerted nucleophile-assisted alkene addition mechanism. Both mechanisms differ from one another by the respective presence or absence of an ionic intermediate phase. Our theoretical results reveal that a concerted mechanism is preferred in some cases. However as the stability of both the generated β-halocarbenium intermediate and halogen source counter-anion increase, a transition towards the classic two-step mechanism is observed. Notably, via NCI analysis it was revealed that the nucleophile can activate the double bond by forming a pre-polarized complex during the concerted as well as the classic two-step mechanism, meaning that the activating role of the nucleophile is not determined by the probability that an intermediate phase is formed. Reactions carried out in this study, resulted in the formation of the syn- and anti-diastereomer product in varying ratios. By scrutinizing the results obtained from the ab initio simulations, syn-directing noncovalent interactions such as hydrogen bonding between the nucleophile and the halogen source are revealed, which control the formation of the syn-product. As this mechanism is in competition with a pathway that generates the anti-product, disruption of these syn-directing interactions by a basic additive or a protic solvent such as MeOH, results in a strongly increased diastereoselectivity towards the anti-product. With that, this study showcases, that through careful selection of reagents and/or reaction conditions, the diastereoselectivity of the halolactonization reaction can be regulated. Moreover, when the syn-directing interactions are negated, and additionally the ionic intermediate phase has a significant lifetime, the activating role of the nucleophile gets diminished. This study affirms the importance of taking dynamic solvent effects explicitly into account when studying a mechanism where ionic intermediates are conceivably formed. We aim for these new insights to assist the field in developing new strategies to control the stereoselective outcome of the halolactonization reaction.Computational methods
Metadynamics
To obtain the dynamic trajectories of the chemical reactions studied in this work, metadynamics (MtD) simulations were performed with the CP2K code (version 6.1) using the Quickstep implementation.69,70 This method improves the sampling efficiency of conventional ab initio molecular dynamics (AIMD) by artificially adding Gaussian potentials along a set of carefully selected collective variables (CVs) that adequately describe the reaction coordinate. In this manner, the potential energy surface is flattened and uniform sampling of the rare event, i.e. chemical reaction, is achieved.71,72All AIMD and MtD simulations were performed at the DFT level using the BLYP functional and the DZVP-MOLOPT-GTH plane wave basis set with the grid level cut-off set at 320 Ry.66,67 For bromine atoms the short range version of the basis set (DZVP-MOLOPT-SR-GTH) was used. Additionally, Grimme's D3 dispersion corrections were used to take into account long range dispersion interactions.73 The dispersion-corrected GGA exchange correlation functional BLYP-D3 has previously shown to adequately describe the dynamical aspects of both concerted and multistep elementary organic reactions.55,74 Simulations were performed in the NVT ensemble where the temperature was set by the CSVR thermostat at 273 K and a timeconstant of 1 fs, matching the experimental reaction conditions. The reactants and solvent molecules were placed in a periodic cubic box with a box edge size of 15 Å and sufficient solvent molecules to match the experimental density of the solvent for CH2Cl2 (1.33 g cm−3) and MeOH (0.792 g cm−3) using the Packmol software.75 Specifications concerning the simulation box can be found in the ESI.†
Each system underwent an equilibration phase before initializing the MtD simulation by running a short AIMD simulation (5000 steps, with a timestep of 1 fs rendering a total simulation time of 5 ps), allowing the system to relax. Following this, Gaussian potentials with a height of 2.0 kJ mol−1 and a width of 0.02 were added every 25 steps along the specified collective variables for the first 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps of the simulation. After this, the hill height was reduced to 1.0 kJ mol−1 to avoid oversampling. If during the simulation the chemical reaction takes place in the first 20
000 steps of the simulation. After this, the hill height was reduced to 1.0 kJ mol−1 to avoid oversampling. If during the simulation the chemical reaction takes place in the first 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, the simulation was repeated with the hill height immediately set to 1.0 kJ mol−1. In all cases the collective variables were defined as coordination numbers (CNs) for which the expression is provided in eqn (1). In this expression rij defines the distance between atom i and j and r0 is a predefined value.
000 steps, the simulation was repeated with the hill height immediately set to 1.0 kJ mol−1. In all cases the collective variables were defined as coordination numbers (CNs) for which the expression is provided in eqn (1). In this expression rij defines the distance between atom i and j and r0 is a predefined value.
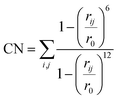 | (1) |
To limit the sampling region, half harmonic biased potentials were added for some simulations and the mass of all protons was set to the mass of tritium to reduce hydrogen vibration frequencies that cause the simulation to be unstable at the 1 fs time step. Detailed information concerning the collective variables and bias potentials of each reactive system and an example input file is provided in the ESI.† In general, MtD simulations sample many forward and reverse rare events to ensure both reactant and product wells are filled and convergence of the simulation is reached. For chemical reactions, however, the reverse step is often unobtainable. For this reason systems for which the activation barrier was determined underwent multiple MtD simulations of the single forward reaction step and results were averaged over these simulations to ensure statistical relevancy. Each simulation ran an excess of 5 ps after the chemical reaction has taken place from which free energy surfaces were constructed.
Analysis of simulations
From the canonical ensemble partition function, the Helmholtz free energy of activation, ΔF‡ was computed by eqn (2). Here, kb denotes the Boltzmann constant, T the temperature, PTS the population at the transition state and Psum the total probability of the reactant state.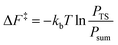 | (2) |
The most accurate transition state was determined as the structure right before a large jump of the collective variable which describes the addition of the electrophilic halogen to the double bond is observed. To determine the lifetime of the charged ionic intermediate, the simulation time between the formation of the carbon–halogen bond and nucleophilic attack was established by tracking the appropriate bond lengths of the reactive system.
Noncovalent interaction indices
When plotting the reduced density gradient (s) against the electron density ρ, noncovalent interaction peaks appear in the plot at low density values (eqn (3)). Furthermore, attractive and repulsive interactions can be discerned from one another by the second eigenvalue of the electron density Hessian matrix (λ2). These aspects form the basis of a noncovalent interaction indices (NCI) analysis.68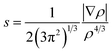 | (3) |
NCI analyses were performed on the transition state structures obtained from the MtD simulations as previously explained. These analyses allowed to elucidate the role of various noncovalent interactions on the mechanistic preference of the reaction. Electron densities were obtained by performing single point energy calculations on the MtD transition state structure at the DFT level of theory using the B3LYP-D3 functional and the double-ζ 6-31G(d) basis set with the Gaussian quantum chemistry package version 16 revision B.01.76 One of the advantages of using the NCI analysis is the exceptional robustness of the technique with respect to the method and basis set used to generate the electron density.66,77,78 During the analysis, explicit solvent molecules which are present during the MtD simulation, were left out to focus on the noncovalent interactions between the reactants and simplify the interpretation of the results. The NCIPLOT program version 3.2.3 was used to perform the analyses and visualization of isosurfaces of the reduced density gradient s was accomplished by the VMD software version 1.9.3.79,80
Author contributions
R. V. L., J. B., U. H. and F. D. P. helped conceptualize and write this research. R. V. L. planned, carried out and analysed the theoretical simulations. J. B. planned, carried out and analysed the experiments in this work. C. G. D. provided the necessary resources and carried out X-ray experiments and analysis. U. H. and F. D. P. supervised the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Tier2 computational resources and services were provided by the Shared ICT Services Centre funded by the Vrije Universiteit Brussel, the Flemish Supercomputer Center (VSC) and FWO. Tier1 computational resources and services that were used in this work were provided by the VSC (Flemish Supercomputer Center), funded by the Research Foundation-Flanders (FWO) and the Flemish Government-department EWI. R. V. L. thanks the FWO for the PhD fellowship received (1185221N). F. D. P. acknowledges the Francqui foundation for a position as “Francqui research professor”.Notes and references
- T. G. Traylor, Acc. Chem. Res., 1969, 2, 152–160 CrossRef CAS.
- J. Bock, S. Guria, V. Wedek and U. Hennecke, Chem.–Eur. J., 2021, 27, 4517–4530 CrossRef CAS PubMed.
- I. Roberts and G. E. Kimball, J. Am. Chem. Soc., 1937, 59, 947–948 CrossRef CAS.
- G. A. Olah and J. M. Bollinger, J. Am. Chem. Soc., 1967, 89, 4744–4752 CrossRef CAS.
- K. Yates and R. S. McDonald, J. Org. Chem., 1973, 38, 2465–2478 CrossRef CAS.
- M. Beller, J. Seayad, A. Tillack and H. Jiao, Angew. Chem., Int. Ed., 2004, 43, 3368–3398 CrossRef CAS PubMed.
- S. E. Denmark, W. E. Kuester and M. T. Burk, Angew. Chem., Int. Ed., 2012, 51, 10938–10953 CrossRef CAS PubMed.
- U. Hennecke, Chem.–Asian J., 2012, 7, 456–465 CrossRef CAS PubMed.
- V. Wedek, R. Van Lommel, C. G. Daniliuc, F. DeProft and U. Hennecke, Angew. Chem., Int. Ed., 2019, 58, 9239–9243 CrossRef CAS PubMed.
- W.-j. Chung and C. D. Vanderwal, Angew. Chem., Int. Ed., 2016, 55, 4396–4434 CrossRef CAS PubMed.
- J. Chen and L. Zhou, Synthesis, 2014, 46, 586–595 CrossRef.
- G. Chen and S. Ma, Angew. Chem., Int. Ed. Engl., 2010, 49, 8306–8308 CrossRef CAS PubMed.
- R. Kristianslund, J. E. Tungen and T. V. Hansen, Org. Biomol. Chem., 2019, 17, 3079–3092 RSC.
- K. Murai and H. Fujioka, Heterocycles, 2013, 87, 763–805 CrossRef CAS.
- E. J. Corey, N. M. Weinshenker, T. K. Schaaf and W. Huber, J. Am. Chem. Soc., 1969, 91, 5675–5677 CrossRef CAS PubMed.
- Y. Shi, L. F. Peng and Y. Kishi, J. Org. Chem., 1997, 62, 5666–5667 CrossRef CAS.
- A. N. French, S. Bissmire and T. Wirth, Chem. Soc. Rev., 2004, 33, 354–362 RSC.
- A. Castellanos and S. P. Fletcher, Chem.–Eur. J., 2011, 17, 5766–5776 CrossRef CAS PubMed.
- C. K. Tan, L. Zhou and Y.-Y. Yeung, Synlett, 2011, 2011, 1335–1339 CrossRef.
- J. M. J. Nolsøe and T. V. Hansen, Eur. J. Org. Chem., 2014, 2014, 3051–3065 CrossRef.
- U. Hennecke, C. Rösner, T. Wald, T. Robert and M. Oestreich, in Comprehensive Organic Synthesis II, ed. P. Knochel, Elsevier, Amsterdam, 2nd edn, 2014, pp. 638–691 Search PubMed.
- S. A. Snyde, D. S. Treitler and A. P. Brucks, Aldrichimica Acta, 2011, 44, 27–40 Search PubMed.
- S. Zheng, C. M. Schienebeck, W. Zhang, H.-Y. Wang and W. Tang, Asian J. Org. Chem., 2014, 3, 366–376 CrossRef CAS.
- S. Ranganathan, K. M. Muraleedharan, N. K. Vaish and N. Jayaraman, Tetrahedron, 2004, 60, 5273–5308 CrossRef CAS.
- D. C. Whitehead, R. Yousefi, A. Jaganathan and B. Borhan, J. Am. Chem. Soc., 2010, 132, 3298–3300 CrossRef CAS PubMed.
- G. E. Veitch and E. N. Jacobsen, Angew. Chem., Int. Ed. Engl., 2010, 49, 7332–7335 CrossRef CAS PubMed.
- L. Zhou, C. K. Tan, X. Jiang, F. Chen and Y. Y. Yeung, J. Am. Chem. Soc., 2010, 132, 15474–15476 CrossRef CAS PubMed.
- K. Murai, T. Matsushita, A. Nakamura, S. Fukushima, M. Shimura and H. Fujioka, Angew. Chem., Int. Ed., 2010, 49, 9174–9177 CrossRef CAS PubMed.
- W. Zhang, S. Zheng, N. Liu, J. B. Werness, I. A. Guzei and W. Tang, J. Am. Chem. Soc., 2010, 132, 3664–3665 CrossRef CAS PubMed.
- M. C. Dobish and J. N. Johnston, J. Am. Chem. Soc., 2012, 134, 6068–6071 CrossRef CAS PubMed.
- D. H. Paull, C. Fang, J. R. Donald, A. D. Pansick and S. F. Martin, J. Am. Chem. Soc., 2012, 134, 11128–11131 CrossRef CAS PubMed.
- J. E. Tungen, J. M. J. Nolsøe and T. V. Hansen, Org. Lett., 2012, 14, 5884–5887 CrossRef CAS PubMed.
- K. Ikeuchi, S. Ido, S. Yoshimura, T. Asakawa, M. Inai, Y. Hamashima and T. Kan, Org. Lett., 2012, 14, 6016–6019 CrossRef CAS PubMed.
- T. Arai, N. Sugiyama, H. Masu, S. Kado, S. Yabe and M. Yamanaka, Chem. Commun., 2014, 50, 8287–8290 RSC.
- M. Wilking, C. Mück-Lichtenfeld, C. G. Daniliuc and U. Hennecke, J. Am. Chem. Soc., 2013, 135, 8133–8136 CrossRef CAS PubMed.
- M. Wilking, C. G. Daniliuc and U. Hennecke, Chem.–Eur. J., 2016, 22, 18601–18607 CrossRef CAS PubMed.
- R. Yousefi, A. Sarkar, K. D. Ashtekar, D. C. Whitehead, T. Kakeshpour, D. Holmes, P. Reed, J. E. Jackson and B. Borhan, J. Am. Chem. Soc., 2020, 142, 7179–7189 CrossRef CAS PubMed.
- N. Salehi Marzijarani, R. Yousefi, A. Jaganathan, K. D. Ashtekar, J. E. Jackson and B. Borhan, Chem. Sci., 2018, 9, 2898–2908 RSC.
- K. D. Ashtekar, M. Vetticatt, R. Yousefi, J. E. Jackson and B. Borhan, J. Am. Chem. Soc., 2016, 138, 8114–8119 CrossRef CAS PubMed.
- E. N. Rengevich, E. A. Shilov and S. Vi, Dokl. Akad. Nauk SSSR, 1962, 146, 111–114 CAS.
- D. L. H. Williams, E. Bienvenüe-Goetz and J. E. Dubois, J. Chem. Soc. B, 1969, 517–522 RSC.
- J. T. Doi, G. W. Luehr, D. Del Carmen and B. C. Lippsmeyer, J. Org. Chem., 1989, 54, 2764–2767 CrossRef CAS.
- S. Ahn, M. Hong, M. Sundararajan, D. H. Ess and M.-H. Baik, Chem. Rev., 2019, 119, 6509–6560 CrossRef CAS PubMed.
- A. F. Zahrt, S. V. Athavale and S. E. Denmark, Chem. Rev., 2020, 120, 1620–1689 CrossRef CAS PubMed.
- T. Sperger, I. A. Sanhueza and F. Schoenebeck, Acc. Chem. Res., 2016, 49, 1311–1319 CrossRef CAS PubMed.
- G.-J. Cheng, X. Zhang, L. W. Chung, L. Xu and Y.-D. Wu, J. Am. Chem. Soc., 2015, 137, 1706–1725 CrossRef CAS PubMed.
- S. Kozuch and S. Shaik, Acc. Chem. Soc., 2011, 44, 101–110 CrossRef CAS PubMed.
- R. B. Sunoj and M. Anand, Phys. Chem. Chem. Phys., 2012, 14, 12715–12736 RSC.
- P. Zimmerman, J. Chem. Theory Comput., 2013, 9, 3043–3050 CrossRef CAS PubMed.
- Y. Basdogan and J. A. Keith, Chem. Sci., 2018, 9, 5341–5346 RSC.
- G. Bussi and A. Laio, Nat. Rev. Phys., 2020, 2, 200–212 CrossRef.
- S. Zheng and J. Pfaendtner, Mol. Simul., 2015, 41, 55–72 CrossRef CAS.
- V. A. Roytman and D. A. Singleton, J. Am. Chem. Soc., 2020, 142, 12865–12877 CrossRef CAS PubMed.
- Y. Fu, L. Bernasconi and P. Liu, J. Am. Chem. Soc., 2021, 143, 1577–1589 CrossRef CAS PubMed.
- S. L. C. Moors, X. Deraet, G. Van Assche, P. Geerlings and F. De Proft, Chem. Sci., 2017, 8, 680–688 RSC.
- R. Van Lommel, S. L. C. Moors and F. De Proft, Chem.–Eur. J., 2018, 24, 7044–7050 CrossRef CAS PubMed.
- G. A. Olah, J. M. Bollinger and J. Brinich, J. Am. Chem. Soc., 1968, 90, 2587–2594 CrossRef CAS.
- C. H. Reynolds, J. Am. Chem. Soc., 1992, 114, 8676–8682 CrossRef CAS.
- V. Nguyen, X. Cheng and T. H. Morton, J. Am. Chem. Soc., 1992, 114, 7127–7132 CrossRef.
- R. Damrauer, M. D. Leavell and C. M. Hadad, J. Org. Chem., 1998, 63, 9476–9485 CrossRef CAS.
- M. Okada, Y. Nakamura, H. Horikawa, T. Inoue and T. Taguchi, J. Fluorine Chem., 1997, 82, 157–161 CrossRef CAS.
- S. C. Wilkinson, O. Lozano, M. Schuler, M. C. Pacheco, R. Salmon and V. Gouverneur, Angew. Chem., Int. Ed., 2009, 48, 7083–7086 CrossRef CAS PubMed.
- H. Slebocka-Tilk, R. G. Ball and R. S. Brown, J. Am. Chem. Soc., 1985, 107, 4504–4508 CrossRef CAS.
- R. S. Brown, R. W. Nagorski, A. J. Bennet, R. E. D. McClung, G. H. M. Aarts, M. Klobukowski, R. McDonald and B. D. Santarsiero, J. Am. Chem. Soc., 1994, 116, 2448–2456 CrossRef CAS.
- R. Rathore, J. Hecht and J. K. Kochi, J. Am. Chem. Soc., 1998, 120, 13278–13279 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS PubMed.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CAS.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS PubMed.
- A. Laio and F. L. Gervasio, Rep. Prog. Phys., 2008, 71 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132 Search PubMed.
- B. Ensing, A. Laio, M. Parrinello and M. L. Klein, J. Phys. Chem. B, 2005, 109, 6676–6687 CrossRef CAS PubMed.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- J. Contreras-Garcia, R. A. Boto, F. Izquierdo-Ruiz, I. Reva, T. Woller and M. Alonso, Theor. Chem. Acc., 2016, 135, 242–254 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, F. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. T. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2056208–2056213. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc01014j |
| ‡ During a metadynamics simulation, a chemical system is forced to move from stable states by means of added Gaussian potentials. As such, these lifetimes are artificially decreased and therefore cannot be directly compared to actual lifetimes. Nevertheless, trends concerning stability of stable states can still be retrieved when the shape and frequency of the added Gaussian potentials remains the same over the different simulations. |
| This journal is © The Royal Society of Chemistry 2021 |