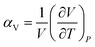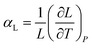Open Access Article
Open Access ArticleThermal expansion properties of organic crystals: a CSD study†
Arie
van der Lee
 *a and
Dan G.
Dumitrescu
*a and
Dan G.
Dumitrescu
 b
b
aInstitut Européen des Membranes, IEM – UMR 5635, ENSCM, CNRS, Université de Montpellier, Montpellier, France. E-mail: arie.van-der-lee@umontpellier.fr
bIndependent researcher, Via D. Bramante, Trieste, Italy
First published on 3rd May 2021
Abstract
The thermal expansion properties of crystalline organic compounds are investigated by data mining of the Cambridge Structural Database (CSD). The mean volumetric thermal expansion coefficient is 168.8 × 10−6 K−1 and the mean uniaxial thermal expansion coefficient is 71.4 × 10−6 K−1, based on 745 and 1129 different observations, respectively. Normal and anomalous coefficients can be identified using these values and the associated standard deviations. The anisotropy of the thermal expansion is also evaluated and found to have a very broad distribution. 4719 different structures, comprising 4093 different molecular compounds and 626 additional polymorphs have been analyzed on their thermal expansion properties. Approximately 34% of these structures may have at least one orthogonal axis with negative thermal expansion, much more than generally believed. Moreover 127 structures have been identified which could have negative volumetric thermal expansion. Experimental validation using a robust protocol with data collected at more than 2 different temperatures is required to validate these cases.
Introduction
Thermal expansion is the shape response of a material exposed to a temperature change. For solid materials the shape response is usually positive with positive temperature change, i.e. the material expands on heating. The isobaric volumetric thermal expansion coefficient expresses the change in volume with temperature per unit volume:Likewise, the isobaric uniaxial thermal expansion coefficient expresses the change along a certain direction with temperature per unit length:
The units of the coefficients are in K−1 but because of its typical magnitudes they are rather expressed in 10−6 K−1, or, more conveniently, in MK−1. Uniaxial does not necessarily mean along a crystallographic axis, since the expansion can be calculated along any direction in space. Thermal expansion is supposed to be mostly linear, but need not be so.
Thermal expansion can be measured using mechanical dilatometry, optical methods such as optical interferometry, and by diffraction techniques.1 However, thermal expansion coefficients measured by dilatometry sometimes give different values than those expected from diffraction measurements. This is especially true for polycrystalline materials with microcracks and microvoids, where the microscopic negative expansion dominates the atomic expansion.2 IR spectroscopy has also been used recently for the measurement of thermal expansion properties of organic semiconducting single crystals.3
Modern diffraction techniques coupled with widely available cryogenic and high-temperature devices have made possible the measurement of thermal expansion with relative ease, provided that the material is available in crystalline form, i.e. either as single crystals or as crystalline powders. Despite these possibilities, systematic studies related to the thermal expansion properties are relatively rare, most possibly due to the fact that the atomic structure is usually the focus of the study. Thermal expansion properties play also a role in crystal structure prediction. It was shown that the errors introduced by neglecting the thermal expansion properties may affect the free-energy among polymorphs which are energetically close.4 Another field where knowledge of volume and density plays a key role is volume-based thermodynamics.5,6
In the last few decades there is a growing interest in materials with anomalous shape properties related to temperature, pressure or strain stimuli. The focus is here on materials with negative or close to zero coefficients, the latter being in particular interesting for numerous applications where shape changes with temperature are undesirable.7–11 The focus is usually on inorganic or hybrid materials that often have nanoporous structures, such as zeolites and metal–organic frameworks (MOFs), which have the advantage of being very flexible with temperature, pressure or uptake of guest species. Uniaxial negative thermal expansion or even volumetric negative thermal expansion have been reported in a number of these structures.12–16 Technological applications require a fine degree of control of the thermal expansion, and this can be achieved through various means, chemical or mechanical, such as the use of pressure.17,18 Devices composed of more than one material and operated in a range of temperatures could show degraded performances when the thermal expansion coefficients do not match. The starting point for the research of controllable thermal expansion is the study of materials having negative thermal expansion.19 Dove & Fang have shown theoretically that negative thermal expansion becomes larger (more negative) with increasing pressure and positive thermal expansion less positive.20 This theoretical behavior is sometimes observed,21 sometimes not.22–24 Chemical modification by intercalation can be used to control the thermal expansion, e.g. by reversible wetting in nanopores of MOFs,25 adsorption of CO2 in a MOF structure to reach a zero expansion material,26 or by polymerizing ethylene in the pores of silicalite, which changes the sign of the volumetric thermal expansion from negative to positive.27 More general design strategies to tune the thermal expansion properties in MOFs by chemical modification have been given recently by Burtch et al.28 and theoretical considerations for these materials have been presented by Sanson.18 General observations to obtain zero expansion functional materials by chemical modification have been given by Chen et al.29
Most of the examples of anomalous and/or tunable thermal expansion properties concern inorganic or hybrid organic/inorganic structures, such as metal–organic framework structures.2,30 Less focus has been given to anomalous thermal expansion properties of organic structures. Some examples of tailored thermal expansion in organic structures include the study by Engel et al.31 who show how the expansion can be tuned by chemical replacement of certain guest species in organic inclusion compounds and the negative thermal expansion in the COV-102 structure.32 An exceptional negative volumetric thermal expansion in 1,4-diazabicyclo[2.2.2]octane hydrochloride was reported by Szafrański (2013);33 the highest reported negative uniaxial thermal expansion was found in chloranilic acid pyrazine.34
In this paper we focus on thermal expansion properties of crystalline organic materials determined by diffraction techniques, using data mining of the Cambridge Structural Database (CSD).35 It is shown that unusual thermal expansion properties exist for a number of crystalline compounds which have not been recognized as such before. The CSD contains at the time of writing somewhat more than one million of entries containing the results of diffraction experiments under a variety of conditions, and thus also possibly unexplored thermal expansion properties of crystalline materials. Crystal structures have been occasionally measured at different temperatures, either for one study by one research group, or by different research groups for unrelated studies. A CSD survey on density properties of organic compounds as a function of temperature has been published in 2007 on the 2004 database version with 325![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 709 entries by a manual search and treatment in an external spreadsheet program.36 In total 373 unique structures were found with temperature dependent data. The CSD Python API37 gives the possibility to extract the data in a more systematic way and to treat the results numerically and statistically. For the present study the 5.41 version of the CSD was used.
709 entries by a manual search and treatment in an external spreadsheet program.36 In total 373 unique structures were found with temperature dependent data. The CSD Python API37 gives the possibility to extract the data in a more systematic way and to treat the results numerically and statistically. For the present study the 5.41 version of the CSD was used.
Extracting thermal expansion coefficients from the CSD
Temperature data in CSD entries
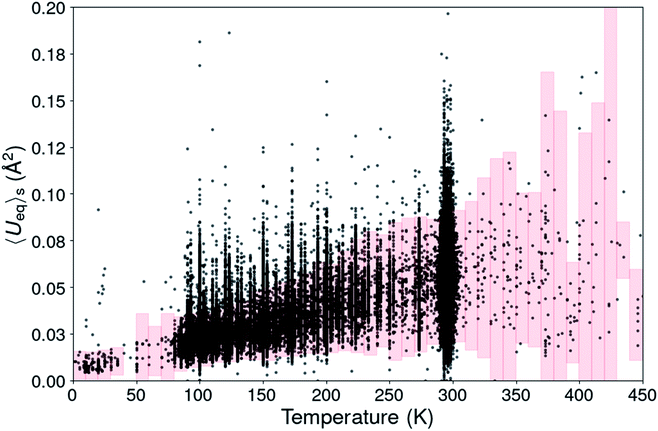 | ||
Fig. 1 Scatterplot of the structural <Ueq>s value from 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 672 organic CSD entries. The pink boxes define the <Ueq>s range for each temperature in which the <Ueq>s values are supposed to be. 672 organic CSD entries. The pink boxes define the <Ueq>s range for each temperature in which the <Ueq>s values are supposed to be. | ||
For temperatures beyond room temperature this ADP analysis method becomes rapidly less reliable, because of the scarcity of experimental observations.
Space group and unit cell information in CSD entries
Determination of thermal expansion coefficients
Expansivities were calculated using the Python NumPy library47 following the method described by Cliffe & Goodwin.48 A number of them were compared to the values obtained by using the on-line calculator PASCAL described in the Cliffe & Goodwin paper, but also with the unit strain calculations implemented in PLATON49 and those on the Bilbao Crystallographic Server.50 The linear expansion coefficients were thus calculated along three orthogonal directions defined by the eigenvectors of the unit strain matrix.In the case of right angles between the cell parameters the uniaxial expansion coefficients coincide with those calculated along the crystallographic axes. When this is not the case, the coefficients are related to directions which are determined by the orthogonalization matrix of the cell metrics. With changing temperatures not only the cell axes change, but also the cell angles for triclinic and monoclinic space groups. In this case it can happen that all three cell axes increase in length with rising temperature, but that one or two orthogonal expansion coefficients are negative. An illustrating case is KUCPED51 without any obvious negative uniaxial thermal expansion if only the cell axes are considered, but which has anyhow one slightly negative uniaxial thermal expansion, one close to zero expansion, and one normal positive expansion (Fig. 2 and Table 1).
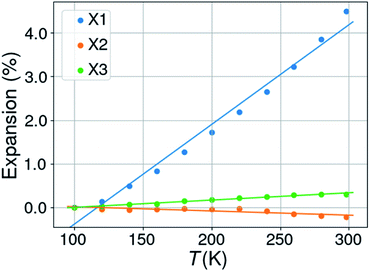 | ||
| Fig. 2 Percentual thermal expansion along the three orthogonal directions in the structure of 3-ethyl-1-methylimidazolium nitrate (KUCPED). | ||
| T (K) | a (Å) | b (Å) | c (Å) | β (°) |
|---|---|---|---|---|
| a Notes: CSD refcode KUCPED. Space group P21/n. Orthogonal thermal expansion coefficients: X1 = 228.6, X2 = −9.7, X3 = 16.7 MK−1. | ||||
| 100 | 8.5306 | 15.778 | 12.4800 | 93.770 |
| 120 | 8.5418 | 15.7812 | 12.4741 | 93.738 |
| 140 | 8.5686 | 15.7871 | 12.4753 | 93.624 |
| 160 | 8.5954 | 15.7896 | 12.4797 | 93.519 |
| 180 | 8.6286 | 15.8000 | 12.4856 | 93.392 |
| 200 | 8.6642 | 15.8053 | 12.4859 | 93.265 |
| 220 | 8.6997 | 15.8123 | 12.4926 | 93.104 |
| 240 | 8.7341 | 15.8150 | 12.4898 | 92.942 |
| 260 | 8.7796 | 15.8229 | 12.4861 | 92.766 |
| 280 | 8.8267 | 15.8236 | 12.4876 | 92.544 |
| 298 | 8.8740 | 15.8256 | 12.4921 | 92.309 |
For structures with more than 2 different temperatures, the mean uniaxial and volumetric expansion coefficients were determined by linear regression of the expansions Ei from the lowest (T0) to the highest temperature TN with i = 0, 1…N. This can be done in two different ways, either by calculating the expansion between subsequent points Ti and Ti+1:
| Ej (Ti) = −1.0 + (1.0 + Ei−1,j) × (1.0 + αij × (Ti − Ti−1)) |
| Ej (Ti) = α′ij × (Ti − T0) |
A problem may arise by the calculation of the eigenvalues and eigenvectors of the strain matrices at more than two temperatures. These are not always in the same order for subsequent calculations. The approach taken in PASCAL is to rearrange the eigenvalues and accompanying eigenvectors in ascending order, but this does not always give satisfactory results. The approach used here is to calculate the angle difference in the crystallographic system between the eigenvectors of the strain matrix between Ti+1 and Ti and those between T1 and T0. The minimum angle difference is taken to be the matching eigenvalue/eigenvector set, and eigenvalues and eigenvectors for the Ti+1/Ti strain matrix are eventually swapped to align them with those between T1 and T0.
Data sets used for thermal expansion properties analysis
From the 355![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 different organic entries in the CSD (5.41), a set of 37308 entries was extracted for 13840 different compounds (including polymorphics) with structures determined at two or more temperatures. After eliminating structures measured at non-ambient pressure, and those with abrupt cell parameter changes, unidentifiable temperatures, and those without space group information, a set of 7478 unique chemical compounds was extracted with data collected at at least two different temperatures and a minimum 50 K temperature interval between lowest and highest temperatures, yielding in total 20826 different entries (refcodes) and consequently an average of 2.78 different temperatures per unique compound. From the 20826 different refcodes, 580 entries were removed because of <Ueq>s values lying outside the trusted interval for their data collection temperature according to the criteria defined before. This could in addition lead to the removal of the chemical compound whenever only one refcode was left. The unit cells of all entries were transformed to the conventional unit cell where needed. Finally, 4719 unique structures comprising 4093 unique molecular compounds and 626 polymorphs have been retained for the analysis of the thermal expansion properties with 11658 different refcodes. The ESI† gives details for all 4719 structures: 14
740 different organic entries in the CSD (5.41), a set of 37308 entries was extracted for 13840 different compounds (including polymorphics) with structures determined at two or more temperatures. After eliminating structures measured at non-ambient pressure, and those with abrupt cell parameter changes, unidentifiable temperatures, and those without space group information, a set of 7478 unique chemical compounds was extracted with data collected at at least two different temperatures and a minimum 50 K temperature interval between lowest and highest temperatures, yielding in total 20826 different entries (refcodes) and consequently an average of 2.78 different temperatures per unique compound. From the 20826 different refcodes, 580 entries were removed because of <Ueq>s values lying outside the trusted interval for their data collection temperature according to the criteria defined before. This could in addition lead to the removal of the chemical compound whenever only one refcode was left. The unit cells of all entries were transformed to the conventional unit cell where needed. Finally, 4719 unique structures comprising 4093 unique molecular compounds and 626 polymorphs have been retained for the analysis of the thermal expansion properties with 11658 different refcodes. The ESI† gives details for all 4719 structures: 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157 (n(αL)) axial and 4719 (n(αV)) volumetric thermal expansion coefficients, 4719 Indicatrix Anisotropy Coefficients (IAC, see below), number of entries per structure, data collection temperatures and hyperlinks to the original publications.
157 (n(αL)) axial and 4719 (n(αV)) volumetric thermal expansion coefficients, 4719 Indicatrix Anisotropy Coefficients (IAC, see below), number of entries per structure, data collection temperatures and hyperlinks to the original publications.
For the determination of the distributions of thermal expansion coefficients a further reduction was applied, since scatter in the data could seriously bias the obtained results. Subsets were defined consisting of only those values from compounds with at least three data collections at different temperatures in a temperature interval larger than 50 K and for which a fit assuming a linear dependency on temperature yielded a goodness of fit value R2 of at least 0.75, 0.80, 0.85, and 0.90. As was outlined elsewhere48 the dependency of the thermal expansion need not be linear, especially at temperatures well below the Debye temperature52 or over continuous first-order (isosymmetric) phase transitions,53,54 but in nearly all practical cases there is no need to go beyond a linear model.
These high-quality subsets contain proportionally more studies than the complete set of compounds in which the same compound was measured in the same laboratory on the same diffractometer and should be qualitatively more homogeneous than the complete set. In the data subset with coefficients determined from only 2 different temperature points, 23% originate from experiments performed in the same study, whereas for the subset with 3 different temperature points this is 26% (with 4: 36%, with 5: 42%, Fig. S1†).
Results and discussion
Distributions of thermal expansion coefficients
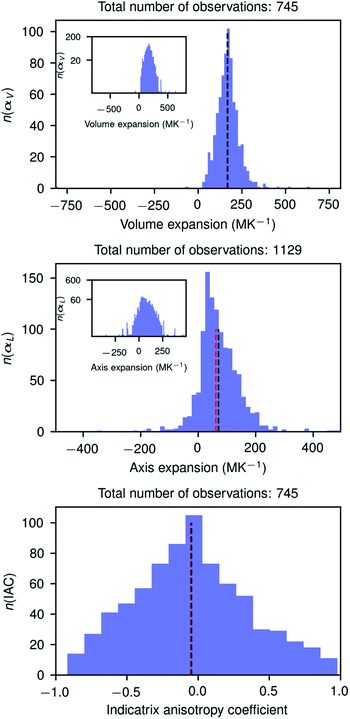
Fig. 3 shows the histograms of uniaxial and linear thermal expansion coefficients based on the data subset corresponding to linear fits with R2 > 0.90, consisting of 745 volumetric and IAC values and 1129 axial values. The mean value (μ) of the volumetric thermal expansion of organic compounds is 168.6 MK−1 (median τ = 168.3 MK−1) with a standard deviation σ of 72.5 MK−1. For the uniaxial expansion these numbers are μ = 71.4 (τ = 62.6) MK−1 with σ = 69.9 MK−1 and for the IAC −0.05 (τ = −0.05) with σ = 0.41. The thermal coefficient samples are not normally distributed according to the D’Agostino and Pearson's test,55,56 but the IACs are. The distribution of the axis thermal expansion coefficients is moderately skewed towards zero. The dependency of the distributions on R2 is relatively low (Table S1 and Fig. S2–S6†), and even the global data set containing 4719 observations has a distribution which is not completely different from the high-quality reduced data set. The obtained mean volumetric thermal and uniaxial expansion coefficients in this way are 156.0 and 51.6 MK−1, respectively, with standard deviations of 68.7 and 73.8 MK−1 for 4719 different volumetric coefficients and 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157 axial values. These mean values are somewhat smaller than those obtained using the reduced subsets and the standard deviations are somewhat larger for the volumetric coefficients, but smaller for the axial coefficients. The values from the global dataset are nevertheless relatively close to the values of the reduced subset, giving confidence that even cell parameters from studies in different laboratories performed on different machines can give valuable thermal expansion information.
157 axial values. These mean values are somewhat smaller than those obtained using the reduced subsets and the standard deviations are somewhat larger for the volumetric coefficients, but smaller for the axial coefficients. The values from the global dataset are nevertheless relatively close to the values of the reduced subset, giving confidence that even cell parameters from studies in different laboratories performed on different machines can give valuable thermal expansion information.
It is interesting to note that the distribution of the IACs is very broad with a standard deviation of 0.41 between limiting values of −1 and 1, and it is slightly more symmetric than the distribution of the volumetric and uniaxial thermal expansion coefficient. The anisotropy of the thermal expansion could thus be considered as rare and large if −1 < IAC < −0.46 or 0.34 < IAC < 1.00 and very rare and extraordinary large when −1 < IAC < −0.86 or 0.74 < IAC < 1.00. In this light the extraordinary anisotropic thermal expansions recently reported for three photosalient crystals57 with IACs of 0.248, 0.342, and −0.06, respectively, are rather normal. The three compounds are, however, metal–organic complexes whose structures could have a different IAC distribution. Although we have no formal proof of the IAC distribution of metal–organic structures, we do not expect it to be very different from the IAC distribution of organic structures.
The highest positive volume expansion coefficient, 2333.5 MK−1, is found for 3-benzoylpropionic acid whose structure was determined at two different temperatures by two different groups,58,59 but needs further experimental verification using a strict experimental protocol (see also Fig. S6 in ESI†), preferably using data sets collected at more than 2 different temperatures spanning a large temperature interval.
Two case studies
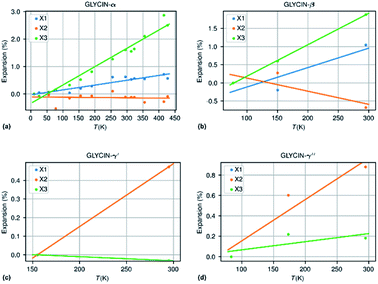
The methodology followed in this paper can be best illustrated by looking into more detail to the thermal expansion coefficients for compounds with a sufficiently large number of experimental structures determined at different temperatures.| Compound | N m | ΔT (K) | α X 1 | α X 2 | α X 3 | α V | χ α | IAC |
|---|---|---|---|---|---|---|---|---|
| a Notes: the thermal expansion coefficients α are in MK−1. χα is the NTE capacity and IAC the Indicatrix Anisotropy Coefficient. | ||||||||
| Glycine-β | 3 | 218 | 53.3 | −36.1 | 86.4 | 103.6 | 2.3 | 0.06 (++) |
| Glycine-α | 14 | 417 | 17.6 | −1.1 | 66.8 | 83.6 | 3.48 | −0.20 (−++) |
| Glycine-γ′ | 2 | 140 | 33.7 | 33.7 | −2.2 | 65.4 | 0.92 | −0.93 (−++) |
| Glycine-γ′′ | 3 | 212 | 40.4 | 40.4 | 8.0 | 89.3 | 1.89 | −0.80 (+++) |
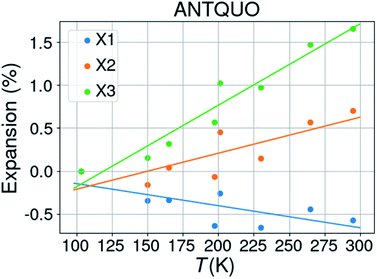
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . The latter was discarded from further analysis and one structure (ANTQUO15) was removed from the analysis because of a strongly deviating cell parameter (doubled a-axis compared to the other structures). The cell parameters of six structures were averaged within the same 10 K temperature bin, leaving 8 structures for thermal expansion analysis. The results from 5 different studies have been included in this compilation. Fig. 5 shows the thermal expansion along the three orthogonal axes of anthraquinone; it gives an idea about the expected variability of the measurements performed at different times, on different laboratories, and on different diffractometers. The extracted thermal expansion coefficients are −35.6, 51.9, 94.8 and 110.9 MK−1 for X1, X2, X3, and V, respectively, with R2 goodness of fit parameters of 0.52, 0.65, 0.93, and 0.67, respectively.
. The latter was discarded from further analysis and one structure (ANTQUO15) was removed from the analysis because of a strongly deviating cell parameter (doubled a-axis compared to the other structures). The cell parameters of six structures were averaged within the same 10 K temperature bin, leaving 8 structures for thermal expansion analysis. The results from 5 different studies have been included in this compilation. Fig. 5 shows the thermal expansion along the three orthogonal axes of anthraquinone; it gives an idea about the expected variability of the measurements performed at different times, on different laboratories, and on different diffractometers. The extracted thermal expansion coefficients are −35.6, 51.9, 94.8 and 110.9 MK−1 for X1, X2, X3, and V, respectively, with R2 goodness of fit parameters of 0.52, 0.65, 0.93, and 0.67, respectively.
Negative volumetric expansion coefficients
Amazingly, 139 structures have been detected with negative volumetric thermal expansion. The different temperature data for each of the compounds have been measured in different laboratories, and most probably on diffractometers of different brands. Additional tests were carried out on these entries to extract the most probable candidates for true negative thermal volumetric expansion. Table S2† gives the 127 compounds remaining after this selection with information about αV, the temperature interval over which it occurs, the number of temperature entries for each compound and the NTE capacity parameter χα which is the product of the relative volume contraction of the compound and the temperature range over which it is observed.63 For each compound it was checked whether <Ueq>s showed a positive tendency with temperature. If not, it was labeled ‘s’. The structures labeled ‘o’ have been reported in the same publication – but not necessarily under the same conditions. For a number of structures, the reliability was checked by inspecting the original publications.Two compounds with extremely large negative volume expansion coefficients (−814.36 MK−1, UFERED;64 −653.79 MK−1, KARGIW65) were eliminated from this set since the refcodes for each compound contained a mixture of structures measured at ambient and not ambient pressures and different temperatures The non-ambient pressure structures had not been flagged as such in the CSD entries.
The crystals of other structures appeared to have different colors at different temperatures. Assignation of color is rather subjective. Although this could indicate a phase transition, it could also be due to a wrong assignment of the color, due to the subjectivity of the assignment process or even due to the physical inability of the researcher to differentiate specific colors.
The histogram of the collected uniaxial thermal expansion coefficients shows that nearly 40% of the values are negative. Out of the 4719 unique compounds 33.1% have one negative thermal coefficient, 5.3% two, and 1.5% three. Only 60.0% of the compounds have three strictly positive uniaxial thermal coefficients, which contradicts the general belief that negative thermal expansion in organic compounds is very rare.19,63,66,67 Isotropic or volumetric negative thermal expansion is however indeed very rare in organic compounds, with only a few confirmed cases.
Anisotropy of thermal expansion
Thermal expansion is rarely completely isotropic – except for compounds crystallizing in cubic space groups – but usually anisotropic to very anisotropic. In order to quantify the anisotropy, the indicatrix anisotropy coefficient was calculated following the method proposed by Doube for quantifying rods, plates, and intermediate forms in 3D ellipsoidal geometries.68 When X1, X2, and X3 are the lengths of the principal axes of an ellipsoid, and X1 ≤ X2 ≤ X3, then IAC = X1/X2 – X2/X3.The Indicatrix Anisotropy Coefficient (IAC) ranges from −1 for very oblate ellipsoids to +1 for strongly prolate ellipsoids when the lengths of the principal axes are all positive. However, in the case of the thermal expansion indicatrix axes may have negative lengths, which means that IAC may range from −infinity to +infinity. A slightly modified definition is therefore used here by using the absolute values of X1, X2, and X3 and adding a suffix to IAC indicating the sign of each value. Thus for example IAC = 0.231(++−) means that the value of IAC is 0.231 and that X1, X2 have a positive sign and X3 a negative sign, but also that the absolute value of X3 is larger than that of X1 and X2. With one or more negative thermal expansion coefficients the ellipsoids are no longer oblate or prolate, but the notion of strong anisotropy remains when IAC is close to 1 or −1.
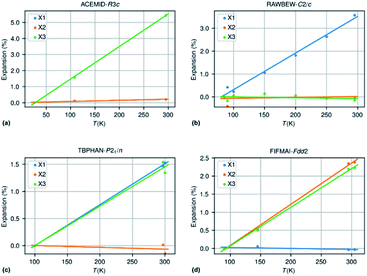
Fig. 3 shows an approximately symmetrical distribution of IAC values, with mean and median values slightly lower than 0.00. A significant proportion of the compounds displays extreme anisotropic thermal expansion of which four examples are given in Fig. 6. They have either very prolate (ACEMID and RAWBEW) or very oblate (TBPHAN & FIFMAI) IAC's. The structures with prolate IAC's have thermal expansions which are close to zero along two principal axes, and in these two cases also along two crystallographic axes (a and b for ACEMID and b and c for RAWBEW, respectively), and a strongly positive thermal expansion along one axis (c for ACEMID and a for RAWBEW). The structures with strongly oblate IAC's have only one axis with close to zero thermal expansion (c for TBPHAN and a for FIFMAI) and two axes with strong positive thermal expansion (a and b for TBPHAN and b and c for FIFMAI).
From the crystal packing it is not always clear why the thermal expansion is very strong in one or two directions and close to zero in the other directions. In the case of the acetamide structure the hydrogen bond network is clearly three dimensional without any preferential directions. The biguanidinium bis(dinitramide) structure does have a quasi two-dimensional structure with the hydrogen network parallel to the bc plane and thus only very weak van der Waals type interactions between the biguanidinium bis(dinitramide). Although this gives a qualitative explanation why the expansion in the direction perpendicular to the layers can be much larger than the expansion within the layers, it does not give a quantitative explanation why the latter is so close to zero. For the structures with extreme oblate IAC's the packing does not give clear clues why the expansion is strongly positive in two directions and close to zero in the third direction. TBPHAN does not have any classical hydrogen bonds, but rather halogen bonds which are not directed along any of the crystallographic axes. In the structure of FIFMAI there is one infinite hydrogen bond chain running along the c-axis, and only weak Waals interactions along the other two directions. The ab initio calculation of thermal expansion coefficients for molecular materials in a quasi-harmonic approximation or using full molecular dynamics simulations is still in its infancy although some progress is made.69–72 The crucial parameters of these calculations are related to the correct description of a wide variety of interactions present in molecular compounds, such as covalent and electrostatic interactions or hydrogen bond and long-range dispersive interactions. This makes it difficult to predict ab initio the thermal expansion properties of even very simple but highly anisotropic systems such as graphite and boron nitride.
Organic negative thermal expansion compounds
The compounds crystallizing in the structures presented in Table S2† which have possible negative volumetric expansion belong to a wide range of classes of compounds of varying complexity, with no apparent clear trend. Also, from a crystallographic point of view, there seems to be no particular clustering of the structures in specific space groups. This study highlighted very simple molecules, such as bis(ammonium) carbonate monohydrate ((NH4)2CO3·H2O; KOYRUN) or carbazole (C12H9N; CRBZOL), but also chiral Z′ = 4 (Ibuprofen)2(4,4′-dipyridyl) co-crystals (IJIJAN) or large ε-cyclodextrin hydrate (NOBBOV) structures. While some of the structures with the lowest thermal expansion coefficient belong to compounds which are hydrogen rich and contain long aliphatic chains, there are also examples of structures containing no hydrogen atoms at all, such as the fluorinated fullerene derivatives WUXNIM and WEDMOI. In the same manner, while most structures are neutral compounds, there are several examples of salts. Furthermore, no heavy atom effect was evident, with iodine being the heaviest element present in the list.As expected, this high structural variability of the compounds reflects in the wide range and type of intermolecular forces binding the structures together. All types of intermolecular interactions expected in organic compounds were observed in the list, ranging from strong ionic or charge-assisted hydrogen bonds, to weak π-stacking, CH⋯π interactions and dihydrogen contacts.
The inability to draw any qualitative structure–property relationship for negative thermal expansion can be attributed on the one hand to the complexity of the balance between the different types of intermolecular interactions and molecular flexibility contributing to the thermal expansion, and on the other hand to the paucity of literature data on any series of compounds. To our knowledge there are no structural studies dealing with the thermal expansion of a homologous series of organic compounds or their salts. This is mainly due to the fact that, in spite of the increasing availability of diffraction as an analytical tool, one X-ray structure is still generally considered adequately sufficient for characterizing an entire series in most synthetic studies.
Experimental validation of negative thermal expansion compounds
The list of structures presented in the current work does not give more than a couple of hints where to look for zero or negative thermal expansion properties. Experimental validation needs to be carried out in the same laboratory on the same diffractometer using a strict thermal and experimental protocol and preferably on the same crystal, although one could think that in order to have better statistics multiple observations of the same structure of a chemical compound should be used in order to obtain a more precise estimate of the thermal expansion coefficients. It could be argued that powder diffraction would be in this sense actually the preferred method for thermal expansion experiments, since the experiment averages over all crystallites present in the sample.73 However, high accuracy in powder diffraction can also only be obtained by strict experimental protocols and proper alignment of the diffractometer. Comparing cell parameters for the same crystalline phase determined on different powder diffractometers give in general different results. Powder diffraction could therefore give higher precision than single crystal diffraction, but not necessarily higher accuracy (“precise estimates are not necessarily accurate”).74–77 A number of single-crystal studies also use powder diffraction analyses, which are much more finely sampled in temperature. A close inspection of several combined powder/single crystal studies gives rather important differences between cell parameters determined by powder diffraction on the one hand and single-crystal diffraction on the other hand. An example is Mg(BH4)2 (refcode BOWMIK78) – which is flagged as ‘organic’ in the CSD – where the single-crystal study performed with synchrotron radiation at 100 K yields a cell volume of 3440 Å3, but the powder diffraction study, also performed with synchrotron radiation, gave 3425 Å3 at 100 K and 3431 Å3 at room temperature. The CSD only reports the single crystal study at 100 K (BOWMIK) and the powder diffraction study at 298 K (BOWMIK01), suggesting therefore that the compound displays negative volumetric thermal expansion, which is clearly not the case as evidenced by the finely sampled cell parameter values determined by powder diffraction between 100 and 500 K. This emphasizes the need to collect data at more than two data points for the extraction of thermal expansion coefficients, since scatter in the data may lead to less reliable values.Two major sources of bias are introduced in the results of this data mining study. The first bias is of course connected to the accuracy of the reported cell parameters. It is not certain that cell parameters from recent studies are necessarily more accurate than cell parameters from studies reported 2–4 decades ago. Related to this is the accurate determination of the temperature at the position of the crystal and its stability during the measurement. The cif-files of more recent structure determination contain often a standard uncertainty for the data collection temperature, since the temperature can be logged continuously during the measurement, but this gives only a hint about the stability of the temperature, not on its accuracy.
The second bias is related to inaccurate or missing information in the cif-files that are deposited at the CSD. A major source of error is the presence of structures measured at non-ambient pressure, usually at room temperature but not only, and which are not flagged as such in the cif-file. The structure of benzoic acid is reported 21 times in the CSD of which 11 have been recorded at room temperature. None are flagged as structures determined at non-ambient pressure. Out of the 11 room temperature structures 7 appeared to originate from the same study by Caia & Katrusiak.79Fig. 7 shows the expansion curves of benzoic acid with and without the structures from the Caia & Katrusiak study.
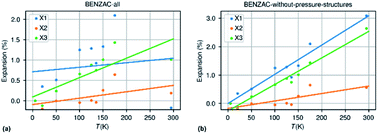 | ||
| Fig. 7 Thermal expansion data for benzoic acid extracted from the CSD with pressure data incorrectly included (a) and with only data collected at ambient pressure but different temperatures (b). | ||
Normal and anomalous values of thermal expansion coefficients
The present study gives an estimate of the mean thermal expansion coefficient to be expected for the crystalline structures of organic compounds. It shows as well that the dispersion of expected values is relatively large. With the actual values in hand it is easier to define when a reported thermal expansion coefficient is anomalous or exceptional. Since the thermal expansion coefficients are far from normally distributed, the Bienaymé–Chebyshev inequality should be applied stating that a minimum of 75% of values must lie within two standard deviations of the mean and 89% within three standard deviations. If a threshold of three standard deviations is retained for the volumetric thermal expansion it means that whenever a reported value is lower than −48.7 MK−1 or larger than 386.3 MK−1, it may be considered as anomalous. For an axial thermal expansion coefficient these values are −138.3 and 281.1 MK−1, respectively.Conclusions and outlook
Data mining studies rely on the availability, diversity and redundancy of data. The Cambridge Structural Database is an extremely important source of available data from very different compounds, and from many different sources and at different times. The importance of redundant data inside this huge data base cannot be underestimated, since this helps in the worst case to discard faulty data and in the best case to increase precision. Therefore, scientists should be even more encouraged than they are now to deposit data from structures that have been published before. All practical crystallographers make very often the decision to skip the full data collection once they discover from the preliminary cell screening and ‘helped’ by fast reduced cell checkers as CellCheckCSD80 hat can be enabled during data collection, that the structure has already been published. In the best case they do not discover this or they decide to perform the data collection anyhow. Then they should take the time to refine the structure and to complete the cif-file, and to deposit them at the CSD labeled as a private communication and, more generally, as a gift to science. This is the best case scenario to advance science from data mining projects.The main conclusion of this study is that negative uniaxial thermal expansion in organic crystal structures is much more common than generally believed. Most papers dealing with negative thermal expansion state that this is a very rare phenomenon, especially in organic crystal structures. We show that about a third of the organic crystal structures may present negative uniaxial thermal expansion. We show – also against general belief – that thermal expansion is commonly very anisotropic in organic crystal structures. We identify about 100 crystal structures which may present negative volumetric thermal expansion. The data present in the Cambridge Structural Database are not 100% trustworthy, which could bias the results of data mining studies as the current one. We present a new simple method to validate or invalidate temperature data in the CSD by an internal check based on the average equivalent atomic displacement parameter of the organic structure is proposed to validate or invalidate the reported temperature in the CSD entry.
Author contributions
The conceptualization, investigation, and validation of the methods and results presented in this study were done by both authors. AvdL performed the methodology and data curation stages and developed the Python scripts used in this study. The paper was written jointly.Conflicts of interest
There are no conflicts to declare.References
- J. D. James, J. A. Spittle, S. G. R. Brown and R. W. Evans, Meas. Sci. Technol., 2001, 12, R1–R15 CrossRef CAS.
- K. Takenaka, Y. Okamoto, T. Shinoda, N. Katayama and Y. Sakai, Nat. Commun., 2017, 8, 14102 CrossRef CAS PubMed.
- J. Mohanraj, E. Capria, L. Benevoli, A. Perucchi, N. Demitri and A. Fraleoni-Morgera, Phys. Chem. Chem. Phys., 2018, 20, 1984–1992 RSC.
- Y. N. Heit and G. J. O. Beran, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 514–529 CrossRef CAS PubMed.
- L. Glasser and H. D. B. Jenkins, J. Chem. Eng. Data, 2011, 56, 874–880 CrossRef CAS.
- L. Glasser, J. Phys. Chem. Solids, 2012, 73, 139–141 CrossRef CAS.
- K. Takenaka and H. Takagi, Appl. Phys. Lett., 2009, 94, 131904 CrossRef.
- A. E. Phillips, G. J. Halder, K. W. Chapman, A. L. Goodwin and C. J. Kepert, J. Am. Chem. Soc., 2010, 132, 10–11 CrossRef CAS PubMed.
- X. Song, Z. Sun, Q. Huang, M. Rettenmayr, X. Liu, M. Seyring, G. Li, G. Rao and F. Yin, Adv. Mater., 2011, 23, 4690–4694 CrossRef CAS PubMed.
- X. Jiang, M. S. Molokeev, P. Gong, Y. Yang, W. Wang, S. Wang, S. Wu, Y. Wang, R. Huang, L. Li, Y. Wu, X. Xing and Z. Lin, Adv. Mater., 2016, 28, 7936–7940 CrossRef CAS PubMed.
- J. Chen, Q. Gao, A. Sanson, X. Jiang, Q. Huang, A. Carnera, C. G. Rodriguez, L. Olivi, L. Wang, L. Hu, K. Lin, Y. Ren, Z. Lin, C. Wang, L. Gu, J. Deng, J. P. Attfield and X. Xing, Nat. Commun., 2017, 8, 14441 CrossRef CAS PubMed.
- P. Lightfoot, D. A. Woodcock, M. J. Maple, L. A. Villaescusa and P. A. Wright, J. Mater. Chem., 2001, 11, 212–216 RSC.
- D. Dubbeldam, K. S. Walton, D. E. Ellis and R. Q. Snurr, Angew. Chem., Int. Ed., 2007, 46, 4496–4499 CrossRef CAS PubMed.
- S. S. Han and W. A. Goddard, J. Phys. Chem. C, 2007, 111, 15185–15191 CrossRef CAS.
- A. F. Sapnik, H. S. Geddes, E. M. Reynolds, H. H. M. Yeung and A. L. Goodwin, Chem. Commun., 2018, 54, 9651–9654 RSC.
- F.-X. Coudert and J. D. Evans, Coord. Chem. Rev., 2019, 388, 48–62 CrossRef CAS.
- A. Sanson and J. Chen, Front. Chem., 2019, 7, 284 CrossRef PubMed.
- A. Sanson, Mater. Res. Lett., 2019, 7, 412–417 CrossRef CAS.
- K. Takenaka, Sci. Technol. Adv. Mater., 2012, 13, 013001 CrossRef PubMed.
- M. T. Dove and H. Fang, Rep. Prog. Phys., 2016, 79, 066503 CrossRef PubMed.
- K. W. Chapman and P. J. Chupas, J. Am. Chem. Soc., 2007, 129, 10090–10091 CrossRef CAS PubMed.
- C. R. Morelock, B. K. Greve, L. C. Gallington, K. W. Chapman and A. P. Wilkinson, J. Appl. Phys., 2013, 114, 213501 CrossRef.
- J. Zhu, J. Zhang, H. Xu, S. C. Vogel, C. Jin, J. Frantti and Y. Zhao, Sci. Rep., 2014, 4, 3700 CrossRef PubMed.
- L. C. Gallington, B. R. Hester, B. S. Kaplan and A. P. Wilkinson, J. Solid State Chem., 2017, 249, 46–50 CrossRef CAS.
- Y. Grosu, A. Faik, J.-M. Nedelec and J.-P. Grolier, J. Phys. Chem. C, 2017, 121, 11499–11507 CrossRef CAS.
- W. L. Queen, C. M. Brown, D. K. Britt, P. Zajdel, M. R. Hudson and O. M. Yaghi, J. Phys. Chem. C, 2011, 115, 24915–24919 CrossRef CAS.
- M. Santoro, F. A. Gorelli, R. Bini, J. Haines and A. van der Lee, Nat. Commun., 2013, 4, 1557 CrossRef PubMed.
- N. C. Burtch, S. J. Baxter, J. Heinen, A. Bird, A. Schneemann, D. Dubbeldam and A. P. Wilkinson, Adv. Funct. Mater., 2019, 29, 1904669 CrossRef CAS.
- J. Chen, L. Hu, J. Deng and X. Xing, Chem. Soc. Rev., 2015, 44, 3522–3567 RSC.
- J. N. Grima, P. S. Farrugia, R. Gatt and V. Zammit, Proc. R. Soc. A, 2007, 463, 1585–1596 CrossRef.
- E. R. Engel, V. J. Smith, C. X. Bezuidenhout and L. J. Barbour, Chem. Mater., 2016, 28, 5073–5079 CrossRef CAS.
- L. Zhao and C. Zhong, J. Phys. Chem. C, 2009, 113, 16860–16862 CrossRef CAS.
- M. Szafrański, J. Mater. Chem. C, 2013, 1, 7904–7913 RSC.
- H. Liu, M. J. Gutmann, H. T. Stokes, B. J. Campbell, I. R. Evans and J. S. O. Evans, Chem. Mater., 2019, 31, 4514–4523 CrossRef CAS.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- C. C. Sun, J. Pharm. Sci., 2007, 96, 1043–1052 CrossRef CAS PubMed.
- P. Sanschagrin, Acta Crystallogr., Sect. A: Found. Adv., 2017, 73, a67 Search PubMed.
- E. M. Melchor-Martínez, D. A. Silva-Mares, E. Torres-López, N. Waksman-Minsky, G. F. Pauli, S.-N. Chen, M. Niemitz, M. Sánchez-Castellanos, A. Toscano, G. Cuevas and V. M. Rivas-Galindo, J. Nat. Prod., 2017, 80, 2252–2262 CrossRef PubMed.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- G. I. Nikonov, L. G. Kuzmina, D. A. Lemenovskii and V. V. Kotov, J. Am. Chem. Soc., 1996, 118, 6333 CrossRef CAS.
- G. I. Nikonov, L. G. Kuzmina, D. A. Lemenovskii and V. V. Kotov, J. Am. Chem. Soc., 1995, 117, 10133–10134 CrossRef CAS.
- F. N. David and J. W. Tukey, Biometrics, 1977, 33, 768 Search PubMed.
- M. Nespolo and M. I. Aroyo, Acta Crystallogr., Sect. A: Found. Adv., 2016, 72, 523–538 CrossRef CAS PubMed.
- J. Rodriguez-Carvajal and J. Gonzalez-Platas, Acta Crystallogr., Sect. A: Found. Crystallogr., 2005, 61, c22 Search PubMed.
- T. Roisnel, CRYSCALC, Centre de Diffractométrie X, UMR6226 CNRS Université de Rennes I, Institut des Sciences Chimiques de Rennes, 35042 Rennes Cedex, France, 2020 Search PubMed.
- L. C. Andrews, H. J. Bernstein and G. A. Pelletier, Acta Crystallogr., Sect. A: Found. Crystallogr., 1980, 36, 248–252 CrossRef.
- C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. F. del Río, M. Wiebe, P. Peterson, P. Gérard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Nature, 2020, 585, 357–362 CrossRef CAS PubMed.
- M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329 CrossRef CAS.
- A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS PubMed.
- E. S. Tasci, G. de la Flor, D. Orobengoa, C. Capillas, J. M. Perez-Mato and M. I. Aroyo, EPJ Web Conf., 2012, 22, 00009 CrossRef.
- J. S. Wilkes and M. J. Zaworotko, J. Chem. Soc., Chem. Commun., 1992, 965 RSC.
- W. I. F. David, R. M. Ibberson and T. Matsuo, Proc. R. Soc. London, Ser. A, 1993, 442, 129–146 CrossRef CAS.
- A. van der Lee, G. H. Roche, G. Wantz, J. J. E. Moreau, O. J. Dautel and J.-S. Filhol, Chem. Sci., 2018, 9, 3948–3956 RSC.
- D. G. Dumitrescu, G. H. Roche, J. J. E. Moreau, O. J. Dautel and A. van der Lee, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 661–673 CrossRef CAS PubMed.
- R. B. D'Agostino, Biometrika, 1971, 58, 341–348 CrossRef.
- R. D'Agostino and E. S. Pearson, Biometrika, 1973, 60, 613–622 Search PubMed.
- K. Yadava, G. Gallo, S. Bette, C. E. Mulijanto, D. P. Karothu, I.-H. Park, R. Medishetty, P. Naumov, R. E. Dinnebier and J. J. Vittal, IUCrJ, 2020, 7, 83–89 CrossRef CAS PubMed.
- S. Selladarai, M. S. Kumar and K. Subramanian, Proc.–Indian Acad. Sci., Chem. Sci., 1990, 102, 39–43 Search PubMed.
- H. W. Thompson, P. A. Vanderhoff and R. A. Lalancette, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1991, 47, 1443–1445 CrossRef.
- G. Albrecht and R. B. Corey, J. Am. Chem. Soc., 1939, 61, 1087–1103 CrossRef CAS.
- Y. Iitaka, Acta Crystallogr., 1958, 11, 225–226 CrossRef CAS.
- Y. Iitaka, Acta Crystallogr., 1960, 13, 35–45 CrossRef CAS.
- C. S. Coates and A. L. Goodwin, Mater. Horiz., 2019, 6, 211–218 RSC.
- L. E. Connor, A. D. Vassileiou, G. W. Halbert, B. F. Johnston and I. D. H. Oswald, CrystEngComm, 2019, 21, 4465–4472 RSC.
- R. Lee, D. S. Yufit, M. R. Probert and J. W. Steed, Cryst. Growth Des., 2017, 17, 1647–1653 CrossRef CAS.
- C. Lind, Materials, 2012, 5, 1125–1154 CrossRef CAS PubMed.
- J. Grima, V. Zammit and R. Gatt, Xjenza, 2006, 11, 17–29 Search PubMed.
- M. Doube, Front. Endocrinol., 2015, 6, 15 Search PubMed.
- A. Erba, J. Maul and B. Civalleri, Chem. Commun., 2016, 52, 1820–1823 RSC.
- J. G. Brandenburg, J. Potticary, H. A. Sparkes, S. L. Price and S. R. Hall, J. Phys. Chem. Lett., 2017, 8, 4319–4324 CrossRef CAS PubMed.
- H.-Y. Ko, R. A. DiStasio, B. Santra and R. Car, Phys. Rev. Mater., 2018, 2(5), 055603 CrossRef CAS.
- J. Hoja, H.-Y. Ko, M. A. Neumann, R. Car, R. A. DiStasio and A. Tkatchenko, Sci. Adv., 2019, 5, eaau3338 CrossRef PubMed.
- J. I. Langford and D. Louër, Rep. Prog. Phys., 1996, 59, 131–234 CrossRef CAS.
- D. Schwarzenbach, S. C. Abrahams, H. D. Flack, W. Gonschorek, T. Hahn, K. Huml, R. E. Marsh, E. Prince, B. E. Robertson, J. S. Rollett and A. J. C. Wilson, Acta Crystallogr., Sect. A: Found. Crystallogr., 1989, 45, 63–75 CrossRef.
- W. Parrish, Acta Crystallogr., 1960, 13, 838–850 CrossRef.
- J. A. Kaduk, Adv. X-Ray Anal., 1997, 40, 352–370 Search PubMed.
- F. H. Herbstein, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 547–557 CrossRef CAS PubMed.
- Y. Filinchuk, R. Ćerný and H. Hagemann, Chem. Mater., 2009, 21, 925–933 CrossRef CAS.
- W. Cai and A. Katrusiak, CrystEngComm, 2012, 14, 4420 RSC.
- P. Wood, CCDC Newsletter, November 2011.
Footnote |
| † Electronic supplementary information (ESI) available: 1. Spreadsheet with details of all structures investigated. 2. Supplementary Fig. S1–S6 and Tables S1–S2. See DOI: 10.1039/d1sc01076j |
| This journal is © The Royal Society of Chemistry 2021 |