Open Access Article
Open Access ArticleCorrelations between ligand field Δo, spin crossover T1/2 and redox potential Epa in a family of five dinuclear helicates†
Sandhya
Singh
 and
Sally
Brooker
and
Sally
Brooker
 *
*
Department of Chemistry, The MacDiarmid Institute for Advanced Materials and Nanotechnology, University of Otago, PO Box 56, Dunedin 9054, New Zealand. E-mail: sbrooker@chemistry.otago.ac.nz
First published on 28th June 2021
Abstract
A family of five new bis-bidentate azole–triazole Rat ligands (1,3-bis(5-(azole)-4-isobutyl-4H-1,2,4-triazol-3-yl)benzene), varying in choice of azole (2-imidazole, 4-imidazole, 1-methyl-4-imidazole, 4-oxazole and 4-thiazole), and the corresponding family of spin-crossover (SCO) and redox active triply bridged dinuclear helicates, [FeII2L3]4+, has been prepared and characterised. X-ray crystal structures show all five Fe(II) helicates are low spin at 100 K. Importantly, DOSY NMR confirms the intactness of these SCO-active dinuclear helicates in D3-MeCN solution, regardless of HS fraction: γHS(298 K) = 0–0.81. Variable temperature 1H NMR Evans and UV-vis studies reveal that the helicates are SCO-active in MeCN solution. Indeed, the choice of azole in the Rat ligand used in [Fe2L3]4+ tunes: (a) solution SCO T1/2 from 247 to 471 K, and (b) reversible redox potential, Em(FeII/III), from 0.25 to 0.67 V for four helicates, whilst one has an irreversible redox process, Epa = 0.78 V, vs. 0.01 M AgNO3/Ag. For the four reversible redox systems, a strong correlation (R2 = 0.99) is observed between T1/2 and Epa. Finally, the analogous Ni(II) helicates have been prepared to obtain Δo, establishing: (a) the ligand field strength order of the ligands: 4-imidazole (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420) ∼ 1-methyl-4-imidazole (11
420) ∼ 1-methyl-4-imidazole (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 430) < 2-imidazole (11
430) < 2-imidazole (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 505) ∼ 4-oxazole (11
505) ∼ 4-oxazole (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 516) < 4-thiazole (11
516) < 4-thiazole (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804 cm−1), (b) that Δo ([NiII2L3]4+) strongly correlates (R2 = 0.87) with T1/2 ([FeII2L3]4+), and (c) interestingly that Δo strongly correlates (R2 = 0.98) with Epa for the four helicates with reversible redox, so the stronger the ligand field strength, the harder it is to oxidise the Fe(II) to Fe(III).
804 cm−1), (b) that Δo ([NiII2L3]4+) strongly correlates (R2 = 0.87) with T1/2 ([FeII2L3]4+), and (c) interestingly that Δo strongly correlates (R2 = 0.98) with Epa for the four helicates with reversible redox, so the stronger the ligand field strength, the harder it is to oxidise the Fe(II) to Fe(III).
Introduction
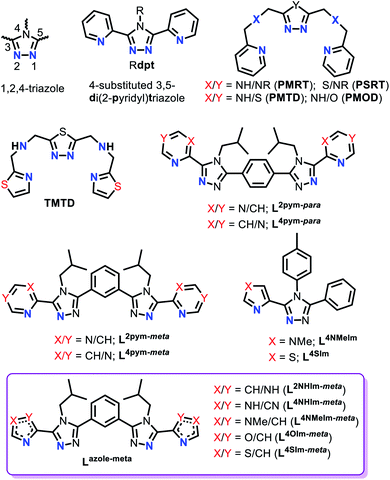
Spin crossover (SCO) is a phenomenon seen in 3d4–3d7 octahedral metal complexes when the ligand field is ‘just right’ so that the application of an external stimulus, including temperature, pressure, light irradiation and guest molecules, causes a reversible switch of spin state, from HS to LS.1–3 This conversion is accompanied by a pronounced change in colour, volume, mechanical, electrical and magnetic properties of the materials; which gives rise to a multitude of potential applications, in sensing, data storage, actuators, thermometers and display devices.1,4,5The study of self-assembled coordination complex architectures6 (metallosupramolecular chemistry)7 has become very popular in the last few decades, not least because of interesting host–guest chemistry, catalysis and sensing ability.8–10 Discrete polynuclear iron(II) supramolecular architectures are particularly interesting for SCO,11–13 as (a) intramolecular interactions, electronic and steric, between the metal centres can influence the SCO, amongst other things enhancing the potential for polynary rather than binary information storage through multistep SCO,4,11 and (b) host–guest interactions can influence the SCO.14,15 Nevertheless, prior to this study, only 12 ligands (Fig. S1.1, ESI,†L1–L12), comprising either azole–pyridine or azole–imine coordinating pockets (Fig. 1), had been employed to form SCO-active dinuclear iron(II) helicates.11,16 The first example of an SCO-active dinuclear helicate, [Fe2L13]4+ (Fig. S1.1, ESI†) was reported by Williams and co-workers in 1998.17 Since then this field has been expanded on by various authors, including Hannon,18 Li,16,19,20 Kruger and Clérac,21–23 Sunatsuki,24,25 and Aromí.26
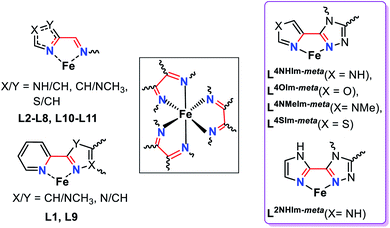 | ||
| Fig. 1 Summary of the common features (black box) of the bidentate binding pockets in the 12 ligands employed to generate the dinuclear SCO-active triply bridged Fe2L3 helicates reported in the literature to date (left, L1–L12, see also Fig. S1.1 ESI†),11 and in the five new ligands presented in this work (right, violet box), L2NHIm-meta, L4NHIm-meta, L4NMeIm-meta, L4OIm-meta and L4SIm-meta. | ||
Despite considerable interest in redox properties, especially of iron complexes due to potential relevance to understanding the function of heme-based metalloproteins, in which spin state changes are also crucial,27–29 studies of SCO and redox in families of complexes are rare:24,30–35 Drago,30 Kadish32,33 and Kuroda-Sowa31 studied mononuclear complexes, whilst Sunatsuki and co-workers have reported the only examples involving dinuclear iron(II) helicates24 (or tetranuclear cages36). Of these, only the Drago30 and Kadish32,33 studies (Fig. S1.2, ESI†) involved solution SCO, which is the most relevant for comparison with the redox potential, also determined in solution.
In the solid state, crystal packing, co-crystallised solvent and intermolecular cooperativity can obscure the electronic modifications imposed by variation of the ligand. In contrast, solution SCO opens the door to investigating the electronic effect arising from ligand modification,37–40 including from a ‘tail’,41–43 as well as the effects of solvent polarity,44 concentration41 and pH.45
1,2,4-Triazole ligands, which can be substituted at the C3, N4 and/or C5 positions on the triazole ring (Fig. 2), provide an appropriate ligand field strength for generating Fe(II) spin crossover materials.46–48
Such ligands have included (Fig. 2): mono- and bis-dentate Rdpt,48 bis-terdentate PMRT/PSRT11,49–51 and the related PMTD/PMOD52–54 or TMTD55 all of which have been reported in the literature to form SCO active Fe(II) complexes. Recently, we reported that our general synthetic strategy for accessing Rdpt ligands38,56 could be extended to access the first examples of ditopic azine-triazole analogues57 and of azole–triazole monotopic Rat ligands.58 The first four ditopic azine-triazole ligands prepared, Lnpym-meta and Lnpym-para (Fig. 2),57 featured n-pyrimidine-triazole binding sites linked by either meta- (for helicates) or para- (for tetrahedral cages) substituted phenylene linkers. All four of the structurally characterised iron(II) complexes, both helicates and cages, of these first ditopic Rat ligand systems were found to be LS.57 Clearly, the ligand field of these new robust ditopic Rat ligands needs to be reduced in order to enable SCO. With this goal in mind, very recently, we reported the first examples of monotopic azole–triazole L4NMe/SIm ligands (Fig. 2), which, as expected, imposed a weaker ligand field: [Fe(L4NMeIm)3](BF4)2 is HS whereas [Fe(L4SIm)3](BF4)2 is SCO-active in both the solid state and in MeCN solution.58
The focus herein is on the development of a new family of robust yet easily modified ligands for the assembly of SCO-active triply bridged iron(II) dinuclear helicates. Hence the ditopic versions of these weaker fields azole–triazole ligands (L4NMe/SIm) are prepared, using a meta-phenylene linker, to enable access to a new class of SCO-active [FeII2L3]4+ dinuclear helicates. Specifically we report the synthesis of five new ditopic Rat ligands (Lazole-meta, Fig. 2, violet box) and the synthesis, structural, spectroscopic, solid and solution spin crossover and redox characterisation of the corresponding triply bridged dinuclear helicates, [FeII2(Lazole-meta)3](BF4)4. Furthermore, to determine the ligand field strengths of these new Rat ligands, the corresponding Ni(II) helicates are also synthesised, two are structurally characterised and all five are studied by UV-vis spectroscopy.
This study of five helicates provides a rare demonstration of the expected, often said but seldom shown, correlation between the SCO switching temperature (T1/2) and the ligand field splitting energy (Δo) for a family of complexes. Somewhat less intuitive is that a connection is also established between these spin crossover properties (Δo, T1/2) and the oxidation potentials (Epa), a combination of properties not often studied together (see above).
Results and discussion
Synthesis
In contrast to the previously published azine-triazole dinuclear helicates featuring a 1,3-phenylene linker ligand, both of which were LS,57 herein the ligand field induced by the ditopic ligands is reduced. So, whilst the same linker is used, both bidentate ligand binding sites are changed from featuring azine-triazole to azole–triazole binding pockets. The five new ditopic ligands of azole–triazole, 2-imidazole L2NHIm-meta, 4-imidazole L4NHIm-meta, 1-methyl-4-imidazole L4NMeIm-meta, 4-oxazole L4OIm-meta and 4-thiazole L4SIm-meta, were synthesised by refluxing the previously reported ethylated bis-thioamide57 and appropriate azole carbohydrazide in n-butanol for three days, and were obtained as analytically pure powders in 31–56% yield (Scheme S1, ESI†).Next, the dinuclear Fe(II) helicates were prepared by a one-pot synthesis at room temperature, reacting a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio of Fe(BF4)2·6H2O and the appropriate ligand L2NHIm-meta or L4XIm-meta (X = NH, NMe, O and S), in acetonitrile except for L4NHIm-meta where nitromethane was used. In addition, nitromethane was used to obtain a solvatomorph of [Fe2L4OIm-meta)3](BF4)4 (crystal structure determined at 100 and 253 K, see below). Similarly, the five [Ni2L3](BF4)4 helicates were obtained, in order to determine Δo from the UV-vis spectra, by using Ni(BF4)2·6H2O and acetonitrile as the solvent.
3 ratio of Fe(BF4)2·6H2O and the appropriate ligand L2NHIm-meta or L4XIm-meta (X = NH, NMe, O and S), in acetonitrile except for L4NHIm-meta where nitromethane was used. In addition, nitromethane was used to obtain a solvatomorph of [Fe2L4OIm-meta)3](BF4)4 (crystal structure determined at 100 and 253 K, see below). Similarly, the five [Ni2L3](BF4)4 helicates were obtained, in order to determine Δo from the UV-vis spectra, by using Ni(BF4)2·6H2O and acetonitrile as the solvent.
All five [FeII2L3](BF4)4 complexes were obtained as single crystals suitable for X-ray crystallography (Fig. S4, ESI†), by slow vapour diffusion of diethyl ether into the reaction solutions: dark orange blocks of [Fe2(L2NHIm-meta)3](BF4)4·2CH3CN·solvent (1·solvents), light brown plates of [Fe2(L4NHIm-meta)3](BF4)4·solvent (2·solvent), light orange-yellow irregular blocks of [Fe2(L4NMeIm-meta)3](BF4)4·6CH3CN·C4H10O (3·6CH3CN·C4H10O), violet-pink needles of [Fe2(L4OIm-meta)3](BF4)4·6CH3CN·solvent (4·solvents), and dark orange blocks of [Fe2(L4SIm-meta)3](BF4)4·solvent (5·solvents). After air drying, compounds 1–5 were obtained, as analytically pure powders (Fig. S6, ESI†), as the following solvatomorphs, all hydrates, in 30–87% yield: 1·4H2O (orange, 73%), 2·6H2O (brown, 30%), 3·5H2O (orange, 87%), 4·6H2O (grey, 37%) and 5·2.5H2O (orange, 87%).
In the same way, the analogous dinuclear Ni(II) helicates were prepared and isolated by vapour diffusion of diethyl ether into the MeCN reaction solutions. After air drying, 1Ni–5Ni were obtained, as analytically pure pale violet/pink powders (Fig. S9, ESI†), as the following solvatomorphs, all hydrates, in 50–96% yield: 1Ni·6H2O (62%), 2Ni·4H2O (50%), 3Ni·5H2O (92%), 4Ni·2.5H2O (62%) and 5Ni·3H2O (96%).
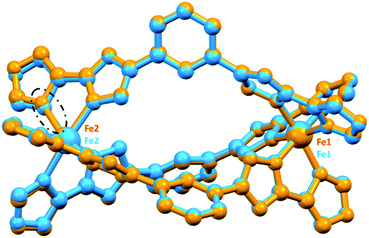
Crystal structure descriptions
Single crystal X-ray data for all five of the Fe(II) dinuclear helicates were collected at 100 K. In all but one case data collection at higher temperatures was not possible due to loss of crystallinity: the exception was 4·5.5NO2CH3, which on warming to 253 K appeared to lose about half a molecule of nitromethane of crystallisation, becoming 4·5NO2CH3 for which data was able to be collected. Modelling of the disorder of some iso-butyl groups, and of some anions, is detailed in ESI.† Due to solvent disorder that could not be modelled satisfactorily, the SQUEEZE59 routine in PLATON59 was applied to five of the datasets: 1·solvents, 2·solvents, 4·solvents 4·5NO2CH3 and 5·solvents, (see ESI† for details).All of the dinuclear helicates (Fig. 3) crystallised in centrosymmetric space groups: 1·solvents (triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), 2·solvents (orthorhombic Pbca), 3·6CH3CN·C4H10O (triclinic P
), 2·solvents (orthorhombic Pbca), 3·6CH3CN·C4H10O (triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), 4·solvents (triclinic P
), 4·solvents (triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), 4·5.5NO2CH3 (100 K, triclinic P
), 4·5.5NO2CH3 (100 K, triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), 4·5NO2CH3 (253 K, triclinic P
), 4·5NO2CH3 (253 K, triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) and 5·solvents (monoclinic C2/c). The entire helicate, [Fe2L3](BF4)4·solvents, was present in the asymmetric unit for all of them, except 5·solvents in which half of the helicate, [FeL1.5](BF4)2·solvents, was present with the other half generated by a 2-fold axis.
) and 5·solvents (monoclinic C2/c). The entire helicate, [Fe2L3](BF4)4·solvents, was present in the asymmetric unit for all of them, except 5·solvents in which half of the helicate, [FeL1.5](BF4)2·solvents, was present with the other half generated by a 2-fold axis.
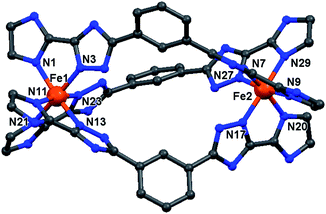 | ||
| Fig. 3 Molecular structure of the cation of the triply bridged dinuclear helicate, [Fe2L2NHIm-meta3]·2CH3CN·solvent (1·solvents). The other four helicates are isostructural with this one (see Fig. S7, ESI†). For clarity, the hydrogen atoms, counter-anions and iso-butyl groups are not shown. Colours: Fe orange; N blue; C grey. | ||
In all cases, the formation of the desired triply bridged dinuclear helicate is confirmed. The N6 coordination sphere forms a distorted octahedral geometry at Fe(II) centre, and comprises the pair of donors from one end of each of the three distinct bis-bidentate azole–triazole Rat ligands (Fig. 3 and S7, ESI†).
Excluding the nitromethane solvatomorphs of 4 (see later), at 100 K all of the Fe–Nazole/triazole distances fall in the range of 1.934–2.000 Å (Table S1, ESI†), which is consistent with LS Fe(II). The octahedral distortion parameters (sum of deviations of the 12 cis angles from 90°) of the Fe(II) centres in 1–5 lie in a narrow range, 56.8–62.0° (Tables 1 and S1, ESI†) that is close to those seen for the LS azine-triazole Fe(II) dinuclear helicates [Fe2L2pym-meta3](BF4)4 (56.7°) and [Fe2L4pym-meta3](BF4)4 (60.3°), and falls in the range seen for all of the SCO-active helicates reported in the literature (51–70°).11,57 The intrahelicate Fe⋯Fe distances in 1–5 lie between 9.971–10.323 Å (Table 1), which falls in the range of 9–12 Å reported for seven of the literature examples SCO-active Fe(II) helicates17,19–21,26,60 (exception ∼ 4 Å (L7/L8),24,25 ∼15 Å (L10/L11)23 and 19 Å (L12),16 Fig. S1.1, ESI†).
| Complexes | Space group | 〈Fe–N〉 (Å) | Σ° | Spin state | M⋯M (Å) |
|---|---|---|---|---|---|
| 1·solvents |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
1.967, 1.962 | 60.9, 59.7 | LS, LS | 10.0361(6) |
| 1 Ni ·solvents | P21/n | 2.097, 2.076 | 75.2, 70.2 | S = 1 | 10.313(1) |
| 2·solvents | Pbca | 1.972, 1.971 | 58.7, 57.8 | LS, LS | 10.1619(9) |
| 2 Ni ·solvents | Ibca | 2.083 | 69.7 | S = 1 | 10.3891(8) |
| 3·6CH3CN·C4H10O |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
1.980, 1.980 | 62.0, 61.5 | LS, LS | 10.3227(7) |
| 4·solvents |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
1.973, 1.964 | 57.0, 56.8 | LS, LS | 10.018(1) |
| 4·5.5NO2CH3 |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
1.967, 2.058 | 62.0, 77.2 | LS, mixLS/HS | 10.1554(7) |
| 4·5NO2CH3 (253 K) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
1.980, 2.181 | 63.0, 95.3 | LS, HS | 10.2281(9) |
| 5·solvents | C2/c | 1.953 | 57.0 | LS | 9.9711(9) |
Only for the nitromethane solvates of the oxazole–triazole helicate could datasets be collected at two temperatures: 4·5.5NO2CH3 at 100 K and 4·5NO2CH3 at 253 K (some nitromethane lost on warming). The resulting parameters (Tables 1 and S1†) are consistent with the helicate being in a [LS–mixedLS/HS] state at 100 K and a [LS–HS] state at 253 K (Fig. 4, Table 1). At 100 K, the [LS–mixedLS/HS] state is proposed as the average Fe–N bond distances and ∑° are 1.967 Å and 62° for Fe1 (LS) and 2.058 Å and 77° for Fe2 (mixedLS/HS). The ∑° value for mixedLS/HS Fe2 is higher than is usual for LS Fe(II) in Fe2L3 helicates (51–70°),11 and is close to that seen for mixedLS/HS [FeII2(L2)3](BF4)4·2MeCN (∑° = 76°).11,60 The average intraligand Nazole–Fe–Ntriazole angles are 80.7 (LS) and 78.5°(mixedLS/HS). At 253 K, 4·5NO2CH3 is in the [LS–HS] state as the SCO at Fe2 is now complete, whilst Fe1 remains LS (Table 1), as shown by the Fe–N and ∑° values 1.980 Å and 63.0° for Fe1 versus 2.181 Å and 95.3° for Fe2 (Table 1 and Fig. 4). On conversion to LS–HS, the average intraligand Nazole–Fe–Ntriazole angles are 80.3 (LS) and 75.8° (HS, a reduction of ∼3°; similar to 75.7° seen for the mononuclear HS 1-methyl-4-imidazole complex58 [FeL3](BF4)2, Table S1, ESI†). The Fe⋯Fe distance expands from 10.1554(7) [LS-mixLS/HS] to 10.2281(9) Å [LS–HS].
The structures of two of the dinuclear Ni(II) helicate analogues, those of the 2- and 4-NH imidazole ligands L2NHIm-meta and L4NHIm-meta, were also obtained at 100 K. The Ni–N distances (2.069–2.103 Å)61 and octahedral distortion values (∑° = 69.7–75.2°) are in between those expected for HS and LS Fe(II). In both cases, the average intraligand Nazole–Fe–Ntriazole angle (78.3/78.7 and 78.8°, Table S1, ESI†) falls in between those seen for HS and LS Fe(II), and an increase of 2–3% in M⋯M distance was observed on LS Fe(II) → Ni(II) (Table 1).
ESI-MS and 1H DOSY NMR spectra
The ESI-MS and 1H DOSY NMR spectra both showed the dinuclear helicates 1–5 are intact in acetonitrile solution (Fig. S67–S95 and S62–S66, ESI†), confirming the robust nature of these [Fe2L3]4+ helicates. Specifically, the ESI-MS spectra showed the presence of [Fe2L3]4+, [Fe2L3](X)3+ and [Fe2L3](X)22+ (X = F or BF4) species.Diffusion ordered 1H NMR spectroscopy (DOSY) was initially developed for use in characterising aggregates such as micelles, protein fragments and coordination polymers.62–64 Further development led to its widespread use in determining the molecular weights65 and size of polymers65,66 and to study molecular interaction between frustrated Lewis acid–base pairs in solution.67,68 Indeed it is now the ‘go to’ technique in supramolecular chemistry for determining the molecular weight and hence n for large diamagnetic self-assembled architectures, as is exemplified by the huge PdnL2n (n = 12, 24 and 30) cages assembled by Fujita and co-workers.64,69–71
Maury, Giraud and co-workers were the first to use DOSY to characterise paramagnetic lanthanide complexes.72 Later on, Byers and co-workers successfully extended the use of DOSY to the determination of molecular weights of paramagnetic 3d transition metal complexes.73 Building on that report, DOSY is used here to analyse the intactness of this family of five paramagnetic dinuclear helicates, 1–5, in MeCN solution at 298 K. The 1H DOSY signals revealed the same diffusion coefficients (D ∼ 6 × 10−6 cm2 s−1; range 6.4–6.7 × 10−6 cm2 s−1) for all five dinuclear helicates, regardless of the variation in HS fraction at 298 K (from 0 to 0.80, see next section). This confirms the ESI-MS finding that all five helicates are robust in MeCN solution.
Regardless of the spin state at 298 K, a plot of the diffusion coefficients vs. molecular weight (Fig. 5), for these five SCO active dinuclear helicates (1–5), along with the previously reported LS helicates [Fe2(L2/4pym-meta)3](BF4)4 and cages [Fe4(L2/4pym-para)3](BF4)8,57 gave an excellent correlation (R2 = 0.98, dark blue line). The results for the pair of mononuclear HS and SCO [Fe(L4NMe/SIm)3](BF4)2 complexes are also shown (stars, Fig. 5) for completeness. Whilst these are not expected to lie on this correlation line (dark blue line, Fig. 5), as they are not members of the Fe2nL3n family, including them in the correlation only drops the R2 to 0.93 (green line, Fig. 5).
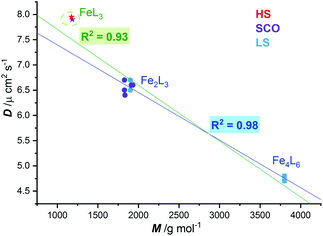 | ||
| Fig. 5 Correlation (dark blue line, R2 = 0.98) of diffusion coefficient (D) with molecular weight (M) observed at 298 K for LS FeII2L3 helicates (blue circles) and FeII4L6 cages (blue squares),57 and the SCO-active FeII2L3 helicates reported here (violet circles). When the two mononuclear FeIIL3 complexes, one HS and one SCO, are included in the fit, the R2 only drops to 0.93 (green line), despite them not being members of the Fe2nL3n family. | ||
Variable temperature 1H NMR Evans method
The magnetic response in solution is not affected by crystal packing effects, intermolecular cooperativity or co-crystallised solvents. The absence of all of these effects in the solution enables the effect of ligand modifications on the ligand field strength imposed on the Fe(II) centres to be clearly seen.39,74,75 Hence, the spin state of the five new dinuclear helicates 1–5 is monitored in acetonitrile solution at variable temperatures using both the 1H NMR Evans method and by UV-vis spectroscopy (discussed in this and the following sections).The Evans method was used to determine magnetic susceptibility of dinuclear helicates 1–5 in accurately prepared, approximately 6 mM CD3CN solution in the temperature range 243–343 K (Fig. S36–S40, ESI†), expected error associated with T1/2 is 5–10% (Fig. S31–S35, ESI†). Four of the complexes, 1·4H2O, 2·6H2O, 3·5H2O and 4·6H2O, undergo partial SCO whereas the fifth complex, 5·2.5H2O, remains mostly LS (Fig. 6). Fitting the data to the regular solution model,76 as a one-step SCO (Fig. 6), gave T1/2 values of 331 K (1·4H2O), 267 K (2·6H2O), 247 K (3·5H2O), 249 K (4·6H2O) and 471 K (5·2.5H2O).
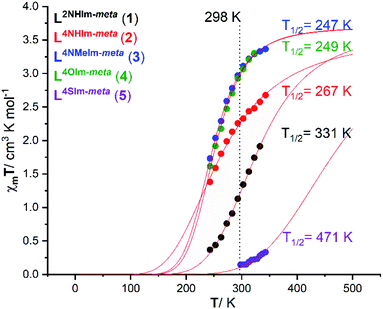 | ||
| Fig. 6 Plot of χmT vs. T for 1·4H2O (black), 2·6H2O (red), 3·5H2O (blue), 4·6H2O (green) and 5·2.5H2O (purple) in CD3CN solution, as determined by Evans method.77,78 The curves correspond to the best fit found for a complete one-step SCO using the regular solution model (see ESI† for details).51,76 | ||
For 1·4H2O, the χmT value (per FeII ion) increased from 0.37 to 1.91 cm3 K mol−1 on increasing the temperature from 243 to 333 K (Fig. 6, black), which corresponds to an increase in high spin fraction (γHS) of 0.1 → 0.5, whilst for 2·6H2O the χmT (per FeII ion) increased from 1.38 to 2.67 cm3 K mol−1 (Fig. 6, red), which corresponds to an increase in γHS of 0.37 → 0.72. The T1/2 of the 2-imidazole helicate 1·4H2O (T1/2 = 331 K) is higher than that of the 4-imidazole helicate 2·6H2O (T1/2 = 267 K) which implies that the ligand field imposed by 2-imidazole is stronger than that imposed by 4-imidazole, consistent with the Kruger's L10 and L11 dinuclear helicates (Fig. S1.1, ESI†),23 and with the relative ligand field strengths calculated from the UV-vis of analogous Ni(II) helicates of L2NHIm-meta and L4NHIm-meta (see later). The χmT value (per FeII ion) for 3·5H2O at 243 K of 1.73 cm3 K mol−1 increased to 3.36 cm3 K mol−1 at 343 K (Fig. 6, blue), which corresponds to an increase in γHS of 0.47 → 0.91. The only difference between the ligands in 2·6H2O (T1/2 = 267 K) and those in 3 (T1/2 = 247 K) is the methylation of the non-coordinated 4-imidazole NH to give the NMe, but this change significantly decreases the ligand field imposed in 3·5H2O. Halcrow previously commented on the hydrogen bonding by 4-imidazole, increasing the acidity of the –NH hydrogen which increases the electron-density of the coordinated N, strengthening the σ bond donation in the N–Fe bond and favouring the LS state, relative to the methylated analogue,40 and the present findings are consistent with this.
Almost identical behaviour to the 1-methyl-4-imidazole helicate 3·5H2O (T1/2 = 247 K) is observed for the 4-oxazole helicate 4·6H2O (Fig. 6, green). The latter, 4·6H2O, had a χmT value (per FeII ion) at 243 K of 1.61 which increased to 3.30 cm3 K mol−1 at 323 K (T1/2 = 249 K), which corresponds to an increase in γHS of 0.44 → 0.89.
In contrast to 1–4, the 4-thiazole helicate 5·2.5H2O remains practically diamagnetic, with a χmT = 0.14 cm3 K mol−1 at 298 K which increased to 0.33 cm3 K mol−1 at 343 K, which corresponds to an increase in γHS from 0.04 → 0.09. Measurements at higher temperatures were not possible due to the boiling point of CD3CN (354 K). The fit to the regular solution model gave T1/2 = 471 K (which should be taken with caution as it involves extrapolation of the data), which is consistent with the 4-thiazole ligand imposing the strongest field ligand of the five studied herein (see later).
In summary, the observed T1/2 values for 1–5, in increasing order, is as follows (3 ∼ 4 < 2 < 1 < 5):
| L4NMeIm-meta (247) ∼ L4OIm-meta (249) < L4NHIm-meta (267) < L2NHIm-meta (331) < L4SIm-meta (471 K) |
Variable temperature solid state magnetic measurements
In contrast to the above, the magnetic studies of the hydrates of these five helicates in the solid state (Fig. S142–146, ESI†) showed that both the 2NH-imidazole L2NHIm-meta (1·4H2O) and 4-thiazole L4SIm-meta (5·2.5H2O) based helicates remain mostly LS, with only small fractions of HS above 300 K. The other three helicates, of the 4NH-imidazole L4NHIm-meta (2·6H2O), 4-oxazole L4OIm-meta (4·6H2O) ligands and 4NMe-imidazole L4NMeIm-meta (3·5H2O), undergo incomplete SCO with T1/2 values of 200, 230 and 280 K, respectively. These T1/2 values place the helicates in a different order, 2·6H2O < 3·5H2O < 4·6H2O < 1·4H2O ∼5·2.5H2O, from the above solution studies, once again demonstrating the often confounding impact of lattice solvent and crystal packing on solid state SCO.Variable temperature UV-vis studies
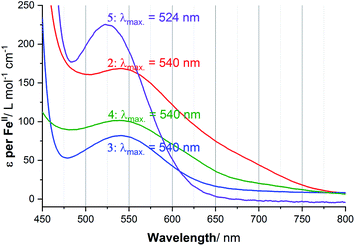
UV-vis spectra of 1–5 in acetonitrile solution were obtained at variable temperatures in our cryostat, in 10 K steps from 253 to 303 K, to probe the SCO of each of these helicates (Fig. S41–S51, ESI†), and the data compared with the Evans NMR method data (Tables S9–S11, ESI†). The spectra of the four complexes at 253 K are shown in Fig. 7, with the Laporte forbidden, spin allowed d–d transition of the LS Fe(II) centres, 1A1g → 1T1g, clearly seen at approximately 540 nm in the case of 2·6H2O, 3·5H2O and 4·6H2O, and at 524 nm for 5·2.5H2O. In contrast, in the case of 1·4H2O, a charge transfer transition (Fig. S41, ESI†), at room temperature 446 nm (ε = 5646 L mol−1 cm−1) obscured this d–d transition, so this charge transfer transition was monitored instead, as such bands have also been used by others to monitor SCO.79For the four complexes that undergo a significant amount of SCO in this temperature range (all but 5·2.5H2O, see later), the ε values obtained from the variable temperature UV-vis study were plotted against the γHS values from the Evans method NMR analysis, enabling a calibration line to be fitted, and in turn conversion of the ε values into γHS values (Table S11, ESI†). In turn, this enables the calculation of an estimated value for the true ε value for the fully LS complexes, εmax (Fig. S52 and S54, ESI†). With that value in hand, the ε vs. T values can be fitted with the regular solution model,51,76 to a full SCO from [LS–LS] → [HS–HS], to obtain the T1/2 values (Fig. S53 and S55, ESI†).
Considering the spectrum of 0.032 mM of the 2-imidazole complex 1·4H2O in acetonitrile, the charge transfer transition band observed at λmax = 446 nm with extinction coefficient per FeII ion of 8597 L mol−1 cm−1 at 253 K (Fig. S42, ESI†) which dropped to 4863 at 303 K, with T1/2 = 306 K. In contrast, d–d transition band were seen at λmax = 524 to 540 nm for the other four complexes (Fig. 7). In the case of the 4-imidazole complex 2·6H2O, the temperature dependence band at 540 nm, ε (per FeII ion) dropped from 174 → 107 L mol−1 cm−1 while heating from 253 K to 303 K, respectively, T1/2 = 267 K (Fig. S44, ESI†). Similarly, for 1-methyl-4-imidazole complex 3·5H2O d–d band at 540 nm ε value per FeII ion vary from 82 to 35 L mol−1 cm−1 (T1/2 of 251 K) (Fig. 8). Further, monitoring of the 540 nm band of 4-oxazole complex (4·6H2O), the ε value (per FeII ion) of 102 L mol−1 cm− 1 at 253 K decreased to 58 L mol−1 cm−1 at 303 K, T1/2 = 265 K (Fig. S47, ESI†).
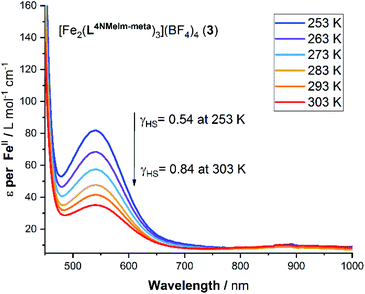 | ||
| Fig. 8 Variable temperature UV-vis spectroscopy study of a 2 mM acetonitrile solution of 3·5H2O. Note: ε is calculated per mole of FeII. | ||
In the 4-thiazole helicate 5·2.5H2O (Fig. 7), the d–d transition occurs at slightly higher energy (524 nm) than for 2–4, and only a small change is observed in the ε value. The apparent ε (per FeII ion) decreased from 225 to 198 L mol−1 cm−1 on warming from 253 K to 303 K (Fig. S51, ESI†). As this temperature range does not overlap with that of the Evans method data in the region where a non-zero Δf and hence χmT value was observed, this could not be analysed in the same way as for the other four complexes.
Ligand field strengths of Lazole-meta ligands
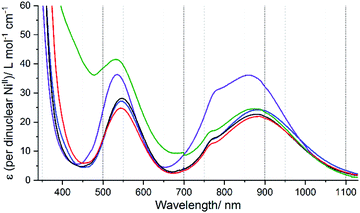
The analogous Ni(II) helicates, 1Ni–5Ni, have been prepared and characterised (see the experimental section, ESI-MS in Fig. S96– S115† and crystal structures of two in Fig. S10, ESI† for details) as analysis of the UV-vis spectra of them (Fig. S56, ESI†) enables the ligand field splitting energy, Δo (10Dq), to be obtained, and compared with the T1/2 values observed for the Fe(II) helicates.Octahedral Ni2+ (d8) has a 3A2g ground state, which gives rise to three spin allowed d–d transitions,80 from highest to lowest energy: 3A2g → 3T1g (P) ≈ 400–310 nm, 3A2g → 3T1g (F) ≈ 715–550 nm, and 3A2g → 3T2g (F) ≈ 1000–800 nm (near IR). This last band corresponds to Δo, but it is often weak and broad, and sometimes the spin forbidden 3A2g → 1Eg transition (which gains some intensity through spin–orbit coupling with 3T2g) can be seen as a shoulder on this band, further complicating the analysis.80,81 Indeed, when Δo is close to 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, as it is herein, mixing of these two bands, 3A2g → 3T2g (F) and 3A2g → 1Eg, becomes more significant and it is not possible to correctly analyse them. To deal with this issue, Hart, Boeyens and Hancock81 developed an empirical relationship:
000 cm−1, as it is herein, mixing of these two bands, 3A2g → 3T2g (F) and 3A2g → 1Eg, becomes more significant and it is not possible to correctly analyse them. To deal with this issue, Hart, Boeyens and Hancock81 developed an empirical relationship:
| 10Dq (corrected) = 10630 + 1370ε1/ε2 |
Using this equation on the ratio of the extinction coefficients corresponding to the shoulder (ε1)/peak (ε2) in the near IR band observed in each of the spectra of 1Ni–5Ni (Fig. 9), the “corrected 10Dq” values, Δo(corr.), have been determined for these five helicates (Table S12, ESI†).
In summary, the resulting Δo(corr.) values, in order of increasing ligand field strength, as follows (cm−1):
L4NHIm-meta (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420) ∼ L4NHIm-meta (11 420) ∼ L4NHIm-meta (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 430) < L2NHIm-meta (11 430) < L2NHIm-meta (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 505) ∼ L4OIm-meta (11 505) ∼ L4OIm-meta (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 516) < L4SIm-meta (11 516) < L4SIm-meta (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804) 804) |
This analysis of the UV-vis spectra of the Ni(II) helicates shows that the effect of changing from –NH, –NMe and –O in the non-coordinating position of the azole moiety in the ligand leads to relatively minor changes in the field strength, whereas changing to –S provides a significant increase in the ligand field strength. The ligand field strengths of these five ligands Δo(corr.) are not entirely consistent with the T1/2 values of the corresponding Fe(II) complexes, but despite this there is a good linear correlation (R2 = 0.87) between them (Fig. 10).
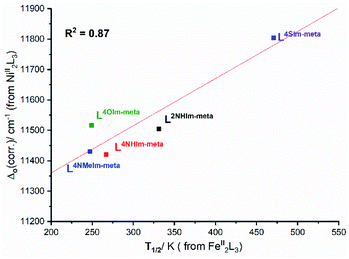 | ||
| Fig. 10 Good correlation (R2 = 0.87) of Δo(corr.) obtained from UV-vis studies of the Ni(II) helicates with solution T1/2 obtained for the analogous Fe(II) helicates. | ||
Electrochemical studies
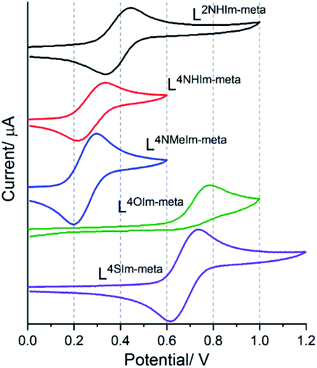
The magnetic response of 1–5 varied considerably with small modifications to the ligand strands, clearly reflecting the effect of changing the heteroatom present in the azole rings of these Rat ligands on the Fe(II) centres, we also expected to see tuning of the FeII/III redox potentials.Cyclic voltammetry was performed on 1 mM MeCN solutions of 1–5, vs. 0.01 M Ag/AgNO3. These solutions also contained 0.1 M TBAClO4, except in the case of 4-thiazole helicate 5·2.5H2O, which was insoluble in 0.1 M TBAClO4 but was soluble in 0.1 M TBAPF6. Four of the five complexes, 1·4H2O (Em = 0.39 V), 2·6H2O (Em = 0.27 V), 3·5H2O (Em = 0.25 V) and 5·2.5H2O (Em = 0.67 V), showed a reversible Fe(II)/Fe(III) redox process. In the case of the 4-oxazole helicate 4·6H2O, an irreversible oxidation event, at higher Epa = 0.78 V than the others, was observed (Fig. 11).
The five helicates, identified by ligand, in order of decreasing Epa, are as follows:
| 4·6H2O (Epa = 0.78 V) ∼5·2.5H2O (Epa = 0.73 V) > 1·4H2O (Epa = 0.44 V) > 2·6H2O (Epa = 0.33 V) ∼3·5H2O (Epa = 0.30 V) |
In general, the presence of an electron donating group pushes more electron density onto a metal centre making it easier to oxidise, and vice versa. Therefore, the oxidation potential (Epa) for 1-methyl-4-imidazole helicate 3·5H2O (0.30 V) is lower than 4-imidazole helicate 2·6H2O (0.33 V), which is attributed to the presence of the electron donating group –NMe in 3·5H2O, making the Fe(II) centre easier to oxidise.36,82
Correlations of SCO T1/2versus Δoversus Epa
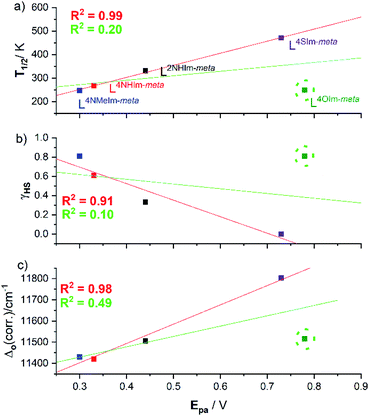
Interestingly, the four helicates with the reversible redox events, 1·4H2O, 2·6H2O, 3·5H2O and 5·2.5H2O, show a strong linear correlations between the (a) oxidation potential Epavs. the SCO T1/2 (R2 = 0.99, Fig. 12a, red line), and (b) γHS (298 K) vs. Epa (R2 = 0.91, Fig. 12b, red line). But when the helicate with the irreversible redox event, 4-oxazole helicate 4·6H2O, included in the linear fit the R2 drops to just 0.20 (Fig. 12a, green line) and 0.10 (Fig. 12b, green line). Given the above, unsurprisingly there is also a strong linear correlation (R2 = 0.98) of Δo and Epa for the four reversible complexes (Fig. 12c, red line), which when 4·6H2O is included again drops, to R2 = 0.49 (Fig. 12c, green line), i.e. in all cases the inclusion of the 4-oxazole helicate 4·6H2O which shows irreversible redox in these correlations leads to a big drop in R2, to 0.10–0.49.In summary, for the four complexes with reversible redox, Epa(FeII/III) is strongly positively correlated with T1/2 and Δo (R2 = 0.91–0.99), and strongly negatively correlated with the γHS fraction at 298 K. This shows that as the ligand field (Δo) and hence fraction LS increases, it gets harder to oxidise, i.e. Epa(FeII/III) increases (Fig. 12 and Table 2).
As noted in the introduction, studies of both redox and SCO across a family of complexes are not common.24,30–33 In the 1980's, in a family of nine solution SCO-active Fe(III) complexes, Kadish and co-workers observed the same trend as is seen here, the lower the γHS the easier it was to reduce (higher E1/2, Fig. S1.2, ESI†).32,33 On the other hand, in 1975 Drago and co-workers30 had studied a family of four solution SCO-active mononuclear Fe(II) complexes of hexadentate ligands varying in number of ortho-methyl groups present, and showed the opposite: the complexes with the highest γHS, rather than those with least electron-donating methyl groups (perhaps due to steric factors), were the most difficult to oxidise.30 Simplistically, SCO T1/2 values are expected to increase with increasing Δo whereas redox potentials E1/2 are expected to increase with decreasing HOMO energy level. So the observation of some correlations between these two distinct properties is intriguing and warrants further attention. Hence a collaborative study probing this family of interesting helicates in detail, using a range of theoretical models, will be carried out in the future in order to better understand the basis of the correlations observed.
| Complexes | E pa (V) | E pc (V) | E m (ΔE) (V) | T 1/2 (K) | γ HS 298 K | Δ o (cm−1) (Ni2L3) |
|---|---|---|---|---|---|---|
| L2NHIm-meta (1·4H2O) | 0.44 | 0.34 | 0.39 (0.10) | 331 | 0.33 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 505 505 |
| L4NHIm-meta (2·6H2O) | 0.33 | 0.22 | 0.27 (0.11) | 267 | 0.61 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420 420 |
| L4NMeIm-meta (3·5H2O) | 0.30 | 0.20 | 0.25 (0.10) | 247 | 0.81 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 430 430 |
| L4OIm-meta (4·6H2O) | 0.78 | Irrev | Irrev | 249 | 0.81 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 516 516 |
| *L4SIm-meta (5·2.5H2O) | 0.73 | 0.61 | 0.67 (0.12) | 471 | 0 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804 804 |
Conclusion
The previously reported ditopic Rat ligands consisted of a pair of pyrimidine-triazole pockets linked through meta-phenylene which resulted in Fe(II) dinuclear helicates that were trapped in the LS state.57 So herein, the strong ligand field pyrimidines (azines) were replaced by lower ligand field azoles. Five such ligands have been prepared (Lazole-meta: L2NHIm-meta, L4NHIm-meta, L4NMeIm-meta, L4OIm-meta and L4SIm-meta) along with the corresponding triply bridged dinuclear helicates [MII2L3](BF4)4·solvents with M = Fe or Ni. Single crystal X-ray structures of the iron(II) helicates (1–5) confirmed that they are indeed helicates, and are in the [LS–LS] state at 100 K.ESI-MS and 1H DOSY NMR spectroscopy studies confirmed the robustness of 1–5 in MeCN solution. Indeed, a strong linear correlation (R2 = 0.98) was seen between the diffusion coefficient and the molecular weight for the nine Fe2L3 helicates (7) and Fe4L6 cages (2) prepared to date,57 regardless of the γHS at 298 K ranging from 0 to 0.81.
VT-NMR Evans method studies of 1–5 in CD3CN solution (243–343 K) revealed that all of the complexes undergo incomplete SCO within this temperature range, with T1/2 values ranging from 247 to 471 K. The SCO was also followed by VT-UV-vis spectroscopy (253–303 K) in CH3CN solution, by monitoring changes in the absorbance of either the charge transfer band for 1, or of the d–d band for 2–5.
UV-vis spectra of the corresponding Ni(II) helicates revealed the ligand field splitting energy Δo(corr.) for four of the Lazole-meta ligands falls in the range 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420–11
420–11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 516 cm−1 (azole = 2-imidazole, 4-imidazole, 1-methyl-4-imidazole and 4-oxazole) whereas the fifth ligand imposes a significantly stronger ligand field, 11
516 cm−1 (azole = 2-imidazole, 4-imidazole, 1-methyl-4-imidazole and 4-oxazole) whereas the fifth ligand imposes a significantly stronger ligand field, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804 cm−1 (azole = 4-thiazole).
804 cm−1 (azole = 4-thiazole).
Cyclic voltammetry studies in acetonitrile solution showed a Fe(II)/Fe(III) redox process that was reversible for four of the helicates, but irreversible for the 4-oxazole helicate 4·6H2O. For the four reversible cases, excellent linear correlations of: Epa with T1/2 (R2 = 0.99), Epa with γHS (R2 = 0.91) and Epa with Δo(corr.) (R2 = 0.98) are observed.
This is a unique study, as it determines all three properties, ligand field splitting energy Δo, SCO T1/2 and oxidation potential Epa across a family of complexes – here for a family of five robust triply bridged dinuclear helicates differing in the choice of non-coordinated diazole heteroatom. In doing so it provides a rare illustration of the textbook statement that the stronger the ligand field (Δo↑) the more the LS state is stabilised over the HS state (T1/2↑; strong correlations, R2 > 0.87). Also, less intuitively, a connection is made between the SCO and redox properties of this family of helicates: for the four reversible systems the stronger the ligand field (Δo↑) and higher the T1/2 (↑), the harder the Fe(II) helicate is to oxidise to Fe(III) (Epa ↑). Future studies will include collaborative theoretical studies to probe these interesting helicates in more detail.
Author contributions
S. S. carried out all of the experimental work. S. B. conceived and supervised the project. S. S. prepared the first draft of the manuscript and S. B. and S. S. refined it to publication standards.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the University of Otago for supporting this work (including a doctoral scholarship and publishing bursary to SS), and Mr Ian Stewart (Otago) for measuring the ESI-MS and NMR spectra.Notes and references
-
M. A. Halcrow, Spin-Crossover Materials: Properties and Applications, John Wiley & Sons, Ltd, Chichester, 1st edn, 2013 Search PubMed
.
- P. Gütlich and H. A. Goodwin, Spin Crossover in Transition Metal Compounds I-III, Top. Curr. Chem., 2004, 233-235 Search PubMed
.
- P. Gütlich, Y. Garcia and T. Woike, Coord. Chem. Rev., 2001, 219–221, 839–879 CrossRef
.
- J.-F. Létard, P. Guionneau and L. Goux-Capes, Top. Curr. Chem., 2004, 235, 221–249 CrossRef
.
- M. Mikolasek, M. D. Manrique-Juarez, H. J. Shepherd, K. Ridier, S. Rat, V. Shalabaeva, A.-C. Bas, I. E. Collings, F. Mathieu, J. Cacheux, T. Leichle, L. Nicu, W. Nicolazzi, L. Salmon, G. Molnár and A. Bousseksou, J. Am. Chem. Soc., 2018, 140, 8970–8979 CrossRef CAS PubMed
.
-
J.-M. Lehn, Supramolecular chemistry: concepts and perspectives, VCH, Weinheim, 1995 Search PubMed
.
- E. C. Constable and A. M. W. Cargill Thompson, J. Chem. Soc., Dalton Trans., 1994, 1409–1418 RSC
.
- A. Lennartson, P. Southon, N. F. Sciortino, C. J. Kepert, C. Frandsen, S. Mørup, S. Piligkos and C. J. McKenzie, Chem.–Eur. J., 2015, 21, 16066–16072 CrossRef CAS PubMed
.
- F. Wang, C.-Y. Zhu, Y.-Q. Zhang, R.-Z. Liao, W. Xia, J.-C. Hu, J. Wu and H. Liu, Dalton Trans., 2018, 47, 13142–13150 RSC
.
- S. Rodríguez-Jiménez and S. Brooker, Inorg. Chem., 2019, 58, 8188–8197 CrossRef
.
- R. W. Hogue, S. Singh and S. Brooker, Chem. Soc. Rev., 2018, 47, 7303–7338 RSC
and inside front cover..
- H. S. Scott, R. W. Staniland and P. E. Kruger, Coord. Chem. Rev., 2018, 362, 24–43 CrossRef CAS
.
- A. J. McConnell, Supramol. Chem., 2018, 30, 858–868 CrossRef CAS
.
- N. Struch, C. Bannwarth, T. K. Ronson, Y. Lorenz, B. Mienert, N. Wagner, M. Engeser, E. Bill, R. Puttreddy, K. Rissanen, J. Beck, S. Grimme, J. R. Nitschke and A. Lützen, Angew. Chem., Int. Ed., 2017, 56, 4930–4935 CrossRef CAS PubMed
.
- R. A. Bilbeisi, S. Zarra, H. L. C. Feltham, G. N. L. Jameson, J. K. Clegg, S. Brooker and J. R. Nitschke, Chem.–Eur. J., 2013, 19, 8058–8062 CrossRef CAS PubMed
.
- K. J. Howard-Smith, A. R. Craze, H. Zenno, J. Yagyu, S. Hayami and F. Li, Chem. Commun., 2020, 56, 8838–8841 RSC
.
- L. J. Charbonnière, A. F. Williams, C. Piguet, G. Bernardinelli and E. Rivara-Minten, Chem.–Eur. J., 1998, 4, 485–493 CrossRef
.
- F. Tuna, M. R. Lees, G. J. Clarkson and M. J. Hannon, Chem.–Eur. J., 2004, 10, 5737–5750 CrossRef CAS
.
- L. Li, A. R. Craze, R. Akiyoshi, A. Tsukiashi, S. Hayami, O. Mustonen, M. M. Bhadbhade, S. Bhattacharyya, C. E. Marjo, Y. Wang, L. F. Lindoy, J. R. Aldrich-Wright and F. Li, Dalton Trans., 2018, 47, 2543–2548 RSC
.
- A. R. Craze, M. M. Bhadbhade, Y. Komatsumaru, C. E. Marjo, S. Hayami and F. Li, Inorg. Chem., 2020, 59, 1274–1283 CrossRef CAS PubMed
.
- D. Pelleteret, R. Clérac, C. Mathonière, E. Harte, W. Schmitt and P. E. Kruger, Chem. Commun., 2009, 221–223 RSC
.
- R. J. Archer, C. S. Hawes, G. N. L. Jameson, V. McKee, B. Moubaraki, N. F. Chilton, K. S. Murray, W. Schmitt and P. E. Kruger, Dalton Trans., 2011, 40, 12368–12373 RSC
.
- R. J. Archer, H. Scott, M. I. J. Polson, B. E. Williamson, C. Mathoniere, M. Rouzieres, R. Clerac and P. Kruger, Dalton Trans., 2018, 47, 7965–7974 RSC
.
- Y. Sunatsuki, R. Kawamoto, K. Fujita, H. Maruyama, T. Suzuki, H. Ishida, M. Kojima, S. Iijima and N. Matsumoto, Inorg. Chem., 2009, 48, 8784–8795 CrossRef CAS PubMed
.
- S. Yukinari, M. Hisashi, F. Kunihiro, S. Takayoshi, K. Masaaki and M. Naohide, Bull. Chem. Soc. Jpn., 2009, 82, 1497–1505 CrossRef
.
- M. Darawsheh, L. A. Barrios, O. Roubeau, S. J. Teat and G. Aromí, Chem.–Eur. J., 2016, 22, 8635–8645 CrossRef CAS PubMed
.
- W. R. Scheidt and C. A. Reed, Chem. Rev., 1981, 81, 543–555 CrossRef CAS
.
- E. V. Dose, M. F. Tweedle, L. J. Wilson and N. Sutin, J. Am. Chem. Soc., 1977, 99, 3886–3888 CrossRef CAS PubMed
.
- S. G. Sligar, Biochemistry, 1976, 15, 5399–5406 CrossRef CAS PubMed
.
- M. A. Hoselton, L. J. Wilson and R. S. Drago, J. Am. Chem. Soc., 1975, 97, 1722–1729 CrossRef CAS
.
- T. Kuroda-Sowa, R. Isobe, N. Yamao, T. Fukumasu, T. Okubo and M. Maekawa, Polyhedron, 2017, 136, 74–78 CrossRef CAS
.
- K. M. Kadish, K. Das, D. Schaeper, C. L. Merrill, B. R. Welch and L. J. Wilson, Inorg. Chem., 1980, 19, 2816–2821 CrossRef CAS
.
- T. Zhu, C. H. Su, D. Schaeper, B. K. Lemke, L. J. Wilson and K. M. Kadish, Inorg. Chem., 1984, 23, 4345–4349 CrossRef CAS
.
- M. G. Cowan, J. Olguín, S. Narayanaswamy, J. L. Tallon and S. Brooker, J. Am. Chem. Soc., 2012, 134, 2892–2894 CrossRef CAS PubMed
and front cover feature..
- J. N. McPherson, R. W. Hogue, F. S. Akogun, L. Bondì, E. T. Luis, J. R. Price, A. L. Garden, S. Brooker and S. B. Colbran, Inorg. Chem., 2019, 58, 2218–2228 CrossRef CAS PubMed
.
- T. Tanaka, Y. Sunatsuki and T. Suzuki, Inorg. Chim. Acta, 2020, 502, 119373 CrossRef CAS
.
- W. Linert, M. Enamullah, V. Gutmann and R. F. Jameson, Monatsh. Chem., 1994, 125, 661–670 CrossRef CAS
.
- S. Rodríguez-Jiménez, M. Yang, I. Stewart, A. L. Garden and S. Brooker, J. Am. Chem. Soc., 2017, 139, 18392–18396 CrossRef PubMed
.
- L. J. Kershaw Cook, R. Kulmaczewski, R. Mohammed, S. Dudley, S. A. Barrett, M. A. Little, R. J. Deeth and M. A. Halcrow, Angew. Chem., Int. Ed., 2016, 55, 4327–4331 CrossRef CAS PubMed
.
- M. Halcrow, Crystals, 2016, 6, 58 CrossRef
.
- C. J. Johnson, G. G. Morgan and M. Albrecht, J. Mater. Chem. C, 2015, 3, 7883–7889 RSC
.
- S. Sundaresan, J. A. Kitchen and S. Brooker, Inorg. Chem. Front., 2020, 7, 2050–2059 RSC
.
- S. Schlamp, P. Thoma and B. Weber, Eur. J. Inorg. Chem., 2012, 2759–2768 CrossRef CAS
.
- S. Rodríguez-Jiménez, A. S. Barltrop, N. G. White, H. L. C. Feltham and S. Brooker, Inorg. Chem., 2018, 57, 6266–6282 CrossRef PubMed
.
- R. Nowak, E. A. Prasetyanto, L. De Cola, B. Bojer, R. Siegel, J. Senker, E. Rossler and B. Weber, Chem. Commun., 2017, 53, 971–974 RSC
.
- J. G. Haasnoot, Coord. Chem. Rev., 2000, 200–202, 131–185 CrossRef CAS
.
- J. A. Kitchen and S. Brooker, Coord. Chem. Rev., 2008, 252, 2072–2092 CrossRef CAS
.
- H. L. C. Feltham, A. S. Barltrop and S. Brooker, Coord. Chem. Rev., 2017, 344, 26–53 CrossRef CAS
.
- R. Kulmaczewski, J. Olguín, J. A. Kitchen, H. L. C. Feltham, G. N. L. Jameson, J. L. Tallon and S. Brooker, J. Am. Chem. Soc., 2014, 136, 878–881 CrossRef CAS PubMed
.
- M. H. Klingele, B. Moubaraki, J. D. Cashion, K. S. Murray and S. Brooker, Chem. Commun., 2005, 987–989 RSC
and front cover feature..
- R. W. Hogue, H. L. C. Feltham, R. G. Miller and S. Brooker, Inorg. Chem., 2016, 55, 4152–4165 CrossRef CAS PubMed
.
- C. F. Herold, L. M. Carrella and E. Rentschler, Eur. J. Inorg. Chem., 2015, 2015, 3632–3636 CrossRef CAS
.
- C. Köhler and E. Rentschler, Eur. J. Inorg. Chem., 2016, 1955–1960 CrossRef
.
- C. F. Herold, S. I. Shylin and E. Rentschler, Inorg. Chem., 2016, 55, 6414–6419 CrossRef CAS PubMed
.
- F. Fürmeyer, L. M. Carrella, V. Ksenofontov, A. Möller and E. Rentschler, Inorg. Chem., 2020, 59, 2843–2852 CrossRef PubMed
.
- M. H. Klingele and S. Brooker, Eur. J. Org. Chem., 2004, 3422–3434 CrossRef CAS
.
- S. Singh, R. W. Hogue, H. L. C. Feltham and S. Brooker, Dalton Trans., 2019, 15435–15444 RSC
.
- S. Singh and S. Brooker, Inorg. Chem., 2020, 59, 1265–1273 CrossRef CAS PubMed
.
- A. Spek, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 9–18 CrossRef CAS PubMed
.
- A. Craze, N. Sciortino, M. Badbhade, C. Kepert, C. Marjo and F. Li, Inorganics, 2017, 5, 62 CrossRef
.
- N. G. White, J. A. Kitchen and S. Brooker, Eur. J. Inorg. Chem., 2009, 2009, 1172–1180 CrossRef
.
- K. F. Morris and C. S. Johnson, J. Am. Chem. Soc., 1993, 115, 4291–4299 CrossRef CAS
.
- K. F. Morris and C. S. Johnson, J. Am. Chem.
Soc., 1992, 114, 3139–3141 CrossRef CAS
.
- D. Fujita, Y. Ueda, S. Sato, N. Mizuno, T. Kumasaka and M. Fujita, Nature, 2016, 540, 563–566 CrossRef CAS PubMed
.
- K. Gu, J. Onorato, S. S. Xiao, C. K. Luscombe and Y.-L. Loo, Chem. Mater., 2018, 30, 570–576 CrossRef CAS
.
- S. Vázquez-Leyva, L. Vallejo-Castillo, C. A. López-Morales, J. E. Herbert-Pucheta, L. G. Zepeda-Vallejo, M. Velasco-Velázquez, L. Pavón, S. M. Pérez-Tapia and E. Medina-Rivero, Anal. Chem., 2019, 91, 14392–14400 CrossRef PubMed
.
- P. S. Pregosin, P. G. A. Kumar and I. Fernández, Chem. Rev., 2005, 105, 2977–2998 CrossRef CAS PubMed
.
- H. Takezawa, T. Murase, G. Resnati, P. Metrangolo and M. Fujita, Angew. Chem., Int. Ed., 2015, 54, 8411–8414 CrossRef CAS PubMed
.
- D. Fujita, Y. Ueda, S. Sato, H. Yokoyama, N. Mizuno, T. Kumasaka and M. Fujita, Chem, 2016, 1, 91–101 CAS
.
- Q. F. Sun, J. Iwasa, D. Ogawa, Y. Ishido, S. Sato, T. Ozeki, Y. Sei, K. Yamaguchi and M. Fujita, Science, 2010, 328, 1144–1147 CrossRef CAS PubMed
.
- M. Tominaga, K. Suzuki, M. Kawano, T. Kusukawa, T. Ozeki, S. Shakamoto, K. Yamaguchi and M. Fujita, Angew. Chem., Int. Ed., 2004, 43, 5621–5625 CrossRef CAS PubMed
.
- S. Denis-Quanquin, F. Riobé, M.-A. Delsuc, O. Maury and N. Giraud, Chem.–Eur. J., 2016, 22, 18123–18131 CrossRef CAS PubMed
.
- M. P. Crockett, H. Zhang, C. M. Thomas and J. A. Byers, Chem. Commun., 2019, 55, 14426–14429 RSC
.
- C. Bartual-Murgui, S. Vela, M. Darawsheh, R. Diego, S. J. Teat, O. Roubeau and G. Aromi, Inorg. Chem. Front., 2017, 4, 1374–1383 RSC
.
- B. Weber and F. A. Walker, Inorg. Chem., 2007, 46, 6794–6803 CrossRef CAS PubMed
.
-
O. Kahn, Molecular Magnetism, VCH Publishers Inc., New York, 1993 Search PubMed
.
- L. A. Yatsunyk and F. A. Walker, Inorg. Chem., 2004, 43, 757–777 CrossRef CAS PubMed
.
- D. F. Evans, J. Chem. Soc., 1959, 2003–2005 RSC
.
- I. Nikovskiy, A. Polezhaev, V. Novikov, D. Aleshin, A. Pavlov, E. Saffiulina, R. Aysin, P. Dorovatovskii, L. Nodaraki, F. Tuna and Y. Nelyubina, Chem.–Eur. J., 2020, 26, 5629–5638 CrossRef CAS PubMed
.
-
F. A. Cotton, G. Wilkinson, C. A. Murillo and M. Bochmann, Advanced Inorganic Chemistry, John Wiley & Sons, Inc., New York, 6th edn, 1999 Search PubMed
.
- S. M. Hart, J. C. A. Boeyens and R. D. Hancock, Inorg. Chem., 1983, 22, 982–986 CrossRef CAS
.
- D. C. Ashley and E. Jakubikova, Inorg. Chem., 2018, 57, 9907–9917 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental section, crystallographic information, DOSY spectra, NMR spectra, MS spectra, UV-vis spectra, cyclic voltammograms, previously reported SCO-active Fe(II) dinuclear helicates, solid state SCO. CCDC 2061247–2061253, 2090518 and 2090519. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc01458g |
| This journal is © The Royal Society of Chemistry 2021 |