 Open Access Article
Open Access ArticleSignature of the neighbor's quantum nuclear dynamics in the electron transfer mediated decay spectra†
Aryya
Ghosh
ab,
Lorenz S.
Cederbaum
 *a and
Kirill
Gokhberg
a
*a and
Kirill
Gokhberg
a
aTheoretische Chemie, Physikalisch-Chemisches Institut, Universität Heidelberg, Im Neuenheimer Feld 229, D-69120 Heidelberg, Germany. E-mail: lorenz.cederbaum@pci.uni-heidelberg.de
bDepartment of Chemistry, Ashoka University, Sonipat, India
First published on 9th June 2021
Abstract
We computed fully quantum nuclear dynamics, which accompanies electron transfer mediated decay (ETMD) in weakly bound polyatomic clusters. We considered two HeLi2 clusters – with Li2 being either in the singlet electronic ground state or in the triplet first excited state – in which ETMD takes place after ionization of He. The electron transfer from Li2 to He+ leads to the emission of another electron from Li2 into the continuum. Due to the weak binding of He to Li2 in the initial states of both clusters, the involved nuclear wavepackets are very extended. This makes both the calculation of their evolution and the interpretation of the results difficult. We showed that despite the highly delocalized nature of the wavepackets the nuclear dynamics in the decaying state is imprinted on the ETMD electron spectra. The analysis of the latter helps understanding the effect which electronic structure and binding strength in the cluster produce on the quantum motion of the nuclei in the decaying state. The results produce a detailed picture of this important charge transfer process in polyatomic systems.
Electron transfer to positive ions in chemical medium can proceed through a variety of processes which involve non-adiabatic effects like the crossing of potential energy surfaces,1 photon emission,2–4 or emission of electrons.5–7 Electron transfer mediated decay or ETMD is a prominent member in the latter group and is most common for singly or multiply charged positive ions, which are produced in clusters or solutions by ionizing radiation.8–22 It occurs whenever the electron attachment energy of the ion exceeds the threshold for double ionization of the surrounding host matrix. In ETMD, electron transfer from a neighboring atom or molecule to the ion leads to its (partial) neutralization and is accompanied by the emission of another electron from the same (ETMD(2)) or a different (ETMD(3)) neighbor.
To estimate its importance we first notice that from the mechanistic standpoint ETMD is an electronic decay process. Therefore, its lifetimes can be computed using established ab initio techniques.7 They were found to be in the picosecond range for van der Waals clusters,8,10,13,23 while for hydrated metal cations the lifetime becomes as short as a few tens of femtoseconds.9,12 As a consequence, if ETMD is energetically allowed, and the ion is in an electronic state for which the other faster electronic decay processes Auger decay or interatomic coulombic decay (ICD) are forbidden, ETMD becomes the leading electron transfer mechanism.23,24 To date it has been experimentally observed in clusters or solutions, where the ion was prepared in the ground or a low-lying electronic state.15–22
ETMD can be seen as incorporating two familiar processes – charge transfer and ionization. Therefore, it is a pathway to either partial neutralization of a cation or double ionization of atoms or molecules in its vicinity. As we demonstrate in our article, by doubly ionizing a molecular neighbor, ETMD can lead to the breaking of covalent bonds. Thus, in aqueous solutions ETMD was shown to efficiently produce radical species by ionizing water molecules,9,12,20 which dissociate as the result. The produced radicals undergo reactions with other molecules present in the vicinity. Radiative damage to DNA is caused by slow electrons and radical species formed in its vicinity.25 ETMD is an efficient process producing such electrons and radicals.
ETMD has been also utilized to produce and study the properties of dications embedded in He nanodroplets. Such droplets are known to serve as ‘refrigerators’ for the immersed dopants.26 Following ionization of He, ETMD takes place with the resulting He+ producing a dication of the dopant which is efficiently cooled and stabilized by the He-matrix. The technique was used to study stability of small doubly charged Mg clusters.17 The formation of dications and the investigation of their stability have been reported in experiments on alkali27 and coronene clusters28 in Hen. Reactions involving molecular dications are of general interest. They occur even under the extreme conditions of the interstellar medium and are responsible for the appearance of polyatomic molecules in the space.29 They can be modeled in doped He nanodroplets, as was demonstrated in the case of the C60–H2O cluster.30
Generation of positive ions in van der Waals clusters or in solutions via photon absorption or charged particle impact is nearly sudden, and leads to highly non-equilibrium nuclear configurations. Since the ETMD lifetimes at these geometries are usually comparable or longer than the characteristic vibrational periods in the ion-neighbor modes, it is usually accompanied by vibrational motion. Computations in atomic van der Waals clusters show10,13 that vibrational motion, which follows ionization of some atom, tends on average to decrease the distance between the resulting ion and its neighbors and leads to the shortening of the effective ETMD lifetimes by as much as an order of magnitude. As a consequence, the spectra of ETMD electrons differ from the spectra which would be obtained at fixed nuclei.13 Importantly, in dimers the vibrational wavepacket is imprinted onto the electron or kinetic energy release of the nuclei (KER) spectra, if the potential energy curve of the final state is repulsive, and the dimer disintegrates at the end of the process.13 This is a common feature in interatomic electronic decay of diatomic clusters.31 It was used to predict and observe the vibrational wave functions in highly excited He2+ which underwent ICD.32 Coupled with ingenious timing techniques such as post collision interaction (PCI) clock,33 this feature was used to experimentally reconstruct the wave packet evolution during ICD in rare gas dimers.34
In ETMD in atomic van der Waals dimers the wave packet evolves over the entire potential energy curve. Since the decay width decreases exponentially with the interatomic distance,8,13,23 ETMD occurs predominantly at the inner repulsive wall.13 This picture simplifies the qualitative analysis of ETMD spectra in dimers. However, no numerical results and no similar picture exist for ETMD in clusters of more than two atoms, due to the complexity of the necessary computations. It becomes more difficult to obtain highly energetic potential energy surfaces (PES) of the decaying electronic states in more than one dimension and calculate the respective position dependent decay widths. Moreover, already for a triatomic system one needs to consider the dynamics of three coupled vibrational modes in the decaying and final states over an extended spatial range. This situation in theory is mirrored by the one in experiment, where ETMD was observed either in dimers or in large clusters but not in trimers.
In this letter we present for the first time the computational results of the full quantum dynamics during ETMD in a triatomic system. Here we choose the HeLi2 cluster which is a basic unit suggested by the experiments on ionization of helium droplets doped with alkali dimers.22 A particular property of these systems is that the alkali dimers can be produced on the surface of a droplet in two different electronic states – the singlet ground state 1Σ+g or the triplet first excited state 3Σ+u – which have widely different binding properties. Thus, Li2(1Σ+g) is a molecule with binding energy of 1 eV, while Li2(3Σ+u) is itself a weakly bound (41 meV) dimer held together by a van der Waals force.35 Correspondingly, following the ionization of He, the HeLi2(1Σ+g) and HeLi2(3Σ+u) clusters are expected to undergo ETMD(2) and ETMD(3) respectively. It is the goal of this investigation to uncover the differences in the quantum nuclear dynamics which accompanies these processes and to relate them to the differences in the observable spectra.
The following equation summarizes the decay process
| He+Li2 → HeLi+Li+ + eETMD, | (1) |
To analyse the nuclear dynamics and to compute the energies of ETMD electrons we numerically solved the following system of equations for the vibrational wavepackets |Ψd(t)〉 and |Ψf(E,t)〉 in the decaying and final states37,38
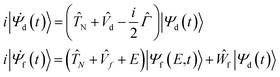 | (2) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) N operator is the operator of the kinetic energy of the nuclei, while
N operator is the operator of the kinetic energy of the nuclei, while ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) d and
d and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) f operators are respectively the PES of the decaying and the final state f, and E is the energy of the emitted ETMD electron. The quantities Ŵf and
f operators are respectively the PES of the decaying and the final state f, and E is the energy of the emitted ETMD electron. The quantities Ŵf and ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) are the ETMD amplitude for the transition to the final state f and the total decay width, which is obtained by summing over all final states accessible from the decaying state. In our case ETMD and radiative charge transfer or RCT3,4 are the only possible decay processes, and RCT is several orders of magnitude slower than ETMD.4,23 Neglecting its contribution to the total width and taking into account that for the cluster in question there is a single ETMD final state we find Γ = 2π|Ŵf|2.
are the ETMD amplitude for the transition to the final state f and the total decay width, which is obtained by summing over all final states accessible from the decaying state. In our case ETMD and radiative charge transfer or RCT3,4 are the only possible decay processes, and RCT is several orders of magnitude slower than ETMD.4,23 Neglecting its contribution to the total width and taking into account that for the cluster in question there is a single ETMD final state we find Γ = 2π|Ŵf|2.
The PES, decay amplitude and width are functions of nuclear coordinates Q. For the system in question we used the Jacobi coordinates R, r, and θ, which stand respectively for the distance from He to the Li2 center of mass, Li–Li distance, and the angle between the Li2 molecular axis and the line connecting He with the center of mass of Li2 (see Fig. 1 in the ESI†). Assuming instantaneous ionization of the cluster we set |Ψd(t = 0)〉 = |Ψi〉 and |Ψf(E,t = 0)〉 = 0, where |Ψi〉 is the vibrational ground state in the initial electronic state of the respective cluster. To avoid wavepacket reflection from the end of the grid we employed cubic complex absorbing potential (CAP). We used the wavepacket |Ψd(t)〉 to analyse the nuclear motion in the decaying state and to estimate the ETMD lifetime from the respective survival probability. The wavepacket |Ψf〉(E,t) is used for computing the electron spectrum as observed either at some time instant t or at some very long time when the decay is essentially over
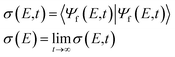 | (3) |
Strong delocalization of the initial wavefunction precludes the analysis of the dynamics in the decaying state in terms of moving wavepackets. However, information about the evolution of the vibrational state can be obtained from the behavior of the survival probability 〈Ψd(t)|Ψd(t)〉 with time. We found that in the HeLi2(1Σ+g) cluster up to t = 15 ps it decays nearly exponentially with the lifetime τ = 12 ps.41 Beyond that time while the decay remains nearly exponential the lifetime τ increases to 17 ps. Additional analysis of the survival probability with Γ set to zero in eqn (2) led to the following picture of the events. In the ionization event the vertical transition of the delocalized initial wavefunction Ψi(Q) to the PES of the decaying state populates vibrational states which lie both below and above the He+/Li2 dissociation threshold. In the nuclear dynamics which follows, He+ is first pulled towards and collides with Li2. Whereupon the continuum part of the wavepacket propagates outwards along the coordinate R until it reaches the CAP and is absorbed by it, while the bound part remains trapped in the potential and decays by ETMD.
The shorter lifetime of |Ψd(t)〉 at the times below 15 ps reflects both the electronic decay via ETMD, and the dissociation of a part of He+Li2 clusters into the He+/Li2 channel. The longer decay lifetime beyond 15 ps reflects only the ETMD of the remaining bound He+Li2(1Σ+g) clusters. While it is difficult to compute the accurate ETMD-to-dissociation branching ratio, our calculations show that up to 30% of HeLi2(1Σ+g) clusters would dissociate following the ionization of He in the absence of ETMD. Similar picture holds for the HeLi2(3Σ+u) clusters, although a larger proportion (57% in the absence of ETMD) of them dissociates after sudden ionization of He due to the breaking of the much weaker Li–Li bond. We also estimated the effective lifetime of He+Li2(1Σ+g) clusters due to ETMD alone as 19.8 ps, while for the He+Li2(3Σ+u) clusters it is 21.5 ps. The difference between them is insignificant, so that the electronic structure of the cluster has little effect on the overall decay rate. However, nuclear dynamics leads to effective ETMD lifetimes which are almost an order of magnitude shorter than the purely electronic lifetimes corresponding to the equilibrium geometries in the initial state.
More information about the dynamics can be derived from the ETMD electron spectra of the respective singlet and triplet HeLi2 clusters. The emitted electron spectrum which results from the decay of the He+Li2(1Σ+g) state is shown in Fig. 1. The ETMD peak is located between 7 eV and 8 eV. Its position coincides with the interval (6.8 eV to 7.8 eV) of expected ETMD electron energies, which we estimated from purely electronic considerations in the previous publication.36 There we assumed that the decay predominantly occurs at the configurations of the nuclei where two conditions are fulfilled: the relative velocities of the nuclei are small and the ETMD rate is large. We also kept the Li–Li distance r constant, under assumption that it would not change much in the strongly bound Li2(1Σ+g) state. While this simple model works surprisingly well in estimating the position and width of the ETMD peak, it fails to reproduce the main finding of the full dynamics, namely, that the spectrum exhibits structure despite the strongly delocalized nuclear wavepacket involved. We observe peaks at 7.24 eV, 7.39 eV, 7.44 eV and a shoulder at 7.58 eV. The distances between the nearest peaks vary between 50 meV and 150 meV. To trace their origin we can compare these numbers with some characteristic frequencies in our system. The fundamental frequencies of Li2(1Σ+g) and in the electronic ground state of He+Li (a possible product) are 42 meV (10.2 THz) and 30 meV (7.3 THz), while the fundamental frequency in the R-mode in He+–Li2 is 32 meV (7.7 THz). None of these numbers can adequately explain the progression observed in the spectrum.
 | ||
| Fig. 1 ETMD electron spectra obtained following the ionization of He in the He–Li2(1Σ+g) cluster. (upper panel) Electron spectrum obtained following wavepacket propagation on the full three-dimensional surface of the decaying state. Red rectangle shows the position of the peak as estimated from electronic properties in ref. 36. (lower panel) Electronic spectra obtained following wavepacket propagation on reduced two-dimensional surfaces of the decaying state. Green line – propagation on the 2D-cut (R, r, θ = 0); red line – propagation on the 2D-cut (R, r, θ = π/2); broken gray line – propagation on the 2D-cut (R, θ, r = req). All spectra are scaled to have the same absolute maximum. | ||
To clarify how the vibrational structure comes about we computed ETMD spectra by running nuclear dynamics on three reduced two-dimensional surfaces of the decaying state. First, we kept the Li–Li distance r fixed at the equilibrium distance req = 2.69 Å of the Li2(1Σ+g) so that He+ moves around and collides with rigid Li2. The resulting spectrum is shown as the broken line in Fig. 1. It appears as a single peak whose position and width coincide with those of the peak in the full three-dimensional spectrum. However, it lacks any vibrational structure observed in the latter. Keeping θ fixed but allowing vibrational motion along the Li–Li coordinate r leads to a dramatic change in the spectral shape. The spectra computed at θ = 0 and θ = π/2 lie both in the same energy window as the spectrum obtained at constant r. However, while the former is a broad featureless peak, the latter two appear as vibrational progressions. The spectrum at θ = π/2 shows peaks with spacings between them being between 80 meV to 180 meV. The spectrum at θ = 0 appears mostly as three peaks spaced by about 200 meV; two of these peaks are in turn split into peaks separated by about 50 meV. Importantly, one can see the correspondence between the peaks in the full spectrum and the structure in the spectra obtained on these reduced 2D surfaces. For example, the leftmost peak at 7.24 eV originates from the leftmost peak (7.31 eV) of the θ = 0 spectrum; likewise, the shoulder at 7.58 eV corresponds to the pronounced peak at 7.64 eV in the θ = π/2 spectrum. The peaks between these two extremes can be also recognized in the two-dimensional spectra.
Consequently, the vibrational structure in the ETMD electron spectra of the He+Li2(1Σ+g) state can be traced to the vibration of the Li2 molecule. The remaining question is why the spacing between the peaks both in the full and reduced two-dimensional spectra at fixed θ is larger than characteristic vibrational frequencies in the decaying or the final states. One arrives at a plausible answer if one follows the chain of processes set off by sudden ionization of He. The appearance of the positive charge on He leads to the change in the Li–Li interaction potential. This change becomes more pronounced as the He–Li2 distance R decreases.36 The sudden perturbation of Li2 due to ionization of He, and the transfer of vibrational energy from the He–Li2 mode during the dynamics that follows lead to the population of excited states in the Li–Li mode. The final state PES, Vf, is repulsive along the coordinate r and behaves nearly as 1/r. Therefore, changing r at which the decay occurs by 0.1 Å about req = 2.69 Å shifts the energy of emitted electrons by 200 meV. On the contrary, the energy of the emitted electrons is less sensitive to changes in the coordinates R and θ. Thus, the vibrational progression in the ETMD electron spectra in Fig. 1 is the imprint of the vibrational wavepacket in the Li–Li mode. This conclusion is supported by the analysis of the vibrational eigenfunctions, ϕn(r), of the Li2(1Σ+g) molecule. Indeed, the distance between the nearest maxima of the |ϕn(r)|2 varies between 0.23 Å for n = 3 to 0.15 Å for n = 10; the projection of these states onto the repulsive Li+–Li+ potential curve would result in the peaks in electron spectra separated by a few hundred meV. This picture of a triatomic cluster is the generalization of observations made in the previous ab initio computations and experiments in diatomic clusters, which demonstrated that electronic decay onto repulsive potential energy curve imprinted the vibrational structure of the decaying state onto the spectra of emitted electrons or kinetic energy release of the nuclei.31,32,34,42
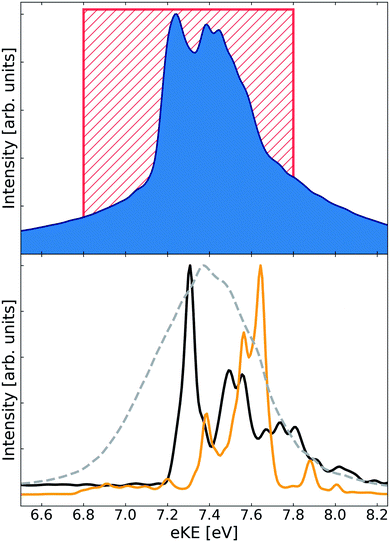
The electron spectra arising from the decay of He+Li2(3Σ+u) are shown in Fig. 2. The ETMD peak is located between 7.75 eV and 9.25 eV. The full spectrum fits less well to the range of electron energies (8.1 eV to 10.2 eV) we determined previously using a simple model similar to the one explained above for the singlet cluster. The only difference between the models was that in the case of the triplet cluster we kept the angle θ = π/2 constant and not the Li–Li distance r. Although unexpected, due to the weak Li–Li bond, the spectrum again shows a pronounced structure with peaks at 8.04 eV, 8.20 eV, 8.38 eV and a shoulder at 8.56 eV. As in the case of the He+Li2(1Σ+g) cluster the spectrum obtained when keeping the Li–Li distance, r, fixed at the respective equilibrium distance appears as a featureless peak. It is relaxing r that leads to the structure appearing in the electron spectrum.
 | ||
| Fig. 2 ETMD electron spectra obtained following the ionization of He in the He–Li2(3Σ+u) cluster. (upper panel) Electronic spectrum obtained following wavepacket propagation on the full three-dimensional surface of the decaying state. Red rectangle shows the position of the peak as estimated from the potential energy surfaces at the T-shaped geometry of the cluster (see ref. 36). (lower panel) Electronic spectra obtained following wavepacket propagation on reduced two-dimensional surfaces of the decaying state. Green line – propagation on the 2D-cut (R, r, θ = 0); red line – propagation on the 2D-cut (R, r, θ = π/2); broken gray line – propagation on the 2D-cut (R, θ, r = req). All spectra are scaled to have the same absolute maximum. | ||
It is interesting to compare the spectra of the two systems, which represent two classes of clusters: a molecule–atom cluster (HeLi2(1Σ+g)), and a triatomic van der Waals cluster (HeLi2(3Σ+u)). The first obvious difference is how well the electron spectra obtained for the reduced two-dimensional PES match the respective full spectra. In the case of the HeLi2(1Σ+g) cluster the three spectra on different reduced surfaces lie within the envelope of the full spectrum. Moreover, there is strong overlap between the full spectrum and the spectra when θ is held constant at 0 and π/2. This indicates that He+ moves around Li2 unhindered and explores the regions characterized by different values of θ with comparable probabilities. In addition, the peaks in the full spectrum correspond to the peaks in spectra obtained at constant θ, and can be related to the vibrational excitations in the Li–Li mode. These results confirm our assumption of an ETMD(2) process between He+ and Li2 in the HeLi2(1Σ+g) cluster. They also explain the excellent correspondence between the computed spectrum and the range of energies of the emitted electrons found assuming rigid Li2 (see Fig. 1).
In the case of the HeLi2(3Σ+u) cluster only one of the spectra obtained on the reduced surfaces (θ = 0) overlaps strongly with the full spectrum. In addition, it becomes more difficult to relate the latter's structure to the peaks in spectra obtained at θ = 0 and θ = π/2. This indicates a breakdown of the atom–molecule model, which worked well in the previous case. Indeed, one would expect the effect of the ionization of He and the subsequent dynamics to be sufficient for breaking the weak Li–Li bond. Thus, the structure in the electron spectra, while carrying the image of the vibrational wavepacket reflected in the dissociative final state PES, cannot be interpreted as arising through the vibrationally excited Li2 molecule. It seems, that in the weakly bound triatomic HeLi2(3Σ+u) cluster all degrees of freedom are equally important in shaping the ETMD electron spectrum, as one would expect for an ETMD(3) process. The structure seen in the spectrum is most probably due to interference effects in the dynamics of an enormously extended wavepacket.
In conclusion, we computed nuclear dynamics which accompanies electronic transfer mediated decay (ETMD) in different metastable electronic states of the weakly bound triatomic HeLi2 cluster. The computations were made particularly challenging by the necessity to compute quantum dynamics on three-dimensional complex surfaces of the decaying states, and by the enormous extent of the wavepackets due to the extremely weak binding of Li2 to He in the initial states. We showed that the nuclear wavepacket which evolves on the PES of the ETMD state following the ionization of He is imprinted on the ETMD electron spectra. This becomes possible since the potential energy surface of the final state is repulsive along the Li–Li coordinate. Due to the extremely weak binding of He to Li2 and strong delocalization of the wavepackets, no semiclassical description of the dynamics is possible. However, the analysis of the spectra helps understanding how the nuclear motion in the decaying state depends on the electronic structure and binding in the cluster. In HeLi2(1Σ+g), where Li–Li bond is strong, the dynamics is dominated by the motion of He+ around the Li2 molecule. The vibrational excitation of Li2 – which occurs both in the sudden ionization of He and through the energy transfer from other modes during the dynamics – appears as a characteristic structure in the electronic peak. In the HeLi2(3Σ+u) cluster the weak Li–Li bond is quickly broken and contributions of dynamics in different modes to the electron spectrum cannot be disentangled. Surprisingly, the spectrum still carries the imprint of the vibrational motion, which disappears if we freeze the dynamics along the Li–Li coordinate.
The effects described in this work can be observed in other experimentally realizable systems. Suitable candidates are the rare-gas trimers NeXe2 and NeKr2. After core ionization of Ne, a fast Auger decay takes place producing of Ne2+(2p−2) cations. The ETMD(3) channel is open in these rare-gas trimers as has been shown before.10,13 Another system of potential interest to experimentalists is Ne–H2O. Despite the high double ionization potential of water (≈39 eV (ref. 43)), the ETMD channel is open in the Franck–Condon region for the Ne2+(2p−2 1S) state. Following ETMD, the doubly ionized H2O would dissociate in a number of channels like OH+/H+ or 2H+/O along strongly repulsive potential surfaces44 such that the signature of the vibrational motion of water can be observed in the ETMD spectra. Importantly, water fragmentation and KER of ions in different dissociation channels were investigated experimentally for the one-photon double ionization of water monomer.45 This also offers an opportunity to compare the KER in the same dicationic states of water produced via different double ionization mechanisms. The simpler systems studied in this letter can thus serve as a model for the ETMD(2) and ETMD(3) processes in such ion–molecule or weakly bound atomic clusters.
Data availability
Additional data are available on request.Author contributions
AG and KG carried out the calculations. All authors equally contributed to writing the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Dieter Meyer and Markus Schröder for their help with the Heidelberg MCTDH package. Financial support by the European Research Council (ERC) (Advanced Investigator Grant No. 692657) is gratefully acknowledged.References
- H. Nakamura, Semiclassical approach to charge-transfer processes in ion-molecule collisions, in Advances in Chemical Physics, John Wiley & Sons, Ltd, 1992, pp. 243–319 Search PubMed.
- R. Johnsen and M. A. Biondi, Measurements of radiative charge-transfer reactions of doubly and singly charged rare-gas ions with rare-gas atoms at thermal energies, Phys. Rev. A: At., Mol., Opt. Phys., 1978, 18, 996–1003 Search PubMed.
- N. Saito, Y. Morishita, I. Suzuki, S. Stoychev, A. Kuleff, L. Cederbaum, X.-J. Liu, H. Fukuzawa, G. Prümper and K. Ueda, Evidence of radiative charge transfer in argon dimers, Chem. Phys. Lett., 2007, 441, 16–19 Search PubMed.
- A. Hans, V. Stumpf, X. Holzapfel, F. Wiegandt, P. Schmidt, C. Ozga, P. Reiß, L. B. Ltaief, C. Küstner-Wetekam, T. Jahnke, A. Ehresmann, P. V. Demekhin, K. Gokhberg and A. Knie, Direct evidence for radiative charge transfer after inner-shell excitation and ionization of large clusters, New J. Phys., 2018, 20, 012001 Search PubMed.
- R. Carmina Monreal, Auger neutralization and ionization processes for charge exchange between slow noble gas atoms and solid surfaces, Prog. Surf. Sci., 2014, 89, 80–125 Search PubMed.
- A. B. Voitkiv, Transfer ionization in collisions with a fast highly charged ion, Phys. Rev. Lett., 2013, 111, 043201 Search PubMed.
- T. Jahnke, U. Hergenhahn, B. Winter, R. Dörner, U. Frühling, P. V. Demekhin, K. Gokhberg, L. S. Cederbaum, A. Ehresmann, A. Knie and A. Dreuw, Interatomic and Intermolecular Coulombic Decay, Chem. Rev., 2020, 120, 11295 Search PubMed.
- J. Zobeley, R. Santra and L. S. Cederbaum, Electronic decay in weakly bound heteroclusters: energy transfer versus electron transfer, J. Chem. Phys., 2001, 115, 5076 Search PubMed.
- I. B. Müller and L. S. Cederbaum, Electronic decay following ionization of aqueous Li+ microsolvation clusters, J. Chem. Phys., 2005, 122, 094305 Search PubMed.
- V. Stumpf, P. Kolorenč, K. Gokhberg and L. S. Cederbaum, Efficient pathway to neutralization of multiply charged ions produced in Auger processes, Phys. Rev. Lett., 2013, 110, 258302 Search PubMed.
- J. P. Zobel, N. V. Kryzhevoi and M. Pernpointner, Communication: electron transfer mediated decay enabled by spin-orbit interaction in small krypton/xenon clusters, J. Chem. Phys., 2014, 140, 161103 Search PubMed.
- V. Stumpf, K. Gokhberg and L. S. Cederbaum, The role of metal ions in X-ray-induced photochemistry, Nat. Chem., 2016, 8, 237 Search PubMed.
- V. Stumpf, S. Scheit, P. Kolorenč and K. Gokhberg, Electron transfer mediated decay in NeXe triggered by K-LL Auger decay of Ne, Chem. Phys., 2017, 482, 192 Search PubMed.
- E. Fasshauer, M. Förstel, M. Mucke, T. Arion and U. Hergenhahn, Theoretical and experimental investigation of Electron Transfer Mediated Decay in ArKr clusters, Chem. Phys., 2017, 482, 226 Search PubMed.
- M. Förstel, M. Mucke, T. Arion, A. M. Bradshaw and U. Hergenhahn, Autoionization mediated by electron transfer, Phys. Rev. Lett., 2011, 106, 033402 Search PubMed.
- K. Sakai, S. Stoychev, T. Ouchi, I. Higuchi, M. Schöffler, T. Mazza, H. Fukuzawa, K. Nagaya, M. Yao, Y. Tamenori, A. I. Kuleff, N. Saito and K. Ueda, Electron-transfer-mediated decay and interatomic coulombic decay from the triply ionized states in argon dimers, Phys. Rev. Lett., 2011, 106, 033401 Search PubMed.
- A. C. LaForge, V. Stumpf, K. Gokhberg, J. von Vangerow, F. Stienkemeier, N. V. Kryzhevoi, P. O'Keeffe, A. Ciavardini, S. R. Krishnan, M. Coreno, K. C. Prince, R. Richter, R. Moshammer, T. Pfeifer, L. S. Cederbaum and M. Mudrich, Enhanced Ionization of Embedded Clusters by Electron-Transfer-Mediated Decay in Helium Nanodroplets, Phys. Rev. Lett., 2016, 116, 203001 Search PubMed.
- T. Ouchi, H. Fukuzawa, K. Sakai, T. Mazza, M. Schöffler, K. Nagaya, Y. Tamenori, N. Saito and K. Ueda, Interatomic coulombic decay and electron-transfer-mediated decay following triple ionization of Ne2 and NeAr, Chem. Phys., 2017, 482, 244 Search PubMed.
- D. You, H. Fukuzawa, Y. Sakakibara, T. Takanashi, Y. Ito, G. G. Maliyar, K. Motomura, K. Nagaya, T. Nishiyama, K. Asa, Y. Sato, N. Saito, M. Oura, M. Schöffler, G. Kastirke, U. Hergenhahn, V. Stumpf, K. Gokhberg, A. I. Kuleff, L. S. Cederbaum and K. Ueda, Charge transfer to ground-state ions produces free electrons, Nat. Commun., 2017, 8, 14277 Search PubMed.
- I. Unger, R. Seidel, S. Thürmer, M. N. Pohl, E. F. Aziz, L. S. Cederbaum, E. Muchová, P. Slavíček, B. Winter and N. V. Kryzhevoi, Observation of electron-transfer-mediated decay in aqueous solution, Nat. Chem., 2017, 9, 708 Search PubMed.
- M. N. Pohl, C. Richter, E. Lugovoy, R. Seidel, P. Slavíček, E. F. Aziz, B. Abel, B. Winter and U. Hergenhahn, Sensitivity of Electron Transfer Mediated Decay to Ion Pairing, J. Phys. Chem. B, 2017, 121, 7709 Search PubMed.
- L. B. Ltaief, M. Shcherbinin, S. Mandal, S. R. Krishnan, R. Richter, T. Pfeifer, M. Bauer, A. Ghosh, M. Mudrich, K. Gokhberg and A. LaForge, Electron transfer mediated decay of alkali dimers attached to He nanodroplets, Phys. Chem. Chem. Phys., 2020, 22, 8557 Search PubMed.
- V. Stumpf, N. V. Kryzhevoi, K. Gokhberg and L. S. Cederbaum, Enhanced one-photon double ionization of atoms and molecules in an environment of different species, Phys. Rev. Lett., 2014, 112, 193001 Search PubMed.
- V. Averbukh and L. S. Cederbaum, “Ab initio calculation of interatomic decay rates by a combination of the Fano ansatz, Green's-function methods, and the Stieltjes imaging technique, J. Chem. Phys., 2005, 123, 204107 Search PubMed.
- E. Alizadeh, T. M. Orlando and L. Sanche, Biomolecular Damage Induced by Ionizing Radiation: The Direct and Indirect Effects of Low-Energy Electrons on DNA, Annu. Rev. Phys. Chem., 2015, 66, 379 Search PubMed.
- S. Yang and A. M. Ellis, Helium droplets: a chemistry perspective, Chem. Soc. Rev., 2013, 42, 472–484 Search PubMed.
- M. Mahmoodi-Darian, S. Raggl, M. Renzler, M. Goulart, S. E. Huber, A. Mauracher, P. Scheier and O. Echt, Doubly charged coronene clusters—much smaller than previously observed, J. Chem. Phys., 2018, 148, 174303 Search PubMed.
- M. Renzler, M. Harnisch, M. Daxner, L. Kranabetter, M. Kuhn, P. Scheier and O. Echt, Fission of multiply charged alkali clusters in helium droplets – approaching the Rayleigh limit, Phys. Chem. Chem. Phys., 2016, 18, 10623–10629 Search PubMed.
- D. K. Böhme, Multiply-charged ions and interstellar chemistry, Phys. Chem. Chem. Phys., 2011, 13, 18253–18263 Search PubMed.
- S. Denifl, F. Zappa, I. Mähr, F. Ferreira da Silva, A. Aleem, A. Mauracher, M. Probst, J. Urban, P. Mach, A. Bacher, O. Echt, T. Märk and P. Scheier, Ion–molecule reactions in helium nanodroplets doped with c60 and water clusters, Angew. Chem., 2009, 48, 8940–8943 Search PubMed.
- N. Moiseyev, R. Santra, J. Zobeley and L. S. Cederbaum, Fingerprints of the nodal structure of autoionizing vibrational wave functions in clusters: interatomic coulombic decay in Ne dimer, J. Chem. Phys., 2001, 114, 7351 Search PubMed.
- N. Sisourat, N. V. Kryzhevoi, P. Kolorenč, S. Scheit, T. Jahnke and L. S. Cederbaum, Ultralong-range energy transfer by interatomic coulombic decay in an extreme quantum system, Nat. Phys., 2010, 6, 508 Search PubMed.
- U. Frühling, F. Trinter, F. Karimi, J. B. Williams and T. Jahnke, Time-resolved studies of interatomic coulombic decay, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 237–244 Search PubMed.
- F. Trinter, J. B. Williams, M. Weller, M. Waitz, M. Pitzer, J. Voigtsberger, C. Schober, G. Kastirke, C. Müller, C. Goihl, P. Burzynski, F. Wiegandt, T. Bauer, R. Wallauer, H. Sann, A. Kalinin, L. Schmidt, M. Schöffler, N. Sisourat and T. Jahnke, Evolution of Interatomic Coulombic Decay in the Time Domain, Phys. Rev. Lett., 2013, 111, 093401 Search PubMed.
- M. Musiał and S. A. Kucharski, First principle calculations of the potential energy curves for electronic states of the lithium dimer, J. Chem. Theory Comput., 2014, 10, 1200–1211 Search PubMed.
- A. Ghosh, L. S. Cederbaum and K. Gokhberg, Electron transfer mediated decay in HeLi2 cluster: potential energy surfaces and decay widths, J. Chem. Phys., 2019, 150, 164309 Search PubMed.
- L. S. Cederbaum and F. Tarantelli, Nuclear dynamics of decaying states: a time-dependent formulation, J. Chem. Phys., 1993, 98, 9691–9706 Search PubMed.
- E. Pahl, H.-D. Meyer and L. Cederbaum, Competition between excitation and electronic decay of short-lived molecular states, Z. Phys. D: At., Mol. Clusters, 1996, 38, 215–232 Search PubMed.
- H.-D. Meyer, U. Manthe and L. Cederbaum, The multi-configurational time-dependent Hartree approach, Chem. Phys. Lett., 1990, 165, 73–78 Search PubMed.
- M. Beck, A. Jäckle, G. Worth and H.-D. Meyer, The multiconfiguration time-dependent Hartree (MCTDH) method: a highly efficient algorithm for propagating wavepackets, Phys. Rep., 2000, 324, 1–105 Search PubMed.
- Electronic decay of an isolated resonance will proceed exponentially in time apart from very short or very long times, in our case, a band of vibronic states with close but different widths decay simultaneuosly. Still, the log–linear plot of the survival probability appears very much like a straight line.
- T. Miteva, Y.-C. Chiang, P. Kolorenč, A. I. Kuleff, K. Gokhberg and L. S. Cederbaum, Interatomic coulombic decay following resonant core excitation of Ar in argon dimer, J. Chem. Phys., 2014, 141, 064307 Search PubMed.
- I. B. Müller and L. S. Cederbaum, Ionization and double ionization of small water clusters, J. Chem. Phys., 2006, 125, 204305 Search PubMed.
- Z. L. Streeter, F. L. Yip, R. R. Lucchese, B. Gervais, T. N. Rescigno and C. W. McCurdy, Dissociation dynamics of the water dication following one-photon double ionization. i. Theory, Phys. Rev. A, 2018, 98, 053429 Search PubMed.
- D. Reedy, J. B. Williams, B. Gaire, A. Gatton, M. Weller, A. Menssen, T. Bauer, K. Henrichs, P. Burzynski, B. Berry, Z. L. Streeter, J. Sartor, I. Ben-Itzhak, T. Jahnke, R. Dörner, T. Weber and A. L. Landers, Dissociation dynamics of the water dication following one-photon double ionization. ii. Experiment, Phys. Rev. A, 2018, 98, 053430 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc01478a |
| This journal is © The Royal Society of Chemistry 2021 |
