Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
How the biomimetic assembly of membrane receptors into multivalent domains is regulated by a small ligand†
Anna
Grochmal
,
Ben
Woods
,
Lilia
Milanesi
,
Manuel
Perez-Soto
 and
Salvador
Tomas
and
Salvador
Tomas
 *
*
Department of Biological Sciences, Institute of Structural and Molecular Biology, School of Science, Birkbeck University of London, Malet Street, London WC1E 7HX, UK. E-mail: s.tomas@bbk.ac.uk
First published on 30th April 2021
Abstract
In living cells, communication requires the action of membrane receptors that are activated following very small environmental changes. A binary all-or-nothing behavior follows, making the organism extremely efficient at responding to specific stimuli. Using a minimal system composed of lipid vesicles, chemical models of a membrane receptor and their ligands, we show that bio-mimetic ON/OFF assembly of high avidity, multivalent domains is triggered by small temperature changes. Moreover, the intensity of the ON signal at the onset of the switch is modulated by the presence of small, weakly binding divalent ligands, reminiscent of the action of primary messengers in biological systems. Based on the analysis of spectroscopic data, we develop a mathematical model that rigorously describes the temperature-dependent switching of the membrane receptor assembly and ligand binding. From this we derive an equation that predicts the intensity of the modulation of the ON signal by the ligand-messenger as a function of the pairwise binding parameters, the number of binding sites that it features and the concentration. The behavior of our system, and the model derived, highlight the usefulness of weakly binding ligands in the regulation of membrane receptors and the pitfalls inherent to their binding promiscuity, such as non-specific binding to the membrane. Our model, and the equations derived from it, offer a valuable tool for the study of membrane receptors in both biological and biomimetic settings. The latter can be exploited to program membrane receptor avidity on sensing vesicles, create hierarchical protocell tissues or develop highly specific drug delivery vehicles.
1. Introduction
Receptors located on the cell membrane bind to ligands present in solution or displayed on other surfaces, and play a central role in cell adhesion and communication processes.1–3 The regulation of receptors involves the participation of complex machinery, tasked with the detection of the appropriate environmental changes and activation of the receptors (for example, by recruiting them at the point of interaction into platforms of high avidity) when the level of a given stimulus reaches a critical threshold.2 Identifying the switches that control the function of these receptors is a very challenging task in the context of the biomolecular complexity of the cell.4–6 Simple models of a cell membrane, in the form of lipid vesicles equipped with minimal synthetic membrane receptors and ligands, have shown that the lateral assembly of receptors enhances both binding to ligands in solution7,8 and membrane adhesion.9,10 These studies have shown that large increases in avidity are largely due to a multivalent effect. The corollary is that ON/OFF regulation of membrane receptor function can be achieved by means of a bimodal control of the receptor assembly, i.e. non-assembled monovalent state (low avidity, OFF state) versus assembled multivalent platforms (high avidity, ON state). On the one hand, identifying and characterizing stimuli that lead to extensive lateral assembly of membrane receptors will improve our understanding of cell communication processes.11 On the other hand, it will inform the design of minimal protocells that are capable of communicating with each other12,13 or to adhere to living cells upon stimulus.14,15 The latter will also facilitate the development of efficient vehicles for targeted drug delivery.In our earlier work, we rigorously characterized the mutual modulation between the lateral assembly of membrane receptors and the binding of ligands in solution.7,16 The mathematical model we developed allowed us to quantify the enhancement of binding due to the formation of multivalent receptor clusters and relate it to a multivalent effect. In the present work we show that changes in the membrane phase (from liquid disordered to gel) lead to an ON/OFF bimodal response in the assembly of the membrane embedded receptor. Moreover, we show that ligands in solution modulate the intensity of the ON response of the bimodal switch, and that efficient modulation of the signal (from virtually non-existent to a maximum response where most of the receptors present in the membrane are assembled) does not require strong ligand binding. We have developed a mathematical assembly-binding model that uses a van't Hoff approach to account for the temperature dependence of the assembly. The fit of this model to UV-visible spectroscopy titration data at different temperatures is excellent, and tracks changes consistent with temperature-induced receptor assembly, ligand induced binding and assembly (or disassembly, when a large excess of ligand is added). These results and the model derived highlight that the bimodal assembly is driven largely by the dramatic increase in lipid–lipid interactions upon phase transition, while ligand binding leads to small changes in receptor assembly that, in the appropriate conditions, are enough to tip the system towards extensive receptor assembly. We reason that any stimulus capable of modulating lipid–lipid interactions (in this instance temperature, but reasonably also lipophilic drugs or hormones) has the potential to trigger this type of switch. The described phenomenon could be programmed into vesicle-based protocells, leading to biomimetic specificity and control of ligand binding and membrane adhesion.
2. Results and discussion
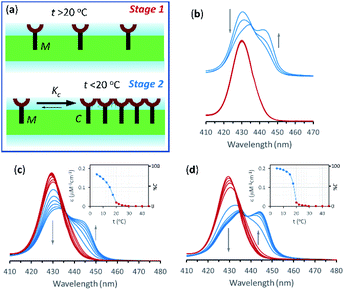
2.1. Lateral assembly of the receptor
Receptor 1Ch (Fig. 1) contains a chromophoric Zn metalloporphyrin headgroup, which allows the monitoring of the lateral assembly and the binding of amine-containing ligands using UV-visible spectroscopy. A cholesterol membrane anchor ensures efficient insertion of 1Ch into the membrane of lipid vesicles.7,16 In our earlier work, we have shown that increasing the in-membrane concentration of 1Ch in lipid vesicles (membrane composition DMPC/cholesterol 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 mol/mol) leads to a red-shift of the Soret band of the porphyrin moieties UV-visible spectrum, characteristic of J-aggregates.17 These changes are attributed to the lateral assembly of 1Ch into domains, or clusters C.
20 mol/mol) leads to a red-shift of the Soret band of the porphyrin moieties UV-visible spectrum, characteristic of J-aggregates.17 These changes are attributed to the lateral assembly of 1Ch into domains, or clusters C.
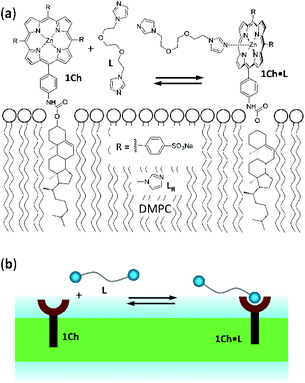 | ||
| Fig. 1 (a) Chemical structures of receptor 1Ch, ligands L and LR and complex 1Ch·L represented embedded in a DMPC membrane. (b) Cartoon representation of the structures shown in (a). | ||
In the current work we use vesicles composed of pure DMPC. Anchored in the membrane of these vesicles, 1Ch does not show any discernible change in the UV-visible spectrum above 20 °C (henceforth temperature stage 1, Fig. 2a) and up to in-membrane concentrations (termed here r1Ch, measured as the molar ratio of 1Ch over that of lipids) of 0.025. This result is consistent with a negligible lateral assembly of the monomeric form of the receptor 1Ch, which we term M, into clustered form C, within this temperature and concentration range (Fig. 2b). However, below 20 °C (henceforth temperature stage 2. Fig. 2a) there is a clear growth of the red-shifted Soret band, indicative of the lateral assembly leading to the clustered form of the receptor C.7,16
The dependence of the spectrum with the temperature was tested with vesicles at constant in-membrane concentration, (r1Ch = 0.01 and 0.025; Fig. 2c and d, respectively). In these conditions the UV-visible spectra initially experience small but clear temperature-dependent changes when cooled from 30 °C to 20 °C. Since the UV-visible spectrum is concentration-independent in this temperature range (Fig. 2b), we attribute these minor changes to variations in the physical properties of the lipid interface leading to a solvatochromic shift of the M form of the receptor as we approach the phase transition temperature.18–20
Below 20 °C (temperature stage 2), the redshifted band, attributed to the laterally assembled C form of 1Ch, grows rapidly when the temperature decreases, which is steeper in samples with a higher in-membrane concentration of 1Ch (Fig. 2c and d). These changes are consistent with a cooperative nucleation-growth mechanism for the assembly of the clusters.21 This behaviour of the receptor is in contrast with our earlier work, where 1Ch was shown to undergo lateral assembly in a weak, non-cooperative isodesmic fashion. However, the earlier work focused on the assembly of the receptor at moderately high temperatures (37 °C), higher receptor loadings (with r1Ch up to 0.1) and different membrane composition.7,16 Nucleation-growth assembly in the membrane can be characterized by the in-membrane solubility of the monomeric form M of the receptor, rM,max, or its reciprocal, the clustering constant Kc:
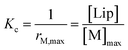 | (1) |
In eqn (1), [M]max and [Lip] are the maximum concentration of the monomeric form of the receptor and that of lipids in relation to the total solution volume. The rise of the red-shifted Soret band (centred at 445 nm c.a.), characteristic of the clustered form C (Fig. 2),7,16 allows us to determine rM,max and Kc at specific temperatures, during temperature stage 2 (i.e., below 20 °C) (See ESI† for details of the model, ESI Fig. S1 and ESI Table S1†). rM,max has a value of 0.007 at 20 °C, (Kc = 140) and reaches values as low as 0.0027 at 5 °C (Kc = 370).
2.2. Ligand binding
As we have previously reported, the binding of a ligand to a membrane-anchored receptor and the lateral assembly of the receptor modulate each other.7,16 The extent of the modulating effect is quantified by the modulation factor, Mf, which is the factor by which the binding affinity for the ligand increases upon lateral assembly, or, conversely, the factor by which the lateral assembly increases upon binding of the ligand. For monovalent ligands the modulation has been attributed to the increased hydrophobicity in the cluster environment, as well as to favourable secondary interactions (e.g., CH–π) between the porphyrin-bound ligand and nearby porphyrins in the cluster.7 It is worth considering that ligand binding may disrupt somewhat porphyrin J-aggregates in the cluster. This may counteract somewhat the benefits of binding to the cluster, leading to the observed weak modulation effect. For divalent ligands the overall modulation is a function of the Mf of each binding and the chelate effect which can lead to a much stronger modulation.7,16For ligand L the binding sites are N-alkyl imidazole moieties (Fig. 1a). Chemically equivalent monovalent ligand methylimidazole LR was used to determine the contribution to receptor binding of each binding site (that is, the microscopic binding constant Km) and the modulation factor Mf per binding site at play in divalent L. We determined the binding affinity of LR for 1Ch by means of a UV-visible titration method, in experimental conditions where either monomeric form of the receptor, M, or the assembled C form are dominant. From these experiments we obtained a value for the binding constant of LR to M, termed, Km, of 38 M−1, which is constant with the temperature within the error of the measure. The modulation factor Mf obtained was 2.2. (see ESI for details of the model used, ESI Fig S2 and ESI Table S2†). Both values are consistent with those obtained in our previous work.16
The interaction of divalent ligand L with membrane anchored receptor 1Ch was studied by means of UV-visible titration on vesicle samples with an in-membrane concentration r1Ch = 0.01 over the temperature range under study. At this concentration the presence of the laterally assembled C form of 1Ch is negligible in temperature stage 1 (above 20 °C). In this temperature stage, titration of L leads to changes in the UV-visible spectrum of 1Ch that do not feature isosbestic points, consistent with the formation of complexes ML and M2L (Fig. 3 and Fig. 4a and b). The overall shape of the binding isotherms (Fig. 4a, b and ESI Fig. S3†) suggests that the binding affinity for the ligand increases as we approach 20 °C. Since Km changes with the temperature are too small to be detectable, we attribute this observed change to an increase in the binding affinity of the ligand to the lipid bilayer that track changes in the membrane interface as seen in the UV-visible spectra of the receptor 1Ch in the absence of ligand (Fig. 2c and d). This phenomenon is characterized by the membrane binding constant Ki (Fig. 3):
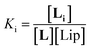 | (2) |
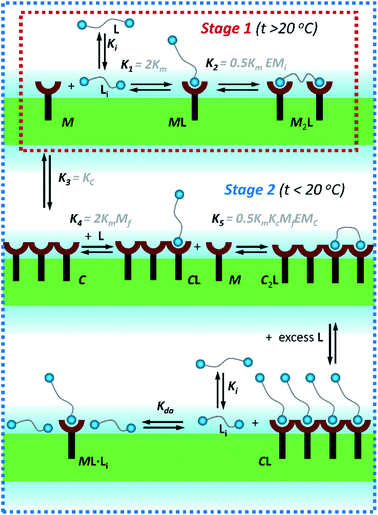 | ||
| Fig. 3 Summary of the main binding and lateral assembly events that dominate each of the temperature stages for membrane embedded receptor 1Ch. The relevant equilibrium constants are written as a function of the pairwise binding parameters. Only one of the possible routes that lead to C2L is shown. See ESI Fig. S4† for an extended illustration of the equilibria involved and their relationship with the pairwise binding parameters. | ||
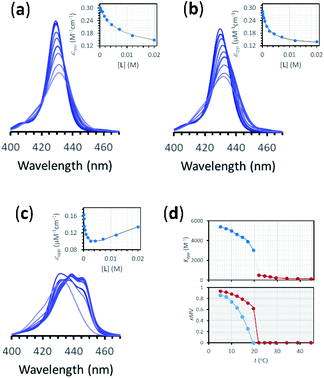 | ||
| Fig. 4 (a) Changes in the Soret band region of the UV-visible spectrum of membrane embedded 1Ch upon addition of increasing amounts of ligand L at 45 °C. Lighter traces signify increasing L concentration. The inset shows the changes in the apparent molar extinction coefficient at 429 nm (blue circles) and the fitting of the data to the corresponding temperature stage 1 binding model (grey line). See main text for details (b) Idem at 25 °C. (c) Idem at 5 °C, using temperature stage 2 binding model to fit the data. (d) (top) Values of the apparent binding constant for receptor 1Ch for L for the addition of the first aliquot of the ligand at the temperatures tested (circles). The colours correspond to temperature stage 1 (red) and temperature stage 2 (blue). (bottom) Fraction of multivalent platform assembled, xMV, calculated as the ratio of all cluster forms of the receptor over total receptor (see eqn (12)) derived from the calculations at the temperatures tested in the absence of ligand (blue circles), and when the concentration of ligand is 2.5 mM (red circles). The lines have been added as visual aids. | ||
In eqn (2) [Li] is the concentration of membrane bound ligand, [L] that of ligand in solution and [Lip] that of lipid molecules, with all the concentrations referred to the total solution volume. The binding constant for the formation of ML, K1 (Fig. 3) can thus be written as a function of Ki as follows:
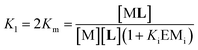 | (3) |
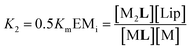 | (4) |
Eqn (2)–(4) (see ESI† for a detailed derivation), in combination with the mass balances, comprise a binding model that was used to fit the UV-visible titration data taken within temperature stage 1. Km was determined from the experiments with LR and was entered as a fixed parameter. EMi was determined from the titrations carried out at the highest temperature end (i.e. above 40 °C) where Ki is negligible. EMi thus calculated has a value of 2.3 M, a reasonable value of effective concentration for molecular recognition events.22 For the fitting of the titration data below 40 °C, EMi as well as Km were entered as fixed parameters, with the Ki at each different temperature obtained as an adjustable parameter from the fitting procedure. The fitting to the model is excellent (Fig. 4a, b and ESI Fig. S3†). The values of Ki are small in all cases and decrease as the temperature increases (ESI Table S3†). At its highest (at 22 °C, the lowest temperature tested) Ki is only 1 M−1. This small affinity for the membrane has, however, a clear impact in increasing the extent of ligand binding to the receptor and the apparent binding affinity (Fig. 4d).
In temperature stage 2, below 20 °C, the monomeric and the laterally assembled cluster form of 1Ch (M and C, respectively) co-exist. Their relative amounts at a given temperature depend on the corresponding in-membrane solubility, rM,max, or its reciprocal, the clustering constant Kc. For the M form, the extent of ligand binding leading to ML depends on Km as described in eqn (3). The clustered form of the receptor, C, has a larger affinity for L than the monomeric form, M, which is attributed to a combination of two factors. Firstly, the intrinsic increase in the binding affinity per binding site quantified by the modulation factor Mf, which has been determined for the alkyl-imidazole binding sites of L using reference ligand LR. Thus, the binding constant for the formation of complex CL, K4, can be written as (Fig. 3):
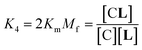 | (5) |
The second factor is the chelate effect at play within the domains or clusters C of receptor, quantified by the effective molarity, EMc. EMc is the apparent concentration of the complementary binding sites for the formation of the complex C2L. The formation of this complex can therefore be written as:
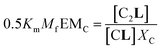 | (6) |
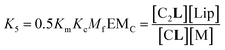 | (7) |
In temperature stage 2, M2L is one of the possible forms of the nucleus that lead to the growth of the clusters, as part of the nucleation-growth mechanism. The accumulation of this complex in this temperature stage can thus be considered negligible. It is noteworthy that when a large excess of L is added, the visible band assigned to C decreases (Fig. 4c). This result is consistent with a scenario in which a ligand-saturated membrane interface causes an increase of the in-membrane solubility of 1Ch, leading to the de-assembly of clusters (Fig. 3 bottom). The ability of Li to stabilize the monomeric form of the receptor is likely rooted, at least in part, on the non-negligible amount of the protonated form of the imidazole moieties of the ligand.23 These cationic, protonated ligands will interact favourably with the anionic sulphonate moieties of 1Ch. To incorporate this possibility to our model, we postulate that the membrane interface bound ligand, Li, binds to the cluster–ligand complex CL, detaching it from the cluster to yield the monomer–ligand complex form ML·Li (Fig. 3 bottom). The disassembly equilibrium constant of this process, Kda, can be written as function of the relevant species as:
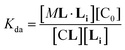 | (8) |
Our model implicitly assumes that, as far as ligand binding is concerned, the behaviour of the receptors C located at the boundary of the cluster or domain is indistinguishable to those located within the domain. The excellent fit of the data to the model is consistent with this assumption. Furthermore, the orientation of the receptors in the membrane also support to this view, as the porphyrin rings are known to sit approximately perpendicular to plane of the membrane.25 For receptors located at the edge there is thus a face that points toward the rest of the domain, where the bound ligand will be exposed to the same environment than those bound within the domain.
Overall, the models presented above allow us to determine speciation from which to derive the apparent binding constant, Kapp, at each temperature analysed at any concentration of L. The temperature trend of Kapp, calculated for the addition of the first aliquot of ligand, mirrors the observed changes in the UV-visible spectra and tracks the formation of the cluster C (Fig. 2c, d and 4d). These show a steep rise at around 20 °C and can be attributed to the multivalent effect at play in the cluster, C, enhanced by a favourable modulation factor, Mf, for our ligand (i.e., Mf > 1). Clearly, the presence of multiple molecules of receptor 1Ch in close proximity within C render these domains multivalent platforms primed for the binding of multivalent ligands. We quantify the extent of formation of the multivalent platform, xMV, as the fraction of all forms of clustered receptor, [C0], over that of the total concentration of receptor, [1Ch]:
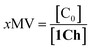 | (9) |
xMV was calculated from the titration data at the different temperature points analysed and the ligand concentrations used. There is a sharper increase of multivalent platform assembly in the presence of a moderate concentration of ligand (i.e. 2.5 mM) than in the absence of ligand (Fig. 4d). The point at 19.5 °C is especially noteworthy, where no platform is assembled (i.e. is switched OFF) unless the ligand is present (i.e., it switches ON). These results point to the combination of two factors playing a role in the assembly of the multivalent platform: (i) the sudden increase in lipid–lipid interactions upon lipid phase transition which for DMPC on the vicinity of 19.5 °C (ref. 18) (ii) the binding of the ligand, which increases the stability of the clustered form and therefore results in an increase of the intensity of the ON switch at the point of phase transition when ligand is present.
Changes in equilibrium constants for self-assembly or phase transition have often been modelled using a van't Hoff approach. In the next section we apply this approach to our system. The aim is two-fold: on the one hand, to test whether the observed behaviour is indeed consistent with the phase change of the lipids. On the other hand, we aim to produce a global model that allows the prediction of the behaviour of the system as a response to multiple stimuli (i.e., not just the concentration of all species involved but also the temperature) and that it is capable of recapitulating the modulation of the intensity of the experimentally observed ON signal.
2.3. Modelling the dependence of lateral assembly and ligand binding with the temperature
The van't Hoff equation is an approximation that assumes that the enthalpy associated to a given chemical reaction does not change with the temperature. This assumption requires that the heat capacity of reagents and products is the same. This is a reasonable assumption when we deal with molecular association processes that do not change the covalent framework of the species involved. In our system, the self-assembly behaviour of the receptor changes drastically around the melting temperature, Tm, with some minor additional changes taking place at either side of Tm. All these changes were modelled using the corresponding van't Hoff equation.For the main change at Tm we used the van't Hoff equation adapted to lipid phase transition.24 We attribute the changes in clustering at Tm to the lower solubility of receptor 1Ch in lipids in the bilayer when in the more rigid gel phase (G, below Tm) compared to lipids in the lipid disordered phase (Ld, above Tm). The G state is characterized by the formation of large domains of ordered lipid molecules; the size of the domains depends on the cooperativity number, nC, which has been estimated at 200 for DMPC.24 It is therefore reasonable to assume that the molecules of the receptor, 1Ch, are driven out of the ordered lipid domains and located preferentially between them, reducing the ability of the membrane to dissolve individual receptor molecules by a factor of nC. We define [Lip]I as the apparent concentration of lipids available for the receptor molecules. Written as a function of the phase composition, [Lip]I is:
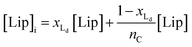 | (10) |
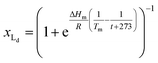 | (11) |
Below Tm the solubility of 1Ch further decreases with the temperature. This is shown by the increase of the clustering constant Kc. We fit the increase of Kc with the temperature to the corresponding van't Hoff equation from which we obtained the apparent molar enthalpy and entropy for the in-membrane receptor clustering, ΔHc and ΔSc (ESI Fig S10,†Table 1).
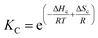 | (12) |
| ΔHmb | T m | ΔHC | ΔSC |
|---|---|---|---|
| a The values of molar enthalpy are reported in units of kJ mol−1, those of molar entropy in units of J mol−1 K−1 and the temperature in K. b Value from ref. 24. The error, measured as twice the standard deviation and derived from the statistical analysis of the data fitting, is on the order of 25%. | |||
| 2930 | 292.6 | −51.5 | −133 |
The changes above Tm are attributed to changes in the lipid interface linked to the main phase transition, which give rise to both the solvatochromic shift observed and the increase in Ki (ESI Fig S5 and S6, Table S4†).
Eqn (10)–(12), together with eqn (1), modified to incorporate the apparent lipid concentration, [Lip]i, rather than the total lipid concentration, [Lip], and the mass balance constitute a model that account for the temperature dependent assembly of the receptor into clusters. Adding in the Lambert–Beer law, the model fits well to the experimental UV-visible data, allowing for small adjustments in the Lambert–Beer law equations to account for the solvatochromic shift experienced by the monomeric form of the receptor M as we approach Tm (see ESI† for details of the model). When fitting the data, the thermodynamic parameters for the lipid phase change and receptor clustering (Table 1) were entered as fixed values, as was the cooperativity number nC (see ESI† for details). Therefore, the only optimized parameters were Tm and the extinction coefficient of the different species. The fit of the model to the UV-visible data is excellent (ESI Fig S11†). The value of Tm obtained from the fitting is 292.6 K (19.6 °C), which is consistent with literature data for vesicles composed of DMPC.18
For the binding of the ligand, we assume that Km is independent of the temperature, based on the lack of a discernible variation of Km for the reference ligand LR (ESI Table S2†). The binding of the ligand to the membrane is described by eqn (2), while the changes in Ki are described by eqn (S76) (see ESI†). The formation of complexes ML and CL are described in eqn (3) and (5). The lateral assembly of 1Ch into C and the formation of M2L and C2L is described by eqn (1), (4) and (7). These equations are modified, replacing the concentration of lipid [Lip] by the apparent concentration [Lip]i, whose temperature dependence is recapitulated by eqn (10) and (11). Changes in Kc with the temperature are described by eqn (12). Together with the corresponding mass balances, these equations comprise a global assembly-ligand binding model that accounts for the speciation and UV-visible spectra observed at any system composition and any temperature (see full model details in the ESI†).
The model was fit to the UV-visible data at all temperatures and ligand concentrations. All the thermodynamic parameters have already been determined and were entered as fixed parameters, with only the colour of the species (i.e., the corresponding extinction coefficients) optimized. The fitting of the global model to the data is excellent, tracking closely all the observed changes, both major and minor (Fig. 5a). Major changes include the sudden increase in UV-visible signal around the Tm. This large change in the UV-visible signal reflects the sudden lateral assembly at Tm, that becomes sharper as the concentration of ligand increases. At very large concentrations of the ligand, the change in the UV-visible signal around Tm becomes very small, reflecting the fact that large excess of ligand inhibits rather than promotes the lateral assembly of the receptor into multivalent clusters or domains.
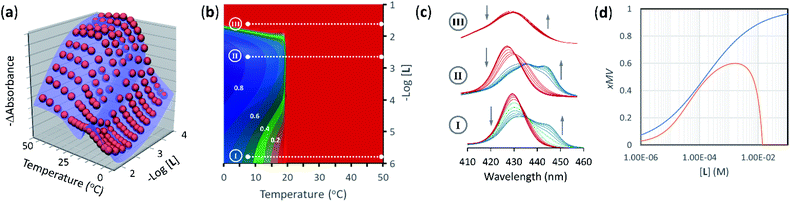 | ||
| Fig. 5 (a) Changes in absorbance at 429 nm of membrane anchored 1Ch in DMPC vesicles upon changes in the temperature and the concentration of ligand (red spheres), fit to a global clustering-binding model (blue surface). The in-membrane concentration of 1Ch was r1Ch = 0.01. (b) Simulated changes in the formation of receptor multivalent platforms (xMV, see eqn. (9)) as a function of the temperature and the concentration of ligand L. Each change of the colour tonality represents an increase of 0.1 in xMV. The dotted white lines labelled I, II and III correspond to the experimental conditions that give rise to the corresponding spectra displayed in panel (c). (c) Changes in the Soret band region of the UV-visible spectra of membrane anchored 1Ch upon changes in the temperature. The grey arrows indicate the direction of change as the temperature is decreased. The concentration of ligand was 0 mM (bottom spectra, I), 2 mM (middle spectra, II) and 20 mM (top spectra, III). r1Ch was 0.01 in all cases. (d). Intensity of the ON signal, measured as the fraction of multivalent platform, xMV, upon switching ON (i.e., cooling to 19.5 °C, just below the Tm) and as a function of the concentration of ligand. The red trace was calculated from speciation derived from the global model. The blue trace was calculated using eqn (14) (r1Ch = 0.01). | ||
The changes in receptor distribution in the membrane are clearly shown when the model is used to simulate the extent of assembly of the multivalent platform, xMV, as the temperature and the ligand concentration are changed (Fig. 5b and c).
Our mathematical model is uncomplicated in that it is built on straightforward algebraic relationships derived from the chemical equilibria involved and the van't Hoff equation to predict the system composition and properties. Although implementation of the global model requires specialist software, the ligand modulation of a bimodal assembly switch can be recapitulated into a simple mathematical expression. For our receptor, we measure the intensity of the ON response as the fraction of receptor that assembles into multivalent platforms xMV (eqn (9)). In the absence of ligand, upon triggering the switch (i.e. cooling below Tm), the value of xMV depends only on the excess of in-membrane concentration of the receptor in relation to the in-membrane solubility. Since the binding of the ligand modulates the in-membrane solubility, xMV can be written as function of the ligand concentration as follows (see ESI† for detailed derivation):
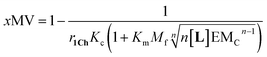 | (13) |
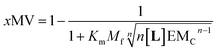 | (14) |
Eqn (14) shows that, in these conditions, the intensity of the ON signal depends on the pairwise binding parameters (i.e. the intrinsic binding affinity), the number of binding sites and the concentration of ligand. Crucially, in these conditions, the ON/OFF deployment of multivalent receptor platforms requires the presence of the ligand. In our experiments, this scenario is observed for samples with r1Ch = 0.01 in the presence of a concentration of ligand in the millimolar region (Fig. 5b, c and d). From eqn (14) we can derive an expression that allows us to determine the minimum concentration of ligand required to obtain the minimum ON signal intensity desired. For example, for the deployment of 50% of the multivalent platform we have that:
| [L] = n−1(KmMf)−nEMCn−1 | (15) |
Eqn (15) clearly shows that the concentration of ligand required to initiate the deployment of the multivalent platform decreases with the number of binding sites, the value of the intrinsic binding affinity (Km), and that of the cooperativity parameters Mf and EMC.
Eqn (13) and (14) are simplifications that nonetheless predict the approximate behaviour of membrane anchored receptors in response to the presence of their ligands. In particular, they show that ligands with small binding affinities can greatly enhance a temperature dependent ON/OFF membrane-receptor multivalent switch, provided that the concentration of the ligand is large enough, or that the ligand is heavily multivalent (i.e., n is large). Such is the case in our system, where an ON/OFF switch is achieved with intrinsic binding constants below 100 M−1. The behaviour of our system also shows the limitations of using a simple equation to describe the system. According to eqn (13), the level of response is larger as the concentration of ligand increases. In reality, at large ligand concentration we see disassembly of the multivalent platforms, due to non-specific interaction of the ligand with both the membrane and the receptor (Fig. 5d). This observation highlights the fact that non-specific interactions are likely to interfere with the molecular switch in those cases where low binding affinity requires the use of large concentration of the ligand.
3. Conclusions
In summary, in this work we have used spectroscopic data of a well-defined, chemically simple lipid membrane system to derive a clustering-binding model and describe its behaviour as a function of the system composition (i.e. the relative concentration of ligand, lipid and receptor) and the temperature. To the best of our knowledge, the development of such a global model based on discrete pairwise binding parameters is unprecedented. Our model clearly shows that the behaviour of the membrane receptors is largely dictated by the properties of the lipid membrane, but that their behaviour can be finely tuned via the self-assembly of the receptor and the presence of a ligand in solution. The model accurately describes the bimodal ON/OFF assembly of the receptor into multivalent platforms, triggered by a temperature switch. The modulation of the ON signal, from nil to full response, is induced by the action of a small ligand in solution. The model also highlights the limitations of weakly binding ligands as modulators of the ON signal, due to the fact that the large concentration required for full deployment leads to additional interactions that may interfere with the function of the switch. The modulation of the signal can be recapitulated into a simple equation (eqn (14)) that offers a good approximation of the system response to the ligand. Current research efforts in our laboratory are focused on developing membrane adhesion and small molecule release switches based on the triggering of the multivalent platforms described here. This work brings their development closer and will open the door to the design of protocells programmed to adhere to other protocells or to living cells upon stimulus, or to allow a fine control of the release of their contents. The former can be applied to the development of hierarchically assembled proto-tissues.12,13 The latter, to develop stimuli-responsive drug delivery vehicles. Our work thus complements the recent development of signal amplification switches in lipid vesicles.26–28 Finally, it is worth noting that the behaviour of our system is reminiscent to that of biological membrane receptors in response to messengers.29 Clearly, many of these biological systems are qualitatively and quantitatively different to the one described here. For example, the well know tyrosine kinase relies on dimerization of a receptor, rather than on the formation of extended domains, with very strong binding affinities.30 Our mathematical model may nonetheless find application in the study of cell adhesion phenomena that rely on assembly of many copies of relatively weakly binding ligands and receptors.31,32Author contributions
AG performed the initial experiments and analysed the data. BW performed additional temperature-variable experimnets, analysed the data and co-worte the manuscript, MP-S performed monovalent ligand control experiments, analysed the data and co-wrote the manuscript. LM analysed the data and co-worte the manuscript, ST designed the research, analysed the data and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Department of Biological Sciences, Birkbeck University of London, and the Leverhulme Trust for funding Dedicated to the memory of Anna Grochmal, 1959–2019.Notes and references
- D. Calebiro, F. Rieken, J. Wagner, T. Sungkaworn, U. Zabel, A. Borzi, E. Cocucci, A. Zurn and M. J. Lohse, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 743 CrossRef CAS PubMed.
- A. Grakoui, S. K. Bromley, C. Sumen, M. M. Davis, A. S. Shaw, P. M. Allen and M. L. Dustin, Science, 1999, 285, 221 CrossRef CAS PubMed.
- C. H. Coles, Y. J. Shen, A. P. Tenney, C. Siebold, G. C. Sutton, W. X. Lu, J. T. Gallagher, E. Y. Jones, J. G. Flanagan and A. R. Aricescu, Science, 2011, 332, 484 CrossRef CAS PubMed.
- M. L. Dustin and D. Depoil, Nat. Rev. Immunol., 2011, 11, 672 CrossRef CAS PubMed.
- J. R. James, M. I. Oliveira, A. M. Carmo, A. Iaboni and S. J. Davis, Nat. Methods, 2006, 3, 1001 CrossRef CAS PubMed.
- B. L. Sprague, R. L. Pego, D. A. Stavreva and J. G. McNally, Biophys. J., 2004, 86, 3473 CrossRef CAS PubMed.
- S. Tomas and L. Milanesi, Nat. Chem., 2010, 2, 1077 CrossRef CAS PubMed.
- B. Gruber, S. Balk, S. Stadlbauer and B. König, Angew. Chem., Int. Ed. Engl., 2012, 51, 10060 CrossRef CAS PubMed.
- S. J. Webb, Acc. Chem. Res., 2013, 46, 2878 CrossRef CAS PubMed.
- M. M. Ma, Y. Gong and D. Bong, J. Am. Chem. Soc., 2009, 131, 16919 CrossRef CAS PubMed.
- P. A. van der Merwe and O. Dushek, Nat. Rev. Immunol., 2011, 11, 47 CrossRef CAS PubMed.
- G. Bolognesi, M. S. Friddin, A. Salehi-Reyhani, N. E. Barlow, N. J. Brooks, O. Ces and Y. Elani, Nat. Commun., 2018, 9, 1882 CrossRef PubMed.
- X. Wang, L. Tian, H. Du, M. Li, W. Mu, D. W. Drinkwater, X. Han and S. Mann, Chem. Sci., 2019, 10, 9446 RSC.
- X. Tian, S. Nyberg, P. S. Sharp, J. Madsen, N. Daneshpour, S. P. Armes, J. Berwick, M. Azzouz, P. Shaw, N. J. Abbott and G. Battaglia, Sci. Rep., 2015, 5, 11990 CrossRef CAS PubMed.
- V. M. Gouveia, L. Rizzello, C. Nunes, A. Poma, L. Ruiz-Perez, A. Oliveira, S. Reis and G. Battaglia, Pharmaceutics, 2019, 11, 614 CrossRef CAS PubMed.
- A. Grochmal, E. Ferrero, L. Milanesi and S. Tomas, J. Am. Chem. Soc., 2013, 135, 10172 CrossRef CAS PubMed.
- J. M. Ribo, J. Crusats, J. A. Farrera and M. L. Valero, J. Chem. Soc., Chem. Commun., 1994, 681 RSC.
- M. Caffrey and J. Hogan, Chem. Phys. Lipids, 1992, 61, 1 CrossRef CAS PubMed.
- E. L. Doyle, C. A. Hunter, H. C. Phillips, S. J. Webb and N. H. Williams, J. Am. Chem. Soc., 2003, 125, 4593 CrossRef CAS PubMed.
- S. Tomas and L. Milanesi, J. Am. Chem. Soc., 2009, 131, 6618 CrossRef CAS PubMed.
- C. Campanella, E. Lopez-Fontal, L. Milanesi and S. Tomas, Phys. Chem. Chem. Phys., 2019, 19, 9617 RSC.
- M. C. Misuraca, T. Grecu, Z. Freixa, V. Garavini, C. A. Hunter, P. van Leeuwen, M. D. Segarra-Maset and S. M. Turega, J. Org. Chem., 2011, 76, 2723 CrossRef CAS PubMed.
- B. Lenarcik and P. Ojczenasz, J. Heterocycl. Chem., 2002, 39, 287 CrossRef CAS.
- O. Enders, A. Ngezahayo, M. Wiechmann, F. Leisten and H. A. Kolb, Biophys. J., 2004, 87, 2522 CrossRef CAS PubMed.
- J. Lahiri, G. D. Fate, S. B. Ungashe and J. T. Groves, J. Am. Chem. Soc., 1996, 118, 2347 CrossRef CAS.
- M. J. Langton, F. Keymeulen, M. Ciaccia, N. H. Williams and C. A. Hunter, Nat. Chem., 2017, 9, 426–430 CrossRef CAS PubMed.
- L. Trevisan, I. Kocsis and C. A. Hunter, Chem. Commun., 2021, 57, 2196 RSC.
- K. Bernitzki, M. Maue and T. Schrader, Chem.–Eur. J., 2012, 18, 13412 CrossRef CAS PubMed.
- D. Raucher, T. Stauffer, W. Chen, K. Shen, S. Guo, J. D. York, M. P. Sheetz and T. Meyer, Cell, 2000, 100, 221 CrossRef CAS PubMed.
- M. A. Lemmon and J. Schlessinge, Cell, 2010, 141, 1117 CrossRef CAS PubMed.
- M. L. Dustin, D. E. Golan, De-M. Zhu, J. M. Miller, W. Meieri, E. A. Davies and P. A. van der Merwe, J. Biol. Chem., 1997, 272, 30889 CrossRef CAS PubMed.
- A. M. Mørch, Š. Bálint, A. M. Santos, S. J. Davis and M. L. Dustin, Front. Cell. Dev. Biol., 2020, 8, 597627 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed experimental methods, detailed derivation of the equations and mathematical model, ESI figures and tables. See DOI: 10.1039/d1sc01598b |
| This journal is © The Royal Society of Chemistry 2021 |