The mechanism behind enhanced reactivity of unsaturated phosphorus(V) electrophiles towards thiols

Abstract

Vinyl- and ethynyl phosphorus(V) electrophiles are a versatile class of thiol-reactive reagents suitable for cysteine-selective peptide and protein modifications, especially for the generation of antibody conjugates. Herein we investigated the reactivity of various P(V) reagents towards thiol addition. Complementing previous studies, we observed that the heteroatoms X (X = S, O, NH) as well as the vinyl- vs. ethynyl-substituent bound to phosphorus greatly influence the overall reactivity. These experimentally observed trends, as well as the high Z-selectivity for thiol additions to ethynyl derivatives, were further elucidated using DFT calculations. Hyperconjugation was a key means of stabilizing the intermediate generated upon the thiol addition, thus determining both the reactivity and stereoselectivity of unsaturated P(V) electrophiles. Specifically, the energetically low-lying σ antibonding orbital of the P–S bond more readily stabilizes the electron density from the lone pair (LP) of the generated carbanion, rendering the phosphonothiolates more reactive compared to the derivatives bearing oxygen and nitrogen. Our studies provide a detailed mechanistic picture for designing P(V)-based electrophiles with fine-tuned reactivity profiles.

---

Introduction

Modifying proteins at the natural amino acid cysteine (Cys) received widespread application both in life science research, and in the development of modern therapeutics such as antibody–drug conjugates.¹ Selective labeling of cysteine's sulfhydryl group in the presence of other functional groups can be achieved with various types of reagents,² many of which are unsaturated electrophiles. In addition to classical maleimides³ and exocyclic maleimide derivatives,⁴ unsaturated carbon–carbon bonds can be activated towards thiol addition by adjacent carbonyl^5–7 or sulfonamide groups,⁸ electron-withdrawing nitro⁹ or tosyl groups,^10,11via pyrimidine¹² and quaternary pyridinium¹³ substituents or by means of ring-strain.^14,15

The phosphoryl (P=O) moiety is another electron-withdrawing moiety that can induce thiol addition to an adjacent vinyl or ethynyl group. Recently, we showed how this electronic feature can be exploited to install unsaturated phosphonamidates^16–18 and phosphonothiolates¹⁹ as handles for selective protein modification at cysteine, resulting in stable thioether conjugates. Ethynylphosphonamidates have been employed for the generation of stable and efficacious antibody–drug conjugates,^18,20 while vinylphosphonamidate derivatives have enabled intramolecular peptide cyclization.¹⁷ Furthermore, an electrophilic vinylphosphonothiolate group installed on a ubiquitin mutant allowed for site-selective protein–protein conjugation.¹⁹

When developing a protein modification method, fast reaction kinetics is an important parameter.²¹ Labeling reagents, such as fluorophores or cytotoxic payloads, which show specificity and high reactivity towards the desired amino acids enable high conversions in a short time, thereby circumventing the use of excess reagents, and facilitating the purification steps. Furthermore, using fewer equivalents of the labeling reagent will avoid competing reactions such as unselective labeling or (re)oxidation of cysteines to disulfides. Therefore, understanding the factors that enhance the reactivity of a certain labeling reagent towards its target amino acid is critical for rationally designing next-generation derivatives that display improved reaction kinetics.

For unsaturated P(V) electrophiles, the substituents around the phosphorus atom influence their thiol addition reactivity. As demonstrated for vinylphosphonamidates, electron-withdrawing substituents at the N- and the O-residue increased the speed of the thiol addition.¹⁷ The fastest derivative in this study (N-phenyl, O-trifluoroethyl) exhibited a second-order rate constant of 0.021 M⁻¹ s⁻¹ with glutathione as a reaction partner at pH 8.5. Another significant rate enhancement can be achieved by replacing the vinyl with an ethynyl group. Under comparable conditions, the second-order rate constant of the glutathione addition to a fluorescent N-phenyl-EDANS-O-ethyl-ethynylphosphonamidate (EDANS = 5-[(2-aminoethyl)amino]naphthalene-1-sulfonic acid) derivative, 9 in Fig. 1b, is 0.62 M⁻¹ s⁻¹.¹⁶ These findings prompted us to investigate in greater detail the effect of the substituents around the phosphorus atom on the reactivity of unsaturated P(V) electrophiles in thiol additions. In particular, we questioned how the vinyl- and ethynyl P(V) electrophiles reacted differently, and how the reactivity of the ethynyl P(V) derivatives changes when the nitrogen atom in phosphonamidates was replaced by an oxygen or a sulfur atom. Furthermore, we aimed to elucidate the origin of the previously reported Z-selectivity¹⁶ for thiol additions to ethynyl P(V) electrophiles.

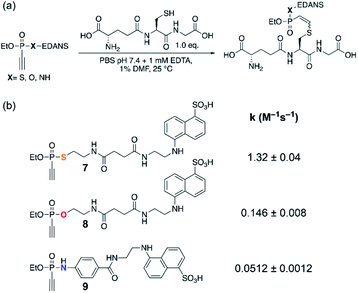Fig. 1 (a) Reaction conditions. (b) Measured second-order rate constants k of the reactions of ethynyl P(V) electrophiles 7–9 with glutathione at pH 7.4.

Based on our previous studies^16,17,19 we envisioned ethynyl-phosphonothiolates and -phosphonates to be promising Cys-selective electrophiles that may potentially display an even higher reactivity compared to the existing unsaturated P(V) systems. Vinylphosphonates have been described by Gao et al.²² in the context of thiol-selective bioconjugation, but rate constants were not reported. In terms of the more reactive ethynyl motif, the synthesis of ethynylphosphonates have been previously reported by Timmer et al.^23,24 and others, though again, reaction rates for thiol additions have not been explored. Thus, we set out to synthesize, and subsequently analyze the electrophilic reactivity of ethynylphosphonate and the novel ethynylphosphonothiolate derivatives.

Results and discussion

We started our studies with the synthesis of fluorescent EDANS-ethynylphosphonothiolate and ethynylphosphonate derivatives, allowing for measuring the thiol addition kinetics by employing a previously established HPLC assay.¹⁶ For both substrates, an ethoxy substituent on the phosphorus atom was retained for consistency with the previous work on EDANS-O-ethyl-ethynylphosphonamidate.¹⁶ The synthetic protocol is summarized in Scheme 1. Subjecting phosphorus trichloride to base-mediated substitutions with ethanol and diisopropylamine, followed by addition of ethynylmagnesium bromide gave the P(III) intermediate 1 in 49% yield after silica gel chromatography. Inspired by aforementioned protocols for the synthesis of unsaturated phosphonates,^23,24 we subjected intermediate 1 to a tetrazole-mediated substitution with either thiol 2 or alcohol 3, followed by in situ oxidation with tert-butyl hydroperoxide to generate phosphonothiolate 4 or phosphonate 5, respectively. The Boc-protected amine was then deprotected with trifluoroacetic acid, and coupled to the carboxylic acid EDANS derivative 6. The targeted ethynylphosphonothiolate 7 and ethynylphosphonate 8 were obtained in 32% and 31% yield, respectively, following the purification by reverse-phase HPLC.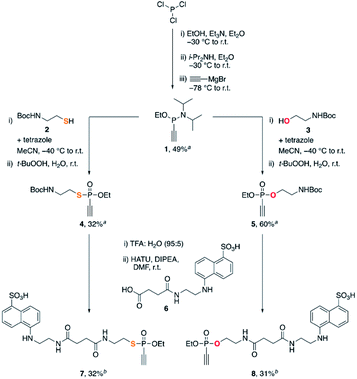

Scheme 1 Synthesis of 7 and 8. ^aIsolated yield after silica flash column chromatography. ^bIsolated yield after reverse phase HPLC purification.

With the desired fluorescent P(V) derivatives synthesized, we next assessed their thiol addition reactivity at physiologically relevant pH of 7.4, using glutathione as a reaction partner in a ratio of 1 : 1 (Fig. 1a). For ethynylphosphonothiolate 7, we measured a second-order rate constant of 1.32 M⁻¹ s⁻¹ (Fig. S1‡), while the glutathione addition to ethynylphosphonate 8 is characterized by a second-order rate constant of 0.146 M⁻¹ s⁻¹ (Fig. S2‡). The previously described ethynylphosphonamidate¹⁶ (9) is the least reactive molecule with a second-order rate constant of 0.0512 M⁻¹ s⁻¹ (Fig. S3‡) at pH 7.4. These results demonstrate that the heteroatoms bound to the central phosphorus atom have a notable influence on the overall thiol addition reactivity and motivated us to pursue a mechanistic rationale. Furthermore, as reported for ethynylphosphonamidates¹⁶ and other electron-deficient alkynes,²⁵ thiol additions to these substrates proceeded with high Z-selectivity. And here, we also observed high Z-selectivity for the thiol addition to an ethynylphosphonothiolate derivative (Fig. S4‡). Another goal of this study was to interpret the origin for the observed Z-selectivity for thiol additions to ethynyl-P(V) electrophiles.

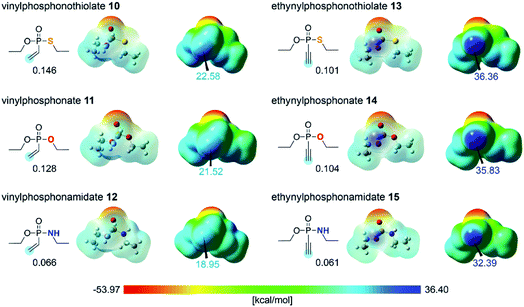
In order to evaluate the different reactivities of unsaturated P(V) electrophiles in thiol addition reactions, the molecular electrostatic potential (MEP) of the electrophiles 10–15 were obtained using density functional theory (DFT) calculations,²⁶ as shown in Fig. 2. The EDANS substituent on the heteroatoms X was modeled as an ethyl substituent for efficient computations. Whereas this structural simplification is somewhat dramatic, the focus of this work lies in understanding the intrinsic reactivity trends centered at the P(V)-oxide functionality. The insight derived from the much simpler ethyl model should be generally valid and transferable for the EDANS substituted system. The MEP results showed that the ethynyl P(V) electrophiles 13–15 have more positively polarized electrostatic potential on the unsaturated terminal carbon compared to the vinyl P(V) electrophiles 10–12, which is in line with the observed kinetics. This is easy to understand considering that the alkynyl group is much more polarizable and will be a more effective acceptor than the vinyl moiety. Within the two classes of electrophiles the positive electrostatic potential on the terminal carbon decreases in the order S > O > NH for both ethynyl- and vinyl series, suggesting that sulfur is most prolific in increasing the positive electrostatic potential at the terminal carbon position, thus rendering 13 to be most susceptible to the nucleophilic attack of the thiol substrate. Although this finding is in good agreement with the experimental observation summarized in Fig. 1, it is fundamentally counter-intuitive, as simple electronegativity considerations (S: 2.5, O: 3.5, N: 3.0) would predict oxygen to be the strongest electron-withdrawing functionality in the series. Although electrostatic potentials offer a reasonable estimate of the reactivity of the electrophiles,²⁷ we sought to characterize the reaction mechanism in greater detail and better understand the origin for different reactivities among the P(V) electrophiles. Thus, several mechanistic possibilities were explored using DFT calculations. The geometry optimizations for the intermediates and the transition state structures were performed with the M06-2X/6-31G(d,p) level of theory^28,29 in conjunction with a continuum solvation model for water (ε = 78.4).^30–33

Fig. 2 MEPs of the unsaturated P(V) electrophiles 10–15. Both transparent and filled maps of the same structures are shown. The CHELPG charges of the reaction site, with hydrogen(s) summed into the terminal carbon, are written in black. The most positive MEP values (in kcal mol⁻¹) found on the edges of the isodensity surface (0.0004 a.u.) are written in blue.

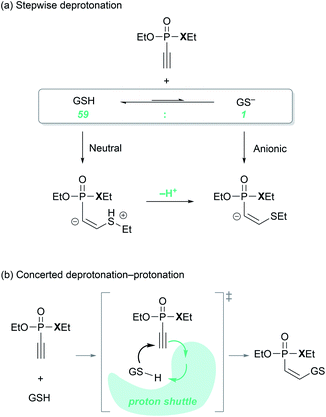
An important mechanistic question relates to the timing of the thiol deprotonation, as shown in Fig. 3. Conceptually, the conjugate base of the thiol, the thiolate, will be a much more powerful nucleophile and we may consider that it is the thiolate formed from the standard Brønsted acid/base equilibrium in water, that attacks the P(V) electrophiles. This possibility is denoted as the ‘anionic’ pathway in Fig. 3a. Given that the pK_a of the thiol group of glutathione is 9.17,³⁴ the equilibrium at the experimental condition of pH = 7.4 lies on the thiol side and the thiolate-to-thiol ratio is 1 : 59. Alternatively, we may consider the thiol to be the reactant and the deprotonation occurs after the C–S bond is formed, labeled as the ‘neutral’ pathway in Fig. 3a. Finally, deprotonation may occur in a synchronous fashion as the two substrates start interacting with each other and form the C–S bond, as visualized in Fig. 3b. Whereas the two extreme possibilities can be captured in a computer simulation, the concerted deprotonation cannot be properly modelled, as weakly bound water solvents will likely serve as proton shuttles along a very shallow potential surface in a highly dynamic fashion, which cannot be handled properly in a simple continuum based solvation model that we employ here. Energetically, the two extreme scenarios can be employed as upper and lower bound estimates.

Fig. 3 (a) Two possible timings for the deprotonation; neutral pathway entails the nucleophilic attack of the thiol followed by deprotonation and anionic pathway assumes that the deprotonation occurs before the nucleophilic attack. (b) Concerted deprotonation and protonation mediated by the reaction medium (‘proton shuttle’). Glutathione is denoted as GSH.

Fig. 4a shows the reaction energy profiles of these two possible pathways, where the glutathione substrate was modeled by ethanethiol (EtSH). In line with the uphill potential energy surface of the Michael addition of a thiol group reported by Matos et al.,³⁵ our calculations show that the thiol cannot form an addition product with 13 without losing the proton. The adduct C13–H⁺, in which the proton remains on sulfur upon C–S bond formation, is not a proper local minimum on the molecular potential energy surface. Forcing the proton to remain on the sulfur, the energy of C13–H⁺ is estimated to be 34.5 kcal mol⁻¹ on the Gibbs energy profile (Fig. S5‡). On the other hand, the deprotonation product C13 is located at 11.8 kcal mol⁻¹, thus the driving force of deprotonation for the putative intermediate C13–H⁺ is ∼23 kcal mol⁻¹ (Fig. 4a). Taking the pK_a of ethanethiol (10.61)³⁶ into consideration, the free energy correction for forming the thiolate at the experimental condition of pH = 7.4 amounts to 4.4 kcal mol⁻¹ (see ESI 5.3‡). Assuming the thiolate as the nucleophile, both the addition product C13 at 11.8 kcal mol⁻¹ and the transition state B-TS13 at 24.7 kcal mol⁻¹ show that the thiolate addition is feasible. Subsequent protonation of the carbanion of C13 is the final step that affords the final product D13 and releases 19.6 kcal mol⁻¹ of Gibbs free energy relative to A13. Fig. 4b illustrates the shape of the general reaction energy profile, indicating that the final protonation step to afford the final product D is the thermodynamic driving force.

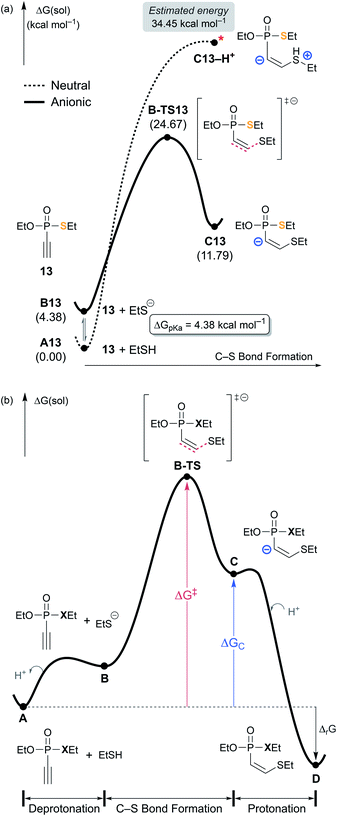Fig. 4 (a) Two possible mechanistic pathways for the nucleophilic attack on 13 by the thiol substrate. (b) General scheme of free energy profile for ethynyl P(V) electrophiles.

According to the kinetic experiments,^17,19 the ethynyl groups are more reactive electrophiles than the vinyl groups. The obvious rationale for the reactivity difference is that the energy of the π* orbital of a C–C triple bond is lower than that of a C–C double bond, thus, a more favorable HOMO–LUMO interaction with an attacking nucleophile is possible. Computationally, this reactivity pattern is well reproduced: for example, the ethynyl P(V) electrophile (13) has a thiol addition barrier of 24.7 kcal mol⁻¹, which is lower than the 27.3 kcal mol⁻¹ barrier predicted for vinyl P(V) electrophile (10). In the light of Hammond's postulate,³⁷ the trends in calculated barriers (ΔG^‡) correlate with the relative stability of the resulting carbanion species, labeled as ΔG_C in Table 1. The substrate 10 undergoes the thiolate addition facing a higher barrier and affording a less stable product intermediate C10. C10 is 20.8 kcal mol⁻¹ uphill in the Gibbs energy profile, whereas the ethynyl derivative C13 is only at 7.7 kcal mol⁻¹. Thus, along with the insight gained from the MEPs illustrated in Fig. 2, we conclude that ethynyl electrophiles are more reactive because of their polarizability and their propensity to form relatively stable carbanion centers.

Table 1 Overall barriers (ΔG^‡) and reaction energies (ΔG_C and Δ_rG) for the nucleophilic thiol addition^a

Substrate			ΔG^‡	ΔGC	ΔrG
a Energies in kcal mol^−1. b Reaction pathway that affords an E-isomer was evaluated. c The barrier is an estimate obtained from the transition state calculation with the constrained geometry of P–C–C–S group (see ESI 5.7 for details).
Vinyl-	X = S	10	27.34	20.82	−6.96
Ethynyl-		13-E	29.67^c	7.69	−21.15
		13	24.67	11.79	−19.63
	X = O	14	26.89	14.96	−20.56
	X = NH	15	30.20	19.98	−17.61

---

Another factor that affects the reactivity is the heteroatom X (X = S, O, NH) bonded to the phosphorus atom. Specifically, substrate 7 (X = S) showed the fastest reaction with a rate constant of 1.32 M⁻¹ s⁻¹, that is larger by few orders of magnitude than that of 8 and 9 (X = O: 0.146, and X = NH: 0.0512 M⁻¹ s⁻¹, respectively). Likewise, calculated barriers of 24.7, 26.9, and 30.2 kcal mol⁻¹ for the computational models 13, 14, and 15, respectively, correlate well with the trends observed in the experimental rates. The effect of the substituent X on the electrophilicity of ethynyl moiety can also be observed from the trends in C–S distances in the transition states, B-TS. As illustrated in Fig. 5, the calculated transitional C–S bond lengths of 2.460 (X = S), 2.402 (X = O), and 2.336 Å (X = NH) reveal that the transition state of 13 (X = S) occurs earlier than those with other substituents.

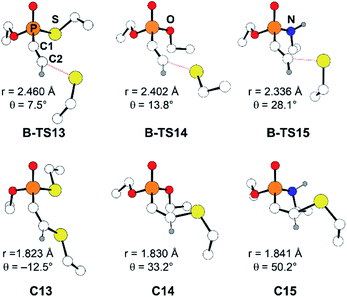Fig. 5 Optimized molecular structures of B-TS and C for the substrates 13–15. The C2–S distance is marked as r, and the X–P–C1–C2 dihedral angle as θ.

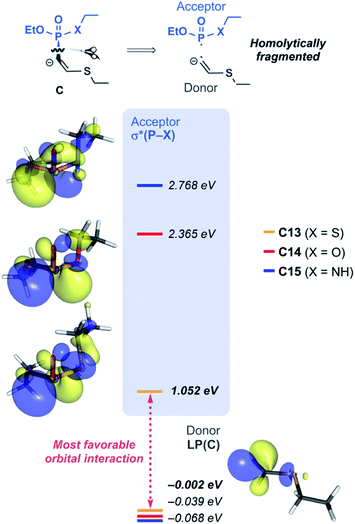
With the reactivity trends in hand, we set out to understand how the heteroatom Xstabilizes the negative charges in the transition state and intermediate. While surveying the geometries of B-TS and C, it was noticeable that the X–P–C1–C2 dihedral angles are within 50°, as illustrated in Fig. 5, hinting at the existence of a stereoelectronic interaction. In this geometry, the carbanion's lone pair is located in an antiperiplanar position to the P–X bond. Anticipating delocalization of the lone pair electrons for stabilizing the carbanion intermediate C, we sought for donor–acceptor orbital interactions using the second-order perturbation theory³⁸ under the natural bond orbital (NBO) formalism.³⁹ Although the orbital interaction energies are not quantitative, the results from NBO provide impartial comparisons of the intramolecular orbital interactions between LP(C) and its neighboring vacant orbitals. The second-order perturbation energies corresponding to the LP(C) → σ*(P–X) interaction are illustrated in Fig. 6, which shows the lone pair delocalization decrease in the order: 22.2 (X = S) > 18.9 (X = O) > 11.6 kcal mol⁻¹ (X = NH). Hence, the P–S antibonding orbital is found to be the best at accepting the electron density through hyperconjugation. Based on this interpretation, we conclude that the orbital interaction involving σ*(P–X) is a key factor in controlling the reactivity of substrates 7–9.

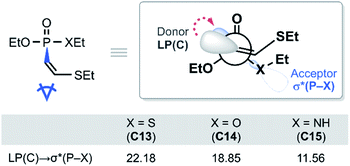Fig. 6 Newman projection of the lowest energy conformer of C13–C15 and the second-order perturbation energies in kcal mol⁻¹.

To investigate the effect of P–X bond on the hyperconjugation, the optimized structures of C13–C15 were fragmented homolytically on the P–C bond, as illustrated in Fig. 7. Molecular orbitals (MOs) generated from the fragments demonstrate that the HOMO of the donor fragment is the lone pair orbital with similar energies; −0.00, −0.04, and −0.07 eV for C13, C14, and C15, respectively. On the other hand, σ*(P–X) orbitals of the acceptor fragment have a large variance in the orbital energies depending on the heteroatom X, in the order of 1.05 (X = S) < 2.37 (X = O) < 2.77 eV (X = NH). The energies of the antibonding orbitals can be further rationalized by the strength of the σ-interaction. P and S loosely interact due to the much larger atomic radius of S, compared to O and N, thus having inefficient overlap of atomic orbitals. The weakest P–S interaction infers the smallest amount of destabilization of the antibonding orbital and imparts the ‘soft’ character of σ*(P–S) that is readily involved in orbital interactions. In the same context, for the substrate 13, significant orbital mixing of σ*(P–S) into the LUMO was found to be responsible to lower the orbital energy compared to 14 and 15 (see Fig. S10 for detailed analysis‡). This is in line with the highest polarizability observed for the phosphonothiolate derivatives, inferred from the highest positive charge in the MEPs of 10 and 13 among the vinyl and ethynyl P(V) derivatives, respectively (Fig. 2). Taken together, the low energy of σ*(P–S) orbital explains why 13 is superior to 14 and 15, in terms of having the most polarizable reaction site towards the nucleophilic attack, and subsequently achieving the most effective electronic delocalization in the intermediate C.

Fig. 7 The intermediates C13–C15 were fragmented homolytically across the P–C bond. Molecular orbitals of the frozen donor and acceptor fragments were visualized with the isodensity value of 0.05 a.u.

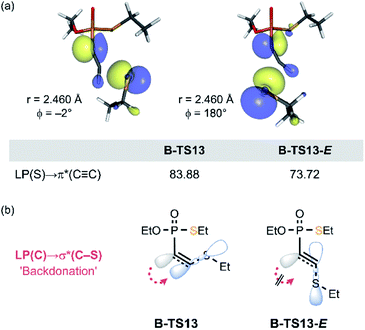
In our previous study of the thiol addition to ethynylphosphonamidates, DFT calculations revealed the higher barrier for the reaction pathway leading to the E-product.¹⁶ Whilst the calculated reaction profile reproduced the trend for the observed Z-selectivity, the origin for this stereochemistry was not explored. Herein, we were able to pinpoint the stereochemical effect that gives rise to the Z-selective C–S bond formation to the ethynyl P(V) derivatives. Consistent with the previous report,¹⁶ the estimated barrier for the E-isomer formation (in 13-E pathway) is 5.0 kcal mol⁻¹ higher than the overall barrier for the Z-selective reaction pathway of 13 (Table 1). In the course of the addition of thiolate, the lone pair orbital of thiolate interacts with the π*(C≡C) orbital, while the negative charge accumulates on the adjacent carbon that eventually transforms into a carbanion's lone pair. As depicted in Fig. 8a, the HOMO of the transition state B-TS13 and the estimated transition state B-TS13-E display the HOMO–LUMO bonding interaction between EtS⁻ and 13, together with the newly forming carbanion lone pair LP(C). The second-order perturbation analysis revealed that B-TS13-E features less LP(S) → π*(C≡C) bonding interaction, having significantly smaller second order perturbation energies of 73.7 kcal mol⁻¹, compared to 83.9 kcal mol⁻¹ in B-TS13 (Fig. 8a). This difference implies that the bond-forming interaction in the transition state is affected by the arrangement of the new bond relative to LP(C). In the E-conformation, the C–S bond is in synperiplanar position to LP(C). Thus, the electronic delocalization through LP(C) → σ*(C–S) interaction (backdonation) is less effective compared to the Z-conformers as illustrated in Fig. 8b. More localized electron density on the carbanion center is also observed in greater distortion of the P–C1–C2 angle, which gives rise to the higher energetic cost to afford the E-product (see ESI 5.7 for detailed analysis‡).

Fig. 8 (a) HOMO (isodensity value = 0.05 a.u.) and the second-order perturbation energies (in kcal mol⁻¹) of B-TS13 and B-TS13-E. The P–C1–C2–S dihedral angle is marked as ϕ. (b) Schematic representation of the electronic delocalization through orbital interactions.

Conclusions

In summary, we have investigated the factors that determine the reactivity of thiol addition to unsaturated P(V) electrophiles. The experimentally measured second-order rate constants revealed that the newly established ethynylphosphonothiolates have the highest reactivity among the tested P(V) derivatives, where the ethynyl groups are more reactive than vinyl groups and the type of heteroatoms bonded to the phosphorus influences the overall reactivity of P(V) derivatives. The DFT calculations on the MEPs gave insights into the sites that are susceptible to a nucleophilic attack. The calculated reaction barriers of nucleophilic addition of the thiol precisely match the trends of the experimentally observed kinetics. NBO analysis enabled us to analyze the electronic structures of the putative carbanion intermediates, and to showcase that hyperconjugation between the lone pair and the vacant σ* orbitals of the vicinal bonds significantly affects the reactivity. Fragment orbital analysis revealed that the phosphonothiolate derivatives possess the lowest σ*(P–X) acceptor orbital and thus achieve the most effective hyperconjugation. In addition, the E/Z stereoselectivity was elucidated in that the newly generated C–S bond is oriented better for hyperconjugation in Z-conformation than in the E-isomer. These fundamental insights into the reactivity of different unsaturated P(V) electrophiles will aid the design of next-generation derivatives with desirable properties. Inspired by these findings, one promising avenue to further enhance the reactivity of P(V) derivatives would be to pursue with even softer phosphorus-substituents and to explore various other unsaturated substituents in greater detail.

Author contributions

Y. P., A. B., H. M., S. B., M.-A. K., M.-H. B. and C. H. conceptualization; Y. P., A. B., H. M., S. B., M.-A. K., and S. H. investigation; Y. P., A. B., H. M., S. B., and M.-A. K. formal analysis; Y. P., A. B., H. M., S. H., M.-H. B. and C. H. writing-original draft; Y. P., A. B., H. M., and M.-H. B. writing-review and editing; H. S., M.-H. B., and C. H. supervision and funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M.-H. B. acknowledges support from the Institute for Basic Science (IBS-R010-A1) in Korea. H. S. thanks Leibniz-Forschungsinstitut für Molekulare Pharmakologie (FMP) and Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC 2008 – 390540038 – UniSysCat. C. P. R. H. is grateful for continuous support by the Deutsche Forschungsgemeinschaft within the SPP1623, the GRK2473 and the SFB765, the Einstein Foundation Berlin (Leibniz-Humboldt Professorship), the Boehringer Ingelheim Fonds (Plus 3 award), the Fonds der Chemischen Industrie and the Leibniz Society (SAW-2018-FMP-4-P5label, T18/2017). A. L. B. acknowledges support from Studienstiftung des Deutschen Volkes for a doctoral fellowship. We thank Mr Bohyun Park for the fruitful discussion.

Notes and references

1. P. Ochtrop and C. P. R. Hackenberger, Curr. Opin. Chem. Biol., 2020, 58, 28–36.
2. R. Tessier, R. K. Nandi, B. G. Dwyer, D. Abegg, C. Sornay, J. Ceballos, S. Erb, S. Cianférani, A. Wagner, G. Chaubet, A. Adibekian and J. Waser, Angew. Chem., Int. Ed., 2020, 59, 10961–10970.
3. J. M. J. M. Ravasco, H. Faustino, A. Trindade and P. M. P. Gois, Chem.–Eur. J., 2019, 25, 43–59.
4. D. Kalia, P. V. Malekar and M. Parthasarathy, Angew. Chem., Int. Ed., 2016, 55, 1432–1435.
5. B. Bernardim, P. M. S. D. Cal, M. J. Matos, B. L. Oliveira, N. Martínez-Sáez, I. S. Albuquerque, E. Perkins, F. Corzana, A. C. B. Burtoloso, G. Jiménez-Osés and G. J. L. Bernardes, Nat. Commun., 2016, 7, 13128.
6. S. Ariyasu, H. Hayashi, B. Xing and S. Chiba, Bioconjugate Chem., 2017, 28, 897–902.
7. T. Wang, A. Riegger, M. Lamla, S. Wiese, P. Oeckl, M. Otto, Y. Wu, S. Fischer, H. Barth, S. L. Kuan and T. Weil, Chem. Sci., 2016, 7, 3234–3239.
8. R. Huang, Z. Li, Y. Sheng, J. Yu, Y. Wu, Y. Zhan, H. Chen and B. Jiang, Org. Lett., 2018, 20, 6526–6529.
9. Q. Luo, Y. Tao, W. Sheng, J. Lu and H. Wang, Nat. Commun., 2019, 10, 142.
10. E. G. de Montes, E. Jiménez-Moreno, B. L. Oliveira, C. D. Navo, P. M. S. D. Cal, G. Jiménez-Osés, I. Robina, A. J. Moreno-Vargas and G. J. L. Bernardes, Chem. Sci., 2019, 10, 4515–4522.
11. E. G. de Montes, A. Istrate, C. D. Navo, E. Jimenez-Moreno, E. A. Hoyt, F. Corzana, I. Robina, G. Jimenez-Oses, A. J. Moreno-Vargas and G. J. L. Bernardes, Angew. Chem., Int. Ed., 2020, 59, 6196–6200.
12. S. J. Walsh, S. Omarjee, W. R. J. D. Galloway, T. T. L. Kwan, H. F. Sore, J. S. Parker, M. Hyvonen, J. S. Carroll and D. R. Spring, Chem. Sci., 2019, 10, 694–700.
13. M. J. Matos, C. D. Navo, T. Hakala, X. Ferhati, A. Guerreiro, D. Hartmann, B. Bernardim, K. L. Saar, I. Companon, F. Corzana, T. P. J. Knowles, G. Jimenez-Oses and G. J. L. Bernardes, Angew. Chem., Int. Ed., 2019, 58, 6640–6644.
14. N. J. Smith, K. Rohlfing, L. A. Sawicki, P. M. Kharkar, S. J. Boyd, A. M. Kloxin and J. M. Fox, Org. Biomol. Chem., 2018, 16, 2164–2169.
15. C. Zhang, P. Dai, A. A. Vinogradov, Z. P. Gates and B. L. Pentelute, Angew. Chem., Int. Ed., 2018, 57, 6459–6463.
16. M.-A. Kasper, M. Glanz, A. Stengl, M. Penkert, S. Klenk, T. Sauer, D. Schumacher, J. Helma, E. Krause, M. C. Cardoso, H. Leonhardt and C. P. R. Hackenberger, Angew. Chem., Int. Ed., 2019, 58, 11625–11630.
17. M.-A. Kasper, M. Glanz, A. Oder, P. Schmieder, J. P. von Kries and C. P. R. Hackenberger, Chem. Sci., 2019, 10, 6322–6329.
18. M.-A. Kasper, A. Stengl, P. Ochtrop, M. Gerlach, T. Stoschek, D. Schumacher, J. Helma, M. Penkert, E. Krause, H. Leonhardt and C. P. R. Hackenberger, Angew. Chem., Int. Ed., 2019, 58, 11631–11636.
19. A. L. Baumann, S. Schwagerus, K. Broi, K. Kemnitz-Hassanin, C. E. Stieger, N. Trieloff, P. Schmieder and C. P. R. Hackenberger, J. Am. Chem. Soc., 2020, 142, 9544–9552.
20. M.-A. Kasper, M. Gerlach, A. F. L. Schneider, C. Groneberg, P. Ochtrop, S. Boldt, D. Schumacher, J. Helma, H. Leonhardt, M. Christmann and C. P. R. Hackenberger, ChemBioChem, 2020, 21, 113–119.
21. F. Saito, H. Noda and J. W. Bode, ACS Chem. Biol., 2015, 10, 1026–1033.
22. F. Gao, X. Yan and K. Auclair, Chem.–Eur. J., 2009, 15, 2064–2070.
23. M. S. M. Timmer, H. Ovaa, D. V. Filippov, G. A. van der Marel and J. H. van Boom, Tetrahedron Lett., 2000, 41, 8635–8638.
24. M. S. M. Timmer, H. Ovaa, D. V. Filippov, G. A. van der Marel and J. H. van Boom, Tetrahedron Lett., 2001, 42, 8231–8233.
25. H. Y. Shiu, T. C. Chan, C. M. Ho, Y. Liu, M. K. Wong and C. M. Che, Chem.–Eur. J., 2009, 15, 3839–3850.
26. The geometry optimizations and generation of the molecular electrostatic potential were carried out using B3LYP/aug-cc-pVTZ level of theory. See ESI 5.1 for details.‡.
27. P. Sjoberg and P. Politzer, J. Phys. Chem., 1990, 94, 3959–3961.
28. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
29. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728.
30. B. Marten, K. Kim, C. Cortis, R. A. Friesner, R. B. Murphy, M. N. Ringnalda, D. Sitkoff and B. Honig, J. Phys. Chem., 1996, 100, 11775–11788.
31. S. R. Edinger, C. Cortis, P. S. Shenkin and R. A. Friesner, J. Phys. Chem. B, 1997, 101, 1190–1197.
32. D. J. Tannor, B. Marten, R. Murphy, R. A. Friesner, D. Sitkoff, A. Nicholls, M. Ringnalda, W. A. Goddard and B. Honig, J. Am. Chem. Soc., 1994, 116, 11875–11882.
33. M. Friedrichs, R. H. Zhou, S. R. Edinger and R. A. Friesner, J. Phys. Chem. B, 1999, 103, 3057–3061.
34. S. S. Tang and G. G. Chang, J. Org. Chem., 1995, 60, 6183–6185.
35. M. J. Matos, B. L. Oliveira, N. Martínez-Sáez, A. Guerreiro, P. M. S. D. Cal, J. Bertoldo, M. Maneiro, E. Perkins, J. Howard, M. J. Deery, J. M. Chalker, F. Corzana, G. Jiménez-Osés and G. J. L. Bernardes, J. Am. Chem. Soc., 2018, 140, 4004–4017.
36. E. P. Serjeant and B. Dempsey, International Union of Pure and Applied Chemistry (IUPAC), Ionisation Constants of Organic Acids in Aqueous Solution, IUPAC Chemical Data Series No. 23, Pergamon Press, Oxford, New York, 1979.
37. G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338.
38. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.
39. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.

---

Footnotes

† Parts of the technology described in the manuscript are part of a pending patent application by C. P. R. H., A. L. B., M.-A. K., S. B.

‡ Electronic supplementary information (ESI) available: Synthetic and experimental procedures, NMR spectral data, Cartesian coordinates of DFT-optimized structures, calculations, and computational details are provided. See DOI: 10.1039/d1sc01730f

§ These authors contributed equally to this work.

---