Open Access Article
Open Access ArticleVibrational Stark shift spectroscopy of catalysts under the influence of electric fields at electrode–solution interfaces†
Dhritiman
Bhattacharyya
 a,
Pablo E.
Videla
b,
Mauricio
Cattaneo
c,
Victor S.
Batista
*b,
Tianquan
Lian
a,
Pablo E.
Videla
b,
Mauricio
Cattaneo
c,
Victor S.
Batista
*b,
Tianquan
Lian
 *a and
Clifford P.
Kubiak
*a and
Clifford P.
Kubiak
 *d
*d
aDepartment of Chemistry, Emory University, 1515 Dickey Drive Northeast, Atlanta, Georgia 30322, USA. E-mail: tlian@emory.edu
bDepartment of Chemistry and Energy Sciences Institute, Yale University, 225 Prospect Street, New Haven, Connecticut 06520, USA. E-mail: victor.batista@yale.edu
cINQUINOA-UNT-CONICET, Facultad de Bioquímica, Química y Farmacia, Instituto de Química Física, Universidad Nacional de Tucumán, Ayacucho 471 (4000), San Miguel de Tucumán, Argentina
dDepartment of Chemistry and Biochemistry, University of California, San Diego, 9500 Gilman Drive, MC 0358, La Jolla, California 92093, USA. E-mail: ckubiak@ucsd.edu
First published on 13th July 2021
Abstract
External control of chemical processes is a subject of widespread interest in chemical research, including control of electrocatalytic processes with significant promise in energy research. The electrochemical double-layer is the nanoscale region next to the electrode/electrolyte interface where chemical reactions typically occur. Understanding the effects of electric fields within the electrochemical double layer requires a combination of synthesis, electrochemistry, spectroscopy, and theory. In particular, vibrational sum frequency generation (VSFG) spectroscopy is a powerful technique to probe the response of molecular catalysts at the electrode interface under bias. Fundamental understanding can be obtained via synthetic tuning of the adsorbed molecular catalysts on the electrode surface and by combining experimental VSFG data with theoretical modelling of the Stark shift response. The resulting insights at the molecular level are particularly valuable for the development of new methodologies to control and characterize catalysts confined to electrode surfaces. This Perspective article is focused on how systematic modifications of molecules anchored to surfaces report information concerning the geometric, energetic, and electronic parameters of catalysts under bias attached to electrode surfaces.
I. Introduction
Electrocatalysis is a major area of industrial and economic relevance with important implications in fine chemical synthesis, solar fuels, and fuel cell development. Conceptual tools to improve electrocatalysis activity, efficiency, mechanisms and addressing challenges regarding various thermodynamic and kinetic parameters are essential to future advances in electrocatalysis technology.1,2 At first sight, achieving control of the local electric field at a catalytic site of an electrode surface might seem to be challenging, particularly considering that the making and breaking of individual bonds would have to be controlled in a complex interfacial environment with rather diffuse macroscopic electric fields. Remarkably, several experiments have already shown that this is precisely what can be accomplished.3–6 The outstanding difficulty, however, is to establish methods for understanding the underlying control mechanisms and to exploit the external field control as applied to important chemical reactions. The integration of synthesis and operando spectro-electrochemical measurements, along with computational modeling is paving the way for precise molecular-level understanding of interfacial electric fields and their effects on heterogenized molecular catalysts.The idea of controlling catalysis with applied electric fields can be traced back to the work of Vayenas et al.7 on non-faradaic electrochemical modification of catalytic activity and selectivity of metal catalysts, with enhancement factors as high as 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, obtained during ethylene and methanol oxidation on Pt, and the work of Sason Shaik8 who theoretically predicted that oriented electric fields could accelerate Diels–Alder reactions and control endo/exo selectivity. Those predictions were subsequently confirmed by experiments.9 Another example is the study of the control of cytochrome P450 catalysis with an external electric field.10 Kanan and coworkers3–5 have shown that subtle alterations to the electronic environment surrounding a catalyst can have notable effects on selectivity. Their experiment featured a Rh porphyrin catalyst immobilized on the surface of a parallel plate capacitor with the surface insulated with metal oxides. Changing the applied voltage across the capacitor swung the product distribution for an organic cyclization reaction from 4
000, obtained during ethylene and methanol oxidation on Pt, and the work of Sason Shaik8 who theoretically predicted that oriented electric fields could accelerate Diels–Alder reactions and control endo/exo selectivity. Those predictions were subsequently confirmed by experiments.9 Another example is the study of the control of cytochrome P450 catalysis with an external electric field.10 Kanan and coworkers3–5 have shown that subtle alterations to the electronic environment surrounding a catalyst can have notable effects on selectivity. Their experiment featured a Rh porphyrin catalyst immobilized on the surface of a parallel plate capacitor with the surface insulated with metal oxides. Changing the applied voltage across the capacitor swung the product distribution for an organic cyclization reaction from 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1
1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, while retaining the chemical composition of the catalyst.3 Furthermore, by modifying the shielding dielectric and ionic composition of the solution, the product ratios were changed substantially from 100
2, while retaining the chemical composition of the catalyst.3 Furthermore, by modifying the shielding dielectric and ionic composition of the solution, the product ratios were changed substantially from 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 all the way to 1
1 all the way to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, which corresponded to a shift from a highly selective catalyst to one that favored a completely different reaction mechanism.3 However, due to the cell design, which involves Si electrodes coated with insulating dielectric layers, very large voltages (∼4.5–5 V) were required to achieve such changes in reactivity. A recent finding by Baik and co-workers6 demonstrates that the base-catalyzed saponification of benzoic esters is fully inhibited at −0.25 V versus open circuit potential; suggesting that the changes in chemical reactivity at electrode interfaces can be achieved at considerably lower voltages. Results by Surendranath and coworkers11–15 revealed that a catalyst conjugated into a graphite electrode can display fundamentally different modes of reactivity than its freely diffusing counterpart. Therefore, it is of paramount importance to characterize the interfacial electric field at the molecular level, including the influence on the catalyst orientation and configuration at the electrode interface, to elucidate the impact on perturbing the electronic structure and the mechanistic behavior of the catalyst that enhances chemical reactivity.
2, which corresponded to a shift from a highly selective catalyst to one that favored a completely different reaction mechanism.3 However, due to the cell design, which involves Si electrodes coated with insulating dielectric layers, very large voltages (∼4.5–5 V) were required to achieve such changes in reactivity. A recent finding by Baik and co-workers6 demonstrates that the base-catalyzed saponification of benzoic esters is fully inhibited at −0.25 V versus open circuit potential; suggesting that the changes in chemical reactivity at electrode interfaces can be achieved at considerably lower voltages. Results by Surendranath and coworkers11–15 revealed that a catalyst conjugated into a graphite electrode can display fundamentally different modes of reactivity than its freely diffusing counterpart. Therefore, it is of paramount importance to characterize the interfacial electric field at the molecular level, including the influence on the catalyst orientation and configuration at the electrode interface, to elucidate the impact on perturbing the electronic structure and the mechanistic behavior of the catalyst that enhances chemical reactivity.
The electrochemical double-layer is a nanoscale region next to the electrode/electrolyte interface where chemistry typically occurs. Recent advances in the study of substrates and electrolytes within the double layer environment have been extensively reviewed.16–21 Along with the conceptual interpretation of the double layer, the dynamic aspect is critical at determining the contact with the electrode surface where the high electric field affects the electronic configuration of the molecule. Chemical induction that manifests itself as molecular Stark shift, often plays an important role by mediating polarization effects and interfacial charge transfer mechanisms critical for reactivity. Stark tuning rates can be measured by surface selective vibrational spectroscopic methods. When combined with theoretical modeling, such spectroscopic methods can provide fundamental understanding of spatial configuration, conformational changes induced by the applied field, and changes in chemical reactivity.
II. Classical models to describe electrode/electrolyte interface
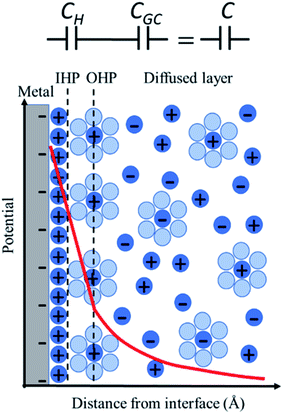
The simplest model to describe an electrode/electrolyte interface is the electrical double layer (EDL) model, which considers the electrodes to be perfectly polarized (metallic) and the electrolyte as a continuum dielectric medium. As proposed by Helmholtz,22 when a charged electrode is immersed in an electrolyte solution, the surface charge of the electrode is neutralized by the oppositely charged counter ions in the solution known as the inner Helmholtz layer or inner Helmholtz plane (IHP), separated by the molecular radius. The solvated ions can only approach the electrode surface from a further distance because of their larger size, and they form an outer Helmholtz plane (OHP) right adjacent to the IHP. The two sheets of opposite charges at the electrode–electrolyte interface resemble a parallel plate capacitor, with a differential capacitance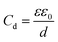 , where ε is the dielectric constant of the medium, ε0 is the permittivity of free space and d is the spacing between the two charge layers. According to this model, the double layer capacitance (Cd) is predicted to be constant, which fails to explain the change in Cd as a function of applied voltage (V) as typically measured by Electrochemical Impedance Spectroscopy (EIS). Later, Gouy23 and Chapman24 independently introduced the idea of a diffuse double layer. It is a continuum mean field approach where ions are considered as point charges in thermodynamic equilibrium with each other. This model assumes that the counter ions are not rigidly held near the electrode surface because of their thermal motion, and therefore can diffuse into the bulk liquid phase. In such a diffuse double layer structure, the concentration of counter ions near the charged surface follows the Boltzmann distribution. Thus, the spacing d between the two charge layers is replaced by the average distance of the ions from the electrode surface, which is dependent on both the applied potential and electrolyte concentration. The Gouy–Chapman model successfully predicts the double layer capacitance in the vicinity of potential of zero charge (PZC) and for low electrolyte concentrations. However, for potentials further away from the PZC, the predicted capacitance rises very rapidly and fails to reproduce the experimental data. To solve this problem, the Gouy–Chapman model was further modified by Stern,25 who introduced the idea that the ions have finite size and therefore, the closest approach between the electrode and the ions in solution is limited by their ionic radii. Stern's model thus combines a compact Helmholtz layer and a Gouy–Chapman diffuse layer that together resemble two parallel-plate capacitors connected in series with the total capacitance (C), with
, where ε is the dielectric constant of the medium, ε0 is the permittivity of free space and d is the spacing between the two charge layers. According to this model, the double layer capacitance (Cd) is predicted to be constant, which fails to explain the change in Cd as a function of applied voltage (V) as typically measured by Electrochemical Impedance Spectroscopy (EIS). Later, Gouy23 and Chapman24 independently introduced the idea of a diffuse double layer. It is a continuum mean field approach where ions are considered as point charges in thermodynamic equilibrium with each other. This model assumes that the counter ions are not rigidly held near the electrode surface because of their thermal motion, and therefore can diffuse into the bulk liquid phase. In such a diffuse double layer structure, the concentration of counter ions near the charged surface follows the Boltzmann distribution. Thus, the spacing d between the two charge layers is replaced by the average distance of the ions from the electrode surface, which is dependent on both the applied potential and electrolyte concentration. The Gouy–Chapman model successfully predicts the double layer capacitance in the vicinity of potential of zero charge (PZC) and for low electrolyte concentrations. However, for potentials further away from the PZC, the predicted capacitance rises very rapidly and fails to reproduce the experimental data. To solve this problem, the Gouy–Chapman model was further modified by Stern,25 who introduced the idea that the ions have finite size and therefore, the closest approach between the electrode and the ions in solution is limited by their ionic radii. Stern's model thus combines a compact Helmholtz layer and a Gouy–Chapman diffuse layer that together resemble two parallel-plate capacitors connected in series with the total capacitance (C), with 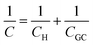 , where CH and CGC are the capacitances of the Helmholtz and the Gouy–Chapman layers, respectively. At high electrolyte concentration and large potentials, the counter ions reside very close to the electrode surface resembling that in the case of the Helmholtz model and giving rise to an almost constant capacitance.
, where CH and CGC are the capacitances of the Helmholtz and the Gouy–Chapman layers, respectively. At high electrolyte concentration and large potentials, the counter ions reside very close to the electrode surface resembling that in the case of the Helmholtz model and giving rise to an almost constant capacitance.
For more than a century, the Gouy–Chapman–Stern (GCS) model has served for the analysis and interpretation of the double layer structure at the electrode/electrolyte interface and to visualize the ionic environment in the vicinity of a charged surface, along with the characterization of the potential profile in the double layer (Fig. 1). According to the GCS model, the electric potential drops linearly within the Helmholtz layer, and in the diffuse layer it falls exponentially. The predictions made by the GCS model, while able to reproduce some gross experimental features in a real system, neglect several finer details including the effects of ion-pairing in the double layer, specific adsorption, and strong nonspecific interaction of the ions with the electrode (ion condensation) that determine the effective surface charge.26 These processes severely affect the electrolyte distribution near the electrode surface and the potential profile in the double layer region (typically on the nanometer scale); but cannot be directly probed using conventional capacitance or surface tension measurements. Stark Shift spectroscopy is one of the ways to directly interrogate the interfacial structure of the double layer and to determine the potential profile away from the electrode surface, which will be discussed in detail later in this article. We refer readers to standard textbooks (e.g., Bard and Faulkner27) for a detailed description and analysis of the electrical double layer structure.
It is worth highlighting that unlike the case of a metallic conductor (described above) where a homogeneous polarization exists throughout the metallic plane, the polarization in the plane of a charged insulator or a metal oxide surface is inhomogeneous and discrete, and should not be described under similar theoretical framework. Girault and coworkers28–30 recently introduced “Discrete Helmholtz” (DH) model, where the discrete nature of the charge carriers at the metal oxide surface drive the formation of a monolayer of counter ions in the solution side, resulting to a large fraction of the interfacial potential drop to take place between these two correlated ionic layers. This ionic correlation, however, is not as strong for these counter ions to be considered as adsorbed or immobile, and these correlated ions in solution can take part in ionic conduction parallel to the plane of the interface, while restricted in the perpendicular direction. The main difference between DH and GCS models is that the former predicts a constant capacitance, while the latter predicts a potential dependent one.28,30 The DH model was also shown to be extended to other interfaces like liquid–liquid interfaces, charged silica–water interfaces, supercapacitors, ion-exchange membranes and even biological membranes.29
III. Electrochemical vibrational Stark effect
The textbook definition of the Stark effect is the shifting, splitting, and broadening of the spectral lines of atoms or molecules in the presence of an external electric field, i.e., the Stark effect is the electric field analogue of the well-known Zeeman effect. From a chemical perspective, the vibrational energy levels of a molecule are shifted under the influence of an electric field since the molecular dipole moment (and thus the strength of the external perturbation) is different for the molecule in the ground and excited vibrational states. As a result, the molecule exhibits vibrational frequency shifts (vibrational Stark shifts) that increase with the strength of the external electric field. For sufficiently weak fields, the Stark shift follows a linear dependence, as follows:| Δν = ν − ν0 = −Δμ·F | (1) |
Prototypical Stark shift reporters are molecules with vibrational modes that are significantly decoupled from other vibrational modes and highly localized along a pair of atoms (e.g., CO or CN stretching modes). The Stark shift Δν of those localized modes can be used to infer the strength of the local electric field F whenever the Stark tuning rates Δμ are readily available from theory, or experimental data. The Stark tuning rate Δμ can be experimentally determined by immobilizing a molecule containing the vibration of interest in a polymer matrix, placing the matrix into a parallel capacitor and applying an external well-defined electric field to measure vibrational Stark shifts.35–38 Alternatively, Δμ can be obtained from ab initio calculations by computing the vibrational frequency shift due to a perturbation of an external electric field added to the Hamiltonian of the system.39–41 Typical values for the vibrational Stark tuning rate of localized vibrational probes (such as CO or CN) are approximately 0.5–2 cm−1 (MV cm−1)−1, i.e. 5–20 cm−1 (V nm−1)−1. Given that solvation and interfacial fields are of the order of tens of MV cm−1, frequency shifts of ∼5–20 cm−1 are typically experienced by Stark shift probes, making the vibrational Stark effect an ideal tool for spectroscopic characterization of interfacial electric fields.
The interfacial electric field F(ϕ,n) is formally a function of both the voltage (ϕ) applied to the electrochemical cell, and the electrolyte ionic strength (n), which are experimentally controllable parameters. In the electrochemical Stark shift experiment, the vibrational frequency of the Stark reporter is typically measured in a self-assembled monolayer (SAM), as a function of ϕ for a fixed value of n. For sufficiently small ϕ, no current flows through the system, so voltage simply polarizes the electrode, and the frequency of the Stark shift reporter changes linearly with ϕ, producing constant values of the Stark tuning slopes dν/dϕ. Once the Stark tuning slopes (dν/dϕ) and Stark tuning rates (Δμ) are known for an electrochemical interface, the absolute strength of the interfacial electric field can be computed according to the following equation:
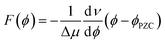 | (2) |
IV. Vibrational sum frequency generation (VSFG) spectroscopy to measure Stark shift
Several operando spectroscopic techniques have been applied for the characterization of interfaces42 and in situ measurements of vibrational Stark shifts, including surface-enhanced infrared absorption spectroscopy (SEIRAS),43 attenuated total reflection infrared (ATR-IR) spectroscopy,44 Fourier-transform infrared reflection-absorption spectroscopy (FT-IRRAS),45 surface-enhanced Raman spectroscopy (SERS),46 sum frequency generation (SFG) spectroscopy40,47 and most recently, shell-isolated nanoparticle enhanced Raman spectroscopy (SHINERS).48 Amongst these techniques, only SFG is inherently surface specific, whereas other IR and Raman based experiments are not and, therefore, they suffer from significant background contribution from the bulk electrolyte solution. The SERS and SEIRAS type measurements work well for roughened electrodes where the surface roughness provides the enhancement of the electric field of the incident light, whereas SFG is particularly valuable to probe planar, single-crystal electrode surfaces. However, we should emphasize that when the spectroscopic entity is tethered to the surface, standard techniques like ATR-IR and SHINERS have sufficient surface sensitivity, despite not being formally surface specific, and provide similar information as one would otherwise get using conventional SFG spectroscopy. There is a considerable volume of literature on these topics; but for the sake of this Perspective, we will only be focusing on the examples related to electrochemical SFG experiments.Sum frequency generation (SFG) spectroscopy provides a valuable platform for operando spectroscopic investigation of buried solid/liquid interfaces, offering intrinsic surface/interface specificity down to sub-monolayer sensitivity. Vibrational sum frequency generation (VSFG) thus offers an ideal method to explore fingerprint bands of molecular species adsorbed on electrode surfaces, including the capability to investigate the interfacial electric field by measuring the Stark shift of vibrational probes. In this Perspective article, we focus on the analysis of various systems probed recently by Stark shift VSFG spectroscopy.
Vibrational sum frequency generation (VSFG) is a second order nonlinear optical spectroscopy that is surface selective since it is electric dipole forbidden in the centrosymmetric medium of the bulk phase.49 Therefore, it is particularly useful to probe molecules at interfaces between two materials where they adopt a preferred orientation.
A typical VSFG experiment is performed by spatially and temporally overlapping a femtosecond broadband tunable IR laser beam and a picosecond narrowband visible laser beam with the sample. The broadband IR pulse creates a vibrational coherence which is upconverted by the visible pulse, and the sum frequency signal can be readily detected since it is emitted along the phase matching direction. The frequency resolution of the VSFG experiment is determined by the bandwidth of the narrowband visible upconverting pulse. The intensity of the VSFG signal (IVSFG) is proportional to the square of the magnitude of the second-order nonlinear susceptibility (χ(2)), and can be fitted by the following equation:50
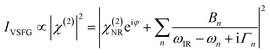 | (3) |
VSFG spectra are recorded for selected polarizations of the input and output pulses. The orientation of the molecular chromophores at the interface can be inferred from direct comparisons to the calculated relative intensities of VSFG signals IVSFG, as obtained from ab initio calculations of χ(2), for different polarization combinations of the incoming and outgoing pulses and/or for different normal modes.52–56Eqn (3) represents the intensity of the VSFG signal that contains both real and imaginary parts of the resonant molecular response (χ(2)R), the non-resonant response (χ(2)NR) from the substrate and the cross terms that are generated because of the interference of these resonant and non-resonant terms. One must rely on complicated spectral fitting procedures to separate out each contribution from such homodyne detected VSFG spectrum, which sometimes can be difficult because of the interference of nearby resonances and in presence of huge non-resonant signal that also interferes with resonant signals. Phase-sensitive VSFG (PS-VSFG) spectroscopy57 or heterodyne-detected VSFG (HD-VSFG) spectroscopy58 paved the way for the determination of both real and imaginary parts of χ(2)R and the phase associated with each resonance, allowing for the accurate subtraction of χ(2)NR. Moreover, unlike the conventional VSFG technique where signal intensity decreases quadratically with decreasing number density of the surface species, the signal intensity scales linearly with surface coverage for HD-VSFG, significantly improving the sensitivity of the measurement with molecular surface coverage as low as 3%.58 However, despite these obvious advantages, there is currently no in situ electrochemical HD-VSFG result reported in the literature to the best of our knowledge. Recent efforts by Hofmann and Koelsch59 introduced a new fitting scheme (iMEMfit) based on iterative phase-matching between complex spectra retrieved from maximum entropy method (MEM) analysis60,61 and fitting of SFG intensity spectrum. This leads to a unique solution of the complex part of χ(2) that shows excellent agreement with that of experimental PS-VSFG spectrum,57,62 enabling quantitative spectral analysis.
To measure the strength of the interfacial electric field and the Stark tuning rate of surface attached, or surface adsorbed species, VSFG experiments are performed under electrochemical conditions. Here, we briefly describe the VSFG experimental set-up from the Lian lab, shown in Fig. 2c. A glass dish is used as an electrochemical cell and is kept inside a home-built chamber which is purged with N2 gas during the experiment. Molecules, typically catalysts, with thiol anchoring groups are used to create a SAM on the Au surface, which serves as the working electrode. To establish the electrical connectivity, copper tape is attached to the gold surface, using an epoxy resin to isolate the copper tape from the electrolyte solution. A 25 μm Teflon spacer is placed on top of the Au surface; above which a 2 mm thick CaF2 window is pressed down in contact. The 25 μm space between the Au slide and the CaF2 window allows for efficient mass (electrolyte) transport during the electrochemistry experiment. The electrochemical cell (glass dish) is then filled with the electrolyte solution. A reference and a counter electrode are immersed into the solution, and all electrodes are connected to a potentiostat (Gamry Instruments) in three-terminal configuration. The VSFG spectrum is typically collected under an applied bias potential for the SAM deposited on a metallic (e.g., Au) or semiconductor (e.g., TiO2) working electrode. A representative potential-dependent VSFG spectra of the nitrile-stretch of 4-mercaptobenzonitrile (4-MBN) on gold is shown in Fig. 2b.63
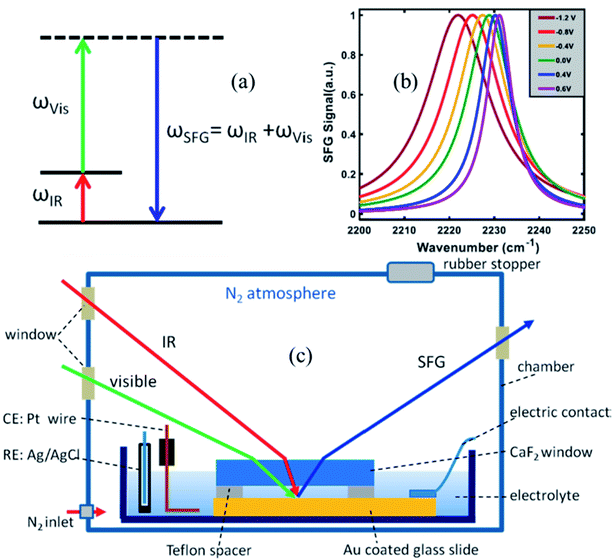 | ||
| Fig. 2 (a) Energy level diagram in a VSFG process. The IR pulse creates a vibrational coherence between v = 0 and v = 1 states, which, in turn, gets upconverted by the visible pulse. The SFG signal is emitted in the phase matching direction with its frequency equal to the sum of the frequencies of the two input pulses. (b) A representative VSFG spectra of the nitrile-stretch of 4-mercaptobenzonitrile (4-MBN) on gold as a function of potential, adapted from a publication by Sarkar et al.63 (c) The electrochemical VSFG set-up used in the Lian lab. Figures (a) and (c) are adapted from a publication by Ge et al.64 | ||
Stark shift measurements have been successfully reported for a range of catalysts attached to various metal and semiconductor surfaces with suitable anchoring groups. Synthetic efforts have contributed significantly by functionalizing the molecules with anchoring groups that attach to Au electrode surfaces with thiolate, nitrile, or isocyanide groups, or to metal-oxide surfaces with carboxylate, or phosphate anchoring groups. It is worth noting that thiolate, cyanide, isocyanide type linkages are not suitable for spectroscopic investigation of the catalyst down to their first reduction potential, as they may be stripped from the electrode surface at potentials below ∼−0.9 V vs. Ag/AgCl. The carboxylate, phosphonate or silatrane anchoring groups on oxide surfaces are relatively more robust. The graphite conjugated catalysts65 or functionalization of the silicon surface via Si–C covalent bond66 pave the way for the development of much robust catalysts that can operate under highly negative voltages. Thus, the combined synthetic, experimental and theoretical efforts by the Kubiak, Lian and Batista groups have enabled fundamental VSFG studies of catalytic systems on electrode surfaces in efforts to provide new insights on catalyst–substrate and catalyst–support interactions, and their response to externally applied bias potential. The integrated approach provides a useful platform to begin studies of chemical reactions at interfaces that could be controlled with externally applied electric fields that modulate the electronic properties of the catalytic sites.
V. Representative examples
(1) Interfacial electric fields at an electrode under polarizing or current-carrying conditions
Dawlaty and coworkers have carried out several studies focusing on the measurement of interfacial fields using 4-mercaptobenzonitrile (4-MBN) as the Stark effect reporter.35,63,67–69 These studies utilize covalent attachment of 4-MBN onto a gold surface and measure the stretching frequency of the nitrile group ν(CN) as a function of different variables to obtain information ranging from the interfacial solvation fields to the correlation between the electrochemical polarization and the Hammett parameters. The ν(CN) stretching frequency varies with applied potential (φ) and ionic-strength concentration (n) of the electrolyte solution (KCl), exhibiting a shift Δν that increases linearly with φ for all n. For a fixed φ, Δν rapidly increases with increasing n from 1–100 mM and beyond that range the change is not significant. These experimental findings were explained by Patrow et al.35 using a model inspired by the work of Smith and White,70 with the following expression of the electric field (F) experienced by the SAM as a function of φ and n: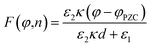 | (4) |
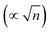 , and φPZC is the potential of zero charge. Eqn (4) combines the Gouy–Chapman model with the capacitive response of the molecular SAM, and in the limiting case of d = 0, i.e., without the SAM on the gold surface, the Gouy–Chapman model can be reclaimed. Starting with this equation, the expression of Δν(φ,n) can be derived, which shows that in the limit of large n values, Δν does not depend on the ionic concentration, thereby explaining the small change in the nitrile stretching frequency once the electrolyte concentration is higher than 100 mM. The interfacial electric field strength (F) as a function of φ and n can be calculated with this model (eqn (4)), as plotted in Fig. 3. Patrow et al.35 showed that the linear change in Δν vs. φ occurs only for positive potentials whereas for negative potentials no change is observed. For the positive bias region, negligible electrochemical current is observed, resulting in charge build-up at the SAM and a resulting increase in φ which increases Δν. On the contrary, significant current is withdrawn for negative potentials, and the magnitude of the current increases with increasing negative voltage, which results in a negligible increase of the field inside the SAM, resembling a “leaky capacitor”. Consequently, Δν does not change with φ in the negative bias region.
, and φPZC is the potential of zero charge. Eqn (4) combines the Gouy–Chapman model with the capacitive response of the molecular SAM, and in the limiting case of d = 0, i.e., without the SAM on the gold surface, the Gouy–Chapman model can be reclaimed. Starting with this equation, the expression of Δν(φ,n) can be derived, which shows that in the limit of large n values, Δν does not depend on the ionic concentration, thereby explaining the small change in the nitrile stretching frequency once the electrolyte concentration is higher than 100 mM. The interfacial electric field strength (F) as a function of φ and n can be calculated with this model (eqn (4)), as plotted in Fig. 3. Patrow et al.35 showed that the linear change in Δν vs. φ occurs only for positive potentials whereas for negative potentials no change is observed. For the positive bias region, negligible electrochemical current is observed, resulting in charge build-up at the SAM and a resulting increase in φ which increases Δν. On the contrary, significant current is withdrawn for negative potentials, and the magnitude of the current increases with increasing negative voltage, which results in a negligible increase of the field inside the SAM, resembling a “leaky capacitor”. Consequently, Δν does not change with φ in the negative bias region.
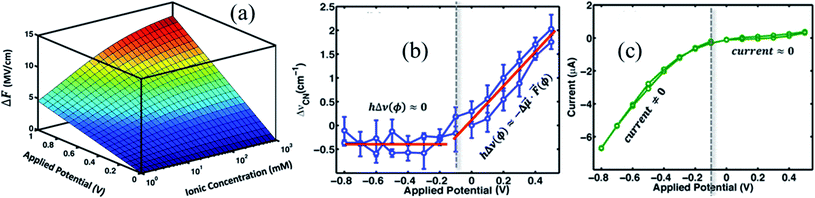 | ||
| Fig. 3 (a) Variation of interfacial electric field experienced by the SAM with applied potential and ionic concentration, ΔF = F(φ,n) − F(0,n). Variation of (b) nitrile stretching frequency, and (c) current as a function of applied potential. Figures are adapted from a publication by Patrow et al.35 | ||
In related work, Shi et al.67 used surface enhanced Raman scattering (SERS) based Stark shift spectroscopy to monitor local electric fields at electrode surfaces during the hydrogen evolution reaction (HER). The onset potential for HER and the PZC at the electrode–electrolyte interface could be determined by current–voltage (I–V) and capacitance–voltage (C–V) measurements, respectively. Comparison of the electric field strength at the onset potential (Eonset = Ereaction = −0.2 V nm−1) and the PZC (EPZC = Esolution = −0.08 V nm−1) provided a way to disentangle the reaction field from the solution field, and the difference corresponds to the field exerted by the electrode (Eelectrode = −0.12 V nm−1) at the onset of HER. The Stark shift measurement of the CN group of benzonitrile reveals a deviation from the linear relationship between the Raman shift and the applied potential when the potential is below −0.3 V vs. Ag/AgCl – i.e., in the HER region that corresponds to an exponential increase in electrochemical current with increase in negative electrode potential. Deviation from linearity stems from a finite voltage drop across the solution (ΔV = IR, where I is the electrochemical current and R is the resistance of the electrolyte solution). The linear dependence of Stark shift is resumed by plotting the frequency as a function of Vapplied − Vsolution, corrected for voltage drop across the solution under current carrying conditions.
(2) Solvation reaction field at the interface
The solvation field is described by the well-known Onsager reaction field theory71 for bulk dielectric media, where a solute molecule is modeled to be residing inside a cavity created by the surrounding solvent. The charge density of the solute polarizes the surrounding solvent, generating the so-called ‘reaction field’ that interacts with the solute molecule itself. The vibrational Stark shift of the chromophore embedded in the solvent cavity provides a quantitative probe of the surrounding field, analogous to the Stark shift of vibrational probes in proteins as demonstrated by Boxer and coworkers.33,72–79 However, the bulk Onsager model cannot be directly translated to the interface due to its inherent asymmetry of the dielectric properties.Dawlaty and coworkers68 constructed a parallel model applicable to the interface, establishing a relation between the vibrational Stark shift of a chromophore tethered to an electrode surface and the interfacial solvation field. To achieve this, a monolayer of 4MBN was formed by covalently attaching 4MBN molecules to the Au surface via thiolate anchoring groups. The VSFG spectra of the monolayer were recorded in the CN stretching region in contact with several solvents (Fig. 4), finding that the frequency of the CN stretch red-shifts when increasing the dielectric constant of the solvent from hexane to DMSO. An expression of the interfacial solvation field analogous to the bulk Onsager model explains the experimental Stark shift as a function of the solvent dielectric constant. The model is based solely on electrostatic interactions, so it does not account for any other type of solute–solvent interaction or even specific interactions due to hydrogen-bonding. Therefore, in the case of chlorinated solvents (CHCl3, CH2Cl2), water and alcohols, the predicted frequency of the CN stretch does not match the experimental observations. The distinct feature of the interfacial solvation field model, when compared to the bulk Onsager model, is that it does not vanish for εr = 1, possibly due to the interaction of the molecular dipole with the metal substrate. Moreover, for most solvents, the interfacial solvation field is smaller than its bulk counterpart and thereby induces a smaller Stark shift of the vibrational chromophore at the interface. The predicted reaction field (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Int) at the 4MBN/Au interface varies from 0.98 V nm−1 for hexane to 2.09 V nm−1 for DMSO.
Int) at the 4MBN/Au interface varies from 0.98 V nm−1 for hexane to 2.09 V nm−1 for DMSO.
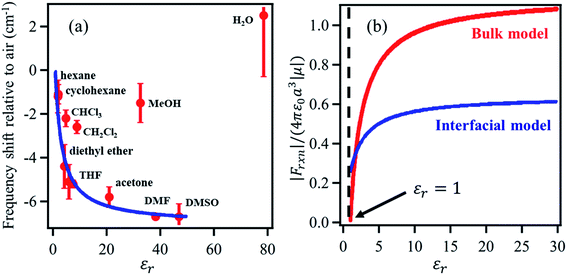 | ||
| Fig. 4 (a) The red dots represent the experimental frequency shift (relative to air) of the nitrile stretch of the 4-MBN molecule adsorbed on gold as a function of the dielectric constant of the solvents. The blue line represents the fit of the experimental results according to the interfacial solvation field model, derived from the bulk Onsager model by Sorenson et al.68 As shown, the interfacial solvation model cannot describe the frequency shifts in the case of chlorinated (CHCl3 and CH2Cl2) and oxygenated (CH3OH and H2O) solvents that participate in H-bonding interactions with the CN moiety. (b) The bulk (red) and the interfacial (blue) reaction fields, in reduced units, as a function of dielectric constant of the solvents. The bulk Onsager field goes to zero at εr = 1; but the interfacial field does not, due to interaction with the metal. These figures are adapted from a publication by Sorenson et al.68 | ||
(3) Electric field strength experienced by surface-immobilized molecular catalysts
Molecular electrocatalysts have been studied extensively in recent years, as they are the key components for a wide range of applications including production of solar fuels, photo-electrochemistry, and sustainable fuel generation.80 In hybrid electrocatalysts where the molecular catalyst is covalently attached to an electrode surface, there is an advantage in the recovery/separation of the products (and catalyst) at the end of the application. To characterize the interfacial structure of such surface-immobilized catalysts, Lian and Batista54,81,82 explored a series of rhenium bipyridine complexes of the general form Re(CnA)(CO)3Cl (CnA = 2,2′-bipyridine-4,4′-(CH2)n-COOH, n = 0–4), bound to single crystalline high-symmetry rutile TiO2 (001) surface by the carboxylate anchoring group. The analysis of molecular orientations based on ab initio DFT calculations of the phase-sensitive VSFG spectra showed that the plane of the bipyridine rings of the Re complex is almost perpendicular to the surface, making an average angle of ∼10–15° from the surface normal (Fig. 5), progressively tilting towards the TiO2 (001) substrate for an increased number of –CH2 units in the linkers.81 The binding geometry and structural heterogeneity are also affected by the crystal facet of the underlying substrate.83,84 For example, an aggregated dimeric structure of the Re catalyst is favored over the monomer on the TiO2 (110) surface, similar to those observed on TiO2 nanoparticles. Information about the interfacial binding geometry/orientation of the electrocatalysts is crucial, as it directly influences the adsorbate–substrate coupling, mechanism of energy and charge transfer and most importantly, the relative stability of the catalytic intermediates.85–87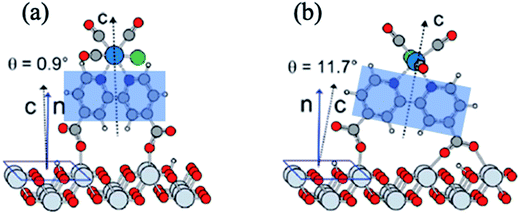 | ||
| Fig. 5 (a and b) Calculated adsorption geometry of Re(CnA)(CO)3Cl on rutile TiO2 (001) substrate, adapted from previous studies.54,82 The shaded blue region shows the plane of the bipyridine rings that is tilted at an angle with respect to the surface normal. | ||
Metal interfaces are particularly important in both heterogeneous and homogeneous catalysis and have enabled in situ monitoring of the potential-dependent electrocatalytic activity of Re catalysts for CO2 reduction. Attachment to Au surfaces has been achieved upon functionalization of the complex bipyridine ligand with CN anchoring groups that covalently bind to the Au surface.88 In contrast to Re catalysts that bind to the TiO2 surface with carboxylate anchoring groups, the plane of the bipyridine rings of the CN substituted catalysts, Re(4-cyano-2,2′-bipyridine)(CO)3Cl and Re(4,4′-dicyano-2,2′-bipyridine)(CO)3Cl, are almost parallel to the metallic surface (∼63° relative to the surface normal), typically exposing the catalytic binding site (Cl ligand) away from the Au substrate. However, the catalytic monolayers are not stable under highly negative voltages and dissociate from the Au surface before any redox reaction of the metal center can take place. This problem can be partially overcome by preparing thiol or disulfide derivatives of the Re complexes which form more robust Au–S bonds and therefore more stable SAMs on the gold surface. In a combined effort by Batista, Lian and Kubiak groups, thiol derivatives of two popular CO2 reduction catalysts, Re(4-mercapto-2,2′-bipyridine) (CO)3Cl (ReS) and Mn(4-mercapto-2,2′-bipyridine) (CO)3Cl (MnS) have been characterized on Au electrode surfaces. The electric field strength at the catalytically active metal center was determined by measuring the Stark tuning rate of the CO ligand stretching vibrations by electrochemical VSFG spectroscopy and DFT calculations.89 It was revealed that the catalysts were significantly tilted by about 65–75° relative to the surface normal (Fig. 6d), with one of the CO groups facing towards the Au surface while exposing the Cl group to the solution, thereby providing in principle a favorable orientation for CO2 binding after exchange with Cl. The potential dependent SFG spectra (Fig. 6a), measured in the range 0.3 to −1.3 V (vs. Ag/AgCl) in a 10 mM aqueous KOH solution shows that the frequency of the CO stretching mode as well as the resonant and non-resonant amplitudes vary reversibly as a function of potential, generating symmetric contour plots between cathodic and anodic sweeps. The non-resonant signal (Fig. 6c) goes through a minimum at −0.2 V for ReS and −0.4 V for MnS, corresponding to the PZC of the Au/SAM/electrolyte system. The frequency shift of the symmetric CO stretching mode can be linearly fitted as a function of the applied bias in the range between 0 to −1.0 V, giving Stark tuning slopes of 21.0 ± 2.0 and 10.0 ± 2.0 cm−1 V−1 for ReS and MnS complexes, respectively. To determine Stark tuning rates of both complexes, DFT calculations were performed to obtain the stretching frequencies of the CO groups as a function of the field strength, when applied normal to the Au surface. The calculated Stark tuning rates Δμ were almost identical for both complexes (−7.5 ± 0.2 cm−1 (V nm−1)−1 for ReS, and −7.7 ± 0.2 cm−1 (V nm−1)−1 for MnS) and twice as large when compared to Δμ for a different binding geometry of the complex where the axial CO group is further away from the surface (∼7.4 Å). Combining the experimental and theoretical results, it has been established that the interfacial electric field strengths at the catalytically active metal centers are on the order of 0.1–1 V nm−1 (108–109 V m−1), as shown in Fig. 6b, for Re and Mn complexes plotted as function of applied potential. The slope of the linear fit, dF/dφ is inversely proportional to the length of the monolayer, and thereby gives a rough estimate of the effective thickness of the SAM formed by these complexes (3.7 ± 0.2 and 7.6 ± 0.2 Å for ReS and MnS, respectively) which are in reasonable agreement with the metal-gold distances calculated by DFT. On the contrary, a simplified Gouy–Chapman-like double-layer model which does not account explicitly for the SAM predicts dF/dφ to be proportional to the inverse Debye length (κ), giving a value of κ−1 = 30 Å for a 0.01 M KOH solution, which differs significantly from the experimental data. These results emphasize that the interfacial electric field is drastically modified by the SAM and cannot be properly described by a simplified Gouy–Chapman-like double-layer model.
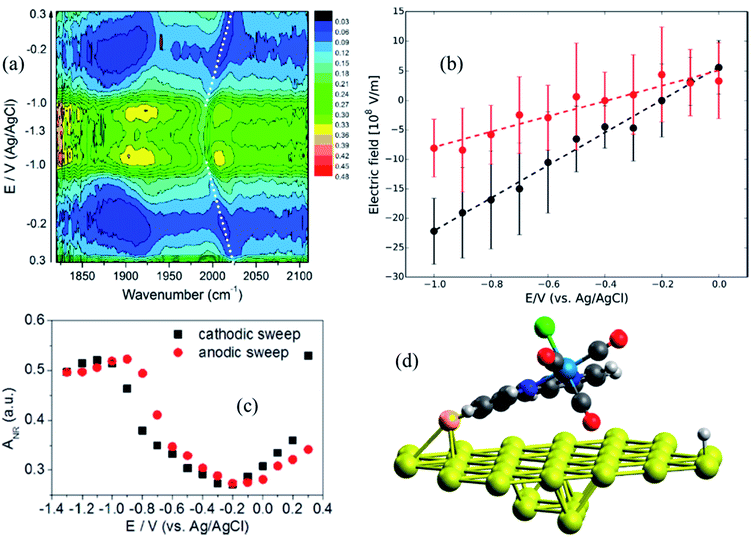 | ||
| Fig. 6 (a) Potential-dependent SFG spectra of Re(4-mercapto-2,2′-bipyridine)(CO)3Cl (ReS) complex attached to Au surface, measured in the potential range from 0.3 to −1.3 V (vs. Ag/AgCl) and using 10 mM KOH aqueous electrolyte solution. (b) Electric field strength as a function of applied potentials; black and red circles correspond to ReS and MnS SAM, respectively. Dashed lines are linear fittings to the data. (c) Potential-dependent amplitude of the non-resonant background obtained from the SFG spectral fitting. (d) DFT-optimized geometry of the ReS SAM on Au; the axial CO group directly points to the Au substrate, while the halogen atom (green color) is facing away. These figures are adapted from a publication by Clark et al.89 | ||
The electrochemical potential window for studies of these catalysts is limited by the stability of the thiolate anchoring group attached to the Au surface. Recent work has been focused on modification of the bipyridine ligand with a disulfide anchoring group, as shown for the complex Re(3,3′-disulfide-2,2′-bipyridine) (CO)3Cl (ReSS) that binds normal to the gold surface.90 Such a binding mode is stabilized by the double-anchoring group exposing the catalyst directly to the CO2 substrate in the solution, an ideal configuration for catalytic functionality. These results further highlight the capabilities of a collaborative approach for design and characterization of heterogenized catalysts at the molecular level.
(4) Correlation between Hammett parameters and electrochemical polarization
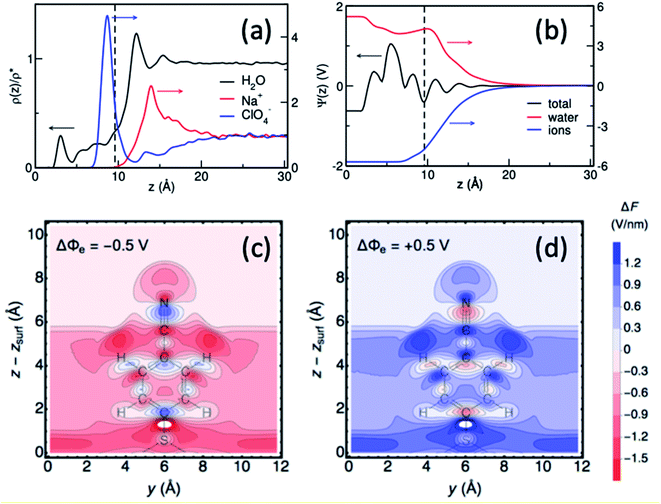
The Hammett parameters (σ) provide a valuable metric to quantify the extent of the polarization effect that a functional group exerts on a molecule by “inductive” effects (i.e., electron withdrawing or donating character). Therefore, the Hammett parameter of a substitutional group typically correlates with the vibrational frequency of a chromophore present in that molecule.91 Hammett parameters are obtained by measuring for example the pKa-shift of benzoic acid substituted with the corresponding functional group (R),92 referencing them with respect to the pK0a = 4.2 of unsubstituted benzoic acid (K0), as follows: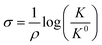 | (5) |
 | ||
| Fig. 7 (a) An illustration of the equivalence of a polarizing electric field at the electrochemical interface and a functional group at the para-position of 4-MBN. The blue arrow shows the shift in electronic charge density. (b) Relation between σp and electric field based on experimental frequency changes (blue), computational frequency changes (green), and charge density changes on nitrogen ρN (red). (c) Stark tuning for the cathodic and anodic sweeps of a1(1) symmetric CO stretch of ReS complex. Solid lines indicate the linear fit in the potential range between 0 and −1.0 V. (d) Plot of frequency vs. Hammett parameters, where frequencies are obtained by measuring the FTIR spectra of ReS complex with substitution at the 4,4′ positions of the bipyridine rings. Figures (a), (b) and (c) are adapted from publications by Sarkar et al.63 and Clark et al.89 respectively. Figure (d) is taken from an unpublished work by the Kubiak group. | ||
The Kubiak–Lian–Batista groups have extended this work for CO2 reduction catalysts, namely Re(4-mercapto-2,2′-bipyridine) (CO)3Cl (ReS), as discussed in the previous section. Their work showed that the observed ν(CO) frequency shifts (>25 cm−1) induced by changing an externally applied electrochemical potential by 1.0 V (Fig. 7c) is four times larger than what has been achieved by synthetic efforts to change the corresponding Hammett parameters of electron donor/acceptor groups on the bipyridine (bpy) ligand (Fig. 7d). For example, by switching from an electron donating OMe group (Hammett σp = −0.27) to an electron withdrawing CN group (Hammett σp = 0.66) on the 4,4′ positions of the bpy ligand, ν(CO) frequency shifts of only 5 cm−1 are observed, consistent with the correlation between Hammett parameters and electrochemical polarization discussed above. Note that it is important to recognize that no current actually flows in these experiments, i.e. there is no redox chemistry. The range of ν(CO) values observed by VSFG spectroscopy of the Re catalyst on the Au electrode under bias corresponds to about half of what would be expected for a change of the Re oxidation state of ±1, or nearly the full range of known Hammett parameters from σp of −0.83 or a N(Me)3 group to +1.11 for a SO2Cl group. Clearly, the electric field at the interface is changing the nature of the attached Re catalyst as much as could ever be achieved by synthesizing vastly different molecules.
(5) Structural transitions in ionic liquids probed by Stark–Shift spectroscopy
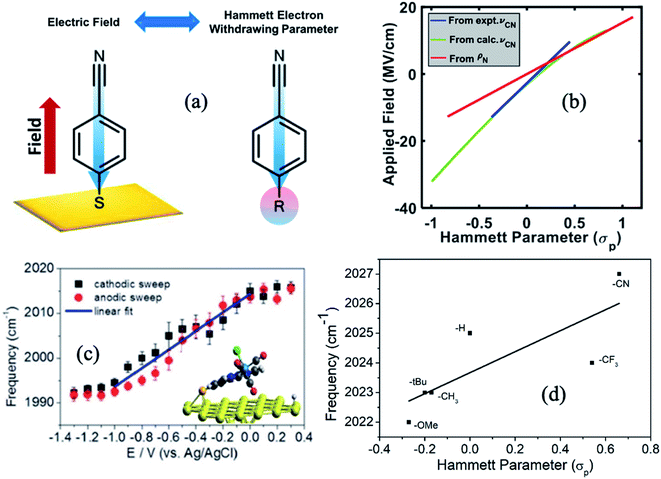
Dlott and coworkers93 have studied, using broadband VSFG spectroscopy, the electrochemical reduction of CO2 to CO on a polycrystalline Ag electrode in the room temperature ionic liquid (RTIL, 1-ethyl-3-methylimidazolium tetrafluoroborate) electrolyte with a small amount of water (0.3 mol%). Several studies had shown that the Ag/RTIL/H2O system is capable of reducing CO2 with a low overpotential. Depending on the amount of water in the electrolyte solution, it is possible to achieve the faradaic efficiency of CO generation approaching nearly 100%.94,95 Cyclic voltammetry measurements showed that the threshold for CO2 reduction in the Ag/RTIL/0.3% H2O system is −1.33 V vs. Ag/AgCl (Fig. 8c). The SFG spectra of surface bound CO were measured as a function of applied potential, revealing that the CO stretching frequency changes drastically at the CO2 reduction threshold; with a slope of 24 cm−1 V−1 in the range between −0.36 and −1.33 V and at more negative potentials, the slope almost doubles (55 cm−1 V−1) due to the presence of a larger field (Fig. 8e). The Stark shift of CO below the CO2 reduction threshold could only be measured during second or third CV cycles, since the concentration of CO adsorbed on the surface was very low during the first cycle. The intensity of the non-resonant (NR) SFG signal exhibits a minimum at around −1.33 V and increases quadratically as the potential is changed in either direction (Fig. 8a). Similar to the change in the Stark slope of CO, the curvature of such quadratic (parabolic) increase also changes drastically as it goes through the minimum, resulting in a much steeper slope for applied voltages below −1.33 V. VSFG experiments with argon purged RTIL solutions show that the minimum of the NR intensity appears at the same potential (−1.33 V), as in the case of the CO2 purged RTIL solution, suggesting that the occurrence of such minima is unrelated to the presence of CO2, thus characteristic property of RTIL itself.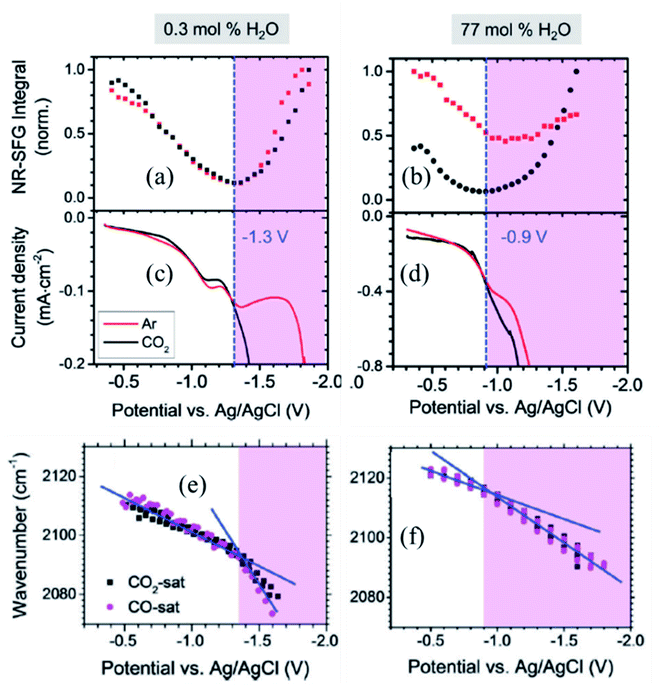 | ||
| Fig. 8 (a and b) Potential dependent non-resonant VSFG signal from Ag/RTIL interface; (c and d) current density vs. potential obtained during cyclic voltammetry measurement; and (e and f) Stark shift of CO adsorbed on Ag electrode surface as a function of applied potential for 0.3 mol% and 77 mol% of water concentrations in Ag/RTIL/H2O system, respectively. The vertical blue dashed line represents the threshold potential for CO2 reduction. These figures are adapted from a publication by Rey et al.96 | ||
In a separate publication, Rey and Dlott96 investigated the effect of water on the CO2 reduction in ionic liquids under low overpotentials. It was observed that the CO2 reduction threshold potential dropped from −1.33 V to −1.21 V and then down to −0.9 V as the water content in the RTIL electrolyte increased from 0.3% to 45%, and then to 77 mol% (Fig. 8d). The minimum of the NR VSFG intensity (Fig. 8b) and the position of the drastic change in the Stark tuning slope of CO (Fig. 8f) also shift in concert with the threshold potential. We note that the minimum position of the NR VSFG intensity in this case is different from that observed for the potential of zero charge (PZC) which is at around −0.6 V for the Ag/RTIL system.96
To explain the behavior of the NR VSFG intensity, Rey et al.96 argued that the SFG measurements at electrified interfaces have contributions from both second (χ(2)) and third (χ(3)) order nonlinear susceptibilities. The χ(2) term arises solely from the electrode surface and surface adsorbates, whereas the χ(3) term originates from the entire double layer (DL) consisting of the electrode surface, adsorbate in the inner layer and electrolyte in the diffused outer layer. In the limit χ(3)φ ≫ χ(2), the non-resonant VSFG intensity INR-VSFG ∝ |χ(3)DL|2φ2 giving a quadratic dependence as a function of applied potential (φ).97 The magnitude of χ(3)DL decreases with increasing negative potential, goes to zero at the threshold potential, and then changes sign and increase in magnitude as the potential becomes more negative. Rey et al.96 proposed that the change in sign and the magnitude of χ(3)DL at the reduction threshold are associated with the structural reorganization of the ionic liquid in the double layer. That interpretation is in line with STM measurements98 and molecular dynamics simulations99 which also predict a potential-dependent monolayer to multilayer structural transitions of RTIL at the electrode surface. As discussed above, such a structural transition in RTIL is independent of whether CO2 is present or not in the medium and controls the CO2 reduction process itself. DFT calculations showed that the imidazolium cations of RTIL form an ordered monolayer on the electrode surface interspersed with anion and water molecules.100,101 With increasing water content, the monolayer adjacent to the Ag surface retains cation-rich character, whereas cations in the subsequent layers are replaced by water molecules. This causes less hindrance to the potential-driven structural rearrangement of RTIL, shifting it to a lower negative potential and thereby triggering the CO2 reduction process at a lower overpotentials.
Using polarization-dependent VSFG spectroscopy, Baldelli and coworkers102 have directly probed the potential-dependent orientational change of ionic liquids at the surface of a platinum electrode. Two different RTILs were investigated, including [BMIM][PF6] and [BMIM][BF4], with 1-butyl-3-methylimidazolium ([BMIM]+) cations, and anions [PF6]− and [BF4]−. The PPP/SSP intensity ratio of different vibrational modes in the range 2750 to 3300 cm−1 (C–H stretching region) change as a function of applied potential, suggesting a change in molecular orientation. At negative surface charge, the plane of the imidazolium ring of the [BMIM]+ cation is relatively parallel to the electrode surface at an angle of ∼60° with respect to the surface normal. Such orientation presumably helps to screen the surface charge well. At positive surface charge, following the law of electrostatics, the negative counter ions tend to come in the vicinity of the electrode surface. To accommodate these negative charges in the Helmholtz layer, the imidazolium ring of [BMIM][BF4] tilts back from the electrode surface, at an angle of ∼35° from the surface normal. For [BMIM][PF6], the tilt angle of the imidazolium ring does not change considerably as a function of applied potential, but the twist angle changes dramatically (by ∼70°) making room for the [PF6]− ions in the Helmholtz layer.
(6) Spatial inhomogeneity of the interfacial electric fields
Interpretations of the vibrational Stark shift are typically based on electric double layer theories, such as Gouy–Chapman, or Gouy–Chapman–Stern models that characterized the interfacial behavior in terms of macroscopic parameters, including permittivity, salt concentration and monolayer thickness. Although critical for advancing our understanding of electrode–solution interfaces, these mean field theories completely neglect the microscopic and dynamical nature of electrochemical interfaces that can give rise to very complex phenomena, including nanoscale structural and dynamical monolayer heterogeneity, monolayer permeability, and solvent and ion structuration. As such, vibrational Stark spectroscopy supplemented with computational modeling of these interfaces can provide atomistic details beyond the capabilities of mean-field theories.In a combined effort by the Batista, Lian and Kubiak groups vibrational Stark spectroscopy was used to determine the interfacial electric field for a series of diisocyanide SAMs with varying length spacers between CN-groups on gold electrodes.40 Remarkably, the analysis of Stark tuning rate revealed that the Helmholtz layer thickness obtained from a Gouy–Chapman–Stern model is shorter than the length of the molecules. Consistently, atomistic molecular dynamics (MD) simulations showed that the solvent and ionic distribution are rather complex, intercalating ions and water in the SAM interface (Fig. 9).40 Moreover, the electrostatic profile obtained from atomistic simulations reveals a complex, oscillatory and inhomogeneous behavior, highlighting the limitations of mean-field theories to treat complex interfaces. Combining MD simulation with theoretical modeling, Limaye et al.103 quantified the electrostatic potential fluctuations experienced by ionic species in the vicinity of an electrode surface and examined the role of image charge effects on such potential fluctuations.
 | ||
| Fig. 9 (a and b) Surface-normal density profiles and mean electric potential profile of a 1,4-phenylene diisocyanide (PDI) monolayer on gold (∼25% surface coverage) in contact with aqueous sodium perchlorate solution.40 The gold slab is located at z = 0 and the vertical dashed line indicates the thickness of the monolayer. (c and d) Contour plots of the surface-normal electric field (relative to the field at the PZC), for the 4-MBN molecule near the Au(111) surface at electrode potentials −0.50 V and +0.50 V.104 Figures (a), (b) and (c), (d) are adapted from publications by Ge et al.40 and Goldsmith et al.104 | ||
More recently, Hammes-Schiffer and coworkers104 have theoretically studied the interfacial electric field probed by the CN stretching of 4-MBN attached to a gold electrode as a function of applied potential, modeled by periodic DFT calculations. Substantial spatial inhomogeneity of the interfacial electric fields and electrostatic potentials were observed (Fig. 9c and d), including oscillations in the region of the molecular probe attached to the electrode. These results further show significant deviations from mean-field electric double layer models and stress the importance of atomistic descriptions for proper characterization of interfacial fields at electrochemical surfaces.
(7) Stark shift: discussion about through bond vs. through space effects
One of the central questions about electrochemical Stark shift spectroscopy is whether the Stark shift is mediated by a through-bond electronic polarization (akin to the inductive effect by functional groups) or via through-space electric field interaction or both. For Stark tuning rates of CO (νCOvs. electric field) adsorbed on metal surfaces, the literature reports of the relative importance of electrostatic field (first-order Stark) effects and adsorbate-surface charge sharing effects are somewhat controversial.105,106 Lambert, however, pointed out that, with proper consideration of metal–adsorbate interactions, interpretations based on an atom superposition and electron delocalization molecular orbital treatment are equivalent to the description in terms of electrostatic interactions of dipole moments and electric fields.107,108 There is a substantial volume of work by Weaver and coworkers37,108–111 who, using DFT calculations for monoatomic adsorbates on finite metal clusters, investigated the dependence of the stretching frequency (ν), binding energy (Eb), and equilibrium bond length (r) of metal–adsorbate bonds as a function of external electric field (F). The static dipole moment (μS), which is field dependent, signifies the direction of metal–adsorbate charge polarization and determines the binding energy–field (Eb–F) slopes to a very good approximation, whereas the dynamic dipole moment (μD), i.e., the r dependent μS value, coupled with the anharmonicity of the potential energy surface primarily control the Stark-tuning behavior.110,111 Using surface enhanced Raman spectroscopy (SERS), Zou and Weaver37 have investigated the dependence of metal–carbon vibrational frequency (νM–C) as a function of electrode potential for saturated CO adlayers on palladium, platinum, rhodium, and iridium film electrodes. Their work showed that the Stark tuning rate of νM–C is negative (from ca. −10 to −20 cm−1 V−1), which is in contrast with the positive value of the Stark tuning rate of the adsorbed CO frequency (νCO) on these Pt group metals (ca. 30 to 60 cm−1 V−1). The authors identified two factors that contribute to the overall electrochemical Stark effect: (1) the presence of an interfacial electrostatic field and (2) the potential dependent chemical bonding due to metal–adsorbate orbital overlap. Korzeniewski et al.112 has performed semiclassical analysis of the Pt–CO system by considering each effect separately and the theoretical results in both cases correctly predict the opposite signs of the Stark tuning rate of νM–C and νCO; whereas the chemical binding model could also approximately reproduce the relative magnitude of these two numbers, i.e. the Stark tuning rate of νM–C being smaller by a factor of 2 as compared to that of νCO. They, therefore, concluded that the chemical binding model plays a major role in describing surface–adsorbate interaction (quite understandably) and to explain the dependence of νM–C as a function of applied voltage. Later in 2011, Mamatkulov and Filhol113 studied electrochemical vibrational and energy properties of CO/Pt(111) in the framework of periodic density functional theory (DFT) calculations. Much like the approach by Zou and Weaver,37 they described the total Stark shift to be split into two competing components. The first corresponds to the direct effect of charging on the C–O chemical bond: it was referred to as electrochemical effect. The second is the consequence of the surface dipole interaction with the applied electric field that modifies the C–O distance, inducing a change of the C–O force constant due to the C–O bond anharmonicity: it was referred to as the electromechanical effect. Their work suggested that in the CO/Pt(111) case, the dominant contribution is electromechanical, i.e. the interaction of the molecular dipole with the electric field.113 In the case of 1,4-phenylenediisocyanide (PDI) adsorbed on gold (one NC group attached to gold, the other NC group is free), we have calculated the relative contribution of regular electromechanical term and the term originating from the coupling of higher order terms of the dipole moment to the electric field, suggesting that the former has the dominant contribution to the Stark tuning rate, being greater than the other by a factor of ∼4.40 Our calculation further suggests that for the free NC group, these contributions are of opposite signs and tend to cancel out giving rise to negligible Stark shift; but for the bound NC both contributions go in the same direction, producing a greater Stark tuning rate.The above examples from the literature suggest that the origin of the electrochemical Stark shift remains an open question. Further collaborative synthetic, spectroscopic, and theoretical studies are needed to disentangle the through-bond and through space effects and to advance the understanding of the nature and distribution of the electric field at the electrode/electrolyte interface.
VI. Outlook and future directions
In this Perspective article, we have reviewed recent efforts focused on the characterization of interfacial electric fields at electrode/electrolyte surfaces with emphasis on Stark shift measurements based on VSFG spectroscopy and interpretation based on theoretical modeling. The reviewed studies have shown that the electric fields at electrochemical interfaces are typically of the same order of magnitude as the ones found at the active sites of enzymes, where strong local electric fields are known to modulate the electronic properties of the substrate, stabilizing transition states and thus lowering the reaction free energy barriers.74,75,77 Recent experimental and theoretical studies have demonstrated that applied electric fields can dramatically modulate the activity and selectivity of catalysts, inducing vast modulation of electrochemical responses under catalytic conditions that open new opportunities for field-driven chemistry and catalysis. However, given the complexity of the electrochemical interface, there is currently little molecular level understanding of how to achieve control of the interfacial electric fields to enhance reactivity or control selectivity of catalytic processes. Future studies to explore these possibilities are of a high priority. The combination of VSFG spectroscopy, electrochemical Stark effect and computational modeling of the interfaces provides a particularly useful unified approach to obtain a comprehensive molecular-level evaluation of the electrified interface.Data availability
The data associated with the publications by V. S. B., T. L. and C. P. K. are available from the corresponding authors upon reasonable request.Author contributions
C. P. K. first conceived the idea for writing this perspective and had given enormous inputs from the beginning. All authors have equally contributed to section I (Introduction); sections II, IV and V have been written by D. B. and T. L.; P. E. V. and V. S. B. wrote sections III, V (subsection 6) and VI; M. C. has contributed to section II.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the AFOSR grants #FA9550-17-0198 (V. S. B., T. L. and C. P. K.), MURI grant FA9550-18-1-0420 (T. L) and DURIP grant FA9550-18-1-0005 (T. L.). V. S. B. acknowledges high-performance computing time from NERSC, DOD Copper, and from the Yale Center for Research Computing.References
- S. Nitopi, E. Bertheussen, S. B. Scott, X. Liu, A. K. Engstfeld, S. Horch, B. Seger, I. E. Stephens, K. Chan and C. Hahn, Progress and Perspectives of Electrochemical CO2 Reduction on Copper in Aqueous Electrolyte, Chem. Rev., 2019, 119, 7610–7672 CrossRef CAS PubMed.
- S. Garg, M. Li, A. Z. Weber, L. Ge, L. Li, V. Rudolph, G. Wang and T. E. Rufford, Advances and Challenges in Electrochemical CO2 Reduction Processes: An Engineering and Design Perspective Looking Beyond New Catalyst Materials, J. Mater. Chem. A, 2020, 8, 1511–1544 RSC.
- C. F. Gorin, E. S. Beh, Q. M. Bui, G. R. Dick and M. W. Kanan, Interfacial Electric Field Effects on a Carbene Reaction Catalyzed by Rh Porphyrins, J. Am. Chem. Soc., 2013, 135, 11257–11265 CrossRef CAS PubMed.
- V. M. Lau, C. F. Gorin and M. W. Kanan, Electrostatic Control of Regioselectivity Via Ion Pairing in a Au(I)-Catalyzed Rearrangement, Chem. Sci., 2014, 5, 4975–4979 RSC.
- V. M. Lau, W. C. Pfalzgraff, T. E. Markland and M. W. Kanan, Electrostatic Control of Regioselectivity in Au(I)-Catalyzed Hydroarylation, J. Am. Chem. Soc., 2017, 139, 4035–4041 CrossRef CAS PubMed.
- J. Heo, H. Ahn, J. Won, J. G. Son, H. K. Shon, T. G. Lee, S. W. Han and M.-H. Baik, Electro-Inductive Effect: Electrodes as Functional Groups with Tunable Electronic Properties, Science, 2020, 370, 214 CrossRef CAS PubMed.
- C. G. Vayenas, S. Bebelis and S. Neophytides, Non-Faradaic Electrochemical Modification of Catalytic Activity, J. Phys. Chem., 1988, 92, 5083–5085 CrossRef CAS.
- R. Meir, H. Chen, W. Lai and S. Shaik, Oriented Electric Fields Accelerate Diels–Alder Reactions and Control the Endo/Exo Selectivity, ChemPhysChem, 2010, 11, 301–310 CrossRef CAS PubMed.
- A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Electrostatic Catalysis of a Diels–Alder Reaction, Nature, 2016, 531, 88–91 CrossRef PubMed.
- S. Shaik, D. Mandal and R. Ramanan, Oriented Electric Fields as Future Smart Reagents in Chemistry, Nat. Chem., 2016, 8, 1091–1098 CrossRef CAS PubMed.
- S. Oh, J. R. Gallagher, J. T. Miller and Y. Surendranath, Graphite-Conjugated Rhenium Catalysts for Carbon Dioxide Reduction, J. Am. Chem. Soc., 2016, 138, 1820–1823 CrossRef CAS PubMed.
- M. N. Jackson, S. Oh, C. J. Kaminsky, S. B. Chu, G. Zhang, J. T. Miller and Y. Surendranath, Strong Electronic Coupling of Molecular Sites to Graphitic Electrodes Via Pyrazine Conjugation, J. Am. Chem. Soc., 2018, 140, 1004–1010 CrossRef CAS PubMed.
- M. N. Jackson, C. J. Kaminsky, S. Oh, J. F. Melville and Y. Surendranath, Graphite Conjugation Eliminates Redox Intermediates in Molecular Electrocatalysis, J. Am. Chem. Soc., 2019, 141, 14160–14167 CrossRef CAS PubMed.
- M. N. Jackson, M. L. Pegis and Y. Surendranath, Graphite-Conjugated Acids Reveal a Molecular Framework for Proton-Coupled Electron Transfer at Electrode Surfaces, ACS Cent. Sci., 2019, 5, 831–841 CAS.
- C. J. Kaminsky, J. Wright and Y. Surendranath, Graphite-Conjugation Enhances Porphyrin Electrocatalysis, ACS Catal., 2019, 9, 3667–3671 CrossRef CAS.
- D. C. Grahame, The Electrical Double Layer and the Theory of Electrocapillarity, Chem. Rev., 1947, 41, 441–501 CrossRef CAS PubMed.
- G. Wang, L. Zhang and J. Zhang, A Review of Electrode Materials for Electrochemical Supercapacitors, Chem. Soc. Rev., 2012, 41, 797–828 RSC.
- C. Zhong, Y. Deng, W. Hu, J. Qiao, L. Zhang and J. Zhang, A Review of Electrolyte Materials and Compositions for Electrochemical Supercapacitors, Chem. Soc. Rev., 2015, 44, 7484–7539 RSC.
- H. Wang, T. K.-J. Köster, N. M. Trease, J. Ségalini, P.-L. Taberna, P. Simon, Y. Gogotsi and C. P. Grey, Real-Time NMR Studies of Electrochemical Double-Layer Capacitors, J. Am. Chem. Soc., 2011, 133, 19270–19273 CrossRef CAS PubMed.
- M. M. Waegele, C. M. Gunathunge, J. Li and X. Li, How Cations Affect the Electric Double Layer and the Rates and Selectivity of Electrocatalytic Processes, J. Chem. Phys., 2019, 151, 160902 CrossRef PubMed.
- R. Burt, G. Birkett and X. Zhao, A Review of Molecular Modelling of Electric Double Layer Capacitors, Phys. Chem. Chem. Phys., 2014, 16, 6519–6538 RSC.
- H. V. Helmholtz, Studien Über Electrische Grenzschichten, Ann. Phys., 1879, 243, 337–382 CrossRef.
- M. Gouy, On the constitution of the electric charge on the surface of an electrolyte, J. Phys. Theor. Appl., 1910, 9, 457–468 CrossRef.
- D. L. Chapman, Li. A Contribution to the Theory of Electrocapillarity, London, Edinburgh Dublin Philos. Mag. J. Sci., 1913, 25, 475–481 CrossRef.
- O. Stern, The Theory of the Electrolytic Double-Layer, Z. Elektrochem., 1924, 30, 1014–1020 Search PubMed.
- P. Attard, Ion Condensation in the Electric Double Layer and the Corresponding Poisson-Boltzmann Effective Surface Charge, J. Phys. Chem., 1995, 99, 14174–14181 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Fundamentals and Applications. Electrochemical Methods, 2001, vol. 2, pp. 580–632 Search PubMed.
- G. C. Gschwend and H. H. Girault, Discrete Helmholtz Charge Distribution at Liquid-Liquid Interfaces: Electrocapillarity, Capacitance and Non-Linear Spectroscopy Studies, J. Electroanal. Chem., 2020, 872, 114240 CrossRef CAS.
- G. C. Gschwend and H. H. Girault, Discrete Helmholtz Model: A Single Layer of Correlated Counter-Ions. Metal Oxides and Silica Interfaces, Ion-Exchange and Biological Membranes, Chem. Sci., 2020, 11, 10304–10312 RSC.
- G. C. Gschwend, A. Olaya and H. H. Girault, How to Polarise an Interface with Ions: The Discrete Helmholtz Model, Chem. Sci., 2020, 11, 10807–10813 RSC.
- C. R. Baiz, B. Błasiak, J. Bredenbeck, M. Cho, J.-H. Choi, S. A. Corcelli, A. G. Dijkstra, C.-J. Feng, S. Garrett-Roe and N.-H. Ge, Vibrational Spectroscopic Map, Vibrational Spectroscopy, and Intermolecular Interaction, Chem. Rev., 2020, 120, 7152–7218 CrossRef CAS PubMed.
- G. U. Bublitz and S. G. Boxer, Stark Spectroscopy: Applications in Chemistry, Biology, and Materials Science, Annu. Rev. Phys. Chem., 1997, 48, 213–242 CrossRef CAS PubMed.
- S. D. Fried and S. G. Boxer, Measuring Electric Fields and Noncovalent Interactions Using the Vibrational Stark Effect, Acc. Chem. Res., 2015, 48, 998–1006 CrossRef CAS PubMed.
- R. Wortmann and D. M. Bishop, Effective Polarizabilities and Local Field Corrections for Nonlinear Optical Experiments in Condensed Media, J. Chem. Phys., 1998, 108, 1001–1007 CrossRef CAS.
- J. G. Patrow, S. A. Sorenson and J. M. Dawlaty, Direct Spectroscopic Measurement of Interfacial Electric Fields near an Electrode under Polarizing or Current-Carrying Conditions, J. Phys. Chem. C, 2017, 121, 11585–11592 CrossRef CAS.
- S. S. Andrews and S. G. Boxer, Vibrational Stark Effects of Nitriles I. Methods and Experimental Results, J. Phys. Chem. A, 2000, 104, 11853–11863 CrossRef CAS.
- S. Zou and M. J. Weaver, Potential-Dependent Metal–Adsorbate Stretching Frequencies for Carbon Monoxide on Transition-Metal Electrodes: Chemical Bonding Versus Electrostatic Field Effects, J. Phys. Chem., 1996, 100, 4237–4242 CrossRef CAS.
- D. K. Lambert, Vibrational Stark Effect of Adsorbates at Electrochemical Interfaces, Electrochim. Acta, 1996, 41, 623–630 CrossRef CAS.
- A. L. Ringer and A. D. MacKerell Jr, Calculation of the Vibrational Stark Effect Using a First-Principles Quantum Mechanical/Molecular Mechanical Approach, J. Phys. Chem. Lett., 2011, 2, 553–556 CrossRef CAS PubMed.
- A. Ge, P. E. Videla, G. L. Lee, B. Rudshteyn, J. Song, C. P. Kubiak, V. S. Batista and T. Lian, Interfacial Structure and Electric Field Probed by In Situ Electrochemical Vibrational Stark Effect Spectroscopy and Computational Modeling, J. Phys. Chem. C, 2017, 121, 18674–18682 CrossRef CAS.
- D. M. Bishop, The Vibrational Stark Effect, J. Chem. Phys., 1993, 98, 3179–3184 CrossRef CAS.
- A. J. Cowan and L. J. Hardwick, Advanced Spectroelectrochemical Techniques to Study Electrode Interfaces within Lithium-Ion and Lithium-Oxygen Batteries, Annu. Rev. Anal. Chem., 2019, 12, 323–346 CrossRef CAS PubMed.
- J. K. Staffa, L. Lorenz, M. Stolarski, D. H. Murgida, I. Zebger, T. Utesch, J. Kozuch and P. Hildebrandt, Determination of the Local Electric Field at Au/Sam Interfaces Using the Vibrational Stark Effect, J. Phys. Chem. C, 2017, 121, 22274–22285 CrossRef CAS.
- S. Zhu, T. Li, W.-B. Cai and M. Shao, CO2 Electrochemical Reduction as Probed through Infrared Spectroscopy, ACS Energy Lett., 2019, 4, 682–689 CrossRef CAS.
- C. Quijada, A. Rodes, F. Huerta and J. Vazquez, In Situ FT–IRRAS Study of SO2 Adlayers Formed on Pt (111) Electrodes from Open-Circuit Adsorption in Acidic Media, Electrochim. Acta, 1998, 44, 1091–1096 CrossRef CAS.
- V. Oklejas, C. Sjostrom and J. M. Harris, Sers Detection of the Vibrational Stark Effect from Nitrile-Terminated SAMs to Probe Electric Fields in the Diffuse Double-Layer, J. Am. Chem. Soc., 2002, 124, 2408–2409 CrossRef CAS PubMed.
- A. Montenegro, C. Dutta, M. Mammetkuliev, H. Shi, B. Hou, D. Bhattacharyya, B. Zhao, S. B. Cronin and A. V. Benderskii, Asymmetric Response of Interfacial Water to Applied Electric Fields, Nature, 2021, 594, 62–65 CrossRef CAS PubMed.
- J.-F. Li, Y.-J. Zhang, A. V. Rudnev, J. R. Anema, S.-B. Li, W.-J. Hong, P. Rajapandiyan, J. Lipkowski, T. Wandlowski and Z.-Q. Tian, Electrochemical Shell-Isolated Nanoparticle-Enhanced Raman Spectroscopy: Correlating Structural Information and Adsorption Processes of Pyridine at the Au (hkl) Single Crystal/Solution Interface, J. Am. Chem. Soc., 2015, 137, 2400–2408 CrossRef CAS PubMed.
- Y. Shen, Surface Properties Probed by Second-Harmonic and Sum-Frequency Generation, Nature, 1989, 337, 519–525 CrossRef CAS.
- D. Bhattacharyya, A. Montenegro, N. T. Plymale, C. Dutta, N. S. Lewis and A. V. Benderskii, Vibrational Sum Frequency Generation Spectroscopy Measurement of the Rotational Barrier of Methyl Groups on Methyl-Terminated Silicon (111) Surfaces, J. Phys. Chem. Lett., 2019, 10, 5434–5439 CrossRef CAS PubMed.
- A. G. Lambert, P. B. Davies and D. J. Neivandt, Implementing the Theory of Sum Frequency Generation Vibrational Spectroscopy: A Tutorial Review, Appl. Spectrosc. Rev., 2005, 40, 103–145 CrossRef CAS.
- D. Bhattacharyya, P. Dhar, Y. Liu, P. I. Djurovich, M. E. Thompson and A. V. Benderskii, A Vibrational Sum Frequency Generation Study of the Interference Effect in a Thin Film of 4,4′-Bis(N-Carbazolyl)-1,10-Biphenyl (Cbp) and the Interfacial Orientation, ACS Appl. Mater. Interfaces, 2020, 12, 26515–26524 CrossRef CAS PubMed.
- D. Bhattacharyya, A. Montenegro, P. Dhar, M. Mammetkuliyev, R. M. Pankow, M. C. Jung, M. E. Thompson, B. C. Thompson and A. V. Benderskii, Molecular Orientation of Poly-3-Hexylthiophene at the Buried Interface with Fullerene, J. Phys. Chem. Lett., 2019, 10, 1757–1762 CrossRef CAS PubMed.
- C. L. Anfuso, R. C. Snoeberger, A. M. Ricks, W. Liu, D. Xiao, V. S. Batista and T. Lian, Covalent Attachment of a Rhenium Bipyridyl CO2 Reduction Catalyst to Rutile TiO2, J. Am. Chem. Soc., 2011, 133, 6922–6925 CrossRef CAS PubMed.
- W. Gan, B.-h. Wu, Z. Zhang, Y. Guo and H.-f. Wang, Vibrational Spectra and Molecular Orientation with Experimental Configuration Analysis in Surface Sum Frequency Generation (SFG), J. Phys. Chem. C, 2007, 111, 8716–8725 CrossRef CAS.
- H.-F. Wang, L. Velarde, W. Gan and L. Fu, Quantitative Sum-Frequency Generation Vibrational Spectroscopy of Molecular Surfaces and Interfaces: Lineshape, Polarization, and Orientation, Annu. Rev. Phys. Chem., 2015, 66, 189–216 CrossRef CAS PubMed.
- N. Ji, V. Ostroverkhov, C.-Y. Chen and Y.-R. Shen, Phase-Sensitive Sum-Frequency Vibrational Spectroscopy and Its Application to Studies of Interfacial Alkyl Chains, J. Am. Chem. Soc., 2007, 129, 10056–10057 CrossRef CAS PubMed.
- I. V. Stiopkin, H. D. Jayathilake, A. N. Bordenyuk and A. V. Benderskii, Heterodyne-Detected Vibrational Sum Frequency Generation Spectroscopy, J. Am. Chem. Soc., 2008, 130, 2271–2275 CrossRef CAS PubMed.
- M. J. Hofmann and P. Koelsch, Retrieval of Complex χ(2) Parts for Quantitative Analysis of Sum-Frequency Generation Intensity Spectra, J. Chem. Phys., 2015, 143, 134112 CrossRef PubMed.
- P.-K. Yang and J. Y. Huang, Phase-Retrieval Problems in Infrared–Visible Sum-Frequency Generation Spectroscopy by the Maximum-Entropy Method, J. Opt. Soc. Am. B, 1997, 14, 2443–2448 CrossRef CAS.
- P.-K. Yang and J. Y. Huang, Model-Independent Maximum-Entropy Method for the Analysis of Sum-Frequency Vibrational Spectroscopy, J. Opt. Soc. Am. B, 2000, 17, 1216–1222 CrossRef CAS.
- S. Nihonyanagi, S. Yamaguchi and T. Tahara, Direct Evidence for Orientational Flip-Flop of Water Molecules at Charged Interfaces: A Heterodyne-Detected Vibrational Sum Frequency Generation Study, J. Chem. Phys., 2009, 130, 204704 CrossRef PubMed.
- S. Sarkar, J. G. Patrow, M. J. Voegtle, A. K. Pennathur and J. M. Dawlaty, Electrodes as Polarizing Functional Groups: Correlation between Hammett Parameters and Electrochemical Polarization, J. Phys. Chem. C, 2019, 123, 4926–4937 CrossRef CAS.
- A. Ge, B. Rudshteyn, P. E. Videla, C. J. Miller, C. P. Kubiak, V. S. Batista and T. Lian, Heterogenized Molecular Catalysts: Vibrational Sum-Frequency Spectroscopic, Electrochemical, and Theoretical Investigations, Acc. Chem. Res., 2019, 52, 1289–1300 CAS.
- M. N. Jackson and Y. Surendranath, Molecular Control of Heterogeneous Electrocatalysis through Graphite Conjugation, Acc. Chem. Res., 2019, 52, 3432–3441 CrossRef CAS PubMed.
- K. Hara, S. Tayama, H. Kano, T. Masuda, S. Takakusagi, T. Kondo, K. Uosaki and M. Sawamura, Functionalization of Silicon Surfaces with Catalytically Active Pd Complexes and Application to the Aerobic Oxidation of Benzylic Alcohols, Chem. Commun., 2007, 4280–4282 RSC.
- H. Shi, Z. Cai, J. Patrow, B. Zhao, Y. Wang, Y. Wang, A. Benderskii, J. Dawlaty and S. B. Cronin, Monitoring Local Electric Fields at Electrode Surfaces Using Surface Enhanced Raman Scattering-Based Stark-Shift Spectroscopy During Hydrogen Evolution Reactions, ACS Appl. Mater. Interfaces, 2018, 10, 33678–33683 CrossRef CAS PubMed.
- S. A. Sorenson, J. G. Patrow and J. M. Dawlaty, Solvation Reaction Field at the Interface Measured by Vibrational Sum Frequency Generation Spectroscopy, J. Am. Chem. Soc., 2017, 139, 2369–2378 CrossRef CAS PubMed.
- S. Sarkar, A. Maitra, S. Banerjee, V. S. Thoi and J. M. Dawlaty, Electric Fields at Metal-Surfactant Interfaces: A Combined Vibrational Spectroscopy and Capacitance Study, J. Phys. Chem. B, 2020, 124, 1311–1321 CrossRef CAS PubMed.
- C. P. Smith and H. S. White, Theory of the Interfacial Potential Distribution and Reversible Voltammetric Response of Electrodes Coated with Electroactive Molecular Films, Anal. Chem., 1992, 64, 2398–2405 CrossRef CAS PubMed.
- L. Onsager, Electric Moments of Molecules in Liquids, J. Am. Chem. Soc., 1936, 58, 1486–1493 CrossRef CAS.
- S. Bagchi, S. G. Boxer and M. D. Fayer, Ribonuclease S Dynamics Measured Using a Nitrile Label with 2d Ir Vibrational Echo Spectroscopy, J. Phys. Chem. B, 2012, 116, 4034–4042 CrossRef CAS PubMed.
- A. T. Fafarman and S. G. Boxer, Nitrile Bonds as Infrared Probes of Electrostatics in Ribonuclease S, J. Phys. Chem. B, 2010, 114, 13536–13544 CrossRef CAS PubMed.
- S. D. Fried, S. Bagchi and S. G. Boxer, Extreme Electric Fields Power Catalysis in the Active Site of Ketosteroid Isomerase, Science, 2014, 346, 1510–1514 CrossRef CAS PubMed.
- S. D. Fried and S. G. Boxer, Electric Fields and Enzyme Catalysis, Annu. Rev. Biochem., 2017, 86, 387–415 CrossRef CAS PubMed.
- S. D. Fried, L.-P. Wang, S. G. Boxer, P. Ren and V. S. Pande, Calculations of the Electric Fields in Liquid Solutions, J. Phys. Chem. B, 2013, 117, 16236–16248 CrossRef CAS PubMed.
- I. T. Suydam, C. D. Snow, V. S. Pande and S. G. Boxer, Electric Fields at the Active Site of an Enzyme: Direct Comparison of Experiment with Theory, Science, 2006, 313, 200 CrossRef CAS PubMed.
- J. P. Layfield and S. Hammes-Schiffer, Calculation of Vibrational Shifts of Nitrile Probes in the Active Site of Ketosteroid Isomerase Upon Ligand Binding, J. Am. Chem. Soc., 2013, 135, 717–725 CrossRef CAS PubMed.
- C. T. Liu, J. P. Layfield, R. J. Stewart III, J. B. French, P. Hanoian, J. B. Asbury, S. Hammes-Schiffer and S. J. Benkovic, Probing the Electrostatics of Active Site Microenvironments Along the Catalytic Cycle for Escherichia Coli Dihydrofolate Reductase, J. Am. Chem. Soc., 2014, 136, 10349–10360 CrossRef CAS PubMed.
- A. Dey, The Way Forward in Molecular Electrocatalysis, Inorg. Chem., 2016, 55, 10831–10834 CrossRef CAS PubMed.
- C. L. Anfuso, D. Xiao, A. M. Ricks, C. F. A. Negre, V. S. Batista and T. Lian, Orientation of a Series of CO2 Reduction Catalysts on Single Crystal TiO2 Probed by Phase-Sensitive Vibrational Sum Frequency Generation Spectroscopy (PS-VSFG), J. Phys. Chem. C, 2012, 116, 24107–24114 CrossRef CAS.
- A. Ge, B. Rudshteyn, B. T. Psciuk, D. Xiao, J. Song, C. L. Anfuso, A. M. Ricks, V. S. Batista and T. Lian, Surface-Induced Anisotropic Binding of a Rhenium CO2-Reduction Catalyst on Rutile TiO2(110) Surfaces, J. Phys. Chem. C, 2016, 120, 20970–20977 CrossRef CAS.
- C. Calabrese, H. Vanselous and P. B. Petersen, Deconstructing the Heterogeneity of Surface-Bound Catalysts: Rutile Surface Structure Affects Molecular Properties, J. Phys. Chem. C, 2016, 120, 1515–1522 CrossRef CAS.
- H. Vanselous, A. M. Stingel and P. B. Petersen, Interferometric 2d Sum Frequency Generation Spectroscopy Reveals Structural Heterogeneity of Catalytic Monolayers on Transparent Materials, J. Phys. Chem. Lett., 2017, 8, 825–830 CrossRef CAS PubMed.
- M. Gruebele and P. G. Wolynes, Vibrational Energy Flow and Chemical Reactions, Acc. Chem. Res., 2004, 37, 261–267 CrossRef CAS PubMed.
- P. L. Houston and R. P. Merrill, Gas-Surface Interactions with Vibrationally Excited Molecules, Chem. Rev., 1988, 88, 657–671 CrossRef CAS.
- V. Zhdanov and K. Zamaraev, Vibrational Relaxation of Adsorbed Molecules. Mechanisms and Manifestations in Chemical Reactions on Solid Surfaces, Catal. Rev., 1982, 24, 373–413 CrossRef CAS.
- M. L. Clark, et al., Orientation of Cyano-Substituted Bipyridine Re(I) Fac-Tricarbonyl Electrocatalysts Bound to Conducting Au Surfaces, J. Phys. Chem. C, 2016, 120, 1657–1665 CrossRef CAS.
- M. L. Clark, A. Ge, P. E. Videla, B. Rudshteyn, C. J. Miller, J. Song, V. S. Batista, T. Lian and C. P. Kubiak, CO2 Reduction Catalysts on Gold Electrode Surfaces Influenced by Large Electric Fields, J. Am. Chem. Soc., 2018, 140, 17643–17655 CrossRef CAS PubMed.
- M. Cattaneo, F. Guo, H. Kelly, P. E. Videla, L. Kiefer, S. Gebre, A. Ge, Q. Liu, S. Wu and T. Lian, Robust Binding of Disulfide-Substituted Rhenium Bipyridyl Complexes for CO2 Reduction on Gold Electrodes, Front. Chem., 2020, 8, 86 CrossRef CAS PubMed.
- L. P. Hammett, The Effect of Structure Upon the Reactions of Organic Compounds. Benzene Derivatives, J. Am. Chem. Soc., 1937, 59, 96–103 CrossRef CAS.
- D. H. McDaniel and H. C. Brown, An Extended Table of Hammett Substituent Constants Based on the Ionization of Substituted Benzoic Acids, J. Org. Chem., 1958, 23, 420–427 CrossRef CAS.
- N. García Rey and D. D. Dlott, Structural Transition in an Ionic Liquid Controls CO2 Electrochemical Reduction, J. Phys. Chem. C, 2015, 119, 20892–20899 CrossRef.
- B. A. Rosen, A. Salehi-Khojin, M. R. Thorson, W. Zhu, D. T. Whipple, P. J. Kenis and R. I. Masel, Ionic Liquid–Mediated Selective Conversion of CO2 to Co at Low Overpotentials, Science, 2011, 334, 643–644 CrossRef CAS PubMed.
- B. A. Rosen, W. Zhu, G. Kaul, A. Salehi-Khojin and R. I. Masel, Water Enhancement of CO2 Conversion on Silver in 1-Ethyl-3-Methylimidazolium Tetrafluoroborate, J. Electrochem. Soc., 2012, 160, H138 CrossRef.
- N. G. Rey and D. D. Dlott, Effects of Water on Low-Overpotential CO2 Reduction in Ionic Liquid Studied by Sum-Frequency Generation Spectroscopy, Phys. Chem. Chem. Phys., 2017, 19, 10491–10501 RSC.
- N. G. Rey and D. D. Dlott, Studies of Electrochemical Interfaces by Broadband Sum Frequency Generation, J. Electroanal. Chem., 2017, 800, 114–125 CrossRef CAS.
- R. Atkin, N. Borisenko, M. Drüschler, S. Z. El Abedin, F. Endres, R. Hayes, B. Huber and B. Roling, An In Situ Stm/Afm and Impedance Spectroscopy Study of the Extremely Pure 1-Butyl-1-Methylpyrrolidinium Tris (Pentafluoroethyl) Trifluorophosphate/Au (111) Interface: Potential Dependent Solvation Layers and the Herringbone Reconstruction, Phys. Chem. Chem. Phys., 2011, 13, 6849–6857 RSC.
- K. Kirchner, T. Kirchner, V. Ivaništšev and M. V. Fedorov, Electrical Double Layer in Ionic Liquids: Structural Transitions from Multilayer to Monolayer Structure at the Interface, Electrochim. Acta, 2013, 110, 762–771 CrossRef CAS.
- M. Urushihara, K. Chan, C. Shi and J. K. Nørskov, Theoretical Study of Emim+ Adsorption on Silver Electrode Surfaces, J. Phys. Chem. C, 2015, 119, 20023–20029 CrossRef CAS.
- S. Baldelli, Probing Electric Fields at the Ionic Liquid–Electrode Interface Using Sum Frequency Generation Spectroscopy and Electrochemistry, J. Phys. Chem. B, 2005, 109, 13049–13051 CrossRef CAS PubMed.
- S. Rivera-Rubero and S. Baldelli, Surface Spectroscopy of Room-Temperature Ionic Liquids on a Platinum Electrode: A Sum Frequency Generation Study, J. Phys. Chem. B, 2004, 108, 15133–15140 CrossRef CAS.
- A. M. Limaye, W. Ding and A. P. Willard, Understanding Attenuated Solvent Reorganization Energies near Electrode Interfaces, J. Chem. Phys., 2020, 152, 114706 CrossRef CAS PubMed.
- Z. K. Goldsmith, M. Secor and S. Hammes-Schiffer, Inhomogeneity of Interfacial Electric Fields at Vibrational Probes on Electrode Surfaces, ACS Cent. Sci., 2020, 6, 304–311 CrossRef CAS PubMed.
- A. B. Anderson, The Influence of Electrochemical Potential on Chemistry at Electrode Surfaces Modeled by Mo Theory, J. Electroanal. Chem. Interfacial Electrochem., 1990, 280, 37–48 CrossRef CAS.
- P. S. Bagus and G. Pacchioni, Theoretical Analysis of the Vibrational Shifts of Co Chemisorbed on Pd (100), Surf. Sci., 1990, 236, 233–240 CrossRef CAS.
- D. K. Lambert, Vibrational Stark Effect of Co on Ni (100), and Co in the Aqueous Double Layer: Experiment, Theory, and Models, J. Chem. Phys., 1988, 89, 3847–3860 CrossRef CAS.
- M. J. Weaver and X. Gao, In Situ Electrochemical Surface Science, Annu. Rev. Phys. Chem., 1993, 44, 459–494 CrossRef CAS.
- M. T. Koper, R. A. van Santen, S. A. Wasileski and M. J. Weaver, Field-Dependent Chemisorption of Carbon Monoxide and Nitric Oxide on Platinum-Group (111) Surfaces: Quantum Chemical Calculations Compared with Infrared Spectroscopy at Electrochemical and Vacuum-Based Interfaces, J. Chem. Phys., 2000, 113, 4392–4407 CrossRef CAS.
- S. A. Wasileski, M. T. Koper and M. J. Weaver, Metal Electrode–Chemisorbate Bonding: General Influence of Surface Bond Polarization on Field-Dependent Binding Energetics and Vibrational Frequencies, J. Chem. Phys., 2001, 115, 8193–8203 CrossRef CAS.
- S. A. Wasileski, M. T. Koper and M. J. Weaver, Field-Dependent Electrode–Chemisorbate Bonding: Sensitivity of Vibrational Stark Effect and Binding Energetics to Nature of Surface Coordination, J. Am. Chem. Soc., 2002, 124, 2796–2805 CrossRef CAS PubMed.
- C. Korzeniewski, S. Pons, P. Schmidt and M. Severson, A Theoretical Analysis of the Vibrational Spectrum of Carbon Monoxide on Platinum Metal Electrodes, J. Chem. Phys., 1986, 85, 4153–4160 CrossRef CAS.
- M. Mamatkulov and J.-S. Filhol, An Ab Initio Study of Electrochemical vs. Electromechanical Properties: The Case of Co Adsorbed on a Pt (111) Surface, Phys. Chem. Chem. Phys., 2011, 13, 7675–7684 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc01876k |
| This journal is © The Royal Society of Chemistry 2021 |