Thermodynamics of ion binding and occupancy in potassium channels

Abstract

Potassium channels modulate various cellular functions through efficient and selective conduction of K⁺ ions. The mechanism of ion conduction in potassium channels has recently emerged as a topic of debate. Crystal structures of potassium channels show four K⁺ ions bound to adjacent binding sites in the selectivity filter, while chemical intuition and molecular modeling suggest that the direct ion contacts are unstable. Molecular dynamics (MD) simulations have been instrumental in the study of conduction and gating mechanisms of ion channels. Based on MD simulations, two hypotheses have been proposed, in which the four-ion configuration is an artifact due to either averaged structures or low temperature in crystallographic experiments. The two hypotheses have been supported or challenged by different experiments. Here, MD simulations with polarizable force fields validated by ab initio calculations were used to investigate the ion binding thermodynamics. Contrary to previous beliefs, the four-ion configuration was predicted to be thermodynamically stable after accounting for the complex electrostatic interactions and dielectric screening. Polarization plays a critical role in the thermodynamic stabilities. As a result, the ion conduction likely operates through a simple single-vacancy and water-free mechanism. The simulations explained crystal structures, ion binding experiments and recent controversial mutagenesis experiments. This work provides a clear view of the mechanism underlying the efficient ion conduction and demonstrates the importance of polarization in ion channel simulations.

---

Introduction

Potassium channels are a family of membrane proteins that controls the rapid and selective conduction of K⁺ and exclusion of Na⁺.¹ The exceptional properties of potassium channels and their importance in regulating cellular processes have stimulated decades of studies on their conduction mechanism.^1–7 The crystal structure of a model potassium channel, KcsA,⁸ shows electron density in the four continuous ion binding sites in the selectivity filter (SF). The close distance of 3–3.5 Å between neighboring sites led to the hypothesis that K⁺ only binds at two non-adjacent sites at a time to avoid strong electrostatic repulsion between ions. In this scheme, overlap between two alternating configurations, i.e. K⁺–water–K⁺–water and water–K⁺–water–K⁺, produces the four peaks in the electron density.^8,9 This two-ion hypothesis, termed the “soft knock-on” mechanism, has been used extensively in ion binding experiments and theoretical studies. Recently, however, this mechanism has been challenged by (i) a reanalysis of crystallography data showing the total occupancy is close to 4,¹⁰ and (ii) long MD simulations of ion permeating events in which the rapid and selective K⁺ conducting pathway contains no water.^10,11

Simulation studies to date have not fully clarified the ion conduction mechanism. On one hand, the four-ion configuration was shown to be stable only in short simulations at 200 K,¹⁰ likely the result of the slow dynamics at low temperature. On the other hand, two-ion and three-ion configurations accounted for more than 90% of long MD trajectories.^10,11 Also, it has been argued that simulation results are sensitive to force field parameters,¹² as reflected by other MD studies that support the soft knock-on mechanism.^13–15 Furthermore, free energy simulations found that a direct knock-on mechanism and the soft knock-on mechanism have comparable free energy barriers.^16,17

There have been numerous experimental studies supporting either mechanism. Crystallographic data are collected at low temperature, while other experiments are conducted at room temperature under either equilibrium or nonequilibrium conditions. Anomalous X-ray diffraction of NaK2K potassium channel showed high K⁺ occupancy in the SF.¹⁸ Solid-state NMR studies of NaK2K detected no water in the SF under physiological conditions.¹⁹ 2-D IR spectroscopy studies found that only the two-water two-ion configurations are compatible with the spectra of the SF,²⁰ while a later study suggested the 2D IR spectra could not differentiate the direct and soft knock-on mechanisms.¹¹ Cuello and coworkers²¹ showed that by removing the S3 site, a KcsA-G77A mutant stabilizes the water–K⁺–water–K⁺ configuration. The G77A mutant has lower conductance but maintains K⁺/Na⁺ selectivity, contrary to the previous conclusion that the direct knock-on mechanism is essential for selectivity.¹¹ The G77A mutant and the wildtype have almost identical structures except at S3, and similar ion binding affinities. Although the G77A mutant may not be directly relevant to wildtype KcsA, it is an interesting model system to study the ion conduction mechanism.

Due to the inconsistent results from various experiments and simulations, there is no consensus on the ion conduction mechanism of KcsA. The stability of ion configurations in the SF results from a competition among the interactions between ions, water and protein in the confined environment.^4,22 The polarization effect is significant for such highly charged systems.^23–25 Polarization is the response of an electron cloud to the electric field generated by its environment. The presence of ions dramatically changes the electric field around the SF. So it is important to account for this effect by allowing protein and water to respond to this change in electric field. Polarization can both enhance electrostatic interactions by increasing molecular dipole moments and reduce them through dielectric screening. For the interactions of ions, such as those in the SF, the screening effect dominates.^25–27 The screening effect can qualitatively affect ion binding. In fact, we showed previously that without the screening effect, Ca²⁺/Mg²⁺ selectivity in most proteins will be inverted.^27–29 The importance of polarization for K⁺ ion binding has also been recognized in recent studies.^30–36 Varma et al. highlighted the complexity of ion–protein interactions because polarization can both enhance and reduce the dipole moments of ion-coordinating molecules.³³ Rossi et al. found that the polarization of the threonine methyl groups at S4 site contribute to a few kcal mol⁻¹ in ion binding energy.³⁴ Peng et al. and Ngo et al. showed that polarization significantly reduces ion conduction barriers.^30,36 Lemkul and coworkers found that polarization is essential for the stability of G-quadruplexes.³⁷ G-quadruplexes are similar to the SF of potassium channels in that they contain a single line of K⁺ ions with interatomic distances of ∼3.4 Å, and each binding site has 8 carbonyl groups surrounded by negatively charged groups. Despite these findings, previous simulations of KcsA predominantly used fixed-charge (nonpolarizable) force fields,² which could cause significant errors for ion interactions.²⁶

Besides inaccuracy in force fields, the observation of both soft and direct knock-on mechanisms in previous simulations could also be related to insufficient sampling. Transitions between configurations in the SF may require long simulations. Since the ion configurations and the structure of the SF are well defined, the relative stabilities can be conveniently calculated by free energy perturbation (FEP).³⁸ FEP utilizes alchemical pathways to calculate free energy differences between thermodynamic states or between molecules. FEP has been used widely for the study of protein–ligand binding, and is an efficient approach for small ligands with rigid binding pockets.

In this work, we endeavored to determine accurately the thermodynamic stabilities of various ion configurations through polarizable MD simulations and free energy calculations. Our results show that in contrast to previous simulations, the four-ion configuration in KcsA is thermodynamically stable and likely a frequent conformation during ion conduction. Additionally, we compared our simulations to the KcsA-G77A mutant data and experimental ion binding affinities.

Results

Ion occupancy in KcsA

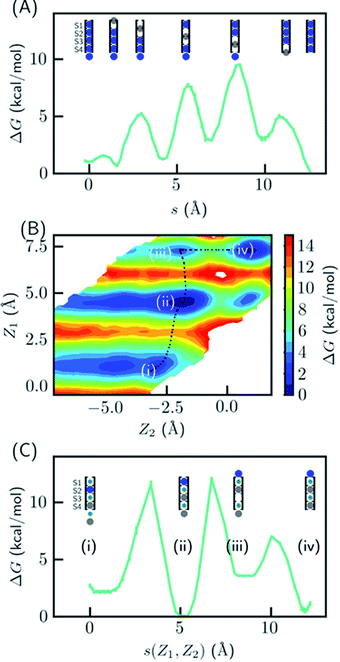
Several hypotheses on ion occupancy have been proposed: full occupancy of 4 based on X-ray crystal structures,^10,18 reduced occupancy of 2–3 in the direct knock-on mechanism based on MD simulations,^10,11 and two-ion two-water configuration (Fig. 1A) based on alternative interpretation of X-ray structures and MD simulations.^9,21 Although the direct knock-on mechanism was considered to be consistent with full occupancy, MD simulations at room temperature have always produced reduced occupancy.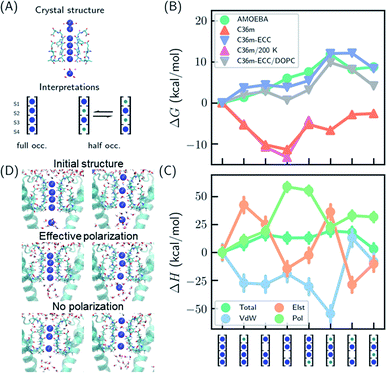

Fig. 1 Thermodynamic stabilities of ion configurations in KcsA. (A) Crystal structures of the SF of KcsA (PDB: 1k4c) and alternative interpretations of ion configurations based on full occupancy or half occupancy. Only two of four subunits in the crystal structures are shown for clarity. The binding sites are S1–S4, from top to bottom. Blue and green circles in the cartoon representations stand for K⁺ and water, respectively. (B) Standard free energies for ion configurations of K⁺ in KcsA calculated from MD simulations. AMOEBA and C36m-ECC include ion polarization while C36m does not. “200 K” indicates the simulation temperature and “DOPC” means simulations of protein embedded in DOPC bilayer. Otherwise, the simulations are for solvated proteins at 298 K. The uncertainties of the free energies are smaller than the size of the symbols. (C) Relative enthalpies and components calculated by AMOEBA. “Elst”, “vdW” and “Pol” denote electrostatics, van der Waals and polarization. (D) Structures of unconstrained MD simulations in DOPC bilayer with two initial structures. “Effective polarization” means simulations with C36m-ECC, and “No polarization” means simulation with C36m. For each combination of initial structure and force field, two 500 ns MD simulations were conducted, and similar structures were observed within 50 ns and remained stable toward the end of simulations.

We predicted the relative stabilities of two-, three- and four-ion configurations from binding free energies of K⁺/water and relative binding free energies between K⁺ and water. Each absolute or relative binding free energy was calculated by FEP and MD simulations. The simulations mimic crystallographic conditions with a model system of KcsA solvated in water solution, while the effect of a lipid bilayer environment is also discussed. Two force fields that account for the polarization effect were chosen, the AMOEBA polarizable force field and the CHARMM36m (C36m) force field with electronic continuum correction (ECC).^25,26 For comparison, simulations with standard CHARMM were also included. AMOEBA explicitly represents polarization through induced dipoles on each atom. It has shown excellent accuracy for ion binding in both gas phase and condensed phase.^27,28,39 We further validated the accuracy of AMOEBA for ion–protein interactions against quantum mechanical (QM) methods (Fig. S1 and S2†). ECC is a framework for modifying standard nonpolarizable force fields to represent polarization through a mean-field approximation. In ECC, the charges of ionized groups and ions are scaled by sqrt(1/2) ≈ 0.7, based on the argument that the electronic screening factor is about 2 for most organic media.²⁶ ECC has also been used in many MD simulation studies²⁵ thanks to its compatibility with popular MD software and computational efficiency.

The results from both AMOEBA and C36m-ECC indicate that the four-ion configuration has the lowest standard free energy (Fig. 1B) despite the perceived strong repulsion between the ions. C36m-ECC simulations in DOPC lipid bilayer (Fig. 1B), and simulations with several variants of AMOEBA parameters (Fig. S3†) also predict similar trends. The differences between the four-ion configuration and some three-ion configurations are moderate: under low K⁺ concentration, reduced occupancy could become more stable. This result is consistent with the experimental observation of reduced ion occupancy in KcsA under low K⁺ concentration of 3 mM.⁸ In contrast, our simulations with the fixed-charge CHARMM force field favored the three-ion and two-ion configurations over the four ion-configuration, with 1,2,4-bound configuration being most stable. This result agrees with previous simulations that used fixed-charge force fields.^10,11 Moreover, the general trend of the calculated free energies is insensitive to temperature (as low as 200 K). Even with the fixed-charge force field, the most stable, 1,2,4-bound configuration has a direct ion–ion contact at S1 and S2. This ion–ion contact occurs because the four negatively charged D80 residues near S1, in addition to the strong dipole moments of the carbonyl groups, favor ion binding at S1 and S2 and the artificially strong ion–ion repulsion prevents binding of three continuous ions. From the comparison between various force fields, especially between C36m-ECC and C36m where the only difference is effective polarization of ions, it can be seen that polarization strongly influences ion binding thermodynamics. Only simulations with polarization are consistent with the full ion occupancy observed in crystal structures.

Despite similar trends regarding the stability of the four-ion configuration, some noticeable differences between AMOEBA and C36m-ECC exist (Fig. 1B). First, the water–K⁺–K⁺–K⁺ configuration is most stable among 3-ion configurations in AMOEBA, while several 3-ion configurations have similar free energies as predicted by C36m-ECC. Second, the free energy difference between water–K⁺–water–K⁺ and water–K⁺–vacancy–K⁺, i.e. the water binding free energy for this configuration, varies significantly. In both AMOEBA and C36m results, the water binding free energy is close to 0, meaning the configurations with and without water at S3 are both possible. With C36m-ECC, the water binding free energy is about −4 kcal mol⁻¹, which seems unusual.

The stability of the four-ion configuration is largely enthalpy-driven (Fig. 1C). The polarization contribution to enthalpy favors the four-ion configuration. The variations in polarization, electrostatics and vdW enthalpies are much larger than the variation in the total enthalpy, indicating compensation between these energy components.

The free energy results were confirmed by long MD simulations of KcsA in lipid bilayer. With effective polarization, starting from the four-ion configuration, the first ion leaves the SF and the fifth ion enters the SF, resulting in a four-ion configuration stable in 500 ns simulations. Without polarization, the SF quickly adopts 1,2,4-bound configuration and remains stable through 500 ns simulations. This result is consistent with our free energy calculation. However, the final structures also depend on the initial structure, which indicates insufficient sampling. Starting from the water–K⁺–water–K⁺ configuration, long-lived configurations K⁺–K⁺–water–K⁺ and K⁺–water–K⁺–vacancy–K⁺ (the first K⁺ at the entry of S1) were observed from simulation with and without effective polarization, respectively.

Multiple binding/unbinding of K⁺ at S1 were observed in two 100 ns AMOEBA simulations of KcsA in 0.15 mM KCl solution. The four-ion configuration accounts for 61% of the last 80 ns simulations, with the rest being three-ion configurations (Fig. S5†). This percentage is converted to a standard binding free energy for the fourth ion of −1.4 ± 0.9 kcal mol⁻¹, in excellent agreement with −1.3 ± 0.6 kcal mol⁻¹ from the free energy calculation (Table 1 and Fig. 1B). AMOEBA simulations of KcsA in DOPC bilayer were stuck in the water–K⁺–K⁺–K⁺ configuration (Fig. S5†), which is also predicted to be a low free energy configuration in water solution (Fig. 1B).

Table 1 Relative and intrinsic binding free energies in KcsA from MD simulations and experiments (kcal mol⁻¹)

Protein	Conformation	AMOEBA		ITC^d
		K^+	Na^+ → K^+	K^+	Na^+ → K^+
a The two values from top to bottom are free energy changes from 2 K^+ to 3 K^+ and 3 K^+ to 4 K^+ in the SF, respectively. 3 K^+ free energy is calculated by sum of partition functions of all four configurations. 2 K^+ free energy is from the water–K^+–water–K^+ configuration. b Free energy change from 2 Na^+ to 1 Na^+/1 K^+ in the SF. c Free energy change from 1 Na^+/3 K^+ to 4 K^+ in the SF. d Experimental binding free energy was calculated from ΔG = −RT ln[Kd/(mol L^−1)], with Kd(K^+) = 67 and 350 μM, Kd(Na^+) = 9 and 0.48 mM in wildtype (conductive) and M96V mutant (collapsed) KcsA, respectively.^47
KcsA-WT	Collapsed	−4.9 ± 0.7	−1.6 ± 0.3^b	−4.7	−2.1
KcsA-WT	Conductive	−6.8 ± 0.6^a	−2.0 ± 0.2^c	−5.7	−2.9
		−1.3 ± 0.6
KcsA-G77A	Conductive	−6.0 ± 0.5	−3.3 ± 0.4^b

---

To better understand the polarization effect on ion binding and ion–ion repulsion, the energy components as a function of ion–ion distance were analyzed. Starting from the crystal structure of KcsA, the first K⁺ ion was gradually moved out of the SF (Fig. 2). AMOEBA and C36m-ECC both predict that structures with the first K⁺ inside and outside the SF have comparable energies separated by a barrier, while C36m and AMOEBA without polarization predict the first K⁺ will be repelled out of the SF with almost no barrier (Fig. 2A). Notably, the barrierless repulsion is an integral part of the previous direct knock-on mechanism.¹⁰ At short ion–ion distance between 3 and 5 Å, the electrostatic interaction is repulsive, while the polarization energy is nearly proportional to the opposite of electrostatic energy, therefore significantly reducing ion–ion repulsion. The polarization comes from the surroundings of the ions. It is long ranged, not fully converging after 10 Å (Fig. 2B). Previous work also pointed out that models that explicitly include the protein environment are more accurate than active-site models.⁴⁰

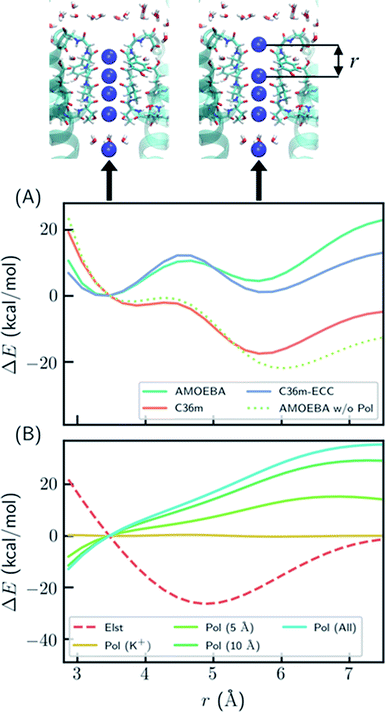Fig. 2 Polarization effect on ion–ion interaction. (A) Relative energy as a function of ion–ion distance. “AMOEBA w/o Pol” means AMEOBA without the polarization term. (B) Electrostatic and polarization energy as a function of ion–ion distance calculated by AMOEBA. The polarization energy for K⁺ and its environment within a certain distance is also computed. “Pol (K⁺)” means polarization energy for four K⁺ in the SF, “Pol (5 Å)” means the polarization energy for K⁺ and atoms that are within 5 Å of K⁺ at any point during the distance scan, and likewise for other polarization energy. The energy was calculated using crystal structure (PDB ID: 1k4c) embedded in DOPC bilayer, except that the coordinate of K⁺ at S1 was modified and two K⁺ ions above S1 were removed.

The reason why polarization effectively reduces ion–ion repulsion is as follows: when the two ions come closer, the combined electric field produced by the two ions also becomes stronger, leading to a much more favorable polarization energy which is proportional to the square of the electric field. This result is a classic example of dielectric screening. If the environment is treated as an electronic continuum, the screening effect can be modeled by a dielectric constant or scaled effective charges.^26,41–44 In addition, because this screening effect mostly acts on ion–ion repulsion, it cannot be straightforwardly modeled by modification of ion–protein vdW interactions as in previous work.⁴⁵

Ion conduction is driven by a membrane potential and/or ion concentration gradient, therefore it is important to consider the effect of membrane potential on the conduction mechanism. The membrane potential of neurons lies between −70 and 40 mV. The holding potential used in electrophysiological experiments is up to 200 mV.¹ The effect of the membrane potential was studied by using the model system in Fig. 2 with either an external electric field or extra ions on each side of the membrane. As shown in Fig. S6,† a membrane potential of 500 mV only shifts the relative energy curve in Fig. 2A by 0.8 kcal mol⁻¹, which is much smaller than the barrier and the effect of polarization. Therefore, the membrane potential has a negligible effect on short-range ion–ion interactions. However, the membrane potential is important for MD simulations of ion permeation since it directly affects ion conduction rate and, in some cases, the conformation of ion channels.

Ion occupancy in KcsA-G77A

One recent piece of evidence for the soft knock-on mechanism comes from the observation of 2,4-bound configuration in KcsA-G77A (Fig. 3A) and KcsA-G77C mutants.²¹ The mutants have abolished binding at S3 due to the rotation of the backbones of V76. The G77A mutant is a K⁺-selective channel with a reduced conductance ∼32 times lower than that of the KcsA wildtype (KcsA-WT). The G77A mutant also has a similar apparent K⁺ binding affinity as KcsA-WT.²¹ Although the mutants could have a different conduction mechanism than the KcsA-WT, they serve as model systems to study how conduction mechanism is affected by the structure of the SF.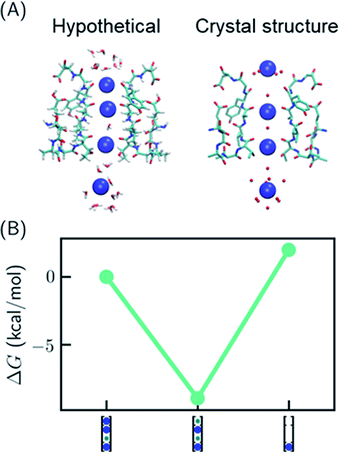

Fig. 3 Relative free energies of ion configurations in KcsA-G77A mutant. (A) Crystal structure of KcsA-G77A (PDB: 6nfu) and a hypothetical 1,2,4-bound configuration from MD simulations; (B) relative free energies of ion configurations calculated from MD simulations. Blue and green circles in the cartoon representations stand for K⁺ and water, respectively. The uncertainties of the free energies are smaller than the size of the symbols.

It was argued that if KcsA-WT has four ions in the SF, KcsA-G77A should have three ions at S1, S2 and S4 (Fig. 3A).²¹ As polarizable force fields produce weak ion–ion repulsion in the SF, it is interesting to see whether the 2,4-bound configuration in KcsA-G77A can be reproduced. The free energy calculation of KcsA-G77A shows that indeed the 2,4-bound K⁺ configuration is more stable than the 1,2,4-bound configuration and the one-ion configuration (Fig. 3B). Although the mutation only affects S2 and S3, both S1 and S3 are free of K⁺ ions. The coupling between S1 and S3 is due to the interaction between ions: K⁺ at S2 is close to an in-plane binding position between S1 and S2 (Fig. 3A), which excludes K⁺ at S1 despite the reduced ion–ion repulsion predicted by polarizable force fields. Previously, the coupling between ion binding at S1 and S3 or between S2 and S4 has been considered as evidence of the two alternating configurations in the soft knock-on mechanism.^21,46 Apparently, the coupling of reduced occupancy at S1 and S3 in KcsA-G77A does not contradict the full ion occupancy in KcsA-WT.

Intrinsic and relative binding free energies

Ion binding experiments provide high-quality thermodynamics data that can be used to validate force fields. Ion binding in potassium channels involves multiple binding events, competition between ions and conformational changes. Thus, it has been difficult to interpret the experimental ion binding data. Lockless and coworkers⁴⁷ showed that K⁺ binding in KcsA and MthK potassium channels in isothermal titration calorimetry (ITC) conditions is the competitive binding between Na⁺ and K⁺. Using ITC with a competitive binding model and several KcsA mutants that only adopt one SF conformation, the intrinsic binding affinities for different conformations were determined. The K⁺ binding affinity was found to be ∼0.1 mM, and the Na⁺/K⁺ selectivity varies between 10² to 10⁴ for different channels and conformations. A much stronger K⁺ binding affinity of ∼2 μM was determined by thermal denaturation experiments.⁴⁸ For the collapsed conformation of KcsA, since the SF is unstable without ions⁴⁸ and there are a maximum of two K⁺, the binding affinity likely corresponds to binding of a second K⁺. The conductive conformation of KcsA is observed at higher K⁺ concentration than the collapsed conformation, so it should contain at least 2 K⁺, and the binding affinity may be related to the binding of the third or the fourth K⁺. The binding free energy for each conformation can be calculated separately by simulations since the simulation time scale is relatively short. By integrating the free energies of various configurations (eqn (S1), Table S1†), we calculated the total free energy for one-ion to four-ion configurations and derived the binding free energy for each binding event (Table 1). The calculated binding free energy for a third K⁺ in the KcsA conductive conformation is −6.8 kcal mol⁻¹, close to the ITC value of −5.6 kcal mol⁻¹,⁴⁷ while the binding of a fourth K⁺ seems too weak (−1.3 kcal mol⁻¹) to be measurable. The calculated K⁺ binding free energy in the collapsed conformation of KcsA (−4.9 kcal mol⁻¹) and Na⁺/K⁺ relative binding free energies (−1.6 to −2.0 kcal mol⁻¹) also agree well with experiments⁴⁷ (−4.7 and −2.1 to −2.9 kcal mol⁻¹, respectively).

One intriguing question from the KcsA-G77A mutant experiments is why KcsA-G77A and KcsA-WT have similar binding affinities (0.30 and 0.29 mM)²¹ if the ion configurations are different. KcsA-WT adopts the collapsed conformation at low K⁺ concentration and transitions to the conductive conformation when K⁺ concentration is above 5 mM, although it is unclear whether the binding takes place before or after the conformational change.^47,49 KcsA-G77A has the conductive conformation at both low and high K⁺ concentrations. In our free energy calculations, the binding free energy for KcsA-G77A (−6.0 kcal mol⁻¹) is close to both the collapsed (−4.9 kcal mol⁻¹) and conductive conformations (−6.8 kcal mol⁻¹) of KcsA-WT, considering the accuracy of MD simulations (Table 1). This data suggests that the binding affinities could be similar despite different conformations or ion configurations.

Ion conduction barriers

Since the SF is saturated by K⁺ at equilibrium, the most likely conduction mechanism is the single vacancy mechanism,⁵⁰ where one vacancy is created by unbinding of the first/last ion and then the vacancy is gradually transferred along the SF. The soft knock-on mechanism, which proceeds though alternating configurations of water–K⁺–water–K⁺ and K⁺–water–K⁺–water,^9,13 is unfavorable due to the high free energy of the two-ion configuration (Fig. 1B), unless it has much lower barrier than the single-vacancy mechanism. To assess the barriers of the single vacancy and the soft knock-on mechanisms, we calculated the potential of mean force (PMF) as a function of ion coordinates by umbrella sampling.^51,52 The intermediate steps in the single vacancy mechanism and the soft knock-on mechanism are illustrated in Fig. 4A and C, respectively. Previous simulations of the soft knock-on mechanism found K⁺–water–K⁺–K⁺ as an intermediate state.¹³ This structure was also sampled in our simulations; it is slightly unfavorable compared to the water–K⁺–vacancy–water–K⁺ configuration (indicated by (iii) in Fig. 4B and C), but does not affect the overall barrier. According to the PMF (Fig. 4A), it is unfavorable for the four-ion configuration to lose one ion at S1 or S4, consistent with the free energy results in Fig. 1. The overall barrier for the single vacancy mechanism is ∼9.5 kcal mol⁻¹ and the highest barrier for individual steps is ∼6.5 kcal mol⁻¹ (Fig. 4A). The barrier is considerably larger than 2–3 kcal mol⁻¹ reported in previous simulations.^13,16 The large barrier is due to the close carbonyl O–O distances in simulations, which in turn is caused by the backbone torsional angles, ion-protein interactions, and the restraints from the protein scaffold. The distances between in-plane diagonal carbonyl oxygen atoms of T75 and V76 in the crystal structures are 4.49 and 4.60 Å. The corresponding distances in equilibrium MD simulations are 4.31 and 4.46 Å. There is also a noticeable difference in the V76 ϕ angle (−78.6° in MD and −68.1° in the crystal structure). The equilibrium K⁺–O distance in K⁺–dialanine dimer is 2.55 Å (Fig. S2†). So the O–O distance needs to increase to ∼5 Å during ion conduction. A stiff protein scaffold or backbone torsions will lead to a large barrier. Fine tuning of the force field parameters is necessary for realistic simulations of the ion conduction. The equilibrium ion binding properties are less affected because the K⁺–O distance at the binding site is larger than at the in-plane position. Nevertheless, the barrier of the single vacancy mechanism is lower than the barrier of the soft knock-on mechanism (∼12.0 kcal mol⁻¹, Fig. 4B and C). The higher barrier for the soft knock-on mechanism can be explained by the stronger ion binding in the half-filled configuration and thus the larger energy cost for ions leaving their favorable binding pose.

Fig. 4 Free energy profile for two ion conduction mechanisms in KcsA. (A) The single vacancy mechanism consisting of only three-ion or four-ion states. The PMF is plotted as a function of the path length of the multistep transition, where each step is a function of one ion coordinate (colored in gray). (B) and (C) The soft knock-on mechanism consisting of ions separated by water. The 2-D PMF in (B) was calculated as a function of the z-coordinates of the bottom two ions (Z₁ and Z₂), where 0 indicate the entry of S4. The minimum free energy path is plotted in (C) as a function of the path length s(Z₁, Z₂) on the 2D surface. The intermediate states are shown in the cartoon representation and the K⁺ ion(s) used for reaction coordinates are colored in gray.

Discussion

The difficulty in inferring ion conduction mechanism of potassium channels mainly comes from the contradiction between strong ion–ion repulsion and the observed ion occupancy at four continuous binding sites in the SF. Initially, the soft knock-on mechanism was proposed to resolve this issue by hypothesizing that ions are separated by one water molecule.⁹ The soft knock-on mechanism requires two energetically balanced configurations, K⁺–water–K⁺–water and water–K⁺–water–K⁺. In the direct knock-on mechanism, ions transiently occupy three continuous sites and the repulsion from the first two ions helps the third ion overcome the barrier.^10,11 The direct knock-on mechanism explains the Na⁺/K⁺ selectivity. However, it contains at most three ions in the SF simultaneously. To explain the ion occupancy in crystal structures, it was argued that the four-ion configuration only exists at very low temperature, which was not verified by converged simulations. Therefore, neither mechanism gives a satisfactory explanation of the crystal structure.

Although ions of like charge strongly repel each other, the SF also has a large negative potential that could possibly compensate for the ion–ion repulsion. To determine the balance between the two forces, accurate electrostatic models are required. Polarization effects are critical for highly charged systems, but they were often neglected in previous simulations of ion channels. Our data show that polarization effectively reduces the ion–ion repulsion through dielectric screening. As a result, the four-ion configuration observed in crystal structures is thermodynamically stable. Considering the thermodynamic stabilities, the most likely conduction mechanism is through reversible binding of ions and the movement of one ion vacancy, or the single-vacancy mechanism. This mechanism is much simplified and consistent with crystal structures.

The single vacancy mechanism suggested by our data is close to the direct knock-on mechanism from previous work, but there are some noticeable differences. In the single vacancy mechanism, the four-ion configuration is stable, and the one-vacancy states incur a small free energy cost. In the previous direct knock-on mechanism, three-ion states are most stable, and the conduction also involves four-ion and two-ion states (see, e.g., Movie (S1) in ref. 10). This difference could affect the conduction rate and the conformation of the selectivity filter, which can be verified by comparing to electrophysiological⁵⁰ and spectroscopic experiments.²⁰ Additionally, previous simulation results were sensitive to force field parameters; slight changes in the parameters could lead to the soft knock-on mechanism.¹² In contrast, our prediction of full ion occupancy is insensitive to force field parameters once polarization is included. Our hypothesis is mainly based on equilibrium ion binding properties using the crystal structures, while actual ion conduction conformations may be different. Future simulations under realistic conditions and at larger time scale are needed to establish the detailed conduction mechanism.

This work has clearly explained the ion occupancy in crystal structures and ITC binding affinities, both of which are directly related to ion binding thermodynamics. In addition, ITC experiments of the MthK K⁺ channel found that there are two K⁺ binding events, each with a Hill coefficient of ∼2 for Na⁺ displacement, which is only possible if there are at least four Na⁺ ions before K⁺ binding.⁵³ Recently, the KcsA-G77A mutant was found to have a stabilized 2,4-bound ion configuration characteristic of the soft knock-on mechanism.²¹ Our data shows that this is because it has a different ion binding property from the wildtype. There have been other experimental studies contradicting the direct knock-on mechanism, and they have been explained partly in recent work of de Groot and coworkers.^10,11 The ion–water coupling ratio derived from streaming potential measurement of KcsA was 1.0,⁵⁴ but the applied osmotic pressure could lead to an ion-depleted, water-permeable state, which is distinct from the conductive state.¹⁰ 2D IR spectroscopy combined with MD simulations found that only a combination of water-separated two-ion configurations, including a structure with one flipped carbonyl group, was compatible with the spectra,²⁰ while it was shown later that the spectra could be reproduced by using only configurations with direct ion–ion contact and the carbonyl-flipped states were unnecessary.¹¹ As most of the structures with direct ion–ion contact also exist in the single vacancy mechanism, the 2D IR study is also compatible with our data.

MD simulations have been valuable for the study of both ion conduction and activation mechanisms of potassium channels.^55–58 Considering the importance of polarization for ion binding thermodynamics, we strongly advocate the use of polarizable force fields (such as AMOEBA, CHARMM Drude⁵⁹) or force fields with effective polarization for ion channel simulations. The charge scaling method (ECC) is a viable approach to effective polarization when computational cost and/or software compatibility are a concern. We have shown that a scaling factor of 0.7 yields the same ion occupancy as explicit polarizable force fields, but deviation exists for the relative stabilities between various configurations. Fine tuning of the scaling factor and possibly vdW parameters²⁵ may be needed for more realistic simulations. Alternative approaches are QM-based methods that properly account for both local and long–range interactions, such as QM/MM⁴⁰ and quasi-chemical theory.^6,35

Materials and methods

System preparation

Systems with KcsA WT in collapsed, partially open⁶⁰ and closed conductive conformations and G77A mutant (PDB codes: 1k4c, 1k4d, 3fb6 and 6nfu) in water boxes or embedded in DOPC bilayers (Fig. S4†) were set up by using the CHARMM-GUI.⁶¹ The box sizes for the water and DOPC systems were about (72 Å)³ and 76 × 76 × 92 Å,³ respectively. Salts were added to give a concentration of 0.15 M NaCl for the water box to mimic the crystallography conditions and 0.4 M KCl for the DOPC bilayer systems to mimic the high local concentration during ion conduction. For the DOPC system, a multistep procedure recommended by CHARMM-GUI was used to for initial relaxation.

Force field validation

The AMOEBA force field parameters were validated by comparing to QM and experimental ion binding energies (Fig. S1 and S2†). The accuracy of our force field is comparable to popular density functional theory methods.

MD simulations

Simulations with the AMOEBA force field were performed using Tinker-OpenMM.^62,63 The AMOEBA 2013 parameters for protein,⁶⁴ the ion parameters developed by Wang⁶⁵ and the DOPC parameters developed by Li and coworkers⁶⁶ were used. Larger polarizabilities for carbonyl groups from Liu et al.⁶⁷ were used since they better describe ionic interactions (see ESI†). Simulations with CHARMM36m force field⁶⁸ were performed using GROMACS 2018.⁶⁹ The water box and DOPC box were used for binding free energy calculations and direct MD simulations, and the DOPC box was used for PMF calculation with AMOEBA and direct MD simulations. The Glu71 sidechains were protonated according to previous studies,¹¹ and all other residues were assigned default protonation states. The collapsed and closed conductive conformations are used for binding free energy calculations and the partially open conformation was used for PMF calculation. To keep the proteins at their starting conformations,²³ flat-bottom position restraints were applied to all alpha carbons except those in the SF (residues 74 to 81). The restraints have a force constant of 5 kcal mol⁻¹ Å⁻¹ for deviations larger than 2 Å.

Long MD simulations without ion restraints were performed, including two 500 ns simulations with DOPC box for each combination of CHARMM/CHARMM-ECC and four-ion/two-ion starting structure, and two 100 ns AMOEBA simulations with either water box (0.15 mM KCl) or DOPC box staring from the four-ion configuration.

Free energy calculation

Free energy perturbation (FEP) and the double decoupling method^70,71 was used to calculate the standard binding free energies in various configurations to derive the relative free energy between different configurations. For example, the ΔG between two configurations K⁺–vacancy–K⁺–K⁺ and K⁺–K⁺–K⁺–K⁺ was calculated as ΔG for moving K⁺ from gas phase to S2 minus ΔG for moving K⁺ from gas phase to the solution. The relative free energy between Na⁺–vacancy–vacancy–Na⁺ and Na⁺–vacancy–vacancy–K⁺ was calculated as ΔG for mutating Na⁺ at S4 to K⁺ minus ΔG for mutating an aqueous Na⁺ to K⁺. The list of FEP calculations is tabulated in Tables S2 and S4.† Each free energy change was calculated through a series of alchemical transitions. For systems with net charge, there is a finite-size effect that depends on not only the box size but also the distribution of charges in the system. To remove such finite-size effect from final ΔG values, the same or similar systems (which differ by four G77A mutations) were used for ΔG in the aqueous phase and ΔG in the SF. Alternatively, the finite size effect can be corrected analytically or by keeping the system charge-neutral during the alchemical transition. Full details of the calculation can be found in the ESI.† In the ECC approach, the solvation free energy consists of a nuclear contribution and an electronic contribution.⁷² The nuclear contribution is calculated by standard FEP using the scaled charge. The electronic contribution can be calculated by the effective Born radius and the electronic dielectric constant, which does not depend on the atomic configurations. Therefore, the electronic contribution is canceled out in the final binding free energy and is omitted in this work. It was shown that traditional nonpolarizable force fields perform well for high-dielectric environment such as aqueous solution because the missing electronic contribution is almost exactly captured by the overestimation of the nuclear contribution, but they perform poorly for low-dielectric environment.⁷²

Energy decomposition calculation

The crystal structure of KcsA (PDB code: 1k4c) was used as a model structure to understand the effect of polarization on ion–ion interaction. The initial structure prepared for free energy calculation of KcsA embedded in DOPC bilayer was first cleaned by energy minimization. Then the two K⁺ ions above S1 were removed. The distance between K⁺ ions at S1 and S2 was varied by modifying the z-coordinate of K⁺ at S1. The vdW cutoff and Ewald parameters were same as those in free energy calculation. The contribution of each atom to the polarization energy was calculated by the ANALYZE program in Tinker 7. Calculation with an external electric field was performed using a modified version of Tinker 8.⁶³

Ion permeation potential of mean force (PMF) calculation

The ion conduction barriers as a function of the z-coordinates of the ions were calculated by 1-D or 2-D WHAM methods using AMOEBA. For the direct knock-on/single vacancy model, each movement of the vacancy involves a different ion, and requires a separate 1-D WHAM calculation. For the soft-knock on mechanism, the positions of the two ions initially at S4 and the cavity were used as reaction coordinates for 2-D WHAM calculation. WHAM consists of simulations in overlapping windows, where reaction coordinates (ion positions in this work) were restrained at different values in each window. This ensures even sampling of the reaction coordinates and helps overcome high barriers. The probability distributions of reaction coordinates in each window are then combined to reconstruct the free energy profile along the reaction coordinates. The WHAM code⁷³ was used for the analysis.

Data availability

The datasets supporting this article have been uploaded as part of the supplementary material. The input coordinate and parameter files are available at Zenodo (DOI: 10.5281/zenodo.4898329).

Author contributions

S. B. R., P. R., J. A. R. and Z. J. designed research, Z. J. and C. L. contributed to new models, Z. J. performed research, Z. J., P. R., S. B. R., J. A. R. and L. R. P. analyzed data, Z. J., S. B. R. and J. A. R. wrote the paper.

Conflicts of interest

The authors declare that they have no competing interests.

Acknowledgements

The authors thank Dr Luis G. Cuello for helpful discussions. This work was supported by the National Institutes of Health (No. R01GM106137 and R01GM114237), National Science Foundation (CHE-1856173), and CPRIT (RP160657). Sandia National Laboratories is a multimission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International, Inc., for the U.S. Department of Energy's NNSA under Contract DE-NA-0003525. This work was supported by Sandia's LDRD program and performed, in part, at the Center for Integrated NanoTechnologies (CINT).

References

1. M. LeMasurier, L. Heginbotham and C. Miller, Kcsa: It's a Potassium Channel, J. Gen. Physiol., 2001, 118(3), 303–314.
2. E. Flood, C. Boiteux, B. Lev, I. Vorobyov and T. W. Allen, Atomistic Simulations of Membrane Ion Channel Conduction, Gating, and Modulation, Chem. Rev., 2019, 119(13), 7737–7832.
3. H. Yu, S. Y. Noskov and B. Roux, Two mechanisms of ion selectivity in protein binding sites, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(47), 20329–20334.
4. S. Varma, D. M. Rogers, L. R. Pratt and S. B. Rempe, Design principles for K⁺ selectivity in membrane transport, J. Gen. Physiol., 2011, 137(6), 479–488.
5. B. Roux, S. Bernèche, B. Egwolf, B. Lev, S. Y. Noskov, C. N. Rowley and H. Yu, Ion selectivity in channels and transporters, J. Gen. Physiol., 2011, 137(5), 415–426.
6. M. I. Chaudhari, J. M. Vanegas, L. R. Pratt, A. Muralidharan and S. B. Rempe, Hydration Mimicry by Membrane Ion Channels, Annu. Rev. Phys. Chem., 2020, 71(1), 461–484.
7. S. W. Lockless, Determinants of cation transport selectivity: equilibrium binding and transport kinetics, J. Gen. Physiol., 2015, 146(1), 3–13.
8. Y. Zhou, J. H. Morais-Cabral, A. Kaufman and R. MacKinnon, Chemistry of ion coordination and hydration revealed by a K⁺ channel–Fab complex at 2.0 Å resolution, Nature, 2001, 414(6859), 43–48.
9. J. H. Morais-Cabral, Y. Zhou and R. MacKinnon, Energetic optimization of ion conduction rate by the K⁺ selectivity filter, Nature, 2001, 414(6859), 37–42.
10. D. A. Köpfer, C. Song, T. Gruene, G. M. Sheldrick, U. Zachariae and B. L. de Groot, Ion permeation in K⁺ channels occurs by direct Coulomb knock-on, Science, 2014, 346(6207), 352–355.
11. W. Kopec, D. A. Köpfer, O. N. Vickery, A. S. Bondarenko, T. L. C. Jansen, B. L. de Groot and U. Zachariae, Direct knock-on of desolvated ions governs strict ion selectivity in K⁺ channels, Nat. Chem., 2018, 10(8), 813–820.
12. F. T. Heer, D. J. Posson, W. Wojtas-Niziurski, C. M. Nimigean and S. Bernèche, Mechanism of activation at the selectivity filter of the KcsA K⁺ channel, eLife, 2017, 6, e25844.
13. S. Bernèche and B. Roux, Energetics of ion conduction through the K⁺ channel, Nature, 2001, 414(6859), 73–77.
14. D. Medovoy, E. Perozo and B. Roux, Multi-ion free energy landscapes underscore the microscopic mechanism of ion selectivity in the KcsA channel, Biochim. Biophys. Acta, Biomembr., 2016, 1858(7), 1722–1732.
15. M. Ø. Jensen, D. W. Borhani, K. Lindorff-Larsen, P. Maragakis, V. Jogini, M. P. Eastwood, R. O. Dror and D. E. Shaw, Principles of conduction and hydrophobic gating in K⁺ channels, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(13), 5833–5838.
16. S. Furini and C. Domene, Atypical mechanism of conduction in potassium channels, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(38), 16074–16077.
17. V. Oakes, S. Furini and C. Domene, Insights into the Mechanisms of K⁺ Permeation in K⁺ Channels from Computer Simulations, J. Chem. Theory Comput., 2020, 16(1), 794–799.
18. P. S. Langan, V. G. Vandavasi, K. L. Weiss, P. V. Afonine, K. el Omari, R. Duman, A. Wagner and L. Coates, Anomalous X-ray diffraction studies of ion transport in K⁺ channels, Nat. Commun., 2018, 9(1), 4540.
19. C. Öster, K. Hendriks, W. Kopec, V. Chevelkov, C. Shi, D. Michl, S. Lange, H. Sun, B. L. de Groot and A. Lange, The conduction pathway of potassium channels is water free under physiological conditions, Sci. Adv., 2019, 5(7), eaaw6756.
20. H. T. Kratochvil, J. K. Carr, K. Matulef, A. W. Annen, H. Li, M. Maj, J. Ostmeyer, A. L. Serrano, H. Raghuraman, S. D. Moran, J. L. Skinner, E. Perozo, B. Roux, F. I. Valiyaveetil and M. T. Zanni, Instantaneous ion configurations in the K⁺ ion channel selectivity filter revealed by 2D IR spectroscopy, Science, 2016, 353(6303), 1040–1044.
21. C. Tilegenova, D. M. Cortes, N. Jahovic, E. Hardy, P. Hariharan, L. Guan and L. G. Cuello, Structure, function, and ion-binding properties of a K⁺ channel stabilized in the 2,4-ion–bound configuration, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(34), 16829–16834.
22. S. Varma and S. B. Rempe, Structural Transitions in Ion Coordination Driven by Changes in Competition for Ligand Binding, J. Am. Chem. Soc., 2008, 130(46), 15405–15419.
23. G. Klesse, S. Rao, S. J. Tucker and M. S. P. Sansom, Induced Polarization in Molecular Dynamics Simulations of the 5-HT3 Receptor Channel, J. Am. Chem. Soc., 2020, 142(20), 9415–9427.
24. R.-N. Sun and H. Gong, Simulating the Activation of Voltage Sensing Domain for a Voltage-Gated Sodium Channel Using Polarizable Force Field, J. Phys. Chem. Lett., 2017, 8(5), 901–908.
25. E. Duboué-Dijon, M. Javanainen, P. Delcroix, P. Jungwirth and H. Martinez-Seara, A practical guide to biologically relevant molecular simulations with charge scaling for electronic polarization, J. Chem. Phys., 2020, 153(5), 050901.
26. I. V. Leontyev and A. A. Stuchebrukhov, Electronic Continuum Model for Molecular Dynamics Simulations of Biological Molecules, J. Chem. Theory Comput., 2010, 6(5), 1498–1508.
27. Z. Jing, C. Liu, R. Qi and P. Ren, Many-body effect determines the selectivity for Ca²⁺ and Mg²⁺ in proteins, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(32), E7495–E7501.
28. Z. Jing, C. Liu, S. Y. Cheng, R. Qi, B. D. Walker, J.-P. Piquemal and P. Ren, Polarizable Force Fields for Biomolecular Simulations: Recent Advances and Applications, Annu. Rev. Biophys., 2019, 48(1), 371–394.
29. J. Litman, A. C. Thiel and M. J. Schnieders, Scalable Indirect Free Energy Method Applied to Divalent Cation-Metalloprotein Binding, J. Chem. Theory Comput., 2019, 15(8), 4602–4614.
30. V. Ngo, H. Li, A. D. MacKerell, T. W. Allen, B. Roux and S. Noskov, Polarization Effects in Water-Mediated Selective Cation Transport across a Narrow Transmembrane Channel, J. Chem. Theory Comput., 2021, 17(3), 1726–1741.
31. S. Varma and S. B. Rempe, Tuning Ion Coordination Architectures to Enable Selective Partitioning, Biophys. J., 2007, 93(4), 1093–1099.
32. S. Varma, D. Sabo and S. B. Rempe, K⁺/Na⁺ Selectivity in K channels and valinomycin: over-coordination versus cavity-size constraints, J. Mol. Biol., 2008, 376(1), 13–22.
33. S. Varma and S. B. Rempe, Multibody Effects in Ion Binding and Selectivity, Biophys. J., 2010, 99(10), 3394–3401.
34. M. Rossi, A. Tkatchenko, S. B. Rempe and S. Varma, Role of methyl-induced polarization in ion binding, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(32), 12978–12983.
35. M. I. Chaudhari and S. B. Rempe, Strontium and barium in aqueous solution and a potassium channel binding site, J. Chem. Phys., 2018, 148(22), 222831.
36. X. Peng, Y. Zhang, H. Chu, Y. Li, D. Zhang, L. Cao and G. Li, Accurate Evaluation of Ion Conductivity of the Gramicidin A Channel Using a Polarizable Force Field without Any Corrections, J. Chem. Theory Comput., 2016, 12(6), 2973–2982.
37. A. M. Salsbury and J. A. Lemkul, Molecular Dynamics Simulations of the c-kit1 Promoter G-Quadruplex: Importance of Electronic Polarization on Stability and Cooperative Ion Binding, J. Phys. Chem. B, 2019, 123(1), 148–159.
38. J. D. Chodera, D. L. Mobley, M. R. Shirts, R. W. Dixon, K. Branson and V. S. Pande, Alchemical free energy methods for drug discovery: progress and challenges, Curr. Opin. Struct. Biol., 2011, 21(2), 150–160.
39. A. Grossfield, P. Ren and J. W. Ponder, Ion Solvation Thermodynamics from Simulation with a Polarizable Force Field, J. Am. Chem. Soc., 2003, 125(50), 15671–15682.
40. L. Rao, Q. Cui and X. Xu, Electronic Properties and Desolvation Penalties of Metal Ions Plus Protein Electrostatics Dictate the Metal Binding Affinity and Selectivity in the Copper Efflux Regulator, J. Am. Chem. Soc., 2010, 132(51), 18092–18102.
41. T. Simonson and C. L. Brooks, Charge Screening and the Dielectric Constant of Proteins: Insights from Molecular Dynamics, J. Am. Chem. Soc., 1996, 118(35), 8452–8458.
42. T. Dudev and C. Lim, Metal Binding in Proteins: The Effect of the Dielectric Medium, J. Phys. Chem. B, 2000, 104(15), 3692–3694.
43. X. You, M. I. Chaudhari, S. B. Rempe and L. R. Pratt, Dielectric Relaxation of Ethylene Carbonate and Propylene Carbonate from Molecular Dynamics Simulations, J. Phys. Chem. B, 2016, 120(8), 1849–1853.
44. P. Ren, J. Chun, D. G. Thomas, M. J. Schnieders, M. Marucho, J. Zhang and N. A. Baker, Biomolecular electrostatics and solvation: a computational perspective, Q. Rev. Biophys., 2012, 45(4), 427–491.
45. L. F. Song, A. Sengupta and K. M. Merz, Thermodynamics of Transition Metal Ion Binding to Proteins, J. Am. Chem. Soc., 2020, 142(13), 6365–6374.
46. M. Zhou and R. MacKinnon, A Mutant KcsA K⁺ Channel with Altered Conduction Properties and Selectivity Filter Ion Distribution, J. Mol. Biol., 2004, 338(4), 839–846.
47. S. Liu, P. J. Focke, K. Matulef, X. Bian, P. Moënne-Loccoz, F. I. Valiyaveetil and S. W. Lockless, Ion-binding properties of a K⁺ channel selectivity filter in different conformations, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(49), 15096–15100.
48. E. Montoya, M. Lourdes Renart, A. Marcela Giudici, J. A. Poveda, A. M. Fernández, A. Morales and J. M. González-Ros, Differential binding of monovalent cations to KcsA: deciphering the mechanisms of potassium channel selectivity, Biochim. Biophys. Acta, Biomembr., 2017, 1859(5), 779–788.
49. S. W. Lockless, M. Zhou and R. MacKinnon, Structural and Thermodynamic Properties of Selective Ion Binding in a K⁺ Channel, PLoS Biol., 2007, 5(5), e121.
50. M. F. Schumaker and R. MacKinnon, A simple model for multi-ion permeation. Single-vacancy conduction in a simple pore model, Biophys. J., 1990, 58(4), 975–984.
51. C. Priest, M. R. VanGordon, C. Rempe, M. I. Chaudhari, M. J. Stevens, S. Rick and S. B. Rempe, Computing Potential of the Mean Force Profiles for Ion Permeation Through Channelrhodopsin Chimera, C1C2, in Channelrhodopsin: Methods and Protocols, ed. R. E. Dempski, Springer US, New York, NY, 2021, pp. 17–28.
52. B. Roux, The calculation of the potential of mean force using computer simulations, Comput. Phys. Commun., 1995, 91(1), 275–282.
53. S. Liu, X. Bian and S. W. Lockless, Preferential binding of K⁺ ions in the selectivity filter at equilibrium explains high selectivity of K⁺ channels, J. Gen. Physiol., 2012, 140(6), 671–679.
54. M. Iwamoto and S. Oiki, Counting Ion and Water Molecules in a Streaming File through the Open-Filter Structure of the K Channel, J. Neurosci., 2011, 31(34), 12180.
55. L. G. Cuello, V. Jogini, D. M. Cortes, A. C. Pan, D. G. Gagnon, O. Dalmas, J. F. Cordero-Morales, S. Chakrapani, B. Roux and E. Perozo, Structural basis for the coupling between activation and inactivation gates in K⁺ channels, Nature, 2010, 466(7303), 272–275.
56. J. Li, J. Ostmeyer, E. Boulanger, H. Rui, E. Perozo and B. Roux, Chemical substitutions in the selectivity filter of potassium channels do not rule out constricted-like conformations for C-type inactivation, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(42), 11145–11150.
57. J. Li, J. Ostmeyer, L. G. Cuello, E. Perozo and B. Roux, Rapid constriction of the selectivity filter underlies C-type inactivation in the KcsA potassium channel, J. Gen. Physiol., 2018, 150(10), 1408–1420.
58. C. Boiteux, D. J. Posson, T. W. Allen and C. M. Nimigean, Selectivity filter ion binding affinity determines inactivation in a potassium channel, Proc. Natl. Acad. Sci. U. S. A., 2020, 202009624.
59. J. A. Lemkul, J. Huang, B. Roux and A. D. MacKerell, An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications, Chem. Rev., 2016, 116(9), 4983–5013.
60. L. G. Cuello, V. Jogini, D. M. Cortes and E. Perozo, Structural mechanism of C-type inactivation in K⁺ channels, Nature, 2010, 466(7303), 203–208.
61. J. Lee, X. Cheng, J. M. Swails, M. S. Yeom, P. K. Eastman, J. A. Lemkul, S. Wei, J. Buckner, J. C. Jeong, Y. Qi, S. Jo, V. S. Pande, D. A. Case, C. L. Brooks, A. D. MacKerell, J. B. Klauda and W. Im, CHARMM-GUI Input Generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM Simulations Using the CHARMM36 Additive Force Field, J. Chem. Theory Comput., 2016, 12(1), 405–413.
62. M. Harger, D. Li, Z. Wang, K. Dalby, L. Lagardère, J.-P. Piquemal, J. Ponder and P. Ren, Tinker-OpenMM: absolute and relative alchemical free energies using AMOEBA on GPUs, J. Comput. Chem., 2017, 38(23), 2047–2055.
63. J. A. Rackers, Z. Wang, C. Lu, M. L. Laury, L. Lagardère, M. J. Schnieders, J.-P. Piquemal, P. Ren and J. W. Ponder, Tinker 8: Software Tools for Molecular Design, J. Chem. Theory Comput., 2018, 14(10), 5273–5289.
64. Y. Shi, Z. Xia, J. Zhang, R. Best, C. Wu, J. W. Ponder and P. Ren, Polarizable Atomic Multipole-Based AMOEBA Force Field for Proteins, J. Chem. Theory Comput., 2013, 9(9), 4046–4063.
65. Z. Wang, Polarizable Force Field Development, and Applications to Conformational Sampling and Free Energy Calculation, Washington University, St. Louis, St. Louis, Missouri, 2018.
66. H. Chu, X. Peng, Y. Li, Y. Zhang, H. Min and G. Li, Polarizable atomic multipole-based force field for DOPC and POPE membrane lipids, Mol. Phys., 2018, 116(7–8), 1037–1050.
67. C. Liu, R. Qi, Q. Wang, J. P. Piquemal and P. Ren, Capturing Many-Body Interactions with Classical Dipole Induction Models, J. Chem. Theory Comput., 2017, 13(6), 2751–2761.
68. J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmüller and A. D. MacKerell, CHARMM36m: an improved force field for folded and intrinsically disordered proteins, Nat. Methods, 2017, 14(1), 71–73.
69. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25.
70. D. R. Bell, R. Qi, Z. Jing, J. Y. Xiang, C. Mejias, M. J. Schnieders, J. W. Ponder and P. Ren, Calculating binding free energies of host–guest systems using the AMOEBA polarizable force field, Phys. Chem. Chem. Phys., 2016, 18(44), 30261–30269.
71. D. Hamelberg and J. A. McCammon, Standard Free Energy of Releasing a Localized Water Molecule from the Binding Pockets of Proteins: Double-Decoupling Method, J. Am. Chem. Soc., 2004, 126(24), 7683–7689.
72. I. Leontyev and A. Stuchebrukhov, Accounting for electronic polarization in non-polarizable force fields, Phys. Chem. Chem. Phys., 2011, 13(7), 2613–2626.
73. A. Grossfield, WHAM: the weighted histogram analysis method, Version 2.0.10.1, http://membrane.urmc.rochester.edu/wordpress/?page_id=126.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc01887f

---