An expanded halogen bonding scale using astatine

Abstract

As a non-covalent interaction, halogen bonding is now acknowledged to be useful in all fields where the control of intermolecular recognition plays a pivotal role. Halogen-bond basicity scales allow quantification of the halogen bonding of referential donors with organic functional groups from a thermodynamic point of view. Herein we present the pK_BAtI basicity scale to provide the community an overview of halogen-bond acceptor strength towards astatine, the most potent halogen-bond donor element. This experimental scale is erected on the basis of complexation constants measured between astatine monoiodide (AtI) and sixteen selected Lewis bases. It spans over 6 log units and culminates with a value of 5.69 ± 0.32 for N,N,N′,N′-tetramethylthiourea. On this scale, the carbon π-bases are the weakest acceptors, the oxygen derivatives cover almost two-thirds of the scale, and sulphur bases exhibit the highest AtI basicity. Regarding the applications of ²¹¹At in targeted radionuclide therapy, stronger labelling of carrier agents could be envisaged on the basis of the pK_BAtI scale.

---

Introduction

A halogen bond (XB) is an attractive and highly directional interaction between the halogen atom X of an R–X compound (XB donor) and a Lewis base B (XB acceptor).¹ XBs have recently been recognized to play an important role in many fields related to molecular recognition,^2–6 as for instance in crystal engineering and the production of liquid crystals,^7,8 in catalyzed reactions in organic synthesis,^9,10 and in chemical biology and medicinal chemistry.^11,12 With respect to the latter applications, halogen bonding has appeared as a reliable tool for designing and optimizing drugs.^13,14 Hence, it is important for chemists to rationalize or anticipate the strength of XB interactions. Because both R–X and B contribute to the XB strength, establishing a universal order is out of reach. The propensity of Lewis bases to form XBs may be discussed by fixing the XB donor, such as ICl, IBr, Br₂, ICN or I₂.¹⁵ In particular, the pioneering diiodine basicity scale pK_BI2 considers the thermodynamic tendency of many substances to interact as XB acceptors with I₂, and this property is measured through the associated complexation constants.¹⁶ Though finer trends may appear with other XB donors, the pK_BI2 scale can be used for semi-quantitative predictions.

Astatine (At, Z = 85) is the heaviest naturally occurring halogen element. By combining liquid/liquid competition experiments and quantum mechanical calculations, we have recently evidenced the first XBs involving At in complexes between astatine monoiodide (AtI) and a few Lewis bases. Among the halogens, we confirmed the highest donating ability of astatine, especially compared to iodine.^17,18 There are fundamental interests to get more experimental data, not only in order to confirm previous findings, but also to increase our understanding of halogen bonding from the perspective of the most potent halogen element, in particular for the refinement of theoretical models.^19,20 On the other hand, the 211 radioisotope of astatine presents potential use in targeted therapy of cancers.^21–23 Practical interests notably lie in the improvement of the radiolabelling strategy for these applications.^24–28 For example, an At-mediated XB can be assumed to explain, in particular, the efficient radiolabelling of bis-(nido-carboranylmethyl)benzene derivatives,²⁹ the latter having been considered as pendant groups for attaching ²¹¹At to carrier biomolecules. Therefore, we proposed to investigate on a more extended and diversified chemical sample the various features (structural, thermodynamic) of XBs involving astatine. One may expect to extend the pK_BI2 scale to astatine species. However, some AtI-mediated complexes show some different behaviors compared to the trends depicted by pK_BI2 (diethyl ether being for instance a significant stronger base compared to hexamethyl benzene according to ref. 17). Moreover, the metallic character of At^30,31 makes its similarity with other halogen elements questionable. In this work, we aim therefore to establish an appropriate basicity scale of At-mediated XBs gathering representative chemical functionalities of Lewis bases, and to look for the strongest XB interactions involving At.

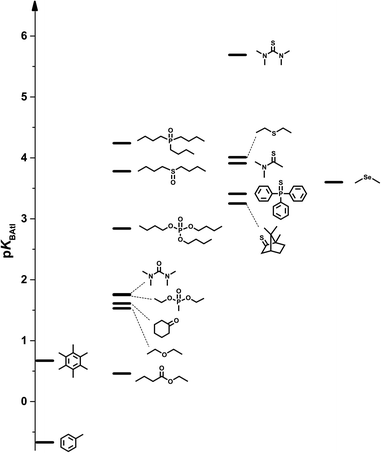
It is worth noting that astatine is considered as an “invisible” element.^21,32 Indeed, it is a short-lived radioelement (t_1/2 ≤ 8.1 h). Only minute quantities can be produced artificially, leading to astatine solutions of concentration typically below 10⁻¹⁰ mol L⁻¹. The conventional spectroscopic tools are therefore inapplicable and most information is obtained by indirect methods. In particular, we successfully evaluated the reactivity of At-compounds by studying the distribution of ²¹¹At radionuclide in biphasic liquid systems.^{17,18,30,31,33} However, a careful selection of the XB donor and acceptors was mandatory to guarantee the occurrence of XB interactions. Among the dihalogens with strong potent donor ability,³⁴ the At₂ and AtF species are still hypothetical. The narrow predominance domains of AtBr and AtCl in aqueous phases and their apparent immiscibility in organic solvents³⁵ prohibit so far any measurements involving these XB donors. As a result, AtI imposes itself as the referential XB donor. Furthermore, the choice of the XB acceptors is severely limited. They must be stable under acidic and oxidizing conditions defining the predominance domain of the AtI species. Therefore, most of the nitrogen Lewis bases, such as amines, pyridines, anilines, guanidines or imines, are experimentally inaccessible owing to their protonation state under the applied conditions. The experimental constraints also imply that the ligands are soluble in organic solvents to promote, upon the formation of XBs, the transfer of astatine species from the aqueous phase to the organic one. Accordingly, we have considered eight new ligands with regard to our previous studies,^17,18 which introduce the following chemical functions: ketone, thioketone, amide, thioamide, urea, thiourea, selenoether and nitrile (Fig. 1).

Fig. 1 The eight Lewis bases experimentally studied in this work.

Results and discussion

Measurements of equilibrium constants

Experimentally, we have tracked the distribution of ²¹¹At in a cyclohexane/aqueous or heptane/aqueous system. A variation of the distribution, arising from a change in experimental conditions, reflects the change of astatine speciation in the biphasic system. The ligand was initially dissolved in the organic phase, while ²¹¹At was doped in the aqueous one. The experimental conditions of the aqueous phase were set to ensure the predominance of the AtI and AtI₂⁻ species (see Section 1.3 in the ESI†). In contrast to AtI₂⁻, AtI can be significantly extracted towards the organic phase,³¹ hence being the only At species able to form an XB complex with the ligand in the organic phase according to eqn (1) (the overlined notation means that these species belong to the organic phase).

The distribution ratio of At (D) is calculated as the ratio of the volumetric activity of ²¹¹At between the organic phase and the aqueous one. In a series of experiments, the ligand concentration in the organic phase is increased, which is supposed to influence the At speciation and thus induce a variation of D.

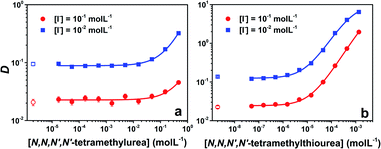
Upon increase of the ligand concentration, the distribution of At can display two typical behaviors. Fig. 2a shows the results for the Lewis base 3, which is also representative of the evolution observed for 1 and 4 (see Fig. S1 in the ESI†). In the low ligand concentration range, the distribution of At is actually ruled by the ratio between AtI and AtI₂⁻ in the aqueous phase and the extraction of AtI in the organic phase; D is thus constant. Then, a sharp increase of D can be observed, which implies the complexation of AtI with ligands in the organic phase, leading to a transfer of At species from the aqueous phase to the organic one. However, as shown in Fig. 2b and S1,† an additional feature appears in the cases of 5, 6 and 7: an inflection point of the distribution vs. concentration curve at the highest ligand concentrations. This behaviour could be rationalized by the hypothesis that B⋯AtI or an additional astatine species is present in the aqueous phase. Because the former possibility is the most probable one under the experimental conditions, as previously shown for other Lewis bases,¹⁷ we here consider that a 1 : 1 complex is also formed in the aqueous phase.

Fig. 2 Astatine distribution ratios as a function of the initial ligand concentration in the organic phase. The hollow symbols indicate data without ligands. (a) Case of N,N,N′,N′-tetramethylurea, solid lines correspond to fitting with model 1 that considers the formation of a 1 : 1 complex between AtI and the ligand in the organic phase; (b) case of N,N,N′,N′-tetramethylthiourea, solid lines are fitting with model 2 that additionally considers the distribution of the 1 : 1 complex in two phases.

The changes of D were reproduced quantitatively from two thermodynamic models of the biphasic system to derive the value of the K_BAtI complexation constant. In this indirect approach, it is noteworthy that we limit as much as possible the number of thermodynamic equilibria involved in the models, i.e., the number of parameters to be adjusted during the fitting. The considered reactions, together with the corresponding analytical expressions of D used to fit the experimental data, are presented in Section 3.3 in the ESI.† The relevance of the chosen models (number of species, equilibrium constants) is notably supported by the results of quantum mechanical calculations (vide infra). For the ligands 2 and 8, the D values remain constant over the whole investigated concentration range, preventing any determination of the complexation constants (see Fig. S2 in the ESI†). Finally, the whole sample of K_BAtI equilibrium constants is reported in Table 1, together with previously determined XB complexation constants.^17,18

Table 1 Equilibrium constants of AtI with different Lewis bases obtained from the distribution ratio measurements and DFT calculations

Lewis base	No.	Solvent	log KBAtI
			Experiment^a	PW6B95/TZVPD	B3LYP/TZVPD
a The values in parenthesis correspond to two standard deviations.
Cyclohexanone	1	Cyclohexane	1.61(37)	1.47	1.66
N,N,N′,N′-Tetramethylurea	3	Heptane	1.76(50)	2.59	2.52
(1R)-(−)-Thiocamphor	4	Heptane	3.25(17)	3.58	3.46
N,N-Dimethyl thioacetamide	5	Heptane	3.91(86)	4.15	4.09
N,N,N′,N′-Tetramethylthiourea	6	Cyclohexane	5.69(32)	5.28	5.02
Dimethyl selenide	7	Cyclohexane	3.60(44)	3.69	3.79
Toluene	9	Cyclohexane	−0.67(24)^17	−0.31	−0.62
Ethyl butanoate	10	Cyclohexane	0.46(56)^17	0.56	0.87
Hexamethylbenzene	11	Cyclohexane	0.67(64)^17	0.92	0.02
Diethyl ether	12	Cyclohexane	1.53(46)^17	0.34	0.15
Diethyl methylphosphonate	13	Cyclohexane	1.75(44)^17	2.41	3.18
Tributyl phosphate	14	Cyclohexane	2.84(26)^17	2.30	3.26
Triphenylphosphine sulfide	15	Cyclohexane	3.41(76)^17	3.81	3.90
Dibutyl sulfoxide	16	Cyclohexane	3.78(40)^17	3.41	3.17
Diethyl sulfide	17	Cyclohexane	4.01(62)^17	3.09	2.87
Tributylphosphine oxide	18	Cyclohexane	4.24(35)^18	4.53	4.51

---

This work also reveals an important advantage of our approach based on biphasic systems. The interactions between the studied compounds can possibly be quantified in the two solvents, and simultaneously. Indeed, for the three strongest Lewis bases, 5, 6 and 7, their interactions with AtI and with water molecules in the aqueous phase become competitive. Therefore, the complexation constants between AtI and these ligands can also be determined in the aqueous phase (K_wBAtI), as detailed in Section 3.2 in the ESI.† The obtained values can be larger (K_wBAtI = 10^3.82 for 7) or smaller (K_wBAtI = 10^3.80 for 5 and 10^4.40 for 6) than the corresponding K_BAtI values. A comprehensive analysis of the influence of the solvent (organic, water) on the strength of the XB interactions becomes feasible, but it goes beyond the scope of this work.³⁶ However, some information can be learned from crude calculations based on an implicit model of water (see Section 2 in the ESI†). The sum of the solvation free energies of AtI and of ligand 5 or 6 exceeds that of the corresponding adduct. Compared to the organic conditions, the adduct in the aqueous phase is therefore destabilized with respect to the reactants and the complexation constant is reduced. The solvation free energy in water of 7 is much weaker than the ones of 5 and 6, which (i) can be justified by the presence of nitrogen functions in 5 and 6, and (ii) is corroborated by a partition coefficient between organic and aqueous phases much bigger for 7 (10^1.40±0.16, see Section 1 in the ESI†) than for 5 and 6 (10^{−0.13±0.01} and 10^{−0.37±0.04}, respectively). The weakest solvation free energy of 7 may explain the relative stabilization of its adduct with AtI when solvated in water, and the increased complexation constant. The K_wBAtI constants can also be compared to constants measured in aqueous phases for the formation of other adducts of AtI, e.g. IAtBr⁻ as the heaviest-known trihalogen species. This species can be viewed as an XB adduct between AtI and Br⁻,³⁷ and the corresponding equilibrium constant in water (10^1.4±0.3)³¹ is weaker by more than two orders of magnitude. This outcome is probably the consequence of the much stronger solvation free energy for the small spherical Br⁻ anion compared to neutral ligands 5–7, making IAtBr⁻ relatively destabilized with respect to the other adducts.

Identification of XB complexes

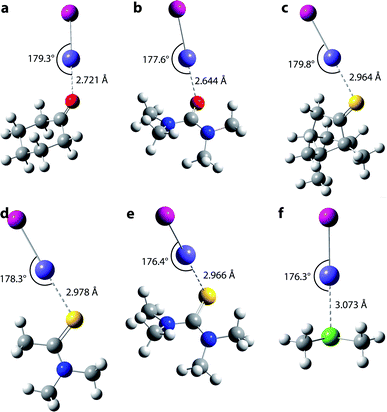
As the experimental data alone do not allow characterizing the species formed with AtI at the molecular scale, we establish their nature by comparing the results of theoretical calculations with the measured equilibrium constants. Relativistic effects (including the spin–orbit coupling) significantly affect the chemical bonds involving astatine. A recent benchmark study focusing on At-compounds has demonstrated that accurate equilibrium constants can be predicted by two-component relativistic density functional theory (DFT).³⁸ Among the 36 DFT functionals tested, the B3LYP and PW6B95 hybrid functionals clearly emerged among the best performing ones. Moreover, these two functionals have also been validated as reliable for investigating compounds stabilized by At-mediated halogen bonds,^17,18,39 notably according to results obtained with the gold-standard CCSD(T) method.^19,20,34 For the studied interactions between AtI and the 16 Lewis bases, the structures have been optimized using double zeta quality basis sets augmented with polarization and diffuse functions (referred to as “AVDZ”). The equilibrium constants have been determined via single-point calculations using triple zeta quality basis sets (referred to as “TZVPD”). The computational methodology is detailed in Section 2 in the ESI.†

As an interhalogen, AtI may form two types of XB interaction, one mediated by the astatine atom and the other one through the iodine atom. A descriptor commonly used to characterize the XB donating ability of a given donor is V_S,max, that is a local maximum value of the electrostatic potential at the molecular surface (molecular electrostatic potential, MEP).² Fig. S3a in the ESI† displays the calculated MEP for AtI at the PW6B95/TZVPD level of theory. Two positive regions are observed, one on the astatine side and the other one on the iodine side. Although astatine presents a significantly higher V_S,max value (180.4 kJ mol⁻¹) than iodine (71.3 kJ mol⁻¹), we have nevertheless investigated the two types of interaction with the selected ligands. Fig. 3 displays the most-stable structures computed for the interactions between AtI and the ligands 1, 3–7, while Fig. S4 in the ESI† presents the structures obtained with the previously investigated ligands (9–18). Whatever the B⋯AtI system, the interaction between the two molecular fragments (AtI and B) is mediated by the astatine atom in the most stable structure. The structures stabilized by an interaction with the iodine atom are significantly less stable, for instance representing less than 7% of the whole population of complexes formed with toluene according to the Boltzmann distribution calculated at the PW6B95/TZVPD level of theory. Halogen bonding with the iodine atom of AtI is a minor phenomenon. Focusing on the At-mediated interactions with the ligands 1 and 3–7, they are all predicted with distances shorter than the sum of the van der Waals radii of the two involved atoms,⁴⁰ by 22% for 7 up to 25% for 3 (see normalized interaction distances r_XB from Table S3 in the ESI†). Furthermore, the angle formed between each ligand and AtI is close to 180°, the largest deviation being 3.7° for 7. These structural features are typical of halogen bonding. Hence, the theoretical calculations suggest that the interactions between AtI and the newly studied Lewis bases are stabilized by At-mediated XBs, as it was previously established for 9–18.^17,18

Fig. 3 Calculated structures (PW6B95/AVDZ) for the most stable conformer of each species corresponding to the interaction between AtI and the newly studied Lewis bases: (a) cyclohexanone, (b) N,N,N′,N′-tetramethylurea, (c) (1R)-(−)-thiocamphor, (d) N,N-dimethyl thioacetamide, (e) N,N,N′,N′-tetramethylthiourea and (f) dimethyl selenide. Atoms' colour code: purple for At, pink for I, red for O, yellow for S, green for Se, grey for C and white for H.

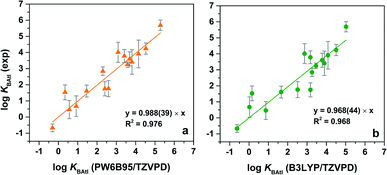
It has previously been shown that the equilibrium constants K_BAtI can be accurately determined,^17,18 provided that the relativistic DFT calculations are carried out on isodesmic-like reactions as detailed in Section 2.2 in the ESI.† If 12 was chosen as the reference ligand, the set of the obtained complexation constants for the 16 B⋯AtI complexes is however translated according to the experimental values; the resulting values are given in Table 1. The PW6B95/TZVPD results are compared with the experimental ones in Fig. 4a. A strong relationship is established. The linear regression slope is very close to one (0.988), which constitutes a first clue that the property calculated corresponds to that measured (i.e., K_BAtI equilibrium constants). The associated coefficient of determination R² (0.976) is also quite good. Furthermore, the mean absolute deviation (MAD) between the experimental and computed log K_BAtI values (0.45) is smaller than the average experimental uncertainty (0.47). The calculated values at the B3LYP/TZVPD level of theory also fairly match the experimental data (R² = 0.968 and MAD = 0.55, see Fig. 4b). Thus, concerning the interactions between AtI and the ligands 1, 3–7, 9–18, the nature of the predicted most stable complexes and the agreement between the calculated K_BAtI constants and the measured property allow us to conclude that the experimentally studied species are At-mediated XB complexes.

Fig. 4 Correlation between experimental and calculated log K_BAtI values at the (a) PW6B95/TZVPD and (b) B3LYP/TZVPD levels of theory. The numbers in parenthesis in the analytical expression correspond to one standard deviation.

The pK_BAtI basicity scale

Based on these XB complexation constants, an astatine monoiodide basicity scale, pK_BAtI, can be built from eqn (2) in which K_BAtI is the equilibrium constant measured in an alkane solvent at 294 ± 3 K.

pK_BAtI = log₁₀(K_BAtI) (2)

Gathering all the chemical functionalities available within the experimental limitations, the pK_BAtI scale spans over 6 log units, as illustrated in Fig. 5. 6 is at the top of this scale with a pK_BAtI value of 5.69. It must be stressed that nitrogen-based Lewis bases are unfortunately absent from this experimental dataset; even 8 which shows a low pK_a value⁴¹ did not lead to any variations of the astatine distribution under our experimental conditions. Scanning the established scale, the carbon π-bases exhibit the weakest XB accepting ability, with pK_BAtI from −0.67 to 0.67. The oxygen acceptor atomic sites are generally stronger XB bases, except the ester derivative 10. Reaching a pK_BAtI value of 4.24 with the phosphine oxide compound 18, the oxygen family, therefore, covers almost 60% of this basicity scale. The sulphur family gathers even stronger XB acceptors, the scale culminating with the thiourea 6. Within the ketone (1vs.4), urea (3vs.6) and ether (12vs.17) families, the sulphur derivatives are systematically found to be stronger acceptors than the oxygen compounds with several orders of magnitude. These trends are fully supported by the computed log K_BAtI values, clearly indicating the much better affinity of sulphur than oxygen for the At-containing XB donor. Conversely, selenoether 7 shows a weaker XB basicity (3.60) than the corresponding thioether 17 (4.01), which is not in line with the DFT calculations.

Fig. 5 Astatine monoiodide basicity chart for common organic functional groups.

Note that the trends which emerge from the pK_BAtI basicity scale can hardly be anticipated from the calculated structural parameters. No correlation exists in particular with the lengths of the interaction distances (R² = 0.019), or even with the normalized interaction distances (r_XB in Table S3†). However, the two carbon π-bases exhibit XBs with the largest deviations from linearity (6.3° and 7.8°) in line with their weak XB accepting ability. In addition, the lengthening of the At–I bond upon complexation is the most important for sulphur bases bearing an sp² S atom, with a maximum of 0.092 Å for 6, in agreement with the thermodynamic trends.

Finally, the pK_BAtI scale of astatine basicity can be compared to the pK_BI2 scale of iodine basicity. As shown in Fig. 6, there is an overall linearity between both sets, with R² = 0.916, supporting again the interactions with AtI through halogen bonding. For 15 Lewis bases among 16, the pK_BAtI value is larger than the pK_BI2 value, which can only be explained by considering a stronger donor ability of At among the halogen elements. Indeed, the propensity of a halogen atom to form XB interactions is commonly assumed to increase with increasing atom polarizability and decreasing atom electronegativity.^2,42 This is supported in addition by the calculated MEP for AtI and I₂. Fig. S3† shows that the value of V_S,max on the At side of AtI, 180.4 kJ mol⁻¹, is significantly higher than that calculated for diiodine, 129.1 kJ mol⁻¹. The comparison to the I₂ donor may also be extended to structural aspects. For instance, the interaction distances here calculated with the AtI donor (Table S3†) can be compared with those known between diiodine and the same or representative XB acceptors. Some interaction distances measured in crystallographic XB complexes with I₂ and observed in the Cambridge structural database⁴³ are gathered in Table S4 in the ESI.† Since the iodine atom is smaller than astatine, it is not unexpected that the lengths of the interactions involving iodine are shorter. This is more surprising if we consider, for the same type of acceptor site, the normalized interaction distances. While distances are weighted by the sum of the van der Waals radii of the two involved atoms, r_XB is 0.722 for the interaction between I₂ and 15, and 0.783 when AtI mediates the interaction. This trend holds for other sulphur bases as for the selenoether 7. Such finding might appear at first sight in contradiction with the stronger donor ability of AtI, but keep in mind that in vacuo calculated values are assessed with respect to crystal distances that endure the packing effects.

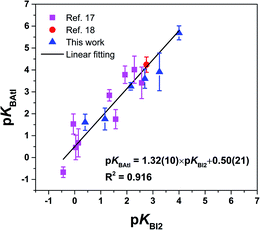Fig. 6 Relationship between the pK_BAtI and pK_BI2 scales for the 16 selected Lewis bases. The numbers in parenthesis in the analytical expression correspond to one standard deviation.

Other interhalogen donors can be indirectly compared with the AtI donor via the pK_BI2 scale. For instance, the pK_BICl and pK_BIBr scales compared to the pK_BI2 scale give linear relationships expressed as pK_BICl = 1.79 × pK_BI2 + 1.42 and pK_BIBr = 1.53 × pK_BI2 + 0.87,^15,16 which lie above the line formed by the pK_BAtI scale (Fig. 6). We can deduce that the donor ability among interhalogens follows the order: I₂ < AtI < IBr < ICl. The ordering between the iodine donors, I₂, IBr and ICl, is in line with the general consensus that more electron-withdrawing groups R, bound to the electrophilic halogen atom X, will lead to more stable complexes of R–X with Lewis bases.^2,42 Conversely, the position of AtI vs. IBr and ICl could not have been anticipated since the donor atom X and the electron-withdrawing group R are both different. Even the calculated values of V_S,max for these XB donors are useless (see Fig. S3 in the ESI†). One may wonder if the pK_BAtI scale encodes different information from that provided by other Lewis basicity scales that are already known, and especially hydrogen bonding scales. However, it has been shown that the pK_BI2 scale, which is in overall linearly correlated with the pK_BAtI scale, as seen above, is orthogonal or quasi-orthogonal to these scales.¹⁶ For instance, the 4-fluorophenol pK_BHX hydrogen-bond basicity scale explains only 36% (on a sample of 265 points) of the variance of the pK_BI2 scale. Although correlations with pK_BAtI could be established within given families of compounds (e.g., oxygen functionalities, or their thio-derivatives), a comprehensive understanding of this behaviour would need specific investigations beyond the scope of this work.

Conclusions

This work is intended to build the very first experimental and homogeneous scale of halogen-bonding basicity specific to astatine, the most potent XB donor atom. The pK_BAtI scale is based on measured equilibrium constants of XB interactions between 16 representative Lewis bases and a reference donor, AtI. This scale, including S, O, Se and π-based ligands, spans over 6 log units and culminates at 5.69 with N,N,N′,N′-tetramethylthiourea. Considering the experimental challenge of studying astatine chemistry, which severely limits the attempts to broaden this scale, it is essential to have powerful tools like the pK_BAtI scale to guide the design of original At-compounds. Regarding the use of ²¹¹At in targeted radionuclide therapy, the propensity of astatine to form strong XBs can help to strengthen the labelling of carrier agents. It is also disclosed that XB interactions can be simultaneously quantified in different solvents thanks to the presented methodology. The pK_BAtI values obtained in an organic phase can be compared to equilibrium constants of At-mediated XBs in the aqueous phase. First, it enables chemists to probe the influence of the solvent, and second, to estimate the strength of XB interactions in media other than alkane solvents. Beyond the direct interest of this scale, the presented methodology can be useful to characterize other XB types today non-quantifiable in the aqueous and/or organic phase (possibly due to the lack of a spectroscopic probe). I-mediated XB complexes can be evaluated for instance by combining studies of the distribution of iodine radioisotopes in biphasic media and theoretical calculations.

Data availability

The data that support the findings of this study are available. Additional information can be requested from the corresponding author upon reasonable request.

Author contributions

Conceptualization, R. M., J. G., J. C., N. G.; methodology, L. L., R. M., G. M., J. G., J. C., N. G.; investigation, L. L., S. R., C. G. P., J. C., N. G.; data curation, L. L., R. M., G. M., J.-Y. L. Q., J. G., J. C., N. G.; writing—original draft preparation, L. L., J. C., N. G.; writing—review and editing, all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported in part by grants from the French National Agency for Research called ‘Investissements d'Avenir’, Equipex Arronax-Plus (ANR-11-EQPX-0004), Labex IRON (ANR-11-LABX-18-01) and ISITE NExT (ANR-16-IDEX-0007). The work was carried out using HPC resources from CCIPL (Centre de Calcul Intensif des Pays de la Loire). The authors acknowledge the GIP ARRONAX for the production of At-211.

Notes and references

1. G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713.
2. G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601.
3. E. Persch, O. Dumele and F. Diederich, Angew. Chem., Int. Ed., 2015, 54, 3290–3327.
4. G. Berger, J. Soubhye and F. Meyer, Polym. Chem., 2015, 6, 3559–3580.
5. B. Li, S.-Q. Zang, L.-Y. Wang and T. C. W. Mak, Coord. Chem. Rev., 2016, 308, 1–21.
6. C. C. Robertson, J. S. Wright, E. J. Carrington, R. N. Perutz, C. A. Hunter and L. Brammer, Chem. Sci., 2017, 8, 5392–5398.
7. H. L. Nguyen, P. N. Horton, M. B. Hursthouse, A. C. Legon and D. W. Bruce, J. Am. Chem. Soc., 2004, 126, 16–17.
8. A. Mukherjee, S. Tothadi and G. R. Desiraju, Acc. Chem. Res., 2014, 47, 2514–2524.
9. D. Bulfield and S. M. Huber, Chem.–Eur. J., 2016, 22, 14434–14450.
10. L. Carreras, M. Serrano-Torné, P. W. N. M. van Leeuwen and A. Vidal-Ferran, Chem. Sci., 2018, 9, 3644–3648.
11. R. Wilcken, M. O. Zimmermann, A. Lange, A. C. Joerger and F. M. Boeckler, J. Med. Chem., 2013, 56, 1363–1388.
12. P. Auffinger, F. A. Hays, E. Westhof and P. S. Ho, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16789–16794.
13. Z. Xu, Z. Yang, Y. Liu, Y. Lu, K. Chen and W. Zhu, J. Chem. Inf. Model., 2014, 54, 69–78.
14. Y. Lu, Y. Liu, Z. Xu, H. Li, H. Liu and W. Zhu, Expert Opin. Drug Discovery, 2012, 7, 375–383.
15. L. Christian and J.-F. Gal, Lewis Basicity and Affinity Scales: Data and Measurement, John Wiley & Sons Ltd, 2010.
16. C. Laurence, J. Graton, M. Berthelot and M. J. El Ghomari, Chem.–Eur. J., 2011, 17, 10431–10444.
17. N. Guo, R. Maurice, D. Teze, J. Graton, J. Champion, G. Montavon and N. Galland, Nat. Chem., 2018, 10, 428–434.
18. L. Liu, N. Guo, J. Champion, J. Graton, G. Montavon, N. Galland and R. Maurice, Chem.–Eur. J., 2020, 26, 3713–3717.
19. N. Galland, G. Montavon, J.-Y. Y. Le Questel and J. Graton, New J. Chem., 2018, 42, 10510–10517.
20. S. Sarr, J. Graton, G. Montavon, J. Pilmé and N. Galland, ChemPhysChem, 2020, 21, 240–250.
21. D. S. Wilbur, Nat. Chem., 2013, 5, 246.
22. G. Vaidyanathan and M. Zalutsky, Curr. Radiopharm., 2008, 1, 177–196.
23. F. Guérard, J.-F. Gestin and M. W. Brechbiel, Cancer Biother.Radiopharm., 2013, 28, 1–20.
24. D. Wilbur, Curr. Radiopharm., 2008, 1, 144–176.
25. D. Teze, D. C. Sergentu, V. Kalichuk, J. Barbet, D. Deniaud, N. Galland, R. Maurice and G. Montavon, Sci. Rep., 2017, 7, 1–9.
26. T. Ayed, J. Pilmé, D. Tézé, F. Bassal, J. Barbet, M. Chérel, J. Champion, R. Maurice, G. Montavon and N. Galland, Eur. J. Med. Chem., 2016, 116, 156–164.
27. K. Fujiki, Y. Kanayama, S. Yano, N. Sato, T. Yokokita, P. Ahmadi, Y. Watanabe, H. Haba and K. Tanaka, Chem. Sci., 2019, 10, 1936–1944.
28. M. Berdal, S. Gouard, R. Eychenne, S. Marionneau-Lambot, M. Croyal, A. Faivre-Chauvet, M. Chérel, J. Gaschet, J.-F. Gestin and F. Guérard, Chem. Sci., 2021, 12, 1458–1468.
29. D. S. Wilbur, M.-K. Chyan, D. K. Hamlin, B. B. Kegley, R. Risler, P. M. Pathare, J. Quinn, R. L. Vessella, C. Foulon, M. Zalutsky, T. J. Wedge and M. F. Hawthorne, Bioconjugate Chem., 2004, 15, 203–223.
30. J. Champion, C. Alliot, E. Renault, B. M. Mokili, M. Chérel, N. Galland and G. Montavon, J. Phys. Chem. A, 2010, 114, 576–582.
31. N. Guo, D.-C. Sergentu, D. Teze, J. Champion, G. Montavon, N. Galland and R. Maurice, Angew. Chem., Int. Ed., 2016, 55, 15369–15372.
32. G.-J. Meyer, J. Labelled Compd. Radiopharm., 2018, 61, 154–164.
33. D.-C. Sergentu, D. Teze, A. Sabatié-Gogova, C. Alliot, N. Guo, F. Bassal, I. Da Silva, D. Deniaud, R. Maurice, J. Champion, N. Galland and G. Montavon, Chem.–Eur. J., 2016, 22, 2964–2971.
34. J. Graton, S. Rahali, J.-Y. Le Questel, G. Montavon, J. Pilmé and N. Galland, Phys. Chem. Chem. Phys., 2018, 20, 29616–29624.
35. J. Champion, M. Seydou, A. Sabatié-Gogova, E. Renault, G. Montavon and N. Galland, Phys. Chem. Chem. Phys., 2011, 13, 14984.
36. C. C. Robertson, R. N. Perutz, L. Brammer and C. A. Hunter, Chem. Sci., 2014, 5, 4179–4183.
37. C. Gomez Pech, P. A. B. Haase, D. C. Sergentu, A. Borschevsky, J. Pilmé, N. Galland and R. Maurice, J. Comput. Chem., 2020, 41, 2055–2065.
38. D.-C. Sergentu, G. David, G. Montavon, R. Maurice and N. Galland, J. Comput. Chem., 2016, 37, 1345–1354.
39. S. Sarr, J. Graton, S. Rahali, G. Montavon and N. Galland, Phys. Chem. Chem. Phys., 2021, 23, 4046–4074.
40. M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806–5812.
41. D. D. Perrin, Dissociation Constants of Organic Bases in Aqueous Solution, Butterworths, London, 1965.
42. M. H. Kolář and P. Hobza, Chem. Rev., 2016, 116, 5155–5187.
43. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.

---

Footnote

† Electronic supplementary information (ESI) available: A description of the experimental and the computational methodologies, and many tables and figures reporting additional data. See DOI: 10.1039/d1sc02133h

---