Comment on “Uncommon structural and bonding properties in Ag₁₆B₄O₁₀” by A. Kovalevskiy, C. Yin, J. Nuss, U. Wedig, and M. Jansen, Chem. Sci., 2020, 11, 962

Abstract

A thorough systematic study of the Electron Localization Function (ELF) in fcc silver metal, the deficient vacant-type Ag₁₆□₄ structure, and the Ag₁₆B₄O₁₀ title compound of the Chem. Sci., 2020, 11, 962 edge article leads to a further understanding of the sub-valent characteristics of silver in the silver borate compound. By visualizing the process in three consecutive steps, (fcc)_eq-Ag → (fcc)_ex-Ag → Ag₁₆□₄ → Ag₁₆B₄O₁₀, the electron reduction of Ag atoms can be traced to be due to (i) the expansion (ex) of the host metallic array from its equilibrium (eq) geometry and (ii) the vacancy creation and subsequent insertion of guest borate clusters. Our ELF analysis also allows us to identify to what extent metallic features remain in the title compound, providing an alternative explanation of why Ag₁₆B₄O₁₀ is not a conductor whereas pure silver is.

---

1 Introduction

As occurs with the chemical bond, the terms valence and oxidation state enclose elusive concepts that are very useful in everyday chemistry but it is difficult to establish a unique agreed definition for them.¹ These concepts lack both the possibility of being measured in the laboratory and a quantum-mechanical operator allowing their calculation. In this context, sub-valent compounds tend to exhibit anomalous compositions and they are compounds where the bonding of one of the atoms involves fewer electrons than expected from the electron counting of its valence shell. In the solid state, sub-valence is associated with oxidation numbers lower than nominal values for any of the atomic constituents of the compound.¹

According to a regular composition, one would expect silver atoms to participate in the electron counting of a chemical bonding network with one electron, that in its 5s valence shell. In the Ag₁₆B₄O₁₀ title compound of the edge article commented here (ref. 2), however, only 8 electrons are needed to account for the charge of the [B₄O₁₀]⁸⁻ electron-precise supertetrahedral unit, which forces silver atoms in this compound to play a sub-valent role (only half electron from each Ag atom is required) to fulfill the observed chemical formula.

The sub-valent behavior of silver is not exclusive to this compound (see for example earlier discussions in ref. 3–5) and has been extensively investigated by the corresponding author of the article commented here who identified the existence of local clustering of Ag atoms hosting electron pairs as a general “new bonding pattern” (see ref. 2 and 6 and references therein).

In this comment, we provide a consistent interpretation of the chemical bonding network of Ag₁₆B₄O₁₀ that contains analogies but also qualitative and quantitative differences with respect to the discussion presented in ref. 2. These differences are essential for the understanding of the structure and bonding in Ag₁₆B₄O₁₀ and are far-reaching since they can be extended to other silver oxide crystals such as Ag₇Pt₂O₇.⁶

The idea that metallic behavior is partially maintained in Ag₁₆B₄O₁₀ is in part suggested in the discussion of ref. 2, where it is pointed out that silver sub-valent oxides present Ag(I) subarrays resembling the structure of the pure fcc-silver metal. However, in our view, it was not explicitly applied to interpret the sub-valent nature of the title compound. To investigate the residual metallic bonding properties of Ag₁₆B₄O₁₀, we propose to follow the electron counting associated with the metallic subarray from the pure silver metal to the borate compound.

Bearing this idea in mind, we provide an alternative interpretation of the bonding network of Ag₁₆B₄O₁₀ supported by a topological analysis of the Electron Localization Function (ELF) in (i) the Ag metal fcc structure, (ii) the Ag deficient fcc sub-array after removal of the [B₄O₁₀] units, and (iii) the Ag₁₆B₄O₁₀ crystal structure. By performing these topological analyses, we will be able to check whether metallic silver features are maintained or not in the title compound, and to what extent.

Our results clearly reveal that [B₄O₁₀]⁸⁻ behaves as an independent anion in agreement with the analysis in ref. 2. The equivalence of [B₄O₁₀]⁸⁻ with the well-known P₄O₁₀ molecule was also justified resorting to the extended Zintl–Klemm concept in ref. 7. However, we found differences with respect to the interpretation of ref. 2 in the peculiarities of the silver subarray. To solve the electron-excess, electron pairs confined in four approximate tetrahedral voids of the Ag₁₆ silver fcc-distorted unit cell are proposed in ref. 2. Although this proposal successfully explains the observed semiconducting behavior and the diamagnetic ordering of this compound, the limited analysis of ELF values at the attractor positions carried out in ref. 2 is not enough to suggest that one electron pair is localized in each of these voids.

2 ELF analysis in fcc silver metal, and defective silver-vacant and silver borate compounds

By combining VASP electronic structure calculations⁸ within the DFT-GGA-PBE approach⁹ with critic2 topological searches of critical points and basin electron density integrations,¹⁰ we perform an extensive ELF analysis in the Ag-related structures detailed in the three subsections below (see computational details in the ESI†). Although other methods such as ELI-D better describe the dynamic electronic correlation and could provide further insight into electron poor metal systems,¹¹ ELF analysis reliably accounts for the valence description of inorganic materials and metals,^12–14 and is simple and illustrative enough to analyze the bonding properties of the title compound.

2.1 fcc pure silver metal

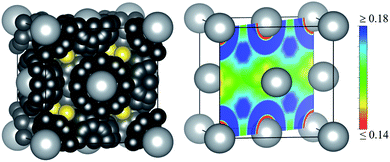
There are three main results in the ELF analysis of pure silver metal that are relevant to understand the structure of Ag₁₆B₄O₁₀. The first one concerns the localization of the ELF attractors associated with the valence electrons of fcc-silver at its room conditions equilibrium geometry (a = 4.146 Å). Two sets of valence attractors become apparent. The first set corresponds to d-electrons located not further away than 1.0 Å from the Ag nuclear positions (small black balls in Fig. 1 (left)) with an ELF value of η = 0.27. The large number of them is a typical consequence of the crystal environment. More interesting are s-valence attractors easily identified at the eight tetrahedral interstices (8c positions) of the fcc unit cell (yellow balls in Fig. 1 (left)). They appear around 1.84 Å away from the four neighbour Ag nuclei with η = 0.20. Electron density integrations inside each of these tetrahedral voids result in 0.53e. This yields a total of 4.24 electrons in the whole unit cell, a value that is consistent with the valence oxidation state (N^v_ox) of +1 for metallic silver, where N^v_ox is defined in this context considering the number of valence electrons hosted in the lattice interstices. This definition is different from the standard N_ox definition which obviously yields a zero value for a pure metal.

Fig. 1 (left) Valence ELF attractors in the fcc pure silver metal structure. Black and yellow balls stand for d- and s-type attractors. Grey balls represent silver atoms. (right) 2D-ELF heat-map plot along the (110) plane highlighting the d-shell structure of the silver atoms and the tetrahedral ELF maxima.

The second ELF feature is that the topology is qualitatively the same when we expand the fcc silver unit cell to the volume corresponding to that of the fcc distorted silver sub-lattice hosting the B₄O₁₀ cluster (a = 4.251 Å). The relevant eight ELF attractors still appear at the tetrahedral positions. However, and in concordance with the generalized stress–redox correlation,¹⁵ the electron population inside the basins of the tetrahedral voids decreases at this expanded sub-lattice. This is a consequence of the lower overlap between the electron density clouds of neighbouring atoms when their internuclear distance increases. In fact, the electron density integration within the ELF tetrahedral-attractor basins estimates now 0.38e in each void. Thus, using these valence electrons as before to evaluate the valence oxidation state of silver, we obtain N^v_ox(Ag) = +0.76 for the expanded fcc-Ag lattice at the same volume of the Ag₁₆B₄O₁₀ compound. Under this perspective, the expanded fcc-Ag already behaves as sub-valent.

Finally, we find that all the ELF attractors at the tetrahedral voids of the fcc-Ag structure (regardless of the unit cell parameter) belong to the same ELF domain. This means that the ELF values at the maxima are linked through ELF first-order saddle points or basin interconnecting points (bips) forming a three dimensional (3D) chemical entity usually called a superbasin. This is the typical ELF picture of metals.¹² The small difference between the ELF value at the attractor (att) and at the bip reflects a highly delocalized nature of the electrons in the 3D-superbasins. Specifically, η_att = 0.20 and 0.19, and η_bip = 0.17 and 0.16 in the room conditions and in the expanded fcc-Ag structures, respectively. The concept of ELF superbasins is not new and has been employed many times to describe the merging of ELF basins belonging to the same atom (see for example ref. 13 and 14) or belonging to different atoms.^16,17 Being a key concept in our alternative interpretation, it is useful to realize that these superbasins constitute 3D channels in the real space that account for the electrical conductivity of metals, as first noted by Silvi and Gatti.¹² In the fcc-Ag structure, the electrical circuit originating from the connection of the tetrahedral ELF attractors belonging to the valence superbasin is easily visualized in Fig. S1.†

2.2 Defective silver-vacant structure

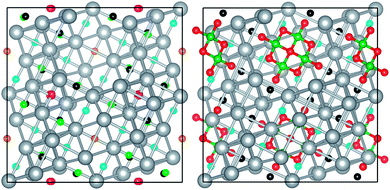
Let us now consider the Ag₁₆□₄ host structure with the same lattice parameters as in Ag₁₆B₄O₁₀. Ag–Ag nearest neighbour distances range from 2.76 Å to 3.23 Å, with an average value of 3.05 Å, pretty close to the Ag–Ag shortest distance of 3.01 Å in the expanded fcc-lattice. Breaking the symmetry of the fcc structure by replacing with a vacancy 4 out of the 20 tetrahedral Ag₄ units of the unit cell (Z = 4) makes tetrahedral attractors not equivalent any more. Up to five different types of ELF attractors identified with different colors in Fig. 2 (left) are found. Among then, four have a multiplicity of 16, whereas the other (cyan) has a multiplicity of 4.

Fig. 2 ELF attractors in the defective Ag₁₆□₄ structure (left) and in the Ag₁₆B₄O₁₀ title compound (right). Colors of small balls denote non-equivalent attractors. Grey, green, and red balls stand for silver, boron, and oxygen atoms, respectively.

Despite the symmetry breaking, there are particular ELF features in the defective silver-vacant structure that resemble the description obtained for the expanded fcc-lattice. For example, the ELF at the tetrahedral maxima keeps similar values around η_att = 0.20 and the average basin population (0.40e) is only a little bit higher that the 0.38e value found in the expanded pure metal. However, basin electron populations oscillate now between 0.50e and 0.30e (see Table S1†). This range of values illustrates how relevant is the position of the attractor relative to the vacancy. Vacancies not only break the symmetry of the structure but also interrupt the connectivity between attractors.

The existence of vacancies reduces the number of available tetrahedral voids which are the only positions where ELF attractors tend to be located in these silver compounds. We observe that this reduction is not balanced by an overall increase of the basin electron populations (see Table S1†). Thus, a lower valence oxidation state of the Ag atoms is produced. Using the basin electron populations, the average valence oxidation state in the defective Ag-vacant structure was found to be N^v_ox(Ag) = +0.42. These values evidence an increase of the sub-valent characteristics of the defective silver-vacant structure.

2.3 Silver borate structure

In the Ag₁₆B₄O₁₀ title compound, ELF analysis allows us to differentiate an ELF domain for the [B₄O₁₀]⁸⁻ unit with equivalent results to those in ref. 2. Attractors between B atoms and the bridge or terminal oxygens are detected, as well as lone pair superbasins containing up to three ELF maxima (see Fig. S2†), reinforcing the structural similarity to the (valence) isoelectronic P₄O₁₀ molecule previously emphasized in ref. 2 and 7.

When the ELF map of the host silver subarray is examined, the same attractors at the tetrahedral voids as in ref. 2 are found with ELF values around 0.25 (black balls of Fig. 2). We found analogies only up to this point with the results of ref. 2. We understand that to be conclusive with respect to the chemical bonding and the structure of the new silver oxide compound, its bonding network should be compared with that of pure silver and the deficient silver structure. As observed in Fig. 2 (right), only two types of attractors at tetrahedral voids (instead of one as in fcc Ag and five in Ag₁₆□₄) are identified. The presence of borate clusters destroys and empties some of the basins at the tetrahedral voids close to the oxygen positions. Oxygen atoms act as electron sinks of the otherwise populated basins in the defective silver-vacant structure. Such an electron transfer to the oxygen atoms reflects an ionic interaction between the two fragments in the Ag₁₆B₄O₁₀ compound. In particular, pink, orange, and green attractors with distances shorter than 2.75 Å to oxygen atoms are not seen in the silver borate compound, whereas only black and cyan attractors beyond 3 Å of any oxygen atom still are present in this compound.

Electron density integrations within each of the basins of these two attractors lead to 0.71e and 0.36e, respectively. We notice that it is the Ag₄ tetrahedra associated with the basins that are more populated where some Ag–Ag distances are especially shorter than those in pure silver metal. Nevertheless, these values show that the number of electrons hosted in these tetrahedral voids is definitely lower than 2, questioning the presence of pairwise electrons. In this way, the sub-valent nature of Ag₁₆B₄O₁₀ might be considered to be inherited from the Ag₁₆□₄ host lattice since we obtain N^v_ox(Ag) = +0.40, almost coincident with the value found in the defective silver-vacant structure.

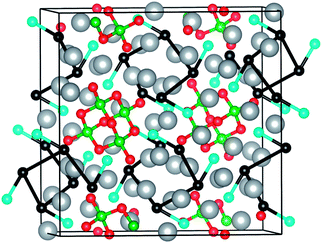
Besides the quantitative picture provided by the electron density integration, the most interesting result of this third ELF analysis comes from the identification of different independent valence superbasins associated with the silver subarray of Ag₁₆B₄O₁₀. These superbasins are equivalent and result from the bips connecting black–black (η_bip ≃ 0.16) and black–cyan (η_bip ≃ 0.19) attractors of values η_att ≃ 0.25 (black) and ≃ 0.23 (cyan). The ELF profile displaying all the possible connections between black and cyan silver attractors is shown in Fig. S3.† Focusing just on one of these equivalent superbasins, we observe that all black attractors are connected with one cyan and two black attractors forming a 1D infinite coil-like chain of helical symmetry with ramifications ending at the cyan attractors. There are four of these electrical circuits per unit cell hosting the electrons delocalized among the tetrahedral voids and running along the c axis of the crystal as shown in Fig. 3. The existence of these unconnected superbasins is used below to explain the different behavior of pure silver metal and the borate compound with respect to metallicity.

Fig. 3 View along the c-axis of 1D-circuits represented by black lines connecting ELF valence attractors (cyan and black small balls) in Ag₁₆B₄O₁₀. Grey, green, and red balls stand for silver, boron, and oxygen atoms, respectively.

3 Discussion and conclusions

We have seen that, in the fcc-silver metal, s-type ELF attractors only appear inside the tetrahedral voids. This fact is noted both in the defective and silver borate compounds, and points towards a general behaviour that could be used to explain other silver sub-valent compounds. Tetrahedral attractors allow the formation of chemical entities called superbasins which identify regions where the metallic bonding properties are maintained. Interestingly, in the pure fcc-silver metal a 3D superbasin is spread out along the whole crystal structure, whereas in the borate compound, it splits up into four independent 1D superbasins per unit cell resembling infinite circuits of helical symmetry along the c axis. Since electron delocalization is an inherent property of superbasins reflected by the close ELF-values at the maxima and the bips, this striking result provides an alternative explanation of why the silver borate compound is a small band gap semiconductor whereas the silver metal is an electrical conductor. Macroscopically, we can understand that borate clusters play the role of crystal defects interrupting the electric conductivity along the three directions of the crystalline space.

The chemical entities associated with these superbasins allow us to discuss the sub-valent characteristics of silver-based compounds too. For the fcc unit cell of silver under room conditions, our ELF analysis and electron density integration lead to a single Ag₄⁴⁺ superbasin. In contrast, four equivalent Ag₁₆^6.4+ entities appear in the unit cell of Ag₁₆B₄O₁₀. From these compositions, it is evident that the sub-valent characteristics of the silver (sub)array originated during the transition from the fcc-metal to the silver borate compound. If we ideally understand the transformation as a three step continuous process involving (i) the expansion of the fcc-structure, (ii) vacancy creation and (iii) borate cluster insertion, we can identify two mechanisms that are able to reduce Ag atoms. The first one is associated with an increase of the lattice parameter. Crystal expansions decrease the electron density inside the tetrahedral voids (and therefore in the superbasins) allowing transfer of the valence electrons to the atomic cores. Firstly, we obtained N^v_ox(Ag) = +1 and N^v_ox(Ag) = +0.76 when a = 4.146 Å and a = 4.251 Å, respectively. Secondly, vacancy creation or cluster (borate) insertion disrupts the 3D superbasin connectivity, reducing the number of tetrahedral positions where silver electrons prefer to be accumulated. As there is no other mechanism to reduce Ag atoms, an almost identical N^v_ox(Ag) value is obtained for the defective (+0.42) and the borate (+0.40) silver compounds.

In conclusion, we believe that these findings may throw light on the interesting experimental observations reported in ref. 2 and might help to interpret the new chemistry exhibited by the silver oxides highlighted in ref. 2 and references therein. Our results emphasize the decisive role that residual metallicity plays in the existence of sub-valent compounds and could represent a promising strategy to be applied to other sub-valent silver oxides showing singular behaviour like the recently published Ag₇Pt₂O₇ compound.⁶ Claimed ‘synergistic interactions among the filled 4d¹⁰-shells’ strengthening silver inter-cluster bonding² may be accounted for by means of the proposed metallic superbasins rather than localized electron pairs. Suggested silver-oxide dispersion interactions need other scalar fields such as reduced gradient density¹⁸ or chemical pressure formalism¹⁹ to reveal so-called non-covalent interactions. We are currently working in that direction.

Data availability

All the revelant computational data of this comment is included in the ESI file.†

Author contributions

All authors have equally contributed to the investigation and writing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors have benefited from discussions with Prof. Gabino A. Carriedo, Prof. A. Vegas and Dr Alberto Otero-de-la-Roza. This work was supported by Spanish MCIU and MINECO through the following projects: PGC2018-094814 B-C2 and RED2018-102612 T, and by the Principado de Asturias (Spain) FICYT Agency through the project FC-GRUPIN-IDI/ 2018/000177. The support provided by the MALTA-Consolider supercomputing center is acknowledged.

Notes and references

1. G. Parkin, J. Chem. Educ., 2006, 83, 791; P. J. Brothers, in Encyclopedia of Inorganic Chemistry, Wiley Online Library ( 2006); M. Jansen and U. Wedig, Angew. Chem., Int. Ed., 2008, 47, 10026–10029.
2. A. Kovalevskiy, C. Yin, J. Nuss, U. Wedig and M. Jansen, Chem. Sci., 2020, 11, 962–969.
3. G. H. Bailey and G. J. Fowler, J. Chem. Soc. Trans., 1887, 51, 416–419.
4. E. T. Blues and D. Bryce-Smith, Discuss. Faraday Soc., 1969, 47, 190–198.
5. E. T. Blues, D. Bryce-Smith, R. Shaoul, H. Hirsch and M. J. Simons, J. Chem. Soc., Perkin Trans. 2, 1993, 2, 1631–1642.
6. G. S. Thakur, R. Dinnebier, T. C. Hansen, W. Assenmacher, C. Felser and M. Jansen, Angew. Chem., Int. Ed., 2020, 59, 19910–19913.
7. A. Vegas and H. D. B. Jenkins, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 865–874.
8. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
9. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
10. A. O. de-la Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018.
11. A. I. Baranov and M. Kohout, J. Comput. Chem., 2008, 29, 2161–2171.
12. B. Silvi and C. Gatti, J. Phys. Chem. A, 2000, 104, 947–953.
13. M. Kohout, F. R. Wagner and Y. Grin, Theor. Chem. Acc., 2002, 108, 150–156.
14. J. Contreras-García, A. M. Pendás, J. M. Recio and B. Silvi, J. Chem. Theory Comput., 2009, 5, 164–173.
15. A. Lobato, H. H. Osman, M. A. Salvadó, P. Pertierra, A. Vegas, V. G. Baonza and J. M. Recio, Inorg. Chem., 2020, 59, 5281–5291.
16. P. Mori-Sánchez, J. M. Recio, B. Silvi, C. Sousa, A. Martín Pendás, V. Luaña and F. Illas, Phys. Rev. B, 2002, 66, 075103.
17. B. Davaasuren, H. Borrmann, E. Dashjav, G. Kreiner, M. Widom, W. Schnelle, F. Wagner and R. Kniep, Angew. Chem., Int. Ed., 2010, 49, 5688–5692.
18. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
19. H. H. Osman, M. A. Salvadó, P. Pertierra, J. Engelkemier, D. C. Fredrickson and J. M. Recio, J. Chem. Theory Comput., 2018, 14, 104–114.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc02152d

‡ Present address: Chalmers University of Technology, SE-41296 Gothenburg, Sweden.

---