 Open Access Article
Open Access ArticleElectrostatic regulation of blue copper sites†
Daniel
Bím
 a and
Anastassia N.
Alexandrova
a and
Anastassia N.
Alexandrova
 *ab
*ab
aDepartment of Chemistry and Biochemistry, University of California, Los Angeles, 607 Charles E. Young Drive East, Los Angeles, CA 90095-1569, USA. E-mail: ana@chem.ucla.edu
bCalifornia NanoSystems Institute, University of California, Los Angeles, 570 Westwood Plaza, Los Angeles, California 90095-1569, USA
First published on 27th July 2021
Abstract
In the last 50 years, the blue copper proteins became central targets of investigation. Extensive experiments focused on the Cu coordination to probe the effect of local perturbations on its properties. We found that local electric fields, generated by charged residues evolutionarily placed throughout the protein edifice, mainly second sphere, but also more remotely, constitute an additional significant factor regulating blue copper proteins. These fields are not random, but exhibit a highly specific directionality, negative with respect to the 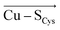 and
and 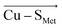 vectors in the Cu first shell. The field magnitude contributes to fine-tuning of the geometric and electronic properties of Cu sites in individual blue copper proteins. Specifically, the local electric fields evidently control the Cu–SMet bond distance, Cu(II)–SCys bond covalency, and the energies of the frontier molecular orbitals, which, in turn, govern the Cu(II/I) reduction potential and the relative absorption intensities at 450 nm and 600 nm.
vectors in the Cu first shell. The field magnitude contributes to fine-tuning of the geometric and electronic properties of Cu sites in individual blue copper proteins. Specifically, the local electric fields evidently control the Cu–SMet bond distance, Cu(II)–SCys bond covalency, and the energies of the frontier molecular orbitals, which, in turn, govern the Cu(II/I) reduction potential and the relative absorption intensities at 450 nm and 600 nm.
Introduction
Blue copper proteins (BC; also type 1 or T1 proteins) are proteins that participate in the rapid long-range biological electron transfers.1–4 Their Cu(II) centers feature an intense 600 nm band in the electronic absorption spectra, giving rise to their blue color and their name. A typical BC active site (e.g., in plastocyanin, azurin, rusticyanin, amicyanin) consists of the Cu(II) coordinated by 2His, Cys, and Met ligands in the pseudotetrahedral geometry.5,6 Since the preferred coordination of Cu(II) complexes is square planar,4 it was initially thought that observed tetrahedral geometry is responsible for their distinct spectral features, including small EPR hyperfine splitting, and high Cu(II/I) reduction potentials.7–15 Additionally, the unusual coordination, along with relatively small geometric changes between oxidized and reduced states (e.g., small angular distortion, small differences in Cu–L bond lengths, and rigidity of proteins upon single-point mutations),16–22 laid the foundations of entatic23 and rack-induced24 concepts in bioinorganic chemistry. According to the entatic/rack hypothesis, the protein function (e.g., electron transfer) is empowered by keeping the active site in a distorted (compromised) structure between the two functional states; such as Cu(I) (tetrahedral) and Cu(II) (square planar) conformations in BC proteins. Hence, the reorganization energy of redox reaction is minimized,4,25 and following the Marcus theory,26 the rate of electron transfer is enhanced. Note that electron-transfer proteins must operate near thermodynamic neutrality, making the argument of small reorganization energy critical for their proper biological function.4However, the entatic/rack concepts were questioned both in computations and in spectroscopic studies.19,27 Solomon and co-workers demonstrated that tetrahedral structure is indeed preferred in Cu(II) BC proteins; however, not due to entatic/rack constraints of Cu(II) coordination geometry in a true sense but rather due to the Cu–SMet bond elongation and Cu–SCys bond shortening in the Cu first ligand shell.19 Such distortions in Cu ligand field lowers the site's symmetry (i.e., orbital degeneracy) and eliminates the Jahn–Teller distorting forces otherwise present in tetrahedral Cu(II) complexes.28 The abnormally elongated axial Cu–SMet and shortened equatorial Cu–SCys bonds are unique, and likely controlled by the constraints produced by the protein.29–31
It was recognized that Cu–SMet and Cu–SCys bonds are electronically and geometrically coupled,2,12,19,32 so that the weak Cu–SMet interaction is compensated by strengthening Cu–SCys, together with increasing the Cu(II)–SCys bond covalency.4,33 In turn, strong Cu–SCys is accountable for a strong electronic absorption at 600 nm due to SCys 3p → Cu(II) 3dx2−y2 π charge transfer.34–36 The high covalency of Cu(II) 3dx2−y2 HOMO also results in a small EPR hyperfine splitting.35 By regulating the strengths of the Cu–SMet and Cu–SCys bonds, the BC proteins might thus tune their properties toward desired functionalities, including adjustment of Cu(II/I) reduction potential or rate of electron transfer.31,35,37,38 However, the mechanism of such regulation remains debated.
Within the Cu(I) sites in the BC proteins, Solomon has argued that Met ligand is held in place by the protein environment – i.e., in the entatic or rack-induced state.39 However, a discussion is complicated by the fact that there is not an unambiguous definition of what entasis is and/or how strain energy in the metal site should be quantified.27,40,41 As an example, Ryde et al. contrariwise proposed that BC proteins are not entatic.27 Instead, the Met residue was foreseen to be selected as a ‘floppy’ ligand with a flat potential energy surface to accommodate facile interchange between the two oxidation states and assist with rapid electron transfer. On the other hand, Hurd et al.42 computed much higher strain energies for plastocyanin when they included not only geometric constraints (i.e., covalent strain) but also protein electrostatics from QM/MM calculations. The strain energies elevated by ∼10 kcal mol−1. In plastocyanin, this suggests that protein electrostatics may play a significant role in Cu–SMet/Cu–SCys regulation and can contribute to plastocyanin function. Electrostatic interactions were also evidenced as predominant determinants of Cu(II/I) reduction potentials in the computational study of BC azurin variants.43
Recently, we have demonstrated that heme-iron proteins exert highly specific intramolecular electric fields on their active sites and that there is a strong correlation between the direction and magnitude of this field and the protein function.44 Herein, we demonstrate that the local electric fields produced by the proteins of the BC family are likewise not randomly oriented and instead appear customized by the evolution to fine-tune the BC centers' properties. This includes modifying the BC site geometry, electronic structure, BC spectral features, and Cu(II/I) reduction potentials.
Results and discussion
The local electric fields in the active sites of blue copper proteins
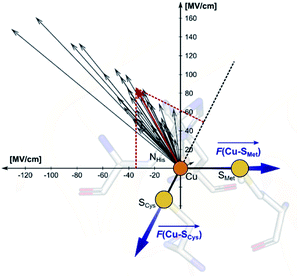
Employing the Erebus PDB protein substructure search server,45 we have identified 36 unique BC proteins with 2His, Cys, Met coordination (see computational details section in the ESI†). For this set of proteins, we analyzed the magnitudes of local electric fields (LEFs) in their active sites' Cu, together with the geometrical features of the proteins' active sites from their crystal structures (Table S1†). Note that the evaluated fields are induced by the entire protein outside of the BC active site, i.e., excluding the effects of their common 2His, Cys, Met coordinating residues and the Cu itself. The coordinating ligands thus do not contribute to the discussed LEFs, and the effect of LEFs is thereby additive to the effect of the first coordination sphere on the metal. By this, we analyze the intramolecular electric field that is exerted by the protein's residues. The electric field produced by the protein outside of the active site is thus calculated separately from any QM calculations, directly from the PDB structures. We then evaluate the effect of the field on the Cu(II) and Cu(I) properties by applying the entire field produced by the protein as a linear external electric field in the QM calculations. Thus, we are investigating the external contributions from the protein edifice on top of the field inherently generated by the active site itself. We also note that in some cases, a fifth ligand (such as backbone carbonyl) can coordinate Cu. To be consistent within the series of studied proteins, the charge on the fifth ligand was not zeroed, and it can thus electrostatically contribute to the Cu site.The overall LEF magnitudes range significantly in the protein series, from 14 MV cm−1 (1a3z; rusticyanin) to 165 MV cm−1 (1ezl; C3A/C26A azurin mutant). However, the LEFs are not randomly oriented (Fig. 1). Instead, the LEFs projected in the 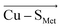 and
and 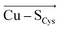 directions are preferentially negative (cf. average F(Cu–SMet) = −35.5 MV cm−1 and F(Cu–SCys) = −47.4 MV cm−1), and the average LEFs projected in the
directions are preferentially negative (cf. average F(Cu–SMet) = −35.5 MV cm−1 and F(Cu–SCys) = −47.4 MV cm−1), and the average LEFs projected in the 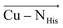 directions are preferentially positive (average F(Cu–NHis) = +36.4 MV cm−1).
directions are preferentially positive (average F(Cu–NHis) = +36.4 MV cm−1).
We indeed found a passable correlation between the computed F(Cu–SMet) projection on this bond and the Cu–SMet distance (d(Cu–SMet)) (Fig. 2). This is consistent with a facile electrostatic regulation of the Cu–SMet bond due to a very flat potential energy surface along this coordinate. However, since a significantly worse correlations were found between LEF (or its projections) and other BC geometric features – such as d(Cu–SCys) or d(Cu–SCys)/d(Cu–SMet) ratio, or the τ angle‡ (Fig. S1–S4†) – it appears that translation to BC site geometry or their spectral properties might be more intricate. As an example, Szuster et al. demonstrated that other factors, e.g., Cu ligand-loop hydrophobicity or water accessibility of the Cu site, also influence the active site geometry, and the Cu(II/I) reduction potentials and electronic absorption intensities in the CuA-based copper sites.46
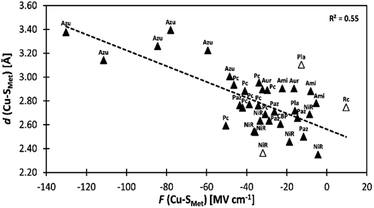 | ||
Fig. 2 A correlation between Cu–SMet bond distances (d(Cu–SMet)) and projections of the LEF vector in the 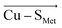 orientation (F(Cu–SMet)) for the BC proteins from Table S1.† The empty triangles represent proteins that were crystallized in the reduced form and are excluded from the fit. Ami = amicyanin, Aur = auracyanin, Azu = azurin, CBP = cucumber basic protein, NiR = nitrite reductase, Pla = plantacyanin, Pc = plastocyanin, Paz = pseudoazurin, Rc = rusticyanin. orientation (F(Cu–SMet)) for the BC proteins from Table S1.† The empty triangles represent proteins that were crystallized in the reduced form and are excluded from the fit. Ami = amicyanin, Aur = auracyanin, Azu = azurin, CBP = cucumber basic protein, NiR = nitrite reductase, Pla = plantacyanin, Pc = plastocyanin, Paz = pseudoazurin, Rc = rusticyanin. | ||
Coupled nature of the Cu–SMet and Cu–SCys bonds
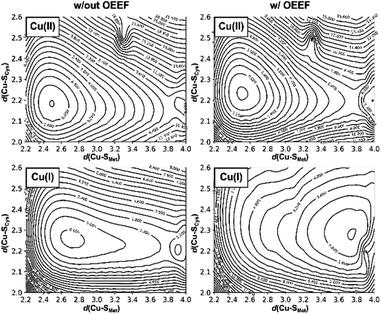
To evaluate how the change of d(Cu–SMet) in the BC site influences d(Cu–SCys), we have performed a constrained two-dimensional potential energy surface scan in the cluster model of the oxidized poplar plastocyanin (PDB code: 4dp9) coordination geometry (Fig. 3, top left).§ The equilibrium structure is found at the d(Cu–SMet) = 2.50 Å and d(Cu–SCys) = 2.20 Å. This is slightly distorted from the oxidized plastocyanin crystal-structure geometry (d(Cu–SMet) = 2.78 Å and d(Cu–SCys) = 2.16 Å);47 however, the energy difference is only ∼1.8 kcal mol−1. Consistent with Ryde's results (based on the cluster-model approach without protein electrostatics),27 we show that Cu–SMet bond is considerably more flexible, with an enthalpic penalty of only ca. 0.3 kcal mol−1, associated with displacement of ∼0.1 Å from the equilibrium geometry. On the other hand, the same displacement of the Cu–SCys bond costs ca. 1.0 kcal mol−1 in enthalpy. In the Cu(I) oxidation state, the lowest-energy structure has the Cu–SMet bond stretched to 2.70 Å and is ca. 0.5 kcal mol−1 below the geometry with d(Cu–SMet) = 2.50 Å preferred in Cu(II) (Fig. 3, bottom left). However, the potential energy surface is yet shallower in the direction toward Cu–SMet dissociation, with a barrier of only ∼2 kcal mol−1 between the two minima with the associated and dissociated Met ligand.Application of oriented external electric field (OEEF) in the average BC site orientation and magnitude (cf.Fig. 1) leads to almost no change in the preferred Cu(II) geometry or potential energy surface (Fig. 3, top right). However, despite small geometric differences, we note that OEEF remarkably reduces the HOMO/LUMO gap between the frontier molecular orbitals (Cu(II) α HOMO and Cu(II) β LUMO) by 28 kcal mol−1 and Cu(II)–SCys bond covalency by ∼24% – as indicated by the change in Cu and SCys spin densities in the Cu(II) equilibrium structure (the calculated spin densities are: Cu = 0.34, SCys = 0.51 at F = 0 and Cu = 0.49, SCys = 0.27 at average F experienced by any BC site) (cf.Table 1). Note that experimental spin populations were provided for some BC proteins that are in close agreement with our theoretical predictions; e.g., in wild-type azurin: SCys = 0.29–0.30 (33S hyperfine coupling),48 0.30 (2H ENDOR),49 0.45 (S K pre-edge XAS);50 NHis = 0.05 (H46) and 0.09 (H117) (15N hyperfine).51
In contrast, there is no stable structure with bonded Met when the OEEF is applied to the Cu(I) site. Instead, the Met ligand dissociates to d(Cu–SMet) = 3.90 Å. This suggests that, although the enzyme geometry would be enthalpically favored in Cu(I) oxidation state without LEF, in the average BC site (with the LEF opposing 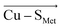 ) the Cu–SMet bond must be covalently constrained by the protein, in order to compensate both the enthalpic and the entropic penalties. Herein, the average LEF was found to introduce an enthalpic strain of ∼4 kcal mol−1 compared to an unconstrained geometry. We suggest the enthalpic penalty should be added to an entropic penalty of ∼4.5 kcal mol−1 proposed by Solomon,35 leading to the total strain energy of ∼8.5 kcal mol−1 that is associated with constraining the Met ligand in an average Cu(I) BC site.
) the Cu–SMet bond must be covalently constrained by the protein, in order to compensate both the enthalpic and the entropic penalties. Herein, the average LEF was found to introduce an enthalpic strain of ∼4 kcal mol−1 compared to an unconstrained geometry. We suggest the enthalpic penalty should be added to an entropic penalty of ∼4.5 kcal mol−1 proposed by Solomon,35 leading to the total strain energy of ∼8.5 kcal mol−1 that is associated with constraining the Met ligand in an average Cu(I) BC site.
Effect of the local electric field on the blue copper properties
Although there is no significant geometrical change in the Cu(II) BC site under OEEF, the quantum chemical calculations revealed that frontier molecular orbitals are substantially altered in energy, along with a decrease of the Cu(II)–SCys bond covalency by ∼24%. A lower covalency is quantified by the lower Mulliken spin population at the SCys atom, indicating smaller SCys 3p and Cu 3dx2−y2 orbitals overlap and hence bonding (Table 1).35 Similarly, smaller bonding in Cu(II) α HOMO can be translated into lower antibonding character in Cu(II) β LUMO, which is exhibited by a significantly decreased Cu(II) β LUMO energy under OEEF, by ∼11.5 kcal mol−1. By evaluating the individual contributions from F(Cu–SCys) and F(Cu–SMet) projections of the LEF (cf. Table S2,† where we applied OEEF only in the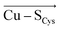 or
or 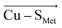 direction), we can conclude that the decreased Cu(II)–SCys bond covalency and Cu(II) β LUMO energy are caused by F(Cu–SCys) projection of the LEF, which exhibits decreased SCys spin population by 0.21e and Cu(II) β LUMO energy by 7.7 kcal mol−1. On the other hand, the average OEEF in
direction), we can conclude that the decreased Cu(II)–SCys bond covalency and Cu(II) β LUMO energy are caused by F(Cu–SCys) projection of the LEF, which exhibits decreased SCys spin population by 0.21e and Cu(II) β LUMO energy by 7.7 kcal mol−1. On the other hand, the average OEEF in 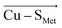 projection increases the Cu(II)–SCys bond covalency by ∼6% with Cu(II) β LUMO decrease by only 0.7 kcal mol−1. Note that the projections are not orthogonal and their effects thus cannot be fully decoupled.
projection increases the Cu(II)–SCys bond covalency by ∼6% with Cu(II) β LUMO decrease by only 0.7 kcal mol−1. Note that the projections are not orthogonal and their effects thus cannot be fully decoupled.
Many BC features were previously correlated with the Cu(II)–SCys bond covalency, and our results therefore suggest that LEF may play a critical role in tuning the BC properties. For instance, the BC proteins' electronic absorption spectra are characterized by the distinctive absorption bands at ∼600 nm and ∼450 nm. The BC proteins have stronger absorption intensity at the lower-energy thiolate π-to-Cu charge-transfer transition and weaker absorption intensity at the higher-energy σ-to-Cu charge-transfer transition (Fig. 4). Inversely, the ε600 and ε450 intensities are reversed for the normal tetragonal cupric complexes and green copper proteins. A lower Cu(II)–SCys bond covalency in our computational model due to lower (more negative) F(Cu–SCys) is thus consistent with a shift toward a more pronounced blue copper absorption features (cf.Fig. 4). Hence, the ε450/ε600 ratio is ∼0.7 for the equilibrium Cu(II) geometry from Fig. 3 without the applied field, while the σ-to-Cu charge-transfer intensity is significantly diminished by the OEEF, leading to an ε450/ε600 ratio of ∼0.2. Significantly, the ε450/ε600 ratio is regularly utilized as a measure of the cupric coordination geometry.2 Its sensitivity to the local intramolecular electric field exerted on the Cu site is striking.
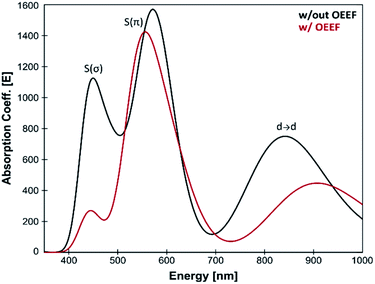 | ||
| Fig. 4 Calculated TD-DFT spectra for the equilibrium structure from Fig. 3; without the applied external electric field (black) and with applied external electric field (corresponding to the average LEF found in the series of BC proteins; red). A lower Cu(II)–SCys bond covalency under applied OEEF is translated into a considerably smaller σ-to-Cu charge-transfer transition at ∼450 nm. | ||
The effect of F(Cu–SCys) on the electronic absorption spectra is further reflected for blue copper and green copper proteins in Table S1.† While the average F(Cu–SCys) is −26.7 MV cm−1 for nitrite reductases (green copper proteins), the remaining proteins exhibit F(Cu–SCys) of −52.3 MV cm−1 (i.e., ∼25 MV cm−1 lower). We also note that F(Cu–SMet) projection of the LEF is as well higher for nitrite reductases by ∼15 MV cm−1, which is consistent with a shorter d(Cu–SMet) witnessed in green copper proteins (cf. correlation of d(Cu–SMet) vs.F(Cu–SMet) for nitrite reductases in Fig. 2).
As for the effect of LEF on the Cu(II/I) reduction potential, a lower Cu(II)–SCys covalency indicates a weaker Cu–SCys bond, which agrees with a destabilization of the oxidized Cu(II) state and thus higher Cu(II/I) reduction potential. According to Hadt et al., the Cu(I) adiabatic ionization energy (i.e., the inverse of the Cu(II) adiabatic electron affinity) is decreased due to lowered Cu(II)–SCys covalency by ∼10 mV per 1% decrease of the spin population on SCys.50 Therefore, on average, we might assign the effect of ∼240 mV increase in the Cu(II) electron affinity due to lowered Cu(II)–SCys covalency in an average BC. Similarly, when the average OEEF is applied, the redox-active molecular orbital (i.e., Cu(II) β LUMO) is decreased in energy by ca. 11.5 kcal mol−1 (cf.Table 1), consistent with an increase in the Cu(II) electron affinity by ca. 500 mV (i.e., the effect that is twice as high as for the Cu(II) electron affinity predicted from a decreased covalency). With simplification, we can thus attribute the increase in the Cu(II) electron affinity to a comparable covalent and non-local electrostatic contributions to the Cu(II) β LUMO energy.
Finally, note that F(Cu–SCys) and F(Cu–SMet) contribute to the overall Cu(II/I) reduction potential in the opposite direction. A negative F(Cu–SMet) leads to a higher Cu(II)–SCys covalency by ∼6% (decreasing the Cu(II) electron affinity by ∼60 mV), and it also contributes to an increased Cu(I) strain energy, additionally decreasing the Cu(II/I) reduction potential by ∼170 mV (vide supra). All in all, the average LEF in BC proteins appears to increase the Cu(II/I) reduction potential on aggregate by ca. 330 mV, coming from the increased Cu(II)–SCys covalency (240 mV), non-local electrostatic contributions to the Cu(II) β LUMO energy (260 mV), and increased Cu(I) strain energy (−170 mV).
We propose that our approach represents a much-simplified procedure as compared to, e.g., QM/MM treatment of the whole proteins, where the electrostatic effects from the surroundings are accounted for via the electrostatic embedding of the QM region in the set of MM point charges. We suggest that, in some cases, the full QM/MM could be approximated by the linear external electric field applied in the QM-only calculations. This offers an attractive alternative for analyzing protein contribution to the active site properties with a single vector, which could be of particular importance for predictions in artificial protein redesign (vide infra). Alternatively, DFT calculations on entire proteins became possible (see, e.g., ref. 52–54), which in principle could capture the same effects. However, such large-QM calculations are rather impractical, far from routine, and exceptionally demanding. Moreover, performing the calculations directly on the PDB structures would likely lead to significant artifacts, while sampling/optimizing structures at the DFT level would become inaccessible. In contrast, our approach provides a cost-efficient protocol, which can be used to sample a large number of proteins, and according to our analysis provides quite a robust methodology how to analyze the internal electric fields in proteins and their contribution to reactivity.
Electrostatic contribution to the azurin Cu(II/I) reduction potentials
To further support the idea of LEF regulating the BC sites' electronic structure, including Cu(II/I) reduction potentials, we have calculated the LEFs in a series of azurin variants from ref. 55. Specifically, we have analyzed all of the variants not containing mutations in the Cu first shell¶ (i.e., N47S, F114N, F114P, and N47S/F114N), which were generated from the available PDB structures of the wild-type azurin (4azu), and N47S/F114N (3jtb) and F114P/M121Q (3in0) azurin variants.As compared to wild-type azurin, the N47S, F114N, and N47S/F114N have higher Cu(II/I) reduction potentials, which are consistent with their more negative F(Cu–SCys) projections of the LEF (Fig. 5A). Oppositely, a higher F(Cu–SCys) of the F114P variant agrees remarkably well with lower Cu(II/I) reduction potential. Since the regression coefficient (R2) in Fig. 5A is close to unity, we can estimate an increase in reduction potential due to F(Cu–SCys) as −12.5 mV/1 MV cm−1. We note in passing that F(Cu–SCys) projection of the LEF in the azurin variants also weakly correlates with the experimentally determined Cu(II)–SCys bond covalencies: 54% for F114P, 45% for wild-type azurin, 43% for F114N, and 31% for N47S.50
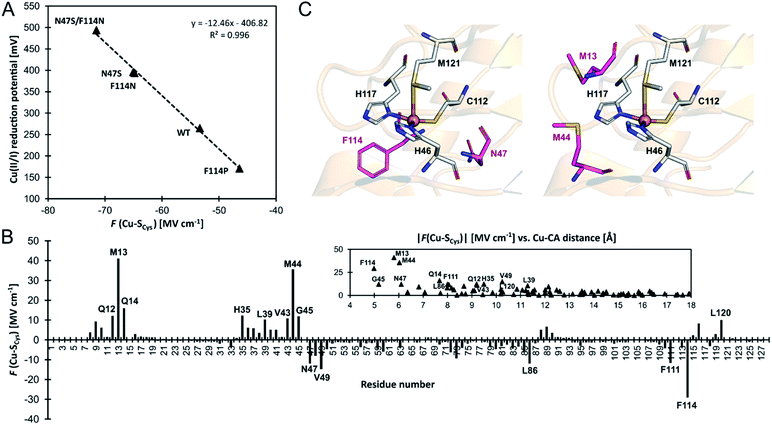 | ||
| Fig. 5 (A) Correlation between experimental one-electron Cu(II/I) reduction potentials (referenced to normal hydrogen electrode) vs.F(Cu–SCys) projection of the LEF in a series of azurin variants from ref. 55. (B) A contribution of each residue's side chain toward F(Cu–SCys) in the wild-type azurin. Note that side chains of the ligating (first-shell) residues are not included. A more significant contribution to F(Cu–SCys) is from the residues closer to the Cu site; the contribution becomes negligible when Cu–Cα distance exceeds ∼15 Å. (C) The second-coordination shell residues subjected to mutation to alter azurin Cu(II/I) reduction potential (in purple) investigated in ref. 55 (left) and suggested in this work (right). | ||
An excellent correlation in Fig. 5A suggests that determinants of the reduction potentials in the azurin variants are purely electrostatic. However, this study benefits from using the crystal structures, which already reflect the effect of the field. For example, the crystal structure of the F114P variant is missing an important hydrogen bond to the S atom of the first-shell C112, donated from the peptide-bond NH group of F114 residue. However, if the F114P mutant is modeled by a simple amino acid replacement in the wild-type azurin, a non-equilibrated structure with that hydrogen bond is yielded, and a much more negative F(Cu–SCys) by ∼14 MV cm−1 is predicted, which significantly deviates from the fit. The crystal structure or a structure produced by extensive molecular dynamics equilibration is needed for accurate predictions. Also, we were not able to reproduce Cu(II/I) reduction potentials between different ‘classes’ of proteins, such as azurin vs. plastocyanin proteins. We believe that reduction potential is governed by overriding effects (e.g., first-shell coordination geometry, hydrogen bonds, water accessibility; cf. ref. 46), whereas the electric field represents a secondary contribution – capable of differentiating systems with alike architecture at the relative scale. Still, the correlation between the change of the reduction potential and the local electric field calculated directly from the crystal structure represents a powerful and economic concept that can be utilized, e.g., for designing analogous BC variants with specific redox properties.
In this regard, we have analyzed the contributions of individual residues in the wild-type azurin (4azu) toward the observed F(Cu–SCys) (see Note S2 in the ESI for details†); the effect of the residues' side chains is presented in Fig. 5B (the overall effect of each residue and the backbone-only contributions are shown in Fig. S6†). Not surprisingly, the electric field beyond the first-coordination sphere is mainly dictated by the side chains of the second sphere residues, and the effect on the F(Cu–SCys) drops significantly with the increasing distance of a residue from Cu (cf.Fig. 5B and S9†). However, some impactful residues in the second sphere have not been experimentally examined. Especially, we hypothesize that M13 and M44 on the opposite side of the first-shell C112 generate substantial dipole moments that should influence the azurin redox properties considerably (Fig. 5B and C).
To estimate the impact of Met residues' mutation on F(Cu–SCys), we have performed a molecular dynamics simulation of the wild-type azurin, azurin variants from ref. 55, and possible M13/M44 variants (see computational details in the ESI†). Despite that we have always introduced mutations into the wild-type azurin crystal structure (PDB: 4azu), the correlation between the experimental Cu(II/I) reduction potentials and the change of the F(Cu–SCys) is reproduced well with R2 = 0.93 (cf. Fig. S8,† which is analogous to Fig. 5A). This suggests that we might also reliably predict changes in the wild-type azurin reduction potential upon proposed M13/M44 mutations. For the M13 or M44 single-mutations, we have observed the greatest decline in F(Cu–SCys) in M44F, M13E, M44S, and M44D variants, steering the F(Cu–SCys) by ∼13–18 MV cm−1 to more negative values (Fig. S7†), corresponding to an upshift of Cu(II/I) reduction potential by ∼150–200 mV. This is comparable to the experimentally tested F114N and N47S single-mutations of azurin protein. Similarly, the double-mutant M13F/M44F can lower the F(Cu–SCys) by ∼26 MV cm−1 (Fig. S7†) and increase Cu(II/I) reduction potential by ∼250 mV. Such change would again be equivalent to a preeminent experimental (second-sphere) double mutant F114N + N47S. Since we propose mutations of unprecedented residues, higher effect could also be achieved by combination of variants in F114/N47 and M13/M44 residues.
Conclusions
By examining an extensive series of blue copper proteins' crystal structures, we show that the protein scaffolds that host blue copper sites are not mere spectators of their function. Instead, the proteins' local electric fields can regulate multiple geometric and electronic properties typical of blue copper sites in biology. Specifically, we demonstrate that the local electric fields are oriented in a definite way throughout the blue copper protein family to modulate the copper interactions with its ligating residues. By orienting the electric field preferentially in the direction opposite of the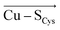 and
and 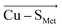 vectors in the copper first shell, the proteins make the Cu–S bonds considerably weaker than those in the isolated blue copper sites in a vacuum.
vectors in the copper first shell, the proteins make the Cu–S bonds considerably weaker than those in the isolated blue copper sites in a vacuum.
In the context of entatic/rack-induced concepts, the F(Cu–SMet) projection of the field pushes the axial Met ligand to dissociate from the Cu(I) center, though the entities are still held together by the protein. Hence, the electric field can be seen as an additional element adding to the Cu(I) sites' covalent strain. In an average blue copper site, we have estimated an enthalpic destabilization of the constrained Cu(I) active site by ∼4 kcal mol−1 due to local electric field.
Importantly, a weakening of the Cu–SCys bond appears to considerably influence many blue copper spectroscopic properties. Besides others, a weaker Cu–SCys is consistent with decreasing the Cu(II)–SCys bond covalency, which, in turn, affects the relative absorption intensities of Cu(II) at 450 nm and 600 nm. We have demonstrated that, while the ε450/ε600 ratio is ∼0.7 for the isolated equilibrium Cu(II) geometry in the plastocyanin active site, the local electric field oriented in the direction opposite of 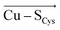 (average projection of F(Cu–SCys) is −47.4 MV cm−1) is necessary to shift the ε450/ε600 to ∼0.2, consistent with that of the regular blue copper sites. On the contrary, the green copper proteins exhibit much lower magnitudes of the local electric fields (average F(Cu–SCys) is −26.7 MV cm−1), in accordance with their higher ε450/ε600 ratio.
(average projection of F(Cu–SCys) is −47.4 MV cm−1) is necessary to shift the ε450/ε600 to ∼0.2, consistent with that of the regular blue copper sites. On the contrary, the green copper proteins exhibit much lower magnitudes of the local electric fields (average F(Cu–SCys) is −26.7 MV cm−1), in accordance with their higher ε450/ε600 ratio.
The electric field also contributes to the high Cu(II/I) reduction potentials of the blue copper sites. On average, it was found to be accountable for an increase of the Cu(II/I) reduction potentials by ca. 330 mV, originating from a lower Cu(II)–SCys covalency (240 mV), non-local contributions to a lower Cu(II) β LUMO energy (260 mV), and increased Cu(I) strain energy (−170 mV).
Last but not least, we have observed that local electric field is a critical determinant of the Cu(II/I) reduction potentials, when comparing different variants of otherwise identical blue copper sites. In a series of azurin variants that introduced mutations in the second-coordination sphere of the Cu site, we have shown that the change of reduction potential can be accurately described by the change in the local electric field exerted on the Cu–SCys bond in the equilibrium structure. We suggest that this concept could be utilized for designing protein variants with desired redox properties. Following our analysis, we propose new targets for mutagenetic studies, which have not been questioned thus far, and which contribute significantly to F(Cu–SCys) and should alter the reduction potential.
Author contributions
The manuscript was written through contributions of all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support comes from the NIH 1R01GM134047 grant to A.N.A. We also acknowledge the UCLA-IDRE cluster Hoffman2 and XSEDE for computational resources.Notes and references
- J. Liu, S. Chakraborty, P. Hosseinzadeh, Y. Yu, S. Tian, I. Petrik, A. Bhagi and Y. Lu, Chem. Rev., 2014, 114, 4366–4469 CrossRef CAS PubMed
.
- E. I. Solomon and R. G. Hadt, Coord. Chem. Rev., 2011, 255, 774–789 CrossRef CAS
.
- E. I. Solomon, R. K. Szilagyi, S. DeBeer George and L. Basumallick, Chem. Rev., 2004, 104, 419–458 CrossRef CAS PubMed
.
- H. B. Gray, B. G. Malmström and R. J. P. Williams, JBIC, J. Biol. Inorg. Chem., 2000, 5, 551–559 CrossRef CAS PubMed
.
- E. I. Solomon, J. W. Hare and H. B. Gray, Proc. Natl. Acad. Sci. U.S.A., 1976, 73, 1389–1393 CrossRef CAS PubMed
.
- J. M. Guss and H. C. Freeman, J. Mol. Biol., 1983, 169, 521–563 CrossRef CAS PubMed
.
- L. Broman, B. G. Malmström, R. Aasa and T. Vänngård, Biochim. Biophys. Acta, 1963, 75, 365–376 CrossRef CAS
.
- E. I. Solomon, M. J. Baldwin and M. D. Lowery, Chem. Rev., 1992, 92, 521–542 CrossRef CAS
.
- E. I. Solomon and M. D. Lowery, Science, 1993, 259, 1575–1581 CrossRef CAS PubMed
.
-
E. I. Solomon, K. W. Penfield and D. E. Wilcox, in Copper, Molybdenum, and Vanadium in Biological Systems, ed. B. A. Averill, L. R. Briggs, N. D. Chasteen, T. R. Gilbert, K. Kustin, G. C. McLeod, K. W. Penfield, E. I. Solomon and D. E. Wilcox, Springer Berlin Heidelberg, Berlin, Heidelberg, 1983, pp. 1–57 Search PubMed
.
- D. W. Randall, S. D. George, B. Hedman, K. O. Hodgson, K. Fujisawa and E. I. Solomon, J. Am. Chem. Soc., 2000, 122, 11620–11631 CrossRef CAS
.
- L. B. LaCroix, S. E. Shadle, Y. Wang, B. A. Averill, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1996, 118, 7755–7768 CrossRef CAS
.
- R. J. P. Williams, Inorg. Chim. Acta. Rev., 1971, 5, 137–155 CrossRef CAS
.
- R. Malkin and B. G. Malmström, Adv. Enzymol. Relat. Areas Mol. Biol., 1970, 177–244 CAS
.
- B. G. Malmström, B. Reinhammar and T. Vänngård, Biochim. Biophys. Acta Bioenerg., 1970, 205, 48–57 CrossRef
.
- A. L. Le Sueur, R. N. Schaugaard, M.-H. Baik and M. C. Thielges, J. Am. Chem. Soc., 2016, 138, 7187–7193 CrossRef CAS PubMed
.
- J. M. Guss, H. D. Bartunik and H. C. Freeman, Acta Crystallogr., Sect. B: Struct. Sci., 1992, 48, 790–811 CrossRef PubMed
.
- J. M. Guss, P. R. Harrowell, M. Murata, V. A. Norris and H. C. Freeman, J. Mol. Biol., 1986, 192, 361–387 CrossRef CAS PubMed
.
- J. A. Guckert, M. D. Lowery and E. I. Solomon, J. Am. Chem. Soc., 1995, 117, 2817–2844 CrossRef CAS
.
- W. E. B. Shepard, B. F. Anderson, D. A. Lewandoski, G. E. Norris and E. N. Baker, J. Am. Chem. Soc., 1990, 112, 7817–7819 CrossRef CAS
.
- A. Romero, C. W. G. Hoitink, H. Nar, R. Huber, A. Messerschmidt and G. W. Canters, J. Mol. Biol., 1993, 229, 1007–1021 CrossRef CAS PubMed
.
- B. G. Karlsson, R. Aasa, B. G. Malmström and L. G. Lundberg, FEBS Lett., 1989, 253, 99–102 CrossRef CAS
.
- B. L. Vallee and R. J. Williams, Proc. Natl. Acad. Sci. U.S.A., 1968, 59, 498–505 CrossRef CAS PubMed
.
- B. G. Malmström, Eur. J. Biochem., 1994, 223, 711–718 CrossRef PubMed
.
- J. R. Winkler, P. Wittung-Stafshede, J. Leckner, B. G. Malmström and H. B. Gray, Proc. Natl. Acad. Sci. U.S.A., 1997, 94, 4246–4249 CrossRef CAS PubMed
.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, Rev. Bioenerg., 1985, 811, 265–322 CrossRef CAS
.
- U. Ryde, M. H. M. Olsson, B. O. Roos, J. O. A. De Kerpel and K. Pierloot, JBIC, J. Biol. Inorg. Chem., 2000, 5, 565–574 CrossRef CAS PubMed
.
- H. A. Jahn, E. Teller and F. G. Donnan, Proc. R. Soc. London, Ser. A, 1937, 161, 220–235 CAS
.
- D. W. Randall, D. R. Gamelin, L. B. LaCroix and E. I. Solomon, JBIC, J. Biol. Inorg. Chem., 2000, 5, 16–29 CrossRef CAS PubMed
.
- R. H. Holm, P. Kennepohl and E. I. Solomon, Chem. Rev., 1996, 96, 2239–2314 CrossRef CAS PubMed
.
- E. I. Solomon, K. W. Penfield, A. A. Gewirth, M. D. Lowery, S. E. Shadle, J. A. Guckert and L. B. LaCroix, Inorg. Chim. Acta., 1996, 243, 67–78 CrossRef CAS
.
- L. B. LaCroix, D. W. Randall, A. M. Nersissian, C. W. G. Hoitink, G. W. Canters, J. S. Valentine and E. I. Solomon, J. Am. Chem. Soc., 1998, 120, 9621–9631 CrossRef CAS
.
- S. E. Shadle, J. E. Penner-Hahn, H. J. Schugar, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1993, 115, 767–776 CrossRef CAS
.
- A. A. Gewirth and E. I. Solomon, J. Am. Chem. Soc., 1988, 110, 3811–3819 CrossRef CAS
.
- K. W. Penfield, A. A. Gewirth and E. I. Solomon, J. Am. Chem. Soc., 1985, 107, 4519–4529 CrossRef CAS
.
- S. Larsson, A. Broo and L. Sjoelin, J. Phys. Chem., 1995, 99, 4860–4865 CrossRef CAS
.
- P. Wittung-Stafshede, M. G. Hill, E. Gomez, A. J. Di Bilio, B. G. Karlsson, J. Leckner, J. R. Winkler, H. B. Gray and B. G. Malmström, JBIC, J. Biol. Inorg. Chem., 1998, 3, 367–370 CrossRef CAS
.
- A. S. Brill, Biophys. Chem., 1999, 80, 129–138 CrossRef CAS PubMed
.
- S. Ghosh, X. Xie, A. Dey, Y. Sun, C. P. Scholes and E. I. Solomon, Proc. Natl. Acad. Sci. U.S.A., 2009, 106, 4969–4974 CrossRef CAS PubMed
.
- W. R. Hagen, Metallomics, 2019, 11, 1768–1778 CrossRef CAS PubMed
.
- J. Stanek, A. Hoffmann and S. Herres-Pawlis, Coord. Chem. Rev., 2018, 365, 103–121 CrossRef CAS
.
- C. A. Hurd, N. A. Besley and D. Robinson, J. Comput. Chem., 2017, 38, 1431–1437 CrossRef CAS PubMed
.
- N. J. Fowler, C. F. Blanford, J. Warwicker and S. P. de Visser, Chem.–Eur. J., 2017, 23, 15436–15445 CrossRef CAS PubMed
.
- D. Bím and A. N. Alexandrova, ACS Catal., 2021, 11, 6534–6546 CrossRef
.
- D. Shirvanyants, A. N. Alexandrova and N. V Dokholyan, Bioinformatics, 2011, 27, 1327–1329 CrossRef CAS PubMed
.
- J. Szuster, U. A. Zitare, M. A. Castro, A. J. Leguto, M. N. Morgada, A. J. Vila and D. H. Murgida, Chem. Sci., 2020, 11, 6193–6201 RSC
.
- G. S. Kachalova, A. C. Shosheva, G. P. Bourenkov, A. A. Donchev, M. I. Dimitrov and H. D. Bartunik, J. Inorg. Biochem., 2012, 115, 174–181 CrossRef CAS PubMed
.
- M. Ramirez Cohen, N. Mendelman, M. Radoul, T. D. Wilson, M. G. Savelieff, H. Zimmermann, I. Kaminker, A. Feintuch, Y. Lu and D. Goldfarb, Inorg. Chem., 2017, 56, 6163–6174 CrossRef CAS PubMed
.
- M. Fittipaldi, G. C. M. Warmerdam, E. C. de Waal, G. W. Canters, D. Cavazzini, G. L. Rossi, M. Huber and E. J. J. Groenen, ChemPhysChem, 2006, 7, 1286–1293 CrossRef CAS PubMed
.
- R. G. Hadt, N. Sun, N. M. Marshall, K. O. Hodgson, B. Hedman, Y. Lu and E. I. Solomon, J. Am. Chem. Soc., 2012, 134, 16701–16716 CrossRef CAS PubMed
.
- J. W. A. Coremans, O. G. Poluektov, E. J. J. Groenen, G. W. Canters, H. Nar and A. Messerschmidt, J. Am. Chem. Soc., 1996, 118, 12141–12153 CrossRef CAS
.
- C. Romero-Muñiz, M. Ortega, J. G. Vilhena, I. Diéz-Pérez, J. C. Cuevas, R. Pérez and L. A. Zotti, Biomolecules, 2019, 9, 506 CrossRef PubMed
.
- K. P. Kepp, J. Inorg. Biochem., 2012, 107, 15–24 CrossRef CAS PubMed
.
- Z. Futera, I. Ide, B. Kayser, K. Garg, X. Jiang, J. H. van Wonderen, J. N. Butt, H. Ishii, I. Pecht, M. Sheves, D. Cahen and J. Blumberger, J. Phys. Chem. Lett., 2020, 11, 9766–9774 CrossRef CAS PubMed
.
- N. M. Marshall, D. K. Garner, T. D. Wilson, Y. G. Gao, H. Robinson, M. J. Nilges and Y. Lu, Nature, 2009, 462, 113–116 CrossRef CAS PubMed
.
- L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955–964 RSC
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc02233d |
| ‡ τ = (360° − (α + β))/(141°), where α and β are the two largest angles between the Cu ligating atoms. The parameter τ was introduced by Yang et al.56 as a four-coordinate geometry index ranging from perfect tetrahedral (τ = 1) to perfect square planar (τ = 0). |
| § In the two-dimensional scan, we incrementally altered the Cu–SCys and Cu–SMet distances by 0.1 Å, while keeping the rest of the coordination geometry (i.e., angles between Cu ligating atoms (τ), and Cu–NHis distances) at the crystal positions. Constraining the τ angle is required to maintain the correct directionality of the external electric field applied at Cu. See computational details section in the ESI.† |
| ¶ In our approach, the LEF is analyzed outside the first-shell sphere of ligands (i.e., charges of the side-chains of ligating residues are zeroed). Therefore, any mutations in the Cu first shell would not result in different LEFs. |
| This journal is © The Royal Society of Chemistry 2021 |

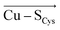
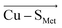
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)