Open Access Article
Open Access ArticleReactions of organic peroxy radicals, RO2, with substituted and biogenic alkenes at room temperature: unsuspected sinks for some RO2 in the atmosphere?†
Barbara
Nozière‡
 *a and
Fabienne
Fache
*a and
Fabienne
Fache
 b
b
aIRCELYON, CNRS, Université Claude Bernard Lyon 1, 2 Avenue Albert Einstein, 69626 Villeurbanne, France. E-mail: noziere@kth.se
bUniversité Lyon 1, CNRS, UMR 5246, Institut de Chimie et Biochimie Moléculaires et Supramoléculaires, 69626 Villeurbanne, France
First published on 27th July 2021
Abstract
Until now the reactions of organic peroxy radicals (RO2) with alkenes in the gas phase have been essentially studied at high temperature (T ≥ 360 K) and in the context of combustion processes, while considered negligible in the Earth's atmosphere. In this work, the reactions of methyl-, 1-pentyl- and acetylperoxy radicals (CH3O2, C5H11O2, and CH3C(O)O2, respectively) with 2-methyl-2-butene, 2,3-dimethyl-2-butene and for the first time the atmospherically relevant isoprene, α-pinene, and limonene were studied at room temperature (298 ± 5 K). Monitoring directly the radicals with chemical ionization mass spectrometry led to rate coefficients larger than expected from previous combustion studies but following similar trends in terms of alkenes, with (in molecule−1 cm3 s−1) 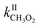 = 10−18 to 10−17 × 2/2 and
= 10−18 to 10−17 × 2/2 and 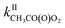 = 10−14 to 10−13 × 5/5. While these reactions would be negligible for CH3O2 and aliphatic RO2 at room temperature, this might not be the case for acyl-, and perhaps hydroxy-, allyl- and other substituted RO2. Combining our results with the Structure–Activity Relationship (SAR) predicts kII(298 K) ∼10−14 molecule−1 cm3 s−1 for hydroxy- and allyl-RO2 from isoprene oxidation, potentially accounting for up to 14% of their sinks in biogenic-rich regions of the atmosphere and much more in laboratory studies.
= 10−14 to 10−13 × 5/5. While these reactions would be negligible for CH3O2 and aliphatic RO2 at room temperature, this might not be the case for acyl-, and perhaps hydroxy-, allyl- and other substituted RO2. Combining our results with the Structure–Activity Relationship (SAR) predicts kII(298 K) ∼10−14 molecule−1 cm3 s−1 for hydroxy- and allyl-RO2 from isoprene oxidation, potentially accounting for up to 14% of their sinks in biogenic-rich regions of the atmosphere and much more in laboratory studies.
Introduction
Gas-phase organic peroxy radicals (RO2, where “R” is an organic moiety) play key roles in the chemistry and oxidizing capacity of the lower atmosphere. Atmospheric RO2 displays a wide variety of molecular structures, providing them with very different reactivities and rate coefficients often spanning over several orders of magnitude. Because of the difficulty in monitoring these radicals in the atmosphere, some unknowns remain in the details of their chemistry, which limit the understanding of atmospheric radical cycles. In particular, the measurements of OH and HO2 radical concentrations in the atmosphere have consistently reported discrepancies with models, especially in organic-rich and vegetation-impacted regions, which were attributed to unknown sinks for RO2.1,2 Over the last decade, the identification of previously overlooked reactions of RO2 was able to reduce these discrepancies.3,4 But recent studies have confirmed the persistence of differences, indicating the occurrence of unknown processes consuming RO2 and producing OH.5,6RO2 can react with a wide range of chemical compounds, including unsaturated organic molecules, such as alkenes, forming the corresponding alkene epoxy as the main product (Scheme 1). Until now, these reactions have been essentially studied for their interest in combustion processes and, with a few exceptions, investigated experimentally at high temperature (T ≥ 360 K).7 Extrapolating these results suggest that these reactions are negligible at room temperature, and thus in the Earth's atmosphere. To our knowledge, they have never been considered in atmospheric chemistry.
Experimental values for the rate coefficients for these reactions, kII (molecule−1 cm3 s−1), are scarce, in particular for CH3O2 (ref. 8) and CH3C(O)O2.9 Ref. 7 summarizes these data and recommends expressions for kII(T), with T = 360–800 K, fitted to the experimental results. For most of the RO2 listed, extrapolating these expressions to 298 K leads to kII ≤ 10−19 molecule−1 cm3 s−1, thus justifying the omission of these reactions in atmospheric chemistry. But for some RO2 such as CH3C(O)O2, the rate coefficients are 5 to 6 orders of magnitude larger than for CH3O2, suggesting that these reactions might not be entirely negligible at room temperature. Extrapolating the expressions in ref. 7 also results in uncertainties on the rate coefficients at 298 K of about ×10/10 for CH3O2 and ×30/30 for CH3C(O)O2, further justifying experimental studies. Finally, as previous studies focused exclusively on combustion systems, atmospherically relevant biogenic alkenes such as isoprene or terpenes have never been investigated. To our knowledge, the reaction of RO2 with conjugated alkenes such as isoprene, prone to allylic rearrangement, has not been studied either. The reactions of RO2 with biogenic alkenes at room temperature are thus worth investigating as a potential sink for at least some RO2 in the atmosphere.
In this work, RO2 + alkene reactions were investigated experimentally for the methyl peroxy radical, CH3O2, 1-pentyl peroxy radical, hereafter referred to as C5H11O2, and peroxy acyl radical, CH3C(O)O2, with 2-methyl-2-butene, 2,3-dimethyl-butene, isoprene, α-pinene, and limonene at 298 ± 5 K.
Experimental section
Experimental conditions
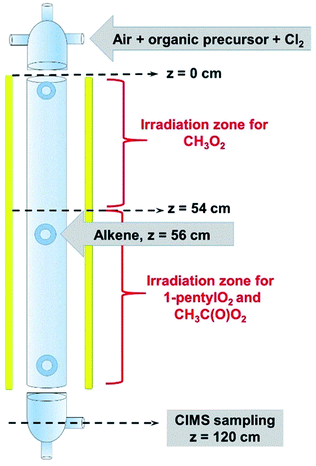
The complete list of experiments is given in Section S1 of the ESI.† The experiments were performed in a vertical quartz reactor of length L = 120 cm and internal diameter d = 5 cm, previously described in ref. 10 (Fig. 1) and operated in a continuous flow. The bath gas (synthetic air, 3–4 sLm, standard temperature = 273 K and pressure = 1 atm) and the radical precursors (CH4, CH3I, C5H11I, CH3CHO and, where necessary, Cl2) were introduced at the top of the reactor. Under these conditions, the gas flow was well in the laminar regime, with a Reynolds number of about 150. At the bottom of the reactor (z = 120 cm in Fig. 1), 1–4% of the flow mixture was sampled into a Chemical Ionization Mass Spectrometer (CIMS) using proton transfer as the ionization method.11,12 The CIMS monitored continuously the RO2 and stable compounds in the reactions at a residence time of 17 s and recorded their changes as alkenes were periodically added to the reactor (Fig. 2A), which were then used in the kinetic analysis.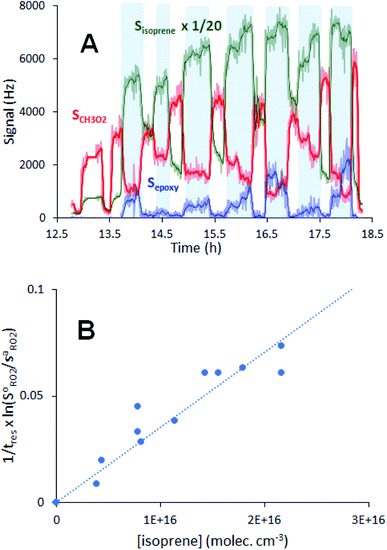 | ||
Fig. 2 Typical experimental profiles and kinetic analysis for the reaction CH3O2 + isoprene (experiment Alk03 in Table S1†): (A) real-time evolution of CH3O2 concentration (red line, m/z = 84), isoprene (green line, m/z = 69) and production of isoprene epoxy (blue line, m/z = 121). The areas shaded in blue correspond to the periodic addition of isoprene; (B) corresponding first-order variation of the ratio 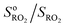 as a function of isoprene concentration providing kII(298 K). as a function of isoprene concentration providing kII(298 K). | ||
The temperature and relative humidity inside the reactor were determined in separate sets of experiments, but under the same conditions of pressure, flow, and UV-light irradiation, by placing an infrared hygrometer (Extech 101) inside the reactor. The uncertainties of ±5 K attributed to the temperature include both the variabilities during the experiments and over the entire time span of the study.
The RO2 were produced photochemically by irradiating the reactor over the wavelengths 280–400 nm with four fluorescent lights (Philips TL12, 40 W). For CH3O2 and CH3C(O)O2, the radical was produced by photolyzing chlorine, Cl2, in the presence of an organic precursor (CH4, and CH3CHO, respectively) as in ref. 11. For CH3O2 the sequence was:
| Cl2 + hν → 2Cl | (2) |
| Cl + CH4 → CH3 + HCl | (3) |
| CH3 + O2 + M → CH3O2 + M | (4) |
And for CH3C(O)O2:
| Cl + CH3CHO → CH3C(O) + HCl | (5) |
| CH3C(O) + O2 + M → CH3C(O)O2 + M | (6) |
Irradiation tests were performed and confirmed that CH3CHO was not photolyzed by the UV lights in the reactor and that its only fate was reaction.5
CH3O2 and C5H11O2 were also produced by photolyzing directly their iodinated precursors, CH3I and C5H11I, respectively, as in ref. 10. For CH3O2:
| CH3l + hν → CH3 + I | (7) |
Followed by reaction.4 For C5H11O2:
| C5H11I + hν → C5H11 + I | (8) |
| C5H11 + O2 + M → C5H11O2 + M | (9) |
CH3O2 was produced from two different precursors, CH4 + Cl2 and CH3I, to rule out potential artefacts due to side-chemistry due to Cl2/Cl or I atoms. Table S1† in the ESI provides the range of concentrations used for the different precursors. Only a small fraction of Cl2 was photolyzed, leading to [Cl] in the range 1011 to 1012 molecule cm−3.12 In the systems using the photolysis of iodinated compounds, the number of radicals produced (thus of I atoms) was in the same range, based on the initial concentrations of RO2 observed in this and previous studies.10,11 In this study, the maximum RO2 concentrations in the reactor were in the range 5 × 1010 to 5 × 1011 molecule cm−3 for CH3O2, 1–2 × 1011 molecule cm−3 for C5H11O2, and 1–3 × 1010 molecule cm−3 for CH3C(O)O2.
Because the radicals studied had very different reactivities, different set-ups were used to study their reactions. CH3O2 was produced in the top half of the reactor (z ≤ 54 cm in Fig. 1) and reacted with alkenes in the dark in the lower half (z ≥ 56 cm), the alkenes being introduced at z = 56 cm (Fig. 1). This was not possible with C5H11O2 and CH3C(O)O2, as producing them in the top half of the reactor resulted in non-measurable concentrations at the bottom (z = 120 cm). These radicals were thus produced in the bottom half of the reactor, the alkenes being still introduced at z = 56 cm. Thus, for these radicals, photochemical production and reactions with alkenes occurred simultaneously in the lower half of the reactor. A separate series of experiments were performed and showed that the photolysis of RO2 in the reactor was negligible, as was that of the stable reaction products (peroxides and aldehydes).
To avoid potential artefacts due to varying flow rate or pressure in the reactor when injecting the alkenes, the total flow through the alkene inlet was maintained continuous throughout the experiments using a flow controller toggled between pure N2 and mixtures of alkenes in N2. The existence of potential artefacts due to insufficient mixing of the alkenes in the reactor was also examined for CH3O2 by varying the total flow rate through the alkene inlet from 5 to 200 sccm, while maintaining the same alkene concentrations (using different dilution factors). The same results were obtained with all flow rates, indicating that such mixing effects were negligible under these conditions.
Chemicals
| A + H3O+(H2O)n → AH+(H2O)m + (n − m + 1)H2O | (10) |
A compound of molecular mass M was thus detected by its ion products at m/z = M + 1, M + 19, M + 37, M + 55, M + 73, etc. Previous studies have shown that a CIMS instrument operating on this principle can detect volatile RO2 in addition to stable molecules.10–12 As in our previous studies,10,11 the potential contribution of other compounds than RO2 at their expected m/z was investigated by adding an excess of NO in the reactor, before or after the series of RO2 + alkene experiments. These tests showed that less than 10% of the signals came from other compounds than RO2, which was attributed to impurities in the system. These constant contributions to the RO2 signals however cancelled out in the first-order kinetic analysis used in this work. In the presence of alkenes, the contribution of other compounds to the RO2m/z was not expected because the latter have even values while stable CxHyOz compounds have odd m/z values with proton transfer.
The CIMS allowed monitoring continuously, with a time resolution of ∼1 s, the evolution of RO2, alkenes, and stable reaction products as the alkenes were periodically added to the reactor (Fig. 2A). Table S3 of the ESI† gives the complete list of the ion masses at which these compounds were detected. Although knowing the absolute concentrations of RO2 in the reactor was not necessary for the first-order kinetic analysis in this work (cf. “Kinetic analysis” below), they were determined in order to constrain the simulations that were used to validate these analyses (see “Kinetic simulations” below). For this, the detection sensitivities determined for these radicals in previous studies were used: 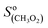 = 5000 Hz ppb−1,10,11
= 5000 Hz ppb−1,10,11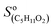 = 200 Hz ppb−1,10 and
= 200 Hz ppb−1,10 and 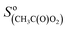 = 2000 Hz ppb−1.11
= 2000 Hz ppb−1.11
For each reaction investigated, the occurrence of the reaction was confirmed by observing both the decrease of the RO2 signal, SRO2, (thus of RO2 concentration) upon alkene addition and by the build-up of stable products at the expected ion masses for the alkene epoxy (Fig. 2A).
Kinetic analysis
The rate coefficients, kII (molecule−1 cm3 s−1), for the reactions RO2 + alkene were determined experimentally from the ratios of the RO2 signal between the absence and the presence of alkene, measured with the CIMS at the bottom of the reactor, and a simple first-order expression.For radicals produced in the top half of the reactor and reacting in the dark in the bottom half (CH3O2 in this study), the maximum radical concentration, [RO2]i, is reached near mid-reactor (z ∼54 cm in Fig. 1), and then decreases as a result of second-order sinks (self-reaction) and first-order sinks (wall losses, reactions with HO2, potential isomerization… see Section S4 of the ESI† for the different RO2) to reach [RO2]o at z = 120 cm. Assuming that the second-order sinks are negligible, [RO2]i and [RO2]o are linked by a simple first-order expression:
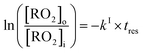 | (11) |
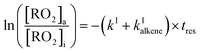 | (12) |
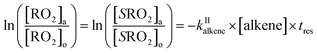 | (13a) |
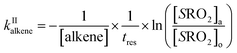 | (13b) |
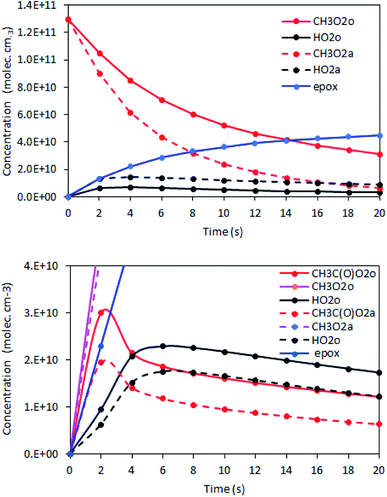
The rate coefficient kII was then determined by applying eqn (13b) to the RO2 signals measured in the absence and in the presence of alkenes with the CIMS. Eqn (13b) is, however, only an approximation of the kinetics for CH3O2 because of the potential contributions of second-order sinks, and even more so for C5H11O2 and CH3C(O)O2 as these radicals were simultaneously produced and consumed in the reactor (Fig. 3 bottom). In addition, for all the radicals, the first-order sinks were not necessarily identical in the absence and in the presence of alkenes, as the concentrations of HO2 (and of CH3O2 in the CH3C(O)O2 system) varied. Thus, kinetic simulations were run (next section) to determine the correction factors to apply to eqn (13b) to determine kII in each series of experiments.
The correction factors for the reactions of CH3O2 were small (see below), implying only small uncertainties in the kinetic results, but larger for C5H11O2 and CH3C(O)O2, implying larger uncertainties. The uncertainties in the values of kII obtained from these analyses were thus estimated to be ×2/2, for CH3O2, mostly based on the statistical dispersion, and ×5/5 for the reactions of C5H11O2 and CH3C(O)O2 because of the larger uncertainties in the correction factors and of the limited range of alkene concentrations that could be used in these experiments.
Kinetic simulations
Kinetic simulations using Chemsimul (V3.90, 2018) were performed to validate our kinetic analysis and to quantify the correction factors to apply to eqn (13b) to determine kII from the experimental data. Complete details on these simulations, including the chemical equations, rate coefficients, and numerical results, are given in Section S4 of the ESI.† Briefly, they consisted of calculating first the concentration profiles in the reactor with [alkene] = 0 and constraining [RO2]o with the experimental RO2 signals. Then, they were run again using alkene concentrations typical of the experiments to determine [RO2]a (Fig. 3). Eqn (13b) was then applied to determine kII. Comparing the kII thus obtained at t = 17 s to the value assumed for this coefficient in the kinetic model gave the correction factor to apply to eqn (13b) in the kinetic analyses.The results showed that, for CH3O2 reactions, the correction factor was 0.76, mostly compensating for neglecting the self-reaction and for the differences in the first-order sinks in the absence and presence of alkenes. For the reactions of C5H11O2 and CH3C(O)O2, these factors were larger, ∼5 and ∼19, respectively, compensating for a number of contributions detailed in Section S4 of the ESI.†
Results and discussion
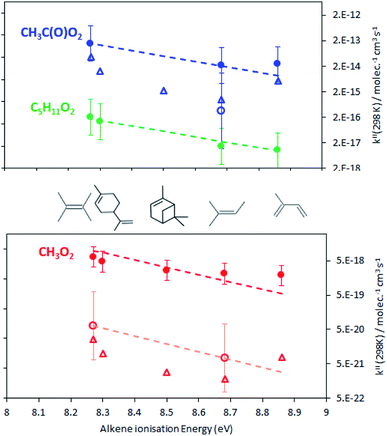
The rate coefficients, kII(298 K), obtained in this work are summarized in Fig. 4 and listed in Table S5† of the ESI. For the alkenes studied in this work they varied between about 2 and 7 × 10−18 molecule−1 cm3 s−1 for CH3O2, 8 to 160 × 10−18 molecule−1 cm3 s−1 for C5H11O2 and 2 to 12 × 10−14 molecule−1 cm3 s−1 for CH3C(O)O2. For all radicals, the rate coefficients followed similar trends in terms of alkene structure, the smallest coefficients being for isoprene and the largest for 2,3-dimethyl-2-butene. These results show that these reactions would be slow at room temperature for CH3O2, C5H11O2, and probably other aliphatic RO2 but not necessarily for CH3C(O)O2. These results also implied that, at room temperature, CH3O2 reacts about 18 times faster than HO2, based on the rate coefficients for HO2 + alkenes in ref. 7.Comparison with high-temperature data and the Structure–Activity Relationship (SAR)
In Fig. 4, the rate coefficients obtained in this work are compared with those extrapolated from previous high-temperature studies (for those available).7–9 The rate coefficients were also calculated for CH3O2, CH3C(O)O2 and the alkenes studied in this work using the Structure–Activity Relationship (SAR) recommended in ref. 7. For C5H11O2, this could not be done because the required parameters were not available in the literature. For CH3O2 and CH3C(O)O2, the activation energy of each reaction, E (kJ mol−1), was calculated from the charge-transfer energy, ΔEc (kJ mol−1), using an equation recommended in ref. 7.| E = 83.0–1.82 × ΔEc | (14) |
| ΔEc = −(χRO2 − χalkene)2/4 × (ηRO2 − ηalkene) | (15) |
| χ = (I + A)/2 | (16) |
| η = (I − A)/2 | (17) |
The pre-exponential factor for the rate coefficients, Ao, used in these SAR calculations was the one recommended in ref. 7 and obtained from empirically fitting the combustion data: Ao = 2.09 × 10−13 molecule−1 cm3 s−1. The ionization energies, I, and electron affinities, A, used in these calculations and the values predicted for kII(298 K) are presented in Table 1.
| I (eV) | A (eV) | χ (eV) | η (eV) | ΔEc (kJ mol−1) | E (kJ mol−1) | k II (298 K) molecule−1 cm3 s−1 | |
|---|---|---|---|---|---|---|---|
| a Ref. 14. b Ref. 15. c Ref. 13. d Based on cyclohexene in ref. 15 but corrected by −0.03 eV for each methyl group. e From ref. 15 but for two double bonds. f Ref. 16. g Ref. 7. | |||||||
| 2,3-Dimethyl-2-butene | 8.27a | −2.27b | 3.0 | 5.3 | |||
| Limonene | 8.30c | −2.10d | 3.1 | 5.2 | |||
| α-pinene | 8.07c | −2.10d | 3.2 | 5.3 | |||
| 2-Methyl-2-butene | 8.68a | −2.24b | 3.2 | 5.5 | |||
| Isoprene | 8.86c | −2.80e | 3.0 | 5.8 | |||
| CH3C(O)O2 | 11.58f | 2.75f | 7.2 | 4.4 | |||
| CH3O2 | 11.18f | 1.21f | 6.2 | 5.0 | |||
| i-C3H7O2 (H3C–CHO2–CH3) | 11.00g | 1.40g | 6.2 | 4.8 | |||
| HOC3H6O2 (HOCH2–CHO2–CH3) | 11.86g | 2.02g | 6.4 | 4.4 | |||
C3H5O2 (H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–CH2O2) CH–CH2O2) |
11.14g | 1.60g | 6.4 | 4.8 | |||
| CH3C(O)O2 + 2,3-dimethyl-2-butene | 43.2 | 4.39 | 3.6 × 10−14 | ||||
| CH3C(O)O2 + limonene | 41.5 | 7.55 | 9.9 × 10−15 | ||||
| CH3C(O)O2 + α-pinene | 39.0 | 11.95 | 1.7 × 10−15 | ||||
| CH3C(O)O2 + 2-methyl-2-butene | 38.0 | 13.85 | 7.8 × 10−16 | ||||
| CH3C(O)O2 + isoprene | 40.3 | 9.73 | 4.1 × 10−15 | ||||
| CH3O2 + 2,3-dimethyl-2-butene | 24.0 | 39.31 | 2.7 × 10−20 | ||||
| CH3O2 + limonene | 22.7 | 41.71 | 1.0 × 10−20 | ||||
| CH3O2 + α-pinene | 21.0 | 44.71 | 3.0 × 10−21 | ||||
| CH3O2 + 2-methyl-2-butene | 20.4 | 45.83 | 1.9 × 10−21 | ||||
| CH3O2 + isoprene | 22.3 | 42.34 | 7.9 × 10−21 | ||||
| i-C3H7O2 + 2,3-dimethyl-2-butene | 24.5 | 38.37 | 3.9 × 10−20 | ||||
| HOC3H6O2 + 2,3-dimethyl-2-butene | 29.4 | 29.40 | 1.5 × 10−18 | ||||
| C3H5O2 + 2,3-dimethyl-2-butene | 27.3 | 33.36 | 3.0 × 10−19 | ||||
Fig. 4 clearly shows that the kII(298 K) obtained in this work is larger than expected from the combustion data, by about a factor 60 for CH3C(O)O2 and 100 to 300 for CH3O2, and by factors 20 and 250 to 1000, respectively, from the SAR predictions. In addition, while the present results indicate that CH3O2 reacts 18 times faster than HO2 (with 2,3-dimethyl-2-butene) the high-temperature data predicted it to react 6 times slower than HO2.
Besides these discrepancies, the rate coefficients obtained in this work followed similar trends to the high-temperature experimental data and SAR previsions in terms of alkene substitution and RO2 structure. In particular, for all the RO2, kII(298 K) increased with alkene substitution, including for the alkenes studied here for the first time, in the sequence isoprene < 2-methyl-2-butene < α-pinene < limonene < 2,3-dimethyl-2-butene. As explained in ref. 7 for an electrophilic addition of a RO2 radical onto a double bond the activation energy, E, is expected to vary proportionally with the alkene ionization energy, which is implicit in eqn (14)–(17). In this work, kII was indeed found to increase with alkene ionization energies (Table 1): isoprene, 8.86;13 2-methyl-2-butene, 8.68;7 limonene, 8.30;13 2,3-dimethyl-2-butene, 8.27.7 Only for α-pinene the ionization energy of 8.07 eV13 found in the literature did not seem consistent with that of the similar molecule limonene. α-pinene was thus arbitrarily assigned an ionization energy of 8.5 eV in Fig. 4 and in the SAR calculations. With this, linear regressions (on the ln scale) were performed on the results, but excluding the data for isoprene (see discussion below).
These linear regressions (dashed lines in Fig. 4) allowed the estimation of kII(298 K) for reactions that had not been studied. For instance, kII(298 K) for CH3C(O)O2 + terpenes was estimated to be in the range 0.5–1 × 10−13 molecule−1 cm3 s−1 (blue line in Fig. 4).
Leaving out the RO2 + isoprene data from the linear regressions revealed that the kII(298 K) for these reactions was systematically larger than the regressions (Fig. 4). These deviations corresponded to a factor 2.8 in average, thus providing an estimate for the excess reactivity due to allylic rearrangement in the RO2 + isoprene reactions.
As explained in ref. 7 and implicit in the SAR calculations, kII for RO2 + alkene also varies strongly with the RO2 structure. In the present work, for the same alkene, CH3C(O)O2 reacts 9000 to 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times faster than CH3O2, while the combustion data predicted a ratio of 36
000 times faster than CH3O2, while the combustion data predicted a ratio of 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 between these radicals with 2-methyl-2-butene. The SAR predicted even larger ratios, between 400
000 between these radicals with 2-methyl-2-butene. The SAR predicted even larger ratios, between 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 1
000 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, but the large discrepancies with the experimental data are likely due to the empirical determination of the preexponential factors.
000, but the large discrepancies with the experimental data are likely due to the empirical determination of the preexponential factors.
The rate coefficients measured for C5H11O2 in this work indicate that this radical reacts about 14 times faster than CH3O2 in average. This seems reasonable as the rate coefficients for other radicals (for instance i-C3H7O2 in Table 1) indicate that kII increases only by a small factor for each additional carbon atom. However, as no other experimental data were available for this radical and its ionization energy and electron affinity were not available, no further comparison could be made with these rate coefficients.
The large discrepancies between the rate coefficients obtained in this work and those reported at high temperature7–9 seem difficult to reconcile, suggesting experimental or analytical artefacts in at least one of the data sets. In the present work, monitoring directly RO2 with only minor potential interference from other compounds should be more selective than monitoring the overall epoxide formation in previous studies.8,9 And using a relative kinetic approach (“alkene off”/”alkene on”) should limit the artefacts in the results by cancelling out a large part of the RO2 sinks other than alkenes. The potential role of side-reactions involving OH radicals or Cl atoms was also investigated and ruled out by performing kinetic simulations (Section S4 of the ESI†). This was further confirmed by the fact that large discrepancies with the high-temperature results were obtained in this work with all types of precursors (Cl2, iodinated compounds) and set-ups. One potential artefact that could account for the large rate coefficients in this work would be insufficient mixing, leading to large underestimations of the alkene concentrations. But, besides the fact that such mixing effects were ruled out by varying the total alkene flow rate (Experimental section), they should affect equally all the rate coefficients, while the discrepancies with the high-temperature data are much larger for CH3O2 than for CH3C(O)O2 reactions (by almost a factor of 5). As a further confirmation, the kinetic simulations showed that such large alkene concentrations would entirely consume RO2, making it impossible to observe profiles such as that in Fig. 2B. While no obvious artefact accounting for the large discrepancies with the high-temperature data can be found in our work, identifying such an artefact in these previous studies8,9 is not easy, especially as little information was provided on their kinetic analysis. In these previous studies, the rate coefficients were determined from the overall formation of the epoxy product. Thus, underestimating the contribution of HO2 to this formation or overestimating the RO2 concentrations, for instance by overlooking side-reactions, could have potentially underestimated the RO2 + alkene rate coefficients.
Other RO2 and alkenes leading to significant reactions at room temperature
Beyond CH3C(O)O2 and the substituted alkenes studied in this work, it would be interesting to identify other alkenes and RO2 leading to significant reaction rates at room temperature. First, previous studies have shown that oxygenated substituents such as carbonyl groups further enhance the reactivity of unsaturated compounds compared to their alkene analogues. In particular the rate coefficient for the reaction of CH3C(O)O2 with C2H3CHO (acrolein)17 was reported to be about 3 times the one with propene. This suggests that oxidation products from isoprene, such as methacrolein and methyl vinyl ketone, or from terpenes, or even unsaturated alcohols such as the biogenic compound 2-methyl-3-butene-ol, might react faster with RO2 than isoprene or terpenes themselves.The SAR, ionization energies and electron affinities in ref. 7 were also used to estimate the rate coefficients with 2,3-dimethyl-2-butene at 298 K for other RO2 than those studied experimentally: isopropylperoxy, i-C3H7O2 or H3C–CH2O2–CH3, 1-hydroxy-2-propylperoxy, HOC3H6O2 or HOCH2–CHO2–CH3, and allylperoxy, C3H5O2 or H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2–CH2O2. The ionization energies, electron affinities, and results for these radicals are presented in Table 1. They show that, at 298 K, HOC3H6O2 reacts about 40 times faster than its aliphatic analogue i-C3H6O2. Allylperoxy, C3H5O2, was predicted to react about 8 times faster than i-C3H6O2, which was assumed to be a typical factor for allyl-substituents, in the absence of ionization energies and electron affinities allowing a comparison with the primary aliphatic analogue 1-C3H6O2. Some RO2 produced by the OH oxidation of isoprene contains both HO- and allyl-substituents, and thus their rate coefficients with alkenes might combine the above factors and be significant at room temperature. The rate coefficient with 2,3-dimethyl-2-butene for such C5-RO2 can be roughly estimated from that of 1-C5H11O2 measured in this work, kII ∼1.5 × 10−16 molecule−1 cm3 s−1, and the factors × 40 and × 8 for the HO- and allyl substituents, leading to 5 × 10−14 molecule−1 cm3 s−1. This estimate has for only purpose to make a first assessment of the importance of these reactions in the laboratory and in the atmosphere, and would obviously need to be confirmed by experimental studies.
CH2–CH2O2. The ionization energies, electron affinities, and results for these radicals are presented in Table 1. They show that, at 298 K, HOC3H6O2 reacts about 40 times faster than its aliphatic analogue i-C3H6O2. Allylperoxy, C3H5O2, was predicted to react about 8 times faster than i-C3H6O2, which was assumed to be a typical factor for allyl-substituents, in the absence of ionization energies and electron affinities allowing a comparison with the primary aliphatic analogue 1-C3H6O2. Some RO2 produced by the OH oxidation of isoprene contains both HO- and allyl-substituents, and thus their rate coefficients with alkenes might combine the above factors and be significant at room temperature. The rate coefficient with 2,3-dimethyl-2-butene for such C5-RO2 can be roughly estimated from that of 1-C5H11O2 measured in this work, kII ∼1.5 × 10−16 molecule−1 cm3 s−1, and the factors × 40 and × 8 for the HO- and allyl substituents, leading to 5 × 10−14 molecule−1 cm3 s−1. This estimate has for only purpose to make a first assessment of the importance of these reactions in the laboratory and in the atmosphere, and would obviously need to be confirmed by experimental studies.
Conclusions and atmospheric implications
The rate coefficients for RO2 + alkene reactions at room temperature measured in this work were larger than expected from previous combustion studies. While those for many RO2, in particular aliphatic ones, would still be small (≤10−15 molecule−1 cm3 s−1), those for acyl-substituted RO2 could be as large as 10−14 to 10−13 molecule−1 cm3 s−1. SAR predictions indicate that other substituents, such as HO- or allyl-, would also contribute to enhance the reactivity of RO2 towards alkenes, especially when combined as for the RO2 produced by the OH-oxidation of multi-unsaturated alkenes (isoprene, terpenes, …).While these estimates await confirmation from further experimental studies, the importance of these reactions in the atmosphere and laboratory for the RO2 produced by the OH-oxidation of isoprene can be determined from the rate coefficient estimated above. Assuming kII (RO2 + isoprene) ∼1/5 × kII (RO2 + 2,3-dimethyl-2-butene) = 10−14 molecule−1 cm3 s−1 and typical isoprene concentrations of 1012 molecule cm−3 in the laboratory or smog chamber would correspond to RO2 sinks of 0.01 s−1. Note that, while some of these RO2 radicals would rapidly undergo H-migration reactions,3,18 their HOOQO2 isomers would also carry HO- and allyl-groups, and thus have similar rate coefficients to alkenes. In the absence of NO, the main other sink for the RO2 would be their reactions with HO2. Typical HO2 concentrations of 109 molecule cm−3 and a rate coefficient of 10−11 molecule−1 cm3 s−1 also correspond to a sink of 0.01 s−1, implying that the reactions with isoprene could represent as much as half of the RO2 sinks under such conditions. If so, they should lead to measurable concentrations of isoprene epoxy, which might have been overlooked or mis-attributed in previous isoprene oxidation studies.19 In the atmosphere, the concentrations reported (for instance in ref. 1) in vegetation-impacted regions, isoprene = 5 × 1010; NO = 5 × 108; HO2 = 108 molecule cm−3, correspond to sinks for isoprene-RO2 (and HOOQO2) of 0.0005, 0.002, and 0.001 s−1, respectively. Reactions with isoprene could thus represent as much as 14% of the sinks for these RO2 radicals, to which their reactions with methacrolein and methyl vinyl ketone would probably have to be added. Thus, for some RO2, RO2 + alkene reactions might not be negligible even in the atmosphere, which emphasizes the need for further experimental investigations at room temperature.
Data availability
Most of the data is presented in the ESI.†Author contributions
BN: conceptualization; methodology; investigation; visualization; writing – original draft; FF: conceptualization; visualization; writing – original draft.Conflicts of interest
The authors have no conflicts to declare.Acknowledgements
This work was part of the ERC Advanced Grant Project EPHEMERAL (grant agreement No 884532) and has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme.References
- J. Lelieveld, T. M. Butler, J. N. Crowley, T. J. Dillon, H. Fischer, L. Ganzeveld, H. Harder, M. G. Lawrence, M. Martinez, D. Taraborrelli and J. Williams, Nature, 2008, 452, 737–740 CrossRef CAS PubMed.
- A. Hofzumahaus, F. Rohrer, K. Lu, B. Bohn, T. Brauers, C.-C. Chang, H. Fuchs, F. Holland, K. Kita, Y. Kondo, X. Li, S. Lou, M. Shao, L. Zeng, A. Wahner and Y. Zhang, Science, 2009, 324, 1702–1704 CrossRef CAS PubMed.
- J. Peeters, T. L. Nguyen and L. Vereecken, Phys. Chem. Chem. Phys., 2009, 11, 5935–5939 RSC.
- J. J. Orlando and G. S. Tyndall, Chem. Soc. Rev., 2012, 41, 6294–6317 RSC.
- K. D. Lu, F. Rohrer, F. Holland, H. Fuchs, B. Bohn, T. Brauers, C. C. Chang, R. Häseler, M. Hu, K. Kita, Y. Kondo, X. Li, S. R. Lou, S. Nehr, M. Shao, L. M. Zeng, A. Wahner, Y. H. Zhang and A. Hofzumahaus, Atmos. Chem. Phys., 2012, 12, 1541–1569 CrossRef CAS.
- Z. Tan, K. Lu, A. Hofzumahaus, H. Fuchs, B. Bohn, F. Holland, Y. Liu, F. Rohrer, M. Shao, K. Sun, Y. Wu, L. Zeng, Y. Zhang, Q. Zou, A. Kiendler-Scharr, A. Wahner and Y. Zhang, Atmos. Chem. Phys., 2019, 19, 7129–7150 CrossRef CAS.
- M. S. Stark, J. Phys. Chem. A, 1997, 101, 8296–8301 CrossRef CAS.
- D. A. Osbourne and D. J. Waddington, J. Chem. Soc., Perkin Trans. 2, 1980, 925–930 RSC.
- R. Ruiz Diaz, K. Selby and D. J. Waddington, J. Chem. Soc., Perkin Trans. 2, 1977, 360–363 RSC.
- B. Nozière and L. Vereecken, Angew. Chem. Int. Ed., 2019, 58, 13976–13982 CrossRef PubMed.
- B. Nozière and D. R. Hanson, J. Phys. Chem. A, 2017, 121, 8453–8464 CrossRef PubMed.
- D. Hanson, J. Orlando, B. Nozière and E. Kosciuch, Int. J. Mass Spectrom., 2004, 239, 147–159 CrossRef CAS.
- J. E. Bartmess, NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, in National Institute of Standards and Technology, Gaithersburg, MD, USA, 2021, DOI:10.18434/T4D303.
- P. Masclet, D. Grosjean, G. Mouvier and J. Dubois, J. Electron. Spectrosc. Relat. Phenom., 1973, 2, 225 CrossRef CAS.
- K. D. Jordan and P. D. Burrow, Acc. Chem. Res., 1978, 11, 341–348 CrossRef CAS.
- M. Jonsson, J. Phys. Chem., 1996, 100, 6814–6818 CrossRef CAS.
- P. J. Roden, M. S. Stark and D. J. Waddington, Int. J. Chem. Kinet., 1999, 31, 277–282 CrossRef CAS.
- L. Vereecken and B. Nozière, Atmos. Chem. Phys., 2020, 20, 7429–7458 CrossRef CAS.
- F. Paulot, J. D. Crounse, H. G. Kjaergaard, A. Kürten, J. M. St Clair, J. H. Seinfeld and P. O. Wennberg, Science, 2009, 325, 730–733 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc02263f |
| ‡ Now at KTH, Royal Institute of Technology, Teknikringen 30, 114 28 Stockholm, Sweden. |
| This journal is © The Royal Society of Chemistry 2021 |