Open Access Article
Open Access ArticleLinker depletion for missing cluster defects in non-UiO metal–organic frameworks†
Isabel Abánades
Lázaro
 a,
Neyvis
Almora-Barrios
a,
Neyvis
Almora-Barrios
 a,
Sergio
Tatay
a,
Sergio
Tatay
 a,
Catalin
Popescu
a,
Catalin
Popescu
 b and
Carlos
Martí-Gastaldo
b and
Carlos
Martí-Gastaldo
 *a
*a
aInstituto de Ciencia Molecular (ICMol), Universidad de Valencia, Catedrático José Beltrán-2, 46980, Paterna, Spain. E-mail: carlos.marti@uv.es
bCELLS-ALBA Synchrotron Light Facility, 08290 Barcelona, Spain
First published on 4th August 2021
Abstract
Defect engineering is a valuable tool to tune the properties of metal–organic frameworks. However, defect chemistry remains still predominantly limited to UiO-type MOFs. We describe the preferential formation of missing cluster defects in heterometallic titanium–organic frameworks of the MUV-10 family when synthesised in sub-stoichiometric linker conditions. Our results show the value of integrating experimental work, computational modelling and thorough characterization in rationalizing the impact of defects over the porosity and structure of this family of materials. Correlation of experiment with computational models reveals the dominance of missing cluster vacancies in the pore size distribution of defective MUV-10. These same models were used to investigate the correlation of defects by synchrotron X-ray diffraction. The diffraction at low reflection angles is dominated by diffuse scattering that is indicative of short-range order and cannot be indexed to the defective structural models generated. In addition to the low atomic scattering factor of titanium, these results confirm the need for high-resolution electron microscopy methods for modelling nanoscale disorder in titanium MOFs.
Introduction
The presence of defects in crystalline structures has a direct impact on the properties of the material.1 This is also the case of metal–organic frameworks (MOFs),2 where the introduction of defects leads to changes in their mechanical and physical properties,3,4 porosity5,6 and density of open metal sites.7,8 This has a direct impact on their performance in applications such as gas storage,9 separation or catalysis10 among others, thus justifying the increasing interest that the chemistry of defects in MOFs has received over the past decade.2,11The possibility of controlling the concentration and distribution of defects by systematic control of the synthetic conditions is arguably key to use defect engineering as a rational tool for the design of functional frameworks. The structural complexity of defective MOFs was initially demonstrated in 2011 for UiO-66(Zr), with thermal decomposition profiles showing a lower linker decomposition step and EXAFS agreeing to a loss of ligands in the first coordinating shell of Zr.12 It was not until 2014, that the possibility of creating structurally correlated defective nano-domains with reo topology was experimentally demonstrated by Cliffe et al. for UiO-66(Hf) by using X-ray scattering and pair distribution function (PDF) measurements.13 This seminal work challenged the accepted randomness of defect chemistry and opened the door to the possibility of gaining synthetic control over the spatial distribution and prevalence of metal–oxo cluster vacancies.
Since then, different groups have dedicated significant efforts to understand the factors that control the formation, relative concentration and structural distribution of the different types of defects (missing linker and cluster) that can be generated in UiO-type MOFs at nanometric14 or even atomic resolutions, by using Scanning Electron Diffraction (SED) or High-Resolution Transmission Electron Microscopy (HRTEM).15 These works highlight the willingness of UiO phases to form correlated defect domains,16 arguably due to the moderate energy penalty between the fcu topology of the perfect framework and the reo, scu, bcu and hcp defective phases that have been identified thus far.15,17,18
Overall, these results suggest that the particular ability of the UiO, and other families of MOFs based on Zr/Hf clusters with high coordination numbers, to generate defective phases is associated with the versatility of 12-connected Zr6O8/Hf6O8 inorganic nodes to reduce their number of connections and accommodate a high concentration of defects while maintaining the stability of the resulting framework.16,19 This has motivated many different groups to use this MOF family as a model to explore the possibilities offered by defect chemistry with very little attention paid to other frameworks or secondary building units (SBUs). To the best of our knowledge, UiO remains the only framework capable of inducing the formation of structurally ordered defective phases even though the number of MOFs reported continues to increase exponentially.20 The possibility of forming structurally correlated domains of defects in other frameworks based on SBUs with different chemistries and connection points remains still an open question.
In this context, we have recently reported a systematic study on the ability of mono- and dicarboxylic modulators to promote defectivity in titanium–organic frameworks.21 Our results confirmed that the nucleation and crystallization of 8–3 connected MUV-10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 (MUV = Materials of the Universitat de València) in acetic acid can be also modulated and the use of isophthalic acid generates defective phases with near 40% of missing linkers, a concentration of defects that is comparable to the values reported for the reo phase of UiO.5,13 Following our interest in tailoring the creation of defects for non-UiO frameworks, here we describe the ability of MUV-10 to accommodate the formation of defective phases with a lower degree of topological connectivity by the controlled generation of missing cluster vacancies when synthesized in sub-stoichiometric concentrations of the linker. Our results also show the value of integrating experimental work, computational modelling and thorough characterization in rationalizing the impact of defects over the porosity and structure of the resulting phases.
22 (MUV = Materials of the Universitat de València) in acetic acid can be also modulated and the use of isophthalic acid generates defective phases with near 40% of missing linkers, a concentration of defects that is comparable to the values reported for the reo phase of UiO.5,13 Following our interest in tailoring the creation of defects for non-UiO frameworks, here we describe the ability of MUV-10 to accommodate the formation of defective phases with a lower degree of topological connectivity by the controlled generation of missing cluster vacancies when synthesized in sub-stoichiometric concentrations of the linker. Our results also show the value of integrating experimental work, computational modelling and thorough characterization in rationalizing the impact of defects over the porosity and structure of the resulting phases.
Results and discussion
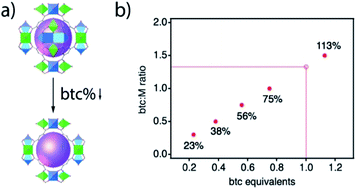
MOFs' self-assembly and growth rely on complex equilibria that can include the deprotonation of organic species, their complexation to metal ions, and the termination of the crystal faces, all with a direct impact on the kinetics of nucleation and crystallisation of the framework and/or on the incorporation of defects.23 These complex equilibria are generally manipulated by the addition of acidic modulators, that compete with the linker for metal-complexation and/or inhibit its deprotonation.24 Recent works show that the concentration of the linker can be also an effective variable to reduce crystal size during MOF synthesis in absence of external modulators.25 In view of these results, we hypothesised that reducing the concentration of the linker below the stoichiometric ratio might also have a significant impact in controlling the assembly and crystal growth of MUV-10 (Fig. 1a). We were particularly interested in whether the unavailability of sufficient linker concentration required for stoichiometric metal-complexation might favour the formation of vacancies for defective phases with lower connectivity. Compared to the use of modulators, linker depletion in less often used as a synthetic tool for controlling the formation of defective MOFs.26,27 We argued the persistent nature of MUV-10 secondary building units, that can be isolated in a broad range of synthetic conditions and are compatible with the assembly of isoreticular frameworks as MUV-12,28 would be ideal for investigating this possibility.Starting with the reported synthesis of [(TiIV2CaII2(μ3-O)2)(H2O)4(btc)2.66] (btc = benzene-1,3,5-tricarboxylate anion), the reaction of stoichiometric amounts of the metal precursors and a slight excess of btc (1.5 ratio, that is 1.13 equivalents) in the presence of acetic acid as a weak acid modulator, we systematically decreased the concentration of btc available for crystal growth by fixing the number of btc equivalents to 0.75, 0.56, 0.38 and 0.23. As shown in Fig. 1b, we carried out 5 reactions for these number of equivalents, and labelled the isolated solids accordingly as 113, 75, 56, 38 and 23%. See ESI Section S2† for the detailed synthetic conditions of all samples.
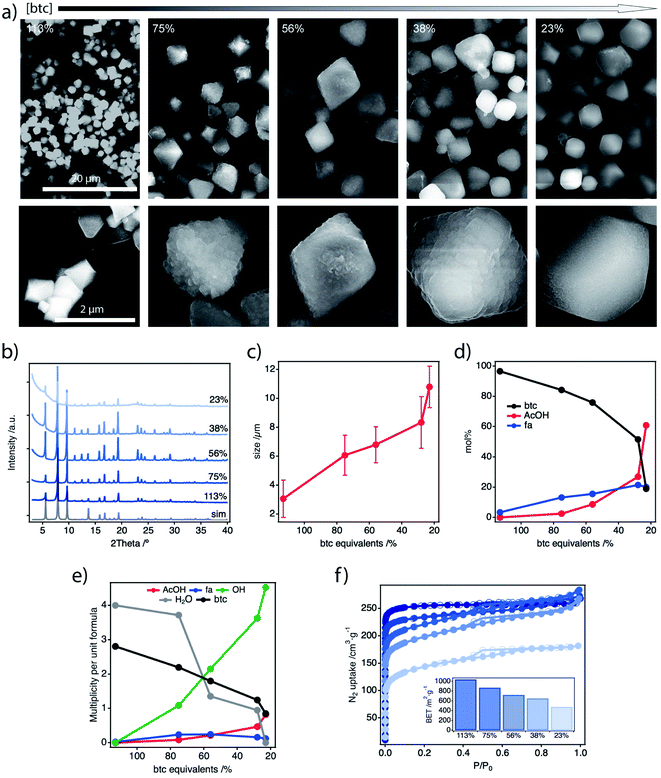
All the samples were isolated and washed thoroughly by Soxhlet extraction in methanol overnight before characterisation unless otherwise stated. The powder X-ray diffraction (PXRD) patterns of all solids confirm the formation of crystalline MUV-10 phases. We observe a significant increase of the scattering at low angular values as the amount of btc is reduced which might be associated to the competing formation of an amorphous phase (Fig. 2b). Scanning Electron Microscopy (SEM) imaging shows changes in the morphology of the particles, with shapes evolving from octahedral to truncated octahedra and more irregular surface terminations (Fig. 2a, ESI Section S3.1†). The size of the crystals progressively increases with the depletion of btc from near 3 μm (113%) to close to 11 μm for 23%, with narrow size dispersions in all cases (Fig. 2c). This behaviour seems to suggest a slower metal-ion complexation for decreasing linker concentrations, that slows down the nucleation and crystallisation kinetics.23 These results contrast with the synthesis of MUV-10 in presence of additional benzoic acid or isophthalic acid acting as modulators,21 for which the particle size was reduced or maintained regardless of their concentration, more indicative of an effective crystal growth capping due to stronger metal coordination ability.
The samples were acid-digested and analysed with 1H-NMR to study the effect of linker depletion on the chemical composition of the resulting frameworks. Fig. 2d and Tables S3–5† show the mole percent (mol%) of acetic (AcOH) and formic acid (fa) incorporated into the solid vs. the equivalents of btc added in the synthesis (ESI Section S3.2†). The amount of fa + AcOH steadily increases for increasingly lower btc concentration. However, while fa content increases rapidly to reach a plateau near to 10% for the 75% sample, and shows slight variations for lower btc concentrations, the AcOH incorporation follows a different trend, with an exponential increase that remains below fa up to 56%. Assuming that the amount of fa generated by the decomposition of DMF in acid media is constant thorough the series, this is consistent with our reported simulations that show that the introduction of fa to the framework is 0.4 eV more favourable thermodynamically than AcOH.21 Fa ligands are mainly incorporated to the structure at higher btc concentrations until its concentration in solution is depleted and AcOH starts to incorporate to the structure. A detailed analysis with energy-dispersive X-ray spectroscopy (EDX) and ICP of the experimental Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca ratios in our defective samples reveals an increase in the titanium content for samples produced at btc below 75%. (ESI Section S3.5†). Though our synthetic controls, in which the totality of linker was removed, did not result in precipitation or turbidity, this experimental divergence from the theoretical value suggests the formation of competing phases rich in titanium upon depletion of the linker. The FT-IR spectra of the samples were used to confirm the absence of free acid in the solids that might compromise the analysis (ESI Section S3.3†). We also observe a broadening of the carboxylate band compared to pristine MUV-10 and new O–C–O sym/assym (ca. 1536 cm−1) and COO-δ (ca. 1019 cm−1) vibrations characteristic of coordinated carboxylate anions, that increase in intensity with btc% reduction and the incorporation of fa/AcOH.
Ca ratios in our defective samples reveals an increase in the titanium content for samples produced at btc below 75%. (ESI Section S3.5†). Though our synthetic controls, in which the totality of linker was removed, did not result in precipitation or turbidity, this experimental divergence from the theoretical value suggests the formation of competing phases rich in titanium upon depletion of the linker. The FT-IR spectra of the samples were used to confirm the absence of free acid in the solids that might compromise the analysis (ESI Section S3.3†). We also observe a broadening of the carboxylate band compared to pristine MUV-10 and new O–C–O sym/assym (ca. 1536 cm−1) and COO-δ (ca. 1019 cm−1) vibrations characteristic of coordinated carboxylate anions, that increase in intensity with btc% reduction and the incorporation of fa/AcOH.
The thermogravimetric decomposition profiles are consistent with a decrease of the btc mass loss at ca. 450 °C concomitant to an increase in the relative weight of defect-compensating species, that decompose between 200 and 400 °C (ESI Section S3.4†). The defective frameworks prepared under linker deficient conditions display only a small decrease in thermal stability of near 55 °C compared to pristine MUV-10. We analysed the thermal decomposition profiles in combination with the information extracted from the 1H-NMR study by using a reported method and assuming a model structure with formula [TiCaO(H2O)w(btc)d(fa)y(AcOH)Z(OH)D].29Fig. 2e shows the evolution of the number of btc and defect-compensating molecules per unit formula with the btc equivalents used in the synthesis. We observe a progressive decrease of btc in the solids that is counterbalanced by the incorporation of hydroxyl, acetate and formate anions for increasing degrees of defectivity. As anticipated by the NMR study, the incorporation of AcOH dominates over fa for the low btc region. However, our analysis shows that OH− anions are the preferred ligands for compensating the charge upon linker removal in all the samples analysed. We argue this is a result of the exchange of fa/AcOH ligands incorporated in the synthesis with OH−/H2O pairs during the Soxhlet treatment in wet MeOH. Ligand replacement in similar conditions has been well documented for defective UiO-66 frameworks.30,31 Our calculations reveal a maximum of near 33% missing linkers in the lattice for the 56% sample. This value is in the range of the reported value for defective MUV-10 synthesized in presence of isophthalic acid, and directly comparable to the values reported for 8-connected bcu and reo topologies for UiO-66 frameworks.15 We collected the N2 adsorption gas isotherms after degassing the samples overnight at 60 °C and 10−6 torr (Fig. 2f). The samples display a progressive decrease in the nitrogen uptake at low pressures upon depletion of the linker, concomitant to the reduction of the BET area values calculated in the microporous region. We also observe the appearance of a hysteresis loop at 0.4 < P/P0 < 0.8 more characteristic of a mesoporous material (ESI Section S.3.6†). The defective samples suggest a stronger deviation from the perfect MUV-10 behaviour with the reduction of the amount of btc. This is possibly due to the competing formation of dense, amorphous phases for a negative impact in the surface area of the resulting materials.
Rather than looking into all the samples available, we decided to analyse in detail the origin of defectivity only for MUV-10 75%, which is the only defective sample that displays a Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ca ratio close to 1. Our compositional analysis [(Ti2Ca2(μ3-O)2)(H2O)4(btc)2.20(fa)0.24(OH)1.10]28 though, cannot establish the origin of the defectivity in MUV-10 samples that could equally arise from missing-linker, missing-cluster defects or the coexistence of both. This complex scenario was beautifully illustrated by Liu et al.,15 that demonstrated with HRTEM at sub-unit-cell resolution the coexistence of different types of defects in UiO-66 crystals with variable populations depending on the synthetic conditions. To tackle this problem, we opted to use a combination of computational modelling, detailed analysis of the changes in the pore size distribution, and synchrotron X-ray diffraction.
Ca ratio close to 1. Our compositional analysis [(Ti2Ca2(μ3-O)2)(H2O)4(btc)2.20(fa)0.24(OH)1.10]28 though, cannot establish the origin of the defectivity in MUV-10 samples that could equally arise from missing-linker, missing-cluster defects or the coexistence of both. This complex scenario was beautifully illustrated by Liu et al.,15 that demonstrated with HRTEM at sub-unit-cell resolution the coexistence of different types of defects in UiO-66 crystals with variable populations depending on the synthetic conditions. To tackle this problem, we opted to use a combination of computational modelling, detailed analysis of the changes in the pore size distribution, and synchrotron X-ray diffraction.
A btc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
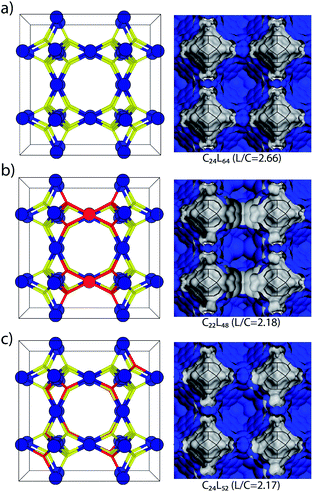
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cluster ratio (L/C) of 2.20 will correspond to 0.25 missing clusters or 1.5 linkers per unit cell (3 clusters and 8 linkers for non-defective MUV-10). Considering a 2 × 2 × 2 supercell (24 clusters and 64 linkers), this would correspond to 2 missing clusters (2MC) or 12 missing linkers (12ML), for simplicity, we focused on isolated missing linker or missing cluster defects and discarded their coexistence for our study (Fig. 3). To support our analysis, we model the defective structures in MUV-10 consistent with the linker-to-cluster ratio of 2.2 estimated for the 75% sample. Fig. 3b and c shows the topological models representative of both types of defects in MUV-10. In this supercell, the introduction of 2 missing clusters generates 7 symmetry inequivalent configurations compared to more than 8.6 × 109 generated by introducing 12 missing linkers.32,33 By using Materials Studio 2017 R2, we generated crystallographic files for all the missing cluster configurations and limited the configurational space to only 12 entries for the missing linker case. All crystallographic files have been included as ESI.†
cluster ratio (L/C) of 2.20 will correspond to 0.25 missing clusters or 1.5 linkers per unit cell (3 clusters and 8 linkers for non-defective MUV-10). Considering a 2 × 2 × 2 supercell (24 clusters and 64 linkers), this would correspond to 2 missing clusters (2MC) or 12 missing linkers (12ML), for simplicity, we focused on isolated missing linker or missing cluster defects and discarded their coexistence for our study (Fig. 3). To support our analysis, we model the defective structures in MUV-10 consistent with the linker-to-cluster ratio of 2.2 estimated for the 75% sample. Fig. 3b and c shows the topological models representative of both types of defects in MUV-10. In this supercell, the introduction of 2 missing clusters generates 7 symmetry inequivalent configurations compared to more than 8.6 × 109 generated by introducing 12 missing linkers.32,33 By using Materials Studio 2017 R2, we generated crystallographic files for all the missing cluster configurations and limited the configurational space to only 12 entries for the missing linker case. All crystallographic files have been included as ESI.†
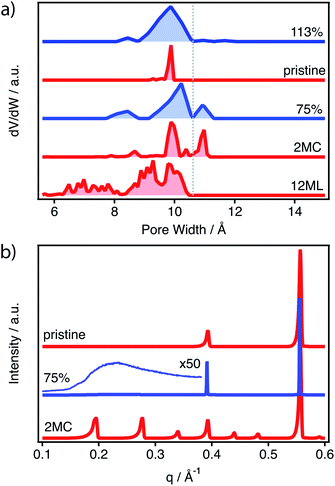
The simulation of the pore size distributions of the different configurations with Zeo++ (ref. 34) shows clear differences that can be associated with each type of defect. Compared to the perfect MUV-10 lattice that shows a single contribution centred around 10 Å, the introduction of missing clusters features a distinctive contribution at 11 Å, which differentiates it from the heterogeneous contributions that are generated only below 10 Å for the missing linker case. The N2 isotherm of MUV-10 75% was used to model its experimental PSD by using Nonlinear Density Functional Theory (NLDFT). Fig. 4a shows that the defective framework combines the micropore intrinsic to the perfect lattice with two additional narrow signals corresponding to smaller and bigger micropores centred at 8.3 and 11 Å, respectively. Comparison with the average PSD curves corresponding to the missing cluster or missing linker type of defects indicates that the porosity in defective MUV-10 75% is dominated by the generation of missing cluster vacancies. For a detailed analysis of the PSD curved calculated for all configurations see ESI Section S4.1.†
To evaluate the possible formation of correlated defect domains in this sample, we analysed this sample with X-ray synchrotron radiation at ALBA (BL04-MSPD).35 PXRD patterns of the defective structures were simulated from the corresponding computational models (ESI Section S4.2†).36Fig. 4b shows the PXRD patterns of pristine MUV-10, MUV-10 75% and the simulation of the 2MC and pristine models. Structurally long-range correlated defects shall result in characteristic superlattice diffraction lines below Q = 0.35 Å−1. However, the high scattering at low angles of the defective sample collected at λ = 0.9532 Å does not permit to identify these characteristic features for definitive confirmation. Superlattice lines are replaced by a diffuse scattering, which forms in the background and can be attributed to short-range ordering.37 In such cases, the scattering at small angles becomes less intense and low broad maxima appear in the pattern. Furthermore, these maxima are usually located at the same angular positions as the sharp superlattice lines formed by long-range ordering.37 In addition, the low scattering factor of titanium seems to impose drastic limitations in this regard. Although this limitation has been nicely overcome in the case of Zr-MOFs by replacement with Hf(IV),13 the synthesis of MUV-10(Hf) derivatives is not straightforward.
Conclusions
We show that the synthesis of MUV-10 at sub-stoichiometric linker regimes facilitates the formation of defected phases dominated by missing cluster vacancies. Preliminary analysis based on compositional NMR/TGA models confirms the formation of defective phases but does not allow for a clear understanding of the predominant type of defects. This is accounted for by complementing the experimental data with computational analysis. The structural models generated for missing cluster and missing linker defects can be used to differentiate between both cases by direct correlation with changes in experimental pore size distribution. Our results confirm that the porosity of MUV-10 75% can be only ascribed to the generation of missing cluster vacancies by the presence of bigger micropores cannot be accounted for by the missing linker defects. Our work also reveals the short-range ordering of Ti-MOFs and the limitations of X-ray diffraction to analyze defect correlation in Ti-MOFs due to the limiting scattering factor of titanium compared to Zr or Hf. Direct proof of correlated disorder in this family of materials will certainly require high-resolution microscopy experiments15 that are currently in progress.Data availability
The structural models that correspond to the defective structures have been uploaded as separate CIF files. Additional experimental information on the synthesis and characterization of the materials are included in the ESI.†Author contributions
I. A.-L. prepared the materials and carried out the characterizations. N. A.-B. and S. T. generated the computational models and performed the corresponding analysis of porosity. C. P. performed the synchrotron diffraction experiments. All authors discussed the results, provided critical insights for the analysis and discussion and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the European Union (ERC Stg Chem-fs-MOF 714122), by the Horizon 2020 research and innovation programme under the Marie Skłodowska grant agreement no 837804 (DefTiMOFs, MSCA-IF-2018) and by the Spanish government (CEX2019-000919-M, RTI2018-098568-A-I00 & RYC-2016-1981). We also thank BSC-RES for computational resources (QS-2020-2-0024) and the University of Valencia for research facilities. C. P is thankful for the financial support of the Spanish Mineco Project No. FIS2017-83295-P. Synchrotron powder x-ray diffraction experiments were performed at the Materials Science and Powder Diffraction beamline of ALBA Synchrotron (Alba Experiment No. 2020094558).References
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. V. de Walle, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- S. Dissegna, K. Epp, W. R. Heinz, G. Kieslich and R. A. Fischer, Adv. Mater., 2018, 140, 11581–11584 CAS.
- S. Dissegna, P. Vervoorts, C. L. Hobday, T. Düren, D. Daisenberger, A. J. Smith, R. A. Fischer and G. Kieslich, J. Am. Chem. Soc., 2018, 140, 11581–11584 CrossRef CAS.
- A. D. Vos, K. Hendrickx, P. V. D. Voort, V. V. Speybroeck and K. Lejaeghere, Chem. Mater., 2017, 29(7), 3006–3019 CrossRef PubMed.
- G. C. Shearer, S. Chavan, S. Bordiga, S. Svelle, U. Olsbye and K. P. Lillerud, Chem. Mater., 2016, 28, 3749–3761 CrossRef CAS.
- W. Liang, C. J. Coghlan, F. Ragon, M. Rubio-Martinez, D. M. D'Alessandro and R. Babarao, Dalton Trans., 2016, 45, 4496–4500 RSC.
- F. G. Cirujano, A. Corma and F. X. L. i Xamena, Catal. Today, 2015, 257, 213–220 CrossRef CAS.
- F. Vermoortele, B. Bueken, G. L. Bars, B. V. de Voorde, M. Vandichel, K. Houthoofd, A. Vimont, M. Daturi, M. Waroquier, V. V. Speybroeck, C. Kirschhock and D. E. D. Vos, J. Am. Chem. Soc., 2013, 135, 11465–11468 CrossRef CAS PubMed.
- L. M. R. Albelo, E. L. Maya, S. Hamad, A. R. Ruiz-Salvador, S. Calero and J. A. R. Navarro, Nat. Commun., 2017, 8, 14457–14467 CrossRef PubMed.
- F. Vermoortele, R. Ameloot, L. Alaerts, R. Matthessen, B. Carlier, E. V. R. Fernandez, J. Gascon, F. Kapteijn and D. E. D. Vos, J. Mater. Chem., 2012, 22, 10313–10321 RSC.
- Z. Fang, B. Bueken, D. E. D. Vos and R. A. Fischer, Angew. Chem., Int. Ed., 2015, 54, 7234–7254 CrossRef CAS.
- L. Valenzano, B. Civalleri, S. Chavan, S. Bordiga, M. H. Nilsen, S. Jakobsen, K. P. Lillerud and C. Lamberti, Chem. Mater., 2011, 23, 1700–1718 CrossRef CAS.
- M. J. Cliffe, W. Wan, X. Zou, P. A. Chater, A. K. Kleppe, M. G. Tucker, H. Wilhelm, N. P. Funnell, F.-X. Coudert and A. L. Goodwin, Nat. Commun., 2014, 5, 4176–4184 CrossRef CAS.
- D. N. Johnstone, F. C. N. Firth, C. P. Grey, P. A. Midgley, M. J. Cliffe and S. M. Collins, J. Am. Chem. Soc., 2020, 142, 13081–13089 CrossRef CAS.
- L. Liu, Z. Chen, J. Wang, D. Zhang, Y. Zhu, S. Ling, K.-W. Huang, Y. Belmabkhout, K. Adil, Y. Zhang, B. Slater, M. Eddaoudi and Y. Han, Nat. Chem., 2019, 11, 622–628 CrossRef CAS PubMed.
- M. Taddei, Coord. Chem. Rev., 2017, 343, 1–24 CrossRef CAS.
- X. Chen, Y. Lyu, Z. Wang, X. Qiao, B. C. Gates and D. Yang, ACS Catal., 2020, 10, 2906–2914 CrossRef CAS.
- F. C. N. Firth, M. J. Cliffe, D. Vulpe, M. Aragones-Anglada, P. Z. Moghadam, D. Fairen-Jimenez, B. Slater and C. P. Grey, J. Mater. Chem. A, 2019, 7, 7459–7469 RSC.
- A. K. Cheetham, T. D. Bennett, F.-X. Coudert and A. L. Goodwin, Dalton Trans., 2016, 45, 4113–4126 RSC.
- P. Z. Moghadam, A. Li, S. B. Wiggin, A. Tao, A. G. P. Maloney, P. A. Wood, S. C. Ward and D. Fairen-Jimenez, Chem. Mater., 2017, 29, 2618–2625 CrossRef CAS.
- I. A. Lázaro, N. Almora-Barrios, S. Tatay and C. Martí-Gastaldo, Chem. Sci., 2020, 12, 2586–2593 RSC.
- J. Castells-Gil, N. M. Padial, N. Almora-Barrios, J. Albero, A. R. Ruiz-Salvador, J. González-Platas, H. García and C. Martí-Gastaldo, Angew. Chem., Int. Ed., 2018, 57, 8453–8457 CrossRef CAS PubMed.
- C. R. Marshall, S. A. Staudhammer and C. K. Brozek, Chem. Sci., 2019, 10, 9396–9408 RSC.
- R. S. Forgan, Chem. Sci., 2020, 11, 4546–4562 RSC.
- C. R. Marshall, E. E. Timmel, S. A. Staudhammer and C. K. Brozek, Chem. Sci., 2020, 11, 11539–11547 RSC.
- B. Bueken, N. V. Velthoven, A. Krajnc, S. Smolders, F. Taulelle, C. Mellot-Draznieks, G. Mali, T. D. Bennett and D. D. Vos, Chem. Mater., 2017, 29, 10478–10486 CrossRef CAS.
- G. Cai and H.-L. Jiang, Angew. Chem., Int. Ed., 2017, 56, 563–567 CrossRef CAS.
- E. López-Maya, N. M. Padial, J. Castells-Gil, C. R. Ganivet, A. Rubio-Gaspar, F. G. Cirujano, N. Almora-Barrios, S. Tatay, S. Navalón and C. Martí-Gastaldo, Angew. Chem., Int. Ed., 2021, 60, 11868–11873 CrossRef.
- I. A. Lázaro, Eur. J. Inorg. Chem., 2020, 2020, 4284–4294 CrossRef.
- J. Marreiros, C. Caratelli, J. Hajek, A. Krajnc, G. Fleury, B. Bueken, D. E. D. Vos, G. Mali, M. B. J. Roeffaers, V. V. Speybroeck and R. Ameloot, Chem. Mater., 2019, 31(4), 1359–1369 CrossRef CAS.
- G. C. Shearer, S. Chavan, J. Ethiraj, J. G. Vitillo, S. Svelle, U. Olsbye, C. Lamberti, S. Bordiga and K. P. Lillerud, Chem. Mater., 2014, 26, 4068–4071 CrossRef CAS.
- K. Okhotnikov, T. Charpentier and S. Cadars, J. Cheminf., 2016, 8, 17–32 Search PubMed.
- R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. de Leeuw, J. Phys.: Condens. Matter, 2007, 19, 256201–256218 CrossRef.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- F. Fauth, I. Peral, C. Popescu and M. Knapp, Powder Diffr., 2013, 28, S360–S370 CrossRef CAS.
- D. Kriegner, E. Wintersberger and J. Stangl, J. Appl. Crystallogr., 2013, 46, 1162–1170 CrossRef CAS PubMed.
- B. D. Cullity and S. R. Stock, Elements of X-ray Diffraction, Prentice Hall, 2001 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc02408f |
| This journal is © The Royal Society of Chemistry 2021 |