Open Access Article
Open Access ArticleResolving the ultrafast dynamics of the anionic green fluorescent protein chromophore in water†
Chey M.
Jones
 ab,
Nanna H.
List
ab,
Nanna H.
List
 ab and
Todd J.
Martínez
ab and
Todd J.
Martínez
 *ab
*ab
aDepartment of Chemistry and the PULSE Institute, Stanford University, Stanford, CA 94305, USA. E-mail: toddjmartinez@gmail.com
bSLAC National Accelerator Laboratory, 2575 Sand Hill Road, Menlo Park, CA 94025, USA
First published on 13th July 2021
Abstract
The chromophore of the green fluorescent protein (GFP) is critical for probing environmental influences on fluorescent protein behavior. Using the aqueous system as a bridge between the unconfined vacuum system and a constricting protein scaffold, we investigate the steric and electronic effects of the environment on the photodynamical behavior of the chromophore. Specifically, we apply ab initio multiple spawning to simulate five picoseconds of nonadiabatic dynamics after photoexcitation, resolving the excited-state pathways responsible for internal conversion in the aqueous chromophore. We identify an ultrafast pathway that proceeds through a short-lived (sub-picosecond) imidazolinone-twisted (I-twisted) species and a slower (several picoseconds) channel that proceeds through a long-lived phenolate-twisted (P-twisted) intermediate. The molecule navigates the non-equilibrium energy landscape via an aborted hula-twist-like motion toward the one-bond-flip dominated conical intersection seams, as opposed to following the pure one-bond-flip paths proposed by the excited-state equilibrium picture. We interpret our simulations in the context of time-resolved fluorescence experiments, which use short- and long-time components to describe the fluorescence decay of the aqueous GFP chromophore. Our results suggest that the longer time component is caused by an energetically uphill approach to the P-twisted intersection seam rather than an excited-state barrier to reach the twisted intramolecular charge-transfer species. Irrespective of the location of the nonadiabatic population events, the twisted intersection seams are inefficient at facilitating isomerization in aqueous solution. The disordered and homogeneous nature of the aqueous solvent environment facilitates non-selective stabilization with respect to I- and P-twisted species, offering an important foundation for understanding the consequences of selective stabilization in heterogeneous and rigid protein environments.
Introduction
Since their initial characterization in Aequorea victoria,1–5 fluorescent proteins (FPs) have emerged as powerful probes for in vivo biological function.6–11 The green fluorescent protein8 (GFP) is the monarch of FPs, and its utility and versatility keep the green fluorophore at the forefront of science. Seminal experiments on the color and protonation state tuning of GFP12–17 inspired novel FP biomarkers, with reversible photoswitchable FPs propelling image resolution beyond the diffraction limit.16–18 Located at the heart of GFP, a tunable chromophore is responsible for GFP's light emission. Because the native characteristics of GFP can be altered significantly by applying point mutations near the site of the chromophore,8 we need a detailed understanding of the chromophore's local steric and electronic environment to optimize the versatility of GFP. Frequently, p-hydroxybenzylidene-2,3-dimethylimidazolinone (HBDI), first synthesized by Kojima et al.,19 serves as a model GFP chromophore. In particular, the anionic form of HBDI (HBDI−) mimics the protonation state of the chromophore responsible for fluorescence in the protein.20,21The overwhelming number of variables in a complex protein environment creates a fundamental roadblock to the rational design of FPs. Due to the rigidity of its 11-stranded β-barrel,22,23 GFP envelops its chromophore in a highly ordered pocket of amino acids. Stiff protein backbones foster heterogeneous electronic and steric fingerprints that can significantly impact the chromophore's behavior.8 Because amino acids in GFP form complex networks of covalent and non-covalent interactions, it is difficult to predict the net effect of various residues acting on the chromophore. To filter out the effects that dictate chromophore behavior, we use HBDI− to monitor the molecule's response to incremental perturbations of the environment. Using the gas-phase dynamics of HBDI− as a baseline,24 we identify the influence of steric and electronic effects on chromophore behavior in solution, focusing on the homogeneous and disordered case of aqueous HBDI−.
Solvated HBDI− straddles the line between the freedom permitted by the gas-phase and the confinement imposed by a protein. In water, HBDI− experiences steric and electronic effects from the solvent, which are absent in vacuo, while in an environment that is less constricting than a protein scaffold. Time-resolved spectroscopies reveal that GFP has an excited-state lifetime on the order of nanoseconds20,25,26 and a fluorescence quantum yield near unity.8 Yet, HBDI− experiences ultrafast internal conversion in vacuum and in solution at ambient temperature.27–31 Twisting around the bridge bonds connecting the imidazolinone (I) and phenolate (P) moieties of the isolated chromophore leads to ultrafast deactivation that decreases fluorescence quantum yield.31–33 As highlighted in previous computational studies,34,35 non-methylated HBDI− (pHBI−) undergoes twisted intramolecular charge-transfer (TICT) as rotations of the I- and P-moieties become sufficiently large. The direction of charge-transfer (CT) on the excited state depends on whether rotation occurs along the I- or P-dihedral (ϕI/ϕP dihedrals illustrated in Fig. 1, respectively). Whereas rotation of ϕI induces CT from the I-ring to the P-ring in the gas-phase, rotation of ϕP induces CT from the P-ring to the I-ring.
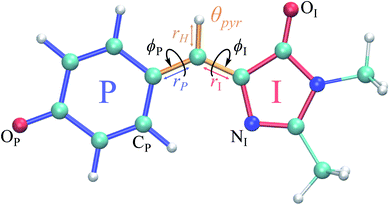 | ||
Fig. 1 Structure of the HBDI− model chromophore illustrating key geometric parameters. Cyan atoms represent carbon, red atoms represent oxygen, blue atoms represent nitrogen, and white atoms represent hydrogen. Blue, red, and orange bonds connect atoms belonging to the P-ring, I-ring, and methine bridge, respectively. ϕI is defined as the dihedral angle formed by NI and the carbon atoms of the methine bridge. ϕP is defined as the dihedral angle formed by the carbon atoms of the methine bridge and CP. The pyramidalization of the central methine carbon atom, θpyr, is calculated as 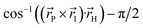 and uses the bridge bond vectors in a method similar to Radhakrishnan et al.71 For reference, the pyramidalization angles of ideal sp2 and sp3 hybridized carbon atoms using this definition are 0° and 55°, respectively. and uses the bridge bond vectors in a method similar to Radhakrishnan et al.71 For reference, the pyramidalization angles of ideal sp2 and sp3 hybridized carbon atoms using this definition are 0° and 55°, respectively. | ||
Using ultrafast fluorescence and polarization spectroscopy experiments,27,36,37 Meech and co-workers identified similar short (hundreds of femtoseconds) and long (picoseconds) decay components for HBDI− across a variety of solvents. In water, time constants of 210 fs and 1.1 ps were reported for fluorescence decay—significantly faster than the 1.3/11.5 ps excited-state lifetimes reported in vacuo.21,30 Early quantum chemical calculations on gas-phase pHBI−38 suggested that a volume-conserving “hula-twist” deactivation mechanism39,40 is responsible for the limited sensitivity of the chromophore's excited-state lifetime on solvent viscosity. However, more recent calculations implicate drastic torsional motion along either of the methine bridge bonds as responsible for the ultrafast deactivation of the anionic chromophore.34,41 This behavior is corroborated by high-level quantum mechanics/molecular mechanics (QM/MM) simulations in water using extended multistate multireference second-order perturbation theory (XMS-CASPT2)42 and spin-flip time-dependent density functional theory.43 These studies found that the dominant decay pathway of pHBI− is through the I-twisted channel. However, the limited simulation time considered (1 ps) did not allow identification of the sources responsible for the multi-timescale decay in solution. To resolve this, we simulate multiple picoseconds of the aqueous HBDI− photodynamics while monitoring important geometric and electronic features of the system.
Ultrafast dispersed pump-dump-probe experiments of HBDI− in water present excited-state decay lifetimes in the 620–940 fs range for twisted excited-state intermediates.44 Although the imperfect selectivity of a dump pulse may make it difficult to attribute time constants to specific processes, the Z/E isomerization quantum yield derived from these experiments was below the detection threshold of ∼5%. Solution-phase studies on the chromophore's protonated counterpart, HBDI, demonstrate that the solvent can have a noticeable impact on isomerization quantum yield.45,46 In aprotic solvents, HBDI recorded Z/E photoisomerization quantum yields of ∼50%. This yield drops to ∼10–20% in protic solvents, where excited-state proton transfer is a competing process. While torsion along ϕI can result in the E-isomer (Z/E isomerization), torsion along ϕP will regenerate the Z-isomer due to the symmetry of the P-ring (Z/Z isomerization). Thus, Z/Z isomerization products are experimentally indistinguishable from decay pathways that do not involve isomerization. For this reason, it remains unclear what ratio of excited-state species proceeds toward photoproduct formation (Z/E isomerization), undergoes P-ring flip (Z/Z isomerization), or re-populates the original ground state (Z-isomer).
A key ingredient of QM/MM (or fully QM) simulations of photochemistry is the proper description of the potential energy surface topography around conical intersections (CIs). Many electronic structure methods are not capable of correctly describing S0/S1 CI regions47–49 (e.g. time-dependent density functional theory and other single-reference methods). Following our recent gas-phase study,24 we use the α-CASSCF method,50 which provides a correct and efficient description of the exact degeneracy and relative energetics along key deactivation coordinates. This enables us to extend our simulations to multiple picoseconds. Consequently, we are able to monitor the chromophore's approach toward the CI seams and provide predictions for the photoproduct branching. The shape of CIs (e.g. peaked vs. sloped) can also be critically important in determining the photoproducts.51–54 Although it appears that the CIs become more peaked upon solvation for the neutral GFP chromophore55,56 (suggesting a shortening of the excited-state lifetime and a larger isomerization quantum yield), the shape of the CIs that govern nonadiabatic transitions for HBDI− in water has been largely unexplored.
Recent femtosecond stimulated Raman spectroscopy (FSRS) and transient absorption experiments of aqueous HBDI−31 fill in some of the gaps left by ultrafast fluorescence experiments. While time-resolved fluorescence experiments elucidate the temporal signatures of highly fluorescent HBDI− species, i.e., closer to the Franck–Condon (FC) point, FSRS is able to track the progression of HBDI− along vibrational modes of dark, non-fluorescent species. FSRS studies yield three time constants for the excited-state dynamics of HBDI−: ∼350 fs, 2–3 ps, and ∼250 ps.31 These were tentatively assigned to the formation of a charge-separated (CS) species, the transition from the CS state to a TICT state, and ground-state recovery of the Z-isomer, respectively.
In this work, we explore the internal conversion dynamics following photoexcitation of explicitly-solvated HBDI−. Using ab initio multiple spawning57–61 (AIMS), we provide insight into the primary deactivation pathways in aqueous solution and each pathway's relative accessibility to CIs. In particular, we investigate the characteristics of HBDI− (i) at the FC region, (ii) out of the FC region as the molecule approaches CI seams, (iii) upon encountering the CI seam, and (iv) away from the CI seam as it returns to the ground state. This non-equilibrium picture (chromophore and solvent response) is compared to the corresponding excited-state equilibrium solvation picture, defined by the free energy surface of aqueous HBDI−. Our results are interpreted in the context of previous experiments performed in silico, in vacuo, and in solution. Using this approach, we discuss the impact of solvation on HBDI− and develop a more complete picture of GFP chromophore photophysics.
Computational details and methods
Because of its efficiency and ability to describe CIs, state-averaged62 complete active space self-consistent field (SA-CASSCF)63–65 was chosen as the electronic structure method for HBDI− in water. To increase the accuracy of SA-CASSCF, we correct for the lack of dynamic electron correlation in SA-CASSCF calculations by using α-CASSCF50 (Fig. S1†). The α-CASSCF method uses energy scaling to approximate the effects of dynamic electron correlation at the cost of traditional SA-CASSCF,66 similar to previous scaling methods introduced by Olivucci and coworkers.67 Orbitals are optimized to minimize the average energy of the three lowest singlet electronic states in SA-CASSCF, as this has been shown to provide an accurate excited-state description of I- and P-torsional pathways.68 In particular, inclusion of three states captures the P-twisted minimum energy conical intersection (MECI) of HBDI−, which can be elusive when using a two-state averaging method with CASSCF.69 An active space of four electrons in three orbitals, i.e., SA3-CASSCF(4,3), incorporates the bonding, non-bonding and anti-bonding π-orbitals relevant to describe the allylic anionic character of the methine bridge (Fig. 2). Unless stated otherwise, the 6-31G* basis set70 is used throughout.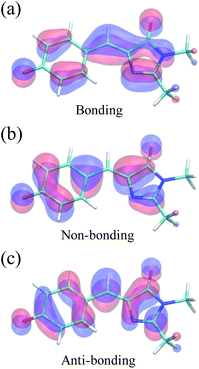 | ||
| Fig. 2 Active space orbitals of HBDI− from α(0.67)-SA3-CASSCF(4,3) at the FC point: the anionic, allylic (a) bonding, (b) non-bonding, and (c) anti-bonding orbitals. | ||
The α parameter was chosen to reproduce the S0 → S1 vertical excitation energy of the planar chromophore in solution, computed with the SA3-XMS-CASPT2(4,3) method72–74 (1s orbitals of heavy atoms were excluded from the perturbation treatment and a level shift of 0.3 a. u. was used). This led to an α value of 0.67 for hydrated HBDI− (Fig. S1†). This is very similar to the α value of 0.64 which we found for isolated HBDI− (used in the gas-phase calculations reported herein).24 As shown in Fig. S1,† this α-CASSCF method reproduces XMS-CASPT2 potential energy profiles along the two bridge torsional coordinates (ϕI and ϕP). Unless otherwise stated, all calculations were performed with α(0.67)-SA3-CASSCF(4,3)/6-31G* in explicit solvent. Relative energies, geometric parameters, and transition dipole moments of representative optimized geometries are provided in the ESI† (Fig. S1–S3 and Tables S1–S4). Fractional occupation number Hartree–Fock (FON–HF) was used to determine initial guess orbitals for the α-CASSCF calculations (using Gaussian broadening with an electronic temperature of 0.3 a. u.).75–78
Critical points were obtained using the DL-FIND geometry optimization library.79 Electronic structure calculations were performed with TeraChem.80–84
Solvated initial conditions
A Boltzmann sampling procedure provided initial conditions (ICs) for the solvated chromophore. Using PACKMOL,85 HBDI− was immersed in a solvent sphere comprised of 2000 water molecules and a sodium counterion. The radius of the solvation sphere was 24.3 Å, consistent with the density of liquid water (0.997 g mL−1). Classical dynamics were run with OpenMM,86 and a restraining spherical force of 10 kcal mol−1 Å−2 was applied to the water sphere during the dynamics. The solvent was equilibrated by performing a 5 ns NVT classical dynamics simulation, using a Langevin thermostat at 300 K, with the geometry of the chromophore fixed. Water molecules were treated with the flexible SPC/Fw model,87 and the sodium ion was modelled using van der Waals parameters previously determined for use in SPC/E water.88 Atomic charges for the chromophore were fit using the restrained electrostatic potential89 procedure with HF/6-31G*, based on the B3LYP-D3/6-31G** optimized geometry of the chromophore in the gas-phase.90–92 Van der Waals parameters for the chromophore were taken from the general Amber force field.93 Other force field parameters (such as equilibrium bond lengths/angles and associated force constants) are irrelevant because the chromophore was kept fixed during the MM simulations used to relax the solvent environment.Following the initial solvent equilibration, the geometric constraints on the chromophore were lifted and a 10 ps ground-state QM/MM molecular dynamics (QM/MM-MD) trajectory, within the NVT ensemble, was run to obtain ICs for the nonadiabatic dynamics simulations. The chromophore was treated at the QM level (described above), whereas the waters and sodium ion were treated at the MM level. A D3 dispersion correction was included for the QM region, using Hartree–Fock parameters.92 Spherical boundary conditions were again employed to avoid evaporation of water molecules. QM/MM-MD simulations were performed with a Langevin thermostat at 300 K, using the time-reversible Niklasson integrator94 and a time step of 0.5 fs. After an equilibration period of 3 ps, a total of 500 temporally-equidistant samples were extracted from the remaining 7 ps of QM/MM-MD to generate an absorption spectrum. The stick spectra were convolved with a Gaussian lineshape function, using a full width at half maximum (FWHM) of 0.40 eV based on solution-phase experiments.95
Nonadiabatic dynamics
A total of 50 ICs were extracted from the 500 QM/MM-MD samples (every tenth IC) and used to initiate AIMS simulations within the independent first generation approximation.60,61 Using this sampling procedure, we minimize the correlation between ICs. Moreover, this sampling procedure enables us to partition ICs based on their location in the aqueous HBDI− absorption spectrum, which is necessary to investigate the wavelength dependence of excited-state deactivation. ICs are classified as either red-shifted or blue-shifted based on their excitation energy relative to the computed absorption maximum (computed as 2.84 eV, compared to the measured value of 2.91 eV (ref. 31 and 95)). When comparing our simulations to experiment, it should be noted that the wavelength of the pump used in previous time-resolved spectroscopy experiments31,96 was on the blue-edge of the spectrum (400 nm, i.e., 0.2 eV blue-shifted from the absorption maximum). The AIMS simulations were continued for 5 ps or until at least 99% of the excited-state population for a given initial trajectory basis function (TBF) was transferred to the ground state. If a TBF on S0 went at least 5 fs without coupling with another TBF (as measured by the TBF overlap, with a threshold of 0.6), the TBF on S0 was removed from the set of coupled TBFs and run independently for the remainder of the simulation. The threshold for spawning (based on the dot product of the nonadiabatic coupling vector and the velocity) was defined as 0.005 a.u. The spherical boundary conditions applied for QM/MM-MD were employed during the AIMS dynamics as well. Error bars for exponential fitting of the S1 population were obtained using a bootstrapping method97 that included 1000 bootstrapping samples. To gauge the branching ratio of photoproducts from AIMS dynamics, each spawned TBF on S0 was propagated independently for an additional 500 fs. By the end of the extended ground-state dynamics, the TBFs were classified based on the ϕI and ϕP values of their S0 nuclear configuration. If the magnitude of either dihedral was above 120°, the product was classified as isomerized with respect to that angle. The resulting photoproducts were used to quantify photoisomerization quantum yield. Geometric analysis of AIMS trajectories was aided by MDTraj.98Umbrella sampling
To provide insight regarding the free energy landscape and entropic effects of HBDI− in water, QM/MM umbrella sampling at 300 K was performed on S1. A two-dimensional mapping was performed along the ϕI and ϕP twisting coordinates (ranging from −120° to 120°, using 10° intervals for a total of 625 sampling windows). To compensate for incomplete sampling of solvent configurations, we augmented the data to incorporate the symmetry with respect to twisting of the ϕI and ϕP dihedral angles (Fig. S4†). Specifically, each data point (i.e., energy, oscillator strength) for an observed geometry contributed to two data points: one for the observed geometry and one for its enantiomer, where ϕenantiomer = −ϕobserved for both ϕI and ϕP. Convergence analysis of the two-dimensional free energy surface indicated that an equilibration time of 1.5 ps for each window provided a sufficient compromise between sampling and computational cost (Fig. S5†). After the equilibration, 2 ps of data was collected for each window to generate the potential of mean force99 (PMF). In total, over 2 ns of excited-state QM/MM-MD simulations were run to obtain the free energy surface. A harmonic biasing potential with a force constant of 100 kcal mol−1 Å−2 was applied to both dihedrals. Contour plots were generated using a cubic interpolation between points on the free energy grid obtained from unbiasing a set of biased sampling windows via the weighted histogram analysis method.100,101Time-resolved fluorescence
Two-dimensional fluorescence spectra of HBDI− were generated based on the AIMS simulations. Spectra were obtained as: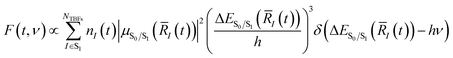 | (1) |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) I) represents the S0/S1 energy gap, and
I) represents the S0/S1 energy gap, and ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) I(t) is the position centroid of the Ith TBF at time t.102 The time-resolved fluorescence spectra were convolved with a Gaussian having FWHM of 0.15 eV in the energy domain (ν) and 100 fs in the temporal domain (t) to simulate the instrument response function of previous fluorescence up-conversion experiments.27,103 For each two-dimensional fluorescence spectrum, the energy was shifted by 0.13 eV to align the fluorescence intensity maxima obtained from theory and experiment (vide infra).31 Once shifted, the decay signal corresponding to an intensity slice at 500 nm was extracted and analyzed to elucidate the fluorescence behavior of HBDI− over the course of the dynamics.
I(t) is the position centroid of the Ith TBF at time t.102 The time-resolved fluorescence spectra were convolved with a Gaussian having FWHM of 0.15 eV in the energy domain (ν) and 100 fs in the temporal domain (t) to simulate the instrument response function of previous fluorescence up-conversion experiments.27,103 For each two-dimensional fluorescence spectrum, the energy was shifted by 0.13 eV to align the fluorescence intensity maxima obtained from theory and experiment (vide infra).31 Once shifted, the decay signal corresponding to an intensity slice at 500 nm was extracted and analyzed to elucidate the fluorescence behavior of HBDI− over the course of the dynamics.
Results and discussion
To begin describing the effects of solvation, we observe how the absorption spectrum of HBDI−changes when the molecule is immersed in water. Fig. 3a compares the simulated and experimental absorption spectra of HBDI− in vacuum24 and aqueous solution. Solvation of HBDI− blue-shifts the absorption maximum (0.41 eV), as is also observed in experiment (0.32 eV).31,95,104 As summarized in Table S5,† the electronic properties of water are primarily responsible for blue-shifting the absorption maximum of HBDI− upon solvation (0.19 eV), whereas the geometric changes have a minimal contribution (0.03 eV) to the spectral shift. Radial distribution functions (RDFs), based on the ground-state QM/MM-MD, between water oxygen atoms and the heteroatoms in HBDI− provide a description of local solvation. As shown in Fig. 3b, the RDF for the OP atom indicates that it is more tightly coordinated to water than the OI atom. This is consistent with the enhanced charge localization on OP, relative to OI, in the ground state (see Fig. S6† for fragment-accumulated Mulliken charges).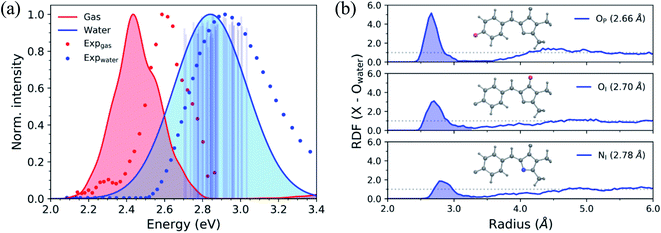 | ||
| Fig. 3 (a) Simulated absorption spectra of HBDI− in gas-phase (red) and water (blue) using 500 ICs from each system. Sticks represent the S0/S1 excitation energy and their relative oscillator strengths for the 50 solvated ICs used for AIMS simulations, at the α(0.67)-SA3-CASSCF(4,3)/6-31G* level. Individual sticks for gas-phase (FWHM of 0.07 eV) and aqueous (FWHM of 0.40 eV) systems were convolved with a Gaussian envelope based on experimental FWHM. Simulated gas-phase data was taken from List et al.,24 sampling from a 300 K harmonic Wigner distribution and using α(0.64)-SA3-CASSCF(4,3)/6-31G*. Experimental gas-phase and solvated chromophore spectra were obtained by digitizing data from Nielsen et al.104 and Andersen et al.,95 respectively. (b) Ground-state radial distribution functions of HBDI− heteroatoms (highlighted in each panel and identified in Fig. 1) in water. Shaded regions represent the first solvation shell. The dotted line represents a value of one, indicating that the solvent has reached bulk-like behavior. | ||
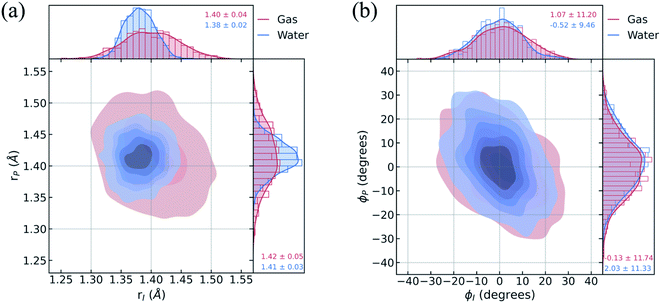
To understand the limited impact of geometric perturbations, we analyze the initial distribution of key geometric parameters to observe how the sampled configuration space changes upon solvation. Fig. 4a shows the bond length distributions for the bridge bonds, rI and rP, from the ground-state QM/MM-MD. In water, the bridge bonds of HBDI− sample a narrower region of configuration space when compared to vacuum. This difference is related to whether a quantum or classical sampling technique is used, as indicated by the similar configuration space sampled by gas-phase and solution-phase HBDI− using QM/MM-MD sampling in both instances (Fig. S7†). Distributions for the solvated ICs used for the AIMS dynamics are shown in Fig. S8.† The average rI-to-rP bond length ratio in water is consistent with a stabilization of the phenolate resonance structure, in line with the RDFs in Fig. 3b. Therefore, we verify that the phenolate resonance structure of HBDI− is favored throughout the ground-state dynamics in water, as suggested by calculations in a polarizable continuum water model.41 While the phenolate and quinoid resonance structures contribute almost equally in gas-phase,24,68 the decrease in the rI-to-rP ratio upon solvation indicates a preference toward the phenolate resonance structure in solution. Interestingly, the distributions along the ϕI and ϕP dihedrals (Fig. 4b) remain almost identical between systems. The striking similarity between these angular distributions indicates that the presence of mobile water molecules does not restrict the chromophore's motion along its twisting dihedrals on the ground state. The concerted rotation around the I- and P-bonds, which are connected by the methine bridge carbon atom and adjacent to one another, is reminiscent of hula-twist motion.39,40 However, we observe conrotatory rotation of ϕI and ϕP, as opposed to the volume-conserving disrotatory motion.105
Electronic effects of equilibrium solvation
Before investigating the photodynamics of HBDI−, we consider the excited-state landscape in the equilibrium solvation regime. Although the difference in time scales of HBDI− intramolecular vibrations and solvent relaxation (e.g. time constants of 0.16 and 1.2 ps were reported for solvent relaxation following photoexcitation of a coumarin dye106) means that an equilibrium picture is unlikely to pertain to the dynamics induced by photoexcitation, an excited-state PMF identifies the energetically favored configurations of aqueous HBDI− following excitation. In other words, the PMF indicates the stability of twisted HBDI− structures that are surrounded by (partially or fully) relaxed solvent configurations. Such insight is useful for categorizing stable excited-state intermediates and interpreting the photodynamics of aqueous HBDI−.The two-dimensional S1 umbrella sampling along the bridge dihedrals in Fig. 5 shows that single-bond twisting about either of the bridge bonds is favored. The resulting PMF highlights four energetic wells located near 90° I- and P-twisted structures on S1. Interestingly, the excited-state dynamics do not follow the minimum free energy path to reach these energetic wells (vide infra). Instead, the chromophore reaches highly-twisted configurations by following either the I- or P-channels illustrated in Fig. 5. Compared to the gas-phase photodynamics of HBDI−,24 the solvated chromophore exhibits more pronounced hula-twist-like (concerted single- and double-bond rotation) motion out of the FC region.
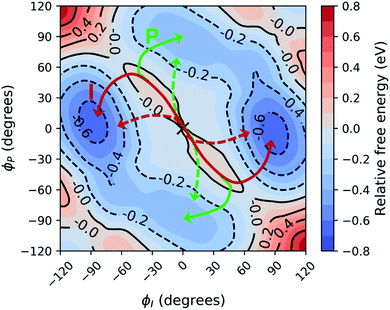 | ||
| Fig. 5 Relative free energy profile on S1 obtained from two-dimensional umbrella sampling along ϕI and ϕP. The zero point (marked with an “X”) corresponds to the planar structure. The observed deactivation pathways through I-twisting (red) and P-twisting (green) are depicted schematically. For reference, arrows with dashed lines represent deactivation pathways observed in gas-phase simulations.24 | ||
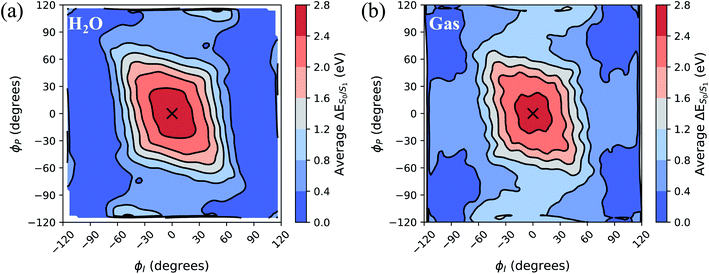
To separate out the electronic effects of equilibrium solvation, Fig. 6 displays the average S0/S1 energy gap across all windows in solvent and solvent-stripped configurations. In water (Fig. 6a), the observed minima along ϕI lie close to the CI seam, whereas rotation along ϕP leads to minima on S1 that are ∼1 eV removed from S0. This suggests that the I-twisted CI seam is more peaked than the P-twisted CI seam. The absence of electronic degeneracy associated with P-twisting hints that energetically and/or entropically unfavorable geometric changes are required to reach degeneracy along this pathway. Fig. 6b shows that I-twisted intermediates have lower S0/S1 energy gaps than those of P-twisted intermediates in the gas-phase, as observed in solution. This energetic asymmetry originates from the differences in electron affinity between the I- and P-rings.24 However, to conclude whether or not water stabilizes one twisted structure over the other, it is necessary to look at the energetic differences caused by solvation. The difference between water and gas-phase energy gaps (Fig. S9†) reveals that water introduces non-selective gap reduction (∼0.3 eV) for highly-twisted (∼90°) structures—the I- and P-twisted energy gaps decrease by approximately the same amount upon solvation. Yet, as previously discussed for Fig. 6a, the consequences of this gap reduction are significant. This equilibrium solvation picture suggests that (i) aqueous HBDI− proceeds along one-bond-flip-dominated coordinates toward the twisted CI seam, as in gas-phase,24 (ii) the I-twisted CI seam is more accessible than its P-twisted counterpart, and (iii) solvation promotes internal conversion through the I-twisted CI seam, similar to its neutral counterpart.55,56 Our nonadiabatic dynamics simulations of HBDI− show that (ii) and (iii) occur in water, while there is no evidence for (i). Rather than participating in a predominantly one-bond-flip mechanism (as in gas-phase), aqueous HBDI− reaches CI seams via an aborted hula-twist-like motion out of the FC region. Note that the concerted torsion is conrotatory as opposed to the more usual (for the hula-twist mechanism) disrotatory motion.
Nonadiabatic dynamics of HBDI− in water
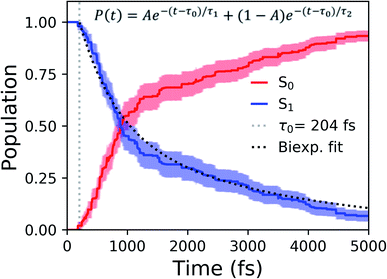
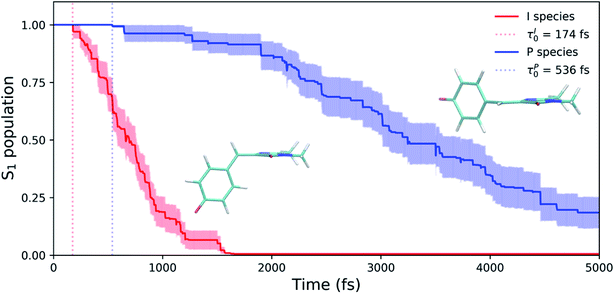
Shifting into the non-equilibrium regime (i.e., the solvent may not have enough time to relax around the chromophore), we analyze the behavior of aqueous HBDI− following photoexcitation. As shown by the S1 population decay in Fig. 7, over half of the excited-state population is transferred to the ground state within the first 1 ps. Such a rapid decay is consistent with the ultrafast deactivation reported in experiments.27,31,44 Yet, despite the sub-ps deactivation, a fraction of the population remains on the excited state for >5 ps. This biphasic pattern inspired a delayed bi-exponential fit to the decay profile: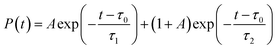 | (2) |
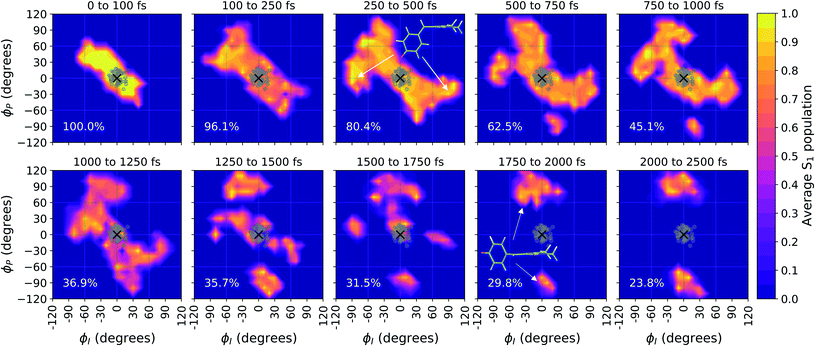
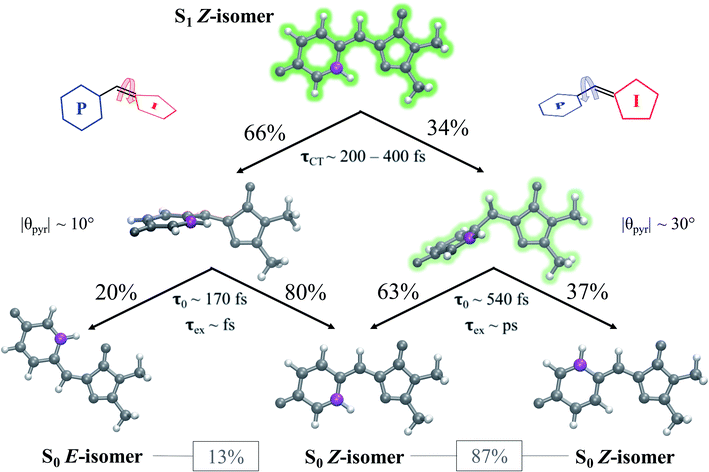
Viewing the dynamics within defined time intervals reveals novel information regarding the time scales of each deactivation pathway available to aqueous HBDI−—two distinct sub-populations exist with different excited-state lifetimes (Fig. 8). In accordance with the decreased electronic density along the methine bridge upon excitation (see Fig. 2) facile rotation along ϕI and ϕP is permitted on the excited state. Monitoring the S1 population over time, with respect to the ϕI and ϕP dihedrals, illustrates (i) the accessibility and (ii) the population transfer efficiency of each internal conversion pathway. During the first 100 fs, the S1 wavepacket remains localized near the FC region. Rather than following the minimum energy path along one-bond-flip coordinates (Fig. 5), the conrotatory hula-twist-like motion exhibited during the ground-state dynamics (Fig. 4b) is preserved. This indicates a non-equilibrium solvation regime where the response of the surrounding waters is too slow to impede the concerted rotation of ϕI and ϕP out of the FC region, which is otherwise associated with a small free energy barrier (less than 0.2 eV). Once the free energy barrier along this path becomes too large to overcome, the wavepacket bifurcates via a process that involves a one-bond-flip-like rotation along either ϕI or ϕP – with one path leading to highly I-twisted structures (I-channel) and the other path leading to highly P-twisted structures (P-channel). The branching associated with this mechanism becomes apparent by 500 fs as exploration into the I- and P-channels enables population transfer to the ground state. By 1 ps, motion along the torsional angles is more prominent as the I- and P-channels arise as the exclusive avenues for population transfer. Essentially no TBFs occupy near-planar configurations after 1.75 ps of dynamics, as four distinct regions in configuration space emerge as dihedral basins. These basins coincide with the energetic wells identified in Fig. 5. Interestingly, 250 fs later, no evidence of the I-twisted species is present while the P-twisted species remains on S1 for several picoseconds. The disappearance of the I-twisted species on S1 is explained by an ultrafast population transfer to the ground state, permitted by the near-degeneracy highlighted in Fig. 6a. For this part of the wavepacket, twisting along ϕI is enough to induce population transfer to the ground state. The persistence of the P-twisted species for several picoseconds on the excited state signifies that dihedral torsion around ϕP alone is insufficient to facilitate efficient population transfer. Rather, additional geometric requirements are necessary for the P-species to participate in internal conversion.
The time scale differences established in Fig. 8 were refined using the S1 population profiles for the I- and P-deactivating species (Fig. 9). In the case of I-twisted deactivation, the entire excited-state population is transferred to the ground state within ∼1.5 ps, with decay initiating at ∼175 fs. This rapid initiation and conclusion of population transfer for the I-species is due to an easily accessible I-twisted CI seam that efficiently transfers population to the ground state, in accordance with Fig. 6. On the other hand, the P-deactivation mechanism is associated with a species that remains on S1 for ∼540 fs before population transfer begins. Furthermore, this mode of population transfer is much slower and less efficient, as ∼10% of the population remains on the excited state after 5 ps. A similar analysis compares the deactivation of red-shifted and blue-shifted ICs (Fig. S10, and Table S6†). Data from this partitioning approach suggests that blue-shifted ICs deactivate faster than red-shifted ICs, but further investigations are required to reach a definitive conclusion.
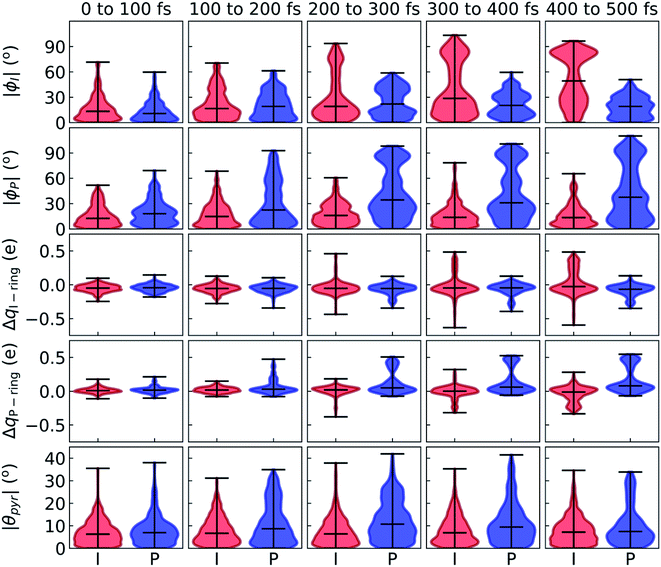
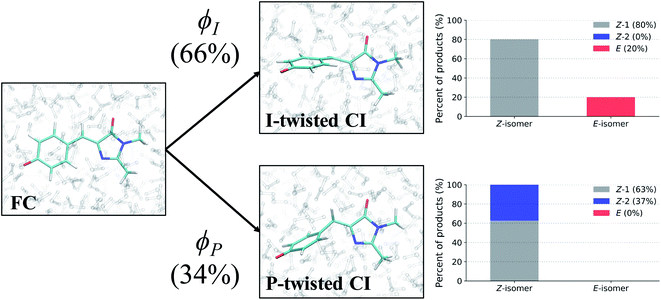
After identifying the characteristic twisting pathways, the dynamics out of the FC region were probed using various electronic and geometric parameters (Fig. 10, and S11†). Here, the parent TBFs are partitioned into I- and P-twisted species based on whether the I- or P-channel was taken, respectively. Our results corroborate that the dominant mode of deactivation (66%) is through torsion along ϕI, in agreement with nonadiabatic dynamics simulations at the XMS-CASPT2 (ref. 42) and spin-flip time-dependent density functional theory43 levels. The violin plots in Fig. 10 present the distribution of key electronic and geometric observables sampled across all parent TBFs of each species during the first 500 fs. Characteristic activity along the ϕI and ϕP twisting dihedrals is observed within the first 500 fs. As expected, the I-species samples along ϕI more aggressively than it does along ϕP, and the opposite behavior is true for the P-species. Worth noting, however, is the time scale at which both species reach ∼90° rotations of their respective dihedrals. Between 200 and 400 fs, both species begin to explore and populate these highly twisted configurations. As in the gas-phase,35 we observe that twisting along ϕI facilitates CT from the I-ring to the P-ring while twisting along ϕP facilitates CT from the P-ring to the I-ring. Furthermore, the molecule's rapid approach toward highly I- and P-twisted structures indicates that access to their respective TICT states is downhill in solution.
In the gas-phase, bond length alternation and bridge pyramidalization are the main coordinates used by HBDI− to reach the CI seam from the respective twisted S1 minimum.24 As shown in Fig. 10 (300–500 fs), displacement along the pyramidalization coordinate is attenuated for the I- and P-twisted species in solution relative to gas-phase (|θpyr| of 30° and 48° for I- and P-twisted MECIs,24 respectively). Because solvation essentially closes the energy gap of the I-twisted species but not completely for the P-twisted, the bridge pyramidalization requirement for reaching the I-twisted CI seam essentially vanishes. Compared to species along the I-channel, larger-amplitude displacements of the pyramidalization coordinate are required to trigger population transfer along the P-channel. This suggests that the path to the I-twisted CI seam is essentially energetically downhill, while it is uphill for the P-twisted case.
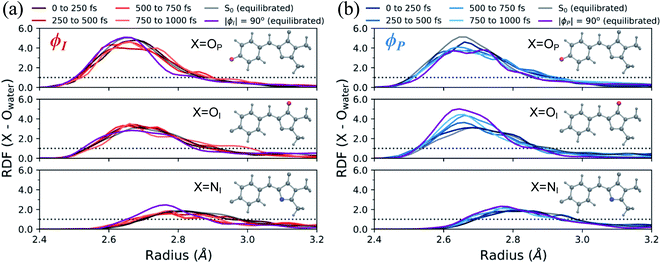
In addition to monitoring the geometric and electronic changes that occur during the first few hundred femtoseconds following photoexcitation, the response of the solvent during the first 1 ps was investigated. Fig. 11 shows the evolution of the first solvation peak for the parts of the wavepacket following the I- and P-twisted pathways. In the case of the I-deactivating species in Fig. 11a, there are no significant changes to the RDF profiles of OP, OI, or NI during the first 1 ps. This contrasts the evolution of RDFs for the same atoms in the P-deactivating species in Fig. 11b. Over the first 1 ps, the maximum of the first solvation peak for OP and OI gradually decreases and increases, respectively, toward the RDFs associated with equilibrated ϕP-twisted structures. This trend is consistent with the TICT behavior identified in Fig. 10. Upon torsion along ϕP, CT occurs from the P-ring to the I-ring. Consequently, a P-twisted intermediate will have (i) a more negative I-ring and (ii) a more positive P-ring than its pre-twisted counterpart. Thus, it is expected that the surrounding solvent would rearrange to compensate for this CT process by shifting increased solvent density from the OP atom toward the OI atom. Interestingly, the opposite trend is absent for the I-species. We attribute this difference to the disparate deactivation time scales along ϕI and ϕP that are presented in Fig. 9. Because deactivation through the I-channel occurs so rapidly, water does not have time to relax fully around I-twisted structures before internal conversion. Furthermore, we suspect that the ground-state solvent arrangement (Fig. 3b) is beneficial for facilitating ultrafast deactivation via I-twisting, since water is already preferentially localized around the P-ring prior to TICT. Such behavior explains the absence of large shifts of excited-state RDF peaks in Fig. 11a. On the other hand, deactivation through the P-channel is more gradual than decay through the I-channel, due to the barrier between the P-twisted CI seam and the corresponding TICT intermediate. Consequently, the solvent has time to reorient itself around P-twisted structures on the excited state. As a result, we observe gradual shifts of excited-state RDF peaks in Fig. 11b.
A geometric analysis at the points of population transfer elucidates the difference between the deactivation profiles of the I- and P-species. For I-deactivation, the spawning events that lead to population transfer generally occur near geometries with ϕI angles near 90° and ϕP angles that lie relatively close to planarity, and vice versa for P-deactivation (Fig. 12). The relationship between key dihedral and pyramidalization angles reveals that, in addition to lasting longer on S1, P-twisted TBFs demand larger pyramidalization angles than I-twisted TBFs to reach their respective CI seams. To investigate the implications of this difference, the absolute population transfer was calculated for each spawning event as a function of the pyramidalization and dihedral angle values upon entering the spawning region (Fig. 12a). Movie S1† provides a time lapse of these population and angle parameters to clarify this point. For a direct comparison of the spawned geometries associated with each pathway, the pyramidalization angle was measured for each spawned geometry of I-deactivating (Fig. 12b) and P-deactivating (Fig. 12c) TBFs. From these distributions, it is clear that pyramidalization requirements for P-deactivating TBFs are more demanding (peaked at ∼30°) than the requirements for I-deactivating TBFs (peaked at ∼10°). The larger pyramidalization angles needed to reach the P-twisted CI gate access to the P-twisted region of the CI seam. Therefore, we conclude that limited access to an uphill CI seam is responsible for the lingering S1 population of the P-species.
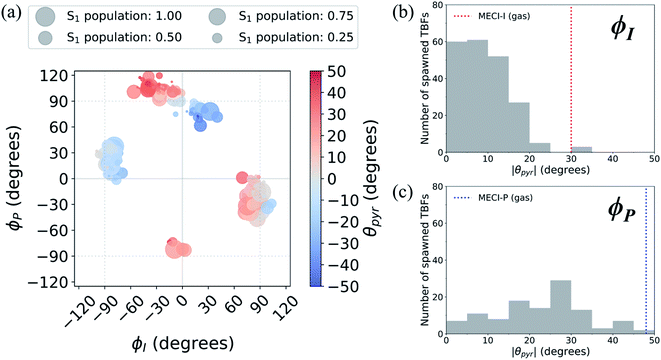 | ||
| Fig. 12 (a) Absolute population transfer and pyramidalization angle associated with the bridge carbon atom for spawned geometries of aqueous HBDI− from parent TBFs. Absolute population transfer is defined by the fraction of original S1 population transferred to S0. Plotted values of ϕI, ϕP, and θpyr characterize geometries that initiate population transfer. A histogram (using 5° bins) of pyramidalization angle magnitudes is provided for spawned TBFs that transfer population through torsion dominated by (b) ϕI or (c) ϕP twisting. Pyramidalization angles measured for I- and P-twisted MECIs in gas-phase24 are represented with vertical lines in (b) and (c). | ||
In addition to being more accessible than the P-twisted CI seam, the I-twisted CI seam appears to be more efficient at transferring population to the ground state. On average, population transfer events mediated by the I- and P-channels transfer 56 ± 32% and 35 ± 26% of the incoming S1 population to S0 per spawning event, respectively (Fig. S12†). This is expected based on the more direct approach toward the I-twisted CI seam, than for its P-twisted counterpart, as supported by Fig. 5 and 6. The uphill pyramidalization requirements and lack of efficiency explain the more gradual deactivation of the P-twisted species.
Relative to gas-phase HBDI−,24 aqueous HBDI− generally demands less pyramidalization to reach I- and P-twisted CI seams (Fig. 12b and c). This difference between systems becomes most apparent when comparing internal conversion tendencies associated with the I-channel. In gas-phase, I-twisted configurations transfer population to S0 while sampling along a larger range of ϕP values than in water. Based on our analysis regarding pyramidalization gating, we conclude that this behavior is due to the topology differences of the I-twisted CI seam across systems. Because solvation reduces the S0/S1 energy gap for I-twisted structures, aqueous HBDI− has smaller pyramidalization requirements to reach the I-twisted CI seam than does gas-phase HBDI−. Thus, I-twisted structures of the solvated chromophore spend less time sampling ϕP torsion than their gas-phase counterparts, as they undergo internal conversion through a near-barrierless process. The I-twisted spawning geometries of aqueous HBDI−, which are associated with ultrafast population transfer, are consistent with rapid accessibility out of the FC region via an aborted hula-twist-like mechanism (as presented in Fig. 8). Because reaching the aqueous P-twisted CI seam from a P-twisted TICT intermediate is an energetically uphill process, P-twisted intermediates significantly sample configurations where ϕP is above 90°. The enhanced sampling along this coordinate may explain the higher proportion of spawning geometries skewed toward the E-isomer, relative to this proportion for ϕI from I-twisted spawns (Fig. S13†).
Based on vibrational signatures obtained from FSRS experiments, Taylor et al. proposed that the formation of a CS species and the transition from this CS state to a TICT state were responsible for measured short (∼350 fs) and long (∼2–3 ps) time components, respectively.31 Our data suggests a different origin of these time constants. As supported by the substantial torsional displacements sampled within the first ∼200 fs (Fig. 10), the formation of TICT states is essentially barrierless. In other words, we do not see evidence of a non-twisted CS intermediate in water. Rather, we observe two competing processes: (i) an I-twisting process that easily reaches a downhill CI seam and (ii) a P-twisting process that encounters a barrier as it approaches an uphill CI seam. As an alternative, we propose that the accessibility of the I- and P-twisted CI seams, from the corresponding TICT states, is the primary factor responsible for the short (caused by mainly I-species) and long (caused by mainly P-species) time components reported from the FSRS experiments. However, rigorously establishing this interpretation of the FSRS fingerprints requires calculation of the vibrational signatures of I- and P-twisted structures and remains a task for future work.
Photoproducts
To evaluate the branching ratio of HBDI− upon deactivation to the ground state, dynamics on S0 were continued for an additional 500 fs (Fig. S14, and Table S7†). Classifying the resulting products provides an estimate for the branching ratio with respect to Z/E isomerization, Z/Z isomerization, and ground-state recovery of the Z-isomer. Most of the population (87%) returns to the Z-isomer (Fig. 13), in line with the low Z/E isomerization quantum yield reported from experiments.44–46 Despite I-torsion being the dominant deactivation pathway, associated CIs are highly inefficient at producing E photoproducts. Thus, HBDI− is much less efficient at generating E photoproducts in solution (∼13% yield) than in gas-phase (∼30% yield).24 Only 20% of the I-twisted spawns undergo Z/E isomerization. P-twisted CIs are more efficient (37%) at producing P-flipped products; however, the symmetry of the P-ring regenerates the Z-isomer whether or not the P-ring isomerizes. Verifying the Z/Z isomerization quantum yield experimentally would require asymmetric substitution on the P-ring. The respective isomerization quantum yields are likely linked to the barrier (or lack thereof) between the TICT state and CI seam associated with each pathway. Because the I-twisted CI seam is reached without significant pyramidalization, I-twisted structures readily proceed through the CI seam as soon as twisting along ϕI nears 90° (Fig. S13a†). On the other hand, the P-twisted CI seam is not reached so easily. As a consequence, P-twisted intermediates sample along ϕP more robustly to reach significantly pyramidalized structures. This results in a majority of spawns with ϕP greater than 90° (Fig. S13b†) and likely contributes to the higher quantum yield for Z/Z isomerization than that of E/Z isomerization.Time-resolved fluorescence
Solvated HBDI− has been the subject of many time-resolved fluorescence experiments.27,37,107–109 To link our simulation data to experimental findings, time-resolved fluorescence spectra were computed over the course of the AIMS simulations (Fig. 14). A line out at 500 nm (based on experiment103) is extracted for various sets of TBFs. Across all TBFs (Fig. 14a), the two-dimensional fluorescence spectrum experiences a significant red-shift spectral evolution after a few hundred femtoseconds. The red-shift and the reduction in fluorescence signal are attributed to a decrease in the S0/S1 energy gap and emission strength, respectively, as the chromophore begins twisting its bridge dihedrals upon departure from the FC region (Table S3, and Fig. S16†). Since twisting along ϕI and ϕP is correlated with a decrease in oscillator strength, we expect that the steeper (compared to XMS-CASPT2) α-CASSCF gradients beyond 30° torsion of ϕI and/or ϕP (Fig. S1†) artificially accelerate fluorescence quenching in our AIMS simulations. The fluorescence spectrum was decomposed to obtain the contributions from the I- and P-deactivating species (Fig. 14b, and c). By comparing the two-dimensional fluorescence spectra, it becomes obvious that the P-twisted channel significantly prolongs the fluorescence intensity of aqueous HBDI− when compared to the signal from the I-twisted channel. From the time-resolved fluorescence spectrum for all TBFs at 500 nm (Fig. 14d), AIMS simulations predict a fluorescence signal that loses roughly 50% of its intensity by 500 fs. Despite this rapid quenching, fluorescence signatures are observed beyond 1.5 ps. An I- and P-pathway decomposition of this signal shows that I-twisting species quench their fluorescence rapidly (within a picosecond). Yet, the P-twisting species has a more pronounced fluorescence signal that survives until ∼1.6 ps. Therefore, the long-lived signal in the time-resolved spectrum, across all TBFs, is attributed to the species that undergoes internal conversion through the P-channel. We attribute the faster fluorescence decay of our simulations, relative to experiment, to the slightly steeper α-CASSCF gradients for partially twisted geometries, when compared to XMS-CASPT2. Furthermore, the underestimated S0/S1 energy gap for I- and P-twisted structures at the α-CASSCF level (Fig. S1†) likely red-shifts the fluorescence signal of I- and P-twisted structures more than expected. However, this issue likely affects the fluorescence signal of P-twisted TBFs, which remain on S1 for several picoseconds, more than the signal of I-twisted TBFs. Another possible contributor to the faster-than-expected simulated fluorescence signal is a higher ratio of P-to-I species in experiment than sampled for our AIMS simulations, which would increase the intensity of the fluorescence tail. Despite these discrepancies, our simulations provide evidence that the deactivation pathway taken by the chromophore has a significant impact on the observed time-resolved fluorescence.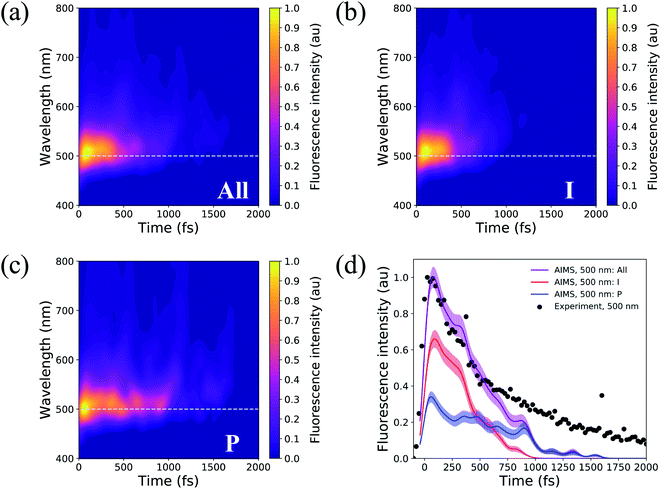 | ||
| Fig. 14 Two-dimensional fluorescence spectrum, probed at 500 nm, for (a) all TBFs, (b) I-deactivating TBFs, and (c) P-deactivating TBFs. (d) Time-resolved fluorescence signals of HBDI− calculated from AIMS simulations in water. The maximum fluorescence intensities of I- and P-deactivating species are scaled based on the relative proportion of ICs that deactivate through the I- and P-channels. Experimental data, following 400 nm excitation, for HBDI− in water was provided by Meech and co-workers.27,103 To align the experimental31 and theoretical fluorescence wavelength maxima, a shift of 0.13 eV was applied to the theory spectra (Fig. S15†). Transparent lines represent the error obtained from bootstrapping analysis. | ||
Conclusions
AIMS dynamics support the presence of two ground-state recovery mechanisms after the photoexcitation of aqueous HBDI− to S1. The dominant mode of deactivation, through I-twisting, proceeds via an ultrafast mechanism and is responsible for the rapidly-decaying signals in time-resolved fluorescence and FSRS experiments. The minor pathway, through P-twisting, remains on S1 for several picoseconds and its access to the CI seam is gated by pyramidalization of the central methine bridge carbon. Our results provide evidence for the following mechanism: (1) evolution from the FC region via near-barrierless motions that are consistent with ground-state QM/MM-MD simulations, (2) formation of a TICT state through an aborted hula-twist-like (conrotatory) mechanism as either ϕI or ϕP approaches 90°, (3) population transfer from S1 to S0 as the two states reach electronic degeneracy (through I-twisting for the I-species and through P-twisting along with pyramidalization for the P-species), and (4) re-population of the ground state with low Z/E and Z/Z isomerization quantum yields. This process is summarized in Fig. 15. The ultrafast differentiation between I- and P-species indicates that both twisted species are accessible from the FC region with little/no energetic barrier, as supported by Fig. 5 and S1.† Relative to the uphill approach needed to reach the P-twisted CI seam, the downhill approach to the I-twisted CI seam makes it easier to transfer population to the ground state through the I-channel. However, the P-twisted species has an isomerization quantum yield about two times as large as its I-twisted counterpart.Our AIMS simulations provide novel mechanistic and electronic insight into the behavior that governs the photodynamics of the GFP chromophore. QM/MM-MD simulations indicate that surrounding HBDI− with mobile solvent molecules has minimal impact on the configuration space sampled by the chromophore in water. Yet, the electronic effects of water blue-shift the absorption spectrum. During gas- and solution-phase dynamics on S0, preferential twisting along ϕI and ϕP in a hula-twist-like (conrotatory) fashion is observed. The subsequent internal conversion mechanisms predominantly occur through rotation of ϕI in both systems.24 The absence of rigid electronic and steric constraints on the chromophore likely explains the ultrafast deactivation tendencies reported by experiments for both systems.21,27,30,31 However, the stabilization of highly-twisted structures and the promotion of electronic degeneracy, especially with respect to ϕI which results in a downhill CI seam, are responsible for shorter lifetimes in water when compared to gas-phase. Furthermore, the fitted time constants for the S1 population decay (609 ± 181 fs and 3.1 ± 1.2 ps) are associated with internal conversion through the I- and P-channels, respectively. Through a direct comparison of AIMS simulations and experimental fluorescence spectra, we provide mechanistic insight to explain the observed fluorescence profile of HBDI− in water.27 We attribute the short experimental time constant (210 fs) describing HBDI− fluorescence in water to the departure from the FC region (of both I- and P-deactivating species), while the longer experimental fluorescence time constant (1.1 ps) corresponds to the longer-lived, P-deactivating species.
Although our simulations do not include an explicit protein environment, our findings imply that the mobility and electronic distribution of residues surrounding the chromophore in a protein can tune the chromophore's behavior on the excited state. From our simulations, we predict that modifications to the protein environment can lead to internal conversion pathways with notably different population transfer rates, fluorescence profiles, and isomerization quantum yields. Using Dronpa2 variants, Romei and co-workers110 have demonstrated that chromophore modifications can bias the preferred directionality of the CT process and modify observables of interest in the protein. Our direct observation of TICT processes in solution provides evidence that steering the chromophore toward a given pathway can significantly alter its properties. To characterize the photochemical processes that drive the dynamics of the chromophore in protein scaffolds, we will extend our simulations and analyses to fluorescent protein systems.
Author contributions
CMJ contributed to data curation, formal analysis, investigation, methodology, visualization and writing (original draft) of the presented work. NHL contributed to data curation, investigation, methodology and project administration. TJM contributed to methodology, project administration, funding acquisition, resources, and supervision. All authors contributed to conceptualization of the project and review and editing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the AMOS program of the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Chemical Sciences, and Biosciences Division. CMJ is a National Science Foundation graduate research fellow, and NHL acknowledges financial support from the Villum Foundation (Grant No. VKR023371). CMJ also acknowledges Sergey Laptenok and Stephen Meech for providing additional experimental data. The authors also acknowledge Matthew Romei, Chi-Yun Lin, and Steven Boxer for their insight and discussions.References
- O. Shimomura, F. H. Johnson and Y. Saiga, J. Cell. Comp. Physiol., 1962, 59, 223–239 CrossRef CAS PubMed.
- F. H. Johnson, O. Shimomura, Y. Saiga, L. C. Gershman, G. T. Reynolds and J. R. Waters, J. Cell. Comp. Physiol., 1962, 60, 85–103 CrossRef CAS.
- J. G. Morin and J. W. Hastings, J. Cell. Physiol., 1971, 77, 313–318 CrossRef CAS PubMed.
- H. Morise, O. Shimomura, F. H. Johnson and J. Winant, Biochemistry, 1974, 13, 2656–2662 CrossRef CAS PubMed.
- O. Shimomura, FEBS Lett., 1979, 104, 220–222 CrossRef CAS.
- M. Chalfie, Y. Tu, G. Euskirchen, W. W. Ward and D. C. Prasher, Science, 1994, 263, 802–805 CrossRef CAS PubMed.
- S. Inouye and F. I. Tsuji, FEBS Lett., 1994, 341, 277–280 CrossRef CAS.
- R. Y. Tsien, Annu. Rev. Biochem., 1998, 67, 509–544 CrossRef CAS PubMed.
- B. J. Feilmeier, G. Iseminger, D. Schroeder, H. Webber and G. J. Phillips, J. Bacteriol., 2000, 182, 4068–4076 CrossRef CAS PubMed.
- J. Lippincott-Schwartz, E. Snapp and A. Kenworthy, Nat. Rev. Mol. Cell Biol., 2001, 2, 444–456 CrossRef CAS PubMed.
- J. Lippincott-Schwartz and G. H. Patterson, Science, 2003, 300, 87–91 CrossRef CAS PubMed.
- W. W. Ward, H. J. Prentice, A. F. Roth, C. W. Cody and S. C. Reeves, Photochem. Photobiol., 1982, 35, 803–808 CrossRef CAS.
- R. Heim, D. C. Prasher and R. Y. Tsien, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 12501–12504 CrossRef CAS.
- R. Heim, A. B. Cubitt and R. Y. Tsien, Nature, 1995, 373, 663–664 CrossRef CAS PubMed.
- R. Heim and R. Y. Tsien, Curr. Biol., 1996, 6, 178–182 CrossRef CAS.
- R. M. Dickson, A. B. Cubitt, R. Y. Tsien and W. E. Moerner, Nature, 1997, 388, 355–358 CrossRef CAS PubMed.
- G. H. Patterson and J. Lippincott-Schwartz, Science, 2002, 297, 1873–1877 CrossRef CAS PubMed.
- M. Hofmann, C. Eggeling, S. Jakobs and S. W. Hell, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17565–17569 CrossRef CAS PubMed.
- S. Kojima, H. Ohkawa, T. Hirano, S. Maki, H. Niwa, M. Ohashi, S. Inouye and F. I. Tsuji, Tetrahedron Lett., 1998, 39, 5239–5242 CrossRef CAS.
- M. Chattoraj, B. A. King, G. U. Bublitz and S. G. Boxer, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 8362–8367 CrossRef CAS.
- A. Svendsen, H. V. Kiefer, H. B. Pedersen, A. V. Bochenkova and L. H. Andersen, J. Am. Chem. Soc., 2017, 139, 8766–8771 CrossRef CAS PubMed.
- F. Yang, L. G. Moss and G. N. Phillips Jr, Nat. Biotechnol., 1996, 14, 1246–1251 CrossRef CAS PubMed.
- M. Ormö, A. B. Cubitt, K. Kallio, L. A. Gross, R. Y. Tsien and S. J. Remington, Science, 1996, 273, 1392–1395 CrossRef PubMed.
- N. H. List, C. M. Jones and T. J. Martínez, 2021, DOI:10.26434/chemrxiv.14544555.
- M. A. Perozzo, K. B. Ward, R. B. Thompson and W. W. Ward, J. Biol. Chem., 1988, 263, 7713–7716 CrossRef CAS.
- G. Striker, V. Subramaniam, C. A. M. Seidel and A. Volkmer, J. Phys. Chem. B, 1999, 103, 8612–8617 CrossRef CAS.
- D. Mandal, T. Tahara and S. R. Meech, J. Phys. Chem. B, 2004, 108, 1102–1108 CrossRef CAS.
- A. Usman, O. F. Mohammed, E. T. Nibbering, J. Dong, K. M. Solntsev and L. M. Tolbert, J. Am. Chem. Soc., 2005, 127, 11214–11215 CrossRef CAS PubMed.
- C. W. West, A. S. Hudson, S. L. Cobb and J. R. Verlet, J. Chem. Phys., 2013, 139, 071104 CrossRef PubMed.
- C. R. S. Mooney, D. A. Horke, A. S. Chatterley, A. Simperler, H. H. Fielding and J. R. R. Verlet, Chem. Sci., 2013, 4, 921–927 RSC.
- M. A. Taylor, L. Zhu, N. D. Rozanov, K. T. Stout, C. Chen and C. Fang, Phys. Chem. Chem. Phys., 2019, 21, 9728–9739 RSC.
- M. W. Forbes and R. A. Jockusch, J. Am. Chem. Soc., 2009, 131, 17038–17039 CrossRef CAS PubMed.
- H. Niwa, S. Inouye, T. Hirano, T. Matsuno, S. Kojima, M. Kubota, M. Ohashi and F. I. Tsuji, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13617–13622 CrossRef CAS PubMed.
- M. E. Martin, F. Negri and M. Olivucci, J. Am. Chem. Soc., 2004, 126, 5452–5464 CrossRef CAS.
- S. Olsen, K. Lamothe and T. J. Martínez, J. Am. Chem. Soc., 2010, 132, 1192–1193 CrossRef CAS PubMed.
- N. M. Webber, K. L. Litvinenko and S. R. Meech, J. Phys. Chem. B, 2001, 105, 8036–8039 CrossRef CAS.
- K. L. Litvinenko, N. M. Webber and S. R. Meech, Bull. Chem. Soc. Jpn., 2002, 75, 1065–1070 CrossRef CAS.
- W. Weber, V. Helms, J. A. McCammon and P. W. Langhoff, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 6177–6182 CrossRef CAS PubMed.
- R. S. Liu and A. E. Asato, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 259–263 CrossRef CAS PubMed.
- R. S. H. Liu and G. S. Hammond, Chem.–Eur. J., 2001, 7, 4536–4545 CrossRef CAS.
- P. Altoe, F. Bernardi, M. Garavelli, G. Orlandi and F. Negri, J. Am. Chem. Soc., 2005, 127, 3952–3963 CrossRef CAS PubMed.
- J. W. Park and T. Shiozaki, J. Chem. Theory Comput., 2017, 13, 3676–3683 CrossRef CAS.
- N. Minezawa and T. Nakajima, J. Chem. Phys., 2020, 152, 024119 CrossRef PubMed.
- M. Vengris, I. H. M. van Stokkum, X. He, A. F. Bell, P. J. Tonge, R. van Grondelle and D. S. Larsen, J. Phys. Chem. A, 2004, 108, 4587–4598 CrossRef CAS.
- J. S. Yang, G. J. Huang, Y. H. Liu and S. M. Peng, Chem. Commun., 2008, 1344–1346, 10.1039/b717714c.
- V. Voliani, R. Bizzarri, R. Nifosi, S. Abbruzzetti, E. Grandi, C. Viappiani and F. Beltram, J. Phys. Chem. B, 2008, 112, 10714–10722 CrossRef CAS.
- B. G. Levine, C. Ko, J. Quenneville and T. J. Martínez, Mol. Phys., 2006, 104, 1039–1051 CrossRef CAS.
- E. F. Kjonstad, R. H. Myhre, T. J. Martínez and H. Koch, J. Chem. Phys., 2017, 147, 164105 CrossRef PubMed.
- D. Tuna, D. Lefrancois, L. Wolanski, S. Gozem, I. Schapiro, T. Andruniow, A. Dreuw and M. Olivucci, J. Chem. Theory Comput., 2015, 11, 5758–5781 CrossRef CAS PubMed.
- J. W. Snyder Jr, R. M. Parrish and T. J. Martínez, J. Phys. Chem. Lett., 2017, 8, 2432–2437 CrossRef.
- G. J. Atchity, S. S. Xantheas and K. Ruedenberg, J. Chem. Phys., 1991, 95, 1862–1876 CrossRef.
- M. Ben-Nun, F. Molnar, K. Schulten and T. J. Martínez, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 1769–1773 CrossRef CAS.
- J. P. Malhado and J. T. Hynes, J. Chem. Phys., 2016, 145, 194104 CrossRef PubMed.
- A. M. Virshup, J. Chen and T. J. Martínez, J. Chem. Phys., 2012, 137, 22A519 CrossRef.
- A. Toniolo, G. Granucci and T. J. Martínez, J. Phys. Chem. A, 2003, 107, 3822–3830 CrossRef CAS.
- A. Toniolo, S. Olsen, L. Manohar and T. J. Martínez, Faraday Discuss., 2004, 127, 149–163 RSC.
- T. J. Martínez, M. Ben-Nun and R. D. Levine, J. Phys. Chem., 1996, 100, 7884–7895 CrossRef.
- M. Ben-Nun and T. J. Martínez, J. Chem. Phys., 1998, 108, 7244–7257 CrossRef CAS.
- M. Ben-Nun, J. Quenneville and T. J. Martínez, J. Phys. Chem. A, 2000, 104, 5161–5175 CrossRef CAS.
- M. Ben-Nun and T. J. Martínez, Adv. Chem. Phys., 2002, 121, 439–512 CrossRef CAS.
- B. F. E. Curchod and T. J. Martínez, Chem. Rev., 2018, 118, 3305–3336 CrossRef CAS.
- K. K. Docken and J. Hinze, J. Chem. Phys., 1972, 57, 4928–4936 CrossRef CAS.
- B. O. Roos, Adv. Chem. Phys., 1987, 69, 399–445 CAS.
- J. W. Snyder Jr, E. G. Hohenstein, N. Luehr and T. J. Martínez, J. Chem. Phys., 2015, 143, 154107 CrossRef.
- J. W. Snyder Jr, B. S. Fales, E. G. Hohenstein, B. G. Levine and T. J. Martínez, J. Chem. Phys., 2017, 146, 174113 CrossRef.
- T. J. A. Wolf, D. M. Sanchez, J. Yang, R. M. Parrish, J. P. F. Nunes, M. Centurion, R. Coffee, J. P. Cryan, M. Guhr, K. Hegazy, A. Kirrander, R. K. Li, J. Ruddock, X. Shen, T. Vecchione, S. P. Weathersby, P. M. Weber, K. Wilkin, H. Yong, Q. Zheng, X. J. Wang, M. P. Minitti and T. J. Martínez, Nat. Chem., 2019, 11, 504–509 CrossRef CAS PubMed.
- L. M. Frutos, T. Andruniow, F. Santoro, N. Ferre and M. Olivucci, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 7764–7769 CrossRef CAS PubMed.
- S. Olsen and R. H. McKenzie, J. Chem. Phys., 2009, 130, 184302 CrossRef PubMed.
- I. V. Polyakov, B. L. Grigorenko, E. M. Epifanovsky, A. I. Krylov and A. V. Nemukhin, J. Chem. Theory Comput., 2010, 6, 2377–2387 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- T. P. Radhakrishnan and I. Agranat, Struct. Chem., 1991, 2, 107–115 CrossRef CAS.
- J. Finley, P. A. Malmqvist, B. O. Roos and L. Serrano-Andres, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef CAS.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef.
- C. Song and T. J. Martínez, J. Chem. Phys., 2020, 152, 234113 CrossRef CAS PubMed.
- N. Gidopoulos and A. Theophilou, Philos. Mag. B, 1994, 69, 1067–1074 CAS.
- G. Granucci and A. Toniolo, Chem. Phys. Lett., 2000, 325, 79–85 CrossRef CAS.
- N. I. Gidopoulos, P. G. Papaconstantinou and E. K. U. Gross, Physica B, 2002, 318, 328–332 CrossRef CAS.
- P. Slavicek and T. J. Martínez, J. Chem. Phys., 2010, 132, 234102 CrossRef PubMed.
- J. Kastner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, J. Phys. Chem. A, 2009, 113, 11856–11865 CrossRef CAS PubMed.
- I. S. Ufimtsev and T. J. Martínez, J. Chem. Theory Comput., 2008, 4, 222–231 CrossRef CAS PubMed.
- I. S. Ufimtsev and T. J. Martínez, J. Chem. Theory Comput., 2009, 5, 1004–1015 CrossRef CAS PubMed.
- I. S. Ufimtsev and T. J. Martínez, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS PubMed.
- S. Seritan, C. Bannwarth, B. S. Fales, E. G. Hohenstein, S. I. L. Kokkila-Schumacher, N. Luehr, J. W. Snyder, Jr., C. Song, A. V. Titov, I. S. Ufimtsev and T. J. Martínez, J. Chem. Phys., 2020, 152, 224110 CrossRef CAS PubMed.
- S. Seritan, C. Bannwarth, B. S. Fales, E. G. Hohenstein, C. M. Isborn, S. I. L. Kokkila-Schumacher, X. Li, F. Liu, N. Luehr, J. W. Snyder, C. Song, A. V. Titov, I. S. Ufimtsev, L. P. Wang and T. J. Martínez, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2020, 11, 1–16 Search PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L. P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, PLoS Comput. Biol., 2017, 13, e1005659 CrossRef.
- Y. Wu, H. L. Tepper and G. A. Voth, J. Chem. Phys., 2006, 124, 024503 CrossRef PubMed.
- I. S. Joung and T. E. Cheatham III, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS.
- C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- A. M. Niklasson, P. Steneteg, A. Odell, N. Bock, M. Challacombe, C. J. Tymczak, E. Holmstrom, G. Zheng and V. Weber, J. Chem. Phys., 2009, 130, 214109 CrossRef PubMed.
- L. H. Andersen, A. Lapierre, S. B. Nielsen, I. B. Nielsen, S. U. Pedersen, U. V. Pedersen and S. Tomita, Eur. Phys. J. D, 2002, 20, 597–600 CrossRef CAS.
- J. R. R. Verlet, Personal communication, 2019.
- B. Efron and R. J. Tibshirani, An Introduction to the Bootstrap, Chapman and Hall/CRC, New York, 1st edn, 1994 Search PubMed.
- R. T. McGibbon, K. A. Beauchamp, M. P. Harrigan, C. Klein, J. M. Swails, C. X. Hernandez, C. R. Schwantes, L. P. Wang, T. J. Lane and V. S. Pande, Biophys. J., 2015, 109, 1528–1532 CrossRef CAS PubMed.
- B. Roux, Comput. Phys. Commun., 1995, 91, 275–282 CrossRef CAS.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- A. Grossfield, WHAM: an implementation of the weighted histogram analysis method, http://membrane.urmc.rochester.edu/content/wham/.
- J. K. Yu, R. Liang, F. Liu and T. J. Martínez, J. Am. Chem. Soc., 2019, 141, 18193–18203 CrossRef CAS PubMed.
- S. Laptenok and S. R. Meech, Personal communication, 2020.
- S. B. Nielsen, A. Lapierre, J. U. Andersen, U. V. Pedersen, S. Tomita and L. H. Andersen, Phys. Rev. Lett., 2001, 87, 228102 CrossRef CAS PubMed.
- R. S. Liu, Acc. Chem. Res., 2001, 34, 555–562 CrossRef CAS PubMed.
- W. Jarzeba, G. C. Walker, A. E. Johnson, M. A. Kahlow and P. F. Barbara, J. Phys. Chem., 1988, 92, 7039–7041 CrossRef CAS.
- D. Mandal, T. Tahara, N. M. Webber and S. R. Meech, Chem. Phys. Lett., 2002, 358, 495–501 CrossRef CAS.
- A. D. Kummer, C. Kompa, H. Niwa, T. Hirano, S. Kojima and M. E. Michel-Beyerle, J. Phys. Chem. B, 2002, 106, 7554–7559 CrossRef CAS.
- K. L. Litvinenko, N. M. Webber and S. R. Meech, J. Phys. Chem. A, 2003, 107, 2616–2623 CrossRef CAS.
- M. G. Romei, C. Y. Lin, I. I. Mathews and S. G. Boxer, Science, 2020, 367, 76–79 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc02508b |
| This journal is © The Royal Society of Chemistry 2021 |