Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evolutionary exploration of polytypism in lead halide perovskites†
Zhenzhu
Li
a,
Ji-Sang
Park
b and
Aron
Walsh
 *ac
*ac
aDepartment of Materials, Imperial College London, London SW7 2AZ, UK. E-mail: a.walsh@imperial.ac.uk
bDepartment of Physics, Kyungpook National University, Daegu 41566, Korea
cDepartment of Materials Science and Engineering, Yonsei University, Seoul 03722, Korea
First published on 10th August 2021
Abstract
The regular ABX3 cubic perovskite structure is composed of close-packed AX3 layers stacked along the 〈111〉 axis. An equivalent hexagonal close-packed network can also be formed, in addition to a series of intermediate polytype sequences. Internally, these correspond to combinations of face- and corner-sharing octahedral chains that can dramatically alter the physical properties of the material. Here, we assess the thermodynamics of polytypism in CsPbI3 and CsPbBr3. The total energies obtained from density functional theory are used to paramaterize an axial Ising-type model Hamiltonian that includes linear and cubic correlation terms of the pseudo-spin. A genetic algorithm is built to explore the polytype phase space that grows exponentially with the number of layers. The ground-state structures of CsPbX3 polytypes are analysed to identify features of polytypism such as the distinct arrangements of layers and symmetry forbidden sequences. A number of polytypes with low ordering energies (around thermal energy at room temperature) are predicted, which could form distinct phases or appear as stacking faults within perovskite grains.
1. Introduction
Perovskite is an important and flexible structure type in solid-state chemistry and physics.1–4 Metal halide perovskites have attracted significant attention as photovoltaic materials since the first report of a photoactive absorber in 2009,5 with the power conversion efficiency (PCE) climbing up from the 3.8% to the current record of 25.5%.6 One key for improving solar cell technologies based on the hybrid organic–inorganic perovskites such as MAPbI3 (MA = CH3NH3+) and FAPbI3 (FA = CH(NH2)2+) or the inorganic lead halide perovskites such as CsPbBr3 and CsPbI3, is to synthesize large-area single-crystal perovskite films, which is challenging due to intense phase competition.MAPbI3 undergoes degradation to release CH3I and NH3 gas at temperatures as low as 80 °C,7 posing a challenge to long-term stability. The compositions used in the state-of-the-art perovskite solar cells are shifting to incorporate FA+ and Cs+ as A-site cations, with reported PCEs up to 25.2%8 and 20.4%,9 respectively. They are comparatively more stable than MAPbI3 at elevated temperatures. However, the photoactive black phases (cubic α-phase) of both FAPbI3 and CsPbI3 can spontaneously transform into photoinactive, non-perovskite yellow phases (hexagonal δ-phase FAPbI3; orthorhombic CsPbI3) at room temperature.10–12 These transformations involve the formation of multiple intermediate phases.13,14
Phases can coexist in as-synthesized perovskite crystals, for instance, the presence of cubic and hexagonal domains in a FAPbI3 nanowire was confirmed with in situ optical micro-spectroscopy.15 The authors proposed a disordered amorphous interfacial layer at the phase boundary where the octahedra are distorted and tilted. Recently the mixed perovskite MA1−xFAxPbI3 (x = 0.5, 1) was also reported with characterisation evidencing the appearance of an intergrain 2H phase.16 On the other hand, the coexistence of cubic and hexagonal phases is often observed for oxide perovskites. For instance, various mixed (ordered or disordered interleaved) packing of hexagonal and cubic layers in BaNiO3, BaCrO3, BaMnO3, and BaRuO3 can form due to the small energetic difference between arrangements, giving rise to strong polytypism.17,18 Polytype engineering can enable novel electronic and ion transport properties as demonstrated for hexagonal oxide perovskites in a range of energy-related technologies.19
Similarly, polytypism of lead halide perovskites has been shown to be energetically accessible. First-principles calculations revealed that the formation enthalpy of δ-FAPbI3 was lower by about 70 meV per formula unit than α-FAPbI3 at 0 K.20 Our density functional theory (DFT) calculations, reported below, also confirmed that the formation enthalpy of a hexagonal CsPbBr3/CsPbI3 phase is 40 meV/90 meV per formula unit higher/lower than the corresponding cubic phases at 0 K.21 It has been reported that the black to yellow phase transitions in FAPbI3 and CsPbI3 are entropy-driven and allow for kinetic trapping of intermediate phases.22 Another aspect is the small lattice mismatch along the 〈111〉 stacking direction between the hexagonal and cubic polytypes, which is just 4.7% for CsPbI3 and 5.4% for CsPbBr3, according to our calculations.
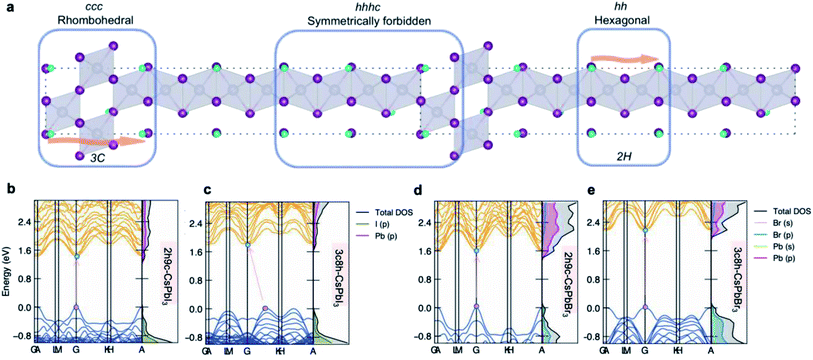
Due to the range of accessible ordered stacking sequences with distinct crystal symmetry and the appearance of stacking faults that break symmetry in halide perovskites, polytypism can bring forth novel physical and chemical phenomena. This includes carrier-blocking effects of hexagonal regions in cubic crystals and a likely contribution to photogenerated carrier recombination in other cases.21 In this work, we aim to shed light on the phase space for polytype formation in lead halide perovskites. To overcome the limitations of standard modelling approaches, we build a workflow based on an evolutionary exploration of a model crystal Hamiltonian. We provide insight into the ordering trends and ground-state structures of CsPbX3 as a prototype system. Universal features such as the accessible layer arrangements and symmetry forbidden sequences are reported.
2. Computational methods
We used a combination of computer simulation approaches in this study. DFT can provide reliable first-principles total energies, but is limited to relatively small polytype stacking sequences. For this reason, a model Hamiltonian approach was employed to rapidly predict polytype energies and assess the extent of polytype disorder. Afterwards, a genetic algorithm with optimisation functions derived from the model Hamiltonian was built to rapidly converge the searching of low energy configurations.Training data
For each polytype in the training set, DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP)23,24 with the standard frozen-core projector augmented-wave (PAW)25,26 method. The cutoff energy for basis functions was 420 eV. The generalized gradient approximation (GGA)27 of the Perdew–Burke–Ernzerhof functional for solids (PBEsol)28 was used for the exchange-correlation. We used a dense 7 × 7 × 5 k-point mesh for structural relaxation until all atoms were relaxed with Hellmann–Feynman forces below 0.01 eV Å−1.Model construction
Genetic algorithm
To quickly identify the ground-state stacking sequences for a given layer number, a genetic algorithm was designed by setting the model Hamiltonian as the objective function. The parameters for running this algorithm include the maximum number of iteration, population size, mutation probability, elite ratio, crossover probability, and parental portion. These parameters can be tuned to monitor and optimise the performance of the algorithm. The converged values are given in the results section.3. Results
Thermodynamic stability of CsPbX3 polytypes
The thermodynamic stability of a CsPbX3 polytype can be evaluated by its ordering energy. Along the stacking chain of a polytype, two adjacent PbX6-octahedra are connected either with a face-sharing (h) or a corner-sharing (c) configuration, forming a unique stacking sequence for each polytype, which in turn determines the interaction between layers and its formability. Given a random CsPbX3 polytype with N layers, its ordering energy (EO) is defined as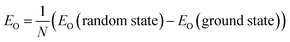 | (1) |
The ordering energy is determined by a combination of electrostatics and crystal strain. Low ordering energy usually indicates the ease of formation. Though similar, the ground state structures of CsPbBr3 and CsPbI3 polytypes are starkly different, allowing us to probe the chemistry of ordering ions.
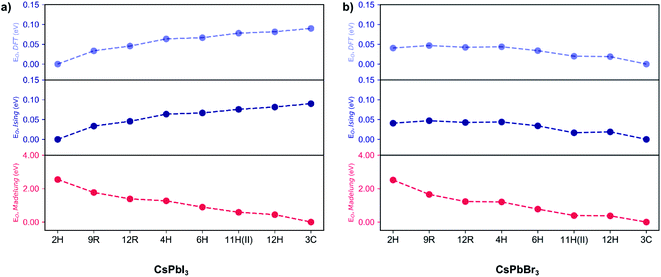
For an ionic crystal, the Madelung energy based on point charges should fully describe phase energetics. However, we found that CsPbX3 is beyond this regime, due to the contribution from the polarisation of ions. As shown in Fig. 2, under the perfect ionic lattice assumption, the Madelung energies of all the polytypes for the two halide perovskites CsPbBr3 and CsPbI3 were calculated, we found that the most stable phase should be cubic 3C. Moreover, the Madelung ordering energies EO,Madelung for the two sets of halide perovskite polytypes are lowered dramatically, by 2.51 eV/layer (CsPbBr3) and 2.55 eV/layer (CsPbI3) respectively, from the hexagonal 2H phase to the cubic 3C phase, indicating that the electrostatic Coulomb energies do influence the ordering preferences. 29 However, as also shown in Fig. 2, first-principles calculations revealed that the most energetically stable phase for CsPbI3 is 2H, while it is 3C for CsPbBr3. The ordering energies EO,DFT are less than 100 meV/layer for both halides, with EO,DFT(CsPbI3) = 90 meV and EO,DFT(CsPbBr3) = 40 meV between the 2H and 3C phase. The greatly reduced ordering energies mean that the bare coulombic interactions are regulated and screened due to the polarisation of ions. Moreover, the reversed order of stability in CsPbI3 and CsPbBr3 polytypes indicates the non-negligible role of anion polarisation; although we note that Pb2+ is also highly polarisable due to its lone pair (6s2) electrons, which contributes to the ionic dielectric response.30
Ising-type model Hamiltonian
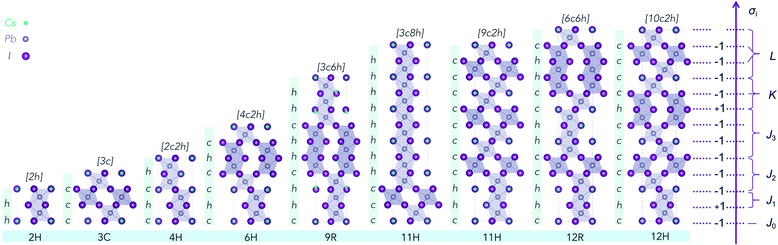
While first-principles calculations can provide reliable total energies, they are limited to relatively small stacking sequences and can only provide a fragmentary picture of the physics of ordering. The other hurdle further stops us from using DFT calculations to explore the phase space directly is the explosion of combinations. Structurally, the ordering of h and c in the stacking chain of a polytype shows a binary nature for each layer. If a polytype has N layers, the possible stacking sequences reach 2N.To overcome this problem, an Ising-type Hamiltonian was built to calculate polytype energies. This model Hamiltonian can not only be used to compute the random-state energies for the 2N stacking sequences of h and c, but also implicitly includes a full set of chemical interactions between the neighbouring layers, manifested by a series of interaction coefficients and their corresponding correlation functions. In Fig. 1, we showed the mapping of a stacking sequence (12H) onto an Ising-type model with σi = 1 for a face-sharing octahedra pair and σi = −1 for a corner-sharing octahedra pair. The first, second and third nearest neighbour interactions are included during the model construction. Thereby, for CsPbX3 polytypes, the random-state total energy of a polytype with N layers can be written as
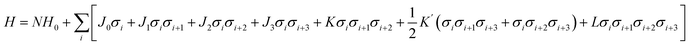 | (2) |
In 1988, Plumer generated an approximate phase diagram for possible ground-state structures of ABX3 perovskite polytypes.31 In this model, limited by available data at the time, the ground-state structures for both CsPbI3 and CsPbBr3 should be 3C, concluded by the sign of their coefficients. However, first-principles calculations have confirmed that, even though both CsPbI3 and CsPbBr3 belong to the ABX3 type perovskite and have similar interaction coefficients, the most stable phase for CsPbI3 is 2H, while for CsPbBr3 it is 3C. This conclusion reflects the underlying chemical complexity and how the choice of elements can play an important role to alter the stability of polytypes with similar stacking sequences.
To obtain the interaction coefficients for CsPbX3, total energies of nine polytype phases (2H (2h), 3C (3c), 4H (2c2h), 6H (4c2h), 9R (3c6h), 11H (3c8h), 11H (9c2h), 12R (6c6h), 12H (10c2h)) with low periodicity (N ≤ 12) for both CsPbI3 and CsPbBr3 were calculated. During the coefficients fitting stage, we randomly chose eight out of the nine structures for parameter fitting in accordance with the eight unknowns (H0 and seven coefficients) in the model Hamiltonian, by solving the linear equations. The resulting interaction coefficients for CsPbI3 and CsPbBr3 are listed in Table 1.
| CsPbX3 | H 0 | J 0 | J 1 | J 2 | J 3 | K | K′ | L |
|---|---|---|---|---|---|---|---|---|
| CsPbI3 | −11.243 | 2.015 | 1.024 | 0.004 | −1.034 | 0.0011 | −2.061 | −1.033 |
| CsPbBr3 | −12.865 | 2.353 | 1.157 | −0.005 | −1.169 | 0.0002 | −2.333 | −1.167 |
Following this procedure, the model Hamiltonian calculated stability trends, denoted as the ordering energies EO,Ising for both CsPbBr3 and CsPbI3 in Fig. 2, in agreement with the DFT results EO,DFT. The Ising-type model Hamiltonian is found to work well, with the largest fitting error being negligible at just 3 meV/layer for the 11H(II, 9c2h)-CsPbBr3 polytype and 2 meV/layer for the 11H(II, 9c2h)-CsPbI3 polytype. Furthermore, the model Hamiltonian predictions have been checked with new (unseen) polytype data, which also confirms the high prediction accuracy of the model Hamiltonian (Table S1†).
The impact of ion choice and ordering for tuning the stability of different stacking sequences is contained within the eight interaction coefficients and their corresponding correlation functions. For instance, the H0 value for the CsPbBr3 stacking sequences is about 1.62 eV/layer lower in energy than that for the CsPbI3 polytypes. Physically, the H0 can be viewed as the energy of the suspended monolayer of octahedra. The more negative H0 value in CsPbBr3 polytypes shows that Br− stabilises the perovskite structure more than I−, in consensus with the conclusion drawn from the perspective of tolerance factors that cubic CsPbBr3 has a more ideal Goldschmidt tolerance factor (t(CsPbBr3) = 0.92; t(CsPbI3) = 0.89). This highlights the key anion role in determining polytype stability. The additional chemical contributions are quantified by the seven interlayer correlation-related coefficients in the model Hamiltonian, which act as gears to tune the stability of a given polytype.
The most striking parameters are the small values for J2 and K, being only several meV. As shown in Fig. 1, J2 denotes the interaction between a layer and its second nearest neighbour, and K denotes the interaction between a group of three neighbouring layers. However, it is not the absolute values of the interaction coefficients that dominates the final ordering effect. The interaction coefficients matter only when the stacking sequence allows it. This can be understood from two aspects. One is that the stacking sequence determines the weight of each type of interaction in the model Hamiltonian through the correlation functions: ∑iσi, ∑iσiσi+1, …; and the other reason is, the impact of a sole interaction coefficient can only be pronounced when such interaction is not quantitatively counterbalanced by other interactions in a given stacking sequence. For instance, for the CsPbX3 polytypes, the total energies of 2H and 3C phases per unit layer are
| H2H/2 = H0 + J0 + J1 + J2 + J3 + K + K′ + L | (3) |
| H3C/3 = H0 − J0 + J1 + J2 + J3 − K − K′ + L | (4) |
Due to the special stacking sequences for 2H and 3C, the ordering effect of their stacking sequences give an equal weight for different interlayer interactions, which only differ in sign. With the absolute values provided in Table 1, the impact of J2 and K become pronounced because the absolute total contribution of interlayer interactions is at the 10 meV level, making the influence from the J2 and K related terms non-negligible. Moreover, from the model Hamiltonian, why the ground state structures for CsPbBr3 and CsPbI3 polytypes prefer different stacking sequences can also be explained. By subtracting eqn (3) and (4), the energy difference between the 2H and 3C phases per layer is
| ΔE2H–3C = 2J0 + 2K + 2K′ | (5) |
Consequently, the three interlayer interactions corresponding to J0, K and K′ are responsible for the ordering energy between the 2H and 3C phases. For magnetic systems, J0 is viewed as the Zeeman-like term linear in σ, representing an externally applied magnetic field pointing along the stacking direction, however in this pseudo-spin model Hamiltonian for polytypism, J0 is a phenomenological parameter with no implicit physical meaning and if the numbers of h and c are equal in a stacking sequence, the weight for J0 will become zero and will not contribute to the total energy. Different from K explained previously, K′ corresponds to the group interaction of three layers consisting of a pair of nearest neighbouring layers and one layer that is the second nearest neighbour to any of them. As a consequence, the ordering energy between the 2H and 3C phases could be quantitatively decided. Taking the 3C phase as the reference, for CsPbI3 ΔE2H–3C is −0.09 eV/layer, meaning that the 2H phase is 90 meV/layer more stable than the 3C phase. For CsPbBr3, the ΔE2H–3C is 0.04 eV/layer, meaning that the 3C phase is 40 meV/layer more stable than its 2H phase. This result arises from the more negative value of K′ for CsPbI3 polytypes, which alters the ground-state structures. Such more negative value of K′ may be also related with the higher polarizability of I− compared to Br−.
Distinct polytypes for an N layer polytype hncm
The Ising-type model Hamiltonian opens up a fast means to compute the energy for an arbitrary hncm polytype. The only computing cost is from the summation over pseudo-spin correlation functions determined by the stacking sequence. An expression to calculate the number of distinct polytypes for an N layer polytype hncm, including periodic boundary conditions, takes the form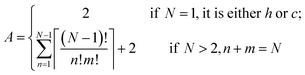 | (6) |
Accordingly, we listed the number of distinct arrangement of h and c for CsPbX3 polytypes in Table 2. For instance, a polytype with 2 layers can have 3 distinct arrangements: hh, cc and hc or ch; a polytype with 3 layers can have 4 distinct arrangements: hhh, hhc, hcc and ccc. With the constraints of periodicity, the space of distinct arrangements of h and c for CsPbX3 polytypes increases slower than the exponential explosion to the 2N for a linear chain of pseudo-spin. There are only 60 distinct arrangements for a 9 layer polytype, which should be 29 = 512 without periodic boundary conditions. Similarly, the space of distinct arrangements for a 12 layer polytype also decreases dramatically by 1–311/(212) = 92.4%.
| Layer number (N) | 2 | 3 | 4 | 6 | 9 | 11 | 12 |
|---|---|---|---|---|---|---|---|
| Arrangements | 3 | 4 | 6 | 14 | 60 | 186 | 311 |
| Representative stacking sequence | 2H | 3C | 4H | 6H | 9R | 11H(I),11H(II) | 12H,12R |
The determination of the distinct polytype set is instructive. Although the energy of a specific polytype hncm can be computed using the model Hamiltonian swiftly, only with the full set of the distinct polytypes, can we grasp the complete thermodynamic landscape of the polytypism. More generally, the number of distinct arrangements determines the number and degeneracy of energy levels that a polytype hncm can possess.
Low energy polytypes
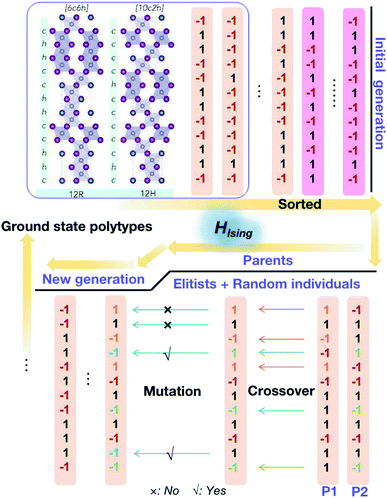
Here, low energy polytypes refer to polytypes whose ordering energies are within the range of ordering energies between the 2H and 3C phases of CsPbI3 and CsPbBr3. These are 90 meV/layer and 40 meV/layer, respectively. In experiments, during the kinetically controlled growth of CsPbI3 and CsPbBr3 crystals, usually the low energy structures would dominate. Along the stacking sequence of the cubic CsPbX3 lattice, the thickness of an octahedral monolayer is around 3.55 Å for the CsPbBr3 and 3.75 Å the for CsPbI3. Thus the domain of a 12 layer stacking faults will be about 4.3–4.5 nm in size, both being much smaller than the typical grain sizes of the cubic phase CsPbI3 and CsPbBr3,32,33 which can extend to microns.A genetic algorithm was adopted to provide an efficient way to locate the ground state structures of polytypes without calculating all energies. At most, it would take 212 = 4096 trials for 12-layer polytypes, but there is an interest to extend to even larger structures in the future. According to evolutionary theory, the gene of a species is a unique DNA sequence. Given the binary nature of each stacking layer, the random stacking sequence of a polytype can also be generated under the biologically inspired operators such as mutation, crossover and selection. Not only that, but also the central idea of natural evolution, ‘survival of the fittest’, is also implemented in genetic algorithms tailored for optimisation problems. The core of a genetic algorithm is the objective function, which here is the Ising-type Hamiltonian for CsPbI3 and CsPbBr3,
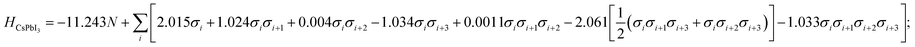 | (7) |
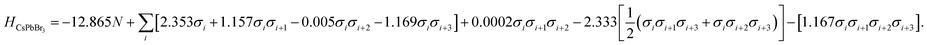 | (8) |
During the optimisation process, because of the binary nature of each layer in the stacking chain, the initial population is generated by a random choice between −1 and 1 for each component layer (see Fig. 3). Then the fitness scores, i.e. values of the objective function corresponding to different stacking sequences, are sorted and normalized. Afterwards, the cumulative probabilities for the initial population are calculated and used for the parent selection. As a result, the parents are formed of elitists and individuals randomly selected from the current population until the set population size is reached. Then, two basic operators are used to generate the new generation: crossover and mutation. The crossover sites are chosen randomly and the number of them is determined by the crossover probability. Here the crossover happens in a uniform way by ‘flipping a coin’ for each site of the parents to decide whether or not it will be included in the next generation; and the mutation takes place randomly within the given mutation probability. Finally amongst the new generation, the new best pseudo-spin sequence to minimize the objective function is generated and compared with the previous generations, which guarantees the algorithm to keep descending to the global minimum for the objective function. The optimisation process will stop when it reaches the set maximum number of iterations.
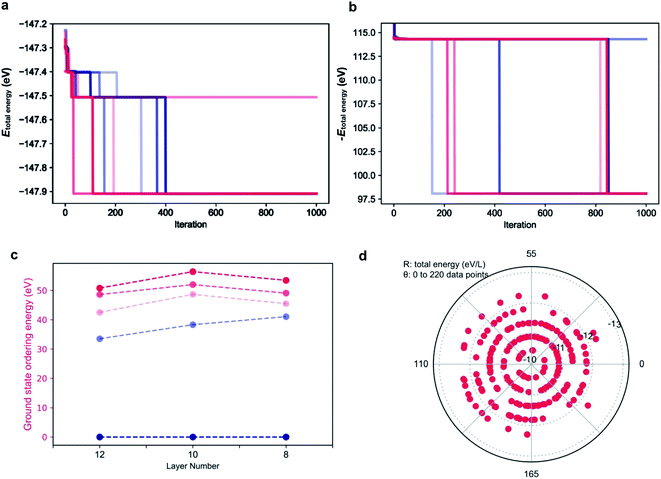
As the parameters used for the genetic algorithm affect the speed and output, a series of tests was conducted to detect the model sensitivity. Taking the 12 layer CsPbI3 polytype as an example, the genetic algorithm converges to the most stable phase of the 12 layer CsPbI3 in only two seconds with the output stacking sequence {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}, i.e. the 2H phase, consist with the DFT results. Interestingly, as shown in Fig. 4a, there are plateaus during the convergence, corresponding to energy levels for distinct polytypes. This also means that other competitive structures can be extracted from the plateaus by tuning the parameters in running the algorithm. Fig. 4c shows the selected ground state structures for the 12, 10, 8 layer CsPbI3 polytypes and their ordering energies compared with the hexagonal 2H phase. Detailed stacking sequences for these ground state polytypes are listed in Table 3. For instance, the 12 layer ground state with an ordering energy of 33 meV per layer in Fig. 4c corresponds to the 12R phase. Such low energy polytypes should be accessible thermodynamically. By considering the thermal energy at room temperature, polytypes with ordering energies lower than 25 meV/layer are more likely to be detected in experimental samples. For example, the 18-layer 2c7h2c7h-CsPbI3 polytype with a 23.5 meV/layer ordering energy is a candidate phase.
| Layer number | Candidate structures | ||||
|---|---|---|---|---|---|
| 12 | 2H | 12R | hhchhcchhchh | ccchhchhchhc | hchhcchchhcc |
| 10 | 2H | hhchhchhcc | hhcchhcchc | ccchhchchh | hhcchhcccc |
| 8 | 2H | hhchhchc | hhcchhcc | hccchhch | chchhchc |
The genetic algorithm can also be used to find the highest energy phases by flipping the sign of the objective function. In principle, the pure 3C phase should be the highest energy. However, as shown in Fig. 4b for the 12 layer polytypes, the output total energy is higher with the global maximum being the stacking sequence of hhhchhhchhhc. The origin of such high energy phases is discussed in the next section.
To validate the predictions, 220 stacking sequences from the 12 layer CsPbI3 polytypes were randomly sampled and their total energies were calculated. As shown in Fig. 4d, a polar coordinate was used to distribute the 220 total energies, with the radius denoting the total energy per layer and the angle representing each polytype. Similar to the plateaus that emerged during the genetic search, the total energies for these 220 polytypes are also discretely distributed, mainly falling upon five energy levels. Taking the total energy per layer of the pure 3C CsPbI3 as the reference, which is −12.23 eV/layer, most of the total energies fall in the inner energy levels, indicating that these stacking sequences will be hard to form. Moreover, typical sequences exhibiting abnormally high total energies per layer are extracted from the learning paleatus, such as hhhc, hhhccc, hchhhc, hhhhcc and hhhhhc. These sequences can be viewed as the high energy gene for a polytype, which are not favored during the evolution, for instance, hhhc and hhhhchhhhchhhc were found to be unstable. Such high energy gene sequences led us to identify symmetry forbidden sequences, which further decrease the number of available arrangements for h and c.
Symmetry forbidden sequences and the electronic impact of stacking sequences
The stacking sequences predicted to be highly unfavourable are in fact forbidden by crystal symmetry. The root cause is the mismatch between different counts of h and c layers in a stacking sequence. Originally, the representation that we use for the 3C unit cell is rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), while the 2H unit cell is hexagonal (P63/mmc). However, as shown in Fig. 5a, for the sequence hhhc, there is no translational symmetry as the start and end of the cell are located at different atomic sites. While the energy of these sequences can be calculated from the model Hamiltonian, which has no atomic resolution, they cannot be mapped onto a valid atomistic supercell. Such sequences should be at least doubled to form a valid centrosymmetric repeat unit. Therefore, for the sequence hhhc, its lowest periodicity is hhhchhhc.
m), while the 2H unit cell is hexagonal (P63/mmc). However, as shown in Fig. 5a, for the sequence hhhc, there is no translational symmetry as the start and end of the cell are located at different atomic sites. While the energy of these sequences can be calculated from the model Hamiltonian, which has no atomic resolution, they cannot be mapped onto a valid atomistic supercell. Such sequences should be at least doubled to form a valid centrosymmetric repeat unit. Therefore, for the sequence hhhc, its lowest periodicity is hhhchhhc.
To preserve translational symmetry for an arbitrary stacking sequence hncm, its minimum periodicity of layer number P can be determined by the following three rules:
(1) If n is odd, then P = 2(n + m), the lattice is hexagonal;
(2) If n is even, then P = 3(n + m), the lattice is rhombohedral;
(3) If n is even and m is 3X, X is zero or an positive integer, then P = (n + m), the lattice is rhombohedral. Thus, the genetically unfavorable stacking sequences, i.e. hhhc, hhhccc, hchhhc, hhhhcc, hhhhhc, are symmetry forbidden. These can only be component sequences for larger lattices and cannot exist alone, so the hhhc should be doubled into the centrosymmetric hexagonal hhhchhhc sequence; the hhhccc should be doubled into the centrosymmetric hexagonal hhhccchhhccc; and the hchhhc should be tripled into the rhombohedral hchhhchchhhchchhhc sequence and so on. The requirement of translational symmetry further decreases the number of distinct polytypes for an N layer polytype hncm.
At last, an example of the impact of stacking sequences on the underlying electronic structures of polytypes is presented in Fig. 5b–e. Taking the 11-layer polytypes as an example, the DFT electronic structures of 2h9c and 3c8h polytypes are shown. The effect of stacking sequence manifests itself by altering the band structures for two CsPbI3 polytypes, that is, from a direct band gap semiconductor (2h9c-CsPbI3) to an indirect band gap semiconductor (3c8h-CsPbI3). Even though a direct band gap is retained for CsPbBr3 polytypes, the 3c8h-CsPbBr3 polytype exhibits a noticeably larger band gap than 2h9c-CsPbBr3. The influence of stacking sequences shows the potential for electronic structures engineering in perovskite polytypes with identical compositions.
4. Conclusions
A family of perovskite polytypes can be represented by sequences of the face- and corner-sharing PbX6 octahedra. The combinatorial explosion arising from the increasing periodicity of the stacking sequence makes it resource and time demanding to perform exhaustive first-principles calculations. To address this problem, an Ising-type model Hamiltonian was constructed and the total energy for any given stacking sequence can be rapidly computed. A genetic algorithm was then built to find the ground state structures for an N layer polytype hncm. The algorithm can converge to the lowest energy sequence in seconds without enumeration over the sequences. Plateaus in the convergence behaviour led us observe symmetry forbidden sequences, which shrinks the possible valid arrangements of h and c to form polytype structures.The energetic and configurational features of the polytypism in CsPbX3 discussed in this work are also instructive for organic–inorganic systems, an extension which would require additional parameterisation for molecular disorder, for example through an on-site electrostatic model. A strong molecular disorder contribution is expected when the A-site cation is methylammonium (MA+) cation, due to its polar nature and relatively fast rotations. The formamidinium (FA+) is less polar and with slower rotations so FAPbI polytypes may be expected to behave more similar to CsPbBr3, considering both its close to ideal tolerance factor (0.99) and ground state 3C phase.
Finally, we note the polytypes discussed here may appear as stacking faults or inclusions rather than as distinct phases for many halide perovskite compositions. We hope that this work will help to bridge the divide between the real-world complexity and atomistic modelling of halide perovskite crystals, and can support future polytype engineering.
Data availability
Structure models and the codes used to generate all structures to parameterize the Ising model Hamiltonian are available in an on-line repository at http://doi.org/10.5281/zenodo.5186354.Author contributions
Z. L. performed all calculations for model building and testing. J. P. wrote the code for polytype generation. A. W. supervised the project. All authors contributed to the analysis and writing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Jacob N. Wilson for constructive discussions in the early stages of this project. We are grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1). Via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202, EP/R029431), this work used the ARCHER UK National Supercomputing Service. This work was also supported by National Research Foundation of Korea (NRF) grants funded by the Korea government (MSIT) (No. 2020R1A5A1019131 and 2020R1F1A1053606).References
- A. M. Glazer, The classification of tilted octahedra in perovskites, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1972, 28, 3384–3392 CrossRef CAS.
- P. M. Woodward, Octahedral tilting in perovskites. I. Geometrical considerations, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1997, 53, 32–43 Search PubMed.
- G. Kieslich, S. Sun and A. K. Cheetham, An extended tolerance factor approach for organic–inorganic perovskites, Chem. Sci., 2015, 6, 3430–3433 RSC.
- W. Travis, E. Glover, H. Bronstein, D. Scanlon and R. Palgrave, On the application of the tolerance factor to inorganic and hybrid halide perovskites: a revised system, Chem. Sci., 2016, 7, 4548–4556 RSC.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- NREL, Best Research-Cell Efficiency Chart, 2021, https://www.nrel.gov/pv/cell-efficiency.html Search PubMed.
- E. J. Juarez-Perez, Z. Hawash, S. R. Raga, L. K. Ono and Y. Qi, Thermal degradation of CH3NH3PbI3 perovskite into NH3 and CH3I gases observed by coupled thermogravimetry–mass spectrometry analysis, Energy Environ. Sci., 2016, 9, 3406–3410 RSC.
- J. J. Yoo, G. Seo, M. R. Chua, T. G. Park, Y. Lu, F. Rotermund, Y.-K. Kim, C. S. Moon, N. J. Jeon, J.-P. Correa-Baena, V. Bulović, S. S. Shin, M. G. Bawendi and J. Seo, Efficient perovskite solar cells via improved carrier management, Nature, 2021, 590, 587–593 CrossRef CAS PubMed.
- S. M. Yoon, H. Min, J. B. Kim, G. Kim, K. S. Lee and S. I. Seok, Surface Engineering of Ambient-Air-Processed Cesium Lead Triiodide Layers for Efficient Solar Cells, Joule, 2021, 5, 183–196 CrossRef CAS.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Semiconducting Tin and Lead Iodide Perovskites with Organic Cations: Phase Transitions, High Mobilities, and Near-Infrared Photoluminescent Properties, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS PubMed.
- A. Marronnier, G. Roma, S. Boyer-Richard, L. Pedesseau, J.-M. Jancu, Y. Bonnassieux, C. Katan, C. C. Stoumpos, M. G. Kanatzidis and J. Even, Anharmonicity and Disorder in the Black Phases of Cesium Lead Iodide Used for Stable Inorganic Perovskite Solar Cells, ACS Nano, 2018, 12, 3477–3486 CrossRef CAS PubMed.
- B. Wang, N. Novendra and A. Navrotsky, Energetics, Structures, and Phase Transitions of Cubic and Orthorhombic Cesium Lead Iodide (CsPbI3) Polymorphs, J. Am. Chem. Soc., 2019, 141, 14501–14504 CrossRef CAS PubMed.
- D. H. Fabini, C. C. Stoumpos, G. Laurita, A. Kaltzoglou, A. G. Kontos, P. Falaras, M. G. Kanatzidis and R. Seshadri, Reentrant Structural and Optical Properties and Large Positive Thermal Expansion in Perovskite Formamidinium Lead Iodide, Angew. Chem., 2016, 55, 15392–15396 CrossRef CAS PubMed.
- C. C. Stoumpos and M. G. Kanatzidis, The Renaissance of Halide Perovskites and Their Evolution as Emerging Semiconductors, Acc. Chem. Res., 2015, 48, 2791–2802 CrossRef CAS PubMed.
- M. Lai, T. Lei, Y. Zhang, J. Jin, J. A. Steele and P. Yang, Phase transition dynamics in one-dimensional halide perovskite crystals, MRS Bull., 2021, 46, 310–316 CrossRef.
- W. Li, M. U. Rothmann, Y. Zhu, W. Chen, C. Yang, Y. Yuan, Y. Y. Choo, X. Wen, Y.-B. Cheng, U. Bach and J. Etheridge, The critical role of composition-dependent intragrain planar defects in the performance of MA1−xFAxPbI3 perovskite solar cells, Nat. Energy, 2021, 6, 624–632 CrossRef.
- C. Rao, in Encyclopedia of Physical Science and Technology, ed. R. A. Meyers, Academic Press, New York, 3rd edn, 2003, pp. 707–714 Search PubMed.
- L. T. Nguyen and R. J. Cava, Hexagonal Perovskites as Quantum Materials, Chem. Rev., 2021, 121, 2935–2965 CrossRef CAS PubMed.
- S. Fop, K. S. McCombie, E. J. Wildman, J. M. S. Skakle, J. T. S. Irvine, P. A. Connor, C. Savaniu, C. Ritter and A. C. Mclaughlin, High oxide ion and proton conductivity in a disordered hexagonal perovskite, Nat. Mater., 2020, 19, 752–757 CrossRef CAS PubMed.
- T. Chen, B. J. Foley, C. Park, C. M. Brown, L. W. Harriger, J. Lee, J. Ruff, M. Yoon, J. J. Choi and S.-H. Lee, Entropy-driven structural transition and kinetic trapping in formamidinium lead iodide perovskite, Sci. Adv., 2016, 2, e1601650 CrossRef PubMed.
- J.-S. Park, Z. Li, J. N. Wilson, W.-J. Yin and A. Walsh, Hexagonal Stacking Faults Act as Hole-Blocking Layers in Lead Halide Perovskites, ACS Energy Lett., 2020, 5, 2231–2233 CrossRef CAS.
- Y. An, J. Hidalgo, C. A. R. Perini, A.-F. Castro-Méndez, J. N. Vagott, K. Bairley, S. Wang, X. Li and J.-P. Correa-Baena, Structural Stability of Formamidinium- and Cesium-Based Halide Perovskites, ACS Energy Lett., 2021, 6(5), 1942–1969 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. I. Csonka, J. P. Perdew, A. Ruzsinszky, P. H. T. Philipsen, S. Lebègue, J. Paier, O. A. Vydrov and J. G. Ángyán, Assessing the performance of recent density functionals for bulk solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 155107 CrossRef.
- R. Magri, S.-H. Wei and A. Zunger, Ground-state structures and the random-state energy of the Madelung lattice, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 11388–11391 CrossRef PubMed.
- J. N. Wilson, J. M. Frost, S. K. Wallace and A. Walsh, Dielectric and ferroic properties of metal halide perovskites, APL Mater., 2019, 7, 010901 CrossRef.
- M. L. Plumer, K. Hood and A. Caille, An Ising-like model of stacking-sequence polytypism in ABX3 compounds, J. Phys. C: Solid State Phys., 1988, 21, 4189–4206 CrossRef.
- J. Shi, Y. Wang and Y. Zhao, Inorganic CsPbI3 Perovskites toward High-Efficiency Photovoltaics, Energy Environ. Mater., 2019, 2, 73–78 CrossRef CAS.
- W. Zhang, X. Liu, B. He, J. Zhu, X. Li, K. Shen, H. Chen, Y. Duan and Q. Tang, Enhanced Efficiency of Air-Stable CsPbBr3 Perovskite Solar Cells by Defect Dual Passivation and Grain Size Enlargement with a Multifunctional Additive, ACS Appl. Mater. Interfaces, 2020, 12, 36092–36101 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc03098a |
| This journal is © The Royal Society of Chemistry 2021 |