Open Access Article
Open Access ArticleExcimer formation dynamics in the isolated tetracene dimer†
Joscha
Hoche
 ,
Marco
Flock
,
Xincheng
Miao
,
Marco
Flock
,
Xincheng
Miao
 ,
Luca Nils
Philipp
,
Michael
Wenzel
,
Ingo
Fischer
,
Luca Nils
Philipp
,
Michael
Wenzel
,
Ingo
Fischer
 * and
Roland
Mitric
* and
Roland
Mitric
 *
*
Institut für Physikalische und Theoretische Chemie, Universität Würzburg, Am Hubland, 97074 Würzburg, Germany. E-mail: ingo.fischer@chemie.uni-wuerzburg.de; roland.mitric@uni-wuerzburg.de
First published on 3rd August 2021
Abstract
The understanding of excimer formation and its interplay with the singlet-correlated triplet pair state 1(TT) is of high significance for the development of efficient organic electronics. Here, we study the photoinduced dynamics of the tetracene dimer in the gas phase by time-resolved photoionisation and photoion imaging experiments as well as nonadiabatic dynamics simulations in order to obtain mechanistic insight into the excimer formation dynamics. The experiments are performed using a picosecond laser system for excitation into the S2 state and reveal a biexponential time dependence. The time constants, obtained as a function of excess energy, lie in the range between ≈10 ps and 100 ps and are assigned to the relaxation of the excimer on the S1 surface and to its deactivation to the ground state. Simulations of the quantum-classical photodynamics are carried out in the frame of the semi-empirical CISD and TD-lc-DFTB methods. Both theoretical approaches reveal a dominating relaxation pathway that is characterised by the formation of a perfectly stacked excimer. TD-lc-DFTB simulations have also uncovered a second relaxation channel into a less stable dimer conformation in the S1 state. Both methods have consistently shown that the electronic and geometric relaxation to the excimer state is completed in less than 10 ps. The inclusion of doubly excited states in the CISD dynamics and their diabatisation further allowed to observe a transient population of the 1(TT) state, which, however, gets depopulated on a timescale of 8 ps, leading finally to the trapping in the excimer minimum.
1. Introduction
Polyacenes are of interest in materials science, because they can act as hole conductors in organic devices. In particular tetracene and pentacene have been identified as candidates that fulfil the photophysical requirements for singlet fission (SF), a process in which an excited singlet state deactivates to two triplets located on neighbouring molecules. The underlying physics has been described in several reviews.1–5 The major condition for SF is the existence of a low-lying triplet state at half the energy of the initially excited singlet state. SF has already been demonstrated to improve the efficiency of solar cells6,7 and thus it receives considerable attention. In tetracene, the T1 state is slightly too high for SF to occur from the S1 origin, but already some vibrational excitation suffices to fulfil the energy condition. Due to its importance as a model for SF, various systems with tetracene chromophores have been studied. SF is envisioned to proceed in two steps, (a) formation of a pair of singlet-correlated triplets from the initially excited state, which then (b) decouples to two triplets on separate molecules.4 However, a consistent picture of the dynamics has not yet emerged. The radiationless relaxation in the tetracene monomer was studied by Spiegelman et al. by employing nonadiabatic dynamics simulations.8 Further nonadiabatic dynamics simulations on covalently linked tetracene dimers and tetracene clusters were conducted to study the exciton localisation process.9,10 Studies by Burdett et al. compared the dynamics in solution with polycrystalline films and revealed an important role of defect states for the dynamics.11 Thin films were investigated by transient absorption in the group of R. Friend and by Schmidt and coworkers, who both observed time-constants of around 80–90 ps. While Friend et al. attributed the time constant to the formation of triplet pairs from S1, i.e. to singlet fission,12 Schmidt and coworkers assigned the transient signal to a transition from S1 to a multi-exciton state that possibly deactivates to separated triplets in a later step.13 Numerous experiments dealt with tetracene units connected by linkers. Bradforth and coworkers recently reported the linker-dependence of SF in such assemblies dissolved in THF, applying a variety of time-resolved and steady-state spectroscopic techniques,14 while Damrauer and coworkers explored structurally rigid dimers extensively.15–18 In contrast, experiments on isolated dimers in a free jet permit a direct comparison with theory and offer an understanding of non-radiative relaxation processes on the molecular level without perturbations by the environment. Such experiments, which could give insight into the relationship between structural changes after excitation and subsequent non-radiative processes are however still scarce. In particular a description of excimer formation, which may compete with or precede the formation of a singlet-correlated triplet pair4,19–21 is lacking. While some studies claimed that excimer formation constitutes an intermediate step in SF, Dover et al. investigated TIPS-tetracene in solution and found excimers to act as traps that hinder SF.22 Very recently, comprehensive benchmarks on tetracene dimers, stacked and T-shaped, were performed by Cardozo et al. showing an overall good agreement between TD-lc-DFTB, TD-DFT, SOS-ADC(2) and DFT/MRCI.23 A thorough investigation of excimer formation in tetracene thus seems to be mandated. Recently, the excimer formation of benzene was studied in detail experimentally by Fujii et al.24 and by simulation by the groups of Krylov25 and Cardozo.26 The excimer formation dynamics was also studied in larger systems like bay-tethered perylene bisimides by Würthner et al., where a single relaxation pathway to the excimer state was found.27 We recently explored the excimer formation in isolated pyrene dimers in a joint computational and experimental study.28 Upon photoexcitation, the parallel displaced dimer relaxed to a stacked geometry, which subsequently leads to excimer formation. The simulations led to the identification of two degrees of freedom associated with this process: (i) local relaxation along the stacking coordinate close to the FC window and (ii) large amplitude oscillations along the parallel shift coordinate accompanied by damped oscillations along the stacking direction. The combined motion leads to the stabilisation of the excimer on a time scale of around 5 ps. Here we address the tetracene system with the goal to understand the deactivation processes occurring in the photoexcited dimers, in particular excimer formation. In the experimental work the dynamics is monitored by time-resolved photoionisation. A picosecond (ps-) laser system is employed, which permits to study the dynamics as a function of excitation energy. The advantages of ps-lasers have been demonstrated in previous work on molecular dimers and clusters.28–31 Nonadiabatic dynamics simulations are performed at the semi-empirical CISD level and in the frame of TD-lc-DFTB in order to explore the processes that set in after the electronic excitation and to identify the dominating relaxation channels.2. Computational details
Structural properties and absorption spectra
The electronic structure of the tetracene dimer has been described in the framework of density functional theory (DFT) employing the hybrid ωB97X-D functional32 as implemented in the Gaussian16 software package33 combined with the def2-SVP basis set.34 The vibrationally resolved absorption spectra for the optically bright S2 ← S0 transition were simulated within the Franck–Condon approximation employing the adiabatic Hessian model (AH) and the vertical gradient method (VG), as implemented in the FCclasses program of J. Cerezo and F. Santoro.35–37Nonadiabatic dynamics simulations
The nonadiabatic dynamics simulations of the excimer formation process have been performed by employing Tully's surface hopping approach38 in combination with a modified calculation scheme for the hopping probabilities39 and using a local diabatisation method to propagate the electronic wavefunction.40,41 A time step of 0.1 fs was used for the surface hopping simulations. Two sets of trajectories were propagated by employing two different levels of theory. In the first set the efficient TD-lc-DFTB method which offers a good compromise between accuracy and computational cost42–45 was used and 34 trajectories were simulated for 10 ps. A reduced active space composed of the highest 24 occupied and the lowest 24 virtual orbitals, denoted as (48e,48o) in what follows, was used for the excited state calculations at the TD-lc-DFTB level. This space provides a good compromise between accuracy of excitation energies and the computational time needed for surface hopping calculations.The second set of trajectories was propagated for up to 20 ps using semi-empirically parameterised configuration interaction with singles and doubles (CISD) with the PM6-D3H4 parameterisation.46–48 Here, an active space of only 2 occupied and 2 virtual orbitals was selected, which shows qualitative agreement with TD-lc-DFTB and TD-DFT(ωB97X-D/def2-SVP) and requires a feasible amount of computational time. CISD allows to include the doubly excited states which are involved in the singlet-fission process (e.g. singlet-correlated triplet pair state). The TD-lc-DFTB calculations were performed using the software package DFTBaby49 while MOPAC2016 (ref. 50) was used for the semi-empirical CISD computations.
The ground-state phase-space distribution, from which the initial conditions were sampled, has been approximated by a canonical Wigner distribution calculated in the harmonic approximation.51,52 For nonadiabatic dynamics simulations employing TD-lc-DFTB, 34 normal mode displacements and momenta were sampled at 50 K. Afterwards, these geometries were equilibrated to 20 K by performing ground-state dynamics at constant temperature using a Berendsen thermostat.53 The Cartesian coordinates and velocities after equilibration were used as initial conditions for the nonadiabatic trajectory simulations. The equilibration step is needed in order to relax the high frequency modes, which tend to be too strongly excited if a harmonic distribution is sampled. For dynamics employing CISD, 100 of such initial conditions were generated. For all the sampled nuclear configurations the S2 ← S0 transition was found to be the most intense one. Therefore, all surface-hopping trajectories were launched from the S2 state.
Analysis of nonadiabatic dynamics in diabatic picture
In order to analyse the electronic character of adiabatic states as computed along nonadiabatic CISD trajectories, one must at first localise the molecular orbitals (MOs) to each monomer. This was realised by using a localisation procedure based on a singular value decomposition (SVD) of the MO coefficients.54–56 The basic idea is to divide the coefficient matrix for n occupied molecular orbitals into rectangular submatrices, each of which contains only AOs on one monomer. Principal component analysis (PCA) was then performed on all submatrices using SVD. The obtained right singular vectors with largest singular values were selected and assigned to the corresponding monomer. Since these vectors in general originate from different submatrices, they were Löwdin orthogonalised57 to form a unitary matrix V, which transforms the original occupied MOs (φi) into localised occupied orbitals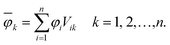 | (1) |
The overline denotes transformed localised orbitals. The same procedure can be applied for the m virtual MOs in the active space, which results in localised virtual orbitals
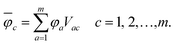 | (2) |
The squared elements from the CI coefficient matrix for the d-th state (Cdia)2 describe the contribution of a specific singly excited configuration. With the help of the unitary matrices Vik and Vac, one can transform the coefficient matrix from the MO basis into the basis of localised orbitals58 giving rise to
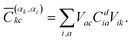 | (3) |
These elements can then be labelled with the initial monomer αk, to which the localised orbital φk belongs, and the final monomer αc, to which φc belongs. This way, one can define the contribution for local excitation (LE) pLE by summing up all squared elements with αk = αc
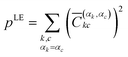 | (4) |
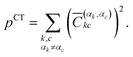 | (5) |
The coefficients for double excitations can be transformed into the basis of localised orbitals in a similar manner using
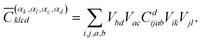 | (6) |
The squared elements with αk = αc and αl = αd, or αk = αd and αl = αc can be summed up to obtain the contribution of the multiexciton (two triplets coupled into a singlet) state (1(TT)) p1(TT),
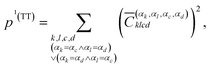 | (7) |
The weight of a specific diabatic state X ∈ {LE, CT, 1(TT), RST} can finally be obtained by normalising the contributions pX
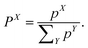 | (8) |
3. Experimental methods
All gas phase experiments were conducted in a differentially pumped vacuum chamber, which has been described in more detail in a previous publication.59 Tetracene (C18H12, 228 g mol−1) was purchased from Sigma-Aldrich and used without further purification. The sample was placed in a home-built oven, heated up to around 200 °C, seeded in argon or helium and expanded into vacuum via a pulsed valve with a 300 µm diameter nozzle. After around 2 cm, the produced supersonic jet passed a conical skimmer (aperture 2 mm) and reached the main chamber of the setup, where it was crossed by the laser beams. The presence of clusters in the molecular beam depended strongly on the expansion conditions. Experiments on monomeric tetracene were carried out at low argon or helium backing pressures (p0 ≈ 1.2 bar), temporally short molecular pulses (FWHM ≈ 150 µs) and at the leading edge of the gas pulse. In contrast, experiments on the dimer required higher backing pressures (p0 ≈ 1.6–1.8 bar) and longer molecular pulses (FWHM ≈ 400 µs) and the laser was synchronised closer to the centre of the pulses. As light source we used a system based on a picosecond Nd:YLF laser that was also described earlier.60 The third harmonic of the 1053 nm fundamental (351 nm, 3.532 eV) was produced via frequency tripling (SHG and SFG) and used to pump an OPG, which generated tuneable laser pulses with a bandwidth of around 10 cm−1. The OPG output pulses were used to excite the molecules, while the fourth harmonic of the setup (263.5 nm, 4.705 eV) was employed as probe wavelength in the two-colour [1 + 1′] REMPI experiments. The instrument response function (IRF) of the laser setup was found to be around 4 ps. Both pulses were overlapped with a dichroic mirror in front of the vacuum chamber and slightly focused into the molecular beam. For experiments aimed at the monomer, unfocused pump pulses were used, since no cluster fragmentation was visible under these conditions. Typically, both laser pulses were vertically polarised, however rotating one of the polarisations did not affect the experimental results.A velocity map imaging ion optics61 accelerated the photoions onto an imaging detector, consisting of two microchannel plates (MCPs) in Chevron configuration and a P43 phosphor screen. In the TOF-MS experiments, the photoion signal was measured by a home-built current monitor. Typically, each data point was averaged over 50 laser shots. For the REMPI spectra, three scans with a step size of 0.2 nm were averaged, while the time-delay traces consist of ten scans with 50 time steps per trace. In the photoion VMI experiments, the light emitted from the phosphor screen was recorded with a CCD camera yielding 2D raw images, each averaged over 1800 laser shots. The images were reconstructed via the pBASEX method,62 employing Legendre polynomials up to the 2nd order. To ensure mass selectivity in the VMI experiments, the voltage applied on the second MCP of the dual-stage detector was gated on the arrival time of the dimer species with a gate width of 150 ns employed by a push/pull switch.
4. Results
Structural properties
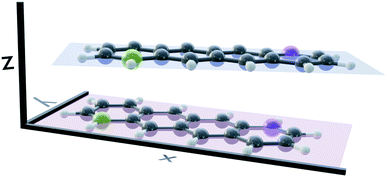
Several stable conformers of the tetracene dimer are described in the literature. Both experimentally and theoretically, a slightly rotated, stacked geometry was found to be the most stable arrangement.23,63 Experimentally, the authors elucidated these structures from angular covariance maps recorded in a strong-field laser ionisation experiment of tetracene in helium nanodroplets. The optimised ground state geometry at the DFT(ωB97X-D/def2-SVP) level is shown in Fig. 1. The two longitudinal axes of the molecules close an angle of approximately 25°. The molecular planes are parallel and their centres are shifted slightly in x-direction. The displacement in x- and y-direction Rx and Ry, as well as the rotation about z-direction Rotz, were evaluated with regard to the coordinate system of the first monomer as shown in Fig. 1. The axes were determined by performing a singular value decomposition (SVD) on the coordinates of all carbon atoms of a single monomer with the centroid subtracted. The right singular vectors sorted by descending singular values were selected as x-, y- and z-axis, respectively. However, since the singular vectors do not possess a consistent direction, the vector spanning from the green carbon atom to the violet one in each monomer (as depicted in Fig. 1) was used to calibrate the positive direction of both x- and y-axis. The positive direction of z-axis follows from the right hand rule. The displacements in x- and y-directions were obtained by projecting the displacement vector between the centroids of both monomers on to x- and y-axis of the first monomer, respectively. The rotation about z-axis is obtained by evaluating the dihedral angle of both monomeric x-axes.Potential energy curves
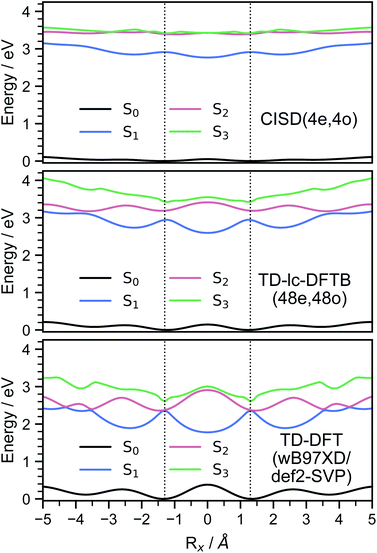
In order to investigate the energetic landscape of the interaction between both monomers, the energies of several electronic states were determined with respect to displacements in x- and z-directions using CISD(4e,4o, PM6-D3H4), TD-lc-DFTB and ωB97X-D/def2-SVP. Starting from a monomer structure that was optimised in its first excited singlet state (S1), the potential energy curves (PECs) along x-displacement were generated by setting Ry to 0 and Rz to a specific value and shifting one monomer rigidly along the x-axis of the other. The value of Rz was chosen to be the distance for which the PEC of S1 has a minimum for Rx = Ry = 0. Optimisations and single-point calculations were performed by using the same method. The PECs along z-displacement were generated by starting from the S1 optimised dimer geometry at SOS-ADC(2) level obtained by Cardozo et al.23 and shifting one monomer rigidly along the z-axis of the other monomer. The distances Rz were determined by measuring distances between the planes obtained using SVD as described above. Our results obtained with TD-lc-DFTB agree very well with the potential energy curves of ref. 23 (see left side of Fig. 2). Despite employing the same method, the results differ slightly quantitatively because we use different Slater–Koster parameters and repulsive potentials in DFTBaby compared to DFTB+.64 We have omitted a comparison to TD-DFT at this point, as we refer the reader to ref. 23 for a more detailed comparison of the quantum chemical methods. There, it is observed that DFT/MRCI predicts a doubly excited state lying below the bright state at the optimised S1 geometry that cannot be described by ordinary TD-DFT(B). In a comparison with the DFT/MRCI results of ref. 23 it is evident that the semi-empirical CISD results agree qualitatively well. The right side of Fig. 2 depicts the potential energy curves at the CISD level, where the red curve shows the doubly excited 31Ag state. Since this double excited state could be important for the excimer relaxation as well as for the formation of the singlet-correlated triplet pair state, we simulated the nonadiabatic dynamics not only using TD-lc-DFTB but also at the semi-empirical CISD(4e, 4o) level.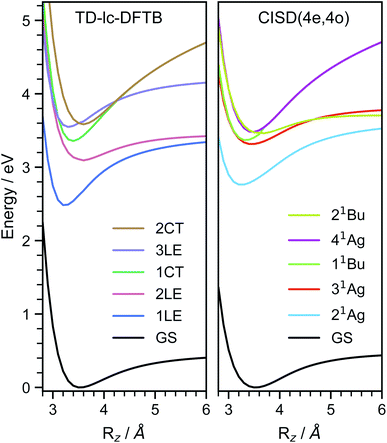 | ||
| Fig. 2 Potential energy curves along the intermolecular stacking coordinate (Rz) as defined in the text. The energies are relative to the minimal energy structure in the electronic ground state. The electronic excited states are adiabatically connected in a similar way as done in ref. 23 to be able to readily compare the performance of the quantum chemical methods. In TD-lc-DFTB case, states are labelled based on their character, while for CISD, symmetry labels are used. | ||
TOF-MS spectra
In a first experiment we recorded one-color REMPI spectra of the transitions into the S1 (B2u) and S2 states in monomeric tetracene, which are depicted in the ESI (Fig. S1 and S2†). It illustrates that at least at low excess energies individual vibronic bands can be resolved. Since the ionisation energy (IE) of the monomers is 6.97 eV (ref. 65) and the S1 origin is located at 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 397 cm−1 (2.78 eV),66 a [1 + 2] REMPI process is required for ionisation via S1. In good agreement with previous work,66–68 the origin was found at 22
397 cm−1 (2.78 eV),66 a [1 + 2] REMPI process is required for ionisation via S1. In good agreement with previous work,66–68 the origin was found at 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 406 cm−1 (446.3 nm). Furthermore, some well resolved vibronic modes were detected in the region up to +2000 cm−1, with the most intense one at +1517 cm−1.
406 cm−1 (446.3 nm). Furthermore, some well resolved vibronic modes were detected in the region up to +2000 cm−1, with the most intense one at +1517 cm−1.
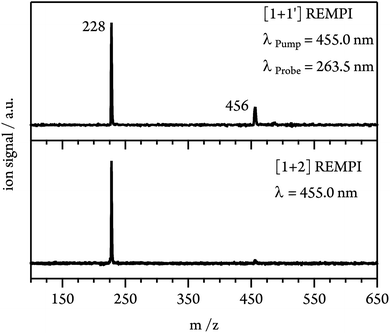
At expansion conditions which favour the formation of multimeric species, even at excitation energies below the S1 origin an intense signal is present in the mass spectrum at m/z = 228 (see Fig. 3, lower trace). The additional small peak at m/z = 456 corresponds to the dimer and indicates strong fragmentation of the dimer cation due to the high excess energy provided in the [1 + 2] REMPI process (1.21 eV relative to the monomer IP at λ = 455.0 nm). To lower the excess energy and to suppress dissociative photoionisation (DPI), we therefore switched to [1 + 1′] REMPI experiments. Using a probe wavelength of λProbe = 263.5 nm (4th harmonic of Nd:YLF laser) gives a total photon energy of 7.43 eV (at λPump = 455.0 nm) and an excess energy of only 0.46 eV relative to the monomer IE. As can be seen in Fig. 3 (upper trace), the dimer signal is significantly enhanced compared to [1 + 2] ionisation. However, the monomer peak still dominates the spectrum and thus fragmentation of clusters has to be taken into account in the interpretation of the experimental data.
REMPI spectra and simulated absorption spectra
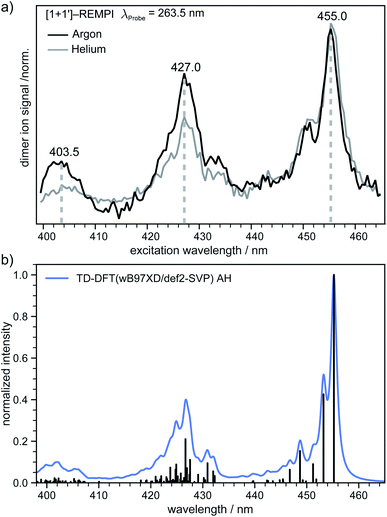
In the next step an absorption spectrum of the tetracene dimer was recorded. The pump–probe delay time was fixed to 20 ps and the dimer ion signal was recorded as a function of the excitation wavelength. The [1 + 1′] REMPI spectra (λProbe = 263.5 nm) obtained in argon and helium as carrier gases are both presented in (Fig. 4a). As can be seen, the spectra show three well defined maxima at 455.0, 427.0 and 403.5 nm. The band positions perfectly match in both spectra, however the higher energy bands are more pronounced in argon. In previous work an absorption spectrum of the tetracene dimer in diethylether/ethanol glasses with an onset around ∼476 nm has been reported69 which is in good agreement with our results.In order to gain further information on the excited dimer species and to check the quality of the quantum-chemical methods, the dimer absorption spectrum was calculated using TD-DFT(ωB97X-D/def2-SVP) and semi-empirically parameterised CISD(4e,4o). The vibrationally resolved absorption spectrum at the TD-DFT level is shown in (Fig. 4b). Note that the transition to the S1 state is Franck–Condon forbidden for a dimer with a structure close to a H-aggregate, so the spectrum corresponds to excitation of the S2 state. However, we also simulated the vibration-resolved absorption spectra of the S1 taking into account Herzberg–Teller (HT) effect that is shown in Fig. S6.† The S1 gains some intensity due to the HT coupling, but the overall intensity is negligible compared to the S2 state. It should be noted, however, that the minimum of S1 is significantly shifted compared to the ground state geometry. Therefore, it is questionable if the harmonic approximation is applicable at all in this case. The spectral envelopes and the relative energy differences between the three dominant peaks match the appearance of the experimental REMPI spectra almost perfectly in the AH model. The second (third) most intense transition is shifted by ∼1458 cm−1 (∼2916 cm−1) with respect to the 0–0 transition and we denote these transitions as the “0–1” and “0–2” transition, respectively. For further comparison the vibrationally resolved absorption spectra were simulated in the frame of TD-DFT and CISD employing the vertical gradient model. These spectra are shown in Fig. S5† and agree very well with the experimental REMPI spectrum.
In addition to the dimer, a signal of the trimer is present in the mass spectrum with small intensity. Fig. S3† shows its REMPI spectrum. As visible, dimer and trimer show separated bands, which allows to excite a given cluster size preferentially. This demonstrates the advantage of a ps-laser for cluster experiments.
Time-resolved photoionisation experiments
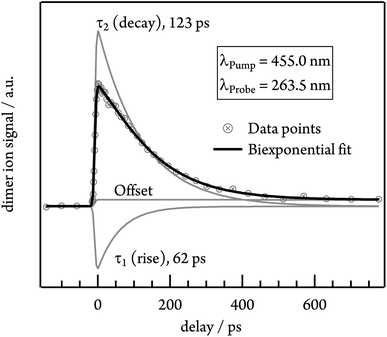
To gain insights into the dynamics of the tetracene dimer, we performed time-resolved photoionisation experiments. The dimers were excited at their absorption maxima (455.0, 427.0 and 403.5 nm) and ionised with a 263.5 nm probe photon. Note that Fig. S3† shows that selective excitation of the dimer is possible even in the presence of trimer. Recording the dimer ion signal as a function of the pump–probe delay yielded ion decay traces as depicted in Fig. 5 for excitation with 455.0 nm.Initially the time-dependence of the signal was fitted with a monoexponential decay function, but no satisfactory match was achieved. Instead, the biexponential fit with two time constants τ1 and τ2 is required for a proper description of the time-dependent signal. τ1 possesses a negative amplitude and thus represents a population increase, while τ2 describes a decay time. The contributions of both time constants to the total fit function in the case of 455.0 nm excitation are depicted in Fig. 5. Both time constants decrease with excitation energy and are slightly smaller in helium, due to the higher temperature of the molecular beam. τ1 ranges from 62 ps in argon at 455.0 nm to 13 ps in helium at 403.5 nm, while the slower time constant τ2 shows values from 123 ps (argon, λPump = 455.0 nm) to 50 ps (helium, λPump = 403.5 nm). A summary of all time constants obtained in both carrier gases is given in Table 1. Note that the transient signal does not decay to zero even at long delay times, but a constant signal offset remains. The origin of this feature will be discussed in more detail in the following section.
| λ Pump [nm] | Argon | Helium | ||
|---|---|---|---|---|
| τ 1 [ps] (rise) | τ 2 [ps] (decay) | τ 1 [ps] (rise) | τ 2 [ps] (decay) | |
| 455.0 | 62 | 123 | 49 | 97 |
| 427.0 | 34 | 69 | 38 | 58 |
| 403.5 | 18 | 54 | 13 | 50 |
Time-resolved VMI experiments
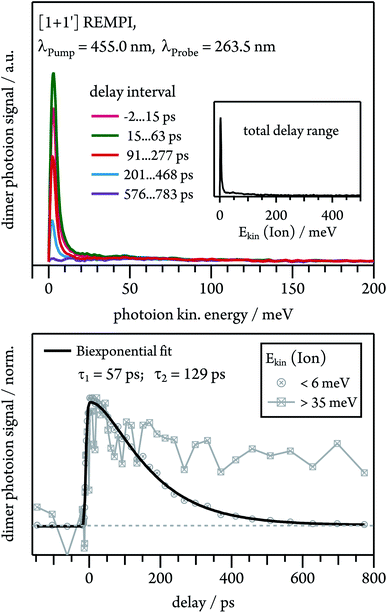
Dissociative photoionisation of larger clusters can contribute to the time-dependence in lower mass channels and thus obscure their dynamics.30 To evaluate the influence of fragmentation processes on the dimer dynamics, we performed time-resolved velocity map imaging (VMI) experiments. While a cation produced through ionisation of a neutral dimer possesses negligible kinetic energy (Ekin(Ion) ≈ 0), because the excess energy is carried away by the electron, fragment ions from dissociative photoionisation of larger clusters show a kinetic energy distributions with Ekin(Ion) > 0. As the VMI technique enables the determination of the photoion kinetic energy, it therefore allows us to distinguish between molecular ion and fragment ion signals, as demonstrated in Fig. 6. We ionised the dimer in a [1 + 1′] process with λPump = 455.0 nm and recorded the ion kinetic energy distribution as a function of the pump–probe delay. The inset in Fig. 6 represents the ion kinetic energy distribution integrated over the complete delay range. It can be seen that the spectrum is dominated by a Gaussian-shaped peak at Ekin(Ion) ≈ 0 meV, which is due to photoionised dimers. In addition, a small contribution is visible at higher kinetic energies up to around 150 meV, which originates from fragment ions. A comparison of the temporal evolution of the Gaussian and the higher energy component shows that the first one drops to zero at long delay times, while the latter one decays to a constant signal offset at long delay times. This leads us to conclude that the long-lived transient observed in the dimer decay traces (see Fig. 5) is due to fragmentation of higher order clusters and thus not related to photoinduced dynamics in tetracene dimers. As visible in Fig. S3,† dimer and trimer exhibit well separated bands, but nevertheless a small amount of trimer will be excited on the maxima of the dimer bands. The time dependence of the Gaussian contribution can again be described with a biexponential fit function with τ1 = 57 ps and τ2 = 129 ps (lower trace of Fig. 6) and thus agrees well with the results obtained in the TOF-MS experiments (see Table 1).Nonadiabatic dynamics of excimer formation
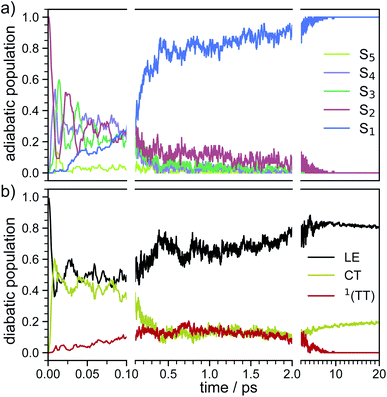
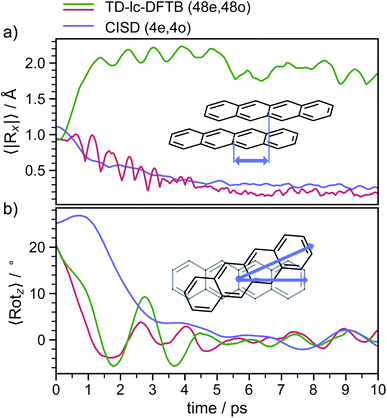
In order to determine the mechanism that governs the excited state relaxation and leads to the subsequent excimer formation, we performed trajectory surface hopping dynamics simulations in the frame of TD-lc-DFTB as well as semi-empirical CISD. The two lowest excited states (S1 and S2) and the ground state have been included in the TD-lc-DFTB dynamics while in the CISD simulation we included the first six electronic states with a singlet multiplicity. The nonadiabatic couplings between all states have been calculated. The time-dependent excited state populations obtained from the CISD nonadiabatic dynamics (cf.Fig. 7) exhibit a decay within ∼500 fs from the S2 state to the S1.The S2 population falls drastically from 1 to about 0.2 in the first 100 fs and decreases gradually to 0 at around 8 ps in an oscillatory manner. This ultrafast population transfer results from the energetic proximity of the S2 state to the higher lying excited states. Almost like its mirror image, the S1 population increases from 0 to about 0.8 rapidly in about 400 fs and then slowly rises to 1 at around 8 ps. Higher excited states, especially the S3 but also the S4 do get populated up to 30 to 40% in the initial decay of S2. The populations however, are rather quickly funnelled to S1 and are basically 0 after about 2.5 ps. The S5 state hardly plays any role in the dynamics because of its very low population throughout the whole simulation. The diabatic states experience a very rapid change similar to the adiabatic ones. The locally excited (LE) state falls from 1 to about 0.5 in the first 10 fs. It then raises oscillatorily to almost 0.9 at 4 ps. Afterwards, the populations of the LE states decrease to a value of 0.8. The charge transfer (CT) population behaves almost like the mirror image of the LE state. It reaches 0.5 in the first 10 fs starting from 0 and decreases to about 0.1 at 2.5 ps. It then gradually increases to its final value 0.2 at the end of the simulation. The population of the singlet-correlated triplet pair state, 1(TT), rises from 0 to about 0.13 in the first 250 fs. It then oscillates around this value, reaching a maximum of 0.2 at about 750 fs and starts to gradually fall at 2 ps. After about 8 ps, the population of the 1(TT) has decreased to zero. The adiabatic state populations of the TD-lc-DFTB dynamics are shown in the ESI (see Fig. S1†) and exhibit a S2 to S1 population transfer on the same time scale as we observed in the CISD simulations. We did not transform the adiabatic TD-lc-DFTB states into a diabatic basis as this single-reference method cannot account for doubly excited states. The Fig. 8 shows scans of the potential energy curves along the longitudinal (x) axis. The upper part shows the curves for CISD(4e,4o), in the middle TD-lc-DFTB and at the bottom the results in the frame of TD-DFT(ωB97X-D/def2-SVP) are shown. It can be seen that the potential energy landscapes of all states are too flat with CISD (assuming the TD-DFT potentials are correct) and both the minimum of the excimer state at Rx = 0 and the other local minima at Rx ≈ 2.5 Å are energetically underestimated. In TD-lc-DFTB, however, the agreement with the TD-DFT results is much better. For this reason, we also performed dynamics simulations with TD-lc-DFTB to check whether the geometric relaxations on the semi-empirical CISD are adequately described. Based on the results of the TD-lc-DFTB nonadiabatic dynamics simulations, two excimer formation channels have been identified in the gas phase: the trajectories either relax to a local minimum in the S1-state close to the FC region and undergo vibrational dynamics mainly along the intermolecular rotation coordinate as the excimer state is formed (see green curve in Fig. 9), or they relax into the perfectly stacked global minimum in the first excited state along the parallel shift coordinate which is accompanied by a simultaneous decrease of the angle around the z-axis (see red curve in Fig. 9). Both relaxation channels can be qualitatively understood based on the shape of the potential energy curves shown in Fig. 8. The PECs exhibit a local minimum in the S2 state close to the FC geometry and a local minimum in the S1 state where Rx ≈ 2.4 Å. The global minimum in the S1 state is characterised by a perfectly stacked geometry. In five trajectories dissociation within 10 ps was observed that was not assigned to one of the relaxation channels shown in Fig. 9. However, at the CISD level (see violet curves in Fig. 9) only one excimer formation channel could be identified. Furthermore, the displacement around the longitudinal coordinate and the rotation around the z-axis are much weaker in the CISD dynamics. These differences can be explained by the differences in the PECs. For one reason, the PECs at the CISD level are much flatter, which is why the large amplitude vibrations will be less pronounced, and for another, the local minima are less stable, so that the excimer cannot be trapped there.
After about 3 to 4 ps the excimer is formed and both the displacement along the x- and y-direction decrease to values representing an almost perfectly stacked geometry. Initially, the angle drops from about 24° to around 0° within the first 3 to 4 ps and exhibits subsequently damped oscillations with a period of ≈2 ps that persist for the whole simulation period of 20 ps. The stabilisation of the excimer requires the removal of energy from the intermolecular coordinates and its internal redistribution over all available vibrational modes.
5. Discussion
Based on the computational and experimental results, a comprehensive picture of the dynamics can be deduced. The photoabsorption visible in the REMPI spectrum corresponds to the S2 ← S0 excitation of the tetracene dimer, as confirmed by computations. Simulations of the nonadiabatic dynamics starting in the S2 state further reveal a fast deactivation to the S1 state on the timescale of ∼500 fs. Such a fast relaxation process is not visible in the experimental data probably due to the limited temporal resolution of our ps laser setup (IRF ≈ 4 ps). Nevertheless, the time-resolved TOF-MS and VMI experiments reveal a biexponential time dependence of the dimer ion signal, with an increasing and a decaying component. Contributions from the photodissociation or dissociative photoionisation of the trimer can be ruled out, based on the different absorption bands and the analysis of the ion images. As the non-radiative deactivation of the optically excited state is not observed, the experimental transients reflect the dynamics on the S1 surface, after it has been populated in a rapid non-radiative transition. Both time constants decrease with excitation energy, which suggests that the rates increase with the density of states. Generally speaking, the ion signal correlates with the ionisation probability at a given delay time. A rise in the transient signal thus can be related to a geometric relaxation into a more ion-like structure and therefore enhanced FC factors for the ionisation step. In contrast, electronic relaxation into vibrationally highly excited states typically leads to lower FC factors and contributes a decay to the transient. We therefore assign τ1 to geometric relaxation within the S1 manifold, associated with excimer-formation and relaxation. Consequently, τ2 is assigned to the deactivation of this excimer state. It is revealing to compare these time constants with data from previous work. In thin films time constants of 80–90 ps were observed in transient absorption spectra. Time-resolved fluorescence measurements on covalently bound stacked tetracene dimers yielded an excimer-emission lifetime of 230 ps.70 These time constants are on the same order of magnitude as the decay time (τ2) observed in the present experiments (123 ps at λPump = 455.0 nm in argon). Thus it is reasonable to assign τ2 to the deactivation of the excimer.As discussed above, tetracene is considered to be a model system for singlet fission. In our CISD dynamics simulations we observed that the 1(TT) state, which is a precursor for singlet fission, is only transiently populated after excitation, before it deactivates to the excimer state. From the simulations we conclude that excimer formation prevents an efficient population of the 1(TT) state in the gas phase. The latter is only an intermediate step between the optical excitation and excimer formation, which indicates an important role of the surrounding in the condensed phase. On the other hand, our interpretation is in accordance with the observations by Dover et al., who conclude that the excimer acts as an excited state trap in TIPS-tetracene, which reduces the singlet-fission yield.22 Experiments on isolated systems, as discussed in the present manuscript, permit to separate the intrinsic properties of the molecular aggregate from the influence of the environment and to validate the theoretical methodology. Studies in solution or crystals will benefit from these investigations, because dynamics absent in the isolated dimer can more easily be assigned to the environment.
6. Conclusion
In this work we investigated excimer formation dynamics in tetracene dimer after optical excitation into the S2 state, both by time-resolved spectroscopy and nonadiabatic dynamics simulations. The picosecond photoionisation experiments were performed in a supersonic jet. Due to the bandwidth of the laser system, dimers and trimers are excited separately and a vibrationally resolved spectrum of the dimer is recorded. Photoion imaging detection permits to distinguish between ∼ true ∼ dimer contributions and contributions from dissociative photoionisation. While the initial depopulation of the S2 state is not resolved, two time constants are observed that are associated with relaxation and deactivation of the excimer state.The nonadiabatic dynamics simulations were performed in the frame of semi-empirical CISD(4e,4o) as well as TD-lc-DFTB(48e,48o) in the gas phase. They led to the identification of a dominant excimer formation channel that is characterised by the relaxation to the global S1 minimum at an almost perfectly stacked geometry. While the TD-lc-DFTB trajectories showed a second relaxation pathway to a geometry that is shifted along the longitudinal axis, this could not be observed in the semi-empirical CISD(4e,4o) simulations. This is explained by the resulting flat potential along this axis. On the other hand, the inclusion of doubly excited states allows to track the population of 1(TT) state. During the electronic relaxation, we observe a population of a 1(TT) state, that could in principle lead to singlet fission. However, this state was only transiently populated for 2 to 3 ps and was depopulated within the next 5 ps by the excimer formation process. In agreement with previous work on the pyrene dimer,28 we observe that large amplitude oscillations play an essential role in the relaxation process after excitation.
In conclusion, the singlet-correlated triplet state 1(TT) is only transiently populated and excimer formation acts as an excited state trap.
Data availability
Data reported in this article are available on demand by contacting the corresponding authors.Author contributions
J. H. contributed to the conceptualisation, simulation and analysis of all theoretical investigations, visualisation and writing of the presented work. M. F. performed and analyzed the experiments and contributed to the writing of the original draft. X. M. contributed to the simulations of the PEC scans, the simulation and analysis of the (CISD) nonadiabatic dynamics and the writing of the presented work. L. N. P. contributed to the simulation of the PEC scans and the simulation of (TD-lc-DFTB) nonadiabatic dynamics simulations. M. W. contributed to the simulation of the vibrationally resolved spectra. I. F. and R. M. conceptualised the project, provided guidance during all stages, and contributed to the writing of the manuscript. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
RM thanks the Bavarian Ministry of Education, Culture, Research, and the Fine Arts for Support within the Solar Technologies Go Hybrid consortium and the financial support within the ERC Consolidator Grant “DYNAMO” (Grant No. 646737). IF acknowledges support by the Deutsche Forschungsgemeinschaft via grant FI575/9-2. XM thanks the Studienstiftung des deutschen Volkes e.V. for a fellowship.References
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- M. B. Smith and J. Michl, Ann. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed.
- J. C. Johnson, A. J. Nozik and J. Michl, Acc. Chem. Res., 2013, 46, 1290–1299 CrossRef CAS PubMed.
- N. V. Korovina, N. F. Pompetti and J. C. Johnson, J. Chem. Phys., 2020, 152, 040904 CrossRef CAS PubMed.
- D. Casanova, Chem. Rev., 2018, 118, 7164–7207 CrossRef CAS PubMed.
- M. Einzinger, T. Wu, J. F. Kompalla, H. L. Smith, C. F. Perkinson, L. Nienhaus, S. Wieghold, D. N. Congreve, A. Kahn and M. G. Bawendi, et al. , Nature, 2019, 571, 90–94 CrossRef CAS PubMed.
- R. W. MacQueen, M. Liebhaber, J. Niederhausen, M. Mews, C. Gersmann, S. Jäckle, K. Jäger, M. J. Y. Tayebjee, T. W. Schmidt, B. Rech and K. Lips, Mater. Horiz., 2018, 5, 1065–1075 RSC.
- E. Posenitskiy, M. Rapacioli, B. Lepetit, D. Lemoine and F. Spiegelman, Phys. Chem. Chem. Phys., 2019, 21, 12139–12149 RSC.
- E. Titov, A. Humeniuk and R. Mitrić, Phys. Chem. Chem. Phys., 2018, 20, 25995–26007 RSC.
- G. Tao, J. Chem. Phys., 2019, 151, 054308 CrossRef.
- J. J. Burdett, A. M. Müller, D. Gosztola and C. J. Bardeen, J. Chem. Phys., 2010, 133, 144506 CrossRef PubMed.
- M. W. B. Wilson, A. Rao, K. Johnson, S. Gelinas, R. di Pietro, J. Clark and R. H. Friend, J. Am. Chem. Soc., 2013, 135, 16680–16688 CrossRef CAS PubMed.
- M. J. Y. Tayebjee, R. G. C. R. Clady and T. W. Schmidt, Phys. Chem. Chem. Phys., 2013, 15, 14797–14805 RSC.
- N. V. Korovina, J. Joy, X. Feng, C. Feltenberger, A. I. Krylov, S. E. Bradforth and M. E. Thompson, J. Am. Chem. Soc., 2018, 140, 10179–10190 CrossRef CAS PubMed.
- P. J. Vallett, J. L. Snyder and N. H. Damrauer, J. Phys. Chem. A, 2013, 117, 10824–10838 CrossRef CAS PubMed.
- J. D. Cook, T. J. Carey and N. H. Damrauer, J. Phys. Chem. A, 2016, 120, 4473–4481 CrossRef CAS PubMed.
- J. D. Cook, T. J. Carey, D. H. Arias, J. C. Johnson and N. H. Damrauer, J. Phys. Chem. A, 2017, 121, 9229–9242 CrossRef CAS PubMed.
- C. J. Imperiale, P. B. Green, E. G. Miller, N. H. Damrauer and M. W. B. Wilson, J. Phys. Chem. Lett., 2019, 10, 7463–7469 CrossRef CAS PubMed.
- P. M. Zimmerman, F. Bell, D. Casanova and M. Head-Gordon, J. Am. Chem. Soc., 2011, 133, 19944–19952 CrossRef CAS PubMed.
- P. M. Zimmerman, C. B. Musgrave and M. Head-Gordon, Acc. Chem. Res., 2013, 46, 1339–1347 CrossRef CAS PubMed.
- X. Feng and A. I. Krylov, Phys. Chem. Chem. Phys., 2016, 18, 7751–7761 RSC.
- C. B. Dover, J. K. Gallaher, L. Frazer, P. C. Tapping, A. J. Petty, M. J. Crossley II, J. E. Anthony, T. W. Kee and T. W. Schmidt, Nat. Chem., 2018, 10, 305–310 CrossRef CAS PubMed.
- D. C. A. Valente, M. T. do Casal, M. Barbatti, T. A. Niehaus, A. J. A. Aquino, H. Lischka and T. M. Cardozo, J. Chem. Phys., 2021, 154, 044306 CrossRef PubMed.
- M. Miyazaki and M. Fujii, Phys. Chem. Chem. Phys., 2015, 17, 25989–25997 RSC.
- E. S. S. Iyer, A. Sadybekov, O. Lioubashevski, A. I. Krylov and S. Ruhman, J. Phys. Chem. A, 2017, 121, 1962–1975 CrossRef CAS PubMed.
- T. M. Cardozo, A. P. Galliez, I. Borges, F. Plasser, A. J. A. Aquino, M. Barbatti and H. Lischka, Phys. Chem. Chem. Phys., 2019, 21, 13916–13924 RSC.
- C. Kaufmann, W. Kim, A. Nowak-Król, Y. Hong, D. Kim and F. Würthner, J. Am. Chem. Soc., 2018, 140, 4253–4258 CrossRef CAS PubMed.
- J. Hoche, H.-C. Schmitt, A. Humeniuk, I. Fischer, R. Mitric and M. I. S. Roehr, Phys. Chem. Chem. Phys., 2017, 19, 25002–25015 RSC.
- R. Knochenmuss, I. Fischer, D. Luhrs and Q. Lin, Isr. J. Chem., 1999, 39, 221–230 CrossRef CAS.
- D. C. Lührs, R. Knochenmuss and I. Fischer, Phys. Chem. Chem. Phys., 2000, 2, 4335–4340 RSC.
- H.-C. Schmitt, I. Fischer, L. Ji, J. Merz, T. B. Marder, J. Hoche, M. I. S. Röhr and R. Mitric, New J. Chem., 2021 10.1039/d0nj02391d.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, et al., Gaussian 16, Rev. A.02, Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1988, 294, 143 CrossRef.
- F. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, J. Chem. Phys., 2007, 126, 084509 CrossRef PubMed.
- F. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, J. Chem. Phys., 2007, 126, 169903 CrossRef.
- F. Santoro, FCclasses: A Fortran 77 Code, 2008, http://www.pi.iccom.cnr.it/fcclasses, last accessed 20/10/2017 Search PubMed.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- P. G. Lisinetskaya and R. Mitrić, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 033408 CrossRef.
- D. Accomasso, G. Granucci, M. Wibowo and M. Persico, J. Chem. Phys., 2020, 152, 244125 CrossRef CAS PubMed.
- F. Plasser, G. Granucci, J. Pittner, M. Barbatti, M. Persico and H. Lischka, J. Chem. Phys., 2012, 137, 22A514 CrossRef PubMed.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268 CrossRef CAS.
- A. Humeniuk and R. Mitrić, J. Chem. Phys., 2015, 143, 134120 CrossRef PubMed.
- J. J. Kranz, M. Elstner, B. Aradi, T. Frauenheim, V. Lutsker, A. D. Garcia and T. A. Niehaus, J. Chem. Theory Comput., 2017, 13, 1737–1747 CrossRef CAS PubMed.
- F. Spiegelman, N. Tarrat, J. Cuny, L. Dontot, E. Posenitskiy, C. Martí, A. Simon and M. Rapacioli, Adv. Phys.: X, 2020, 5, 1710252 CAS.
- J. J. Stewart, J. Mol. Model., 2007, 13, 1173–1213 CrossRef CAS PubMed.
- J. Rezac and P. Hobza, J. Chem. Theory Comput., 2012, 8, 141–151 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. Humeniuk and R. Mitrić, Comput. Phys. Commun., 2017, 221, 174–202 CrossRef CAS.
- J. J. P. Stewart, Stewart Computational Chemistry, 2016 Search PubMed.
- E. Wigner, Phys. Rev., 1932, 40, 749–759 CrossRef CAS.
- V. Bonačić-Koutecký and R. Mitrić, Chem. Rev., 2005, 105, 11–65 CrossRef PubMed.
- H. J. Berendsen, J. v. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- A. Luzanov, A. Sukhorukov and V. Umanskii, Theor. Exp. Chem., 1976, 10, 354–361 CrossRef.
- A. Luzanov and V. Pedash, Theor. Exp. Chem., 1980, 15, 338–341 CrossRef.
- D. Accomasso, G. Granucci and M. Persico, ChemPhotoChem, 2019, 3, 933–944 CrossRef CAS.
- P.-O. Löwdin, in Advances in quantum chemistry, Elsevier, 1970, vol. 5, pp. 185–199 Search PubMed.
- W. Liu, B. Lunkenheimer, V. Settels, B. Engels, R. F. Fink and A. Köhn, J. Chem. Phys., 2015, 143, 084106 CrossRef PubMed.
- M. Flock, L. Bosse, D. Kaiser, B. Engels and I. Fischer, Phys. Chem. Chem. Phys., 2019, 21, 13157–13164 RSC.
- J. Auerswald, B. Engels, I. Fischer, T. Gerbich, J. Herterich, A. Krueger, M. Lang, H.-C. Schmitt, C. Schon and C. Walter, Phys. Chem. Chem. Phys., 2013, 15, 8151 RSC.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484 CrossRef CAS.
- G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989–4996 CrossRef CAS.
- C. Schouder, A. S. Chatterley, F. Calvo, L. Christiansen and H. Stapelfeldt, Struct. Dyn., 2019, 6, 044301 CrossRef PubMed.
- B. Hourahine, B. Aradi, V. Blum, F. Bonafé, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrică, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Köhler, T. Kowalczyk, T. Kubař, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Řezáč, C. G. Sánchez, M. Sternberg, M. Stöhr, F. Stuckenberg, A. Tkatchenko, V. W.-z. Yu and T. Frauenheim, J. Chem. Phys., 2020, 152, 124101 CrossRef CAS PubMed.
- W. Schmidt, J. Chem. Phys., 1977, 66, 828–845 CrossRef CAS.
- B. Dick, E. Zinghar and Y. Haas, Chem. Phys. Lett., 1991, 187, 571–578 CrossRef CAS.
- A. Amirav, U. Even and J. Jortner, J. Chem. Phys., 1981, 75, 3770–3793 CrossRef CAS.
- A. M. Griffiths and P. A. Freedman, J. Chem. Soc., Faraday Trans. 2, 1982, 78, 391–398 RSC.
- J. A. Katul and A. B. Zahlan, J. Chem. Phys., 1967, 47, 1012–1014 CrossRef CAS.
- H. Liu, V. M. Nichols, L. Shen, S. Jahansouz, Y. Chen, K. M. Hanson, C. J. Bardeen and X. Li, Phys. Chem. Chem. Phys., 2015, 17, 6523–6531 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Additional experimental and simulated data. See DOI: 10.1039/d1sc03214c |
| This journal is © The Royal Society of Chemistry 2021 |