Open Access Article
Open Access ArticleActinide arene-metalates: ion pairing effects on the electronic structure of unsupported uranium–arenide sandwich complexes†
Jesse
Murillo
 a,
Rina
Bhowmick
b,
Katie L. M.
Harriman
c,
Alejandra
Gomez-Torres
a,
Rina
Bhowmick
b,
Katie L. M.
Harriman
c,
Alejandra
Gomez-Torres
 a,
Joshua
Wright
d,
Robert W.
Meulenberg
e,
Pere
Miró
a,
Joshua
Wright
d,
Robert W.
Meulenberg
e,
Pere
Miró
 b,
Alejandro
Metta-Magaña
b,
Alejandro
Metta-Magaña
 a,
Muralee
Murugesu
a,
Muralee
Murugesu
 c,
Bess
Vlaisavljevich
c,
Bess
Vlaisavljevich
 *b and
Skye
Fortier
*b and
Skye
Fortier
 *a
*a
aDepartment of Chemistry and Biochemistry, University of Texas at El Paso, El Paso, Texas 79968, USA. E-mail: asfortier@utep.edu
bDepartment of Chemistry, University of South Dakota, Vermillion, South Dakota 57069, USA. E-mail: Bess.Vlaisavljevich@usd.edu
cDepartment of Chemistry and Biomolecular Sciences, University of Ottawa, Ottawa, Ontario K1N 6N5, Canada
dDepartment of Physics, Illinois Institute of Technology, Chicago, Illinois 60616, USA
eDepartment of Physics and Astronomy and Frontier Institute for Research in Sensor Technologies, University of Maine, Orono, Maine 04469, USA
First published on 9th September 2021
Abstract
Addition of [UI2(THF)3(μ-OMe)]2·THF (2·THF) to THF solutions containing 6 equiv. of K[C14H10] generates the heteroleptic dimeric complexes [K(18-crown-6)(THF)2]2[U(η6-C14H10)(η4-C14H10)(μ-OMe)]2·4THF (118C6·4THF) and {[K(THF)3][U(η6-C14H10)(η4-C14H10)(μ-OMe)]}2 (1THF) upon crystallization of the products in THF in the presence or absence of 18-crown-6, respectively. Both 118C6·4THF and 1THF are thermally stable in the solid-state at room temperature; however, after crystallization, they become insoluble in THF or DME solutions and instead gradually decompose upon standing. X-ray diffraction analysis reveals 118C6·4THF and 1THF to be structurally similar, possessing uranium centres sandwiched between bent anthracenide ligands of mixed tetrahapto and hexahapto ligation modes. Yet, the two complexes are distinguished by the close contact potassium-arenide ion pairing that is seen in 1THF but absent in 118C6·4THF, which is observed to have a significant effect on the electronic characteristics of the two complexes. Structural analysis, SQUID magnetometry data, XANES spectral characterization, and computational analyses are generally consistent with U(IV) formal assignments for the metal centres in both 118C6·4THF and 1THF, though noticeable differences are detected between the two species. For instance, the effective magnetic moment of 1THF (3.74 μB) is significantly lower than that of 118C6·4THF (4.40 μB) at 300 K. Furthermore, the XANES data shows the U LIII-edge absorption energy for 1THF to be 0.9 eV higher than that of 118C6·4THF, suggestive of more oxidized metal centres in the former. Of note, CASSCF calculations on the model complex {[U(η6-C14H10)(η4-C14H10)(μ-OMe)]2}2− (1*) shows highly polarized uranium–arenide interactions defined by π-type bonds where the metal contributions are primarily comprised by the 6d-orbitals (7.3 ± 0.6%) with minor participation from the 5f-orbitals (1.5 ± 0.5%). These unique complexes provide new insights into actinide–arenide bonding interactions and show the sensitivity of the electronic structures of the uranium atoms to coordination sphere effects.
Introduction
The structural elucidation of bis(benzene)chromium, Cr(η6-C6H6)2, by E. O. Fischer was a landmark discovery as it established a new chemical bonding paradigm for both transition metal and carbon molecules alike,1 expanding upon the seminal structural characterization of ferrocene a few years earlier.2,3 In Cr(η6-C6H6)2, the molecule features a formally chromium(0) atom sandwiched between two neutral benzene rings wherein stabilization is bidirectional: donation of the benzene π-electrons into empty metal orbitals accompanied by backbonding of occupied metal orbitals into the empty benzene π*-orbitals.4,5 This contrasts the bonding scheme in Cp2Fe (Cp = η5-C5H5), which is considered to contain an iron(II) centre sandwiched between two π-donating, anionic, aromatic Cp-ligands with negligible backbonding character.6 Indeed, subsequent analysis of the bonding in Cr(η6-C6H6)2 suggests that chromium δ-backdonation is the largest contributor to the bonding interactions.6 Not surprisingly, Cr(η6-C6H6)2 has been the focus of several structural studies, providing valuable insights into metal bonding and chemistry.7 Notably, Cr(η6-C6H6)2 is more than a simple curiosity as chromium mono- and bis(arene) complexes have become important reagents for organic synthesis and catalysis.8Consequently, Cr(η6-C6H6)2 has spawned a rich and diverse field of investigation that has studied the complexation of arenes9 to metals spanning from the d-block to the main group element series.10,11 On the other hand, glaringly lacking are metal-arene sandwich complexes belonging to the 4f- and 5f-metals.12,13 Using electron-beam vaporization techniques, Cloke and co-workers accomplished the remarkable synthesis of a few, thermally stable homoleptic lanthanide-arene sandwich compounds of the type Ln(η6-tBu3C6H3)2 (Ln = Nd, Gd, Tb, Dy, Ho, Er, and Lu) and the thermally unstable species Ln(η6-tBu3C6H3)2 (Ln = La, Pr, Sm).14–16 Electronic structure calculations show substantial lanthanide d-orbital → π*-arene backbonding.17–19 This is illuminating and surprising in many regards as the bonding of the lanthanide metals is typically considered to be predominantly ionic in nature, yet it is still possible for these metals to participate in covalent backbonding interactions through 5d-orbital contributions. Furthermore, the study validates the core-like nature of the 4f-orbitals and their unavailability for bonding. Though, in 2017, Mazzanti and co-workers reported the synthesis of the triple decker complex [K(2.2.2-crypt)]2{[(KL3Ce)(μ-η6:η6-C7H8)]2Ce} (L = −OSi(OtBu)3) from the reduction of [KCeL4].20 This trinuclear compound features a [Ce(η6-C7H8)2]2− core, and DFT calculations show that each of the cerium atoms engages the (C7H8)2− moieties through δ-bonding involving the 4f-orbitals.
Homoleptic actinide–arene sandwich complexes would be particularly noteworthy and important for studying actinide bonding behaviour as the 5f-orbitals extend beyond the core. Compounds such as these may give way to interesting molecules possessing exotic φ-type bonds.21,22 Understanding these types of molecules and their bonding character are important for addressing one of the more poorly understood areas of actinide science, namely the role and participation of the 5f- and 6d/7s/7p-valence orbital combinations to chemical bonding.23
Yet, with respect to the actinides, all efforts to use similar vaporization techniques to produce the analogous An(arene)2 compounds have failed,18 though gas-phase reactions have successfully detected the formation of [U(η6-tBu3C6H3)2]+,24 suggesting an achievability for such molecules. In fact, quantum calculations predict U(η6-tBu3C6H3)2 to have a metal-arene bond disruption enthalpy of 88 kcal mol−1, exceeding that of the analogous Ln(η6-tBu3C6H3)2 (Ln = Ce – Yb) (28–72 kcal mol−1) and M(η6-tBu3C6H3)2 (M = Group 4, Group 5; 49–79 kcal mol−1) complexes;19 though, the reliability of the calculated enthalpy value for uranium has been called into question due to the complicated electronic structure of the actinides.17
In 1970, Cesari et al. demonstrated that unsupported actinide–monoarene adducts could be accessed by applying Fischer's reductive Friedel–Crafts conditions used in the synthesis of Cr(η6-C6H6)2. Specifically, the treatment of UCl4 with an excess of AlCl3 and Al0 in benzene gives the U(III) complex [(η6-C6H6)U(AlCl4)3].25 Following a similar strategy, Cotton, Schwotzer, and others subsequently reported the synthesis and structural characterization of a handful of uranium–monoarene adducts including the first U(IV) arene complex {[(η6-C6Me6)UCl2]2(μ-Cl)3}[AlCl4].26–29 Later, Ephritikhine et al. showed that thermal decomposition of U(BH4)4 in mesitylene affords (η6-C6H3Me3)U(BH4)3, which undergoes facile ligand displacement with hexamethylbenzene to give (η6-C6Me6)U(BH4)3.30 The U–arene bonding in these complexes is likely to be electrostatic in nature with the neutral arene coordinating through the π-electron cloud as a Lewis base to the highly electron deficient uranium centres. Consequently, inspection of the Caryl–Caryl distances reveals no bond length distortions,29 indicating a lack of metal backbonding, with the arene readily displaced by coordinating solvents such as THF.26 More recently, Braunschweig et al. reported the first actinide π-complexes with neutral 1,4-diborabenzene to give (dbb)AnCl4L (dbb = 1,4-bis(cAAC)2-1,4-diborabenzene; An = Th, U; L = THF, MeCN). In this case, the dbb-An bond was found to be strong, though, also primarily electrostatic in character.31 In specific regards to thorium, Gambarotta and co-workers have reported the synthesis of the thorium naphthalenide complexes [Li(DME)3]{[K(DME)][(Et8-calix[4]tetrapyrrole)Th(η4-C10H8)]}, {[K(DME)][(Et8-calix[4]tetrapyrrole)Th(μ-η4:η6-C10H8-μ-K)]}n,32 and [O-2,4-tBu2-C6H2(CH2)]2Th(η4-C10H8)2[K(18-crown-6)]2.33 The latter is the only reported actinide–arenide sandwich complex; however, low yields and persistent impurities prevented characterization beyond the determination of its solid-state molecular structure.
Compounds containing actinide–arene/arenide interactions have become increasingly important moieties in 5f-element chemistry. So called inverted sandwich complexes featuring An-arenide-An cores have become nearly commonplace in uranium organometallic chemistry in recent years.34 These complexes have provided valuable electronic insight into actinide bonding, particularly with respect to δ-interactions, while enabling rich redox chemistry and other novel reactivity patterns such as the C–H borylation of arenes.34–46 For example, U(O-2,6-tBu2C6H3)3 reacts with benzene in the presence of HBBN (HBBN = 9-bora-9-bicylononane) to give the inverted sandwich product [U(O-2,6-tBu2C6H3)2]2[μ:η6:η6-C6H5(BBN)].45 Moreover, uranium–arene interactions play key roles in the stabilization of the rare U(II) oxidation state in [K(2.2.2-cryptand)]{[(Ad,MeArO)3Mes]U} ((Ad,MeArO)3Mes = κ3:η6-C6Me3[CH2(O–C6H2MeAd)]3)47 and U(κ1:η6-NHAriPr6)2 (AriPr6 = (2,4,6-iPr3C6H2)2C6H3),48 where the uranium–arene bonds are enforced through intramolecular ligand tethering. Interestingly, it has been predicted by means of density functional theory (DFT) that uranium–arene complexes may also provide access to the unknown U(I) oxidation state.49
On this note, the use of tethered ligand manifolds to encourage supported actinide–arene interactions has become a popular approach within recent years.47,48,50–59 Bart, Meyer, and coworkers first demonstrated that uranium–arene δ-bonding was a key feature of their U(III) complex [(tBu,tBuArO)3Mes]U,50 while Arnold and coworkers showed that redox isomerization of the trans-calix[2]benzene[2]pyrollide (bz2pyr22−) uranium complex gives rise to the supported sandwich compound (κ2-η6:η6-bz2pyr2)UIII(X) (X = I, BH4, O-2,6-tBu2C6H3, N(SiMe3)2).54,55 In our own work, we have utilized an N,N′-tethered uranium–arene platform, viz [(κ2:η6-LAr)UIII]+ ((LAr)2− = 2,2′-bis(2,6-iPr2C6H3N)-p-terphenyl), to stabilize a rare U–Fe bond and separately generate a highly reactive uranium–nitride species.57,58 Regardless, the ancillary ligand coordination in these systems provides additional bonding contributions and potential ligand strain effects that can compete with or affect the actinide–arene bonding.
Considering the soft nature of neutral aromatic hydrocarbons and the hard Lewis acidic character of the actinide ions, we hypothesized that the formation of unsupported 5f-sandwich arene complexes would be best accessed through the use of Chatt reaction conditions as popularized by Ellis and others.11 This method specifically refers to the reaction of a metal salt with a reduced arenide anion to give metal-arenide products through salt metathesis. The compounds produced in these reactions are often found to form “-ate” complexes, which have been referred to as “arene-metalates”.11
Through these means, we herein report the synthesis and characterization of the first unsupported uranium arenide-metalate sandwich complexes, namely [K(18-crown-6)(THF)2]2[U(η6-C14H10)(η4-C14H10)(μ-OMe)]2·4THF (118C6·4THF) and ion contact paired {[K(THF)3][U(η6-C14H10)(η4-C14H10)(μ-OMe)]}2 (1THF), formed from the reaction of K[C14H10] with the methoxy-iodide dimer [UI2(THF)3(μ-OMe)]2 (2). Compounds 118C6·4THF and 1THF are isolated in modest yields, and their structural and electronic properties have been thoroughly characterized through X-ray diffraction analysis, SQUID magnetometry, XANES spectroscopy, DFT, and multireference wavefunction-based computational methods. The magnetism and XANES data show a clear difference in the electronic properties of 118C6·4THF from 1THF, revealing a key sensitivity of the electronic structure to coordination sphere ion pairing effects.
A word of note regarding the nomenclature of arene-complexed metal compounds. These interactions are commonly referred to as metal-arene bonds, regardless of the formal charge state of the arene moiety. This general terminology stems from the fact that the redox level of a coordinated aromatic hydrocarbon to d- or f-block metals can be difficult to ascertain due to orbital mixing and backbonding contributions, not unlike the coordination of CO to low-valent metals.60 Futhermore, in his recent review of arene-metalates, Ellis contends the term “arenide” can be confused with the conjugate base of the arene.11 For the purposes of this work, in the instances where reduction of the arene ligand is clear, such as in the cases of 118C6·4THF from 1THF, the term arenide will be used to acknowledge an anionic charge state.
Results and discussion
Synthesis
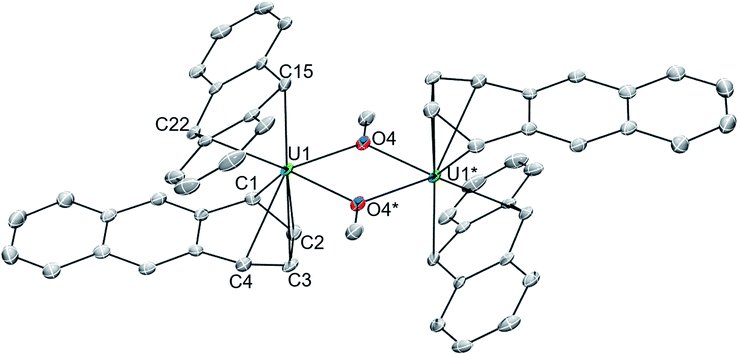
In one instance, addition of UI3(dioxane)1.5 to a stirring solution of 6 equiv. of K[C14H10] (prepared in situ) in DME at −35 °C produced an intensely dark blue solution. Filtration of the reaction mixture at room temperature afforded a dark blue solid that solubilized in THF to which excess 18-crown-6 was added, resulting in the formation of a few single crystals after 12 h at −35 °C. Single crystal X-ray diffraction analysis revealed the formation of the heteroleptic, bent uranium bis(anthracenide) sandwich dimer 118C6·4THF (Fig. 1 and S2†), with the units conjoined through two bridging methoxide ligands. The formation of the methoxide groups in 118C6 was unexpected but is presumably formed from the reductive cleavage of the DME solvent, a phenomenon that is precedented in f-element reduction chemistry.61–63 Multiple attempts to reproduce this synthesis failed, giving [K(18-crown-6)(THF)2][C14H10]64 as the only isolable product.We postulate that the uncontrolled reductive cleavage of the reaction solvent to form the methoxy ligands of 118C6 is primarily responsible for the irreproducibility of the reaction and therefore set out to pre-install the methoxy groups on uranium prior to K[C14H10] addition. Adding one equiv. of K[OMe] to UI3(dioxane)1.5 in THF gives 2·THF as a blue crystalline solid upon workup in 60% yield (eqn (1)) (Fig. S1†).
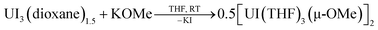 | (1) |
This uranium(III) methoxy-bridged precursor, 2, proved ideal as conversion to 118C6 can be accomplished directly through salt metathesis, thus avoiding the necessity for adventitious DME cleavage. Addition of 2·THF to a cold, stirring solution of 6 equiv. of K[C14H10] in THF followed by filtration and addition of 2 equiv. of 18-crown-6 reproducibly generates 118C6·4THF in modest yields of 36% as a highly crystalline, midnight-blue coloured product (Scheme 1). Forgoing the use of 18-crown-6 produces the THF-solvated complex 1THF in comparable yields (Scheme 1) (Fig. S6†). In these reactions, 2 equiv. of anthracene are also produced that can co-deposit in the product mixture. Yet, after crystallization, both 118C6·4THF and 1THF exhibit insolubility in DME and THF with the residual anthracene readily removed by thorough washing of the crystalline material with THF to give analytically pure products as shown by combustion analyses. These compounds are also insoluble in non-polar solvents and aromatics such as toluene.
Compounds 118C6·4THF and 1THF are exceedingly air-sensitive, instantaneously bleaching in colour upon exposure. On the other hand, they are thermally stable as solids and can be stored indefinitely under dinitrogen or argon atmospheres. Suspensions of isolated samples of 118C6·4THF and 1THF in THF are unstable, and despite their insolubility, will gradually decompose (under N2 or Ar) to give black insoluble material and dark blue solutions with K[C14H10] as the only product detectable by electronic absorption spectroscopy (UV-vis/NIR). This solution-phase instability suggests that 118C6·4THF and 1THF are likely the kinetic products of the reaction.
The solid-state molecular structures of 118C6·4THF (Fig. 1 and S2†) and 1THF (Fig. S6†) are nearly isostructural with the differences arising from the potassium ion pairing, yielding a charge-separated, non-interacting pair in the former and a close contact pair in the latter, possessing K–Canth interactions. Otherwise, both complexes feature a {[U(η6-C14H10)(η4-C14H10)(μ-OMe)]2}2− dimeric core. By far, the most salient feature of 118C6·4THF and 1THF is the sandwiching of each uranium centre between two bent anthracenide units that are observed to adopt distinct η4-and η6-coordination. The mixed binding modes of the anthracenides is an uncommon feature for electronically unsaturated bis(arene)-metalates and, to the best of our knowledge, has been documented in only a few cases.65–67
The solid-state molecular structure of 1THF is afflicted with severe positional disorder of its potassium-coordinated THF molecules, consequently affecting the data quality, leading to slightly reduced precision of the bond metrics. Therefore, only the structural features of 118C6·4THF are discussed here in detail.
Complex 118C6·4THF crystallizes in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with one half of the molecule in the asymmetric unit, generating the full complex through crystallographic inversion symmetry, rendering the metrics within the monomeric units identical. The U1-(η4-Canth) distances narrowly range from 2.638(5) to 2.676(6) Å. Tetrahapto coordination of aromatic or carbocyclic ligands to the actinides is rare, but a handful of terminal cyclobutadienide complexes are known.68–71 The U1-(η4-Canth) distances in 118C6·4THF are significantly longer than the uranium–cyclobutadienide distances found in [Na(12-crown-4)2]{[η4-C4(SiMe3)4]U(BH4)3} (U–CCb = 2.522(5)–2.556(4) Å) and {U[η4-C4(SiMe3)4](μ-BH4)3[K(THF)2]}2 (U–CCb = 2.46(2)–2.56(2) Å) but fall within the upper range of those in {U[η4-C4(SiMe3)4][η3-C4H(SiMe3)3-κ-CH2SiMe2(BH4)]}- (U–CCb = 2.550(5)–2.650(6) Å).68 Closer comparison can be made to the thorium compound {[O-2,4-tBu2-C6H2(CH2)]2Th(η4-C10H8)2}[K(18-crown-6)]2 which features Th-Cnaphth bonds that range from 2.671(8) to 2.784(8) Å,31 where the elongation of the thorium-arenide distances as compared to 118C6·4THF possibly result from the slight size difference in the ionic radii between thorium and uranium (e.g., Th(IV), C.N. = 6, r = 0.94 Å vs. U(IV), C.N. = 6, r = 0.89 Å).72
with one half of the molecule in the asymmetric unit, generating the full complex through crystallographic inversion symmetry, rendering the metrics within the monomeric units identical. The U1-(η4-Canth) distances narrowly range from 2.638(5) to 2.676(6) Å. Tetrahapto coordination of aromatic or carbocyclic ligands to the actinides is rare, but a handful of terminal cyclobutadienide complexes are known.68–71 The U1-(η4-Canth) distances in 118C6·4THF are significantly longer than the uranium–cyclobutadienide distances found in [Na(12-crown-4)2]{[η4-C4(SiMe3)4]U(BH4)3} (U–CCb = 2.522(5)–2.556(4) Å) and {U[η4-C4(SiMe3)4](μ-BH4)3[K(THF)2]}2 (U–CCb = 2.46(2)–2.56(2) Å) but fall within the upper range of those in {U[η4-C4(SiMe3)4][η3-C4H(SiMe3)3-κ-CH2SiMe2(BH4)]}- (U–CCb = 2.550(5)–2.650(6) Å).68 Closer comparison can be made to the thorium compound {[O-2,4-tBu2-C6H2(CH2)]2Th(η4-C10H8)2}[K(18-crown-6)]2 which features Th-Cnaphth bonds that range from 2.671(8) to 2.784(8) Å,31 where the elongation of the thorium-arenide distances as compared to 118C6·4THF possibly result from the slight size difference in the ionic radii between thorium and uranium (e.g., Th(IV), C.N. = 6, r = 0.94 Å vs. U(IV), C.N. = 6, r = 0.89 Å).72
Inspection of the U1-(η6-Canth) distances reveals two sets of bond lengths, two shorter (U1-Canth = 2.557(5)–2.571(6) Å) and four longer (U1-Canth = 2.766(5)–2.797(5) Å), that differ by approximately 0.2 Å, a consequence of the observed ring puckering of the anthracenide ligand (vide infra). The range of the U1-Canth distances along with the nominal uranium-centroid distance U1-(η6-Ccent) = 2.31 Å of 118C6·4THF are significantly shorter than those found in the monoarene Friedel–Crafts type complexes [(η6-C6H6)U(AlCl4)3] (U–Ccent = 2.56 Å, avg. U–Carene = 2.91 Å) and {[(η6-C6Me6)UCl2]2(μ-Cl)3}[AlCl4] (avg. U–Ccent = 2.55 Å, avg. U–Carene = 2.92 Å).25,26 Comparison to inverted sandwich complexes,34 namely the organometallic inverted benzene sandwich (Cp*2U)2(μ-η6:η6-C6H6) (Cp* = η5-C5Me5),44 possessing a puckered benzene ring, shows an avg. U–Ccent = 2.20 Å distance that is sizably shorter than 118C6·4THF but with a comparable U–Carenide = 2.51(1) – 2.73(1) Å bond range. The shorter U-C distances in 118C6·4THF, as compared to [(η6-C6H6)U(AlCl4)3] and {[(η6-C6Me6)UCl2]2(μ-Cl)3}[AlCl4] with their neutral arene ligands, suggests a strong bonding interaction that may be due to increased charge accumulation within the anthracenide moieties. As such, the U–Canth bond metrics in 118C6·4THF better match the parameters of (Cp*2U)2(μ-η6:η6-C6H6), where the bridging benzene moiety is assigned a dianionic charge.
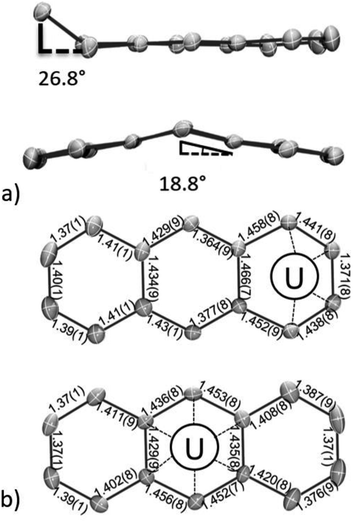
In line with this, both the η6-C14H10 and η4-C14H10 rings of 118C6·4THF show distortions from planarity (Fig. 2a), which is typically considered an indication of localized anionic charge character in monometallic arene-metalate systems.73 For instance, in magnesium anthracenides featuring (C14R10)2−, the central ring fold angles are 28.6° in [Mg(η2-C14H10)(THF)3] and 41.0° in [Mg(η2-1,4-Me2C14H8)(THF)3].74,75 Along these lines, a few examples of mononuclear 4f-element anthracenide complexes are known, and they too show similar folding (cf. CpLu(η2-C14H10),76 35.8°; (η2-C14H10)TmI(DME)2,77 37.8°). In comparison, the η6-C14H10 ligand in 118C6·4THF shows a shallow bend angle of 18.8° across the central, bridgehead C15/C22 bond vector (Fig. 2a and S2†). The more acute folding of the anthracenide ring in 118C6·4THF suggests carbon atom hybridization at C15 and C22 that is closer to sp2-character. In support of this idea, the fold angle in dibenzo-7-dimethylgermanobornadiene (Me2GeA; A = C14H10) is 56.8°, wherein the germanium atom is bound to sp3-hybridized bridgehead carbons.78 In addition, the η4-C14H10 ligand of 118C6·4THF exhibits a bend angle of 26.8° from planarity at its terminal, coordinating ring. Similar η4-C14H10 bending has been observed in a number of complexes,11 and the deviation from planarity is comparable to that found in the bis(anthracenide) niobium compound {[K(18-crown-6)(THF)](η4-C14H10)2Nb[P(OMe)3]2} (28.4°).79
The structural distortion of these arene rings can be accounted through localized population of C–C π*-orbitals. Consequently, it would be expected that formal reduction of the anthracene ring should also manifest in elongated C–C bonds; though, in uranium inverted sandwich complexes, it is not unusual to find planar, bridging arenides with little to no obvious C–C bond lengthening.34
Inspection of the C–C bond lengths within the η6-C14H10 and η4-C14H10 rings of 118C6·4THF shows obvious bond distance perturbations as compared to neutral, aromatic anthracene,80 and the C–C ring distances of 118C6·4THF are shown in Fig. 2b. In the case of η6-C14H10, the C–C bond distances of the central, coordinated ring narrowly range from 1.429(9) to 1.456(8) Å with an average distance of 1.44 Å, which is slightly longer than the average C–C distances within the peripheral rings, both 1.40 Å, the latter falling nicely within the expected C–C bond length of 1.41 Å for aromatic hydrocarbon bonds.81 Turning to the η4-C14H10 ring, the bond distances of the coordinated carbon atoms are C1–C2 = 1.441(8) Å; C2–C3 = 1.371(8) Å; and C3–C4 = 1.438(8) Å with the three adjoining, non-coordinating bonds ranging from 1.452(9)–1.466(7) Å, while the remaining C–C distances of the η4-C14H10 ring conform to standard aromatic bond lengths (avg. 1.39 Å) (note that the pattern in the bond distances is present in the DFT geometries (Table S15†), vide infra). This long-short-long bond pattern of the C2 to C4 moiety is consistent with a localized ‘-ene’ dianion form having the charge centres at C1 and C4. Yet, while the structural parameters clearly indicate negative charge accumulation on the coordinated η6-C14H10 and η4-C14H10 rings, the ability of anthracene to access and sustain both monoanionic and dianionic forms complicates the charge picture.
Magnetic susceptibility
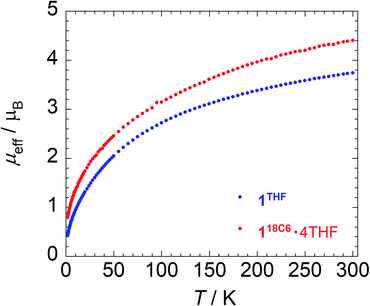
To provide further insight into the paramagnetic character of these complexes, magnetic susceptibility studies were performed on crushed polycrystalline samples of 118C6·4THF and 1THF using SQUID magnetometry in the temperature range of 1.8–300 K at 0.1 T. A plot of the effective magnetic moment (μeff) versus temperature is shown in Fig. 3. The data for 118C6·4THF and 1THF follow a similar trend as the μeff gradually decreases as a function of temperature, curving downwards to 0.80 and 0.43 μB at 1.8 K, respectively. Curiously, despite their structural similarity at uranium, the overall μeff values for 1THF are lower than that of 118C6·4THF. For instance, at 300 K, 118C6·4THF and 1THF exhibit μeff values of 4.40 μB and 3.74 μB per molecule, respectively, with a sizable Δ(μeff) = 0.66 μB at room temperature that reduces to Δ(μeff) = 0.37 μB at lower temperatures. This indicates that the contact pairing of the potassium cations plays a critical role in the modulation of the electronic structure of the {[U(η6-C14H10)(η4-C14H10)(μ-OMe)]2}2− cores in 118C6·4THF and 1THF. We postulate that the Lewis acidity of the contact-paired potassium cations in 1THF polarizes and concentrates electron density onto the coordinated portion of the η4-anthracenide ligands, thus giving rise to point charge accumulation that leads to a stronger crystal field splitting effect, and consequently lower μeff for 1THF. This enhanced charge build-up is supported by analysing DFT atomic charges as discussed below (see Electronic structure analysis).Qualitatively, the curvatures of both magnetization plots in Fig. 3 are characteristic of U(IV) complexes that approach singlet ground states upon cooling to low temperatures due to thermal depopulation of the metal excited states.82,83 However, the μeff of 118C6·4THF and 1THF at 300 K, possible ligand radical contributions aside, are much lower than that expected for a U(IV) dimer, assuming 3.58 μB per 5f2, 3H4 ion in the Russell-Saunders coupling scheme.82,83 Though, reported complexes of U(IV) often do not possess a room temperature value of 3.58 μB per ion owing partly to the quenching or the orbital angular momenta as result of low symmetry or increased covalency.84,85
In relation to select inverted sandwich complexes, the μeff of 118C6·4THF and 1THF are higher than those found for (Cp*2UIII)2(μ-η6:η6-C6H6) (μeff = 2.1 μB, Evans method),44 [K2{UIV[OSi(OtBu)3]3}2(μ-η6:η6-C7H8)] (μeff = 3.15 μB),42 and [{HC[SiMe2N(4-MeC6H4)]3}UV]2(μ-η6:η6-C7H8) (μeff = 3.32 μB)41 at room temperature. Moreover, factoring in potential ligand radical contributions, while maintaining U(IV) assignments, gives near room temperature calculated values that range from μeff = 5.35 μB (one ligand radical) to μeff = 6.14 μB (four, non-interacting ligand radicals) and higher. The analysis is further confounded by the fact that μeff values for uranium are highly variable,82 and this does not factor in possible uranium super-exchange and other magnetic coupling interactions between spin carriers. In comparison to the U(IV) dimer [(MesPDIMe)UIVI]2 (MesPDIMe = [2,6-(MesN = CMe)(NC5H3)˙]3−) possessing ligand-centred PDI-radicals, its μeff displays a much narrower range from μeff = 1.03–2.66 μB (2–300 K), where the low temperature μeff is said to derive from the unquenched spins of the ligand radicals.86
XANES
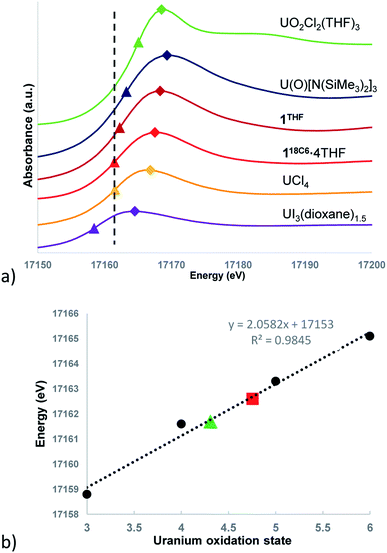
Given the difficulty of definitively assigning charge states to the ligands and uranium centres for 118C6·4THF and 1THF based upon the intermediacy of the structural parameters and magnetism data, transmission mode U LIII-edge X-ray absorption near edge spectroscopy (XANES) measurements were performed at room temperature. The samples consisted of pulverized, compressed pellets of 118C6·4THF and 1THF diluted in X-ray transparent boron nitride matrices vacuum sealed in polyethylene envelopes (see ESI† for further detail).XANES spectroscopy has become an effective tool for the delineation of metal oxidation states in actinide compounds.39,40,86–89 With regards to uranium, the U LIII-edge energy corresponds to an electric-dipole allowed (2p63d10)5fn6d0→ (2p53d10)5fn6d1 photoexcited core electron transition,86,87 where the excitation energy is dependent upon the shielding environment of the 2p-electrons and their relative binding energies, providing insights into the effective nuclear charge of the uranium. Consequently, the X-ray absorption energy correlates to the charge character of the absorbing uranium ion, a correlation that has been utilized in the assignment of formal oxidation states in uranium compounds. This can be quantified through the absorption threshold of the edge energy, defined as the inflection point in the first derivative of the XANES spectrum, as well as the peak “white line” energy.
The background-subtracted and intensity normalized XANES spectra for 118C6·4THF and 1THF is presented in Fig. 4a and is plotted alongside spectra collected for the respective U(III)–U(VI) standards UI3(dioxane)1.5, UCl4, U(O)[N(SiMe3)2]3, and UO2Cl2(THF)3. The inflection point energies for 118C6·4THF and 1THF are much higher than that of UI3(dioxane)1.5 by 2.9 and 3.8 eV, respectively, but closer in range to that found for UCl4 (Δ (eV) = +0.1 eV (118C6·4THF); +1.0 eV (1THF)) (Table S2†). However, 1THF is only 0.7 eV lower than that of pentavalent U(O)[N(SiMe3)2]3. Turning to the white line energies for further comparison, the peaks of 118C6·4THF and 1THF exceed that of UCl4 by 1.1 and 2.4 eV, respectively, with the latter compound falling 0.6 eV below the white line value of U(O)[N(SiMe3)2]3.
Based upon these comparisons, the data appears generally consistent with a tetravalent oxidation state assignment for the uranium centres in 118C6·4THF and 1THF. The data also clearly indicates a more oxidized uranium species in the case of 1THF. This provides a possible explanation for the observed disparity in their μeff plots (Fig. 3). Namely, the more oxidized uranium centres in ion-paired 1THF show a lower overall μeff as compared to more electron rich 118C6·4THF. As such, the contact pairing of the potassium cations in 1THF seem to have an effect on the relative charge state of the uranium metal centres, despite the ion-pairing taking place beyond the immediate coordination sphere of uranium. A somewhat related phenomenon has been observed in the inverted sandwich complex {UIV[OSi(OtBu)3]3}2(μ-η6:η6-C7H8) where addition of K[OTf] results in the cation-mediated disproportionation to U(IV)/U(IV) and U(IV)/U(V) complexes, a feature that does not occur upon treatment with non-coordinating cations such as [NBu4]+.42 These observations signal that the electronic structure of uranium is highly sensitive to subtle perturbations within its ligand environment, especially when adding other interacting Lewis acid cations.
Caution must be exercised here in defining definitive oxidation states as the ligands and coordination geometries in 118C6·4THF and 1THF are unique, thus direct correlations to the standards may not be possible due to significant differences in their electronic environments. In an effort to verify the merits of the comparative analysis and in an attempt to provide formal charge assignments, the oxidation states of the standards versus their edge energies was plotted to generate a linear regression line (Fig. 4b). Linear regressions have been previously applied to XANES data for the corroboration of oxidation state assignments in isostructural uranium coordination compounds.88 The edge energy values for 118C6·4THF and 1THF fall nicely along the regression line, giving calculated oxidation states of U+4.31 and U+4.76, respectively.
Assuming U(IV) assignments for the uranium centres in 118C6·4THF and 1THF, yields a charge formulation of (C14H10)2− for each of the anthracene ligands. Nevertheless, each anthracene still adopts a distinctive coordination mode to uranium. In order to gain further insights into the electronic structure and the bonding interactions between uranium and the anthracenes, electronic structure analyses were performed.
Electronic Structure Analysis
Density functional theory (DFT) calculations (RI-PBE-D3/def2-TZVP,90–93 def-TZVP for U94–96) were performed in the Turbomole program package97 to study the model systems {[U(η6-C14H10)(η4-C14H10)(μ-OMe)]2}2− (1*) and {K[U(η6-C14H10)(η4-C14H10)(μ-OMe)]}2 (1-K*) (see SI for full computational details). Both 1* and 1-K* were optimized in the triplet, quintet, and septet spin states and confirmed as minima by harmonic vibrational analysis. The optimized structures for all three spin states were compared to those obtained from the X-ray determined structures by comparing U–C bond distances as summarized in Table S20† and detailed in Tables S4 and S5.† The root-mean-square deviation (RMSD) for each DFT optimized structure was also calculated. The geometry from the ground state quintet is in closest agreement with both experimental structures (Fig. S2 and S6†); however, comparing the RMSD values for all three spin states suggests that all of the calculated geometries are in satisfactory agreement with the experimental data. For 1*, the RMSD for the triplet, quintet, and septet states are 0.311, 0.326, and 0.331 Å, respectively. Similarly, the RMSD values for the same states are 0.348, 0.320, and 0.360 Å for 1-K*. With respect to the relative calculated energies, the quintet ground state is favoured for both 1* and 1-K* (Table S3, Fig. S21†) as both the triplet and septet states lie approximately 7 kcal mol−1 higher in comparison. The electronic structures of 1* and 1-K* in the quintet state are comparable; though, the calculated average U–C bond distances of 1-K* are found to be slightly shorter than for 1* (Table S20†). In the quintet state, each uranium is in a 5f2 electronic configuration, supporting the U(IV) assignments determined from the XANES data (Fig. 4) and the curvature of the temperature dependent μeff plots (Fig. 3).To provide insight into the nature of the U–C bonds, bond orders were calculated using the Amsterdam Density Functional program package (ADF)98 at the PBE/TZP level of theory. Generally, a Mayer bond order of 1, 2, or 3 corresponds to a single, double, or triple bond between two atoms, respectively, although deviations from integer values are expected for highly polarized bonds.99 The average Mayer bond order of the U–C(η4) bonds in 1* and 1-K* are 0.40 and 0.33, respectively (Tables S7 and S9†). This indicates slightly greater orbital overlap between the η4-C14H10 ligands and the uranium atoms in 1*versus that of 1-K*. Though, no significant differences are observed when determining the total bond orders through Gopinathan-Jug or Nalewajski–Mrozek methods (Tables S7 and S9†). In comparison, the Mayer bond orders for the U–C(η6) interactions are unaffected by the presence of the potassium ion and found to range from 0.22 to 0.50 (avg. 0.31) for 1* (Table S7†) and 0.23 to 0.52 (avg. 0.32) for 1-K* (Table S9†). The nature of the U–C(η4) and U–C(η6) interactions was also studied by dividing the molecule into two fragments along the U–anthracenide bonds of each ligand type in order to perform energy decomposition analysis (EDA) (Table S19†). The bond energy for 1* is −150.37 and −154.86 kcal mol−1 for the η4-and η6-anthracenide ligands, respectively. Furthermore, orbital interactions contribute 49.4% and 50.7% to the attractive energy. Both values indicate a slightly stronger interaction with the η6-anthracenide ligand.
Quantum theory of atoms in molecules (QTAIM) analyses for 1* and 1-K* identified two bond critical points (BCPs) between the uranium centres and the η6-rings and three bond critical points for the η4-anthracenide ligands. At all BCPs, the total electronic energy density, E(r), is negative (1*: −0.0077 to −0.0116; 1-K*: −0.0075 to −0.0125), and the Laplacian of the density, ∇2(ρ), is positive (1*: 0.0825–0.1149; 1-K*: 0.0800–0.1261) (Table S6†). In addition, the electron density values, ρ, are small (1*: 0.0471–0.0554; 1-K*: 0.0490–0.0572), altogether indicating U–C dative bonding where the interactions can be described as primarily ionic or exhibiting strongly polarized bonding character.100
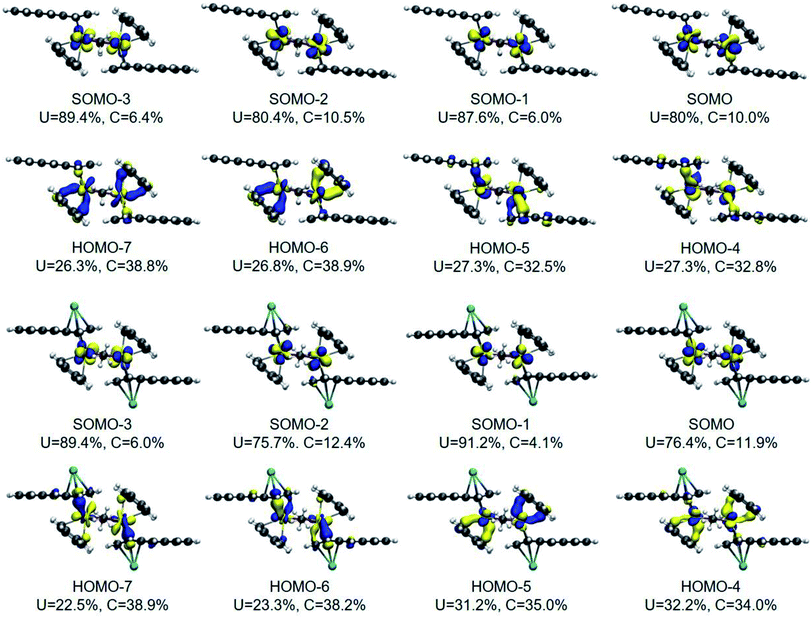
The DFT frontier molecular orbitals of 1* and 1-K* are illustrated in Fig. 5 and show that the U–C(η6) interactions for both 1* and 1-K*, as defined by the crystallographically determined uranium–carbon bond lengths for 118C6·4THF and 1THF (vide supra), are nominally hexahapto. The electronic structure shows the coordination mode of this anthracenide to be better described as bidentate with the strongest interactions occurring through π-bonding at the bridgehead carbon atoms with negligible contributions from the remaining carbons of the central ring, consistent with the findings of the QTAIM BCPs. With respect to the U–C(η4) fragments of 1* and 1-K*, orbital overlap is observed with all four carbon atoms, albeit more so at the C1/C4 fold atoms.
The DFT-calculated frontier molecular orbitals of 1* and 1-K* in Fig. 5 are displayed with the total percent electronic contribution of the uranium centres and sum of the carbon orbitals involved in the bonds. In both cases, the singly occupied molecular orbitals (SOMOs), SOMO to SOMO-3, are predominately 5f in character with HOMO-4 through HOMO-7 defining the U–C interactions. In 1*, HOMO-6 and HOMO-7 are also primarily defined by the orbitals of the U–C(η6) interactions. Yet, in 1-K*, the corresponding frontier orbitals are comprised by the U–C(η4) bonding compositions. In either case, the bonds appear highly polarized with the contributions from the uranium atoms approaching 25% and those from the carbon atoms nearing 40%.
The Charge Model 5 (CM5) atomic charges were found for each system (Table S11†). The average charge of each uranium ion is +1.0 for both 1* and 1-K*. On the other hand, the ion pairing has a significant effect on the relative charges of the arenide anions. The combined partial charges for the carbon atoms for each of the η4-C14H10 and η6-C14H10 ligands in 1* are −0.87 and −0.77, respectively. This decreases in 1-K* to −0.55 for the η6-C14H10 ligands but increases to −0.95 for the η4-C14H10 anthracenides, where the presence of the coordinated potassium cations allows for greater charge accumulation in the latter. Note that in both cases, the relative charge on the η4-C14H10 ligands exceed those of the η6-C14H10 arenides.
Since uranium complexes often exhibit multiconfigurational electronic structures not adequately treated with DFT, the electronic structure was studied by the complete active space self-consistent field (CASSCF) method along with second-order energy corrections (CASPT2)101,102 for 1*. In CASPT2, including only the 5f-orbitals and their corresponding electrons in the active space (4e,14o), the singlet, triplet, and quintet states are effectively degenerate lying within 0.3 kcal mol−1 of one another. As such, we cannot assign a single spin state as the ground state. We expect that the true ground state is a spin–orbit coupled state with contributions from the singlet, triplet, and quintet spin-free states.
Since the DFT shows covalent interactions between the uranium centres and the arenide ligands, the bonding in dimer 1* was also studied with the restricted active space self-consistent field (RASSCF) method with corrections from second-order perturbation theory (RASPT2),103,104 allowing for larger active spaces to be studied than in CASSCF. All CASPT2 and RASPT2 calculations were performed in Open Molcas.105
The active space would ideally include all of the molecular orbitals that are linear combinations of uranium 5f-orbitals and orbitals that include bonding or antibonding interactions between uranium and the arenide ligands. While there are total of 14 5f-orbitals in 1*, they are not all occupied due to crystal field effects. Therefore, after the aforementioned (4e,14o) active space was used, it was determined that only 8 of these orbitals need be included, (4e,8o) (Fig. S26 to S28†). By inspection of the (4e,8o) orbitals, 10 pairs of π-bonding and anti-bonding orbitals were also identified. This surpasses the number of orbitals one can include in CASSCF; therefore, the RASSCF method was used to restrict excitations in a subset of the active space.
Specifically, RASSCF/RASPT2 calculations were performed including the 10 π-orbitals in the so-called RAS1 space, eight 5f-orbitals in the RAS2 space, and 10 π*-orbitals in the RAS3 space. All excitations are allowed within RAS2 but only configurations with up to two holes are allowed in RAS1 and up to two electrons in RAS3, denoted (24e,2h,2e;10o,8o,10o) using the notation of Sauri et al.104 The calculations yield occupation numbers for the π-orbitals in RAS1 that are 1.96 or higher, consistent with a doubly occupied orbital. Likewise, those in RAS3 have occupation numbers of 0.04 or less, signalling empty orbitals. Based on the RASSCF results, the active space can be further reduced to (8e,12o), the results of which remain similar to RASSCF (Tables S12 and S13†).
RASPT2 predicts that the singlet, triplet, and quintet states are within 0.3 kcal mol−1 of one another. Note that DFT cannot describe the multiconfigurational singlet and triplet states in which the 5f-electrons are weakly coupled with one another; however, both CASPT2 and RASPT2 suggest interpreting the DFT high-spin quintet state to understand the uranium–carbon interactions is reasonable.
The RASSCF natural orbitals for the quintet state are included in Fig. S34† although the singlet and triplet orbitals are qualitatively the same (Fig. S32 and S33†). In the RAS1 space, the total uranium orbital contribution to the U–C π-interactions across the U–C(η6) and U–C(η4) bonds range from 11.7% to 17.7% in 1*. The average uranium contribution between the U–C(η6) (avg. 14.3%) and U–C(η4) bonds (avg. 14.2%) are comparable. Of particular note, in contrast to the DFT orbital picture, the 5f-orbitals play a minimal to negligible role in the U–C bonding of 1* (Fig. S34†). The average contributions of the uranium orbitals to the bonding scheme in the quintet state is 7.3 ± 0.6% (6d), 2.5 ± 0.4% (6p), 1.5 ± 0.4% (5f), and 1.4 ± 1.4% (7s). Accordingly, the uranium 6d-orbitals are the dominant contributors accompanied by some semi-core 6p-orbital participation.
Noticeably absent are metal-arene bonding interactions that can be described as δ-bonds, which is a significant departure from the bonding schemes determined for actinide inverted sandwich complexes.34 For example, CASSCF analyses on (μ-η6:η6-C7H8)U2[N(tBu)(3,5-C6H3Me2)]439 and [U(BIPM)]6(μ-I)3(μ-η6:η6-C6H6)3 (BIPM = (C(PH2NH)2)2−)40 both show significant δ-bonding overlap between the π*-orbitals of the arenides and filled 5f-orbitals. The sandwiched rings in these compounds are formally tetraanions and bound by two metals, which together limits structural distortions and favours the δ-bonding. In our case, formal two-electron reduction of each of the anthracene ligands leads to ring folding that greatly diminishes the possibility for uranium–anthracenide δ-bonding.
Conclusions
Metal-arene sandwich complexes are an important class of molecules that have been instrumental in understanding the electronic properties and orbital characteristics of the d-block series while providing access to important arene-functionalization chemistry. Extension of these systems to the f-elements has been limited to only a handful of lanthanide-arene sandwich complexes, mainly synthesized by electron beam vaporization techniques,14–16 and the poorly characterized, heteroleptic thorium species {[O-2,4-tBu2-C6H2(CH2)]2Th(η4-C10H8)2}[K(18-crown-6)]2.33 Utilizing Chatt reaction protocols popularized by Ellis,11 we have shown that the reaction of [UI2(THF)3(μ-OMe)]2 (2) with 6 equiv. of K[C14H10] produces the unprecedented and unsupported bent uranium arene-metalate sandwiches [K(18-crown-6)(THF)2]2[U(η6-C14H10)(η4-C14H10)(μ-OMe)]2 (118C6) and {[K(THF)3][U(η6-C14H10)(η4-C14H10)(μ-OMe)]}2 (1THF) in the presence and absence of 18-crown-6, respectively.As shown through X-ray diffractometry, the arenide ligands in both complexes display notable ring fold angles, indicative of formal reduction and partial dearomatization of the anthracene moieties. While the cores of both 118C6 and 1THF comprise of a dimeric {[U(η6-C14H10)(η4-C14H10)(μ-OMe)]2}2− unit, the two systems are distinguished by close-contact arenide-pairing of the potassium cation that occurs in 1THF but is missing in 118C6·4THF, due to polyether sequestration of the potassium cations in the latter. Despite their structural similarity, XANES analysis and magnetic characterization of 118C6·4THF and 1THF show appreciable differences in their electronic and magnetic properties. For instance, the effective magnetic moment of 118C6·4THF (μeff = 4.40 μB) is significantly higher than 1THF (μeff = 3.74 μB) at 300 K, though both complexes show a temperature dependent μeff response in line with U(IV) centres (Fig. 3). The XANES spectra shows an obvious difference in the level of oxidation between the uranium atoms of 118C6·4THF and 1THF (Fig. 4a), with the linear regression fitting of the edge energies yielding formal charges of U+4.31 for 118C6·4THF and U+4.76 for 1THF (Fig. 4b). Together, the data clearly signals that the close-contact ion pairing of the potassium cations has a direct effect on the electronic structure of the actinide centres and the oxidation states of the metal centres. We attribute this to enhanced bond polarization effects enabled by the coordinated, Lewis acidic potassium cations, which leads to greater localized charge character at the η4-anthracenide ligands.
Electronic structure analysis of the isolated diuranium complexes 1* and 1-K* by DFT calculations and 1* by RASPT2 methods indicates that the uranium–carbon bonding is highly polarized with modest orbital contributions from the uranium atoms. DFT analysis of 1-K* also substantiates increased charge polarization at the potassium-bound anthracenes. In stark contrast to thorium and uranium inverted sandwich complexes, δ-bonding between uranium and the arenide moieties is not observed in 1* or 1-K*, which we ascribe to the bent nature of the anthracenide ligands that prevents metal-arene δ-symmetry orbital overlap. Instead, the metal–ligand bonding is best described as comprising of π-type bonds. Interestingly, RASSCF calculations reveal little participation of the 5f-orbitals to the uranium–carbon interactions, with the 6d-orbitals providing the greatest contributions.
Efforts are currently underway to modify the reaction conditions and choice of arene ligands in order to obtain homoleptic uranium–arenide sandwich complexes to further probe the electronic and chemical properties of this unique class of molecules.
Data availability
The synthetic details of the compounds and their characterization data, including XANES analyses, is provided as part of the ESI.† The optimized geometries are also provided as .xyz files. Complete crystallographic data has been deposited at the Cambridge Crystallographic Data Center (CCDC No. 2071454 (118C6·4THF), 2072886 (1THF), 2071450 (2THF)).Author contributions
J. M. performed synthetic experimental work, data duration, and formal analysis related to characterization, and assisted in the writing of original draft. R. B. performed theoretical investigations and supplied graphical analysis. K. L. M. H performed magnetic measurements, formal analysis of data, and supplied graphical content. A. G.-T. assisted in synthetic experimental work and data collection related to XANES measurements. J. W. supervised the collection and analysis of XANES spectra as well as assisted in the development of sample preparation methodology. R. W. M. collaborated on XANES measurements and provided data analysis and experimental methodology contributions. P. M. assisted in the EDA theoretical calculations and provided use of ADF software for theoretical analysis. A. M.-M. supervised single crystal X-ray data collection. M. M. supervised magnetic measurements and validated formal analysis. B. V. supervised theoretical investigations, conceptualization of theoretical methodology, and contributed to the writing of the original draft. S. F. conceptualized the synthesis of reported compounds, assisted in synthetic work, and was primarily responsible for the original writing and reviewing of the manuscript. All authors contributed to the review and editing of the final draft of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to the Welch Foundation (AH-1922-20200401; S.F.) and the NSF (DMR-1827745; CHE-1827875) for financial support of this work. S. F. is an Alfred P. Sloan Foundation research fellow and is thankful for their support. MRCAT operations are supported by the Department of Energy and the MRCAT member institutions. This research used resources of the Advanced Photon Source; a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. Computations supporting this project were performed on High Performance Computing systems at the University of South Dakota, funded by NSF Award OAC-1626516. B. V. would like to thank the University of South Dakota for start-up funds. B. V., P. M., and R. B. acknowledge that the land their research was performed on is the original homelands of the Dakota, Lakota, and Nakota tribal nations. K. L. M. H. and M. M. are grateful for the support and funds from the University of Ottawa, the Natural Sciences and Engineering Research Council of Canada, and the Canadian Foundation for Innovation.Notes and references
- D. Seyferth, Organometallics, 2002, 21, 2800–2820 CrossRef CAS.
- D. Astruc, Eur. J. Inorg. Chem., 2017, 1, 6–29 CrossRef.
- H. Werner, Angew. Chem., Int. Ed., 2012, 51, 6052–6058 CrossRef CAS PubMed.
- J. H. Osborne, W. C. Trogler, P. D. Morand and C. G. Francis, Organometallics, 1987, 6, 94–100 CrossRef CAS.
- J. Weber, E. P. Kundig, A. Goursot and E. Penigault, Can. J. Chem., 1985, 63, 1734–1740 CrossRef CAS.
- V. M. Rayón and G. Frenking, Organometallics, 2003, 22, 3304–3308 CrossRef.
- R. Sahnoun and C. Mijoule, J. Phy. Chem. A, 2001, 105, 6176–6181 CrossRef CAS.
- M. Rosillo, G. Domínguez and J. Pérez-Castells, Chem. Soc. Rev., 2007, 36, 1589–1604 RSC.
- The word arene is here used in the context of a neutral aromatic hydrocarbon and is distinguished from other carbocyclic ligands, such as Cp-, which only acheive aromaticity upon deprotonation or redox change.
- G. Pampaloni, Coord. Chem. Rev., 2010, 254, 402–419 CrossRef CAS.
- J. E. Ellis, Dalton Trans., 2019, 48, 9538–9563 RSC.
- W. Huang and P. L. Diaconescu, Dalton Trans., 2015, 44, 15360–15371 RSC.
- M. N. Bochkarev, Chem. Rev., 2002, 102, 2089–2118 CrossRef CAS PubMed.
- J. G. Brennan, F. G. N. Cloke, A. A. Sameh and A. Zalkin, J. Chem. Soc. Chem. Comm., 1987, 1668–1669, 10.1039/C39870001668.
- D. M. Anderson, F. G. N. Cloke, P. A. Cox, N. Edelstein, J. C. Green, T. Pang, A. A. Sameh and G. Shalimoff, J. Chem. Soc. Chem. Comm., 1989, 1, 53–55 RSC.
- F. G. N. Cloke, Chem. Soc. Rev., 1993, 22, 17–24 RSC.
- G. Y. Hong, F. Schautz and M. Dolg, J. Am. Chem. Soc., 1999, 121, 1502–1512 CrossRef CAS.
- M. Dolg, J. Chem. Inf. Model., 2001, 41, 18–21 CrossRef CAS PubMed.
- W. A. King, S. DiBella, G. Lanza, K. Khan, D. J. Duncalf, F. G. N. Cloke, I. L. Fragala and T. J. Marks, J. Am. Chem. Soc., 1996, 118, 627–635 CrossRef CAS.
- R. P. Kelly, L. Maron, R. Scopelliti and M. Mazzanti, Angew. Chem., Int. Ed., 2017, 56, 15663–15666 CrossRef CAS PubMed.
- S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, D. L. Clark, S. A. Kozimor, R. L. Martin, D. K. Shuh and T. Tyliszczak, Chem. Sci., 2014, 5, 351–359 RSC.
- M. P. Kelley, I. A. Popov, J. Jung, E. R. Batista and P. Yang, Nat. Commun., 2020, 11 Search PubMed.
- M. L. Neidig, D. L. Clark and R. L. Martin, Coord. Chem. Rev., 2013, 257, 394–406 CrossRef CAS.
- W. W. Yin, A. G. Marshall, J. Marcalo and A. P. Dematos, J. Am. Chem. Soc., 1994, 116, 8666–8672 CrossRef CAS.
- M. Cesari, U. Pedretti, Z. Zazzetta, g. Lugli and W. Marconi, Inorg. Chim. Acta, 1971, 5, 439–444 CrossRef CAS.
- F. A. Cotton and W. Schwotzer, Organometallics, 1985, 4, 942–943 CrossRef CAS.
- G. C. Campbell, F. A. Cotton, J. F. Haw and W. Schwotzer, Organometallics, 1986, 5, 274–279 CrossRef CAS.
- F. A. Cotton, W. Schwotzer and C. Q. Simpson, Angew. Chem., Int. Ed., 1986, 25, 637–639 CrossRef.
- F. A. Cotton and W. Schwotzer, Organometallics, 1987, 6, 1275–1280 CrossRef CAS.
- D. Baudry, E. Bulot, P. Charpin, M. Ephritikhine, M. Lance, M. Nierlich and J. Vigner, J. Organomet. Chem., 1989, 371, 155–162 CrossRef CAS.
- V. Paprocki, P. Hrobárik, K. L. M. Harriman, M. S. Luff, T. Kupfer, M. Kaupp, M. Murugesu and H. Braunschweig, Angew. Chem., Int. Ed., 2020, 31, 13109–13115 CrossRef PubMed.
- I. Korobkov, S. Gambarotta and G. P. A. Yap, Angew. Chem., Int. Ed., 2003, 42, 814–818 CrossRef CAS PubMed.
- I. Korobkov, S. Gambarotta and G. P. A. Yap, Angew. Chem., Int. Ed., 2003, 42, 4958–4961 CrossRef CAS PubMed.
- S. T. Liddle, Coord. Chem. Rev., 2015, 293–294, 211–227 CrossRef CAS.
- J. Murillo and S. Fortier, Encyclopedia of Inorganic and Bioinorganic Chemistry, 2018, pp. 1–19 Search PubMed.
- T. W. Hayton and N. Kaltsoyannis, Experimental and Theoretical Approaches to Actinide Chemistry, 2018, ch. 4, pp. 181–236 Search PubMed.
- P. L. Diaconescu, P. L. Arnold, T. A. Baker, D. J. Mindiola and C. C. Cummins, J. Am. Chem. Soc., 2000, 122, 6108–6109 CrossRef CAS.
- P. L. Diaconescu and C. C. Cummins, J. Am. Chem. Soc., 2002, 124, 7660–7661 CrossRef CAS PubMed.
- B. Vlaisayljevich, P. L. Diaconescu, W. L. Lukens, L. Gagliardi and C. C. Cummins, Organometallics, 2013, 32, 1341–1352 CrossRef.
- A. J. Wooles, D. P. Mills, F. Tuna, E. J. L. McInnes, G. T. W. Law, A. J. Fuller, F. Kremer, M. Ridgway, W. Lewis, L. Gagliardi, B. Vlaisavljevich and S. T. Liddle, Nat. Commun., 2018, 9, 2097 CrossRef PubMed.
- D. Patel, F. Tuna, E. J. L. McInnes, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Dalton Trans., 2013, 42, 5224–5227 RSC.
- C. Camp, V. Mougel, J. Pécaut, L. Maron and M. Mazzanti, Chem.-Eur. J., 2013, 19, 17528–17540 CrossRef CAS PubMed.
- C. Yu, J. F. Liang, C. Deng, G. Lefevre, T. Cantat, P. L. Diaconescu and W. L. Huang, J. Am. Chem. Soc., 2020, 142, 21292–21297 CrossRef CAS PubMed.
- W. J. Evans, S. A. Kozimor, J. W. Ziller and N. Kaltsoyannis, J. Am. Chem. Soc., 2004, 126, 14533–14547 CrossRef CAS PubMed.
- P. L. Arnold, S. M. Mansell, L. Maron and D. McKay, Nat. Chem., 2012, 4, 668–674 CrossRef CAS PubMed.
- P. L. Arnold, C. J. V. Halliday, L. Puig-Urrea and G. S. Nichol, Inorg. Chem., 2021, 60, 4162–4170 CrossRef CAS PubMed.
- H. S. La Pierre, A. Scheurer, F. W. Heinemann, W. Hieringer and K. Meyer, Angew. Chem. Int. Edit., 2014, 53, 7158–7162 CrossRef CAS PubMed.
- B. S. Billow, B. N. Livesay, C. C. Mokhtarzadeh, J. McCracken, M. P. Shores, J. M. Boncella and A. L. Odom, J. Am. Chem. Soc., 2018, 140, 17369–17373 CrossRef CAS PubMed.
- J. N. Tian, M. Zheng, L. Li, G. Schreckenbach, Y. R. Guo and Q. J. Pan, New J. Chem., 2019, 43, 1469–1477 RSC.
- S. C. Bart, F. W. Heinemann, C. Anthon, C. Hauser and K. Meyer, Inorg. Chem., 2009, 48, 9419–9426 CrossRef CAS PubMed.
- D. P. Halter, H. S. La Pierre, F. W. Heinemann and K. Meyer, Inorg. Chem., 2014, 53, 8418–8424 CrossRef CAS PubMed.
- H. S. La Pierre, H. Kameo, D. P. Halter, F. W. Heinemann and K. Meyer, Angew. Chem., Int. Ed., 2014, 53, 7154–7157 CrossRef CAS PubMed.
- S. M. Franke, B. L. Tran, F. W. Heinemann, W. Hieringer, D. J. Mindiola and K. Meyer, Inorg. Chem., 2013, 52, 10552–10558 CrossRef CAS PubMed.
- P. L. Arnold, J. H. Farnaby, R. C. White, N. Kaltsoyannis, M. G. Gardiner and J. B. Love, Chem. Sci., 2014, 5, 756–765 RSC.
- P. L. Arnold, J. H. Farnaby, M. G. Gardiner and J. B. Love, Organometallics, 2015, 34, 2114–2117 CrossRef CAS.
- M. Suvova, K. T. P. O'Brien, J. H. Farnaby, J. B. Love, N. Kaltsoyannis and P. L. Arnold, Organometallics, 2017, 36, 4669–4681 CrossRef CAS.
- S. Fortier, J. R. Aguilar-Calderon, B. Vlaisavljevich, A. J. Metta-Magana, A. G. Goos and C. E. Botez, Organometallics, 2017, 36, 4591–4599 CrossRef CAS.
- M. Yadav, A. J. Metta-Magana and S. Fortier, Chem. Sci., 2020, 11, 2381–2387 RSC.
- C. J. Inman, A. S. P. Frey, A. F. R. Kilpatrick, F. G. N. Cloke and S. M. Roe, Organometallics, 2017, 36, 4539–4545 CrossRef CAS.
- P. T. Wolczanski, Organometallics, 2017, 36, 622–631 CrossRef CAS.
- A. Arunachalampillai, P. Crewdson, I. Korobkov and S. Gambarotta, Organometallics, 2006, 25, 3856–3866 CrossRef CAS.
- I. Korobkov, S. Gorelsky and S. Gambarotta, J. Am. Chem. Soc., 2009, 131, 10406–10420 CrossRef CAS PubMed.
- Y. K. Gunko, P. B. Hitchcock and M. F. Lappert, J. Organomet. Chem., 1995, 499, 213–219 CrossRef CAS.
- M. Castillo, A. J. Metta-Magaña and S. Fortier, New J. Chem., 2016, 40, 1923–1926 RSC.
- J. K. Seaburg, P. J. Fischer, J. Young, G. Victor and J. E. Ellis, Angew. Chem., Int. Ed., 1998, 37, 155–158 CrossRef CAS.
- M. N. Bochkarev, I. L. Fedushkin, A. A. Fagin, H. Schumann and J. Demtschuk, Chem. Commun., 1997, 18, 1783–1784 RSC.
- N. S. Labrum, Y. Losovyj and K. G. Caulton, Chem. Commun., 2018, 54, 12397–12399 RSC.
- N. Tsoureas, A. Mansikkamaki and R. A. Layfield, Chem. Commun., 2020, 56, 944–947 RSC.
- J. T. Boronski and S. T. Liddle, Eur. J. Inorg. Chem., 2020, 2020, 2851–2861 CrossRef CAS.
- N. Tsoureas, A. Mansikkamäki and R. A. Layfield, Chem. Sci., 2021, 12, 2948–2954 RSC.
- J. T. Boronski, L. R. Doyle, A. J. Wooles, J. A. Seed and S. T. Liddle, Organometallics, 2020, 39, 1824–1831 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr. A, 1976, 32, 751–767 CrossRef.
- A. Falceto, D. Casanova, P. Alemany and S. Alvarez, Chem.-Eur. J., 2014, 20, 14674–14689 CrossRef CAS PubMed.
- L. M. Engelhardt, S. Harvey, C. L. Raston and A. H. White, J. Organomet. Chem., 1988, 341, 39–51 CrossRef CAS.
- B. Bogdanovic, Acc. Chem. Res., 1988, 21, 261–267 CrossRef CAS.
- D. M. Roitershtein, A. M. Ellern, M. Y. Antipin, L. F. Rybakova, Y. T. Struchkov and E. S. Petrov, Mendeleev Commun., 1992, 2, 118–120 CrossRef.
- I. L. Fedushkin, M. N. Bochkarev, S. Dechert and H. Schumann, Chem.-Eur. J., 2001, 7, 3558–3563 CrossRef CAS.
- A. Velian, W. J. Transue and C. C. Cummins, Organometallics, 2015, 34, 4644–4646 CrossRef CAS.
- W. W. Brennessel, J. E. Ellis, S. N. Roush, B. R. Strandberg, O. E. Woisetschlager and V. G. Young, Chem. Commun., 2002, 20, 2356–2357 RSC.
- M. Lusi, I. J. Vitorica-Yrezabal and M. J. Zaworotko, Cryst. Growth Des., 2015, 15, 4098–4103 CrossRef CAS.
- R. C. Fortenberry, C. M. Novak, T. J. Lee, P. P. Bera and J. E. Rice, ACS Omega, 2018, 3, 16035–16039 CrossRef CAS PubMed.
- D. R. Kindra and W. J. Evans, Chem. Rev., 2014, 114, 8865–8882 CrossRef CAS PubMed.
- S. Fortier, B. C. Melot, G. Wu and T. W. Hayton, J. Am. Chem. Soc., 2009, 131, 15512–15521 CrossRef CAS PubMed.
- I. Castro-Rodriguez, K. Olsen, P. Gantzel and K. Meyer, J. Am. Chem. Soc., 2003, 125, 4565–4571 CrossRef CAS PubMed.
- E. M. Broderick, N. P. Gutzwiller and P. L. Diaconescu, Organometallics, 2010, 29, 3242–3251 CrossRef CAS.
- N. H. Anderson, S. O. Odoh, U. J. Williams, A. J. Lewis, G. L. Wagner, J. L. Pacheco, S. A. Kozimor, L. Gagliardi, E. J. Schelter and S. C. Bart, J. Am. Chem. Soc., 2015, 137, 4690–4700 CrossRef CAS PubMed.
- R. Bes, M. Rivenet, P. L. Solari, K. O. Kvashnina, A. C. Scheinost and P. M. Martin, Inorg. Chem., 2016, 55, 4260–4270 CrossRef CAS PubMed.
- B. Kosog, H. S. La Pierre, M. A. Denecke, F. W. Heinemann and K. Meyer, Inorg. Chem., 2012, 51, 7940–7944 CrossRef CAS PubMed.
- S. J. Kraft, U. J. Williams, S. R. Daly, E. J. Schelter, S. A. Kozimor, K. S. Boland, J. M. Kikkawa, W. P. Forrest, C. N. Christensen, D. E. Schwarz, P. E. Fanwick, D. L. Clark, S. D. Conradson and S. C. Bart, Inorg. Chem., 2011, 50, 9838–9848 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed.
- W. Küchle, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1994, 100, 7535–7542 CrossRef.
- X. Cao, M. Dolg and H. Stoll, J. Chem. Phys., 2003, 118, 487–496 CrossRef CAS.
- TURBMOLE V7.3 2018, a development of the University of Karlsruhe and Forschungszentrum Karlsruhe GmBH, 1989-2007, TURBMOLE GmbH, since 2007; available from http://www.turbomole.com Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- I. Mayer, Int. J. Quantum Chem., 1986, 29, 477–483 CrossRef CAS.
- Q.-R. Huang, J. R. Kingham and N. Kaltsoyannis, Dalton Trans., 2015, 44, 2554–2566 RSC.
- K. Andersson, P. A. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- P. A. Malmqvist, K. Pierloot, A. R. M. Shahi, C. J. Cramer and L. Gagliardi, J. Chem. Phys., 2008, 128, 204109 CrossRef PubMed.
- V. Sauri, L. Serrano-Andres, A. R. M. Shahi, L. Gagliardi, S. Vancoillie and K. Pierloot, J. Chem. Theory Comput., 2011, 7, 153–168 CrossRef CAS PubMed.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galvan, N. Ferre, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. X. Ma, P. A. Malmqvist, T. Muller, A. Nenov, M. Olivucci, T. B. Pedersen, D. L. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Marti, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2071450, 2071454 and 2072886. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1sc03275e |
| This journal is © The Royal Society of Chemistry 2021 |