Open Access Article
Open Access ArticleMD simulations and QM/MM calculations reveal the key mechanistic elements which are responsible for the efficient C–H amination reaction performed by a bioengineered P450 enzyme†
Surajit
Kalita
 a,
Sason
Shaik
a,
Sason
Shaik
 *b and
Kshatresh Dutta
Dubey
*b and
Kshatresh Dutta
Dubey
 *a
*a
aDepartment of Chemistry and Center for Informatics, School of Natural Sciences, Shiv Nadar University, Dadri, Gautam Buddha Nagar, Uttar Pradesh 201314, India. E-mail: kshatresh.dubey@snu.edu.in
bInstitute of Chemistry, The Hebrew University of Jerusalem, Edmond J Safra Campus, Givat Ram, Jerusalem, 9140401, Israel. E-mail: sason@yfaat.ch.huji.ac.il
First published on 13th October 2021
Abstract
An enzyme which is capable of catalyzing C–H amination reactions is considered to be a dream tool for chemists due to its pharmaceutical potential and greener approach. Recently, the Arnold group achieved this feat using an engineered CYP411 enzyme, which further undergoes a random directed evolution which increases its efficiency and selectivity. The present study provides mechanistic insight and the root cause of the success of these mutations to enhance the reactivity and selectivity of the mutant enzyme. This is achieved by means of comprehensive MD simulations and hybrid QM/MM calculations. The study shows that the efficient C–H amination by the engineered CYP411 is a combined outcome of electronic and steric effects. The mutation of the axial cysteine ligand to serine relays electron density to the Fe ion in the heme, and thereby enhances the bonding capability of the heme-iron to the nitrogen atom of the tosyl azide. In comparison, the native cysteine-ligated P450 cannot bind the tosyl azide. Additionally, the A78V and A82L mutations in P411 provide ‘bulk’ to the active site which increases the enantioselectivity via a steric effect. At the same time, the QM/MM calculations elucidate the C–H amination by the iron nitrenoid, revealing a mechanism analogous to Compound I in the native C–H hydroxylation by P450.
1. Introduction
Enzymes are efficient nanomachines which have usually evolved for some specific functions. One such example is the cytochrome P450 enzymes that have evolved, inter alia, for the metabolism of various administered drugs and toxic xenobiotics. Therefore, tweaking enzymes for functional versatility and harnessing their catalytic efficiency for commercial applications has become a holy grail for bioengineers. Due to its versatility in function and the capability of activating the C–H bond, which is a commercially important process, cytochrome P450 (CYP450) provides an ideal scaffold for bioengineering through directed evolution. The native CYP450 uses molecular oxygen and attaches one oxygen to the substrate while the second oxygen is reduced as a water molecule.1–18 An axial thiolate ligand (cysteine) that controls the electron density via the push–pull effect is the hallmark residue of all CYP450 enzymes.19,20 Among the members of the P450 family, CYP450BM3 possesses the widest and most exposed substrate-access channel, and exhibits as such the highest degree of promiscuity among CYP450s. Wild type CYP450BM3 is well known for hydroxylation and epoxidation reactions in fatty acids via monooxygenation.21,22 As such, CYP450BM3 has been widely used as a scaffold for bioengineering of non-native reactions such as carbene- and nitrene-transfer reactions.23,24Generally, the naturally occurring CYP450s perform C–H activation through monooxygenation but none of the natural enzymes exhibit in their repertoire C–H bond amination. Since more than 75% of all drugs involve a N-containing heterocyclic ring, this has started a race among biochemists to develop an effective biocatalyst for C–N bond formation using inert C–H bonds.25,26 Such bioengineering was demonstrated by Gellman in 1985 using a porphyrin mimetic, and pioneered by Arnold group in 2013![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 then followed by the Fasan group in 2014 through intra-molecular C–H amination catalyzed by CYP450, albeit with a low yield.8,27 Recently, the Arnold group bioengineered an efficient enzyme, P411, which is a variant of CYP450BM3, by mutating the most conserved axial-ligand cysteine to serine.28 This newly engineered CYP450 variant was sufficiently powerful to accomplish the C–H amination reaction, although the regioselectivity remained uncontrolled. In a subsequent feat of engineering, the Arnold group used P411 as a scaffold, and reported the first-ever intermolecular C–H amination with significant enantioselectivity.24 This required the following three key mutations in the P411 scaffold (Fig. 1).
7 then followed by the Fasan group in 2014 through intra-molecular C–H amination catalyzed by CYP450, albeit with a low yield.8,27 Recently, the Arnold group bioengineered an efficient enzyme, P411, which is a variant of CYP450BM3, by mutating the most conserved axial-ligand cysteine to serine.28 This newly engineered CYP450 variant was sufficiently powerful to accomplish the C–H amination reaction, although the regioselectivity remained uncontrolled. In a subsequent feat of engineering, the Arnold group used P411 as a scaffold, and reported the first-ever intermolecular C–H amination with significant enantioselectivity.24 This required the following three key mutations in the P411 scaffold (Fig. 1).
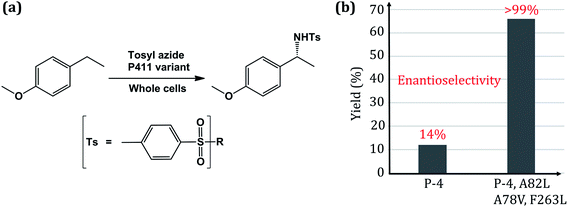 | ||
| Fig. 1 (a) Scheme of the intermolecular C–H amination reaction catalyzed by engineered whole-cell P450. (b) Reactivity plot showing the percentage of yield and enantioselectivity for two different mutated variants of P450. Here P4 is an engineered P411 (ref. 24). | ||
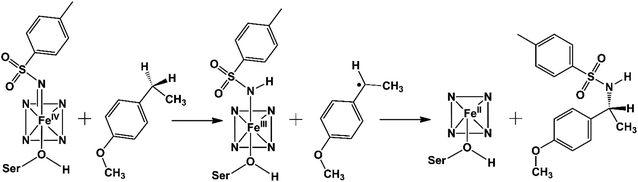
The C–H amination reaction in Fig. 1a is supposed to be mediated by an active iron-nitrenoid oxidant (complex 3 in Scheme 1), in a catalytic cycle shown in Scheme 1 (note that 3 is a Compound I (Cpd I) analog). As can be seen, the scheme involves three main catalytic steps that begin with a single electron reduction of the resting ferric complex, 1. The so-formed reduced ferrous complex, 2, readily reacts with the nitrene source (tosyl azide) and forms a short-lived active oxidant ‘iron nitrenoid’, 3, that directly facilitates the C–H activation. The third step may bifurcate into either an unproductive nitrene reduction or the productive nitrene transfer, which affects the efficacy of the so-engineered enzyme. The root cause of this bifurcation remains an enigma, which is the focus of this work.
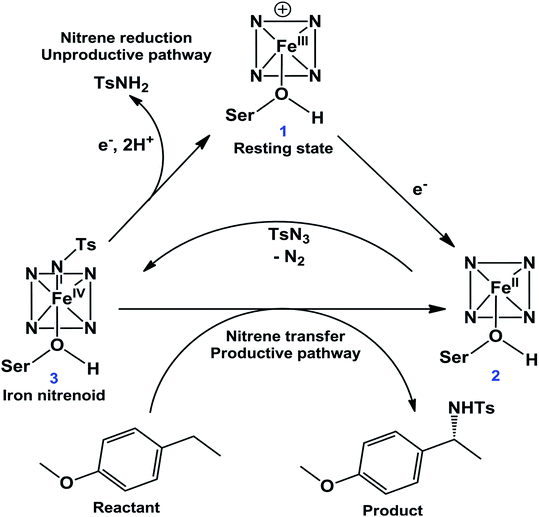 | ||
| Scheme 1 A proposed24 catalytic cycle of a P450 variant for the intermolecular C–H amination reaction. | ||
Thus, this great feat of bioengineering of C–H amination by mutating the axial cysteinate ligand in CYP450 raises several mechanistic puzzles: (1) how does the assumed iron-nitrenoid active species differ from Cpd I, and how does the swapping of the axial thiolate with serine bring about the unorthodox C–H amination reactions? (2) How do the three-point mutations drastically increase the reactivity and enantioselectivity of the P411 enzyme (Fig. 1b)?
Guided by the above mechanistic questions, we have carried out several MD simulations, Density Functional Theory (DFT) calculations, and hybrid QM/MM calculations. We have performed a comprehensive and sequential study starting with the characterization of the electronic states of different catalytic steps in Scheme 1, studied the topology of key protein residues with the help of several MD simulations, verified the mechanism of C–H amination through hybrid QM/MM calculations, and revealed the root cause that triggers the unorthodox C–H amination due to serine mutation. We will see how theoretical calculations coherently explain the elegant choreography of the protein matrix engineered by directed evolution, ultimately leading to an efficient and selective C–H amination.
2. Computational methods
We used molecular docking to generate enzyme–cofactor complexes, MD simulations for the conformational sampling of wild type (WT) and mutant complexes, Density Functional Theory (DFT) calculations for characterization of electronic states, and hybrid QM/MM calculations for exploring the catalytic mechanism. Each of these steps is discussed in detail in the subsequent section.2.1 System setup
The starting coordinates for the geometry of the CYP450 variant were taken from the protein data bank of PDB id 5UCW24 and processed with MODELLER29 to add the missing non-terminal residues. Hydrogen atoms in protein were added using the LEAP module of AMBER20 employing the ff14SB force field. Parametrization for the metal coordinated cluster (iron porphyrin and axial serine) was performed using a python based AMBER20 inbuilt Metal Centre Parameter Builder tool.30 Since the metal coordination of the engineered P411 enzyme is different from that of its parent CYP450BM3 enzyme, we characterized the correct ground state geometry of the ferrous complex 2. The details of the optimized geometry can be found in the ESI (see Fig. S2†). Since the triplet-state is the ground state, charges and other parameters for the subsequent MD simulations were generated for this state. The ligands tosyl azide and 4-ethylanisole were docked in the active site of protein using AutoDock Vina,31 and the best pose was considered for MD simulations. The force field parameters for ligands were produced using a generalized AMBER force field (GAFF2) in the antechamber module of AMBER20. The associated partial atomic charges were also generated by applying the restraint electrostatic potential (RESP) method32,33 of QM calculated charges at the HF/6-31G(d) level of theory. Subsequently, the systems were solvated in an octahedral box of TIP3P34 water extending up to 10 Å from the protein surface. Based on the overall charge of the prepared solvated system, a corresponding total number of 9 Na+ ions were added to neutralize it. We used the protonated form of serine for all MD simulations and subsequent QM/MM calculations.24 In the absence of the proton, the enzyme would not be active. More on the rationale for using a protonated serine can be found in ESI S1.†2.2 MD simulations
After proper system setup, the target complexes were subjected to minimization in two steps to remove the poor contacts during system setup. In the first step, only water molecules were minimized while in the second step the entire complex was minimized using 5000 steps of steepest descent and subsequently 5000 steps of conjugate gradient algorithm. Afterward, the systems were gently heated from 10 to 300 K using an NVT ensemble for 50 ps. Following that, we normalized the system under the NPT ensemble for 1 ns at a target temperature and pressure of 300 K and 1.0 atm using the Langevin thermostat35 and Berendsen barostat,36 respectively. Along with that, a collision frequency of 2 ps was also applied where the pressure relaxation time was 1 ps. Systems were then equilibrated for the next ∼3 ns under the same conditions. The equilibrated systems underwent a further productive MD run of at least 100 ns (depending on the system) using a multi-trajectory approach in which we restarted the simulation after completion of each 50 ns of simulation at a random velocity. The algorithms SHAKE37 and particle mesh Ewald (PME)38 were used to constrain the hydrogen bonds and treat the long-range electrostatic forces, respectively. All MD simulations were carried out in the GPU version of the AMBER20 package.392.3 QM/MM calculations
For the mechanistic study, we used QM/MM calculations employing Chemshell40,41 that combines Turbomole,42 for the QM region, and DL_POLY43 using the AMBER force field, for the MM part. All QM/MM calculations were performed on the representative snapshots taken from the MD simulation of complexes 2 and 3 (see Scheme 1). In all cases, a truncated heme-porphyrin ring and the proximal serine (HO–C2H5) residue were kept in the QM zone along with the reactive ligand of the respective complexes. The representative snapshots were based on the closest available distance of interest of the most populated MD trajectories.The QM optimizations were performed using the UB3LYP/def2-SVP level of theory44–48 followed by a single point energy calculation using UB3LYP/def2-TZVP as a higher level of theory. The basis set and QM theory were employed here based on similar previous studies in P450 chemistry.49–51 The energetics were further improved using ZPE (zero-point energy) corrections followed by frequency calculations of the optimized reactant (RC), transition state (TS), and product (PC) geometries at the UB3LYP/def2-SVP level of theory. Grimme dispersion (G-D3)52 was used to add dispersion correction in energetics. The part of protein and water molecules residing up to 8 Å from the QM zone were considered as active atoms and their electrostatic as well as van der Waals effects were accounted for by QM calculations. Moreover, an electronic embedding scheme53 was employed to account for the polarizing effect of the enzyme environment on the QM region. While treating the QM/MM boundary, we used hydrogen link atoms with the charge-shift model.40,41
2.4 QM only DFT calculations
In the native P450 enzymes, the doublet and quartet are the two relevant spin states in the active species, Compound I (Cpd I).17,18,49 However, our investigated reactive species (heme + serine + nitrene) is significantly different from the native one.24 Therefore, prior to MD simulations and time-consuming QM/MM calculations, we performed DFT calculations for the reactive species in three different spin states (singlet, triplet and quintet) to ascertain the correct ground state electronic state (see Fig. S3†). Our calculations show the triplet spin as the ground state of the reactive species; therefore, all further calculations were reported for the triplet state only. The QM-only DFT calculations were performed in Gaussian 09 software54 using the UB3LYP/B1 level of theory where B1 contains the LANL2DZ basis set for the Fe atom55–57 and 6-31G(d) for all other atoms.58,59 The optimized energies were further refined by calculating single-point energy using an all-electron basis set, def2-TZVP, coupled with UB3LYP. All reported energies are zero-point energy (ZPE) and Grimme dispersion (G-D3) corrected where ZPE values were obtained from frequency calculation. We optimized the geometry in the gas phase to determine the lowest energy ground state multiplicity followed by a further re-optimization of energetically lowest geometry in chlorobenzene solvent using the SMD solvent model.60 We chose the chlorobenzene solvent to mimic the non-polar nature of the enzyme environment based on previous studies.61,62 The natural- and spin natural-orbital calculations were carried out to identify the presence of singly occupied molecular orbitals and the nature of the electron spin.3. Results and discussion
We start our study by decoding the enhanced C–H amination activity and regiospecificity due to several site mutations as depicted in Fig. 1b.3.1. Decoding the enhanced activity due to site-directed mutations in the P411 enzyme
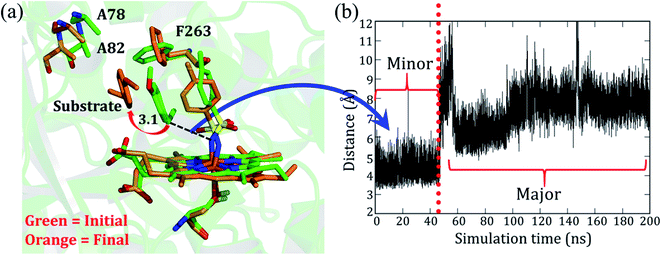
As mentioned, the site-directed mutations (see Fig. 1b) of the engineered P411 enzyme enhance the catalytic turnover of C–H amination by several fold and also provide an enantioselective product.24 However, the rationale for the increased activity and selectivity is not apparent and requires elucidation. As such, we intend to show here how theory complements the directed-evolution experiment by providing the underlying mechanistic principles which drive these effects. For simplicity, we named the P-4 variant as variant1, while P-4 with additional mutations of A82L, A78V, and F263L was named as variant2. Note that variant1 is less reactive and less enantioselective vis-à-visvariant2.The simulation of variant1 reveals two conformations: (a) the initial and less populated (∼20%) conformation, which we refer to as the minor basin (shown in green in Fig. 2a), and the highly populated conformation (80%), which is the major basin (shown in orange in Fig. 2a). In the minor basin, the substrate is close to the iron nitrenoid (∼3.5 Å), and at the same time, an active site residue, F263, is located perpendicular to the substrate. The perpendicular orientation of F263 (green in Fig. 2a) applies a restraint on the substrate and limits its flexibility. On the other hand, as shown in Fig. 2a, in the major basin (orange colored) the substrate moves away from the active oxidant (7–10 Å), and subsequently, the F263 residue flips to a parallel position vis-à-vis the substrate. This reorientation of F263 frees the substrate from constraints and provides flexibility to it. This might be the root cause for the low activity and less specificity of the substrate in variant1. It is apparent, therefore, that the MD simulation concisely explains the low activity and specificity for variant1. In addition, we also found two additional water molecules in the major conformation which might be due to the additional space freed by the substrate. In summary, the phenylalanine residue (F263) acts as a ringmaster which controls the substrate movement inside the active site by changing its conformation from a perpendicular to a parallel orientation.
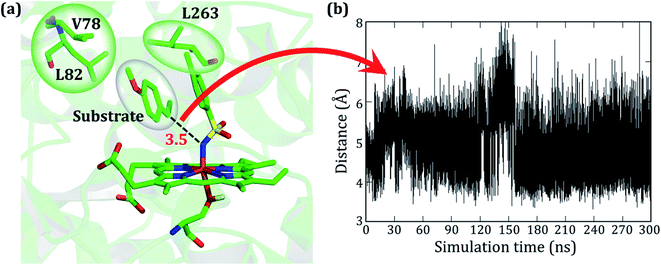
As stated earlier, the mutations of A82L, A78V, and F263L in variant2 significantly enhance the C–H amination activity and enantioselectivity (>99%) relative to variant1. Therefore, we performed MD simulations for this variant to uncover the roots for this change in activity. Interestingly, during the MD simulations of variant2, the substrate stays close to the oxidant (∼4 Å) for more than 90% of the entire 300 ns simulations and remains quite stable (see Fig. 3).
As seen in variant1, the substrate was trapped by F263 (Phe 263) via a strong π–π interaction, and therefore a mutation of Phe to Leu in variant2 removes the π–π interaction and allows the substrate to change its orientation. At the same instant, the substrate finds a new π–π interaction with the aromatic ring of the tosyl moiety of the iron nitrenoid. Due to the new π–π interaction, the substrate remains close to the tosyl moiety of the oxidant for the entire simulation. Therefore, the F263L mutation exerts a binding advantage that contributes to the enhanced activity.
How do the mutations of A78V and A82L augment the enantioselectivity of the reaction? Being non-polar residues, valine (V) and leucine (L) do not change the electrostatic and polar environment of the active site, and at the same time, these mutations increase the rigidity of the active site due to elongated side chains vis-à-vis alanine (A). This extra “filling” of the active site is necessary for enantioselectivity. Thus, the smart bioengineering which enhances the C–H amination is efficiently decoded by the MD simulation.
3.2. MD simulation explains the product enantioselectivity
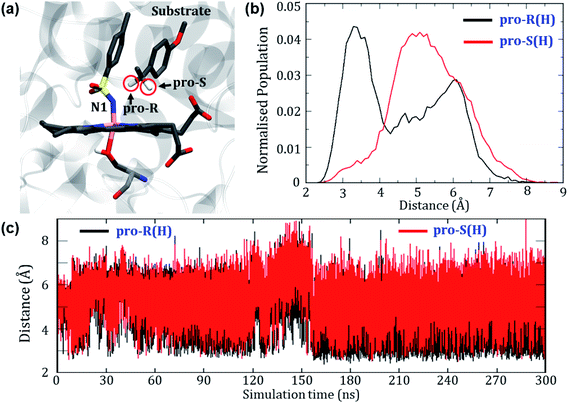
Can the simulation also predict the observed pro-R selectivity over pro-S? The answer is yes, and this is shown in Fig. 4.Fig. 4a depicts a representative snapshot from the MD simulations and highlights the pro-R and pro-S hydrogens. Fig. 4c shows the evolution of distances of these hydrogens from the reactive N1 atom of the oxidant. It is therefore apparent that the pro-R hydrogen is significantly closer to N1 compared with the pro-S hydrogen. We further calculated the Boltzmann population of the pro-R and pro-S distances over the entire 300 ns as shown in Fig. 4b. Using Fig. 4b, it is quite clear that the pro-R(H) is populated close to the region of 3 Å for most of the simulation time while pro-S(H) stays at a distance of 5–6 Å from N1 (see Fig. S4† for similar results of another replica simulation). Since we started the simulations from a docked position where the methyl group points towards the iron center, the pro-R(H) preference might be anticipated due to the unique starting conformation. To rule out this possibility, we performed a separate simulation where the substrate was flipped upside down. Surprisingly, the substrate reorients and restores the conformation wherein the pro-R comes closer than the pro-S conformation even in the flipped conformations (see Fig. S5† for details). In contrast, the enantioselectivity of variant1 shows a non-selective pattern since both pro-R and pro-S hydrogens were equidistant from the reactive center (see Fig. S6 of the ESI†). Therefore, these predictions of enantioselectivity of pro-R(H) for variant2 and non-selectivity for variant1 are in good agreement with the experimental observation of Arnold et. al.24 and hence show that our MD simulations are sufficiently accurate to mimic the experimental enantioselectivity.
3.3. QM/MM mechanistic investigation of the intermolecular C–H amination reaction
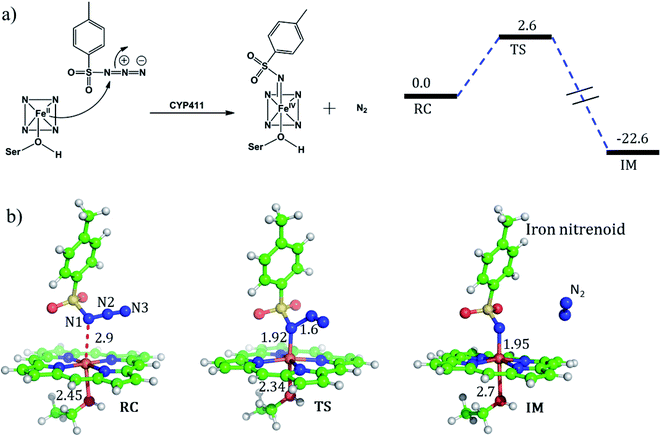
As can be seen, the engineered P411 is entirely different from its parent P450 due to its novel serine-ligated heme-porphyrin structure. The electronic features which dictate the catalytic mechanism of P411 should be established by means of quantum mechanical calculations. We, therefore, performed a comprehensive mechanistic study of C–H amination using hybrid QM/MM calculations.Scheme 2 shows a possible mechanism of this reaction. Initially, the nitrogen atom (N1) abstracts the benzylic Csp3–H atom and forms a reactive intermediate and a radical substrate. Subsequently, these two newly formed species mutually couple to generate the C–H aminated product and a ferrous complex of P411.
To validate this mechanism, we started our QM/MM calculations by optimizing a representative MD snapshot from the simulation of variant2. The snapshot was chosen based on the closest distance between the benzylic pro-R(H) of the substrate and N1 of the nitrenoid. An energy scanning was carried out for abstracting the pro-R(H), leading to the formation of a highly reactive intermediate complex as well as a radical substrate. Subsequent energy scanning resulted in product formation via a rebound mechanism as found in native P450 enzymes. The energy profile diagram and the key geometries are presented in Fig. 5.
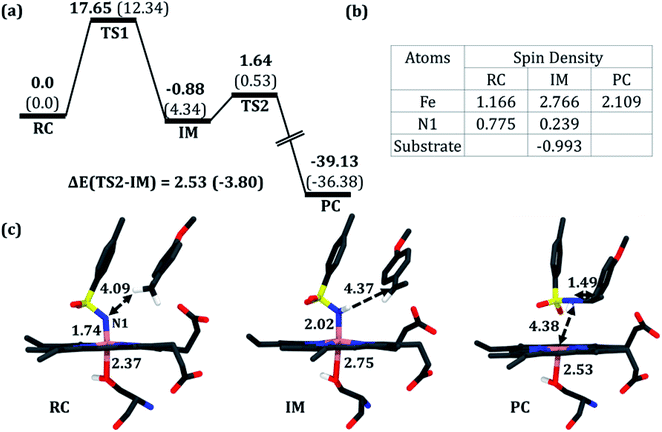 | ||
| Fig. 5 (a) A complete reaction profile for the intermolecular C–H amination. Energies (in kcal mol−1) are relative to the reaction complex (RC). Values in parentheses are single-point energies in the better basis set. All energies are corrected for zero-point energy (ZPE) and G-D3 dispersion. Note that all energetics were evaluated relative to the iron nitrenoid complex, not from the separated reactants. (b) Spin densities in RC, the reaction intermediate (IM), and the product cluster (PC). (c) Optimized geometries for RC, IM, and PC (from left to right); respective bond lengths are in Å. The optimized geometry of TS1 and TS2 can be found in the ESI (see Fig. S8†). | ||
In the first step, the reactive intermediate complex (IM) is formed by abstracting the pro-R hydrogen at the cost of a moderate energy barrier of 17.7 kcal mol−1, which is lowered to 12.3 kcal mol−1 using the more extensive basis set. This less exothermic step is rate-determining. Subsequently, IM proceeds through the radical rebound mechanism that possesses a tiny energy barrier of 2.5 kcal mol−1 and forms the C–H aminated product. Furthermore, a PES scanning for the pro-S H-abstraction exhibits an energy barrier of 20.47 kcal mol−1 which is 2.82 kcal mol−1 higher than that of its counterpart (see Fig. S7 in the ESI†).
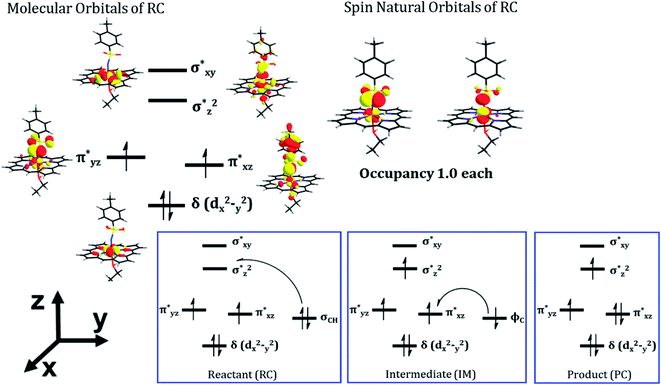
As can be seen, the QM/MM calculations show that the mechanism of the C–H amination reaction with the engineered P411 is essentially similar to the C–H oxidation mechanism with the native P450 enzyme. However, whether it is completely identical to the native P450 enzyme including the involvement of the porphyrin radical cation and Compound II type intermediate is not clear from the energy profile. Therefore, we calculated the spin density of the RC, IM, and PC species in Fig. 5b and detailed electronic structures of RC. The calculations reveal in Fig. 6 two unpaired electrons at the antibonding π orbitals of the Fe–N bond in RC which is also supported by the spin natural orbital calculations shown in Fig. 6. This electronic structure of RC (iron nitrenoid) resembles Compound I except for a radical cation at the porphyrin.63
Using the spin densities as shown in Fig. 5b we further depicted the occupation of the key orbitals throughout the reaction pathway shown in Fig. 6. In the H-abstraction step, an electron, initially in a σCH orbital of the substrate, shifts to the unoccupied high energy  orbital of the active oxidant and produces the intermediate IM. In this species, there are three identical-spin electrons (due to orbital delocalization, only 2.8 according to population analysis), while one down-spin electron is localized at the benzylic C-atom of the substrate, with a small extent of delocalization to the phenyl ring (hence, population analysis gives a value of −0.993). In the rebound step, the substrate formally donates its electron to the Fe atom resulting in the formation of the product molecule and the ferrous heme-porphyrin complex.
orbital of the active oxidant and produces the intermediate IM. In this species, there are three identical-spin electrons (due to orbital delocalization, only 2.8 according to population analysis), while one down-spin electron is localized at the benzylic C-atom of the substrate, with a small extent of delocalization to the phenyl ring (hence, population analysis gives a value of −0.993). In the rebound step, the substrate formally donates its electron to the Fe atom resulting in the formation of the product molecule and the ferrous heme-porphyrin complex.
As such, the active species of P411 is an analog of the oxo-iron(IV) Cpd II intermediate in native P450s, having two singly occupied π* orbitals, which here acts as a H-abstractor. Thus, QM/MM mechanistic studies provide us with strong energetic and electronic evidence supporting our proposed pathway and reveal a native P450-like mechanism despite the absence of a Cpd I-like species.
3.4. Formation of the iron nitrenoid active oxidant in P411
While we achieved an understanding of the C–H amination reaction by the bioengineered P411, this creates an additional mechanistic puzzle: why is the native cysteine ligand unable to promote the C–H amination? This obviously requires us to understand the role of the mutation of the most conserved cysteine residue to serine. To this end, we performed several MD simulations and QM/MM calculations which are discussed below.We believe that the key to solving the above mechanistic puzzle might be associated with the ease of formation of the iron-nitrenoid active oxidant. We therefore proceeded to compare the mechanisms of formations of the serine-ligated vs. cysteine-ligated iron-nitrenoid P411 species.
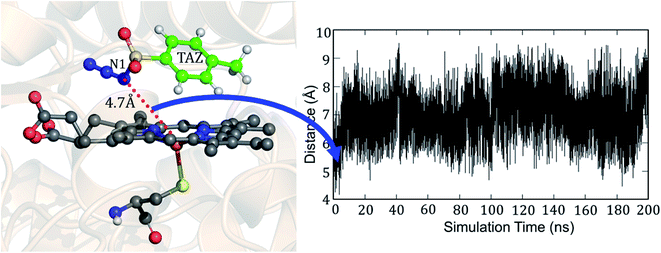
Fig. 7 shows the two conformations of the distal tosyl azide (TAZ) of P411, before and after MD simulations. As can be seen from Fig. 7a, the TAZ is initially far from the heme iron (the respective distance between N1 and Fe is 4.6 Å). However, during the simulation, the distance reduces to 2.53 Å (see Fig. 7b) for 30% of the sampled MD trajectory. A closer inspection of the MD trajectory also shows that the proximity of the distal ligand with heme-iron is strongly correlated with the juxtapositions of L263 and V328 (see Fig. S9† for graphs showing the correlation with distance). It is apparent that these residues provide a tight packing to the distal ligand, and therefore, the relative position of these residues directly affects the orientation of the ligand.
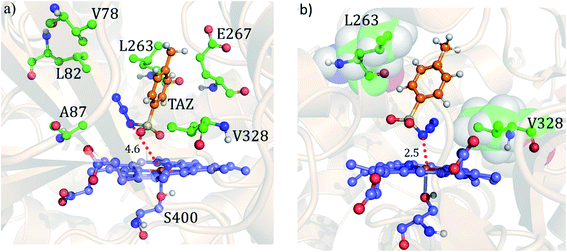 | ||
| Fig. 7 The precursor enzyme with a serine axial ligand (S400): (a) geometry of the docked tosyl azide (TAZ), and the identified active site residues based on ref. 24. (b) A representative MD snapshot showing the most probable interaction of the TAZ ligand with different residues of the enzyme. All distances are in Å. | ||
For the mechanism of formation of the active oxidant, iron nitrenoid, we performed QM/MM calculations for a representative snapshot from MD simulations. We started the calculations with the optimization of the reactant followed by potential energy scanning to trace the reaction coordinate for the formation of the iron nitrenoid. The energy profile for the reaction is shown in Fig. 8a. As can be seen, the activation barrier for the formation of the active oxidant, i.e. iron nitrenoid, is just 2.6 kcal mol−1. Moreover, this process takes place in a concerted displacement reaction; the Fe–N1 bond is formed and at the same time the N1–N2 bond is broken leaving behind the iron nitrenoid active oxidant and molecular nitrogen.
As such, our QM/MM calculations show that the rate of formation of the iron nitrenoid active oxidant is by far faster than that of the analogous process which generates Cpd I for the native CYP450BM3 enzyme where cysteine is the axial ligand.51 The corresponding barrier for this Cpd I formation process is 15.7 kcal mol−1.51Hence, our theoretical mechanistic investigation shows that the engineered enzyme produces the iron nitrenoid more efficiently than its functional analog Cpd I in the native P450 enzyme.
But why does the native enzyme with the cysteine ligand fail to create the iron nitrenoid oxidant? To answer this question, we mutated in the engineered P411 the proximal serine to cysteine and performed 200 ns of MD simulation. Interestingly, now, the tosyl azide ligand never approaches the heme-porphyrin during the entire 200 ns of simulation of the cysteine-ligated P411 complex. As can be seen in Fig. 9, the average distance between Fe and N1 is ∼7 Å and the lowest possible distance is 4.7 Å. In fact, the QM/MM optimization (see Fig. S10†) also reveals that the ligand moves away from its original position by a large distance, much the same as the MD results. Moreover, a QM/MM scanning for cysteine-ligated P411 iron shows nitrenoid formation as an unfavorable process (see Fig. S11†).
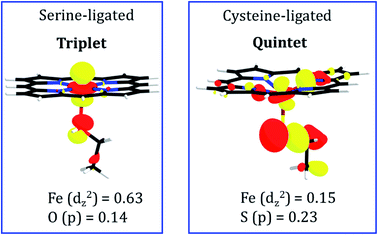
To pinpoint the cause of this change in the distance of FeII---TAZ when serine is replaced by cysteine, we plotted in Fig. 10 the molecular orbitals which are responsible for the FeII–N1 σ bonds between the ferrous ion and TAZ. Thus, the serine-ligated complex exhibits a bond-making orbital which is well-located on the FeII ion (see Fig. 10; the weight contribution of Fe to the dz2 MO is 0.63). In contrast, the cysteine-ligated ferrous complex has a quintet ground spin state (see Fig. S10†), and its FeII–N1 bond making orbital has a small weight contribution of FeII (0.15) in the respective MO. It is apparent therefore that the corresponding iron ion, in the cysteine-ligated heme, will coordinate the TAZ very feebly. On the other hand, the high orbital density for the serine-ligated iron creates a stronger binding site for TAZ.
3.5. Revealing the path of nitrenoid reduction
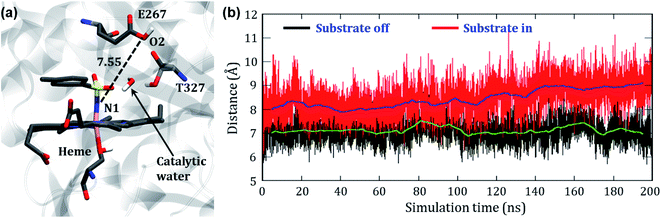
In the engineered P411, the nitrenoid reduction by subsequent delivery of two protons is believed to constitute a nonproductive machinery for the C–H amination. Therefore, an understanding of this proton-delivery machinery could be helpful in further site-directed mutagenesis that blocks the unproductive pathway. Keeping this in mind, we studied the possible route of the protonation in P411.In the crystal structure, we see a Glu267 residue which usually acts as an acid or a traditional proton donor for native P450BM3 in the monooxygenation pathway. We, therefore, have thoroughly studied the conformational position of the Glu267 residue to investigate whether it can play the same role in the engineered enzymes too. The initial distance between Fe and O2 of the protonating Glu267 was found to be 12.2 Å which is too long for protonation. However, we observed a small curl in the position of the Glu267 residue in the iron nitrenoid intermediate, but still, the distance (∼7 Å) is too long to transfer the proton (see Fig. 11). Therefore, we performed two different MD simulations of variant2 in the presence and absence of the substrate to account for the involved route of protonation. For the “substrate off” system, we found a water molecule constantly present at the active site for a longer period of the simulation as shown in Fig. 11a. On the other hand, we did not observe any such water molecule when the substrate was present in the heme site. We, therefore, propose a crucial role of this water molecule for the proton relay through the Glu267 to the iron nitrenoid. Besides, the threonine molecule (Thr327) present close to the Glu267 may play the role of alcohol as is done by Thr268 in wild type P450BM3.51 The distance evolution between N1 of the nitrenoid and O2 of Glu267 reveals that the “curl in” position of Glu267 remains almost constant for the “substrate off” system while it opens up slowly when the substrate is around (see Fig. 11b). This observation also shows the crucial role of substrate entry at the catalytic cycle after the formation of the iron nitrenoid. In a sense, we can assume that the substrate mediates the reductive ability of the iron nitrenoid. Moreover, our simulation results also indicate that the point mutation of Glu267 can reduce the formation of the unproductive reduced product.
Though the mechanism of the CH amination for the P411 enzyme has been studied previously,64–68 the present work provides the following novel findings: (a) in previous studies, a deprotonated serine was used. In contrast, our present study shows that the deprotonation of serine is unfavorable, since it destructs the porphyrin group by protonating the nearby porphyrin nitrogen, and otherwise breaking the O–H bond heterolytically is a high energy process (see ESI† S.1). Therefore, the use of deprotonated serine as in previous studies may not have been tested properly. Furthermore, our study points out that protonated serine (i.e. the natural form of serine) could be more reactive relative to deprotonated serine. (b) The present work elaborates on the effect of axial Cys → Ser mutation using electronic structure calculations. We have highlighted the pivotal role of the electron density along the proximal axis which controls the formation of the active oxidant (iron nitrenoid). This finding is novel and may have further implications in bioengineering of proximal ligation in P450s. (c) The present study deciphers the novel mechanism of the unproductive reduction of a nitrenoid (see Section 3.4).
In a nutshell, our theoretical investigation decisively explains the enhanced activity of the C–H amination in cysteine → serine mutation and complements the experimentally observed results.24
4. Conclusions
The present study provides a rationale and logical explanation for the highly successful engineering that leads to the unorthodox C–H amination reaction. Using MD simulations and hybrid QM/MM calculations we have shown that the enhanced C–H amination activity and its enantioselectivity are jointly determined by well-defined electronic and steric effects. The mutation of cysteine → serine of the proximal ligand in the engineered P411 enzyme provides a favorable electronic effect that increases the orbital population on the Fe atom vis-à-vis the native cysteine-ligated P450, which in turn triggers the C–H amination reactions in the P411 enzyme. Similarly, the mutations of A78V and A82L in variant2 of the P411 enzyme provide ‘bulk’ to the active site which increases the enantioselectivity via a steric effect. Moreover, MD simulations lucidly explain how a mutation of F263 to L263 can significantly enhance the reactivity by switching its interacting partner from a 4-ethylanisole substrate to a distal ligand. Our study supplemented by QM/MM calculations provides a valuable insight that engineered enzyme P411 follows a native P450-like mechanism of H-abstraction where an iron-nitrenoid acts as an active oxidant, which is analogous to but more potent than the native Cpd II.As such, the present study shows that the MD simulations and QM/MM calculations complement the bioengineering involved in directed evolution, elucidating the factors which make this engineering so successful.
Author contributions
SK performed all calculations. KDD and SS designed the project and wrote the manuscript.Conflicts of interest
The authors declare no conflict of interest.Data availability
Optimized geometries of all key structures are available as part of the ESI.†Acknowledgements
KDD acknowledges the Department of Biotechnology, Govt of India for the Ramalingaswami re-entry grant. SS acknowledges the Israel Science Foundation for an ISF 520/18 grant. SK acknowledges the Council of Scientific and Industrial Research for JRF.References
- F. H. Arnold, Acc. Chem. Res., 1998, 31, 125–131 CrossRef CAS.
- P. A. Romero and F. H. Arnold, Nat. Rev. Mol. Cell Biol., 2009, 10, 866–876 CrossRef CAS PubMed.
- F. H. Arnold, Angew. Chem., Int. Ed., 2019, 58, 14420–14426 CrossRef CAS PubMed.
- K. Chen and F. H. Arnold, Nat. Catal., 2020, 3, 203–213 CrossRef CAS.
- J. B. Wang, G. Li and M. T. Reetz, Chem. Commun., 2017, 53, 3916–3928 RSC.
- H. Renata, Z. J. Wang and F. H. Arnold, Angew. Chem., Int. Ed., 2015, 54, 3351–3367 CrossRef CAS PubMed.
- J. A. McIntosh, P. S. Coelho, C. C. Farwell, Z. J. Wang, J. C. Lewis, T. R. Brown and F. H. Arnold, Angew. Chem., Int. Ed., 2013, 52, 9309–9312 CrossRef CAS PubMed.
- R. Singh, M. Bordeaux and R. Fasan, ACS Catal., 2014, 4, 546–552 CrossRef CAS PubMed.
- C. K. Prier, T. K. Hyster, C. C. Farwell, A. Huang and F. H. Arnold, Angew. Chem., Int. Ed., 2016, 55, 4711–4715 CrossRef CAS PubMed.
- S. Kille, F. E. Zilly, J. P. Acevedo and M. T. Reetz, Nat. Chem., 2011, 3, 738–743 CrossRef CAS PubMed.
- M. T. Reetz, J. Am. Chem. Soc., 2013, 135, 12480–12496 CrossRef CAS PubMed.
- F. P. Guengerich, Toxicol. Res., 2021, 37, 1–23 CrossRef PubMed.
- F. P. Guengerich and F. K. Yoshimoto, Chem. Rev., 2018, 118, 6573–6655 CrossRef CAS PubMed.
- A. W. Munro, K. J. McLean, J. L. Grant and T. M. Makris, Biochem. Soc. Trans., 2018, 46, 183–196 CrossRef CAS PubMed.
- K. D. Dubey and S. Shaik, Acc. Chem. Res., 2019, 52, 389–399 CrossRef PubMed.
- H. M. Girvan and A. W. Munro, Curr. Opin. Chem. Biol., 2016, 31, 136–145 CrossRef CAS PubMed.
- Cytochrome P450: Structure, Mechanism and Biochemistry, ed. P. R. and O. de Montellano, Plenum Press, New York, 2nd edn, 1995 Search PubMed.
- B. Meunier, S. P. de Visser and S. Shaik, Chem. Rev., 2004, 104, 3947–3980 CrossRef CAS PubMed.
- J. H. Dawson, Science, 1988, 240, 433–439 CrossRef CAS PubMed.
- J. T. Groves, Nat. Chem., 2014, 6, 89–91 CrossRef CAS PubMed.
- C. J. C. Whitehouse, S. G. Bell and L. L. Wong, Chem. Soc. Rev., 2012, 41, 1218–1260 RSC.
- A. W. Munro, D. G. Leys, K. J. McLean, K. R. Marshall, T. W. B. Ost, S. Daff, C. S. Miles, S. K. Chapman, D. A. Lysek, C. C. Moser, C. C. Page and P. L. Dutton, Trends Biochem. Sci., 2002, 27, 250–257 CrossRef CAS PubMed.
- P. S. Coelho, E. M. Brustad, A. Kannan and F. H. Arnold, Science, 2013, 339, 307–310 CrossRef CAS PubMed.
- C. K. Prier, R. K. Zhang, A. R. Buller, S. B. Chen and F. H. Arnold, Nat. Chem., 2017, 9, 629–634 CrossRef CAS PubMed.
- N. Kerru, L. Gummidi, S. Maddila, K. K. Gangu and S. B. Jonnalagadda, Molecules, 2020, 25, 1909 CrossRef CAS PubMed.
- D. Schroder and H. Schwartz, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18114–18119 CrossRef CAS PubMed.
- E. W. Svastits, J. H. Dawson, R. Breslow and S. H. Gellman, J. Am. Chem. Soc., 1985, 107, 6427–6428 CrossRef CAS.
- P. S. Coelho, Z. J. Wang, M. E. Ener, S. A. Baril, A. Kannan, F. H. Arnold and E. M. Brustad, Nat. Chem. Biol., 2013, 9, 485–487 CrossRef CAS PubMed.
- A. Šali and T. L. Blundell, J. Mol. Biol., 1993, 234, 779–815 CrossRef PubMed.
- P. Li and K. M. Merz Jr, J. Chem. Inf. Model., 2016, 56, 599–604 CrossRef CAS PubMed.
- O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31, 455–461 CAS.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- W. D. Cornell, P. Cieplak, C. I. Bayly and P. A. Kollman, J. Am. Chem. Soc., 1993, 115, 9620–9631 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J. A. Izaguirre, D. P. Catarello, J. M. Wozniak and R. D. Skeel, J. Chem. Phys., 2001, 114, 2090–2098 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- T. Darden, D. York and L. Pederson, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- R. S. Ferrer, A. W. Götz, D. Poole, S. L. Grand and R. C. Walker, J. Chem. Theory Comput., 2013, 9, 3878–3888 CrossRef PubMed.
- P. Sherwood, A. H. de Vries, M. F. Guest, G. Schreckenbach, C. R. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjøvoll, A. Fahmi, A. Schäfer and C. Lennartz, J. Mol. Struct.: THEOCHEM, 2003, 632, 1–28 CrossRef CAS.
- S. Metz, J. Kästner, A. A. Sokol, T. W. Keal and P. Sherwood, Comput. Mol. Sci., 2014, 4, 101–110 CrossRef CAS.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- W. Smith and T. R. Forester, J. Mol. Graphics, 1996, 14, 136–141 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1992, 96, 2155–2160 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- F. Weigenda and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigenda, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- S. Shaik, S. Cohen, Y. Wang, H. Chen, D. Kumar and W. Thiel, Chem. Rev., 2010, 110, 949–1017 CrossRef CAS PubMed.
- K. D. Dubey, B. Wang and S. Shaik, J. Am. Chem. Soc., 2016, 138, 837–845 CrossRef CAS PubMed.
- S. Kalita, S. Shaik, H. K. Kisan and K. D. Dubey, ACS Catal., 2020, 10, 11481–11492 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- D. Bakowies and W. Thiel, J. Phys. Chem., 1996, 100, 10580–10594 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- D. Usharani, D. Janardanan and S. Shaik, J. Am. Chem. Soc., 2011, 133, 176–179 CrossRef CAS PubMed.
- D. A. Sharon, D. Mallick, B. Wang and S. Shaik, J. Am. Chem. Soc., 2016, 138, 9597–9610 CrossRef CAS PubMed.
- Y. Moreau, H. Chen, E. Derat, H. Hirao, C. Bolm and S. Shaik, J. Phys. Chem. B, 2007, 111, 10288–10299 CrossRef CAS PubMed.
- J. Wang, H. Gao, L. Yang and Y. Q. Gao, ACS Catal., 2020, 10, 5318–5327 CrossRef CAS.
- K. Chen, S. Q. Zhang, O. F. Brandenberg, X. Hong and F. H. Arnold, J. Am. Chem. Soc., 2018, 140, 16402–16407 CrossRef CAS PubMed.
- Y. Yang, I. Cho, X. Qi, P. Liu and F. H. Arnold, Nat. Chem., 2019, 11, 987–993 CrossRef CAS PubMed.
- Z. Li, D. J. Burnell and R. J. Boyd, J. Phys. Chem. B, 2017, 121, 10859–10868 CrossRef CAS PubMed.
- X. Li, L. Dong and Y. Liu, Inorg. Chem., 2020, 59, 1622–1632 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc03489h |
| This journal is © The Royal Society of Chemistry 2021 |