Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Why halides enhance heterogeneous metal ion charge transfer reactions†
Jacob
Florian
 ab,
Harsh
Agarwal
ab,
Harsh
Agarwal
 ab,
Nirala
Singh
ab,
Nirala
Singh
 *ab and
Bryan R.
Goldsmith
*ab and
Bryan R.
Goldsmith
 *ab
*ab
aDepartment of Chemical Engineering, University of Michigan, Ann Arbor, Michigan 48109-2136, USA. E-mail: bgoldsm@umich.edu; snirala@umich.edu
bCatalysis Science and Technology Institute, University of Michigan, Ann Arbor, Michigan 48109-2136, USA
First published on 26th August 2021
Abstract
The reaction kinetics of many metal redox couples on electrode surfaces are enhanced in the presence of halides (i.e., Cl−, Br−, I−). Using first-principles metadynamics simulations, we show a correlation between calculated desorption barriers of V3+–anion complexes bound to graphite via an inner-sphere anion bridge and experimental V2+/V3+ kinetic measurements on edge plane pyrolytic graphite in H2SO4, HCl, and HI. We extend this analysis to V2+/V3+, Cr2+/Cr3+, and Cd0/Cd2+ reactions on a mercury electrode and demonstrate that reported kinetics in acidic electrolytes for these redox couples also correlate with the predicted desorption barriers of metal–anion complexes. Therefore, the desorption barrier of the metal–anion surface intermediate is a descriptor of kinetics for many metal redox couple/electrode combinations in the presence of halides. Knowledge of the metal–anion surface intermediates can guide the design of electrolytes and electrocatalysts with faster kinetics for redox reactions of relevance to energy and environmental applications.
Introduction
Electrochemical charge transfer of metal ions has applications in energy storage,1 wastewater remediation,2 organic synthesis,3 and chemical production.4 Understanding and controlling charge transfer at the electrode surface would increase energy efficiency and product selectivity, and reduce capital cost of devices. Interestingly, halides accelerate the kinetics of many electrochemical reactions in aqueous solution, Fig. 1. For example, heterogeneous charge transfer reactions including V2+/V3+,5,6 Cr2+/Cr3+,7,8 Fe2+/Fe3+,9,10 and Eu2+/Eu3+,11 and metal electrodeposition reactions, such as Cd0/Cd2+ and Zn0/Zn2+,12,13 show rate constants (k) that are up to 103 higher in the presence of chloride (Cl−), bromide (Br−), or iodide (I−). Kinetic enhancement by halides is observed on many electrodes, including glassy carbon (GC),14 Hg,15 Au,7,10 and Pt,9,16 where the increase in k typically is the largest for I−, followed by Br−, and then Cl−. Thus, understanding the cause of these enhancements would guide electrolyte and electrode selection.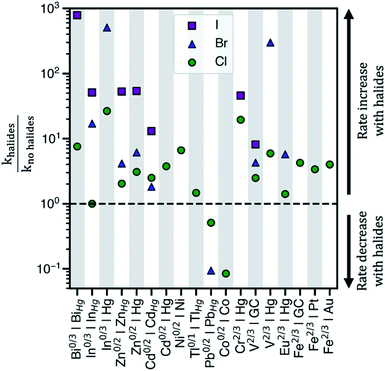 | ||
| Fig. 1 The observed ratios of rate constants with and without halides for various redox couples and electrodes in aqueous electrolytes. khalides corresponds to the rate constant in the presence of halides, whereas kno halides corresponds to the rate constant in sulfate or perchlorate electrolytes. The abscissa shows ‘redox couple|electrode surface’ combinations where rate data has been reported. The halides present in the electrolytes considered are either chloride, bromide, or iodide. GC = glassy carbon electrode and MHg = metal–Hg amalgam alloy electrode. Table S1 in the ESI† contains the standard rate constants for these redox couples. | ||
Halide-induced rate enhancements may arise from the halide ions being adsorbed on electrodes to serve as sites for adsorption and charge transfer of metal ions. This mechanism, whereby the halide anion adsorbed on the electrode acts as a bridge in the electron transfer between metal ion and electrode, has been called anion bridging.15 The anion bridging mechanism has been invoked to explain rate enhancements for Cr2+/Cr3+, V2+/V3+, Sb3+/Sb5+, and Fe2+/Fe3+ redox couples.10,14,15,17,18 A two-step inner-sphere mechanism for how an adsorbed anion (*X) promotes oxidation of a metal ion (Mn+) through the formation of an adsorbed metal–anion intermediate (*XMn+1) is written in eqn (1) and (2). Although here we write Mn+1 as the product leaving behind *X, it is also possible that the halide becomes part of the desorbed complex as XMn+1.
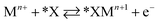 | (1) |
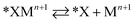 | (2) |
Although this mechanism is plausible, there is little knowledge of how the metal ion and the bridging anion together promote charge transfer and why the rate enhancement relative to non-complexing electrolytes (i.e., through *OH bridge) typically follows the order of Cl− < Br− < I−. This order of rate enhancement correlates with increasing free anion polarizability,19,20 that is, polarizable anions can more easily transfer one of their outer shell electrons to the metal cation while the other electron is being transferred from the electrode surface to the anion bridge. However, free anion polarizability does not account for the electrode and redox couple identity. Interfacial potential shifts due to anion adsorption can also increase the rate of metal ion redox couples, as has been reported previously.21 However, some studies have found that electrostatic effects alone are insufficient to explain the large increases (khalide/kno halides > 10) in the observed rate constants and postulated that anion bridging may be responsible.8,10,15,18
Herein, we test our hypothesis that anion bridging on electrodes increases the kinetics for many metal redox couples by changing the energy of the surface intermediate (*XMn+1) and its adsorption and desorption barriers. The energy of *XMn+1 controls the fraction of active sites that the intermediate occupies and the apparent activation barriers for the redox reaction. In Scheme 1a we show an energy diagram of a metal ion charge transfer reaction involving the adsorbed intermediate written in eqn (1) and (2). We assume that electron transfer is fast so that it occurs concurrently with either adsorption or desorption. This assumption is consistent with observations that rate enhancements arise from changes in the barrier associated with the formation of adsorbed complexes as opposed to the intrinsic barrier for electron transfer.15,17 At equilibrium, the reduced and oxidized species are the same energy, and the forward and reverse rates are equal and opposite. The magnitude of these rates is proportional to the experimental rate constant (k) and exchange current density (io).
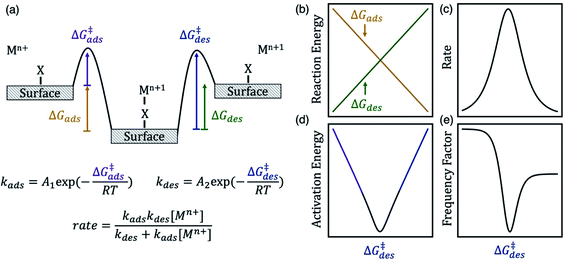 | ||
| Scheme 1 (a) Energy diagram of a metal ion charge transfer reaction involving an adsorbed intermediate. The desorption free energy barrier (ΔG‡des) of the metal–anion surface intermediate can be a descriptor for kinetics of a Mn+/Mn+1 redox couple. The diagrams on the right show the dependence of (b) reaction energy, (c) rate (proportional to exchange current density and observed rate constant), (d) apparent activation energy, and (e) apparent frequency factor on ΔG‡des, assuming Brønsted–Evans–Polanyi scaling relations hold. The rate law derivation is included in the ESI.† Here kads has units of s−1, kdes has units of mol L−1 s−1, and overall rate has units of mol L−1 s−1. | ||
The energy of the surface intermediate should correlate with the ease at which the intermediate desorbs from the surface, thus we hypothesize the desorption free energy barrier (ΔG‡des) is a descriptor for redox kinetics. For chemically similar surface reactions, the activation barrier of an elementary step is often linearly correlated to the reaction energy of that step, referred to as a Brønsted–Evans–Polanyi (BEP) relation.22 Therefore, the adsorption barrier (ΔG‡ads) linearly correlates with the adsorption energy (ΔGads) and the desorption barrier (ΔG‡des) linearly correlates with the desorption energy (ΔGdes) if a BEP relation holds. If true, ΔG‡des positively correlates with ΔGdes and negatively correlates with ΔGads (Scheme 1b). The oxidation rate is a function of the concentration of the reduced species ([Mn+]) and the rate constants for adsorption (kads) and desorption (kdes) on the surface (derivation in ESI†). Adsorption is rate-limiting at low values of ΔG‡des, whereas desorption is rate-limiting at high values of ΔG‡des, thus the rate is maximized at intermediate ΔG‡des values at the top of the volcano curve in Scheme 1c.23 The rate has contributions from the apparent, or experimentally observed activation energy and frequency factor. The apparent activation energy (Scheme 1d) correlates with ΔG‡ads (ΔG‡des) when ΔG‡des is low (high). Similarly, neglecting entropic changes, the apparent frequency factor (Scheme 1e) approaches the frequency factor for the adsorption step, A1 (desorption step, A2) at low (high) values of ΔG‡des.
We establish a relationship between desorption free energy barriers of metal–anion complexes and the kinetics of various redox reactions that rationalizes the enhancement by halides following the model discussed in Scheme 1. If BEP relations exist, any of the free energies in Scheme 1 could be calculated, but here we focus on ΔG‡des due to work showing its relevance to metal ion redox kinetics24 and because it can be relatively straightforwardly computed. Using density functional theory (DFT)-based metadynamics simulations, we predict ΔG‡des of V3+–anion complexes on the graphite edge plane (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) [graphite(11
0) [graphite(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0)] and compare to our V2+/V3+ kinetic measurements on edge plane pyrolytic graphite (EPPG) in H2SO4 and hydrohalic acids. We evaluate V2+/V3+ experimental exchange current densities (io), apparent frequency factors, and apparent activation energies (Ea) on EPPG in sulfuric (H2SO4), hydrochloric (HCl), and hydriodic (HI) acids, and show that these parameters correlate with the predicted desorption barriers. Desorption barriers of V3+–, Cr3+–, and Cd2+–anion complexes are also calculated on a model mercury Hg(111) electrode to examine whether ΔG‡des correlates with rate constants across different redox couples and electrodes. These metal ions are chosen because of the availability of experimental rate data displaying an increase in activity in the presence of halides (Fig. 1).
0)] and compare to our V2+/V3+ kinetic measurements on edge plane pyrolytic graphite (EPPG) in H2SO4 and hydrohalic acids. We evaluate V2+/V3+ experimental exchange current densities (io), apparent frequency factors, and apparent activation energies (Ea) on EPPG in sulfuric (H2SO4), hydrochloric (HCl), and hydriodic (HI) acids, and show that these parameters correlate with the predicted desorption barriers. Desorption barriers of V3+–, Cr3+–, and Cd2+–anion complexes are also calculated on a model mercury Hg(111) electrode to examine whether ΔG‡des correlates with rate constants across different redox couples and electrodes. These metal ions are chosen because of the availability of experimental rate data displaying an increase in activity in the presence of halides (Fig. 1).
Our results show that desorption barriers of metal–anion complexes on model surfaces correlate with rate constants on polycrystalline electrodes, but inner-sphere electron transfer rates and adsorption of anions are also dependent on the surface structure of the electrode.25 When rates of Fe2+/Fe3+ electron transfer on different facets of Pt26 and Au27 were examined in non-complexing perchloric acid, the rates correlated with the potential of zero charge (PZC) of the different facets. This finding suggests that the dependence of the rate constant on the local electrode structure comes, at least in part, from variations in the PZC, which affect the structure of the double layer. When Fe2+/Fe3+ kinetics were measured in sulfuric acid, which is reported to follow an inner-sphere mechanism,28 a 30-fold increase in activity was observed at the grain boundaries of a polycrystalline Pt electrode compared to on the grains themselves.26 Clearly, the rates for heterogeneous charge transfer reactions are not uniform on a polycrystalline electrode, and corresponding desorption barriers of metal–anion complexes on different facets are likely to change. Although we limit our calculation of desorption barriers to a single facet for different electrodes, we elucidate qualitative trends by correlating desorption barriers of predicted metal–anion surface intermediates to experimental kinetic data on a given electrode surface. Our findings show that desorption barriers of metal–anion surface intermediates are descriptors for redox couple activity across a constant electrode surface and support the hypothesis that halides increase the activity of redox couples by changing the energy and transition states of the adsorbed intermediate.
Results and discussion
V2+/V3+ on graphite edge plane
We study the V2+/V3+ reaction because its solution-phase structure is known in various electrolytes, and a prior study showed that the desorption barrier of the V3+ intermediate in non-complexing solution can be related to redox kinetics.24 In HCl, HBr, and HI, V3+ complexes with halides to form [V(H2O)5X]2+ (X = Cl, Br, or I).5,14 V3+ exists predominantly as [V(H2O)5SO4]+ in H2SO4.5,14 V2+ prefers to form [V(H2O)6]2+ in all the considered electrolytes (i.e., HCl, HBr, HI, and H2SO4).5,29 A metadynamics study predicted the adsorption and desorption barriers of [V(H2O)6]2+ and [V(H2O)6]3+ through an oxygen bridge on graphite(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) and found that [V(H2O)6]3+ desorption had a larger barrier and was rate limiting.24 Thus, a lower desorption barrier for the V3+-complex should result in faster kinetics.
0) and found that [V(H2O)6]3+ desorption had a larger barrier and was rate limiting.24 Thus, a lower desorption barrier for the V3+-complex should result in faster kinetics.
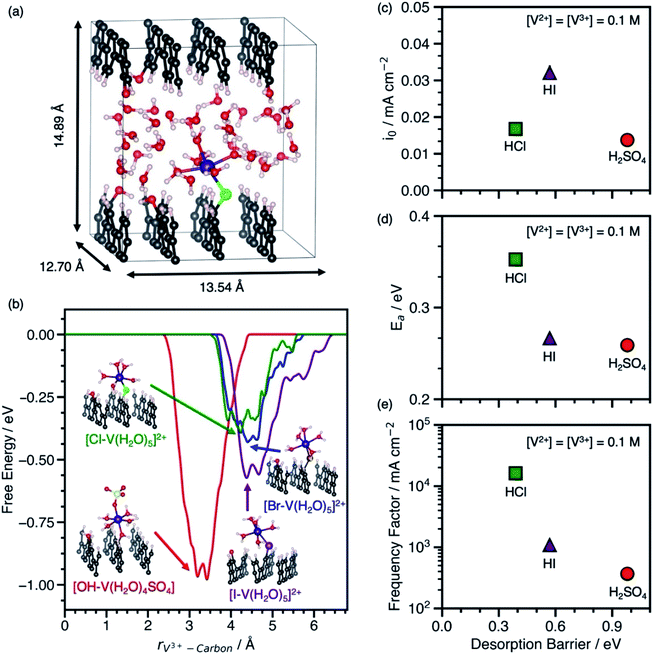
Our predicted desorption barriers of V3+–anion complexes on graphite(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) and experimental kinetic parameters of V2+/V3+ on EPPG in H2SO4, HCl, and HI are shown in Fig. 2. The cell and graphite(11
0) and experimental kinetic parameters of V2+/V3+ on EPPG in H2SO4, HCl, and HI are shown in Fig. 2. The cell and graphite(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) model used in metadynamics simulations to predict ΔG‡des are shown in Fig. 2a. The EPPG used in experiments consists of multiple parallel edge facets, which resembles graphite(11
0) model used in metadynamics simulations to predict ΔG‡des are shown in Fig. 2a. The EPPG used in experiments consists of multiple parallel edge facets, which resembles graphite(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0). The kinetic measurements are conducted at various V2+ and V3+ concentrations using a rotating disk electrode setup to prevent mass transfer limitations. The change in Ea at various V2+ and V3+ concentrations in each electrolyte (Fig. S5 and S6†) indicates that the V2+/V3+ charge transfer is an inner-sphere reaction that involves an adsorbed intermediate, as opposed to an outer-sphere reaction where Ea is independent of vanadium concentration. This dependence of apparent activation energy on vanadium concentrations arises because of the dependence of coverage on temperature, which causes the apparent activation energy to include contributions both from the rate constant and enthalpies of adsorption/desorption steps.14 The full set of kinetic measurements are provided in Fig. S1–S6, Scheme S1, and Tables S2–S4 and discussed in the ESI.†
0). The kinetic measurements are conducted at various V2+ and V3+ concentrations using a rotating disk electrode setup to prevent mass transfer limitations. The change in Ea at various V2+ and V3+ concentrations in each electrolyte (Fig. S5 and S6†) indicates that the V2+/V3+ charge transfer is an inner-sphere reaction that involves an adsorbed intermediate, as opposed to an outer-sphere reaction where Ea is independent of vanadium concentration. This dependence of apparent activation energy on vanadium concentrations arises because of the dependence of coverage on temperature, which causes the apparent activation energy to include contributions both from the rate constant and enthalpies of adsorption/desorption steps.14 The full set of kinetic measurements are provided in Fig. S1–S6, Scheme S1, and Tables S2–S4 and discussed in the ESI.†
The adsorbed [*X–V(H2O)5] (where X = Cl, Br, or I) and [*OH–V(H2O)4SO4] were used as models for the adsorbed metal–anion complex in hydrohalic acids and H2SO4, because they preserve the V3+ structure in solution and are adsorbed through an anion bridge. The [*OH–V(H2O)4SO4] complex is modeled through an *OH bridge, because *SO4 is unstable on carbon surfaces.14Fig. 2b shows the desorption free energy profiles of V3+–anion complexes from graphite(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) based on metadynamics simulations using spin-polarized DFT with the PBE functional. To calculate ΔG‡des, the distance between the metal ion and the surface was biased until the complex desorbs. Desorption barriers through halide bridges are lower than through an *OH bridge on graphite(11
0) based on metadynamics simulations using spin-polarized DFT with the PBE functional. To calculate ΔG‡des, the distance between the metal ion and the surface was biased until the complex desorbs. Desorption barriers through halide bridges are lower than through an *OH bridge on graphite(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) in the order *OH > *I > *Br > *Cl. Snapshots of desorbed metal–anion complexes are shown in Fig. S7.† Additional DFT and metadynamics modeling details are given in the ESI (Fig. S8–S10 and Table S5†).
0) in the order *OH > *I > *Br > *Cl. Snapshots of desorbed metal–anion complexes are shown in Fig. S7.† Additional DFT and metadynamics modeling details are given in the ESI (Fig. S8–S10 and Table S5†).
The behavior between the measured io in each electrolyte and ΔG‡des of the V3+–anion complexes in Fig. 2c matches the volcano-like relationship in Scheme 1c. V3+ adsorbs too strongly in H2SO4 such that desorption is rate-limiting, and as ΔG‡des decreases due to weaker V3+ adsorption in HI, the rate begins to increase. However, once ΔG‡des is too low, the adsorption of species become rate-limiting as suggested by rate measurements in HCl. The io has contributions from both Ea and the apparent frequency factor, which are shown in Fig. 2d and e. The data in Fig. 2d resembles the inverse volcano in Scheme 1d with a hypothetical minimum between [*I–V(H2O)5]2+ in HI and [*OH–V(H2O)4SO4] in H2SO4. Assuming BEP relations hold, the ideal desorption barrier with the lowest Ea will be located at that minimum. Despite having the lowest measured Ea among the electrolytes studied, the V2+/V3+ exchange current density is lowest in H2SO4 because it has a low frequency factor, as shown in Fig. 2e. Using this as a model, we predict that the io, Ea, and apparent frequency factor of V2+/V3+ in HBr will be between that in HCl and HI, because the desorption barrier of [*Br–V(H2O)5]2+ is between [*Cl–V(H2O)5]2+ and [*I–V(H2O)5]2+. We also find that the Ea observed on EPPG in the presence of halides does not correlate with increasing free anion polarizability. This finding highlights the importance of understanding the surface intermediate structure and that using anion physicochemical properties alone are insufficient to explain the observed kinetic behavior.
V2+/V3+, Cr2+/Cr3+, and Cd0/Cd2+ on mercury
To assess the transferability of the desorption barrier as a descriptor, we compare the ΔG‡des of V3+–, Cr3+–, and Cd2+–anion complexes on a mercury (Hg) electrode to standard rate constants in sulfuric and hydrohalic acids. Mercury is the most widely reported electrode for anion-promoted electrocatalysis of metal redox couples with several experimental rate constants available in the literature (Table S1†). Anion-promoted electrocatalysis has also been reported on surfaces such as Au, Pt, and carbon, but data is sparse and often consists of only one or two redox couple/electrolyte combinations. We predict the desorption barriers of V3+–, Cr3+–, and Cd2+–anion complexes on a Hg(111) electrode through halide and hydroxyl bridges, Fig. 3. Hg(111) is often used as a model surface (Fig. S8†) for mercury electrodes to study qualitative trends.30–33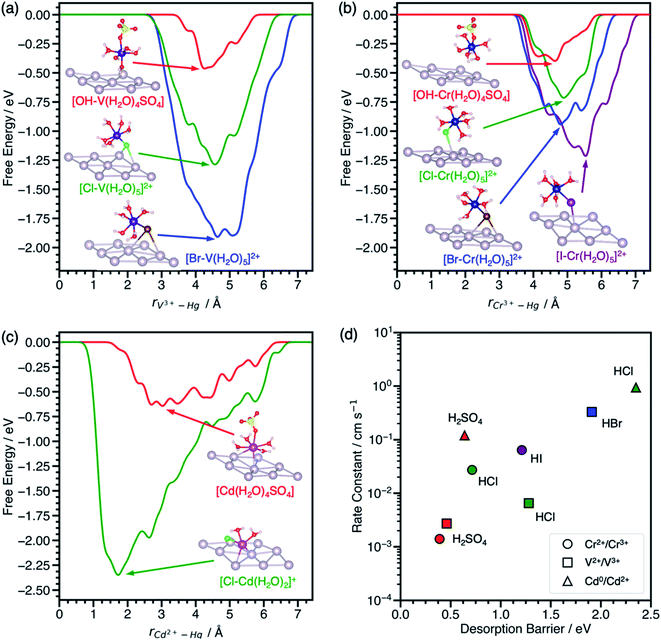 | ||
| Fig. 3 Metadynamics-based free energy profiles for desorption of (a) V3+–, (b) Cr3+–, and (c) Cd2+–anion complexes from Hg(111) through an *OH, *Cl, *Br, or *I bridge at 300 K. Snapshots of the adsorbed metal–anion complexes are shown at the free energy minima. (d) Experimental standard rate constants of the metal charge transfer reactions on mercury drop electrodes plotted against the corresponding predicted desorption barriers from (a–c). Colors denote the acid, namely H2SO4 (red), HCl (green), HBr (blue), and HI (purple). Rate constants for these reactions were reproduced from ref. 11, 12 and 41. Atom color legend: Hg = gray, V = dark purple, Cr = blue, Cd = pink, O = red, S = yellow, H = white, Cl = green, Br = dark brown, I = purple. | ||
The effect of halides on the desorption barrier for V3+ complexes on Hg(111) are different than on graphite(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0). In the case of V3+ desorption on Hg(111) (Fig. 3a), [*Br–V(H2O)5]2+ has a desorption barrier of 1.91 eV, followed by [*Cl–V(H2O)5]2+ at 1.28 eV, and [*OH–V(H2O)4SO4] at 0.46 eV. This trend for V3+ complexes on Hg(111) is opposite to that of graphite(11
0). In the case of V3+ desorption on Hg(111) (Fig. 3a), [*Br–V(H2O)5]2+ has a desorption barrier of 1.91 eV, followed by [*Cl–V(H2O)5]2+ at 1.28 eV, and [*OH–V(H2O)4SO4] at 0.46 eV. This trend for V3+ complexes on Hg(111) is opposite to that of graphite(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0), where ΔG‡des is largest in sulfate electrolytes. This change in trends of desorption barriers for the same redox couple must arise due to the difference in nature of the interaction of the intermediate with Hg(111) and graphite(11
0), where ΔG‡des is largest in sulfate electrolytes. This change in trends of desorption barriers for the same redox couple must arise due to the difference in nature of the interaction of the intermediate with Hg(111) and graphite(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0). Hg, being noble, has chemisorption that is dominated by Pauli repulsion (especially for electronegative adsorbates such as halides), while chemisorption on graphite is dominated by covalent interactions.34 Generally, ΔG‡des is much larger on Hg(111) than graphite(11
0). Hg, being noble, has chemisorption that is dominated by Pauli repulsion (especially for electronegative adsorbates such as halides), while chemisorption on graphite is dominated by covalent interactions.34 Generally, ΔG‡des is much larger on Hg(111) than graphite(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0).
0).
Cr3+ complexes with anions in its first solvation sphere, and charge transfer is predicted to take place through a Cr3+–anion bridge on Hg.15,35 We predict that Cr3+ behaves similarly to V3+ on Hg(111), where halides increase the ΔG‡des relative to sulfate in the same order (*OH < *Cl < *Br < *I), Fig. 3b. The [*OH–Cr(H2O)4SO4] complex only physisorbs on the surface, consistent with experiments suggesting that Cr2+/Cr3+ charge transfer is outer sphere in the presence of sulfate on Hg electrodes.8
We also model the desorption of Cd2+ on Hg(111), but only in H2SO4 and HCl, where rate data for Cd0/Cd2+ is available.12 Cd2+–anion complexes have been proposed as the adsorbing species on Hg electrodes in hydrohalic acids.36,37 From Fig. 3c, the desorption barrier of the Cd2+–chloride complex is 2.35 eV, which is much higher than the Cd2+–sulfate complex at 0.64 eV. In the initial geometry, Cd2+ was coordinated with five water molecules and one chloride or sulfate ligand, consistent with a report that aqueous Cd2+ has a coordination number of six.38 During the simulation, Cd2+ adsorbed directly onto Hg(111) and formed a [*Cl–Cd(H2O)2]+ complex. After Cd2+ desorbed, the solvent waters were reincorporated into the first solvation sphere to form the [Cd(H2O)5Cl]+ complex. The desorption barriers of Cd2+ complexes are higher than V3+ and Cr3+ complexes in the same electrolyte.
The desorption barriers of V3+, Cr3+, and Cd2+ on Hg(111) show a positive correlation with previously measured standard rate constants of the V2+/V3+, Cr2+/Cr3+, and Cd0/Cd2+ reactions on mercury drop electrodes in Fig. 3d. Although Cd0/Cd2+ metal electrodeposition is expected to follow a different reaction mechanism than the inner-sphere charge transfer of aqueous ions, the correlation still holds. This may occur because the first electron transfer step (i.e., Cd+/Cd2+) is slower than the solid metal formation (i.e., Cd0/Cd+), making the kinetic trends more closely resemble that of aqueous charge transfer.39,40 This positive correlation between desorption barrier and rate constant suggests that these points are on the left side of the volcano curve in Scheme 1c where adsorption is rate limiting and not around the maximum like V2+/V3+ on EPPG. For a given redox couple in Fig. 3d, the rate constant and desorption barriers increase going from H2SO4 (*OH bridge) < HCl (*Cl bridge) < HBr (*Br bridge) < HI (*I bridge). This observation suggests that the more polarizable halides decrease the energy of the active metal–anion intermediate on Hg, thus increasing surface coverage and leading to higher reaction rates. Unlike V2+/V3+ on EPPG, we do not have experimental apparent activation energies for a more detailed comparison of kinetics on Hg electrodes. We hypothesize that activation energies for V2+/V3+, Cr2+/Cr3+, and Cd0/Cd2+ on Hg will negatively correlate with the desorption barrier and the rate constant.
We also compute desorption barriers of Fe2+/Fe3+ on Au(111) through *OH, *Cl and *Br bridges (Fig. S11†). Qualitative enhancements in rate constants have been reported for Fe2+/Fe3+ on gold with increasing concentrations of Cl− and Br− compared to H2SO4.10 The desorption barriers for the [OH–Fe(H2O)4SO4], [Cl–Fe(H2O)5]2+, and [Br–Fe(H2O)5]2+ complexes are predicted to be 0.82, 0.67, and 0.55 eV, respectively, on Au(111). Thus, the rate enhancements in the presence of chloride and bromide may arise due to decreasing the desorption barrier. However, because the reports of enhancements with halides for Fe2+/Fe3+ on Au(111) are only qualitative, we are unable to obtain quantitative correlations.
The desorption barrier of the electroactive species is a new way to rationalize and predict rate enhancement by halides for inner-sphere aqueous metal ion charge transfer reactions. However, we stress that the desorption barrier is only a valid descriptor among inner-sphere reactions on chemically similar surfaces. When examined together, the rate constants for V2+/V3+ on Hg(111) and graphite(11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) in hydrohalic electrolytes do not correlate in the same way with ΔG‡des (Fig. S12†). The inability of ΔG‡des to describe kinetics across different electrodes for a given redox couple can arise due to three major factors: (1) reactions on different surfaces do not necessarily obey the same BEP relations, (2) discrepancies exist between the modeled surface and the actual electrode active site, and (3) different mechanisms occur on different electrodes. By comparing desorption barriers of different metal–anion complexes on the same surface, these factors will be similar and qualitative insights can be gained. Different mechanisms and explanations for anion enhancements may also be valid. Theories have been developed for how electrostatics can be used to explain outer-sphere electron transfer,42 and how electrode modification can be used to enhance rates by changing the potential of zero charge.43,44 Rate enhancements can also arise from a change in mechanism from outer-sphere to inner-sphere, as is reported to occur for Cr2+/Cr3+ when halides are added to the electrolyte.8 The applicability of using ΔG‡des as a descriptor for kinetics of the same redox couple on multiple surfaces could be tested by conducting kinetic measurements for a fixed redox couple on chemically similar surfaces such as metal electrodes. Fig. S12,† shows a possible correlation between the desorption barriers for V3+ on two noble metals (Au and Hg) and V2+/V3+ rate constants, but more data is needed for a conclusive analysis. Future work should examine how changes in the desorption barrier on different crystal facets compare to the experimental rate constants on the corresponding single crystal electrodes, which may improve predicted volcano relations and give deeper insight into the structure-sensitivity of inner-sphere metal ion charge transfer.
0) in hydrohalic electrolytes do not correlate in the same way with ΔG‡des (Fig. S12†). The inability of ΔG‡des to describe kinetics across different electrodes for a given redox couple can arise due to three major factors: (1) reactions on different surfaces do not necessarily obey the same BEP relations, (2) discrepancies exist between the modeled surface and the actual electrode active site, and (3) different mechanisms occur on different electrodes. By comparing desorption barriers of different metal–anion complexes on the same surface, these factors will be similar and qualitative insights can be gained. Different mechanisms and explanations for anion enhancements may also be valid. Theories have been developed for how electrostatics can be used to explain outer-sphere electron transfer,42 and how electrode modification can be used to enhance rates by changing the potential of zero charge.43,44 Rate enhancements can also arise from a change in mechanism from outer-sphere to inner-sphere, as is reported to occur for Cr2+/Cr3+ when halides are added to the electrolyte.8 The applicability of using ΔG‡des as a descriptor for kinetics of the same redox couple on multiple surfaces could be tested by conducting kinetic measurements for a fixed redox couple on chemically similar surfaces such as metal electrodes. Fig. S12,† shows a possible correlation between the desorption barriers for V3+ on two noble metals (Au and Hg) and V2+/V3+ rate constants, but more data is needed for a conclusive analysis. Future work should examine how changes in the desorption barrier on different crystal facets compare to the experimental rate constants on the corresponding single crystal electrodes, which may improve predicted volcano relations and give deeper insight into the structure-sensitivity of inner-sphere metal ion charge transfer.
Conclusions
This work demonstrates the role of halides in promoting inner-sphere heterogeneous metal charge transfer by changing the transition state energies and energy of the metal–anion surface intermediate. Experimental kinetic measurements combined with metadynamics simulations show that halide bridges increase kinetics of the V2+/V3+ redox couple on EPPG by decreasing the desorption barrier of the adsorbed V3+–anion complex, until an optimum is reached. For V2+/V3+, Cr2+/Cr3+, and Cd0/Cd2+ on Hg, desorption is not rate limiting and halides stabilize the metal ion on the Hg surface, thus increasing surface coverage and promoting the reaction rate. When BEP relations hold for chemically similar reactions, desorption barriers correlate with redox kinetics. This knowledge can guide anion bridge design so reactive intermediates adsorb on electrodes with optimal strength. Because the charge transfer kinetics of many metal ion redox couples are increased in the presence of halides, these findings apply broadly and highlight the importance of understanding the combined role of the redox couple, electrode, and electrolyte when engineering electrochemical systems.Data availability
Data for this paper, including VASP output files and geometries, are available at the NOMAD Repository at https://dx.doi.org/10.17172/NOMAD/2021.07.03-1.Author contributions
B. R. G. and N. S. conceived the project. J. F. performed all the molecular simulations and DFT modeling under the guidance of B. R. G. H. A. carried out all electrochemical measurements and data analysis under the guidance of N. S. All authors were involved in analysis and writing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by the University of Michigan Office of Research Grant (UMOR-29814), as well as assistant professor start-up funds provided by the Goldsmith and Singh Labs. This research used the resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231. This work also used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562.References
- E. Sánchez-Díez, E. Ventosa, M. Guarnieri, A. Trovò, C. Flox, R. Marcilla, F. Soavi, P. Mazur, E. Aranzabe and R. Ferret, J. Power Sources, 2021, 481, 228804 CrossRef
.
- P. Srimuk, X. Su, J. Yoon, D. Aurbach and V. Presser, Nat. Rev. Mater., 2020, 5, 517–538 CrossRef CAS
.
- S. Möhle, M. Zirbes, E. Rodrigo, T. Gieshoff, A. Wiebe and S. R. Waldvogel, Angew. Chem., Int. Ed., 2018, 57, 6018–6041 CrossRef PubMed
.
- M. J. Orella, Y. Román-Leshkov and F. R. Brushett, Curr. Opin. Chem. Eng., 2018, 20, 159–167 CrossRef
.
- H. Agarwal, J. Florian, B. R. Goldsmith and N. Singh, ACS Energy Lett., 2019, 4, 2368–2377 CrossRef CAS
.
- M. Park, I. Y. Jeon, J. Ryu, H. Jang, J. B. Back and J. Cho, Nano Energy, 2016, 26, 233–240 CrossRef CAS
.
- A. Rodes, J. M. Feliu, A. Aldaz and J. Clavilier, J. Electroanal. Chem., 1989, 271, 127–139 CrossRef CAS
.
- M. Weaver and F. Anson, Inorg. Chem., 1976, 15, 1871–1881 CrossRef CAS
.
- D. C. Johnson and E. W. Resnlck, Anal. Chem., 1977, 49, 1918–1924 CrossRef CAS
.
- J. Weber, Z. Samec and V. Mareček, J. Electroanal. Chem., 1978, 89, 271–288 CrossRef CAS
.
- K. Niki and H. Mizota, J. Electroanal. Chem., 1976, 72, 307–317 CrossRef CAS
.
- J. K. Frischmann and A. Timnick, Anal. Chem., 1967, 39, 507–511 CrossRef CAS
.
- E. Eriksrud, J. Electroanal. Chem., 1977, 76, 27–49 CrossRef CAS
.
- H. Agarwal, J. Florian, B. Goldsmith and N. Singh, Cell Rep. Phys. Sci., 2021, 2, 100307 CrossRef CAS
.
- R. de Levie, J. Electrochem. Soc., 1971, 118, 185–192 CrossRef
.
- R. J. Davenport and D. C. Johnson, Anal. Chem., 1973, 45, 1755–1756 CrossRef CAS
.
- M. J. Weaver, Isr. J. Chem., 1979, 18, 35–44 CrossRef CAS
.
- L. R. Taylor, B. A. Parkinson and D. C. Johnson, Electrochim. Acta, 1975, 20, 1005–1009 CrossRef CAS
.
- A. G. Sykes, Adv. Inorg. Chem. Radiochem., 1968, 10, 153–245 CrossRef
.
- J. Heyrovsky, Discuss. Faraday Soc., 1947, 1, 212–225 RSC
.
- M. J. Weaver and F. C. Anson, J. Electroanal. Chem., 1975, 65, 737–758 CrossRef CAS
.
- T. Bligaard, J. K. Nørskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, J. Catal., 2004, 224, 206–217 CrossRef CAS
.
-
J. K. Norskov, F. Studt, F. Ablid-Pederson and T. Bligaard, Fundamental Concepts in Heterogeneous Catalysis, John Wiley & Sons, Hoboken, New Jersey, 2014 Search PubMed
.
- Z. Jiang, K. Klyukin and V. Alexandrov, Phys. Chem. Chem. Phys., 2017, 19, 14897–14901 RSC
.
- Y. B. Vogel, J. Zhang, N. Darwish and S. Ciampi, ACS Nano, 2018, 12, 8071–8080 CrossRef CAS PubMed
.
- B. D. B. Aaronson, C. H. Chen, H. Li, M. T. M. Koper, S. C. S. Lai and P. R. Unwin, J. Am. Chem. Soc., 2013, 135, 3873–3880 CrossRef CAS PubMed
.
- M. Hromadová and W. R. Fawcett, J. Phys. Chem. A, 2001, 105, 104–111 CrossRef
.
- H. G. Bochmann and W. Vielstich, Electrochim. Acta, 1987, 33, 805–809 CrossRef
.
- F. J. Oldenburg, M. Bon, D. Perego, D. Polino, T. Laino, L. Gubler and T. J. Schmidt, Phys. Chem. Chem. Phys., 2018, 20, 23664–23673 RSC
.
- S. A. Wasileski and M. J. Weaver, J. Phys. Chem. B, 2002, 106, 4782–4788 CrossRef CAS
.
- D. I. Dimitrov and N. D. Raev, J. Electroanal. Chem., 2000, 486, 1–8 CrossRef CAS
.
- V. Ivaništšev, R. R. Nazmutdinov and E. Lust, Surf. Sci., 2013, 609, 91–99 CrossRef
.
- G. Toth, E. Spohr and K. Heinzinger, Chem. Phys., 1995, 200, 347–355 CrossRef CAS
.
- H. Xin and S. Linic, J. Chem. Phys., 2010, 132, 12–15 Search PubMed
.
- I. Dellien and L. G. Hepler, Can. J. Chem., 1976, 54, 1383–1387 CrossRef CAS
.
- F. C. Anson and D. J. Barclay, Anal. Chem., 1968, 40, 1791–1798 CrossRef CAS
.
- J. J. H. Ackerman, T. V. Orr, V. J. Bartuska and G. E. Maciel, J. Am. Chem. Soc., 1979, 101, 341–347 CrossRef CAS
.
- R. J. Frick, T. S. Hofer, A. B. Pribil, B. R. Randolf and B. M. Rode, Phys. Chem. Chem. Phys., 2010, 12, 11736–11743 RSC
.
- F. Van der Pol, M. Sluyters-Rehbach and J. H. Sluyters, J. Electroanal. Chem. Interfacial Electrochem., 1975, 58, 177–188 CrossRef CAS
.
- C. P. M. Bongenaar, A. G. Remijnse, M. Sluyters-Rehbach and J. H. Sluyters, J. Electroanal. Chem., 1980, 111, 139–153 CrossRef CAS
.
- J. Jones Ulrich and F. C. Anson, Inorg. Chem., 1969, 8, 195–200 CrossRef
.
- R. Kant, J. Kaur and G. K. Mishra, J. Phys. Chem. C, 2020, 124, 2273–2288 CrossRef CAS
.
- J. Kaur and R. Kant, J. Phys. Chem. C, 2017, 121, 13059–13069 CrossRef CAS
.
- J. Kaur and R. Kant, J. Phys. Chem. C, 2018, 122, 911–918 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc03642d |
| This journal is © The Royal Society of Chemistry 2021 |