Open Access Article
Open Access ArticleSelective crystallization via vibrational strong coupling†
Kenji
Hirai
 *abc,
Hiroto
Ishikawa
ac,
Thibault
Chervy
d,
James A.
Hutchison
*abc,
Hiroto
Ishikawa
ac,
Thibault
Chervy
d,
James A.
Hutchison
 e and
Hiroshi
Uji-i
*acfg
e and
Hiroshi
Uji-i
*acfg
aDivision of Photonics and Optical Science, Research Institute for Electronic Science (RIES), Hokkaido University, North 20 West 10, Kita Ward, Sapporo, Hokkaido, Japan. E-mail: hirai@es.hokudai.ac.jp
bPrecursory Research for Embryonic Science and Technology (PRESTO), Japan Science and Technology Agency (JST), 4-1-8 Honcho, Kawaguchi, Saitama, Japan
cDivision of Information Science and Technology, Graduate School of Information Science and Technology, Hokkaido University, North 14 West 9, Kita Ward, Sapporo, Hokkaido, Japan
dPhysics and Informatics Laboratories, NTT Research Inc., 940 Stewart Dr, Sunnyvale, CA 94085, USA
eSchool of Chemistry, The University of Melbourne, Masson Rd, Parkville VIC 3052, Melbourne, Australia
fDepartment of Chemistry, KU Leuven, Celestijnenlaan 200F, 3001 Heverlee, Leuven, Belgium
gInstitute for Integrated Cell–Material Science (WPI–iCeMS), Kyoto University, Yoshida Sakyo-ku, Kyoto 606-8501, Japan
First published on 10th August 2021
Abstract
The coupling of (photo)chemical processes to optical cavity vacuum fields is an emerging method for modulating molecular and material properties. Recent reports have shown that strong coupling of the vibrational modes of solvents to cavity vacuum fields can influence the chemical reaction kinetics of dissolved solutes. This suggests that vibrational strong coupling might also effect other important solution-based processes, such as crystallization from solution. Here we test this hitherto unexplored notion, investigating pseudopolymorphism in the crystallization from water of ZIF metal–organic frameworks inside optical microcavities. We find that ZIF-8 crystals are selectively obtained from solution inside optical microcavities, where the OH stretching vibration of water is strongly coupled to cavity vacuum fields, whereas mixtures of ZIF-8 and ZIF-L are obtained otherwise. Moreover, ZIF crystallization is accelerated by solvent vibrational strong coupling. This work suggests that cavity vacuum fields might become a tool for materials synthesis, biasing molecular self-assembly and driving macroscopic material outcomes.
Introduction
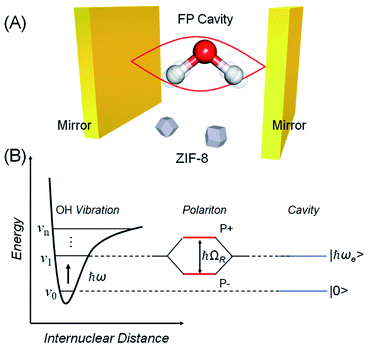
Over the last decade it has been realized that many chemical phenomena that can be modulated by intense optical fields in free space, can also be influenced by vacuum optical fields in confined cavities. The modulation of chemical reactivity by the strong coupling of molecular absorptions to cavity vacuum fields is a prominent example,1–4 thought to occur by the re-shaping of the reaction potential energy surface as occurs in ‘bond-softening’ using intense laser fields.5When, for example, the vibrational modes of molecules couple strongly to the optical modes of a Fabry–Perot (FP) cavity, new vibro-polaritonic states, denoted by P+ and P−, are formed and are separated at resonance by the vacuum Rabi splitting energy (ħΩR)6,7 (Fig. 1a and b). The extent of Rabi splitting is proportional to the number of molecules N in the cavity field as 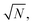 and proportional to the number of photons n in the cavity mode as
and proportional to the number of photons n in the cavity mode as 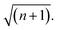 In the vacuum limit (n = 0), the interaction remains finite, occurring between the molecule and the zero-point energy of the cavity mode. Vibrational strong coupling (VSC) has been shown to effectively influence the kinetics of chemical reactions in a growing number of systems, attributed to a reordering of the energy landscape of the system that is the subject of much current experimental and theoretical investigation.8–14 VSC of solvent molecules can also alter the kinetics of organic reactions,10,15–17 most relevant here being the modification of enzyme kinetics by VSC of the OH stretch of water in the vacuum field regime.10,17 The latter results suggest that the nature of solvation can be changed under VSC, i.e. VSC could potentially be used to control many other solution-based processes including crystallization from solution and solubility-based purification (phase changes have also been shown to be modified by electronic strong coupling).18 Indeed, while impressive studies have demonstrated control of crystal nucleation and growth using high intensity beams, so-called ‘laser trapping crystallization’,19 crystallization under VSC of solvent molecules investigated here utilizes cavity vacuum fields and thus will rely on different mechanisms.
In the vacuum limit (n = 0), the interaction remains finite, occurring between the molecule and the zero-point energy of the cavity mode. Vibrational strong coupling (VSC) has been shown to effectively influence the kinetics of chemical reactions in a growing number of systems, attributed to a reordering of the energy landscape of the system that is the subject of much current experimental and theoretical investigation.8–14 VSC of solvent molecules can also alter the kinetics of organic reactions,10,15–17 most relevant here being the modification of enzyme kinetics by VSC of the OH stretch of water in the vacuum field regime.10,17 The latter results suggest that the nature of solvation can be changed under VSC, i.e. VSC could potentially be used to control many other solution-based processes including crystallization from solution and solubility-based purification (phase changes have also been shown to be modified by electronic strong coupling).18 Indeed, while impressive studies have demonstrated control of crystal nucleation and growth using high intensity beams, so-called ‘laser trapping crystallization’,19 crystallization under VSC of solvent molecules investigated here utilizes cavity vacuum fields and thus will rely on different mechanisms.
One of the key issues in crystallization is polymorphism: the same dissolved molecular components can assemble and precipitate in multiple crystalline phases. For example, the anti-inflammatory drug indomethacin gives three different crystal structures depending on the crystallization conditions.20 The medical efficacy of indomethacin depends on the crystal structure because the crystal structure significantly influences its solubility in the human body. Another example is the synthesis of metal–organic frameworks (MOFs).21–23 MOFs are porous crystalline materials that are of enormous interest for applications including gas adsorption, chemical sensing, and catalysis. However, it is sometimes found that the same combination of metal ions and organic ligands in solution yields MOFs with various crystal structures,24–26 causing heterogeneity in their porous properties that may compromise performance. In general, the selectivity of crystalline phases relies on the energy landscape connecting free dissolved components and crystals. Classical nucleation models input thermodynamic quantities such as the crystal surface and bulk free energies as a function of size to predict behaviour. Since VSC of (solvent) molecules has been shown to modify the energy levels of ground states and activated complexes,6 it might also be a new tool for selective crystallization.
These considerations inspired us to investigate the influence of VSC of solvent molecules on MOF crystallization. Zeolitic imidazolate frameworks (ZIFs) are a subfamily of MOFs.27 They consist of tetrahedral metal nodes interconnected by imidazolate derivatives. Self-assembly of Zn(II) and 2-methylimidazole (Hmeim) gives dimorphic structures, i.e., [Zn(meim)2]n (ZIF-8, Fig. S1†) and [Zn(meim)2(Hmeim)]n (ZIF-L, Fig. S1†).28–30 In principle, the ZIF-L and ZIF-8 forms constitute a pseudopolymorphism due to the difference in their chemical composition. The extent of this pseudopolymorphism is highly sensitive to experimental conditions and is therefore an excellent testing ground for the notion that cavity vacuum fields may influence crystallization processes. To demonstrate our idea, we show that ZIF crystallization inside optical cavities, and specifically under conditions of VSC of the solvent (water) to cavity vacuum fields, does indeed influence ZIF pseudopolymorphism. We find that ZIF-8 is selectively obtained inside the optical cavities, whereas mixtures of ZIF-8 and ZIF-L are obtained otherwise. Furthermore, the rate of ZIF crystallization is accelerated by VSC. These results suggest new avenues for addressing the challenge of crystal polymorphism and to our knowledge is the first example of cavity vacuum field interactions leading to macroscopic materials synthesis outcomes.
Results and discussion
Selective crystallization under vibrational strong coupling
Prior to performing experiments in a Fabry–Perot (FP) cavity, crystallization of ZIF in open solution under ambient conditions was conducted as a control. In brief, an aqueous solution of Zn(NO3)2 and 2-methylimidazole (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41.6 mole ratio) was left to stand at room temperature for 2 h. White powders were collected, centrifuged, and washed with ethanol to remove unreacted components. The powder was examined by scanning electron microscopy (SEM). A mixture of cuboctahedral crystals (ZIF-8) and flake-like crystals (ZIF-L) was obtained under these conditions (Fig. 2A). These morphologies are in very good agreement with previous reports on this well studied MOF system, in which ZIF-8 exhibits cuboctahedron or cubic structures and ZIF-L exhibits flake or crosshair-star structures (Fig. 2B).28–30 X-ray diffraction (XRD) further confirmed that the crystals were a mixture of ZIF-8 and ZIF-L (Fig. S2†). The ratio of ZIF-8 to ZIF-L was estimated to be 74
41.6 mole ratio) was left to stand at room temperature for 2 h. White powders were collected, centrifuged, and washed with ethanol to remove unreacted components. The powder was examined by scanning electron microscopy (SEM). A mixture of cuboctahedral crystals (ZIF-8) and flake-like crystals (ZIF-L) was obtained under these conditions (Fig. 2A). These morphologies are in very good agreement with previous reports on this well studied MOF system, in which ZIF-8 exhibits cuboctahedron or cubic structures and ZIF-L exhibits flake or crosshair-star structures (Fig. 2B).28–30 X-ray diffraction (XRD) further confirmed that the crystals were a mixture of ZIF-8 and ZIF-L (Fig. S2†). The ratio of ZIF-8 to ZIF-L was estimated to be 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 by physical counting of several hundred crystals with different morphologies.
26 by physical counting of several hundred crystals with different morphologies.
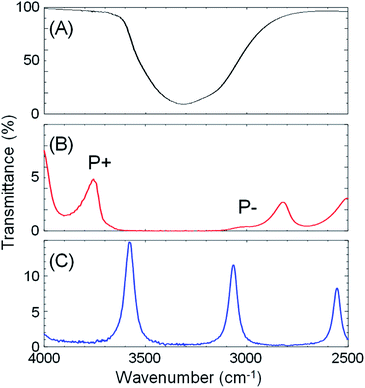
Next, optical cavities were constructed, within which the same crystallization could be undertaken under conditions of strong coupling of the solvent (water) OH stretching vibration to cavity vacuum fields. The OH stretching vibration was chosen as the target vibrational mode because of its strong absorbance. A FP cavity consisting of two parallel mirrors separated by a ca. 10 μm film spacer was prepared. The mirrors were fabricated by sputtering 10 nm Au on 2 mm ZnSe windows, followed by spin-coating of a ca. 100 nm polydimethylsiloxane (PDMS) film to isolate the metal from solutions (Fig. S3†). A transmission spectrum of the empty (air-filled) FP cavity is shown in Fig. 3C, blue curve, showing the progression of optical cavity modes. The energy of these transmission peaks when the cavity is filled with water, but in the absence of the OH stretch absorption at 3360 cm−1 (i.e. a flat background refractive index of 1.33) was simulated using the Transfer Matrix Method (TMM, in-house code). Example mode energies and their angular dispersion are shown with dashed green lines in Fig. 4B. These simulations suggest that adjusting the mirror separation to 8.75 μm brings the 8th mode of the cavity into resonance with the OH stretching mode at 3360 cm−1 at normal incidence, with a free spectral range (FSR, the peak-to-peak separation of cavity modes) of 420 cm−1. This mirror separation was accurately achieved in experimental contexts by monitoring transmission spectra of the water-filled FP cavity and adjusting the FSR of cavity modes far from any solvent absorptions.
We note here that the resonance energies of all the simulated and experimental transmission spectra were in excellent agreement over a very broad energy range irrespective of conditions (air or water-filled), however the observed widths of the cavity modes were always much broader than predicted by simulation (compare Fig. 4A and B). We attribute the broadening not to a degradation of the Q-factor of the FP cavity locally, but to the fact that the waist of the FTIR spectrometer probe beam is large (millimetre diameter) and probed a range of cavity separations as the FP mirrors are not able to be held perfectly flat against each other in the liquid cell holder. Simulations of this situation suggested a normal distribution of probed mirror separations over the range 8.75 ± 0.2 μm (see ESI, Fig. S4†).
When an aqueous solution of Zn(NO3)2 and 2-methylimidazole (same 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
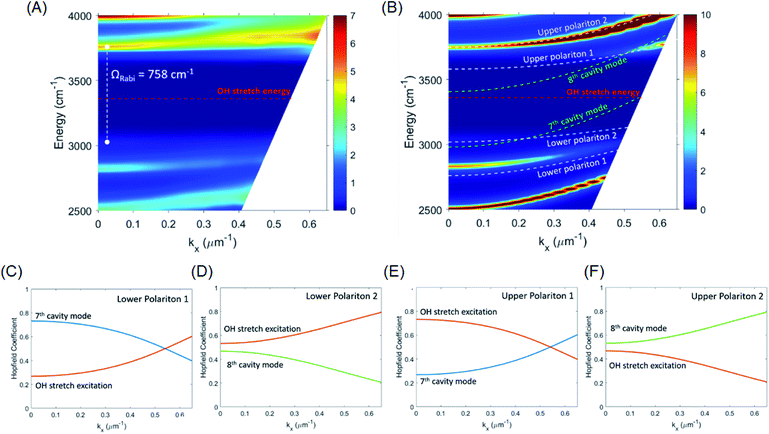
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41.6 mole ratio) was placed in a FP cavity with mirrors adjusted to a separation of 8.75 μm, the normal incidence transmission spectrum shows a clear band gap at the energy of the OH stretching mode of water (Fig. 3B, red curve, note that the solutes are present in only millimolar concentrations and the mode structure is dominated by the solvent refractive index). The eighth-order cavity mode is split into two new vibro-polaritonic states, denoted by P+ and P− around the OH stretching vibration (3360 cm−1, Fig. 3A, black line), with the intensity of P− relatively reduced due to the asymmetric shape of the OH absorption. The energy gap (Rabi splitting) between P+ and P− is 758 cm−1 (Fig. 3B), a value larger than both the width of the OH stretching band (FWHM = 480 cm−1) and the cavity mode (FWHM = 82 cm−1), confirming that the system is well inside the strong coupling regime (a Rabi splitting of 728 cm−1 is predicted in the simulations).
41.6 mole ratio) was placed in a FP cavity with mirrors adjusted to a separation of 8.75 μm, the normal incidence transmission spectrum shows a clear band gap at the energy of the OH stretching mode of water (Fig. 3B, red curve, note that the solutes are present in only millimolar concentrations and the mode structure is dominated by the solvent refractive index). The eighth-order cavity mode is split into two new vibro-polaritonic states, denoted by P+ and P− around the OH stretching vibration (3360 cm−1, Fig. 3A, black line), with the intensity of P− relatively reduced due to the asymmetric shape of the OH absorption. The energy gap (Rabi splitting) between P+ and P− is 758 cm−1 (Fig. 3B), a value larger than both the width of the OH stretching band (FWHM = 480 cm−1) and the cavity mode (FWHM = 82 cm−1), confirming that the system is well inside the strong coupling regime (a Rabi splitting of 728 cm−1 is predicted in the simulations).
Angle-dependent transmission spectra (0–15°) reveal a relatively flat dispersion of the upper and lower polariton peaks around the anti-crossing at the OH stretch absorption peak position (Fig. 4A and S5†). Again, simulated dispersion curves facilitate interpretation of the coupling behaviour (Fig. 4B). At normal incidence (in-plane momentum, kx = 0 μm−1) the 8th cavity mode is resonant with the OH stretch and disperses to higher energy as incidence angle is increased, but at 15° incidence (kx = 0.53 μm−1) the 7th cavity mode has already moved into resonance with the OH stretch with similarly strong interaction (see Fig. 4B). The overall observed result of this strong coupling of successive cavity modes is a relatively flat polariton dispersion. Other consequences of the cavity FSR being similar to the width of the OH stretch band are discussed further on.
To give more insight into the mode structure for the water-filled optical cavity, we performed a multi-mode coupled oscillator analysis, assuming the absence of losses and accounting for the simultaneous hybridization of different cavity modes to the non-radiatively broadened water OH stretch band. Since the different longitudinal modes of the FP cavity form an orthogonal set of modes, each mode independently couples to the OH stretch, resulting in a Rabi doublet for each longitudinal mode of the cavity. This independent coupling is based on the fact that hybridization of the nth and (n + 1)th cavity modes in a homogeneous medium is forbidden by symmetry along the z-axis and no mixing of the original cavity eigenmodes can occur.31,32 Thus for the simultaneous interaction of the 7th and 8th FP modes (with energies E7thcav and E8thcav) with the OH stretch (with energy EEx) in Fig. 4, the appropriate Hopfield matrix is:
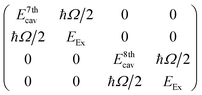 | (1) |
Four eigenstates result, being two independent pairs of upper and lower polariton branches per bare FP mode-vibration interaction. These are plotted in white dashed lines in Fig. 4B assuming equal interaction energies for each mode-vibration interaction (ħΩ/2 = 364 cm−1), EEx = 3360 cm−1, and with the bare cavity mode energies extracted from TMM simulations for the 8.75 μm mirror cavity filled with a flat background refractive index of 1.33 (green dashed lines in Fig. 4B). The eigenvector decomposition for each of the polariton branches (the Hopfield coefficients) are shown in Fig. 4C–F.
The agreement between this coupled oscillator analysis and the TMM-calculated theoretical angular dispersion of the water-filled cavity in Fig. 4B is good for the upper polariton branches, but only reasonable for the lower polariton branches, understandable since the coupled oscillator model does not consider the asymmetric lineshape of the OH stretch. Nevertheless, the analysis confirms that the system is indeed in the strong coupling regime, and clarifies the mode structure in the experimental dispersion in Fig. 4A where broadening of the modes makes the lower polariton 2 and upper polariton 1 branches difficult to resolve as they disperse towards the OH stretch band and are strongly damped.
We note that we also fitted the experimental angular dispersion data in Fig. 4A to a multi-mode Hopfield model, again accounting for the simultaneous hybridization of different cavity modes to the OH stretching band of water, but also including corrections for the ultra-strong coupling regime (counter-rotating terms of the dipolar interaction as well as the depolarization shift of the vibrational mode).31 The ultra-strong coupling regime is entered when the Rabi splitting is a significant fraction (typically >10%) of the coupled transition's energy. The ultra-strong coupling corrections did not significantly affect the results, justifying their neglect in the analysis above (i.e. justifying the use of the rotating wave approximation).
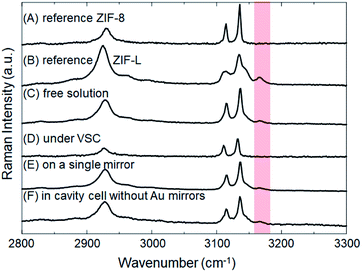
The crystallization of ZIFs was carried out inside optical microcavity under VSC of OH stretch of water. Two hours after the aqueous solution of Zn(NO3)2 and 2-methylimidazole was placed in the FP cavity, the cavity was opened and the solution including crystals was collected by a syringe. The collected crystals were washed by repeated centrifugation, removal of supernatant solution, and redispersal in fresh solvent (see the detail of Materials and methods). SEM images showed the formation of cuboctahedral crystals of 262 ± 48 nm in size (Fig. 2C, D and Table S1†), however in contrast with the experiment in free solution, no formation of star/flake-like crystals was observed suggesting selective formation of ZIF-8. Furthermore, ZIF-8 and ZIF-L can also be distinguished by Raman spectroscopy. The spectra in Fig. 5A and B show the Raman signatures of pure samples of ZIF-8 and ZIF-L, respectively (Fig. S6†), where the band at 3165 cm−1 assigned to the N–H related vibration is clearly present for only ZIF-L.33 The Raman spectrum of the product of crystallization in free solution clearly shows that a mixture of ZIF-8 and ZIF-L is present (Fig. 5C). However microscopic Raman spectroscopy of the washed crystals extracted from the FP cavity (Fig. 5D) shows no sign of the 3160 cm−1 band, in very good agreement with the morphological result (Fig. 2C and D) and confirming that ZIF-8 was selectively formed in the FP cavity.
To confirm that this selectivity is an optical effect rather than a consequence of physical confinement, the same aqueous Zn(NO3)2/2-methylimidazole solution was placed in a ca. 9 μm width cavity but where the ZnSe/Au/PDMS mirrors were replaced with PDMS-coated ZnSe. In the absence of Au layers, the cavity cell does not support well-defined confined vacuum fields but merely provides a microscopic confined space with equivalent PDMS surfaces in contact with solution as before. Two hours after the aqueous solution had been placed in that confined space, a mixture of ZIF-8 and ZIF-L was obtained morphologically very similar to that obtained in free solution (Fig. S7a†). Microscopic Raman spectroscopy confirms the similarity with the relative intensity of the characteristic peak (∼3165 cm−1) against the strongest peak (∼3140 cm−1) very similar for the no-mirror cavity and the free solution crystallization (compare Fig. 5F and C). Given that 26 ± 3% of the crystals formed in the ZIF-L phase in free solution crystallization (as determined by counting), ca. 20 ± 6% of the crystals were estimated to be in the ZIF-L phase for the no-mirror sample based on the Raman intensity ratios obtained by peak fitting (based on pure reference samples of ZIF-8 and ZIF-L, see Table 1 and Fig. S8†). As another control the same aqueous Zn(NO3)2/2-methylimidazole solution was placed on a single mirror consisting of PDMS-coated, Au-sputtered ZnSe and left for 2 h. The resultant crystals morphology (Fig. S7b†) and Raman spectrum (Fig. 5E) both indicated once again that a mixture of ZIF-8 and ZIF-L were obtained with very similar morphology to the free solution experiment (equivalent 22 ± 4% ZIF-L crystals, Table 1). Once again, the selectivity for ZIF-8 is only observed inside the mirror cavity. The effect of physical confinement34 in a no-mirror cavity does not alter the ratio of polymorphs formed compared to free solution, but it does affect the average size of the crystals formed. In the cell without mirrors the crystals were formed with ca. 0.97 ± 0.14 μm diameter, which was smaller than the crystals obtained on a single mirror and in free solution (2.42 ± 0.54 μm, Table S1†). The studies above also confirm that the PDMS buffer layers did not contribute to selective crystallization of ZIF-8.
| Samples | Ratio of ZIF-L to ZIF-8a (%) |
|---|---|
| a Estimated based on relative intensity at ∼3165 cm−1 against the strongest peak at 3140 cm−1. The signals were fitted as shown in Fig. S8. The uncertainties are the standard deviation of five separate experiments. | |
| Pure ZIF-8 | 0 |
| Pure ZIF-L | 100 |
| ZIF crystals formed in free solution | 26 ± 3 |
| ZIF crystals formed inside optical cavity | 0 |
| ZIF crystals formed on a single mirror | 22 ± 4 |
| ZIF crystals formed in cavity without mirrors | 20 ± 6 |
The density of vacuum field modes for a ca. 9 μm mirror separation cavity makes it difficult to tune the cavity modes to be non-resonant with the OH stretching vibration (the cavity FSR and the width of the OH stretch band are both in the order of 500 cm−1, see Fig. 4). Making cavities with significantly reduced mirror separation (<5 μm) would be desirable to test a genuinely non-resonant FP cavity control, however this is technically difficult to fabricate and the resulting much smaller solution volume and crystal numbers would be difficult again to characterize accurately. Nevertheless, we attribute the optical cavity-induced selectivity of crystallization of ZIF-8 to the interaction of the cavity fields with the OH stretch of the solvent as there are no other strong cavity field–water interactions detected over a 1–25 micron spectral range (some weak interactions are evident with the OH bending mode at 1640 cm−1).
To further confirm the mirror cavity-induced selectivity is indeed an optical effect, we tuned the mirrors to larger separations to assess the effect on polymorph selectivity (using Raman spectroscopy to estimate the ratio). In Fig. S10† the ratio of ZIF-8 to ZIF-L crystals obtained in the mirror cavity (no-mirror cavity) is plotted versus mirror (wall) separation over the range 8–100 μm. For the no-mirror cavity, ca. 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25% ratio of ZIF-8 to ZIF-L was obtained over the whole separation range, the same as observed in free solution, again confirming that physical confinement alone does not affect polymorph selectivity. For the mirror cavity, 100% selectivity for ZIF-8 was maintained as mirror separation increased from 8.75 μm to 17 μm. Strong coupling is maintained over this tuning range due to the similarity between the cavity Free Spectral Range (FSR) and the width of the OH stretching vibration (∼500 cm−1) over this range of mirror separations (consistent with the dispersion curve in Fig. 4 showing a large and constant Rabi splitting for angle-tuning near the 7th and 8th cavity modes). However, as mirror separation is increased out to 100 μm, polymorph selectivity is gradually lost, approaching the ca. 75
25% ratio of ZIF-8 to ZIF-L was obtained over the whole separation range, the same as observed in free solution, again confirming that physical confinement alone does not affect polymorph selectivity. For the mirror cavity, 100% selectivity for ZIF-8 was maintained as mirror separation increased from 8.75 μm to 17 μm. Strong coupling is maintained over this tuning range due to the similarity between the cavity Free Spectral Range (FSR) and the width of the OH stretching vibration (∼500 cm−1) over this range of mirror separations (consistent with the dispersion curve in Fig. 4 showing a large and constant Rabi splitting for angle-tuning near the 7th and 8th cavity modes). However, as mirror separation is increased out to 100 μm, polymorph selectivity is gradually lost, approaching the ca. 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25% ratio of ZIF-8 to ZIF-L observed in free solution and in the no-mirror cavity. At around 100 μm separation, the cavity FSR reduces to below 50 cm−1, meaning that more than 10 optical modes with sizeable spectral overlaps interact with the OH stretch simultaneously (Fig. S9†). This begins to approximate the continuum of modes that would interact with the water stretch in the limit of infinite cavity mirror separation (i.e. no mirror effect at all).
25% ratio of ZIF-8 to ZIF-L observed in free solution and in the no-mirror cavity. At around 100 μm separation, the cavity FSR reduces to below 50 cm−1, meaning that more than 10 optical modes with sizeable spectral overlaps interact with the OH stretch simultaneously (Fig. S9†). This begins to approximate the continuum of modes that would interact with the water stretch in the limit of infinite cavity mirror separation (i.e. no mirror effect at all).
Moreover, while a simple model of radiatively broadened vibrational mode coupled to photons always leads to the formation of polaritons, even in the long cavity limit (i.e. 3D polaritons), it should be noted that this is not the case when the absorbers have substantial non-radiative decay pathways as in the present experiment. In such a scenario, for a long cavity filled with high oscillator strength dissipative absorbers, the photonic resonances are overdamped in a large spectral range around the central absorption wavelength and no polariton modes are formed as the energy likely decays before the photon can complete a single cavity round-trip (this over-damping is clear in the transmission of the water-filled, 100 μm separation mirror cavity, Fig. S9†). To summarize, the limit of a long mirror cavity filled with absorbers corresponds to the weak coupling regime due to the combined effects of optical mode overlap, and dissipation within the absorbing medium over a single round-trip. Both effects originate from the dissipative dynamics of the photons and molecular vibrations, and thus cannot be captured by a simple loss-less model which would predict a constant Rabi coupling for arbitrary cavity length, as long as the concentration of absorbers is maintained (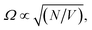 where N is the number of molecules within the cavity mode volume V). Therefore, while it was impossible to detune the OH-stretch from cavity modes, transition from the strong coupling to the weak coupling regime was possible by increasing the mirror cavity length >50 μm. That the observed polymorph selectivity approaches that of the no-mirror cavity/free solution at the same time confirms that strong light–matter interactions drive the mirror cavity-induced polymorph selectivity reported here (Fig. S10†).
where N is the number of molecules within the cavity mode volume V). Therefore, while it was impossible to detune the OH-stretch from cavity modes, transition from the strong coupling to the weak coupling regime was possible by increasing the mirror cavity length >50 μm. That the observed polymorph selectivity approaches that of the no-mirror cavity/free solution at the same time confirms that strong light–matter interactions drive the mirror cavity-induced polymorph selectivity reported here (Fig. S10†).
In another attempt at a detuning experiment, the crystallization was performed in a mixed solvent, equal parts H2O and D2O. The reduced peak intensity of the OH stretch allows one to better-detune it from the cavity modes and study ON-resonance (Fig. S11,† blue spectrum) and OFF-resonance cavities (Fig. S11,† red spectrum). The crystals obtained in each cavity were characterized by SEM and Raman spectroscopy (Fig. S12 and S13†). The morphological results are consistent with ZIF-8 being selectively formed under VSC of OH stretching vibrations in the ON-resonance cavity, and this selectivity being lost for the OFF-resonance cavity. However, the ratio of ZIF-8 to ZIF-L cannot be estimated reliably by Raman signals due to the exchange of deuterium ions in solution and proton of 2-methylimidazole.35 This exchange weakens the characteristic signal of N–H vibrations of 2-methylimidazole in ZIF-L. However, the signal of NH vibration is still observable despite the intensity reductions (Fig. S13†), suggesting the formation of ZIF-L under OFF-resonance condition. This result also supports the notion that VSC of the OH stretch of water induces the selective crystallization of ZIF-8.
There is a possibility that VSC of N–H vibration in 2-methylimidazole also influences the crystallization of ZIF. To clarify this, we performed the crystallization studies in neat D2O under VSC of the OD stretching vibration, shifted far from the 2-methylimidazole N–H stretch (Fig. S14†). Morphological studies suggest that ZIF-8 is still selectively formed under VSC of the OD stretching vibration (Fig. S15 and S16†), supporting the VSC effect of OH stretch of water on selective crystallization of ZIF-8.
We also assessed the effect of cavity quality (Q) factor on the observed polymorph selectivity. We kept the mirror separation constant (at 8.75 μm, resonant conditions) and varied the Q-factor of the cavity modes by changing the mirror thickness. The thickness of the Au layers was reduced from 10 to 6 nm, reducing the Q-factor of the optical cavity modes from ca. 32 to 24. Despite this mirror thickness reduction, when the aqueous Zn(NO3)2/2-methylimidazole solution (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41.6 mole ratio) was included in the 6 nm gold mirror cavity, the Rabi splitting was barely altered from the 10 nm case and still within the strong coupling regime (Fig. S17†). Consistent with the previous observations for 10 nm mirror cavity mirrors, crystals obtained from the 6 nm Au mirror cavity were morphologically and spectroscopically consistent with 100% selectivity for the ZIF-8 polymorph (Fig. S18 and S19†). We note here that the no-mirror cavity, which does not display polymorph selectivity, supports very low Q-factor modes (<5) due to reflections at the ZnSe/water interface.
41.6 mole ratio) was included in the 6 nm gold mirror cavity, the Rabi splitting was barely altered from the 10 nm case and still within the strong coupling regime (Fig. S17†). Consistent with the previous observations for 10 nm mirror cavity mirrors, crystals obtained from the 6 nm Au mirror cavity were morphologically and spectroscopically consistent with 100% selectivity for the ZIF-8 polymorph (Fig. S18 and S19†). We note here that the no-mirror cavity, which does not display polymorph selectivity, supports very low Q-factor modes (<5) due to reflections at the ZnSe/water interface.
Role of vibrational strong coupling on crystallization
One scenario to explain the effect of solvent VSC on selective crystallization is stabilization of the ZIF-8 phase over ZIF-L phase. This relies on the stabilization/activation of one phase over the other one under strong coupling. To investigate the relative stability of crystal polymorphs in this system, we investigated the influence of the relative number of starting materials on the ratio of ZIF-8 and ZIF-L. In all the above experiments, a Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Hmeim ratio of 1
Hmeim ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41.6 was employed to give significant yields of both ZIF-8 (74%) and ZIF-L (26%) crystals in free solution (and giving 100% ZIF-8 in the FP cavity). However it is well known for ZIF crystallization that the ratio of ZIF-L obtained increases with increasing relative amount of 2-methylimidazole over Zn(NO3)2. For example, a 1
41.6 was employed to give significant yields of both ZIF-8 (74%) and ZIF-L (26%) crystals in free solution (and giving 100% ZIF-8 in the FP cavity). However it is well known for ZIF crystallization that the ratio of ZIF-L obtained increases with increasing relative amount of 2-methylimidazole over Zn(NO3)2. For example, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 Zn
28 Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Hmeim ratio affords majority (68%) ZIF-L crystals in free solution. We checked a range of ratios of starting materials and found in all cases a cavity-induced modification of the crystal phase in favour of ZIF-8, but not always leading to complete suppression (Tables S2, S3 and Fig. S20†). For the 1
Hmeim ratio affords majority (68%) ZIF-L crystals in free solution. We checked a range of ratios of starting materials and found in all cases a cavity-induced modification of the crystal phase in favour of ZIF-8, but not always leading to complete suppression (Tables S2, S3 and Fig. S20†). For the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 Zn
28 Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Hmeim ratio experiment, the 68 ± 5% ZIF-L crystal majority in free solution, becomes a 24 ± 7% minority inside the FP cavity, for example.
Hmeim ratio experiment, the 68 ± 5% ZIF-L crystal majority in free solution, becomes a 24 ± 7% minority inside the FP cavity, for example.
The relative stability of crystal polymorphs can be estimated from their solubility (s) ratio as:
ΔGB→A = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(sB/sA) ln(sB/sA) | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 Zn
28 Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Hmeim ratio starting material experiment, this yields an estimated 395 cm−1 stabilization energy. We note cautiously that this energy is of the same order as half the Rabi splitting (376 cm−1) which is the expected stabilization of the first vibrational state of the water OH stretch in the cavity due to VSC (Fig. 1B, energy gap between the first vibrational state and lower polariton). One of the central propositions of the field of polaritonic chemistry is that spectral shifts due to polariton formation correspond to changes in the potential energy landscape of the material under strong coupling, affecting reaction rates, work functions etc. A direct connection here between stabilization of the first vibrational state of the solvent, and the stabilization of ZIF-8 over ZIF-L in the cavity is not well-understood yet, hence we do not draw any strong conclusions and simply note this correspondence.
Hmeim ratio starting material experiment, this yields an estimated 395 cm−1 stabilization energy. We note cautiously that this energy is of the same order as half the Rabi splitting (376 cm−1) which is the expected stabilization of the first vibrational state of the water OH stretch in the cavity due to VSC (Fig. 1B, energy gap between the first vibrational state and lower polariton). One of the central propositions of the field of polaritonic chemistry is that spectral shifts due to polariton formation correspond to changes in the potential energy landscape of the material under strong coupling, affecting reaction rates, work functions etc. A direct connection here between stabilization of the first vibrational state of the solvent, and the stabilization of ZIF-8 over ZIF-L in the cavity is not well-understood yet, hence we do not draw any strong conclusions and simply note this correspondence.
The mechanism of cavity-induced stabilization of the ZIF-8 phase over ZIF-L, and whether the absolute energies of just one or both phases are affected, is a matter for speculation at this stage. The other scenario to explain the selective crystallization is influence on the crystallization process rather than the free energies of final products. Theoretical and experimental studies of the effects of VSC are yet to merge into a single satisfactory picture, with recent theoretical work even suggesting that the Morse potential picture of the coupled bond (Fig. 1B) is perturbed beyond recognition under VSC. One common thread is that several experimental works have measured reductions in chemical reactivity as a result of VSC, in concert with some theory that has predicted a strengthening/shortening of the coupled bond (a squeezed Morse potential, see Fig. S21†).6 If any of these energy and bond strength changes are occurring for the water OH stretch in the cavity due to VSC herein, the critical parameters for crystal nucleation and growth, the crystal surface and bulk free energies, are both likely to be affected as water can enter inside the pores of both ZIF-8 and ZIF-L. Whether the size-dependence of the crystal surface and bulk free energies is changed inside the optical cavity, and thus if the ‘burst nucleation’ of the La Mer model and Ostwald ripening still operate, is also an open and fertile question.
Further clues might be gained by observing the solvent dependence of ZIF pseudopolymorphism. Leaving bulk alcohol solutions of Zn(NO3)2·6H2O and 2-methylimidazole to stand for 2 h leads to the exclusive formation of ZIF-8 for methanol, ethanol, and isopropanol (Fig. S22–S24†). Since alcoholic solvents give similar selectivity for ZIF-8 as does water under VSC in optical cavities, some parallels may be drawn. The polarity of alcoholic OH groups is weaker than that of water, thus we speculate that VSC may change the solvation properties of water to be closer to those of alcohols. This picture consistent with the squeezed the Morse potential picture of VSC where the average displacement of a polar bond is reduced in excited states (Fig. S21†).
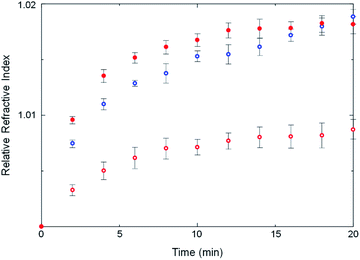
Some strength can be lent to this speculation by monitoring the kinetics of ZIF crystallization. Crystallization slightly changes the refractive index of the solution owing to the formation of tiny crystalline particles. The crystallization in an optical cavity can be monitored by temporal shift of cavity modes derived from the change of refractive index.37 The temporal shift of cavity modes far from the OH stretch energy was used to estimate the crystallization rate. This is also possible for a no-mirror cavity as the water/ZnSe interface provides sufficient reflectivity to generate optical cavity modes, albeit of low Q-factor. In no-mirror cavities, the change of the refractive index due to MOF crystallization occurred slightly faster in ethanol compared to in water (Fig. 6 and S25†), in good agreement with previous work in which a weakly polar solvent accelerated crystallization of ZIF structures.38 More interestingly, the change of the refractive index due to crystallization in water was faster in the mirror cavity under VSC compared to in the no-mirror cavity. VSC apparently alters the crystallization rate in water to be more like that in ethanol, a similar trend to what was observed for polymorph selectivity. This suggests again that the solvation properties of water under VSC may be modified.
Conclusions
In this work, we investigated VSC of solvent molecules in MOF synthesis. ZIF-8 was selectively obtained under VSC of the OH stretching absorption in water, whereas mixtures of ZIF-8 and ZIF-L were obtained without VSC of OH. Control experiments showed that the mirror surface and microscopic confinement had no effects on the selectivity of ZIF-8. The array of possible mechanisms testifies to the rich opportunities afforded by coupling chemical processes such as crystallization to cavity vacuum fields, and the broad array of work that is still to be done to deepen understanding in this area. The ability to selectively control (pseudo)polymorphism using cavity vacuum fields demonstrated here has enormous potential in the domain of crystallography with particular application in biomedical materials. This may also be the first example of VSC applied to self-assembly of macroscopic structures, opening a new cross-disciplinary domain between quantum photonics and materials synthesis.Materials and methods
Cavity setup
A cavity cell was made by TTC Inc., Japan. Mylar film of thickness 1 μm was purchased from Micron Wings, Australia. ZnSe windows were purchased from Specac Ltd, UK. The ZnSe windows were sputter-coated with an Au layer of thickness 10 nm. The Au layer was spin-coated with Sylgard and then the assembly was dried in an oven.Crystallization
Zn(NO3)2·6H2O and 2-methylimidazole were purchased from the FUJIFILM Wako Pure Chemical Corporation. Zn(NO3)2·6H2O (7.44 mg, 2.5 × 10−2 mmol) and 2-methylimidazole (86.2 mg, 1.05 mmol) were dissolved in MilliQ water (2 mL). A portion of the solution was placed in or outside the cavity at room temperature. After crystallization, the solution containing the white precipitate was collected from the FP cavity by a syringe. The precipitate was washed with ethanol three times to remove unreacted components. The washing process repeated the following procedure: centrifugation to collect the precipitate, removal of supernatant solution, addition of neat ethanol, and shaking the solution to wash/redisperse the crystals. The final washed solution was drop-cast onto substrates and dried for Raman spectroscopy and SEM observations. Although SEM observations and microscopic Raman spectroscopy are local measurements, we checked that they reflected the ensemble heterogeneous distribution of each crystal type on the substrate for each sample. The crystallization experiments were repeated five times to determine the average ratio of ZIF-8 to ZIF-L, with the statistical error associated with the ratio determination estimated from the standard deviation of the result for the five experiments.The crystallization experiments were repeated five times to determine the average ratio of ZIF-8 to ZIF-L, with the statistical error associated with the ratio determination estimated from the standard deviation of the result for the five experiments.
Instrumentation
IR spectra were recorded with a JASCO FT-IR 6800 instrument. Au sputtering was performed with an ACS-4000-C3-HS instrument (ULVAC, Inc., Japan) or MSP-1S vacuum device (Japan). SEM was performed with a Phenom Pro desktop instrument. XRD patterns were recorded with a Rigaku SmartLab system. Microscopic Raman spectroscopy was performed with a Renishaw inVia™ instrument.Data availability
The experimental details and datasets supporting this article are available in the ESI.†Author contributions
K. H. and H. U. conceived the project. K. H. and J. A. H. designed the experiments. H. I. and K. H. performed the experiments, J. A. H. and T. C. performed the simulations. All authors discussed the results and commented on the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was supported by JSPS KAKENHI (Grant No. JP18K19085, JP21H01899) and JST PRESTO (JPMJPR18TA) to K. H., and partially supported by the JSPS Core-to-Core Program A. Advanced Research Networks and KU Leuven internal funds (C14/15/053, C14/19/079) to H. U. J. A. H. acknowledges an Australian Research Council (ARC) Future Fellowship award (FT180100295). We thank the Open Facility at Hokkaido University for allowing us to carry out X-ray diffraction measurements, microscopic Raman spectroscopy and sputtering.References
- T. W. Ebbesen, Acc. Chem. Res., 2016, 49, 2403–2412 CrossRef CAS.
- J. A. Hutchison, T. Schwartz, C. Genet, E. Devaux and T. W. Ebbesen, Angew. Chem., Int. Ed., 2012, 51, 1592–1596 CrossRef CAS PubMed.
- R. Damari, O. Weinberg, D. Krotkov, N. Demina, K. Akulov, A. Golombek, T. Schwartz and S. Fleischer, Nat. Commun., 2019, 10, 3248 CrossRef PubMed.
- G. L. Paravicini-Bagliani, F. Appugliese, E. Richter, F. Valmorra, J. Keller, M. Beck, N. Bartolo, C. Rössler, T. Ihn, K. Ensslin, C. Ciuti, G. Scalari and J. Faist, Nat. Phys., 2019, 15, 186–190 Search PubMed.
- P. H. Bucksbaum, A. Zavriyev, H. G. Muller and D. W. Schumacher, Phys. Rev. Lett., 1990, 64, 1883–1886 CrossRef CAS.
- J. Flick, M. Ruggenthaler, H. Appel and A. Rubio, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3026–3034 CrossRef CAS PubMed.
- F. Herrera and F. C. Spano, Phys. Rev. Lett., 2016, 116, 238301 CrossRef.
- A. Thomas, J. George, A. Shalabney, M. Dryzhakov, S. J. Varma, J. Moran, T. Chervy, X. Zhong, E. Devaux, C. Genet, J. A. Hutchison and T. W. Ebbesen, Angew. Chem., Int. Ed., 2016, 55, 11462–11466 CrossRef CAS PubMed.
- A. Thomas, L. Lethuillier-Karl, K. Nagarajan, R. M. A. Vergauwe, J. George, T. Chervy, A. Shalabney, E. Devaux, C. Genet, J. Moran and T. W. Ebbesen, Science, 2019, 363, 615–619 CrossRef CAS.
- R. M. A. Vergauwe, A. Thomas, K. Nagarajan, A. Shalabney, J. George, T. Chervy, M. Seidel, E. Devaux, V. Torbeev and T. W. Ebbesen, Angew. Chem., Int. Ed., 2019, 58, 15324–15328 CrossRef CAS.
- K. Hirai, R. Takeda, J. A. Hutchison and H. Uji-i, Angew. Chem., Int. Ed., 2020, 59, 5332–5335 CrossRef CAS PubMed.
- A. Sau, K. Nagarajan, B. Patrahau, L. Lethuillier-Karl, R. M. A. Vergauwe, A. Thomas, J. Moran, C. Genet and T. W. Ebbesen, Angew. Chem., 2021, 133, 5776–5781 CrossRef.
- F. Herrera and J. Owrutsky, J. Chem. Phys., 2020, 152, 100902 CrossRef CAS PubMed.
- K. Hirai, J. A. Hutchison and H. Uji-i, ChemPlusChem, 2020, 85, 1981–1988 CrossRef CAS PubMed.
- J. Lather, P. Bhatt, A. Thomas, T. W. Ebbesen and J. George, Angew. Chem., Int. Ed., 2019, 58, 10635–11063 CrossRef CAS PubMed.
- H. Hiura and A. Shalabney, ChemRxiv, 2019 DOI:10.26434/chemrxiv.7234721.v5.
- J. Lather and J. George, J. Phys. Chem. Lett., 2021, 12, 379–384 CrossRef CAS.
- S. Wang, A. Mika, J. A. Hutchison, C. Genet, A. Jouaiti, M. W. Hosseini and T. W. Ebbesen, Nanoscale, 2014, 6, 7243–7248 RSC.
- T. Sugiyama and H. Masuhara, Chem.–Asian J., 2011, 6, 2878–2889 CrossRef CAS.
- T. Minamisono and H. Takiyama, J. Cryst. Growth, 2013, 362, 135–139 CrossRef CAS.
- S. Kitagawa, R. Kitaura and S. I. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334–2375 CrossRef CAS.
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O’Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472 CrossRef CAS PubMed.
- K. Barthelet, J. Marrot, D. Riou and G. Férey, Angew. Chem., Int. Ed., 2002, 41, 281–284 CrossRef CAS PubMed.
- A. Ferguson, L. Liu, S. J. Tapperwijn, D. Perl, F. X. Coudert, S. Van Cleuvenbergen, T. Verbiest, M. A. Van Der Veen and S. G. Telfer, Nat. Chem., 2016, 8, 250–257 CrossRef CAS PubMed.
- R. N. Widmer, G. I. Lampronti, S. Chibani, C. W. Wilson, S. Anzellini, S. Farsang, A. K. Kleppe, N. P. M. Casati, S. G. Macleod, S. A. T. Redfern, F. X. Coudert and T. D. Bennett, J. Am. Chem. Soc., 2019, 141, 9330–9337 CrossRef PubMed.
- N. Zhu, M. J. Lennox, T. Düren and W. Schmitt, Chem. Commun., 2014, 50, 4207–4210 RSC.
- H. Hayashi, A. P. Côté, H. Furukawa, M. O'Keeffe and O. M. Yaghi, Nat. Mater., 2007, 6, 501–506 CrossRef CAS.
- H. Fu, Z. Wang, X. Wang, P. Wang and C. C. Wang, CrystEngComm, 2018, 20, 1473–1477 RSC.
- Z. X. Low, J. Yao, Q. Liu, M. He, Z. Wang, A. K. Suresh, J. Bellare and H. Wang, Cryst. Growth Des., 2014, 14, 6589–6598 CrossRef CAS.
- Y. Lo, C. H. Lam, C. W. Chang, A. C. Yang and D. Y. Kang, RSC Adv., 2016, 6, 89148–89156 RSC.
- J. George, T. Chervy, A. Shalabney, E. Devaux, H. Hiura, C. Genet and T. W. Ebbesen, Phys. Rev. Lett., 2016, 117, 153601 CrossRef PubMed.
- D. Meiser and P. Meystre, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 065801 CrossRef.
- T. Forsting, J. Zischang, M. A. Suhm, M. Eckhoff, B. Schröder and R. A. Mata, Phys. Chem. Chem. Phys., 2019, 21, 5989–5998 RSC.
- B. Chang, Y. Yang, H. Jansen, F. Ding, K. Mølhave and H. Sun, Adv. Mater. Interfaces, 2018, 5, 1–8 Search PubMed.
- M. Cebo, M. Kielmas, J. Adamczyk, M. Cebrat, Z. Szewczuk and P. Stefanowicz, Anal. Bioanal. Chem., 2014, 406, 8013–8020 CrossRef CAS.
- P. Upadhyay, A. K. Dantuluri, L. Kumar and A. K. Bansal, J. Pharm. Sci., 2012, 101, 1843–1851 CrossRef CAS.
- H. Liu, F. Pang, L. Hong, Z. Ma, L. Huang, Z. Wang, J. Wen, Z. Chen and T. Wang, Optics Exp., 2019, 27, 6201–6209 CrossRef CAS.
- X. Feng, T. Wu and M. A. Carreon, J. Cryst. Growth, 2016, 455, 152–156 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc03706d |
| This journal is © The Royal Society of Chemistry 2021 |