Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unveiling the complex pattern of intermolecular interactions responsible for the stability of the DNA duplex†
Ahmet
Altun
 ,
Miquel
Garcia-Ratés
,
Miquel
Garcia-Ratés
 ,
Frank
Neese
,
Frank
Neese
 and
Giovanni
Bistoni
and
Giovanni
Bistoni
 *
*
Max-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, D-45470 Mülheim an der Ruhr, Germany. E-mail: giovanni.bistoni@kofo.mpg.de
First published on 2nd September 2021
Abstract
Herein, we provide new insights into the intermolecular interactions responsible for the intrinsic stability of the duplex structure of a large portion of human B-DNA by using advanced quantum mechanical methods. Our results indicate that (i) the effect of non-neighboring bases on the inter-strand interaction is negligibly small, (ii) London dispersion effects are essential for the stability of the duplex structure, (iii) the largest contribution to the stability of the duplex structure is the Watson–Crick base pairing – consistent with previous computational investigations, (iv) the effect of stacking between adjacent bases is relatively small but still essential for the duplex structure stability and (v) there are no cooperativity effects between intra-strand stacking and inter-strand base pairing interactions. These results are consistent with atomic force microscope measurements and provide the first theoretical validation of nearest neighbor approaches for predicting thermodynamic data of arbitrary DNA sequences.
Introduction
The double-stranded DNA structure encodes the genetic information necessary for the development and functioning of all living organisms1 and understanding the complex pattern of interactions responsible for the structural features of DNA is of fundamental importance in biology.The bases of each strand of a DNA duplex lay nearly parallel on top of each other and their relative orientation is influenced by intra-strand stacking (S) interactions (Fig. 1).2 In addition, the two strands of DNA are held together by inter-strand S and inter-strand H-bonding interactions between Watson–Crick (WC, i.e., A–T and G–C) base pairs (BPs).
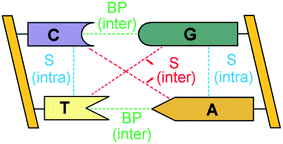 | ||
| Fig. 1 Inter-strand and intra-strand interactions of a section of double-strand DNA. BP and S denote base-pairing and stacking, respectively. | ||
In standard biology textbooks,3,4 inter-strand H-bonding is regarded as the major factor responsible for the stability of the DNA duplex, based on the observation that the melting temperature of DNA increases linearly with the increase of its G–C content.5 However, a quantitative understanding of the relative importance of base pairing vs. stacking interactions on the stability of the DNA duplex is still lacking.6 This stimulated the development of experimental probes aimed at quantifying the total stacking and the base-pairing contributions to the stability of DNA.7–12 These include (i) single molecule study on blunt-end DNA origami thick fibers pulled by mechanical forces;7 (ii) temperature-dependent polyacrylamide gel electrophoresis (PAGE) of nicked and kinked DNA molecules at different denaturating conditions;8,9 (iii) nano-differential scanning calorimeter (nano-DSC) and nano-isothermal titration calorimetry (nano-ITC) measurements in dilute solutions10,11 and (iv) stretching and unzipping of DNA for rupture force measurements under atomic force microscope (AFM).12 Interestingly, while mechanical studies, i.e., AFM measurements, confirmed the classical textbook description by finding the rupture forces of G–C, A–T and stacking as 20, 14 and 2 piconewtons, respectively, the solution free-energy parameters derived from PAGE, nano-DSC and nano-ITC measurements8–11 indicate that the stability of duplex DNA arises almost entirely from stacking. Moreover, the PAGE-based stacking parameters are still consistent with the linearity of predicted DNA melting temperature on the G–C content.8,9 These somehow contradicting findings originate from the fact that the experimental observables that are commonly associated with the stability of DNA are influenced by a number of contributions that are difficult to disentangle experimentally, such as the concentration of the ions interacting with the backbones, temperature-dependent enthalpic and entropic effects and the intermolecular interactions between the DNA strands. In this study, rather than dissecting such contributions, we provide an in-depth, quantitative characterization of the intermolecular interactions responsible for the intrinsic stability of B-DNA at its biologically relevant duplex structure using advanced quantum mechanical (QM) methods.
Energy decomposition analysis (EDA)13–15 and symmetry adapted perturbation theory (SAPT)16 methods breakdown the QM interaction energy into physically meaningful components, and have proven instrumental in exploring such conflicting issues. However, such studies focused mostly on H-bonding and stacking interactions between just two bases17–21 or between two base pairs oriented at different twist angles (called base step) in the gas phase and in different dielectric media.22–25 The main findings of these studies can be summarized as follows: (i) the interaction between the bases in the G–C pair is significantly stronger than that in the A–T pair in the gas phase;17–23 (ii) due to its complex nature, there is still no consensus on the mechanism responsible for the synergistic stabilization originating from multiple H-bonds in base pairs, as discussed in a recent review paper of Guerra and coworkers;26 (iii) The sugar-phosphate backbone imposes geometrical constraints that destabilize base-pairing interactions27 and it is also essential for properly describing DNA–protein interactions, as emphasized by Hobza and coworkers;28 (iv) the interaction energy between base pairs or base steps decreases in solution proportional to the polarity of the solvent;22,23 (v) the base-pairing contribution to the stability is significantly larger than the stacking contribution, as initially demonstrated by Hessellman et al.21 and then confirmed by many subsequent computational studies20,22,23 (vi) inter-strand stacking is a crucial element of structural stability, especially in the GC-rich sequences.22 Finally, all previous computational investigations17–23 agree that electrostatic and London dispersion interactions are the major contribution to the base pair stability.
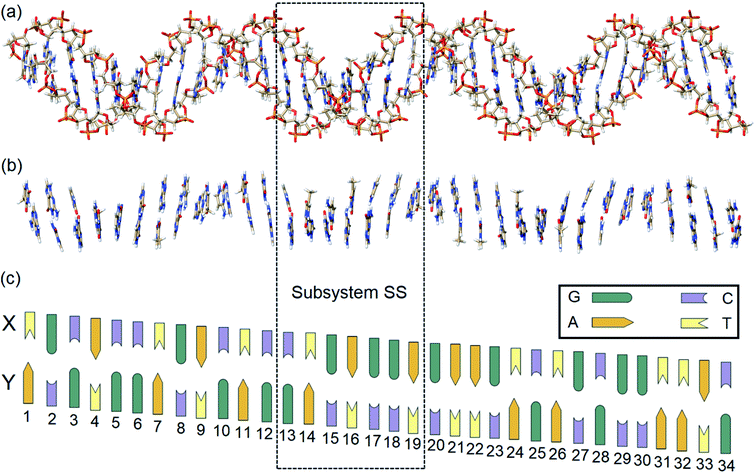
In this work, state-of-the-art QM methods are used to elucidate the intermolecular interactions responsible for the intrinsic stability of human B-DNA by considering realistic DNA models of different size, including a thirty-four nucleobase-long duplex model (Fig. 2). To this aim, we apply the well-established Local Energy Decomposition (LED) scheme,29–32 which allows for a chemically meaningful decomposition of the interaction energy obtained at the accurate domain-based local pair natural orbital coupled cluster DLPNO-CCSD(T) level33 for a system containing an arbitrary number of fragments. This method has already found widespread applications in chemistry.34–39
In particular, our analysis relies on the recently developed Hartree–Fock plus London Dispersion (HFLD) scheme for the efficient and accurate quantification and analysis of noncovalent interaction (NCI) energies.40 In the HFLD scheme, the interaction between the fragments is treated at the DLPNO-CCSD level of theory, while the fragments themselves are kept at the HF level. The LED analysis is then used to single out the dispersion contribution from the other inter-fragment terms, which is then used to correct interaction energies at the HF level. On challenging benchmark sets for NCIs, this scheme provides an accuracy between that of CCSD and of the gold standard CCSD(T) method, while showing an efficiency that is comparable to that of standard mean-field approaches.40 Therefore, our combined HFLD/LED approach allows us to uniquely probe the nature of the interactions between all the nucleobases and the backbones in DNA at its biologically relevant structure. It is worth mentioning here that many dispersion-corrected HF approaches have been proposed,41–47 and semi-empirical schemes like HF-D3(BJ)46 or HF-3c47 have proven instrumental in computational studies of large biomolecular systems.47–51
Computational details
Unless otherwise specified, all calculations were performed with a development version of the ORCA program package based on version 5.0.52–54 Very tight SCF convergence criteria were used for the isolated base pairs, while tight SCF criteria were used for all other systems. The default grid settings of ORCA 5.0, which are very conservative, were used throughout the study.Model systems
In order to identify and quantify the key intermolecular interactions in the DNA duplex, we defined a series of model systems of different size and charge. The initial coordinates of the thirty-four nucleobase-long duplex portion of human B-DNA (denoted hereafter as the large system LS), which is responsible for the synthesis of β-hemoglobin,55 were obtained using the DNA modeling server 3D-DART.56 The 5′-TGCACCTGACTCCTGAGGAGAAGTCTGCGGTTAC-3′ sequence (strand X) and its corresponding complementary sequence (strand Y) were considered. The 3′ and 5′ terminals of the strands were saturated with hydrogen atoms. The charged anionic phosphate groups of the sugar-phosphate backbones were kept negatively charged (total system size: 2162 atoms). The resulting coordinates were then fully optimized with the GFN2-xTB variant of the density functional tight binding method, by treating the water environment implicitly.57 The resulting charged model is denoted hereafter as LSBACK-C (Fig. 2a). A simplified model was obtained by removing the backbones from LSBACK-C and saturating the covalent bonds cut with hydrogen atoms, following the standard link atom58 placement protocol in ORCA. The model thus obtained (1001 atoms) is neutral and it is denoted as LSN(BACK-C) (Fig. 2b).For the sake of simplicity and unless stated otherwise, the results obtained from our extensive analyses are discussed in detail only for the subsystem SS (enclosed by a dashed box in Fig. 2), with the sequence 5′-CTGAGGA-3′. This model was built by: (i) protonating the 3′ and 5′ terminals for the subsystem extracted from LSBACK-C, (ii) optimizing the resulting structure at the GFN2-xTB level. The resulting model is negatively charged and it is denoted hereafter as SSBACK-C (448 atoms). To assess the effect of the charge of the system on the stability of the DNA duplex, a neutral model was built by adding one hydrogen atom to one of the non-bridging oxygen atoms of each phosphate group. The resulting structure was optimized at the GFN2-xTB level and the optimized geometry is denoted as SSBACK-N (462 atoms). Two simplified models were obtained by removing the backbone from SSBACK-C and SSBACK-N and saturating the covalent bonds cut with hydrogen atoms. The resulting SSN(BACK-C) and SSN(BACK-N) models feature 220 atoms. A preliminary benchmark study on smaller model systems demonstrated that the results of our analysis are essentially independent by the specific method used for the geometry optimization, as detailed in the ESI.† The HFLD/LED data obtained for all the SS and LS models are given in the ESI.†
Calculations on isolated nucleobase dimers
In order to compare the results obtained with different computational methodologies, the interaction energies of the H-bonded WC and stacked (S) conformers of A–T and G–C pairs in the gas phase were computed using different electronic structure methods. All correlation calculations were performed with the default frozen core settings.59Geometry optimizations for all conformers were carried out at the MP2 level of theory60 using the RIJK approach61–63 for the two-electron integrals in the reference calculation. The cc-pVTZ basis set was used in conjunction with its auxiliary counterparts.64–67
Single point DLPNO-CCSD(T)33 calculations were carried out using TightPNO68 settings. All electron pairs were included in the coupled cluster treatment. The Foster-Boys (FB)69 scheme was used for localizing the occupied orbitals. To approach the complete basis set (CBS) limit, two-point extrapolation was performed using the aug-cc-pVTZ and aug-cc-pVQZ basis sets,64–66 as described previously.40 Interaction energies were also corrected for the basis set superposition error (BSSE).70
HFLD calculations were carried out using the RIJCOSX approach62,63,71,72 in the SCF part. The FB scheme was employed for localizing both the occupied orbitals and the pair natural orbitals (PNOs). The default NormalPNO* settings (TCutPairs = 10−5) of HFLD40 were used. The def2-TZVP(-f) basis set was used with its corresponding matching auxiliary basis set.73
Our results were compared with those obtained with HF and MP2 calculations60 as well as with the previous composite MP2/CCSD(T)74,75 and SAPT21 calculations. Density functional theory (DFT) calculations were also carried out, using the B3LYP76–79 exchange–correlation functional in conjunction with the D3(BJ)46,80 dispersion correction and the def2-TZVP(-f)73 basis set. For the large DNA models, the effect of the three-body (ABC) contribution80 to the D3(BJ) correction was also discussed.
HFLD/LED analysis of the DNA duplex
DFT calculations have proven instrumental in elucidating many interesting aspects of the stability of the DNA duplex. However, different authors have emphasized the importance of benchmarking DFT results against those obtained from accurate wave function-based methods in order to test the accuracy of exchange–correlation functionals on realistic DNA models.81,82 In this work, our analysis relies on the HFLD scheme,40 which is a correlated wave function-based method that is free from any empirical parameterization. Accordingly, the dispersion interactions between the X and Y strands of the DNA were treated using conservative PNO settings, whilst intra-strand correlation effects were neglected. By combining the HFLD approach with the LED scheme,29–31 the HFLD interaction energy between DNA strands can be expressed as:| ΔEint = ΔEel-prep,X + ΔEel-prep,Y + Eelstat(X↔Y) + Eexch(X↔Y) + Edisp(X↔Y) | (1) |
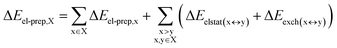 | (2) |
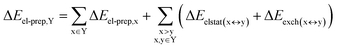 | (3) |
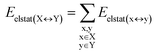 | (4) |
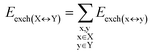 | (5) |
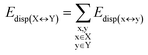 | (6) |
For the sake of simplicity, for the model systems without the backbone (e.g., LSN(BACK-C)), all the LED contributions were presented in the form of heat maps (the so-called LED interaction maps).83 The diagonal elements denote the repulsive ΔEel-prep,x contributions associated with the individual nucleobases and backbones. Non-diagonal elements involving bases/backbones within same strand represent the changes of intra-strand electrostatic and exchange interactions upon duplex formation, i.e., ΔEelstat(x↔y) and ΔEexch(x↔y). Non-diagonal elements involving nucleobases on different strands represent electrostatic, exchange and dispersion interactions between nucleobases on different strands, i.e., Eelstat(x↔y), Eexch(x↔y) and Edisp(x↔y), respectively.
The same computational settings described in the previous subsection for isolated nucleobase dimers were used for HFLD/LED calculations on the DNA system. However, since the ΔEint values obtained with TCutPairs = 10−5 and 5 × 10−5 were found to be identical to each other for the SSN(BACK-C/N) model, the looser TCutPairs = 5 × 10−5 threshold was used for the large LSN(BACK-C) calculations. The effect of water environment on the energetics was assessed using the Conductor-like Polarizable Continuum Model (CPCM),84 as implemented in ORCA.85,86 The results obtained were found to be largely independent by the specific method87,88 used for incorporating solvation corrections in the correlated calculations (see the ESI†).89 Unless otherwise specified, the results of this paper were obtained using the perturbation theory and energy PTE scheme.87
HFLD/LED/def2-TZVP(-f) calculations on the duplex of SSN(BACK-C), SSBACK-C and LSN(BACK-C) require 3630, 7938 and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 998 contracted basis functions, respectively. The corresponding computations on the DNA duplex required about 6 hours, 1.5 days and 10 days, respectively, by using four cores of a single cluster node equipped with 4 Intel Xeon CPUs. HFLD interaction energies were already shown to provide essentially converged interaction energies by using double-ζ basis sets and NormalPNO* settings on challenging benchmark sets of closed-shell adducts held together by NCIs.40
998 contracted basis functions, respectively. The corresponding computations on the DNA duplex required about 6 hours, 1.5 days and 10 days, respectively, by using four cores of a single cluster node equipped with 4 Intel Xeon CPUs. HFLD interaction energies were already shown to provide essentially converged interaction energies by using double-ζ basis sets and NormalPNO* settings on challenging benchmark sets of closed-shell adducts held together by NCIs.40
Results and discussion
Benchmark study on base pairs
Before starting our discussion on the intermolecular interactions in the DNA duplex, we tested the accuracy of the HFLD scheme on smaller systems of similar nature. The interaction energies obtained at the HFLD/def2-TZVP(-f) level of theory for the nucleobase dimers were compared with those obtained at different levels of theory as shown in Table 1.| HF | MP2 | MP2/CCSD(T) | DFT-SAPT | DLPNO-CCSD(T) | HFLD | B3LYP-D3(BJ) | |
|---|---|---|---|---|---|---|---|
| WC | |||||||
| A–T | −9.9 | −16.9 | −16.9 | −15.7 | −16.6 | −16.2 | −18.0 |
| G–C | −24.6 | −31.6 | −32.1 | −30.5 | −31.5 | −32.8 | −33.2 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| S | |||||||
| A–T | 5.6 | −15.1 | −12.3 | −10.9 | −10.5 | −11.9 | −12.1 |
| G–C | −3.4 | −20.8 | −19.0 | −17.8 | −17.7 | −20.0 | −19.4 |
For both H-bonded WC and stacked (S) conformers, HFLD results reproduce the reference DLPNO-CCSD(T)/CBS interaction energies extremely well, providing results that are also reasonably close to those obtained previously using the popular MP2/CCSD(T)/CBS74,75 method as well as with DFT-SAPT/CBS21 (Table 1). HF underestimates all the interaction energies significantly, whilst MP2 significantly overestimates those of the stacked (S) conformers. Therefore, HFLD can be considered to be a cost-effective yet accurate method for the quantification of non-covalent interactions between nucleobases.
The role of the backbone
The inter-strand interaction energy computed for the SSBACK-C, SSBACK-N and SSN(BACK-C) models of DNA at the HF, HFLD, B3LYP-D3(BJ) and B3LYP-D3(BJ,ABC) levels in the gas phase and in water is given in Table 2. For the simplified SSN(BACK-C) model in the gas phase, the DLPNO-CCSD(T1)/TightPNO/def2-TZVP(-f) interaction energy amounts to −177.4 kcal mol−1, which is very close to −178.9 kcal mol−1 value obtained at the HFLD/def2-TZVP(-f) level. These results provide additional evidence for the great accuracy of the HFLD method in this context. In comparison, the interaction energy obtained at the HF level of theory is significantly underestimated (−86.0 kcal mol−1), whilst B3LYP-D3(BJ) without and with the three-body ABC dispersion term predicts an interaction energy of −194.4 and −190.5 kcal mol−1, respectively. The fact that HF underestimates the inter-strand interaction with respect to DLPNO-CCSD(T), whilst B3LYP-D3(BJ) overestimates it, is consistent with the results obtained in the previous subsection for the interaction of the individual bases.| System | HF | HFLD | B3LYP-D3(BJ) | B3LYP-D3(BJ,ABC) |
|---|---|---|---|---|
| a The corresponding DLPNO-CCSD(T1)/TightPNO/def2-TZVP(-f) interaction energy is −177.4 kcal mol−1. | ||||
| Gas phase | ||||
| SSBACK-N | −86.0 | −185.9 | −204.4 | −199.0 |
| SSN(BACK-C) | −86.0 | −178.9a | −194.4 | −190.5 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| In water | ||||
| SSBACK-C | 27.4 | −75.0 | −104.1 | −98.8 |
| SSBACK-N | 12.4 | −88.9 | −118.6 | −113.2 |
| SSN(BACK-C) | 13.5 | −80.7 | −107.1 | −103.2 |
In the gas phase, the interaction energy of large charged models of DNA, such as SSBACK-C, is known to be highly repulsive, because of the negative charge of the phosphate groups on the backbones, which leads to an insurmountable repulsive interaction in the gas phase.90 A common practice91 in QM studies of DNA for suppressing the excessive electrostatics is to artificially protonate one of the non-bridging oxygens of each phosphate group, as we have done in SSBACK-N. For this model, the inter-strand interaction becomes significantly attractive also in the gas phase, being −86.0, −185.9, −204.4 and −199.0 kcal mol−1 with HF, HFLD, B3LYP-D3(BJ) and B3LYP-D3(BJ,ABC) levels, respectively. These values are analogous to those obtained for SSN(BACK-C), which indicates that, for neutral systems, the backbone provides a small contribution to the overall interaction between the DNA strands.
In addition, by incorporating the effect of the water solvent implicitly in the energetics,86 all models provide similar interaction energies, including SSBACK-C. This suggests that the interaction between the DNA and the environment counteracts the repulsion between the negatively charged DNA strands in SSBACK-C. Thus, in solution, the net contribution of the backbones to the interaction appears to be small, irrespective of the particular DNA model used.
It is also worth emphasizing that the inclusion of the solvent lowers the overall interaction in neutral model systems. This effect can be explained by looking at the results shown in Table 3, in which the overall solvation correction at the HFLD level is decomposed into a contribution from the CPCM dielectric, representing direct DNA-solvent interactions, plus a polarization contribution, representing how the environment influences the electronic interaction between the DNA strands (see the ESI† for a detailed discussion of how these terms are computed and for a discussion of the importance of non-electrostatic solvation corrections). The contributions from the CPCM dielectric and polarization are both very similar to each other for neutral systems with and without backbones. The contribution from the CPCM dielectric is large and positive, which causes the overall interaction to decrease in solution. In contrast, the effect of the environment on the electronic interaction between the strands is small and essentially the same irrespective of the particular DNA model employed.
| Total solvation contribution | Direct DNA-solvent contribution | DNA polarization contribution | |
|---|---|---|---|
| SSBACK-N | 97.0 | 123.2 | −26.2 |
| SSN(BACK-C) | 98.1 | 125.0 | −26.9 |
Importantly, for SSBACK-N and SSN(BACK-C), the calculated Edisp contribution to the inter-strand stability of the duplex is −99.9 and −92.9 kcal mol−1 in the gas phase (only ∼1 kcal mol−1 larger for both models in water), respectively. Therefore, the dispersion contribution to the backbone–backbone interaction is noticeable but weak compared to base–base dispersion interactions.
All these findings demonstrate that:
(i) The two DNA strands are held together by the interaction of the bases;
(ii) In solution, the net effect of the backbone to the interaction is small compared to that originating from the interaction between the bases. However, its residual contribution is likely to be very sensitive to the environment, e.g., to the concentration of ions in solution. A complete theoretical characterization of temperature and ion concentration effects is beyond the scope of the present work;
(iii) London dispersion provides a fundamental contribution to the stability of the DNA duplex structure.
In the following section, we will elucidate the details of the interaction between the bases in DNA, which are responsible for the intrinsic stability of the DNA duplex. For the sake of simplicity, we will focus on the SSN(BACK-C) model.
HFLD/LED analysis of the inter-strand interaction
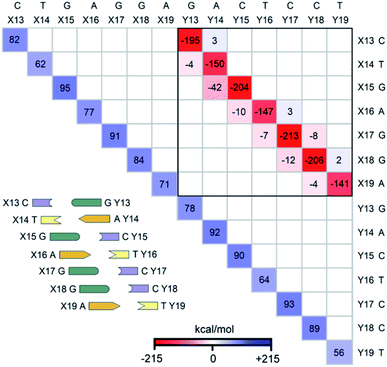
The LED interaction map provides a clear-cut visual representation of the interactions between the nucleobases and it is given in Fig. 3 for the SSN(BACK-C) model system. The corresponding metadata are given in the ESI.† Note that the sum of all the elements in Fig. 3, plus the repulsive CPCM dielectric correction (direct DNA-solvent contribution in Table 3), provides the exact inter-strand interaction energy computed at the HFLD level in water, i.e., −80.7 kcal mol−1. As discussed in the ESI,† the LED maps are only weakly affected by the specific DNA model considered or by the level of theory used for describing environmental effect.We consider first the submatrix enclosed by a solid black square in Fig. 3, which represents the pairwise interactions between the bases on different strands, i.e., the interactions of bases X13–X19 with bases Y13–Y19.
The first eye catching feature of this matrix is that the strongest inter-strand interaction is due to WC base pairing, which corresponds to the diagonal elements of this submatrix. In contrast, inter-strand stacking is effective only for the bases on neighboring sites, i.e., for the X(x)⋯Y(x + 1) and X(x + 1)⋯Y(x) interactions. These results are remarkable because they provide a first theoretical validation of popular nearest neighbor (NN) models92–100 for predicting thermodynamic data of given DNA sequences. In fact, NN models assume no interaction between distant bases and consider only the interaction between adjacent pairs.
Moreover, our analysis also demonstrates that, due to the right-handed helical structure of B-DNA, the bases at sites X(x + 1) and Y(x) show larger overlaps than those at X(x) and Y(x + 1). Thus, the X(x + 1)⋯Y(x) stacking interactions are attractive and much stronger than the X(x)⋯Y(x + 1) stacking interactions, with the latter being usually very small or even repulsive (see the non-diagonal elements of the submatrix). We have illustrated this feature of B-DNA by plotting the schematic ladders tilted. This interesting pattern of stacking interactions is consistent with the observation that DNA sequences having the same GC-content do not necessarily have the same interaction energies,101 and stacking interactions among unnatural nucleobases that cannot form H-bonds are strong enough to keep the two strands together.102
The non-diagonal elements in the upper and lower triangular submatrices in Fig. 3 show how interactions between the base pairs on the same strand are affected by the inter-strand interaction. These numbers are essentially negligible in all cases, demonstrating that there is essentially no cooperativity between intra-strand stacking and inter-strand base pairing.
Finally, the diagonal elements in Fig. 3 represent the energy needed to distort the electronic structure of the bases on one DNA strand to prepare them for the interaction with the bases on the other DNA strand. They are repulsive by definition and their magnitude is slightly larger for G and C than for A and T. This effect originates from the fact that the electronic structure of G and C is perturbed by the formation of three H-bonds, whilst that of the latter by just two.
Electrostatics, exchange and dispersion interactions
To gain further insights into the nature of the stability of DNA duplex, the submatrix of the LED interaction energy map corresponding to the interaction between bases on different strands can be further decomposed into electrostatic, exchange and dispersion components. Such decompositions are provided for SSN(BACK-C) in Fig. 4.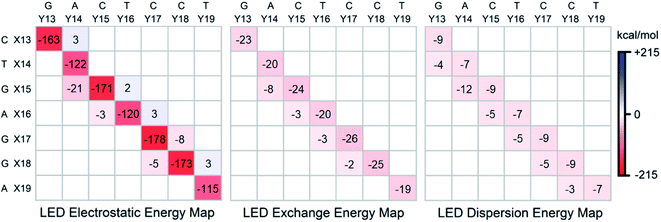 | ||
| Fig. 4 Electrostatic, exchange and dispersion energy submatrices of the LED interaction energy map for SSN(BACK-C) in water. | ||
Consistent with previously published results on isolated dimers and base steps,17–23 these decompositions demonstrate that base pairing (H-bonding) is mainly of electrostatic origin also when the base pairs are in their biologically relevant structure. Exchange and dispersion also play a smaller but important role. All these attractive components are consistently larger for the G–C pair than for the A–T pair. Therefore, the stability of DNA increases with the increase of its GC-content, consistent with the above mentioned textbook explanation based on melting temperature data.5
As discussed above, the stabilizing effect associated with the inter-strand stacking, which is much smaller than that originating from base pairing, arises from X(x + 1)⋯Y(x) interactions. This stabilization originates from London dispersion forces to a large extent, with a smaller but noticeable contribution from the exchange interactions. The X(x + 1)⋯Y(x) inter-strand stacking interaction demonstrates some common patterns based on the size of the bases, i.e., based on their overlap: it is the largest when both the X(x + 1) and the Y(x) bases are double-ringed (A or G). The interaction is still noticeably large when just one of the bases is double-ringed. However, when both of these bases are single-ringed (T or C), the X(x + 1)⋯Y(x) interaction is the smallest (even repulsive in some cases due to electrostatics), with essentially negligibly small contributions from the attractive exchange and dispersion interactions. Abbreviating the double-ringed G or A as “d”, and the single-ringed C or T as “s”, the stability sequence of the inter-strand stacking in base steps is thus sd⋯ds > dd⋯ss ≈ ss⋯dd > ds⋯sd. Finally, it is worth emphasizing here that the results just discussed remains valid irrespective of the size of the model system considered, as demonstrated in the ESI† of this work on the LSN(BACK-C) model, featuring more than 1000 atoms and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 basis functions.
000 basis functions.
Conclusions
Our analysis suggests that the interaction between the two strands of large DNA models are dominated by the contribution of neighboring bases, which provides a first theoretical validation of nearest neighbor models. Consistent with previous AFM studies of large DNAs and the previous computational studies on much smaller model systems, we have found that the largest contribution to the stability of the duplex structure is the Watson–Crick base pairing, while the effect of stacking between adjacent bases is relatively small but still important for the stability of the DNA duplex. London dispersion effects were found to be essential for the stability of the duplex, while cooperativity effects between intra-strand stacking and inter-strand base pairing interactions provide a negligible contribution. To the best of our knowledge, this is the first time that a quantitative, QM-based multi-fragment energy decomposition analysis is reported for a realistic DNA model.Data availability
The Cartesian coordinates of all structures, the results of benchmark calculations on solvation schemes and geometries, the detailed decomposed energy terms of the inter-strand interaction energy for different B-DNA models, the corresponding heat maps, the average base step contributions and the generic references for the methods used are provided in the ESI.†Author contributions
G. B. devised the project, designed the computational framework and supervised the study. A. A. carried out all the calculations and wrote the original draft. G. B., A. A., M. G.-R. and F. N. contributed to the analysis of the results and to the writing of the manuscript. M. G.-R. implemented coupled-cluster solvation schemes in ORCA.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the Priority Program “Control of Dispersion Interactions in Molecular Chemistry” (SPP 1807) of the Deutsche Forschungsgemeinschaft for financial support.References
- J. Watson and A. Berry, DNA: The Secret of Life, Arrow Books, Croydon, UK, 2004 Search PubMed.
- D. B. McIntosh, G. Duggan, Q. Gouil and O. A. Saleh, Biophys. J., 2014, 106, 659–666 CrossRef CAS PubMed.
- G. H. Fried and G. J. Hademenos, Schaum's Outline of Biology, McGraw Hill Canada, 5th edn, 2019 Search PubMed.
- D. L. Nelson and M. Cox, Lehninger Principles of Biochemistry, Macmillan Learning, 7th edn, 2017 Search PubMed.
- J. Marmur and P. Doty, J. Mol. Biol., 1962, 5, 109–118 CrossRef CAS.
- E. T. Kool, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 1–22 CrossRef CAS PubMed.
- F. Kilchherr, C. Wachauf, B. Pelz, M. Rief, M. Zacharias and H. Dietz, Science, 2016, 353, aaf5508 CrossRef PubMed.
- P. Yakovchuk, E. Protozanova and M. D. Frank-Kamenetskii, Nucleic Acids Res., 2006, 34, 564–574 CrossRef CAS PubMed.
- A. Vologodskii and M. D. Frank-Kamenetskii, Phys. Life Rev., 2018, 25, 1–21 CrossRef PubMed.
- P. L. Privalov and C. Crane-Robinson, Eur. Biophys. J., 2020, 49, 315–321 CrossRef CAS PubMed.
- P. L. Privalov, J. Biophys. Struct. Biol., 2020, 8, 1–7 CrossRef.
- T.-B. Zhang, C.-L. Zhang, Z.-L. Dong and Y.-F. Guan, Sci. Rep., 2015, 5, 9143 CrossRef CAS PubMed.
- E. Pastorczak and C. Corminboeuf, J. Chem. Phys., 2017, 146, 120901 CrossRef PubMed.
- M. von Hopffgarten and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43–62 CAS.
- M. J. S. Phipps, T. Fox, C. S. Tautermann and C.-K. Skylaris, Chem. Soc. Rev., 2015, 44, 3177–3211 RSC.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS.
- R. Sedlák, P. Jurečka and P. Hobza, J. Chem. Phys., 2007, 127, 075104 CrossRef PubMed.
- J. F. Gonthier and C. D. Sherrill, J. Chem. Phys., 2016, 145, 134106 CrossRef PubMed.
- J. Šponer, K. E. Riley and P. Hobza, Phys. Chem. Chem. Phys., 2008, 10, 2595 RSC.
- P. R. Horn, Y. Mao and M. H. Gordon, Phys. Chem. Chem. Phys., 2016, 18, 23067–23079 RSC.
- A. Hesselmann, G. Jansen and M. Schütz, J. Am. Chem. Soc., 2006, 128, 11730–11731 CrossRef CAS PubMed.
- J. Poater, M. Swart, F. M. Bickelhaupt and C. F. Guerra, Org. Biomol. Chem., 2014, 12, 4691–4700 RSC.
- T. A. Hamlin, J. Poater, C. Fonseca Guerra and F. M. Bickelhaupt, Phys. Chem. Chem. Phys., 2017, 19, 16969–16978 RSC.
- H. Kruse, P. Banáš and J. Šponer, J. Chem. Theory Comput., 2019, 15, 95–115 CrossRef CAS PubMed.
- T. M. Parker, E. G. Hohenstein, R. M. Parrish, N. V. Hud and C. D. Sherrill, J. Am. Chem. Soc., 2013, 135, 1306–1316 CrossRef CAS PubMed.
- S. C. C. van der Lubbe and C. Fonseca Guerra, Chem.–Asian J., 2019, 14, 2760–2769 CAS.
- G. Barone, C. Fonseca Guerra and F. M. Bickelhaupt, ChemistryOpen, 2013, 2, 186–193 CrossRef CAS PubMed.
- O. A. Stasyuk, D. Jakubec, J. Vondrášek and P. Hobza, J. Chem. Theory Comput., 2017, 13, 877–885 CrossRef CAS PubMed.
- W. B. Schneider, G. Bistoni, M. Sparta, M. Saitow, C. Riplinger, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2016, 12, 4778–4792 CrossRef CAS PubMed.
- A. Altun, F. Neese and G. Bistoni, J. Chem. Theory Comput., 2019, 15, 215–228 CrossRef CAS PubMed.
- A. Altun, M. Saitow, F. Neese and G. Bistoni, J. Chem. Theory Comput., 2019, 15, 1616–1632 CrossRef CAS PubMed.
- G. Bistoni, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, e1442 Search PubMed.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed.
- A. Altun, F. Neese and G. Bistoni, Beilstein J. Org. Chem., 2018, 14, 919–929 CrossRef CAS PubMed.
- F. Neese, M. Atanasov, G. Bistoni, D. Manganas and S. Ye, J. Am. Chem. Soc., 2019, 141, 2814–2824 CrossRef CAS PubMed.
- Q. Lu, F. Neese and G. Bistoni, Phys. Chem. Chem. Phys., 2019, 2019, 11569–11577 RSC.
- Q. Lu, F. Neese and G. Bistoni, Angew. Chem., Int. Ed., 2018, 57, 4760–4764 CrossRef CAS PubMed.
- G. Bistoni, A. A. Auer and F. Neese, Chem.–Eur. J., 2017, 23, 865–873 CrossRef CAS PubMed.
- A. Altun, R. Izsák and G. Bistoni, Int. J. Quantum Chem., 2021, 121, e26339 CrossRef CAS.
- A. Altun, F. Neese and G. Bistoni, J. Chem. Theory Comput., 2019, 15, 5894–5907 CrossRef CAS PubMed.
- J. Hepburn, G. Scoles and R. Penco, Chem. Phys. Lett., 1975, 36, 451–456 CrossRef CAS.
- R. Podeszwa, K. Pernal, K. Patkowski and K. Szalewicz, J. Phys. Chem. Lett., 2010, 1, 550–555 CrossRef CAS.
- E. B. Guidez and M. S. Gordon, J. Phys. Chem. A, 2015, 119, 2161–2168 CrossRef CAS PubMed.
- B. Jeziorski, M. van Hemert and B. Jeziorski, Mol. Phys., 1976, 31, 713–729 CrossRef CAS.
- T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 094106 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- R. Sure and S. Grimme, J. Comput. Chem., 2013, 34, 1672–1685 CrossRef CAS PubMed.
- L. Goerigk and J. R. Reimers, J. Chem. Theory Comput., 2013, 9, 3240–3251 CrossRef CAS PubMed.
- L. Goerigk, C. A. Collyer and J. R. Reimers, J. Phys. Chem. B, 2014, 118, 14612–14626 CrossRef CAS PubMed.
- H. Kruse and S. Grimme, J. Chem. Phys., 2012, 136, 154101 CrossRef PubMed.
- J. A. Conrad and M. S. Gordon, J. Phys. Chem. A, 2015, 119, 5377–5385 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- G. Honig and J. Adams, Human Hemoglobin Genetics, Springer-Verlag, 2012 Search PubMed.
- M. van Dijk and A. M. J. J. Bonvin, Nucleic Acids Res., 2009, 37, W235–W239 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- G. Bistoni, C. Riplinger, Y. Minenkov, L. Cavallo, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2017, 13, 3220–3227 CrossRef CAS PubMed.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503–506 CrossRef CAS.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS.
- F. Neese, J. Comput. Chem., 2003, 24, 1740–1747 CrossRef CAS PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 064107 CrossRef PubMed.
- K. A. Peterson and T. H. Dunning, J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 2975–2988 CrossRef CAS.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. L. Martin and F. Neese, J. Chem. Theory Comput., 2015, 11, 1525–1539 CrossRef CAS PubMed.
- S. F. Boys, Rev. Mod. Phys., 1960, 32, 296–299 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- R. Izsák and F. Neese, J. Chem. Phys., 2011, 135, 144105 CrossRef PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef.
- P. Jurečka, J. Šponer, J. Černý and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985–1993 RSC.
- J. Šponer, M. Zgarbová, P. Jurečka, K. E. Riley, J. E. Šponer and P. Hobza, J. Chem. Theory Comput., 2009, 5, 1166–1179 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 2002, 98, 11623–11627 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- D. Wu and D. G. Truhlar, J. Chem. Theory Comput., 2021, 17, 3967–3973 CrossRef CAS PubMed.
- A. Mládek, M. Krepl, D. Svozil, P. Čech, M. Otyepka, P. Banáš, M. Zgarbová, P. Jurečka and J. Šponer, Phys. Chem. Chem. Phys., 2013, 15, 7295–7310 RSC.
- M. E. Beck, C. Riplinger, F. Neese and G. Bistoni, J. Comput. Chem., 2021, 42, 293–302 CrossRef CAS PubMed.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Garcia-Ratés and F. Neese, J. Comput. Chem., 2019, 40, 1816–1828 CrossRef PubMed.
- M. Garcia-Ratés and F. Neese, J. Comput. Chem., 2020, 41, 922–939 CrossRef PubMed.
- R. Cammi, J. Chem. Phys., 2009, 131, 164104 CrossRef CAS PubMed.
- M. Caricato, J. Chem. Phys., 2011, 135, 074113 CrossRef PubMed.
- M. Garcia-Ratés, U. Becker and F. Neese, J. Comput. Chem., 2021, 42, 1959–1973 CrossRef PubMed.
- J. Šponer, A. Mládek, J. E. Šponer, D. Svozil, M. Zgarbová, P. Banáš, P. Jurečka and M. Otyepka, Phys. Chem. Chem. Phys., 2012, 14, 15257–15277 RSC.
- H. Y. Chen, C. L. Kao and S. C. N. Hsu, J. Am. Chem. Soc., 2009, 131, 15930–15938 CrossRef CAS PubMed.
- O. Gotoh and Y. Tagashira, Biopolymers, 1981, 20, 1033–1042 CrossRef CAS.
- A. V. Vologodskii, B. R. Amirikyan, Y. L. Lyubchenko and M. D. Frank- Kamenetskii, J. Biomol. Struct. Dyn., 1984, 2, 131–148 CrossRef CAS PubMed.
- K. J. Breslauer, R. Frank, H. Blocker and L. A. Marky, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 3746–3750 CrossRef CAS PubMed.
- S. G. Delcourt and R. D. Blake, J. Biol. Chem., 1991, 266, 15160–15169 CrossRef CAS.
- M. J. Doktycz, R. F. Goldstein, T. M. Paner, F. J. Gallo and A. S. Benight, Biopolymers, 1992, 32, 849–864 CrossRef CAS PubMed.
- J. SantaLucia, H. T. Allawi and P. A. Seneviratne, Biochemistry, 1996, 35, 3555–3562 CrossRef CAS PubMed.
- N. Sugimoto, S. Nakano, M. Yoneyama and K. Honda, Nucleic Acids Res., 1996, 24, 4501–4505 CrossRef CAS PubMed.
- H. T. Allawi and J. Santalucia, Biochemistry, 1997, 36, 10581–10594 CrossRef CAS PubMed.
- J. SantaLucia, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 1460–1465 CrossRef CAS PubMed.
- H. Chen and C. K. Skylaris, Phys. Chem. Chem. Phys., 2021, 23, 8891–8899 RSC.
- S. Jahiruddin and A. Datta, J. Phys. Chem. B, 2015, 119, 5839–5845 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The optimized coordinates of the structures and their detailed energetics (XLSX). See DOI: 10.1039/d1sc03868k |
| This journal is © The Royal Society of Chemistry 2021 |