Open Access Article
Open Access ArticleAttaining record-high magnetic exchange, magnetic anisotropy and blocking barriers in dilanthanofullerenes†
Sourav
Dey
 and
Gopalan
Rajaraman
and
Gopalan
Rajaraman
 *
*
Department of Chemistry, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India. E-mail: rajaraman@chem.iitb.ac.in
First published on 6th October 2021
Abstract
While the blocking barrier (Ueff) and blocking temperature (TB) for “Dysprocenium” SIMs have been increased beyond liquid N2 temperature, device fabrication of these molecules remains a challenge as low-coordinate Ln3+ complexes are very unstable. Encapsulating the lanthanide ion inside a cage such as a fullerene (called endohedral metallofullerene or EMF) opens up a new avenue leading to several Ln@EMF SMMs. The ab initio CASSCF calculations play a pivotal role in identifying target metal ions and suitable cages in this area. Encouraged by our earlier prediction on Ln2@C79N, which was verified by experiments, here we have undertaken a search to enhance the exchange coupling in this class of molecules beyond the highest reported value. Using DFT and ab initio calculations, we have studied a series of Gd2@C2n (30 ≤ 2n ≤ 80), where an antiferromagnetic JGd⋯Gd of −43 cm−1 was found for a stable Gd2@C38-D3h cage. This extremely large and exceptionally rare 4f⋯4f interaction results from a direct overlap of 4f orbitals due to the confinement effect. In larger cages such as Gd2@C60 and Gd2@C80, the formation of two centre-one-electron (2c-1e−) Gd–Gd bonds is perceived. This results in a radical formation in the fullerene cage leading to its instability. To avoid this, we have studied heterofullerenes where one of the carbon atoms is replaced by a nitrogen atom. Specifically, we have studied Ln2@C59N and Ln2@C79N, where strong delocalisation of the electron yields a mixed valence-like behaviour. This suggests a double-exchange (B) is operational, and CASSCF calculations yield a B value of 434.8 cm−1 and resultant JGd–rad of 869.5 cm−1 for the Gd2@C59N complex. These parameters are found to be two times larger than the world-record J reported for Gd2@C79N. Further ab initio calculations reveal an unprecedented Ucal of 1183 and 1501 cm−1 for Dy2@C59N and Tb2@C59N, respectively. Thus, this study offers strong exchange coupling as criteria for new generation SMMs as the existing idea of enhancing the blocking barrier via crystal field modulation has reached its saturation point.
Introduction
Single molecule magnets (SMMs) are of prime interest in molecular magnetism due to their potential application in memory storage devices, qubits, etc.1,2 The figure of merit of an SMM is determined by the blocking barrier for magnetisation reversal (Ueff) and blocking temperature (TB), the temperature below which opening of magnetic hysteresis is observed. These Ueff and TB values are generally very high for lanthanides, thanks to their strong spin–orbit coupling.3–10 The enhancement of TB as high as 80 K in “Dysprocenium” complexes was an important breakthrough, replenishing the hope for potential applications in information storage devices.11–15 Among others, important bottlenecks that are likely to hamper the futuristic application of these SMMs are (i) enhancing the blocking temperature beyond 80 K (ii) obtaining molecules that are stable under ambient conditions so that fabrication can be attempted (iii) retaining their intriguing magnetic properties upon fabrication – many of the best transition metal SMMs failed these criteria.16–21To address the first challenge, among other strategies that could help enhance the barrier height/blocking temperature is the quenching of quantum tunnelling of magnetisation (QTM), which is prevalent at low temperatures. If a robust magnetic exchange between two Ln3+ ions is induced, it can act as a perturbation to reduce the degeneracy of Kramers doublets (KDs). This quenches the QTM and gives rise to large Ueff and TB values.22–24 However, obtaining a large exchange coupling between two Ln3+ metal ions is a formidable task as 4f orbitals are deeply buried, leading to a weak/no interaction in dinuclear or polynuclear Ln3+ complexes.8,25–30
In this regard, lanthanide encapsulated fullerenes (called endohedral metallofullerenes or EMFs) are gaining tremendous attention for various reasons: (a) they offer stability to guest molecules which are otherwise unstable;31 (b) thanks to their strong π cloud, fabrication of such molecules on graphene/HOPG/CNTs and other surfaces is straightforward;31–39 (c) during this process guest molecules stay intact, and hence they are unlikely to lose their characteristics upon fabrication;31 (d) as fullerenes are made of pure carbon, and the source of nuclear spin of the guest molecules can be controlled, they offer a nuclear spin free system – a key criterion for some qubit applications.31,40 These key advantages mentioned here directly address the aforementioned goals (ii) and (iii), making them superior to traditional coordination chemistry/organometallic SMMs/SIMs.
One way to attain strong exchange coupling in lanthanide SMMs is to employ radical–Ln exchange which is substantially larger due to the direct exchange between 4f–2p orbitals.41–43 In the search for a stronger exchange in Ln–radical systems, using a combination of DFT and ab initio methods, we have predicted a record high magnetic exchange coupling for a Gd2@C79N radical fullerene complex and also suggested a very large blocking barrier for the Dy analogue.44,45 Both these predictions were proved in a span of few years independently by two groups,46–49 and Gd2@C79N is found to have a very large spin relaxation time opening up a new avenue in spin-based qubits.40,46 While a Ln–radical exchange could solve this problem,41 the majority of the conventional lanthanide–radical systems are highly reactive and could pose a challenge in accomplishing the aforementioned goals (ii) and (iii).41,43,50–55
In this connection, if a robust exchange is induced between two Ln3+ ions, this will be very rewarding. One strategy to enhance the exchange coupling is to induce a weak Ln⋯Ln bond, which is possible if two ions are brought very close to each other directly. The metal–metal bonds in transition metal complexes are common but are scarce for lanthanides.56–58 Inspired from the report that even noble gas elements such as He form He⋯He bonds under confinement, we devise such models for lanthanides that can offer very large 4f–4f exchange interactions.59–63 In line with this idea, we have explored various Gd2@C2n (2n = 30–52, 60, 80) complexes in search of a stronger exchange and found Gd3+⋯Gd3+ exchange as high as −43 cm−1. In the second approach, we have extended our study to air-stable azafullerene radical analogues such as Ln2@C59/79N (Ln = Gd, Tb, Dy). Using ab initio calculations, we have computed the double-exchange parameter B in these azafullerene cages. We have exploited the presence of double exchange to design SMMs based on Dy and Tb and unveil a new line of prediction with models exhibiting a Ueff value exceeding 1500 cm−1.
Results and discussion
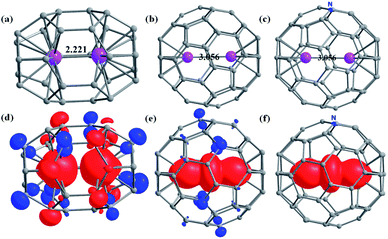
Achieving large exchange coupling in lanthanides is challenging as the 4f orbitals of lanthanides are deeply buried and interact weakly with ligand orbitals. The highest magnetic exchange between two Ln3+ ions is estimated in a {Gd2Cr2} complex where JGd–Gd is +1.4 cm−1 (Ĥ = −JŜ1Ŝ2).28 As the Ln⋯Ln distance plays a crucial role in controlling the 4f–4f exchange interaction, a large J is expected if two Ln3+ ions are confined in a fullerene cage. With this goal, we begin our study with Gd2 endohedral fullerenes by varying the cage size from C30 to C80. We have analysed the structure, binding energy, and magnetic properties within the DFT framework for two low energy conformers of the fullerene cages among various close-lying isomers.Structure and bonding in Gd2@C2n (2n = 30–48, 52, 40, 80)
The C30 fullerene is the smallest cage where encapsulation leads to a stable geometry, as steric strain dominates over the metal-cage stabilisation in C28 and lower cages (Fig. 1, Table S1 and Appendix S1–S25†). For Gd2@C30, a C2v isomer is found to be stable by 52.3 kJ mol−1 compared to the D5h isomer due to stronger Gd–C interactions in the former as affirmed by the AIM analysis (see Table 1 for larger cages and Tables S1–S4 in the ESI†). In larger cages, the stability can be rationalised using (i) the number of APRs (Table S2†) and (ii) the nature of Gd–C interaction as obtained from the AIM analysis (see Fig. 1, S1–S26 and Tables S3–S27 in the ESI†).| Gd2@C2n | J Gd⋯Gd (cm−1) | Binding energy (kJ mol−1) | ΔE (kJ mol−1) | |||
|---|---|---|---|---|---|---|
| a The binding energy has been calculated with respect to electronic energy. In all other isomers, the binding energy has been calculated with respect to electronic and thermal free energies. b Here ‘n’ represents the total number of atoms, including the one nitrogen atom. | ||||||
| 2n = 30 | C 2v (2.185) | D 5h (2.224) | C 2v | D 5h | C 2v | D 5h |
| J Gd–Gd = −49.8 (6.96; 6.95) | J Gd–Gd = −62.7 (6.94; 6.94) | 1160.9 | 1149.8 | 0.0 | 52.3 | |
| 2n = 32 | C 2 (2.207) | D 3 (2.272) | C 2 | D 3 | C 2 | D 3 |
| J Gd–Gd = −12.0 (6.93; 6.95) | J Gd–Gd = −15.5 (6.93; 6.93) | 907.3 | 620.2 | 166.5 | 0.0 | |
| 2n = 34 | C s (2.283) | C 2 (2.266) | C s | C 2 | C s | C 2 |
| J Gd–Gd = −11.6 (6.94; 6.94) | J Gd–Gd = −13.7 (6.94; 6.94) | 279.1 | 392.1 | 73.0 | 0.0 | |
| 2n = 36 | C s (2.400) | D 2d (2.269) | C s | D 2d | C s | D 2d |
| J Gd–Gd = −8.3 (6.92; 6.97) | J Gd–Gd = −26.3 (6.96; 6.95) | 61.0 | 330.0 | 0.0 | 37.2 | |
| 2n = 38 | C 1 (2.443) | D 3h (2.734) | C 1 | D 3h | C 1 | D 3h |
| J Gd–Gd = −7.0 (6.97; 6.93) | J Gd–Gd = −43.4 (6.99; 6.99) | −108.1 | −63.0 | 0.0 | 478.1 | |
| 2n = 40 | C 2v (2.376) | D 2 (2.400) | C 2v | D 2 | C 2v | D 2 |
| J Gd–Gd = −4.9 (7.00; 7.00) | J Gd–Gd = −10.3 (6.99; 6.99) | 0.7 | −173.2 | 320.6 | 0.0 | |
| 2n = 42 | C 1 (2.495) | D 3 (2.430) | C 1 | D 3 | C 1 | D 3 |
| J Gd–Gd = −3.0 (6.99; 6.99) | J Gd–Gd = −7.6 (7.00; 7.00) | −337.3 | −193.1 | 0.0 | 60.8 | |
| 2n = 44 | C s (2.608) | D 2 (2.549) | C s | D 2 | C s | D 2 |
| J Gd–Gd = 0.2 (6.98; 7.02) | J Gd–Gd = −8.4 (7.00; 7.00) | −386.9 | −308.0 | 157.1 | 0.0 | |
| 2n = 46 | C 1 (2.728) | C s (2.796) | C 1 | C s | C 1 | C s |
| J Gd–Gd = −1.4 (6.99; 7.00) | J Gd–Gd = −0.3 (6.98; 6.98) | −494.8 | −537.0 | 42.1 | 0.0 | |
| 2n = 48 | C 1 (2.836) | C 2v (3.002) | C 1 | C 2v | C 1 | C 2v |
| J Gd–Gd = −0.4 (7.00; 7.00) | J Gd–Gd = 0.7 (6.99; 6.99) | −560.2 | −534.3 | 0.0 | 410.6 | |
| 2n = 52 | C s (3.282) | D 2d (2.324) | C s | D 2d | C s | D 2d |
| J Gd–Gd = −1.3 (7.02; 6.99) | J Gd–Gd = 2.7 (7.04; 7.04) | −595.2 | −991.4 | 224.3 | 0.0 | |
| 2n = 60b | Gd2@C60-Ih (3.056) | Gd2@C59N-Cs (3.056) | Gd2@C60-Ih | Gd2@C59N-Cs | ||
| J 1 = 869.8, J2 = 0.08, J3 = 40.2, B = 434.8 (7.53; 7.53) | J 1 = 869.8, J2 = 0.08, B = 434.8 (7.54; 7.54) | −369.4a | −389.1a | |||
| 2n = 80b | D 5h (3.818) | C 2v (4.074) | D 5h | C 2v | D 5h | C 2v |
| J 1 = 404.6, J2 = 0.03, B = 202.1, J3 = −41.3 (7.54; 7.54) | J 1 = 351.3, J2 = 0.03, B = 175.6, J3 = −95.5 (7.52; 7.53) | −987.6a | −840.5a | 0.0 | 96.7 | |
| 2n = 80b | Gd2@C79N-Cs-1 (3.816) | Gd2@C79N-Cs-2 (4.107) | Gd2@C79N-Cs-1 | Gd2@C79N-Cs-2 | Gd2@C79N-Cs-1 | Gd2@C79N-Cs-2 |
| J 1 = 404.6, J2 = 0.03, B = 202.1 (7.55; 7.55) | J 1 = 351.3, J2 = 0.03, B = 175.6 (7.51; 7.53) | −958.0a | −733.7a | 0.0 | 157.7 | |
Considering the Gd3+ ionic radius,64 a Gd⋯Gd distance less than 2.5 Å (van der Walls radii) is likely to suggest a weak interaction or even a metal–metal bond. Such interactions are expected to reflect on JGd–Gd values with smaller values indicate weaker Gd⋯Gd interactions and not a metal–metal bond. Therefore, to compare the metal–metal interaction in Gd2@C2n with 30 ≤ 2n ≤ 52, the magnetic exchange JGd–Gd between two Gd3+ ions has been estimated using DFT calculations (B3LYP/TZV, Ĥ = −JŜGd1ŜGd2, see computational details and Table 1). The JGd–Gd is found to be antiferromagnetic in all Gd2@C2n (2n ≤ 52) EMFs with the exception of Gd2@C44-Cs, Gd2@C48-C2v, and Gd2@C52-D2d EMFs having a ferromagnetic coupling (Table 1). The value in Table 1 suggests the decrease in antiferromagnetic interaction with the decrease in cage size. Within the same cage, the JGd–Gd value increases for a higher symmetry isomer. The largest antiferromagnetic JGd–Gd was estimated for Gd2@C30-D5h (−62.7 cm−1). This is several orders of magnitude larger than the experimentally known largest 4f–4f interaction. For the Gd2@C30-C2v isomer, the JGd–Gd decreases to −49.6 cm−1 despite a shorter Gd⋯Gd distance compared to the D5h isomer. This is due to stronger 4f–4f overlaps (Tables S28–S29†). Although the Gd⋯Gd distances are very similar for C30 and C32, the JGd–Gd value is significantly smaller in Gd2@C32 (see Table 1) due to symmetry constraints and the associated 4f–4f overlaps (see Tables S30–S49 in ESI†). Further increase in the cage size only nominally decreases the JGd–Gd values with several exceptions, though lower symmetry models follow the trend (see Fig. S27†). A net ferromagnetic interaction is observed in Gd2@C44-Cs, Gd2@C48-C2v and Gd2@C52-D2d cages due to a meagre contribution to the antiferromagnetic part of J (see Tables S42, S46 and S48†). Orbital orthogonality of 4f-orbitals and dipolar contributions due to shorter Gd⋯Gd distance leads to a net ferromagnetic coupling in these examples. A very large 4f–4f overlap suggests a possibility of direct 4f–4f interactions between two lanthanide ions, which are hard to observe in classical coordination chemistry. The binding energy becomes positive for Gd2@C2n with 2n ≤ 36 and negative for Gd2@C2n with 2n > 36 (see Table 1) except for the Gd2@C40-C2v isomer, where it is thermoneutral (0.7 kJ mol−1). Thus, it suggests that the large antiferromagnetic interaction is feasible for the isomers of Gd2@C2n with 2n > 36.
The magnitude of the spin density of the two Gd3+ ions increases with an increase in ring size, supported by the contour plots of the electron density map obtained from AIM analysis (Fig. S28–S54 and Tables S50, S51†). Particularly a sudden jump in the magnitude of spin density is noted for Gd2@C60, with nearly one electron found between the two Gd ions (see Fig. 1, S50–S52†). Our NBO analysis reveals that this electron is delocalised in the formally empty orbitals, which are hybridised among 6s, 6p, and 5d orbitals (6s6p0.115d0.33, see Fig. S55†). Thus, it suggests a strong valence delocalisation where one unpaired electron is delocalised to vacant 5d/6s/6p orbitals of each Gd3+ ion leading to a type-III class of mixed valence systems (Gd2.5+⋯Gd2.5+, see later).65
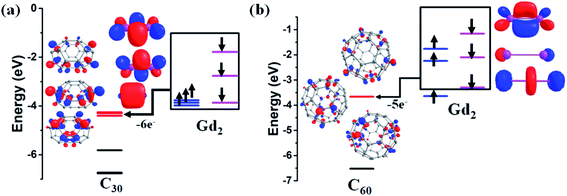
Mechanism of the formation of Gd2@C2n
To further investigate the unusual behaviour wherein the cage size decides the magnitude of the spin density present between the Gd3+ ion, we have analysed the formation of Gd2@C2n from the HOMO–LUMO gap perspective. In the formation of dimetallofullerene Gd2@C2n, we can presume that two Gd atoms donate three electrons each from their frontier orbitals (5d and 6s orbitals) to the three lowest unoccupied molecular orbitals (LUMOs) of the C2n cage resulting in Gd26+@C2n6−.66 Thus, the formation of Gd2@C2n depends on the energy gap between the frontier orbitals of Gd2 and the LUMOs of the C2n cage. If the LUMOs of the C2n cage are found to be lower in energy than the frontier orbitals of the Gd2 fragment, a large stabilisation occurs after the electron transfer. Quite interestingly, this is the case for the C2n cage with 2n ≤ 52, which favours the transfer of six electrons from Gd2 (with the Gd–Gd distance <3.0 Å, ignoring 4f orbitals, the valence electron configuration is σ2gσ1uπ1gπ2u)67 to the C2n cage (Fig. 2a for Gd2@C30 and Fig. S56 and S57† for Gd2@C52-D2d and Gd2@C48-C2v). As the ring size increases, the LUMOs of the C2n cage destabilised. In Gd2@C60 with the Gd⋯Gd distance of 3.056 Å, the bonding in the Gd2 fragment before encapsulation is found to be σ2gπ3uσ1u (ignoring the 4f orbitals, Fig. 2b). After encapsulation, the five electrons are fully transferred to the cage except one σ1g electron (here the β electron in Fig. 2b for Gd2@C60-Ih) resulting in a 2c-1e− bond between two Gd atoms. This is due to the comparable energy of the beta (6s/5d) σ1g orbital with the LUMO of the C2n cage.Estimation of magnetic exchange in Gd2@C59N-Cs, Gd2@C79N-Cs-1, and Gd2@C79N-Cs-2
The most sensitive parameter that yields insight into the spin density distribution discussed in the last section is the corresponding exchange coupling JGd–Gd. Here we intend to compute this parameter and analyse this with respect to the cage size. The mechanism of formation of Gd2@C2n suggests the presence of one unpaired electron between two Gd3+ ions and another conjugate electron in the fullerene cage for Gd2@C60-Ih, Gd2@C80-D5h, and Gd2@C80-C2v isomers (see Table S50†). For these molecules, a complex set of magnetic coupling emerges: (i) the coupling between Gd3+ and the radical that reside inside the cage (J1), (ii) the second one describes the coupling between two Gd3+ ions (J2), (iii) the third one describes the coupling between two radicals (J3) and (iv) in addition to these isotropic exchange coupling values, a strong electron delocalisation of the radical between two Gd3+ ions suggests a double-exchange (parameter B) being operative between two Gd ions (in a fully delocalised case, Gd22.5+). All these exchanges have been illustrated in Scheme S2.† This is similar to a type-III mixed-valence system68,69 where the spin Hamiltonian parameters are estimated using the following Hamiltonian70| H = −J(SA·SB·OA + SA·SB·OB) + BTAB, | (1) |
The presence of one unpaired electron in the fullerene cage of Gd2@C60-Ih, Gd2@C80-D5h, and Gd2@C80-C2v leads to polymerisation or aggregation, and often, these complexes are not isolable.71,72 There are two strategies available to demonstrate their existence (i) by transforming them into a chemically stable form with one-electron reduction/substitution at the ring position. This has been adapted to stabilise the Dy2@C80-Ih molecule by chemically transforming it to Dy2@C80(CH2Ph).72–75 (ii) By substituting one of the carbon with the nitrogen atom yielding azafullerenes such as Ln2@C79N and other analogues.49,70,76–79 Here, we have adopted the second approach where one carbon atom is substituted by nitrogen in Gd2@C60/80 isomers yielding Gd2@C59/79N molecules (see Appendix S26–S28† for optimised coordinates) possessing Cs symmetry (here Gd2@C79N-Cs-1 is derived from Gd2@C80-D5h and Gd2@C79N-Cs-2 is derived from Gd2@C80-C2v, see Table 1). Upon substitution, as expected, the spin density of the cage in Gd2@C59/79N was seized (see Fig. 1e and f for the 665 isomer, see ref. 44). While Gd2@C79N is a well-characterised and thoroughly studied molecule, Gd2@C59N is not known. However, the X-ray structure of C59N and encapsulation of some metal ions are experimentally studied, and their existence has been proved beyond ambiguity.35,80–86 Particularly, K6C59N has been isolated and characterised thoroughly. This suggests that the C59N6− cage is a stable molecular fragment and can encapsulate Ln3+ cations similar to those hypothesised here.87–89
This type-III mix valence moiety of Gd2@C59N-Cs, Gd2@C79N-Cs-1, and Gd2@C79N-Cs-2 isomer represents a multireference wave function as the unpaired electron is not localised on a particular centre. Therefore, a multireference method such as the state-average CAS(15,15)SCF set up was employed to estimate the double exchange parameter (B) (Fig. 3, see computational details).90 As per the CASSCF calculations, the additional radical electron resides in a hybrid orbital containing coefficients from 6s, 5pz, 6pz, and 5dz2 orbitals of Gd1 and Gd2 centres (see Table S55† for composition). The set of spin Hamiltonian parameters obtained from the CASSCF calculations are as follows, Gd2@C59N-Cs (Gd2@C79N-Cs-1) [Gd2@C79N-Cs-2]: J1 = +869.8 (+404.6) [+351.3] cm−1, J2 = 0.08 (0.03) [0.03] cm−1 and B = +434.8 (+202.1) [+175.6] cm−1 (Table 1). For all three complexes, the J1 interaction is found to be extremely large, and this is due to the involvement of the diffuse virtual 6s and 6pz and 5dz2 orbitals of Gd ions, while the J2 coupling between two Gd3+ ions is found to be very small as the 4f orbitals are only weakly interacting here. It is worth mentioning that we have previously reported a very large J1 value of +400 cm−1 (Ĥ = −JŜ1Ŝ2) in Gd2@C79N using the UB3LYP/TZV setup.44 The estimated J1 value by our ab initio approach for Gd2@C79N lies in the range of 350–405 cm−1, and this is in line with the DFT calculations and experimental reports (−350 ± 20 cm−1 using Ĥ = J1(ŜGd1Ŝrad + ŜGd2Ŝrad) + J2(ŜGd1ŜGd2) in ref. 40 and a J1 value of 170 ± 10 cm−1 using the Hamiltonian Ĥ = −2J1(ŜGd1Ŝrad + ŜGd2Ŝrad) − 2J2(ŜGd1ŜGd2) in ref. 76; see ESI† for the discussion of J3). These large exchange values have potential application in qubits as they enhance the quantum coherence required for qubit applications.40
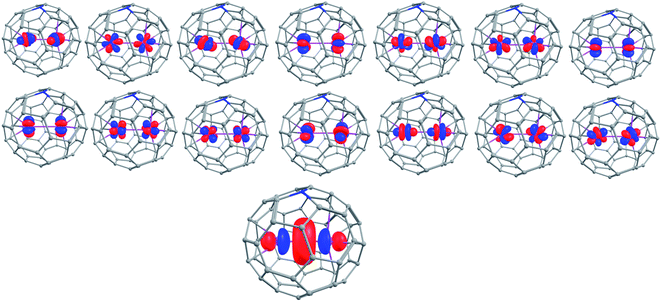 | ||
| Fig. 3 The fifteen active orbitals of Gd2@C59N with CAS (15,15) active space for the S = 15/2 state. Colour code: Gd-pink, C-grey, N-blue. | ||
A case study of magnetic anisotropy in Dy2@C59N and Tb2@C59N
As heterofullerenes yield larger Js and homofullerene yields relatively smaller antiferromagnetic Js, the former is the best suited to design SMMs. The antiferromagnetic Js in homofullerene yields diamagnetic ground states, and smaller ferromagnetic Js observed in larger cage sizes such as C52 did not yield any appealing SMM characteristics. To harness SMMs in this class, heterodinuclear lanthanides with unequal mJ states were modelled. Models such as PrEr@C38-D3h yield a reasonable Ucal value with robust QTM quenching (ca. 109 cm−1, see ESI†) but are not substantial to serve as a synthetic target.Therefore, we aim to estimate the magnetic anisotropy in the Dy2@C59N and Tb2@C59N. It is noteworthy to mention that the record-breaking magnetic anisotropy is previously achieved in Dy2@C79N and Tb2@C79N molecules.44,77 The metal centre in Dy2@C59N is found to interact in an η6 fashion with the C59N cage, which creates a strong uniaxial anisotropy (see Fig. 1c) as a long Dy⋯Dy bond (3.056 Å) induces a weak ligand field in the opposite site of cage binding. Thus, the coordination can be compared with Dy3+–O, which perfectly suits the oblate ground state.91,92 The easy axis of magnetisation is found to be nearly collinear with the Dy–Dy axis with a very small angle (2.0 (1.1°) for Dy1(Dy2), Fig. S72†). The calculated gz values of KD1 (∼19.97) imply an Ising ground state for both the Dy centres (Tables S70, S71 and Fig. S71†), with the relaxation predicted to proceed via the first excited state for Dy2 (Ucal = 250.5 cm−1) and third excited state for the Dy1 centre (Ucal = 483.7 cm−1, Fig. S71 and Tables S70, S71†). The very large axial crystal field parameter93Bkq (k = 0, q = 0) compared to the non-axial crystal field parameter Bkq (k = 0, q ≠ 0) suggests significant axiality for both the Dy centres in Dy2@C59N (see Table S72†). Furthermore, the axial CF parameters are found to be slightly larger in Dy2@C59N compared to Dy2@C79N, suggesting a larger axiality of the former compared to the latter.44
The ab initio calculations on Tb2@C59N reveal a negligible tunnel splitting in the ground pKDs (0.025(0.013) cm−1 for Tb1(Tb2), see Tables S73, S74 and Fig. S73†). Further, the ground state gz value (gz = 17.921(17.919) for Tb1(Tb2) centre94,95) suggests the Ising nature of the ground state. The ground anisotropy axis of the Tb1(Tb2) centre is oriented along the pseudo C6 axis of the hexagonal ring and nearly collinear with the Tb–Tb axis (the tilting angle becomes 0.45 and 1.50° for Tb1 and Tb2 centres, respectively, Fig. 4). However, the significant tunnel splitting (0.115 and 0.102 cm−1 for Tb1(Tb2), Fig. S73†) in the first excited pKDs reinforces the magnetisation relaxation via this state. This leads to the Ucal value of 227.6 and 233.2 cm−1 for Tb1 and Tb2 centres, respectively (see Tables S73, S74 and S70†).
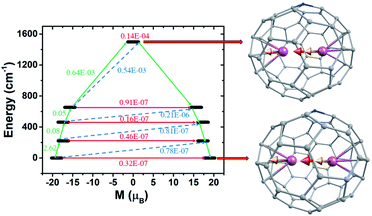
To explore the mechanism of magnetisation relaxation in the exchange-coupled Dy2@C79N and Tb2@C79N systems, we have simulated the exchange-coupled energy spectrum using the POLY_ANISO module (see Table 1 and computational details). For the computed ground state, a large magnetic moment of ca. 21 and 19 μB for Dy2@C59N and Tb2@C59N respectively, was obtained (see Fig. 4 and S72†) with negligible tunnel splitting or QTM effects. The first, second, and third excited states are found to possess negligible tunnel splitting/TA-QTM, which is reflected in negligible gx/gy and very large gz values (see Tables S75, S76, Fig. 4 and S72†). The magnetic moment in the fourth excited state is very small, and it results in sizeable QTM for Dy2@C59N and Tb2@C59N. Therefore, the magnetisation relaxation for this exchange-coupled system is expected via the fourth excited state yielding a record-high Ucal value of 1183.3 and 1501.8 cm−1 for Dy2@C59N and Tb2@C59N, respectively (see Fig. 4, 5, and S72†). These gigantic Ucal values are two times larger than Dy2@C79N/Tb2@C79N estimates, thanks to a very large ferromagnetic exchange.44,77 The other relaxation process due to intermolecular interactions is expected to be minimal due to confinement, which is likely to yield large TB values. As our predictions on Gd2@C79N and Dy2@C79N are proved by experiments lately, with Dy2@C79N yielding an attractive blocking temperature (24 K), these smaller cages, if made, could enhance TB values even further.40,44,47,76
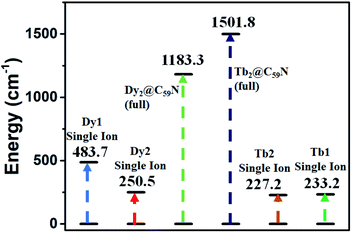 | ||
| Fig. 5 Diagrammatic representation of the estimated single ion and exchange-coupled Ucal for Dy2@C59N-Cs and Tb2@C59N-Cs. | ||
Conclusions
To this end, we have employed an array of theoretical tools in search of finding lanthanide encapsulated fullerenes with very large blocking barriers and blocking temperatures. Various ideas, such as enhancing the coupling between two lanthanide ions by bringing them close to each other in the confined space, have been tested, and the main conclusions drawn from this works are summarised below.(i) Sourcing the large JGd–Gd exchange via confinement: in search of increasing the magnetic exchange (JGd–Gd) between two lanthanide ions via confinement, we have varied the cage size from C30 to C80 where the Gd⋯Gd distance ranging from 2.185 Å to 4.107 Å is observed. Here smaller cages (C2n, 2n ≤ 52) yield a weaker Gd⋯Gd interactions with a stable Gd2@C38-D3h complex having a record-high exchange for any 4f–4f interaction (JGd⋯Gd = −43.4 cm−1). A strong 4f–4f orbital overlap between two Gd3+ ions suggests the Gd–Gd bond formation under confinement. As the exchange is antiferromagnetic, these are not ideal for SMMs, however among hetero dilanthanide EMFs, some promising SMMs are identified.
(ii) Ab initio estimation of double exchange in endohedral azafullerenes: the larger cages (Gd2@C60 and Gd2@C80) lead to the formation of a two-centre-one-electron Gd–Gd bond due to the comparable energy of the highest occupied orbitals of Gd2 and lowest unoccupied orbitals of the fullerene cage. Here we have studied Gd2@C59/79N complexes where the delocalisation of the electron between two Gd centres is treated via a double-exchange parameter. A protocol to compute the double-exchange using ab initio CASSCF calculations is proposed, and this methodology yields spin Hamiltonian parameters that are in excellent agreement with experiments for Gd2@C79N. The application of this method in Gd2@C59N unveils a massive JGd–rad exchange (JGd–rad = +869 cm−1) which is two times larger than the record-high J reported for Gd2@C79N.
(iii) Record-high blocking barrier for Dy2@C59N and Tb2@C59N: the huge ferromagnetic JGd–rad exchange found in the C59N cage quenches the QTM significantly and yields a very high Ucal value of 1502 cm−1 for Tb2@C59N – the largest reported for any lanthanide EMF. This opens up the possibility of generating large magnetic anisotropy without relying on a stronger ligand field.
Computational details
All the DFT calculations have been performed using the Gaussian09 suite with the B3LYP functional.96,97 There are several isomers with different symmetries possible for a chosen fullerene cage. To estimate the effect of symmetry of the fullerene cage in the associated magnetic properties, we have chosen two low energy conformers of the C2n (n = 15–24, 26, 30, 40) fullerene from http://www.nanotube.msu.edu/ and encapsulated two Gd atoms.98 The optimisation of the resulting Gd2@C2n has been performed using the UB3LYP/CSDZ(Gd), SVP (rest) methodology.99,100 Further single point energy calculations were performed with an Ahlrichs' triple-ξ valence (TZV) basis set to obtain an excellent numerical estimate of energy/magnetic coupling.101 A quadratic convergence SCF method was used throughout all the calculations.102 One high spin (HS, the spin on both Gd3+ centres is “up”) and one broken symmetry (BS, the spin on one Gd3+ centre is “up” and another Gd3+ centre is “down”) configuration was used to estimate the magnetic exchange. The magnetic exchange has been calculated using the Hamiltonian Ĥ = −JŜ1Ŝ2, where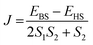 .103,104 Additionally, we have performed AIM (atoms in molecules) analysis with the AIM2000 programme package to determine the coordination number of the Gd3+ ion inside the fullerene cage along with the nature of Gd–C and Gd–Gd bonds.105
.103,104 Additionally, we have performed AIM (atoms in molecules) analysis with the AIM2000 programme package to determine the coordination number of the Gd3+ ion inside the fullerene cage along with the nature of Gd–C and Gd–Gd bonds.105
To estimate the double exchange in Gd2@C79N and Gd2@C59N molecules, ab initio CASSCF calculations have been performed using the MOLCAS 8.4 programme package.106 We have employed [Ln·ANO-RCC⋯8s7p5d3f2g1h], [C·ANO-RCC⋯3s2p1d] and [N·ANO-RCC⋯3s2p1d] contraction schemes in the basis set for Gd, C and N, respectively.106,107 The DKH Hamiltonian was used to take into account the scaler relativistic effect.108 The Cholesky decomposition technique was used to reduce the size of the disk space.109 The CASSCF calculations have been performed with the CAS (15,15) active space.90 The active space includes seven 4f orbitals from each Gd atom and one orbital for the unpaired electron. Within the active space, we have computed the energy of the S = 13/2, 11/2, 9/2, 7/2, 5/2 and 3/2 states with two roots while the energy of S = 15/2 and 1/2 states has been estimated using only one root. Further details on the computational methods are elaborated in the ESI.†
The magnetic anisotropy in the Gd2@C38-D3h and Gd2@C52-D2d isomer has been estimated by replacing the isotropic Gd metal centres with Dy, Er and Pr. For Gd2@C59N model, anisotropic calculations were perforemd using Dy and Tb ions. The CASSCF calculations have been performed with minimal CAS(n,7) active space (n = number of 4f electrons) for Pr, Dy, Tb and Er using the MOLCAS 8.4 programme package.106 We have computed the energies of the 21 triplets and 28 singlets of Pr3+, 7 septets, 140 quintets and 195 triplets for Tb3+, 21 sextets for Dy3+, and 35 quartets and 112 doublets for Er3+ within the size of the active space. Thereafter, the computed spin-free states (7 septets, 105 quintets and 112 triplets for Tb3+) have been mixed in RASSI-SO to obtain the spin–orbit coupled energies. Finally, the g tensors, QTM/TA-QTM, etc. of the metal centre have been computed by SINGLE_ANISO, which interfaces with the RASSI-SO. After calculating the magnetic anisotropy of the individual metal centres, they have been coupled by POLY_ANISO using the Lines model to compute the energy of the exchange-coupled system.110 The magnetic exchange computed with the DFT and ab initio approach has been scaled with 5/7, 6/7, and 3/7 for Dy, Tb and Er centres, respectively, to estimate exchange coupled energy levels.
Author contributions
GR conceived the idea and SD performed all the calculations and interpret and analyse the data. Both wrote the manuscript together.Conflicts of interest
There are no conflicts to declare.Acknowledgements
SD would like to thank UGC for the SRF fellowship and Dr Hélène Bolvin, UPS, Toulouse for her helpful suggestions. GR would like to thank DST/SERB (CRG/2018/000430, DST/SJF/CSA03/2018-10; SB/SJF/2019–20/12; SPR/2019/001145) for funding.Notes and references
- R. Sessoli, D. Gatteschi, A. Caneschi and M. Novak, Nature, 1993, 365, 141–143 CrossRef CAS
.
- E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501–513 RSC
.
- N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed
.
- A. B. Canaj, S. Dey, E. R. Martí, C. Wilson, G. Rajaraman and M. Murrie, Angew. Chem., Int. Ed., 2019, 131, 14284–14289 CrossRef
.
- A. B. Canaj, S. Dey, C. Wilson, O. Céspedes, G. Rajaraman and M. Murrie, Chem. Commun., 2020, 56, 12037–12040 RSC
.
- S. Dey, G. Velmurugan and G. Rajaraman, Dalton Trans., 2019, 48, 8976–8988 RSC
.
- M. S. Norre, C. Gao, S. Dey, S. K. Gupta, A. Borah, R. Murugavel, G. Rajaraman and J. Overgaard, Inorg. Chem., 2019, 59, 717–729 CrossRef PubMed
.
- S. Dey and G. Rajaraman, Dalton Trans., 2020, 49, 14781–14785 RSC
.
- Y. S. Ding, N. F. Chilton, R. E. Winpenny and Y. Z. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074 CrossRef CAS PubMed
.
- S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Sci., 2016, 7, 5181–5191 RSC
.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS PubMed
.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed
.
- D. Reta, J. G. Kragskow and N. F. Chilton, J. Am. Chem. Soc., 2021, 143(15), 5943–5950 CrossRef CAS PubMed
.
- K. R. McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503 RSC
.
- P. Evans, D. Reta, G. F. Whitehead, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2019, 141, 19935–19940 CrossRef CAS PubMed
.
- R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804–1816 CrossRef CAS
.
- V. E. Campbell, M. Tonelli, I. Cimatti, J. B. Moussy, L. Tortech, Y. J. Dappe, E. Riviere, R. Guillot, S. Delprat, R. Mattana, P. Seneor, P. Ohresser, F. Choueikani, E. Otero, F. Koprowiak, V. G. Chilkuri, N. Suaud, N. Guihery, A. Galtayries, F. Miserque, M. A. Arrio, P. Sainctavit and T. Mallah, Nat. Commun., 2016, 7, 13646 CrossRef CAS PubMed
.
- L. Rosado Piquer, E. Jiménez Romero, Y. Lan, W. Wernsdorfer, G. Aromí and E. C. Sañudo, Inorg. Chem. Front., 2017, 4, 595–603 RSC
.
- C. Wäckerlin, F. Donati, A. Singha, R. Baltic, S. Rusponi, K. Diller, F. Patthey, M. Pivetta, Y. Lan and S. Klyatskaya, Adv. Mater., 2016, 28, 5195–5199 CrossRef PubMed
.
- V. E. Campbell, M. Tonelli, I. Cimatti, J.-B. Moussy, L. Tortech, Y. J. Dappe, E. Rivière, R. Guillot, S. Delprat and R. Mattana, Nat. Commun., 2016, 7, 1–10 Search PubMed
.
- M. Mannini, F. Pineider, C. Danieli, F. Totti, L. Sorace, P. Sainctavit, M.-A. Arrio, E. Otero, L. Joly and J. C. Cezar, Nature, 2010, 468, 417 CrossRef CAS PubMed
.
- D. N. Woodruff, R. E. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed
.
- Y.-N. Guo, G.-F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. Tang, H.-J. Zhang, L. F. Chibotaru and A. K. Powell, J. Am. Chem. Soc., 2011, 133, 11948–11951 CrossRef CAS PubMed
.
- F. Habib, G. Brunet, V. Vieru, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2013, 135, 13242–13245 CrossRef CAS PubMed
.
- P. Evans, D. Reta, C. A. P. Goodwin, F. Ortu, N. F. Chilton and D. P. Mills, Chem. Commun., 2020, 56, 5677–5680 RSC
.
- T. Han, Y.-S. Ding, Z.-H. Li, K.-X. Yu, Y.-Q. Zhai, N. F. Chilton and Y.-Z. Zheng, Chem. Commun., 2019, 55, 7930–7933 RSC
.
- J. Long, F. Habib, P.-H. Lin, I. Korobkov, G. Enright, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 5319–5328 CrossRef CAS PubMed
.
- S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, B. F. Abrahams, L. F. Chibotaru and K. S. Murray, Angew. Chem., Int. Ed., 2013, 52, 12014–12019 CrossRef CAS PubMed
.
- A. Venugopal, F. Tuna, T. P. Spaniol, L. Ungur, L. F. Chibotaru, J. Okuda and R. A. Layfield, Chem. Commun., 2013, 49, 901–903 RSC
.
- H. Tian, L. Ungur, L. Zhao, S. Ding, J. Tang and L. F. Chibotaru, Chem.–Eur. J., 2018, 24, 9928–9939 CrossRef CAS PubMed
.
- A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113 CrossRef CAS PubMed
.
- R. Nakanishi, J. Satoh, K. Katoh, H. Zhang, B. K. Breedlove, M. Nishijima, Y. Nakanishi, H. Omachi, H. Shinohara and M. Yamashita, J. Am. Chem. Soc., 2018, 140, 10955–10959 CrossRef CAS PubMed
.
- C. H. Chen, L. Spree, E. Koutsouflakis, D. S. Krylov, F. Liu, A. Brandenburg, G. Velkos, S. Schimmel, S. M. Avdoshenko and A. Fedorov, Adv. Sci., 2021, 8, 2000777 CrossRef CAS PubMed
.
- D. S. Krylov, S. Schimmel, V. Dubrovin, F. Liu, T. N. Nguyen, L. Spree, C. H. Chen, G. Velkos, C. Bulbucan and R. Westerström, Angew. Chem., Int. Ed., 2020, 59, 5756–5764 CrossRef CAS PubMed
.
- T. Zuo, L. Xu, C. M. Beavers, M. M. Olmstead, W. Fu, T. D. Crawford, A. L. Balch and H. C. Dorn, J. Am. Chem. Soc., 2008, 130, 12992–12997 CrossRef CAS PubMed
.
- T. Greber, A. P. Seitsonen, A. Hemmi, J. Dreiser, R. Stania, F. Matsui, M. Muntwiler, A. Popov and R. Westerström, Phys. Rev. Mater., 2019, 3, 014409 CrossRef CAS
.
- C.-H. Chen, D. Krylov, S. Avdoshenko, F. Liu, L. Spree, R. Westerström, C. Bulbucan, M. Studniarek, J. Dreiser and A. Wolter, Nanoscale, 2018, 10, 11287–11292 RSC
.
- S. Schimmel, Z. Sun, D. Baumann, D. Krylov, N. Samoylova, A. Popov, B. Büchner and C. Hess, Beilstein J. Nanotechnol., 2017, 8, 1127–1134 CrossRef CAS PubMed
.
- V. Martinez, B. Karadeniz, N. Biliškov, I. Lončarić, S. Muratović, D. Zilic, S. M. Avdoshenko, M. Roslova, A. A. Popov and K. Uzarevic, Chem. Mater., 2020, 32, 10628–10640 CrossRef CAS
.
- Z. Hu, B. W. Dong, Z. Liu, J. J. Liu, J. Su, C. Yu, J. Xiong, D. E. Shi, Y. Wang, B. W. Wang, A. Ardavan, Z. Shi, S. D. Jiang and S. Gao, J. Am. Chem. Soc., 2018, 140, 1123–1130 CrossRef CAS PubMed
.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236–14239 CrossRef CAS PubMed
.
- V. Vieru, N. Iwahara, L. Ungur and L. F. Chibotaru, Sci. Rep., 2016, 6, 1–8 CrossRef PubMed
.
- S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Nat. Commun., 2017, 8, 1–9 CrossRef CAS PubMed
.
- M. K. Singh, N. Yadav and G. Rajaraman, Chem. Commun., 2015, 51, 17732–17735 RSC
.
- M. K. Singh and G. Rajaraman, Chem. Commun., 2016, 52, 14047–14050 RSC
.
- Z. Hu, B.-W. Dong, Z. Liu, J.-J. Liu, J. Su, C. Yu, J. Xiong, D.-E. Shi, Y. Wang and B.-W. Wang, J. Am. Chem. Soc., 2018, 140, 1123–1130 CrossRef CAS PubMed
.
- F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. B. Wolter, B. Buchner and A. A. Popov, Nat. Commun., 2017, 8, 16098 CrossRef CAS PubMed
.
- G. Velkos, D. S. Krylov, K. Kirkpatrick, X. Liu, L. Spree, A. U. B. Wolter, B. Buchner, H. C. Dorn and A. A. Popov, Chem. Commun., 2018, 54, 2902–2905 RSC
.
- Y. Wang, J. Xiong, J. Su, Z. Hu, F. Ma, R. Sun, X. Tan, H.-L. Sun, B.-W. Wang and Z. Shi, Nanoscale, 2020, 12, 11130–11135 RSC
.
- C. A. Gould, L. E. Darago, M. I. Gonzalez, S. Demir and J. R. Long, Angew. Chem., Int. Ed., 2017, 129, 10237–10241 CrossRef
.
- S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289, 149–176 CrossRef
.
- K. R. Meihaus, J. F. Corbey, M. Fang, J. W. Ziller, J. R. Long and W. J. Evans, Inorg. Chem., 2014, 53, 3099–3107 CrossRef CAS PubMed
.
- S. Demir, J. M. Zadrozny, M. Nippe and J. R. Long, J. Am. Chem. Soc., 2012, 134, 18546–18549 CrossRef CAS PubMed
.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542 CrossRef CAS PubMed
.
- C. A. Gould, E. Mu, V. Vieru, L. E. Darago, K. Chakarawet, M. I. Gonzalez, S. Demir and J. R. Long, J. Am. Chem. Soc., 2020, 142, 21197–21209 CrossRef CAS PubMed
.
- P. Sharma, D. R. Pahls, B. L. Ramirez, C. C. Lu and L. Gagliardi, Inorg. Chem., 2019, 58, 10139–10147 CrossRef CAS PubMed
.
- S. X. Hu, E. Lu and S. T. Liddle, Dalton Trans., 2019, 48, 12867–12879 RSC
.
- C. Jones, C. Schulten, R. P. Rose, A. Stasch, S. Aldridge, W. D. Woodul, K. S. Murray, B. Moubaraki, M. Brynda, G. La Macchia and L. Gagliardi, Angew. Chem., Int. Ed., 2009, 48, 7406–7410 CrossRef CAS PubMed
.
- A. Khong, H. A. Jiménez-Vázquez, M. Saunders, R. J. Cross, J. Laskin, T. Peres, C. Lifshitz, R. Strongin and A. B. Smith, J. Am. Chem. Soc., 1998, 120, 6380–6383 CrossRef CAS
.
- R.-F. Peng, S.-J. Chu, Y.-M. Huang, H.-J. Yu, T.-S. Wang, B. Jin, Y.-B. Fu and C.-R. Wang, J. Mater. Chem., 2009, 19, 3602–3605 RSC
.
- T. Yu. Nikolaienko, E. S. Kryachko and G. A. Dolgonos, J. Comput. Chem., 2018, 39, 1090–1102 CrossRef PubMed
.
- E. Cerpa, A. Krapp, R. Flores-Moreno, K. J. Donald and G. Merino, Chem.–Eur. J., 2009, 15, 1985–1990 CrossRef CAS PubMed
.
- S. Jalife, S. Mondal, J. L. Cabellos, S. Pan, M. A. Mendez-Rojas, I. Fernández, G. Frenking and G. Merino, ChemistrySelect, 2016, 1, 2405–2408 CrossRef CAS
.
- K. Li, H. Lian and R. V. Deun, J. Lumin., 2018, 198, 155–162 CrossRef CAS
.
- M. Parthey and M. Kaupp, Chem. Soc. Rev., 2014, 43, 5067–5088 RSC
.
- F. Liu, L. Spree, D. S. Krylov, G. Velkos, S. M. Avdoshenko and A. A. Popov, Acc. Chem. Res., 2019, 52, 2981–2993 CrossRef CAS PubMed
.
- X. Cao and M. Dolg, Theor. Chem. Acc., 2002, 108, 143–149 Search PubMed
.
- S. Ghosh, S. K. Singh, S. Tewary and G. Rajaraman, Dalton Trans., 2013, 42, 16490–16493 RSC
.
- B. Bechlars, D. M. D'alessandro, D. M. Jenkins, A. T. Iavarone, S. D. Glover, C. P. Kubiak and J. R. Long, Nat. Chem., 2010, 2, 362–368 CrossRef CAS PubMed
.
-
O. Kahn, Molecular Magnetism, VCH Publishers, Inc., USA, 1993 Search PubMed
.
- A. A. Popov, Curr. Opin. Electrochem., 2018, 8, 73–80 CrossRef CAS PubMed
.
- F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. Wolter and B. Büchner, Nat. Commun., 2017, 8, 1–9 CrossRef CAS PubMed
.
- A. A. Popov, S. M. Avdoshenko, A. M. Pendás and L. Dunsch, Chem. Commun., 2012, 48, 8031–8050 RSC
.
- L. Bao, M. Chen, C. Pan, T. Yamaguchi, T. Kato, M. M. Olmstead, A. L. Balch, T. Akasaka and X. Lu, Angew. Chem., Int. Ed., 2016, 128, 4314–4318 CrossRef
.
- F. Liu, G. Velkos, D. S. Krylov, L. Spree, M. Zalibera, R. Ray, N. A. Samoylova, C.-H. Chen, M. Rosenkranz and S. Schiemenz, Nat. Commun., 2019, 10, 1–11 CrossRef PubMed
.
- G. Velkos, D. Krylov, K. Kirkpatrick, X. Liu, L. Spree, A. Wolter, B. Büchner, H. Dorn and A. Popov, Chem. Commun., 2018, 54, 2902–2905 RSC
.
- G. Velkos, D. S. Krylov, K. Kirkpatrick, L. Spree, V. Dubrovin, B. Büchner, S. M. Avdoshenko, V. Bezmelnitsyn, S. Davis and P. Faust, Angew. Chem., Int. Ed., 2019, 58, 5891–5896 CrossRef CAS PubMed
.
- A. Kostanyan, R. Westerström, D. Kunhardt, B. Büchner, A. A. Popov and T. Greber, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 101, 134429 CrossRef CAS
.
- W. Fu, J. Zhang, T. Fuhrer, H. Champion, K. Furukawa, T. Kato, J. E. Mahaney, B. G. Burke, K. A. Williams and K. Walker, J. Am. Chem. Soc., 2011, 133, 9741–9750 CrossRef CAS PubMed
.
- T. Kaneko, Y. Li, S. Nishigaki and R. Hatakeyama, J. Am. Chem. Soc., 2008, 130, 2714–2715 CrossRef CAS PubMed
.
- S. Ostrowski, P. Garnuszek and J. C. Dobrowolski, Spectrochim. Acta Mol. Biomol. Spectrosc., 2020, 231, 117791 CrossRef CAS PubMed
.
- C. Brown, L. Cristofolini, K. Kordatos, K. Prassides, C. Bellavia, R. Gonzalez, M. Keshavarz-K, F. Wudl, A. Cheetham and J. Zhang, Chem. Mater., 1996, 8, 2548–2550 CrossRef CAS
.
- W. Si, X. Zhang, N. Asao, Y. Yamamoto and T. Jin, Chem. Commun., 2015, 51, 6392–6394 RSC
.
- K. Hedberg, L. Hedberg, D. S. Bethune, C. Brown, H. Dorn, R. D. Johnson and M. de Vries, Science, 1991, 254, 410–412 CrossRef CAS PubMed
.
- R. D. Johnson, C. S. Yannoni, H. C. Dorn, J. R. Salem and D. S. Bethune, Science, 1992, 255, 1235–1238 CrossRef CAS PubMed
.
- Y.-F. Yang and L. S. Cederbaum, Phys. Chem. Chem. Phys., 2021, 23, 11837–11843 RSC
.
- K. Prassides, M. Keshavarz-K, J. C. Hummelen, W. Andreoni, P. Giannozzi, E. Beer, C. Bellavia, L. Cristofolini, R. González and A. Lappas, Science, 1996, 271, 1833–1835 CrossRef CAS
.
- W. Andreoni, A. Curioni, K. Holczer, K. Prassides, M. Keshavarz-K, J.-C. Hummelen and F. Wudl, J. Am. Chem. Soc., 1996, 118, 11335–11336 CrossRef CAS
.
- M. Keshavarz-K, R. González, R. G. Hicks, G. Srdanov, V. I. Srdanov, T. G. Collins, J. C. Hummelen, C. Bellavia-Lund, J. Pavlovich and F. Wudl, Nature, 1996, 383, 147–150 CrossRef CAS
.
- F. Cimpoesu, B. Frecus, C. I. Oprea, H. Ramanantoanina, W. Urland and C. Daul, Mol. Phys., 2015, 113, 1712–1727 CrossRef CAS
.
- L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Inorg. Chem., 2013, 52, 6328–6337 CrossRef CAS PubMed
.
- L. Ungur and L. F. Chibotaru, Phys. Chem. Chem. Phys., 2011, 13, 20086–20090 RSC
.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed
.
- J. Griffith, Phys. Rev., 1963, 132, 316 CrossRef
.
-
J. S. Griffith, The theory of transition-metal ions, Cambridge University Press, 1964 Search PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed
.
- A. D. Beck, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef
.
-
D. Tománek, Guide through the nanocarbon jungle, 2014 Search PubMed
.
- T. R. Cundari and W. J. Stevens, J. Chem. Phys., 1993, 98, 5555–5565 CrossRef CAS
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef
.
-
C. Ögretir and I. G. Csizmadia, Computational advances in organic chemistry: molecular structure and reactivity, Springer Science & Business Media, 2012 Search PubMed
.
- E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391–1400 CrossRef CAS
.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS
.
- F. Biegler-König and J. Schönbohm, J. Comput. Chem., 2002, 23, 1489–1494 CrossRef PubMed
.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos and L. Gagliardi, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed
.
- B. O. Roos, V. Veryazov and P.-O. Widmark, Theor. Chem. Acc., 2004, 111, 345–351 Search PubMed
.
- M. Reiher, Theor. Chem. Acc., 2006, 116, 241–252 Search PubMed
.
- F. Aquilante, P.-Å. Malmqvist, T. B. Pedersen, A. Ghosh and B. O. Roos, J. Chem. Theory Comput., 2008, 4, 694–702 CrossRef CAS PubMed
.
- M. Lines, J. Chem. Phys., 1971, 55, 2977–2984 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc03925c |
| This journal is © The Royal Society of Chemistry 2021 |