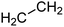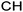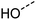Open Access Article
Open Access ArticleA framework for automated structure elucidation from routine NMR spectra†
Zhaorui
Huang
 ,
Michael S.
Chen
,
Michael S.
Chen
 ,
Cristian P.
Woroch
,
Cristian P.
Woroch
 ,
Thomas E.
Markland
,
Thomas E.
Markland
 * and
Matthew W.
Kanan
* and
Matthew W.
Kanan
 *
*
Department of Chemistry, Stanford University, Stanford, CA 94305, USA. E-mail: tmarkland@stanford.edu; mkanan@stanford.edu
First published on 9th November 2021
Abstract
Methods to automate structure elucidation that can be applied broadly across chemical structure space have the potential to greatly accelerate chemical discovery. NMR spectroscopy is the most widely used and arguably the most powerful method for elucidating structures of organic molecules. Here we introduce a machine learning (ML) framework that provides a quantitative probabilistic ranking of the most likely structural connectivity of an unknown compound when given routine, experimental one dimensional 1H and/or 13C NMR spectra. In particular, our ML-based algorithm takes input NMR spectra and (i) predicts the presence of specific substructures out of hundreds of substructures it has learned to identify; (ii) annotates the spectrum to label peaks with predicted substructures; and (iii) uses the substructures to construct candidate constitutional isomers and assign to them a probabilistic ranking. Using experimental spectra and molecular formulae for molecules containing up to 10 non-hydrogen atoms, the correct constitutional isomer was the highest-ranking prediction made by our model in 67.4% of the cases and one of the top-ten predictions in 95.8% of the cases. This advance will aid in solving the structure of unknown compounds, and thus further the development of automated structure elucidation tools that could enable the creation of fully autonomous reaction discovery platforms.
Introduction
Solving the structure of unknown compounds is a major bottleneck in the chemical sciences that limits the pace of molecular and reaction discovery for innumerable applications. As advances are made in automating the planning and execution of experiments, this bottleneck will become more acute because the rate at which previously unknown compounds are generated will increase. Methods to automate structure elucidation that can be applied broadly across chemical structure space will therefore aid researchers in accelerating chemical discovery and will ultimately prove essential for creating fully autonomous molecular and reaction discovery platforms.NMR is the most widely used technique for characterizing the structure of organic molecules. NMR spectra encode the local environments of the atoms that make up a molecule, providing molecular “fingerprints” that can be used to deduce connectivity and relative stereochemistry. While sample preparation and data collection for routine 1D NMR experiments are facile, data interpretation is often time-consuming and error-prone. Even relatively small molecules may have a large number of 1H NMR peaks with complex splitting patterns, which are often obscured by peak overlaps. In practice, chemists thus frequently resort to the use of 2D NMR experiments to deduce structures from complex spectra, at the expense of considerable additional time and resources. The forward problem of automated prediction of NMR peak shifts and splittings for a given molecule has seen much success using ab initio calculations,1–3 simple empirical methods (e.g. database similarity searches4 or additivity rules5–7), and machine learning (ML) models.8–18 However, the inverse problem of automated prediction of the structure of a molecule from its NMR spectrum is much more challenging because of the enormity of molecular structure space.
Computer-assisted structure elucidation (CASE) programs have been developed to help interpret 2D and 1D NMR spectra. However, these programs still require a large amount of human intervention to pick out the relevant peaks from complex 2D NMR spectra.19,20 Another recently developed method uses a bottom-up rule-based approach to solve molecular structure from a combination of tabulated infrared (IR) spectroscopy peaks, 1H and 13C NMR peaks, and mass spectra.21 This approach requires picking 1H NMR peaks and their multiplicities, which varies based on user interpretation, and is prone to failure if even a single expected peak is missing. Other approaches to automating NMR interpretation leverage the use of NMR databases. However, the structure space of even moderately sized organic molecules is astronomically large (e.g. 166 billion molecules with up to 17 C, N, O, S, and/or halogen atoms22) making it impossible to assemble a database that represents a meaningful fraction of this space. Database methods are also prone to failure if there are small variations in spectra due to differences in experimental conditions.23
Machine learning algorithms have shown great promise in their ability to solve ill-defined inverse problems24 and thus offer an appealing route to obtain fully automated structure elucidation using NMR data as input. ML methods have previously been used to identify the presence of functional groups using IR spectra,25–29 NMR spectra,30,31 and mass spectrometry data.32–34 However, these existing methods only predict the presence of a small set of functional groups and thus do not provide enough information to elucidate full molecular structures. Recently, Jonas described a deep neural network to predict molecular structure from the molecular formula and augmented 13C NMR spectra.35 The neural network is trained using imitation learning to generate bonds between the atoms based on the information about the C atoms encoded in the 13C NMR spectrum and outputs a probabilistic ranking of molecular structures. In order to have sufficient information for structure generation, the model requires the 13C peak shifts to be augmented with the expected multiplicities arising from coupling with adjacent 1H nuclei, which effectively amounts to an idealized, pre-assigned 1H-coupled 13C NMR spectrum. However, 1H-coupled 13C spectra are rarely obtained in practice because peak overlaps, large disparities in relaxation times, and long-range couplings make it infeasible to accurately assign 13C multiplets. Thus, this model can only be applied to experimental 13C shifts from 1H-decoupled spectra where the peak multiplicities have already been assigned based on the known molecular structure, limiting its real-world applicability.
Here we introduce a ML framework that provides automated elucidation of the connectivity (constitutional isomer) of an unknown compound using routine, experimental 1D 1H and/or 13C NMR spectra. Our approach to structure elucidation is inspired by the way chemists approach NMR spectra. When presented with a spectrum of an unknown compound, chemists typically identify structural fragments (substructures) based on individual peaks or peak combinations and then combine these substructures to propose a molecular structure. While a person can only consider a handful of substructures in a reasonable amount of time, our ML model is able to learn and predict the presence of hundreds of substructures simultaneously. We thus provide a deep learning based ML architecture that, when trained on simulated and experimental NMR data using a supervised learning protocol, predicts the likelihood of a given substructure being present in the compound and highlights the part of the spectrum that corresponds to it. We then show how we can use these substructure probability predictions in conjunction with a graph generation algorithm to direct the automated generation of the most probable constitutional isomers for the unknown compound. Although this 1st generation structure prediction framework does not predict relative stereochemistry (diastereomers), we discuss strategies to incorporate stereochemical predictions in subsequent generations.
Results and discussion
An overview of our automated structure prediction framework is shown in Fig. 1, which outlines how the NMR data is first fed into a substructure prediction neural network and then the output is used to build and rank candidate structures. The input data consists of the full 1H NMR spectrum, the 13C NMR peak shifts, and the molecular formula. The full 1H spectrum is used because the peak multiplicities and areas provide abundant information about the molecular structures present. In contrast, only the 13C peak shifts are used because routine 13C NMR experiments do not produce reliable integrations and peak multiplicities. This data is first passed through the substructure prediction model, which is a neural network trained to identify substructures. The output of this model is a substructure probability profile – a vector that indicates the probability of each substructure being present. The substructure probability profile can also be used to annotate the NMR spectra with likely substructures. Molecular structures are then generated using a graph generation algorithm that takes as its inputs the molecular formula and substructure probability profile. This graph-based algorithm generates molecular structures as graphs one edge (bond) at a time using the substructure information as a guide. The output of this framework is a set of constitutional isomers and their probabilistic ranking.Our substructure prediction model is composed of a convolutional neural network (CNN) with two sets of 1-D convolutional layers and max pooling layers that feeds into several fully connected layers (Fig. S1†). The rationale behind this design is that the first layer learns simple features such as dips, peaks, and slopes in a spectrum, while the second layer learns more complex features such as peak multiplets.36 To perform substructure predictions, the full 1H spectrum is passed through the CNN, whose outputs are combined with the 13C NMR peaks and the molecular formula before being collectively passed through the fully connected layers to output the predicted substructure probabilities.
To develop the set of substructures targeted for prediction, we first generated thousands of candidate substructures composed of C, H, O, and/or N by using (i) an automated method starting with a central C atom and systematically adding atoms up to two bonds away and (ii) a procedure based on randomly selecting two different molecules in the training set and identifying new substructures that could be used to differentiate them using NMR. The latter was used to generate larger substructures such as rings that can capture relationships more than two bonds away. The substructure candidates were then filtered based on their ability to differentiate the molecules in the training set and their prevalence in it to arrive at a selection of 957 substructures (ESI† section 3.2). Predicting for the presence of 957 substructures requires a large training dataset to provide sufficient examples of each substructure. Although there are published 1H NMR data for millions of compounds, the vast majority are in the form of listed peaks or images instead of the original full spectral data used by our model. To create a suitable training set, we therefore simulated 1H and 13C NMR spectra for ∼100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecular structures containing H, C, O, and/or N with up to 9 non-hydrogen atoms selected from the GDB-13 database (Fig. S2†).37 For each of the 957 substructures, there are at least 100 occurrences in the training set molecules (Fig. S3†). Simulated spectra were generated using MestReNova38 and augmented by applying a random peak width factor to mimic the variability in experimental spectra (ESI† section 2.2).
000 molecular structures containing H, C, O, and/or N with up to 9 non-hydrogen atoms selected from the GDB-13 database (Fig. S2†).37 For each of the 957 substructures, there are at least 100 occurrences in the training set molecules (Fig. S3†). Simulated spectra were generated using MestReNova38 and augmented by applying a random peak width factor to mimic the variability in experimental spectra (ESI† section 2.2).
While simulated data was used for training, because large amounts can be generated efficiently, the data used to validate and test the model were experimental 1H and 13C NMR spectra sourced from the Human Metabolome Database (HMDB),39 SDBS,50 and our own measurements. The full experimental dataset consisted of 309 sets of experimental spectra for molecules containing H, C, O, and/or N with up to 10 non-hydrogen atoms (Fig. S2† and supplementary files). The experimental 1H NMR data was processed using MestReNova only to remove the NMR solvent peak, peaks corresponding to labile protons (e.g. OH and NH2) and impurity peaks (ESI† section 2.3). However, it is important to note that the there was only a mild decrement in the performance of the model when raw experimental spectra were used (see below). The samples were randomly split into a validation set (214 examples) and a test set (95 examples). The simulated training set and the experimental validation and test sets contain no common molecules.
The overall substructure prediction model can be configured as multiple single task models that each only predict the probability of a single substructure being present or as multitask models that predict for many substructures simultaneously. We employed multitask models in order to reduce the total training time, decrease overfitting, and take advantage of transfer learning between different substructure predictions. Rather than training one model that predicts 957 substructures, we obtained more accurate results by training 3 sets of models that each predict for the probabilities of 319 substructures (Table S1†). In our supervised learning protocol, the weights in the CNN were fitted with respect to the training set for multiple epochs (complete passes over the training set). We used the validation set to mitigate overfitting by applying an early stopping procedure, where once the validation error started to rise, training was halted. Since the training of different substructures can occur at different rates, we applied task-based early stopping where the training was stopped individually for each substructure according to its error in the validation set. Thus, 957 models were generated by stopping training at the optimal time for each substructure. To tame the erratic predictions that can occur from any single model, we used an ensemble average of five sets of models, each trained with different weight initializations. The final 957 substructure predictions were therefore constructed from a total of 957 × 5 = 4785 models. We note, however, that it is possible to systematically reduce the total number of models to as few as 100 with only a small reduction in prediction performance (ESI† section 3.4 and Table S2).
Since predictions are made for 957 substructures, the correct probability profile for each molecule is dominated by zeroes, i.e. most substructures are not in a given molecule. In the test set, only 2.4% of the 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 915 substructure labels (957 substructures per molecule × 95 test set molecules) are ones, so even a null model that predicts all zeroes (i.e. that no substructure is ever present) would achieve an accuracy of 97.6%. Hence, it is vital to assess our substructure prediction model's success rate in achieving both true positives and true negatives while also avoiding false positives and false negatives. Fig. 2 shows the distribution of these four outcomes given a particular probability prediction from the substructure prediction model and where a predicted probability of 0.5 is taken as the threshold between a negative and positive classification. When the model predicts that a given substructure is highly unlikely to be present (<0.1), it is 99.89% accurate, i.e. it gives only 0.11% false negatives, which is more than 20-fold better than the null model. In addition, when the model predicts a substructure is highly likely to be present (>0.9), it is 99.27% accurate, in contrast to the null model which would have 0% accuracy in these cases. In between these limits, a range that accounts for only 3.3% of all of the test set substructure predictions, the model is less accurate and the proportion of false positives and false negatives increases as the predicted substructure probabilities approach 0.5. The utility of such probabilistic predictions provided by the model is that the predictions can be weighted appropriately when used to elucidate molecular structure. Thus, if one obtains a prediction for the presence of a substructure that is ∼0.5 for a given set of input NMR data, then it is clear that the prediction should carry low weight compared to predictions close to 0 or 1 when it comes to elucidating the structure of the unknown molecule.
915 substructure labels (957 substructures per molecule × 95 test set molecules) are ones, so even a null model that predicts all zeroes (i.e. that no substructure is ever present) would achieve an accuracy of 97.6%. Hence, it is vital to assess our substructure prediction model's success rate in achieving both true positives and true negatives while also avoiding false positives and false negatives. Fig. 2 shows the distribution of these four outcomes given a particular probability prediction from the substructure prediction model and where a predicted probability of 0.5 is taken as the threshold between a negative and positive classification. When the model predicts that a given substructure is highly unlikely to be present (<0.1), it is 99.89% accurate, i.e. it gives only 0.11% false negatives, which is more than 20-fold better than the null model. In addition, when the model predicts a substructure is highly likely to be present (>0.9), it is 99.27% accurate, in contrast to the null model which would have 0% accuracy in these cases. In between these limits, a range that accounts for only 3.3% of all of the test set substructure predictions, the model is less accurate and the proportion of false positives and false negatives increases as the predicted substructure probabilities approach 0.5. The utility of such probabilistic predictions provided by the model is that the predictions can be weighted appropriately when used to elucidate molecular structure. Thus, if one obtains a prediction for the presence of a substructure that is ∼0.5 for a given set of input NMR data, then it is clear that the prediction should carry low weight compared to predictions close to 0 or 1 when it comes to elucidating the structure of the unknown molecule.
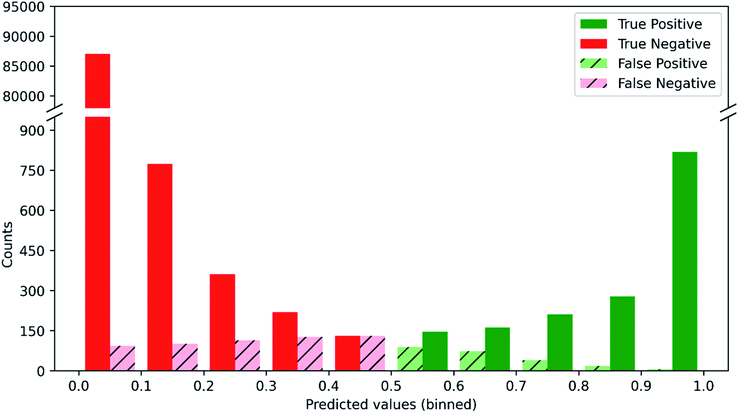 | ||
| Fig. 2 Distribution of true/false positives and true/false negatives as a function of the probability predicted by our substructure prediction model for the test set. | ||
In order to succinctly quantify the classification performance of our model accounting for both the rate of false positives and false negatives, we use F1 scores and precision recall curve (PRC) area under the curve (PRC-AUC) scores. While the F1 score reflects the ability of a model to accurately classify whether a particular substructure is present or not for a particular decision threshold (in our case 0.5), the PRC-AUC reflects a model's ability to provide a correct relative ranking of more vs. less likely examples independent of a particular threshold. The PRC-AUC is particularly important when we use the substructure probability profile to build and rank full molecules since the ranking is based on comparative binary cross entropy (BCE) loss and therefore the absolute values of the probabilities for each substructure are less important than their relative values. For a more detailed description of the PRC-AUC score see ESI† section 3.3.
The substructure prediction results for both the validation and test sets are shown in Table 1 based on using just 1H spectra, just 13C spectra, or both 1H and 13C spectra as input. With both 1H and 13C inputs, the model achieved a micro-average F1 score of 0.803 and a PRC-AUC score of 0.904 for the test set (see Fig. S4† for the PRC), which is significantly better than the performance using either 1H or 13C alone (F1 of 0.720 and 0.672 respectively). This result agrees with the intuition that 1H and 13C data are complementary – 1H NMR provides local structure information arising from the proton splittings while 13C NMR provides more general structure information (e.g. the presence of a carbonyl). The F1 score of the validation set, 0.869, is higher than that of the test set, which indicates some overfitting to the validation set. This overfitting is likely a consequence of the relatively small number of structures in the validation set.
| Dataset | Inputs | Substructure prediction | Molecular structure prediction | |||
|---|---|---|---|---|---|---|
| Micro-average F1 score | PRC-AUC score | Top-1 acc. (%) | Top-10 acc. (%) | Mean reciprocal rank | ||
| Validation | 13C | 0.718 | 0.850 | 61.7 | 90.7 | 0.726 |
| 1H | 0.747 | 0.871 | 63.6 | 84.1 | 0.710 | |
| 1H, 13C | 0.869 | 0.953 | 85.5 | 96.3 | 0.890 | |
| Test | 13C | 0.672 | 0.792 | 38.9 | 87.4 | 0.541 |
| 1H | 0.720 | 0.823 | 47.4 | 85.3 | 0.604 | |
| 1H, 13C | 0.803 | 0.904 | 67.4 | 95.8 | 0.777 | |
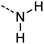
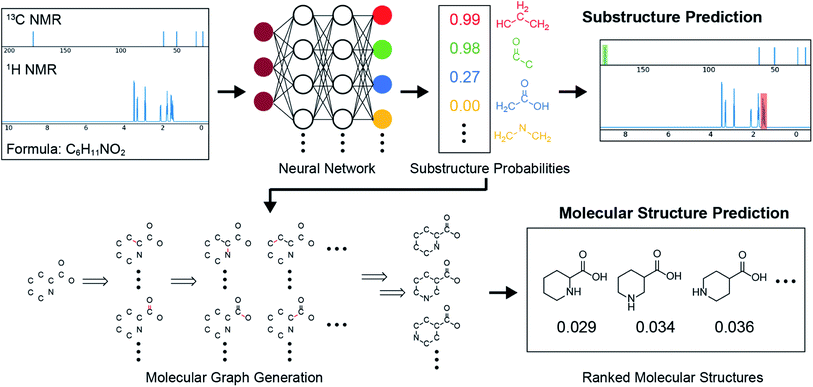
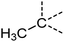
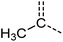
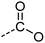
Examination of the results for individual substructure predictions shows how performance depends on the nature of the substructure (Table 2 and ESI† section 4.1). For a substructure consisting of a completely generic methyl group (CH3 attached to any C, N, or O), the model achieved an F1 score of 0.950 and a PRC-AUC score of 0.993 (entry 1). This result shows that it is possible to learn a substructure that has substantially different peak shapes and peak shifts depending on the specific molecular context. The performance in predicting more specific methyl substructures is shown in entries 2–5. The model performed perfectly for a methyl group attached to a quaternary carbon (entry 2), whereas for a methoxy group (entry 5) the model performed worse. This difference likely reflects the fact that there are more substructures with shifts and peak shapes similar to a methoxy group compared to the more unique shift of a methyl attached to a quaternary C (upfield singlet). The model performed well (F1 >0.877) for substructures containing a carbonyl (entries 6–8), aromatic C–H (entries 9 and 10), adjacent methylenes (entry 11), and even a generic substructure consisting of a C bound to a single H (entry 12). Remarkably, the model also performed well (F1 >0.816) for a generic –OH or –NH2 (entries 13 and 14) even though peaks for labile protons were not included in the 1H NMR test data. The model implicitly learns to identify these substructures via their correlation with related substructures such as those with C–O or C–N bonds. However, the performance in predicting the substructure consisting of a N bound to a single H (entry 15) was much worse (F1 = 0.222), which may be a consequence of the wider variety of NMR features that can arise in this case.
We also examined how well our substructure prediction model performs when applied to experimental data obtained from a set of 8 larger molecules containing between 12 and 14 non-hydrogen atoms (Fig. S5†). Although our substructure prediction model was trained on structures with 9 or fewer non-hydrogen atoms, the degradation in performance is mild (F1 = 0.730) for molecules containing 12 to 14 non-hydrogen atoms compared to that obtained on the original test set (F1 = 0.803). This result demonstrates that our current model is able to make accurate substructure predictions for larger molecules than those in the test set.
We now assess how the substructure probability profiles that predict for the presence of 957 substructures can be leveraged to predict molecular structure. For relatively small molecules (∼10 non-hydrogen atoms), it is computationally tractable to generate all the possible constitutional isomers corresponding to a particular molecular formula using existing algorithms.40,41 One can then systematically rank them by comparing the BCE loss between the actual substructure profile for each isomer and the profile predicted from the NMR data by our substructure prediction model. However, the number of possible constitutional isomers grows exponentially with the number of atoms, quickly surpassing the limit of what can feasibly be generated. Circumventing this problem requires a way to use the predicted substructure probability profile to efficiently generate only those candidate structures with low BCE loss.
To efficiently generate constitutional isomers from the substructure probability profile, we developed a beam search algorithm42 that generates candidate structures one bond at a time (Fig. S6†). For this process, a structure is represented as a graph with the nodes corresponding to non-hydrogen atoms and the edges to bonds. The inputs to our graph generation algorithm are the molecular formula and the substructure probability profile generated by our substructure prediction model. Our approach is based on the concept that when iteratively building up molecular graphs, incomplete graphs with low BCE loss are more likely to lead to completed graphs with minimal BCE loss. For example, if the substructure prediction model predicts there is a very low probability of alkenes being present, then intermediate candidate structures that contain alkenes will have a high loss and should not be built up any further. On the other hand, if the model predicts there is a high probability of alkenes being present, intermediate candidates with alkenes should be prioritized. Starting with a set of nodes that correspond to the molecular formula, edges (bonds) are added to the graph one at a time. At each step, all possible single-edge additions are generated to create a set of candidate incomplete graphs. Pruning is then performed to remove candidates with chemically implausible substructures or substructures specifically excluded (Table S3 and ESI† section 3.5). The remaining candidates are then ranked according to the BCE loss between their substructure profiles and the predicted substructure probability profile. The top k candidates are retained for the next step, where k is the beam size. Once the graph matches the molecular formula, and hence is complete, the structure's BCE is then used to rank it amongst the other structures that have been generated by the algorithm. We note that in its current form our model does not predict stereochemistry and there are also no molecules with multiple stereogenic centers in the test set. Hence, we are primarily evaluating the performance of our framework in predicting the correct constitutional isomer. Strategies to predict for relative stereochemistry are discussed below.
The results for molecular structure prediction for the test set are shown alongside the substructure prediction results in Table 1. The key metric for molecular structure prediction is the percentage of cases in which the correct molecular structure was ranked within the top-X candidates generated by the molecular graph generation algorithm. The total number of possible constitutional isomers corresponding to the molecular formula for each molecule in the test set is shown in Fig. S7.† The majority of the formulae have >1000 and 22% have >10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 possible isomers. Remarkably, using substructure probability profiles predicted from 13C and 1H NMR spectra and using a beam size of 1000, the top-ranking molecular structure prediction (top-1) was the correct structure for 67.4% of the test set and the correct structure was within the top ten predicted structures in 95.8% of the cases. The cases where the actual structure was incorrectly ranked can arise either when (i) the correct candidate molecular structure was not generated by the graph algorithm or (ii) it was misranked owing to a poorly predicted substructure probability profile. To assess the former, we generated all the possible constitutional isomers corresponding to the molecular formula for each test set example using the Open Molecular Generator (OMG)40 and then ranked them according to their BCE loss using the substructure probability profile generated from the NMR data, yielding a top-1 of 68.4% and top-10 of 95.8% (Table S4†). Hence, with a beam size of 1000, there is only a 1% drop in top-1 and 0% drop in top-10 structure prediction ability arising from the molecular structure generation algorithm, indicating that the error primarily arises from the substructure predictions. To assess how the accuracy of molecular structure predictions depends on the processing of the experimental spectra (i.e. the removal of solvent and impurity peaks), we repeated the predictions using unprocessed experimental 1H NMR spectra (see ESI† section 2.3). Using raw spectra yielded only a 12% loss in top-1 and 2% loss in top-10 prediction ability over the test set (Table S5†), indicating that the predictions are relatively tolerant to extraneous peaks.
000 possible isomers. Remarkably, using substructure probability profiles predicted from 13C and 1H NMR spectra and using a beam size of 1000, the top-ranking molecular structure prediction (top-1) was the correct structure for 67.4% of the test set and the correct structure was within the top ten predicted structures in 95.8% of the cases. The cases where the actual structure was incorrectly ranked can arise either when (i) the correct candidate molecular structure was not generated by the graph algorithm or (ii) it was misranked owing to a poorly predicted substructure probability profile. To assess the former, we generated all the possible constitutional isomers corresponding to the molecular formula for each test set example using the Open Molecular Generator (OMG)40 and then ranked them according to their BCE loss using the substructure probability profile generated from the NMR data, yielding a top-1 of 68.4% and top-10 of 95.8% (Table S4†). Hence, with a beam size of 1000, there is only a 1% drop in top-1 and 0% drop in top-10 structure prediction ability arising from the molecular structure generation algorithm, indicating that the error primarily arises from the substructure predictions. To assess how the accuracy of molecular structure predictions depends on the processing of the experimental spectra (i.e. the removal of solvent and impurity peaks), we repeated the predictions using unprocessed experimental 1H NMR spectra (see ESI† section 2.3). Using raw spectra yielded only a 12% loss in top-1 and 2% loss in top-10 prediction ability over the test set (Table S5†), indicating that the predictions are relatively tolerant to extraneous peaks.
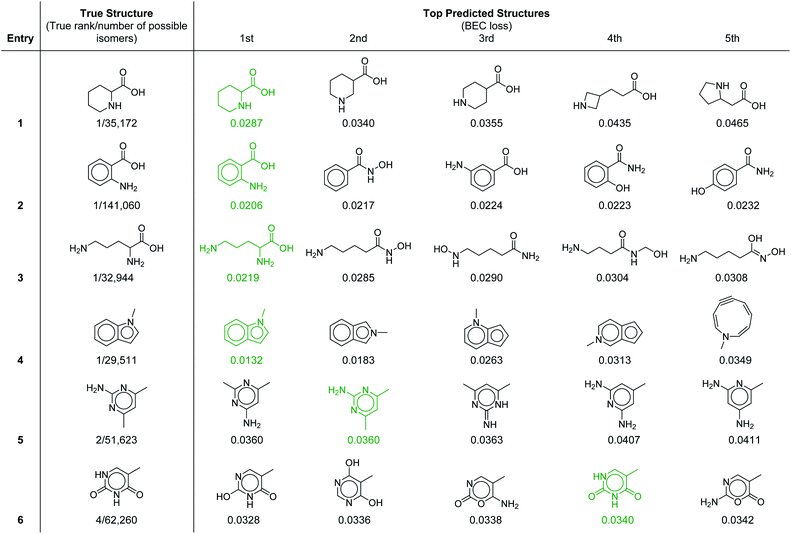
To provide further insight into the molecular prediction performance of our framework, Table 3 shows the top-5 ranked molecular structures as well as the true structure for six molecules in the test set. In all the cases shown, the number of possible constitutional isomers corresponding to the molecular formula ranges from ∼30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to ∼140
000 to ∼140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. For the first four entries where the most probable structure predicted by the model was the correct structure, the lower ranked molecules are very structurally similar, demonstrating that in these cases the model can effectively discern subtle molecular differences. Notably, the 1H–1H coupling in the first entry, piperidine-2-carboxylic acid, is fairly complex because of the ring conformation and would be laborious to parse out manually. In the final two entries the true structure was ranked in the top-2 and top-4 respectively. In the former, the top two structures were calculated to have equal probability (identical loss values) because with our current set of 957 substructures both molecules have identical substructure profiles. For the latter (entry 6), the highest ranked structure is a tautomer of the correct structure (thymine), which is the 4th ranked prediction. A detailed breakdown of the inputs and predicted structures for each of the test set examples is provided in ESI† section 4.3.
000. For the first four entries where the most probable structure predicted by the model was the correct structure, the lower ranked molecules are very structurally similar, demonstrating that in these cases the model can effectively discern subtle molecular differences. Notably, the 1H–1H coupling in the first entry, piperidine-2-carboxylic acid, is fairly complex because of the ring conformation and would be laborious to parse out manually. In the final two entries the true structure was ranked in the top-2 and top-4 respectively. In the former, the top two structures were calculated to have equal probability (identical loss values) because with our current set of 957 substructures both molecules have identical substructure profiles. For the latter (entry 6), the highest ranked structure is a tautomer of the correct structure (thymine), which is the 4th ranked prediction. A detailed breakdown of the inputs and predicted structures for each of the test set examples is provided in ESI† section 4.3.
One additional benefit of our approach to structure prediction is that the model and its outputs can easily be utilized to annotate the NMR spectra. For this process, part of the spectrum (e.g. one peak) is set to zero to generate a “masked” input, which is then passed through the substructure prediction model to generate a set of substructure probabilities. By comparing the substructure probabilities obtained with masked vs. unmasked input, the substructures can then be ranked according to the change in magnitude of their predicted probabilities. The substructures with large probability changes can then be associated with the part of the spectrum that is masked. Two examples are shown in Fig. 3. In the first example, the model correctly identifies the carbonyl carbon and a methylene carbon in the 13C NMR, as well as one of the peaks corresponding to the methylene next to the nitrogen in the 1H NMR. In the second example, the model correctly identifies methylene and methine substructures in the 13C NMR and the methylene next to the N in the 1H NMR. This masking approach can be easily applied to any region of the spectrum to assess which substructures are most likely to be associated with peaks in that region. Annotation can greatly assist the interpretation process and help the user understand why the model is making certain predictions. A detailed breakdown of annotations of a subset of the test set examples is provided in ESI† section 4.4.
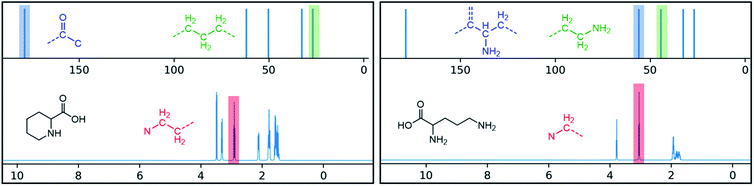 | ||
| Fig. 3 Annotated spectra generated by the substructure prediction model for two examples in the test set. The top predicted substructure is shown for each highlighted peak. | ||
Conclusions
In summary, we have demonstrated that our ML-powered framework provides an accurate and efficient approach to predict the structures of small (<11 non-hydrogen atoms) organic molecules and the substructures they contain using routine 1D 1H and 13C spectra. Using never-seen-before experimental spectra for a set of molecules including those with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000's or even over 100
000's or even over 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 possible constitutional isomers, our probabilistic substructure prediction model achieved 99.3% accuracy in true positive predictions and 99.9% in true negative predictions for 96.7% of the total substructure predictions. Leveraging this substructure information, our molecular generator achieved a top-1 accuracy of 67.4% and a top-10 accuracy of 95.8% for prediction of the molecular structure. By assigning peaks and regions of the NMR spectra to their most likely substructures, our framework also provides insights into the reasons for the overall structure determination it has made.
000 possible constitutional isomers, our probabilistic substructure prediction model achieved 99.3% accuracy in true positive predictions and 99.9% in true negative predictions for 96.7% of the total substructure predictions. Leveraging this substructure information, our molecular generator achieved a top-1 accuracy of 67.4% and a top-10 accuracy of 95.8% for prediction of the molecular structure. By assigning peaks and regions of the NMR spectra to their most likely substructures, our framework also provides insights into the reasons for the overall structure determination it has made.
We envision expanding this framework to enable accurate predictions for much larger and more complex molecules. In principle, the set of predicted substructures can readily be expanded to include other elements, larger and more specific motifs (e.g. substituted ring systems), and groups commonly encountered in synthesis (e.g. protecting groups). The ability to predict, in a probabilistic manner, for many thousands of substructures could itself greatly aid human interpretation of NMR spectra for novel complex molecules or unexpected products synthesized in the development of new reactions.
Many potential applications of automated structure elucidation require the ability to predict relative stereochemistry, which is absent from our current framework. A straightforward approach to this problem is to combine our prediction of constitutional isomers with a separate algorithm to rank the possible diastereomers. For each of the top n-ranked constitutional isomers identified by our model (with a user specified cutoff n), the 1H and 13C peak shifts and coupling constants of all possible diastereomers could be predicted using quantum mechanical calculations43–45 or recently developed machine learning protocols.10,17,18,46 These predictions could then be compared with the experimental spectra to generate a ranked list of molecular structures with defined stereochemistry. A complementary approach is to expand our substructure prediction model to include substructures with defined stereochemical relationships using 3D fingerprints47,48(e.g. syn vs. anti diols, cis vs. trans fused rings, etc.). The substructures with defined stereochemistry could then be used to distinguish between diastereomers of the candidate constitutional isomers generated by the graph generator.
Expanding the substructures predicted by our model will require an even greater expansion of the training set. Since we have demonstrated that training on simulated spectra is sufficient for predicting from experimental spectra, it is straightforward to expand the training set by selecting molecules with targeted substructures and simulating their spectra. However, accurate prediction of substructures with defined stereochemistry will likely require using experimental 1H NMR spectra for the training set molecules containing these substructures because it can be very computationally expensive to calculate peak splittings for different diastereomers. Regardless, incorporating experimental spectra in the training set is expected to improve performance, and, more importantly, large datasets of experimental spectra will be needed to expand the validation set in order to optimize early stopping. Large sets of experimental NMR data suitable for our framework could become available if it becomes common practice to include FIDs in supplementary data.49
Predicting the molecular structures for much larger and more complex molecules than what we have demonstrated here will also likely require improving the efficiency of generating molecular graphs utilizing substructure probabilities as a guide. We emphasize that our substructure prediction model can be utilized regardless of whether the molecular complexity exceeds what can be accommodated by the molecular generator. With the framework provided here, expanding and improving both substructure and molecular structure prediction has the potential to streamline and automate structure elucidation for diverse applications.
Data availability
The data for the test and validation sets are included as supplementary files test_results.pdf and validation_results.pdf. The list of all the structures used to generate data for the training set is included as SMILES strings in the supplementary file training_smiles.txt. Additional information about the data sets is provided in the ESI.† The code developed for substructure and molecular structure prediction will be made available upon reasonable request.Author contributions
MWK and TEM conceptualized and supervised the project. ZH and MSC designed and developed the substructure prediction algorithm with early contributions from CPW. ZH designed the substructures and designed and developed the graph generator. ZH, MSC, and CPW obtained the simulated and experimental datasets. MWK, TEM, ZH, and MSC wrote the original draft and all authors contributed to editing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Office of Naval Research (N00014-18-1-2659 to M. W. K.) and the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences (DE-SC0020203 to T. E. M.). Z. H. and M. S. C. thank the Stanford Center for Molecular Analysis and Design (CMAD) for fellowships. M. S. C. also acknowledges support from the Weldon G. Brown fellowship.References
- T. Helgaker, M. Jaszuński and K. Ruud, Ab initio methods for the calculation of NMR shielding and indirect spin–spin coupling constants, Chem. Rev., 1999, 99, 293–352 CrossRef CAS PubMed.
- L. B. Casabianca and A. C. De Dios, Ab initio calculations of NMR chemical shifts, J. Chem. Phys., 2008, 128, 052201 CrossRef PubMed.
- M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Computational prediction of 1H and 13C chemical shifts: A useful tool for natural product, mechanistic, and synthetic organic chemistry, Chem. Rev., 2012, 112, 1839–1862 CrossRef CAS PubMed.
- W. Bremser, Hose – a novel substructure code, Anal. Chim. Acta, 1978, 103, 355–365 CrossRef CAS.
- D. M. Grant and E. G. Paul, Carbon-13 Magnetic Resonance. II. Chemical Shift Data for the Alkanes, J. Am. Chem. Soc., 1964, 86, 2984–2990 CrossRef CAS.
- E. Pretsch, T. Clerc, J. Seibl and W. SimonTables of Spectral Data for Structure Determination of Organic Compounds, Springer-Verlag, Berlin, Heidelberg, 1983 Search PubMed.
- R. B. Schaller, C. Arnold and E. Pretsch, New parameters for predicting 1H NMR chemical shifts of protons attached to carbon atoms, Anal. Chim. Acta, 1995, 312, 95–105 CrossRef.
- J. Aires-de-Sousa, M. C. Hemmer and J. Gasteiger, Prediction of 1H NMR chemical shifts using neural networks, Anal. Chem., 2002, 74, 80–90 CrossRef CAS PubMed.
- J. Meiler, PROSHIFT: Protein chemical shift prediction using artificial neural networks, J. Biomol. NMR, 2003, 26, 25–37 CrossRef CAS PubMed.
- Y. Guan, S. V. S. Sowndarya, L. C. Gallegos, P. C. S. John and R. S. Paton, Real-time prediction of 1H and 13C chemical shifts with DFT accuracy using a 3D graph neural network, Chem. Sci., 2021, 12, 12012–12026 RSC.
- Y. D. Smurnyy, K. A. Blinov, T. S. Churanova, M. E. Elyashberg and A. J. Williams, Toward more reliable 13C and 1H chemical shift prediction: A systematic comparison of neural-network and least-squares regression based approaches, J. Chem. Inf. Model., 2008, 48, 128–134 CrossRef CAS PubMed.
- S. Kuhn, B. Egert, S. Neumann and C. Steinbeck, Building blocks for automated elucidation of metabolites: Machine learning methods for NMR prediction, BMC Bioinf., 2008, 9, 1–19 CrossRef PubMed.
- Y. Shen and A. Bax, SPARTA+: a modest improvement in empirical NMR chemical shift prediction by means of an artificial neural network, J. Biomol. NMR, 2010, 48, 13–22 CrossRef CAS PubMed.
- B. Han, Y. Liu, S. W. Ginzinger and D. S. Wishart, SHIFTX2: Significantly improved protein chemical shift prediction, J. Biomol. NMR, 2011, 50, 43–57 CrossRef CAS PubMed.
- S. Liu, et al., Multiresolution 3D-DenseNet for Chemical Shift Prediction in NMR Crystallography, J. Phys. Chem. Lett., 2019, 10, 4558–4565 CrossRef CAS PubMed.
- E. Jonas and S. Kuhn, Rapid prediction of NMR spectral properties with quantified uncertainty, J. Cheminf., 2019, 11, 1–7 CAS.
- W. Gerrard, et al., IMPRESSION – prediction of NMR parameters for 3-dimensional chemical structures using machine learning with near quantum chemical accuracy, Chem. Sci., 2020, 11, 508–515 RSC.
- Z. Yang, M. Chakraborty and A. D. White, Predicting chemical shifts with graph neural networks, Chem. Sci., 2021, 12, 10802–10809 RSC.
- D. C. Burns, E. P. Mazzola and W. F. Reynolds, The role of computer-assisted structure elucidation (CASE) programs in the structure elucidation of complex natural products, Nat. Prod. Rep., 2019, 36, 919–933 RSC.
- M. Valli, et al., Computational methods for NMR and MS for structure elucidation I: software for basic NMR, Phys. Sci. Rev., 2019, 4, 1–17 Search PubMed.
- M. Pesek, et al.,Database Independent Automated Structure Elucidation of Organic Molecules Based on IR, 1H NMR, 13C NMR, and MS Data, J. Chem. Inf. Model., 2021, 61, 756–763 CrossRef CAS PubMed.
- L. Ruddigkeit, R. Van Deursen, L. C. Blum and J. L. Reymond, Enumeration of 166 billion organic small molecules in the chemical universe database GDB-17, J. Chem. Inf. Model., 2012, 52, 2864–2875 CrossRef CAS PubMed.
- M. Valli, et al., Computational methods for NMR and MS for structure elucidation II: Database resources and advanced methods, Phys. Sci. Rev., 2019, 4, 1–16 Search PubMed.
- G. Ongie, et al., Deep learning techniques for inverse problems in imaging, IEEE J. Sel. Areas Inf. Theory, 2020, 1, 39–56 Search PubMed.
- E. W. Robb and M. E. Munk, A neural network approach to infrared spectrum interpretation, Mikrochim. Acta, 1990, 100, 131–155 CrossRef.
- R. J. Fessenden and L. Gyorgyi, Identifying Functional Groups in IR Spectra Using an Artificial Neural Network, J. Chem. Soc., Perkin Trans. 2, 1991, 1755–1762 RSC.
- C. Klawun and C. L. Wilkins, Optimization of functional group prediction from infrared spectra using neural networks, J. Chem. Inf. Comput. Sci., 1996, 36, 69–81 CrossRef CAS.
- R. Nalla, R. Pinge, M. Narwaria and B. Chaudhury, Priority based functional group identification of organic molecules using machine learning, CoDS-COMAD'18, 2018, DOI:10.1145/3152494.3152522.
- Z. Wang, X. Feng, J. Liu, M. Lu and M. Li, Functional groups prediction from infrared spectra based on computer-assist approaches, Microchem. J., 2020, 159, 105395 CrossRef CAS.
- C. L. Wilkins and T. L. Isenhour, Multiple Discriminant Function Analysis of Carbon-13 Nuclear Magnetic Resonance Spectra. Functional Group Identification by Pattern Recognition, Anal. Chem., 1975, 47, 1849–1851 CrossRef CAS.
- T. Specht, K. Münnemann, H. Hasse and F. Jirasek, Automated Methods for Identification and Quantification of Structural Groups from Nuclear Magnetic Resonance Spectra Using Support Vector Classification, J. Chem. Inf. Model., 2021, 61, 143–155 CrossRef CAS PubMed.
- B. Curry and D. E. Rumelhart, MSnet: A Neural Network which Classifies Mass Spectra, Tetrahedron Comput. Methodol., 1990, 3, 213–237 CrossRef CAS.
- J. Hummel, N. Strehmel, J. Selbig, D. Walther and J. Kopka, Decision tree supported substructure prediction of metabolites from GC-MS profiles, Metabolomics, 2010, 6, 322–333 CrossRef CAS PubMed.
- J. A. Fine, A. A. Rajasekar, K. P. Jethava and G. Chopra, Spectral deep learning for prediction and prospective validation of functional groups, Chem. Sci., 2020, 11, 4618–4630 RSC.
- E. Jonas, Deep imitation learning for molecular inverse problems, Adv. Neural Inf. Process. Syst., 2019, 32 Search PubMed , https://papers.nips.cc/paper/2019.
- M. H. Mozaffari and L.-L. Tay, A Review of 1D Convolutional Neural Networks toward Unknown Substance Identification in Portable Raman Spectrometer, 2020, https://arxiv.org/abs/2006.10575.
- L. C. Blum and J. L. Reymond, 970 Million druglike small molecules for virtual screening in the chemical universe database GDB-13, J. Am. Chem. Soc., 2009, 131, 8732–8733 CrossRef CAS PubMed.
- Mestrelab Research S.L., MestReNova 14.2.0, https://mestrelab.com/, 2020 Search PubMed.
- D. S. Wishart, et al., HMDB 4.0: The human metabolome database for 2018, Nucleic Acids Res., 2018, 46, D608–D617 CrossRef CAS PubMed.
- J. E. Peironcely, et al., OMG: Open molecule generator, J. Cheminf., 2012, 4, 1–13 Search PubMed.
- R. Gugisch, et al., MOLGEN 5.0, A Molecular Structure Generator, Advances in Mathematical Chemistry and Applications, Elsevier Ltd, 2015, vol. 1 Search PubMed.
- S. J. Russell and P. Norvig, Artificial Intelligence: A Modern Approach, Pearson Education, 2009 Search PubMed.
- A. Howarth, K. Ermanis and J. M. Goodman, DP4-AI automated NMR data analysis: straight from spectrometer to structure, Chem. Sci., 2020, 11, 4351–4359 RSC.
- F. Hoffmann, D.-W. Li, D. Sebastiani and R. Brüschweiler, Improved Quantum Chemical NMR Chemical Shift Prediction of Metabolites in Aqueous Solution toward the Validation of Unknowns, J. Phys. Chem. A, 2017, 121, 3071–3078 CrossRef CAS PubMed.
- P. S. Achanta, et al., Quantum mechanical NMR full spin analysis in pharmaceutical identity testing and quality control, J. Pharm. Biomed. Anal., 2021, 192, 113601 CrossRef CAS PubMed.
- J. Fang, L. Hu and J. Dong, et al., Predicting scalar coupling constants by graph angle-attention neural network, Sci. Rep., 2021, 11, 18686 CrossRef CAS PubMed.
- M. Awale, X. Jin and J. L. Reymond, Stereoselective virtual screening of the ZINC database using atom pair 3D-fingerprints, J. Cheminf., 2015, 7, 3 Search PubMed.
- S. D. Axen, X.-P. Huang, E. L. Cáceres, L. Gendelev, B. L. Roth and M. J. Keiser, A simple representation of three-dimensional molecular structure, J. Med. Chem., 2017, 60(17), 7393–7409 CrossRef CAS PubMed.
- A. M. Hunter, E. M. Carreira and S. J. Miller, Encouraging Submission of FAIR Data at The Journal of Organic Chemistry and Organic Letters, Org. Lett., 2020, 22, 1231–1232 CrossRef CAS PubMed.
- SDBSWeb: https://sdbs.db.aist.go.jp (National Institute of Advanced Industrial Science and Technology, p. 2021).
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc04105c |
| This journal is © The Royal Society of Chemistry 2021 |

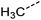
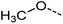
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [OX1])O
[OX1])O